Abstract
Supervised learning and pattern recognition is a crucial area of research in information retrieval, knowledge engineering, image processing, medical imaging, and intrusion detection. Numerous algorithms have been designed to address such complex application domains. Despite an enormous array of supervised classifiers, researchers are yet to recognize a robust classification mechanism that accurately and quickly classifies the target dataset, especially in the field of intrusion detection systems (IDSs). Most of the existing literature considers the accuracy and false-positive rate for assessing the performance of classification algorithms. The absence of other performance measures, such as model build time, misclassification rate, and precision, should be considered the main limitation for classifier performance evaluation. This paper’s main contribution is to analyze the current literature status in the field of network intrusion detection, highlighting the number of classifiers used, dataset size, performance outputs, inferences, and research gaps. Therefore, fifty-four state-of-the-art classifiers of various different groups, i.e., Bayes, functions, lazy, rule-based, and decision tree, have been analyzed and explored in detail, considering the sixteen most popular performance measures. This research work aims to recognize a robust classifier, which is suitable for consideration as the base learner, while designing a host-based or network-based intrusion detection system. The NSLKDD, ISCXIDS2012, and CICIDS2017 datasets have been used for training and testing purposes. Furthermore, a widespread decision-making algorithm, referred to as Techniques for Order Preference by Similarity to the Ideal Solution (TOPSIS), allocated ranks to the classifiers based on observed performance reading on the concern datasets. The J48Consolidated provided the highest accuracy of 99.868%, a misclassification rate of 0.1319%, and a Kappa value of 0.998. Therefore, this classifier has been proposed as the ideal classifier for designing IDSs.
1. Introduction
The footprint of artificial intelligence-enabled Internet of Things (IoT) devices [1] in our day-to-day life attracts hackers and potential intrusions. In 2017, WannaCry ransomware, a self-propagating malware, devastatingly impacted computing resources by infecting more than 50,000 NHS systems [2]. The network threats such as WannaCry become a nightmare for the security manager and remain an open research area. Many intrusion detection schemes have been proposed to counter malicious activities in a computer network [3,4,5,6]. All the network anomaly counter mechanisms are either unsupervised, supervised, or a combination of both. The supervised algorithms are rigorously used to design state-of-the-art intrusion detectors. This is because the ability to learn from examples makes the supervised classifiers robust and powerful. In data science, an array of supervised classifiers exists, and each one of them claims to be the best among others. However, in the real world of classification processes, the scenario is somewhat different. The supervised classifiers are susceptible to misclassification if overfit or underfit during the training process [7]. Another aspect is a class-imbalance issue [8] in the underlying dataset of a classification model. A supervised classifier always favors the majority class if the training is incorporated on a high class-imbalance dataset [9,10]. Apart from the class-imbalance issue, the data purity also decides the performance of the supervised classifiers. The data are stored and are available in numerous formats and include several outliers such as missing class information, NULL, and NaN values. The raw data with outliers drastically limit the performance of the classifiers. The classifiers reveal unrealistic results with the data of outliers [11,12]. This leads to the development of robust and versatile classifiers for impure data. In this regard, numerous researchers are concerned about pattern recognition, and data extraction [13,14], which is the main objective of data mining, and perhaps one of the motivational aspects for exploring [15,16,17] supervised machine learning algorithms. Numerous classification mechanisms are available in the literature to handle impure data, especially in designing full-bodied network intrusion detection systems (IDS). However, the central question of the researchers is associated with the selection of the optimum classifiers to develop a base learner for IDS.
Furthermore, there is a lack of a standard guideline to select the most suitable classifier for their datasets. Multiple studies have been conducted on the before-mentioned problem. However, most of the proposed studies available in the literature evaluate the classifiers using standard performance measures such as classification accuracy and false-positive rate [18,19,20,21,22]. It is worth mentioning that the quality of a classifier does not depend only on the classification accuracy. Other performance measures such as misclassification rate, precision, recall, and F-Score empirically define the classifier’s performance quality. Therefore, it is necessary to study a comprehensive review that can be used as a guideline to analyze classifiers using various performance measures in various datasets. Therefore, the main objective of this paper is to examine several research papers in the field of host-based and network-based intrusion detection considering multiple aspects. This study analyzes the type of classification used, the datasets used to consider the sample size, performance measures discussed in evaluating classifier performance, inferences, and research gaps encountered.
Moreover, the proposed study provides a guideline for designing a host-based or network-based intrusion detection system. This study’s main contribution is to present an in-depth analysis of fifty-four widely used classifiers considering six different classifier groups across thirteen performance measures. These classifiers are comprehensively analyzed through three well-recognized binary and multiclass NSLKDD, ISCXIDS2012, and CICIDS2017 datasets. The decision-making algorithm referred to as Techniques for Order Preference by Similarity to the Ideal Solution (TOPSIS) [23,24] is incorporated as a reliable feature to allocate weight to these classifiers. These weights are subsequently used for ranking the performance of the classifiers. Consequently, the best classifier for a dataset and the best of each group of classifiers is proposed. Moreover, the best classifier across all the datasets is suggested as the most generic classifier for designing an IDS.
The research of this analysis is structured as follows. In Section 2, the most recent study of supervised classifiers is delineated; the materials and methods has been mentioned in Section 3. Furthermore, in Section 4, the results of the analysis has been discussed. Section 5 is dedicated for J48Consolidated classifier, followed by the conclusion in Section 6.
2. Related Works
Supervised classifiers are extensively used in the field of network security. The most potential applications of machine learning techniques are in risk assessment after the deployment of various security apparatus [25], identifying risks associated with various network attacks and in predicting the extent of damage a network threat can do. Apart from these, supervised classification techniques have been explored and analyzed by numerous researchers in a variety of application areas. Most of those studies’ analyses focused on a detailed exploration to validate a theory or performance evaluation to come across a versatile classifier [26,27,28]. The performance of supervised classifiers has been explored in intrusion detection [29], robotics [18], semantic web [19], human posture recognition [30], face recognition [20], biomedical data classification [31], handwritten character recognition [22] and land cover classification [21]. Furthermore, an innovative semi-supervised heterogeneous ensemble classifier called Multi-train [32] was also proposed, where a justifiable comparison was made with other supervised classifiers, such as k-Nearest Neighbour (kNN), J48, Naïve Bayes, and random tree. Multi-train was also successfully achieved, and its prediction accuracy of unlabeled data was improved, which, therefore, can reduce the risk of incorrectly labeling the unlabeled data. A study on this topic, which exclusively deals with classifiers’ accuracy measures using multiple standard datasets, is proposed by Labatut et al. [33]. An empirical analysis of supervised classifiers was carried out by Caruana et al. [34] using eleven datasets with eight performance measures, where the calibrated boosted trees appeared as the best learning algorithm. Besides, a systematic analysis of supervised classifiers was carried out by Amancio et al. [35] under varying classifiers’ settings.
The focus of this paper is to analyze the performance of various supervised classifiers using IDS datasets. Therefore, the authors have decided to review related articles in the literature that examined different classifiers using IDS datasets. The classifier analysis is expected to provide a platform for the researchers to devise state-of-the-art IDSs and quantitative risk assessment schemes for various cyber defense systems. Numerous studies and their detailed analytical findings related to supervised classifiers have been outlined in Table 1.

Table 1.
Detailed findings and analysis of supervised classifiers.
Table 1 summarizes the taxonomy of analyzed articles. In the last column, an attempt has been made to outline the inferences/limitation or research gaps encountered. The summarization of these analyses provides scope for meta-analysis about the supervised classifiers, which ultimately shows direction or justification for further investigation in the field of supervised classification using intrusion detection datasets. From Table 1, it has been observed that the decision tree and function-based approaches are mostly explored. The usage statistics of supervised classifiers are presented in Figure 1.
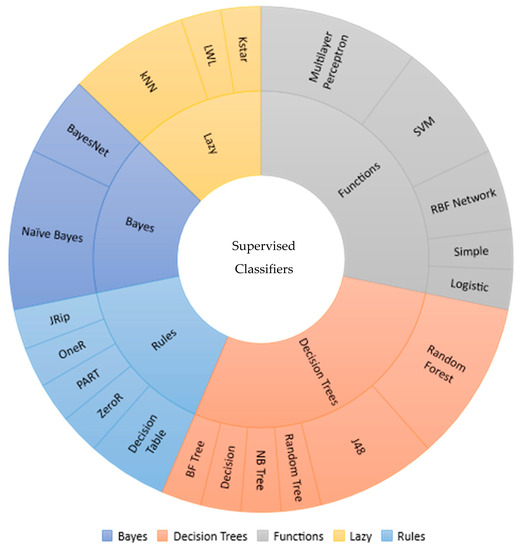
Figure 1.
Usage statistics of supervised classifiers.
According to Figure 1, J48 (C4.5) and Random Forest of decision trees and function-based SVM and Multilayer Perceptron (Neural Network) have been analyzed considerably by numerous researchers. In this work, the authors have tried to understand the reason behind decision trees’ popularity and function-based approaches. Therefore, the authors have summarized the performance metrics results used to explore those classifiers in the analyzed papers. Most of the researchers focused on accuracy scores; therefore, the authors used the accuracy score as a base measure to understand the reason behind the use of decision trees and function-based classifiers.
Therefore, in this study, the authors have calculated the minimum, maximum, and average accuracy of Bayes, Decision trees, Functions, Lazy, and Rules group of classifiers concerning the literature outlined in Table 1. The calculated detection accuracy of the research papers surveyed is presented in Figure 2. In Figure 2, almost all groups of classifiers show a maximum accuracy rate of more than 99%.
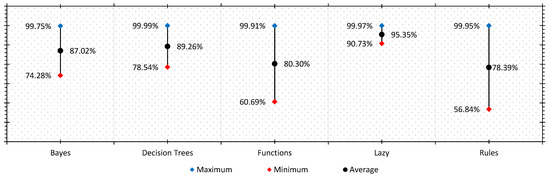
Figure 2.
Comparison of classification accuracy in various classifier groups found in the literature.
Similarly, considering the average accuracy, the Lazy classifiers are far ahead of different groups of classifiers. Despite having an impressive accuracy rate, the Lazy group classifiers were deeply analyzed by a handful of researchers [48,49,50]. On the other hand, decision trees and function-based classifiers were the center point of many research papers. Consequently, in this paper, the authors have decided to explore multiple classifiers of all the classifier groups. In this work, fifty-four state-of-the-art classifiers of six different classifier groups were analyzed. The classifier groups were created based on their functionality and the guidelines presented by Frank et al. [59]. The classifiers under evaluation and their groups are presented in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 under six different classifier groups.

Table 2.
Bayes classifiers for evaluation.

Table 3.
Functions classifiers.

Table 4.
Lazy group classifiers.

Table 5.
Rule-based classifiers.

Table 6.
Decision tree classifiers.

Table 7.
Miscellaneous classifiers.
3. Materials and Methods
The authors used Weka 3.8.1 [59] software in a CentOS platform on the Param Shavak supercomputing facility provided by the Centre for Development of Advanced Computing (CDAC), India. The supercomputing system consists of 64 GB RAM with two multicore CPUs, each with 12 cores having a performance of 2.3 Teraflops. To evaluate all the classifiers of Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, the authors have considered samples of NSLKDD [118,119,120], ISCXIDS2012 [121], and CICIDS2017 [122] datasets. The training and testing sample size for each dataset is outlined in Table 8. The training and testing samples were generated with 66% and a 34% split of the total sample size.

Table 8.
Miscellaneous classifiers.
All three NSLKDD, CICIDS2017 and ISCXIDS2012, have a high-class imbalance. Additionally, NSLKDD and CICIDS2017 are multi-class, and the ISCXIDS2012 dataset contains binary class information. The performance of a classifier cannot be explored only through its accuracy and detection rate. Therefore, the authors have considered a variety of performance measures such as training time, testing time, model accuracy, misclassification rate, kappa, mean absolute error, root mean squared error, relative absolute error, root relative squared error, true positive rate, false-positive rate, precision, and receiver operating curve (ROC). The ROC value reveals the real performance on class imbalance datasets such as the CICIDS2017 and the NSL-KDD. Similarly, the Matthews correlation coefficient (MCC) and precision-recall curve (PRC) are useful for evaluating binary classification on the ISCXIDS2012 dataset.
The experiment for evaluating classifiers covers five essential steps [123], such as dataset selection, classification, weight calculation using multi-criteria decision making, weight to rank transformation, and finally, global rank generation. Figure 3 shows the methodology used by the authors.
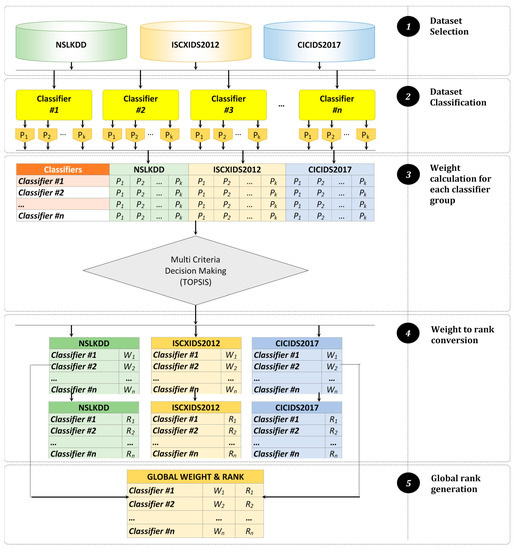
Figure 3.
The methodology of classification to rank allocations of supervised classifiers.
The authors have conducted all five steps iteratively for all datasets and classifiers under evaluation. In the initial steps from the pool of datasets, a dataset has been selected. The dataset initially contains several tuples with variable class densities. From each dataset, the requisite number of random samples were generated. The output of this step has been presented in Table 8. This procedure was conducted deliberately to ensure that all the classifiers were not biased for a specific dataset. The second step began by classifying each dataset using each classifier that is presented in the classifier pool. The performance of each classifier was tabulated for future reference. The process has been recursively conducted for each dataset.
The third and fourth steps jointly work to achieve the research objectives. In this process, the average performance score of each group of classifiers has been analyzed. Additionally, each group’s ranking has also been calculated to retrieve the best classifier group specific to the dataset. All the group’s classifiers with better results were considered to evaluate their consistent performance across the three datasets. Furthermore, considering the performances of the best performing group’s classifiers, the authors have calculated the weight and rank of each classifier of that group, specific to each dataset. The authors aimed to provide a reliable evaluation of the best classifier for each dataset.
The final step involved global weight and rank calculation. At this stage, the global weight of a classifier of the best performing group was calculated based on the ranking received for each dataset. The average performance results of those included in the group with the better score across the three datasets were based on the individual score of each classifier. The scores were further arranged in ascending order to provide a clear presentation about the best performance classifier.
All the five steps of methodologies included a two-stage procedure. First, the best classifier group was selected, and the second-best classifier was proposed. The best classifier and classifier group were based on an extensively used conventional multiple-criteria decision-making (MCDM) method named TOPSIS. Before applying TOPSIS, the performance outcome of each classifier and each classifier group were calculated. Therefore, the authors have calculated 13 performance metrics of the classifiers.
Furthermore, the authors considered only eight performance measures, i.e., testing time per instance, accuracy, kappa value, mean absolute error, false-positive rate, precision, and receiver operating curve value for weighting and ranking purpose. On the one hand, these eight measures are in line with the aim of this research. On the other hand, all the other performance metrics can be calculated through one of these measures that are considered in this study. Consequently, the significance of those 17 measures did not affect the weighting and ranking process. The algorithmic method of the weighting of each classifier and classifier group based on TOPSIS has been demonstrated in Table 9.

Table 9.
The algorithm algoWeighting.
It should be noted that in algoWeighting, C1, C2, C3,………, Cn are the classifier or classifier group labels, and P1, P2, P3,………, Pk are the performance or average performance score, respectively.
The algorithm begins with constructing a decision matrix Md, where the nth classifier or classifier group is the performance outcome for kth performance measure. The decision matrix is the basis for the evaluation of the best classifier. It helps the decision-making module (TOPSIS) to calculate the weight for each feature.
At the second stage, a weightage normalized decision matrix has been calculated, which is the weight of the jth performance measures.
The idea behind allocating appropriate weight to performance measures is in its ability to rank classifiers specific to domain area and learning environment. For instance, in high class-imbalance learning, the performance measure Matthews correlation coefficient (MCC), Kappa, and receiver operating curve (ROC) value should be given more weightage than other performance matrices. The datasets used here were class imbalance in nature; therefore, more emphasis has been given to performance matrices suitable for the class imbalance environment. In this regard, eight performance matrices have been shortlisted, and corresponding weights have been allocated for TOPSIS processing. The weight for eight performance measures is presented in Table 10. Another reason for not considering all the performance matrices is because other performance measures themselves can be derived from the matrices presented in Table 10. For instance, detection accuracy can be calculated from True Positives (TP) and True Negatives (TN). Therefore, the True Positive Rate (TPR) and True Negative Rate (TNR) have been dropped from calculating weight for classifiers. In this way, out of the 13 performance measures, only eight performance measures have been selected.

Table 10.
Weights allocated to various performance measures.
The algorithm includes a positive and negative ideal solution to calculate the separation measure of each classifier/classifier group, which supports the calculation of each classifier or group’s score. The scores are used to rank the classifiers. The procedure followed here for calculating the rank of classifiers has been presented in Table 11.

Table 11.
The algorithm rankClassifiers.
4. Results and Discussion
The presented analysis to reach the best classifier was conducted through a top-to-bottom approach. Firstly, the best classifier group has been identified through intergroup analysis. Secondly, the best performing classifier of that best classifier group has been acknowledged through intragroup analysis.
4.1. Intergroup Performance Analysis
Under intergroup performance analysis, the authors have calculated the classifier group performance as a whole. The classifier’s group performances for NSLKDD, ISCXIDS2012, and CICIDS2017 datasets have been listed in Table 12, Table 13 and Table 14, respectively.

Table 12.
Overall performance of classifier groups for NSLKDD dataset.

Table 13.
Overall performance of classifier groups for ISCXIDS2012 dataset.

Table 14.
Overall performance of classifier groups for CICIDS2017 dataset.
According to Table 12, decision tree classifiers present reliable results in all the fields of performance metrics, except training and testing time. On the one hand, the decision tree classifiers consume training and testing times of 4.18 s and 0.03 s, respectively. Similarly, the Bayes group of classifiers has a fast response in training and testing time but presents low-quality performance metrics. The ROC and MCC values are suitable for evaluating classifier groups’ performance, considering the class imbalance learning. Therefore, by observing the average ROC and MCC of classifier groups on the NSL-KDD dataset, the authors have seen that the decision tree behaves far better than other classifier groups. The authors found a similar observation concerning the ISCXIDS2012 dataset. Table 6 shows the group performance of supervised classifiers for the ISCXIDS2012 dataset. The decision tree classifiers showed the highest amount of average accuracy of 97.3519%, but the average testing time per instance was low and on par with Bayes and Miscellaneous classifiers. Nevertheless, decision tree classifiers were far ahead of their peer classifier groups, with a higher average ROC value of 0.985. The authors have also conducted intergroup performance analysis on CICIDS2017. The average, maximum, and minimum performance reading has been outlined in Table 12. The decision tree classifiers reveal an impressive amount of accuracy and ROC values of 99.635 and 0.999, respectively.
Furthermore, the decision tree classifiers present consistent performance metrics for all three intrusion detection datasets NSLKDD, ISCXIDS2012, and CICIDS2017. However, before concluding that decision trees are best for these datasets by considering a limited number of parameters, the authors have decided to identify all these classifier groups’ actual weight and rank through TOPSIS. The classifier group with the highest weight and rank will be pointed out as the best classifier for these IDS datasets. This will improve the proposed study’s relevance and background to find the best classifier within the winning classifier group.
Figure 4 presents the weights and ranks of classifier groups for all three IDS datasets. The decision tree classifier presents the highest performance. Moreover, the decision trees present a consistent performance for all the IDS datasets. Therefore, the decision tree can be considered as the best method for the development of reliable IDSs.
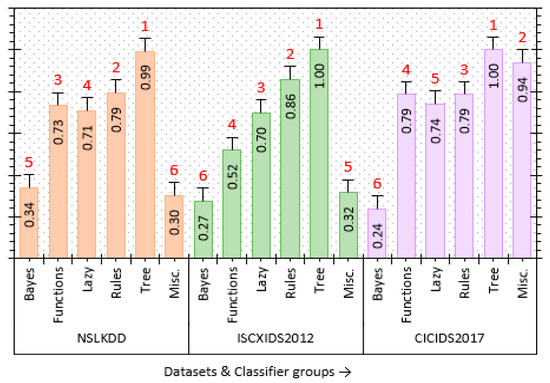
Figure 4.
Weights and ranks of supervised classifier groups.
4.2. Intragroup Performance Analysis
In the intergroup analysis, the authors conclude that decision tree classifiers reveal the best performance for imbalanced IDS datasets. The authors have decided to conduct an intragroup analysis of decision trees for NSLKDD, ISCXIDS2012, and CICIDS2017 datasets. The intragroup study aims to identify the best decision tree within the decision tree group of classifiers for the concerned datasets. Several performance outcomes of decision tree classifiers for NSLKDD, ISCXIDS2012, and CICIDS2017 datasets have been analyzed through Figure 5, Figure 6 and Figure 7.
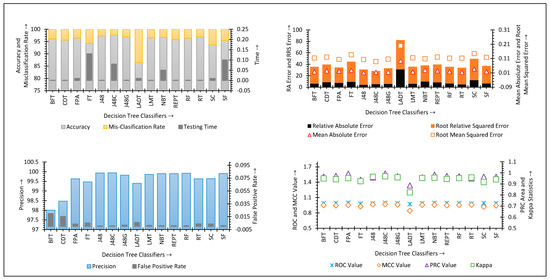
Figure 5.
Performance of decision tree classifiers for NSLKDD dataset.
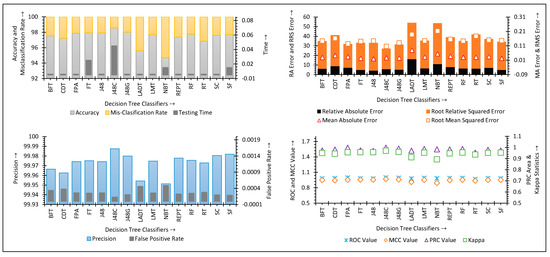
Figure 6.
Performance of decision tree classifiers for ISCXIDS2012 dataset.
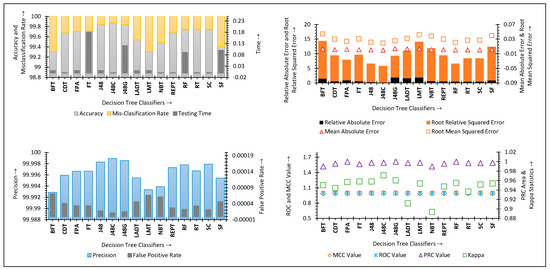
Figure 7.
Performance of decision tree classifiers for CICIDS2017 dataset.
The J48Consolidated classifier shows better accuracy for the NSL-KDD dataset. The sample size of NSLKDD here is an imbalance in nature. Therefore, these measures play a significant role in finding the best classifier. Considering the ROC value, the ForestPA performs better as compared to J48Consolidated. Additionally, both ForestPA and J48Consolidated show similar performance in terms of the MCC value. Consequently, the authors did not find sufficient scope for deciding an ideal decision tree classifier for the NSLKDD dataset.
Furthermore, the decision tree classifiers’ performance on a sample of the ISCXIDS2012 dataset is presented in Figure 6. The Functional Trees (FT), J48Consolidated, NBTree, and SysFor classifiers consumed a significant amount of computational time. Nevertheless, the rest of the decision trees consumed 0.001 s of testing time per instance. The J48Consolidated algorithm was limited by presenting the longest amount of time to detect an anomalous instance. However, this computation time consumption supports the fact that J48Consolidated provides the highest accuracy of 98.5546%, which leads to the lowest misclassification rate of 1.4454%. Moreover, J48Consolidated seems to lead the decision trees group with the best Kappa value (0.9711).
The test results of decision trees on a CICIDS2017 dataset are presented in Figure 7. The J48Consolidated algorithm provides high-quality results in the class imbalance instances of the CICIDS2017 dataset. J48Consolidated scores the highest accuracy with a low misclassification rate. However, considering the ROC and MCC values, the J48 presents better performance than the J48Consolidated. Therefore, it is not clear about the best classifiers, which can be considered as the base learner for future IDS.
In the case of ISCXIDS2012, J48Consolidated also presents consistent results in all performance measures. However, in the case of NSL-KDD and CICIDS2017, it was not possible to find the best classifier. Therefore, the authors have also considered TOPSIS to allocate individual decision tree classifiers’ weight and rank. The average weight and rank of decision tree classifiers for all datasets have also been calculated to find the best classifier for all the datasets. The average weight and rank across all the datasets are not significant in identifying a suitable classifier because an IDS is designed considering a specific dataset or environment. However, average weight and rank will play a relevant role in the conclusion concerning the most versatile classifier conducted in this study. The average ranks and weights of all the classifiers for all the three IDS datasets are represented in Figure 8.
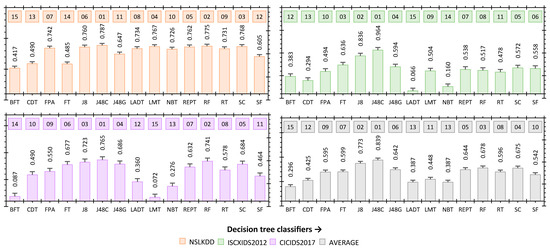
Figure 8.
Techniques for Order Preference by Similarity to the Ideal Solution (TOPSIS) weights and ranks of decision tree classifiers for NSLKDD, ISCXIDS2012 and CICIIDS2017 dataset.
The J48Consolidated classifier has the highest rank across all the datasets. Moreover, J48Consolidated presents the highest weight of 0.964 for the ISCXIDS2012 dataset. The J48Consolidated decision tree classifier is best for the high-class imbalance NSLKDD and CICIDS2017 and ISCXIDS2012 datasets. Therefore, J48Consolidated will be a suitable classifier for designing IDS base learners using either NSLKDD, ISCXIDS2012, and CICIDS2017 datasets.
4.3. Detailed Performance Reading of All the Classifiers
Table 15, Table 16 and Table 17 provide a detailed insight of all the supervised classifiers in six distinct groups. These tables outlined thirteen performance metrics. However, the authors have identified the best classifier group (decision tree) and the best classifier (J48Consolidated). Nevertheless, other classifiers can have different performances considering other datasets. Therefore, while designing IDSs, the authors suggest further evaluation of supervised classifiers based on specific computing and network environments.

Table 15.
Performance outcome of supervised classifiers on NSL-KDD dataset.

Table 16.
Performance outcome of supervised classifiers on ISCXIDS2012 dataset.

Table 17.
Performance outcome of supervised classifiers on CICIDS2017 dataset.
5. J48Consolidated—A C4.5 Classifier Based on C4.5
J48Consolidated has been presented as the best classifier considering the decision tree group. Therefore, this section provides an in-depth analysis of J48Consodated.
5.1. Detection Capabilities of J48Consolidated
In this section, the J48Consolidated classifier is analyzed, considering the classification of the attack detection process. The classification threshold and the percentage of detection have been taken into consideration while analyzing attack classes. The attack-wise classification output for NSLKDD, ISCXIDS, and CICIDS2017 datasets has been presented in Figure 9, Figure 10 and Figure 11, respectively.
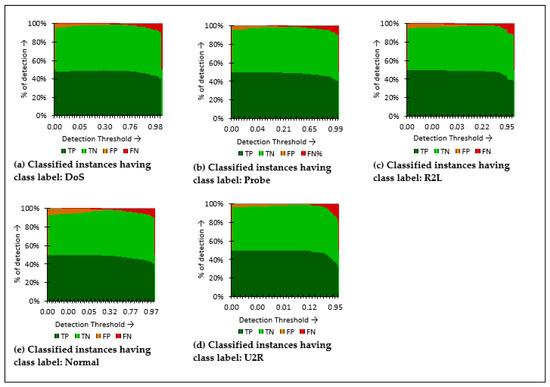
Figure 9.
Detection (%) of attacks and normal class labels of NSL-KDD multi-class dataset.
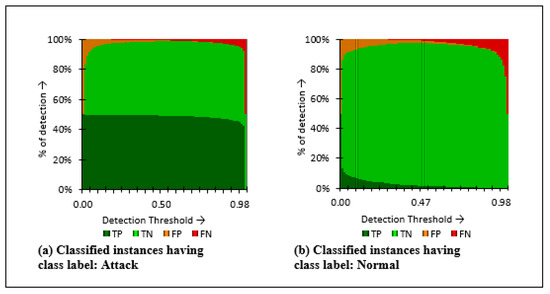
Figure 10.
Detection (%) of attacks and normal class labels of ISCXIDS2012 binary class dataset.
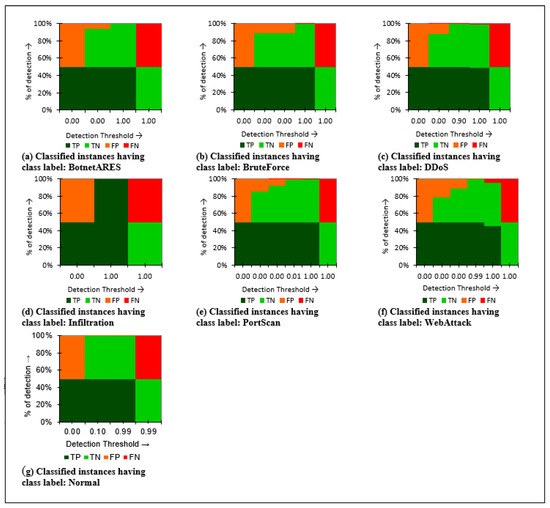
Figure 11.
Detection (%) of attacks and normal class labels of CICIDS2017 multi class dataset.
The detection output for the NSLKDD dataset remains consistently good for DoS, Probe, R2L, U2R, and Normal classes with the increase in detection threshold. The U2R attack class shows low false positives, whereas few regular instances are misclassified during the classification process. Overall, the J48Consolidated classifier exhibited satisfactory performance for the NSLKDD dataset.
ISCXIDS2012 is a binary class dataset; therefore, J48Consolidated seems to generate false alarms. However, the presented results are low compared to the number of correctly classified instances (true positives and true negatives).
Finally, the individual J48Consolidated evaluation presents an effective classification considering six attack groups of the CICIDS2017 dataset. The classifier also differentiates regular instances with attack instances during the classification process.
5.2. Classification Output of J48Consolidated
The three IDS datasets are considered for a specific environment. The correlation of attributes, attacks, and benign instances varied from dataset to dataset. Therefore, J48Consolidated shows a different classification performance considering different IDS datasets. The classification output of J48Consolidated for NSLKDD, ISCXIDS2012, and CICIDS2017 datasets has been outlined in Figure 12, Figure 13 and Figure 14, respectively.
Figure 12.
Classification of J48Consolidated on NSL-KDD dataset.
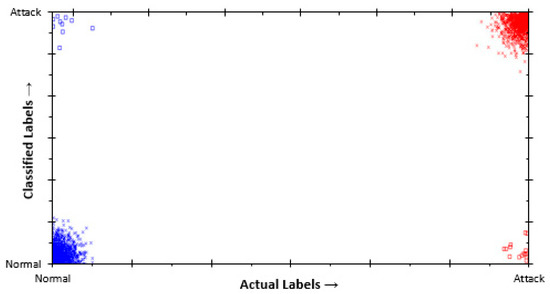
Figure 13.
Classification of J48Consolidated on ISCXIDS2012 dataset.
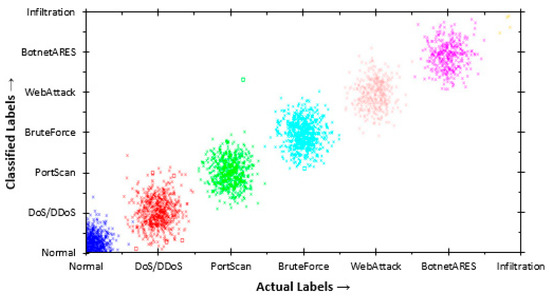
Figure 14.
Classification of J48Consolidated on CICIDS2017 dataset.
Figure 12 shows that the J48Consolidated classifier presents a reliable classification in the NSLKDD dataset. Nevertheless, J48Consolidated also produced false alarms for positive and negative instances. Therefore, the authors recommend incorporating filter components such as data standardization and effective feature selection while designing IDSs using J48Considated. A filter component not only smooths the underlying data, but will also improve classification performance.
On the one hand, for the ISCXIDS2012 dataset, J48Consolidated dramatically showed improvement in classification. The classifier showed few false alarms. On the other hand, J48Consolidated successfully detected almost all the instances of the ISCXIDS2012 binary dataset. Therefore, the classifier achieved the highest TOPSIS score of 0.964 (Figure 8); thus, contributing to the highest average rank.
Finally, for the CICIDS2017 dataset, the J48Consolidated classifier presented a low number of false alarms. The six attack groups of the CICIDS2017 dataset presented a consistent classification with a detection accuracy of 99.868% (Table 17) and a low false positive of 0.000011.
A reliable IDS benchmark dataset must fulfill 11 criteria [122], such as complete network configuration, attack diversity, overall traffic, thorough interaction, labeled dataset, full capture, existing protocols, heterogeneity, feature set, anonymity, and metadata. The CICIDS2017 [123] dataset fulfills these criteria. Furthermore, CICIDS2017 is recent and focuses on the latest attack scenarios. The J48Consolidated classifier presented the best results for the CICIDS2017 dataset with an accuracy of 99.868%. Consequently, the J48Consolidated classifier can be assumed as an effective IDS with the CICIDS2017 dataset. Nevertheless, the authors recommend the incorporation of feature selection procedures at the preprocessing stage to extract the most relevant features of the dataset and promote system performance.
6. Conclusions
This paper analyzed fifty-four widely used classifiers spanning six different groups. These classifiers were evaluated on the three most popular intrusion detection datasets, i.e., NSLKDD, ISCXIDS2012 and CICIDS2017. The authors have extracted a sufficient number of random samples from these datasets, which retained the same class imbalance property of the original datasets. Consequently, multi-criteria decision-making has been used to allocate weight to these classifiers for different datasets. The rank of the classifiers was also finalized using those weights. First, an intragroup analysis has been conducted to find the best classifier group. Secondly, an intragroup analysis of the best classifier group has been made to find the best classifiers for the intrusion detection datasets. The authors analyzed thirteen performance metrics. Therefore, the best classifier has been selected impartially. On the one hand, the intergroup analysis presented the decision tree group of classifiers as the best classifier group, followed by the Rule-based classifiers, whereas the intragroup study identified J48Consolidated as the best classifier for high-class imbalance considering NSLKDD, CICIDS2017 and ISCXIDS2012 datasets. The J48Consolidated classifier provided the highest accuracy of 99.868%, a misclassification rate of 0.1319%, and a Kappa value of 0.998.
This study presented an in-depth analysis that provides numerous outcomes for IDS designers. Comparing fifty-four classifiers on intrusion detection datasets through thirteen performance matrices and ranking them is the main contributory work of this article. Nevertheless, the present study has limitations. Further investigation is required considering other datasets and other specific application domains. Moreover, the number of classes, class-wise performance observation, and classifiers’ performance based on varying sample sizes should be carried out to understand the detailed aspects of the classifiers. The scalability and robustness of the classifiers were not tested. As a future work, many other IDS datasets can be used for ascertaining performance of the classifiers. Many recent ranking algorithms can be used as voting principle to obtain exact ranks of classifiers. Many other recent rule-based, decision forest classifiers were covered in this article; those classifiers can be analyzed to understand the real performance of the classifiers and classifier groups. Finally, J48Consolidated, which evolved as an ideal classifier out of this analysis, can be used along with a suitable feature selection technique to design robust intrusion detection systems.
Author Contributions
The individual contributions for this research are specified below: Conceptualization, R.P., S.B. and M.F.I.; Data curation, R.P. and M.F.I.; Formal analysis, A.K.B., M.P., C.L.C. and R.H.J.; Funding acquisition, R.H.J., C.L.C. and M.F.I.; Investigation; R.P., S.B., M.F.I. and A.K.B.; Methodology, R.P., S.B., C.L.C., M.F.I. and M.P.; Project administration, S.B., R.H.J., C.L.C. and A.K.B.; Resources, S.B., A.K.B., C.L.C. and M.P.; Software, R.P., C.L.C., M.F.I. and M.P.; Supervision, S.B., A.K.B., R.H.J.; Validation, R.P., M.F.I., C.L.C. and M.P.; Visualization, R.P., S.B., M.F.I., R.H.J. and A.K.B.; Writing—Review and editing, R.P., M.F.I., S.B., C.L.C., M.P., R.H.J. and A.K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Sejong University research fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: NSL-KDD—https://www.unb.ca/cic/datasets/nsl.html (accessed on 1 February 2021), ISCXIDS2012—https://www.unb.ca/cic/datasets/ids.html (accessed on 1 February 2021), CICIDS2017—https://www.unb.ca/cic/datasets/ids-2017.html (accessed on 1 February 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Abbreviation | Description |
| TT | Testing Time |
| ACC | Accuracy |
| KV | Kappa Value |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| RAE | Relative Absolute Error |
| RRSE | Root Relative Squared Error |
| FPR | False Positive Rate |
| PRE | Precession |
| ROC | Receiver Operating Curve |
| MCC | Matthews Correlation Coefficient |
| PRC | Precision Recall Curve |
| TOPSIS | Techniques for Order Preference by Similarity to the Ideal Solution |
| IDS | Intrusion Detection System |
| IoT | Internet of Things |
| LWL | Locally Weighted Learning |
| RLKNN | Rseslib K-Nearest Neighbor |
| CR | Conjunctive Rule |
| DTBL | Decision Table |
| DTNB | Decision Table Naïve Bayes |
| FURIA | Fuzzy Rule Induction |
| NNGE | Nearest Neighbor with Generalization |
| OLM | Ordinal Learning Method |
| RIDOR | RIpple-DOwn Rule learner |
| BFT | Best-First Decision Tree |
| CDT | Criteria Based Decision Tree |
| LADT | Logit Boost based Alternating Decision Tree |
| LMT | Logistic Model Trees |
| NBT | Naïve Bayes based Decision Tree |
| REPT | Reduces Error Pruning Tree |
| RF | Random Forest |
| RT | Random Tree |
| SC | Simple Cart |
| CHIRP | Composite Hypercubes on Iterated Random Projections |
| FLR | Fuzzy Lattice Reasoning |
| HP | Hyper Pipes |
| VFI | Voting Feature Intervals |
| TP | True Positives |
| TN | True Negatives |
| TPR | True Positive Rate |
| TNR | True Negative Rate |
| FT | Functional Trees |
References
- Chavhan, S.; Gupta, D.; Chandana, B.N.; Khanna, A.; Rodrigues, J.J.P.C. IoT-based Context-Aware Intelligent Public Transport System in a metropolitan area. IEEE Internet Things J. 2019, 7, 6023–6034. [Google Scholar] [CrossRef]
- Chen, Q.; Bridges, R.A. Automated behavioral analysis of malware: A case study of wannacry ransomware. In Proceedings of the 16th IEEE International Conference on Machine Learning and Applications, ICMLA 2017, Cancun, Mexico, 18–21 December 2017; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, December 2017; Volume 2017, pp. 454–460. [Google Scholar]
- Liang, W.; Li, K.C.; Long, J.; Kui, X.; Zomaya, A.Y. An Industrial Network Intrusion Detection Algorithm Based on Multifeature Data Clustering Optimization Model. IEEE Trans. Ind. Inform. 2020, 16, 2063–2071. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, W.; Wang, A.; Wu, H. Network Intrusion Detection Combined Hybrid Sampling with Deep Hierarchical Network. IEEE Access 2020, 8, 32464–32476. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Wang, X. Intrusion Detection for IoT Based on Improved Genetic Algorithm and Deep Belief Network. IEEE Access 2019, 7, 31711–31722. [Google Scholar] [CrossRef]
- Yang, H.; Wang, F. Wireless Network Intrusion Detection Based on Improved Convolutional Neural Network. IEEE Access 2019, 7, 64366–64374. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Model selection and overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Pes, B. Learning from high-dimensional biomedical datasets: The issue of class imbalance. IEEE Access 2020, 8, 13527–13540. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Multiclass imbalance problems: Analysis and potential solutions. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Ho, T.K.; Basu, M. Complexity measures of supervised classification problems. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 289–300. [Google Scholar]
- Kelly, M.G.; Hand, D.J.; Adams, N.M. Supervised classification problems: How to be both judge and jury. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin, Germany, 1999; Volume 1642, pp. 235–244. [Google Scholar]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms: Second Edition; Wiley: Hoboken, NJ, USA, 2014; Volume 9781118315, ISBN 9781118914564. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Lashkari, A.H.; Gil, G.D.; Mamun, M.S.I.; Ghorbani, A.A. Characterization of tor traffic using time based features. In Proceedings of the ICISSP 2017 3rd International Conference on Information Systems Security and Privacy, Porto, Portugal, 19–21 February 2017; SciTePress: Setúbal, Portugal, 2017; Volume 2017-Janua, pp. 253–262. [Google Scholar]
- Robert, C. Machine Learning, a Probabilistic Perspective. CHANCE 2014, 27, 62–63. [Google Scholar] [CrossRef]
- Maindonald, J. Pattern Recognition and Machine Learning; Journal of Statistical Software: Los Angeles, CA, USA, 2007; Volume 17. [Google Scholar]
- Frasca, T.M.; Sestito, A.G.; Versek, C.; Dow, D.E.; Husowitz, B.C.; Derbinsky, N. A Comparison of Supervised Learning Algorithms for Telerobotic Control Using Electromyography Signals. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, AAAI 2016, Phoenix, AZ, USA, 12–17 February 2016; pp. 4208–4209. Available online: www.aaai.org (accessed on 12 May 2020).
- Soru, T.; Ngomo, A.C.N. A comparison of supervised learning classifiers for link discovery. ACM Int. Conf. Proceeding Ser. 2014, 41–44. [Google Scholar] [CrossRef]
- Arriaga-Gómez, M.F.; De Mendizábal-Vázquez, I.; Ros-Gómez, R.; Sánchez-Ávila, C. A comparative survey on supervised classifiers for face recognition. In Proceedings of the International Carnahan Conference on Security Technology, Hatfield, UK, 13–16 October 2014; Volume 2014, pp. 1–6. [Google Scholar]
- Shiraishi, T.; Motohka, T.; Thapa, R.B.; Watanabe, M.; Shimada, M. Comparative assessment of supervised classifiers for land use-land cover classification in a tropical region using time-series PALSAR mosaic data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1186–1199. [Google Scholar] [CrossRef]
- Micó, L.; Oncina, J. Comparison of fast nearest neighbour classifiers for handwritten character recognition. Pattern Recognit. Lett. 1998, 19, 351–356. [Google Scholar] [CrossRef]
- Sianaki, O.A. Intelligent Decision Support System for Energy Management in Demand Response Programs and Residential and Industrial Sectors of the Smart Grid. Ph.D. Thesis, Curtin University, Bentley, WA, Australia, 2015. [Google Scholar]
- Hwang, C.; Masud, A. Multiple Objective Decision Making—Methods and Applications: A State-Of-The-Art Survey; Springer: New York, NY, USA, 2012. [Google Scholar]
- Radanliev, P.; De Roure, D.; Page, K.; Van Kleek, M.; Santos, O.; Maddox, L.; Burnap, P.; Anthi, E.; Maple, C. Design of a dynamic and self-adapting system, supported with artificial intelligence, machine learning and real-time intelligence for predictive cyber risk analytics in extreme environments—Cyber risk in the colonisation of Mars. Saf. Extrem. Environ. 2021, 1–12. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Ross, Q.J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. in Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Demusar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Chand, N.; Mishra, P.; Krishna, C.R.; Pilli, E.S.; Govil, M.C. A comparative analysis of SVM and its stacking with other classification algorithm for intrusion detection. In Proceedings of the 2016 International Conference on Advances in Computing, Communication and Automation, ICACCA, Dehradun, India, 8–9 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Htike, K.K.; Khalifa, O.O. Comparison of supervised and unsupervised learning classifiers for human posture recognition. In Proceedings of the International Conference on Computer and Communication Engineering (ICCCE 2010), Kuala Lumpur, Malaysia, 11–13 May 2010. [Google Scholar] [CrossRef]
- Tuysuzoglu, G.; Yaslan, Y. Gözetimli Siniflandiricilar ve Topluluk Temelli Sözlükler ile Biyomedikal Veri Siniflandirilmasi. In Proceedings of the 25th Signal Processing and Communications Applications Conference, SIU 2017, Antalya, Turkey, 15–18 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Gu, S.; Jin, Y. Multi-train: A semi-supervised heterogeneous ensemble classifier. Neurocomputing 2017, 249, 202–211. [Google Scholar] [CrossRef]
- Labatut, V.; Cherifi, H. Accuracy Measures for the Comparison of Classifiers. arXiv 2012, arXiv:abs/1207.3790. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Hong Kong, China, 18–22 December 2006; Volume 148, pp. 161–168. [Google Scholar]
- Amancio, D.R.; Comin, C.H.; Casanova, D.; Travieso, G.; Bruno, O.M.; Rodrigues, F.A.; Da Fontoura Costa, L. A systematic comparison of supervised classifiers. PLoS ONE 2014, 9, e94137. [Google Scholar] [CrossRef]
- Araar, A.; Bouslama, R. A comparative study of classification models for detection in ip networks intrusions. J. Theor. Appl. Inf. Technol. 2014, 64, 107–114. [Google Scholar]
- Gharibian, F.; Ghorbani, A.A. Comparative study of supervised machine learning techniques for intrusion detection. In Proceedings of the Fifth Annual Conference on Communication Networks and Services Research (CNSR 2007), Fredericton, NB, Canada, 14–17 May 2007; pp. 350–355. [Google Scholar]
- Panda, M.; Patra, M.R. A comparative study of data mining algorithms for network intrusion detection. In Proceedings of the 1st International Conference on Emerging Trends in Engineering and Technology, ICETET 2008, Maharashtra, India, 16–18 July 2008; pp. 504–507. [Google Scholar]
- Srinivasulu, P.; Nagaraju, D.; Kumar, P.R.; Rao, K.N. Classifying the network intrusion attacks using data mining classification methods and their performance comparison. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 11–18. [Google Scholar]
- Wu, S.Y.; Yen, E. Data mining-based intrusion detectors. Expert Syst. Appl. 2009, 36, 5605–5612. [Google Scholar] [CrossRef]
- Jalil, K.A.; Kamarudin, M.H.; Masrek, M.N. Comparison of machine learning algorithms performance in detecting network intrusion. In Proceedings of the 2010 International Conference on Networking and Information Technology, Manila, Philippines, 11–12 June 2010; pp. 221–226. [Google Scholar] [CrossRef]
- Amudha, P.; Rauf, H.A. Performance analysis of data mining approaches in intrusion detection. In Proceedings of the 2011 International Conference on Process Automation, Control and Computing, Coimbatore, India, 20–22 July 2011. [Google Scholar]
- China Appala Naidu, R.; Avadhani, P.S. A comparison of data mining techniques for intrusion detection. In Proceedings of the IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 23–25 August 2012; pp. 41–44. [Google Scholar]
- Kalyani, G. Performance Assessment of Different Classification Techniques for Intrusion Detection. IOSR J. Comput. Eng. 2012, 7, 25–29. [Google Scholar] [CrossRef]
- Thaseen, S.; Kumar, C.A. An analysis of supervised tree based classifiers for intrusion detection system. In Proceedings of the 2013 International Conference on Pattern Recognition, Informatics and Mobile Engineering, Salem, India, 21–22 February 2013; pp. 294–299. [Google Scholar]
- Revathi, S.; Malathi, A. A Detailed Analysis on NSL-KDD Dataset Using Various Machine Learning Techniques for Intrusion Detection. Int. J. Eng. Res. Technol. 2013, 2, 1848–1853. [Google Scholar]
- Robinson, R.R.R.; Thomas, C. Ranking of machine learning algorithms based on the performance in classifying DDoS attacks. In Proceedings of the 2015 IEEE Recent Advances in Intelligent Computational Systems, RAICS 2015, Trivandrum, Kerala, 10–12 December 2015; pp. 185–190. [Google Scholar]
- Choudhury, S.; Bhowal, A. Comparative analysis of machine learning algorithms along with classifiers for network intrusion detection. In Proceedings of the 2015 International Conference on Smart Technologies and Management for Computing, Communication, Controls, Energy and Materials (ICSTM), Avadi, India, 6–8 May 2015; pp. 89–95. [Google Scholar]
- Jain, A.; Rana, J.L. Classifier Selection Models for Intrusion Detection System (Ids). Inform. Eng. Int. J. 2016, 4, 1–11. [Google Scholar]
- Bostani, H.; Sheikhan, M. Modification of supervised OPF-based intrusion detection systems using unsupervised learning and social network concept. Pattern Recognit. 2017, 62, 56–72. [Google Scholar] [CrossRef]
- Belavagi, M.C.; Muniyal, B. Performance Evaluation of Supervised Machine Learning Algorithms for Intrusion Detection. Procedia Comput. Sci. 2016, 89, 117–123. [Google Scholar] [CrossRef]
- Almseidin, M.; Alzubi, M.; Kovacs, S.; Alkasassbeh, M. Evaluation of Machine Learning Algorithms for Intrusion Detection System. In Proceedings of the 2017 IEEE 15th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 14–16 September 2017. [Google Scholar]
- Amira, A.S.; Hanafi, S.E.O.; Hassanien, A.E. Comparison of classification techniques applied for network intrusion detection and classification. J. Appl. Log. 2017, 24, 109–118. [Google Scholar]
- Aksu, D.; Üstebay, S.; Aydin, M.A.; Atmaca, T. Intrusion detection with comparative analysis of supervised learning techniques and fisher score feature selection algorithm. In Communications in Computer and Information Science; Springer: Berlin, Germany, 2018; Volume 935, pp. 141–149. [Google Scholar]
- Nehra, D.; Kumar, K.; Mangat, V. Pragmatic Analysis of Machine Learning Techniques in Network Based IDS. In Proceedings of the International Conference on Advanced Informatics for Computing Research; Springer: Berlin/Heidelberg, Germany, 2019; pp. 422–430. [Google Scholar]
- Mahfouz, A.M.; Venugopal, D.; Shiva, S.G. Comparative Analysis of ML Classifiers for Network Intrusion Detection; Springer: Berlin/Heidelberg, Germany, 2020; pp. 193–207. [Google Scholar]
- Rajagopal, S.; Siddaramappa Hareesha, K.; Panduranga Kundapur, P. Performance analysis of binary and multiclass models using azure machine learning. Int. J. Electr. Comput. Eng. 2020, 10, 978. [Google Scholar] [CrossRef]
- Ahmim, A.; Ferrag, M.A.; Maglaras, L.; Derdour, M.; Janicke, H. A Detailed Analysis of Using Supervised Machine Learning for Intrusion Detection; Springer: Berlin/Heidelberg, Germany, 2020; pp. 629–639. [Google Scholar]
- Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques.”; Morgan Kaufmann: Burlington, VT, USA, 2016; p. 128. [Google Scholar]
- Su, J.; Zhang, H.; Ling, C.X.; Matwin, S. Discriminative parameter learning for Bayesian networks. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1016–1023. [Google Scholar]
- Yu, S.-Z. Hidden semi-Markov models. Artif. Intell. 2010, 174, 215–243. [Google Scholar] [CrossRef]
- Ghahramani, Z. An introduction to Hidden Markov Models and Bayesian Networks. In Hidden Markov Models; World Scientific: Singapore, 2001; Volume 15. [Google Scholar]
- Zhang, H. Exploring conditions for the optimality of naïve bayes. Proc. Int. J. Pattern Recognit. Artif. Intell. 2005, 19, 183–198. [Google Scholar] [CrossRef]
- John, G.H.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers George. Proc. Elev. Conf. Uncertain. Artif. Intell. 1995, 42, 338–345. [Google Scholar]
- Puurula, A. Scalable Text Classification with Sparse Generative Modeling. In Lecture Notes in Computer Science; Springer: New York, NY, USA, 2012; pp. 458–469. [Google Scholar]
- Balakrishnama, S.; Ganapathiraju, A. Linear Discriminant Analysis—A Brief Tutorial; Institute for Signal and information Processing: Philadelphia, PA, USA, 1998; Volume 18, pp. 1–8. [Google Scholar]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large Linear Classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Introduction to Logistic Regression; Springer: New York, NY, USA, 2010; pp. 1–39. [Google Scholar]
- Windeatt, T. Accuracy/diversity and ensemble MLP classifier design. IEEE Trans. Neural Netw. 2006, 17, 1194–1211. [Google Scholar] [CrossRef]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; Elsevier Science Publishers: Amsterdam, The Netherlands, 2018; ISBN 9780429968211. [Google Scholar]
- Yang, Q.; Cheng, G. Quadratic Discriminant Analysis under Moderate Dimension. Stat. Theory. 2018. Available online: http://arxiv.org/abs/1808.10065 (accessed on 12 May 2020).
- Frank, E. Fully Supervised Training of Gaussian Radial Basis Function Networks in WEKA; University of Waikato: Hamilton, New Zealand, 2014; Volume 04. [Google Scholar]
- Schwenker, F.; Kestler, H.A.; Palm, G. Unsupervised and Supervised Learning in Radial-Basis-Function Networks. In Self-Organizing Neural Networks; Physica Verlag: Heidelberg, Germany, 2002; pp. 217–243. [Google Scholar]
- Kyburg, H.E. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference by Judea Pearl. J. Philos. 1991, 88, 434–437. [Google Scholar] [CrossRef]
- Kecman, V. Support Vector Machines—An Introduction; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–47. [Google Scholar]
- Keerthi, S.S.; Shevade, S.K.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to Platt’s SMO algorithm for SVM classifier design. Neural Comput. 2001, 13, 637–649. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-Based Learning Algorithms. In Machine Learning; Springer: Berlin, Germany, 1991; Volume 6, pp. 37–66. [Google Scholar]
- Cleary, J.G.; Trigg, L.E. K*: An Instance-based Learner Using an Entropic Distance Measure. In Machine Learning Proceedings 1995; Morgan Kaufmann: New York, NY, USA, 1995. [Google Scholar]
- Wojna, A.; Latkowski, R. Rseslib 3: Library of rough set and machine learning methods with extensible architecture. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2019; Volume 10810 LNCS, pp. 301–323. [Google Scholar]
- Frank, E.; Hall, M.; Pfahringer, B. Locally Weighted Naive Bayes; University of Waikato: Hamilton, New Zealand, 2012. [Google Scholar]
- Atkeson, C.G.; Moore, A.W.; Schaal, S. Locally Weighted Learning. Artif. Intell. Rev. 1997, 11, 11–73. [Google Scholar] [CrossRef]
- Zimek EM (Documentation for extended WEKA including Ensembles of Hierarchically Nested Dichotomies). Available online: http://www.dbs.ifi.lmu.de/~zimek/diplomathesis/implementations/EHNDs/doc/weka/clusterers/FarthestFirst.html (accessed on 12 May 2020).
- Kohavi, R. The power of decision tables. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 1995; Volume 912, pp. 174–189. [Google Scholar]
- Hall, M.A.; Frank, E. Combining naive bayes and decision tables. In Proceedings of the FLAIRS Conference, Coconut Grove, FL, USA, 15–17 May 2008; Volume 2118, pp. 318–319. [Google Scholar]
- Hühn, J.; Hüllermeier, E. FURIA: An algorithm for unordered fuzzy rule induction. Data Min. Knowl. Discov. 2009, 19, 293–319. [Google Scholar] [CrossRef]
- Cohen, W.W. Fast Effective Rule Induction. In Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995. [Google Scholar]
- Stefanowski, J. Rough set based rule induction techniques for classification problems. In Rough Set Based Rule Induction Techniques for Classification Problems; Intelligent Techniques & Soft Computing: Aachen, Germany, 1998; Volume 1, pp. 109–113. [Google Scholar]
- Sylvain, R. Nearest Neighbor with Generalization; University of Canterbury: Christchurch, New Zealand, 2002. [Google Scholar]
- Martin, B. Instance-Based Learning: Nearest Neighbor with Generalization; University of Waikato: Hamilton, New Zealand, 1995. [Google Scholar]
- Ben-David, A. Automatic Generation of Symbolic Multiattribute Ordinal Knowledge-Based DSSs: Methodology and Applications. Decis. Sci. 1992, 23, 1357–1372. [Google Scholar] [CrossRef]
- Holte, R.C. Very Simple Classification Rules Perform Well on Most Commonly Used Datasets. Mach. Learn. 1993, 11, 63–90. [Google Scholar] [CrossRef]
- Frank, E.; Wang, Y.; Inglis, S.; Holmes, G.; Witten, I.H. Using model trees for classification. Mach. Learn. 1998, 32, 63–76. [Google Scholar] [CrossRef]
- Thangaraj, M. Vijayalakshmi Performance Study on Rule-based Classification Techniques across Multiple Database Relations. Int. J. Appl. Inf. Syst. 2013, 5, 1–7. [Google Scholar]
- Pawlak, Z. Rough set theory and its applications to data analysis. Cybern. Syst. 1998, 29, 661–688. [Google Scholar] [CrossRef]
- Frank, E. ZeroR. Weka 3.8 Documentation. 2019. Available online: https://weka.sourceforge.io/doc.stable-3-8/weka/classifiers/rules/ZeroR.html (accessed on 12 May 2020).
- Suthaharan, S. Decision Tree Learning. In Machine Learning Models and Algorithms for Big Data Classification. Integrated Series in Information Systems; Springer: Berlin/Heidelberg, Germany, 2016; pp. 237–269. [Google Scholar]
- Abellán, J.; Moral, S. Building Classification Trees Using the Total Uncertainty Criterion. Int. J. Intell. Syst. 2003, 18, 1215–1225. [Google Scholar] [CrossRef]
- Adnan, M.N.; Islam, M.Z. Forest PA: Constructing a decision forest by penalizing attributes used in previous trees. Expert Syst. Appl. 2017, 89, 389–403. [Google Scholar] [CrossRef]
- Gama, J. Functional trees. Mach. Learn. 2004, 55, 219–250. [Google Scholar] [CrossRef]
- Salzberg, S.L. C4.5: Programs for Machine Learning by J. Ross Quinlan. In Machine Learning; Morgan Kaufmann Publishers, Inc.: New York, NY, USA, 1993; Volume 16, pp. 235–240. [Google Scholar]
- Ibarguren, I.; Pérez, J.M.; Muguerza, J.; Gurrutxaga, I.; Arbelaitz, O. Coverage-based resampling: Building robust consolidated decision trees. Knowledge-Based Syst. 2015, 79, 51–67. [Google Scholar] [CrossRef]
- Hayashi, Y.; Tanaka, Y.; Takagi, T.; Saito, T.; Iiduka, H.; Kikuchi, H.; Bologna, G.; Mitra, S. Recursive-rule extraction algorithm with J48graft and applications to generating credit scores. J. Artif. Intell. Soft Comput. Res. 2016, 6, 35–44. [Google Scholar] [CrossRef]
- Holmes, G.; Pfahringer, B.; Kirkby, R.; Frank, E.; Hall, M. Multiclass alternating decision trees. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2002; Volume 2430, pp. 161–172. [Google Scholar]
- Landwehr, N.; Hall, M.; Frank, E. Logistic model trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef]
- Sumner, M.; Frank, E.; Hall, M. Speeding up Logistic Model Tree induction. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Samos, Greece, 18–20 July 2005; Volume 3721 LNAI, pp. 675–683. [Google Scholar]
- Jiang, L.; Li, C. Scaling up the accuracy of decision-tree classifiers: A naive-bayes combination. J. Comput. 2011, 6, 1325–1331. [Google Scholar] [CrossRef]
- Kalmegh, S. Analysis of WEKA Data Mining Algorithm REPTree, Simple Cart and RandomTree for Classification of Indian News. Int. J. Innov. Sci. Eng. Technol. 2015, 2, 438–446. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 9780128042915. [Google Scholar]
- Islam, Z.; Giggins, H. Knowledge Discovery through SysFor: A Systematically Developed Forest of Multiple Decision Trees kDMI: A Novel Method for Missing Values Imputation Using Two Levels of Horizontal Partitioning in a Data set View project A Hybrid Clustering Technique Combining a Novel Genetic Algorithm with K-Means View project Knowledge Discovery through SysFor-a Systematically Developed Forest of Multiple Decision Trees. 2011. Available online: https://www.researchgate.net/publication/236894348 (accessed on 11 May 2020).
- Wilkinson, L.; Anand, A.; Tuan, D.N. CHIRP: A new classifier based on composite hypercubes on iterated random projections. In Proceedings of the Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 6–14. [Google Scholar]
- Athanasiadis, I.N.; Kaburlasos, V.G.; Mitkas, P.A.; Petridis, V. Applying Machine Learning Techniques on Air Quality Data for Real-Time Decision Support 1 Introduction 2 Decision support systems for assessing air quality in real—time 3 The σ—FLNMAP Classifier. First Int. Symp. Inf. Technol. Environ. Eng. 2003, 2–7. Available online: http://www.academia.edu/download/53083886/Applying_machine_learning_techniques_on_20170511-3627-1jgoy73.pdf (accessed on 11 May 2020).
- Deeb, Z.A.; Devine, T. Randomized Decimation HyperPipes; Penn State University: University Park, PA, USA, 2010. [Google Scholar]
- Demiröz, G.; Altay Güvenir, H. Classification by voting feature intervals. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 1997; Volume 1224, pp. 85–92. [Google Scholar]
- Ingre, B.; Yadav, A. Performance analysis of NSL-KDD dataset using ANN. In Proceedings of the 2015 International Conference on Signal Processing and Communication Engineering Systems, Guntur, India, 2–3 January 2015; pp. 92–96. [Google Scholar] [CrossRef]
- Ibrahim, L.M.; Taha, D.B.; Mahmod, M.S. A comparison study for intrusion database (KDD99, NSL-KDD) based on self organization map (SOM) artificial neural network. J. Eng. Sci. Technol. 2013, 8, 107–119. [Google Scholar]
- Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A detailed analysis of the KDD CUP 99 data set. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; pp. 1–6. [Google Scholar]
- Shiravi, A.; Shiravi, H.; Tavallaee, M.; Ghorbani, A.A. Toward developing a systematic approach to generate benchmark datasets for intrusion detection. Comput. Secur. 2012, 31, 357–374. [Google Scholar] [CrossRef]
- Gharib, A.; Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. An Evaluation Framework for Intrusion Detection Dataset. In Proceedings of the ICISS 2016—2016 International Conference on Information Science and Security, Jaipur, India, 19–22 December 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017. [Google Scholar]
- Panigrahi, R.; Borah, S. Design and Development of a Host Based Intrusion Detection System with Classification of Alerts; Sikkim Manipal University: Sikkim, India, 2020. [Google Scholar]
- Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward Generating a New Intrusion Detection Dataset and Intrusion Traffic Characterization. In Proceedings of the ICISSP 2018, Madeira, Portugal, 22–24 January 2018; pp. 108–116. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).