Yule–Walker Equations Using a Gini Covariance Matrix for the High-Dimensional Heavy-Tailed PVAR Model

Abstract

Gini covariance plays a vital role in analyzing the relationship between random variables with heavy-tailed distributions. In this papaer, with the existence of a finite second moment, we establish the Gini–Yule–Walker equation to estimate the transition matrix of high-dimensional periodic vector autoregressive (PVAR) processes, the asymptotic results of estimators have been established. We apply this method to study the Granger causality of the heavy-tailed PVAR process, and the results show that the robust transfer matrix estimation induces sign consistency in the value of Granger causality. Effectiveness of the proposed method is verified by both synthetic and real data.

1. Introduction

The heavy-tailed distribution is graphically thicker in the tails and sharper in the peaks than the normal distribution. Intuitively, this means that the probability of extreme values is greater for these data than for normally distributed data. The heavy-tailed phenomenon has been encountered empirically in various fields: physics, earth sciences, economics and political science, etc. Periodicity is a wave-like or oscillatory movement around a long-term trend presented in a time series. It is well-known that cyclicality caused by business and economic activities is usually different from trend movements, not in a single direction of continuous movement, but in alternating fluctuations between ups and downs. When these components, trend and cyclicality, do not evolve independently, traditional differencing filters may not be suitable (see for example, Franses and Paap [1], Bell et al. [2], Aliat and Hamdi [3]). Periodic time series models are used to model periodically stationary time series. Periodic vector autoregressive (PVAR) models extend the classical vector autoregressive (VAR) models by allowing the parameters to vary with the cyclicality.

$$X_{iT+v}=\sum _{k=1}^{q\left(v\right)}{\alpha }_k\left(v\right)X_{iT+v-k}+{ϵ}_{iT+v}.$$

(1)

For fixed v and predetermined value T, the random vector $X_{iT+v}$ represents the realization during the vth season, with $v\in \{1,\dots ,T\}$, at year $i,i\in \{1,\dots ,n\}$. The PVAR model order at season v is given by $q\left(v\right)$, whereas ${\alpha }_k\left(v\right),k=1,\cdots ,v$, represent the PVAR model coefficients during season v. The error process $ϵ=\left\{{ϵ}_{iT+v}\right\}$ corresponds to a periodic white noise, with $E\left({ϵ}_{iT+v}\right)=\mathbf{0}$ and $var\left({ϵ}_{iT+v}\right)={\sigma }^2\left(v\right)\mathbf{I}$, where $\mathbf{0}$ is a zero vector of order d and $\mathbf{I}$ is a unit matrix of order d.

This paper seeks to establish a PVAR model to simulate the heavy-tailed time series. Let random vectors $X_1,...,X_n$ be from a stationary stochastic process ${\left(X_k\right)}_{k=-\infty }^{\infty }$, $X_k={(X_{kT+1},\dots ,X_{kT+T})}^{\top },$ where the transpose (indicated by ⊤) of a row vector is a column vector.

We consider first-order PVAR model,

$$X_{kT+v}=A{X}_{kT+v-1}+E_{kT+v},$$

(2)

where $k\in \{1,\cdots ,n\},v\in \{2,\cdots ,T\}$, T is the period of $X_k$, $E_{kT+v}$ denotes the latent heavy-tailed innovation, and A is the transition matrix. In this paper, we assume that the entries of the heavy-tailed innovation $E_{kT+v}={(E_{kT+v1},\cdots ,E_{kT+vd})}^{\top }$ obey a power-law distribution with $P(|E_{kT+vi}|>x)\sim C{x}^{-{\alpha }_i}$ and ${\alpha }_i\le 2$, then the second moment is finite and the third moment is infinite. From the Equation (2) we know that, given k, the vector $X_k$ follows a first-order vector autoregressive (VAR). We call the first-order PVAR process stable if all eigenvalues of transition matrix A have modulus less than 1, the condition is equivalent to $det\left(I_d-Az\right)\ne 0$ for all $|z|\le 1$ (see for example, Section 2.1 in Lütkepohl [4]). The transition matrix characterizes the temporal dependence for sequence data, and plays a fundamental role in forecasting. Moreover, the zero and nonzero entries of the transition matrix is often closely related to Granger causality. This manuscript focuses on estimating the transition matrix of high-dimensional heavy-tailed PVAR processes.

PVAR models have been extensively studied under the Gaussian assumption, the Gaussian PVAR models assume that the latent innovations are independent identity distribution Gaussian random vectors. Under this model, there are two kinds of methods to estimate the transition matrix under high dimensional setting, one is the Lasso-based estimation procedures, see [5,6,7,8], and the other is Dantzig-selector-type estimators, see [9,10,11,12]. Under the non-Gaussian VAR process, Qiu et al. [13] proposed a quantile-based dantzig-selector-type estimator of the transition matrix for elliptical VAR process. Wong et al. [14] provided an alternative proof of the consistency of the Lasso for sparse non-Gaussian VAR models. Maleki et al. [15] extended the multivariate setting of autoregressive process, by considering the multivariate scale mixture of skew-normal distributions for VAR innovations.

The statistical second-order information contained in the data is usually expressed by the variance and covariance, most of the literature dealing with time series measure dependence using the variance and covariance. To investigate the validity of the variance estimates, we need the presence of the fourth order moment of the random variables. For the heavy-tailed nature of financial data, the third-order moments of random variables are usually non-existent. Schechtman and Yitzhaki [16] proposed the concept of Gini covariance, which has been used widely to measure the dependence of heavy-tailed distributions. Let H be the joint distribution of the random variables X and Y with the marginal distribution functions $F_1$ and $F_2$, respectively. The standard Gini covariance is defined as

$$\mathrm{Gcov}(X,Y)=\mathrm{cov}(X,F_2\left(Y\right))\mathrm{and}\mathrm{Gcov}(Y,X)=\mathrm{cov}(Y,F_1\left(X\right)),$$

(3)

assuming the random variables with only a finite first moment. The Gini covariance has an advantage when analyzing bivariate data defined by both variate values and ranks of the values. The representation of Gini covariance $\mathrm{Gcov}(X,Y)$ indicates that it has mixed properties of the variable X and the rank of the variable Y, and thus complements the usual covariance and rank covariance [16,17,18]. In terms of balance between effciency and robustness, Gini covariance plays an important role in measuring association for variables from heavy-tailed distributions [19].

The Yule–Walker equations arise naturally in the problem of linear prediction of any zero-mean weakly stationary process based on a finite number of contiguous observations. The Yule–Walker equations provide a straightforward connection between the autoregressive model parameters and the covariance function of the process. In this paper, relaxing the strong assumption of the existence of higher order moments of the regressors, we use a non-parametric method to estimate the Gini covariance matrix, establish the Gini–Yule–Walker equation to estimate the sparse transition matrix of stationary PVAR processes. The estimator falls into the category of Dantzig-selector-type estimators. With existence of a finite second moment, we investigate the asymptotic behavior of the estimator in high dimensions.

The paper is orginazed as follows: In Section 2, we establish the Gini–Yule–Walker equation and estimate the sample Gini covariance matrix. In Section 3, we derive the convergence rate of transfer matrix estimation. In Section 4, we discuss the characterization and estimation of Granger causality under the heavy-tailed PVAR model. In Section 5, both synthetic and real data are used to demonstrate the empirical performance of the proposed methodology.

2. Model

In this section, the notations are set. Then, we establish the Gini–Yule–Walker equation, obtain simple non-parametric estimators for Gini covariance matrix and investigate the convergence rate of the sample Gini covariance matrix.

2.1. Notation

Let $v={(v_1,...,v_d)}^{\top }$ be a d-dimensional real vector, and $M=\left[M_{ji}\right]\in R^{d_1\times d_2}$ be a $d_1\times d_2$ matrix. For $0<q<\infty$, we define the vector $l_q$ norm of v as ${||v||}_q={({\sum }_{j=1}^d\mid v_j{\mid }^q)}^{1/q}$, and the vector $l_{\infty }$ norm of v as ${||v||}_{\infty }={\max }_{j=1}^d\mid v_j\mid$. Let the matrix $l_1$ norm of M as ${||M||}_1={\max }_i{\sum }_{j=1}^d\mid M_{ji}\mid$, the matrix $l_{\infty }$ norm ${||M||}_{\infty }={\max }_j{\sum }_{i=1}^d\mid M_{ji}\mid$, $X_k={(X_{1k},...,X_{dk})}^{\top }$ and $Y_k={(Y_{1k},...,Y_{dk})}^{\top }$ be two random vectors.

2.2. Gini–Yule–Walker Equation

In this paper, we model the time series vector by a stationary PVAR process under the existence of second moment. For each $k,1\le k\le n$, $X_{1k},...,X_{Tk}\in R^d$ follow a lag-one VAR process, with $E_{tk}$ independent of $X_{(t-1)k}$, and $E\left(X_{tk}\right)=0,E\left(E_{tk}\right)=0$.

We define

$$X_k={(X_{1k},···,X_{(T-1)k})}^{\top },$$

this VAR process may be performed by concatenating the equation systems to analyze the following equation,

$$y_k=Y_k\beta +{\epsilon }_k,$$

(4)

where $Y_k=X_k\otimes {\mathrm{I}}_d$, and

$$y_k=\left[\begin{array}{c}{y}_{1k}\\ y_{2k}\\ ⋮\\ y_{dk}\end{array}\right],y_{ik}=\left[\begin{array}{c}{X}_{2ik}\\ X_{3ik}\\ ⋮\\ X_{Tik}\end{array}\right],\beta =\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_d\end{array}\right],{\beta }_i=\left[\begin{array}{c}{A}_{i1}\\ A_{i2}\\ ⋮\\ A_{id}\end{array}\right],{\epsilon }_k=\left[\begin{array}{c}{\epsilon }_{1k}\\ {\epsilon }_{2k}\\ ⋮\\ {\epsilon }_{dk}\end{array}\right],{\epsilon }_{ik}=\left[\begin{array}{c}{E}_{2ik}\\ E_{3ik}\\ ⋮\\ E_{Tik}\end{array}\right],$$

the ⊗ is a Kronecker product operator.

Since the matrix $Y_k$ is a block diagonal matrix, the estimation problem can be decomposed into d independent sub-problems. Let us consider the i-th equation of the system.

$$\left[\begin{array}{c}{X}_{2ik}\\ X_{3ik}\\ ⋮\\ X_{Tik}\end{array}\right]=\left[\begin{array}{cccc}{X}_{11k}& X_{12k}& \cdots & X_{1dk}\\ X_{21k}& X_{22k}& \cdots & X_{2dk}\\ ⋮& ⋮& ⋮& ⋮\\ X_{(T-1)1k}& X_{(T-1)2k}& \cdots & X_{(T-1)dk}\end{array}\right]\left[\begin{array}{c}{A}_{i1}\\ A_{i2}\\ ⋮\\ A_{id}\end{array}\right]+\left[\begin{array}{c}{E}_{2ik}\\ E_{3ik}\\ ⋮\\ E_{Tik}\end{array}\right],$$

the above equation system can be considered as a multiple regression

$$X_{tik}=X_{(t-1)1k}{A}_{i1}+X_{(t-1)2k}{A}_{i2}+...+X_{(t-1)dk}{A}_{id}+{ϵ}_{tik},t\in \{2,3,\cdots ,T\},$$

this equation system can be abbreviated as

$$z_{ik}=x_{1k}{A}_{i1}+x_{2k}{A}_{i2}+...+x_{dk}{A}_{id}+{\widetilde{ϵ}}_{ik},$$

(5)

with $T-1$ samples to estimate the i-th line of transition matrix A.

Let $F\left(x_{ik}\right)$ be the distribution of $x_{ik}$, we assume the independence between ${\widetilde{ϵ}}_{ik}$ and $F\left(x_{ik}\right)$, for $i=1,2,...,d$. Then we get the Gini covariance matrix equation issue from Equation (5),

$$\left[\begin{array}{c}\mathrm{cov}(z_{ik},F\left(x_{1k}\right))\\ \mathrm{cov}(z_{ik},F\left(x_{2k}\right))\\ ⋮\\ \mathrm{cov}(z_{ik},F\left(x_{dk}\right))\end{array}\right]=\left[\begin{array}{cccc}\mathrm{cov}(x_{1k},F\left(x_{1k}\right))& \mathrm{cov}(x_{2k},F\left(x_{1k}\right))& \cdots & \mathrm{cov}(x_{dk},F\left(x_{1k}\right))\\ \mathrm{cov}(x_{1k},F\left(x_{2k}\right))& \mathrm{cov}(x_{2k},F\left(x_{2k}\right))& \cdots & \mathrm{cov}(x_{dk},F\left(x_{2k}\right))\\ ⋮& ⋮& ⋮& ⋮\\ \mathrm{cov}(x_{1k},F\left(x_{dk}\right))& \mathrm{cov}(x_{2k},F\left(x_{kd}\right))& \cdots & \mathrm{cov}(x_{dk},F\left(x_{dk}\right))\end{array}\right]\left[\begin{array}{c}{A}_{i1}\\ A_{i2}\\ ⋮\\ A_{id}\end{array}\right].$$

From the above equation, we obtain the so called Gini–Yule–Walker Equation

$$G=\tilde{G}{A}^{\top },$$

(6)

where $G=\frac{1}{n}{\sum }_{k=1}^n{G}_k$, $\tilde{G}=\frac{1}{n}{\sum }_{k=1}^n{\tilde{G}}_k$. The entries of $G_k$ are given by $G_{ijk}=\mathrm{Gcov}(z_{jk},x_{ik})$, and the entries of ${\tilde{G}}_k$ are given by ${\tilde{G}}_{ijk}=\mathrm{Gcov}(x_{jk},x_{ik})$.

2.3. Sample Gini Covariance Matrix

We use a $U-$statistic method to estimate the Gini covariance matrix $G_k$ and ${\tilde{G}}_k$. From Equation (6), the elements of the covariance matrix $G_k$ and ${\tilde{G}}_k$ can be divided into two categories: Gini covariance $\mathrm{Gcov}({\tilde{X}}_k,{\tilde{Y}}_k)$ and Gini mean difference $\mathrm{Gcov}({\tilde{Y}}_k,{\tilde{Y}}_k)$, ${\tilde{X}}_k\ne {\tilde{Y}}_k$ with ${\tilde{X}}_k\in \left\{z_{1k},z_{2k},\cdots ,z_{dk},x_{1k},x_{2k},\cdots ,x_{dk}\right\},{\tilde{Y}}_k\in \left\{x_{1k},x_{2k},\cdots ,x_{dk}\right\}$.

For the Gini covariance $\mathrm{Gcov}({\tilde{X}}_k,{\tilde{Y}}_k)$, we have sample space

$$\{({\tilde{X}}_{1k},{\tilde{Y}}_{1k}),({\tilde{X}}_{2k},{\tilde{Y}}_{2k}),\cdots ,({\tilde{X}}_{(T-1)k},{\tilde{Y}}_{(T-1)k})\}.$$

The i-th ordered variable of ${\tilde{X}}_k$ is expressed by ${\tilde{X}}_{i:(T-1)k}$ and the associated variable of ${\tilde{Y}}_k$ (matched with ${\tilde{X}}_{i:(T-1)k}$ ) is expressed by ${\tilde{Y}}_{[i:(T-1)]k}$, which is the concomitant of the i-th order statistic. In this set-up, in the context of non-parametric estimation of a regression function, Yang [20] proposed a statistic of the form

$$R\left(F_{(T-1)}({\tilde{X}}_k,{\tilde{Y}}_k)\right)=\frac{1}{(T-1)}\sum _{i=1}^{(T-1)}J\left(\frac{i}{(T-1)}\right)h\left({\tilde{X}}_{i:(T-1)k},{\tilde{Y}}_{[i:(T-1)]k}\right),$$

(7)

where $J(.)$ is a bounded smooth function, $h(.)$ is a real valued function of $({\tilde{X}}_k,{\tilde{Y}}_k),$ and $F_{T-1}(.)$ is the empirical distribution function corresponding to $F_{{\tilde{X}}_k,{\tilde{Y}}_k}(.)$. The Gini covariance defined in Equation (3) can be rewritten as

$$\mathrm{Gcov}({\tilde{X}}_k,{\tilde{Y}}_k)={\int }_0^{\infty }{\int }_0^{\infty }\frac{1}{2}\tilde{x}\left(2F_{{\tilde{Y}}_k}\left(\tilde{y}\right)-1\right)d{F}_{{\tilde{X}}_k,{\tilde{Y}}_k}(\tilde{x},\tilde{y}).$$

Choosing $J\left(F_{{\tilde{Y}}_k}\left(\tilde{y}\right)\right)=2F_{{\tilde{Y}}_k}\left(\tilde{y}\right)-1$ and $h(\tilde{x},\tilde{y})=\frac{1}{2}\tilde{x},$ from Equation (7), we obtain an estimator of $G({\tilde{X}}_k,{\tilde{Y}}_k)$ as

$$U({\tilde{X}}_k,{\tilde{Y}}_k)=\frac{2}{{(T-1)}^2}\sum _{i=1}^{T-1}(2i-T){\tilde{X}}_{[i:(T-1\left)\right]k}.$$

(8)

For the Gini mean difference $\mathrm{Gcov}({\tilde{Y}}_k,{\tilde{Y}}_k)$, we have sample space $\{{\tilde{Y}}_{1k},{\tilde{Y}}_{2k},...,{\tilde{Y}}_{(T-1)k}\}$. Let ${\tilde{Y}}_{1k}$ and ${\tilde{Y}}_{2k}$ be two independent random variables with distribution function $F_{{\tilde{Y}}_k}$, the Gini mean difference $\mathrm{Gcov}({\tilde{Y}}_k,{\tilde{Y}}_k)$ can be expressed as

$$\begin{array}{cc}\hfill \mathrm{Gcov}({\tilde{Y}}_k,{\tilde{Y}}_k)& =\frac{1}{2}\left({\int }_0^{\infty }2\tilde{y}{F}_{{\tilde{Y}}_k}\left(\tilde{y}\right)d{F}_{{\tilde{Y}}_k}\left(\tilde{y}\right)-{\int }_0^{\infty }\tilde{y}d{F}_{{\tilde{Y}}_k}\left(\tilde{y}\right)\right)\hfill \\ \hfill & =\frac{1}{2}E\left(max\left({\tilde{Y}}_{1k},{\tilde{Y}}_{2k}\right)-{\tilde{Y}}_{1k}\right).\hfill \end{array}$$

The estimator of $\mathrm{Gcov}({\tilde{Y}}_k,{\tilde{Y}}_k)$ based on U-statistics is given by

$$U({\tilde{Y}}_k,{\tilde{Y}}_k)=\frac{1}{\left(\genfrac{}{}{0pt}{}{T-1}{2}\right)}\sum _{i=1}^{T-1}\sum _{i<j,j=2}^{T-1}k\left({\tilde{Y}}_{ik},{\tilde{Y}}_{jk}\right),$$

where $k\left({\tilde{Y}}_{1k},{\tilde{Y}}_{2k}\right)=\frac{1}{4}\left(2max\left({\tilde{Y}}_{1k},{\tilde{Y}}_{2k}\right)-{\tilde{Y}}_{1k}-{\tilde{Y}}_{2k}\right)$. After some simplification, we obtain

$$U({\tilde{Y}}_k,{\tilde{Y}}_k)=\frac{1}{2(T-1)(T-2)}\sum _{i=1}^{T-1}(2i-T-2){\tilde{Y}}_{i:(T-1)k},$$

(9)

where ${\tilde{Y}}_{i:(T-1)k}$ is the i -th order statistic based on the sample space $\{{\tilde{Y}}_{1k},\dots ,{\tilde{Y}}_{(T-1)k}\}$.

2.4. Convergence Rates of the Estimator $U({\tilde{X}}_k,{\tilde{Y}}_k)$ and $U({\tilde{Y}}_k,{\tilde{Y}}_k)$

In this subsection, with the truncation method, we use the Bernstein’s inequality to investigate the convergence rates of the estimator $U({\tilde{X}}_k,{\tilde{Y}}_k)$ and $U({\tilde{Y}}_k,{\tilde{Y}}_k)$. From Equations (8) and (9), we define ${\gamma }_k=U({\tilde{X}}_k,{\tilde{Y}}_k),{\eta }_k=U({\tilde{Y}}_k,{\tilde{Y}}_k),1\le k\le n$, and $\mathrm{\Delta }=\max \{D\left({\gamma }_k\right),D\left({\eta }_k\right)\}$, where $D\left({\gamma }_k\right)$ is the variance of the variable ${\gamma }_k$.

For analysis, we require the following three assumptions on the time series and the size of variables $(d,T,n)$:

Assumption A1.

From Equation (2), suppose that the entries of the heavy-tailed innovation $E_{kT+v}={(E_{kT+v1},\cdots ,E_{kT+vd})}^{\top }$ obey a power-law distribution with $P(|E_{kT+vi}|>x)\sim C{x}^{-{\alpha }_i}$ and ${\alpha }_i\le 2$, then the second moment is finite and the third moment is infinite.

Assumption A2.

Suppose that $\frac{logn}{T}\to 0$, $\frac{dT}{\sqrt{n}}\le c$, c is a finite constant, for $T\to \infty ,n\to \infty$.

Assumption A3.

Suppose $\frac{d}{n}\to 0$, for $n\to \infty .$

Lemma 1.

Let ${\left\{X_k\right\}}_{k\in Z}$ be a stationary PVAR process from Equation (2), and $X_1,\cdots ,X_n$ be a sequence of observations from ${\left\{X_k\right\}}_{k\in \mathbb{Z}}$. Suppose that Assumptions (A1)–(A2) are satisfied. Then, for T and n large enough, with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}),$ we have

$$|\frac{1}{n}\sum _{k=1}^n({\gamma }_k-E{\gamma }_k)|\le d\sqrt{\frac{8Tlogn}{n}},$$

(10)

$$|\frac{1}{n}\sum _{k=1}^n({\eta }_k-E{\eta }_k)|\le d\sqrt{\frac{8Tlogn}{n}}.$$

(11)

Proof. 

Assuming that m and $\lambda$ are constants greater than 0, and

$${\tilde{\gamma }}_k=({\gamma }_k-E{\gamma }_k)1_{|{\gamma }_k-E{\gamma }_k|\le m}.$$

Then, ${\tilde{\gamma }}_k$ is a bounded random variable and satisfies the property of independent identical distribution, it follows from the Bernstein’s inequality that

$$\mathbb{P}(|\sum _{k=1}^n{\tilde{\gamma }}_k|\ge \lambda )\le 2exp\left(-{\lambda }^2{(2{\sigma }^2+\frac{2}{3}m\lambda )}^{-1}\right),$$

(12)

where ${\sigma }^2=nD\left({\tilde{\gamma }}_k\right)\le n\mathrm{\Delta }$.

Let $m=d\sqrt{\frac{Tn}{8logn}},\delta =d\sqrt{\frac{8Tlogn}{n}}$ and $\lambda =n\delta$, we have

$$\begin{array}{cc}\hfill \mathbb{P}(|\frac{1}{n}\sum _{k=1}^n({\gamma }_k-E{\gamma }_k)|\ge & \delta )\le n\mathbb{P}(|{\gamma }_k-E{\gamma }_k|>m)+\mathbb{P}(|\sum _{k=1}^n{\tilde{\gamma }}_k|\ge n\delta )\hfill \\ \hfill \le & \frac{nD\left({\gamma }_k\right)}{m^2}+2exp\left(-\frac{8d^{2}Tlogn}{2D\left({\gamma }_k\right)+\frac{2}{3}{d}^{2}T}\right)\hfill \\ \hfill \le & \frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}.\hfill \end{array}$$

As $T\to \infty$ and $n\to \infty$, assuming $\frac{logn}{T}\to 0$ and $\frac{dT}{\sqrt{n}}\le c$, then $\frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}\to 0$.

With similar proof methods, we obtain that

$$\mathbb{P}(|\frac{1}{n}\sum _{k=1}^n({\eta }_k-E{\eta }_k)|\ge \delta )\le \frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}.$$

This completes the proof. □

From Equations (5) and (6), we define the sample estimation of Gini covariance matrix G as $\widehat{G}=\left({\widehat{G}}_{ij}\right),{\widehat{G}}_{ij}=\frac{1}{n}{\sum }_{k=1}^{n}U(z_{jk},x_{ik})$ and the sample estimation of Gini covariance matrix $\tilde{G}$ as $\widehat{\tilde{G}}=\left({\widehat{\tilde{G}}}_{ij}\right),{\widehat{\tilde{G}}}_{ij}=\frac{1}{n}{\sum }_{k=1}^{n}U(x_{jk},x_{ik})$, $1\le i,j\le d$.

Next, we investigate the convergence rates of the estimator $\widehat{G}$ and $\widehat{\tilde{G}}$ under the $l_{\infty }$ norm.

Lemma 2.

Let ${\left\{X_k\right\}}_{k\in Z}$ be a stationary PVAR process from Equation (2), and $X_1,\cdots ,X_n$ be a sequence of observations from ${\left\{X_k\right\}}_{k\in \mathbb{Z}}$. Suppose that Assumptions (A1)–(A3) are satisfied. Then, for T and n large enough, with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2}),$ we have

$$||\widehat{G}{-G||}_{\infty }\le d\sqrt{\frac{8Tlogn}{n}},$$

(13)

$$||\widehat{\tilde{G}}-\tilde{G}{||}_{\infty }\le d\sqrt{\frac{8Tlogn}{n}}.$$

(14)

Proof. 

Let $\delta =d\sqrt{\frac{8Tlogn}{n}}$, based on the Lemma 1, we have

$$\begin{array}{cc}\hfill \mathbb{P}\left\{{∥\widehat{G}-G∥}_{\infty }\ge \delta \right\}\le & \sum _{i,j=1}^d\mathbb{P}\left(|{\widehat{G}}_{ij}-G_{ij}|\ge \delta \right)\hfill \\ \hfill \le & d^2\mathbb{P}\left(|{\widehat{G}}_{ij}-G_{ij}|\ge \delta \right)\hfill \\ \hfill =& d^2\mathbb{P}\left(|\frac{1}{n}\sum _{k=1}^n\left(U(z_{jk},x_{ik})-\mathrm{Gcov}(z_{jk},x_{ik})\right)|\ge \delta \right)\hfill \\ \hfill \le & d^2\mathbb{P}\left(|\frac{1}{n}\sum _{k=1}^n({\gamma }_k-E{\gamma }_k)|\ge \delta \right)\hfill \\ \hfill \le & \frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2}.\hfill \end{array}$$

As $T\to \infty$ and $n\to \infty$, assuming $\frac{logn}{T}\to 0$, $\frac{dT}{\sqrt{n}}\le c$ and $\frac{d}{n}\to 0$, then $\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2}\to 0$.

Next, we study the convergence of sample Gini covariance matrix $\widehat{\tilde{G}}$.

Let $\delta =d\sqrt{\frac{8Tlogn}{n}}$, based on the Lemma 1,

$$\begin{array}{cc}\hfill \mathbb{P}\left(|{\widehat{\tilde{G}}}_{jj}-{\tilde{G}}_{jj}|\ge \delta \right)=& \mathbb{P}\left(|\frac{1}{n}\sum _{k=1}^n\left(U(x_{jk},x_{jk})-\mathrm{Gcov}(x_{jk},x_{jk})\right)|\ge \delta \right)\hfill \\ \hfill =& \mathbb{P}(|\frac{1}{n}\sum _{k=1}^n({\eta }_k-E{\eta }_k)|\ge \delta )\hfill \\ \hfill \le & \frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}.\hfill \end{array}$$

(15)

Now, for the off-diagonal entries, we have

$$\begin{array}{cc}\hfill \mathbb{P}\left(|{\widehat{\tilde{G}}}_{ij}-{\tilde{G}}_{ij}|\ge \delta \right)=& \mathbb{P}\left(|\frac{1}{n}\sum _{k=1}^n\left(U(x_{jk},x_{ik})-\mathrm{Gcov}(x_{jk},x_{ik})\right)|\ge \delta \right)\hfill \\ \hfill =& \mathbb{P}(|\frac{1}{n}\sum _{k=1}^n({\gamma }_k-E{\gamma }_k)|\ge \delta )\hfill \\ \hfill \le & \frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}.\hfill \end{array}$$

(16)

Combining Equations (15) and (16), we obtain

$$\begin{array}{cc}\hfill \mathbb{P}\left\{{∥\widehat{\tilde{G}}-\tilde{G}∥}_{\infty }\ge \delta \right\}\le & \sum _{i,j=1}^d\mathbb{P}\left(|{\widehat{\tilde{G}}}_{ij}-{\tilde{G}}_{ij}|\ge \delta \right)\hfill \\ \hfill \le & d^2\left(\frac{8\mathrm{\Delta }logn}{d^{2}T}+\frac{2}{n^2}\right)\hfill \\ \hfill =& \frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2}.\hfill \end{array}$$

This completes the proof. □

3. Theoretical Properties

Using the Gini covariance matrix Equation (6), we propose to estimate A by

$$\widehat{A}=\underset{M\in R^{d\times d}}{argmin}||M_{jk}||s.t.||\widehat{G}-\widehat{\tilde{G}}{M}^{\top }{||}_{\infty }\le \tilde{\lambda }.$$

(17)

The above optimization problem can be further decomposed into d subproblems. The i-th row of transition matrix A by

$${\widehat{A}}_{i*}=\underset{v\in R^{d\times 1}}{argmin}{||v||}_{1}s.t.{||{\widehat{G}}_{*i}-\widehat{\tilde{G}}v||}_{\infty }\le \tilde{\lambda }.$$

(18)

Compared to the lasso-type procedures, the proposed method can be solved in parallel and Equation (17) can be solved efficiency using the parametric simplex method for sparse learning in [21].

Based on Lemma 2, we can further deliver the rates of convergence of $\widehat{A}$ under the matrix $l_{\infty }$ norm and $l_1$ norm. We start with some additional notation. For $\alpha \in [0,1),\eta >0,$ and $M_d>0$ that may scale with d, we define the matrix class

$$\mathcal{M}(\alpha ,\eta ,M_d)=\{\mathbf{M}\in {\mathbb{R}}^{d\times d}:\underset{1\le j\le d}{max}\sum _{k=1}^d|{\mathbf{M}}_{jk}{|}^{\alpha }\le {\eta ,||\mathbf{M}||}_1\le M_d\}.$$

(19)

$\mathcal{M}(\alpha ,\eta ,M_d)$ requires the transition matrices are sparse in rows. If $\alpha =0$, then the maximum number of nonzeros in rows of transition matrice is at most $\eta$. $\mathcal{M}(\alpha ,\eta ,M_d)$ is also investigated in [12].

Theorem 1.

Let ${\left\{X_k\right\}}_{k\in Z}$ be a stationary PVAR process from Equation (2). Suppose that Assumptions (A1)–(A3) are satisfied. The transition matrix $A^{\top }\in \mathcal{M}(\alpha ,\eta ,M_d)$, if we choose the tuning parameter $\tilde{\lambda }=(1+M_d)d\sqrt{\frac{8Tlogn}{n}}$. Then, for T and n large enough, with probability no small than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$, we have

$$||{\widehat{A}}^{\top }-A^{\top }{||}_{\infty }\le 2\tilde{\lambda }{||{\left(\tilde{G}\right)}^{-1}||}_1,$$

(20)

$$||{\widehat{A}}^{\top }-A^{\top }{||}_1\le 4\eta (2\tilde{\lambda }||{\tilde{G}}^{-1}{{||}_1)}^{1-\alpha }.$$

(21)

Proof. 

We first show that with large probability, A is feasible to the optimization problem. By the Gini–Yule–Walker equation, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}||\widehat{\tilde{G}}{A}^{\top }-\widehat{G}{||}_{\infty }\hfill & =\hfill & ||\widehat{\tilde{G}}{\tilde{G}}^{-1}G-\widehat{G}{||}_{\infty }\hfill \\ & =\hfill & ||\widehat{\tilde{G}}{\tilde{G}}^{-1}G-G+G-\widehat{G}{||}_{\infty }\hfill \\ & \le \hfill & ||(\widehat{\tilde{G}}{\tilde{G}}^{-1}-I){G||}_{\infty }+{||G-\widehat{G}||}_{\infty }\hfill \\ & \le \hfill & ||\widehat{\tilde{G}}-\tilde{G}{||}_{\infty }||A^{\top }{||}_1+{||G-\widehat{G}||}_{\infty }\hfill \\ & \le \hfill & ||\widehat{\tilde{G}}-\tilde{G}{||}_{\infty }{M}_d+{||G-\widehat{G}||}_{\infty }.\hfill \end{array}\end{array}$$

The last inequality is due to $A^{\top }\in \mathcal{M}(\alpha ,\eta ,M_d)$, by Lemma 2, with probability no small than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$ that,

$$||\widehat{\tilde{G}}{A}^{\top }-\widehat{G}{||}_{\infty }\le (1+M_d)d\sqrt{\frac{8Tlogn}{n}}=\tilde{\lambda }.$$

A is feasible in the optimization equation, by checking the Equation (17), we have $||\widehat{A}||\le ∥A∥$ with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$.

Next, we prove Equation (20). Let $A^{\top }={\tilde{G}}^{-1}G$, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}||{\widehat{A}}^{\top }-A^{\top }{||}_{\infty }\hfill & =\hfill & ||{\widehat{A}}^{\top }-{\tilde{G}}^{-1}{G||}_{\infty }\hfill \\ & =\hfill & ||{\tilde{G}}^{-1}(\tilde{G}{\widehat{A}}^{\top }-G){||}_{\infty }\hfill \\ & =\hfill & ||{\tilde{G}}^{-1}(\tilde{G}{\widehat{A}}^{\top }-\widehat{\tilde{G}}{\widehat{A}}^{\top }+\widehat{G}-G+\widehat{\tilde{G}}{\widehat{A}}^{\top }-\widehat{G}){||}_{\infty }\hfill \\ & \le \hfill & ||{\tilde{G}}^{-1}{||}_1(||\tilde{G}-\widehat{\tilde{G}}{||}_{\infty }||{\widehat{A}}^{\top }{||}_1+||\widehat{G}{-G||}_{\infty }+||\widehat{\tilde{G}}{\widehat{A}}^{\top }-\widehat{G}{)||}_{\infty })\hfill \\ & \le \hfill & 2\tilde{\lambda }{||{\tilde{G}}^{-1}||}_1\hfill \end{array}\end{array}$$

with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$.

Let ${\lambda }_1\ge 0$ and $S_j=\{m:|A_{jm}|\ge {\lambda }_1\},j=1,\cdots ,d$. Define

$$\tilde{D}\left({\lambda }_1\right)=\underset{j\le d}{max}\sum _{j=1}^{d}min\left\{|A_{jm}^{\top }|\wedge {\lambda }_1,1\right\}.$$

Then, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}||{({\widehat{A}}^{\top }-A^{\top })}_{j*}{||}_1\hfill & \le \hfill & ||{\widehat{A}}_{j,S_j^c}^{\top }{||}_1+||A_{j,S_j^c}^{\top }{||}_1+{||{({\widehat{A}}^{\top }-A^{\top })}_{j,S_j}||}_1\hfill \\ & =\hfill & ||A_{j*}^{\top }{||}_1-||{\widehat{A}}_{j,S_j}^{\top }{||}_1+||A_{j,S_j^c}^{\top }{||}_1+{||{({\widehat{A}}^{\top }-A^{\top })}_{j,S_j}||}_1\hfill \\ & \le \hfill & 2||A_{j,S_j^c}^{\top }{||}_1+2{||{({\widehat{A}}^{\top }-A^{\top })}_{j,S_j}||}_1\hfill \\ & \le \hfill & 2||A_{j,S_j^c}^{\top }{||}_1+2||{\widehat{A}}^{\top }-A^{\top }{||}_{\infty }·|S_j|\hfill \\ & \le \hfill & 2\tilde{D}\left({\lambda }_1\right)({\lambda }_1+2\tilde{\lambda }||{\tilde{G}}^{-1}{||}_1).\hfill \end{array}\end{array}$$

Suppose ${max}_j{\sum }_{i=1}^d{\left|{\left(A^{\top }\right)}_{ij}\right|}^{\alpha }\le \eta$ and setting ${\lambda }_1=2\tilde{\lambda }{||{\tilde{G}}^{-1}||}_1,$ we have

$${\lambda }_1{S}_j=\underset{1\le j\le d}{max}\sum _{i=1}^{d}min\left\{\left|{\left(A\right)}_{ij}\right|,{\lambda }_1\right\}\le {\lambda }_1\underset{1\le j\le d}{max}\sum _{i=1}^{d}min\left\{{\left|{\left(A\right)}_{ij}\right|}^{\alpha }/{\lambda }_1^{\alpha },1\right\}\le {\lambda }_1^{1-\alpha }\eta .$$

Therefore, we have

$$||{({\widehat{A}}^{\top }-A^{\top })}_{j*}{||}_1\le 4{\lambda }_1\tilde{D}\left({\lambda }_1\right)\le 4\eta {\lambda }_1^{1-\alpha }=4\eta (2\tilde{\lambda }||{\tilde{G}}^{-1}{{||}_1)}^{1-\alpha }.$$

Since the above equation holds for any $j=1,\cdots ,d$, we complete the proof.

□

4. Granger Causality

In this section, the practical example is conducted to verify the effectiveness of the proposed methods, moreover, the characterization and estimation of Granger causality under the heavy-tailed PVAR model are discussed. Firstly, we give the definition of Granger causality.

Definition 1.(Granger [22]) Let $\left\{X_t\right\}\in \mathbb{Z}$ be a stationary process, where $X_t={\left(X_{t1},\dots ,X_{td}\right)}^T$. For $j\ne k\in \{1,\dots ,d\},$ ${\left\{X_{tk}\right\}}_{t\in \mathbb{Z}}$ Granger causes ${\left\{X_{tj}\right\}}_{t\in \mathbb{Z}}$ if and only if there exists a measurable set A such that

$$\mathbb{P}\left(X_{(t+1)j}\in A\mid {\left\{X_s\right\}}_{s\le t}\right)\ne \mathbb{P}\left(X_{(t+1)j}\in A\mid {\left\{X_{s,\backslash k}\right\}}_{s\le t}\right)$$

for all $t\in \mathbb{Z},$ where $X_{s,\backslash k}$ is the subvector obtained by removing $X_{sk}$ from $X_s$

For a Gaussian VAR process ${\left\{X_t\right\}}_{t\in \mathbb{Z}},$ we have that ${\left\{X_{tk}\right\}}_{t\in \mathbb{Z}}$ Granger causes ${\left\{X_{tj}\right\}}_{t\in \mathbb{Z}}$ if and only if the $(j,k)$ entry of the transition matrix is non-zero [4]. For the heavy-tailed PVAR process, let ${\left\{X_k\right\}}_{k\in \mathbb{Z}}$ be a stationary PVAR process from Equation (2), we define

$${\check{X}}_t=\frac{1}{n}\sum _{k=1}^n{X}_{tk},{\check{E}}_t=\frac{1}{n}\sum _{k=1}^n{E}_{tk},1\le t\le T.$$

In the next theorem, we show that a similar property holds for the heavy-tailed PVAR process.

Theorem 2.

Let ${\left\{X_k\right\}}_{k\in \mathbb{Z}}$ be a stationary PVAR process from Equation (2). Suppose that Assumptions (A1)–(A3) are satisfied, and $\mathrm{Gcov}{\left({\check{X}}_{ti},{\check{X}}_{si}\mid {\check{X}}_{s,\backslash t}\right)}_{s\le t}\ne 0$ for any $i\in \{1,\dots ,d\}.$ Then, for $j\ne i\in \{1,$ $\dots ,d\},$ we have

1. 

If $A_{ji}\ne 0,$ then ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ Granger causes ${\left\{{\check{X}}_{tj}\right\}}_{t\in \mathbb{Z}}$.

2. 

If we further assume that ${\check{E}}_{t+1}$ is independent of ${\left\{{\check{X}}_s\right\}}_{s\le t}$ for any $t\in \mathbb{Z},$ we have that ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ Granger causes ${\left\{{\check{X}}_{tj}\right\}}_{t\in \mathbb{Z}}$ if and only if $A_{ji}\ne 0$.

Proof. 

In order to prove Issue $1,$ we only need to prove that ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ doesn’t Granger cause ${\left\{{\check{X}}_{tj}\right\}}_{t\in \mathbb{Z}}$ implies $A_{ji}=0.$ Suppose for some $t\in \mathbb{Z},$ we have

$$\mathbb{P}\left({\check{X}}_{(t+1)j}\in A\mid {\left\{{\check{X}}_s\right\}}_{s⩽t}\right)=\mathbb{P}\left({\check{X}}_{(t+1)j}\in A\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)$$

for any measurable set A. The above equation implies that conditioning on ${\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}$, ${\check{X}}_{(t+1)j}$ is independent of ${\left\{{\check{X}}_{sj}\right\}}_{s⩽t}.$ Hence, we have

$$\mathrm{Gcov}\left({\check{X}}_{(t+1)j},{\check{X}}_{ti}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)=0.$$

Plugging ${\check{X}}_{(t+1)j}={\sum }_{i=1}^d{A}_{ji}{\check{X}}_{ti}+{\check{E}}_{(t+1)j}$ into the above equation, we have

$$\begin{array}{c}\hfill 0=\mathrm{Gcov}\left(A_{ji}{\check{X}}_{ti},{\check{X}}_{ti}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)+\\ \hfill \mathrm{Gcov}\left(\sum _{i\ne j}{A}_{ji}{\check{X}}_{ti},{\check{X}}_{tj}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)+\\ \hfill \mathrm{Gcov}\left({\check{E}}_{(t+1)j},{\check{X}}_{ti}\mid {\left\{{\check{X}}_{s,i}\right\}}_{s⩽t}\right).\end{array}$$

The second term on the right hand side is $0,$ since given ${\left\{{\check{X}}_{si}\right\}}_{s⩽t},{\sum }_{i\ne j}{A}_{ji}{\check{X}}_{ti}$ is constant. Since ${\check{E}}_{tk}$ and ${\left({\check{X}}_s\right)}_{s<t}$ are independent for any $t\in \mathbb{Z}$, we have $\mathrm{Gcov}\left({\check{E}}_{(t+1)j},{\check{X}}_{si}\right)=0$ for any $s⩽t$. Using Theorem 2.18 in Fang et al. [23], we have the third term is also $0.$ Thus, we have $\mathrm{Gcov}\left({\check{X}}_{ti},{\check{X}}_{ti}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)=0$ and hence $A_{ji}=0.$ This proves Issue 1.

Given Issue $1,$ to prove Issue $2,$ it remains to prove that $A_{ji}=0$ implies that ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ doesn’t Granger cause ${\left\{{\check{X}}_{tj}\right\}}_{t\in \mathbb{Z}}.$ Since $A_{ji}=0,$ we have

$$\begin{array}{cc}\hfill & p\left({\check{X}}_{(t+1)j},{\left\{{\check{X}}_{si}\right\}}_{s⩽t}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)\hfill \\ \hfill =& p\left({\check{X}}_{(t+1)j}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)p\left({\left\{{\check{X}}_{si}\right\}}_{s⩽t}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right).\hfill \end{array}$$

(22)

Here p is the conditional probability density function. The last equation is because $E_{t+1k}$ is independent of ${\left\{{\check{X}}_s\right\}}_{s⩽t},$ and the fact that ${\sum }_{i\ne k}{A}_{ji}{\check{X}}_{ti}$ is constant given ${\left\{{\check{X}}_s\backslash i\right\}}_{s\le t}.$ Hence, we have

$$\begin{array}{cc}\hfill & p\left({\check{X}}_{(t+1)j},{\left\{{\check{X}}_{si}\right\}}_{s⩽t}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)\hfill \\ \hfill =& p\left({\check{X}}_{(t+1)j}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)p\left({\left\{{\check{X}}_{si}\right\}}_{s⩽t}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right)\hfill \end{array}$$

(23)

and thus

$$p\left({\check{X}}_{(t+1)j}\mid {\left\{{\check{X}}_s\right\}}_{s⩽t}\right)=p\left({\check{X}}_{(t+1)j}\mid {\left\{{\check{X}}_{s,\backslash i}\right\}}_{s⩽t}\right).$$

□

Remark 1.

The assumption that $\mathrm{Gcov}{\left({\check{X}}_{ti},{\check{X}}_{s\backslash i}\mid {\check{X}}_{s,\backslash i}\right)}_{s\le t}\ne 0$ requires that ${\check{X}}_{ti}$ cannot be perfectly predictable from the past or from the other observed random variables at time t. Otherwise, we can simply remove ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ from the process ${\left\{{\check{X}}_t\right\}}_{t\in \mathbb{Z}},$ since predicting ${\left\{{\check{X}}_{ti}\right\}}_{t\in \mathbb{Z}}$ is trivial. Assuming that ${\check{E}}_{t+1}$ is independent of ${\left\{{\check{X}}_s\right\}}_{s\le t}$ for any $t\in \mathbb{Z},$ the Granger causality relations among the processes $\left\{{\left\{{\check{X}}_{jt}\right\}}_{t\in \mathbb{Z}}:j=1,\dots ,d\right\}$ is characterized by the non-zero entries of $A.$ To estimate the Granger causality relations, we define $\tilde{A}=\left[{\tilde{A}}_{ji}\right],$ where

$${\tilde{A}}_{ji}:={\widehat{A}}_{ji}I\left(\left|{\widehat{A}}_{ji}\right|\ge \gamma \right)$$

for some threshold parameter γ. To evaluate the consistency between $\tilde{A}$ and A regarding sparsity pattern, we define function $sign\left(x\right):=I(x>0)-I(x<0)$. For a matrix M, define $sign\left(M\right):=\left[sign\left(M_{ji}\right)\right]$. The next theorem gives the rate of γ such that $\tilde{A}$ recovers the sparsity pattern of A with high probability.

Theorem 3.

Let ${\left\{X_k\right\}}_{k\in \mathbb{Z}}$ be a stationary PVAR process from Equation (2). Suppose that Assumptions 1–3 are satisfied. The transition matrix $A^{\top }\in \mathcal{M}(\alpha ,\eta ,M_d)$, if we set

$$\gamma =2\tilde{\lambda }{||{\left(\tilde{G}\right)}^{-1}||}_1,$$

(24)

then, with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$, we have $sign\left(\tilde{A}\right)=sign\left(A\right),$ provided that

$$\underset{\left\{(j,i):A_{ji}>0\right\}}{min}\left|A_{ji}\right|\ge 2\gamma .$$

(25)

Proof. 

The proof is a consequence of Theorem 1. In detail, if $A_{ji}>0,$ by Equation (25), we have $A_{ji}⩾2\gamma .$ By Theorem 1, with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$, we have $\left|{\widehat{A}}_{ji}-A_{ji}\right|⩽\gamma$. Thus, we have ${\widehat{A}}_{ji}⩾\gamma$ with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$. By the definition of A, we have ${\tilde{A}}_{ji}={\widehat{A}}_{ji}⩾\gamma >0$.

If $A_{ji}<0,$ by Equation (25), we have $A_{ji}⩽-2\gamma .$ Using Theorem 1, we have ${\widehat{A}}_{ji}⩽-\gamma$ with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$, By the definition of $\tilde{A},$ we have ${\tilde{A}}_{ji}={\widehat{A}}_{ji}⩽-\gamma <0$.

If $A_{ji}=0$, using Theorem 1, we have ${\widehat{A}}_{ji}<\gamma$ with probability no smaller than $1-(\frac{8\mathrm{\Delta }logn}{T}+\frac{2d^2}{n^2})$, since $\mathbb{P}\left({\widehat{A}}_{ji}=\gamma \right)=$ 0. By the definition of $\tilde{A},$ we have ${\tilde{A}}_{ji}=0$.

□

5. Experiments

This section provides some numerical results on synthetic and real data. We consider Lasso and Dantzig selector for comparison.

• Lasso: an $l_1$ regularized estimator defined as

  $$\widehat{A}=\underset{M\in {\mathbb{R}}^{d\times d}}{argmin\frac{1}{n}{\sum }_{k=1}^n}{||Y_k-M{X}_k||}_F^2+\rho \sum _{ij}{M}_{ij},$$

  where $Y_k:=\left(X_{1k},\dots ,X_{(T-1)k}\right)\in {\mathbb{R}}^{d\times (T-1)}$, $X_k:=\left(X_{2k},\dots ,X_{Tk}\right)\in {\mathbb{R}}^{d\times (T-1)}$.
• Dantzig selector: the estimator proposed in [12],

  $$\widehat{A}=\underset{M\in R^{d\times d}}{argmin}\sum _{jk}|M_{jk}|\mathrm{s}.\mathrm{t}.\frac{1}{n}\sum _{k=1}^n{||S_{k}M-S_{1k}^{\top }||}_{max}\le \lambda ,$$
  $S_k$ and $S_{1k}$ be the marginal and lag one sample covariance matrices of Equation (2).
• G-Dantzig selector: the estimator described in Equation (17).

5.1. Synthetic Data

In this subsection, we compare the performance of our method with the lasso and Dantzig under synthetic data. The “flare” package in R is used to create the transition matrix according to three patterns: cluster, hub, random. We rescale A such that ${||A||}_2=0.8$, generate $\mathrm{\Sigma }$ such that ${||\mathrm{\Sigma }||}_2=2{||A||}_2$, then calculate the covariance matrix $\mathrm{\Psi }$ of the noise vector $E_t$ as $\mathrm{\Psi }=\mathrm{\Sigma }-A^T\mathrm{\Sigma }A$. Let the periodical time series length $n=2000$, the period length $T=100$ and the dimension $d=150$, with $A,\mathrm{\Sigma }$ and $\mathrm{\Psi }$, we simulate periodical time series according to the model described in Equation (2). Specifically, we consider three models:

• Model 1: Data generated from Equation (2), where the errors $E_t\sim N(0,\mathrm{\Psi })$. There is no outliers under Model 1.
• Model 2: Data generated from Equation (2), where the errors $E_t\sim t(0,\mathrm{\Psi },2)$. No outliers appear and the tail of the error distribution is heavier than that of the normal distribution.
• Model 3: Data generated from Equation (2) with the same error distribution as Model 1. Then replace $X_i$ by $X_i+{(-1)}^{I(U_1<1/2)}(20+10U_2)I$ for $i=1,...,T/5$, where $U_1$ and $U_2$ are independently generated from $U[0,1]$ distribution, there are $T/5$ outliers that deviate from the majority of the observations.

The tuning parameter $\lambda$ is chosen by cross validation. We construct 20,000 replicates and compare the three methods described above. Table 1 presents averaged estimation errors under three matrix norms. From this table, we have the following findings: Under the Gaussian model (Model 1), G-Dantzig selector has comparable performance as Dantzig selector and out performs Lasso. Under Model 2 and 3, our methods are more stable than Lasso and Dantzig selector. Thus, we conclude that the G-Dantzig selector is robust to the heavy-tailedness of data and the possible presence of outliers.

Table 1. Comparison of estimation errors of three methods under different setups. The standard deviations are shown in parentheses. Here $L_1$, $L_{\infty }$, $L_F$ are the $L_1$, $L_{\infty }$ and Frobenius matrix norms respectively.

		Lasso			Dantzig			Our Method
		${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\infty }$	${\mathit{L}}_{\mathit{F}}$	${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\infty }$	${\mathit{L}}_{\mathit{F}}$	${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\infty }$	${\mathit{L}}_{\mathit{F}}$
Model 1	$cluster$	1.13	1.62	1.67	1.03	1.55	1.58	1.23	1.74	1.79
		(0.17)	(0.16)	(0.55)	(0.16)	(0.07)	(0.03)	(0.27)	(0.37)	(0.43)
	$hub$	1.37	2.16	2.39	1.18	1.25	1.36	1.09	1.17	1.28
		(0.34)	(0.45)	(0.22)	(0.17)	(0.07)	(0.08)	(0.46)	(0.28)	(0.09)
	$random$	1.41	2.58	2.18	0.97	1.08	1.75	1.46	1.17	1.95
		(0.43)	(0.67)	(0.17)	(0.36)	(0.73)	(0.18)	(0.13)	(0.25)	(0.15)
Model 2	$cluster$	1.25	1.76	1.79	1.13	1.64	1.77	0.95	0.96	1.18
		(0.64)	(0.45)	(0.37)	(0.21)	(0.36)	(0.27)	(0.38)	(0.46)	(0.47)
	$hub$	1.51	2.76	1.58	1.58	1.64	1.78	1.18	1.59	1.09
		(0.41)	(0.56)	(0.14)	(0.19)	(0.43)	(0.54)	(0.85)	(1.12)	(0.93)
	$random$	1.36	2.24	2.17	1.24	1.45	1.85	1.13	1.06	1.07
		(0.32)	(0.17)	(0.17)	(0.29)	(0.15)	(0.09)	(0.22)	(0.19)	(0.27)
Model 3	$cluster$	1.54	2.13	1.96	1.12	1.32	1.71	1.05	1.29	1.59
		(0.29)	(0.13)	(0.18)	(0.25)	(0.46)	(0.52)	(0.17)	(0.19)	(0.19)
	$hub$	1.52	2.67	1.41	1.45	1.91	1.45	1.11	1.29	1.31
		(0.26)	(0.18)	(0.16)	(0.07)	(0.09)	(0.12)	(0.24)	(0.06)	(0.09)
	$random$	1.78	2.56	2.21	1.66	1.34	2.15	1.03	1.23	1.76
		(0.22)	(0.26)	(0.54)	(0.18)	(0.09)	(0.12)	(0.11)	(0.18)	(0.06)

Figure 1 plots the prediction errors against sparsity for the three transition matrix estimators. We observe that G-Dantzig selector achieves smaller prediction errors compared to Lasso and Dantzig selector.

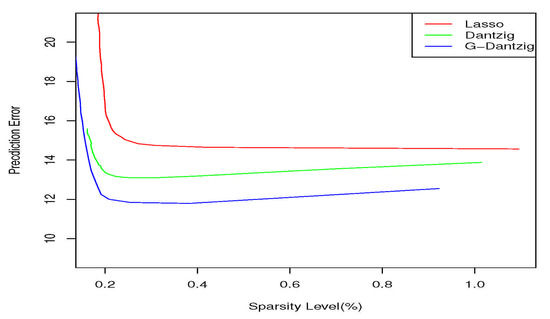
Figure 1. Prediction errors in stock prices plotted against the sparsity of the estimated transition matrix.

5.2. Real Data

We further compared the three methods on a real equity data from Yahoo Finance. We collected the 10-minutes time intervals price in Monday of each week for 50 stocks with the highest volatility that were consistently in the $S\&P$ 500 index from 1 January 2008 to 31 December 2020. Then, the periodical time series length was $n=672$, the period length was $T=36$ and the dimension was $d=50$. Since we chose the data points on the Monday of each week, the data points can be seen as independent of each other. Estimations of the transition matrix ${\widehat{A}}_s$ were obtained by the Lasso, Dantzig selector and G-Dantzig selector, where $s\in [0,1]$ is the fraction of non-zero entries of ${\widehat{A}}_s$ and can be controled by the tuning parameters $\lambda$ and $\rho$. We define the prediction error associated with ${\widehat{A}}_s$ to be

$${ϵ}_s:=\frac{1}{n}\sum _{k=1}^n\left(\frac{1}{T-1}\sum _{t=2}^T{||X_{tk}-{\widehat{A}}_s{X}_{(t-1)k}||}_2\right).$$

6. Conclusions

In this paper, we developed a Gini–Yule–Walker equation for modeling and estimating the heavy-tailedness data and the possible presence of outliers in high dimensions. Our contributions are three-fold. (i) At the model level, we generalized the Gaussian process to time series with the existence of merely second order moments. (ii) Methodologically, we proposed a Gini–Yule–Walker-based estimator of the transition matrix. Experimental results demonstrate that the proposed estimator is robust to heavy-tailedness of data and the possible presence of outliers. (iii) Theoretically, we proved that the adopted method yields a parametric convergence rate in the matrix $l_{\infty }\mathrm{and}{l}_1$ norm. In this manuscript, we focused on the stationary vector autoregressive model and our method is designed for such stationary process. The stationary requirement is a common assumption in analysis and is adopted by most recent works, for example, see and [14,24]. We notice that there are works in handling time-varying PVAR models, checking for example in [25]. We would like to explore this problem in the future.