Abstract
For a simple graph with no isolated vertices, a total Roman {3}-dominating function(TR3DF) on G is a function having the property that (i) if ; (ii) if ; and (iii) every vertex v with has a neighbor u with for every vertex . The weight of a TR3DF f is the sum and the minimum weight of a total Roman {3}-dominating function on G is called the total Roman {3}-domination number denoted by . In this paper, we show that the total Roman {3}-domination problem is NP-complete for planar graphs and chordal bipartite graphs. Finally, we present a linear-time algorithm to compute the value of for trees.
1. Introduction
Let be a graph with vertex set and edge set . For every vertex , the open neighborhood and the closed neighborhood . We denote the degree of v by . A vertex of degree one is called a leaf and its neighbor is a support vertex, and a support vertex is called a strong support if it is adjacent to at least two leaves. Let be a star with order n. A tree T is an acyclic connected graph. is a union graph G such that and .
Given a graph G and a positive integer k, assume that is a function, and suppose that is the ordered partition of V introduced by f, where for . Then we can write and is the weight of a function f of G.
A subset S of a vertex set is a dominating set of G if for every vertex , there exists a vertex such that is an edge of G. The domination number of G denoted by is the smallest cardinality of a dominating set S of G [1]. A function is called a dominating function(DF) on G if every vertex u with has a vertex such that [2]. The dominating set problem(DSP) is to find the domination number of G, which has been deeply and widely studied in recent years [3,4,5,6,7].
A subset S of a vertex set is a total dominating set of G if . The total domination number of G denoted by is the smallest cardinality of a total dominating set S of G [8]. The literature on the subject of total domination in graphs has been surveyed and provided in detail in a recent book [9]. Moreover, Michael A. Henning et al. presented a survey of selected recent results on total domination in graphs [10].
The mathematical concept of Roman domination is originally defined and discussed by Stewart et al. [11] and ReVelle et al. [12]. A Roman dominating function(RDF) on graph G is a function such that every vertex for which is adjacent to at least one vertex u with [13]. The Roman domination number of G is the minimum weight overall s, denoted by [14]. On the basis of Roman domination, signed Roman domination [15], double Roman domination [16] and total Roman domination [17] have been proposed recently.
The total Roman dominating function(TRDF) on G is an RDF f on G with an additional property that every vertex with has a neighbor u with . Let denote the minimum weight of all TRDFs on G. A TRDF on G with weight is called a -function. The conception of TRDF was first defined by Hossein Ahangar et al. [18]. In addition, Nicolás Campanelli et al. studied the total Roman domination number of the lexicographic product of graphs [17] and Chloe Lampman et al. presented some basic results of Edge-Critical Graphs [19].
The Roman -dominating function (also named Italian domination) f [20] introduced by Chellali et al. which is defined as follows: has the property that for [21]. Chellali et al. proved that the Roman -domination problem is NP-complete for bipartite graphs [21]. Hangdi Chen showed that the Roman -domination problem is NP-complete for split graphs, and gave a linear-time algorithm for finding the minimum weight of Roman -dominating function in block graphs [22]. As a generalization of Roman domination, Michael A. Henning et al. studied the relationship between Roman -domination and dominating set parameters in trees [20].
A Roman -dominating function(R{3}DF) f defined by Mojdeh et al. [23], which is defined as follows: has the property that for every vertex with and . Mojdeh et al. presented an upper bound on the Roman -domination number of a connected graph G, characterized the graphs attaining upper bound and showed that the Roman -domination problem is NP-complete, even restricted to bipartite graphs [23].
The total Roman -domination [24] was studied recently. The total Roman -dominating function(TR3DF) on a graph G is an R{3}DF on G with the additional property that every vertex with has a neighbor w with . The minimum weight of a total Roman -dominating function on G denoted by is named the total Roman -domination number of G. A -function is a total Roman -dominating function on G with weight . Doost Ali Mojdeh et al. showed the relationship among total Roman -domination, total domination, and total Roman-domination parameters. They also presented an upper bound on the total Roman -domination number of a connected graph G and characterized the graphs arriving this bound. Finally, they investigated that total Roman -domination problem is NP-complete for bipartite graphs [24].
In this paper, we further investigate the complexity of total Roman -domination in planar graphs and chordal bipartite graphs. Moreover, we give a linear-time algorithm to compute the for trees which answer the problem that it is possible to construct a polynomial algorithm for computing the number of total Roman -domination for trees [24].
2. Complexity
In this section, we study the complexity of total Roman {3}-domination of graph. We show that the total Roman {3}-domination problem is NP-complete for planar graphs and chordal bipartite graphs. Consider the following decision problem.
- Total Roman {3}-Domination Problem TR3DP.Instance: Graph , and a positive integer m.Question: Does G have a total Roman {3}-function with weight at most m?
Please note that the dominating set problem is NP-complete for planar graphs [25] and chordal bipartite graphs [26]. We show the NP-completeness results by reducing the well-known NP-complete problem, dominating set, to TR3D.
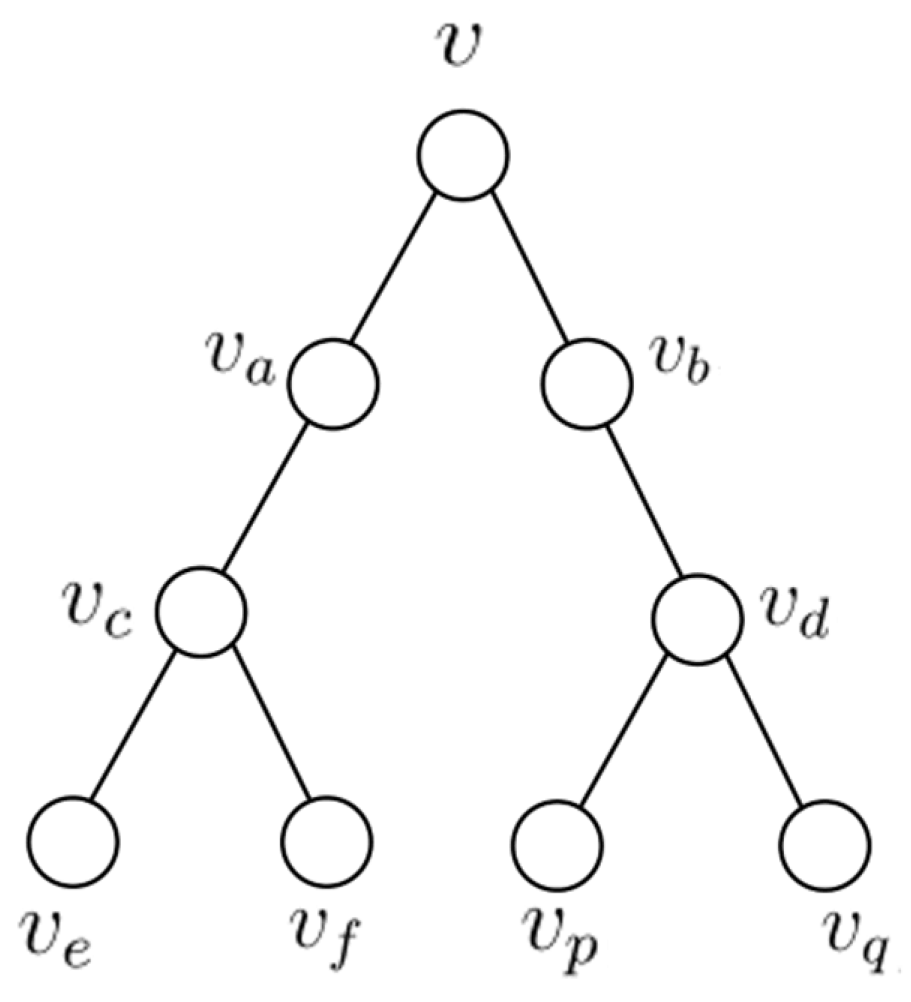
Let G be a graph on n vertices. Let be the tree with , , as depicted in Figure 1.
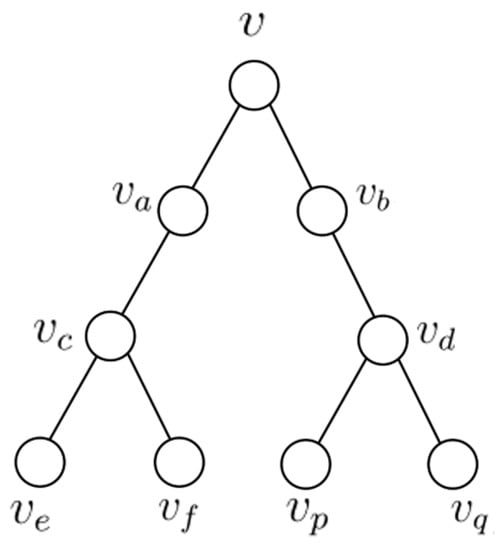
Figure 1.
The tree .
Let be the graph obtained by adding edges between and if from the union of the trees for . Please note that and .
Lemma 1.
If G is a planar graph or chordal bipartite graph, so is .
Lemma 2.
([24]) Let be a star with , then .
Lemma 3.
Let g be a TR3DF of G. If v is a strong support vertex of G, then .
Proof of Lemma 3.
Let be leaves of v with . Since for , we have for . Then . If , it is clear that . If , there exists a vertex with . Then . □
Lemma 4.
If f is a of G with , then there exists a g of with .
Proof of Lemma 4.
For each , we define g as follows: , , , , otherwise. It is clear that g is a of . Therefore we have that . □
Claim 1.
Let g be a of , then .
Proof of Claim 1.
By Lemmas 2, 3 and definition, we have that and . Since , then we can reduce . □
Claim 2.
If there exists a h of with for , then there exists a g of such that and .
Proof of Claim 2.
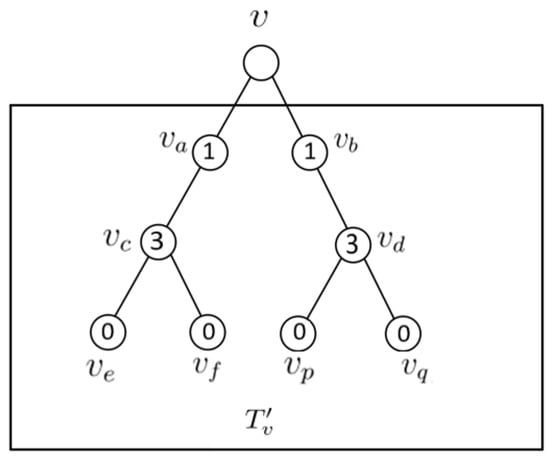
By the definition of , we have and , then we have .
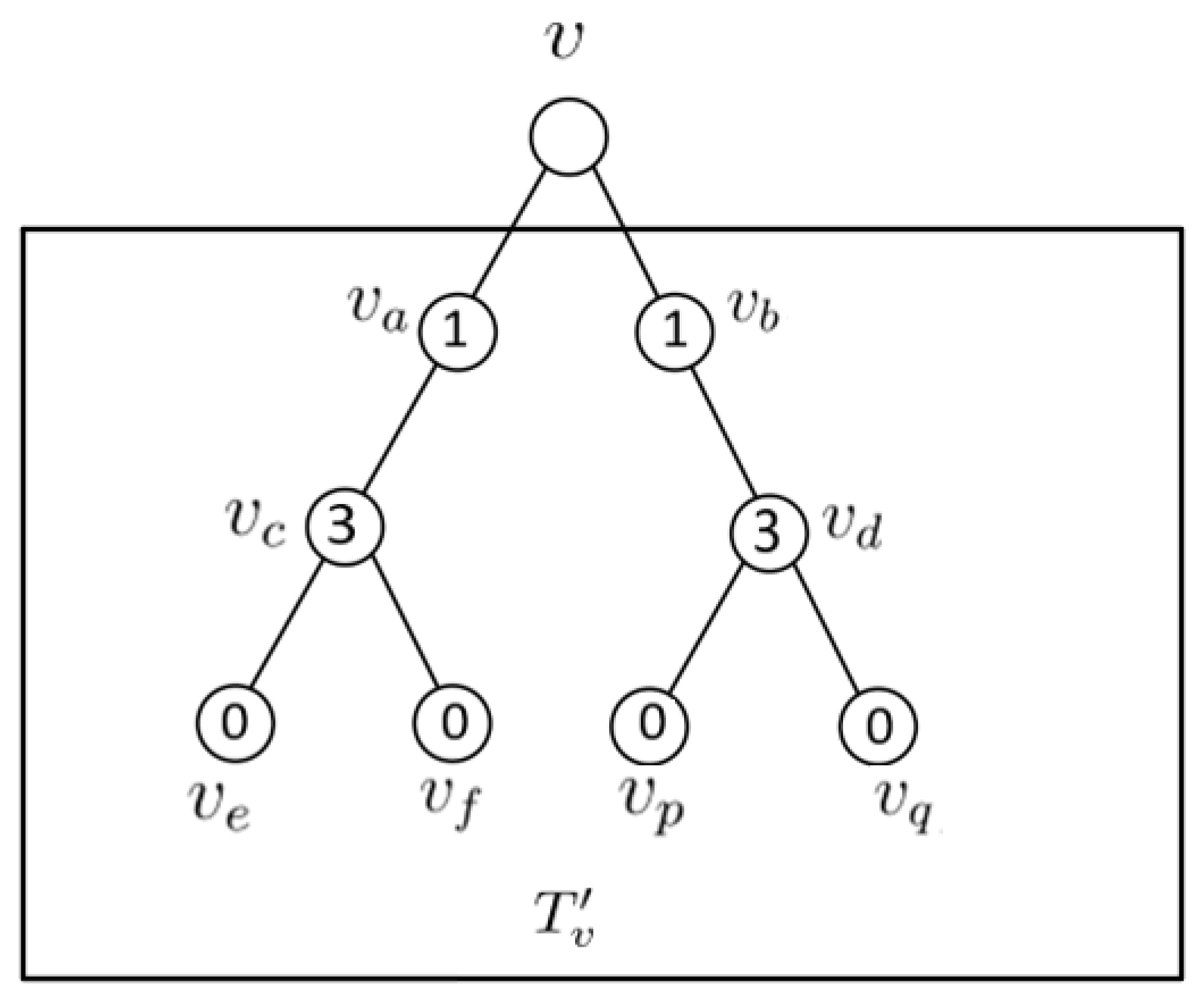
If , then we define such that , , , otherwise, seeing Figure 2. Therefore g is a of such that and .

Figure 2.
Pre-labeling of g.
If , then we define such that , , , otherwise. Therefore g is a of such that and . □
Lemma 5.
If g is a of G with , then there exists a f of G with .
Proof of Lemma 5.
By Claim 2, w.l.o.g, let g be a of with for , . Define such that if , and if . For each vertex , since , we have or there exists a vertex such that . Therefore f is of G and by Claim 1. □
Theorem 1.
By Lemmas 1, 4, 5, the total Roman {3}-domination problem is NP-complete for planar graphs and chordal bipartite graphs.
3. A Linear-Time Algorithm for Total Roman {3}-Domination in Trees
In this section, we present a linear-time algorithm to compute the minimum weight of total Roman -dominating function for trees. First, we define the following concepts:
Definition 1.
Let u be a vertex of G, and let on G be a function having the property that (i) , ; (ii) , if and if .
Definition 2.
The minimum weight overall functions on G denoted by is the number of G, and a -function is an function on G with weight .
Definition 3.
Let be a function defined as follows: =
Lemma 6.
For any graph G with specific vertex u, we have
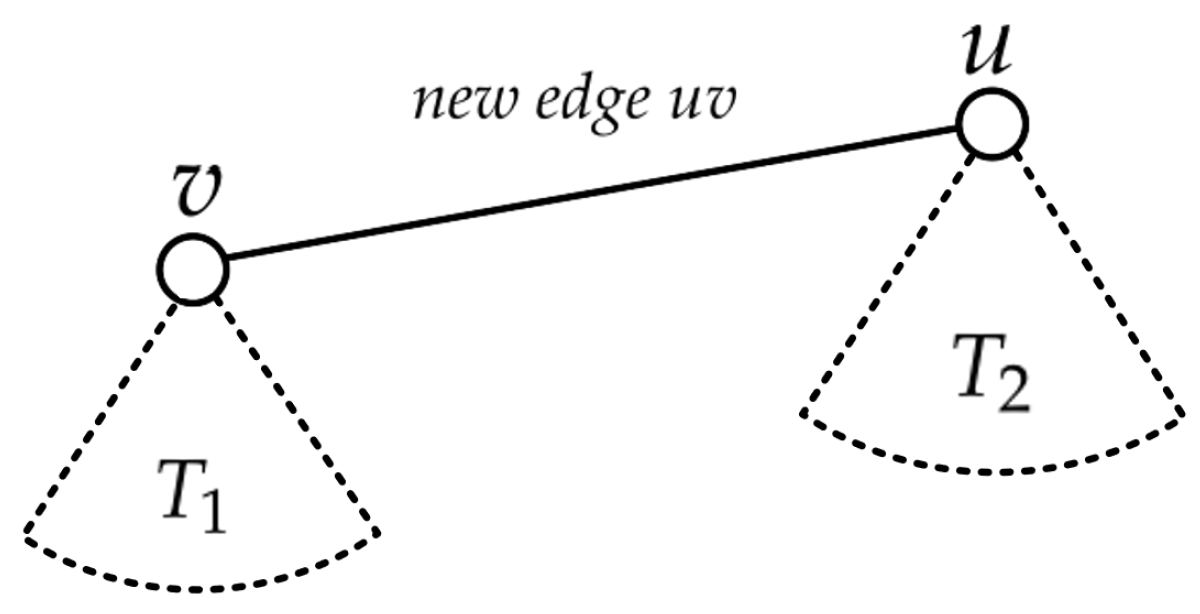
Lemma 7.
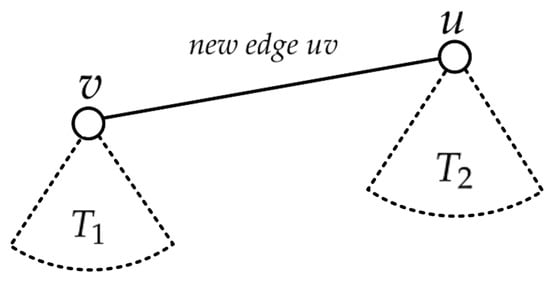
Suppose and are trees with specific vertices v and u, respectively. Let be the tree with the specific vertex u, which is obtained by joining a new edge from the union of and , as depicted in Figure 3.

Figure 3.
.
Then the following statements hold for .
For , , we have:
For , , we have:
Proof of Lemma 7.
Let , , f be a -function of , be the restriction of f on and be the restriction of f on .
(a) If f is a -function on , for . By the definition of -function, we have that if , then . It follows from the fact that f is a -function of if and only if , where at least one of followings holds: (i) is a -function of , is a -function of ; (ii) is a -function of , is a -function of , for .
(b) It follows from the fact that f is a -function of , for , if and only if f = , where is a -function of and is a -function of , for . □
Lemmas 6 and 7 give the following dynamic programming algorithm 1 for the total Roman -domination problem in trees.
| Algorithm 1 Counting in trees. |
 |
4. Conclusions
The total Roman {3}-domination problem was introduced and studied in [24], and it was proven to be NP-complete for bipartite graphs. In this paper, we prove that the total Roman {3}-domination problem is NP-complete for planar graphs or chordal bipartite graphs, and showed a linear-time algorithm for total Roman {3}-domination problem on trees. For the algorithmic aspects of the total Roman {3}-domination problem, designing exact algorithms or approximation algorithms on general graphs, or polynomial algorithms for total Roman {3}-domination problem on some special classes graphs deserve further research.
Author Contributions
Conceptualization, X.L., H.J. and Z.S.; writing, X.L. and Z.S.; review, H.J. and Z.S.; investigation: P.W. All authors have contributed equally to this work. All authors have read and agreed to the possible publication of the manuscript.
Funding
This work is supported by the Natural Science Foundation of Guangdong Province under Grant 2018A0303130115.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DF | Dominating function |
| DSP | Dominating set problem |
| TRDF | Total Roman dominating function |
| R3DF | Roman -domination |
| TR3DF | Total Roman -domination |
References
- Mojdeh, D.A.; Firoozi, P.; Hasni, R. On Connected (γ, k)-critical Graphs. Australas. J. Comb. 2010, 46, 25–36. [Google Scholar]
- Thulasiraman, K.; Swamy, M.N.S. Graphs: Theory and Algorithms; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Stojmenovic, I.; Seddigh, M.; Zunic, J. Dominating Sets and Neighbor Elimination-Based Broadcasting Algorithms in Wireless Networks. IEEE Trans. Parallel Distrib. Syst. 2002, 13, 14–25. [Google Scholar] [CrossRef]
- Haynes, T.W.; Henning, M.A. Domination in Graphs; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Lund, C.; Yannakakis, M. On the Hardness of Approximating Minimization Problems. J. ACM 1994, 41, 960–981. [Google Scholar] [CrossRef]
- Kinnersley, W.B.; West, D.B.; Zamani, R. Extremal Problems for Game domination Number. SIAM J. Discret. Math. 2013, 27, 2090–2107. [Google Scholar] [CrossRef]
- Haynes, T.W.; Hedetniemi, S.; Slater, P. Fundamentals of Domination in Graphs; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Cockayne, E.J.; Dawes, R.M.; Hedetniemi, S.T. Total domination in Graphs. Networks 1980, 10, 211–219. [Google Scholar] [CrossRef]
- Henning, M.A.; Yeo, A. Total Domination in Graphs; Springer: Berlin, Germany, 2013. [Google Scholar]
- Henning, M.A. A Survey of Selected Recent Results On Total domination in Graphs. Discret. Math. 2009, 309, 32–63. [Google Scholar] [CrossRef]
- Stewart, I. Defend the Roman Empire. Sci. Am. 1999, 281, 136–138. [Google Scholar] [CrossRef]
- ReVelle, C.S.; Rosing, K.E. Defendens Imperium Romanum*: A Classical Problem in Military Strategy. Am. Math. Mon. 2000, 107, 585–594. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Dreyer, P.A.; Hedetniemi, S.M.; Hedetniemi, S.T. Roman Domination in Graphs. Discret. Math. 2004, 278, 11–22. [Google Scholar] [CrossRef]
- Chambers, E.W.; Kinnersley, B.; Prince, N.; West, D.B. Extremal Problems for Roman Domination. SIAM J. Discret. Math. 2009, 23, 1575–1586. [Google Scholar] [CrossRef]
- Abdollahzadeh, H.A.; Henning, A.M.; Löwenstein, C.; Zhao, Y.; Samodivkin, V. Signed Roman domination in Graphs. J. Comb. Optim. 2014, 27, 241–255. [Google Scholar] [CrossRef]
- Beeler, R.A.; Haynes, T.W.; Hedetniemi, S.T. Double Roman domination. Discret. Appl. Math. 2016, 211, 23–29. [Google Scholar]
- Campanelli, N.; Kuziak, D. Total Roman domination in the Lexicographic Product of Graphs. Discret. Appl. Math. 2019, 263, 88–95. [Google Scholar] [CrossRef]
- Abdollahzadeh, H.A.; Henning, A.M.; Samodivkin, V.; Yero, G.I. Total Roman domination in Graphs. Appl. Anal. Discret. Math. 2016, 10, 501–517. [Google Scholar] [CrossRef]
- Lampman, C.; Mynhardt, K.; Ogden, S. Total Roman domination Edge-Critical Graphs. Involv. J. Math. 2019, 12, 1423–1439. [Google Scholar] [CrossRef]
- Henning, M.A.; Klostermeyer, W.F. Italian Domination in Trees. Discret. Appl. Math. 2017, 217, 557–564. [Google Scholar] [CrossRef]
- Chellali, M.; Haynes, T.W.; Hedetniemi, S.T.; McRae, A.A. Roman {2}-domination. Discret. Appl. Math. 2016, 204, 22–28. [Google Scholar] [CrossRef]
- Chen, H.; Lu, C. A Note on Roman {2}-domination Problem in Graphs. arXiv 2018, arXiv:1804.09338. [Google Scholar]
- Mojdeh, D.A.; Volkmann, L. Roman {3}-domination (Double Italian domination). Discret. Appl. Math. 2020, 283, 555–564. [Google Scholar] [CrossRef]
- Shao, Z.; Mojdeh, D.A.; Volkmann, L. Total Roman {3}-domination in Graphs. Symmetry 2020, 12, 268. [Google Scholar] [CrossRef]
- Zverovich, I.E.; Zverovich, V.E. An Induced Subgraph Characterization of Domination Perfect Graphs. J. Graph Theory 1995, 20, 375–395. [Google Scholar] [CrossRef]
- Müller, H.; Brandstädt, A. The NP-completeness of Steiner Tree and Dominating set for Chordal Bipartite Graphs. Theor. Comput. Sci. 1987, 53, 257–265. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).