A Simple and Effective Approach for Tackling the Permutation Flow Shop Scheduling Problem

Abstract

In this research, a new approach for tackling the permutation flow shop scheduling problem (PFSSP) is proposed. This algorithm is based on the steps of the elitism continuous genetic algorithm improved by two strategies and used the largest rank value (LRV) rule to transform the continuous values into discrete ones for enabling of solving the combinatorial PFSSP. The first strategy is combining the arithmetic crossover with the uniform crossover to give the algorithm a high capability on exploitation in addition to reducing stuck into local minima. The second one is re-initializing an individual selected randomly from the population to increase the exploration for avoiding stuck into local minima. Afterward, those two strategies are combined with the proposed algorithm to produce an improved one known as the improved efficient genetic algorithm (IEGA). To increase the exploitation capability of the IEGA, it is hybridized a local search strategy in a version abbreviated as HIEGA. HIEGA and IEGA are validated on three common benchmarks and compared with a number of well-known robust evolutionary and meta-heuristic algorithms to check their efficacy. The experimental results show that HIEGA and IEGA are competitive with others for the datasets incorporated in the comparison, such as Carlier, Reeves, and Heller.

1. Introduction

Recently, the flow shop scheduling problem (FSSP) has attracted the attention of the researchers for overcoming it due to its importance in industries, such as transportation, procurement, computing designs, information processing, and communication. Because this problem is NP-hard, which finding a solution in polynomial time is to hard, many algorithms in the literature were proposed to overcome this problem. Some of which will be reviewed within the next subsections. Johnson [1] in 1954 introduced and formulated FSSP for the first time. Using a limited range up to a 3-machine problem, Johnson was able to overcome this problem for a restricted case. Afterward, Nawaz et al. [2] proposed a meta-heuristic approach known as Nawaz-Enscore-Ham (NEH) algorithm for tacking this problem with m-machine and n-job.

Due to succeeding achieved by the NEH algorithm, the researchers have been work on improving its performance or integrating it with other optimization algorithms for overcoming this problem [3,4]. Before speaking of the optimization algorithms, we start reviewing the literature which is devoted to the improvement of the standard NEHheuristic method. Kalczynski [5] improved the performance of the NEH algorithm by using a new priority order integrated with a simple tie-breaking method that proved its superiority over all the problem sizes. Additionally, Dong [6] proposed an improvement on the standard NEH heuristic to minimize the makespan. This improvement is summarized as follows: (1) using the priority rule, which integrates the average processing time of jobs and their standard deviations to replace the one in the standard NEH, and (2) using the new tie-breaking strategy to significantly improve the performance of the standard one. Furthermore, Sauvey, and Sauer [3] proposed an improvement on the standard NEH algorithm using two strategies: (1) the first one used the factorial basis decomposition method to ensure testing all the possible orders for the small-scale instances, and allow to randomly choose a particular order of all the possible orders, and (2) the second strategy was based on keeping a list of the best partial sequences, rather than just one.

The evolutionary and meta-heuristic algorithms play a crucial role in solving several problems. According to the significant success achieved by those algorithms, they are extensively used in tackling the FSSP. Zhang et al. [7], presented an improved discrete migrating birds optimization for overcoming the no-wait FSSP (NWFSSP) using the makespan criterion. A decision tree in Govindan et al. [8] is further combined with scatter search (SS) algorithms for solving the permutation FSSP (PFSSP) by reducing the make-span. Furthermore, Liu [9] proposed an efficient hybrid differential evolution with Greedy-based local search and the individual improved scheme for overcoming the permutation PFSSP. In Ding et al. [10], the simulated annealing algorithm was embedded with a block-shifting operation for overcoming NWFSP to reduce the makespan. Sanjeev Kumar [11] proposed an algorithm for overcoming the permutation FSSP based on minimizing the makespan and total flowtime using the modified gravitational emulation local search algorithm. Finally, Reeves [12], proposed a genetic algorithm (GA) for overcoming the FSSP.

Moreover, in Liu et al. [13] the particle swarm optimization (PSO) which rely on the memetic algorithm was suggested for tackling the PFSSP for minimizing the makespan. In [14], the teaching-learning based optimization algorithm integrated with a variable neighborhood search (VNS) for fast solution improvement was suggested for tackling the PFSSP. Zhao et al. [15] developed the discrete water wave optimization algorithm for tackling the NWFSP with respect to maximizing the makespan. A new cuckoo search (CS) [4] combined with the NEH and the smallest position rule(SPR) was proposed for overcoming FSSP. For the open shop scheduling problem, a bat algorithm (BA) [16] improved using ColReuse, and substitution meta-heuristic functions have been proposed. Li [17] proposed a hybrid approach based on PSO for tackling the multi-objective PFSSP. It uses several local search methods to improve the exploitation capability of the algorithm for reaching better outcomes. In [18], a multi-objective approach based on the genetic algorithm and Pareto optimality has been proposed for overcoming the PFSSP. Additionally, Pang et al. [19] solved the PFSSP and the hybrid FSSP using the fireworks algorithm employing three strategies: (1) using a nonlinear radius, in addition to checking the minimum explosion amplitude to avoid the waste of the optimal fireworks, (2) integrating the Cauchy distribution and the Gaussian distribution to replace the original Gaussian distribution for improving the search process, and (3) using the elite group selection strategy to decrease the computing costs. The improved fireworks algorithm (IFWA) was compared with the standard fireworks algorithm and validated on two instances from the PFSSP and the hybrid FSSP. Mishra [20] proposed a discrete version of the Jaya algorithm for tackling the PFSSP with the objective of optimizing the makespan based on two strategies: (1) allocating a random priority to each job in a permutation sequence, and (2) the random priority vector was mapped to job permutation vector using the largest order value (LOV).

In the last few years, quite strong techniques for PFSSP have been proposed, but those techniques still suffer from numerous problems: local minima as a result of lack the solutions diversity, and convergence speed toward the near-optimal solution in less number of function evaluations. Those drawbacks motivate us to propose this work.

The evolutionary algorithms are considered one of the best choice for tackling a combinatorial problem due to its ability on checking several permutations that may contain the best permutation for this combinatorial problem. Although of the high ability of the evolutionary algorithm for solving this type of problems, the need for operators in genetic algorithms to help in improving their performance is still open even today. Therefore, within our research, we study the performance of the elitism based-GA (EGA) when integrating the Arithmetic crossover with the uniform crossover for tackling the PFSSP. Since the arithmetic crossover operator generates continuous values and PFSSP is discrete in nature, the LRV rule will be applied to transform those continuous values into discrete ones. In addition, to increase the exploration rate of EGA and an individual selected randomly form, the population will be re-initialized randomly within the search space of the problem. The incorporation between the uniform crossover and Arithmetic crossover in addition to the re-initialization process is integrated with the EGA to improve its performance when tackling the PFSSP in a version abbreviated as IEGA. Additionally, to improve dramatically the performance of IEGA when tackling PFSSP, it was hybridized with a local search strategy (LSS). In our work, we used a number of well-established optimization algorithms such as slap swarm algorithm (SSA) [21], whale optimization algorithm (WOA) [22], and sine cosine algorithm (SCA) [23] due to their significant success for solving several optimization problems [23,24,25,26,27,28,29]. Additionally, the hybrid whale algorithm (HWA) [30] as the most competitive algorithm for solving the permutation flow shop scheduling are used in our comparison with the proposed to see its strength to tackle this problem as an alternative to the strong existing algorithm. Furthermore, a genetic algorithm based on the uniform crossover (GA), elitism genetic algorithm based on the uniform crossover (EGA), and genetic algorithm based on the order-based crossover (OEGA) are additionally used to see the efficacy of the proposed over some the evolutionary algorithms.

Generally, our contributions within this paper are summarized in the following points:

• Using the continuous values in the approach instead of discrete values, by employing LRV to convert those continuous values into discrete, for tackling PFSSP.
• Combining the uniform crossover and the arithmetic crossover (UAC) to help in increasing the exploitation capability in addition to reducing stuck into local minima.
• Proposing a version of the efficient GA, abbreviated as IEGA, improved by dynamic mutation and crossover probability (DMCP) and UAC for tacking the PFSSP.
• Additionally, IEGA is enhanced by integrating with a LSS and insert-reversed block (IRB) operator for tackling the PFSSP, in a version abbreviated as HIEGA.
• IEGA and HIEGA were tested on the benchmarks Reeves, Carlier, and Heller to check their performance.

The remainder of this paper is structured as: Section 2 illustrates the permutation flow shop scheduling problem; Section 3, introduces the proposed algorithms (IEGA, and HIEGA) and, in particular, Section 3.7 exposes the experiments outcomes, discussion, and comparison between results. Finally, Section 4 shows the conclusions about our proposed work in addition to our future work.

2. The Permutation Flow Shop Scheduling Problem

The permutation FSSP indicates employment n jobs over m machines consecutively and on the same permutation under the criterion of decreasing the make-span. Generally, this problem could be summarized in the following points:

• Each job $j_b$ could be run only one time on each machine. $b=1,2,3,\dots ,n$
• Each machine $i_z$ could address only a job at a time, $z=1,2,3,\dots ,m$
• Each machine will address a job in a time known as the processing time and abbreviated as PT.
• A completion time c is a time needed by each job $j_b$ on a machine $i_z$ and symbolized as $c(j_b,i_z)$.
• The processing time of each job is a phrase about the running time added with the set-up time of the machine.
• At the start, each job takes time of 0.
• PFSSP is solved with the objective of finding the best permutation that will minimize the makespan $c^{\ast }$ that is known as the maximum completion time or until the last job on the final machine was completed.

Mathematically, PFSSP could be modeled as follows:

$$\begin{array}{c}\hfill c(j_1,i_1)=P{T}_{(j_1,i_1)},b=1,z=1,\end{array}$$

(1)

$$\begin{array}{c}\hfill c(j_b,i_1)=c(j_{b-1},i_1)+P{T}_{(j_b,i_1)},b=2,3,\dots ,n.\end{array}$$

(2)

$$\begin{array}{c}\hfill c(j_b,i_z)=c(j_1,i_{z-1})+P{T}_{(j_1,i_z)},z=2,3,\dots ,m.\end{array}$$

(3)

$$\begin{array}{c}\hfill c(j_b,i_z)=max(c(j_{b-1},i_z),c(j_b,i_{z-1}))+P{T}_{(j_b,i_z)},\\ \hfill b=2,3,\dots ,n,z=2,3,\dots ,m.\end{array}$$

(4)

The permutation refers to the different sequences of the jobs on the machine. The objective of FSSP is finding the best permutation that will minimize the maximum completion time (makespan) and defined as follows:

$$c^{\ast }=c(j_b,i_z)$$

(5)

Equation (5) is considered the objective function that will be used to be minimized by our proposed algorithm until the best job permutation is found.

3. The Proposed Algorithm

In this section, the main steps of the proposed algorithm will be discussed in detail. GA is an approach inspired by the Darwinian theory of natural evolutionary [31,32,33]. In GA, a set consisting of N solutions, each one known as individual, will be initialized within the search space of the problem. After distribution, the fitness value for each individual will be calculated and a number of the best individuals will be selected to generate better individuals within the next generation. Specifically, the genetic algorithm depends on three basic operators: selection, crossover, and mutation operators.

3.1. Initialization

At the start, a population consisting of N individuals is generated with n dimension for each job and initialized with distinct random numbers to generate a permutation of the job sequence. After generating the random numbers within each individual, those numbers must be checked to prevent duplication of any number within the same individual. Since the random number generated within the individual is continuous, the need for a method to convert them into a job sequence permutation is necessary. According to the study performed by Li and Yin [34], LRV could effectively map the continuous values into job permutation. In LRV, the continuous value is ranked in decreasing order. Until LRV could generate the job permutation without any mistake, duplication of any value within each individual must be removed. For instance, Figure 1a present a solution with duplicated values, hence, this duplication need to be removed until the LRV could be used to estimate the job permutation. Therefore, this duplication is removed by inserting other values not found in this solution. Finally, this solution is mapped into job permutation by sorting in descending order as shown in Figure 1c; the index of the largest value in the unsorted solution is selected in the first position of the mapped solution, the position of second largest one is inserted into the second position of the mapped solution, and so on. After generating and checking the duplication in each solution, the algorithm must be evaluated to extract its makespan using Equation (5) to measure its quality in solving PFSSP in comparison with the others.

Figure 1. Illustration for a real-value solution.

3.2. Selection Operator

The selection operator specifies the way of selecting the parents that will be used to generate the offspring in the next generation. Recently, many selection operators have been proposed, but within our research, we will use a selection operator known as tournament selection mechanism [35]. In this mechanism, a number K, known as tournament size, will be chosen and the solution with the best fitness will be taken as a parent for the next generation. After selecting the parents using the tournament section operator, the second operator known as the crossover operator will be used to generate the offspring within the next generation.

3.3. Crossover Operator

This operator works on generating the individuals within the next generation under the supervision of the best individual, selected according to the selection operator. Among all the available crossover operators, within our experiment, we selected Uniform crossover [36] and the arithmetic crossover. In the uniform crossover, a binary vector with a length equal to the size of the individuals will be created and initialized by generating a random number within the range 0 and 1 and if this number is smaller than the crossover rate (CR), the current position in this vector is assigned a value of 1. Otherwise, it will take a value of 0. Note that, 0 indicates that the current position of the offspring will be taken from the first parent, while 1 indicates the second individual, and this binary vector, called mask, will be used to generate the first individual. For the second individual, the values within this mask will be flipped to convert 0 into 1 and 1 into 0. Then the second one will be generated. Figure 2a illustrates two offspring, $O_1$ and $O_2$, using two parents, $P_1$ and $P_2$, using uniform crossover. In this figure, at the start, the mask $M_1$ will be initialized with 0 and 1 and its flipping is shown in $M_2$. After that, $O_1$ will be generated according to $M_1$, and $M_2$ will be used to generate $O_2$.

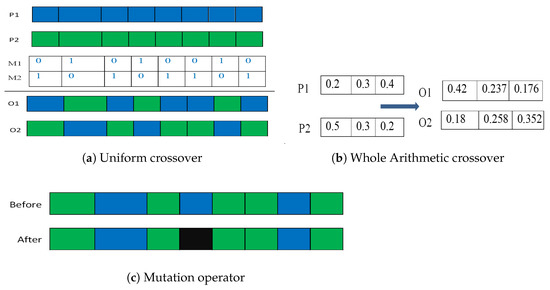
Figure 2. Different genetic operators.

Regarding the Arithmetic crossover, in this operator, the two parents are used to generate two offspring under the following formula:

$$\begin{array}{c}\hfill O_1=\sigma \ast P_1+(1-\sigma )\ast P_2.\end{array}$$

(6)

$$\begin{array}{c}\hfill O_2=\sigma \ast P_2+(1-\sigma )\ast P_1.\end{array}$$

(7)

For example, Figure 2b shows the outcomes of the generated two offspring, $O_1$, and $O_2$, using two parents, $P_1$ and $P_2$, under this crossover operator, assuming $\sigma =0.2$.

3.4. Mutation Operator

In the end, the mutation operator based on a certain probability, known as mutation probability (MR), will be applied to each offspring as an attempt to generate a better solution and preventing stuck into local minima problems. MR is used until the GA is not converted into a primitive random search. Figure 2c shows the influence before using the mutation and after applying mutation.

3.5. Combination of Uniform Crossover and Arithmetic Crossover (UAC)

In this part, we will combine both uniform crossover and the Arithmetic crossover with each other according to the $CRU$, to recombine the two individuals together. The formula of this combination is as follows:

$$O=\nu \ast P+r\ast M,$$

(8)

where O is the generated offspring, P is the first parent selected using tournament selection, M is the second selected parent, r is a random number created to determine the weight of the second in relative to the generated offspring, and $\nu$ is used to determine the weight of P, we recommend $0.8$ as discussed later. In the end, Algorithm 1 shows the steps of the combination of uniform crossover and the arithmetic crossover.

Algorithm 1 Uniform Arithmetic crossover (UAC)

1:  P // is the first parent selected using tournament selection. 2:   3:  M // is the second parent selected using tournament selection. 4:   5:  O; // indicates the offspring. 6:   7:  i=0; 8:   9:  while $i<n$ do 10:   11:   $r_1:isanumberassignedrandomlybetween0and$ 1 12:   13:   if $r_1\le CRU$ then 14:   15:    $O_i=\nu \ast P_i+r\ast M_i$;//(Equation (8)) 16:   17:   else 18:   19:    $O_i=M_i$ 20:   21:   end if 22:   23:   $i++$ 24:   25:  end while 26:   27:  Return O 28:

3.6. Local Search Strategy (LSS)

LSS works on exploring the solutions around the best-so-far solution to find a better one. Each job in the best-so-far individual will be tried in all the positions within this best based on a certain a probability known as LSP (LSP = 0.01 as recommended in [30]) and the permutation that will reduce the makespan in comparison to the original will be taken as the best-so-far one as illustrated in Algorithm 2.

Finally, the UAC with re-initializing selected an individual randomly from the population. This selection promotes the exploration capability for avoiding stuck into local minima, which improves the performance of the EGA to produce a version abbreviated as IEGA. After that, IEGA is integrated with LSS as shown in Algorithm 3 to increase the exploitation capability of the algorithm.

Algorithm 2 LSS

1:  $X^{\ast }$: The best so-far solution 2:   3:  for i = 1 to n do 4:   5:   $X=X^{\ast }$ 6:   7:   for j = 1 to n do 8:   9:    r: random number between 0 and 1 10:   11:    if $r<LSP$ then 12:   13:     $X_j=X_i^{\ast }$ 14:   15:     Applying LRV on X 16:   17:     Calculate the fitness of X. 18:   19:     Update $X^{\ast }$ if X is better. 20:   21:    end if 22:   23:   end for 24:   25:  end for 26:   27:  Return $X^{\ast }$ 28:

Algorithm 3 HIEGA

1:  [Initialization] create a population $x_i$ of N individuals, $i=1,2,3,\dots ,N$. 2:   3:  [Fitness] evaluate each $x_i$. 4:   5:  $t=0$// current iteration. 6:   7:  $t_{max}$//the maximum iteration. 8:   9:  MR// mutation rate 10:   11:  CR// crossover rate. 12:   13:  $X^{\ast }$: The best-so-far solution. 14:   15:  $n{x}_i$ is a new population. 16:   17:  while $(t<t_{max)}$ do 18:   19:   Re-initialize an individual selected randomly from the population. 20:   21:   //Elitism operation 22:   23:   if elitism then 24:   25:    $n{x}_0$: the best-so-far solution, $X^{\ast }$ 26:   27:   end if 28:   29:   ///crossover operation 30:   31:   for $eachi\ge 1in{x}_i$ do 32:   33:    $n{x}_i$= generate a new individual using Algorithm 2 34:   35:   end for 36:   37:   ///mutation operation. 38:   39:   for $eachi\ge 1toN$ do 40:   41:    for j = 1 to n do 42:   43:     $r_2$: Create a random number between 0 and 1. 44:   45:     if $r_2\le MRU$ then 46:   47:      $r_3$: Create a random number between 0 and 1. 48:   49:      $n{x}_{i,j}+=r_3$ 50:   51:     end if 52:   53:    end for 54:   55:   end for 56:   57:   for $eachi\ge 1toN$ do 58:   59:    $x_i=n{x}_i$ 60:   61:    Applying LRV on each individual, $x_i$ 62:   63:    Calculate the fitness of each individual $x_i$. 64:   65:    Update $X^{\ast }$ if there is better. 66:   67:    Applying Algorithm 2 on $x_i$ if it was better than $X^{\ast }$. 68:   69:   end for 70:   71:   $t++$ 72:   73:  end while 74:   75:  Return: $X^{\ast }$ 76:

3.7. Time Complexity

In this subsection, the time complexity of the HIEGA as the proposed algorithm in big-O will be computed to find its speedup for solving the PFSSP. First, lets show the components that will affect the speedup of the algorithm for one generation:

• The first one is the generating process of offspring that need time complexity of $O\left(nN\right)$.
• The second one is LRV which will need time complexity of $O(nlogn)$ [37] for the Quicksort algorithm. And totally for all population, the time complexity with LRV will be $O(Nnlogn)$.
• The last one is the LSS that need $O\left(n^2\right)$ for single individual. For all individual, the time complexity is as $O\left(N{n}^2\right)$.

Finally, after summing the time complexity of the previous three components as shown in Equation (9), it is concluded that the time complexity of the proposed algorithm is $O\left(N{n}^2\right)$

$$T\left(HIEGA\right)=O\left(nN\right)+O(Nnlogn)+O\left(N{n}^2\right)$$

(9)

In this section, three different widely-used well-known datasets will be tested to justify the effectiveness of our proposed approach. Those datasets are: (1) the Carlier dataset [38] with eight instances, (2) the second one was introduced by Reeves [12] and contains 21 instances, only 14 instances of this datasets will be used within our experiments, and (3) the last one is created by Heller [39] and consist of two instances. The data sets used, can be found in http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/flowshop1.txt, and their descriptions are shown in Table 1 that shows the optimal known makespan symbolized as $Z^{\ast }$. According to researches in the literature [30,34,40], the best-known value for each instance is used in our work to be compared with the proposed algorithm outcomes to see its efficacy. Also, in [30,40], the authors could reach less value than the best-known value for Hel1 as mentioned in [34]. Therefore, in our proposed work, we set the value of Hel1 as mentioned in most literature and show to the readers that the proposed could reach less value than the best-known ones.

Table 1. The dataset descriptions.

Carlier, Heller, Reeves Benchmarks
Name	n	m	$Z^{\ast }$	Name	n	m	$Z^{\ast }$
Car01	11	5	7038	Rec05	20	5	1242
Car02	13	4	7166	Rec07	20	10	1566
Car03	12	5	7312	Rec09	20	10	1537
Car04	14	4	8003	Rec11	20	10	1431
Car05	10	6	7720	Rec13	20	15	1930
Car06	8	9	8505	Rec15	20	15	1950
Car07	7	7	6590	Rec17	20	15	1902
Car08	8	8	8366	Rec19	30	10	2017
Hel1	20	10	516	Rec21	30	10	2011
Hel2	100	10	136	Rec37	75	20	4951
Rec01	20	5	1247	Rec39	75	20	5087
Rec03	20	5	1109	Rec41	75	20	4960

The algorithms used in our experiments within this section are coded using java programming language on a device with 32GB of RAM, and Intel(R) Core(TM) i7-4700MQ CPU $@2.40$ GHz. Our proposed approach is experimentally compared with a number of the meta-heuristic and evolutionary algorithms, such as slap swarm algorithm (SSA) [21], whale optimization algorithm (WOA) [22], sine cosine algorithm (SCA) [23], hybrid whale algorithm (HWA) [30], a genetic algorithm dependent on the uniform crossover (GA), elitism GA based on the uniform crossover (EGA), and genetic algorithm based on the order-based crossover (OEGA). The genetic algorithms (GA) have two important parameters: CR and MR that significantly affect their performance. For getting the optimal values for those two parameters, Figure 3b,c are introduced to tell that the best values for them are $0.8$ and $0.02$, respectively. Regarding IEGA, there is another parameter: P that must be accurately picked until getting to the optimality in its performance. After conducting several experiments with different values for P that are shown in Figure 3a, we found that the best value was $0.8$. Regarding the parameters of SCA, SSA, and WOA, they are equal to the ones used in the cited papers. Table 2 introduces the parameters of the other compared algorithms. The maximum iteration and N are set to 100 and 20, respectively, to ensure a fair comparison with the other algorithms. The block size (BS) of the insert-reversed block operation is assigned to 5 as recommended in [30]. All the algorithms were running 30 independent times.

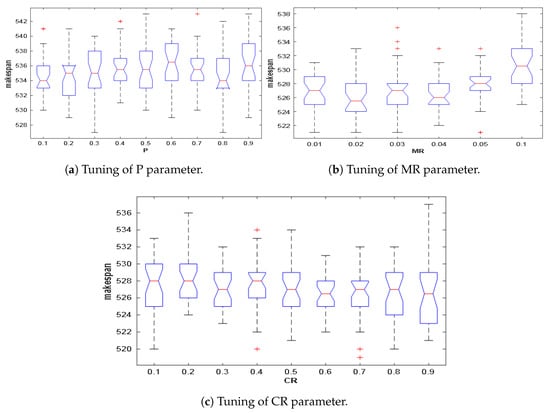
Figure 3. The sensitivity analysis for the genetic parameters introduced.

Table 2. The parameters of the algorithms.

GA, EGA, IEGA, OEGA and IEGA		HWA, HIEGA
CR	0.8	LSP	0.01
MR	0.02	BS P	5 0.8

3.8. Performance Metric

In our experiments, three performance metrics are used to observe the performance of the compared algorithms: Worst Relative Error (WRE), Average Relative Error (ARE), and Best Relative Error (BRE). Each one of which could be mathematically formulated as follows:

$$\begin{array}{c}\hfill WRE=\frac{Z^{\ast }-Z_w}{Z^{\ast }}\end{array}$$

(10)

$$\begin{array}{c}\hfill ARE=\frac{Z^{\ast }-Z_{Avg}}{Z^{\ast }}\end{array}$$

(11)

$$\begin{array}{c}\hfill BRE=\frac{Z^{\ast }-Z_B}{Z^{\ast }}\end{array}$$

(12)

$Z^{\ast }$ indicates the best-known result, $Z_w$ is the worst value obtained within the independent runs, $Z_{Avg}$ is the average of the values obtained within 30 independent runs, and $Z_B$ is the best value obtained within the independent runs.

3.9. Comparison under Carlier

In this experiment, our proposed algorithm is compared with eight algorithms on benchmark Car to check its superiority. In the following figures, 0 values mean that the algorithms could come true to the optimal value. Figure 4a is introduced to sum the average of BRE obtained by each algorithm on each instance within 30 independent runs with each other to see the best one that could come true to the lowest BRE value. This figure shows that HIEGA and HWA could outperform all the other and come true values of 0 for BRE as the lowest possible value which algorithm could reach. For the average of ARE on all the Car instances, Figure 4b is introduced to show that our proposed algorithm could outperform all the other algorithm with a value of $0.001$ and come in the first rank, and IEGA comes as the third-best one after HIEGA with a value of $0.012$, while HWA occupies the second rank with a value of $0.002$ and SCA come in the last rank with a value of $0.091$. Concerning the mean of WRE on all the Car instances, Figure 4c is introduced to expose the superiority of IEGA with a value of $0.01$ on the others with the exception of HWA that could get to the same value.

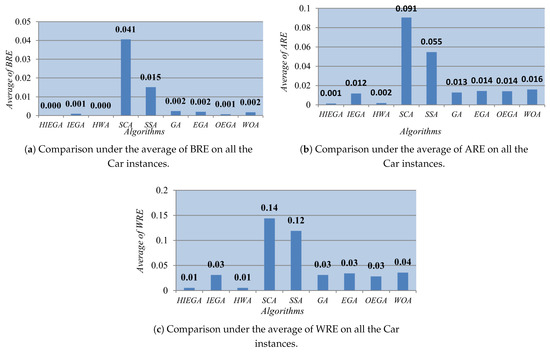
Figure 4. Comparison among algorithms on the car instances.

Furthermore, Table 3 and Table 4 show the BRE, ARE, WRE, $Z_{Avg}$, and standard deviation (SD) obtained by each algorithm on each Car instance. According to these tables, HIEGA could outperform the others for Car03, Car05, Car06, and Car07 instances in terms of the ARE, WRE, $Z_{Avg}$, and SD, while was competitive with the others for the rest of the instances.

Table 3. Outcomes of different performance metrics on the Car instances (Car01–Car06).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Car01	HIEGA	7038	0	0	0	7038	0
	IEGA		0	0	0	7038	0
	HWA		0	0	0	7038	0
	SCA		0	0.171213	0.088562	7661.3	305.406849
	SSA		0	0.122336	0.064303	7490.566667	226.370593
	GA		0	0	0	7038	0
	EGA		0	0.002699	0.000090	7038.633333	3.410604
	OEGA		0	0	0	7038	0
	WOA		0	0.042484	0.004244	7067.866667	66.693195
Car02	HIEGA	7166	0	0	0	7166	0
	IEGA		0	0.029305	0.018504	7298.6	94.769756
	HWA		0	0	0	7166	0
	SCA		0.084706	0.171365	0.130398	8100.433333	158.832130
	SSA		0.056377	0.143734	0.099660	7880.166667	139.553116
	GA		0.007257	0.055679	0.031352	7390.666667	62.308016
	EGA		0	0.094334	0.037957	7438	118.735279
	OEGA		0	0.059029	0.033078	7403.033333	94.837223
	WOA		0	0.063634	0.037687	7436.066667	119.013146
Car03	HIEGA	7312	0	0.011898	0.003597	7338.3	28.709058
	IEGA		0.007385	0.049644	0.027922	7516.166667	85.491942
	HWA		0	0.011898	0.006524	7359.7	34.085334
	SCA		0.056483	0.184628	0.127010	8240.7	268.999771
	SSA		0.035968	0.111324	0.076067	7868.2	170.196044
	GA		0.011898	0.054431	0.028679	7521.7	87.041044
	EGA		0.011898	0.044037	0.026044	7502.433333	72.344861
	OEGA		0.006018	0.054431	0.032891	7552.5	65.858308
	WOA		0.011898	0.056483	0.035161	7569.1	73.710402
Car04	HIEGA	8003	0	0	0	8003	0
	IEGA		0	0.011746	0.001141	8012.133333	22.399008
	HWA		0	0	0	8003	0
	SCA		0.052480	0.148819	0.091095	8732.033333	218.220146
	SSA		0.018618	0.134699	0.070865	8570.133333	200.441468
	GA		0	0.025366	0.004823	8041.6	56.202372
	EGA		0	0.016244	0.006702	8056.633333	58.819772
	OEGA		0	0.028239	0.012475	8102.833333	67.356803
	WOA		0.000625	0.052480	0.015965	8130.766667	77.604847
Car05	HIEGA	7720	0	0.013083	0.002988	7743.066667	33.402528
	IEGA		0	0.034845	0.010734	7802.866667	49.143147
	HWA		0	0.013083	0.003105	7743.966667	31.594813
	SCA		0.038472	0.118005	0.078001	8322.166667	164.803536
	SSA		0.002332	0.118912	0.024188	7906.733333	207.587079
	GA		0	0.019819	0.010289	7799.433333	40.596948
	EGA		0.003886	0.017358	0.010406	7800.333333	29.777322
	OEGA		0	0.013989	0.006503	7770.2	29.221453
	WOA		0.001554	0.018782	0.010622	7802	43.109937
Car06	HIEGA	8505	0	0.007643	0.002802	8528.833333	31.3231366
	IEGA		0	0.061023	0.021105	8684.5	147.216337
	HWA		0	0.007643	0.003821	8537.5	32.5
	SCA		0.054321	0.144386	0.088309	9256.066667	184.081311
	SSA		0.007643	0.123691	0.044158	8880.566667	251.156483
	GA		0	0.058554	0.016477	8645.133333	127.213923
	EGA		0	0.051382	0.019075	8667.233333	131.723115
	OEGA		0	0.041152	0.016899	8648.733333	105.884507
	WOA		0	0.029277	0.011515	8602.933333	96.881004

Bold values indicate the best outcomes.

Table 4. Outcomes of different performance metrics on the Car instances (Car07–Car08).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Car07	HIEGA	6590	0	0.008043	0	6591.766667	0
	IEGA		0	0.008043	0.001877	6602.366667	22.416487
	HWA		0	0.008043	0.001340	6598.833333	19.751934
	SCA		0.014416	0.130197	0.071259	7059.6	195.841024
	SSA		0	0.145827	0.035225	6822.133333	230.693842
	GA		0	0.025797	0.002155	6604.2	36.750873
	EGA		0	0.025797	0.002403	6605.833333	37.018989
	OEGA		0	0.008346	0.002155	6604.2	23.550513
	WOA		0	0.008346	0.001897	6602.5	22.662377
Car08	HIEGA	8366	0	0.008346	0.001897	6602.5	22.662377
	IEGA		0	0	0	8366	0
	HWA		0	0.035620	0.008179	8434.433333	64.081554
	SCA		0	0	0	8366	0
	SSA		0.010877	0.093593	0.059527	8864	169.176239
	GA		0.005139	0.071002	0.025922	8582.866667	127.503656
	EGA		0	0.031198	0.011017	8458.166667	65.852909
	OEGA		0	0.030002	0.010774	8456.133333	53.485658
	WOA		0	0.012789	0.005610	8412.933333	35.052278

Bold values indicate the best outcomes.

3.10. Comparison of Reeves

After proving the superiority of HIEGA and IEGA on the other genetic algorithms under the benchmark car in the previous experiment, through this part, they will be compared with the other entire algorithm on the benchmark Reeve to observe its superiority. To measure the performance of the algorithms, each algorithm is executed 30 independent runs on each Reeve instance, and then the different performance metrics: BRE, WRE, ARE, $Z_{Avg}$, and SD though those runs are introduced in Table 5, Table 6, Table 7 and Table 8 for all Reeves instances. For both ARE and $Z_{Avg}$, HIEGA could outperform the others in 16 out of 21, while equal with HWA in another and loser in others. Likewise, for WRE, the proposed could be superior to the others for 11 instances and equal in three others, unfortunately could not outperform the HWA for 7 others. For BRE, HIEGA could come true the best for 10 instances, and equal with the HWA for 7 instances.

Table 5. Outcomes of different performance metrics on the Reeve instances (Rec01–Rec11).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Rec01	HIEGA	1247	0	0.019246	0.002834	1250.533333	4.828618
	IEGA		0.052125	0.106656	0.070783	1335.266667	14.534862
	HWA		0.001604	0.051323	0.006977	1255.7	14.744829
	SCA		0.109864	0.198075	0.157017	1442.8	20.972045
	SSA		0.086608	0.178027	0.137423	1418.366667	25.921013
	GA		0.063352	0.100241	0.082625	1350.033333	13.816616
	EGA		0.063352	0.109864	0.082304	1349.633333	13.352861
	OEGA		0.058541	0.103448	0.081476	1348.6	15.098786
	WOA		0.074579	0.120289	0.092515	1362.366667	14.155054
Rec03	HIEGA	1109	0	0.021641	0.002164	1111.4	4.644710
	IEGA		0.007214	0.061317	0.040517	1153.933333	13.921047
	HWA		0	0.021641	0.002946	1112.266667	6.065934
	SCA		0.102795	0.210099	0.152901	1278.566667	32.871146
	SSA		0.078449	0.167719	0.119748	1241.8	31.186963
	GA		0.030658	0.067629	0.052329	1167.033333	11.223438
	EGA		0.029757	0.089269	0.056748	1171.933333	14.449759
	OEGA		0.032462	0.069432	0.052059	1166.733333	9.688252
	WOA		0.038774	0.099189	0.073129	1190.1	14.839924
Rec05	HIEGA	1242	0.002416	0.018519	0.006871	1250.533333	5.481687
	IEGA		0.012077	0.056361	0.034568	1284.933333	11.744313
	HWA		0.002416	0.011272	0.004938	1248.133333	4.177187
	SCA		0.042673	0.153784	0.115996	1386.066667	26.293134
	SSA		0.045894	0.134461	0.097236	1362.766667	26.297888
	GA		0.024959	0.060387	0.043156	1295.6	9.704295
	EGA		0.017713	0.070048	0.043774	1296.366667	14.969933
	OEGA		0.026570	0.058776	0.042002	1294.166667	9.757333
	WOA		0.029791	0.060387	0.048282	1301.966667	9.809802
Rec07	HIEGA	1566	0	0.011494	0.007663	1578	8.485281
	IEGA		0.035759	0.087484	0.056939	1655.166667	20.448445
	HWA		0	0.011494	0.007791	1578.2	8.268011
	SCA		0.093231	0.188378	0.147829	1797.5	33.795217
	SSA		0.082376	0.173052	0.120945	1755.4	39.244193
	GA		0.042146	0.100894	0.069199	1674.366667	18.948146
	EGA		0.045338	0.101533	0.073159	1680.566667	22.496938
	OEGA		0.044699	0.084929	0.067497	1671.7	14.512409
	WOA		0.051086	0.096424	0.077203	1686.9	15.712734
Rec09	HIEGA	1537	0	0.063761	0.014769	1559.7	21.506820
	IEGA		0.051399	0.116461	0.089091	1673.933333	22.152401
	HWA		0	0.042290	0.017393	1563.733333	16.958643
	SCA		0.130124	0.202342	0.164867	1790.4	28.841637
	SSA		0.068315	0.162004	0.118174	1718.633333	35.250989
	GA		0.074171	0.117111	0.094860	1682.8	19.482299
	EGA		0.062459	0.121015	0.097636	1687.066667	20.602481
	OEGA		0.065712	0.113208	0.095316	1683.5	17.659275
	WOA		0.060508	0.124268	0.099349	1689.7	22.564205
Rec11	HIEGA	1431	0	0.0433263	0.014256	1451.4	17.779388
	IEGA		0.093640	0.141858	0.117027	1598.466667	18.990758
	HWA		0	0.040531	0.017353	1455.833333	17.384060
	SCA		0.149545	0.220824	0.194805	1709.766667	27.304069
	SSA		0.095737	0.198462	0.156836	1655.433333	30.650376
	GA		0.096436	0.145352	0.122362	1606.1	16.213882
	EGA		0.082459	0.150943	0.123526	1607.766667	19.653130
	OEGA		0.100628	0.139063	0.119613	1602.166667	14.973495
	WOA		0.088050	0.136268	0.118518	1600.6	15.632444

Bold values indicate the best outcomes.

Table 6. Outcomes of different performance metrics on the Reeve instances (Rec13–Rec25).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Rec13	HIEGA	1930	0	0.038342	0.015664	1960.233333	15.683714
	IEGA		0.046632	0.118134	0.076131	2076.933333	29.532957
	HWA		0.002072	0.044559	0.019153	1966.966667	16.592133
	SCA		0.122797	0.214507	0.164162	2246.833333	35.753865
	SSA		0.109844	0.182383	0.135716	2191.933333	32.857199
	GA		0.078238	0.121761	0.096269	2115.8	22.456476
	EGA		0.069948	0.130569	0.094801	2112.966667	29.238654
	OEGA		0.088082	0.119171	0.100690	2124.333333	17.376868
	WOA		0.096373	0.127979	0.109706	2141.733333	14.042633
Rec15	HIEGA	1950	0.004615	0.098974	0.024290	1997.366667	35.095567
	IEGA		0.047692	0.098974	0.068974	2084.5	19.416058
	HWA		0.005128	0.042564	0.018461	1986	21.594752
	SCA		0.090769	0.168205	0.141538	2226	34.466408
	SSA		0.070256	0.131794	0.108085	2160.766667	30.206713
	GA		0.063589	0.106666	0.084700	2115.166667	22.764128
	EGA		0.061538	0.101025	0.083641	2113.1	18.758731
	OEGA		0.06	0.097948	0.080700	2107.366667	19.027144
	WOA		0.055384	0.092307	0.081982	2109.866667	14.548157
Rec17	HIEGA	1902	0.017350	0.082544	0.035173	1968.9	25.981211
	IEGA		0.067297	0.114090	0.093305	2079.466667	24.349857
	HWA		0	0.058359	0.027024	1953.4	20.878378
	SCA		0.127760	0.206624	0.170347	2226	32.794308
	SSA		0.107781	0.179285	0.135278	2159.3	32.444979
	GA		0.074658	0.121976	0.106151	2103.9	20.932192
	EGA		0.088853	0.137224	0.108307	2108	19.832633
	OEGA		0.090431	0.128811	0.114335	2119.466667	16.995555
	WOA		0.097791	0.136172	0.114879	2120.5	18.067927
Rec19	HIEGA	2017	0.044124	0.187902	0.058139	2134.266667	49.683621
	IEGA		0.123946	0.163113	0.144752	2308.966667	21.393898
	HWA		0.042141	0.069410	0.055197	2128.333333	11.950825
	SCA		0.176995	0.258800	0.230325	2481.566667	36.693944
	SSA		0.153197	0.238968	0.205982	2432.466667	35.916322
	GA		0.143777	0.179970	0.163427	2346.633333	19.460187
	EGA		0.136836	0.184928	0.163609	2347	21.776133
	OEGA		0.143777	0.174020	0.160337	2340.4	18.045498
	WOA		0.134358	0.195835	0.175260	2370.5	26.722961
Rec21	HIEGA	2011	0.013426	0.019393	0.018680	2048.566667	2.603629
	IEGA		0.074589	0.138736	0.108238	2228.666667	28.311756
	HWA		0.009945	0.019393	0.018680	2048.566667	3.630273
	SCA		0.165092	0.228741	0.196784	2406.733333	33.423478
	SSA		0.128294	0.203381	0.168788	2350.433333	34.844113
	GA		0.087021	0.150174	0.126255	2264.9	24.064288
	EGA		0.104922	0.148185	0.127697	2267.8	21.487050
	OEGA		0.108403	0.152163	0.129355	2271.133333	20.170495
	WOA		0.109895	0.148185	0.133731	2279.933333	19.177996
Rec23	HIEGA	2011	0.004972	0.034808	0.017918	2047.033333	14.855937
	IEGA		0.085529	0.141223	0.110923	2234.066667	27.282391
	HWA		0.004972	0.036300	0.016194	2043.566667	14.247066
	SCA		0.137245	0.220288	0.186507	2386.066667	39.107487
	SSA		0.139234	0.206365	0.165108	2343.033333	32.162590
	GA		0.110890	0.158130	0.129587	2271.6	19.491194
	EGA		0.104425	0.151665	0.128244	2268.9	20.799599
	OEGA		0.116360	0.146195	0.131990	2276.433333	15.329021
	WOA		0.112879	0.151168	0.131659	2275.766667	18.322451
Rec25	HIEGA	2513	0.007958	0.044966	0.026754	2580.233333	19.095694
	IEGA		0.082371	0.121368	0.106685	2781.1	22.530497
	HWA		0.014325	0.045364	0.027616	2582.4	16.987446
	SCA		0.155590	0.204934	0.176588	2956.766667	36.271828
	SSA		0.108635	0.188221	0.150245	2890.566667	41.364786
	GA		0.102268	0.139673	0.122735	2821.433333	20.817754
	EGA		0.092319	0.147632	0.127749	2834.033333	25.235534
	OEGA		0.097493	0.136490	0.122708	2821.366667	19.693456
	WOA		0.107043	0.149224	0.127152	2832.533333	24.555696

Bold values indicate the best outcomes.

Table 7. Outcomes of different performance metrics on the Reeve instances (Rec27–Rec37).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Rec27	HIEGA	2373	0.008006	0.036662	0.019272	2418.733333	16.641180
	IEGA		0.096923	0.147071	0.119047	2655.5	30.93945
	HWA		0.010535	0.032027	0.019525	2419.333333	13.842767
	SCA		0.170670	0.235988	0.202612	2853.8	46.058947
	SSA		0.139907	0.209860	0.179898	2799.9	40.539980
	GA		0.102823	0.160977	0.136311	2696.466667	36.165115
	EGA		0.115887	0.153813	0.137772	2699.933333	20.720253
	OEGA		0.088074	0.160556	0.139120	2703.133333	34.369301
	WOA		0.112937	0.156342	0.137435	2699.133333	26.572834
Rec29	HIEGA	2287	0.006121	0.042850	0.023597	2340.966667	22.394170
	IEGA		0.101442	0.174901	0.142661	2613.266667	37.883974
	HWA		0.007870	0.050284	0.027969	2350.966667	24.183304
	SCA		0.195452	0.254044	0.225200	2802.033333	37.867737
	SSA		0.157848	0.239178	0.192042	2726.2	43.699275
	GA		0.140358	0.188019	0.162789	2659.3	27.098770
	EGA		0.137297	0.191954	0.162075	2657.666667	25.819028
	OEGA		0.132488	0.177962	0.159860	2652.6	25.210579
	WOA		0.144731	0.186270	0.165573	2665.666667	25.373652
Rec31	HIEGA	3045	0.002627	0.027586	0.016934	3096.566667	22.008609
	IEGA		0.104433	0.146798	0.125473	3427.066667	39.693772
	HWA		0.008867	0.037766	0.022375	3113.133333	20.418510
	SCA		0.154351	0.210837	0.186097	3611.666667	34.852387
	SSA		0.134318	0.198358	0.177329	3584.966667	42.869167
	GA		0.127422	0.157635	0.140634	3473.233333	23.531090
	EGA		0.122824	0.162233	0.142200	3478	23.359509
	OEGA		0.122495	0.159277	0.143940	3483.3	27.282656
	WOA		0.131362	0.159277	0.147071	3492.833333	25.139720
Rec33	HIEGA	3114	0.001284	0.020231	0.008188	3139.5	10.883473
	IEGA		0.074181	0.115606	0.098126	3419.566667	29.809040
	HWA		0.001284	0.010276	0.008295	3139.833333	4.305681
	SCA		0.150610	0.198137	0.173560	3654.466667	36.446063
	SSA		0.121066	0.193962	0.162952	3621.433333	49.127509
	GA		0.102761	0.136159	0.115403	3473.366667	22.817366
	EGA		0.094091	0.137443	0.113690	3468.033333	33.271091
	OEGA		0.107899	0.128131	0.118946	3484.4	18.307739
	WOA		0.106294	0.140976	0.123389	3498.233333	27.813286
Rec35	HIEGA	3277	0	0	0	3277	0
	IEGA		0.044552	0.083918	0.063452	3484.933333	29.017159
	HWA		0	0.000915	0.000030	3277.1	0.538516
	SCA		0.105584	0.158986	0.132478	3711.133333	42.568950
	SSA		0.089105	0.145865	0.120587	3672.166667	44.570605
	GA		0.064693	0.092767	0.080327	3540.233333	25.608180
	EGA		0.057064	0.101617	0.083084	3549.266667	34.247076
	OEGA		0.065913	0.091852	0.083653	3551.133333	19.057340
	WOA		0.046689	0.098870	0.085433	3556.966667	33.488787
Rec37	HIEGA	4951	0.032922	0.056756	0.042227	5160.066667	27.546243
	IEGA		0.146435	0.182791	0.167528	5780.433333	40.535320
	HWA		0.023833	0.058372	0.044206	5169.866667	38.933904
	SCA		0.185215	0.235710	0.216064	6020.733333	62.100957
	SSA		0.184407	0.213492	0.198215	5932.366667	35.673971
	GA		0.157140	0.188850	0.175708	5820.933333	35.789135
	EGA		0.166229	0.191072	0.176395	5824.333333	31.882422
	OEGA		0.154918	0.188244	0.176806	5826.366667	39.860994
	WOA		0.153706	0.186225	0.176408	5824.4	31.813623

Bold values indicate the best outcomes.

Table 8. Outcomes of different performance metrics on the Reeve instances (Rec39–Rec41).

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Rec39	HIEGA	5087	0.013564	0.034598	0.022980	5203.9	27.544327
	IEGA		0.113033	0.168665	0.145888	5829.133333	71.492066
	HWA		0.011401	0.039512	0.025273	5215.566667	31.597134
	SCA		0.179083	0.222528	0.198853	6098.566667	53.726271
	SSA		0.159622	0.206211	0.182412	6014.933333	57.731524
	GA		0.145862	0.170434	0.15824	5891.966667	33.412057
	EGA		0.141930	0.175152	0.159229	5897	47.012055
	OEGA		0.140554	0.167682	0.155527	5878.166667	35.096137
	WOA		0.148810	0.177118	0.164635	5924.5	28.965209
Rec41	HIEGA	4960	0.025637	0.050806	0.039227	5154.566667	28.312168
	IEGA		0.146572	0.194354	0.169731	5801.866667	44.835055
	HWA		0.028830	0.059072	0.043131	5173.933333	33.260520
	SCA		0.197782	0.246774	0.227210	6086.966667	54.319108
	SSA		0.194354	0.237903	0.213608	6019.5	52.392588
	GA		0.170161	0.208467	0.187332	5889.166667	45.649449
	EGA		0.171371	0.205040	0.187022	5887.633333	36.043014
	OEGA		0.169758	0.198790	0.186444	5884.766667	30.707961
	WOA		0.178225	0.201612	0.190732	5906.033333	29.825585

Bold values indicate the best outcomes.

Regarding ARE, the average of each algorithm on all the Reeves instances is introduced in Figure 5. Inspecting this figure we can draws the superiority of our proposed algorithm under the average of the ARE on the entire Reeves instance, where it could win with a value of $0.102$ as the best one and IEGA come in the third rank after HIEGA and HWA, while SCA comes in the last rank with a value of $0.179$. After completing this experiment, it is concluded that the proposed algorithm is competitive with the HWA as a robust algorithm suggested recently for this problem, and subsequently it is considered a strong alternative to this algorithm for tackling the PFSSP.

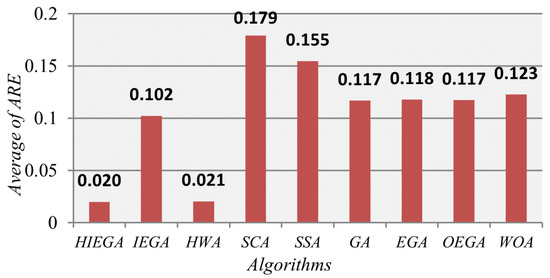
Figure 5. Comparison under the average of ARE on all the Reeve instances.

3.11. Comparison of Heller

This dataset was created by Heller and consist of two instances. In this part, we compare the proposed algorithms with the other algorithms under this dataset. For doing that, Figure 6a–c are presented to illustrate the average of BRE, to see the summation of the ratio of the error between the best value obtained by each algorithm within the independent runs and the best-known value on each instance, the average of ARE, and the average of the WRE, respectively. According to those figures, our proposed algorithm is the best in comparison with the other algorithms in terms of the ARE, and WRE, meanwhile competitive with HIEGA in terms of the BRE. Moreover, Table 9 is introduced to show the outcomes of BRE, WRE, ARE, $Z_{Avg}$ and SD obtained by each algorithm on the two Heller instances that confirms our suppositions to the superiority of the proposed algorithm over the others for the five performance metrics used.

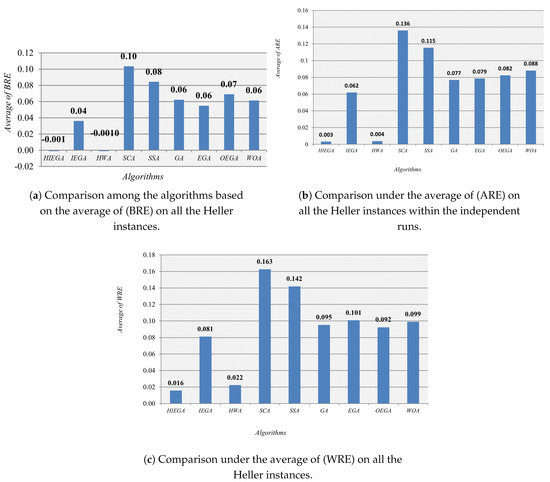
Figure 6. Comparison among algorithms on the Heller instances.

Table 9. Outcomes of the performance metrics on the Heller instances.

Instances	Algorithm	${\mathit{Z}}^{\ast }$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	SD
Hel1	HIEGA	516	−0.001938	0.001938	0.000129	516.066666	0.442216
	IEGA		0.042635	0.081395	0.067441	550.8	4.460194
	HWA		−0.001938	0.007751	0.000710	516.366666	1.079609
	SCA		0.089147	0.141472	0.116085	575.9	4.928488
	SSA		0.094961	0.122093	0.109043	572.266666	3.687215
	GA		0.065891	0.094961	0.079715	557.133333	3.621540
	EGA		0.065891	0.091085	0.079328	556.933333	3.511251
	OEGA		0.071705	0.089147	0.080943	557.766666	2.499111
	WOA		0.063953	0.094961	0.086627	560.7	2.876919
Hel3	HIEGA	136	0	0.029411	0.006372	136.866666	0.718022
	IEGA		0.029411	0.080882	0.056372	143.666666	1.776388
	HWA		0	0.036764	0.007107	136.966666	0.982626
	SCA		0.117647	0.183823	0.155882	157.2	2.150968
	SSA		0.073529	0.161764	0.121813	152.566666	2.679344
	GA		0.058823	0.095588	0.074019	146.066666	1.364632
	EGA		0.044117	0.110294	0.077941	146.6	2.154065
	OEGA		0.066176	0.095588	0.083823	147.4	1.113552

Bold values indicate the best outcomes.

3.12. Comparison under CPU Time and BoxPLot

For knowing the speedup of each algorithm, we calculate the average of the CPU time needed by each algorithm until finishing implementing the instances of the Carlier and Heller, and this average value is introduced in Figure 7a. This figure told us that our proposed algorithm outperforms HWA, IEGA, GA, EGA, and OEGA and wins the first rank with a value of $2.59$ after SSA, SCA, and WOA. When comparing HIEGA with SSA, SCA, and WOA in terms of CPU time and MS, our proposed algorithm could significantly come true better outcomes at a reasonable time. In Figure 7b,c we compare the algorithms under the Boxplot for the values obtained by each one within 30 independent runs on Hel1 and Hel2, respectively. Inspecting this figure shows that IEGA could outperform all the algorithms except HIEGA and HWA. Also from this figure, we found that HIEGA could overcome HWA under the boxplot of Hel1 and Hel2. Generally, our proposed algorithms, IEGA and HIEGA, are competitive in comparison with the others.

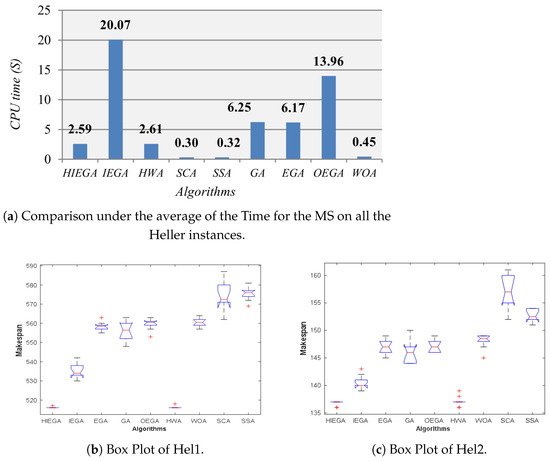
Figure 7. Comparison among algorithms under CPU time and Box-plot for the makespan on the Heller instances.

4. Conclusions

This work presents the integration between the uniform crossover and the arithmetic crossover (UAC) to enhance the exploitation capability and alleviate stuck into local minima problems. After that, the UAC with re-initializing an individual selected randomly from the population through each iteration are combined in the EGA, to enhance its performance when tackling the PFSSP, which is a well-known scheduling problem applied in several industrial applications in a version, abbreviated as IEGA. Additionally, we integrate a LSS with the IEGA for strength its performance toward solving PFSSP; this version is abbreviated as HIEGA. HIEGA and IEGA are experimentally validated on three well-known benchmarks: Reeves, Heller, and Carlier, and compared with a number of the robust evolutionary and meta-heuristic algorithms. On the car instances, the proposed algorithm could reach a value of 0.001 for ARE; while for the Heller instances, it reaches a value of 0.003 for the same metric mentioned before; ultimately for the Reeve instances, a value of 0.020 for ARE is obtained by the proposed. The experimental outcomes show that IEGA and HIEGA is competitive with those algorithms.

Unfortunately, the computational cost of the proposed algorithm is slightly higher than some of the others used in comparison as our main limitation. Therefore, in our future work, we will work on overcoming the time complexity of those proposed by integrating them with some of the strategies like levy flight, and opposition theory until accelerating the convergence toward the best solution in less number of iterations. Additionally, we will incorporate extending our proposed algorithms to solve the open shop.