Abstract
Genomic heterogeneity constitutes one of the most distinctive features of cancer diseases, limiting the efficacy and availability of medical treatments. Tumorigenesis emerges as a strongly stochastic process, producing a variable landscape of genomic configurations. In this context, matrix factorisation techniques represent a suitable approach for modelling such complex patterns of variability. In this work, we present a hierarchical factorisation model conceived from a systems biology point of view. The model integrates the topology of molecular pathways, allowing to simultaneously factorise genes and pathways activity matrices. The protocol was evaluated by using simulations, showing a high degree of accuracy. Furthermore, the analysis with a real cohort of breast cancer patients depicted the internal composition of some of the most relevant altered biological processes in the disease, describing gene and pathway level strategies and their observed combinations in the population of patients. We envision that this kind of approaches will be essential to better understand the hallmarks of cancer.
1. Introduction
The term cancer describes a group of heterogeneous diseases characterised by the uncontrolled growth of a group of cells known as tumour. In spite of the vast amount of resources invested in biomedical research during the last decades, it still represents a group of pathologies with one of the highest mortality rates worldwide [1].
The tumourigenesis process initiates after the accumulation of specific DNA somatic alterations, affecting essential components of cells. As a result, biological processes, such as cell growth or cell proliferation, are overstimulated within the tumour, while other control mechanisms evolved to eliminate erratic cells are inhibited. In this context, cancer research over the last two decades revealed a set of common patterns shared by all types of tumours, irrespective of their tissue of origin. These patterns are represented in the so-called hallmarks of cancer [2], which constitutes a general description of the abilities that any tumour needs to acquire in order to survive, grow and evade the surrounding tissue control.
In a wide range of cases, the disease is caused by continuous exposure to a harmful agent, such as UV radiation. In addition, other mechanisms at a molecular level, such as sporadic errors in the replication machinery [3], oxidative damage, or inherited germline mutations [4], may play a relevant role in the onset and development of the disease. Despite the selective pressure imposed by the surrounding environment, the origin of somatic alterations emerges as a strongly stochastic process, resulting in a wide variety of genetic configurations at the intra-tumour level. This phenomenon is, in turn, propagated to the population of patients, exhibiting a large amount of variability even within those individuals with the same subtype of cancer. A clear example of this fundamental property of cancers is represented by the low population frequency of recurrently mutated genes, which severely hampers the design of general purpose therapies.
An interesting approach for modelling complex patterns of variability is the use of matrix factorisation (MF) techniques [5,6]. These methodologies aim at obtaining a finite set of latent patterns representing the basic building blocks that constitute the observations, usually obtained as a linear combination of them. MF has been addressed by many different approaches, imposing different constraints to shape the properties of the final set of latent components. Among the most common methods are principal component analysis (PCA) [7], which defines components as principal directions of variability, or independent component analysis (ICA) [8], which imposes statistical independence between components. Additionally, non-negative matrix factorisation (NMF) [9] is becoming a very popular technique among data analysts, which performs a decomposition imposing positive values in the matrices of the model. This restriction provides a parts-based representation of observations that facilitates the individual interpretation of each component, as there are no negative values that need to be cancelled combining other components.
In the context of computational biology, NMF works under the assumption that individuals belonging to the same group share common genomic features, ultimately represented by specific components in the model. The obtained model is usually a low-rank representation, describing in some cases NMF as a dimensionality reduction technique. NMF has been particularly useful in computational biology, providing relevant contributions in the field of clustering [10], protein–protein interaction analysis [11], deconvolution of mutational patterns [12,13], as well as inferring the proportion of different cell types in tissue samples [14,15], among others.
On the other hand, NMF-derived models have also been applied to jointly factorise two or more input matrices. One of the most pioneering works in this context was proposed by Zhang et al. [16], designed for extracting a set of multi-dimensional modules from the joint factorisation of different types of omics, with the restriction of using the same component matrix. A similar approach was followed in the work of Ray et al. [17], where the authors proposed a new multiview approach to combine phosphoproteomics data with other compatible omics, restricting the factorisation to use the same mixing matrix for deconvoluting all input matrices. Subsequently, Zhang et al. [18] proposed a new approach to integrate different omics, decomposing each input matrix into a sum of different components that collect both specific and common patterns. Additionally, in the field of graph community estimation, Ding et al. [19] suggested jointly factorising the correlation matrices of different omics in order to find latent graph communities.
The properties of MF techniques enable a natural integration into the field of systems biology, which describes living entities (such as cells, tissues, or organs) as complex systems whose functioning depends on a densely interconnected network of more fundamental parts. In the particular context of computational biology, systems biology has led to the inference of a collection of molecular pathways describing how proteins interact in order to carry out the different biological processes that cells required during their life cycle. This task promoted the creation of large repositories of biological knowledge as Gene Ontology [20], which defines an ontology of biological terms to describe cellular processes, or KEGG [21], which provides a graphical description of the most relevant molecular pathways. These repositories, in turn, boosted the scientific community to develop a wide variety of statistical and computational methods [22,23,24] to infer the activity of molecular pathways by using gene expression values as a proxy of protein activity, hence allowing to quantify cell activities beyond the classic reductionist gene-based approaches. Interestingly, some of these tools [25,26,27,28,29] integrated a topological description of molecular pathways, allowing to appropriately weight the relevance of each gene involved in each pathway. One of the most interesting methodologies in this context is represented by the tool Hipathia [29,30,31], which allows the modelling and quantification of a set of essential signalling pathways, recurrently altered in cancer.
The combination of systems and computational biology provides an ideal framework to understand the different levels of heterogeneity in cancer, represented as a hierarchical system with different layers of information. First, the wide variety of somatic alterations that arise within a tumour establishes the first level of heterogeneity, where the most relevant genes in the disease may show a range of different genomic alterations, with a similar effect on their function. Next, the low population frequency observed in recurrently mutated genes, necessarily suggests that altering different combinations of genes can lead to cellular phenotypes with similar properties. In this case, the natural structure of molecular pathways explains this second level of heterogeneity, since somatic alterations in different genes within the same network could potentially have the capacity to inhibit or overactivate its functioning. Illustrative examples of this concept are the alteration of different proteins belonging to the same complex (disrupting the complex and, thus, its function in the cell), the disruption of different essential proteins within the same pathway (thereby blocking its activity), or the alteration of different inhibitory proteins within the same signalling cascade (leading to its overactivation) [29]. Furthermore, it is also possible to contextualise a missing part of variability by analyzing how different molecular pathways regulate the same biological processes in cells. This point establishes the third level of heterogeneity, where different molecular signals could potentially enhance the same altered biological processes.
This representation, conceived from a systems biology perspective, provides a hierarchical view of genomic heterogeneity in cancer, encompassing gene mutations, molecular pathways, and the biological functions that ultimately underpin cancer hallmarks. With this perspective, in this work, we describe a protocol of analysis designed to study the different levels of genomic heterogeneity in a group of patients with the same type of cancer. The protocol is based on a joint factorisation model that simultaneously decomposes two different matrices representing the activity of genes and signalling pathways in the same individuals. Unlike previous alternatives, the model establishes a hierarchical relationship between the two sets of components, and integrates into the optimisation specific biological knowledge to represent how genes interact in the context of signalling pathways. As a result, the model obtains two sets of latent components describing the different strategies that patient tumours implement in order to carry out the hallmarks of cancer.
2. Materials and Methods
The first step in our protocol is the estimation of the matrix that stores the gene activity in the set of selected individuals. With genes and n individuals, is obtained by multiplying the gene expression matrix by the mutation effect matrix :
where ⊙ corresponds to the element-wise product (e.g., ). Although corresponds to the normalised gene expression matrix, describes on each individual the effect of the observed somatic mutations on the structure of measured genes (see Supplementary Section S1 for details). The combination of gene expression and somatic mutations allows for (i) estimating the global activity of each gene in the analyzed tissue, while (ii) taking into account somatic mutations that potentially affect the gene activity without modifying their expression levels. Illustrative examples are somatic mutations that do not block the translation of the corresponding protein but alter its interactions by modifying essential amino acids on its sequence.
The resulting gene activity matrix is then used to estimate the activity of signalling pathways in the same individuals, represented by the matrix . To this end, we use the tool Hipathia [29], which decomposes cell signalling into individual cascades describing the sequence of protein interactions required to activate effector proteins in the cell. In the model, we represent Hipathia by the function (see Supplementary Section S3 for details) where () corresponds to the individual equation used to estimate the activity of the ith signalling cascade. In practice, ℏ takes the gene activity matrix () as input and returns the activity matrix of signalling cascades ():
and matrices describe tumour activities from two different biological levels. Since the activity of the signalling pathways is directly dependent on the activity of their constituent genes, we can assume that the two matrices are connected, and, therefore, the latent components that constitute them. This approach suggests that addressing the problem through a joint factorisation should provide a more accurate decomposition of the latent components present at each space.
The connection between both sets of latent components must be addressed from a biological perspective. A naive approximation could be defining a 1-to-1 relationship between both levels, where each gene-level component would produce a particular component at the pathway level, having , with , and k corresponding to the number of components employed at both levels. However, the natural topology of molecular pathways suggests that altering different combinations of genes interacting in the same biological processes can produce a similar response at the molecular pathway level. A common example of this effect would be the inhibition of the cellular response to a particular environmental stimulus by altering any of the proteins involved in the signalling cascade responsible for triggering that response. In the model, this effect would lead to observing groups of gene-level components translating into a very similar result at the pathway level, thereby producing a set of pathway-level components () with many repeated elements.
To solve this limitation we change the connection between and from a 1-to-1, to a 1-to-many scheme, where each individual pathway-level component is hierarchically associated with 1 or more gene-level components, implying that , with and as the group of associated gene-level components. This characteristic causes to be typically much smaller than , which in biological terms translates into greater variability at the gene level compared to the pathway level, biologically consistent with the results observed in patients with the same type of cancer.
2.1. Hierarchical Model of Factorisation
In our approach, the factorisation model focuses on a subset of biological processes significantly altered in the disease under study. Illustrative examples in the study of cancer are the regulation of the cell cycle, or in the particular case of breast cancer, the regulation of the response to hormones.
In practice, we perform individual factorisations for each biological process of interest in the disease. In each factorisation, the model takes as input the subset of and that contains only the genes and signalling cascades involved in the regulation of the selected biological process (see Supplementary Section S2 for details). This approach reduces the complexity of the factorisation, helping the model to easily establish the hierarchical relationship between the activity of the selected genes and their effect on the involved signalling pathways.
Let and be the subset of and only containing the genes and signalling cascades involved in the regulation of a particular biological process under study (e.g., response to hormones). Following a classic NMF, we define the general problem for genes and pathways as:
where and correspond to the component matrices, and and to the mixing matrices, for genes and pathways, respectively, with and being the number of components used in the factorisation, having typically .
In a general case, the objective function of NMF independently applied to each activity matrix tries to minimise the following expression:
where corresponds to the Frobenius norm, used to evaluate the distance between the input matrix X and the solution obtained in each interaction. Here, the norm is solved as:
from which we can derive the partial derivatives with respect to W and H:
In this case, as suggested by Lee and Seung [9], we can use multiplicative updates, hence avoiding possible negative values that could be obtained from the standard gradient descent rule:
Following this idea, we can reformulate the original multiplicative updates to our particular case for genes and pathways as:
To establish the hierarchical relationship (Figure 1) between each pathway-level component and their associated gene-level components we need to define the binary matrix . In practice, S concentrates the essence of the hierarchical model, since it allows us to determine how the components at both levels are interconnected. In particular, if corresponds to a group of gene-level components that are associated with the same pathway-level component j, then , with .
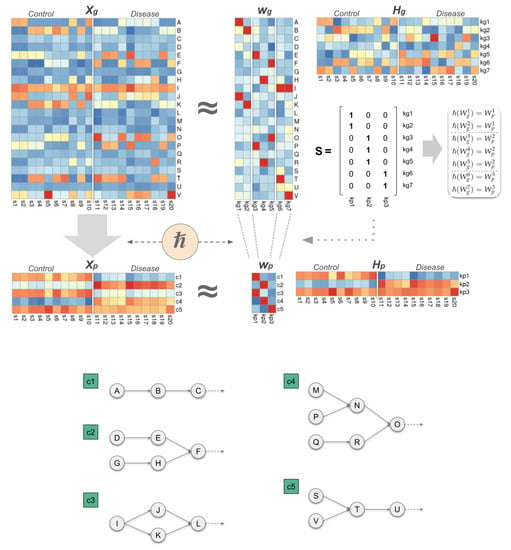
Figure 1.
Description of the obtained hierarchical model applied to a controlled simulation, representing a cohort of 20 individuals divided into 2 different phenotypic groups (Control and Disease). The use of the Hipathia function on provides the pathway activity matrix () composed of 5 rows, corresponding to the 5 signalling cascades ([c1, c2, c3, c4, c5]) modelled by Hipathia (below). These 5 cascades involve 22 genes (from A to V) responsible for regulating the biological process under study. The S matrix shows the hierarchical relationship between the 3 components obtained at the pathway level () and the 7 components obtained at the gene level (). As can be seen, the first component at the pathway level (kp1) regulates the biological process by overactivating the c1 and c3 signalling cascades. In this case, the hierarchical model obtains two different strategies (components) at the gene level to produce this effect: while kg1 overactivates the genes A and J, kg2 overactivates the genes B and K. Likewise, the mixing matrix obtained at the pathway level () shows two different configurations for the two groups of individuals. In this case, while the Control group weights the first component (kp1), the Disease group focuses on the second component (kp2), with kp3 being shared by both groups.
Since both component levels use a different number of components (usually < ), S is essential to estimate the distance between the two sets of components at pathways space. More precisely, to determine the compatibility between the two sets of components, we add the following term to the cost function:
Here, the product allows the pathway-level components to be properly expanded to have the same order and dimensions of , which represents the activity of the gene-level components at the pathway space.
Similarly, S helps to reinforce the consistency of the model by enabling the two sets of mixing matrices to be compared through the following term:
In this case, compacts the gene-level weights around their associated pathway-level components, thereby allowing to directly compare against the obtained pathway-level weights ().
Because of its binary structure, to produce a smooth convergence S is approximated during optimisation by using a sigmoid expression such as:
where Y, with the same dimensions of S, will exhibit at the end of the optimisation large positive and negative values, thereby producing close to 0 or 1 values in S.
Additionally, in order to obtain a consistent S matrix, it is important to penalise solutions with more than one non-zero value by row, which would lead gene-level components to be simultaneously assigned to more than one pathway-level component. With this aim, the following term is added:
where and correspond to column vectors with all their values equal to 1, with a and size, respectively. In this case, the product allows us to sum the values of S per row and, therefore, to assess whether each gene-level component is distributed across more than one pathway-level component.
On the other hand, it is important to converge to S solutions with balanced correspondence between gene and pathway components, avoiding cases in which a reduced number of pathway components attract the majority of gene components. To solve this limitation, we add this term:
where represents the expected average number of gene components associated to the same pathway component in an ideal case. In this case, the product allows summing the values of S per column, which is equivalent to accumulating the contribution of each pathway-level component across all gene-level components. This approach helps to detect an unbalanced weight between the pathway-level components.
Finally, the complete objective function is defined as:
where we added specific weights for each term. Each term of this equation is expanded as explained in Equation (7), and subsequently used to derive the partial derivatives with respect to each matrix. From the derivatives we obtain the following update rules, specifically using for , , and matrices a similar multiplicative approach as defined by Lee and Seung [9]:
with as the learning rate used to optimise the Y matrix. In this case, we define
corresponding to the derivative of a sigmoid function. Additionally, in order to complete the model we need to assess how gene variability affects pathway activity. This characteristic is represented by the partial derivative , with and as the number of genes and signalling cascades included in the model. To evaluate how the variability of a particular gene g affects the variability of given signalling cascade c we need to sum the result of the partial derivate of with respect to g across all columns:
where i corresponds to each column of , and with the particular equation that defines the activity of the signalling cascade c within the Hipathia function (ℏ), according to the Q genes that compose it.
Finally, each term weight allows the user to balance which is the most important aspect in the optimisation. In this work, we customise the weight of each factorised biological term using the R package DEoptim [32], which, through a genetic algorithm, explores the error space by trying different combinations of weight values. In this case, for the model validation we used a total of 50 generations in the genetic algorithm, with 25 runs per generation, employing 100 iterations in each run, selecting the final combination of weights that provided the lowest error at the end of the search.
2.2. Deriving the Internal Composition from Model Matrices
The results obtained by the hierarchical model provide a detailed description of the internal composition of a cohort of individuals, mainly composed by the set of components found at both levels ( and ), and their weight across the individuals ( and ). On a practical level, the hierarchical model allows us to determine which components have a more relevant contribution to a particular individual. These components describe, at the molecular level, the main strategies that the tumour has implemented to alter the biological process under study.
In a more detailed analysis, we can compare the components with each other, allowing us to determine which are the most active elements within each component. This approach reveals the most relevant genes for each gene-level component (see Supplementary Section S5 for details), providing a more concise description of the role of the component in those individuals in which it is integrated. At the biological level, the most relevant elements define groups of genes that are simultaneously overactivated in order to carry out their function, paving the way to define more effective personalised treatments designed to simultaneously target several essential drivers in the tumour. At the pathway level, the approach is equivalent, revealing in each component which signalling cascades are more active. Furthermore, the hierarchical point of view of the model provides a direct link between the most relevant genes within a given gene-level component to the most active signalling cascades in its associated pathway-level counterpart.
Similarly, the model matrices can be used to characterise groups of patients. At a practical level, this approach defines the most important molecular characteristics of a given subtype, and subsequently its differences and similarities with other subtypes of the disease. An interesting approach in this context is to obtain a binarised version of the mixture matrices, which provides a more comprehensive view of those components that are required in a certain subtype. Formally, binarised versions are obtained as follows:
where ♭ is the binarisation function. In this case, if then the weight of the component i in the individual j is at least greater than the 25% of the maximum weight of that component across all individuals.
This transformation allows us to establish more concisely which are the most frequent combinations of components observed when building the individuals in the cohort. Then, these combinations can be used to build meta-sample profiles, obtained by adding up those components included in each particular observed combination, thereby producing canonical representations of each subtype.
Following these ideas we formally define the internal composition of a cohort of patients as:
where S defines the components hierarchy, and the latent components, and the weights across individuals, and their binarised versions, and the observed combinations, and their frequencies in the cohort, and and the obtained meta-samples, for genes and pathways, respectively, and G as a matrix that defines the relevance of each gene on each particular gene-level component.
2.3. Estimating the Optimal Number of Components
The characteristic parameter of any MF technique is the number of latent components to be used in the process. This parameter is typically unknown and its adequate selection becomes crucial, since selecting a too low value would lead to a suboptimal factorisation, and a too high would produce an excessive fragmentation of the original components.
The most common approach to this problem consists of carrying out successive runs using a sufficiently wide range of candidate values, to then determine the number of components that gives the most suitable factorisation. This approach, although robust, shows some important limitations. First, the computational load could be unacceptable when using an excessively wide range of values. Second, the process should introduce specific metrics to balance the model complexity against the obtained goodness of fit, since a higher number of components will generally produce a more accurate fitting.
A usual approach involves the cophenetic correlation coefficient [33] that evaluates the agreement between the sample Euclidean distance and the distance obtained from a hierarchical clustering performed with the mixing matrix. Likewise, the silhouette method was also used in this context, since it allows estimating the distance of each observation to other adjacent groups of samples included in the hierarchical clustering, which implicitly provides a mechanism to evaluate the consistency obtained from model matrices.
The present hierarchical factorisation model provides a natural constraint to estimate an appropriate number of components, since the optimal pair of values for genes () and pathways () is the one that maximises the compatibility between both sets of components (see Equation (16)). Unfortunately, given that the model simultaneously factorises both activity matrices, this approach becomes infeasible, requiring a large number of executions, with and as the set of candidate values for pathways and genes, respectively, and their sizes.
With the aim of keeping this strategy while reducing the computational burden, we use a hybrid approach (Figure 2) that consists of an initial phase of successive independent factorisations for genes and pathways, using the classic NMF [9] method. The objective here is to restrict the search to a narrow interval that potentially would contain the optimal value for and , to then apply the hierarchical model only to this subset of values. This solution reduces the number of factorisations to only , with and corresponding to the bounded interval.
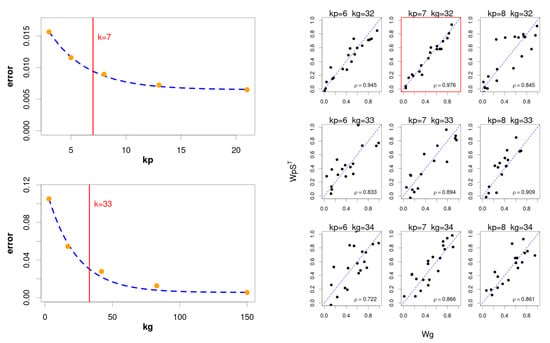
Figure 2.
Illustrative example to describe the designed protocol to estimate the optimal number of components ( and ). On the left, we see the result obtained after fitting the error curve (dashed blue lines) from 5 independent factorisations (orange dots) performed for pathways (top) and genes (bottom), respectively. The result of this process defines the values and as potential “elbow points”. From these two values we define the intervals and to be explored by the hierarchical model, giving a total of 9 joint factorisations to be performed. On the right, we show the scatter plots comparing the values of the gene-level components () and their associated pathway-level components () for the 9 joint factorisations performed by the hierarchical model. The graphs show that the pair of values and provides the best correlation between the components obtained at both levels, being therefore the pair of values to be used for subsequent factorisations.
The selection of the interval is based on the evolution of the goodness of fit, as we increase the number of components in the factorisation. In particular, we try to select an “elbow point” on the fitting curve from which the increase in the number of components does not provide a relevant improvement, since the quadratic error falls below a certain threshold. In this case, the “elbow point” is defined as follows:
where represents the selected value, K the whole tested interval, y the fitting error, and w a normalisation constant (typically ).
Furthermore, due to the goodness of fit typically exhibits a predictable exponential trend, in practice we can obtain an estimation for without needing to test all possible values within the range. In this case, the error curve is parametrised by minimising the following expression:
where , corresponding to the normalised error obtained by using k components, and z to the unknown parameter to be optimised by using a gradient descend algorithm.
The exponential fitting permits to reduce the number of independent runs to only few candidate values adequately distributed over the range. Thus, the final intervals explored by the hierarchical model is defined for genes and pathways as and , with d (with a typical value of 1) defining the interval width. Finally, the hierarchical factorisation model selects the pair of values that maximises the coherence between both sets of components:
with and being the selected number of components.
2.4. Model Validation
The proposed hierarchical factorisation model was evaluated using two complementary strategies. First, a set of specially designed simulations (see Supplementary Section S4 for details) was used to perform an exhaustive evaluation of the the accuracy of the model. The simulations allowed us to know a priori the optimal number of components ( and ) to estimate on each run. In this case, the protocol followed by the hierarchical model was compared against two classic estimation strategies: the cophenetic correlation coefficient [33] and the silhouette method [34]. In addition, we evaluated the ability of the hierarchical model to recover the matrices used to build the simulated samples (, , , y S), comparing its result against the classic NMF methodology [9] and the alternating non-negative least squares [35] approach. Furthermore, we evaluated the coherence between both sets of components ( vs. ) and their corresponding mixing matrices ( vs. ), hence determining whether the models properly reconstructed the hierarchical structure of simulated samples.
On the other hand, the hierarchical factorisation model was also evaluated using a cohort of breast cancer patients obtained from the International Cancer Genome Consortium [36]. In this case, with the aim of having the patient subtype as the main variable of interest, only patients with stage II disease were selected. To prepare the sample the gene expression data in MAF format was downloaded from the official repository (https://dcc.icgc.org/releases/current, (accessed on 1 January 2021)) and converted to a CSV file by using a custom R script. Then, the read counts by gene were normalised by means of the DeSeq2 [37] R package. Additionally, the somatic mutations of the same cohort of patients were also downloaded in MAF format, and converted into the corresponding VCF file. Finally, the clinical information was obtained from the GDAC repository (https://gdac.broadinstitute.org/, (accessed on 1 January 2021)) at the Broad Institute.
3. Results
In a first step, the hierarchical model was evaluated by using a set of 100 simulations, designed to reproduce the hierarchical structure that genes and molecular pathways show in the cell.
First, the protocol used to estimate the optimal number of components was evaluated, comparing its accuracy against two classic selection methods: the cophenetic correlation coefficient [33] and the silhouette method [34]. Figure 3 shows the difference between the expected number of components and the value provided by the three compared methods.
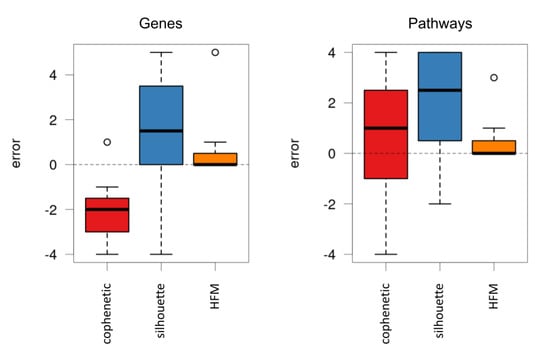
Figure 3.
Difference between the expected number of components and those estimated over 100 simulations using the cophenetic correlation coefficient, the silhouette method and the hierarchical factorisation model (HFM), for genes and pathways, respectively. As can be seen, the hierarchical model provides the smallest differences in both spaces, providing in most cases the exact number of expected components.
As can be seen, the estimation of our protocol showed a much lower error compared to the other alternatives, also reproducing the same results for both genes and pathways. Remarkably, the proposed protocol provided the exact number of components in a considerable number of cases.
On the other hand, the simulations were used to evaluate the ability of our model to recover the previously introduced components and mixing matrices. Figure 4 shows the correlation values obtained between the simulated and the estimated matrices obtained by the original NMF method [9], the alternating non-negative least squares (NNLS) approach [35], and the proposed hierarchical factorisation model.
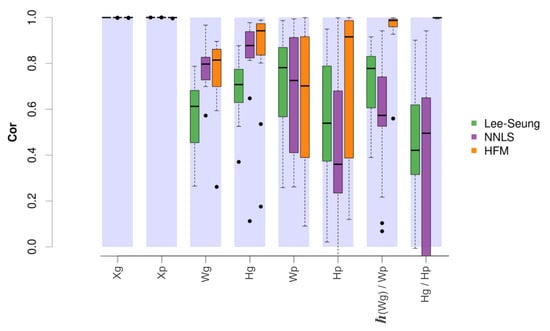
Figure 4.
Distribution of the correlation values obtained between the simulated and the optimised matrices by using the original NMF, the alternating non-negative least squares method (NNLS) and the hierarchical factorisation model (HFM). As can be seen, the hierarchical model provides the highest correlations, especially when comparing the coherence between both sets of components ( vs. ) and their corresponding mixtures ( vs. ).
In this case, the results showed for all compared methods a close to 1 correlation between the original activity matrices ( and ) and their corresponding estimated matrices, both at the gene and pathway level. Additionally, the hierarchical model obtained the best estimates for the component and mixing matrices, with the exception of the pathway level components, where the model provided slightly worse correlations. Remarkably, the distribution of correlations obtained between the pathway level component matrices and their associated gene level components after using Hipathia were considerably higher in the hierarchical model. In a similar way, the mixing matrices also showed greater correlations between both levels, providing a distribution of values close to 1.
On the other hand, real samples selected from the BRCA-US project were also analysed by the hierarchical factorisation model, with the aim of extracting the main strategies implemented in each individual tumour. For illustrative purposes, the model was used to analyse a set of selected biological functions known to be altered in the disease subtypes. In this context, the assessment of the most important genes per component (see Supplementary Section S5 for details) played an important role in interpreting the results, as their specific combination of values (and their over- and under-activation) provides a detailed characterisation of the main role of each component in the tumours.
The hierarchical factorisation model has provided a detailed view to characterise the internal composition of the individuals included in this study. The model depicts how the different gene-level components are hierarchically grouped to produce the same pathway-level responses, and how these, in turn, regulate the biological function under study. How the different components at both levels contribute to building the individuals provides a direct portrait of genomic heterogeneity observed in the cohort.
Figure 5 provides a graphical description of the internal composition of Her2 subtype patients. In particular, the different panels (see Supplementary Figure S2 for a complete description) present the component matrices obtained by the model for pathways () and genes (), respectively. In addition, the mixing matrices are shown through their binarised version ( and ) to facilitate biological interpretation. Each pathway-level component () is tagged with a distinctive colour at the top of the heatmap. Both colour and order are maintained in the corresponding rows of the mixing matrix (). Likewise, the gene-level components () and their corresponding mixtures () show the same order and colour as the pathway-level components they are associated with in the hierarchical model. On the other hand, on the right of each binarised mixture matrix, the combinations of observed components in the set of analysed patients are shown by using UpSet plots [38], ordered from left to right according to the population frequency they show at the pathway level. Similarly, the combinations at the gene level also follow the same order defined at the pathway level, and are grouped (and separated by blue dashed lines) according to the particular combination they belong to. Below each UpSet plot, the combinations are shown as a heatmap obtained by adding the set of components included on each particular observed combination.
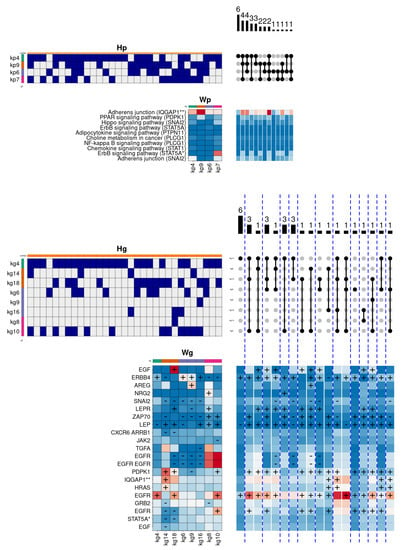
Figure 5.
Graphical representation of the hierarchical model obtained for the biological function cellular response to epidermal growth factor stimulus, applied to the Her2 subtype. The most frequent combination observed at the pathway level relies on the kp4 component (coloured green), overactivating two signalling cascades of the Adherens junction pathway. In the gene space, the kp4 component is associated with the kg4 component, having as relevant genes ERBB4 and EGFR, both belonging to the epidermal growth factor receptor family.
In this example, Figure 5 describes the internal composition of the Her2 subtype in the biological function cellular response to epidermal growth factor stimulus. This subtype is characterised by very low oestrogen and progesterone hormone receptor activity, and by showing a high degree of over-activation in the gene ERBB2. This gene belongs to the epidermal growth factor membrane receptor family, responsible for regulating, among other functions, cell proliferation, contributing significantly to the higher mortality of Her2 subtype compared to other subtypes. In this case, the model shows that the most frequent pathway-level component combination consists of the exclusive use of the kp4 component (coloured in green), mainly showing the overactivation of two signalling cascades of the Adherens junction pathway. In the gene space, the kp4 component is associated with a single combination represented by the gene-level component kg4, containing the relevant genes ERBB4 and EGFR, also belonging to the epidermal growth factor receptor family. Likewise, two secondary combinations are observed, including the kp9 component (coloured in orange), that partially activates PPAR signalling pathway. In this case, the kp9 component is represented in the gene space by two distinct components, corresponding to the kg14, which simultaneously overactivates the genes PDPK1 (involved in the response to growth factors and insulin), IQGAP1 (involved in cell cycle regulation) and HRAS (belonging to the RAS family of oncogenes), and the kg18 component, which again overactivates PDPK1 and EGFR, and adding the epidermal growth factor gene (EGF). In addition, the two secondary combinations incorporate the pathway component kp7 (coloured in pink), leading to an increase in the ErbB signalling pathway activity, and the component kp6 (coloured in magenta), overactivating again one of the two cascades of the Adherens junction pathway. These components are represented in the gene space by the components kg6/8/16 and kg8/10, respectively, contributing to the overactivation of other relevant genes, such as AREG (also belonging to the epidermal growth factor receptor family) or NREG2 (involved in the growth and differentiation of epithelial cells).
The same approach has been applied to understand the heterogeneity observed in patients belonging to the Basal subtype. The Basal subtype tumours are recognised by being usually negative for both hormone and the ERBB2 receptors. This circumstance impedes the use of the most usual treatments, showing greater tumour growth, aggressiveness, and higher mortality compared to other subtypes. One of the most altered signalling pathways in the Basal subtype is the Notch signalling pathway. This is a highly conserved pathway in mammals, with an essential role in embryonic development and cell fate regulation in mammary glands throughout different stages of development. The Figure 6 shows the internal composition of the Basal subtype in this biological function.
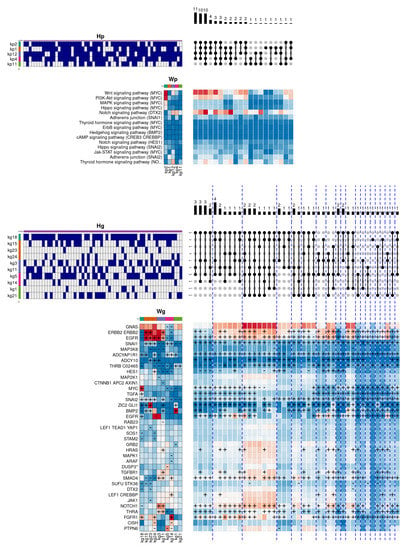
Figure 6.
Graphical representation of the hierarchical model obtained for the biological function Notch signalling, applied to the Basal subtype.The most frequent pathway-level combination relies on the components kp2 (dark green), kp12 (magenta), and kp4 (pink) components, overactivating signalling cascades from the Wnt, PI3K-Akt, MAPK, Hippo, and Adherens junction pathways. Interestingly, the combination also activates the Notch signalling pathway, highly relevant in the Basal subtype. At the gene space, these components include several cancer-related genes such as MYC, EGFR, SNAI1, or NOTCH1, among others.
As can be seen, the hierarchical model provides a more variable description than the previous one. Here, three main combinations are observed, representing the majority of individuals, where the Wnt and Notch signalling pathways appear heavily activated. In this case, the combinations share the components kp2 (dark green), kp12 (magenta), and kp4 (pink). The first component (kp2) describes the overactivation of signalling cascades from the Wnt, PI3K-Akt, MAPK, and Hippo signalling pathways, commonly altered in different types of cancer. This component is associated in gene space with the kg18 component, which simultaneously overactivates the genes MYC (an oncogene involved in cell cycle regulation and apoptosis), TGFA (a natural ligand of the epidermal growth factor receptor), SNAI2 (a natural repressor of the e-cadherin complex, commonly inhibited in carcinomas), EGFR and FGFR1 (previously involved in tumour growth and metastasis). On the other hand, the component kp12 contributes activating the signalling pathway Notch, highly relevant in the Basal subtype, as well as the signalling pathway that regulates the thyroid hormone reception. This component is associated in gene space with the kg3/11 components that, besides to overactivate the EGFR and ERBB2 receptors, contribute to the composition overactivating the genes TGFBR1 (another transforming growth factor beta receptor), SMAD4 (activated by the transforming growth factor beta), THRA (a nuclear thyroid hormone receptor) and, notably, NOTCH1 (involved in the regulation of cell fate, differentiation, and proliferation). For its part, the kp4 component contributes by reinforcing the activation of the Notch pathway, including the Adherens junction pathway. This component is associated in the gene space with the kg5/14 components, which, besides increasing the activation of the SMAD4 and FGFR1 genes, contributes by overactivating the SNAI1 gene (also a repressor of the e-caderin complex, and involved in the epithelial-mesenchymal transition). Apart from the three described components, the two secondary combinations involve the kp1 (orange) and kp11 (light green) components. In this case, the kp1 component helps to reinforce the activation of the PI3K-Akt, Notch, and Adherence junction pathways. In particular, this component associates in the gene space with the kg15/23/24 components, which prominently overactivate the previously described ERBB2 and EGFR receptors. In addition, they also overactivate the genes SNAI1, SNAI2 and BMP2 (a natural ligand of transforming growth factor beta, involved in the regulation of cell proliferation, differentiation, and immune response). Finally, the kp11 component, which again reinforces the thyroid hormone reception and the activation of the Notch pathway, is associated with the gene-level components kg1/21, responsible for overactivating the genes THRB (also a nuclear thyroid hormone receptor), BMP2 and ZIC2 (a natural repressor of the dopamine receptor).
Unlike the Basal and Her2 subtypes, the Luminal A and B are characterised by showing high activity in hormone receptors, especially the oestrogen receptor. These are the most common subtypes in breast cancer, showing the best prognosis.
Figure 7 shows the result obtained by the hierarchical model for the luminal subtypes in the biological function Response to oestrogen. In this case, the figure also describes the components that are specific to the Luminal A subtype (in green), to the Luminal B subtype (in red), and those that are common to both subtypes (in black). Additionally, the gene labels show the same colour code, depending on the components in which they are relevant.
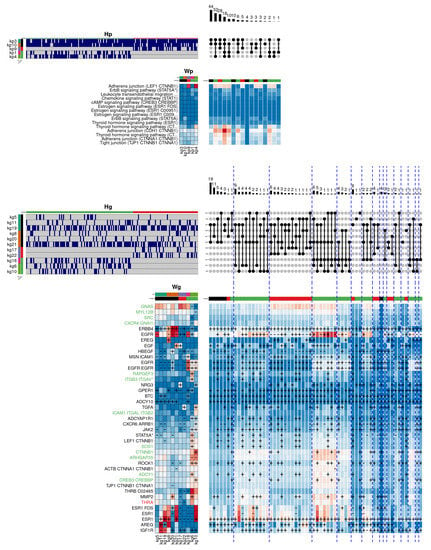
Figure 7.
Graphical representation of the hierarchical model obtained in the biological function response to oestrogen, applied to the subtypes Luminal A and Luminal B. The most frequent pathway-level combination is shared between both luminal subtypes, involving the kp3 and kp10 components. These components mainly activate thyroid hormone reception, as well as Adherens junction, Tight junction and ErbB signalling pathways. At the gene level, the associated components activate relevant genes as the growth factor receptors ERBB4 and AREG, as well as ESR1, one of the oestrogen receptor isoforms.
In this example, the most frequent pathway-level combination is shared between both luminal subtypes, involving the kp3 and kp10 components. The first component shows a reasonable activation of thyroid hormone reception, as well as Adherens junction and Tight junction pathways, related to the physical interaction that occurs between adjacent cells. In this case, the kp3 component is related in gene space to the kg5/11/19 components. These components have as relevant genes the epidermal growth factor receptors ERBB4 and AREG, and notably, the ESR1 gene, encoding the major oestrogen receptor isoform. The second pathway-level component (kp10), contributes to activating the same pathways, although adding in this case the ErbB signalling pathway, involved in the regulation of several essential biological functions. The component associates with kg8/20/21 components, contributing again to the activation of the ERBB4 and ESR1 genes. In addition, one of the components (kg8) specifically activates the genes EREG (a specific ligand of the epidermal growth factor receptors) and GPER1 (whose protein preferentially binds oestrogens). Likewise, the genes HBEGF (an important paralog of the AREG gene) and MMP2 (belonging to a family of enzymes responsible for degrading some components of the extracellular matrix) are also activated in the same group.
The second most frequent combination at the pathway level is specifically associated with the Luminal A subtype. The combination adds the kp4 component to the previous two components, and notably activates a distinct cascade of the Adherens junction pathway, as well as an additional cascade of the thyroid hormone response. Here, the component is associated with the gene-level components kg10/6/10, that simultaneously activate a large groups of genes, especially the kg6 component, which activates the genes EGFR, RAPGEF3 (involved in angiogenesis), ITGB3, GPER1, STAT5A (which regulates the expression of milk proteins during lactation), LEF1, SOS1, ROCK1, ADCY1, and MMP2. On the other hand, the kg10 component also simultaneously activates a large number of genes, some shared with the kg6 component, but specifically activating the genes NRG3 (a specific ligand of the ERBB4 receptor), TGFA, CTNNB1, and CREB3 (involved in cell cycle regulation), among others. On the other hand, the third combination is specific to the Luminal B subtype, adding the kp9 component, which notably activates the previous Adherens junction cascade, and reasonably reinforcing other already activated cascades. The kp9 component specifically associates in the gene space with the kg17/22 components that show a quite heterogeneous pattern: whereas the kg17 component clearly activates the EGF and NRG3 genes, the kg22 component activates TGFA and partially HBEGF. Finally, the hierarchical model identifies a significant number of genes associated with the Luminal A subtype (in green). This view suggests that the two luminal subtypes, in spite of sharing a common hormone receptor activity, show clear differences in the oestrogen response regulation.
Another important difference between the two luminal subtypes is the higher level of cellular proliferation observed in tumours of Luminal B subtype, producing a significant increase in mortality rates compared to individuals of Luminal A subtype. In order to determine the molecular differences between the two subtypes in cell proliferation, Figure 8 describes the regulation of the G2 M transition of mitotic cell cycle function, which describes an essential part of the cell cycle.
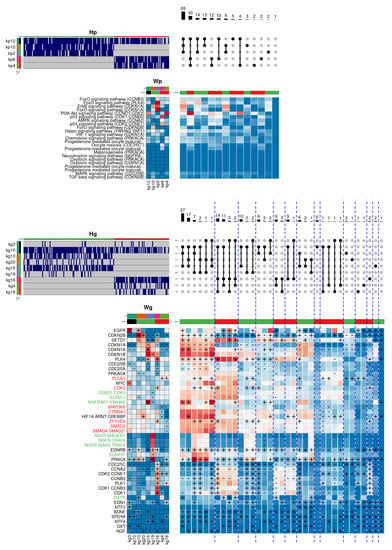
Figure 8.
Graphical representation of the hierarchical model obtained in the biological function G2 M transition of mitotic cell cycle, applied to the subtypes Luminal A and Luminal B. The model found two dominant pathway-level combinations concentrating the majority of individuals. Both combinations share the kp12 component (green), that overactivates the PI3K-Akt pathway. Interestingly, the first combination is specific to the Luminal A subtype and adds the kp10 (orange) and kp2 (magenta) components, that activate mainly FoxO and ErbB signalling pathways, and partially the MAPK and TGF-beta pathways. These components are associated in the gene space with the kg13/20 and kg15/19 components, respectively, which characteristically activate the cyclin inhibitors CDKN1A, CDKN1B, and CDKN2B. On the other hand, the second combination is specific to the Luminal B subtype, incorporating the components kp6 (pink) and kp4 (light green), which significantly activate the PI3K-Akt pathway and the P53 protein activation pathway. These components are associated in the gene space with the kg16 and kg4/18 components, activating a set of genes that positively regulates cell proliferation, such as PLK1, or the cyclins CDC25C, CCNA2, CDK1, and CDK2.
In this case, the figure shows two pathway-level combinations concentrating the majority of individuals. Both combinations make use of the kp12 component (green), responsible for partially activating the signalling pathways FoxO, Hippo, AMPK, Chemokine, and Progesterone mediated oocyte maturation, as well as the overactivation of the PI3K-Akt pathway. This component is associated in gene space with the kg3/10 components. In this case, the kg10 component is associated with both subtypes, having as relevant genes PRKCA (involved in cell adhesion, differentiation, and proliferation) BDNF, and SPDYA (involved in cell cycle phase transition).
The first combination is specific to the Luminal A subtype and, besides the kp12 component, it adds the kp10 (orange) and kp2 (magenta) components, which highly activate the FoxO and ErbB signalling pathways, and partially the MAPK and TGF-beta pathways. These components are associated in gene space with the kg13/20 and kg15/19 components, respectively, which characteristically activate the cyclin inhibitors CDKN1A, CDKN1B, and CDKN2B, in addition to activating a block of genes consisting of NGFR, NGFRAP1, EDRNB, PRKCA, EDF1, and NTF4. The second combination is specific to the Luminal B subtype and, besides the global component kp12, it incorporates the components kp6 (pink) and kp4 (light green), which significantly activate the PI3K-Akt pathway and the P53 protein activation pathway. These components are associated in the gene space with the kg16 and kg4/18 components, respectively. In this case, the kg16 component, which shows a major prevalence, is responsible for characteristically overactivating a set of genes directly related to the positive regulation of the cell cycle. In particular, the component activates the cyclin genes CDC25C, CCNA2, CDK1, CDK2, CCNB3, as well as PLK1. Interestingly, the observed differences between the two combinations explain, in turn, the differences between the two luminal subtypes, whereas the Luminal A subtype clearly activates some cell cycle inhibitors, the components associated with the Luminal B subtype simultaneously overactivate a block of genes that promote this biological function [39].
4. Discussion
The proposed methodology has been designed to address the statistical modelling of cell function. In this work, modelling is performed both at the gene and molecular pathway level, establishing relevant connections between both spaces that allow explaining a substantial part of the genomic variability observed in patients with the same type of cancer. To this end, the model integrates a set of equations derived from the Hipathia tool that implicitly represent the structure and topology of the signalling networks, describing the influence of each constituent gene on the activity of those cascades where it participates.
The statistical modelling has been approached by using NMF. This technique, which imposes a positivity constraint in the model matrices, describes the observations as a positive-sum of more fundamental parts, facilitating the direct interpretation of individual components. In this case, we developed a statistical model that simultaneously factorises the activity of genes and pathways within the same group of patients. To this end, the model imposes a series of constraints during optimisation to guarantee the extraction of two sets of hierarchically compatible components, and, therefore, also coherent at the biological level.
Unlike other approaches used to perform a joint factorisation between two or more input matrices, the proposed model establishes a hierarchical relationship between the components of both levels. This approach provides a practical mechanism for clustering groups of gene-level components with a similar response at the molecular pathway level, thereby allowing the modelling of genomic variability due to the natural structure of molecular pathways. To perform this task, the model integrates the topology of signalling pathways. This information provides very specific knowledge about the nature of the input matrices, allowing to precisely establish the hierarchical connections between both sets of components.
Furthermore, we provided a formal definition to describe the internal composition () as a mathematical object composed of the hierarchical model matrix (S), the latent components found at both levels ( and ), their corresponding binarised mixture matrices ( and ), the observed component combinations ( and ), their frequencies in the population of samples ( and ), the derived meta-samples ( and ) and the gene relevance matrix (G). Together, these matrices yield a very detailed portrait about the molecular composition of patients, providing a valuable tool for the design of future treatments.
The application of the hierarchical factorisation model has provided accurate results. The first part of its evaluation has been carried out by using a set of simulations specially designed to reproduce the hierarchical structure that the cells show in their functioning. In this case, the simulations allowed to accurately evaluate the ability of the model to find a set of previously introduced latent components, showing a higher performance compared to non-hierarchical classic NMF approaches. Likewise, the simulations have allowed us to assess the expected error when estimating the optimal number of components to be used in the model, offering a much higher accuracy than other classic approaches such as the cophenetic correlation coefficient or the silhouette method.
In a similar way, the application of the hierarchical model to a set of real patients also produced interesting results. In particular, a comprehensive view of the hierarchical model results has been graphically presented, describing internal features of the altered biological functions that could potentially explain the differences between subtypes. In this case, the graphical representation not only allowed us to determine which were the main components at the pathway level for each subtype, but also the most frequent combinations of components in the cohort, which is a direct representation of the genomic heterogeneity within a group of samples. Additionally, the hierarchical model allowed us to determine the existence of components and combinations associated with more than one subtype in the disease, potentially describing common features of interest to design more generic treatments. In this sense, the hierarchical model also helped to identify the most frequent gene-level components within the observed combinations, thus suggesting possible combined therapies that target the set of genes that are simultaneously activated within the same gene-level component, considered essential in one or more subtypes.
At the biological level, hierarchical models allowed understanding the internal structure of the Her2 subtype in the regulation of epidermal growth factor, the inner composition of the Basal subtype in the Notch signalling pathway and the differences between the Luminal A and Luminal B subtypes in the regulation of oestrogen response and the cell cycle regulation. These results confirm previous findings in the disease and will validate new future results obtained by analysing lesser-known biological processes in the study of cancer.
5. Conclusions
The model presented in this work has been designed to address the study of genomic heterogeneity in a group of patients with cancer disease, representing one of the most inherent aspects of tumours. The model, conceived from a systems biology point of view, has provided a portrait of the internal composition of patients, describing in detail a set of cellular strategies that individual tumours implement to regulate a certain biological function altered in the disease.
In this work, the hierarchical model has been applied to analyse a set of biological processes classically altered in breast cancer, obtaining a detailed description of them. As a future step, we plan to extend this analysis to the study of a broader set of biological processes. This work will provide a much more general description of the cellular alterations caused by the disease, providing valuable clues to understand the regulation of biological processes that are less understood.
To develop this work, it has been essential to adopt a factorisation technique, such as NMF, extended in our case to factorise the activity of genes and pathways simultaneously, converging to biologically compatible solutions. In addition, the proposed model integrates the topology of signalling pathways, thus providing a factorisation method that integrates specific prior knowledge about the context in which it is applied.
We envisage that the use of hierarchical designs, such as the one proposed in this work, will be essential to better understand how the different levels of heterogeneity in the cell are connected, and how they produce different initial genomic configurations that ultimately lead to the development of the same hallmarks of cancer.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/math9212833/s1, Figure S1: Protocol to obtained the customised Hipathia function, Figure S2: Guide to understand the internal composition plot, Table S1: Categories to define somatic mutation effect.
Author Contributions
Conceptualisation, J.C.-C.; Methodology, J.C.-C.; Software, J.C.-C.; Writing— original draft preparation, J.C.-C.; Writing—review and editing, A.L.-Q., D.C. and J.D.; Supervision, A.L.-Q., D.C. and J.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by grants PID2020-117979RB-I00 from the Spanish Ministry of Science and Innovation, PT17/0009/0006 from the Instituto de Salud Carlos III (ISCIII), co-funded with European Regional Development Funds (ERDF). Additionally, D.C. and A.L.-Q. would like to thank the Spanish Ministerio de Ciencia e Innovación—Agencia Estatal de Investigación for grant PID2019-106341GB-I00 (jointly financed by the European Regional Development Fund, FEDER).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Breast cancer data was obtained from the ICGC official repository at https://dcc.icgc.org/releases/current (accessed on 1 January 2021). Clinical information was obtained from the GDAC repository at https://gdac.broadinstitute.org/ (accessed on 1 January 2021) hosted at the Broad Institute.
Acknowledgments
The authors want to thank Eva Alloza for her comments and suggestions on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Torre, L.A.; Siegel, R.L.; Ward, E.M.; Jemal, A. Global Cancer Incidence and Mortality Rates and Trends—An Update. Cancer Epidemiol. Biomarkers Prev. 2016, 25, 16–27. [Google Scholar] [CrossRef] [Green Version]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martincorena, I.; Campbell, P.J. Somatic mutation in cancer and normal cells. Science 2015, 349, 1483–1489. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Fang, Q.; Ge, Z.; Yu, N.; Xu, S.; Fan, X. Common BRCA1 and BRCA2 mutations in breast cancer families: A meta-analysis from systematic review. Mol. Biol. Rep. 2012, 39, 2109–2118. [Google Scholar] [CrossRef] [PubMed]
- Stein-O’Brien, G.L.; Arora, R.; Culhane, A.C.; Favorov, A.V.; Garmire, L.X.; Greene, C.S.; Goff, L.A.; Li, Y.; Ngom, A.; Ochs, M.F.; et al. Enter the Matrix: Factorization Uncovers Knowledge from Omics. Trends Genet. 2018, 34, 790–805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kossenkov, A.V.; Ochs, M.F. Matrix factorisation methods applied in microarray data analysis. Int. J. Data Min. Bioinform. 2010, 4, 72–90. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Türkmen, A.C. A Review of Nonnegative Matrix Factorization Methods for Clustering. 2015, pp. 1–23. Available online: https://arxiv.org/abs/1507.03194 (accessed on 1 April 2019).
- Hofree, M.; Shen, J.P.; Carter, H.; Gross, A.; Ideker, T. Network-based stratification of tumor mutations. Nat. Methods 2013, 10, 1108–1115. [Google Scholar] [CrossRef]
- Alexandrov, L.B.; Nik-Zainal, S.; Wedge, D.C.; Campbell, P.J.; Stratton, M.R. Deciphering signatures of mutational processes operative in human cancer. Cell Rep. 2013, 3, 246–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayati, M.; Rabiee, H.R.; Mehrbod, M.; Vafaee, F.; Ebrahimi, D.; Forrest, A.R.R.; Alinejad-Rokny, H. CANCERSIGN: A user-friendly and robust tool for identification and classification of mutational signatures and patterns in cancer genomes. Sci. Rep. 2020, 10, 1286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Repsilber, D.; Kern, S.; Telaar, A.; Walzl, G.; Black, G.F.; Selbig, J.; Parida, S.K.; Kaufmann, S.H.; Jacobsen, M. Biomarker discovery in heterogeneous tissue samples -taking the in-silico deconfounding approach. BMC Bioinform. 2010, 11, 27. [Google Scholar] [CrossRef] [Green Version]
- Gaujoux, R.; Seoighe, C. Semi-supervised Nonnegative Matrix Factorization for gene expression deconvolution: A case study. Infect. Genet. Evol. 2012, 12, 913–921. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Liu, C.C.; Li, W.; Shen, H.; Laird, P.W.; Zhou, X.J. Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucleic Acids Res. 2012, 40, 9379–9391. [Google Scholar] [CrossRef]
- Ray, B.; Liu, W.; Fenyo, D. Adaptive multiview nonnegative matrix factorization algorithm for integration of Multimodal Biomedical Data. Cancer Inform. 2017, 16, 1176935117725727. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, S. Learning common and specific patterns from data of multiple interrelated biological scenarios with matrix factorization. Nucleic Acids Res. 2019, 47, 6606–6617. [Google Scholar] [CrossRef] [PubMed]
- Ding, Q.; Sun, Y.; Shang, J.; Li, F.; Zhang, Y.; Liu, J.X. NMFNA: A Non-negative Matrix Factorization Network Analysis Method for Identifying Modules and Characteristic Genes of Pancreatic Cancer. Front. Genet. 2021, 12, 1115. [Google Scholar] [CrossRef]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Subramanian, A.; Tamayo, P.; Mootha, V.K.; Mukherjee, S.; Ebert, B.L.; Gillette, M.A.; Paulovich, A.; Pomeroy, S.L.; Golub, T.R.; Lander, E.S.; et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 2005, 102, 15545–15550. [Google Scholar] [CrossRef] [Green Version]
- Al-Shahrour, F.; Arbiza, L.; Dopazo, H.; Huerta-Cepas, J.; Minguez, P.; Montaner, D.; Dopazo, J. From genes to functional classes in the study of biological systems. BMC Bioinform. 2007, 8, 114. [Google Scholar] [CrossRef] [Green Version]
- Sebastián-León, P.; Carbonell, J.; Salavert, F.; Sanchez, R.; Medina, I.; Dopazo, J. Inferring the functional effect of gene expression changes in signaling pathways. Nucleic Acids Res 2013, 41, W213–W217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarca, A.L.; Draghici, S.; Khatri, P.; Hassan, S.S.; Mittal, P.; Kim, J.S.; Kim, C.J.; Kusanovic, J.P.; Romero, R. A novel signaling pathway impact analysis. Bioinformatics 2009, 25, 75–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martini, P.; Sales, G.; Massa, M.S.; Chiogna, M.; Romualdi, C. Along signal paths: An empirical gene set approach exploiting pathway topology. Nucleic Acids Res. 2013, 41, e19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haynes, W.A.; Higdon, R.; Stanberry, L.; Collins, D.; Kolker, E. Differential expression analysis for pathways. PLoS Comput. Biol. 2013, 9, e1002967. [Google Scholar] [CrossRef]
- Jacob, L.; Neuvial, P.; Dudoit, S. More power via graph-structured tests for differential expression of gene networks. Ann. Appl. Stat. 2012, 6, 561–600. [Google Scholar] [CrossRef]
- Hidalgo, M.R.; Cubuk, C.; Amadoz, A.; Salavert, F.; Carbonell-Caballero, J.; Dopazo, J. High throughput estimation of functional cell activities reveals disease mechanisms and predicts relevant clinical outcomes. Oncotarget 2016, 8, 5160. [Google Scholar] [CrossRef] [Green Version]
- Amadoz, A.; Hidalgo, M.R. A comparison of mechanistic signaling pathway activity analysis methods. Briefings Bioinform. 2019, 20, 1655–1668. [Google Scholar] [CrossRef]
- Rian, K.; Hidalgo, M.R.; Çubuk, C.; Falco, M.M.; Loucera, C.; Esteban-Medina, M.; Alamo-Alvarez, I.; Peña-Chilet, M.; Dopazo, J. Genome-scale mechanistic modeling of signaling pathways made easy: A bioconductor/cytoscape/web server framework for the analysis of omic data. Comput. Struct. Biotechnol. J. 2021, 19, 2968–2978. [Google Scholar] [CrossRef]
- Ardia, D.; Boudt, K.; Carl, P.; Mullen, K.M.; Peterson, B.G. Differential Evolution with DEoptim: An Application to Non-Convex Portfolio Optimization. R. J. 2011, 3, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Saraçli, S.; Doǧan, N.; Doǧan, I. Comparison of hierarchical cluster analysis methods by cophenetic correlation. J. Inequalities Appl. 2013, 2013, 203. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Park, H. Nonnegative Matrix Factorization Based on Alternating Nonnegativity Constrained Least Squares and Active Set Method. SIAM J. Matrix Anal. Appl. 2008, 30, 713–730. [Google Scholar] [CrossRef]
- Hudson, T.J.; Anderson, W.; Aretz, A.; Barker, A.D.; Bell, C.; Bernabé, R.R.; Bhan, M.K.; Calvo, F.; Eerola, I.; Gerhard, D.S.; et al. International network of cancer genome projects. Nature 2010, 464, 993–998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conway, J.R.; Lex, A.; Gehlenborg, N. UpSetR: An R package for the visualization of intersecting sets and their properties. Bioinformatics 2017, 33, 2938–2940. [Google Scholar] [CrossRef] [Green Version]
- Gampenrieder, S.P.; Rinnerthaler, G.; Greil, R. CDK4/6 inhibition in luminal breast cancer. Memo 2016, 9, 76–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).