Structural Properties of Connected Domination Critical Graphs

Abstract

A graph G is said to be k-${\gamma }_c$-critical if the connected domination number ${\gamma }_c\left(G\right)$ is equal to k and ${\gamma }_c(G+uv)<k$ for any pair of non-adjacent vertices u and v of G. Let $\zeta$ be the number of cut vertices of G and let ${\zeta }_0$ be the maximum number of cut vertices that can be contained in one block. For an integer $\ell \ge 0$, a graph G is ℓ-factor critical if $G-S$ has a perfect matching for any subset S of vertices of size ℓ. It was proved by Ananchuen in 2007 for $k=3$, Kaemawichanurat and Ananchuen in 2010 for $k=4$ and by Kaemawichanurat and Ananchuen in 2020 for $k\ge 5$ that every k-${\gamma }_c$-critical graph has at most $k-2$ cut vertices and the graphs with maximum number of cut vertices were characterized. In 2020, Kaemawichanurat and Ananchuen proved further that, for $k\ge 4$, every k-${\gamma }_c$-critical graphs satisfies the inequality ${\zeta }_0\left(G\right)\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$. In this paper, we characterize all k-${\gamma }_c$-critical graphs having $k-3$ cut vertices. Further, we establish realizability that, for given $k\ge 4$, $2\le \zeta \le k-2$ and $2\le {\zeta }_0\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$, there exists a k-${\gamma }_c$-critical graph with $\zeta$ cut vertices having a block which contains ${\zeta }_0$ cut vertices. Finally, we proved that every k-${\gamma }_c$-critical graph of odd order with minimum degree two is 1-factor critical if and only if $1\le k\le 2$. Further, we proved that every k-${\gamma }_c$-critical $K_{1,3}$-free graph of even order with minimum degree three is 2-factor critical if and only if $1\le k\le 2$.

1. Introduction

For a natural number n, we let $\left[n\right]=\{1,2,\dots ,n\}$. For standard terminology of graphs, we refer the reader to [1,2]. All graphs in this paper are finite, undirected and simple (no loops or multiple edges). For a graph G, let $V\left(G\right)$ denote the set of vertices of G and let $E\left(G\right)$ denote the set of edges of G. For $S\subseteq V\left(G\right)$, $G\left[S\right]$ denotes the subgraph of G induced by S. The open neighborhood $N_G\left(v\right)$ of a vertex v in G is $\{u\in V(G):uv\in E(G\left)\right\}$. Further, the closed neighborhood $N_G\left[v\right]$ of a vertex v in G is $N_G\left(v\right)\cup \left\{v\right\}$. For subsets X and Y of $V\left(G\right)$, $N_Y\left(X\right)$ is the set $\{y\in Y:yx\in E(G)$ for some $x\in X\}$. For a subgraph H of G, we use $N_Y\left(H\right)$ instead of $N_Y\left(V\left(H\right)\right)$ and we use $N_H\left(X\right)$ instead of $N_{V\left(H\right)}\left(X\right)$. If $X=\left\{x\right\}$, we use $N_Y\left(x\right)$ instead of $N_Y\left(\left\{x\right\}\right)$. The degree $deg\left(x\right)$ of a vertex x in G is $|N_G\left(x\right)|$. The minimum degree of G is denoted by $\delta \left(G\right)$. When no ambiguity occur, we write $N\left(x\right),N\left(X\right)$ and $\delta$ instead of $N_G\left(x\right),N_G\left(X\right)$ and $\delta \left(G\right)$, respectively. An end vertex is a vertex of degree one and a support vertex is the vertex which is adjacent to an end vertex. A tree is a connected graph with no cycle. A star $K_{1,n}$ is a tree containing one support vertex and n end vertices. The support vertex of a star is called the center. For a connected graph G, a vertex subset S of G is called a cut set if $G-S$ is not connected. We let ${\omega }_o(G-S)$ be the number of components of $G-S$ containing odd number of vertices. In particular, if $S=\left\{v\right\}$, then v is called a cut vertex of G. That is, $G-v$ is not connected. A block B of a graph G is a maximal connected subgraph such that B has no cut vertex. An end block of G is a block containing exactly one cut vertex of G. For graphs H and G, a graph G is said to be H-free if G does not contain H as an induced subgraph. For a connected graph G, a bridge $xy$ of G is an edge such that $G-xy$ is not connected.

For a finite sequence of graphs $G_1,\dots ,G_l$ for $l\ge 2$, the sequential joins $G_1\vee \cdots \vee G_l$ is the graph consisting of the disjoint union of $G_1,\dots ,G_l$ and joining edges from every vertex of $G_i$ to every vertex of $G_{i+1}$ for $1\le i\le l-1$. In particular, for a subgraph H of $G_2$, the join $G_1\vee {}_{H}G{}_2$ is the graph consisting of the disjoint union of $G_1$ and $G_2$ and joining edges from every vertex of $G_1$ to every vertex of H. As the join operation is run over vertices, for a vertex x and a set X of vertices, the join $x\vee X$ is the graph consisting of the disjoint union of $\left\{x\right\}$ and X and joining edges from x to every vertex in X. In the following, we may call the sequential joins shortly the joins while the operation is still the same, that is, to add all edges between only two consecutive graphs in the order. For a subgraph H of G, H is maximal complete subgraph of G if for any complete subgraph $H^{\prime }$ of G such that $V\left(H\right)\subseteq V\left(H^{\prime }\right)$, we have $V\left(H\right)=V\left(H^{\prime }\right)$.

The distance $d(u,v)$ between vertices u and v of G is the length of a shortest $(u,v)$-path in G. The diameter of G $diam\left(G\right)$ is the maximum distance of any two vertices of G. For a non-negative integer k, a graph G is k-diameter critical if $diam\left(G\right)=k$ and $diam(G-uv)>k$ for any edge $uv\in E\left(G\right)$. A matching of a graph G is a set of edges which are not incident to a common vertex. A matching M of a graph G is perfect if $V\left(M\right)=V\left(G\right)$. For a non-negative integer ℓ, a graph G is ℓ-factor critical if $G-S$ has a perfect matching where S is any set of ℓ vertices, in particular, a graph G has a perfect matching if $\ell =0$, further, G is factor critical if $\ell =1$ and is bi-critical if $\ell =2$. For subsets D and X of $V\left(G\right)$, D dominates X if every vertex in X is either in D or adjacent to a vertex in D. If D dominates X, then we write $D\succ X$ and we also write $a\succ X$ when $D=\left\{a\right\}$. Moreover, if $X=V\left(G\right)$, then D is a dominating set of G and we write $D\succ G$ instead of $D\succ V\left(G\right)$. A connected dominating set of a graph G is a dominating set D of G such that $G\left[D\right]$ is connected. If D is a connected dominating set of G, we then write $D{\succ }_{c}G$. A smallest connected dominating set is called a ${\gamma }_c$-set. The cardinality of a ${\gamma }_c$-set is called the connected domination number of G and is denoted by ${\gamma }_c\left(G\right)$. A graph G is said to be k-${\gamma }_c$-critical if ${\gamma }_c\left(G\right)=k$ and ${\gamma }_c(G+uv)<k$ for any pair of non-adjacent vertices u and v of G.

In the structural characterizations of k-${\gamma }_c$-critical graphs, Chen et al. [3] showed that every 1-${\gamma }_c$-critical graph is a complete graph while every 2-${\gamma }_c$-critical graph is the complement of the disjoint union of at least two stars. However, for $k=3$, it turns out that the k-${\gamma }_c$-critical graphs have no complete characterization in the sense of free graphs (see in [4], Chapter 5). Interestingly, it was proved by Hanson and Wang [5] that for a connected graph G, the graph G is 3-${\gamma }_c$-critical if and only if the complement of G is 2-diameter critical. For a study on k-diameter critical graphs see Almalki [6]. In [7], Ananchuen proved that every 3-${\gamma }_c$-critical graph contains at most one cut vertex and also established characterizations of 3-${\gamma }_c$-critical graphs having a cut vertex. For more studies related with 3-${\gamma }_c$-critical graphs see the works in [8,9,10]. For $k=4$, Kaemawichanurat and Ananchuen [11] proved that every 4-${\gamma }_c$-critical graph contains at most two cut vertices and the characterization of the such graphs having two cut vertices was given. Further, Kaemawichanurat and Ananchuen [12] established that every k-${\gamma }_c$-critical graphs contains at most $k-2$ cut vertices when $k\ge 5$. They also characterized that there is exactly one class of k-${\gamma }_c$-critical graphs having $k-2$ cut vertices. In the same paper, the authors established the maximum number of cut vertices that every block of the graph can have. That is:

Theorem 1

([12]). Let G be a k-${\gamma }_c$-critical graph containing ζ cut vertices and let ${\zeta }_0\left(G\right)$ be the maximum number of cut vertices of G that can be in a block of G. Then,

$${\zeta }_0\left(G\right)\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}.$$

Very recently, Henning and Kaemawichanurat [13] characterized all the eleven classes of k-${\gamma }_c$-critical graphs satisfying the upper bound of Theorem 1. For more related works on connected domination critical graphs see [14,15,16,17,18,19,20,21].

In this paper, for $k\ge 5$, we characterize all k-${\gamma }_c$-critical graphs having $k-3$ cut vertices. Further, we establish realizability that, for given $k\ge 4$, $2\le \zeta \le k-2$ and $2\le {\zeta }_0\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$, there exists a k-${\gamma }_c$-critical graph with $\zeta$ cut vertices having a block which contains ${\zeta }_0$ cut vertices. We also proved that every k-${\gamma }_c$-critical graph of odd order with $\delta \ge 2$ is factor critical if and only if $1\le k\le 2$. We prove that every k-${\gamma }_c$-critical $K_{1,3}$-free graph of even order with $\delta \ge 2$ is factor critical if and only if $1\le k\le 2$. All the main results are shown in Section 2, while their proofs are given in Section 4. We present some useful results that are used in the proofs in Section 3.

2. Main Results

First, we give constructions of two classes of such graphs which will be the characterizations of k-${\gamma }_c$-critical graphs with $k-3$ cut vertices. Let

$$\mathit{i}=(i_1,i_2,\dots ,i_{k-3})$$

be a $k-3$ tuple such that $i_1,i_2,\dots ,i_{k-3}\in \{0,1\}$ and ${\mathsf{\Sigma }}_{j=1}^{k-3}{i}_j=1$ (there is exactly one $l\in \{1,2,\dots ,k-3\}$ such that $i_l=1$ and $i_{l^{\prime }}=0$ for all $l^{\prime }\in \{1,2,\dots ,k-3\}-\left\{l\right\}$).

The class${\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$

For a $k-3$ tuple $\mathit{i}=(0,0,\dots ,i_l,\dots ,0)$ where $i_l=1$ and $i_{l^{\prime }}=0$ for $1\le l\ne l^{\prime }\le$$k-3$, a graph G in the class ${\mathcal{G}}_1\mathit{i}$ can be constructed from paths $c_0,c_1,\dots ,c_{l-1}$ and $c_l,c_{l+1},\dots ,c_{k-4}$, a copy of a complete graph $K_{n_l}$ and a block $B\in {\mathcal{B}}_{2,2}$ (the construction of the class ${\mathcal{B}}_{2,2}$ will be given in Section 3 as it was established earlier in [12]) by adding edges according the join operations:

• $c_{l-1}\vee K_{n_l}\vee c_l$ and
• $c_{k-4}\vee c$

where we call c the head of B. Examples of graphs in this case are illustrated by Figure 1 and Figure 2. Further, for a $k-3$ tuple $\mathit{i}=(0,0,\dots ,1)$ where $i_{k-3}=1$ and $i_{l^{\prime }}=0$ for $1\le l^{\prime }\le k-2$, a graph G in the class ${\mathcal{G}}_1\mathit{i}$ can be constructed from paths $c_0,c_1,\dots ,c_{k-4}$, a copy of a complete graph $K_{n_{k-3}}$ and a block $B\in {\mathcal{B}}_{2,2}$ by adding edges according the join operation:

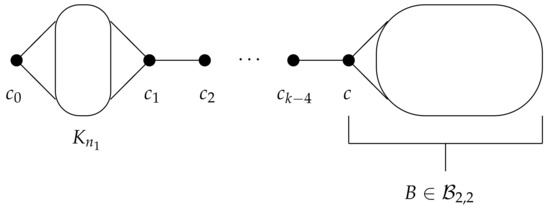
Figure 1. A graph G in the class ${\mathcal{G}}_1(1,0,0,\dots ,0)$.

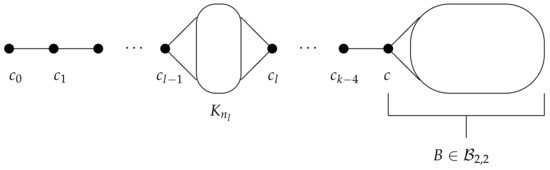
Figure 2. A graph G in the class ${\mathcal{G}}_1(0,0,\dots ,i_l=1,0,\dots ,0)$.

• $c_{k-4}\vee K_{n_{k-3}}\vee c$

where we call c the head of B. Example of a graph in this case is illustrated by Figure 3.

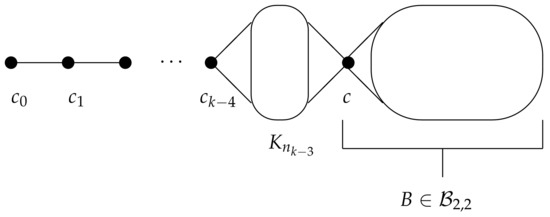
Figure 3. A graph G in the class ${\mathcal{G}}_1(0,0,\dots ,1)$.

Next, we will construct another class of k-${\gamma }_c$-critical graphs with $k-3$ cut vertices. Before giving the construction, we introduce the following class of end blocks.

The class${\mathcal{B}}_3$

An end block $B\in {\mathcal{B}}_3$ has b as the head. Let $N_B\left(b\right)=A$ and $\check{B}=G[V\left(B\right)-\left\{b\right\}]$. Moreover, B has the following properties:

(1)

Every vertex $v\in V\left(\check{B}\right)$, there exists a ${\gamma }_c$-set $D_v$ of B of size 3 such that $v\in D_v$.

(2)

For every non-adjacent vertices x and y of $\check{B}$, there exists a ${\gamma }_c$-set $D_{xy}^B$ of $B+xy$ such that $D_{xy}^B\cap \{x,y\}\ne \varnothing$, $|D_{xy}^B|=2$ and $D_{xy}^B\cap A\ne \varnothing$.

For an example of a graph in the class ${\mathcal{B}}_3$, we let B be the graph obtained from a vertex b and $C_5$, a cycle of length 5, by joining b to a pair of consecutive vertices of $C_5$. It can be checked that B satisfies $\left(1\right)$ and $\left(2\right)$ of the class ${\mathcal{B}}_3$. Thus, $B\in {\mathcal{B}}_3$. Figure 4 illustrates the graph B. Further, it is worth noting that $D_v$ in the property $\left(1\right)$ satisfies $D_v\cap A\ne \varnothing$ in order to dominate b. We are ready to give the construction.

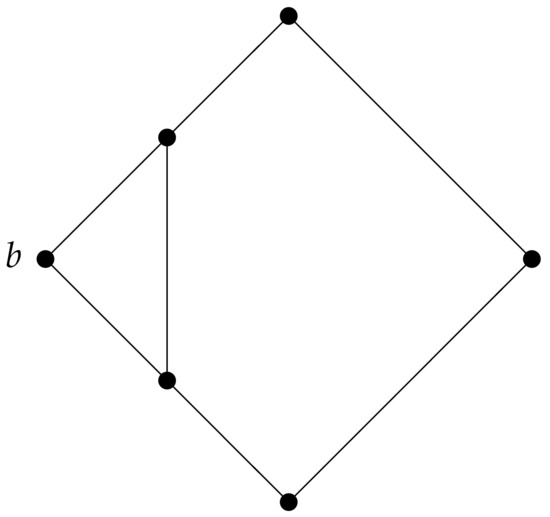
Figure 4. A graph B in the class ${\mathcal{B}}_3$.

The class${\mathcal{G}}_2\left(k\right)$

For $k\ge 5$, a graph G in this class can be constructed from a path $c_0,c_1,\dots ,c_{k-4}$ and an end block $B\in {\mathcal{B}}_3$ with the head b by adding the edge $c_{k-4}b$. For the sake of convenience, we may relabel b as $c_{k-3}$.

Then, we let

$\mathcal{Z}(k,\zeta ):$ the class of k-${\gamma }_c$-critical graphs containing $\zeta$ cut vertices.

Our first main result is as follows:

Theorem 2.

For an integer $k\ge 4$, $\mathcal{Z}(k,k-3)={\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})\cup {\mathcal{G}}_2\left(k\right)$.

For our next main results, we let B be a block of G. We further define the following notation. We let $\mathcal{C}\left(G\right)$ be the set of all cut vertices of G. That is

$\mathcal{C}\left(G\right)=\{v\in V(G):v$ is a cut vertex of $G\}$,

$\zeta \left(G\right)=\left|\mathcal{C}\right(G\left)\right|$,

$\mathcal{C}\left(B\right)=V\left(B\right)\cap \mathcal{C}\left(G\right)$,

$\zeta \left(B\right)=\left|\mathcal{C}\right(B\left)\right|$ and

${\zeta }_0\left(G\right)=max\{\zeta \left(B\right):B$ is a block of $G\}$.

We prove that:

Theorem 3.

For all $k\ge 4$, $2\le \zeta \le k-2$ and $2\le {\zeta }_0\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$, there exists a k-${\gamma }_c$-critical graph with ζ cut vertices having a block that contains ${\zeta }_0$ cut vertices.

Finally, we establish constructive proofs to show that:

Theorem 4.

Every k-${\gamma }_c$-critical graph of odd order with $\delta \ge 2$ is factor critical if and only if $k\in \left[2\right]$.

Theorem 5.

Every k-${\gamma }_c$-critical $K_{1,3}$-free graph of even order with $\delta \ge 3$ is bi-critical if and only if $k\in \left[2\right]$.

3. Preliminaries

In this section, we state a number of results that are used in establishing our theorems. We begin with a result of Favaron [22] which gives matching properties of graphs according to the toughness.

Theorem 6

([22]). For an integer $\ell \ge 0$, let G be a graph with minimum degree $\delta \ge \ell +1$. Then, G is ℓ-factor critical if and only if ${\omega }_o(G-S)\le \left|S\right|-\ell$ for any cut set S of G such that $\left|S\right|\ge \ell$.

In the context of k-${\gamma }_c$-critical graphs, Ananchuen et al. [23] established some matching properties of such graphs when $k=3$.

Theorem 7

([23]). Every 3-${\gamma }_c$-critical graph of even order with $\delta \ge 2$ has a perfect matching.

However, for factor criticality, they found a 3-${\gamma }_c$-critical graph of odd order with $\delta \ge 2$ which is not factor critical. The graph is constructed from a complete graph $K_n$, a star $K_{1,n}$ by joining every end vertex of the star to every vertex of $K_n$ and then remove all edges of a perfect matching between these two graphs. The resulting graph is detailed in Figure 5.

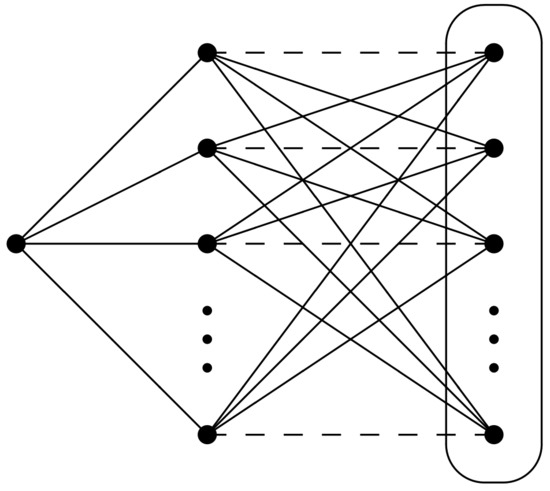
Figure 5. A 3-${\gamma }_c$-critical graph which is non-factor critical.

Chen et al. [3] characterized all k-${\gamma }_c$-critical graphs when $1\le k\le 2$.

Theorem 8

([3]). A graph G is 1-${\gamma }_c$-critical graph if and only if G is a complete graph. Moreover, a graph G is 2-${\gamma }_c$-critical graph if and only if $\overline{G}={\cup }_{i=1}^n{K}_{1,n_i}$ where $n\ge 2$ and $n_i\ge 1$ for all $1\le i\le n$.

We then obtain the following observations as a consequence of Theorem 8.

Observation 1.

For $k\in \left[2\right]$ every k-${\gamma }_c$-critical graph of odd order is factor critical.

Observation 2.

For $k\in \left[2\right]$ every k-${\gamma }_c$-critical graph of even order with minimum degree $\delta \ge 3$ is bi-critical.

By Theorem 8, we observe further that a k-${\gamma }_c$-critical graph does not contain a cut vertex when $1\le k\le 2$.

Observation 3.

Let G be a k-${\gamma }_c$-critical graph with $1\le k\le 2$. Then G has no cut vertex.

Further, Chen et al. [3] established fundamental properties of k-${\gamma }_c$-critical graphs for $k\ge 2$.

Lemma 1

([3]). Let G be a k-${\gamma }_c$-critical graph, x and y a pair of non-adjacent vertices of G and $D_{xy}$ a ${\gamma }_c$-set of $G+xy$. Then

(1) 

$k-2\le |D_{xy}|\le k-1$,

(2) 

$D_{xy}\cap \{x,y\}\ne \varnothing$,

(3) 

if $\left\{x\right\}=\{x,y\}\cap D_{xy}$, then $N_G\left(y\right)\cap D_{xy}=\varnothing$.

Ananchuen [7] established structures of k-${\gamma }_c$-critical graphs with a cut vertex.

Lemma 2

([7]). For $k\ge 3$, let G be a k-${\gamma }_c$-critical graph with a cut vertex c and D a connected dominating set. Then,

(1) 

$G-c$ contains exactly two components,

(2) 

if $C_1$ and $C_2$ are the components of $G-c$, then $G\left[N_{C_1}\left(c\right)\right]$ and $G\left[N_{C_2}\left(c\right)\right]$ are complete,

(3) 

$c\in D$.

All the following results of this section were established in [12]. The first result is the construction of a forbidden subgraph of k-${\gamma }_c$-critical graphs. For a connected graph G, let $X,Y,X_1$ and $Y_1$ be disjoint vertex subsets of $V\left(G\right)$. The induced subgraph $G[X\cup X_1\cup Y\cup Y_1]$ is called a bad subgraph if

(i) 

$x_1\succ X\cup X_1$ for any vertex $x_1\in X_1$,

(ii) 

$N\left[x\right]\subseteq X\cup X_1$ for any vertex $x\in X$,

(iii) 

$y_1\succ Y\cup Y_1$ for any vertex $y_1\in Y_1$ and

(iv) 

$N\left[y\right]\subseteq Y\cup Y_1$ for any vertex $y\in Y$.

An example of a bad subgraph is illustrated in Figure 6.

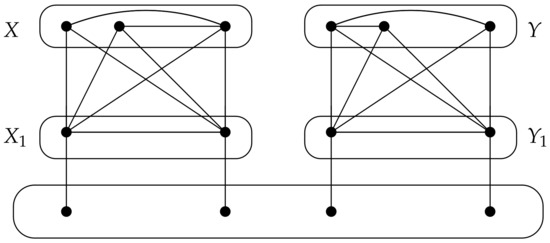
Figure 6. The induced subgraph $G[X\cup X_1\cup Y\cup Y_1]$.

The authors showed, in [12], that:

Lemma 3

([12]). For $k\ge 3$, let G be a k-${\gamma }_c$-critical graph. Then G does not contain a bad subgraph.

They also provided characterizations of some blocks of k-${\gamma }_c$-critical graphs. Recall that

• $\mathcal{C}\left(G\right)$ is the set of all cut vertices of G and, for a block B of G,
• $\mathcal{C}\left(B\right)=V\left(B\right)\cap \mathcal{C}\left(G\right)$ and $\zeta \left(G\right)=\left|\mathcal{C}\right(G\left)\right|$.

when no ambiguity occur, we write $\mathcal{C}$ rather than $\mathcal{C}\left(G\right)$. In the same paper, the authors showed further that for a connected graph G and a pair of non-adjacent vertices x and y of G, $\mathcal{C}\left(G\right)=\mathcal{C}(G+xy)$ if x and y are in the same block of G.

Lemma 4

([12]). For a connected graph G, let B be a block of G and $x,y\in V\left(B\right)$ such that $xy\notin E\left(G\right)$. Then, $\mathcal{C}\left(G\right)=\mathcal{C}(G+xy)$.

Let D be a ${\gamma }_c$-set of G. The followings are the characterization of four classes of end blocks of k-${\gamma }_c$-critical graphs that contains at most 3 vertices from D. For vertices $c,z_1$ and $z_2$, let

• ${\mathcal{B}}_0=\{c\vee K_{t_1}:$ for an integer $t_1\ge 1\}$,
• ${\mathcal{B}}_1=\{c\vee K_{t_2}\vee z_1:$ for an integer $t_2\ge 2\}$ and
• ${\mathcal{B}}_{2,1}=\{c\vee K_{t_3}\vee K_{t_4}\vee z_2:$ for integers $t_3,t_4\ge 2\}$.

The following is a part of the construction of ${\mathcal{B}}_{2,2}$. For integers $l\ge 2,m_i\ge 1$ and $r\ge 0$, we let $\mathcal{S}={\cup }_{i=1}^l{K}_{1,m_i}$ and $T=\mathcal{S}\cup \overline{K_r}$. When $r=0$, we let $T=\mathcal{S}$. Then, for $1\le i\le l$, let $s_0^i,s_1^i,s_2^i,\dots ,s_{m_i}^i$ be the vertices of a star $K_{1,m_i}$ which $s_0^i$ is the center. Further, let $S={\cup }_{i=1}^l\{s_1^i,s_2^i,\dots ,s_{m_i}^i\}$ and $S^{\prime }={\cup }_{i=1}^l\left\{s_0^i\right\}$, moreover, let $S^{″}=V\left(\overline{K_r}\right)$ if $T=\mathcal{S}\cup \overline{K_r}$ and $S^{″}=\varnothing$ if $T=\mathcal{S}$. Therefore,

$$\overline{T}=\left\{\begin{array}{cc}\overline{\mathcal{S}}\hfill & or\hfill \\ \overline{\mathcal{S}}\vee K_r.\hfill \end{array}\right.$$

That is, $\overline{T}$ can be obtained by removing the edges in the stars of $\mathcal{S}$ from a complete graph on $S\cup S^{\prime }\cup S^{″}$. Then, the blocks in ${\mathcal{B}}_{2,2}$ are defined as follows.

${\mathcal{B}}_{2,2}=\{c\vee {}_{\overline{T}\left[S\right]}\overline{T}:$ for integers $l\ge 2,r\ge 0$ and $m_i\ge 1\}$.

A graph in this class is illustrated by Figure 7. According to the figure, an oval denotes a complete subgraph, double lines between subgraphs denote all possible edges between the subgraphs and a dash line denotes a removed edge.

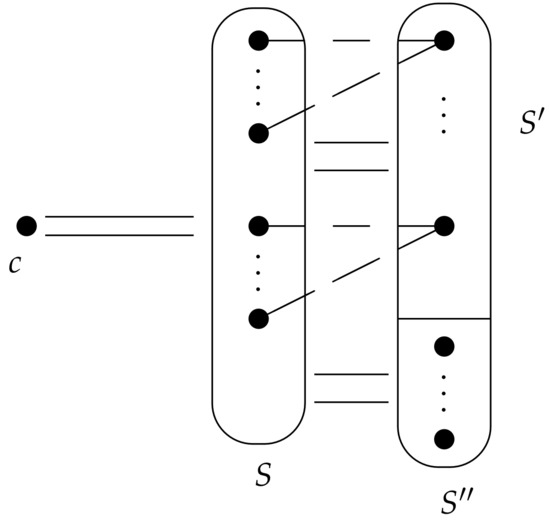
Figure 7. A block B in the class ${\mathcal{B}}_{2,2}$.

For a block $B\in {\mathcal{B}}_0\cup {\mathcal{B}}_1\cup {\mathcal{B}}_{2,1}\cup {\mathcal{B}}_{2,2}$, the vertex c is called the head of B. The following are the characterizations of an end block B such that $|D\cap V(B\left)\right|\le 3$.

Lemma 5

([12]). Let G be a k-${\gamma }_c$-critical graph with a ${\gamma }_c$-set D and let B be an end block of G. If $\left|\right(D\cap V\left(B\right))-\mathcal{C}|=0$, then $B\in {\mathcal{B}}_0$.

Lemma 6

([12]). Let G be a k-${\gamma }_c$-critical graph with a ${\gamma }_c$-set D and let B be an end block of G. If $\left|\right(D\cap V\left(B\right))-\mathcal{C}|=1$, then $B\in {\mathcal{B}}_1$.

Lemma 7

([12]). Let G be a k-${\gamma }_c$-critical graph with a ${\gamma }_c$-set D and let B be an end block of G. Suppose that $\left|\right(D\cap V\left(B\right))-\mathcal{C}|=2$. Then, $B\in {\mathcal{B}}_{2,1}\cup {\mathcal{B}}_{2,2}$.

Lemma 8

([12]). For $k\ge 3$, let G be a k-${\gamma }_c$-critical graph. Then, G contains at most one end block B such that $B\in {\mathcal{B}}_0\cup {\mathcal{B}}_1$.

Finally, we conclude this section by the following two lemmas which are structures of blocks of k-${\gamma }_c$-critical graphs. Recall from Section 2 that

$\mathcal{Z}(k,\zeta ):$ the class of k-${\gamma }_c$-critical graphs containing $\zeta$ cut vertices.

Lemma 9

([12]). Let $G\in \mathcal{Z}(k,\zeta )$ where $\zeta \in \{k-3,k-2\}$. Then, G has only two end blocks and all other blocks contain exactly two cut vertices.

Lemma 10

([12]). Let $G\in \mathcal{Z}(k,\zeta )$ with a ${\gamma }_c$-set D where $\zeta \in \{k-3,k-2\}$ and B be a block of G containing two cut vertices c and $c^{\prime }$. If $(D\cap V(B\left)\right)-\mathcal{C}=\varnothing$. Then, $B=c{c}^{\prime }$.

In [24], the authors established a construction of the class $\mathcal{P}\left(k\right)$ which, for any graph $G\in \mathcal{P}\left(k\right)$ and integer $l\ge 1$, there exists a $(k+l)$-${\gamma }_c$-critical graph containing G as an induced subgraph. Recall that, for a subgraph H of G, H is a maximal complete subgraph of G if for any complete subgraph $H^{\prime }$ of G such that $V\left(H\right)\subseteq V\left(H^{\prime }\right)$, we have $V\left(H\right)=V\left(H^{\prime }\right)$.

The class $\mathcal{P}\left(k\right)$

A k-${\gamma }_c$-critical graph G is in this class if there exists a maximal complete subgraph H of order at least two of G satisfying the following properties:

(i) 

for any vertex x of G, there exists a ${\gamma }_c$-set D of G such that $x\in D$ and $D\cap V\left(H\right)\ne \varnothing$ and

(ii) 

for any non-adjacent vertices x and y of G, there exists a set $D_{xy}^{\prime }$ that is a connected dominating set of $G+xy$ and satisfies $D_{xy}^{\prime }\cap V\left(H\right)\ne \varnothing$ and $|D_{xy}^{\prime }|<k$.

We next give a construction of a $(k+l)$-${\gamma }_c$-critical graph containing G in the class $\mathcal{P}\left(k\right)$ as an induced subgraph. Let H be a maximal complete subgraph of G having properties $\left(i\right)$ and $\left(ii\right)$. The graph $G(n_1,n_2,\dots ,n_l)$ can be constructed from a vertex $x_0$, l copies of complete graphs $K_{n_1},K_{n_2},\dots ,K_{n_{l-1}}$ which $n_i\ge 1$ for $1\le i\le l$ and the graph G by adding edges according to the join operations:

$$x_0\vee K_{n_1}\vee K_{n_2}\vee \dots \vee K_{n_l}\vee {}_{H}G.$$

The graph is illustrated by Figure 8.

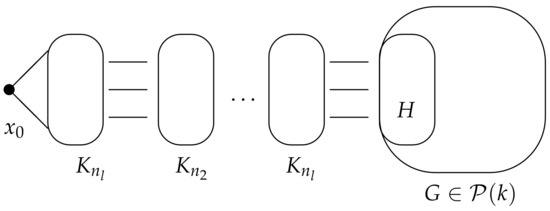
Figure 8. The graph $G(n_1,n_2,\dots ,n_l)$.

Thus, they proved that

Theorem 9

([24]). For an integer $k\ge 3$, let $G\in \mathcal{P}\left(k\right)$. Then, $G(n_1,n_2,\dots ,n_l)$ is a $(k+l)$-${\gamma }_c$-critical graph for all $l\ge 1$.

4. Proofs

4.1. Connected Dominating Set of Blocks

Let

$\mathfrak{B}\left(G\right)$ be the family of all blocks of G.

when no ambiguity can occur, we use $\mathfrak{B}$ to denote $\mathfrak{B}\left(G\right)$. For a k-${\gamma }_c$-critical graph G with a cut vertex, let B be a block of G containing non-adjacent vertices x and y. Clearly, $V(B+xy)=V\left(B\right)$. Let D be a ${\gamma }_c$-set of G.

Lemma 11.

Let B be a block of G and $x,y\in V\left(B\right)$ such that $xy\notin E\left(G\right)$. Then, $D\cap \mathcal{C}=D_{xy}\cap \mathcal{C}$, in particular, $D\cap \mathcal{C}\left(B^{\prime }\right)=D_{xy}\cap \mathcal{C}\left(B^{\prime }\right)$ for all $B^{\prime }\in \mathfrak{B}(G+xy)$.

Proof. 

We first show that $D\cap \mathcal{C}\subseteq D_{xy}\cap \mathcal{C}$. Let $c\in D\cap \mathcal{C}$. By Lemma 4, $c\in \mathcal{C}(G+xy)$. By the connectedness of $(G+xy)\left[D_{xy}\right]$, $c\in D_{xy}$. Thus $D\cap \mathcal{C}\subseteq D_{xy}\cap \mathcal{C}$. We now show that $D_{xy}\cap \mathcal{C}\subseteq D\cap \mathcal{C}$. Let $c\in D_{xy}\cap \mathcal{C}$. That is, $c\in \mathcal{C}$. Lemma 2(3) yields that $c\in D$. Therefore, $c\in D\cap \mathcal{C}$ and, thus, $D_{xy}\cap \mathcal{C}\subseteq D\cap \mathcal{C}$, as required.

In view of Lemma 4, $V\left(B^{\prime }\right)\cap \mathcal{C}(G+xy)=V\left(B^{\prime }\right)\cap \mathcal{C}$ for all $B^{\prime }\in \mathfrak{B}(G+xy)$. Because $D\cap \mathcal{C}=D_{xy}\cap \mathcal{C}$, it follows that

$$D\cap \mathcal{C}\left(B^{\prime }\right)=D\cap \mathcal{C}\cap V\left(B^{\prime }\right)=D_{xy}\cap \mathcal{C}\cap V\left(B^{\prime }\right)=D_{xy}\cap \mathcal{C}\left(B^{\prime }\right).$$

This completes the proof. □

It is worth noting that in [12], this result was proved only for end blocks. Therefore, our result in Lemma 11 is more general. For non-adjacent vertices x and y of the block B, the following lemma gives the number of vertices of a ${\gamma }_c$-set of $G+xy$ in B.

Lemma 12.

For all $x,y\in V\left(B\right)$ such that $xy\notin E\left(G\right)$, $|D_{xy}\cap V\left(B\right)|<|D\cap V\left(B\right)|$.

Proof. 

We first establish the following claim.

Claim: For any block $B^{\prime }$ which is not B, $|D\cap V\left(B^{\prime }\right)|\le |D_{xy}\cap V\left(B^{\prime }\right)|$.

Suppose to the contrary that $|D\cap V\left(B^{\prime }\right)|>|D_{xy}\cap V\left(B^{\prime }\right)|$. Lemma 11 gives that $D\cap \mathcal{C}\left(B^{\prime }\right)=D_{xy}\cap \mathcal{C}\left(B^{\prime }\right)$. Because $x,y\notin V\left(B^{\prime }\right)$, $G[(D-V\left(B^{\prime }\right))\cup (D_{xy}\cap V\left(B^{\prime }\right))]$ is connected. Moreover, $(D-V\left(B^{\prime }\right))\cup (D_{xy}\cap V\left(B^{\prime }\right)){\succ }_{c}G$. This implies that

$$\begin{array}{cc}\hfill k=\left|D\right|=|(D-V\left(B^{\prime }\right))\cup (D\cap V\left(B^{\prime }\right))|& =|D-V\left(B^{\prime }\right)|+|D\cap V\left(B^{\prime }\right)|\hfill \\ \hfill & >|D-V\left(B^{\prime }\right)|+|D_{xy}\cap V\left(B^{\prime }\right)|\hfill \\ \hfill & =|(D-V\left(B^{\prime }\right))\cup (D_{xy}\cap V\left(B^{\prime }\right))|,\hfill \end{array}$$

contradicting the minimality of D. Thus establishing the claim.

We now prove Lemma 12. Suppose to the contrary that $|D_{xy}\cap V\left(B\right)|\ge |D\cap V\left(B\right)|$. Lemma 11 yields that $D\cap \mathcal{C}=D_{xy}\cap \mathcal{C}$. Clearly $D={\cup }_{\tilde{B}\in \mathfrak{B}}(D\cap V\left(\tilde{B}\right))$ and $D_{xy}={\cup }_{\tilde{B}\in \mathfrak{B}(G+xy)}(D_{xy}\cap V\left(\tilde{B}\right))$. Lemma 2(1) yields, further, that each cut vertex is contained in exactly two blocks. Thus each cut vertex is counted twice in ${\sum }_{\tilde{B}\in \mathfrak{B}}\left|(D\cap V\left(\tilde{B}\right))\right|$ and ${\sum }_{\tilde{B}\in \mathfrak{B}(G+xy)}\left|(D_{xy}\cap V\left(\tilde{B}\right))\right|$. Therefore, $\left|D\right|={\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}}|D\cap V\left(\tilde{B}\right)|-|\mathcal{C}|$ and ${\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}(G+xy)}|D_{xy}\cap V\left(\tilde{B}\right)|-|\mathcal{C}(G+xy)|=|D_{xy}|$. We note by Lemma 4 that $\left|\mathcal{C}\right|=\left|\mathcal{C}\right(G+xy\left)\right|$. By the claim and the assumption that $|D_{xy}\cap V\left(B\right)|\ge |D\cap V\left(B\right)|$, we have

$$\begin{array}{cc}\hfill k=\left|D\right|& ={\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}}|D\cap V\left(\tilde{B}\right)|-|\mathcal{C}|\hfill \\ \hfill & =|D\cap V\left(B\right)|+{\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}-\left\{B\right\}}|D\cap V\left(\tilde{B}\right)|-|\mathcal{C}|\hfill \\ \hfill & \le |D_{xy}\cap V\left(B\right)|+{\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}-\left\{B\right\}}|D\cap V\left(\tilde{B}\right)|-|\mathcal{C}|\left(bytheassumption\right)\hfill \\ \hfill & \le |D_{xy}\cap V\left(B\right)|+{\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}(G+xy)-\left\{B\right\}}|D_{xy}\cap V\left(\tilde{B}\right)|-|\mathcal{C}|\left(bytheclaim\right)\hfill \\ \hfill & ={\mathsf{\Sigma }}_{\tilde{B}\in \mathfrak{B}(G+xy)}|D_{xy}\cap V\left(\tilde{B}\right)|-|\mathcal{C}(G+xy)|=|D_{xy}|.\hfill \end{array}$$

This contradicts Lemma 1(1). Thus, $|D_{xy}\cap V\left(B\right)|<|D\cap V\left(B\right)|$, and this completes the proof. □

Corollary 1.

For any block B of G and $x,y\in V\left(B\right)$ such that $xy\notin E\left(G\right)$, $|(D_{xy}\cap V\left(B\right))-\mathcal{C}|<|(D\cap V\left(B\right))-\mathcal{C}|$.

Proof. 

In view of Lemma 11, $D\cap V\left(B\right)\cap \mathcal{C}=D_{xy}\cap V\left(B\right)\cap \mathcal{C}$. Lemma 12 then implies that

$$\begin{array}{cc}\hfill \left|\right(D_{xy}\cap V\left(B\right))-\mathcal{C}|& =|D_{xy}\cap V\left(B\right)|-|D_{xy}\cap V\left(B\right)\cap \mathcal{C}|\hfill \\ \hfill & <|D\cap V(B\left)\right|-|D\cap V(B)\cap \mathcal{C}|\hfill \\ \hfill & =\left|\right(D\cap V\left(B\right))-\mathcal{C}|\hfill \end{array}$$

and this completes the proof. □

4.2. The k-${\gamma }_c$-Critical Graphs with $\zeta \left(G\right)=k-3$

In this subsection, we characterize k-${\gamma }_c$-critical graphs with $k-3$ cut vertices. We recall the classes ${\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$ and ${\mathcal{G}}_2\left(k\right)$ from Section 2. First, we will prove that all graphs in these two classes are k-${\gamma }_c$-critical with $k-3$ cut vertices.

Lemma 13.

Let G be a graph in the class ${\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$, then G is a k-${\gamma }_c$-critical graph with $k-3$ cut vertices.

Proof. 

Clearly G has $c_1,c_2,\dots ,c_{k-4}$ and c as the $k-3$ cut vertices. Observe that, for any $\mathit{i}=(i_1,i_2,\dots ,,i_{k-3})$, a graph $G\in {\mathcal{G}}_1\mathit{i}$ has the path $P=c_0,c_1,\dots ,c_{l-1},a,c_l,\dots ,c_{k-4},c$ from $c_0$ to c where $a\in V\left(K_{n_l}\right)$. To prove all cases of $\mathit{i}$, we may relabel the path P to be $x_1,\dots ,x_{k-1}$. Therefore, $c_0=x_1,c_1=x_2,\dots c_{k-4}=x_{k-2}$ and $c=x_{k-1}$. We see that $\{x_2,x_3,\dots ,x_{k-2},x_{k-1},s_1^1,s_0^2\}{\succ }_{c}G$ where $s_1^1,s_0^2$ are vertices in $B\in {\mathcal{B}}_{2,2}$ defined in Section 3. Therefore, ${\gamma }_c\left(G\right)\le k$.

Let D be a ${\gamma }_c$-set of G. If $x_1\notin D$, then, to dominate $x_1$, we have $x_2\in D$. If $x_1\in D$, then $x_2\in D$ as $G\left[D\right]$ is connected. In both cases, $x_2\in D$.

Suppose that $D\cap S^{″}=\varnothing$. Because $B\in {\mathcal{B}}_{2,2}$, to dominate B, $|D\cap (S\cup S^{\prime }\left)\right|\ge 2$. By the connectedness of $G\left[D\right]$, we have $\{x_3,x_4,\dots ,x_{k-2},x_{k-1}\}\subseteq D$. Thus, ${\gamma }_c\left(G\right)\ge k$ implying that ${\gamma }_c\left(G\right)=k$. Hence, suppose that $D\cap S^{″}\ne \varnothing$. As $x_2\in D$ and $G\left[D\right]$ is connected, it follows that $\{x_3,x_4,\dots ,x_{k-2},$$x_{k-1},y\}\subseteq D$ where $y\in D\cap S$. Thus, ${\gamma }_c\left(G\right)=\left|D\right|\ge k$ implying that ${\gamma }_c\left(G\right)=k$.

Now, we will establish the criticality. Let u and v be a pair of non-adjacent vertices of G and let $S_1=S\cup S^{\prime }\cup S^{″}$. We first assume that $|\{u,v\}\cap S_1|=0$. Therefore, $\{u,v\}\subseteq \{x_1,x_2,\dots ,x_{k-2},$$x_{k-1}\}$. Thus, $u=x_i$ and $v=x_j$ for some $i,j\in \{1,2,\dots ,k-1\}$. Without loss of generality let $i<j$. Clearly $i+2\le j$. We see that

$\{x_2,x_3,\dots ,x_i,x_{i+2},x_{i+3},\dots ,x_j,\dots ,x_{k-1},s_1^1,s_0^2\}{\succ }_{c}G+uv$. Therefore, ${\gamma }_c(G+uv)\le k-1$.

Thus, we assume that $|\{u,v\}\cap S_1|=1$. If $\{u,v\}=\{x_{k-1},s\}$ for some $s\in S_1$, then $s\notin S$ and, clearly, $\{x_{k-1},s\}\succ S_1$. Thus, $\{x_2,x_3,\dots ,x_{k-1},s_1\}{\succ }_{c}G+uv$. Therefore ${\gamma }_c(G+uv)\le k-1$. Let $v\in S_1$. As $\left|\mathcal{S}\right|\ge 2$, there exists $v^{\prime }\in S-\left\{v\right\}$ such that $\{v,v^{\prime }\}{\succ }_c{S}_1$. Suppose that $u\in \{x_2,x_3,\dots ,x_{k-2}\}$. Thus, $\{x_2,x_3,\dots ,u,\dots ,x_{k-2},v,v^{\prime }\}{\succ }_{c}G+uv$. Therefore, ${\gamma }_c(G+uv)\le k-1$. If $u=x_1$, then $\{x_3,x_4,\dots ,$$x_{k-1}$$,v,v^{\prime }\}{\succ }_{c}G+uv$ implying that ${\gamma }_c(G+uv)\le k-1$.

Finally, we assume that $\{u,v\}\subseteq S_1$. Thus, $\{u,v\}=\{s_j^i,s_0^i\}$ for some $i\in \{1,2,\dots ,|\mathcal{S}\left|\right\}$ and $j\in \{1,2,\dots ,m_i\}$. Clearly $\{x_2,x_3,\dots ,x_{k-1},s_j^i\}{\succ }_{c}G+uv$ and ${\gamma }_c(G+uv)\le k-1$. Thus, G is a k-${\gamma }_c$-critical graph and this completes the proof. □

Lemma 14.

Let G be a graph in the class ${\mathcal{G}}_2\left(k\right)$. Then, G is a k-${\gamma }_c$-critical graph with $k-3$ cut vertices.

Proof. 

Let D be a ${\gamma }_c$-set of G. As $c_1,c_2,\dots ,c_{k-3}$ are cut vertices, by Lemma 2(3), $c_1,c_2,\dots ,c_{k-3}$$\in D$. Recall that $N_B\left(c_{k-3}\right)=A$. Because $D{\succ }_{c}B$, we can let $w\in A\cap D$. Thus $w\in V\left(\check{B}\right)\cap D$. By Lemma 2(2), $N_B\left(c_{k-3}\right)\subseteq N_B\left[w\right]$. So, $V\left(\check{B}\right)\cap D$ is a connected dominating set of B. By $\left(1\right)$, there exists a ${\gamma }_c$-set $D_w$ of B of size 3. By the minimality of $D_w$, $|V\left(\check{B}\right)\cap D|\ge |D_w|=3$. Therefore, ${\gamma }_c\left(G\right)=\left|D\right|=|\{c_1,c_2,\dots ,c_{k-3}\}|+|V\left(\check{B}\right)\cap D|\ge k$. Further, because $D_w{\succ }_{c}B$ and $w\in D_w\cap A$, it follows that $\{c_1,c_2,\dots ,c_{k-3}\}\cup D_w{\succ }_{c}G$. Therefore, ${\gamma }_c\left(G\right)\le |\{c_1,c_2,\dots ,c_{k-3}\}|+|D_w|=k$ and this implies that ${\gamma }_c\left(G\right)=k$.

We will prove the criticality. Let u and v be non-adjacent vertices of G. Suppose first that $c_0\in \{u,v\}$, $c_0=u$ say. If $v\in \{c_2,c_3,\dots ,c_{k-3}\}$, then $D-\left\{c_1\right\}{\succ }_{c}G+uv$. If $v\in V\left(\check{B}\right)$, then, by Property $\left(1\right)$ of the class ${\mathcal{B}}_3$, there exists a ${\gamma }_c$-set $D_v$ of size 3 of B such that $v\in D_v$ and $A\cap D_v\ne \varnothing$. So $\{c_2,c_3,\dots ,c_{k-3}\}\cup D_v{\succ }_{c}G+uv$. These imply that ${\gamma }_c(G+uv)<{\gamma }_c\left(G\right)$.

We then suppose that $c_0\notin \{u,v\}$. If $\{u,v\}\subseteq \{c_1,c_2,\dots ,c_{k-3}\}$, then there exists i and j such that $c_i=u$ and $c_j=v$. Without loss of generality let $i<j$. Clearly, $i+2\le j$. Therefore, $D-\left\{c_{i+1}\right\}{\succ }_{c}G+uv$. For the case when $|\{u,v\}\cap \{c_1,c_2,\dots ,c_{k-3}\}|=1$, we have $v\in \check{B}$ and thus $\{c_1,\dots ,c_i,\dots ,c_{k-4}\}\cup D_v{\succ }_{c}G+uv$. Finally, if $\{u,v\}\subseteq V\left(B\right)$, then, by Property $\left(2\right)$ of the class ${\mathcal{B}}_3$, there exists a ${\gamma }_c$-set $D_{uv}^B$ such that $D_{uv}^B\cap \{u,v\}\ne \varnothing$, $|D_{uv}^B|=2$ and $D_{uv}^B\cap A\ne \varnothing$. Thus, $\{c_1,c_2,\dots ,c_{k-3}\}\cup D_{uv}^B{\succ }_{c}G+uv$. This implies that ${\gamma }_c(G+uv)<{\gamma }_c\left(G\right)$. Clearly, $c_1,c_2,..,c_{k-3}$ are the $k-3$ cut vertices of G. This completes the proof. □

In the following, we let $G\in \mathcal{Z}(k,k-3)$ having a ${\gamma }_c$-set D. In view of Lemma 9, G has only two end blocks and all other blocks contain two cut vertices. Thus, we let $B_1$ and $B_{k-2}$ be the two end blocks and all other blocks $B_2,B_3,\dots ,B_{k-3}$ contain two cut vertices. Without loss of generality let $c_1\in V\left(B_1\right),c_{k-3}\in V\left(B_{k-2}\right)$ and $c_{i-1},c_i\in V\left(B_i\right)$ for $2\le i\le k-3$. Moreover, let $C_i=V\left(B_i\right)-\mathcal{C}$ for all $1\le i\le k-2$. If $D^{\prime }$ is a ${\gamma }_c$-set of G such that $D^{\prime }\ne D$, by the minimality of k, we have $|V\left(B_i\right)\cap D|=|V\left(B_i\right)\cap D^{\prime }|$ for all i. Thus, we can let

$\mathcal{H}(b_1,b_2,b_3,\dots ,b_{k-2}):$ the class of a graph $G\in \mathcal{Z}(k,k-3)$ such that

$|V\left(C_i\right)\cap D|=b_i$ for $1\le i\le k-2$.

Lemma 15.

For a ${\gamma }_c$-set of G, either $\left|V\right(C_1)\cap D|\ge 2$ or $\left|V\right(C_{k-2})\cap D|\ge 2$.

Proof. 

Suppose to the contrary that $\left|V\right(C_1)\cap D|\le 1$ and $\left|V\right(C_{k-2})\cap D|\le 1$. Lemmas 5 and 6 imply that $B_1,B_{k-2}\in {\mathcal{B}}_0\cup {\mathcal{B}}_1$. This contradicts Lemma 8. Thus, either $\left|V\right(C_1)\cap D|\ge 2$ or $\left|V\right(C_{k-2})\cap D|\ge 2$ and this completes the proof. □

By Lemma 15, we may suppose without loss of generality that $|V\left(C_{k-2}\right)\cap D|\ge |V\left(C_1\right)\cap D|$.

Lemma 16.

$\mathcal{Z}(k,k-3)=\mathcal{H}(0,0,0,\dots ,3)\cup \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$ where $b_i=1$ for some $1\le i\le k-3$ and $b_j=0$ for all $1\le j\ne i\le k-3$.

Proof. 

By the definition, $\mathcal{H}(0,0,0,\dots ,3)\cup \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)\subseteq \mathcal{Z}(k,k-3)$.

Conversely, let $G\in \mathcal{Z}(k,k-3)$. Thus, by Lemma 9, G has only two end blocks $B_1$ and $B_{k-2}$ and all other blocks $B_2,B_3,\dots ,B_{k-2}$ contain two cut vertices. Moreover, $c_1\in V\left(B_1\right),c_{k-3}\in V\left(B_{k-1}\right)$ and $c_{i-1},c_i\in V\left(B_i\right)$ for $2\le i\le k-3$. In view of Lemma 2(3), $c_1,c_2,\dots ,c_{k-3}$ $\in D$. So $|D-\mathcal{C}|=3$. Thus, $\left|V\right(C_i)\cap D|\le 3$ for all $i\in \{1,k-2\}$. Recall that $|V\left(C_{k-2}\right)\cap D|\ge |V\left(C_1\right)\cap D|$. Lemma 15 implies that either $\left|V\right(C_{k-2})\cap D|=3$ or $\left|V\right(C_{k-2})\cap D|=2$. That is, $G\in \mathcal{H}(0,0,0,\dots ,3)\cup \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$. This completes the proof. □

By Lemma 16, to characterize a graph G in the class $\mathcal{Z}(k,k-3)$, it suffices to consider when G is either in $\mathcal{H}(0,0,0,\dots ,3)$ or $\mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$. We first consider the case when $G\in \mathcal{H}(b_1,b_2,\dots ,$$b_{k-3},2)$. Let $c_i$ and $c_{i+1}$ be vertices and $K_{n_i}$ a copy of a complete graph.

Lemma 17.

Let $G\in \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$ with a block $B_i$ containing two cut vertices $c_{i-1}$ and $c_i$ and $b_i=1$. Then, $B_i=c_{i-1}\vee K_{n_i}\vee c_i$ where $n_i\ge 2$.

Proof. 

As $G\in \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$ and $b_i=1$ for some $1\le i\le k-3$, we must have $b_j=0$ for all $1\le j\ne i\le k-3$. Because $B_i$ contains two cut vertices, $i>1$. Therefore, $b_1=0$. Lemma 5 then implies that

$$B_1=K_{n_1}\vee c_1.$$

Let $B^{\prime }=B_i-c_{i-1}-c_i$. We first show that $B^{\prime }$ is complete. Let x and y be non-adjacent vertices of $B^{\prime }$. Consider $G+xy$. Lemma 1(2) implies that $|D_{xy}\cap \{x,y\}|\ge 1$. As $x,y\in V\left(B^{\prime }\right)$, we must have $|D_{xy}\cap (V\left(B_i\right)-\mathcal{C})|\ge 1=b_i=|D\cap (V\left(B_i\right)-\mathcal{C})|$ contradicting Corollary 1. Therefore, $B^{\prime }$ is complete.

We will show that $c_{i-1}{c}_i\notin E\left(G\right)$. Thus, we may assume to the contrary that $c_{i-1}{c}_i\in E\left(G\right)$. We let

$X_1=N_{B_i}\left(\{c_{i-1},c_i\}\right)$ and

$X=V\left(B^{\prime }\right)-X_1$.

As $|D\cap (V\left(B_i\right)-\{c_{i-1},c_i\}\left)\right|=1$, it follows that $X\ne \varnothing$. Because $B^{\prime }$ is complete, $G[X_1\cup X]$ is complete. In fact, $X_1$ and X satisfy $\left(i\right)$ and $\left(ii\right)$ of bad subgraphs. We then let

$Y_1=\left\{c_1\right\}$ and

$Y=V\left(K_{n_1}\right)$.

Thus, G has $X,$$X_1$$,Y$ and $Y_1$ as a bad subgraph. This contradicts Lemma 3. Therefore, $c_{i-1}{c}_i\notin E\left(G\right)$.

We finally show that $N_{B_i}\left(c_i\right)=N_{B_i}\left(c_{i-1}\right)=V\left(B^{\prime }\right)$. We may assume to the contrary that there exists a vertex u of $B^{\prime }$ which is not adjacent to $c_{i-1}$. Consider $G+u{c}_{i-1}$. Corollary 1 gives that $|D_{u{c}_{i-1}}\cap V\left(B^{\prime }\right)|=0$. Lemma 4 gives further that $\{c_{i-1},c_i\}\subseteq D_{u{c}_{i-1}}$. As $c_{i-1}{c}_i\notin E\left(G\right)$, it follows that $(G+u{c}_{i-1})\left[D_{u{c}_{i-1}}\right]$ is not connected, a contradiction. Therefore, $N_{B_i}\left(c_{i-1}\right)=V\left(B^{\prime }\right)$ and, similarly, $N_{B_i}\left(c_i\right)=V\left(B^{\prime }\right)$. As $B_i$ is a block, $n_i\ge 2$ and this completes the proof. □

We will prove the following two theorems, both of which give main contribution to the proof of our first main theorem, Theorem 2.

Theorem 10.

For $k\ge 4$, $\mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)={\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$ where $b_j=i_j$ for all $1\le j\le k-3$.

Proof. 

Let $b_j=i_j$ for all $1\le j\le k-3$. In views of Lemma 13, we have that ${\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$$\subseteq \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$. Thus, it suffices to show that $\mathcal{H}(b_1,b_2,\dots ,$$b_{k-3},2)\subseteq {\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})$.

We will show that $B_{k-2}\in {\mathcal{B}}_{2,2}$. Clearly, $b_1$ is either 0 or 1. If $b_1=0$, then Lemma 5 implies that $B_1=K_{n_1}\vee c_1$. However, if $b_1=1$, then Lemma 6 implies that $B_1=c_0\vee K_{n_1}\vee c_1$. Thus, we let

$$X_1=\left\{\begin{array}{cc}\left\{c_1\right\}\hfill & if{b}_1=0and\hfill \\ V\left(K_{n_1}\right)\hfill & if{b}_1=1.\hfill \end{array}\right.$$

and

$$X=\left\{\begin{array}{cc}V\left(K_{n_1}\right)\hfill & if{b}_1=0and\hfill \\ \left\{c_0\right\}\hfill & if{b}_1=1.\hfill \end{array}\right.$$

As $b_{k-2}=2$, by Lemma 7, $B_{k-2}\in {\mathcal{B}}_{2,1}\cup {\mathcal{B}}_{2,2}$. If $B_{k-2}\in {\mathcal{B}}_{2,1}$, then $B_{k-2}=c_{k-3}\vee K_{n_1}\vee K_{n_2}\vee z_2$ where $z_2$ is given at the definition of ${\mathcal{B}}_{2,1}$. We then let

$Y_1=V\left(K_{n_2}\right)$ and $Y=\left\{z_2\right\}$

Clearly, G has a bad subgraph, contradicting Lemma 3. Thus, $B_{k-2}\in {\mathcal{B}}_{2,2}$.

We now consider the case when $b_1=1$. Thus, $b_2=b_3=\dots =b_{k-3}=0$. By Lemma 6, $B_1\in {\mathcal{B}}_1$ implying that $B_1=c_0\vee K_{n_1}\vee c_1$. Further, Lemma 10 implies also that $B_i=c_{i-1}{c}_i$ for $2\le i\le k-3$. Thus, $G\in {\mathcal{G}}_1(1,0,\dots ,0)$.

We finally consider the case when $b_1=0$. Thus, $b_j=1$ for some $2\le j\le k-3$ and $b_j=0$ for $2\le j^{\prime }\ne j\le k-3$. Similarly, $B_{j^{\prime }}=c_{j^{\prime }-1}{c}_{j^{\prime }}$ for all $j^{\prime }$ by Lemma 10. Moreover, Lemma 17 yields that $B_j=c_{j-1}\vee K_{n_j}\vee c_i$. Let $c_0\in V\left(B_1\right)\setminus \left\{c_1\right\}$. We will show that $B_1=c_0{c}_1$. We let a be a vertex in $V\left(B_2\right)-\{c_1,c_2\}$ if $j=2$. Then, we let

$$x=\left\{\begin{array}{cc}a\hfill & ifj=2and\hfill \\ c_2\hfill & ifj>2.\hfill \end{array}\right.$$

Consider $G+c_{0}x$. As $c_2$ is a cut vertex of $G+c_{0}x$, $c_2\in D_{c_{0}x}$ by Lemma 2(3). That is $x\in D_{c_{0}x}$ when $j>2$. When $j=2$, by Lemma 17, $x{c}_2\in E\left(G\right)$. As $c_2\in D_{c_{0}x}$, by Lemma 1(3), $x\in D_{c_{0}x}$. In both cases, $x\in D_{c_{0}x}$. If $|D_{c_{0}x}\cap \left({\cup }_{i=2}^{k-2}V\left(B_i\right)\right)|\le k-2$, then $(D_{c_{0}x}\cap \left({\cup }_{i=2}^{k-2}V\left(B_i\right)\right))\cup \left\{c_1\right\}{\succ }_{c}G$ contradicting ${\gamma }_c\left(G\right)=k$. Therefore, $|D_{c_{0}x}\cap \left({\cup }_{i=2}^{k-2}V\left(B_i\right)\right)|=k-1$ by Lemma 1(1). Thus, $c_1,c_0\notin D_{c_{0}x}$ implying that $B_1=c_0{c}_1$. Therefore, $G\in {\mathcal{G}}_1(0,0,\dots ,i_j=1,\dots ,0)$. This completes the proof. □

Theorem 11.

For $k\ge 4$, $\mathcal{H}(0,0,\dots ,0,3)={\mathcal{G}}_2\left(k\right)$.

Proof. 

By Lemma 14, ${\mathcal{G}}_2\left(k\right)\subseteq \mathcal{H}(0,0,\dots ,3)$. Thus, it is sufficient to show that $\mathcal{H}(0,0,\dots ,3)\subseteq {\mathcal{G}}_2\left(k\right)$.

As $b_i=0$ for all $2\le i\le k-3$, by Lemma 10, $B_i=c_{i-1}{c}_i$. By Lemma 5 and similar arguments in Theorem 10, we have that $B_1=c_0{c}_1$.

We will show that $B_{k-2}$ satisfies $\left(1\right)$ of the class ${\mathcal{B}}_3$. Recall that ${\check{B}}_{k-2}=B_{k-2}-c_{k-3}$. Let $D^{\prime }$ be a ${\gamma }_c$-set of $B_{k-2}$. Suppose that $|D^{\prime }|\le 2$. To dominate $c_{k-3}$, we have $D^{\prime }\cap A\ne \varnothing$. Thus, $\{c_1,\dots ,c_{k-3}\}\cup D^{\prime }{\succ }_{c}G$. However, $|\{c_1,\dots ,c_{k-3}\}\cup D^{\prime }|=k-1$ contradicting the minimality of k. Therefore, $\left|D\right|=3$. Thus, to prove that $B_{k-2}$ satisfies $\left(1\right)$, it suffices to give a connected dominating set of size 3 of $B_{k-2}$ containing a chosen vertex from ${\check{B}}_{k-2}$. For a vertex v of ${\check{B}}_{k-2}$, consider $G+c_{0}v$. Lemma 1(2) implies that $\{c_0,v\}\cap D_{c_{0}v}\ne \varnothing$. Lemma 1(1) implies also that $|D_{c_{0}v}|\le k-1$. We first show that $\left\{c_0\right\}\ne D_{c_{0}v}\cap \{c_0,v\}$. Suppose to the contrary that $\left\{c_0\right\}=D_{c_{0}v}\cap \{c_0,v\}$. As $(G+uv)\left[D_{uv}\right]$ is connected, there exists $w\in V\left({\check{B}}_{k-2}\right)$ which is adjacent to v. Because $D_{c_{0}v}{\succ }_{c}G+c_{0}v$, w is adjacent to a vertex of $D_{uv}\cap V(B_{k-2}-v)$. Thus,

$$(D_{uv}-\left\{c_0\right\})\cup \left\{w\right\}{\succ }_{c}G.$$

This contradicts the minimality of k. Thus, $\left\{c_0\right\}\ne D_{c_{0}v}\cap \{c_0,v\}$. Therefore, $\{c_0,v\}\subseteq D_{c_{0}v}$ or $\left\{v\right\}=D_{c_{0}v}\cap \{c_0,v\}$.

$\mathbf{Case}\mathbf{1}:$$\{c_0,v\}\subseteq D_{c_{0}v}$

Let

$$i=max\{0\le j\le k-3:\{c_0,c_1,c_2,\dots ,c_j\}\subseteq D_{c_{0}y}\}.$$

We first consider the case when $i=k-3$. Thus $\{c_1,c_2,\dots ,c_{k-3}\}\subseteq D_{c_{0}v}$. As $|D_{c_{0}v}|\le k-1$ and $\{c_0,v\}\subseteq D_{c_{0}v}$, we must have

$$D_{c_{0}v}=\{c_0,c_1,\dots ,c_{k-3},v\}.$$

Therefore, $v\succ V\left(B_{k-2}\right)-A$ and $N_A\left(v\right)=\varnothing$, otherwise $\{c_1,\dots ,c_{k-3},w,v\}{\succ }_{c}G$ where $w\in N_A\left(v\right)$, contradicting the minimality of k. Let $u\in N_{B_{k-2}}\left(v\right)$ such that u is adjacent to a vertex a in A. Thus, $\{v,u,a\}{\succ }_c{B}_{k-2}$ and so $B_{k-2}$ satisfies $\left(1\right)$.

We now consider the case when $i=k-4$. Let $D_{c_{0}v}^{\prime }=D_{c_{0}v}\cap V\left({\check{B}}_{k-2}\right)$. Clearly, $v\in D_{c_{0}v}^{\prime }$. As $\{c_0,c_1,\dots ,c_{k-4}\}\subseteq D_{c_{0}v}$ and $|D_{c_{0}v}|\le k-1$, it follows that $|D_{c_{0}v}^{\prime }|\le 2$. If $|D_{c_{0}v}^{\prime }|=1$, then $D_{c_{0}v}^{\prime }=\left\{v\right\}$ implying that $v\succ {\check{B}}_{k-2}$, in particular, $v\succ A$. Thus, $\{c_1,\dots ,c_{k-3},w,v\}{\succ }_{c}G$ where $w\in N_A\left(v\right)$ contradicting the minimality of D. Therefore, we let $D_{c_{0}v}^{\prime }=\{v,v^{\prime }\}$. As $D_{c_{0}v}{\succ }_{c}G+c_{0}v$, $D_{c_{0}v}^{\prime }{\succ }_c{\check{B}}_{k-2}$. Thus, for a vertex a in A, $D_{c_{0}v}^{\prime }\cup \left\{a\right\}{\succ }_c{B}_{k-2}$. Therefore, $B_{k-2}$ satisfies $\left(1\right)$.

We now consider the case when $i=k-5$. Thus $\{c_0,c_1,\dots ,c_{k-5}\}\subseteq D_{c_{0}v}$. Therefore, $|D_{c_{0}v}^{\prime }|\le 3$ and, $D_{c_{0}v}^{\prime }\cap A\ne \varnothing$ to dominate $c_{k-3}$. So, $B_{k-2}$ satisfies $\left(1\right)$.

We finally consider the case when $i\le k-6$. To dominate $c_{i+2}$, we have that $c_{i+3}\in D_{c_{0}v}$. By the connectedness of $(G+c_{0}v)\left[D_{c_{0}v}\right]$, $\{c_{i+3},\dots ,c_{k-3}\}\subseteq D_{c_{0}v}$. Thus, $\{c_0,c_1,\dots ,c_i\}\cup \{c_{i+3},\dots ,c_{k-3}\}\cup D_{c_{0}v}^{\prime }\subseteq D_{c_{0}v}$ implying that

$k-4+|D_{c_{0}v}^{\prime }|=(i+1)+((k-3)-(i+3)+1)+|D_{c_{0}v}^{\prime }|\le k-1$.

Therefore, $|D_{c_{0}v}^{\prime }|\le 3$. To dominate $c_{k-3}$, $D_{c_{0}v}^{\prime }\cap A\ne \varnothing$. Thus $B_{k-2}$ satisfies $\left(1\right)$ and this completes the proof of Case 1.

$\mathbf{Case}\mathbf{2}:$$\left\{v\right\}=D_{c_{0}v}\cap \{c_0,v\}$

To dominate $c_1$, we have that $c_2\in D_{c_{0}v}$. By the connectedness of $(G+c_{0}v)\left[D_{c_{0}v}\right]$, $\{c_2,c_3,\dots ,$$c_{k-3}\}\subseteq D_{c_{0}v}$ and $D_{c_{0}v}\cap A\ne \varnothing$. As $|D_{c_{0}v}|\le k-1$, we must have $|D_{c_{0}v}-\{c_2,c_3,\dots ,c_{k-3}\}|\le 3$. So $B_{k-2}$ satisfies $\left(1\right)$. This completes the proof of Case 2.

We finally show that $B_{k-2}$ satisfies $\left(2\right)$ of the class ${\mathcal{B}}_2$. Let x and y be non-adjacent vertices of $B_{k-2}$. Lemma 1(2) implies that $\{x,y\}\cap D_{xy}\ne \varnothing$. Lemma 1(1) implies also that $|D_{xy}|\le k-1$. To dominate $c_0$, we have that $c_1\in D_{xy}$. Let $D_{xy}^B=D_{xy}\cap V\left({\check{B}}_{k-2}\right)$. By the connectedness of $(G+xy)\left[D_{xy}\right]$, $D_{xy}^B\cap A\ne \varnothing$ and $\{c_1,c_2,\dots ,c_{k-3}\}\subseteq D_{xy}$. As $|D_{xy}|\le k-1$, we must have $|D_{xy}^B|=|D_{xy}\cap V\left({\check{B}}_{k-2}\right)|=|D_{xy}-\{c_1,c_2,\dots ,c_{k-3}\}|\le 2$. Thus, $B_{k-2}$ satisfies $\left(2\right)$. Therefore, $B_{k-2}\in {\mathcal{B}}_3$. This completes the proof. □

Now, we are ready to prove our first main result, Theorem 2. For completeness, we restate the theorem.

Theorem 2.

For an integer $k\ge 4$, $\mathcal{Z}(k,k-3)={\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})\cup {\mathcal{G}}_2\left(k\right)$.

Proof. 

In view of Lemma 16, $\mathcal{Z}(k,k-3)=\mathcal{H}(0,0,0,\dots ,3)\cup \mathcal{H}(b_1,b_2,\dots ,b_{k-3},2)$ where $b_i=1$ for some $1\le i\le k-3$ and $b_j=0$ for all $1\le j\ne i\le k-3$. Moreover, Theorems 10 and 11 imply that $\mathcal{Z}(k,k-3)={\mathcal{G}}_1(i_1,i_2,\dots ,i_{k-3})\cup {\mathcal{G}}_2\left(k\right)$. This completes the proof. □

4.3. k-${\gamma }_c$-Critical Graphs with Prescribed Cut Vertices

In this section, we prove Theorem 3. First, we introduce structure of some subgraphs. For any block H of a graph G, H is called a block ${\mathcal{H}}_{\ell }$ for $\ell \ge 2$ if H consists of a vertex x and $U_1,U_2,\dots ,U_{\ell }$ as vertex sets of order at least 2 and

• $G[\left\{x\right\}\cup U_1]$, $G[U_1\cup U_2],G[U_2\cup U_3],\dots ,G[U_{\ell -2}\cup U_{\ell -1}]$ and $G\left[U_{\ell }\right]$ are complete.
• For each $u\in V\left(U_{\ell -1}\right)$, $|N_{U_{\ell }}\left(u\right)|=|U_{\ell }|-1$.
• For each $u^{\prime }\in V\left(U_{\ell }\right)$, there exists $u\in V\left(U_{\ell -1}\right)$ such that $u{u}^{\prime }\in E\left(G\right)$.

We say that x is the head of a block ${\mathcal{H}}_{\ell }$. Note that when $\ell =2$, we have ${\mathcal{H}}_2={\mathcal{B}}_{2,2}$.

Let $\mathcal{D}(k,\zeta ,{\zeta }_0):$ the class of all k-${\gamma }_c$-critical graphs with $\zeta$ cut vertices containing a block B such that $\zeta \left(B\right)={\zeta }_0$.

We next introduce the following class that we use to establish the existence of graphs in $\mathcal{D}(k,\zeta ,{\zeta }_0)$.

The class $\mathcal{F}(p,q,r)$:

Let $H_1,H_2,\dots ,H_p$ be p ${\mathcal{H}}_2$ blocks. Further, we let $H_{p+1}$ be $P_q$ (a path of q vertices), and let $H_{p+2}$ be an ${\mathcal{H}}_r$ block. Let $c_i$ be the head of $H_i$ for $1\le i\le p+2$. A graph $G\in \mathcal{F}(p,q,r)$ is obtained from $H_1,\dots ,H_{p+2}$ by joining edges between vertices in $\{c_i:1\le i\le p+2\}$ to form a clique.

Lemma 18.

If a graph G is in the class $\mathcal{F}(p,q,r)$, then G is $(r+q+3p)$-${\gamma }_c$-critical with $p+q$ cut vertices having a block that contains $p+2$ cut vertices.

Proof. 

For $i\in \left[p\right]$, let $U_1^i=N_{H_i}\left(c_i\right)$ and $U_2^i=V\left(H_i\right)-U_1^i$. We see that $U_1^i$ and $U_2^i$ are, respectively, the same as $U_1$ and $U_2$ of the block ${\mathcal{H}}_2$. Let $a_i\in U_1^i$. By the construction of the block ${\mathcal{H}}_2$, there exists $b_i\in U_2^i$ such that $a_i{b}_i\in E\left(G\right)$ and $a_i$ is not adjacent to the vertex $a_i^{\prime }\in U_2^i$. Let $H_{p+1}=d_0,d_1,\dots ,d_{q-1}$ where $c_{p+1}=d_0$. For the block $H_{p+2}$, let ${\tilde{U}}_i$ be a vertex subset of $V\left(H_{p+2}\right)$ which is the same as $U_i$ of the block ${\mathcal{H}}_r$ and $u_i\in {\tilde{U}}_i$ for $i\in \left[r\right]$.

Lemma 2(3) implies that $c_i\in D$ for $i\in [p+2]$. Consider $H_{p+2}$. By the connectedness of $G\left[D\right]$, $|{\tilde{U}}_i\cap D_c|\ge 1$ for $i\in [r-1]$. Because every vertex in ${\tilde{U}}_{r-1}$ does not dominate ${\tilde{U}}_r$, $|D\cap ({\tilde{U}}_{r-1}\cup {\tilde{U}}_r\left)\right|\ge 2$. Since $c_{p+2}\in D$, $|D\cap V(H_{p+2}\left)\right|\ge r+1$. By the same arguments, $|D\cap V(H_i\left)\right|\ge 3$ for $i=1,2,\dots ,p$. Finally, to dominate $d_{q-1}$, $\{c_{p+1},d_1,d_2,\dots ,d_{q-2}\}\subseteq D$. So $\left|D\right|\ge (r+1)+3p+(q-1)=r+q+3p$. It is not difficult to see that $\left({\cup }_{i=1}^p\{a_i,b_i\}\right)\cup \{c_1,c_2,\dots ,c_{p+2}\}\cup \{d_1,..,d_{q-2}\}\cup \{u_1,u_2,\dots ,u_r\}{\succ }_{c}G$. Therefore, $\left|D\right|\le 2p+(p+2)+(q-2)+r=r+q+3p$. Thus, ${\gamma }_c\left(G\right)=r+q+3p$.

Let $k=r+q+3p$. For a pair of non adjacent vertices $u,v\in V\left(G\right)$. Consider $G+uv$. To establish the criticality, it suffices to show that there exists a dominating set $D_{uv}$ of $G+uv$ containing less than k vertices. For $i\in [p+2]$, let $D_i=D\cap V\left(H_i\right)$. We distinguish 3 cases.

Case 1:$\{u,v\}\cap \left({\cup }_{i=1}^p{H}_i\right)\ne \varnothing$.

Without loss of generality, let $u\in V\left(H_1\right)$.

Subcase 1.1:$u=c_1$. Clearly, $v\notin \{c_2,c_3,\dots ,c_{p+2}\}$.

• If $v\in U_2^1$, then let $D_{uv}=\{u,v\}\cup \left({\cup }_{i=2}^{p+2}{D}_i\right)$.

For $j\ge 2$,

• if $v\in U_1^j$, then let $D_{uv}=\left({\cup }_{i\ne j}{D}_i\right)\cup \{v,w\}$ where $w\in N_{U_2^j}\left(v\right)$, and
• if $v\in U_2^j$, then let $D_{uv}=\left({\cup }_{i\ne j}{D}_i\right)\cup \{v,c_j\}$.

We now consider the case when $v\in V\left(H_{p+1}\right)$. We let $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)\cup \{d_1,d_2,\dots ,$$v,\dots ,d_{q-2}\}$ if $v\ne d_{q-1}$ and let $D_{uv}=D-\left\{d_{q-2}\right\}$ if $v=d_{q-1}$. When $v\in V\left(H_{p+2}\right)$, we let $D_{uv}=\left({\cup }_{i\ne p+2}{D}_i\right)\cup \{u_1,u_2,\dots ,v,\dots ,u_r\}$ where $u_1,u_2,\dots ,v,\dots ,u_r$ is a path such that $v=u_j$ for some $j\in \left[r\right]$.

Subcase 1.2:$u\in U_1^1$. Without loss of generality let $u=a_1$. So $u{a}_1^{\prime }\notin E\left(G\right)$ and $u{b}_1\in E\left(G\right)$. Clearly, $v\ne c_1$. If $v=c_i$ for some $\{2,\dots ,p\}$, then we can find $D_{uv}$ by the same arguments as Subcase 1.1. Thus, we may consider when $v\ne c_i$ for $i=1,2,\dots ,p$. If $v=a_1^{\prime }$, then let $D_{uv}=\left({\cup }_{i\ne 1}{D}_i\right)\cup \{a_1,c_1\}$. For $j\ge 2$,

• if $v\in U_1^j$, then let $D_{uv}=\left({\cup }_{i\ne 1,j}{D}_i\right)\cup \{c_1,u,b_1,v,w\}$ where $w\in N_{U_2^j}\left(v\right)$, and
• if $v\in U_2^j$, then let $D_{uv}=\left({\cup }_{i\ne 1,j}{D}_i\right)\cup \{c_1,u,b_1,v,c_j\}$.

We now consider the case when $v\in V\left(H_{p+1}\right)\cup V\left(H_{p+2}\right)$. If $v\in \{c_{p+1},c_{p+2}\}$, then $D_{uv}=\left({\cup }_{i\ne 1}{D}_i\right)\cup \{u,b_1\}$. Thus, we may assume that $v\notin \{c_{p+1},c_{p+2}\}$. We let $\tilde{D}=\left({\cup }_{i=2}^p{D}_i\right)\cup \{c_1,u,b_1\}$. If $v=d_i$ for some $i\in [q-2]$, then we let $D_{uv}=\tilde{D}\cup \{d_1,\dots ,d_{q-2}\}\cup D_{p+2}$. If $v=d_{q-1}$, then we let $D_{uv}=\tilde{D}\cup \{d_0,\dots ,d_{q-3}\}\cup D_{p+2}$. Finally, if $v=u_i\in {\tilde{U}}_i$ for some $i\in \left[r\right]$, then we let $D_{uv}=\tilde{D}\cup D_{p+1}\cup \{u_1,u_2,\dots ,v,\dots ,u_r\}$.

Subcase 1.3:$u\in U_2^1$. Without loss of generality let $u=b_1$. Clearly, $u{a}_1\in E\left(G\right)$. By the same arguments as Subcases 1.1 and 1.2, we consider only when $v\notin {\cup }_{i=2}^p(\left\{c_i\right\}\cup U_1^i)$. If $v\in U_1^1$, then let $D_{uv}=\{v,c_1\}\cup \left({\cup }_{i\ne 1}{D}_i\right)$. If $v\in U_2^j$, then let $D_{uv}=\left({\cup }_{i\ne 1,j}{D}_i\right)$$\cup \{u,v,a_1,c_1\}$. If $v\in \{c_{p+1},c_{p+2}\}$, then $D_{uv}=\left({\cup }_{i\ne 1}{D}_i\right)\cup \{u,c_1\}$. Thus, we may assume that $v\in V\left(H_{p+1}\right)\cup V\left(H_{p+2}\right)-\{c_{p+1},c_{p+2}\}$. We let $\tilde{D}=D_{uv}=\left({\cup }_{i=2}^p{D}_i\right)\cup \{c_1,u,a_1\}$ and we can find $D_{uv}$ by same arguments as Subcase 1.2.

Case 2:$\{u,v\}\cap \left({\cup }_{i=1}^{p}V\left(H_i\right)\right)=\varnothing$ and $\{u,v\}\cap V\left(H_{p+1}\right)\ne \varnothing$.

Without loss of generality let $u\in V\left(H_{p+1}\right)$.

Subcase 2.1:$u=c_{p+1}$. Suppose first that $v\in V\left(H_{p+1}\right)$. Thus, $v=d_j$ for some $j>2$. If $j=3$, then let $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)\cup \{c_{p+1},d_3,d_4,\dots ,d_{q-2}\}$. If $3<j<q-1$, then $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)\cup \{c_{p+1},d_4,\dots ,v\dots ,d_{q-2}\}$. If $j=q-1$, then let $D_{uv}=D-\left\{d_{q-2}\right\}$. If $v\in V\left(H_{p+2}\right)$, then we let $D_{uv}=\left({\cup }_{i\ne p+2}{D}_i\right)\cup \{u_1,u_2,\dots ,v,\dots ,u_r\}$.

Subcase 2.2:$u\in V\left(H_{p+1}\right)-\left\{c_{p+1}\right\}$. Suppose that $v\in V\left(H_{p+1}\right)$. By the same arguments as Subcase 2.1, $v\in V\left(H_{p+1}\right)-\left\{c_{p+1}\right\}$. Without loss of generality let $u=d_j$ and $v=d_{j^{\prime }}$ such that $j<j^{\prime }$. If $j^{\prime }<q-1$, then let $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)\cup \{c_{p+1},d_1,d_2,\dots ,d_{j-1},u,d_{j+2},\dots ,v,\dots ,d_{q-2}\}$. If $j^{\prime }=q-1$, then let $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)$$\cup \{c_{p+1},d_1,\dots ,u,\dots ,d_{q-3}\}$. Suppose that $v\in V\left(H_{p+2}\right)$. If $v=c_{p+2}$ and $j<q-1$, then let $D_{uv}=\left({\cup }_{i\ne p+1}{D}_i\right)\cup \{d_1,\dots ,u,\dots ,d_{q-2}\}$. If $v=c_{p+2}$ and $j=q-1$, then let $D_{uv}=D-\left\{d_{q-2}\right\}$. We now consider the case when $v\in V\left(H_{p+2}\right)-\left\{c_{p+2}\right\}$. Let ${\tilde{D}}_{p+2}=\{c_{p+2},u_1,\dots ,u_r\}$ and ${\tilde{D}}_{p+1}=\{d_1,d_2,\dots ,d_{q-2}\}$. Let $D_{uv}=\left({\cup }_{i=1}^p{D}_i\right)\cup ({\tilde{D}}_{p+1}\cup {\tilde{D}}_{p+2})$ by the same arguments as Subcase 2.1.

Case 3:$\{u,v\}\subseteq V\left(H_{p+2}\right)$. Without loss of generality let $u\in {\tilde{U}}_j$ and $v\in {\tilde{U}}_{j^{\prime }}$ where $j<j^{\prime }$. Let $c_{p+2}=U_0$. If $u\notin {\tilde{U}}_{r-1}$, then there exists a path $u_0,u_1,\dots ,u_r$ such that $u=u_j$ and $v=u_{j^{\prime }}$ where $u_i\in {\tilde{U}}_i$ for $0\le i\le r$. Let $D_{uv}=\left({\cup }_{i\ne p+2}{D}_i\right)\cup \{u_0,u_1,\dots ,u_{j-1},u,u_{j+2},\dots ,v,\dots ,u_r\}$. If $u\in {\tilde{U}}_{r-1}$, then v is the only one vertex in ${\tilde{U}}_r$ which u is not adjacent. Thus, $D_{uv}=\left({\cup }_{i\ne p+2}{D}_i\right)\cup \{U_0,U_1,\dots ,U_{r-2},u\}$.

Finally, we see that $c_1,\dots ,c_{p+2},d_1,\dots ,d_{q-2}$ are all the cut vertices of G. Thus, G has $p+q$ cut vertices. Further, the block $G\left[\{c_1,\dots ,c_{p+2}\}\right]$ has $c_1,\dots ,c_{p+2}$ as the cut vertices of G. Therefore, there is a block containing $p+2$ cut vertices. This completes the proof. □

Now, we are ready to prove Theorem 12. For completeness, we restate the theorem.

Theorem 12.

For all $k\ge 4$, $2\le \zeta \le k-2$ and $2\le {\zeta }_0\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$, there exists a k-${\gamma }_c$-critical graph with $\zeta$ cut vertices having a block that contains ${\zeta }_0$ cut vertices, namely, $\mathcal{D}(k,\zeta ,{\zeta }_0)\ne \varnothing$.

Proof. 

In view of Lemma 18, for all $k\ge 4$, $2\le \zeta \le k-2$ and $2\le {\zeta }_0\le min\left\{⌊\frac{k+2}{3}⌋,\zeta \right\}$, we have $\mathcal{F}({\zeta }_0-2,\zeta -{\zeta }_0+2,k-\zeta -2{\zeta }_0+4)\subseteq \mathcal{D}(k,\zeta ,{\zeta }_0)$. This completes the proof. □

4.4. Factor Criticality of k-${\gamma }_c$-Critical Graphs

In this section, for $k\ge 3$, we will use the property of graphs in the class $\mathcal{P}\left(k\right)$ which is given in Section 3. First, we may prove that the class $\mathcal{P}\left(k\right)$ is non-empty for $k\ge 3$.

Lemma 19.

For all $k\ge 3$, $\mathcal{P}\left(k\right)\ne \varnothing$.

Proof. 

For an integer $k\ge 3$, we let $C_{k+2}=c_1,c_2,\dots ,c_{k+2},c_1$ be a cycle of length $k+2$. It is well known that $C_{k+2}$ is a k-${\gamma }_c$-critical graph. In this proof, all subscripts are taken modulo $k+2$. Observe that $C_{k+2}\left[\{c_j,c_{j+1}\}\right]$ is a maximal complete subgraph for all $1\le j\le k+2$. Thus, without loss of generality, it suffices to show that complete subgraph $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(i\right)$ and $\left(ii\right)$ of $\mathcal{P}\left(k\right)$.

For a vertex $c_j$ where $1\le j\le k+2$, let

$S_j=\{c_j,c_{j+1},\dots ,c_{k+2},c_1,\dots ,c_{j-3}\}{\succ }_c{C}_{k+2}$.

Clearly, $S_j\cap \{c_1,c_2\}\ne \varnothing$ if $j\ne 3$. Thus, we consider the case when $j=3$. In this case $c_{k+2}\in S_3$. Let $S^{\prime }=(S_3-\left\{c_{k+2}\right\})\cup \left\{c_2\right\}$. Therefore, $S^{\prime }{\succ }_c{C}_{k+2}$. Moreover, $S^{\prime }\cap \{c_1,c_2\}\ne \varnothing$. Therefore, $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(i\right)$.

We now let $c_j$ and $c_l$ be non-adjacent vertices of $C_{k+2}$. So $|j-l|\ge 2$. Consider $C_{k+2}+c_j{c}_l$. We partition $V\left(C_{k+2}\right)$ to

$C^1=\{c_j,c_{j+1},\dots ,c_{l-1}\}$ and $C^2=\{c_l,c_{l+1},\dots ,c_{j-1}\}$.

As $k+2\ge 5$, at least one of $C^1$ or $C^2$ must have at least three vertices. Without loss of generality let it be $C^1$. We further let

$$D=\left\{\begin{array}{cc}\{c_j,c_{j+1},\dots ,c_{l-3}\}\cup \{c_l,c_{l+1},\dots ,c_{j-3}\},\hfill & if|C^2|\ge 3and\hfill \\ \{c_j,c_{j+1},\dots ,c_{l-2}\},\hfill & otherwise.\hfill \end{array}\right.$$

Clearly, $D{\succ }_c{C}_{k+2}$ and $\left|D\right|<k$. We first consider the case when $|C^2|\ge 3$. Note that D in this case contains $k-2$ vertices. If $\{c_1,c_2\}$ is neither $\{c_{l-1},c_{l-2}\}$ nor $\{c_{j-1},c_{j-2}\}$, then $D\cap \{c_1,c_2\}\ne \varnothing$. This implies that $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(ii\right)$. Thus, we may assume that $\{c_1,c_2\}=\{c_{l-1},c_{l-2}\}$. As $\left|D\right|=k-2$, we must have $|D\cup \{c_{l-1}\left\}\right|<k$. Moreover, $D\cup \left\{c_{l-1}\right\}{\succ }_c{C}_{k+2}+c_j{c}_l$ because $D{\succ }_c{C}_{k+2}+c_j{c}_l$. Thus, $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(ii\right)$. The case $\{c_1,c_2\}=\{c_{j-1},c_{j-2}\}$ can be proved by the same arguments.

We now consider the case when $|C^2|<3$, in fact $C^2=\{c_l,c_{l+1}\}$ and $c_{l+2}=c_j$. If $\{c_1,c_2\}$ is neither $\{c_{l-1},c_l\}$ nor $\{c_l,c_{l+1}\}$, then $D\cap \{c_1,c_2\}$ and this implies that $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(ii\right)$. Thus we may assume that $\{c_1,c_2\}$ is $\{c_{l-1},c_l\}$ or $\{c_l,c_{l+1}\}$. We observe that $c_1=c_{l-1}$ and $c_2=c_l$ when $\{c_1,c_2\}=\{c_{l-1},c_l\}$, moreover, $c_1=c_l$ and $c_2=c_{l+1}$ when $\{c_1,c_2\}=\{c_l,c_{l+1}\}$. In both cases, $c_l\in \{c_1,c_2\}$. Let $D^{\prime }=(D-\left\{c_{l-2}\right\})\cup \left\{c_l\right\}$. We see that $D^{\prime }{\succ }_c{C}_{k+2}+c_j{c}_l$. So $D^{\prime }\cap \{c_1,c_2\}\ne \varnothing$ because $c_l\in \{c_1,c_2\}$ and $c_l\in D^{\prime }$. Therefore $C_{k+2}\left[\{c_1,c_2\}\right]$ satisfies $\left(ii\right)$. Therefore, $C_{k+2}\in \mathcal{P}\left(k\right)$ and this completes the proof. □

In the following, we show how to apply the construction of some graphs in the class $\mathcal{P}\left(k\right)$ to establish the existence of $(k+l)$-${\gamma }_c$-critical graphs with some property. For an integer $k\ge 1$ and $\ell \ge 1$, we let

$\mathcal{Q}(k,\ell ):$ the class of k-${\gamma }_c$-critical graphs G with $\delta \ge \ell +1$ such that $\left|V\right(G\left)\right|\equiv \ell \left(\mathrm{mod}2\right)$

G is not ℓ-factor critical.

Therefore, we may rewrite Observation 1 in term of the class $\mathcal{Q}(k,1)$.

Observation 4.

$\mathcal{Q}(k,1)=\varnothing$ for $k\in \left[2\right]$.

For $k=3$, Figure 5 shows that there exists a 3-${\gamma }_c$-critical graph of odd order and $\delta \ge 2$ which is non-factor critical. Thus $\mathcal{Q}(3,1)\ne \varnothing$. In the following, for $k\ge 4$, we show further that there exists a k-${\gamma }_c$-critical graph which is non-factor critical.

The class$\mathcal{X}\left(s\right)$

For an integer $s\ge 3$, let $A=\{a_1,a_2,\dots ,a_s\}$ and $B=\{b_1,b_2,\dots ,b_s\}$ be two disjoint sets of vertices. We further let $K_s$ be a copy of a complete graph of order s such that $V\left(K_s\right)=\{y_1,y_2,\dots ,y_s\}$. A graph G in the class $\mathcal{X}\left(s\right)$ can be constructed from $A,B$ and $K_s$ by adding edges according to the join operations that, for $1\le i\le s$,

• $a_i\vee (B-\left\{b_i\right\})$ and
• $a_i\vee (K_s-y_i)$.

A graph in this class is illustrated by Figure 9.

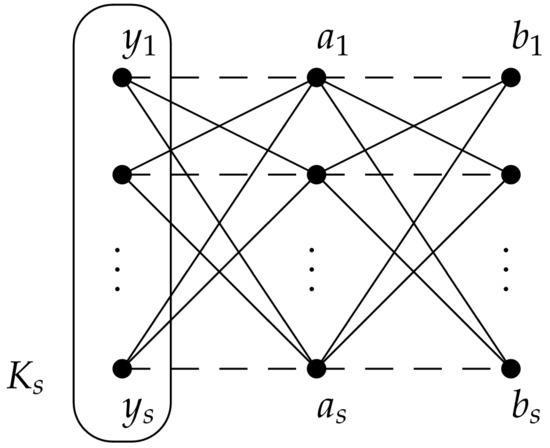
Figure 9. A graph G in the class $\mathcal{X}\left(s\right)$.

The following lemma gives that $\mathcal{X}\left(s\right)\subseteq \mathcal{P}\left(4\right)\cap \mathcal{Q}(4,1)$ for integer $s\ge 3$.

Lemma 20.

For an integer $s\ge 3$, $\mathcal{X}\left(s\right)\subseteq \mathcal{P}\left(4\right)\cap \mathcal{Q}(4,1)$.

Proof. 

For a given $s\ge 3$, let G be in the class $\mathcal{X}\left(s\right)$. We first show that ${\gamma }_c\left(G\right)=4$. Suppose to the contrary that there exists a connected dominating set D of size less than 4. We first consider the case when $D\cap V\left(K_s\right)\ne \varnothing$. To dominate B, $|D\cap A|\ge 2$. Therefore, $D=\{y_i,a_j,a_l\}$. By the connectedness of $G\left[D\right]$, $i\notin \{j,l\}$. Thus, D does not dominate $a_i$, a contradiction. Thus, we consider the case when $D\cap V\left(K_s\right)=\varnothing$. Therefore, to dominate $K_s$, $|D\cap A|\ge 2$. As A is an independent set, by the connectedness of $G\left[D\right]$, $|D\cap B|\ge 1$. Therefore, $D=\{a_j,a_l,b_i\}$. Similarly, $i\notin \{j,l\}$, and this implies that D does not dominate $a_i$, a contradiction. Thus, ${\gamma }_c\left(G\right)\ge 4$.

We observe that $K_s$ is a maximal complete subgraph of G. We do not only show that ${\gamma }_c\left(G\right)\le 4$, but we also show that, for a vertex a of G, there exists a connected dominating set $D_a$ of G containing a and $D\cap V\left(K_s\right)\ne \varnothing$. That is, we show that $K_s$ satisfies $\left(i\right)$ of graphs in the class $\mathcal{P}\left(k\right)$. For $1\le i\ne i^{\prime }\ne i^{″}\le s$, we have

$D_{y_i}=D_{a_i}=\{y_i,y_{i^{\prime }},a_i,a_{i^{\prime }}\}$ and

$D_{b_i}=\{b_i,a_{i^{\prime }},y_{i^{\prime \prime }},a_i\}$

Therefore, ${\gamma }_c\left(G\right)\le 4$ and thus ${\gamma }_c\left(G\right)=4$. Moreover, $K_s$ satisfies $\left(i\right)$.

We finally establish the criticality. Further, we show that, for non-adjacent vertices x and y of G, $D_{xy}\cap V\left(K_s\right)\ne \varnothing$. That is, we will show that $K_s$ satisfies $\left(ii\right)$ of graphs in the class $\mathcal{P}\left(k\right)$. We first consider the case when $\{x,y\}\cap B\ne \varnothing$. If $\{x,y\}=\{b_i,b_j\}$, then $D_{xy}=\{b_i,a_j,y_l\}$. If $\{x,y\}=\{a_i,b_i\}$, then $D_{xy}=\{a_i,y_j,y_l\}$. If $\{x,y\}=\{b_i,y_j\}$ (in this case $y_j$ could be $y_i$), then $D_{xy}=\{y_j,y_l,a_i\}$. We now consider the case when $\{x,y\}\cap B=\varnothing$. Thus, $\{x,y\}$ is either $\{a_i,a_j\}$ or $\{a_i,y_i\}$. In both cases, $D_{xy}=\{a_i,a_j,y_i\}$. Thus, G is a 4-${\gamma }_c$-critical graph, in particular, $G\in \mathcal{P}\left(4\right)$.

Finally, let s be odd number and $S=A$. Thus, ${\omega }_o(G-S)$ has $K_s$ and $b_1,\dots ,b_s$ as $s+1$ odd components. Thus ${\omega }_o(G-S)=s+1>s-1=\left|S\right|-1$. By Theorem 6, G is non-factor critical. Thus, $G\in \mathcal{Q}(4,1)$ and this completes the proof. □

We will use a graph in the class $\mathcal{P}\left(4\right)$ to show that $\mathcal{Q}(k,1)\ne \varnothing$ for all $k\ge 6$. For $k=5$, we also provide a graph $G_5(l_1,l_2)$ in the class $\mathcal{Q}(5,1)$ by the following construction. Let $u,x,y,z$ and w be five different vertices. We also let $P_2=x^{\prime },y^{\prime }$ be a path of length one and $K_{l_1},K_{l_2}$ be two copies of complete graphs of order $l_1\ge 2$ and $l_2\ge 2$, respectively, moreover, $l_1+l_2$ is even number. The graph $G_5(l_1,l_2)$ is constructed by adding edges according to the join operations:

• $u\vee K_{l_1}\vee K_{l_2}\vee P_2$
• $x\vee x^{\prime },y\vee y^{\prime }$
• $w\vee P_2$ and
• $z\vee \{x,y,w\}$.

Figure 10 illustrates the graph $G_5(l_1,l_2)$.

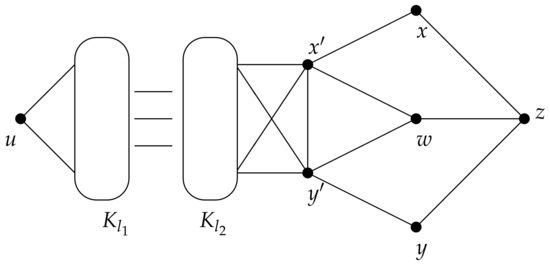
Figure 10. The graph $G_5(l_1,l_2)$.

It is not difficult to show that $G_5(l_1,l_2)$ is 5-${\gamma }_c$-critical graph. Moreover, $G_5(l_1,l_2)$ has $S=\{x^{\prime },y^{\prime },z\}$ as a cut set such that ${\omega }_o(G_5(l_1,l_2)-S)=4=\left|S\right|+1>\left|S\right|-1$. By Theorem 6, $G_5(l_1,l_2)$ is not factor critical.

Now, we are ready to prove Theorem 4. For completeness, we restate the theorem.

Theorem 13.

Every k-${\gamma }_c$-critical graph of odd order with $\delta \ge 2$ is factor critical if and only if $k\in \left[2\right]$. Namely, $\mathcal{Q}(k,1)=\varnothing$ if and only if $k\in \left[2\right]$.

Proof. 

Observation 4 implies that if $k=1$ or 2, then $\mathcal{Q}(k,1)=\varnothing$.

Conversely, Figure 5 in Section 3 yields that $\mathcal{Q}(3,1)\ne \varnothing$. Lemma 20 yields that $\mathcal{Q}(4,1)\ne \varnothing$. Moreover, as $G_5(l_1,l_2)\in \mathcal{Q}\left(5\right)$, we must have $\mathcal{Q}(5,1)\ne \varnothing$. We assume that $k\ge 6$. For an odd integer $s\ge 3$, we let $G\in \mathcal{X}\left(s\right)$ with $K_s=H$ satisfies $\left(i\right)$ and $\left(ii\right)$ of graphs in the class $\mathcal{P}\left(k\right)$. We moreover let integers $n_1,n_2,\dots ,n_{l-1}\ge 2$ and $n_l=1$ be such that $n_1+n_2+\dots +n_{l-1}+1$ is odd number.

$G(n_1,n_2,\dots ,n_{l-1},1)=x_0\vee K_{n_1}\vee K_{n_2}\vee \dots \vee K_{n_{l-1}}\vee K_{n_l}\vee {}_{H}G$. In view of Theorem 9, $G(n_1,n_2,\dots ,n_{l-1},1)$ is a $(4+l)$-${\gamma }_c$-critical graph. Let $V\left(K_{n_l}\right)=\left\{y\right\}$. Thus, $G(n_1,n_2,\dots ,n_{l-1},1)$ has $S=\{y,a_1,a_2,\dots ,a_s\}$ as a cut set such that

${\omega }_o(G(n_1,n_2,\dots ,n_{l-1},1)-S)=\left|S\right|+2>\left|S\right|-1$. Theorem 6 then gives that $G(n_1,n_2,\dots ,n_{l-1},1)$ is non-factor critical. Therefore $\mathcal{Q}(k,1)\ne \varnothing$ for all $k\ge 6$. These imply that if $\mathcal{Q}(k,1)=\varnothing$, then $k=1$ or 2. This completes the proof. □

In view of Theorem 4, it is natural to think of the bi-criticality of k-${\gamma }_c$-critical graphs with $\delta \ge 3$. Although, we know that if a graph G is not factor critical, then there exists a cut set S such that

$$\begin{array}{c}\hfill {\omega }_o(G-S)>\left|S\right|-1>\left|S\right|-2.\end{array}$$

By Theorem 6, regardless with the parity of the orders of graphs, it is most likely there exist k-${\gamma }_c$-critical graphs that are not bi-critical. However, we notice that the graphs that are obtained from the construction in Figure 10 and Theorem 4 contain a claw, $K_{1,3}$, as an induced subgraphs. Therefore, we may ask if every k-${\gamma }_c$-critical $K_{1,3}$-free graph with $\delta \ge 3$ is bi-critical. By Theorem 8, for $1\le k\le 2$, every k-${\gamma }_c$-critical graph is $K_{1,3}$-free with $\delta \ge 3$ of even order is bi-critical. Therefore, we obtain the following corollary by Observation 2.

Corollary 2.

If $k\in \left[2\right]$, then every k-${\gamma }_c$-critical $K_{1,3}$-free graph with $\delta \ge 3$ is bi-critical.

When $k\ge 3$, it turns out that there exist k-${\gamma }_c$-critical graph with $\delta \ge 3$ which is not bi-critical even they do not contain $K_{1,3}$ as an induced subgraph.

Let

$\tilde{\mathcal{Q}}(k,\ell ):$ the class of k-${\gamma }_c$-critical $K_{1,3}$-free graphs G with $\delta \ge \ell +1$ such that

G is not ℓ-factor critical.

The class $\mathcal{A}(t_1,t_2)$

For an odd number $t_1\ge 2$ and an even number $t_2\ge 2$, the graph G in this class is obtained from vertices $x_1,x_2,x_3$ and copies of complete graphs $K_{t_1},K_{t_2}$ by adding edges according to the join operations:

• $x_1\vee K_{t_l}\vee x_2\vee x_3$ and
• $x_1\vee K_{t_2}\vee x_3$.

The graph in this class is illustrated by Figure 11.

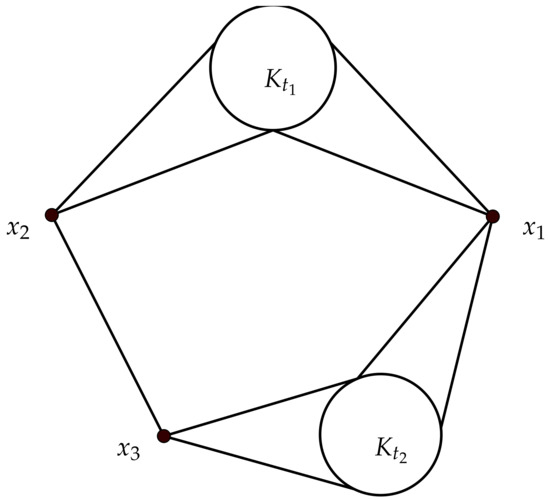
Figure 11. The graph G in the class $\mathcal{A}(t_1,t_2)$.

Lemma 21.

If $G\in \mathcal{A}(t_1,t_2)$, then $G\in \mathcal{P}\left(3\right)\cap \tilde{\mathcal{Q}}(3,2)$.

Proof. 

It is easy to see that all graphs in the class $\mathcal{A}(t_1,t_2)$ is 3-${\gamma }_c$-critical and $K_{1,3}$-free with $\delta \ge 3$. Further, by removing $x_1$ and $x_2$, the resulting graph has two odd components: $K_{t_1}$ and $G[V\left(K_{t_2}\right)\cup \left\{x_3\right\}]$. Thus, G is not bi-critical. Therefore, $G\in \tilde{\mathcal{Q}}(3,2)$. It is easy to see that every graph G in the class $\mathcal{A}(t_1,t_2)$ satisfies the Properties (i) and (ii) of the class $\mathcal{P}\left(k\right)$ by selecting $G[V\left(K_{t_2}\right)\cup \left\{x_3\right\}]$ as a maximal complete subgraph. Thus, $G\in \mathcal{P}\left(3\right)\cap \tilde{\mathcal{Q}}(3,2)$ and this completes the proof. □

Finally, we will establish the existence of k-${\gamma }_c$-critical $K_{1,3}$-free graphs with $\delta \ge 3$ which are not bi-critical for $k\ge 4$ by proving Theorem 14. For completeness, we restate theorem.

Theorem 14.

Every k-${\gamma }_c$-critical $K_{1,3}$-free graph of even order with $\delta \ge 3$ is bi-critical if and only if $k\in \left[2\right]$. Namely, $\tilde{\mathcal{Q}}(k,2)=\varnothing$ if and only if $k\in \left[2\right]$.

Proof. 

By Observation 2, we have that if $k\in \left[2\right]$, then $\tilde{\mathcal{Q}}(k,2)=\varnothing$.

Conversely, we will show that if $k\ge 3$, then $\tilde{\mathcal{Q}}(k,2)\ne \varnothing$. By Lemma 21, we have that $\tilde{\mathcal{Q}}(3,2)\ne \varnothing$. For $k\ge 4$, we let $G\in \mathcal{A}(t_1,t_2)$ such that $t_1\ge 3$ is an odd number and $t_2\ge 2$ is an even number. Further, we let $x_0$ be a vertex and, for $n_1,\dots ,n_{k-3}\ge 2$ such that $n_1+\cdots +n_{k-3}$ is an odd number, we let $K_{n_1},\dots ,K_{n-k}$ be $k-3$ copies of complete graphs of order $n_1,\dots ,n_{k-3}$, respectively. Let $H=G[V\left(K_{t_2}\right)\cup \left\{x_3\right\}]$ and

$G^{\prime }=G^{\prime }(n_1,\dots ,k_{k-3},t_1,t_2)=x_0\vee K_{n_1}\vee \cdots \vee K_{n_{k-3}}\vee {}_{H}G$.

By Theorem 9, we have that $G^{\prime }$ is k-${\gamma }_c$-critical graphs. Clearly, $G^{\prime }$ is $K_{1,3}$-free and $\delta \left(G^{\prime }\right)\ge 3$. By removing $x_1$ and $x_2$ from $G^{\prime }$, we have that $G^{\prime }-x_1-x_2$ has $K_{t_1}$ and $x_0\vee K_{n_1}\vee \cdots \vee K_{n_{k-3}}\vee H$ as the two odd components. Therefore,

$${\omega }_o(G^{\prime }-\{x_1,x_2\})=2>0=\left|\{x_1,x_2\}\right|-2$$

implying that $G^{\prime }$ is not bi-critical. This completes the proof. □