Abstract
A graph G is said to be k--critical if the connected domination number is equal to k and for any pair of non-adjacent vertices u and v of G. Let be the number of cut vertices of G and let be the maximum number of cut vertices that can be contained in one block. For an integer , a graph G is ℓ-factor critical if has a perfect matching for any subset S of vertices of size ℓ. It was proved by Ananchuen in 2007 for , Kaemawichanurat and Ananchuen in 2010 for and by Kaemawichanurat and Ananchuen in 2020 for that every k--critical graph has at most cut vertices and the graphs with maximum number of cut vertices were characterized. In 2020, Kaemawichanurat and Ananchuen proved further that, for , every k--critical graphs satisfies the inequality . In this paper, we characterize all k--critical graphs having cut vertices. Further, we establish realizability that, for given , and , there exists a k--critical graph with cut vertices having a block which contains cut vertices. Finally, we proved that every k--critical graph of odd order with minimum degree two is 1-factor critical if and only if . Further, we proved that every k--critical -free graph of even order with minimum degree three is 2-factor critical if and only if .
1. Introduction
For a natural number n, we let . For standard terminology of graphs, we refer the reader to [1,2]. All graphs in this paper are finite, undirected and simple (no loops or multiple edges). For a graph G, let denote the set of vertices of G and let denote the set of edges of G. For , denotes the subgraph of G induced by S. The open neighborhood of a vertex v in G is . Further, the closed neighborhood of a vertex v in G is . For subsets X and Y of , is the set for some . For a subgraph H of G, we use instead of and we use instead of . If , we use instead of . The degree of a vertex x in G is . The minimum degree of G is denoted by . When no ambiguity occur, we write and instead of and , respectively. An end vertex is a vertex of degree one and a support vertex is the vertex which is adjacent to an end vertex. A tree is a connected graph with no cycle. A star is a tree containing one support vertex and n end vertices. The support vertex of a star is called the center. For a connected graph G, a vertex subset S of G is called a cut set if is not connected. We let be the number of components of containing odd number of vertices. In particular, if , then v is called a cut vertex of G. That is, is not connected. A block B of a graph G is a maximal connected subgraph such that B has no cut vertex. An end block of G is a block containing exactly one cut vertex of G. For graphs H and G, a graph G is said to be H-free if G does not contain H as an induced subgraph. For a connected graph G, a bridge of G is an edge such that is not connected.
For a finite sequence of graphs for , the sequential joins is the graph consisting of the disjoint union of and joining edges from every vertex of to every vertex of for . In particular, for a subgraph H of , the join is the graph consisting of the disjoint union of and and joining edges from every vertex of to every vertex of H. As the join operation is run over vertices, for a vertex x and a set X of vertices, the join is the graph consisting of the disjoint union of and X and joining edges from x to every vertex in X. In the following, we may call the sequential joins shortly the joins while the operation is still the same, that is, to add all edges between only two consecutive graphs in the order. For a subgraph H of G, H is maximal complete subgraph of G if for any complete subgraph of G such that , we have .
The distance between vertices u and v of G is the length of a shortest -path in G. The diameter of G is the maximum distance of any two vertices of G. For a non-negative integer k, a graph G is k-diameter critical if and for any edge . A matching of a graph G is a set of edges which are not incident to a common vertex. A matching M of a graph G is perfect if . For a non-negative integer ℓ, a graph G is ℓ-factor critical if has a perfect matching where S is any set of ℓ vertices, in particular, a graph G has a perfect matching if , further, G is factor critical if and is bi-critical if . For subsets D and X of , D dominates X if every vertex in X is either in D or adjacent to a vertex in D. If D dominates X, then we write and we also write when . Moreover, if , then D is a dominating set of G and we write instead of . A connected dominating set of a graph G is a dominating set D of G such that is connected. If D is a connected dominating set of G, we then write . A smallest connected dominating set is called a -set. The cardinality of a -set is called the connected domination number of G and is denoted by . A graph G is said to be k--critical if and for any pair of non-adjacent vertices u and v of G.
In the structural characterizations of k--critical graphs, Chen et al. [3] showed that every 1--critical graph is a complete graph while every 2--critical graph is the complement of the disjoint union of at least two stars. However, for , it turns out that the k--critical graphs have no complete characterization in the sense of free graphs (see in [4], Chapter 5). Interestingly, it was proved by Hanson and Wang [5] that for a connected graph G, the graph G is 3--critical if and only if the complement of G is 2-diameter critical. For a study on k-diameter critical graphs see Almalki [6]. In [7], Ananchuen proved that every 3--critical graph contains at most one cut vertex and also established characterizations of 3--critical graphs having a cut vertex. For more studies related with 3--critical graphs see the works in [8,9,10]. For , Kaemawichanurat and Ananchuen [11] proved that every 4--critical graph contains at most two cut vertices and the characterization of the such graphs having two cut vertices was given. Further, Kaemawichanurat and Ananchuen [12] established that every k--critical graphs contains at most cut vertices when . They also characterized that there is exactly one class of k--critical graphs having cut vertices. In the same paper, the authors established the maximum number of cut vertices that every block of the graph can have. That is:
Theorem 1
([12]). Let G be a k--critical graph containing ζ cut vertices and let be the maximum number of cut vertices of G that can be in a block of G. Then,
Very recently, Henning and Kaemawichanurat [13] characterized all the eleven classes of k--critical graphs satisfying the upper bound of Theorem 1. For more related works on connected domination critical graphs see [14,15,16,17,18,19,20,21].
In this paper, for , we characterize all k--critical graphs having cut vertices. Further, we establish realizability that, for given , and , there exists a k--critical graph with cut vertices having a block which contains cut vertices. We also proved that every k--critical graph of odd order with is factor critical if and only if . We prove that every k--critical -free graph of even order with is factor critical if and only if . All the main results are shown in Section 2, while their proofs are given in Section 4. We present some useful results that are used in the proofs in Section 3.
2. Main Results
First, we give constructions of two classes of such graphs which will be the characterizations of k--critical graphs with cut vertices. Let
be a tuple such that and (there is exactly one such that and for all ).
The class
For a tuple where and for , a graph G in the class can be constructed from paths and , a copy of a complete graph and a block (the construction of the class will be given in Section 3 as it was established earlier in [12]) by adding edges according the join operations:
- and
where we call c the head of B. Examples of graphs in this case are illustrated by Figure 1 and Figure 2. Further, for a tuple where and for , a graph G in the class can be constructed from paths , a copy of a complete graph and a block by adding edges according the join operation:
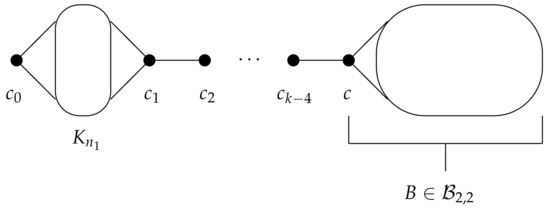
Figure 1.
A graph G in the class .
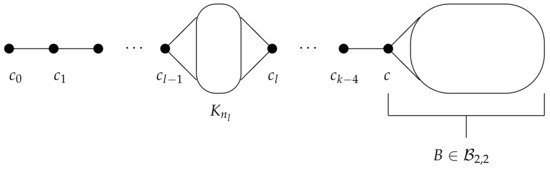
Figure 2.
A graph G in the class .
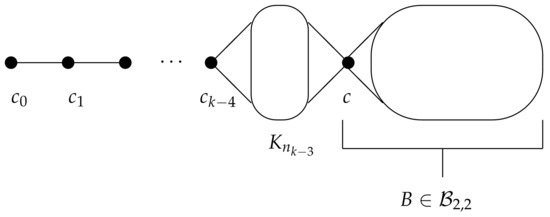
Figure 3.
A graph G in the class .
Next, we will construct another class of k--critical graphs with cut vertices. Before giving the construction, we introduce the following class of end blocks.
The class
An end block has b as the head. Let and . Moreover, B has the following properties:
- (1)
- Every vertex , there exists a -set of B of size 3 such that .
- (2)
- For every non-adjacent vertices x and y of , there exists a -set of such that , and .
For an example of a graph in the class , we let B be the graph obtained from a vertex b and , a cycle of length 5, by joining b to a pair of consecutive vertices of . It can be checked that B satisfies and of the class . Thus, . Figure 4 illustrates the graph B. Further, it is worth noting that in the property satisfies in order to dominate b. We are ready to give the construction.
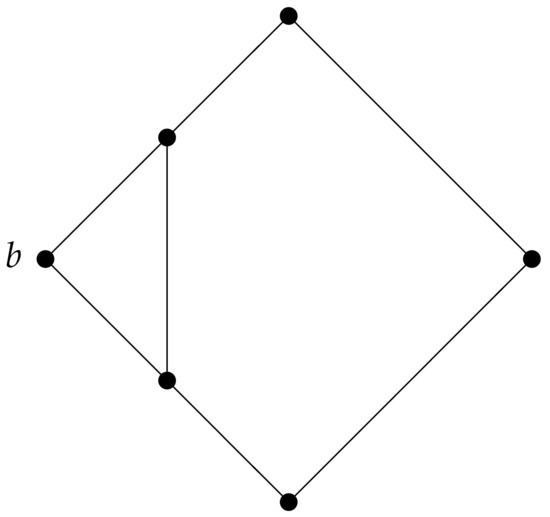
Figure 4.
A graph B in the class .
The class
For , a graph G in this class can be constructed from a path and an end block with the head b by adding the edge . For the sake of convenience, we may relabel b as .
Then, we let
the class of k--critical graphs containing cut vertices.
Our first main result is as follows:
Theorem 2.
For an integer , .
For our next main results, we let B be a block of G. We further define the following notation. We let be the set of all cut vertices of G. That is
is a cut vertex of ,
,
,
and
is a block of .
We prove that:
Theorem 3.
For all , and , there exists a k--critical graph with ζ cut vertices having a block that contains cut vertices.
Finally, we establish constructive proofs to show that:
Theorem 4.
Every k--critical graph of odd order with is factor critical if and only if .
Theorem 5.
Every k--critical -free graph of even order with is bi-critical if and only if .
3. Preliminaries
In this section, we state a number of results that are used in establishing our theorems. We begin with a result of Favaron [22] which gives matching properties of graphs according to the toughness.
Theorem 6
([22]). For an integer , let G be a graph with minimum degree . Then, G is ℓ-factor critical if and only if for any cut set S of G such that .
In the context of k--critical graphs, Ananchuen et al. [23] established some matching properties of such graphs when .
Theorem 7
([23]). Every 3--critical graph of even order with has a perfect matching.
However, for factor criticality, they found a 3--critical graph of odd order with which is not factor critical. The graph is constructed from a complete graph , a star by joining every end vertex of the star to every vertex of and then remove all edges of a perfect matching between these two graphs. The resulting graph is detailed in Figure 5.
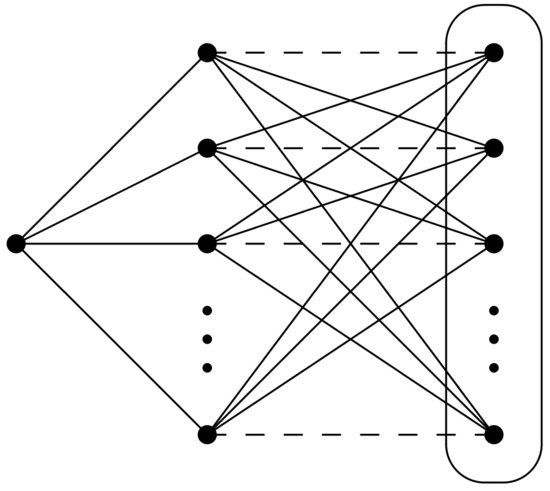
Figure 5.
A 3--critical graph which is non-factor critical.
Chen et al. [3] characterized all k--critical graphs when .
Theorem 8
([3]). A graph G is 1--critical graph if and only if G is a complete graph. Moreover, a graph G is 2--critical graph if and only if where and for all .
We then obtain the following observations as a consequence of Theorem 8.
Observation 1.
For every k--critical graph of odd order is factor critical.
Observation 2.
For every k--critical graph of even order with minimum degree is bi-critical.
By Theorem 8, we observe further that a k--critical graph does not contain a cut vertex when .
Observation 3.
Let G be a k--critical graph with . Then G has no cut vertex.
Further, Chen et al. [3] established fundamental properties of k--critical graphs for .
Lemma 1
([3]). Let G be a k--critical graph, x and y a pair of non-adjacent vertices of G and a -set of . Then
- (1)
- ,
- (2)
- ,
- (3)
- if , then .
Ananchuen [7] established structures of k--critical graphs with a cut vertex.
Lemma 2
([7]). For , let G be a k--critical graph with a cut vertex c and D a connected dominating set. Then,
- (1)
- contains exactly two components,
- (2)
- if and are the components of , then and are complete,
- (3)
- .
All the following results of this section were established in [12]. The first result is the construction of a forbidden subgraph of k--critical graphs. For a connected graph G, let and be disjoint vertex subsets of . The induced subgraph is called a bad subgraph if
- (i)
- for any vertex ,
- (ii)
- for any vertex ,
- (iii)
- for any vertex and
- (iv)
- for any vertex .
An example of a bad subgraph is illustrated in Figure 6.
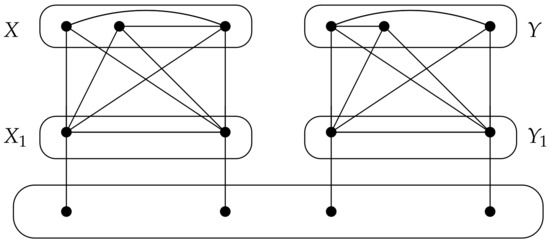
Figure 6.
The induced subgraph .
The authors showed, in [12], that:
Lemma 3
([12]). For , let G be a k--critical graph. Then G does not contain a bad subgraph.
They also provided characterizations of some blocks of k--critical graphs. Recall that
- is the set of all cut vertices of G and, for a block B of G,
- and .
when no ambiguity occur, we write rather than . In the same paper, the authors showed further that for a connected graph G and a pair of non-adjacent vertices x and y of G, if x and y are in the same block of G.
Lemma 4
([12]). For a connected graph G, let B be a block of G and such that . Then, .
Let D be a -set of G. The followings are the characterization of four classes of end blocks of k--critical graphs that contains at most 3 vertices from D. For vertices and , let
- for an integer ,
- for an integer and
- for integers .
The following is a part of the construction of . For integers and , we let and . When , we let . Then, for , let be the vertices of a star which is the center. Further, let and , moreover, let if and if . Therefore,
That is, can be obtained by removing the edges in the stars of from a complete graph on . Then, the blocks in are defined as follows.
for integers and .
A graph in this class is illustrated by Figure 7. According to the figure, an oval denotes a complete subgraph, double lines between subgraphs denote all possible edges between the subgraphs and a dash line denotes a removed edge.
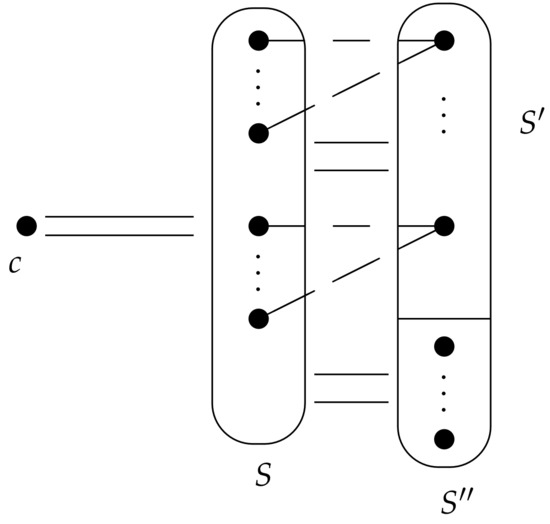
Figure 7.
A block B in the class .
For a block , the vertex c is called the head of B. The following are the characterizations of an end block B such that .
Lemma 5
([12]). Let G be a k--critical graph with a -set D and let B be an end block of G. If , then .
Lemma 6
([12]). Let G be a k--critical graph with a -set D and let B be an end block of G. If , then .
Lemma 7
([12]). Let G be a k--critical graph with a -set D and let B be an end block of G. Suppose that . Then, .
Lemma 8
([12]). For , let G be a k--critical graph. Then, G contains at most one end block B such that .
Finally, we conclude this section by the following two lemmas which are structures of blocks of k--critical graphs. Recall from Section 2 that
the class of k--critical graphs containing cut vertices.
Lemma 9
([12]). Let where . Then, G has only two end blocks and all other blocks contain exactly two cut vertices.
Lemma 10
([12]). Let with a -set D where and B be a block of G containing two cut vertices c and . If . Then, .
In [24], the authors established a construction of the class which, for any graph and integer , there exists a --critical graph containing G as an induced subgraph. Recall that, for a subgraph H of G, H is a maximal complete subgraph of G if for any complete subgraph of G such that , we have .
The class
A k--critical graph G is in this class if there exists a maximal complete subgraph H of order at least two of G satisfying the following properties:
- (i)
- for any vertex x of G, there exists a -set D of G such that and and
- (ii)
- for any non-adjacent vertices x and y of G, there exists a set that is a connected dominating set of and satisfies and .
We next give a construction of a --critical graph containing G in the class as an induced subgraph. Let H be a maximal complete subgraph of G having properties and . The graph can be constructed from a vertex , l copies of complete graphs which for and the graph G by adding edges according to the join operations:
The graph is illustrated by Figure 8.
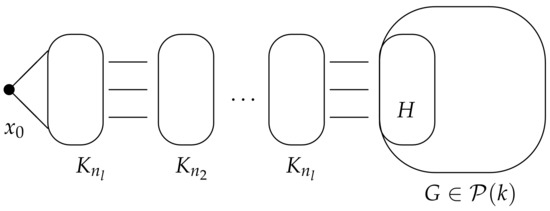
Figure 8.
The graph .
Thus, they proved that
Theorem 9
([24]). For an integer , let . Then, is a --critical graph for all .
4. Proofs
4.1. Connected Dominating Set of Blocks
Let
be the family of all blocks of G.
when no ambiguity can occur, we use to denote . For a k--critical graph G with a cut vertex, let B be a block of G containing non-adjacent vertices x and y. Clearly, . Let D be a -set of G.
Lemma 11.
Let B be a block of G and such that . Then, , in particular, for all .
Proof.
We first show that . Let . By Lemma 4, . By the connectedness of , . Thus . We now show that . Let . That is, . Lemma 2(3) yields that . Therefore, and, thus, , as required.
In view of Lemma 4, for all . Because , it follows that
This completes the proof. □
It is worth noting that in [12], this result was proved only for end blocks. Therefore, our result in Lemma 11 is more general. For non-adjacent vertices x and y of the block B, the following lemma gives the number of vertices of a -set of in B.
Lemma 12.
For all such that , .
Proof.
We first establish the following claim.
Claim: For any block which is not B, .
Suppose to the contrary that . Lemma 11 gives that . Because , is connected. Moreover, . This implies that
contradicting the minimality of D. Thus establishing the claim.
We now prove Lemma 12. Suppose to the contrary that . Lemma 11 yields that . Clearly and . Lemma 2(1) yields, further, that each cut vertex is contained in exactly two blocks. Thus each cut vertex is counted twice in and . Therefore, and . We note by Lemma 4 that . By the claim and the assumption that , we have
This contradicts Lemma 1(1). Thus, , and this completes the proof. □
Corollary 1.
For any block B of G and such that , .
Proof.
In view of Lemma 11, . Lemma 12 then implies that
and this completes the proof. □
4.2. The k--Critical Graphs with
In this subsection, we characterize k--critical graphs with cut vertices. We recall the classes and from Section 2. First, we will prove that all graphs in these two classes are k--critical with cut vertices.
Lemma 13.
Let G be a graph in the class , then G is a k--critical graph with cut vertices.
Proof.
Clearly G has and c as the cut vertices. Observe that, for any , a graph has the path from to c where . To prove all cases of , we may relabel the path P to be . Therefore, and . We see that where are vertices in defined in Section 3. Therefore, .
Let D be a -set of G. If , then, to dominate , we have . If , then as is connected. In both cases, .
Suppose that . Because , to dominate B, . By the connectedness of , we have . Thus, implying that . Hence, suppose that . As and is connected, it follows that where . Thus, implying that .
Now, we will establish the criticality. Let u and v be a pair of non-adjacent vertices of G and let . We first assume that . Therefore, . Thus, and for some . Without loss of generality let . Clearly . We see that
.
Therefore, .
Thus, we assume that . If for some , then and, clearly, . Thus, . Therefore . Let . As , there exists such that . Suppose that . Thus, . Therefore, . If , then implying that .
Finally, we assume that . Thus, for some and . Clearly and . Thus, G is a k--critical graph and this completes the proof. □
Lemma 14.
Let G be a graph in the class . Then, G is a k--critical graph with cut vertices.
Proof.
Let D be a -set of G. As are cut vertices, by Lemma 2(3), . Recall that . Because , we can let . Thus . By Lemma 2(2), . So, is a connected dominating set of B. By , there exists a -set of B of size 3. By the minimality of , . Therefore, . Further, because and , it follows that . Therefore, and this implies that .
We will prove the criticality. Let u and v be non-adjacent vertices of G. Suppose first that , say. If , then . If , then, by Property of the class , there exists a -set of size 3 of B such that and . So . These imply that .
We then suppose that . If , then there exists i and j such that and . Without loss of generality let . Clearly, . Therefore, . For the case when , we have and thus . Finally, if , then, by Property of the class , there exists a -set such that , and . Thus, . This implies that . Clearly, are the cut vertices of G. This completes the proof. □
In the following, we let having a -set D. In view of Lemma 9, G has only two end blocks and all other blocks contain two cut vertices. Thus, we let and be the two end blocks and all other blocks contain two cut vertices. Without loss of generality let and for . Moreover, let for all . If is a -set of G such that , by the minimality of k, we have for all i. Thus, we can let
the class of a graph such that
for .
Lemma 15.
For a -set of G, either or .
Proof.
Suppose to the contrary that and . Lemmas 5 and 6 imply that . This contradicts Lemma 8. Thus, either or and this completes the proof. □
By Lemma 15, we may suppose without loss of generality that .
Lemma 16.
where for some and for all .
Proof.
By the definition, .
Conversely, let . Thus, by Lemma 9, G has only two end blocks and and all other blocks contain two cut vertices. Moreover, and for . In view of Lemma 2(3), . So . Thus, for all . Recall that . Lemma 15 implies that either or . That is, . This completes the proof. □
By Lemma 16, to characterize a graph G in the class , it suffices to consider when G is either in or . We first consider the case when . Let and be vertices and a copy of a complete graph.
Lemma 17.
Let with a block containing two cut vertices and and . Then, where .
Proof.
As and for some , we must have for all . Because contains two cut vertices, . Therefore, . Lemma 5 then implies that
Let . We first show that is complete. Let x and y be non-adjacent vertices of . Consider . Lemma 1(2) implies that . As , we must have contradicting Corollary 1. Therefore, is complete.
We will show that . Thus, we may assume to the contrary that . We let
and
.
As , it follows that . Because is complete, is complete. In fact, and X satisfy and of bad subgraphs. We then let
and
.
Thus, G has and as a bad subgraph. This contradicts Lemma 3. Therefore, .
We finally show that . We may assume to the contrary that there exists a vertex u of which is not adjacent to . Consider . Corollary 1 gives that . Lemma 4 gives further that . As , it follows that is not connected, a contradiction. Therefore, and, similarly, . As is a block, and this completes the proof. □
We will prove the following two theorems, both of which give main contribution to the proof of our first main theorem, Theorem 2.
Theorem 10.
For , where for all .
Proof.
Let for all . In views of Lemma 13, we have that . Thus, it suffices to show that .
We will show that . Clearly, is either 0 or 1. If , then Lemma 5 implies that . However, if , then Lemma 6 implies that . Thus, we let
and
As , by Lemma 7, . If , then where is given at the definition of . We then let
and
Clearly, G has a bad subgraph, contradicting Lemma 3. Thus, .
We now consider the case when . Thus, . By Lemma 6, implying that . Further, Lemma 10 implies also that for . Thus, .
We finally consider the case when . Thus, for some and for . Similarly, for all by Lemma 10. Moreover, Lemma 17 yields that . Let . We will show that . We let a be a vertex in if . Then, we let
Consider . As is a cut vertex of , by Lemma 2(3). That is when . When , by Lemma 17, . As , by Lemma 1(3), . In both cases, . If , then contradicting . Therefore, by Lemma 1(1). Thus, implying that . Therefore, . This completes the proof. □
Theorem 11.
For , .
Proof.
By Lemma 14, . Thus, it is sufficient to show that .
As for all , by Lemma 10, . By Lemma 5 and similar arguments in Theorem 10, we have that .
We will show that satisfies of the class . Recall that . Let be a -set of . Suppose that . To dominate , we have . Thus, . However, contradicting the minimality of k. Therefore, . Thus, to prove that satisfies , it suffices to give a connected dominating set of size 3 of containing a chosen vertex from . For a vertex v of , consider . Lemma 1(2) implies that . Lemma 1(1) implies also that . We first show that . Suppose to the contrary that . As is connected, there exists which is adjacent to v. Because , w is adjacent to a vertex of . Thus,
This contradicts the minimality of k. Thus, . Therefore, or .
Let
We first consider the case when . Thus . As and , we must have
Therefore, and , otherwise where , contradicting the minimality of k. Let such that u is adjacent to a vertex a in A. Thus, and so satisfies .
We now consider the case when . Let . Clearly, . As and , it follows that . If , then implying that , in particular, . Thus, where contradicting the minimality of D. Therefore, we let . As , . Thus, for a vertex a in A, . Therefore, satisfies .
We now consider the case when . Thus . Therefore, and, to dominate . So, satisfies .
We finally consider the case when . To dominate , we have that . By the connectedness of , . Thus, implying that
.
Therefore, . To dominate , . Thus satisfies and this completes the proof of Case 1.
To dominate , we have that . By the connectedness of , and . As , we must have . So satisfies . This completes the proof of Case 2.
We finally show that satisfies of the class . Let x and y be non-adjacent vertices of . Lemma 1(2) implies that . Lemma 1(1) implies also that . To dominate , we have that . Let . By the connectedness of , and . As , we must have . Thus, satisfies . Therefore, . This completes the proof. □
Now, we are ready to prove our first main result, Theorem 2. For completeness, we restate the theorem.
Theorem 2.
For an integer , .
Proof.
In view of Lemma 16, where for some and for all . Moreover, Theorems 10 and 11 imply that . This completes the proof. □
4.3. k--Critical Graphs with Prescribed Cut Vertices
In this section, we prove Theorem 3. First, we introduce structure of some subgraphs. For any block H of a graph G, H is called a block for if H consists of a vertex x and as vertex sets of order at least 2 and
- , and are complete.
- For each , .
- For each , there exists such that .
We say that x is the head of a block . Note that when , we have .
Let the class of all k--critical graphs with cut vertices containing a block B such that .
We next introduce the following class that we use to establish the existence of graphs in .
The class :
Let be p blocks. Further, we let be (a path of q vertices), and let be an block. Let be the head of for . A graph is obtained from by joining edges between vertices in to form a clique.
Lemma 18.
If a graph G is in the class , then G is --critical with cut vertices having a block that contains cut vertices.
Proof.
For , let and . We see that and are, respectively, the same as and of the block . Let . By the construction of the block , there exists such that and is not adjacent to the vertex . Let where . For the block , let be a vertex subset of which is the same as of the block and for .
Lemma 2(3) implies that for . Consider . By the connectedness of , for . Because every vertex in does not dominate , . Since , . By the same arguments, for . Finally, to dominate , . So . It is not difficult to see that . Therefore, . Thus, .
Let . For a pair of non adjacent vertices . Consider . To establish the criticality, it suffices to show that there exists a dominating set of containing less than k vertices. For , let . We distinguish 3 cases.
Case 1:.
Without loss of generality, let .
Subcase 1.1:. Clearly, .
- If , then let .
For ,
- if , then let where , and
- if , then let .
We now consider the case when . We let if and let if . When , we let where is a path such that for some .
Subcase 1.2:. Without loss of generality let . So and . Clearly, . If for some , then we can find by the same arguments as Subcase 1.1. Thus, we may consider when for . If , then let . For ,
- if , then let where , and
- if , then let .
We now consider the case when . If , then . Thus, we may assume that . We let . If for some , then we let . If , then we let . Finally, if for some , then we let .
Subcase 1.3:. Without loss of generality let . Clearly, . By the same arguments as Subcases 1.1 and 1.2, we consider only when . If , then let . If , then let . If , then . Thus, we may assume that . We let and we can find by same arguments as Subcase 1.2.
Case 2: and .
Without loss of generality let .
Subcase 2.1:. Suppose first that . Thus, for some . If , then let . If , then . If , then let . If , then we let .
Subcase 2.2:. Suppose that . By the same arguments as Subcase 2.1, . Without loss of generality let and such that . If , then let . If , then let . Suppose that . If and , then let . If and , then let . We now consider the case when . Let and . Let by the same arguments as Subcase 2.1.
Case 3:. Without loss of generality let and where . Let . If , then there exists a path such that and where for . Let . If , then v is the only one vertex in which u is not adjacent. Thus, .
Finally, we see that are all the cut vertices of G. Thus, G has cut vertices. Further, the block has as the cut vertices of G. Therefore, there is a block containing cut vertices. This completes the proof. □
Now, we are ready to prove Theorem 12. For completeness, we restate the theorem.
Theorem 12.
For all , and , there exists a k--critical graph with cut vertices having a block that contains cut vertices, namely, .
Proof.
In view of Lemma 18, for all , and , we have . This completes the proof. □
4.4. Factor Criticality of k--Critical Graphs
In this section, for , we will use the property of graphs in the class which is given in Section 3. First, we may prove that the class is non-empty for .
Lemma 19.
For all , .
Proof.
For an integer , we let be a cycle of length . It is well known that is a k--critical graph. In this proof, all subscripts are taken modulo . Observe that is a maximal complete subgraph for all . Thus, without loss of generality, it suffices to show that complete subgraph satisfies and of .
For a vertex where , let
.
Clearly, if . Thus, we consider the case when . In this case . Let . Therefore, . Moreover, . Therefore, satisfies .
We now let and be non-adjacent vertices of . So . Consider . We partition to
and .
As , at least one of or must have at least three vertices. Without loss of generality let it be . We further let
Clearly, and . We first consider the case when . Note that D in this case contains vertices. If is neither nor , then . This implies that satisfies . Thus, we may assume that . As , we must have . Moreover, because . Thus, satisfies . The case can be proved by the same arguments.
We now consider the case when , in fact and . If is neither nor , then and this implies that satisfies . Thus we may assume that is or . We observe that and when , moreover, and when . In both cases, . Let . We see that . So because and . Therefore satisfies . Therefore, and this completes the proof. □
In the following, we show how to apply the construction of some graphs in the class to establish the existence of --critical graphs with some property. For an integer and , we let
the class of k--critical graphs G with such that
G is not ℓ-factor critical.
Therefore, we may rewrite Observation 1 in term of the class .
Observation 4.
for .
For , Figure 5 shows that there exists a 3--critical graph of odd order and which is non-factor critical. Thus . In the following, for , we show further that there exists a k--critical graph which is non-factor critical.
The class
For an integer , let and be two disjoint sets of vertices. We further let be a copy of a complete graph of order s such that . A graph G in the class can be constructed from and by adding edges according to the join operations that, for ,
- and
- .
A graph in this class is illustrated by Figure 9.
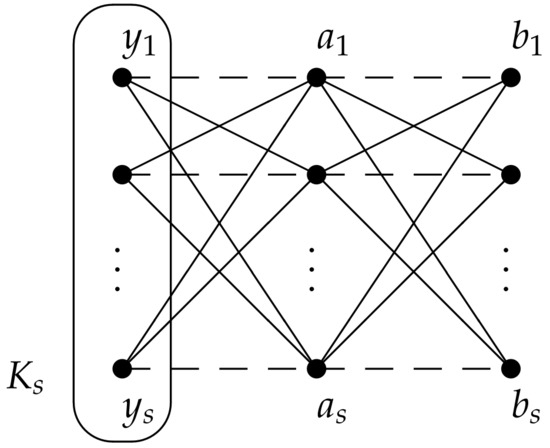
Figure 9.
A graph G in the class .
The following lemma gives that for integer .
Lemma 20.
For an integer , .
Proof.
For a given , let G be in the class . We first show that . Suppose to the contrary that there exists a connected dominating set D of size less than 4. We first consider the case when . To dominate B, . Therefore, . By the connectedness of , . Thus, D does not dominate , a contradiction. Thus, we consider the case when . Therefore, to dominate , . As A is an independent set, by the connectedness of , . Therefore, . Similarly, , and this implies that D does not dominate , a contradiction. Thus, .
We observe that is a maximal complete subgraph of G. We do not only show that , but we also show that, for a vertex a of G, there exists a connected dominating set of G containing a and . That is, we show that satisfies of graphs in the class . For , we have
and
Therefore, and thus . Moreover, satisfies .
We finally establish the criticality. Further, we show that, for non-adjacent vertices x and y of G, . That is, we will show that satisfies of graphs in the class . We first consider the case when . If , then . If , then . If (in this case could be ), then . We now consider the case when . Thus, is either or . In both cases, . Thus, G is a 4--critical graph, in particular, .
Finally, let s be odd number and . Thus, has and as odd components. Thus . By Theorem 6, G is non-factor critical. Thus, and this completes the proof. □
We will use a graph in the class to show that for all . For , we also provide a graph in the class by the following construction. Let and w be five different vertices. We also let be a path of length one and be two copies of complete graphs of order and , respectively, moreover, is even number. The graph is constructed by adding edges according to the join operations:
- and
- .
Figure 10 illustrates the graph .
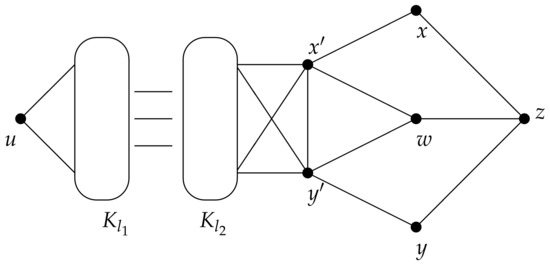
Figure 10.
The graph .
It is not difficult to show that is 5--critical graph. Moreover, has as a cut set such that . By Theorem 6, is not factor critical.
Now, we are ready to prove Theorem 4. For completeness, we restate the theorem.
Theorem 13.
Every k--critical graph of odd order with is factor critical if and only if . Namely, if and only if .
Proof.
Observation 4 implies that if or 2, then .
Conversely, Figure 5 in Section 3 yields that . Lemma 20 yields that . Moreover, as , we must have . We assume that . For an odd integer , we let with satisfies and of graphs in the class . We moreover let integers and be such that is odd number.
.
In view of Theorem 9, is a --critical graph. Let . Thus, has as a cut set such that
.
Theorem 6 then gives that is non-factor critical. Therefore for all . These imply that if , then or 2. This completes the proof. □
In view of Theorem 4, it is natural to think of the bi-criticality of k--critical graphs with . Although, we know that if a graph G is not factor critical, then there exists a cut set S such that
By Theorem 6, regardless with the parity of the orders of graphs, it is most likely there exist k--critical graphs that are not bi-critical. However, we notice that the graphs that are obtained from the construction in Figure 10 and Theorem 4 contain a claw, , as an induced subgraphs. Therefore, we may ask if every k--critical -free graph with is bi-critical. By Theorem 8, for , every k--critical graph is -free with of even order is bi-critical. Therefore, we obtain the following corollary by Observation 2.
Corollary 2.
If , then every k--critical -free graph with is bi-critical.
When , it turns out that there exist k--critical graph with which is not bi-critical even they do not contain as an induced subgraph.
Let
the class of k--critical -free graphs G with such that
G is not ℓ-factor critical.
The class
For an odd number and an even number , the graph G in this class is obtained from vertices and copies of complete graphs by adding edges according to the join operations:
- and
- .
The graph in this class is illustrated by Figure 11.
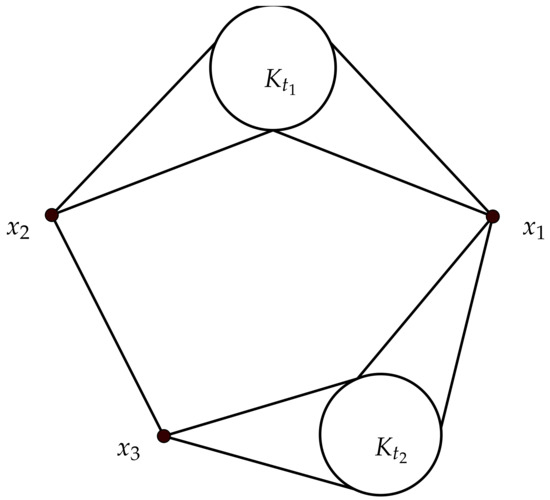
Figure 11.
The graph G in the class .
Lemma 21.
If , then .
Proof.
It is easy to see that all graphs in the class is 3--critical and -free with . Further, by removing and , the resulting graph has two odd components: and . Thus, G is not bi-critical. Therefore, . It is easy to see that every graph G in the class satisfies the Properties (i) and (ii) of the class by selecting as a maximal complete subgraph. Thus, and this completes the proof. □
Finally, we will establish the existence of k--critical -free graphs with which are not bi-critical for by proving Theorem 14. For completeness, we restate theorem.
Theorem 14.
Every k--critical -free graph of even order with is bi-critical if and only if . Namely, if and only if .
Proof.
By Observation 2, we have that if , then .
Conversely, we will show that if , then . By Lemma 21, we have that . For , we let such that is an odd number and is an even number. Further, we let be a vertex and, for such that is an odd number, we let be copies of complete graphs of order , respectively. Let and
.
By Theorem 9, we have that is k--critical graphs. Clearly, is -free and . By removing and from , we have that has and as the two odd components. Therefore,
implying that is not bi-critical. This completes the proof. □
Author Contributions
N.A.: Conceptualization, Investigation, Methodology, Validation, Writing—original draft, Writing—reviewing and editing. P.K.: Supervision, Project administration, Investigation, Methodology, Validation, Writing—original draft, Writing—reviewing and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The second author has been supported by Thailand Research Fund (MRG 6080139).
Conflicts of Interest
The authors declare no conflict of interest. All results are only for an academic purpose.
References
- Bondy, J.A.; Murty, U.S.R. Graphs Theory with Applications; The Macmillan Press: London, UK, 1976. [Google Scholar]
- Chatrand, G.; Oellermann, O.R. Applied and Algorithmic Graph Theory; Mcgraw-Holl. Inc.: New York, NY, USA, 1993. [Google Scholar]
- Chen, X.G.; Sun, L.; Ma, D.X. Connected Domination Critical Graphs. Appl. Math. Lett. 2004, 17, 503–507. [Google Scholar] [CrossRef][Green Version]
- Kaemawichanurat, P. Connected Domination Critical Graphs. Ph.D. Thesis, Curtin University, Bentley, Australia, 2016. [Google Scholar]
- Hanson, D.; Wang, P. A note on extremal total domination edge critical graphs. Util. Math. 2003, 63, 89–96. [Google Scholar]
- Almalki, N. The Existence of Diameter-Edge-Critical Graphs. Ph.D. Thesis, Curtin University, Bentley, Australia, 2016. [Google Scholar]
- Ananchuen, N. On Domination Critical Graphs with Cut Vertices having Connected Domination Number 3. Int. Math. Forum 2007, 2, 3041–3052. [Google Scholar] [CrossRef][Green Version]
- Ananchuen, N.; Ananchuen, W. A Characterization of 3-(γc,2)-Critical Claw-Free Graphs which are not 3-γc-Critical. Graphs Combin. 2010, 26, 315–328. [Google Scholar] [CrossRef]
- Lemańska, M.; Patyk, A. Weakly connected domination critical graphs. Opusc. Math. 2008, 28, 325–330. [Google Scholar]
- Mamart, S.; Ananchuen, N. Some Structure of 3-(γc,2)-Critical Graphs which are not 3-γc-Critical. Util. Math. 2015, 97, 3–21. [Google Scholar]
- Kaemawichanurat, P.; Ananchuen, N. On 4-γc-Critical Graphs with Cut Vertices. Util. Math. 2010, 82, 253–268. [Google Scholar]
- Kaemawichanurat, P.; Ananchuen, N. Connected Domination Critical Graphs with Cut Vertices. Discuss. Math. Graph Theory 2020, 40, 1035–1055. [Google Scholar]
- Henning, M.A.; Kaemawichanurat, P. Connected domination critical graphs with a block having maximum number of cut vertices. Appl. Math. Comput. 2021, 406, 126248. [Google Scholar]
- Ananchuen, N. On Local Edge Connected Domination Critical Graphs. Utilitas Math. 2010, 82, 11–23. [Google Scholar]
- Kaemawichanurat, P.; Caccetta, L.; Ananchuen, N. Critical Graphs with respect to Total Domination and Connected Domination. Australas. J. Combin. 2016, 65, 1–13. [Google Scholar]
- Kaemawichanurat, P.; Caccetta, L. Hamiltonicity of domination critical claw-free graphs. J. Comb. Math. Comb. Comput. 2017, 103, 39–62. [Google Scholar]
- Kaemawichanurat, P.; Caccetta, L. Bounds on the order of connected domination vertex critical graphs. J. Combin. Math. Combin. Comput. 2018, 107, 73–96. [Google Scholar]
- Kaemawichanurat, P.; Caccetta, L.; Ananchuen, W. Hamiltonicity of connected domination critical graphs. Ars Comb. 2018, 136, 127–151. [Google Scholar]
- Plummer, M.D. On the structure of graphs vertex critical with respect to connected domination. In Research Trends in Combinatorial Optimization; Springer: Berlin, Germany, 2009; pp. 303–315. [Google Scholar]
- Sampathkumar, E.; Walikar, H.B. The connected domination number of a graph. J. Math. Phys. Sci. 1979, 13, 607–613. [Google Scholar]
- Taylor, J.D.; van der Merwe, L.C. A note on connected domination critical graphs. J. Combin. Math. Combin. Comput. 2017, 100, 3–8. [Google Scholar]
- Favaron, O. On k-Factor Critical Graphs. Discuss. Math. Graph Theory 1996, 16, 41–51. [Google Scholar] [CrossRef]
- Ananchuen, N.; Ananchuen, W.; Plummer, M.D. Matching Properties in Connected Dominaion Critical Graphs. Discret. Math. 2008, 38, 1260–1267. [Google Scholar] [CrossRef][Green Version]
- Henning, M.A.; Ananchuen, N.; Kaemawichanurat, P. Traceability of connected domination critical graphs. Appl. Math. Comput. 2020, 386, 125455. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).