Weak and Strong Convergence Theorems for Common Attractive Points of Widely More Generalized Hybrid Mappings in Hilbert Spaces

Abstract

In this work, we study iterative methods for the approximation of common attractive points of two widely more generalized hybrid mappings in Hilbert spaces and obtain weak and strong convergence theorems without assuming the closedness for the domain. A numerical example supporting our main result is also presented. As a consequence, our main results can be applied to solving a common fixed point problem.

1. Introduction

Let H be a real Hilbert space and C be a nonempty subset of H. For a mapping T from C into H, we will denote by $F\left(T\right)$ the set of all fixed points, i.e.,

$$F\left(T\right)=\{x\in C:Tx=x\}.$$

In 2010, Kocourek et al. [1] introduced the notion of a generalized hybrid mapping $T:C\to H$ by the condition that there exist $\alpha ,\beta \in \mathbb{R}$ such that

$${\alpha \parallel Tx-Ty\parallel }^2{+(1-\alpha )\parallel Ty-x\parallel }^2\le {\beta \parallel Tx-y\parallel }^2+(1-\beta ){\parallel x-y\parallel }^2$$

for all $x,y\in C$ and proved a fixed point theorem of this kind of mapping; see [2,3] for more results for fixed point theorems of generalized hybrid mappings.

In 2011, the notion of attractive points for nonlinear mappings in Hilbert spaces was introduced by Takahashi and Takeuchi [4]. For a mapping of T from C into H, we will denote by $A\left(T\right)$ the set of all attractive points, i.e.,

$$A\left(T\right)=\{z\in H:\parallel Tx-z\parallel \le \parallel x-z\parallel ,\forall x\in C\}.$$

They also proved an existence theorem for attractive points for generalized hybrid mappings without convexity in Hilbert spaces.

In 2013, Kawasaki and Takahashi [5] defined a class of widely more generalized hybrid mappings. A mapping $T:C\to H$ is called a widely more generalized hybrid if there exists $\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta \in \mathbb{R}$ such that

$$\begin{array}{cc}\hfill \alpha \parallel Tx& {-Ty\parallel }^2{+\beta \parallel x-Ty\parallel }^2{+\gamma \parallel Tx-y\parallel }^2{+\delta \parallel x-y\parallel }^2+ϵ{\parallel x-Tx\parallel }^2\hfill \\ \hfill & {+\xi \parallel y-Ty\parallel }^2+\eta {\parallel (x-Tx)-(y-Ty)\parallel }^2\le 0,\forall x,y\in C.\hfill \end{array}$$

(1)

We call such mapping an $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mapping.

In 2018, Khan [6] introduced the concept of common attractive points for two nonlinear mappings. For two mappings $S,T:C\to H$, we will denote by $A(S,T)$ the set of common attractive points of S and T, i.e.,

$$A(S,T)=\{z\in H:max(\parallel Sx-z\parallel ,\parallel Tx-z\parallel )\le \parallel x-z\parallel ,\forall x\in C\}.$$

It is obvious that $A(S,T)=A\left(S\right)\cap A\left(T\right).$ The author also introduced a new mapping, which is more general than generalized hybrid mappings, called further generalized hybrid mappings. A mapping $T:C\to H$ is called a further generalized hybrid if there exists $\alpha ,\beta ,\gamma ,\delta ,ϵ\in \mathbb{R}$ such that

$${\alpha \parallel Tx-Ty\parallel }^2{+\beta \parallel x-Ty\parallel }^2{+\gamma \parallel Tx-y\parallel }^2{+\delta \parallel x-y\parallel }^2+ϵ{\parallel x-Tx\parallel }^2\le 0,\forall x,y\in C.$$

Obviously, this is a special case of widely more generalized hybrid mappings when $\xi =\eta =0$ in (1).

In 2015, Zheng [7] guaranteed the weak and strong convergence theorems of attractive points for generalized hybrid mappings in Hilbert spaces by using the iterative scheme (2), known as Ishikawa iteration [8],

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}=(1-{\beta }_n)x_n+{\beta }_{n}T{y}_n,\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n,\hfill \end{array}\right.$$

(2)

where $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ are sequences in $(0,1)$.

To approximate the common fixed points of two mappings, Das and Debata [9] and Takahashi and Tamura [10] generalized the Ishikawa iterative for mappings S and T as follows:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}=(1-{\beta }_n)x_n+{\beta }_{n}S{y}_n,\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n,\hfill \end{array}\right.$$

(3)

where $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ are sequences in $(0,1)$. Note that when $S=T$, (3) can be reduced to (2). It is worth noting that the approximation of common fixed points of a two mappings case has its own importance as there is a direct link with minimization problems; see [11] for examples.

In 2020, Thongpaen and Inthakon [12] used the iteration (3) to prove a weak convergence theorem for common attractive points of two widely more generalized hybrid mappings in Hilbert spaces and applied the main result to some common fixed point problems. Furthermore, see [13,14] and references therein for more results of common attractive points theorems.

For another approximation algorithm, Khan [15] employed iterative scheme of Yao and Chen [16] to obtain weak and strong convergence results of the sequence defined by:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

(4)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1),S$ and T are quasi-asymptotically nonexpansive mappings in uniformly convex Banach spaces. As far as the author’s observation, (3) and (4) are independent.

In 2019, Ali and Ali [17] proved some weak and strong convergence theorems for common fixed points of two generalized nonexpansive mappings using the iteration presented in (4) in uniformly Banach spaces.

The convergence of several iterations to a fixed point is usually established under the assumption that the domain of those above mappings is closed and convex.

Motivated by [17] and abovementioned works, our goal in this paper is to employ the iteration (4) for finding common attractive points of two widely more generalized hybrid mappings without assuming the closedness of the domain and prove weak and strong convergence theorems of (4). Furthermore, we complete this paper by applying our main results to some common fixed point theorems together with some numerical experiments.

2. Preliminaries

Throughout this paper, the set of positive integers and real numbers will be denoted by $\mathbb{N}$ and $\mathbb{R}$. Let H be a real Hilbert space with an inner product $⟨·,·⟩$ that induces its norm $\parallel ·\parallel$. We use → for the strong convergence and ⇀ for the weak convergence. One of the most important properties in Hilbert spaces is Opial’s property:

Theorem 1

([18]). Let $\left\{x_n\right\}$ be a sequence in H and $x_0\in H$. If $x_n\rightharpoonup x_0$, then

$$\underset{n\to \infty }{lim\; inf}\parallel x_n-x_0\parallel <\underset{n\to \infty }{lim\; inf}\parallel x_n-x\parallel$$

for all $x\in H\backslash \left\{x_0\right\}.$

Next, we recall the following property of a Hilbert space H which is useful for proving our main result.

Theorem 2

([18]). Let C be a nonempty closed convex subset of H. Then for each $x\in H$, there exists a unique element $P_{C}x\in C$ such that

$$\parallel x-P_{C}x\parallel =d(x,C),$$

where $d(x,C)=inf\{\parallel x-y\parallel :y\in C\}$ and $P_C$ is called the metric projection of H on C.

We have the following lemma from Khan [6].

Lemma 1.

Let C be a nonempty subset of H and let $S,T$ be two mappings from C into H. Then $A(S,T)$ is a closed and convex subset of H.

Moreover, the following result of Guu and Takahashi [19] also plays an important role for our main results.

Lemma 2.

Let C be a nonempty subset of $H.$ Suppose $T:C\to H$ is an $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mapping satisfying either of the conditions(1) or (2):

(1)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\gamma >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$;

(2)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\beta >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0.$

If $x_n\rightharpoonup x_0$ and $x_n-T{x}_n\to 0,$ then $x_0\in A\left(T\right)$.

Recall that a mapping $T:C\to H$ is quasi-nonexpansive if $F\left(T\right)\ne \varnothing$ and

$$\parallel T\left(x\right)-p\parallel \le \parallel x-p\parallel$$

for all $p\in F\left(T\right),x\in C$. Furthermore, Takahashi et al. [20] proved the following result for quasi-nonexpansive mappings.

Lemma 3.

Let C be a nonempty subset of $H.$ Suppose T is a quasi-nonexpansive mapping from C into H. Then $A\left(T\right)\cap C=F\left(T\right)$.

We know from [5] that the following condition provides widely more generalized hybrid mappings to be quasi-nonexpansive.

Lemma 4

([5]). Let C be a nonempty closed convex subset of $H.$ Suppose $T:C\to H$ is an $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mapping such that $F\left(T\right)\ne \varnothing$ and satisfying either of the conditions(1)or(2):

(1)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\gamma >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$;

(2)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\beta >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0.$

Then T is quasi-nonexpansive.

We also need the following result to prove our main theorem.

Lemma 5

([21]). Let X be a uniformly convex Banach space. Suppose $d>0$ and two sequences $\left\{x_n\right\}$ and $\left\{y_n\right\}$ in X satisfy the following:

(i) 

${lim\; sup}_{n\to \infty }\parallel x_n\parallel \le d;$

(ii) 

${lim\; sup}_{n\to \infty }\parallel y_n\parallel \le d;$

(iii) 

${lim\; sup}_{n\to \infty }\parallel {\alpha }_n{x}_n+(1-{\alpha }_n)y_n\parallel =d,$

where $0<p\le {\alpha }_n\le q<1$ for all $n\ge 1.$ Then ${lim}_{n\to \infty }\parallel x_n-y_n\parallel =0.$

3. Main Results

In this section, we present weak and strong convergence theorems using the iteration (4) for two widely more generalized hybrid mappings in a Hilbert space. Before proving the main theorem, the following results are required.

Lemma 6.

Let C be a nonempty convex subset of H. Suppose $S,T:C\to C$ are two mappings with $A(S,T)\ne \varnothing$. If $\left\{x_n\right\}$ is defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$. Then ${lim}_{n\to \infty }\parallel x_n-z\parallel$ exists for all $z\in A(S,T).$

Proof. 

Let $z\in A(S,T)$. Then,

$$\parallel S{x}_n-z\parallel \le \parallel x_n-z\parallel and\parallel T{x}_n-z\parallel \le \parallel x_n-z\parallel .$$

Consider,

$$\begin{array}{cc}\hfill \parallel x_{n+1}-z\parallel & =\parallel {\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n-z\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel x_n-z\parallel +{\beta }_n\parallel S{x}_n-z\parallel +{\gamma }_n\parallel T{x}_n-z\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel x_n-z\parallel +{\beta }_n\parallel x_n-z\parallel +{\gamma }_n\parallel x_n-z\parallel \hfill \\ \hfill & =\parallel x_n-z\parallel .\hfill \end{array}$$

Therefore, $\{\parallel x_n-z\parallel \}$ is nonincreasing and bounded for all $z\in A(S,T)$ which implies that ${lim}_{n\to \infty }\parallel x_n-z\parallel$ exists. □

Lemma 7.

Let C be a nonempty convex subset of H. Suppose $S,T:C\to C$ are two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings with $A(S,T)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and there exist $a,b\in \mathbb{R}$ such that $0<a\le {\gamma }_n\le b<1$, for every $n\in \mathbb{N}$. Then ${lim}_{n\to \infty }\parallel x_n-S{x}_n\parallel =0$ and ${lim}_{n\to \infty }\parallel x_n-T{x}_n\parallel =0.$

Proof. 

Let $z\in A(S,T).$ By Lemma 6, let ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\parallel =p.}$ Since $z\in A(S,T),$ we have

$$\parallel S{x}_n-z\parallel \le \parallel x_n-z\parallel and\parallel T{x}_n-z\parallel \le \parallel x_n-z\parallel .$$

Thus,

$$\underset{n\to \infty }{lim\; sup}\parallel S{x}_n-z\parallel \le \underset{n\to \infty }{lim\; sup}\parallel x_n-z\parallel =p$$

(5)

and

$$\underset{n\to \infty }{lim\; sup}\parallel T{x}_n-z\parallel \le \underset{n\to \infty }{lim\; sup}\parallel x_n-z\parallel =p.$$

(6)

Using the control conditions of $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$, we have

$$\begin{array}{cc}\hfill p& =\underset{n\to \infty }{lim}\parallel x_{n+1}-z\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel {\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n-z\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}∥(1-{\gamma }_n)\left[\frac{{\alpha }_n}{1-{\gamma }_n}(x_n-z)+\frac{{\beta }_n}{1-{\gamma }_n}(S{x}_n-z)\right]+{\gamma }_n(T{x}_n-z)∥\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}& ∥\frac{{\alpha }_n}{1-{\gamma }_n}(x_n-z)+\frac{{\beta }_n}{1-{\gamma }_n}(S{x}_n-z)∥\hfill \\ \hfill & \le \underset{n\to \infty }{lim\; sup}\left[\frac{{\alpha }_n}{1-{\gamma }_n}\parallel x_n-z\parallel +\frac{{\beta }_n}{1-{\gamma }_n}\parallel S{x}_n-z\parallel \right]\hfill \\ \hfill & \le \underset{n\to \infty }{lim\; sup}\left[\frac{{\alpha }_n}{1-{\gamma }_n}\parallel x_n-z\parallel +\frac{{\beta }_n}{1-{\gamma }_n}\parallel x_n-z\parallel \right]\hfill \\ \hfill & =\underset{n\to \infty }{lim\; sup}\frac{{\alpha }_n+{\beta }_n}{1-{\gamma }_n}\parallel x_n-z\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim\; sup}\parallel x_n-z\parallel \hfill \\ \hfill & =p.\hfill \end{array}$$

(8)

Applying Lemma 5 to (6), (7) and (8), we obtain

$$\begin{array}{cc}\hfill 0& =\underset{n\to \infty }{lim}∥\frac{{\alpha }_n}{1-{\gamma }_n}(x_n-z)+\frac{{\beta }_n}{1-{\gamma }_n}(S{x}_n-z)-(T{x}_n-z)∥\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{1}{1-{\gamma }_n}∥{\alpha }_n(x_n-z)+{\beta }_n(S{x}_n-z)-(1-{\gamma }_n)(T{x}_n-z)∥\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{1}{1-{\gamma }_n}\parallel {\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n-({\alpha }_n+{\beta }_n+{\gamma }_n)z+z-T{x}_n\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{1}{1-{\gamma }_n}\parallel x_{n+1}-T{x}_n\parallel .\hfill \end{array}$$

Since ${\gamma }_n\le b<1$ for every $n\in \mathbb{N}$, we get

$$\underset{n\to \infty }{lim}\parallel x_{n+1}-T{x}_n\parallel =0.$$

We can show in a similar way that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_{n+1}-S{x}_n\parallel =0}$ and ${\displaystyle \underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =0.}$ Therefore,

$$\underset{n\to \infty }{lim}\parallel x_n-S{x}_n\parallel \le \underset{n\to \infty }{lim}\parallel x_n-x_{n+1}\parallel +\underset{n\to \infty }{lim}\parallel x_{n+1}-S{x}_n\parallel =0$$

and

$$\underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel \le \underset{n\to \infty }{lim}\parallel x_n-x_{n+1}\parallel +\underset{n\to \infty }{lim}\parallel x_{n+1}-T{x}_n\parallel =0.$$

□

3.1. Weak Convergence Theorems

We are now proving weak convergence theorems for two widely more generalized hybrid mappings in a Hilbert space.

Theorem 3.

Let C be a nonempty convex subset of $H.$ Suppose $S,T:C\to C$ are two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings satisfying either the following condition (1) or (2) holds:

(1)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\gamma >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$;

(2)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\beta >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$

with $A(S,T)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and there exist $a,b\in \mathbb{R}$ such that $0<a\le {\gamma }_n\le b<1$, for every $n\in \mathbb{N}$. Then $\left\{x_n\right\}$ converges weakly to $z\in A(S,T).$

Proof. 

By Lemma 6, we know $\left\{x_n\right\}$ is bounded and hence there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup z.$ Lemma 2 and Lemma 7 imply that $z\in A(S,T)$. Let $\left\{x_{n_j}\right\}$ be any weakly convergent subsequence of $\left\{x_n\right\}$, then there exists $z_1\in H$ such that $x_{n_j}\rightharpoonup z_1.$ Using the same argument, we get $z_1\in A(S,T)$. By the way, the weak limit is unique. Indeed, if $z\ne z_1,$ then by Opial’s condition and Lemma 6, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel x_n-z\parallel & =\underset{k\to \infty }{lim}\parallel x_{n_k}-z\parallel \hfill \\ \hfill & <\underset{k\to \infty }{lim}\parallel x_{n_k}-z_1\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel x_n-z_1\parallel \hfill \\ \hfill & =\underset{j\to \infty }{lim}\parallel x_{n_j}-z_1\parallel \hfill \\ \hfill & <\underset{j\to \infty }{lim}\parallel x_{n_j}-z\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel x_n-z\parallel .\hfill \end{array}$$

This is a contradiction, that is $z=z_1.$ Therefore $x_n\rightharpoonup z\in A(S,T)$. □

Furthermore, if the subset C in Theorem 3 is closed, we also obtain a weak convergence theorem for common fixed points of two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings in Hilbert spaces as follows.

Corollary 1.

Let C be a nonempty closed convex subset of $H.$ Suppose $S,T:C\to C$ are two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings satisfying either the following condition (1) or (2) holds:

(1)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\gamma >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$;

(2)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\beta >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$

with $F\left(S\right)\cap F\left(T\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and there exist $a,b\in \mathbb{R}$ such that $0<a\le {\gamma }_n\le b<1$, for every $n\in \mathbb{N}$. Then $\left\{x_n\right\}$ converges weakly to $z\in F\left(S\right)\cap F\left(T\right).$

Proof. 

By Lemma 4, we get S and T are quasi-nonexpansive. It is derived from Lemma 3 that

$$A(S,T)\cap C=F\left(S\right)\cap F\left(T\right).$$

The fact $F\left(S\right)\cap F\left(T\right)\ne \varnothing$ in assumption implies the set $A(S,T)\ne \varnothing$. By Theorem 3, we have $x_n\rightharpoonup z\in A(S,T)$. Since C is closed and convex, C is weakly closed which implies that $z\in C$. Therefore, we can conclude that $z\in F\left(S\right)\cap F\left(T\right).$ □

3.2. Strong Convergence Theorems

Firstly, we give one important result as follows.

Theorem 4.

Let C be a nonempty convex subset of H. Suppose $S,T:C\to C$ are two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings with $A(S,T)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and there exist $a,b\in \mathbb{R}$ such that $0<a\le {\gamma }_n\le b<1$, for every $n\in \mathbb{N}$. Then $\left\{x_n\right\}$ converges strongly to $z\in A(S,T)$ if and only if ${\displaystyle \underset{n\to \infty }{lim\; inf}d(x_n,A)=0}$ or ${\displaystyle \underset{n\to \infty }{lim\; sup}d(x_n,A)=0}$, where $A=A(S,T)$ and $d(x,A):=inf\{\parallel x-y\parallel :y\in A\}.$

Proof. 

Put $A=A(S,T)$. Suppose that $\left\{x_n\right\}$ converges strongly to $z\in A$. Then, for $\epsilon >0$, there exists $k\in \mathbb{N}$ such that

$$\parallel x_n-z\parallel <\epsilon \mathrm{for\; all}n\ge k.$$

Therefore, we obtain

$$d(x_n,A)=inf\{\parallel x_n-u\parallel :u\in A\}\le \parallel x_n-z\parallel <\epsilon \mathrm{for\; all}n\ge k.$$

It follows that ${\displaystyle \underset{n\to \infty }{lim}d(x_n,A)=0,}$ and hence

$$\underset{n\to \infty }{lim\; inf}d(x_n,A)=0=\underset{n\to \infty }{lim\; sup}d(x_n,A).$$

Conversely, if ${\displaystyle \underset{n\to \infty }{lim\; sup}d(x_n,A)=0,}$ then ${\displaystyle \underset{n\to \infty }{lim}d(x_n,A)=0.}$ Assume that ${\displaystyle \underset{n\to \infty }{lim\; inf}}$$d(x_n,A)=0$. We obtain from Lemma 5 that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\parallel }$ exists for all $z\in A.$ By assumption, we get ${\displaystyle \underset{n\to \infty }{lim}d(x_n,A)=0}$ and hence for any $k\in \mathbb{N},$ there exists $N_k\in \mathbb{N}$ such that

$$d\left(x_n,A\right)<\frac{1}{2^k}\mathrm{for\; all}n\ge N_k.$$

(9)

For $k=1,$ put $n_1=N_1+1>N_1.$ It follows from (3) that ${\displaystyle d(x_{n_1},A)<\frac{1}{2}}$ and hence by Lemma 1 and Theorem 2, there exists $z_1\in A$ such that

$$\parallel x_{n_1}-z_1\parallel <\frac{1}{2}.$$

For $k=2$, put $n_2=max\{n_1,N_2\}+1.$ Then $n_2>n_1$ and $n_2>N_2$. From (3), we have ${\displaystyle d(x_{n_2},A)<\frac{1}{2^2}}$ and obtain $z_2\in A$ such that

$$\parallel x_{n_2}-z_2\parallel <\frac{1}{2^2}.$$

Continuing this process, we can choose $n_k=max\{n_{k-1},N_k\}+1$, where $n_0=0$ such that

$$n_k>N_k,n_k>n_{k-1}and\parallel x_{n_k}-z_k\parallel <\frac{1}{2^k}\mathrm{for\; all}k\in \mathbb{N}.$$

Therefore, there exist a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ and a sequence $\left\{z_k\right\}$ in A such that

$$\parallel x_{n_k}-z_k\parallel <\frac{1}{2^k}\mathrm{for\; all}k\in \mathbb{N}.$$

Since $\{\parallel x_n-z\parallel \}$ is nonincreasing for every $z\in A$, we get that

$$\parallel x_{n_{k+1}}-z_k\parallel \le \parallel x_{n_k}-z_k\parallel$$

and

$$\begin{array}{cc}\hfill \parallel z_{k+1}-z_k\parallel & =\parallel z_{k+1}-x_{n_{k+1}}+x_{n_{k+1}}-z_k\parallel \hfill \\ \hfill & \le \parallel x_{n_{k+1}}-z_{k+1}\parallel +\parallel x_{n_{k+1}}-z_k\parallel \hfill \\ \hfill & \le \parallel x_{n_{k+1}}-z_{k+1}\parallel +\parallel x_{n_k}-z_k\parallel \hfill \\ \hfill & <\frac{1}{2^{k+1}}+\frac{1}{2^k}\hfill \\ \hfill & <\frac{1}{2^{k-1}}\hfill \end{array}$$

for all $k\in \mathbb{N}.$ If $m>n,$ we employ the triangle inequality to obtain

$$\begin{array}{cc}\hfill \parallel z_m-z_n\parallel & \le \parallel z_n-z_{n+1}\parallel +\parallel z_{n+1}-z_{n+2}\parallel +\parallel z_{n+2}-z_{n+3}\parallel +\cdots +\parallel z_{m-1}-z_m\parallel \hfill \\ \hfill & <\frac{1}{2^{n-1}}+\frac{1}{2^n}+\frac{1}{2^{n+1}}+\cdots +\frac{1}{2^{m-2}}\hfill \\ \hfill & =\frac{1}{2^{n-1}}\left(1+\frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^{m-n-1}}\right)\hfill \\ \hfill & \le \frac{1}{2^{n-2}}.\hfill \end{array}$$

Therefore, $\left\{z_k\right\}$ is a Cauchy sequence in A which implies that $\left\{z_k\right\}$ is convergent. Since A is closed, we obtain $z_k\to z\in A$. Moreover,

$$\begin{array}{cc}\hfill \parallel x_{n_k}-z\parallel & =\parallel x_{n_k}-z_k+z_k-z\parallel \hfill \\ \hfill & \le \parallel x_{n_k}-z_k\parallel +\parallel z_k-z\parallel \hfill \\ \hfill & <\frac{1}{2^k}+\parallel z_k-z\parallel .\hfill \end{array}$$

Let $k\to \infty$, we get that ${\displaystyle \underset{k\to \infty }{lim}\parallel x_{n_k}-z\parallel =0.}$

Since ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\parallel }$ exists, we obtain ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\parallel =0}$ and the proof is complete. □

By the way, one idea to prove strong convergence is employing the concept introduced by Senter and Dotson [22] called condition A. Let C be a subset of Hilbert space H. A mapping T satisfies condition A if there exists a nondecreasing function $f:[0,\infty )\to [0,\infty )$ with $f\left(0\right)=0,f\left(r\right)>0$ for all $r\in (0,\infty )$ such that

$$f\left(d\right(x,A\left(T\right)\left)\right)\le \parallel x-Tx\parallel$$

for all $x\in C$, where $d(x,A(T\left)\right):=inf\{\parallel x-y\parallel :y\in A(T\left)\right\}$. Moreover, the examples of mappings satisfying condition A was also given in [22].

In 2007, Chidume [23] extended the condition A for two mappings, called condition $A^{\prime }$. Two mappings $S,T:C\to C$ satisfy condition $A^{\prime }$ if there exists a nondecreasing function $f:[0,\infty )\to [0,\infty )$ with $f\left(0\right)=0,f\left(r\right)>0$ for all $r\in (0,\infty )$ such that either

$$f\left(d\right(x,A(S,T))\le \parallel x-Sx\parallel orf(d(x,A(S,T\left)\right)\le \parallel x-Tx\parallel$$

for all $x\in C$, where $d(x,A(S,T\left)\right):=inf\{\parallel x-y\parallel :y\in A(S,T\left)\right\}$.

As a consequence of Theorem 4, we obtain a strong convergence theorem for common attractive points of two widely more generalized hybrid mappings satisfying condition $A^{\prime }.$

Theorem 5.

Let C be a nonempty convex subset of $H.$ Suppose $S,T:C\to C$ are two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings with $A(S,T)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and $0<a\le {\gamma }_n\le b<1$. If S and T satisfy condition $A^{\prime }$, then $\left\{x_n\right\}$ converges strongly to $z\in A(S,T).$

Proof. 

By Lemma 7, we have

$$\underset{n\to \infty }{lim}\parallel x_n-S{x}_n\parallel =0=\underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel .$$

Since S and T satisfy condition $A^{\prime }$, we obtain that there exists a nondecreasing function $f:[0,\infty )\to [0,\infty )$ with $f\left(0\right)=0,f\left(r\right)>0$ for all $r\in (0,\infty )$ such that either

$$0\le \underset{n\to \infty }{lim}f(d(x_n,A(S,T))\le \underset{n\to \infty }{lim}\parallel x_n-S{x}_n\parallel =0,$$

or

$$0\le \underset{n\to \infty }{lim}f\left(d(x_n,A(S,T))\right)\le \underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.$$

In both case, it follows that ${\displaystyle \underset{n\to \infty }{lim}d(x_n,A(S,T))=0.}$ By Theorem 4, we conclude that $\left\{x_n\right\}$ converges strongly to a common attractive point of S and T. □

Furthermore, if the subset C and both two mappings S and T in Theorem 5 satisfy the same conditions in Corollary 1, then we obtain the following corollary.

Corollary 2.

Let C be a nonempty closed convex subset of $H.$ Let $S,T:C\to C$ be two $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings. Suppose that either the following condition (1) or (2) holds:

(1)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\gamma >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$;

(2)

$\alpha +\beta +\gamma +\delta \ge 0,\alpha +\beta >0,ϵ+\eta \ge 0$ and $\xi +\eta \ge 0$

with $F\left(S\right)\cap F\left(T\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be defined by (4) as:

$$\left\{\begin{array}{c}{x}_1\in C,\hfill \\ x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}S{x}_n+{\gamma }_{n}T{x}_n,\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and $0<a\le {\gamma }_n\le b<1$. If S and T satisfy condition $A^{\prime }$, then $\left\{x_n\right\}$ converges strongly to $z\in F\left(S\right)\cap F\left(T\right).$

Proof. 

By Theorem 5, we can prove similarly to the proof of Corollary 1. □

We end this section with formally constructing an example to support our main results.

Example 1.

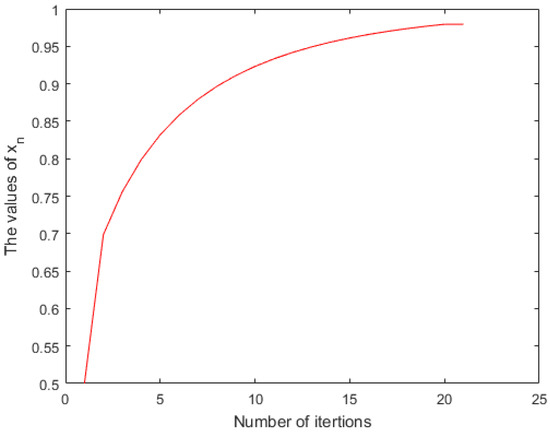
Let $H=\mathbb{R}$ and $C=(0,1]$. Then C is a nonempty convex subset of H. Suppose $S,T:C\to C$ are defined by $Sx=\frac{x^3+2}{3}$ and $Tx=e^{x-1}$ for all $x\in C.$ It can be easily investigated that S and T are $(\alpha ,\beta ,\gamma ,\delta ,ϵ,\xi ,\eta )$-widely more generalized hybrid mappings because they are nonexpansive and $1\in A\left(S\right)\cap A\left(T\right)$. We choose the parameters ${\alpha }_n={\beta }_n={\gamma }_n=\frac{1}{3}$ and initial point $x_1=\frac{1}{2}$. Then, we compute the sequence $\left\{x_n\right\}$ generated by (4) as seen in Table 1.

Table 1. The values of $\left\{x_n\right\}$ for different number of iterations.

Iteration No.	${\mathit{x}}_{\mathit{n}}$	$|{\mathit{x}}_{\mathit{n}}-1|$	$|{\mathit{x}}_{\mathit{n}}-{\mathit{S}}_{\mathit{n}}{\mathit{x}}_{\mathit{n}}|$	$|{\mathit{x}}_{\mathit{n}}-{\mathit{T}}_{\mathit{n}}{\mathit{x}}_{\mathit{n}}|$	$\left|\frac{{\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}}{{\mathit{x}}_{\mathit{n}}}\right|$
1	$0.5000$	$0.5000$	$0.2500$	$0.1065$	$0.2377$
2	$0.6987$	$0.3821$	$0.1755$	$0.0642$	$0.1291$
3	$0.7560$	$0.3013$	$0.1307$	$0.0411$	$0.0820$
4	$0.7989$	$0.2440$	$0.1012$	$0.0275$	$0.0567$
5	$0.8320$	$0.2011$	$0.0805$	$0.0189$	$0.0415$
6	$0.8583$	$0.1680$	$0.0654$	$0.0133$	$0.0315$
7	$0.8795$	$0.1417$	$0.0539$	$0.0096$	$0.0247$
8	$0.8968$	$0.1205$	$0.0450$	$0.0070$	$0.0197$
9	$0.9112$	$0.1032$	$0.0380$	$0.0051$	$0.0160$
10	$0.9232$	$0.0888$	$0.0322$	$0.0038$	$0.0132$
11	$0.9333$	$0.0768$	$0.0276$	$0.0029$	$0.0110$
12	$0.9420$	$0.0667$	$0.0237$	$0.0022$	$0.0092$
13	$0.9493$	$0.0580$	$0.0205$	$0.0017$	$0.0078$
14	$0.9557$	$0.0507$	$0.0177$	$0.0013$	$0.0067$
15	$0.9611$	$0.0443$	$0.0154$	$9.6815\times {10}^{-4}$	$0.0057$
16	$0.9659$	$0.0389$	$0.0135$	$7.4544\times {10}^{-4}$	$0.0049$
17	$0.9700$	$0.0341$	$0.0118$	$5.7579\times {10}^{-4}$	$0.0043$
18	$0.9736$	$0.0300$	$0.0103$	$4.4596\times {10}^{-4}$	$0.0037$
19	$0.9767$	$0.0264$	$0.0090$	$3.4624\times {10}^{-4}$	$0.0032$
20	$0.9794$	$0.0233$	$0.0079$	$2.6937\times {10}^{-4}$	$0.0028$

It is seen from Table 1 that $x_n\to 1\in A\left(S\right)\cap A\left(T\right),$ the error $|x_n-1|\to 0,|x_n-S_n{x}_n|\to 0,|x_n-T_n{x}_n|\to 0$ and $\left|\frac{x_{n+1}-x_n}{x_n}\right|\to 0.$ Furthermore, the result of convergence behavior of iterative method (4) is shown in Figure 1.

Figure 1. The graph of convergence behavior of our iterative method.

4. Conclusions

In this paper, by using the iterative scheme (4), we proved weak and strong convergence theorems for common attractive points of two widely more generalized hybrid mappings in a Hilbert space without assuming the closedness of the domain. Using our main results, we can apply them to some common fixed point problems. Moreover, we presented a numerical example, Example 1, to support our main result.