Inertial Krasnoselski–Mann Iterative Method for Solving Hierarchical Fixed Point and Split Monotone Variational Inclusion Problems with Its Applications

Abstract

In this article, we discuss the hierarchical fixed point and split monotone variational inclusion problems and propose a new iterative method with the inertial terms involving a step size to avoid the difficulty of calculating the operator norm in real Hilbert spaces. A strong convergence theorem of the proposed method is established under some suitable control conditions. Furthermore, the proposed method is modified and used to derive a scheme for solving the split problems. Finally, we compare and demonstrate the efficiency and applicability of our schemes for numerical experiments as well as an example in the field of image restoration.

1. Introduction

The variational inequality problem (VIP for short) is a significant branch of mathematics. Over the decades, this problem has been extensively studied for solving many real-world problems in various applied research areas such as physics, economics, finance, optimization, network analysis, medical images, water resources and structural analysis. Moreover, it contains fixed point problems, optimization problems arising in machine learning, signal processing and linear inverse problems, (see [1,2,3]). The set of solutions of the variational inequality problem is denoted by

$$VI(C,A)=\{u\in C:⟨v-u,Au⟩\ge 0\},\forall v\in C,$$

where C is a nonempty closed convex subset of the Hilbert space H and $A:C\to H$ is a mapping.

Moudafi and Mainge [4] established the hierarchical fixed point problem for a nonexpansive mapping T with respect to another nonexpansive mapping S on H by utilizing the concept of the variational inequality problem: Find $x^{\ast }\in Fix\left(T\right)$ such that

$$⟨x^{\ast }-S{x}^{\ast },x^{\ast }-x⟩\le 0,\forall x\in Fix\left(T\right),$$

(1)

where $S:H\to H$ is a nonexpansive mapping and $Fix\left(T\right)=\{x\in C:x=Tx\}$. It is easy to see that (1) is equivalent to the following fixed point problem: Find $x^{\ast }\in H$ such that

$$x^{\ast }\in P_{Fix\left(T\right)}S{x}^{\ast },$$

(2)

where $P_{Fix\left(T\right)}$ stands for the metric projection on the closed convex set $Fix\left(T\right)$. The solution set of HFPP (1) is denoted by $\Phi =\{x^{\ast }\in H:⟨x^{\ast }-S{x}^{\ast },x^{\ast }-x⟩\le 0,\forall x\in Fix\left(T\right)\}$. It is obvious that $\Phi =VI\left(Fix\right(T),I-S)$. It is worth noting (1) covers monotone variational inequality on fixed point sets as well as minimization problem, etc. For several fixed point theory and solving the hierarchical fixed point problem in (1), many iterative methods have been studied and developed, (see [4,5,6,7,8]).

On the other hand, The split monotone variational inclusion problem (in short, SpMVIP) is proposed and studied by Moudafi [9]. It had been applied to the intensity-modulated radiation therapy treatment planning as a model, (see [10]). This concept has appeared in many inverse problems which emerge in phase retrieval and other real-world problems such as sensor networks, data compression as well as comprised tomography, (see [11,12]): Find $x^{\ast }\in H_1$ such that

$$0\in f\left(x^{\ast }\right)+F\left(x^{\ast }\right)$$

(3)

and such that

$$y^{\ast }=A{x}^{\ast }\mathrm{solves}0\in g\left(y^{\ast }\right)+G\left(y^{\ast }\right),$$

(4)

where $F:H_1\to 2^{H_1}$ and $G:H_2\to 2^{H_2}$ are multi-valued monotone operators, $f:H_1\to H_1$, $g:H_2\to H_2$ are two single-valued operators and $A:H_1\to H_2$ is a bounded linear operator. The solution set of SpMVIP is denoted by $\Omega =\{x^{\ast }\in H_1:x^{\ast }\in \mathrm{Sol}(\mathrm{MVIP}(3\left)\right)\}\mathrm{and}A{x}^{\ast }\in \mathrm{Sol}(\mathrm{MVIP}\left(4\left)\right)\right\}$.

They introduced the following iterative method and studied the weak convergence theorem for SpMVIP: For a given $x_0\in H_1$, compute iterative sequence $\left\{x_n\right\}$ generated by the following scheme:

$$x_{n+1}=U(x_n+r{A}^{\ast }(V-I)A{x}_n),\mathrm{for}r>0,$$

where $U=J_{\lambda }^F(I-\lambda f)$, $V=J_{\lambda }^G(I-\lambda g)$ such that $J_{\lambda }^F$ and $J_{\lambda }^G$ are the resolvent mappings of F and G, respectively (see the definition in Section 2) and I is the identity mapping. The operator A is a bounded linear operator with $A^{\ast }$ is adjoint of A and $r\in (0,\frac{1}{L})$ with L being the spectral radius of the operator $A^{\ast }A$. They proved that the sequence $\left\{x_n\right\}$ converges weakly to a solution of hierarchical fixed point and split monotone variational inclusion problems.

In 2017, Kazmi et al. [13] developed a Krasnoselski–Mann type iterative method to approximate a common solution set of a hierarchical fixed point problem for nonexpansive mappings $S,T$ and a split monotone variational inclusion problem which was defined as follows:

$$\begin{array}{ccc}\hfill x_0& \in & C;\hfill \\ \hfill u_n& =& (1-{\alpha }_n)x_n+{\alpha }_n({\beta }_{n}S{x}_n+(1-{\beta }_n)T{x}_n);\hfill \\ \hfill x_{n+1}& =& U(u_n+\lambda A^{\ast }(V-I)A{u}_n),\forall n\ge 0,\hfill \end{array}$$

(5)

where $U=J_{\lambda }^F(I-{\lambda }_{n}f)$, $V=J_{\lambda }^G(I-{\lambda }_{n}g)$ and the step size $\lambda \in (0,\frac{1}{L})$ where L is the spectral radius of the operator $A^{\ast }A$. Under some suitable conditions on $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{r_n\right\}$:

$$(C1){\sum }_{n=0}^{\infty }{\beta }_n<\infty ; (C2){lim}_{n\to \infty }\frac{\parallel x_n-u_n\parallel }{{\alpha }_n{\beta }_n}=0; (C3){lim\; inf}_{n\to \infty }{\lambda }_n>0$$

.

They proved that the sequence $\left\{x_n\right\}$ converges weakly to a solution of hierarchical fixed point and split monotone variational inclusion problems. Normally, an interesting question is how to construct the strongly convergence results which approximate the solution of the split monotone variational inclusion and hierarchical fixed point problems.

In 2021, Dao-Jun Wen [14] modified Krasnoselski–Mann type iteration (5) which replaced operator T with $(I-{\mu }_{n}D)$ where D is a strongly monotone operator and L-Lipschitzian. Define a sequence $\left\{x_n\right\}$ in the following manner:

$$\begin{array}{ccc}\hfill u_n& =& (1-{\alpha }_n)x_n+{\alpha }_{n}T({\beta }_{n}S{x}_n+(1-{\beta }_n)(I-{\mu }_{n}D)x_n),\hfill \\ \hfill x_{n+1}& =& U(u_n+\lambda A^{\ast }(V-I)Au),\hfill \end{array}$$

where $U=J_{\lambda }^F(I-\lambda f)$, $V=J_{\lambda }^G(I-\lambda g)$, $T,S$ are two nonexpansive mappings and the step size $\lambda \in (0,\frac{1}{L})$ where L is the spectral radius of the operator $A^{\ast }A$. They established the strong convergence result and constructed the new condition of coefficients which replaced of condition (C2).

If $f=0$ and $g=0$, then the split monotone variational inclusion problem reduced to the following split variational inclusion problem (SVIP): Find $x^{\ast }\in H_1$ such that

$$0\in F\left(x^{\ast }\right)\mathrm{and}\mathrm{such}\mathrm{that}{y}^{\ast }=A{x}^{\ast }\mathrm{solves}0\in G\left(y^{\ast }\right).$$

(6)

Byrne et al. [15] have attempted to solve a special case of (6) and defined $\left\{x_n\right\}$ in the following: $x_{n+1}=J_{\lambda }^F(x_n+r{A}^{\ast }(J_{\lambda }^G-I)A{x}_n).$ Moreover, they obtained the weak and strong convergence results of problem (6) with resolvent operator technique and the stepsize $r\in (0,\frac{2}{\parallel A^{\ast }A\parallel })$. In order to speed up the convergence speed, Alvarez and Attouch [16] considered the following iterative scheme: $x_{n+1}=J_{\lambda }^F(x_n+{\theta }_n(x_n-x_{n-1}))$, where F is a maximal monotone operator, $\lambda >0$ and ${\theta }_n\in [0,1]$, such the iterative scheme is called the inertial proximal method, and ${\theta }_n(x_n-x_{n-1})$ is referred to as the inertial extrapolation term which is a procedure of speeding up the convergence properties under the condition that ${\sum }_{n=1}^{\infty }{\parallel x_n-x_{n-1}\parallel }^2<\infty$ (see [17]). At the same time, the idea of the inertial technique plays an important role in the optimization community as a technology to build an accelerating iterative method, (see [18,19]).

On the other hand, the iterative methods mentioned above share a common manner, that is, their step size requires a knowlegde of the prior information of the operator (matrix) norm $\parallel A\parallel$. It may be difficult to calculate $\parallel A\parallel$ and the fixed step size of iterative methods have an impact on the implementation. To conquer, the construction of self-adaptive step size has aroused interest among researchers. Recently, there are many iterative methods that do not require the prior information of the operator (matrix) norm, (see [20,21,22]).

Motivated and inspired by the work mentioned above, we further investigate the self-adaptive inertial Krasnoselski-mann iterative method for solving hierarchical fixed point and split monotone variational inclusion problems. This manuscript aims to suggest modifications of the results that appeared in [14] by applying the inertial scheme that is effective for speeding up the iteration process and adding the step size that the prior information of the operator (matrix) norm is not required. A strong convergence theorem of the proposed iterative method is established under some suitable conditions. Furthermore, we also present some numerical experiments to demonstrate the advantages of the stated iterative method over other existing methods [9,13,14] and apply our main results to solving the image restoration problem.

2. Materials and Methods

In this section, we recall some basic definitions and properties which will be frequently used in our later investigation. Some useful results proved already in the literature are also summarized.

Definition 1.

A mapping $f:H\to H$ is said to be:

(i)

monotone, if

$$⟨fx-fy,x-y⟩\ge 0,\forall x,y\in H;$$

(ii)

α-inverse strongly monotone, if there exists a constant $\alpha >0$ such that

$$⟨fx-fy,x-y⟩\ge {\alpha \parallel fx-fy\parallel }^2,\forall x,y\in H;$$

(iii)

β-Lipschitz continuous, if there exists a constant $\beta >0$ such that

$$\parallel fx-fy\parallel \le \beta \parallel x-y\parallel \forall x,y\in H.$$

Let $F:H\to 2^H$ be a multivalued operator on H. Then the graph $G\left(F\right)$ of F is defined by

$$G\left(F\right)=\left\{\right(x,y)\in H\times H:y\in F(x\left)\right\},$$

and

(i)

the operator F is called a monotone operator, if

$$⟨u-v,x-y⟩\ge 0,\mathrm{whenever}u\in F\left(x\right),v\in F\left(y\right);$$

(ii)

the operator F is called a maximal monotone operator, if F is monotone and the graph of F is not properly contained in the graph of other monotone mappings.

Let $F:H\to 2^H$ be a set-valued maximal monotone mapping, which Graph (F) is not property contained in the graph of any other monotone mapping. Then the resolvent operator $J_{\lambda }^F:H\to H$ is defined by

$$J_{\lambda }^F={(I+\lambda F)}^{-1}\left(x\right),\forall x\in H,$$

where I stands for the identity operator on H. It is well known that resolvent operator $J_{\lambda }^F$ is single-valued, nonexpansive and firmly nonexpansive for $\lambda >0$.

Lemma 1.

Let f be a κ-inverse strongly monotone mapping and F be a maximal monotone mapping, then $J_{\lambda }^F(I-\lambda F)$ is averaged for all $\lambda \in (0,2\kappa )$.

Lemma 2

([9]). Let f be a mapping and F be a maximal monotone mapping, then $0\in f\left(x^{\ast }\right)+F\left(x^{\ast }\right)$ if and only if $x^{\ast }=J_{\lambda }^F(I-\lambda f)x^{\ast }$, i.e., $x^{\ast }\in Fix\left(J_{\lambda }^F(I-\lambda f)\right)$ for $\lambda >0$.

Lemma 3.

For any $x,y\in H$, the following results hold:

(i)

${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2⟨y,x+y⟩;$

(ii)

${\parallel tx+(1-t)y\parallel }^2={t\parallel x\parallel }^2+{(1-t)\parallel y\parallel }^2-t(1-t){\parallel x-y\parallel }^2,\forall t\in [0,1].$

Lemma 4

([23]). Let $D:H\to H$ be η-strongly monotone and L-Lipschitz continuous. Then $I-{\mu }_{n}D$ is a $(1-{\mu }_n\rho )$-contraction, i.e.,

$$\parallel (I-{\mu }_{n}D)x-(I-{\mu }_{n}D)y\parallel \le (1-{\mu }_n\rho )\parallel x-y\parallel ,\forall x,y\in H,$$

where $\left\{{\mu }_n\right\}$ is a sequence such that ${\mu }_n\in (0,\mu ]$ and $\rho =\frac{2\eta -\mu L^2}{2}$ with $\mu <\frac{2\mu }{L^2}$.

Lemma 5

([24]). Let $\left\{a_n\right\}$ and $\left\{c_n\right\}$ be two sequences of non-negative real numbers such that

$$a_{n+1}\le (1-{\tau }_n)a_n+b_n+c_n,n\ge 0,$$

where $\left\{{\tau }_n\right\}$ is a sequence in $(0,1)$ and $\left\{b_n\right\}$ is a sequence in $\mathbb{R}$. Assume that ${\mathsf{\Sigma }}_{n=0}^{\infty }{c}_n<\infty$. If $b_n\le {\tau }_{n}M$ for some $M\ge 0$, then $\left\{a_n\right\}$ is a bounded sequence.

Lemma 6

([25]). Let $\left\{a_n\right\}$ be a sequence of non-negative real numbers, $\left\{{\tau }_n\right\}$ be a sequence of real numbers in $(0,1)$ with ${\mathsf{\Sigma }}_{n=1}^{\infty }{\tau }_n=\infty$ and $\left\{b_n\right\}$ be a sequence of real numbers such that

$$a_{n+1}\le (1-{\tau }_n)a_n+{\tau }_n{b}_n,\forall n\ge 1.$$

If ${lim\; sup}_{k\to \infty }{b}_{n_k}\le 0$ for every subsequence $\left\{a_{n_k}\right\}$ of $\left\{a_n\right\}$ satisfying ${lim\; inf}_{k\to \infty }(a_{n_k+1}-a_{n_k})\ge 0$, then ${lim}_{n\to \infty }{a}_n=0$.

3. Results

In this section, we propose a self-adaptive method with inertial extrapolation term for solving hierarchical fixed point and split variational inclusion problems. To begin with, the control conditions need to be satisfied by Condition 1:

(A1)

$\left\{{\theta }_n\right\}\subset (0,\theta )$ for some $\theta >0$ such that ${\theta }_n=O\left({\tau }_n\right)$, i.e., ${lim}_{n\to \infty }\frac{{\theta }_n}{{\tau }_n}=0;$

(A2)

$\left\{{\tau }_n\right\}\subset (0,1)$ such that ${lim}_{n\to \infty }{\tau }_n=0$ and ${\sum }_{n=0}^{\infty }{\tau }_n=\infty$;

(A3)

$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}\subset (a,b)\subset (0,1)$ such that ${lim\; inf}_{n\to \infty }{\alpha }_n>0$, ${\sum }_{n=0}^{\infty }{\beta }_n<\infty$;

(A4)

$\left\{{\mu }_n\right\}$ is a positive sequence such that ${lim}_{n\to \infty }{\mu }_n=0$ and ${\sum }_{n=0}^{\infty }{\mu }_n=\infty$;

(A5)

$\left\{{\delta }_n\right\}\subset (a,b)\subset (0,1-{\tau }_n)$, $\left\{{\alpha }_n{\beta }_n\right\}\subset (a,b)\subset (0,{\tau }_n)$ and ${\sum }_{n=0}^{\infty }{\alpha }_n{\beta }_n{\mu }_n<\infty .$

Remark 1.

From $\overline{{\theta }_n}$ = $\left\{\begin{array}{ccc}& min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\},\hfill & \mathrm{if}{x}_n\ne x_{n-1},\hfill \\ & \theta ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$ and Algorithm 1, we have

$${\theta }_n\parallel x_n-x_{n-1}\parallel \le \overline{{\theta }_n}\parallel x_n-x_{n-1}\parallel \le {ϵ}_n.$$

Therefore ${\mathsf{\Sigma }}_{n=1}^{\infty }{\theta }_n(x_n-x_{n-1})<\infty .$

Algorithm 1: Inertial Krasnoselski-Mann Iterative Method

Initialization: Let $x_0,x_1\in H_1$, $\theta >0$, $\left\{{\sigma }_n\right\}\subset (0,1),$ $\left\{{ϵ}_n\right\}\subset [0,\infty )$ and  ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty$.

Iterative steps: Calculate $x_{n+1}$ follows:

Step 1. Given the iterates $x_{n-1}$ and $x_n$ for each $n\ge 1$, choose $0\le {\theta }_n\le \overline{{\theta }_n}$ where   $\overline{{\theta }_n}$ = $\left\{\begin{array}{ccc}& min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\},\hfill & \mathrm{if}{x}_n\ne x_{n-1};\hfill \\ & \theta ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Step 2. Compute   $w_n=x_n+{\theta }_n(x_n-x_{n-1})$; $u_n=(1-{\alpha }_n)w_n+{\alpha }_{n}T((1-{\beta }_n)S{w}_n+{\beta }_n(1-{\mu }_{n}D)w_n)$.

Step 3. Compute $U=J_{\lambda }^F(I-\lambda f)$, $V=J_{\lambda }^G(I-\lambda g)$ and   $y_n=U(u_n+r_n\left(A^{\ast }(V-I)A{u}_n\right))$, where   $r_n$ = $\left\{\begin{array}{ccc}& {\displaystyle \frac{{\sigma }_n{\parallel (V-I)A{u}_n\parallel }^2}{\parallel A^{\ast }(V-I)A{u}_n{\parallel }^2},}\hfill & \mathrm{if}\parallel A^{\ast }(V-I)A{u}_n{\parallel }^2\ne 0;\hfill \\ & 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Step 4. Compute   $x_{n+1}=(1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n$.   Set $n=n+1$, and return to Step 1.

Lemma 7.

Assume that $H_1$ and $H_2$ are real Hilbert spaces and $A:H_1\to H_2$ is a bounded linear operator with its adjoint operator $A^{\ast }.$ Let $F:H_1\to 2^{H_1}$ and $G:H_2\to 2^{H_2}$ be set-valued maximal monotone operators. Let $f:H_1\to H_1$ and $g:H_2\to H_2$ be ${\kappa }_1,{\kappa }_2$-inverse strongly monotone mappings with $\kappa =min\{{\kappa }_1,{\kappa }_2\}$. Then, for any $x,y\in H$, $\lambda \in (0,2\kappa )$ and $L={\parallel A\parallel }^2$, the following statements hold:

(i)

$U=J_{\lambda }^F(I-\lambda f)$ and $V=J_{\lambda }^G(I-\lambda g)$ are nonexpansive;

(ii)

${\parallel Wx-Wy\parallel }^2\le {\parallel x-y\parallel }^2-r_n(1-r_{n}L){\parallel (V-I)Ax-(V-I)Ay\parallel }^2,$where $W=I+r_{n}A\ast (V-I)A$.

Proof.

(i) Since f and g are ${\kappa }_1,{\kappa }_2$-inverse strongly monotone mappings, respectively. From Lemma 1, we obtain that $U=J_{\lambda }^F(I-\lambda f)$ is averaged. So U is nonexpansive for $\lambda \in (0,2\kappa )$. Similarly, we can prove that $V=J_{\lambda }^G(I-\lambda g)$ is nonexpansive.

(ii) From $V=J_{\lambda }^G(I-\lambda g)$ is nonexpansive, we have

$$\begin{array}{ccc}\hfill {\parallel (I-V)Ax-(I-V)Ay\parallel }^2& =& ⟨(I-V)(Ax-Ay),(I-V)(Ax-Ay)⟩\hfill \\ & =& {\parallel (Ax-Ay)-(V\left(Ax\right)-V\left(Ay\right))\parallel }^2\hfill \\ & =& {\parallel Ax-Ay\parallel }^2-2⟨Ax-Ay,V\left(Ax\right)-V\left(Ay\right)⟩\hfill \\ & & +{\parallel V(Ax-Ay)\parallel }^2\hfill \\ & \le & {2\parallel Ax-Ay\parallel }^2-2⟨Ax-Ay,V\left(Ax\right)-V\left(Ay\right)⟩\hfill \\ & =& 2⟨Ax-Ay,(Ax-Ay)-\left(V\right(Ax-Ay\left)\right)⟩\hfill \\ & =& 2⟨Ax-Ay,(I-V)Ax-(I-V)Ay⟩.\hfill \end{array}$$

It follows that

$$\begin{array}{ccc}\hfill {\parallel Wx-Wy\parallel }^2& =& \parallel (I+r_n{A}^{\ast }(V-I)A)x-(I+r_n{A}^{\ast }(V-I)A){y\parallel }^2\hfill \\ & =& {\parallel x-y\parallel }^2-2r_n⟨x-y,A^{\ast }(I-V)Ax-A^{\ast }(I-V)Ay⟩\hfill \\ & & +r_n^2{\parallel A^{\ast }(I-V)Ax-A^{\ast }(I-V)Ay\parallel }^2\hfill \\ & \le & {\parallel x-y\parallel }^2-r_n{\parallel (I-V)Ax-(I-V)Ay\parallel }^2\hfill \\ & & +r_n^2{\parallel A\parallel }^2{\parallel (I-V)Ax-(I-V)Ay\parallel }^2\hfill \\ & =& {\parallel x-y\parallel }^2-r_n(1-r_{n}L){\parallel (V-I)Ax-(V-I)Ay\parallel }^2.\hfill \end{array}$$

□

Lemma 8.

The sequence $\left\{r_n\right\}$ formed by Algorithm 1, then $\left\{r_n\right\}$ is bounded.

Proof.

If $\parallel A^{\ast }(J_{\lambda }^G(I-\lambda g)-I)A{u}_n{\parallel }^2\ne 0$, then

$${\displaystyle inf\left\{\frac{1\parallel (J_{\lambda }^G(I-\lambda g)-I)A{u}_n{\parallel }^2}{\parallel A^{\ast }(J_{\lambda }^G(I-\lambda g)-I)A{u}_n{\parallel }^2}-r_n\right\}>0.}$$

From A is bounded and linear, we get

$$\begin{array}{ccc}\hfill \frac{{\sigma }_n{\parallel (J_{\lambda }^G(I-\lambda g)-I)A{u}_n\parallel }^2}{\parallel A^{\ast }(J_{\lambda }^G(I-\lambda g)-I)A{u}_n{\parallel }^2}& \ge & \frac{{\sigma }_n{\parallel (J_{\lambda }^G(I-\lambda g)-I)A{u}_n\parallel }^2}{{\parallel A\parallel }^2{\parallel (J_{\lambda }^G(I-\lambda g)-I)A{u}_n\parallel }^2}\hfill \\ & =& \frac{{\sigma }_n}{{\parallel A\parallel }^2}.\hfill \end{array}$$

(7)

Hence $sup{r}_n>\infty$, thus $\left\{r_n\right\}$ is bounded. □

Lemma 9.

Assume that $\left\{y_n\right\}$ and $\left\{u_n\right\}$ are formed by Algorithm 1. If $\left\{u_{n_k}\right\}$ converges weakly to z and ${\displaystyle \underset{k\to \infty }{lim}\parallel u_{n_k}-y_{n_k}\parallel =\underset{k\to \infty }{lim}\parallel (V-I)A{u}_{n_k}\parallel =0}$, then $z\in \Omega =\{x^{\ast }\in H_1:x^{\ast }\in \mathrm{Sol}(\mathrm{MVIP}(3\left)\right)\}\mathrm{and}A{x}^{\ast }\in \mathrm{Sol}(\mathrm{MVIP}\left(4\left)\right)\right\}$.

Proof.

Since U is nonexpansive, we get

$$\begin{array}{ccc}\hfill \parallel y_{n_k}-U{u}_{n_k}\parallel & =& \parallel U(u_{n_k}+r_{n_k}{A}^{\ast }(V-I)A{u}_{n_k})-U{u}_{n_k}\parallel \hfill \\ & \le & \parallel r_{n_k}\left(A^{\ast }(V-I)A{u}_{n_k}\right)\parallel \hfill \\ & =& r_{n_k}\parallel A\parallel \parallel (V-I)A{u}_{n_k}\parallel ,\hfill \end{array}$$

which together ${lim}_{k\to \infty }\parallel (V-I)A{u}_{n_k}\parallel =0$ gives that

$$\underset{k\to \infty }{lim}\parallel y_{n_k}-U{u}_{n_k}\parallel =0.$$

Since

$$\parallel u_{n_k}-U{u}_{n_k}\parallel =\parallel u_{n_k}-y_{n_k}\parallel +\parallel y_{n_k}-U{u}_{n_k}\parallel ,$$

we get

$$\underset{k\to \infty }{lim}\parallel u_{n_k}-U{u}_{n_k}\parallel =0.$$

This combines with Lemma 2 and $u_{n_k}\rightharpoonup z$ yields $z\in Fix\left(J_{\lambda }^F(I-\lambda f)\right)$. In view of the fact A is a linear operator, we get $A{u}_{n_k}\rightharpoonup Az$. From ${lim}_{k\to \infty }\parallel (V-I)A{u}_{n_k}\parallel =0$, we obtain $Az\in Fix\left(J_{\lambda }^G(I-\lambda g)\right)$. Therefore $z\in \Omega .$ □

Theorem 1.

Let $H_1$ and $H_2$ be are two real Hilbert spaces and C be a nonempty closed convex subset of $H_1$ and $A:H_1\to H_2$ be a bounded linear operator with its adjoint operator $A^{\ast }$. Assume that $F:H_1\to 2^{H_1}$ and $G:H_2\to 2^{H_2}$ are set-valued maximal monotone operators. Let $f:H_1\to H_1$ and $g:H_2\to H_2$ be are ${\kappa }_1,{\kappa }_2$-inverse strongly monotone mappings with $\kappa =min\{{\kappa }_1,{\kappa }_2\}$. Let $D:C\to C$ be η-strongly monotone and L-Lipschitzian, $T:C\to C$ be a nonexpansive mapping, $S:C\to C$ be a continuous quasi-nonexpansive mapping such that $I-S$ is monotone and $\Psi =\Phi \cap \Omega \cap \mathrm{Fix}\left(S\right)\ne \varnothing .$ Let $\left\{x_n\right\}$ be the sequence defined by Algorithm 1 and the Condition 1 holds. Then the sequence $\left\{x_n\right\}$ converges strongly to $x^{\ast }\in \Psi$ in the norm, where $\parallel x^{\ast }\parallel =min\{\parallel z\parallel :z\in \Omega \}.$

Proof.

This proof is divided the remaining proof into several steps.

Step 1. We will show that $\left\{x_n\right\}$ is bounded. Let us assume that $x^{\ast }\in \Psi$. From the definition of $w_n$, we get

$$\begin{array}{ccc}\hfill \parallel w_n-x^{\ast }\parallel & =& \parallel x_n+{\theta }_n(x_n-x_{n-1})-x^{\ast }\parallel \hfill \\ & \le & \parallel x_n-x^{\ast }\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \hfill \\ & =& \parallel x_n-x^{\ast }\parallel +{\tau }_n\frac{{\theta }_n}{{\tau }_n}\parallel x_n-x_{n-1}\parallel .\hfill \end{array}$$

(8)

According to Condition 1, one has $\frac{{\theta }_n}{{\tau }_n}\parallel x_n-x_{n-1}\parallel \to 0$. Therefore, there exists a constant $M_1>0$ such that

$$\frac{{\theta }_n}{{\tau }_n}\parallel x_n-x_{n-1}\parallel \le M_1,\forall n\ge 1.$$

(9)

Combining (8) and (9), we obtain

$$\parallel w_n-x^{\ast }\parallel \le \parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1,\forall n\ge 1.$$

(10)

Set $v_n=(1-{\beta }_n)S{w}_n+{\beta }_n{B}_n{w}_n$ and $B_n=I-{\mu }_{n}D$, we get

$$\begin{array}{ccc}\hfill \parallel u_n-x^{\ast }\parallel & =& \parallel (1-{\alpha }_n)w_n+{\alpha }_n\left(T{v}_n\right)-x^{\ast }\parallel \hfill \\ & =& \parallel (1-{\alpha }_n)(w_n-x^{\ast })+{\alpha }_n(T{v}_n-x^{\ast })\parallel \hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }\parallel +{\alpha }_n\parallel T{v}_n-x^{\ast }\parallel \hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }\parallel +{\alpha }_n\parallel v_n-x^{\ast }\parallel .\hfill \end{array}$$

(11)

From Lemma 4, we have

$$\begin{array}{ccc}\hfill \parallel v_n-x^{\ast }\parallel & =& \parallel (1-{\beta }_n)S{w}_n+{\beta }_n{B}_n{w}_n-x^{\ast }\parallel \hfill \\ & \le & (1-{\beta }_n)\parallel S{w}_n-x^{\ast }\parallel +{\beta }_n\parallel B_n{w}_n-x^{\ast }\parallel \hfill \\ & \le & (1-{\beta }_n)\parallel w_n-x^{\ast }\parallel +{\beta }_n\left(\parallel B_n{w}_n-B_n{x}^{\ast }\parallel +\parallel B_n{x}^{\ast }-x^{\ast }\parallel \right)\hfill \\ & \le & (1-{\beta }_n)\parallel w_n-x^{\ast }\parallel +{\beta }_n\left((1-{\mu }_n\rho )\parallel w_n-x^{\ast }\parallel +{\mu }_n\parallel D{x}^{\ast }\parallel \right)\hfill \\ & \le & \parallel w_n-x^{\ast }\parallel +{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel .\hfill \end{array}$$

(12)

From (11) and (12), we get

$$\begin{array}{ccc}\hfill \parallel u_n-x^{\ast }\parallel & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }\parallel +{\alpha }_n\parallel v_n-x^{\ast }\parallel \hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }\parallel +{\alpha }_n\left(\parallel w_n-x^{\ast }\parallel +{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \right)\hfill \\ & \le & \parallel w_n-x^{\ast }\parallel +{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel .\hfill \end{array}$$

(13)

Indeed, it follows Lemma 7, $A{x}^{\ast }=V\left(A{x}^{\ast }\right)$ and (7), we have

$$\begin{array}{ccc}\hfill \parallel y_n-x^{\ast }{\parallel }^2& \le & \parallel u_n-x^{\ast }{\parallel }^2-r_n(1-r_n{\parallel A\parallel }^2)\parallel (V-I)A{u}_n{\parallel }^2\hfill \\ & \le & \parallel u_n-x^{\ast }{\parallel }^2-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2.\hfill \end{array}$$

(14)

It follows from $\left\{{\sigma }_n\right\}\subset (0,1)$, we obtain

$$\parallel y_n-x^{\ast }\parallel \le \parallel u_n-x^{\ast }\parallel .$$

(15)

Combining (10), (13) and (15), we get

$$\begin{array}{c}\hfill \parallel y_n-x^{\ast }\parallel \le \parallel w_n-x^{\ast }\parallel +{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \le \parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel .\end{array}$$

Set $M_2={\tau }_n{M}_1+{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \ge 0$, it follows that

$$\begin{array}{c}\hfill \parallel y_n-x^{\ast }\parallel \le \parallel x_n-x^{\ast }\parallel +M_2.\end{array}$$

(16)

By the definition of $x_{n+1}$, we also have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }\parallel & =& \parallel (1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n-x^{\ast }\parallel \hfill \\ & =& \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast })+{\tau }_n{x}^{\ast }\parallel \hfill \\ & \le & \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast })\parallel +{\tau }_n\parallel x^{\ast }\parallel .\hfill \end{array}$$

(17)

Further, we have

$$\begin{array}{ccc}\hfill \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2& =& {(1-{\delta }_n-{\tau }_n)}^2\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n^2{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & & +2(1-{\delta }_n-{\tau }_n){\delta }_n⟨x_n-x^{\ast },y_n-x^{\ast }⟩\hfill \\ & \le & {(1-{\delta }_n-{\tau }_n)}^2\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n^2{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & & +(1-{\delta }_n-{\tau }_n){\delta }_n{\parallel x_n-x^{\ast }\parallel }^2\hfill \\ & & +(1-{\delta }_n-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & =& (1-{\delta }_n-{\tau }_n)(1-{\tau }_n){\parallel x_n-x^{\ast }\parallel }^2\hfill \\ & & +(1-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2.\hfill \end{array}$$

(18)

By (16) and Condition 1, we get

$$\begin{array}{ccc}\hfill & & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & \le & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n){\parallel x_n-x^{\ast }\parallel }^2+(1-{\tau }_n){\delta }_n{\left(\parallel x_n-x^{\ast }\parallel +M_2\right)}^2\hfill \\ & =& (1-{\delta }_n-{\tau }_n)(1-{\tau }_n){\parallel x_n-x^{\ast }\parallel }^2+(1-{\tau }_n){\delta }_n\left(\parallel x_n-x^{\ast }{\parallel }^2+2M_2\parallel x_n-x^{\ast }\parallel +M_2^2\right)\hfill \\ & =& {(1-{\tau }_n)}^2{\parallel x_n-x^{\ast }\parallel }^2+(1-{\tau }_n){\delta }_n\left(2M_2\parallel x_n-x^{\ast }\parallel +M_2^2\right)\hfill \\ & =& {(1-{\tau }_n)}^2\parallel x_n-x^{\ast }{\parallel }^2+2(1-{\tau }_n){\delta }_n{M}_2\parallel x_n-x^{\ast }\parallel +(1-{\tau }_n){\delta }_n{M}_2^2\hfill \\ & \le & {\left((1-{\tau }_n)\parallel x_n-x^{\ast }\parallel +M_2\right)}^2.\hfill \end{array}$$

(19)

Substituting (19) into (17), we obtain

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }\parallel & \le & \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast })\parallel +{\tau }_n\parallel x^{\ast }\parallel \hfill \\ & \le & (1-{\tau }_n)\parallel x_n-x^{\ast }\parallel +M_2+{\tau }_n\parallel x^{\ast }\parallel \hfill \\ & =& (1-{\tau }_n)\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel +{\tau }_n\parallel x^{\ast }\parallel \hfill \\ & =& (1-{\tau }_n)\parallel x_n-x^{\ast }\parallel +{\tau }_n(M_1+\parallel x^{\ast }\parallel )+{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel .\hfill \end{array}$$

From Lemma 5, this implies that $\left\{x_n\right\}$ is bounded. Together with (10), (13) and (16), we get $\left\{w_n\right\}$, $\left\{u_n\right\}$ and $\left\{y_n\right\}$ are also bounded.

Step 2. We will show that

$$\begin{array}{ccc}& & {\delta }_n(1-{\tau }_n)\left({\alpha }_n(1-{\alpha }_n)\parallel T{v}_n-w_n{\parallel }^2+{\delta }_n{r}_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2\right)\hfill \\ & & \le \parallel x_n-x^{\ast }{\parallel }^2-{\parallel x_{n+1}-x^{\ast }\parallel }^2+{\tau }_n{M}_5.\hfill \end{array}$$

By the definition of $w_n$, we get

$$\begin{array}{ccc}\hfill \parallel w_n-x^{\ast }{\parallel }^2& =& \parallel x_n+{\theta }_n(x_n-x_{n-1})-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (x_n-x^{\ast })+{\theta }_n(x_n-x_{n-1}){\parallel }^2\hfill \\ & =& \parallel x_n-x^{\ast }{\parallel }^2+{\theta }_n^2{\parallel x_n-x_{n-1}\parallel }^2+2{\theta }_n⟨x_n-x^{\ast },x_n-x_{n-1}⟩\hfill \\ & \le & \parallel x_n-x^{\ast }{\parallel }^2+{\theta }_n^2\parallel x_n-x_{n-1}{\parallel }^2+2{\theta }_n\parallel x_n-x^{\ast }\parallel \parallel x_n-x_{n-1}\parallel \hfill \\ & =& \parallel x_n-x^{\ast }{\parallel }^2+{\theta }_n\parallel x_n-x_{n-1}\parallel \left({\theta }_n\parallel x_n-x_{n-1}\parallel +2\parallel x_n-x^{\ast }\parallel \right)\hfill \\ & \le & \parallel x_n-x^{\ast }{\parallel }^2+{\tau }_n{M}_3,\hfill \end{array}$$

(20)

for some $M_3>0.$ From Lemma 3, we have

$$\begin{array}{ccc}\hfill \parallel u_n-x^{\ast }{\parallel }^2& =& \parallel (1-{\alpha }_n)w_n+{\alpha }_n\left(T{v}_n\right)-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\alpha }_n)(w_n-x^{\ast })+{\alpha }_n(T{v}_n-x^{\ast }){\parallel }^2\hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }{\parallel }^2+{\alpha }_n\parallel T{v}_n-x^{\ast }{\parallel }^2-{\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2\hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }{\parallel }^2+{\alpha }_n\parallel v_n-x^{\ast }{\parallel }^2-{\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2.\hfill \end{array}$$

(21)

From Lemma 3, Lemma 4 and (10), we obtain

$$\begin{array}{ccc}\hfill \parallel v_n-x^{\ast }{\parallel }^2& =& \parallel (1-{\beta }_n)S{w}_n+{\beta }_n{B}_n{w}_n-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\beta }_n)(S{w}_n-x^{\ast })+{\beta }_n(B_n{w}_n-x^{\ast }){\parallel }^2\hfill \\ & =& \parallel (1-{\beta }_n)(S{w}_n-x^{\ast })+{\beta }_n((1-{\mu }_{n}D)w_n-x^{\ast }){\parallel }^2\hfill \\ & =& \parallel (1-{\beta }_n)(S{w}_n-x^{\ast })+{\beta }_n\left((1-{\mu }_{n}D)(w_n-x^{\ast })-{\mu }_{n}D{x}^{\ast }\right){\parallel }^2\hfill \\ & \le & (1-{\beta }_n)\parallel S{w}_n-x^{\ast }{\parallel }^2+{\beta }_n{\parallel (1-{\mu }_{n}D)(w_n-x^{\ast })-{\mu }_{n}D{x}^{\ast }\parallel }^2\hfill \\ & & -(1-{\beta }_n){\beta }_n{\parallel S{w}_n-B_n{w}_n\parallel }^2\hfill \\ & \le & (1-{\beta }_n)\parallel S{w}_n-x^{\ast }{\parallel }^2+{\beta }_n({(1-{\mu }_{n}D)}^2{\parallel w_n-x^{\ast }\parallel }^2\hfill \\ & & -2⟨{\mu }_{n}D{x}^{\ast },(1-{\mu }_{n}D)(w_n-x^{\ast })-{\mu }_{n}D{x}^{\ast }⟩)\hfill \\ & \le & (1-{\beta }_n)\parallel w_n-x^{\ast }{\parallel }^2+{\beta }_n((1-{\mu }_n\rho ){\parallel w_n-x^{\ast }\parallel }^2\hfill \\ & & -2⟨{\mu }_{n}D{x}^{\ast },(1-{\mu }_{n}D)(w_n-x^{\ast })-{\mu }_{n}D{x}^{\ast }⟩)\hfill \\ & \le & \parallel w_n-x^{\ast }{\parallel }^2+2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x^{\ast }-w_n\parallel +{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & \le & \parallel w_n-x^{\ast }{\parallel }^2+2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right).\hfill \end{array}$$

(22)

Substituting (20) and (22) into (21), we get

$$\begin{array}{ccc}\hfill \parallel u_n-x^{\ast }{\parallel }^2& \le & (1-{\alpha }_n)\parallel w_n-x^{\ast }{\parallel }^2+{\alpha }_n(\parallel w_n-x^{\ast }{\parallel }^2+2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel \hfill \\ & & +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \left)\right)-{\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2\hfill \\ & \le & \parallel w_n-x^{\ast }{\parallel }^2+2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & -{\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2.\hfill \end{array}$$

(23)

From (14) and (23), it follows that

$$\begin{array}{ccc}\hfill \parallel y_n-x^{\ast }{\parallel }^2& \le & \parallel u_n-x^{\ast }{\parallel }^2-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2\hfill \\ & \le & \parallel w_n-x^{\ast }{\parallel }^2+2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & -{\alpha }_n(1-{\alpha }_n)\parallel T{v}_n-w_n{\parallel }^2-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2.\hfill \end{array}$$

(24)

By the definition of $x_{n+1}$, we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& =& \parallel (1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast })-{\tau }_n{x}^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2+{\tau }_n^2{\parallel x^{\ast }\parallel }^2\hfill \\ & & -{\tau }_n⟨(1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }),x^{\ast }⟩\hfill \\ & \le & \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2+{\tau }_n{M}_4,\hfill \end{array}$$

(25)

for some $M_4>0$. Substituting (18), (24) and using Condition 1 into (25), we obtain

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& \le & \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2+{\tau }_n{M}_4\hfill \\ & \le & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2+{\tau }_n{M}_4\hfill \\ & \le & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\parallel x_n-x^{\ast }\parallel }^2+{\tau }_n{M}_3\hfill \\ & & +2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & -{\alpha }_n(1-{\alpha }_n)\parallel T{v}_n-w_n{\parallel }^2-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2)+{\tau }_n{M}_4\hfill \\ & \le & (1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\tau }_n{M}_3+2{\tau }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel \hfill \\ & & +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel )-{\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2\hfill \\ & & -r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2)+{\tau }_n{M}_4\hfill \\ & \le & \parallel x_n-x^{\ast }{\parallel }^2+{\tau }_n{M}_5-{\delta }_n(1-{\tau }_n)({\alpha }_n(1-{\alpha }_n){\parallel T{v}_n-w_n\parallel }^2\hfill \\ & & -r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2),\hfill \end{array}$$

(26)

for some $M_5>0$. Thus

$$\begin{array}{ccc}& & {\delta }_n(1-{\tau }_n)\left({\alpha }_n(1-{\alpha }_n)\parallel T{v}_n-w_n{\parallel }^2+{\delta }_n{r}_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2\right)\hfill \\ & & \le \parallel x_n-x^{\ast }{\parallel }^2-{\parallel x_{n+1}-x^{\ast }\parallel }^2+{\tau }_n{M}_5.\hfill \end{array}$$

Step 3. We will show that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& =& (1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\tau }_n({\delta }_n{M}_3+2{\delta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel \hfill \\ & & +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel )+2{\delta }_n\parallel y_n-x_n\parallel \parallel x^{\ast }-x_{n+1}\parallel +2⟨x^{\ast },x^{\ast }-x_{n+1}⟩).\hfill \end{array}$$

From the definition of $x_{n+1}$, we get

$$\begin{array}{ccc}\hfill x_{n+1}& =& (1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n\hfill \\ & =& (1-{\delta }_n)x_n+{\delta }_n{y}_n-{\tau }_n{x}_n.\hfill \end{array}$$

Let $t_n=(1-{\delta }_n)x_n+{\delta }_n{y}_n$. Then we have $x_n-t_n={\delta }_n(y_n-x_n)$ and

$$\begin{array}{ccc}\hfill \parallel t_n-x^{\ast }{\parallel }^2& =& \parallel (1-{\delta }_n)x_n+{\delta }_n{y}_n-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\delta }_n)(x_n-x^{\ast })+{\delta }_n{(y_n-x^{\ast }\parallel }^2\hfill \\ & \le & (1-{\delta }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n\parallel y_n-x^{\ast }{\parallel }^2-{\delta }_n(1-{\delta }_n){\parallel x_n-y_n\parallel }^2\hfill \\ & \le & (1-{\delta }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n{\parallel y_n-x^{\ast }\parallel }^2.\hfill \end{array}$$

(27)

From the definition of $t_n$, we obtain

$$\begin{array}{ccc}\hfill x_{n+1}& =& t_n-{\tau }_n{x}_n\hfill \\ & =& (1-{\tau }_n)t_n-{\tau }_n(x_n-t_n)\hfill \\ & =& (1-{\tau }_n)t_n-{\tau }_n{\delta }_n(y_n-x_n).\hfill \end{array}$$

(28)

This implies that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& =& \parallel (1-{\tau }_n)t_n-{\tau }_n{\delta }_n(y_n-x_n)-x_{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\tau }_n)(t_n-x^{\ast })-{\tau }_n({\delta }_n(y_n-x_n)-x^{\ast }){\parallel }^2\hfill \\ & \le & (1-{\tau }_n){\parallel t_n-x^{\ast }\parallel }^2+2⟨{\tau }_n{\delta }_n(y_n-x_n)+{\tau }_n{x}^{\ast },x^{\ast }-x_{n+1}⟩\hfill \\ & \le & (1-{\tau }_n){\parallel t_n-x^{\ast }\parallel }^2+2{\tau }_n{\delta }_n⟨y_n-x_n,x^{\ast }-x_{n+1}⟩+2{\tau }_n⟨x^{\ast },x^{\ast }-x_{n+1}⟩\hfill \\ & \le & (1-{\tau }_n)\parallel t_n-x^{\ast }{\parallel }^2+2{\tau }_n{\delta }_n\parallel y_n-x_n\parallel \parallel x^{\ast }-x_{n+1}\parallel +2{\tau }_n⟨x^{\ast },x^{\ast }-x_{n+1}⟩.\hfill \end{array}$$

(29)

From (20), (24), (27) and (29), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& \le & (1-{\tau }_n)\left((1-{\delta }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n{\parallel y_n-x^{\ast }\parallel }^2\right)\hfill \\ & & +2{\tau }_n{\delta }_n\parallel y_n-x_n\parallel \parallel x^{\ast }-x_{n+1}\parallel +2{\tau }_n⟨x^{\ast },x^{\ast }-x_{n+1}⟩\hfill \\ & \le & (1-{\tau }_n)((1-{\delta }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\delta }_n({\parallel x_n-x^{\ast }\parallel }^2+{\tau }_n{M}_3\hfill \\ & & +2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & -{\alpha }_n(1-{\alpha }_n)\parallel T{v}_n-w_n{\parallel }^2-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2\left)\right)\hfill \\ & & +2{\tau }_n{\delta }_n\parallel y_n-x_n\parallel \parallel x^{\ast }-x_{n+1}\parallel +2{\tau }_n⟨x^{\ast },x^{\ast }-x_{n+1}⟩\hfill \\ & \le & (1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+{\tau }_n({\delta }_n{M}_3+2{\delta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1\hfill \\ & & +{\mu }_n\parallel D{w}_n\parallel \left)\right)+2{\delta }_n\parallel y_n-x_n\parallel \parallel x^{\ast }-x_{n+1}\parallel +2⟨x^{\ast },x^{\ast }-x_{n+1}⟩.\hfill \end{array}$$

(30)

Step 4. We will show $x^{\ast }\in \Psi$. Assume that $\{\parallel x_{n_k}-x^{\ast }\parallel \}$ is a subsequence of $\{\parallel x_n-x^{\ast }\parallel \}$ such that

$$\underset{k\to \infty }{lim\; inf}\left(\parallel x_{n_k+1}-x^{\ast }\parallel -\parallel x_{n_k}-x^{\ast }\parallel \right)\ge 0.$$

Then,

$$\begin{array}{ccc}& & \underset{k\to \infty }{lim\; inf}\left(\parallel x_{n_k+1}-x^{\ast }{\parallel }^2-{\parallel x_{n_k}-x^{\ast }\parallel }^2\right)\hfill \\ & & =\underset{k\to \infty }{lim\; inf}\left(\parallel x_{n_k+1}-x^{\ast }\parallel -\parallel x_{n_k}-x^{\ast }\parallel \right)\left(\parallel x_{n_{k+1}}-x^{\ast }\parallel +\parallel x_{n_k}-x^{\ast }\parallel \right)\ge 0.\hfill \end{array}$$

From Step 2, we see that

$$\begin{array}{ccc}& & {\delta }_{n_k}{\alpha }_{n_k}(1-{\alpha }_{n_k})\parallel T{v}_{n_k}-w_{n_k}{\parallel }^2+{\delta }_{n_k}{r}_{n_k}(1-{\sigma }_{n_k}){\parallel (V-I)A{u}_{n_k}\parallel }^2\hfill \\ & & \le \underset{k\to \infty }{lim\; sup}\left(\parallel x_{n_k}-x^{\ast }{\parallel }^2-{\parallel x_{n_k+1}-x^{\ast }\parallel }^2+{\tau }_{n_k}{M}_5\right)\hfill \\ & & \le \underset{k\to \infty }{lim\; sup}\left(\parallel x_{n_k}-x^{\ast }{\parallel }^2-{\parallel x_{n_k+1}-x^{\ast }\parallel }^2\right)+\underset{k\to \infty }{lim\; sup}{\tau }_{n_k}{M}_5\hfill \\ & & \le 0,\hfill \end{array}$$

which indicates that

$$\underset{k\to \infty }{lim}\parallel T{v}_{n_k}-w_{n_k}\parallel =0\mathrm{and}\underset{k\to \infty }{lim}\parallel (V-I)A{u}_{n_k}\parallel =0.$$

(31)

From the definition of $u_n$, we get

$$\parallel u_{n_k}-w_{n_k}\parallel ={\alpha }_{n_k}\parallel T{v}_{n_k}-w_{n_k}\parallel .$$

Thus

$$\underset{k\to \infty }{lim}\parallel u_{n_k}-w_{n_k}\parallel =0.$$

(32)

From $w_{n_k}-x_{n_k}={\theta }_{n_k}(x_{n_k}-x_{n_k-1})$, we have

$$\begin{array}{ccc}\hfill \parallel u_{n_k}-x_n\parallel & \le & \parallel u_{n_k}-w_{n_k}\parallel +\parallel w_{n_k}-x_{n_k}\parallel \hfill \\ & =& \parallel u_{n_k}-w_{n_k}\parallel +{\theta }_{n_k}\parallel x_{n_k}-x_{n_{k-1}}\parallel \hfill \\ & =& \parallel u_{n_k}-w_{n_k}\parallel +{\tau }_{n_k}\frac{{\theta }_{n_k}}{{\tau }_{n_k}}\parallel x_{n_k}-x_{n_{k-1}}\parallel .\hfill \end{array}$$

So

$$\underset{k\to \infty }{lim}\parallel u_{n_k}-x_{n_k}\parallel =0.$$

(33)

Since T is nonexpansive, S is a continuous quasi-nonexpansive mapping, we have

$$\begin{array}{ccc}\hfill \parallel T{v}_{n_k}-x^{\ast }{\parallel }^2& \le & \parallel v_{n_k}-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel ((1-{\beta }_{n_k})S{w}_{n_k}+{\beta }_{n_k}{B}_{n_k}{w}_{n_k})-x^{\ast }{\parallel }^2\hfill \\ & =& \parallel (1-{\beta }_{n_k})(S{w}_{n_k}-x^{\ast })+{\beta }_{n_k}(w_{n_k}-x^{\ast })-{\beta }_{n_k}{\mu }_{n_k}D{w}_{n_k}{\parallel }^2\hfill \\ & \le & \parallel (1-{\beta }_{n_k})(S{w}_{n_k}-x^{\ast })+{\beta }_{n_k}(w_{n_k}-x^{\ast }){\parallel }^2-2{\beta }_{n_k}{\mu }_{n_k}⟨D{w}_{n_k},v_{n_k}-x^{\ast }⟩\hfill \\ & \le & (1-{\beta }_{n_k})\parallel S{w}_{n_k}-x^{\ast }{\parallel }^2+{\beta }_{n_k}\parallel w_{n_k}-x^{\ast }{\parallel }^2-{\beta }_{n_k}(1-{\beta }_{n_k}){\parallel S{w}_{n_k}-w_{n_k}\parallel }^2\hfill \\ & & -2{\beta }_{n_k}{\mu }_{n_k}⟨D{w}_{n_k},v_{n_k}-x^{\ast }⟩\hfill \\ & \le & \parallel w_{n_k}-x^{\ast }{\parallel }^2-{\beta }_{n_k}(1-{\beta }_{n_k}){\parallel S{w}_{n_k}-w_{n_k}\parallel }^2-2{\beta }_{n_k}{\mu }_{n_k}⟨D{w}_{n_k},v_{n_k}-x⟩.\hfill \end{array}$$

(34)

So

$$\begin{array}{ccc}\hfill {\beta }_{n_k}(1-{\beta }_{n_k}){\parallel S{w}_{n_k}-w_{n_k}\parallel }^2& \le & \parallel w_{n_k}-x^{\ast }{\parallel }^2-{\parallel T{v}_{n_k}-x^{\ast }\parallel }^2-2{\beta }_{n_k}{\mu }_{n_k}⟨D{w}_{n_k},v_{n_k}-x^{\ast }⟩\hfill \\ & \le & \parallel w_{n_k}-T{v}_{n_k}\parallel (\parallel w_{n_k}-x^{\ast }\parallel -\parallel T{v}_{n_k}-x^{\ast }\parallel )\hfill \\ & & -2{\beta }_{n_k}{\mu }_{n_k}⟨D{w}_{n_k},v_{n_k}-x^{\ast }⟩.\hfill \end{array}$$

Thus

$$\underset{k\to \infty }{lim}\parallel S{w}_{n_k}-w_{n_k}\parallel =0.$$

(35)

Note that

$$\begin{array}{ccc}\hfill \parallel w_{n_k}-v_{n_k}\parallel & =& \parallel w_{n_k}-\left((1-{\beta }_{n_k})S{w}_{n_k}+{\beta }_{n_k}(1-{\mu }_{n_k}D)w_{n_k}\right)\parallel \hfill \\ & =& \parallel (1-{\beta }_{n_k})(S{w}_{n_k}-w_{n_k})+{\beta }_{n_k}{\mu }_{n_k}D{w}_{n_k}\parallel \hfill \\ & \le & (1-{\beta }_{n_k})\parallel S{w}_{n_k}-w_{n_k}\parallel +{\beta }_{n_k}{\mu }_{n_k}\parallel D{w}_{n_k}\parallel .\hfill \end{array}$$

(36)

From (35) and Condition 1, we get

$$\underset{k\to \infty }{lim}\parallel w_{n_k}-v_{n_k}\parallel =0.$$

(37)

By the definition of $u_n$, we have

$$\begin{array}{ccc}\hfill \parallel v_{n_k}-T{v}_{n_k}\parallel & =& \parallel v_{n_k}-w_{n_k}\parallel +\parallel w_{n_k}-u_{n_k}\parallel +\parallel u_{n_k}-T{v}_{n_k}\parallel \hfill \\ & =& \parallel v_{n_k}-w_{n_k}\parallel +\parallel w_{n_k}-u_{n_k}\parallel +(1-{\alpha }_{n_k})\parallel w_{n_k}-T{v}_{n_k}\parallel \hfill \\ & =& \parallel v_{n_k}-w_{n_k}\parallel +{\alpha }_{n_k}\parallel w_{n_k}-T{v}_{n_k}\parallel +(1-{\alpha }_{n_k})\parallel w_{n_k}-T{v}_{n_k}\parallel \hfill \\ & =& \parallel v_{n_k}-w_{n_k}\parallel +\parallel w_{n_k}-T{v}_{n_k}\parallel .\hfill \end{array}$$

From (31) and (37), we obtain

$$\underset{k\to \infty }{lim}\parallel v_{n_k}-T{v}_{n_k}\parallel =0.$$

(38)

Since $w_n=x_n+{\theta }_n(x_n-x_{n-1})$, we have $w_n-x_n={\theta }_n(x_n-x_{n-1})$. It follows that

$$\parallel w_n-x_n\parallel ={\tau }_n\frac{{\theta }_n}{{\tau }_n}\parallel x_n-x_{n-1}\parallel .$$

So

$$\underset{k\to \infty }{lim}\parallel w_{n_k}-x_{n_k}\parallel =0.$$

(39)

Set $q_n=u_n+r_n{A}^{\ast }(V-I)A{u}_n$. Now we estimate

$$\begin{array}{ccc}\hfill \parallel q_{n_k}-x_{n_k}\parallel & =& \parallel u_{n_k}+r_{n_k}{A}^{\ast }(V-I)A{u}_{n_k}-x_{n_k}\parallel \hfill \\ & \le & \parallel u_{n_k}-x_{n_k}\parallel +r_{n_k}\parallel A\parallel \parallel (V-I)A{u}_{n_k}\parallel .\hfill \end{array}$$

From (31) and (33), we get

$$\underset{k\to \infty }{lim}\parallel q_{n_k}-x_{n_k}\parallel =0.$$

(40)

Since

$$\parallel u_{n_k}-q_{n_k}\parallel \le \parallel u_{n_k}-x_{n_k}\parallel +\parallel x_{n_k}-q_{n_k}\parallel ,$$

by (33) and (40), we have

$$\underset{k\to \infty }{lim}\parallel u_{n_k}-q_{n_k}\parallel =0.$$

(41)

By the definition of $y_n$ and Lemma 7, we get

$$\begin{array}{ccc}\hfill \parallel y_{n_k}-x^{\ast }{\parallel }^2& =& \parallel J_{\lambda }^F(I-\lambda f)q_{n_k}-J_{\lambda }^F(I-\lambda f)x^{\ast }{\parallel }^2\hfill \\ & \le & \parallel (q_{n_k}-x^{\ast })-\lambda (f{q}_n-f{x}^{\ast }){\parallel }^2\hfill \\ & =& \parallel q_{n_k}-x^{\ast }{\parallel }^2+{\lambda }^2{\parallel f{q}_n-f{x}^{\ast }\parallel }^2-2\lambda ⟨q_n-x^{\ast },f{q}_n-f{x}^{\ast }⟩\hfill \\ & \le & \parallel q_{n_k}-x^{\ast }{\parallel }^2+{\lambda }^2\parallel f{q}_n-f{x}^{\ast }{\parallel }^2-2{\kappa }_1\lambda \parallel f{q}_n-f{x}^{\ast }\parallel \hfill \\ & =& \parallel q_{n_k}-x^{\ast }{\parallel }^2-\lambda (2{\kappa }_1-\lambda )\parallel f{q}_n-f{x}^{\ast }\parallel .\hfill \end{array}$$

(42)

By the definition of $x_{n+1}$ and (21), (22), (25), (42), we have

$$\begin{array}{ccc}& & \parallel x_{n+1}-x^{\ast }{\parallel }^2\hfill \\ & & \le \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2+{\tau }_n{M}_4\hfill \\ & & \le (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2+{\tau }_n{M}_4\hfill \\ & & \le (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\parallel x_n-x^{\ast }\parallel }^2+{\tau }_n{M}_3\hfill \\ & & +{\alpha }_n\left(2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\right)-r_n(1-{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2\hfill \\ & & -\lambda (2{\kappa }_1-\lambda )\parallel f{q}_n-f{x}^{\ast }\parallel )+{\tau }_n{M}_4\hfill \\ & & \le (1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\tau }_n{M}_3+{\alpha }_n(2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1\hfill \\ & & +{\mu }_n\parallel D{w}_n\parallel \left)\right)-r_n(1-{\sigma }_n)\parallel (V-I)A{u}_n{\parallel }^2-\lambda (2{\kappa }_1-\lambda )\parallel f{q}_n-f{x}^{\ast }\parallel )+{\tau }_n{M}_4.\hfill \end{array}$$

(43)

Thus

$$\begin{array}{ccc}\hfill (1-{\tau }_n){\delta }_n\lambda (2{\kappa }_1-\lambda )\parallel f{q}_n-f{x}^{\ast }\parallel & \le & \parallel x_n-x^{\ast }{\parallel }^2-{\parallel x_{n+1}-x^{\ast }\parallel }^2+(1-{\tau }_n){\delta }_n({\tau }_n{M}_3\hfill \\ & & +{\alpha }_n(2{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & -r_n(1-r_n{\sigma }_n){\parallel (V-I)A{u}_n\parallel }^2)+{\tau }_n{M}_4.\hfill \end{array}$$

(44)

Substituting n into $n_k$, from the boundness of $\left\{x_n\right\}$, Condition 1, (31), and taking $k\to \infty$, we get

$$\underset{k\to \infty }{lim}\parallel f{q}_{n_k}-f{x}^{\ast }\parallel =0.$$

(45)

Since $J_{\lambda }^F$ is firmly nonexpansive, we obtain

$$\begin{array}{ccc}\hfill \parallel y_n-x^{\ast }{\parallel }^2& =& \parallel J_{\lambda }^F(I-\lambda f)q_n-J_{\lambda }^F(I-\lambda f)x^{\ast }\parallel \hfill \\ & \le & ⟨(I-\lambda f)q_n-(I-\lambda f)x^{\ast },y_n-x^{\ast }⟩\hfill \\ & =& \frac{1}{2}\left(\parallel (I-\lambda f)q_n-(I-\lambda f)x^{\ast }{\parallel }^2+\parallel y_n-x^{\ast }{\parallel }^2-{\parallel q_n-y_n-\lambda (f{q}_n-f{x}^{\ast })\parallel }^2\right)\hfill \\ & =& \frac{1}{2}(\parallel q_n-x^{\ast }{\parallel }^2+{\lambda }^2\parallel f{q}_n-f{x}^{\ast }{\parallel }^2-2\lambda ⟨q_n-x^{\ast },f{q}_n-f{x}^{\ast }⟩+{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & & -\parallel q_n-y_n-\lambda (f{q}_n-f{x}^{\ast }){\parallel }^2)\hfill \\ & =& \frac{1}{2}(\parallel q_n-x^{\ast }{\parallel }^2+{\lambda }^2\parallel f{q}_n-f{x}^{\ast }{\parallel }^2-2\lambda ⟨q_n-x^{\ast },f{q}_n-f{x}^{\ast }⟩+{\parallel y_n-x^{\ast }\parallel }^2\hfill \\ & & -\left(\parallel q_n-y_n{\parallel }^2+\lambda {\parallel f{q}_n-f{x}^{\ast }\parallel }^2-2\lambda ⟨q_n-y_n,f{q}_n-f{x}^{\ast }⟩\right))\hfill \\ & \le & \frac{1}{2}\left(\parallel q_n-x^{\ast }{\parallel }^2+2\lambda \parallel x^{\ast }-y_n\parallel \parallel f{q}_n-f{x}^{\ast }\parallel +\parallel y_n-x^{\ast }{\parallel }^2-{\parallel q_n-y_n\parallel }^2\right).\hfill \end{array}$$

So

$$\begin{array}{c}\hfill \parallel y_n-x^{\ast }{\parallel }^2\le \parallel q_n-x^{\ast }{\parallel }^2+2\lambda \parallel x^{\ast }-y_n\parallel \parallel f{q}_n-f{x}^{\ast }\parallel -\parallel q_n-y_n{\parallel }^2.\end{array}$$

(46)

From (23), (25) and (46), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{\ast }{\parallel }^2& \le & \parallel (1-{\delta }_n-{\tau }_n)(x_n-x^{\ast })+{\delta }_n(y_n-x^{\ast }){\parallel }^2+{\tau }_n{M}_4\hfill \\ & \le & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n{\parallel y_n-x^{\ast }\parallel }^2+{\tau }_n{M}_4\hfill \\ & \le & (1-{\delta }_n-{\tau }_n)(1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\parallel x_n-x^{\ast }\parallel }^2+{\tau }_n{M}_3\hfill \\ & & +2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel \left(\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel \right)\hfill \\ & & +2\lambda \parallel x^{\ast }-y_n\parallel \parallel f{q}_n-f{x}^{\ast }\parallel -\parallel q_n-y_n{\parallel }^2)+{\tau }_n{M}_4\hfill \\ & \le & (1-{\tau }_n)\parallel x_n-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\tau }_n{M}_3+2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel \hfill \\ & & +{\tau }_n{M}_1+{\mu }_n\parallel D{w}_n\parallel )+2\lambda \parallel x^{\ast }-y_n\parallel \parallel f{q}_n-f{x}^{\ast }\parallel -\parallel q_n-y_n{\parallel }^2)+{\tau }_n{M}_4.\hfill \end{array}$$

(47)

Therefore

$$\begin{array}{ccc}& & (1-{\tau }_n){\delta }_n{\parallel q_n-y_n\parallel }^2\hfill \\ & & \le \parallel x_n-x^{\ast }{\parallel }^2-\parallel x_{n+1}-x^{\ast }{\parallel }^2+(1-{\tau }_n){\delta }_n({\tau }_n{M}_3+2{\alpha }_n{\beta }_n{\mu }_n\parallel D{x}^{\ast }\parallel (\parallel x_n-x^{\ast }\parallel +{\tau }_n{M}_1\hfill \\ & & +{\mu }_n\parallel D{w}_n\parallel )+2\lambda \parallel x^{\ast }-y_n\parallel \parallel f{q}_n-f{x}^{\ast }\parallel -\parallel q_n-y_n{\parallel }^2)+{\tau }_n{M}_4.\hfill \end{array}$$

Substituting n into $n_k$, from the boundness of $\left\{x_n\right\}$, Condition 1, (45) and taking limit $k\to \infty$, we get

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel q_{n_k}-y_{n_k}\parallel =0.\end{array}$$

(48)

Since

$$\parallel y_{n_k}-u_{n_k}\parallel \le \parallel y_{n_k}-q_{n_k}\parallel +\parallel q_{n_k}-u_{n_k}\parallel ,$$

it follows from (41) and (48), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel y_{n_k}-u_{n_k}\parallel =0.\end{array}$$

(49)

Since

$$\begin{array}{c}\hfill \parallel x_{n_k}-y_{n_k}\parallel =\parallel x_{n_k}-q_{n_k}\parallel +\parallel q_{n_k}-y_{n_k}\parallel ,\end{array}$$

we have

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel x_{n_k}-y_{n_k}\parallel =0.\end{array}$$

(50)

By the definition of $x_{n+1}$, we get

$$\begin{array}{c}\hfill \parallel x_{n_{k+1}}-x_{n_k}\parallel ={\delta }_{n_k}\parallel y_{n_k}-x_{n_k}\parallel -{\tau }_{n_k}{x}_{n_k}.\end{array}$$

(51)

Using (50) and Condition 1, we have

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel x_{n_{k+1}}-x_{n_k}\parallel =0.\end{array}$$

(52)

Note that

$$\begin{array}{ccc}\hfill \parallel x_{n_k}-T{x}_{n_k}\parallel & =& \parallel x_{n_k}-v_{n_k}\parallel +\parallel v_{n_k}-T{v}_{n_k}\parallel +\parallel T{v}_{n_k}-T{x}_{n_k}\parallel \hfill \\ & \le & 2\parallel x_{n_k}-v_{n_k}\parallel +\parallel v_{n_k}-T{v}_{n_k}\parallel .\hfill \end{array}$$

Since $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_k}\right\}$ which converges weakly to $x^{\ast }$. Assume that $x^{\ast }\ne T{x}^{\ast }$, by Opial property

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-x^{\ast }\parallel & <& \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-T{x}^{\ast }\parallel \hfill \\ & \le & \underset{k\to \infty }{lim\; inf}\left(\parallel x_{n_k}-T{x}_{n_k}\parallel +\parallel T{x}_{n_k}-T{x}^{\ast }\parallel \right)\hfill \\ & \le & \underset{k\to \infty }{lim\; inf}\left(2\parallel x_{n_k}-v_{n_k}\parallel +\parallel v_{n_k}-T{v}_{n_k}\parallel +\parallel x_{n_k}-x^{\ast }\parallel \right)\hfill \\ & =& \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-x^{\ast }\parallel .\hfill \end{array}$$

This is a contradiction. Hence $x^{\ast }=T{x}^{\ast }$ and $x^{\ast }\in Fix\left(T\right)$. On the other hand, we note that $u_n=(1-{\alpha }_n)w_n+{\alpha }_{n}T{v}_n$ and

$$\begin{array}{ccc}\hfill w_n-T{v}_n& =& (w_n-v_n)+(v_n-T{v}_n)\hfill \\ & =& ((1-{\beta }_n)(w_n-S{w}_n)-{\beta }_n{\mu }_{n}D{w}_n)+(v_n-T{v}_n).\hfill \end{array}$$

Setting

$$\begin{array}{ccc}\hfill {\phi }_n=\frac{w_n-u_n}{{\alpha }_n(1-{\beta }_n)}& =& (w_n-S{w}_n)-\frac{{\beta }_n}{(1-{\beta }_n)}{\mu }_{n}D{w}_n+\frac{1}{(1-{\beta }_n)}(v_n-T{v}_n).\hfill \end{array}$$

In particular, for each $z\in Fix\left(T\right)$, we have

$$\begin{array}{ccc}\hfill ⟨{\phi }_n,w_n-z⟩& =& ⟨(I-S)w_n-\frac{{\beta }_n}{(1-{\beta }_n)}{\mu }_{n}D{w}_n+\frac{1}{(1-{\beta }_n)}(I-T)v_n,w_n-z⟩\hfill \\ & =& ⟨(I-S)w_n-(I-S)z,w_n-z⟩+⟨(I-S)z,w_n-z⟩\hfill \\ & & -\frac{{\beta }_n}{(1-{\beta }_n)}{\mu }_n⟨D{w}_n,w_n-z⟩+\frac{1}{(1-{\beta }_n)}⟨(I-T)v_n,w_n-z⟩\hfill \\ & =& ⟨(I-S)w_n-(I-S)z,w_n-z⟩+⟨(I-S)z,w_n-z⟩\hfill \\ & & -\frac{{\beta }_n}{(1-{\beta }_n)}{\mu }_n⟨D{w}_n,w_n-z⟩+\frac{1}{(1-{\beta }_n)}⟨(I-T)v_n,w_n-v_n⟩\hfill \\ & & +\frac{1}{(1-{\beta }_n)}⟨(I-T)v_n,v_n-z⟩,\hfill \end{array}$$

which comes from the monotonicity of $I-S$ and $I-T,$

$$\begin{array}{c}\hfill ⟨{\phi }_n,w_n-z⟩\ge ⟨(I-S)z,w_n-z⟩+\frac{1}{(1-{\beta }_n)}⟨(I-T)v_n,w_n-v_n⟩-\frac{{\beta }_n}{(1-{\beta }_n)}{\mu }_n⟨D{w}_n,w_n-z⟩.\end{array}$$

Replacing n with $n_k$, we have

$$\begin{array}{ccc}\hfill & & ⟨{\phi }_{n_k},w_{n_k}-z⟩\hfill \\ & & \ge ⟨(I-S)z,w_{n_k}-z⟩+\frac{1}{(1-{\beta }_{n_k})}⟨(I-T)v_{n_k},w_{n_k}-v_{n_k}⟩-\frac{{\beta }_{n_k}}{(1-{\beta }_{n_k})}{\mu }_{n_k}⟨D{w}_{n_k},w_{n_k}-z⟩.\hfill \end{array}$$

(53)

Moreover, by (32) and Condition 1, we get

$$\underset{k\to \infty }{lim}{\phi }_{n_k}=\underset{k\to \infty }{lim}\frac{w_{n_k}-u_{n_k}}{{\alpha }_{n_k}(1-{\beta }_{n_k})}=0.$$

Since $\parallel x_{n_k}-w_{n_k}\parallel \to 0$, one has $w_{n_k}\rightharpoonup x^{\ast }$. Taking limit on both sides of (53) for $k\to \infty$, it follows from (37) and (38) that

$$⟨(I-S)z,x^{\ast }-z⟩\le 0,\forall z\in Fix\left(T\right).$$

If z is substituted by $tz+(1-t)x^{\ast }$ for $t\in (0,1)$, we get

$$⟨(I-S)(tz+(1-t)x^{\ast }),x^{\ast }-z⟩\le 0,\forall z\in Fix\left(T\right).$$

Since $(I-S)$ is continuous, on taking limit $t\to 0^{+}$, we have

$$⟨(I-S)x^{\ast },x^{\ast }-z⟩\le 0,\forall z\in Fix\left(T\right).$$

That is $x^{\ast }\in \Phi$. Next we will show that $x^{\ast }\in \Omega .$

Note that $y_{n_k}=U(u_{n_k}+r_{n_k}\left(A^{\ast }(V-I)A{u}_{n_k}\right))$ can be rewritten as

$$\begin{array}{c}\hfill \frac{y_{n_k}-u_{n_k}+r_{n_k}(A^{\ast }(V-I)A{u}_{n_k}}{\lambda }\in f\left(W{u}_{n_k}\right)-F\left(y_{n_k}\right),\end{array}$$

(54)

where $W=I+r_n{A}^{\ast }(I-V)A$ is nonexpansive for Lemma 7. Taking $k\to \infty$ in (54) by (31), (49) and the graph of maximal monotone mapping is weakly strongly closed, we obtain $0\in f\left(x^{\ast }\right)+F\left(x^{\ast }\right)$. Moreover, since $\left\{x_n\right\}$ and $\left\{u_n\right\}$ have the same asymptotical behavior, we have $A{u}_{n_k}\to A{x}^{\ast }$. Since the resolvent operator $V=J_{\lambda }^G(I-\lambda g)$ is average and hence nonexpansive, we can obtain

$$0\in g\left(A{x}^{\ast }\right)+G\left(A{x}^{\ast }\right).$$

This shows that $x^{\ast }\in \Omega$ and so $x^{\ast }\in \Psi$.

Step 5. We will show that $x_n\to x^{\ast }$ where $\parallel x^{\ast }\parallel =min\{\parallel z\parallel :z\in \Omega \}.$ Since $\left\{x_{n_k}\right\}$ is bounded, there exists a subsequence $\left\{x_{n_j}\right\}$ of $\left\{x_{n_k}\right\}$ such that $x_{n_j}\rightharpoonup z$. Moreover,

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; sup}⟨x^{\ast },x^{\ast }-x_{n_k}⟩& =& \underset{j\to \infty }{lim\; sup}⟨x^{\ast },x^{\ast }-x_{n_j}⟩\hfill \\ & =& ⟨x^{\ast },x^{\ast }-z⟩.\hfill \end{array}$$

(55)

Since $\parallel x_{n_k}-u_{n_k}\parallel \to 0$, one has $u_{n_j}\rightharpoonup z$, which together with $\parallel y_{n_k}-u_{n_k}\parallel \to 0$ and Lemma 9, we get $z\in \Omega$. From the definition of $x^{\ast }$ and (55), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}⟨x^{\ast },x^{\ast }-x_{n_k}⟩=⟨x^{\ast },x^{\ast }-z⟩\le 0.\end{array}$$

(56)

Combining (56) and (52), we obtain

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; sup}⟨x^{\ast },x^{\ast }-x_{n_{k+1}}⟩& \le & \underset{k\to \infty }{lim\; sup}⟨x^{\ast },x^{\ast }-x_{n_k}⟩\hfill \\ & \le & ⟨x^{\ast },x^{\ast }-z⟩\le 0.\hfill \end{array}$$

(57)

This together with (50), Step 3. and Lemma 6, we can conclude that $\left\{x_n\right\}$ strongly converges to $x^{\ast }\in \Psi$. Hence we obtain the desired conclusion. □

Remark 2.

We note that our results directly improve and extend some known results in the literature as follows:

(i)

Our proposed iterative method has a strong convergence in real Hilbert spaces which is more preferable than the weak convergence results of Kazmi et al. [7].

(ii)

We improve and extend Theorem 3.1 of Dao-Jun Wen [14]. Especially, we use the quasi-nonexpansive mappings instead of the nonexpansive mappings.

(iii)

The selection of the step size in the iterative method provided by Dao-Jun Wen [14] and Kazmi et al. [7] requires the prior information of the operator (matrix) norm while our iterative method can update the step size of each iteration.

(iv)

Our iterative method improve and extend iterative method of Dao-Jun Wen [14] and Kazmi et al. [7].

4. Theoretical Applications

In this section, we derive a scheme for solving hierarchical fixed point and the split problems from Algorithm 1 and also extend and generalize the known results.

4.1. Split Variational Inclusion Problem

The split variational inclusion problem is one of the important special case of the split monotone variational inclusion problem. This is a fundamental problem in optimization theory, which is applied in a wide range of disciplines. In other words, if $f=0$ and $g=0$, then the split monotone variational inclusion problem is reduced to split variational inclusion problem. Let us denote Sol(SVIP) $=\{x^{\ast }\in H_1:0\in F\left(x^{\ast }\right)\mathrm{and}0\in G\left(A{x}^{\ast }\right)\}$ by the solution set of the split variational inclusion problem.

Theorem 2.

Let $H_1$ and $H_2$ be are two real Hilbert spaces and C be a nonempty closed convex subset of $H_1$ and $A:H_1\to H_2$ be a bounded linear operator with its adjoint operator $A^{\ast }$. Assume that $F:H_1\to 2^{H_1}$ and $G:H_2\to 2^{H_2}$ are set-valued maximal monotone operators. Let $D:C\to C$ be η-strongly monotone and L-Lipschitzian, $T:C\to C$ be a nonexpansive mapping, $S:C\to C$ be a continuous quasi-nonexpansive mapping such that $I-S$ is monotone and $\Gamma =Sol\left(SVIP\right)\cap \Phi \cap Fix\left(S\right)\ne \varnothing .$ Let $\left\{x_n\right\}$ be the a sequence which satisfies the Condition 1 generated by the following scheme:

$$\left\{\begin{array}{c}{w}_n=x_n+{\theta }_n(x_n-x_{n-1});\hfill \\ u_n=(1-{\alpha }_n)w_n+{\alpha }_{n}T((1-{\beta }_n)S{w}_n+{\beta }_n(1-{\mu }_{n}D)w_n);\hfill \\ y_n=J_{\lambda }^F(u_n+r_n\left(A^{\ast }(J_{\lambda }^G-I)A{u}_n\right));\hfill \\ x_{n+1}=(1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n,\hfill \end{array}\right.$$

where $\left\{r_n\right\}$ and $\left\{{\theta }_n\right\}$ satisfy the Algorithm 1. Then the sequence $\left\{x_n\right\}$ converges strongly to $x^{\ast }\in \Gamma$ in the norm, where $\parallel x^{\ast }\parallel =min\{\parallel z\parallel :z\in \Gamma \}.$

4.2. Split Variational Inequality Problem

Let C be a nonempty closed convex subset of a Hilbert space $H_1$. Define the normal cone $N_C\left(x\right)$ of C at a point $x\in C$ by

$$N_C\left(x\right)=\{z\in H_1:⟨z,y-x⟩\le 0,\forall y\in C\}.$$

It is known that for each $\lambda >0$, we get

$$\begin{array}{ccc}\hfill y& =& {(I+\lambda N_C)}^{-1}x\iff x\in y+\lambda N_C\left(y\right)\iff x-y\in \lambda N_C\left(y\right)\hfill \\ & \iff & ⟨x-y,z-y⟩\le 0,\forall z\in C\hfill \\ & \iff & y\in P_{C}x.\hfill \end{array}$$

This implies that ${(I+\lambda N_C)}^{-1}x=P_{C}x$. Let C and Q be nonempty closed convex subsets of Hilbert spaces of $H_1$ and $H_2$, respectively. If $F=N_C$ and $G=N_Q$ in the split monotone variational inclusion problem, the following split variational inequality problem is obtained: Find $x^{\ast }\in C$ such that

$$⟨f\left(x^{\ast }\right),x-x^{\ast }⟩\ge 0\forall x\in C\mathrm{and}⟨g\left(A{x}^{\ast }\right),y-A{x}^{\ast }⟩\ge 0\forall y\in Q,$$

where $f:H_1\to H_1$ and $g:H_2\to H_2$ are ${\kappa }_1,{\kappa }_2$-inverse strongly monotone mappings with $\kappa =min\{{\kappa }_1,{\kappa }_2\}$. In particular, if f is a ${\kappa }_1$-inverse strongly monotone mapping with $\lambda \in (0,2{\kappa }_1)$, then $P_C(I-\lambda f)$ is average. Then, the following results can be obtained from our Theorem 1.

Theorem 3.

Let $H_1,H_2,C,Q,f,g$ be the same as above. Let $A:H_1\to H_2$ be a bounded linear operator with adjoint operator $A^{\ast }$. Select arbitrary initial points $x_0,x_1\in H_1$, $\left\{x_n\right\}$ is generated by the following scheme:

$$\left\{\begin{array}{c}{w}_n=x_n+{\theta }_n(x_n-x_{n-1});\hfill \\ u_n=(1-{\alpha }_n)w_n+{\alpha }_{n}T((1-{\beta }_n)S{w}_n+{\beta }_n(1-{\mu }_{n}D)w_n);\hfill \\ y_n=P_C(I-\lambda f)(u_n+r_n\left(A^{\ast }(P_Q(I-\lambda g)-I)A{u}_n\right));\hfill \\ x_{n+1}=(1-{\delta }_n-{\tau }_n)x_n+{\delta }_n{y}_n,\hfill \end{array}\right.$$

where $\left\{r_n\right\}$ and $\left\{{\theta }_n\right\}$ satisfy the Algorithm 1. Suppose that Condition 1 are satisfied and ${\rm Y}=\mathrm{Sol}\left(\mathrm{SVIP}\right)\cap \Phi \cap \mathrm{Fix}\left(S\right)\ne \varnothing$. Then the sequence $\left\{x_n\right\}$ converges strongly to $x^{\ast }\in {\rm Y}$ in the norm, where $\parallel x^{\ast }\parallel =min\{\parallel z\parallel :z\in {\rm Y}\}.$

5. Numerical Experiments

Some numerical results will be presented in this section to demonstate the effeciveness of our proposed method. The MATLAB codes were run in MATLAB version 9.5 (R2018b) on MacBook Pro 13-inch, 2019 with 2.4 GHz Quad-Core Intel Core i5 processor. RAM 8.00 GB.

Example 1.

We consider an example in infinite dimensional Hilbert spaces. Assume $H_1=H_2=L^2\left([0,1]\right)$ with inner product ${\displaystyle ⟨x,y⟩={\int }_0^{1}x\left(t\right)y\left(t\right)dt}$ and induced norm ${\displaystyle \parallel x\parallel =\sqrt{{\int }_0^1{\left|x\left(t\right)\right|}^{2}dt}}$ for all $x,y\in L^2\left([0,1]\right)$. Let $F,G:L_2(0,1)\to L_2(0,1)$ be defined by $Fx\left(t\right)=3x\left(t\right)$ and $Gx\left(t\right)=5x\left(t\right)$ where $x\left(t\right)\in L^2\left([0,1]\right),t\in [0,1]$. Let $f,g:L_2(0,1)\to L_2(0,1)$ be defined by $fx\left(t\right)=2x\left(t\right)$ and $gx\left(t\right)=4x\left(t\right)$ where $x\left(t\right)\in L^2\left([0,1]\right),t\in [0,1]$. Then f is 2-inverse strongly monotone, g is 4-inverse strongly monotone and $F,G$ are maximal monotone. Further, we have $\lambda >0$ by a direct calculation that

$$\begin{array}{ccc}\hfill J_{\lambda }^F(x-\lambda fx)& =& {(I+\lambda F)}^{-1}(x-\lambda fx)\hfill \\ & =& \left(\frac{1-2\lambda }{1+3\lambda }\right)x\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill J_{\lambda }^G(x-\lambda gx)& =& {(I+\lambda G)}^{-1}(x-\lambda gx)\hfill \\ & =& \left(\frac{1-4\lambda }{1+5\lambda }\right)x\left(t\right),\hfill \end{array}$$

where $x\left(t\right)\in L^2[0,1],$$t\in [0,1]$. Choose $\theta =0.6$ and ${\epsilon }_n=\frac{1}{{(n+1)}^3}$, we have

$$\overline{{\theta }_n}=\left\{\begin{array}{ccc}& min\{0.6,\frac{1}{{(n+1)}^3\parallel x_n-x_{n-1}\parallel }\},\hfill & \mathrm{if}{x}_n\ne x_{n-1};\hfill \\ & 0.6,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The mapping $A:H_1\to H_2$ is defined by $Ax\left(t\right)=-\frac{9}{4}x\left(t\right)$ and $\parallel A\parallel =\parallel A^{\ast }\parallel =\frac{9}{4}$. Let $Tx\left(t\right)=x\left(t\right)$, $Sx\left(t\right)=x\left(t\right)cos\left(x\right(t\left)\right)$ and $Dx\left(t\right)=10x\left(t\right)$ where $x\left(t\right)\in L^2\left([0,1]\right)$, $t\in [0,1].$ Then T is a nonexpansive mapping with $Fix\left(T\right)=(-\infty ,\infty )$ and S is a continuous qusi-nonexpansive mapping with $Fix\left(S\right)=\left\{0\right\}$ and $(I-S)$ is monotone but S is not a nonexpansive mapping. Hence $\Phi =\mathrm{Sol}\left(\mathrm{HFPP}\right)=\left\{0\right\}$. Furthermore, it easy to prove that $\Omega =\left\{0\right\}$. Therefore $\Psi =\Psi \cap \Omega =\left\{0\right\}\ne \varnothing$. We choose the iterative coefficients

$${\alpha }_n=\frac{1}{2},{\beta }_n=\frac{1}{n^2},{\mu }_n=\frac{1}{2n},{\delta }_n=0.98-{\tau }_n,{\tau }_n=\frac{1}{n+2}.$$

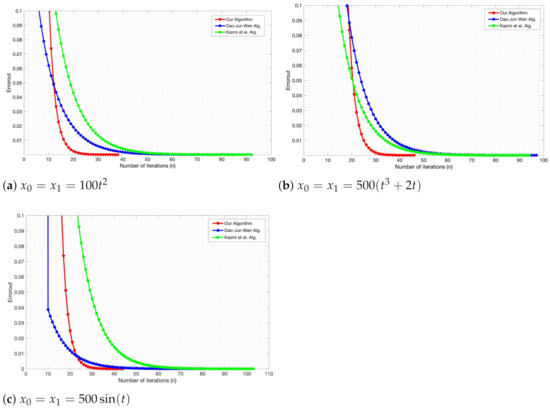
The further comparison of convergence behavior between our proposed method and Dao-Jun Wen. [14] and Kazmi et al. [7] is displayed in Figure 1 and Table 1 with the stopping criteria $\parallel x_n-x^{\ast }\parallel \le {10}^{-5}$.

Figure 1. Numerical behavior of all algorithms with different initial values in Example 1.

Table 1. The result of all algorithms with different inertial points in Example 1.

Algorithms	$x_1=100t^2$		$x_1=500(t^3+2t)$		$x_1=500sin\left(t\right)$
	Iter.	Time (s)	Iter.	Time (s)	Iter.	Time (s)
Our Algorithm	38	0.13	47	0.13	45	0.12
Dao-Jun Wen Alg.	86	0.15	97	0.12	81	0.16
Kazmi et al. Alg.	93	0.18	95	0.24	103	0.21

Remark 3.

Table 1 shows that the different inertial points $x_0=x_1$ have almost on effect on the number of iterations and shows that our proposed method has a better number of iterations and CPU time than Dao-Jun Wen. [14] and Kazmi et al. [7].

Example 2.

In this example, we apply our main result to solve the image restoration problem by using Algorithm 1. We consider the convex minimization problem as follows:

$$\underset{x}{min}\{h\left(x\right)+g\left(x\right)\},$$

(58)

where $h:{\mathbb{R}}^n\to \mathbb{R}$ is a smooth convex loss function and differentiable with L-Lipschitz continuous gradient $\nabla h$ where $L>0$ and $g:{\mathbb{R}}^n\to \mathbb{R}$ is a continuous convex function. It is well known that the convex minimization problem (58) is equivalent to the following problem:

$$findapoint{x}^{\ast }\in Csuchthat0\in \nabla h\left(x^{\ast }\right)+\partial g\left(x^{\ast }\right).$$

(59)

We consider the degradation model that represents image restoration problems as the following mathematical model:

$$b=Ax+\epsilon ,$$

(60)

where $A\in {\mathbb{R}}^{m\times n}$ is a blurring matrix and $\epsilon \in {\mathbb{R}}^{m\times 1}$ is a noise term. The goal is to recover the original image $x\in {\mathbb{R}}^{n\times 1}$ by minimizing a noise term. We consider a model which produces the restored image given by the following minimization problem:

$$\underset{x}{min}\{\frac{1}{2}{\parallel Ax-b\parallel }_2^2+{\omega \parallel x\parallel }_1\},$$

(61)

for some regularization parameter $\omega >0$. In this situation, we choose $h\left(x\right)=\frac{1}{2}{\parallel Ax-b\parallel }_2^2$ and $g\left(x\right)={\mu \parallel x\parallel }_1$ and set operators $f=\nabla h$, $F=\partial g$, $A=-\frac{9x}{4}$, $D=10x$, $G=0$, $T=\frac{3nx}{3n+1}$, $S=pro{x}_{rg}(I-r\nabla h)$ and ${\theta }_n$ is defined as Example 1. We set parameters as follows:

$${\alpha }_n=\frac{60n-9}{100n},{\beta }_n=\frac{1}{150n^2},{\tau }_n=\frac{1}{2000(2n+1)},{\delta }_n=0.4-{\tau }_n,{\mu }_n=0.5.$$

For this example, we choose the regularization parameter $\omega ={10}^{-3}$ and the original gray and RGB images (see in Figure 2a,f). We use an average and motion blur create the blurred and noise images (see in Figure 2b,g). The performance for image restoring process is quantitatively measured by signal-to-noise ratio (SNR), which is defined as

$$SNR=20{log}_{10}\left(\frac{{\parallel x\parallel }_2^2}{\parallel x-x_n{\parallel }_2^2}\right),$$

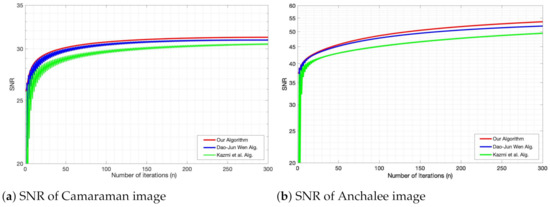
where x and $x_n$ denote the original image and the restored image at iteration n, respectively. A higher SNR implies that the recovered image is of higher quality. Our numerical results are explained in Table 2 and Figure 3.

Figure 2. The original images are shown as (a) “Cameraman image” and (f) “Anchalee image”, Degradation images by an average and motion blur are shown as (b,g), repectively. (c,h) show the reconstruction by our algorithm, (d,i) show the reconstruction by Dao-Jun Wen algorithm and (e,j) show the reconstruction by Kazmi et al. algorithm.

Table 2. The performance of signal-to-noise ratio (SNR) in the gray and RGB images.

SNR
	Cameraman Image			Anchalee Image
n	Our Alg.	Dao-Jun Wen	Kazmi et al.	Our Alg.	Dao-Jun Wen	Kazmi et al.
1	26.2564	8.1116	4.0332	37.2865	9.5366	4.7484
50	30.1687	30.0091	29.2302	45.6664	45.1171	42.9992
100	30.7660	30.5809	29.8699	48.5931	47.7755	45.0396
200	31.1938	30.9517	30.3947	51.7846	50.5634	47.7038
300	31.2939	31.0011	30.5988	53.5650	51.9977	49.4282
400	31.2432	30.9072	30.6739	54.7291	52.8411	50.6422

Figure 3. Numerical behavior of all algorithms with SNR in Example 2.

Remark 4.

It can be observed from Figure 2 that the restoration quality of the the gray and RGB images restored by our algorithm is better than the quality of the image restored by Dao-Jun Wen. Alg. [14] and Kazmi et al. Alg. [7], and Table 2 and Figure 3 are verified by the higher SNR values of our algorithm.

6. Conclusions

In this article, the main contribution is to introduce a novel self-adaptive inertial Krasnoselski-mann iterative method for solving hierarchical fixed point and split monotone variational inclusion problems in Hilbert speaces. The main advantage of this scheme involves both the use of an inertial technique and the self-adaptive step size criterion which does not require prior knowledge of the Lipschitz constant of the cost operator. Under standard assumptions, the strong convergence of the proposed method is established. A modified scheme derived from the proposed method is given for solving hierarchical fixed points and the split problems. The application of the proposed method in image recovery and comparison with Dao-Jun Wen. Alg. [14] and Kazmi et al. Alg. [7] are presented.