Abstract
The Estrada index of a graph G is defined as , where are the eigenvalues of the adjacency matrix of G. A unicyclic graph is a connected graph with a unique cycle. Let be the set of all unicyclic graphs with n vertices and diameter d. In this paper, we give some transformations which can be used to compare the Estrada indices of two graphs. Using these transformations, we determine the graphs with the maximum Estrada indices among . We characterize two candidate graphs with the maximum Estrada index if d is odd and three candidate graphs with the maximum Estrada index if d is even.
1. Introduction
In this paper, we only consider simple undirected graphs. Let be a graph with n vertices and m edges. Let be the set of vertices adjacent to v in G. The degree of v in G, denoted by , is equal to . A vertex of degree one is called a pendant vertex. The edge incident with a pendant vertex is known as a pendant edge. Let . Then denote by the subgraph induced by S. If (or ), then we write for the graph obtained from G by deleting all of its edges (or vertices, resp.) in D. If , then we denote by the graph obtained from G by adding all of edges in D to the graph.
Let be the adjacency matrix of G. Denote the eigenvalues of by and assume . Then , usually denoted by , is called the spectral radius of G. The Estrada index of G is defined as
This graph invariant was first proposed as a measure of the degree of folding of a protein [1] and now has been found multiple applications in various fields, such as measurements of the subgraph centrality and the centrality of complex networks [2,3] and the extended molecular branching [4]. Recently, the correlation between the Estrada index and -electronic energies for benzenoid hydrocarbons was investigated in [5], the results of which warrant its further usage in quantitative structure–activity relationships. Given these prominent applications of the Estrada index, the research on it is of theoretical and practical significance. In the last few decades, some mathematical properties of the Estrada index, including various bounds for it, have been established [6,7,8,9,10,11,12].
In 1986, Brualdi and Solheid [13] proposed the following problem concerning the spectral radii of graphs: Given a set of graphs, find an upper bound for the spectral radius of graphs in and characterize the graphs for which the maximal spectral radius is attained. The corresponding problem of a given graph invariant has been widely studied (see [14,15,16], for example). Motivated by this, many results have been obtained on characterizing graphs that maximize (or minimize) the Estrada index among a given set of graphs. For example, some interesting results were obtained for the general trees [17], trees with a given matching number [18], trees with a fixed diameter [19], trees with perfect matching and a fixed maximum degree [20], and trees with a fixed number of pendant vertices [21]. Du and Zhou [22] showed a graph with the maximal Estrada index and two candidate graphs with the minimum Estrada index among all unicyclic graphs. Moreover, they determined the unique graphs with maximum Estrada indices among graphs with given parameters [23]. Wang et al. [24] and Zhu et al. [25] characterized the bicyclic graph and the tricyclic graph with maximum Estrada indices, respectively. E. Andrade et al. [26] presented the graph having the largest Estrada index of its line graph among all graphs on n vertices with connectivity less than or equal to a fixed number. For more results on the Estrada index and its variations, the readers may refer to [27,28,29,30].
A unicyclic graph is a connected graph with a unique cycle. Let and be the path and the cycle on n vertices, respectively. Denote by the set of all unicyclic graphs with n vertices and diameter d. In this paper, we characterize the graphs with the maximum Estrada index in .
This paper is organized as follows. In Section 2, we list some transformations which can be used to compare the Estrada indices of two graphs. In Section 3, we determine the graphs with the maximum Estrada index among unicyclic graphs in . We show two candidate graphs with the maximal Estrada index if d is odd and three candidate graphs with the maximal Estrada index if d is even. We also propose a hypothesis on the structure of the extremal graph with the maximum Estrada index in .
2. Preliminaries
In order to obtain the main results of this paper, we give some definitions and lemmas here.
A walk of length k in a graph G is any sequence of vertices and edges in G, , such that for every . For a subsequence of W, we refer to it as a -section of W. Usually, we write instead for simplicity and call it a -walk. Let . Then is called the reverse of W. If , then W is called a closed walk.
Let be the kth spectral moment of the graph G defined as . It is well-known that equals the number of closed walks of length k in G; see [31]. Then by the Taylor expansion of the exponential function , we have
Let G and H be two graphs with , and . Suppose k is an arbitrary positive integer. Let be the set of all -walks of length k going through the edge e in G and let . Let be the set of all -walks of length k in G and let . If for all positive integers k, then we write . If , and for some positive integer , then we write . For convenience, let , and .
The following four results are often used to compare the Estrada indices of two graphs.
Lemma 1
([28]). Let H be a graph (not necessarily connected) with . Suppose that , and for . Let and . Let and . If and for , then .
Lemma 2
([32]). Let and be two non-trivial graphs with , . Let be the graph obtained from and by identifying u with w, and be the graph obtained from and by identifying v with w. If , then .
Lemma 3
([32]). Let and be two connected graphs with and . Let G be the graph obtained by joining u and v with and edge, and let be the graph obtained by identifying u with v, and attaching a pendant vertex to the common vertex. If , then .
Theorem 1
([27]). Let G be a connected graph and be the graph obtained from G by attaching p and q pendant edges to u and v, respectively, where and . Then or . Furthermore, if or if .
3. Lemmas
In this section, we give some lemmas that can be used to prove in a graph G, where .
Lemma 4.
Let G be a simple graph and . If , then , and for each . Moreover, if , then .
Proof of Lemma 4.
Since G is simple, implies . Let and . Then W can be written as , where . Let . Since and , the map : , defined as is an injection. Thus, . Since is arbitrary, we get . Note that and . Therefore, if further holds. Similarly, we can show for each . □
Lemma 5.
Let G be a graph and such that . If , then . Moreover, if , then .
Proof of Lemma 5.
For each and , by the definition of ,
Since , we have . Therefore, there exits an injection . In order to prove , it suffices to show .
Let . Then either or must be contained in W. If W does not contain the section , or appears earlier than in W, then W can be decomposed uniquely to such that for some and for some . In this case, we define . Then .
If W does not contain the section , or appears earlier than in W, then W can be decomposed uniquely to , where is a -walk in G for each , and is a -walk in H. Here, either contains no e, or contains no , or appears earlier than . Without loss of generality, we suppose appears earlier than in . Then can be decomposed to such that for some and is a -walk in H. In this case, we define . Then . Now it is easy to show that the map defined as above is an injection. Therefore, .
Moreover, if , then for some . Thus, by (2), which implies . □
Lemma 6.
Let G be a graph and be a path in G such that . Let q and l be two nonnegative integers such that and . Suppose and are two vertices in P such that for each . Let . Then
- (1)
- ;
- (2)
- If , or and the condition does not hold, then , where is: and for each .
- (3)
- If is even, then for each .
Proof of Lemma 6.
Let for each . For each walk W in , , denote by the walk obtained from W by replacing each vertex with and the corresponding edges, where . We distinguish the following two cases:
Case 1. is even.
Let and . Then has the same distance from v and u in P. If W contains more than once, then it can be decomposed uniquely to , such that which is as long as possible, is a -walk in G, and is a -walk in G. In this case, let . Then . If W contains at most once, then let . Obviously, the map defined as above is an injection. Since k is arbitrary, we have .
If , then does not cover the walk .
Now suppose and the condition does not hold. Without loss of generality, suppose there exists some with . Then there exists a vertex such that . If , then does not cover the walk . If , then does not cover the walk . Therefore, if , or and the condition does not hold, then for some . This implies Lemma 6 (2) holds.
Let and . Then W must contain . Thus, W can be decomposed uniquely to such that which is as long as possible and is a -walk in G. Then the map : defined as is an injection. Therefore, .
Case 2. is odd.
Let , , and . If W contains , then it must contain at least twice and can be decomposed uniquely to , such that , which contains only once; , which does not contain ; , which is as long as possible; and , which does not contain . In this case, let . If W does not contain , let . Then the map defined as above is an injection. Thus, .
The proof of (Case 2) when is odd is the same as that of Case 1. □
Remark 1.
Lemma 6 (3) does not hold if is odd. For example, let G be the graph obtained from and a new vertex w by adding the edge . Let and . Then and . Thus, does not hold in G.
4. Graphs with the Maximum Estrada Index in
In this section, we determine the graphs with the maximum Estrada index among .
Let be the graph obtained from the cycle by attaching vertices to for . Let and . Let be the set of all unicyclc graphs of order n.
The following theorem characterizes the graphs with greatest, second-greatest, smallest, and second-smallest Estrada indices among the unicyclic graphs in .
Theorem 2
([33]). Among the unicyclic graphs in ,
- (i)
- According to references [22,34], the cycle has smalles tindex and the graph has second-smallest Estrada index;
- (ii)
- According to references [22,34], the graph has the greatest Estrada index;
- (iii)
- The graph has the second-greatest Estrada index.
For , we have and . If , then . By Theorem 2, the graphs with the maximum Estrada indices among the graphs in and are and , respectively. Therefore, we assume and in the following. Now we give some lemmas.
Lemma 7.
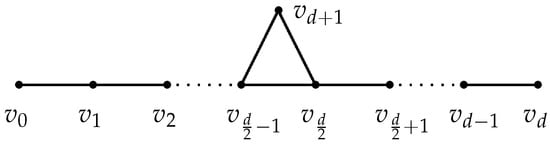
Let be a path, where is even. Let H be the graph obtained from P and a new vertex by adding the edges and ; see Figure 1. Then .

Figure 1.
Graph H in Lemma 7.
Proof of Lemma 7.
Let for each . Let and . For each walk W in and each , denote by the walk obtained from W by replacing with and the corresponding edges. Let and . If W does not contain , then define . If W contains , then W can be decomposed uniquely to , such that for some , for some , which is as long as possible, or , or . Obviously, neither nor contains . In this case, we define . Then it is easy to show that the map defined as above is an injection. Since does not cover the walk , we have . □
Lemma 8.
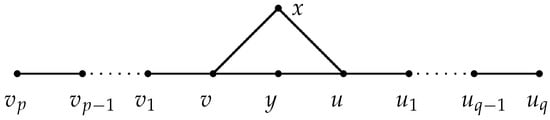
Let be a 4-cycle. Denote by H the graph obtained from by attaching two paths and at vertices v and u, respectively; see Figure 2. If , then .

Figure 2.
Graph H in Lemmas 8 and 9.
Proof of Lemma 8.
For each walk W in and each , denote by the walk obtained from W by replacing with , v with u and the corresponding edges. Let and . If W contains neither x nor y, then let . If W contains x or y, then W can be decomposed uniquely to , such that is a -walk; is a -walk which is as long as possible, where ; and is a -walk. It is obvious that both of and are walks in . In this case, we define . Then it is easy to show that the map defined as above is an injection. Since , does not cover the walk . Therefore, we have . □
Lemma 9.
Let H be the graph depicted in Figure 2. If and , then .
Proof of Lemma 9.
Let be an arbitrary integer. By the definition of the walk, we have
and
Since , in order to prove , it suffices to show , i.e., for each . We prove this by induction on k.
If , . If , . Now suppose and let . We consider the edge e preceding the last vertex v in W. If , then W can be written as . In this case, let . If , then W can be written as . In this case, let . If , then W can be uniquely decomposed to , such that for some which is as large as possible, and for some . Obviously, is a walk in . Define the walk obtained from by replacing with for each , v with u, and the corresponding edges. By the inductive hypothesis, there is an injection . In this case, let . Then it is easy to show that the map defined as above is an injection. Therefore, .
Since , . Thus, . This completes the proof. □
Let be a path of length d with . Let be the graph obtained from P and a new vertex by adding the edges and , and attaching pendant edges at the vertex (see Figure 3).
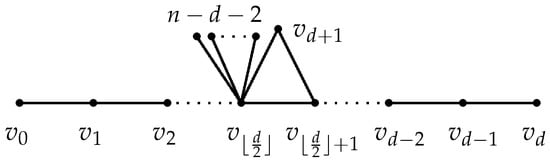
Figure 3.
Graph .
Lemma 10.
Let be a path of length . Let be the graph with diameter d obtained from P and a new vertex by adding the edges and , and attaching pendant edges at one vertex , where and . Then , with equality if and only if , where is depicted in Figure 3.
Proof of Lemma 10.
Denote by the set of all graphs . Let be the graph in with the maximum Estrada index. Then there exists some such that is obtained from P and by adding the edges and , and attaching pendant edges at a vertex v for some vertex . We show that , i.e., . For each vertex in P, let . We distinguish the following two cases.
Case 1. d is odd.
We show that for each , we have .
Let t be the minimum index with . Suppose . If , then and is even. Let . By Lemma 6, , and for each , . Define . Then and by Lemma 1, a contradiction to the choice of . Therefore, , i.e., for each . Similarly, we have for each . Thus, and .
Obviously, if . Now we suppose . Then . Suppose . Let and . Then and . Thus, we have by Lemma 4 and by Lemma 5. Note that for each , . By Lemma 1, we get , a contradiction to the choice of . Therefore, , i.e., .
Case 2. d is even.
By an argument similar to that of Case 1, we have for each and . Thus, or , and . Without loss of generality, we may suppose . Then if . Now suppose . By an argument similar to that in Case 1, we have . Suppose or . Let be the set of all pendant vertices adjacent to v and . Then by Lemmas 6 and 7, , and for each , . By Lemma 1, , a contradiction to the choice of . Therefore, , i.e., . This completes the proof. □
Lemma 11.
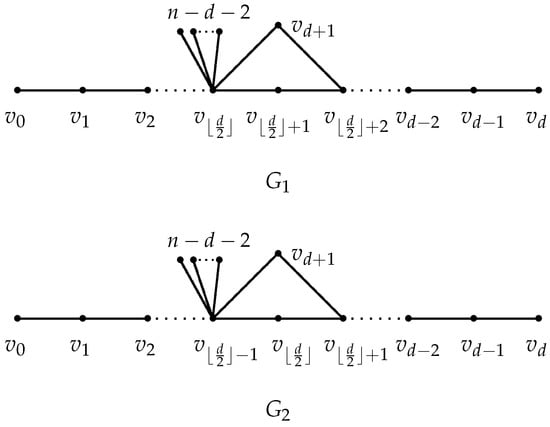
Let be a path of length . Let be the graph with diameter d obtained from P and a new vertex by adding the edges and , and attaching pendant edges at , where , and . Let and be depicted in Figure 4.

Figure 4.
Graphs and .
- (i)
- If d is odd, then , with equality if and only if .
- (ii)
- If d is even, then , with equality if and only if is isomorphic to the graph with a larger Estrada index between and .
Proof of Lemma 11.
Denote by the set of all graphs . Let be the graph in with the maximum Estrada index. Then there exists some and such that is obtained from P and by adding the edges and , and attaching pendant edges at the vertex . We distinguish the following two cases.
Case 1. d is odd.
Without loss of generality, we suppose . Let be the set of all pendant vertices adjacent to . Let . We show in the following that either , or .
Suppose . Then and is even. Moreover, for each by Lemma 6, and by Lemmas 8 and 9. Thus, by Lemma 1. Now let . Then and by Lemmas 1 and 6, a contradiction to the choice of . Therefore, . Similarly, . Thus, or . Suppose . Then for each with by Lemmas 6, 8, and 9. Thus, from the choice of . Similarly, if . Since d is odd, we get .
Case 2. d is even.
By a similar argument to that in Case 1, we can show that either , or , or , or . Note that has a maximum among . Therefore, is isomorphic to the graph between and with a larger Estrada index. □
Now we give our main results.
Theorem 3.
Proof of Theorem 3.
If , then . If or 3, then by Theorem 2. Thus, the result holds when . We assume below.
By Theorem 2, . Let be an induced path of length d and be the unique cycle in G. Since , —say, . Thus, we can make some claims.
Claim 1.
.
Proof of Claim 1.
Otherwise, since G is connected, there exists a shortest path connecting and , where and , and and . Denote by and the connected components containing and in , respectively. Let be the graph obtained from and by identifying with , and attaching a pendant vertex to the common vertex. Then and by Lemma 3, a contradiction. □
By Claim 1, . Denote , where and . By a similar argument, we have
Claim 2.
for each vertex .
By Theorem 1, we have
Claim 3.
All pendant vertices except and in G are adjacent to one common vertex v.
Claim 4.
.
Proof of Claim 4.
Suppose . Then and . Since , we can assume (otherwise, relabel the vertices in ). Let , and . Then , and . By Lemma 4, we have and for each vertex , . Thus, by Lemma 1, a contradiction. □
Claim 5.
If then ; and if , then and .
Proof of Claim 5.
Suppose . If , by letting , and , then , and . Moreover, and for each vertex by Lemma 4. Thus, by Lemma 1, a contradiction. Hence, or . □
Suppose when . Since , we can assume (otherwise, relabel the vertices in ). Let , and . Then , and . By Lemma 4, and for each vertex , . Thus, by Lemma 1, a contradiction. This implies if .
Now suppose . Suppose . Let , and . Then , and . By Lemma 4, and for each vertex , . Thus, by Lemma 1, a contradiction. Therefore, . Since , we have .
By Claims 5 and 3, if , then G is the unicyclic graph with maximum Estrada index of diameter d obtained from and by adding the edges and , and attaching pendant edges at one vertex for some . By Lemma 10, we get
Claim 6.
If , then .
By Claims 5 and 3, if , then G is the unicyclic graph with the maximum Estrada index of diameter d obtained from and by adding the edges and , and attaching pendant edges at one vertex for some . By Lemma 11, we get
Claim 7.
If , then if d is odd, and if d is even.
Now the proof is complete. □
By Theorem 3, we can easily obtain the following corollary.
Corollary 1.
Let G be a graph in . If the girth of G is odd, then , with equality if and only if .
Liu et al. in [35] showed the following result on the spectral radii of unicyclic graphs.
Theorem 4
([35]). Let G be a graph in , . Then , and equality holds if and only if .
Based on Theorems 3 and 4 and previous results on extremal values of Estrada index and spectral radius, we propose the following hypothesis.
Hypothesis 1.
Let G be a graph in . Then , with equality if and only if .
Remark 2.
To prove Hypothesis 1, it suffices to show that and by Theorem 3. To show this, by previous methods and (1), it suffices to show that for , the inequality holds for each and is strict for some . However, this can not happen since for . Notice that and are both bipartite graphs. The hypothesis is true if we can show that for , holds for all and is strict for some .
5. Conclusions
In [1], Estrada proposed a graph invariant (the Estrada index) based on a Taylor series expansion of spectral moments. In this paper, we gave some transformations that can be used to compare the Estrada indices of two graphs. As applications, we determined the graphs with the maximum Estrada indices among all unicyclic graphs with fixed diameter d. We showed two candidate extremal graphs if d is odd and three candidate extremal graphs if d is even. For future research, it would be interesting to study Hypothesis 1.
Author Contributions
Methodology, W.N. and K.W.; investigation, W.N. and K.W.; writing—original draft preparation, K.W.; writing—review and editing, W.N.; funding acquisition, W.N. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (number 11801568).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Estrada, E. Characterization of 3D molecular structure. Chem. Phys. Lett. 2000, 319, 713–718. [Google Scholar] [CrossRef]
- Estrada, E.; Rodríguez-Valázquez, J.A. Subgraph centrality in complex networks. Phys. Rev. E 2005, 71, 056103. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Rodríguez-Valázquez, J.A. Spectral measures of bipartivity in complex networks. Phys. Rev. E 2005, 72, 046105. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Rodríguez-Valázquez, J.A.; Randić, M. Atomic branching in molecules. Int. J. Quantum Chem. 2006, 106, 823–832. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M.; Liu, J. Correlation between the Estrada index and π-electronic energies for benzenoid hydrocarbons with applications to boron nanotubes. Int. J. Quantum Chem. 2019, 119, e26016. [Google Scholar] [CrossRef]
- Du, Z. An edge grafting theorem on the Estrada index of graphs and its applications. Discret. Appl. Math. 2013, 161, 134–139. [Google Scholar] [CrossRef][Green Version]
- Shang, Y. Estrada and L-Estrada Indices of Edge-Independent Random Graphs. Symmetry 2015, 7, 1455–1462. [Google Scholar] [CrossRef]
- Rodríguez, J. A note on new bounds for the Estrada Index. Linear Algebra Appl. 2019, 580, 121–127. [Google Scholar] [CrossRef]
- Carmona, J.R.; Rodríguez, J. An increasing sequence of lower bounds for the Estrada index of graphs and matrices. Linear Algebra Appl. 2019, 580, 200–211. [Google Scholar] [CrossRef]
- Shang, Y. Estrada Index and Laplacian Estrada Index of Random Interdependent Graphs. Mathematics 2020, 8, 1063. [Google Scholar] [CrossRef]
- Rodríguez, J.; Aguayo, J.L.; Carmona, J.R.; Jahanbani, A. A note lower bounds for the Estrada index. Discret. Math. 2021, 344, 112303. [Google Scholar] [CrossRef]
- Rashid, M.A.; Ahmad, S.; Siddiqui, M.K.; Jahanbani, A.; Sheikholeslami, S.M.; Shao, Z. New Bounds for the Estrada Index of Phenylenes. Polycycl. Aromat Comp. 2020, 1–17. [Google Scholar] [CrossRef]
- Brualdi, R.A.; Solheid, E.S. On the spectral radius of complementary acyclic matrices of zero and ones. SIAM J. Algebr. Discret. Methods 1986, 7, 265–272. [Google Scholar] [CrossRef]
- He, S.; Li, S. On the signless Laplacian index of unicyclic graphs with fixed diameter. Linear Algebra Appl. 2012, 436, 252–261. [Google Scholar] [CrossRef]
- Sun, Q.; Ikica, B.; Škrekovski, R.; Vukašinović, V. Graphs with a given diameter that maximize the Wiener index. Appl. Math. Comput. 2019, 356, 438–448. [Google Scholar]
- Vukićević, Z.K.; Vujošević, S.; Popivoda, G. Unicyclic graphs with extremal values of arithmetic–geometric index. Discret. Appl. Math. 2021, 302, 67–75. [Google Scholar] [CrossRef]
- Deng, H. A proof of a conjecture on the Estrada index. MATCH Commun. Math. Comput. Chem. 2009, 62, 599–606. [Google Scholar]
- Zhai, C.; Wang, W. Minimal Estrada indices of the trees with a perfect matching. Electron. J. Linear Algebra 2016, 31, 134–146. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, B.; Li, J. On Estrada index of trees. Linear Algebra Appl. 2011, 434, 215–223. [Google Scholar] [CrossRef][Green Version]
- Ilić, A.; Stevanović, D. The Estrada index of chemical trees. J. Math. Chem. 2010, 47, 305–314. [Google Scholar] [CrossRef]
- Du, Z.; Zhou, B. The Estrada index of trees. Linear Algebra Appl. 2011, 435, 2462–2467. [Google Scholar] [CrossRef][Green Version]
- Du, Z.; Zhou, B. The Estrada index of unicyclic graphs. Linear Algebra Appl. 2012, 436, 3149–3159. [Google Scholar] [CrossRef]
- Du, Z.; Zhou, B.; Xing, R. On maximum Estrada indices of graphs with given parameters. Linear Algebra Appl. 2012, 436, 3767–3772. [Google Scholar] [CrossRef][Green Version]
- Wang, L.; Fan, Y.; Wang, Y. Maximum Estrada index of bicyclic graphs. Discret. Appl. Math. 2015, 180, 194–199. [Google Scholar] [CrossRef]
- Zhu, Z.; Tan, L.; Qiu, Z. Tricyclic graph with maximal Estrada index. Discret. Appl. Math. 2014, 162, 364–372. [Google Scholar] [CrossRef]
- Andrade, E.; Lenes, E.; Mallea-Zepeda, E.; Robbiano, M.; Rodríguez, J. Extremal graphs for Estrada indices. Linear Algebra Appl. 2020, 588, 54–73. [Google Scholar] [CrossRef]
- Wang, W.; Xu, W. Graphs with the maximal Estrada indices. Linear Algebra Appl. 2014, 446, 314–328. [Google Scholar] [CrossRef]
- Du, Z.; Liu, Z. On the Estrada and Laplacian Estrada indices of graphs. Linear Algebra Appl. 2011, 435, 2065–2076. [Google Scholar] [CrossRef][Green Version]
- Zhu, Z. Maximal Estrada index of unicyclic graphs with perfect matching. J. Appl. Math. Comput. 2017, 54, 381–393. [Google Scholar] [CrossRef]
- Liu, C.; Pan, Y.; Li, J. On the geometric-arithmetic Estrada index of graphs. Appl. Math. Comput. 2021, 391, 125700. [Google Scholar] [CrossRef]
- Cvetković, D.; Doob, M.; Sachs, H. Spectra of Graphs-Theory and Application; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Du, Z.; Zhou, B. On the Estrada index of graphs with given number of cut edges. Electron. J. Linear Algebra 2011, 22, 586–592. [Google Scholar] [CrossRef][Green Version]
- Zhu, Z. Some extremal properties of the resolvent energy, Estrada and resolvent Estrada indices of graphs. J. Math. Anal. Appl. 2017, 447, 957–970. [Google Scholar] [CrossRef]
- Allem, L.; Capaverde, J.; Trevisan, V.; Gutman, I.; Zogić, E.; Glogić, E. Resolvent energy of unicyclic, bicyclic and tricyclic graphs. MATCH Commun. Math. Comput. Chem. 2017, 77, 95–104. [Google Scholar]
- Liu, H.; Lu, M.; Tian, F. On the spectral radius of unicyclic graphs with fixed diameter. Linear Algebra Appl. 2007, 420, 449–457. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).