Geometric Invariants of Surjective Isometries between Unit Spheres

Abstract

In this paper we provide new geometric invariants of surjective isometries between unit spheres of Banach spaces. Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. The most relevant geometric invariants under surjective isometries such as T are known to be the starlike sets, the maximal faces of the unit ball, and the antipodal points (in the finite-dimensional case). Here, new geometric invariants are found, such as almost flat sets, flat sets, starlike compatible sets, and starlike generated sets. Also, in this work, it is proved that if F is a maximal face of the unit ball containing inner points, then $T(-F)=-T\left(F\right)$. We also show that if $[x,y]$ is a non-trivial segment contained in the unit sphere such that $T\left(\right[x,y\left]\right)$ is convex, then T is affine on $[x,y]$. As a consequence, T is affine on every segment that is a maximal face. On the other hand, we introduce a new geometric property called property P, which states that every face of the unit ball is the intersection of all maximal faces containing it. This property has turned out to be, in a implicit way, a very useful tool to show that many Banach spaces enjoy the Mazur-Ulam property. Following this line, in this manuscript it is proved that every reflexive or separable Banach space with dimension greater than or equal to 2 can be equivalently renormed to fail property P.

1. Introduction

The isometric extension problem is a prolific topic in the area of Functional Analysis inspired by the so-called Mazur-Ulam Theorem [1], which affirms that an isometry defined between two real Banach spaces is affine, understanding an isometry as a mapping $T:X\to Y$ preserving distances (where X and Y are two normed spaces), that means $\Vert T\left(x\right)-T\left(y\right)\Vert =\Vert x-y\Vert$ for all $x,y\in X$. The interest hiding on this result is the identification between the algebraic structure of the underline vector space and the metric one, whose distance is defined by its norm. A subtle generalization of this result is due to Mankiewicz [2], which states that it is sufficient to define the isometry between two convex bodies (convex sets with non-empty interior) of the real normed spaces to uniquely extend to an affine isometry between the whole spaces. A notable convex body in Banach spaces is the unit ball, which motivates the next step in the isometric extension problem: reducing the domain and co-domain to the unit spheres of both spaces. This question is known as Tingley’s Problem, due to Tingley [3].

Problem 1

(Tingley’s Problem). Is it always possible to extend a surjective isometry defined between the unit spheres of two real Banach spaces to a surjective linear isometry between the whole spaces?

In the last thirty years, quite a few researchers have given several positive answers to the above problem for particular Banach spaces, as well as many geometric and algebraic tools to tackle it [4,5,6,7,8,9,10,11,12,13,14,15]. Despite this wide list, nowadays Problem 1 is still open, even for the 2-dimensional case.

A variation of Tingley’s Problem was introduced in [6] by considering an arbitrary Banach space Y. This is a more general question in the isometric extension topic known as the Mazur-Ulam property.

Definition 1

(Mazur-Ulam property). A Banach space X satisfies the Mazur-Ulam property (MUp) if for an arbitrary Banach space Y, any surjective isometry between the unit spheres of X and Y is the restriction of a surjective linear isometry between the whole spaces.

The natural question that arises is what conditions allow X to satisfy the MUp. Some concrete examples of Banach spaces satisfying the MUp are polyhedral spaces, $c_0(\Gamma ),{\ell }^p(\Gamma )(1\le p<\infty ),{\ell }^{\infty }(\Gamma ),C(\Omega )$, (see [5,8,16,17,18]). This issue is currently a hot topic at the same level as Tingley’s Problem (recent articles about the MUp are [19,20,21,22]). Finally, in [21,23] the authors prove that non-strictly convex 2-dimensional Banach spaces and non-smooth 2-dimensional Banach spaces satisfy MUp.

In this work, the authors give some new geometric invariants under surjective isometries and simpler proofs about well-known results. Section 2 is devoted to make a review about the more relevant concepts, useful tools and results in the geometrical study of Banach spaces, in particular, the extremal structure, the starlike structure, smoothness, inner points and the Minkowski functional. These notions will play a fundamental role along the article. Moreover, property P is newly introduced in this section: we shall say that a normed space has property P if every proper face is the intersection of all maximal faces containing it. This property will be utilised as an implement in the study of the MUp (see Problem 2). Section 3 is a compilation of geometric results concerning the terms presented above. In the first place, we present several examples of Banach spaces failing property P under particular hypotheses. Later, we make a comprehension about the behaviour of facets and frames of the unit ball. In particular, we point out Theorem 7 as a straightforward characterisation of the frame of the unit ball. The next subsection is a deep study of the flatness properties of the unit sphere, where we present new definitions in search for more geometric invariants under surjective isometries. In particular, Theorems 9 and 10 show an identification between starlike sets and maximal faces when they are convex or centred in a smooth point. To end this section, we prove the invariance of the frame (Theorem 11), starlike envelopes (Theorem 12) and faces, when the large space satisfies property P (Theorem 13). Even more, surjective isometries preserve antipodal rotund points (Theorem 14), antipodal maximal faces with inner points (Theorem 15) and segments of the unit ball, when its image is convex (Theorem 17). Section 4 and Section 5 close the article with a proposal of a new approach to show that 2-dimensional real Banach spaces enjoy MUp by strongly relying on [23].

2. Materials and Methods

All vector spaces considered throughout this manuscript will be over the reals. If X is a normed space, then $B_X,U_X,S_X$ will stand for its (closed) unit ball, its open unit ball, and its unit sphere, respectively. If $x\in X$ and $r>0$, then $B_X(x,r),U_X(x,r),S_X(x,r)$ will denote, as expected, the (closed) ball of center x and radius $r>0$, the open ball of center x and radius $r>0$, and the sphere of center x and radius $r>0$. For metric spaces, we will keep using the same notation for the closed balls, the open balls and the spheres.

If X is now a topological space and $A\subseteq X$, then $\mathrm{int}\left(A\right),\mathrm{cl}\left(A\right),\mathrm{bd}\left(A\right)$ stand for the interior of A, the closure of A, and the boundary of A, respectively. If $B\subseteq A$, then ${\mathrm{int}}_A\left(B\right),{\mathrm{cl}}_A\left(B\right),{\mathrm{bd}}_A\left(B\right)$ stand, as expected, for the relative interior of B with respect to A, the relative closure of B with respect to A, and the relative boundary of B with respect to A, respectively.

2.1. Extremal Structure

The following definitions are well known among the Banach Space Geometers and belong to the folklore of classic literature of Banach Space Theory. For further reading on these topics, we refer the reader to the classical texts [24,25,26].

Definition 2

(Extremal subset, Extremal point). Let X be a vector space. Let $E\subseteq F\subseteq X$. We say that E satisfies the extremal condition with respect to F provided that the following property is satisfied:

$$\forall x,y\in F,\forall t\in (0,1):tx+(1-t)y\in E\Rightarrow x,y\in E.$$

(1)

Under this situation, we say that E is extremal in F. When an extremal subset $E=\left\{e\right\}$ is a singleton, then $\left\{e\right\}$ is called a extremal point of F. The set of extremal points of F is denoted by $\mathrm{ext}\left(F\right)$.

Notice that the non-empty intersection of any arbitrary family of extremal subsets is extremal as well. Also, if E is extremal in F and D is extremal in E, then D is extremal in F. Observe that if E is extremal in F, then $\mathrm{ext}\left(E\right)\subseteq \mathrm{ext}\left(F\right)$.

Example 1

(Supporting hyperplane). Let A be a non-empty subset of a vector space X and consider $f\in X^{*}$. The supporting hyperplane relative to f in A

$$F(f,A):=\{x\in A:f(x)=maxf(A\left)\right\}$$

is a extremal subset of A, provided that $F(f,A)\ne ⌀$. If X is normed and $A=B_X$, then we will simply write $F\left(f\right)$.

The extremal condition allows to define the geometrical concepts of face and facet. We would like to make the reader beware that the notions of face and facet in [3] is what we call later on in this manuscript an exposed face and a maximal face, respectively.

Definition 3

(Face, Extreme point). Let X be a normed space. Let $A\subseteq B_X$ be a subset of $B_X$. We shall say that A is a face of $B_X$ if A is convex and extremal in $B_X$. The extremal points of a convex subset $A\subseteq B_X$ are called extreme points.

It is easy to check that every extremal subset E of $B_X$ satisfies that either $E=B_X$ or $E\subseteq S_X$. As a consequence, proper faces of the unit ball are always contained in the unit sphere. Also, a point x is an extreme point of a convex set A if and only if $A\setminus \left\{x\right\}$ is also convex.

Definition 4

(Exposed face, Exposed point, Edge). Let X be a normed space. An exposed face of $B_X$ is a set of the form $F\left(f\right)$ for some $f\in S_{X^{*}}$. When an exposed face $F\left(f\right)=\left\{x\right\}$ is a singleton, then $\left\{x\right\}$ is called an exposed point of $B_X$. The set of exposed points of $B_X$ is denoted by $exp\left(B_X\right)$. Besides, we define an edge $E\left(f\right)$ of the unit ball with respect to $f\in S_{X^{*}}$ as $E\left(f\right)={\mathrm{bd}}_{f^{-1}\left(\left\{1\right\}\right)}\left(F\left(f\right)\right)$.

Observe that exposed faces are trivial examples of proper faces. On the other hand, it is trivial that $exp\left(B_X\right)\subseteq \mathrm{ext}\left(B_X\right)$. We want to make the reader notice that the definition of edge right above agrees with the one given in ([9], Theorem 1.1) and ([10], Section 3), and it differs from the one provided in ([27], Definition 1.2(2)).

Remark 1.

Let X be a normed space. If ${\left(C_n\right)}_{n\in \mathbb{N}}$ is a family of exposed faces of $B_X$ such that ${\bigcap }_{n\in \mathbb{N}}{C}_n\ne ⌀$, then ${\bigcap }_{n\in \mathbb{N}}{C}_n$ is an exposed face of $B_X$. Indeed, take $f_n\in S_{X^{*}}$ with $C_n=F\left(f_n\right)$ for all $n\in \mathbb{N}$. Then ${\bigcap }_{n\in \mathbb{N}}{C}_n=F\left(f\right)$ where $f:={\sum }_{n=1}^{\infty }\frac{1}{2^n}{f}_n$.

Definition 5

(Maximal face, Rotund point). Let X be a normed space. A maximal face of $B_X$ is a proper face that is a maximal element of the set of proper faces of $B_X$ endowed with the inclusion. When a maximal face $C=\left\{x\right\}$ of $B_X$ is a singleton, we call x a rotund point of $B_X$. The set of rotund points of $B_X$ is denoted by $rot\left(B_X\right)$.

In view of the Hahn-Banach Separation Theorem, one can see that every maximal face of the unit ball is an exposed face. In fact, maximal faces can be characterized as follows. Recall that a convex component is, by definition, a maximal convex subset. We refer the reader to [28] for a wider perspective on convex components. By relaying on the Hahn-Banach Separation Theorem, it is not hard to check (see also ([3], Lemma 1) or ([27], Lemma 2.7)) that the following are equivalent for a subset $C\subseteq S_X$:

• C is a convex component of $S_X$.
• C is a maximal face of $B_X$.
• C is a maximal exposed face of $B_X$.

Therefore, we will indistinctly talk about maximal faces of the unit ball and maximal convex subsets of the unit sphere. Also, note that $rot\left(B_X\right)\subseteq exp\left(B_X\right)\subseteq \mathrm{ext}\left(B_X\right)$. The following examples show the above contentions are strict for some kind of Banach spaces.

Example 2.

In ${\ell }_{\infty }^2$, each corner of the unit sphere is an example of an exposed point which is not rotund. If we smoothen the corners of $B_{{\ell }_{\infty }^2}$, then each extreme of any of the four edges is an extreme point which is not an exposed point.

The following result can be found in ([6], Lemma 5.1), ([10], Lemma 3.5), and ([11], Lemma 6.3).

Theorem 1

([6,10,11]). Let $X,Y$ be Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry and $C\subseteq S_X$ a maximal convex subset of $S_X$. Then $T\left(C\right)$ is a maximal face of $B_Y$.

The above theorem was originally proved in ([3], Lemma 13) in the finite dimensional case. In Corollary 7(1), we provide a new and simpler proof of Theorem 1 for a wide class of Banach spaces including the finite-dimensional spaces.

Definition 6

(Pre-maximal face, Proper exposed point). Let X be a normed space. A proper face A of $B_X$ is said to be a pre-maximal face of $B_X$ if A is the intersection of all maximal faces containing A. When a pre-maximal face is a singleton $A=\left\{x\right\}$, it is called a proper exposed point, and the set of all proper exposed points of $B_X$ is denoted by $pexp\left(B_X\right)$.

The term of proper exposed point defined right above was already coined by Tanaka in ([11], Definition 3.2). The following chain of inclusions is verified:

$$\mathrm{rot}\left(B_X\right)\subseteq \mathrm{pexp}\left(B_X\right)\subseteq \mathrm{ext}\left(B_X\right).$$

If X is separable, one can see by relying on Remark 1 or on ([11], Proposition 3.4) that:

$$\mathrm{rot}\left(B_X\right)\subseteq \mathrm{pexp}\left(B_X\right)\subseteq exp\left(B_X\right)\subseteq \mathrm{ext}\left(B_X\right).$$

The following interesting property, original from this work, is strongly motivated by ([11], Definition 3.2). It constitutes a very helpful tool to prove that certain spaces enjoy the MUp.

Definition 7

(Property P). Let X be a normed space. We say that X has property P or the P-property (Pp) if every proper face of $B_X$ is a pre-maximal face.

It is an interesting question whether every Banach space satisfying Pp also enjoys the MUp.

Problem 2.

If X is a Banach space enjoying Pp, does X have the MUp?

If the answer to the above problem was positive, then the next step would be to determine or characterize which Banach spaces verify Pp. This motivates the following question:

Problem 3.

Can every Banach space be equivalently renormed to satisfy Pp?

In Corollary 3, we approach the above question negatively by proving that reflexive Banach spaces and separable Banach spaces with dimension greater than or equal to 2 can be equivalently renormed to fail Pp.

As we mentioned before, in [3], Tingley calls facets to the maximal faces of the unit ball. Here, following ([27], Definition 1.2), we will give a different meaning to the notion of facet.

Definition 8

(Facet). Let X be a normed space. A proper face A of $B_X$ is called a facet of $B_X$ provided that ${\mathrm{int}}_{S_X}\left(A\right)\ne ⌀$. We will denote ${\mathcal{C}}_X:=\{C\subset S_X:C\mathrm{is}\mathrm{a}\mathrm{facet}\}$.

Remark 2.

Let $X,Y$ be Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry and $C\subseteq S_X$ a facet. Then ${\mathrm{int}}_{S_X}\left(C\right)\ne ⌀$, so ${\mathrm{int}}_{S_Y}\left(T\left(C\right)\right)\ne ⌀$ because T is a homeomorphism.

In ([27], Theorem 2.8), it was proved that facets of the unit ball are convex components of the unit sphere, hence they are maximal faces of the unit ball. A direct consequence of this fact together with Theorem 1 and Remark 2 is that surjective isometries between unit sphere preserve facets of the unit ball.

Corollary 1.

Let $X,Y$ be Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry. If $C\subseteq S_X$ a facet, then $T\left(C\right)$ is a facet of $B_Y$. In other words, $T\left({\mathcal{C}}_X\right)={\mathcal{C}}_Y$.

2.2. Starlike Structure

Starlike sets were originally introduced in [3] and characterized in ([3], Lemma 4 and Corollary 5).

Definition 9

(Starlike set). Let X be a normed space. The starlike set of a point $x\in S_X$ is defined as $\mathrm{s}\mathrm{t}(x,B_X):=\{y\in B_X:\Vert x+y\Vert =2\}$.

Observe that $\mathrm{s}\mathrm{t}(x,B_X)\subseteq S_X$ and $\mathrm{s}\mathrm{t}(-x,B_X)=-\mathrm{s}\mathrm{t}(x,B_X)$. Using metric spaces notation, the starlike set of x is precisely the sphere of center $-x$ and radius 2 in the metric space given by the unit sphere, that is, $\mathrm{s}\mathrm{t}(x,B_X)=S_{S_X}(-x,2)$. Another trivial way of characterizing the starlike set is the following:

$$\mathrm{s}\mathrm{t}(x,B_X)=\left\{y\in S_X:[y,x]\subseteq S_X\right\}=\bigcup \left\{C\subseteq S_X:C\mathrm{is}\mathrm{a}\mathrm{maximal}\mathrm{face}\mathrm{containing}x\right\}.$$

(2)

Remark 3.

Let $X,Y$ be metric spaces. Every isometry $T:X\to Y$ clearly satisfies, for all $x\in X$ and all $r>0$, that $T\left(B_X(x,r)\right)\subseteq B_Y(T\left(x\right),r)$, $T\left(U_X(x,r)\right)\subseteq U_Y(T\left(x\right),r)$, $T\left(S_X(x,r)\right)\subseteq S_Y(T\left(x\right),r)$. Furthermore, if T is surjective, then $T\left(B_X(x,r)\right)=B_Y(T\left(x\right),r)$, $T\left(U_X(x,r)\right)=U_Y(T\left(x\right),r)$, $T\left(S_X(x,r)\right)=S_Y(T\left(x\right),r)$.

In view of the previous remark, the following is immediate (see also ([3], Lemma 10 and Corollary 11)).

Remark 4.

Let $X,Y$ be Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry. For every $x\in S_X$,

$$T\mathrm{s}\mathrm{t}\left((x,B_X)\right)=T\left(S_{S_X}(-x,2)\right)=S_{S_Y}(T(-x),2)=S_{S_Y}(-(-T(-x)),2)=\mathrm{s}\mathrm{t}(-T(-x),B_Y).$$

The main theorem of [3], which is stated right below, shows that surjective isometries between unit spheres of finite dimensional Banach spaces preserve antipodal points.

Theorem 2

([3]). Let $X,Y$ be finite dimensional Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry. Then $T(-x)=-T\left(x\right)$ for every $x\in S_X$.

In ([5], Corollary 2.2), the following result was stated and proved. In ([6], Corollary 5.2), the same result was stated but its proof was omitted. Here, simply for the sake of completeness, we will include a different (and more direct) proof than the one given in ([5], Corollary 2.2). This proof strongly relies on Theorem 1.

Theorem 3

([5,6]). Let $X,Y$ be Banach spaces. Let $T:S_X\to S_Y$ be a surjective isometry. Then $T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(T\left(x\right),B_Y)$ for every $x\in S_X$.

Proof. 

In virtue of (2) together with Theorem 1, we have that

$$\begin{array}{ccc}\hfill T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)& =& T\left(\bigcup \left\{C\subseteq S_X:C\mathrm{is}\mathrm{a}\mathrm{maximal}\mathrm{face}\mathrm{containing}x\right\}\right)\hfill \\ & =& \bigcup \left\{T\left(C\right):C\mathrm{is}\mathrm{a}\mathrm{maximal}\mathrm{face}\mathrm{of}{B}_X\mathrm{containing}x\right\}\hfill \\ & =& \bigcup \left\{D\subseteq S_Y:D\mathrm{is}\mathrm{a}\mathrm{maximal}\mathrm{face}\mathrm{of}{B}_Y\mathrm{containing}T\left(x\right)\right\}\hfill \\ & =& \mathrm{s}\mathrm{t}(T\left(x\right),B_Y).\hfill \end{array}$$

□

In Corollary 7(2), we provide a different and more direct proof of Theorem 3 for a wide class of Banach spaces containing the finite-dimensional Banach spaces. On the other hand, a direct consequence of Theorem 3 together with Remark 4 is the following corollary, original from this work.

Corollary 2.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. Then $T(-\mathrm{s}\mathrm{t}(x,B_X))=-T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)$ for all $x\in S_X$.

Proof. 

It only suffices to rely on Theorem 3 and Remark 4:

$$T(-\mathrm{s}\mathrm{t}(x,B_X))=T\left(\mathrm{s}\mathrm{t}(-x,B_X)\right)=(T\mathrm{s}\mathrm{t}(-x),B_Y)=-\mathrm{s}\mathrm{t}(-T(-x),B_Y))=-T\left(\mathrm{s}\mathrm{t}(x,B_X)\right).$$

□

2.3. Smoothness

The following concepts are related to the smoothness properties of the unit ball. We refer the reader to [25,26,29] for a wider perspective on smoothness. First of all, we recall the definition of smoothness.

Definition 10

(Smooth space, smooth point). Let X be a normed space. A point $x\in S_X$ is called a smooth point of $B_X$ if there exists a unique functional $f\in S_{X^{*}}$ attaining its norm at x, in other words, $f\left(x\right)=1$. The set of smooth points of $B_X$ is denoted as $\mathrm{smo}\left(B_X\right)$. The normed space X is said to be smooth provided that $\mathrm{smo}\left(B_X\right)=S_X$.

Geometrically speaking, x is smooth if the unit ball $B_X$ has a unique supporting hyperplane at x. Notice that all the exposed faces of the unit ball are pairwise disjoint in smooth spaces.

Definition 11

(Dualilty mapping). Let X be a normed space. The duality mapping of X is defined as

$$\begin{array}{cccc}\hfill J:& \hfill X& \to & \mathcal{P}\left(X^{*}\right)\hfill \\ & \hfill x& \mapsto & J\left(x\right):=\left\{x^{*}\in X^{*}:x^{*}\left(x\right)=∥x^{*}∥\Vert x\Vert \right\}.\hfill \end{array}$$

(3)

The duality mapping induces the spherical image map.

Definition 12

(Spherical image map). Let X be a normed space. The spherical image map of X is defined as

$$\begin{array}{cccc}\hfill \nu :& \hfill S_X& \to & \mathcal{P}\left(S_{X^{*}}\right)\hfill \\ & \hfill x& \mapsto & \nu \left(x\right):=\left\{x^{*}\in S_{X^{*}}:x^{*}\left(x\right)=1\right\}.\hfill \end{array}$$

(4)

Notice that, for each $x\in S_X$, $\nu \left(x\right)=J\left(x\right)\cap S_{X^{*}}$, that is, $\nu \left(x\right)$ is the subset of $S_{X^{*}}$ whose members are the supporting functionals for $B_X$ at x. On the other hand, it is easy to understand that $\nu \left(x\right)=F\left(x\right)$, where x is seen as an element of $X^{**}$. Note that if $x\in \mathrm{smo}\left(B_X\right)$, then $\nu \left(x\right)$ is a singleton, so we will identify $\nu \left(x\right)$ with its only element. In this situation, $F\left(\nu \right(x\left)\right)$ is the only exposed face of $B_X$ containing x, thus $F\left(\nu \right(x\left)\right)$ is the only maximal face of $B_X$ containing x.

With the help of the spherical image map, we can provide an easy reformulation of the frame of a Banach space (see ([9], Theorem 1.1) and ([10], Section 3)).

Definition 13

(Frame). Let X be a normed space. The frame of $B_X$ is defined as

$$\mathrm{frm}\left(B_X\right):=\bigcup \left\{E\left(f\right):f\in \bigcup _{x\in S_X}\nu \left(x\right)\right\}.$$

In ([10], Theorem 3.7), it was proved that the frame of a Banach space is preserved under surjective isomeries between unit spheres.

Theorem 4

([10]). If $T:S_X\to S_Y$ is a surjective isometry between the unit spheres of Banach spaces $X,Y$, then $T\left(\mathrm{frm}\left(B_X\right)\right)=\mathrm{frm}\left(B_Y\right)$.

In Theorem 7, we provide a topological reformulation of the frame in terms of the relative topology of the unit sphere, which allows to provide a very simple proof ([10], Theorem 3.7) (see Theorem 11).

2.4. Inner Structure

We refer the reader to [30,31,32,33] for a wider perspective on these concepts. Inner structure was introduced for the first time in ([30], Definition 1.2) for non-convex sets, although it appears implicitly in [34,35] for convex sets. In this manuscript, we will only make use of inner structure of convex sets.

Definition 14

(Inner points). Let X be a vector space. Let M be a convex subset of X with at least two points. We define the set of inner points of M as

$$\mathrm{inn}\left(M\right):=\left\{x\in X:\forall m\in M\setminus \left\{x\right\}\exists n\in M\setminus \{m,x\}\mathrm{such}\mathrm{that}x\in (m,n)\right\}.$$

The set of inner points of a convex set is the infinite dimensional version of what Tingley calls “relative interior” of convex subsets of ${\mathbb{R}}^n$ in [3]. In fact, in ([30], Theorem 5.1) it is proved that every non-singleton convex subset of any finite dimensional vector space has inner points. However, in ([30], Corollary 5.3) it was shown that every infinite dimensional vector space possesses a non-singleton convex subset free of inner points.

Remark 5.

Under the settings of the previous definition, we convey that if M is a singleton, then $\mathrm{inn}\left(M\right)=⌀$. It is trivial that $\mathrm{inn}\left(M\right)\subseteq M$. In view of ([32], Remark 1.1), if $x\in \mathrm{inn}\left(M\right)$, then $[x,m)\subseteq \mathrm{inn}\left(M\right)$ for all $m\in M$. As a consequence, $\mathrm{inn}\left(M\right)$ is convex and $\mathrm{cl}\left(\mathrm{inn}\right(M\left)\right)=\mathrm{cl}\left(M\right)$. On the other hand, in ([32], Lemma 2.1), it was proved that if F is a extremal subset of M, then $F\cap \mathrm{inn}\left(M\right)=⌀$.

The following trivial remark we will be made use of later on and it will turn out to be crucial.

Remark 6.

Let X be a vector space. If $x,y,z\in X$ are three different points not aligned, then

$$\begin{array}{ccc}\hfill \mathrm{inn}\left(\mathrm{co}\right(\{x,y,z\}\left)\right)& =& \mathrm{co}\left(\right\{x,y,z\left\}\right)\setminus \left(\right[x,y]\cup [y,z]\cup [x,z\left]\right)\hfill \\ & =& \{rx+sy+tz:r,s,t\in (0,1),r+s+t=1\}.\hfill \end{array}$$

In ([6], Definition 2.1), the notion of non-supporting point was introduced.

Definition 15

(Non-support point). Let X be a vector space. Let A be a non-empty subset of X. Let $h\left(A\right):=\{f\in X^{*}:f\mathrm{attains}\mathrm{its}\sup \mathrm{at}A\mathrm{and}\mathrm{it}\mathrm{is}\mathrm{not}\mathrm{constant}\mathrm{on}A\}$. The set of non-support points of A is defined as $\mathrm{nsupp}\left(A\right):=A\setminus {\bigcup }_{f\in h\left(A\right)}F(f,A)$.

Notice that in the above definition it might occur that $h\left(A\right)$ be empty. For instance, if A is the open unit ball of a normed space, then $h\left(A\right)=⌀$. The following result, which is original from this work, unveils the relation between inner points and non-support points.

Theorem 5.

Let X be a vector space. Let C be a convex subset of X. If $h\left(C\right)\ne ⌀$, then $\mathrm{inn}\left(C\right)\subseteq \mathrm{nsupp}\left(C\right)$.

Proof. 

Fix an arbitrary $f\in h\left(C\right)$. By bearing in mind Example 1, we have that $F(f,C)$ is extremal in C. Next, we call on ([32], Lemma 2.1) (see also Remark 5) to conclude that $\mathrm{inn}\left(C\right)\cap F(f,C)=⌀$. This means that $\mathrm{inn}\left(C\right)\subseteq C\setminus F(f,C)$. The arbitrariness of $f\in h\left(C\right)$ implies that

$$\mathrm{inn}\left(C\right)\subseteq \bigcap _{f\in h\left(C\right)}C\setminus F(f,C)=C\setminus \bigcup _{f\in h\left(C\right)}F(f,C)=\mathrm{nsupp}\left(C\right).$$

□

The following remark is crucial towards finding geometric invariants under surjective isometries between unit spheres.

Remark 7.

Let X be a normed space. For every $x,y\in X\setminus \left\{0\right\}$, $\Vert x+y\Vert =\Vert x\Vert +\Vert y\Vert$ if and only if $\left[\frac{x}{\Vert x\Vert },\frac{y}{\Vert y\Vert }\right]\subseteq S_X$. Indeed, if $\Vert x+y\Vert =\Vert x\Vert +\Vert y\Vert$, then

$$\frac{\Vert x\Vert }{\Vert x+y\Vert }\frac{x}{\Vert x\Vert }+\frac{\Vert y\Vert }{\Vert x+y\Vert }\frac{y}{\Vert y\Vert }=\frac{x+y}{\Vert x+y\Vert }$$

is a strict convex combination contained in $S_X$, so then the whole segment $\left[\frac{x}{\Vert x\Vert },\frac{y}{\Vert y\Vert }\right]$ is contained in $S_X$. Conversely, if $\left[\frac{x}{\Vert x\Vert },\frac{y}{\Vert y\Vert }\right]\subseteq S_X$, then

$$\frac{x+y}{\Vert x\Vert +\Vert y\Vert }=\frac{\Vert x\Vert }{\Vert x\Vert +\Vert y\Vert }\frac{x}{\Vert x\Vert }+\frac{\Vert y\Vert }{\Vert x\Vert +\Vert y\Vert }\frac{y}{\Vert y\Vert }\in \left[\frac{x}{\Vert x\Vert },\frac{y}{\Vert y\Vert }\right]\subseteq S_X,$$

therefore, $\Vert x+y\Vert =\Vert x\Vert +\Vert y\Vert$.

Recall that a normed space X is said to be rotund or strictly convex provided that its unit sphere is free of non-trivial segments. This is equivalent to $\mathrm{ext}\left(B_X\right)=S_X$.

Remark 8.

Let X be a normed space. If $C\subseteq X$ is a convex subset containing at least three points not aligned, then $C\setminus \left\{c\right\}$ is connected for every $c\in C$.

2.5. Minkowski Functional

The following definition forms part of the folklore of the literature of Geometry of Topological Vector Spaces. We refer the reader to [36,37,38] for a deep perspective on the following concepts and on the Minkowski functional.

Definition 16.

Let X denote a vector space. A subset $A\subseteq X$ is said to be:

• Balanced provided that $[-1,1]A\subseteq A$.
• Absorbing provided that for all $x\in X$ there exists $\delta >0$ satisfying that $[-\delta ,\delta ]x\subseteq A$.
• Absolutely convex if A is balanced and convex.
• Linearly bounded if A does not contain straight lines or rays.

The Minkowski functional assures that every absorbing absolutely convex subset $A\subseteq X$ defines a seminorm on X:

$${\Vert x\Vert }_A:=inf\{\lambda \ge 0:x\in \lambda A\}.$$

If we let $U_X,B_X$ denote the open, closed unit balls of $(X,\Vert ·{\Vert }_A)$, respectively, then it is easy to check that $U_X=\mathrm{int}\left(A\right)$ and $B_X=\mathrm{cl}\left(A\right)$. Another trivial fact is that ${\Vert ·\Vert }_A$ is a norm on X if and only if A is linearly bounded.

Suppose now that X is a Banach space and A is a bounded, closed, absolutely convex subset of X with non-empty interior. Then the Minkowski functional on A defines an equivalent norm in X (keep in mind that every absolutely convex subset with non-empty interior in a topological vector space is a neighbourhood of 0).

We will rely on the following remark to construct a new unit ball in ${\mathbb{R}}^3$ that will serve as counterexample for several intuitive conjectures.

Remark 9.

Let X be a finite dimensional Banach space. Let K be a convex compact subset of X with non-empty interior. Suppose that there exists $x^{*}\in S_{X^{*}}$ such that $x^{*}\left(x\right)>0$ for all $x\in K$. Take $A:=\mathrm{co}(K\cup -K)$. Then A is compact, absolutely convex and a neighbourhood of 0. As a consequence, A defines an equivalent norm on X.

Lemma 1.

Under the settings of Remark 9, $\mathrm{ext}\left(A\right)\subseteq \mathrm{ext}\left(K\right)\cup \mathrm{ext}(-K)$.

Proof. 

Fix any $a\in \mathrm{ext}\left(A\right)$. There are $t\in [0,1]$ and $k_1,k_2\in K$ with $a=t{k}_1+(1-t)(-k_2)$. Since a is an extreme point of A, either $a=k_1$ or $a=-k_2$. Suppose without any loss of generality that $a=k_1$. Then $a\in \mathrm{ext}\left(A\right)\cap K\subseteq \mathrm{ext}\left(K\right)$. □

Recall that the Krein-Milman Theorem [39] assures that if X is a Hausdorff locally convex topological vector space and $K\subseteq X$ compact, then $\mathrm{ext}\left(K\right)\ne ⌀$. If, in addition, K is compact and convex, then $K=\overline{\mathrm{co}}\left(\mathrm{ext}\left(K\right)\right)$. As a consequence, if X is a reflexive Banach space and $C\subseteq X$ is closed, convex and bounded, then C is weakly closed and bounded, and thus weakly compact. Therefore, $\mathrm{ext}\left(C\right)\ne ⌀$.

3. Results

In this section, we will present the main results derived from this work on Tingley’s Problem.

3.1. Banach Spaces Lacking Pp

Our first result provides a sufficient condition for a Banach space to fail Pp.

Lemma 2.

Let X be a Banach space. If X is smooth and $\mathrm{ext}\left(B_X\right)\setminus \mathrm{rot}\left(B_X\right)\ne ⌀$, then X fails Pp.

Proof. 

Take any $e\in \mathrm{ext}\left(B_X\right)\setminus \mathrm{rot}\left(B_X\right)$. We will show X fails P by proving that $\left\{e\right\}$ is a face of $B_X$ that is not the intersection of all maximal faces containing it. Indeed, there exists a maximal face $C\subseteq S_X$ containing e. If D is another maximal face containing $\left\{e\right\}$, then there exists $x^{*}\in S_{X^{*}}$ such that $D=\{x\in S_X:x^{*}\left(x\right)=1\}$. Now, C is another maximal face, so there exists $y^{*}\in S_{X^{*}}$ such that $C=\{x\in S_X:y^{*}\left(x\right)=1\}$. Then $x^{*}\left(e\right)=1=y^{*}\left(e\right)$, which implies that $x^{*}=y^{*}$ because of the smoothness of X. As a consequence, $C=D$ is the only maximal face containing $\left\{e\right\}$. Finally, since $e\notin \mathrm{rot}\left(B_X\right)$, $C\ne \left\{e\right\}$. □

Lemma 3.

If Y is a 2-dimensional Banach space, then Y is isomorphic to a smooth space $Y^{\prime }$ such that $\mathrm{ext}\left(B_{Y^{\prime }}\right)\setminus \mathrm{rot}\left(B_{Y^{\prime }}\right)\ne ⌀$. If, in addition, Z is another Banach space, then $\mathrm{ext}\left(B_{Y^{\prime }}\right)\setminus \mathrm{rot}\left(B_{Y^{\prime }}\right)\subseteq \left(B_{X^{\prime }}\right)\setminus \mathrm{rot}\left(B_{X^{\prime }}\right)$, where $X^{\prime }:=Y^{\prime }{\oplus }_{2}Z$.

Proof. 

It suffices to smoothen the corners of $B_{{\ell }_{\infty }^2}$ and take $Y^{\prime }$ equal to ${\mathbb{R}}^2$ endowed with the norm given by this new unit ball. Since $Y^{\prime }$ is not strictly convex and its unit ball is compact, any non-singleton maximal face of $B_{Y^{\prime }}$ contains extreme points in view of the Krein-Milman Theorem. These extreme points are clearly not rotund points. □

We are now in the right position to state and prove the main theorem in this subsection.

Theorem 6.

If a Banach space X with dimension greater than or equal to 2 admits a smooth equivalent norm, then it can be equivalently renormed to be smooth and to verify that $\mathrm{ext}\left(B_X\right)\setminus \mathrm{rot}\left(B_X\right)\ne ⌀$. Thus, X fails Pp with this equivalent norm by Lemma 2.

Proof. 

First off, let us assume that X is already endowed with an equivalent smooth norm. Fix a 2-dimensional subspace Y of X. According to Lemma 3, Y is isomorphic to a smooth, but not strictly convex, 2-dimensional Banach space $Y^{\prime }$. Let Z be a closed subspace of X such that $X=Y\oplus Z$. Observe that X is isomorphic to $X^{\prime }:=Y^{\prime }{\oplus }_{2}Z$. Also, notice that $Y^{\prime }{\oplus }_{2}Z$ is smooth. In view of Lemma 3, we can find $e\in \mathrm{ext}\left(B_{Y^{\prime }}\right)\setminus \mathrm{rot}\left(B_{Y^{\prime }}\right)$. Finally, $e\in \left(B_{X^{\prime }}\right)\setminus \mathrm{rot}\left(B_{X^{\prime }}\right)$ in virtue of Lemma 3. □

Corollary 3.

Every reflexive or separable Banach space with dimension greater than or equal to 2 can be equivalently renormed to fail Pp.

Proof. 

It only suffices to take into consideration that reflexive Banach spaces ([40], Corollary 4) and separable Banach spaces ([29], Corollary 4.3(i)) admit an equivalent smooth renorming. □

We also refer the reader to [41] for other interesting renormings of reflexive spaces.

3.2. Geometric Structure of Facets and Frames

Some of the results in this subsection appear in a light version and in a scattered manner throughout the literature of the Geometry of Banach spaces. Those results are generalized here and all the proofs are provided for the sake of completeness. We refer the reader to [25,26,27,28,32] for more details about facets and frames.

Remark 10.

Let X be a normed space, $x\in X$, $r>0$ and $y\in B_X(x,r)\setminus \left\{x\right\}$. The extremes of the maximal segment of $B_X(x,r)$ containing $[x,y]$ are given by

$$\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y\mathrm{and}\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y.$$

(5)

Notice that these two points are in $S_X(x,r)$ and they are the only points of the segment

$$\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]$$

lying on $S_X(x,r)$.

Lemma 4.

Let X be a normed space with $dim\left(X\right)\ge 2$. Let $x\in S_X$, $f\in S_{X^{*}}$ with $f\left(x\right)=1$, and $r>0$. Then:

• If $B_X(x,r)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$, then $B_X\left(x,\frac{r}{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$.
• If $y\in S_X\setminus \left\{x\right\}$ is so that $[x,y]\subseteq S_X\cap f^{-1}\left(\left\{1\right\}\right)$, and $[u,v]$ is the maximal segment of $S_X$ containing $[x,y]$, then $u,v\in \mathrm{cl}\left(S_X\setminus f^{-1}\left(\left\{1\right\}\right)\right)$.
• If $B_X(x,r)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$, then $B_X(x,r)\cap S_X$ is convex and $r\le 1$. Even more, if $y\in \left(B_X(x,r)\cap S_X\right)\setminus \left\{x\right\}$, then $\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]\subseteq S_X$.
• If $B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$, then $r\le 1$ and there exists $0<s<r$ such that $B_X\left(x,s\right)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$.

Proof.

• Take any $y\in B_X\left(x,\frac{r}{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)$. Observe that $1=f\left(y\right)\le \Vert y\Vert$. Next,

  $$\begin{array}{ccc}\hfill ∥x-\frac{y}{\Vert y\Vert }∥& \le & \Vert x-y\Vert +∥y-\frac{y}{\Vert y\Vert }∥\hfill \\ & =& \Vert x-y\Vert +\frac{∥\Vert y\Vert y-y∥}{\Vert y\Vert }\hfill \\ & =& \Vert x-y\Vert +\frac{\left|\Vert y\Vert -1\right|\Vert y\Vert }{\Vert y\Vert }\hfill \\ & =& \Vert x-y\Vert +\left|\Vert y\Vert -1\right|\hfill \\ & =& \Vert x-y\Vert +\left|\Vert y\Vert -\Vert x\Vert \right|\hfill \\ & \le & 2\Vert y-x\Vert \hfill \\ & \le & r.\hfill \end{array}$$
  Therefore, $\frac{y}{\Vert y\Vert }\in B_X(x,r)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$. As a consequence, $f\left(\frac{y}{\Vert y\Vert }\right)=1$, which implies that $\Vert y\Vert =1$.
• It suffices to show that $u,v\notin {\mathrm{int}}_{S_X}\left(S_X\cap f^{-1}\left(\left\{1\right\}\right)\right)$. Suppose to the contrary that, for instance, $u\in {\mathrm{int}}_{S_X}\left(S_X\cap f^{-1}\left(\left\{1\right\}\right)\right)$. There exists $\alpha >0$ such that $B_X(u,\alpha )\cap S_X\subseteq S_X\cap f^{-1}\left(\left\{1\right\}\right)$. In virtue of Lemma 4(1), $B_X\left(u,\frac{\alpha }{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$. Then we can find $s<0$ sufficiently small such that $(1-s)u+sv\in B_X\left(u,\frac{\alpha }{2}\right)$. Clearly, $(1-s)u+sv\in f^{-1}\left(\left\{1\right\}\right)$ because $[x,y]\subseteq [u,v]$ and $[x,y]\subseteq f^{-1}\left(\left\{1\right\}\right)$, so $[u,v]\subseteq f^{-1}\left(\left\{1\right\}\right)$. As a consequence, $(1-s)u+sv\in B_X\left(u,\frac{\alpha }{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$. In particular, $[(1-s)u+sv,v]\subseteq B_X\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$. Finally, notice that $[u,v]⊊[(1-s)u+sv,v]\subseteq S_X$, contradicting the maximality of $[u,v]$.
• We will show first that $B_X(x,r)\cap S_X$ is convex. Take $y,z\in B_X(x,r)\cap S_X$ and $t\in [0,1]$. Notice that $ty+(1-t)z\in B_X(x,r)\cap B_X$. By hypothesis, $ty+(1-t)z\in f^{-1}\left(\left\{1\right\}\right)$, which implies that $\Vert ty+(1-t)z\Vert \ge \left|f\right(ty+(1-t)z\left)\right|=1$. As a consequence, $ty+(1-t)z\in S_X$. This shows that $B_X(x,r)\cap S_X$ is convex. Next, let us prove that $r\le 1$. Assume on the contrary that $r>1$. Observe that $x\in S_X=\mathrm{cl}\left(S_X\setminus \left\{x\right\}\right)$ because $dim\left(X\right)\ge 2$. Therefore, we can take $y\in \left(B_X(x,r)\cap S_X\right)\setminus \left\{x\right\}$. Since $B_X(x,r)\cap S_X$ is convex, we have that $[x,y]\subseteq B_X(x,r)\cap S_X$. According to Remark 10, the maximal segment of $B_X(x,r)$ containing $[x,y]$ is given by

  $$\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right].$$
  Denote by $[u,v]$ to the maximal segment of $S_X$ containing $[x,y]$. Let us distinguish between several cases:
  • $\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]\subseteq [u,v]$. In this case, since $[u,v]\subseteq S_X$, we obtain that

    $$\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\in S_X,$$

    reaching the contradiction that

    $$\begin{array}{ccc}\hfill 2& =& \mathrm{diam}\left(B_X\right)\hfill \\ & \ge & ∥\left[\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]-\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y\right]∥\hfill \\ & =& ∥2\frac{r}{\Vert x-y\Vert }(y-x)∥=2r>2.\hfill \end{array}$$
  • $\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]⊊[u,v]$. In this case, either u or v is in in the interior of the segment

    $$\left(\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right).$$
    By Remark 10,

    $$\left(\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right)\subseteq U_X(x,r).$$
    We can assume without any loss of generality that $u\in U_X(x,r)$. Let $\delta >0$ such that $B_X(u,\delta )\subseteq U_X(x,r)$. Notice that $[u,v]\subseteq f^{-1}\left(\left\{1\right\}\right)$ since $[x,y]\subseteq [u,v]$ and $[x,y]\subseteq B_X(x,r)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$. In accordance with Lemma 4(2), $u\in \mathrm{cl}\left(S_X\setminus f^{-1}\left(\left\{1\right\}\right)\right)$, so we can find $u^{\prime }\in \left(S_X\setminus f^{-1}\left(\left\{1\right\}\right)\right)\cap B_X(u,\delta )\subseteq U_X(x,r)\subseteq B_X(x,r)$. Finally, $u^{\prime }\in \left(B_X(x,r)\cap S_X\right)\setminus f^{-1}\left(\left\{1\right\}\right)$, which contradicts our hypothesis that $B_X(x,r)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$.
  As a consequence, $r\le 1$. Notice that, with $r\le 1$, for every $y\in \left(B_X(x,r)\cap S_X\right)\setminus \left\{x\right\}$ the first one of the above two bullets is possible, but not the second one, which implies that

  $$\left[\left(1+\frac{r}{\Vert x-y\Vert }\right)x-\frac{r}{\Vert x-y\Vert }y,\left(1-\frac{r}{\Vert x-y\Vert }\right)x+\frac{r}{\Vert x-y\Vert }y\right]\subseteq S_X.$$
• Suppose to the contrary that $r>1$. Since $dim\left(X\right)\ge 2$, we can find

  $$y\in \left(B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\right)\setminus \left\{x\right\}.$$
  Suppose that $\Vert y-x\Vert >1$. Then $2x-y\in B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$. Therefore, we reach the contradiction that

  $$2=\mathrm{diam}\left(B_X\right)\ge \Vert (2x-y)-y\Vert =2\Vert x-y\Vert >2.$$
  If $\Vert y-x\Vert \le 1$, then

  $$z:=\frac{r}{\Vert y-x\Vert }y+\left(1-\frac{r}{\Vert y-x\Vert }\right)x\in B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)$$

  and $\Vert z-x\Vert =r>1$. By using the same reasoning as before, we reach the contradiction that $\mathrm{diam}\left(B_X\right)>2$. As a consequence, $r\le 1$. Finally, let us show the existence of $0<s<r$ such that $B_X\left(x,s\right)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$. Take $0<s<r$ such that $s+\frac{s}{1-s}\le r$. Take any $y\in B_X\left(x,s\right)\cap S_X$. Observe that $f\left(y\right)=f\left(x\right)-f(x-y)=1-f(x-y)\ge 1-\Vert x-y\Vert \ge 1-s$. Next,

  $$\begin{array}{ccc}\hfill ∥x-\frac{y}{f\left(y\right)}∥& \le & \Vert x-y\Vert +∥y-\frac{y}{f\left(y\right)}∥\hfill \\ & =& \Vert x-y\Vert +\frac{∥f\left(y\right)y-y∥}{\left|f\right(y\left)\right|}\hfill \\ & =& \Vert x-y\Vert +\frac{\left|f\left(y\right)-1\right|\Vert y\Vert }{\left|f\right(y\left)\right|}\hfill \\ & =& \Vert x-y\Vert +\frac{\left|f\left(y\right)-f\left(x\right)\right|}{\left|f\right(y\left)\right|}\hfill \\ & \le & \Vert x-y\Vert +\frac{∥y-x∥}{\left|f\right(y\left)\right|}\hfill \\ & \le & s+\frac{s}{1-s}\hfill \\ & \le & r.\hfill \end{array}$$
  Therefore, $\frac{y}{f\left(y\right)}\in B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$. As a consequence, $∥\frac{y}{f\left(y\right)}∥=1$, which implies that $f\left(y\right)=1$.

□

The following proposition is an extension of ([27], Lemma 2.1).

Proposition 1.

Let X be a normed space. Let $C\subset S_X$ be a convex subset, and let $f\in S_{X^{*}}$ such that $C\subseteq F\left(f\right)$. Then ${\mathrm{int}}_{S_X}\left(C\right)={\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$ and ${\mathrm{bd}}_{S_X}\left(C\right)={\mathrm{bd}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$. In particular, $E\left(f\right)={\mathrm{bd}}_{S_X}\left(F\left(f\right)\right)$.

Proof. 

Fix an arbitrary $x\in {\mathrm{int}}_{S_X}\left(C\right)\ne ⌀$. There exists $r>0$ such that $B_X(x,r)\cap S_X\subseteq C$. We will show that $B_X\left(x,\frac{r}{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq C$, which implies that $x\in {\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$. For this, by taking into consideration that $B_X(x,r)\cap S_X\subseteq C$, it only suffices to show that $B_X\left(x,\frac{r}{2}\right)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq S_X$, which is already given by Lemma 4(1). Conversely, fix an arbitrary $x\in {\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)\ne ⌀$. There exists $r>0$ such that $B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq C$. In view of Lemma 4(4), we know that $r\le 1$ and there exists $0<s<r$ such that $B_X\left(x,s\right)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$. We will prove that $B_X\left(x,s\right)\cap S_X\subseteq C$, which implies that $x\in {\mathrm{int}}_{S_X}\left(C\right)$. However, by taking into consideration that $B_X(x,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq C$, it only suffices with $B_X\left(x,s\right)\cap S_X\subseteq f^{-1}\left(\left\{1\right\}\right)$. Finally, since both $S_X$ and $f^{-1}\left(\left\{1\right\}\right)$ are closed in X, we have that $\mathrm{cl}\left(C\right)={\mathrm{cl}}_{S_X}\left(C\right)={\mathrm{cl}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$, therefore

$${\mathrm{bd}}_{S_X}\left(C\right)={\mathrm{cl}}_{S_X}\left(C\right)\setminus {\mathrm{int}}_{S_X}\left(C\right)={\mathrm{cl}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)\setminus {\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)={\mathrm{bd}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right).$$

□

Lemma 5.

Let X be a normed space. If $C\subset S_X$ is a facet, then:

• C is a convex component of $S_X$, that is, a maximal convex subset of $S_X$.
• There exists a unique $f\in S_{X^{*}}$ such that $C\subseteq F\left(f\right)$, which verifies that $C=F\left(f\right)$.
• If $c\in {\mathrm{int}}_{S_X}\left(C\right)$ and $f\in \nu \left(c\right)$, then $C=F\left(f\right)$.
• ${\mathrm{int}}_{S_X}\left(C\right)\subseteq \mathrm{smo}\left(B_X\right)$.
• If $c\in in{t}_{S_X}\left(C\right)$ and $f\in \nu \left(c\right)$, then $C-c$ is a closed convex neighbourhood of 0 in $ker\left(f\right)$. In particular, ${\mathrm{int}}_{S_X}\left(C\right)$ is dense in C and $\mathrm{inn}\left(C\right)={\mathrm{int}}_{S_X}\left(C\right)$.

Proof.

• Let D be a convex subset of $S_X$ strictly containing C. Fix an arbitrary $d\in D\setminus C$. Take any $c\in {\mathrm{int}}_{S_X}\left(C\right)$. By relying on the Hahn-Banach Separation Theorem, there exists $f\in S_{X^{*}}$ such that $C\subseteq D\subseteq F\left(f\right)$. In view of Proposition 1, $c\in {\mathrm{int}}_{S_X}\left(C\right)={\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$, so there exists a ball $B_X(c,r)$ such that $B_X(c,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq C$. There exists $t>1$ sufficiently closed to 1 such that $tc+(1-t)d\in B_X(c,r)$. Notice that $tc+(1-t)d\in f^{-1}\left(\left\{1\right\}\right)$, thus $tc+(1-t)d\in B_X(c,r)\cap f^{-1}\left(\left\{1\right\}\right)\subseteq C$. Since C is a face of $B_X$, we conclude that $d\in C$.
• The maximality of C already implies the existence of $f\in S_{X^{*}}$ such that $C=F\left(f\right)$. Suppose that there exists other $g\in S_{X^{*}}$ such that $C=F\left(g\right)$. In view of Proposition 1, we have that ${\mathrm{int}}_{S_X}\left(C\right)={\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)={\mathrm{int}}_{g^{-1}\left(\left\{1\right\}\right)}\left(C\right)$. Fix any arbitrary $c\in in{t}_{S_X}\left(C\right)$. Observe that ${\mathrm{int}}_{ker\left(f\right)}(C-c)={\mathrm{int}}_{ker\left(g\right)}(C-c).$ Next, observe that $C\subseteq f^{-1}\left(\left\{1\right\}\right)\cap g^{-1}\left(\left\{1\right\}\right)$, thus $C-c\subseteq ker\left(f\right)\cap ker\left(g\right)$. This implies that $ker\left(f\right)=ker\left(g\right)$ and so $f=g$.
• Suppose that there exists $y\in C\setminus F\left(f\right)$. Then $f\left(y\right)<1$. Take $g\in S_{X^{*}}$ such that $C=F\left(g\right)$. According to Proposition 1, we can fix $r>0$ such that $B_X(c,r)\cap g^{-1}\left(\left\{1\right\}\right)\subseteq C$. We can find $t<0$ sufficiently closed to 0 such that $ty+(1-t)c\in B_X(c,r)$.Note that $y,c\in C=F\left(g\right)$, thus $ty+(1-t)c\in F\left(g\right)=C$. As a consequence, $ty+(1-t)c\in B_X(c,r)\cap g^{-1}\left(\left\{1\right\}\right)\subseteq C\subseteq S_X$. However, we obtain the contradiction $1\ge f(ty+(1-t\left)c\right)=tf\left(y\right)+1-t=1-t(1-f(y\left)\right)>1$.
• If $c\in {\mathrm{int}}_{S_X}\left(C\right)$ and $f,g\in \nu \left(c\right)$, then by the previous item $C=F\left(f\right)=F\left(g\right)$. Finally, by (2) we have that $f=g$. This shows that $x\in \mathrm{smo}\left(B_X\right)$.
• It only suffices to take into consideration that ${\mathrm{int}}_{S_X}\left(C\right)={\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$ and that the translation

  $$\begin{array}{ccc}\hfill X& \to & X\hfill \\ \hfill x& \mapsto & x-c\hfill \end{array}$$

  is a homeomorphism mapping $f^{-1}\left(\left\{1\right\}\right)$ to $ker\left(f\right)$, C to $C-c$, ${\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)$ to ${\mathrm{int}}_{ker\left(f\right)}(C-c)$, and c to 0. In order to show that ${\mathrm{int}}_{S_X}\left(C\right)$ is dense in C, note that $C-c$ is a convex set with non-empty interior in $ker\left(f\right)$, so it is well known that ${\mathrm{cl}}_{ker\left(f\right)}\left({\mathrm{int}}_{ker\left(f\right)}(C-c)\right)={\mathrm{cl}}_{ker\left(f\right)}\left(C-c\right).$ Thus, by undoing the translation, we obtain $\mathrm{cl}\left({\mathrm{int}}_{S_X}\left(C\right)\right)=\mathrm{cl}\left({\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)\right)={\mathrm{cl}}_{f^{-1}\left(\left\{1\right\}\right)}\left({\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)\right)={\mathrm{cl}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)=\mathrm{cl}\left(C\right).$ Finally, let us see that $\mathrm{inn}\left(C\right)={\mathrm{int}}_{S_X}\left(C\right)$. Indeed, we use again the fact that $C-c$ is a convex set with non-empty interior in $ker\left(f\right)$, so we call on ([33], Lemma 5(6)) to conclude that $\mathrm{inn}(C-c)={\mathrm{int}}_{ker\left(f\right)}(C-c)$. Since translations preserve inner points ([30], Proposition 1.3), we conclude that $\mathrm{inn}\left(C\right)={\mathrm{int}}_{f^{-1}\left(\left\{1\right\}\right)}\left(C\right)={\mathrm{int}}_{S_X}\left(C\right)$.

□

The final result in this section is a characterization of frames. This characterization serves to provide an immediate proof of ([10], Theorem 3.7) (see also Theorem 4).

Theorem 7.

Let X be a normed space. Then

$$\mathrm{frm}\left(B_X\right)=S_X\setminus \bigcup _{C\in {\mathcal{C}}_X}{\mathrm{int}}_{S_X}\left(C\right).$$

Proof. 

We will strongly rely on Proposition 1. Let $x\in S_X\setminus {\bigcup }_{C\in {\mathcal{C}}_X}{\mathrm{int}}_{S_X}\left(C\right)$. By Hahn-Banach, there exists $x^{*}\in S_{X^{*}}$ such that $x\in F\left(x^{*}\right)$. If ${\mathrm{int}}_{S_X}\left(F\left(x^{*}\right)\right)=⌀$, then $F\left(x^{*}\right)=E\left(x^{*}\right)$, so $x\in E\left(x^{*}\right)\subseteq \mathrm{frm}\left(B_X\right)$. If ${\mathrm{int}}_{S_X}\left(F\left(x^{*}\right)\right)\ne ⌀$, then $F\left(x^{*}\right)\in {\mathcal{C}}_X$, therefore $x\notin {\mathrm{int}}_{S_X}\left(F\left(x^{*}\right)\right)$ therefore $x\in F\left(x^{*}\right)\setminus {\mathrm{int}}_{S_X}\left(F\left(x^{*}\right)\right)={\mathrm{bd}}_{S_X}\left(F\left(x^{*}\right)\right)=E\left(x^{*}\right)$. Conversely, let $x\in \mathrm{frm}\left(B_X\right)$. Suppose on the contrary that there exists $C\in {\mathcal{C}}_X$ such that $x\in {\mathrm{int}}_{S_X}\left(C\right)$. Since ${\mathrm{int}}_{S_X}\left(C\right)\subseteq \mathrm{smo}\left(B_X\right)$, there exists a unique $f\in S_{X^{*}}$ such that $C=F\left(f\right)$. By hypothesis, there exists $g\in S_{X^{*}}$ such that $x\in E\left(g\right)\subseteq F\left(g\right)$. Since x is a smooth point, $f=g$, which produces the following contradiction: $x\in {\mathrm{int}}_{S_X}\left(C\right)={\mathrm{int}}_{S_X}\left(F\left(g\right)\right)$ and $x\in {\mathrm{bd}}_{S_X}\left(F\left(g\right)\right)$. □

As a direct consequence of Theorem 7, we obtain the following corollary, the details of whose proof we spare to the reader as a simple topology exercise.

Corollary 4.

Let X be a normed space. The following conditions are equivalent:

• ${\mathrm{int}}_{S_X}\left(\mathrm{frm}\left(B_X\right)\right)=⌀$.
• ${\bigcup }_{C\in {\mathcal{C}}_X}{\mathrm{int}}_{S_X}\left(C\right)$ is dense in $S_X$.

3.3. Flatness

In ([42], Definition 11), the notion of starlike hull was introduced and studied for general starlike sets. Here, we propose the term of starlike envelope for subsets of the unit sphere of a normed space, which fits our purposes much better.

Definition 17.

Let X be a normed space. Let $E\subseteq S_X$. The starlike envelope of E is defined as

$$\mathrm{s}\mathrm{t}\left(E\right):=\bigcap _{e\in E}\mathrm{s}\mathrm{t}(e,B_X).$$

Furthermore, we will say that:

• E is almost flat if $[e,f]\subseteq S_X$ for all $e,f\in E$.
• E is flat if $\mathrm{co}\left(E\right)\subseteq S_X$.
• E is starlike compatible if $E\subseteq \mathrm{s}\mathrm{t}\left(E\right)$.
• E is starlike generated if $E=\mathrm{s}\mathrm{t}\left(E\right)$.

It is clear that every flat set is almost flat. It is also trivial to check that a subset of the unit sphere is almost flat if and only if E is starlike compatible. We will explore next the relations between the previous concepts and will provide an example of a unit ball in ${\mathbb{R}}^3$ containing an almost flat set which is not flat.

Notice that convex subsets of the unit sphere are trivially flat. In general, any subset of the unit sphere who is contained in a convex subset of the unit sphere is flat. As a consequence, in view of the Hahn-Banach Separation Theorem, a subset of the unit sphere is flat if and only if it is contained in a exposed face of the unit ball.

Lemma 6.

Let X be a normed space. Let $E\subseteq S_X$. Then:

• If E is convex, then E is flat and starlike compatible.
• E is almost flat if and only if E is starlike compatible.
• If E is flat, then E is almost flat.
• E is flat if and only if $\mathrm{co}\left(E\right)\subseteq \mathrm{s}\mathrm{t}\left(E\right)$.
• If E is flat and D is a convex component of $S_X$ containing E, then $D\subseteq \mathrm{s}\mathrm{t}\left(E\right)$.
• If E is a convex component of $S_X$, then E is starlike generated.
• If E is convex and starlike generated, then E is a convex component.

Proof.

• It is trivial that E is flat. In order to check that E is starlike compatible, it only suffices to notice that if $e,f\in E$, then $[e,f]\subseteq S_X$, therefore $f\in \mathrm{s}\mathrm{t}(e,B_X)$, that is, $E\subseteq \mathrm{s}\mathrm{t}(e,B_X)$ for all $e\in E$.
• Immediate by bearing in mind (2).
• Trivial by definition.
• Suppose first that E is flat, then $\mathrm{co}\left(E\right)\subseteq S_X$, so $[x,e]\subseteq \mathrm{co}\left(E\right)\subseteq S_X$ for all $x\in \mathrm{co}\left(E\right)$, meaning that $x\in \mathrm{s}\mathrm{t}(e,B_X)$ for all $x\in \mathrm{co}\left(E\right)$ and all $e\in E$, that is, $\mathrm{co}\left(E\right)\subseteq \mathrm{s}\mathrm{t}\left(E\right)$. Conversely, assume that $\mathrm{co}\left(E\right)\subseteq \mathrm{s}\mathrm{t}\left(E\right)$, then $\mathrm{co}\left(E\right)\subseteq \mathrm{s}\mathrm{t}\left(E\right)\subseteq S_X$, so E is flat.
• Fix an arbitrary $d\in D$. For every $e\in E$, $[e,d]\subseteq D\subseteq S_X$, thus $d\in \mathrm{s}\mathrm{t}\left(E\right)$. The arbitrariness of $d\in D$ means that $D\subseteq \mathrm{s}\mathrm{t}\left(E\right)$.
• We know by (1) that $E\subseteq \mathrm{s}\mathrm{t}\left(E\right)$. Fix an arbitrary $x\in \mathrm{s}\mathrm{t}\left(E\right)$. Notice that

  $$\mathrm{co}(E\cup \left\{x\right\})=\bigcup _{e\in E}[e,x]\subseteq S_X$$

  because $[x,e]\subseteq S_X$ for all $e\in E$. The maximality of E implies that $E=\mathrm{co}\left(\right\{x\}\cup E)$, so $x\in E$. This shows that $E=\mathrm{s}\mathrm{t}\left(E\right)$, hence E is starlike generated.
• By (1) we know that E is flat. Let us show now that E is a convex component of $S_X$. Indeed, let D be any convex subset of $S_X$ containing E. Fix an arbitrary $d\in D$. Take any $e\in E$. Then $[d,e]\subseteq D\subseteq S_X$. By (2), $d\in \mathrm{s}\mathrm{t}(e,B_X)$. The arbitrariness of $e\in E$ shows that

  $$d\in \bigcap _{e\in E}\mathrm{s}\mathrm{t}(e,B_X)=\mathrm{s}\mathrm{t}\left(E\right)=E.$$
  The arbitrariness of $d\in D$ implies that $D\subseteq E$. This proves that E is a convex component of $S_X$.

□

Example 3

(Almost flat set which is not flat). This example serves to show the existence of almost flat sets which are not flat. It strongly relies on Remark 9 and Lemma 1. The unit ball displayed in the next figures is a convex polyhedron whose facets are equilateral triangles and diamonds. An easy way to construct this unit ball is by taking a regular octahedron and placing a regular tetrahedron (with the same triangles) on top and the opposite tetrahedron on the bottom. If E denotes the set of all four vertices of the top regular tetrahedron, then E is clearly almost flat but not flat, since $\mathrm{co}\left(E\right)$ is the whole regular tetrahedron, which is clearly not contained in the boundary of the previous unit ball.

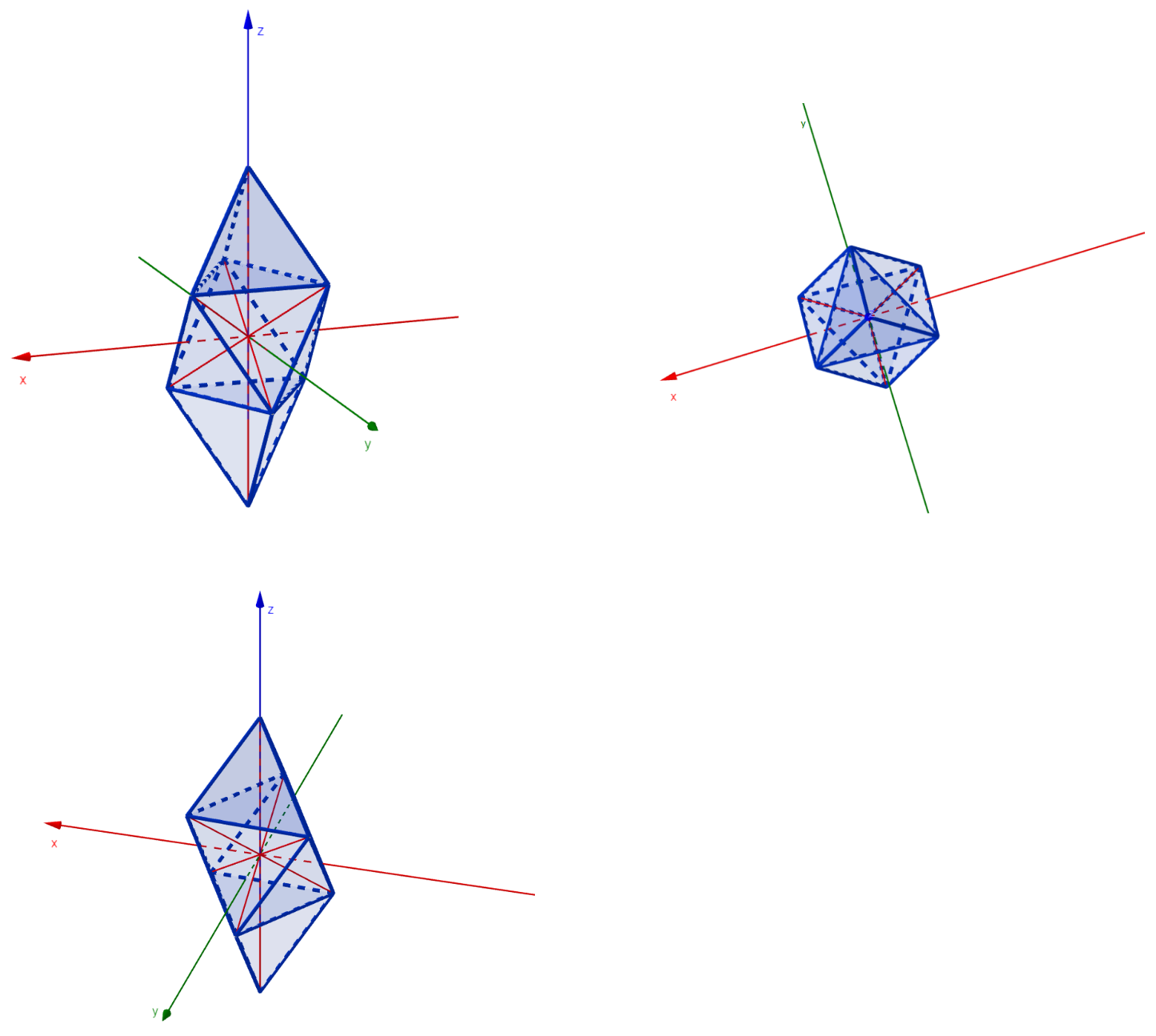
The previous example motivates the following definition.

Definition 18

(Flat property). A normed space is said to have the flat property or the F-property (Fp) if every almost flat subset of its unit sphere is flat.

Example 3 shows the existence of Banach spaces lacking the Fp. In fact, the next theorem shows that every Banach space with dimension greater than or equal to 3 can be equivalently renormed to fail Fp.

Theorem 8.

Let X be a Banach space with $dim\left(X\right)\ge 3$. There exists an equivalent norm on X for which X fails Fp.

Proof. 

Let Y be a 3-dimensional subspace of X. There exists a closed subspace Z of X such that $X=Y\oplus Z$. Since Y is isomorphic to the 3-dimensional Banach space given in Example 3, we may endow Y with the equivalent norm provided by the unit ball of Example 3, which we can call $Y^{\prime }$. If we keep the same norm in Z, then X is clearly isomorphic to $X^{\prime }:=Y^{\prime }{\oplus }_{2}Z$, which trivially fails Fp because so does $Y^{\prime }$. □

The following lemma shall be an useful tool to determine conditions for a convex subset of the unit ball to be contained in the unit sphere. It also provides a sufficient condition for an almost flat set to be flat.

Lemma 7.

Let X be a normed space. Let D be a convex subset of $B_X$. Then:

• If $\mathrm{inn}\left(D\right)\cap S_X\ne ⌀$, then $D\subseteq S_X$.
• If $D\subseteq S_X$ is almost flat and there exists $d\in D$ such that $d\in \mathrm{inn}\left(\mathrm{co}\right(D\left)\right)$, then D is flat.

Proof.

• Fix $d_0\in \mathrm{inn}\left(D\right)\cap S_X$. Take any $d\in D\setminus \left\{d_0\right\}$. By hypothesis, there exists $e\in D\setminus \{d_0,d\}$ such that $d_0\in (d,e)$. Since $d,e\in D\subseteq B_X$, it must necessarily occur that $[d,e]\subseteq S_X$.
• Notice that $d\in \mathrm{inn}\left(\mathrm{co}\left(D\right)\right)\cap S_X$, thus, by Lemma 7(1), $\mathrm{co}\left(D\right)\subseteq S_X$.

□

Lemma 8(1) constitutes the generalization of ([3], Lemma 2) to infinite dimensions. Lemma 8(2,5) are the infinite dimensional version of ([3], Corollary 3).

Lemma 8.

Let X be a normed space. Let $E\subseteq S_X$. Then:

• If E is a face of $B_X$, $e\in \mathrm{inn}\left(E\right)$ and $y\in S_X$ is so that $[e,y]\subseteq S_X$, then $\mathrm{co}(E\cup \left\{y\right\})\subseteq S_X$ and $E\subseteq \mathrm{s}\mathrm{t}(y,B_X)$.
• If E is a convex component of $S_X$ and there exists $e\in E$ such that E is the only convex component of $S_X$ containing e, then $E=\mathrm{s}\mathrm{t}(e,B_X)$.
• If E is a facet of $B_X$, then every $e\in {\mathrm{int}}_{S_X}\left(E\right)$ satisfies that E is the only convex component of $S_X$ containing e.
• If E is a convex component of $S_X$ for which there exists a dense sequence ${\left(e_n\right)}_{n\in \mathbb{N}}$ in E such that $e:={\sum }_{n=1}^{\infty }\frac{e_n}{2^n}$ is convergent, then E is the only convex component of $S_X$ containing e.
• If E is a maximal face of $B_X$ with $\mathrm{inn}\left(E\right)\ne ⌀$, then every $e\in \mathrm{inn}\left(E\right)$ satisfies that E is the only convex component of $S_X$ containing e.

Proof.

• Observe that $\mathrm{co}(E\cup \left\{y\right\})={\bigcup }_{d\in E}[d,y]$. By hypothesis, we already know that $[e,y]\subseteq S_X$. So, fix an arbitrary $d\in E\setminus \left\{e\right\}$. Since $e\in \mathrm{inn}\left(E\right)$, there exists $c\in E\setminus \{e,d\}$ such that $e\in (d,c)$. If $d,c,y$ are aligned, then the convexity and the extremal condition satisfied by E force that $y\in E$, hence we trivially obtain that $\mathrm{co}(E\cup \left\{y\right\})=E\subseteq S_X$ and $E\subseteq \mathrm{s}\mathrm{t}(y,B_X)$. Thus, let us assume that $d,c,y$ are not aligned. Then we can call on Remark 6 to conclude that $(e,y)\subseteq \mathrm{inn}\left(\mathrm{co}\right(\{d,c,y\}\left)\right)$. Finally, since $(e,y)\subseteq S_X$, by applying Lemma 7, we have that $\mathrm{co}\left(\{d,c,y\}\right)\subseteq S_X$. In particular, $[d,y]\subseteq S_X$. The arbitrariness of $d\in E\setminus \left\{e\right\}$ shows that $\mathrm{co}(E\cup \left\{y\right\})\subseteq S_X$, hence $E\subseteq \mathrm{s}\mathrm{t}(y,B_X)$.
• We know by Lemma 6(1) that $E\subseteq \mathrm{s}\mathrm{t}(e,B_X)$. Take any $x\in \mathrm{s}\mathrm{t}(e,B_X)$. Then $\Vert x+e\Vert =2$, that is, $[x,e]\subseteq S_X$. We can find a convex component D of $S_X$ containing $[x,e]$. By hypothesis, $E=D$, thus $x\in E$.
• It is sufficient to call on Lemma 5(3) to conclude that every $e\in {\mathrm{int}}_{S_X}\left(E\right)$ is a smooth point of $B_X$ and then it clearly satisfies that E is the only convex component of $S_X$ containing e.
• Let $D\subseteq S_X$ be a convex component of $S_X$ containing e. There exists a functional $g\in S_{X^{*}}$ such that $D=F\left(g\right)$. Since $e\in D$, we have that $g\left(e\right)=1$, which implies that $g\left(e_n\right)=1$ for all $n\in \mathbb{N}$. The density of ${\left(e_n\right)}_{n\in \mathbb{N}}$ in E assures that $g\left(E\right)=\left\{1\right\}$, in other words, $E\subseteq F\left(g\right)=D$. This fact contradicts the maximality of E.
• Let F be another maximal face of $B_X$ containing e. Fix any arbitrary $d\in E\setminus \left\{e\right\}$. There exists $c\in E\setminus \{d,e\}$ such that $e\in (d,c)$. The extremal condition satisfied by F forces that $d,c\in F$. The arbitrariness of $d\in E\setminus \left\{e\right\}$ implies that $E\subseteq F$. The maximality of E means that $E=F$.

□

Theorem 9.

Let X be a normed space. For every $x\in S_X$, $\mathrm{s}\mathrm{t}(x,B_X)$ satisfies the extremal condition with respect to $B_X$. Even more, if $\mathrm{s}\mathrm{t}(x,B_X)$ is convex, then $\mathrm{s}\mathrm{t}(x,B_X)$ is the only maximal face of $B_X$ containing x.

Proof. 

Take any $x_1,x_2\in B_X$ and $t\in (0,1)$ such that $t{x}_1+(1-t)x_2\in \mathrm{s}\mathrm{t}(x,B_X)$. By $\left(\right)$, there exists a maximal face C such that $t{x}_1+(1-t)x_2\in C$, in particular, C satisfies the extremal condition, which implies that $x_1,x_2\in C\subseteq \mathrm{s}\mathrm{t}(x,B_X)$. Now suppose that $\mathrm{s}\mathrm{t}(x,B_X)$ is also convex, and therefore it is a face by definition. Let D be a maximal face of $B_X$ containing x. By using again (2), $D\subseteq \mathrm{s}\mathrm{t}(x,B_X)$. As a consequence, $\mathrm{s}\mathrm{t}(x,B_X)$ is the only maximal face of $B_X$ containing x. □

The set of rotund points of the unit ball can be described in terms of starlike sets.

Remark 11.

Let X be a normed space. Then

$$\mathrm{rot}\left(B_X\right)=\left\{x\in S_X:\mathrm{s}\mathrm{t}(x,B_X)=\left\{x\right\}\right\}.$$

The following result combined with Theorem 9 constitute a generalization of ([43], Lemma 2.7).

Theorem 10.

Let X be a normed space. If $x\in \mathrm{smo}\left(B_X\right)$, then $\mathrm{s}\mathrm{t}(x,B_X)$ is convex. Even more, $\mathrm{s}\mathrm{t}(x,B_X)=F\left(\nu \left(x\right)\right)$.

Proof. 

The smoothness of x implies that there is only one exposed face of $B_X$ containing x, which is precisely $F\left(\nu \right(x\left)\right)$, hence there is only one maximal face of $B_X$ containing x. By (2), $\mathrm{s}\mathrm{t}(x,B_X)$ coincides with that maximal face. □

3.4. Preservation of Flatness and Faces under Surjective Isometries

We will begin by providing a very simple proof of ([10], Theorem 3.7), by simply relying on Theorem 1, Remark 2, and Theorem 7.

Theorem 11.

If $T:S_X\to S_Y$ is a surjective isometry between the unit spheres of Banach spaces $X,Y$, then $T\left(\mathrm{frm}\left(B_X\right)\right)=\mathrm{frm}\left(B_Y\right)$.

Proof. 

By relying on Theorem 7, by taking into consideration that T is a homeomorphism, and by noticing that $T\left({\mathcal{C}}_X\right)={\mathcal{C}}_Y$ (see Theorem 1 together with Remark 2), we have that

$$\begin{array}{ccc}\hfill T\left(\mathrm{frm}\left(B_X\right)\right)& =& T\left(S_X\setminus \bigcup _{C\in {\mathcal{C}}_X}{\mathrm{int}}_{S_X}\left(C\right)\right)=T\left(S_X\right)\setminus \bigcup _{C\in {\mathcal{C}}_X}T\left({\mathrm{int}}_{S_X}\left(C\right)\right)\hfill \\ & =& T\left(S_X\right)\setminus \bigcup _{C\in {\mathcal{C}}_X}{\mathrm{int}}_{S_Y}\left(T\left(C\right)\right)=S_Y\setminus \bigcup _{D\in {\mathcal{C}}_Y}{\mathrm{int}}_{S_Y}\left(D\right)\hfill \\ & =& \mathrm{frm}\left(B_Y\right).\hfill \end{array}$$

□

Example 4.

Let X be a Banach space such that the frame of its unit ball has empty interior relative to the unit sphere, that is, ${\mathrm{int}}_{S_X}\left(\mathrm{frm}\left(B_X\right)\right)=⌀$. If Y is another Banach space such that there exists a surjective isometry $T:S_X\to S_Y$, then $T\left(\mathrm{frm}\left(B_X\right)\right)=\mathrm{frm}\left(B_Y\right)$ according to Theorem 11. Even more, since T is a homeomorphism, we conclude that

$${\mathrm{int}}_{S_Y}\left(\mathrm{frm}\left(B_Y\right)\right)={\mathrm{int}}_{S_Y}\left(T\left(\mathrm{frm}\left(B_X\right)\right)\right)=T\left({\mathrm{int}}_{S_X}\left(\mathrm{frm}\left(B_X\right)\right)\right)=T(⌀)=⌀.$$

We would like to make the reader beware that Theorem 12(2) and Theorem 12(5) state the same sentence in view of Lemma 6(2). We have just included both items in the following theorem because Theorem 12(5) does not need to rely on Theorem 3 whereas Theorem 12(2) does.

Theorem 12.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. Let $E\subseteq S_X$. Then:

• $T\left(\mathrm{s}\mathrm{t}\right(E\left)\right)=\mathrm{s}\mathrm{t}\left(T\right(E\left)\right)$.
• If E is starlike compatible, then $T\left(E\right)$ is starlike compatible.
• If E is starlike generated, then $T\left(E\right)$ is starlike generated.
• If E is flat, then $T\left(E\right)$ is flat.
• If E is almost flat, then $T\left(E\right)$ is almost flat.

Proof.

• Simply keep in mind Theorem 3 to observe that

  $$\begin{array}{ccc}\hfill T\left(\mathrm{s}\mathrm{t}\right(E\left)\right)& =& T\left(\bigcap _{e\in E}\mathrm{s}\mathrm{t}(e,B_X)\right)=\bigcap _{e\in E}T\left(\mathrm{s}\mathrm{t}(e,B_X)\right)\hfill \\ & =& \bigcap _{e\in E}\mathrm{s}\mathrm{t}(T\left(e\right),B_Y)=\bigcap _{d\in T\left(E\right)}\mathrm{s}\mathrm{t}(d,B_Y)=\mathrm{s}\mathrm{t}\left(T\left(E\right)\right).\hfill \end{array}$$
• By definition, $E\subseteq \mathrm{s}\mathrm{t}\left(E\right)$, so $T\left(E\right)\subseteq T\left(\mathrm{s}\mathrm{t}\right(E\left)\right)=\mathrm{s}\mathrm{t}\left(T\right(E\left)\right)$, meaning that $T\left(E\right)$ is starlike compatible.
• Follows a similar proof as right above.
• By definition, $\mathrm{co}\left(E\right)\subseteq S_X$. Let D be a convex component of $S_X$ containing $\mathrm{co}\left(E\right)$. In view of Theorem 1, $T\left(D\right)$ is a convex component of $S_Y$. Since $E\subseteq \mathrm{co}\left(E\right)\subseteq D$, we obtain that $T\left(E\right)\subseteq T\left(\mathrm{co}\right(E\left)\right)\subseteq T\left(D\right)$. The convexity of $T\left(D\right)$ allows that $\mathrm{co}\left(T\left(E\right)\right)\subseteq T\left(D\right)\subseteq S_Y$, meaning that $T\left(E\right)$ is flat.
• Fix arbitrary elements $e,f\in E$. We have to prove that $[T\left(e\right),T\left(f\right)]\subseteq S_Y$. By hypothesis, since E is almost flat, we have that $[e,f]\subseteq S_X$. There exists a convex component F of $S_X$ containing $[e,f]$. By Theorem 1, $T\left(F\right)$ is a maximal face of $B_Y$. Notice also that $T\left(\right[e,f\left]\right)\subseteq T\left(F\right)$ since $[e,f]\subseteq F$. Therefore, $T\left(e\right),T\left(f\right)\in T\left(F\right)$. Finally, the convexity of $T\left(F\right)$ allows that $[T\left(e\right),T\left(f\right)]\subseteq T\left(F\right)\subseteq S_Y$.

□

Example 5.

Let us consider ${\mathbb{R}}^3$ endowed with the unit ball given in Example 3. In the first place, note that this unit ball is a convex polyhedron, therefore, ${\mathbb{R}}^3$ endowed with this unit ball satisfies MUp by keeping in mind ([8], Theorem 4.5). On the other hand, we have already seen in Example 3 that the set E consisting of all four vertices of the top regular tetrahedron is almost flat but not flat. Finally, any of the diamonds that compose the boundary of the unit ball is a maximal convex component, hence starlike generated in view of Lemma 6(6).

Let X be a normed space. For every flat subset C of $S_X$, we will denote

$$M_C:=\left\{D\subseteq S_X:D\mathrm{is}\mathrm{a}\mathrm{maximal}\mathrm{face}\mathrm{of}{B}_X\mathrm{containing}C\right\}.$$

Notice that $M_C=M_{\mathrm{co}\left(C\right)}$. If $C=\left\{c\right\}$ is a singleton, then we will simply write $M_c$. The following result relies on Theorem 1.

Theorem 13.

Let $X,Y$ be Banach spaces and consider a surjective isometry $T:S_X\to S_Y$. Let E be a flat subset of $S_X$. Then:

• $T\left(M_E\right)=M_{T\left(E\right)}$.
• If X has Pp and E is a face of $B_X$, then $T\left(E\right)$ is a face of $B_Y$.

Proof.

• Fix any arbitrary $D\in M_E$. By Theorem 1, $T\left(D\right)$ is a maximal face of $B_Y$ containing $T\left(E\right)$. Therefore, $T\left(D\right)\in M_{T\left(E\right)}$. This shows that $T\left(M_E\right)\subseteq M_{T\left(E\right)}$. The reverse inclusion can be accomplished by using $T^{-1}$.
• By hypothesis, since X has Pp, $E={\bigcap }_{D\in M_E}D$. Next, $T\left(E\right)$ is flat by Theorem 12(4), therefore, $T\left(M_E\right)=M_{T\left(E\right)}$ by (1). Notice,

  $$T\left(E\right)=T\left(\bigcap _{D\in M_E}D\right)=\bigcap _{D\in M_E}T\left(D\right)=\bigcap _{C\in M_{T\left(E\right)}}C.$$
  This means that $T\left(E\right)$ is an intersection of (maximal) faces of $B_Y$, thus $T\left(E\right)$ is a face of $B_Y$.

□

Lemma 9.

Let X be a normed space and let $x,y\in S_X$. Then:

• If $\nu \left(x\right)\subseteq \nu \left(y\right)$, then $M_x\subseteq M_y$.
• If $x,y\in \mathrm{smo}\left(B_X\right)$ and $M_x\subseteq M_y$, then $M_x=M_y$ and $\nu \left(x\right)=\nu \left(y\right)$.
• $\mathrm{s}\mathrm{t}(x,B_X)\subseteq \mathrm{s}\mathrm{t}(y,B_X)$ if and only if $M_x\subseteq M_y$.
• $\mathrm{s}\mathrm{t}(x,B_X)=\mathrm{s}\mathrm{t}(y,B_X)$ if and only if $M_x=M_y$.

Proof.

• Take any $D\in M_x$. Since maximal faces are exposed faces, there exists $f\in S_{X^{*}}$ such that $D=F\left(f\right)$. Then $f\in \nu \left(x\right)\subseteq \nu \left(y\right)$. This implies that $f\left(y\right)=1$, hence $y\in F\left(f\right)=D$ and $D\in M_y$.
• In accordance with Theorems 9 and 10, we have that $M_x=\left\{\mathrm{s}\mathrm{t}(x,B_X)\right\}$ and $M_y=\left\{\mathrm{s}\mathrm{t}(y,B_X)\right\}$, so both $M_x$ and $M_y$ are singletons, so they must be equal because $M_x\subseteq M_y$. By calling again on Theorem 10, we have that $F\left(\nu \left(x\right)\right)=\mathrm{s}\mathrm{t}(x,B_X)=\mathrm{s}\mathrm{t}(y,B_X)=F\left(\nu \left(y\right)\right)$. The smoothness of x and y forces that $\nu \left(x\right)=\nu \left(y\right)$.
• Suppose first that $\mathrm{s}\mathrm{t}(x,B_X)\subseteq \mathrm{s}\mathrm{t}(y,B_X)$. Let $D\in M_x$. It is clear that $D\subseteq \mathrm{s}\mathrm{t}(x,B_X)$ in view of (2). We will show that $\mathrm{co}(D\cup \left\{y\right\})\subseteq S_X$. Indeed, notice that $\mathrm{co}(D\cup \left\{y\right\})={\bigcup }_{d\in D}[d,y]$. Notice that, by assumption $D\subseteq \mathrm{s}\mathrm{t}(x,B_X)\subseteq \mathrm{s}\mathrm{t}(y,B_X)$, so $[d,y]\subseteq S_X$ for every $d\in D$. As a consequence, $\mathrm{co}(D\cup \left\{y\right\})={\bigcup }_{d\in D}[d,y]\subseteq S_X$. Since D is a maximal face of $B_X$, we conclude that $\mathrm{co}(D\cup \{y\left\}\right)=D$, hence $y\in D$. This proves that $D\in M_y$. The arbitrariness of $D\in M_x$ shows that $M_x\subseteq M_y$. Conversely, suppose that $M_x\subseteq M_y$. By relying again on (2), we have that

  $$\mathrm{s}\mathrm{t}(x,B_X)=\bigcup M_x\subseteq \bigcup M_y=\mathrm{s}\mathrm{t}(y,B_X).$$
• It is a direct consequence of Lemma 9(3).

□

The converse to Lemma 9(1) does not hold true as shown in the following example.

Example 6.

Let $X:={\mathbb{R}}^2$ endowed with the norm provided by the unit ball resulting from the intersection of the Euclidean ball $B_{{\ell }_2^2}$ with the band $\left\{(x_1,x_2)\in {\mathbb{R}}^2:-\frac{1}{2}\le x_2\le \frac{1}{2}\right\}$. Take $x:=\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)$ and $y:=\left(0,\frac{1}{2}\right)$. Notice that $M_x=M_y=\left\{\left[\left(\frac{-\sqrt{3}}{2},\frac{1}{2}\right),\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)\right]\right\}$. However, $\nu \left(x\right)⊈\nu \left(y\right)$ because $y\in \mathrm{smo}\left(B_X\right)$ and $x\notin \mathrm{smo}\left(B_X\right)$, which implies that $\nu \left(y\right)$ is a singleton and $\nu \left(x\right)$ is infinite.

Corollary 5.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. If Y is smooth, then $\nu \left(T\right(-x\left)\right)=-\nu \left(T\right(x\left)\right)$.

Proof. 

On the one hand, $T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=(-T(-x),B_Y)$ by Remark 4. On the other hand, $T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(T\left(x\right),B_X)$ by Theorem 3. By combining the two previous equalities, we obtain that $\mathrm{s}\mathrm{t}(-T(-x),B_Y)=\mathrm{s}\mathrm{t}(T\left(x\right),B_Y)$. In accordance with Lemma 9(4), $M_{-T(-x)}=M_{T\left(x\right)}$, and Lemma 9(2) assures that $-\nu \left(T\right(-x\left)\right)=\nu (-T(-x\left)\right)=\nu \left(T\right(x\left)\right)$. □

The following result provides a very simple proof of Theorem 1 for singleton maximal faces of the unit ball. Recall that singleton maximal faces of the unit ball are precisely the rotund points.

Theorem 14.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. Then $T\left(\mathrm{rot}\left(B_X\right)\right)=\mathrm{rot}\left(B_Y\right)$. Even more, $T(-x)=-T\left(x\right)$ for all $x\in \mathrm{rot}\left(B_X\right)$.

Proof. 

Fix an arbitrary $x\in \mathrm{rot}\left(B_X\right)$. Since $\left\{x\right\}$ is a maximal face of $B_X$, we have that $\left\{x\right\}=\mathrm{s}\mathrm{t}(x,B_X)$ (see Remark 11). Then, by Remark 4,

$$\left\{T\left(x\right)\right\}=T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(-T(-x),B_Y).$$

Since $-T(-x)\in \mathrm{s}\mathrm{t}(-T(-x),B_Y)$, we conclude that $-T(-x)=T\left(x\right)$ and $\{-T(-x)\}=\mathrm{s}\mathrm{t}(-T(-x),B_Y)$, which implies that $-T(-x)\in \mathrm{rot}\left(B_Y\right)$ in virtue of Remark 11, hence $T(-x)\in \mathrm{rot}\left(B_Y\right)$. If we repeat the same argument with $-x\in \mathrm{rot}\left(B_X\right)$, we end up having that $T\left(x\right)\in \mathrm{rot}\left(B_Y\right)$. This shows that $T\left(\mathrm{rot}\left(B_X\right)\right)\subseteq \mathrm{rot}\left(B_Y\right)$. By using the same reasoning with $T^{-1}$, we obtain the desired equality. □

Corollary 6.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. If X is strictly convex, then so is Y.

The previous results motivate the following definition.

Definition 19

(Inner property). A normed space X is said to have the inner property or the I-property (Ip) if it is strictly convex or all the non-singleton maximal faces of $B_X$ have inner points.

According to ([30], Theorem 5.1), every finite dimensional Banach space satisfies the Ip. The following example shows the existence of infinite dimensional Banach spaces lacking the Ip.

Example 7.

A Banach space X is called transitive if for every $x,y\in S_X$ there exists a surjective linear isometry $T:X\to X$ such that $T\left(x\right)=y$. In ([44], Corollary 2.21), it is shown that every Banach space can be isometrically regarded as a subspace of a suitable transitive Banach space. With this in hand, if we take any non-strictly convex Banach space Y, there exists a transitive Banach space X such that X contains a subspace isomometrically isomorphic to Y. Then X cannot be strictly convex because it contains a non-strictly convex subspace. According to ([45], Theorem 3.2), all non-singleton maximal faces of $B_X$ are free of inner points. As a consequence, X does not satisfy the Ip.

Another example of Banach space lacking the Ip follows.

Example 8.

Consider the space of all absolute summable sequences

$${\ell }_1:=\left\{{\left(x_n\right)}_{n\in \mathbb{N}}\in {\mathbb{R}}^{\mathbb{N}}:\sum _{n=1}^{\infty }\left|x_n\right|<\infty \right\},$$

with the norm given by

$${∥{\left(x_n\right)}_{n\in \mathbb{N}}∥}_1:=\sum _{n=1}^{\infty }\left|x_n\right|.$$

Notice that

$$D:=\left\{{\left(x_n\right)}_{n\in \mathbb{N}}\in S_{{\ell }_1}:x_n\ge 0\forall n\in \mathbb{N}\right\}$$

is a maximal face of $B_{{\ell }_1}$. In virtue of ([30], Theorem 5.4), $\mathrm{inn}\left(D\right)=⌀$. As a consequence, ${\ell }_1$ fails Ip.

The following theorem generalizes ([3], Lemmas 12 and 13) to infinite dimensions.

Theorem 15.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. Let $F\subseteq S_X$ be a maximal face with $\mathrm{inn}\left(F\right)\ne ⌀$. Then:

• $T(-F)=-T\left(F\right)$.
• If there exists $x\in \mathrm{inn}\left(F\right)$ for which there exists $E\in M_{T\left(x\right)}$ with $\mathrm{inn}\left(E\right)\ne ⌀$, then $T\left(F\right)\subseteq E$.

Proof.

• Fix an arbitrary $x\in \mathrm{inn}\left(F\right)$. In virtue of Lemma 8(2,5), we have that $F=\mathrm{s}\mathrm{t}(x,B_X)$. By Remark 6, $T\left(F\right)=T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(-T(-x),B_Y)$, so $-T(-x)\in T\left(F\right)$, hence $T(-x)\in -T\left(F\right)$. The arbitrariness of $x\in \mathrm{inn}\left(F\right)$ means that $T(-\mathrm{inn}(F\left)\right)\subseteq -T\left(F\right)$. Since $\mathrm{inn}\left(F\right)$ is dense in F by Remark 5, T is continuous, and $T\left(F\right)$ is closed in $S_Y$, we deduce that $T(-F)\subseteq -T\left(F\right)$. Finally, $-F$ is also a maximal face of $B_X$ with $\mathrm{inn}\left(F\right)\ne ⌀$, so $T\left(F\right)\subseteq -T(-F)$, obtaining the desired equality.
• Fix any $e\in \mathrm{inn}\left(E\right)$. By Lemma 8(2,5), we have that $E=\mathrm{s}\mathrm{t}(e,B_Y)$. By Remark 4, $T^{-1}\left(E\right)=\left(-T^{-1}(-e),B_X\right)$. Since $x\in T^{-1}\left(E\right)$, we obtain that $\left[x,-T^{-1}(-e)\right]\subseteq S_X$, hence, by Lemma 8(1), $F\subseteq \left(-T^{-1}(-e),B_X\right)$. Thus, $F\subseteq T^{-1}\left(E\right)$ and $T\left(F\right)\subseteq E$.

□

The reader may observe that ([3], Lemma 13) has already been fully generalize to infinite dimensions in |([6], Lemma 5.1) and in ([10], Lemma 3.5) (see also Theorem 1). However, here in Corollary 7(1) we propose an alternative and simpler proof for the case that the Banach spaces satisfy the Ip. In Corollary 7(2), we propose an alternative and easier proof of Theorem 3 without having to rely on Theorem 1.

Corollary 7.

Let $X,Y$ be Banach spaces and let $T:S_X\to S_Y$ be a surjective isometry. Suppose that both $X,Y$ satisfy the Ip. Then:

• If $F\subseteq S_X$ is a maximal face of $B_X$, then $T\left(F\right)$ is a maximal face of $B_Y$.
• $T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(T\left(x\right),B_Y)$ for all $x\in S_X$.

Proof.

• If $F=\left\{x\right\}$ is a singleton, then $x\in \mathrm{rot}\left(B_X\right)$ and we only need to call on Theorem 14. Thus, let us assume that F is not a singleton. BY hypothesis, $\mathrm{inn}\left(F\right)\ne ⌀$, hence we can fix any $x\in \mathrm{inn}\left(F\right)$. Take any $E\in M_{T\left(x\right)}$. By hypothesis, $\mathrm{inn}\left(E\right)\ne ⌀$, therefore, by Theorem 15(2), $T\left(F\right)\subseteq E$. Next, take any $e\in \mathrm{inn}\left(E\right)$ and any $D\in M_{T^{-1}\left(e\right)}$. Since $\mathrm{inn}\left(D\right)\ne ⌀$ by hypothesis, we can apply again Theorem 15(2) to conclude that $T^{-1}\left(E\right)\subseteq D$. Thus, we end up with the chain of inclusions $F\subseteq T^{-1}\left(E\right)\subseteq D$. The maximality of F forces that $F=T^{-1}\left(E\right)=D$.
• We will rely on Lemma 9, so it only suffices to prove that $M_{T\left(x\right)}=M_{-T(-x)}$ because $T\left(\mathrm{s}\mathrm{t}(x,B_X)\right)=\mathrm{s}\mathrm{t}(-T(-x),B_Y)$ in view of Remark 4. Indeed, let $C\in M_{T\left(x\right)}$. Then $x\in T^{-1}\left(C\right)$, so $-x\in -T^{-1}\left(C\right)=T^{-1}(-C)$ in virtue of Theorem 15(1), therefore $T(-x)\in -C$, that is, $-T(-x)\in C$, hence $C\in M_{-T(-x)}$. The arbitrariness of $C\in M_{T\left(x\right)}$ means that $M_{T\left(x\right)}\subseteq M_{-T(-x)}$. Following a similar reasoning, we obtain the reverse inclusion, concluding with the desired equality.

□

Example 9.

According to Example 7, there exists a Banach space X which is transitive, not strictly convex, and whose unit ball $B_X$ contains a maximal face C such that $\mathrm{inn}\left(C\right)=⌀$. Notice that $\mathrm{rot}\left(B_X\right)=⌀$, since otherwise, the transitivity of X forces that $\mathrm{rot}\left(B_X\right)=S_X$, meaning that X is strictly convex. As a consequence, $\mathrm{rot}\left(B_X\right)=⌀$. If Y is another Banach space and $T:S_X\to S_Y$ is a surjective isometry, then we can conclude that $T\left(C\right)$ is a maximal face of $B_Y$ in view of Theorem 1 and $\mathrm{rot}\left(B_Y\right)=⌀$ according to Theorem 14.

Example 9 motivates the following result. First, let us recall that a topological space is said to be homogeneous provided that any two points there exists a homeomorphism on the space mapping one to another.

Theorem 16.

Let X be a transitive Banach space, Y a Banach space, and $T:S_X\to S_Y$ a surjective isometry. Then $S_Y$ is homogeneous. If, in addition, X is separable, then Y is strictly convex.

Proof. 

Fix arbitrary elements $y_1,y_2\in S_Y$. Since X is transitive, there exists a surjective linear isometry $S:X\to X$ such that $S\left(T^{-1}\left(y_1\right)\right)=T^{-1}\left(y_2\right)$. Next, it only suffices to consider the surjective isometry $T\circ S\circ T^{-1}:S_Y\to S_Y$, which is clearly a homeormorphism and maps $y_1$ to $y_2$. Finally, if X is separable, then X is strictly convex in view of ([46], Theorem 28). As a consequence, Y is strictly convex as well by bearing in mind Corollary 6. □

3.5. Invariance of Segments

This final subsection is aimed at studying the invariance of segments under surjective isometries between unit spheres.

Theorem 17.

Let $X,Y$ be Banach spaces and $T:S_X\to S_Y$ a surjective isometry. Let $x,y\in S_X$ with $x\ne y$ and $[x,y]\subseteq S_X$. If $T\left(\right[x,y\left]\right)$ is convex, then $T\left(\right[x,y\left]\right)=\left[T\right(x),T(y\left)\right]$ and T is affine on $[x,y]$, that is, $T(tx+(1-t\left)y\right)=tT\left(x\right)+(1-t)T\left(y\right)$ for all $t\in [0,1]$.

Proof. 

Note that $T\left(\right[x,y\left]\right)$ is compact and convex. In fact, $T\left(\right[x,y\left]\right)$ is homeomorphic to $[x,y]$. Let us prove first that $T\left(\right[x,y\left]\right)$ is a segment. Suppose on the contrary that $T\left(\right[x,y\left]\right)$ is not a segment. Since it is convex by hypothesis, it contains at least three points not aligned. Then $[x,y]\setminus \left\{\frac{x+y}{2}\right\}$ is not connected, thus $T\left([x,y]\setminus \left\{\frac{x+y}{2}\right\}\right)=T\left([x,y]\right)\setminus \left\{T\left(\frac{x+y}{2}\right)\right\}$ is not connected either. However, Remark 8 assures that it is connected. As a consequence, $T\left(\right[x,y\left]\right)$ is a segment, so $T\left(\right[x,y\left]\right)=[a,b]$ for some $a,b\in S_Y$. Let $t,s\in [0,1]$ in such a way that $T(tx+(1-t\left)y\right)=a$ and $T(sx+(1-s\left)y\right)=b$. Since isometries preserve diameters, we obtain that

$$\begin{array}{ccc}\hfill \Vert x-y\Vert & =& \mathrm{diam}\left(\right[x,y\left]\right)\hfill \\ & =& \mathrm{diam}\left(T\right([x,y]\left)\right)\hfill \\ & =& \Vert a-b\Vert \hfill \\ & =& \Vert T(tx+(1-t\left)y\right)-T(sx+(1-s\left)y\right)\Vert \hfill \\ & =& \Vert tx+(1-t)y-(sx+(1-s\left)y\right)\Vert \hfill \\ & =& |t-s|\Vert x-y\Vert .\hfill \end{array}$$

Thus, the only possibility is that $|t-s|=1$, hence either $t=0$ and $s=1$, or $t=0$ and $s=1$. In any case, $T\left(\right[x,y\left]\right)=\left[T\right(x),T(y\left)\right]$. Let us finally prove that T is affine on $[x,y]$. Indeed, fix an arbitrary $t\in (0,1)$. There exists $s\in (0,1)$ such that $T(tx+(1-t\left)y\right)=sT\left(x\right)+(1-s)T\left(y\right)$. Following similar reasoning as above,

$$\begin{array}{ccc}\hfill (1-s)\Vert x-y\Vert & =& (1-s)\Vert T\left(x\right)-T\left(y\right)\Vert \hfill \\ & =& \Vert \left(sT\right(x)+(1-s\left)T\right(y\left)\right)-T\left(x\right)\Vert \hfill \\ & =& \Vert T(tx+(1-t\left)y\right)-T\left(x\right)\Vert \hfill \\ & =& \Vert (tx+(1-t\left)y\right)-x\Vert \hfill \\ & =& (1-t)\Vert x-y\Vert .\hfill \end{array}$$

As a consequence, we obtain that $t=s$. □

As a direct consequence of Theorem 17 together with Theorem 1, we obtain the following corollary.

Corollary 8.

Let $X,Y$ be Banach spaces and $T:S_X\to S_Y$ a surjective isometry. Let $x,y\in S_X$ with $x\ne y$ and $[x,y]\subseteq S_X$. If $[x,y]$ is a maximal face of $B_X$, then T is affine on $[x,y]$, that is, $T(tx+(1-t\left)y\right)=tT\left(x\right)+(1-t)T\left(y\right)$ for all $t\in [0,1]$.

Proof. 

By Theorem 1, $T\left(\right[x,y\left]\right)$ is a maximal face of $B_Y$, so it is convex. Finally, Theorem 17 does the rest. □

Example 10.

In ([47], Example 3.8), a 3-dimensional Banach space was constructed whose unit ball only contains rotund points except for two maximal segments. These two maximal segments are, in fact, maximal faces, so this unit ball satisfies the conditions of Corollary 8.

4. Discussion

As we mention in the introduction, in ([23], Corollary 3.8) it is proved that every 2-dimensional non-strictly convex Banach space satisfies the MUp. Here, we propose the following idea to prove that every 2-dimensional strictly convex Banach space satisfies the MUp, by relying on ([23], Corollary 3.8). The idea is to make a slight perturbation on the unit ball of a strictly convex 2-dimensional Banach space to introduce a small segment in its unit sphere. This way we obtain a non-strictly convex 2-dimensional Banach space whose unit ball is very similar to the one of the strictly convex space. The point is to redefine an isometry.

This renorming technique to introduce a facet in the unit sphere has already been used in [48,49,50]. Let X be a Banach space. For every $0<t<1$ and every $x^{*}\in X^{*}$ with $\Vert x^{*}\Vert =1$,

$$\mathcal{B}:=B_X\cap {\left(x^{*}\right)}^{-1}\left([-t,t]\right)$$

(6)

is a bounded, closed, absolutely convex subset of X with nonempty interior, thus it defines an equivalent norm on X, ${\Vert ·\Vert }_{\mathcal{B}}$, satisfying that:

• $\mathcal{B}\subseteq B_X$, hence $\Vert ·\Vert \le {\Vert ·\Vert }_{\mathcal{B}}$.
• $\mathrm{int}\left(\mathcal{B}\right)=U_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right)$.
• $\mathrm{bd}\left(\mathcal{B}\right)=\left[S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right)\right]\cup \left[B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right)\right]$.
• $B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t\}\right)$ and $B_X\cap {\left(x^{*}\right)}^{-1}\left(\left\{t\right\}\right)$ are maximal faces of $\mathcal{B}$ with non-empty interior relative to $\mathrm{bd}\left(\mathcal{B}\right)$.

Now, let $X,Y$ be Banach spaces and $T:S_X\to S_Y$ a surjective isometry between their unit spheres. Now we apply the renorming given by (6) to both $X,Y$ to obtain ${\mathcal{B}}_X,{\mathcal{B}}_Y$, respectively. In order to obtain ${\mathcal{B}}_X$, the idea is to choose $0<t<1$ very small and to take $x^{*}\in S_{X^{*}}$ in such a way that $x^{*}$ attains its norm at a smooth point a of $B_X$, that is, $x^{*}=\nu \left(a\right)$. To obtain ${\mathcal{B}}_Y$, we choose the same t and an element $y^{*}\in \nu \left(T\left(a\right)\right).$ Next, it is precise to transport T to a surjective isometry $\tilde{T}:\mathrm{bd}\left({\mathcal{B}}_X\right)\to \mathrm{bd}\left({\mathcal{B}}_Y\right)$ in such a way that $\tilde{T}\left(x\right)=T\left(x\right)$ for all $x\in S_X\cap {\left(x^{*}\right)}^{-1}\left([-t,t]\right)$. To accomplish this, it is necessary to compute $\Vert x_1-x_2{\Vert }_{{\mathcal{B}}_X}$ and $\Vert y_1-y_2{\Vert }_{{\mathcal{B}}_Y}$ for all $x_1,x_2\in \mathrm{bd}\left({\mathcal{B}}_X\right)$ and all $y_1,y_2\in \mathrm{bd}\left({\mathcal{B}}_Y\right)$. The following technical lemmas are devoted to achieve this.

Lemma 10.

Let X be a Banach space. Let $0<t<1$ and $x^{*}\in X^{*}$ with $\Vert x^{*}\Vert =1$. Let $\mathcal{B}:=B_X\cap {\left(x^{*}\right)}^{-1}\left([-t,t]\right)$. For every $x\in X\setminus \left\{0\right\}$,

$${\Vert x\Vert }_{\mathcal{B}}=\left\{\begin{array}{cc}\hfill \Vert x\Vert & \mathrm{if}\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right),\hfill \\ \hfill \frac{|x^{*}\left(x\right)|}{t}& \mathrm{if}\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right).\hfill \end{array}\right.$$

Proof. 

Fix an arbitrary $x\in X\setminus \left\{0\right\}$. Notice that $\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in \mathrm{bd}\left(\mathcal{B}\right)=\left[S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right)\right]\cup \left[B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right)\right]$. Therefore, we have two possibilities:

• $\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right)$. In this case, $∥\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}∥=1$, so $\Vert x\Vert ={\Vert x\Vert }_{\mathcal{B}}$.
• $\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right).$ In this case, $\left|x^{*}\left(\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\right)\right|=t$, hence ${\Vert x\Vert }_{\mathcal{B}}=\frac{|x^{*}\left(x\right)|}{t}$.

□

Notice that, under the settings of the previous lemma, if $\frac{x}{{\Vert x\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right)$, then ${\Vert x\Vert }_{\mathcal{B}}=\Vert x\Vert =\frac{|x^{*}\left(x\right)|}{t}$.

Lemma 11.

Let X be a Banach space. Let $0<t<1$ and $x^{*}\in X^{*}$ with $\Vert x^{*}\Vert =1$. Let $\mathcal{B}:=B_X\cap {\left(x^{*}\right)}^{-1}\left([-t,t]\right)$. Let $x,y\in \mathrm{bd}\left(\mathcal{B}\right)$ with $x\ne y$ such $x,y\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right)$. Then:

• If $x^{*}\left(x\right)=x^{*}\left(y\right)$, then $\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right).$
• If $x^{*}\left(x\right)\ne x^{*}\left(y\right)$, then $\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right).$

In particular,

$${\Vert x-y\Vert }_{\mathcal{B}}=\left\{\begin{array}{cc}\hfill \Vert x-y\Vert & \mathrm{if}{x}^{*}\left(x\right)=x^{*}\left(y\right),\hfill \\ \hfill 2& \mathrm{if}{x}^{*}\left(x\right)\ne x^{*}\left(y\right).\hfill \end{array}\right.$$

Proof. 

Notice that

$$\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in \mathrm{bd}\left(\mathcal{B}\right)=\left[S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right)\right]\cup \left[B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right)\right].$$

• Suppose on the contrary that

  $$\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right).$$
  Then

  $$t=\left|x^{*}\left(\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\right)\right|$$

  so ${t\Vert x-y\Vert }_{\mathcal{B}}=\left|x^{*}\left(x-y\right)\right|=\left|x^{*}\left(x\right)-x^{*}\left(y\right)\right|=0$, which is not possible since $x\ne y$ and $t>0$. Therefore,

  $$\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right).$$
  In particular,

  $$∥\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}∥=1,$$

  so ${\Vert x-y\Vert }_{\mathcal{B}}=∥x-y∥$.
• Suppose on the contrary that

  $$\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in S_X\cap {\left(x^{*}\right)}^{-1}\left((-t,t)\right).$$
  Observe that

  $$t>\left|x^{*}\left(\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\right)\right|=\frac{2t}{{\Vert x-y\Vert }_{\mathcal{B}}},$$

  meaning that ${\Vert x-y\Vert }_{\mathcal{B}}>2$, which is impossible since $x,y\in \mathcal{B}$. As a consequence,

  $$\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\in B_X\cap {\left(x^{*}\right)}^{-1}\left(\{-t,t\}\right).$$
  In particular,

  $$t=\left|x^{*}\left(\frac{x-y}{{\Vert x-y\Vert }_{\mathcal{B}}}\right)\right|=\frac{2t}{{\Vert x-y\Vert }_{\mathcal{B}}},$$

  which implies that ${\Vert x-y\Vert }_{\mathcal{B}}=2$.

□

5. Conclusions

The main conclusion that we infer from this work is that still there are plenty of geometric invariants under surjective isometries to be found. Before this work, the main geometric invariants known were starlike sets, maximal faces, and facets in the general case and antipodal points in the finite-dimensional case. After this work, we know new geometric invariants such as flat sets, starlike envelopes, starlike compatible sets, and starlike generated sets. This list should be enlarged with convex sets, faces, and segments. It is particularly interesting to prove that surjective isometries between unit spheres map segments to segments, which leads to the surjective isometry being affine on segments in the unit sphere. In this work, we have accomplished this if the segment is a convex component of the unit sphere.