A Closed-Form Solution without Small-Rotation-Angle Assumption for Circular Membranes under Gas Pressure Loading

Abstract

The closed-form solution of circular membranes subjected to gas pressure loading plays an extremely important role in technical applications such as characterization of mechanical properties for freestanding thin films or thin-film/substrate systems based on pressured bulge or blister tests. However, the only two relevant closed-form solutions available in the literature are suitable only for the case where the rotation angle of membrane is relatively small, because they are derived with the small-rotation-angle assumption of membrane, that is, the rotation angle θ of membrane is assumed to be small so that “sinθ = 1/(1 + 1/tan²θ)^1/2” can be approximated by “sinθ = tanθ”. Therefore, the two closed-form solutions with small-rotation-angle assumption cannot meet the requirements of these technical applications. Such a bottleneck to these technical applications is solved in this study, and a new and more refined closed-form solution without small-rotation-angle assumption is given in power series form, which is derived with “sinθ = 1/(1 + 1/tan²θ)^1/2”, rather than “sinθ = tanθ”, thus being suitable for the case where the rotation angle of membrane is relatively large. This closed-form solution without small-rotation-angle assumption can naturally satisfy the remaining unused boundary condition, and numerically shows satisfactory convergence, agrees well with the closed-form solution with small-rotation-angle assumption for lightly loaded membranes with small rotation angles, and diverges distinctly for heavily loaded membranes with large rotation angles. The confirmatory experiment conducted shows that the closed-form solution without small-rotation-angle assumption is reliable and has a satisfactory calculation accuracy in comparison with the closed-form solution with small-rotation-angle assumption, particularly for heavily loaded membranes with large rotation angles.

1. Introduction

The so-called Föppl–Hencky membrane problem is well known: that is, the problem of large deflection of a peripherally fixed, initially flat circular membrane subjected to uniformly distributed out-of-plane loads. The initially flat circular membrane may be either stress-free or prestressed (by applying in-plane loads along the outer edge of the circular membrane before it is fixed), and the pre-stress can be either tensile or compressive, but in most cases it is tensile. The uniformly distributed out-of-plane loads is generally achieved by means of uniform transverse (lateral) or normal loading, where the uniformly distributed transverse loads refer primarily to the self-weight per unit area of the circular membrane in practice, while the uniformly distributed normal loads refer primarily to the gas or liquid pressure applied to the surface of the circular membrane. However, attention is mainly focused on the case of uniform transverse loading in the existing literature, while the closed-form solutions suitable for uniform normal loading are available in a few cases.

Föppl originally derived a system of equations of large deflection of membranes (thin plates with vanishing bending stiffness) from the classical Föppl–von Kármán equations of large deflection of thin plates [1,2,3]. Hencky used the power series method to solve this system of equations for the case of a circular membrane under uniform loading, and presented the first analytical solution for the circular membrane problem [4]. This is the reason why the circular membrane problem is usually called Föppl–Hencky membrane problem or simply well-known Hencky problem, but Hencky originally dealt only with the case of a stress-free circular membrane subjected to uniform transverse loading [4]. A computational error in the power series solution which was presented originally by Hencky in 1915 [4] was corrected subsequently by Chien in 1948 [5] and Alekseev in 1953 [6], respectively. This solution is usually called the well-known Hencky solution, and is often cited in some studies of related issues [7,8,9,10,11,12].

In the existing literature, however, the closed-form solutions of circular membranes subjected to uniform normal loading are available in a few cases [13,14,15]. Fichter was the first scholar to deal analytically with the circular membrane problem for uniform normal loading, who presented an analytical solution of a stress-free circular membrane under gas pressure for the anticipated use for predicting the shape of orbiting inflatable reflectors [13]. The horizontal component of the gas pressure applied is an extra component from the point of view of the problem for uniform transverse loading, and was really included during the mathematical formulation in [13] but was actually neglected in Campbell [14]. Therefore, the solution presented in Campbell [14] was actually still suitable for the circular membrane problem for uniform transverse loading rather than uniform normal loading, although the title of the Campbell’s paper [14] is “on the theory of initially tensioned circular membranes subjected to uniform pressure”. Shi et al. [15] presented the closed-form solution for circular membranes under in-plane radial stretching or compressing and out-of-plane gas pressure loading, extending the closed-form solution presented in Fichter [13] to include the case of pre-stress.

The closed-form solutions are often found to be necessary in some engineering or technical applications. In fact, the closed-form solutions suitable for uniform normal loading are far more often needed than the ones suitable for uniform transverse loading, for instance, the characterization of mechanical properties for freestanding thin films or thin-film/substrate systems based on pressured bulge or blister tests [9,16,17,18,19,20,21], also including the anticipated use for predicting the orbiting reflector shape upon inflation [13], all need the closed-form solution of a circular membrane subjected to uniform normal loading due to the fact that all of these circular membranes are actually subjected to gas pressure loading rather than uniform transverse loading. As has been described above, however, the opposite is true in the existing literature, where there are far more of the closed-form solutions suitable for uniform transverse loading than the closed-form solutions suitable for uniform normal loading. In particular, the calculation accuracy of the existing closed-form solutions suitable for uniform transverse loading has been greatly improved, while the calculation accuracy of the existing closed-form solutions for uniform normal loading [13,15] is far from ideal.

It may be observed from Fichter [13] or Shi et al. [15] that the closed-form solution presented was actually obtained under the condition that the rotation angle θ of the circular membrane is so small that “sinθ = tanθ” can be used in place of “sinθ = 1/(1 + 1/tan²θ)^1/2”, which is usually called the small-rotation-angle assumption of the membrane (see Equations (37) or (2) in Fichter [13] or Equations (1) through (3) in Shi et al. [15]). This assumption inevitably leads to the loss of computational accuracy of the closed-form solutions, especially when the rotation angle θ of the circular membrane is relatively large. However, in technical applications such as the mechanical properties characterization or orbiting inflatable reflectors mentioned above [9,16,17,18,19,20,21], the rotation angle θ of the circular membrane is often larger. Especially in the mechanical property characterization, the maximum deflection of the bulge or blister membrane may be close to the radius of the circular membrane, such that the rotation angle θ may be as high as 50 degrees. In this case, if the small-rotation-angle assumption of membrane is adopted, then the calculation error which is caused only by substituting “sinθ = tanθ” for “sinθ = 1/(1 + 1/tan²θ)^1/2” is about 1.54% when θ = 10 degrees, 6.42% when θ = 20 degrees, 15.47% when θ = 30 degrees, and 30.54% when θ = 40 degrees. Therefore, it is necessary and worthwhile for these technical applications to give up the so-called small-rotation-angle assumption of membrane during the mathematical formulation of the problem under consideration.

In the following section, the problem of large deflection of a peripherally fixed, initially flat, stress-free circular membrane subjected to uniform normal loading is reformulated, where the small-rotation-angle assumption of membrane adopted in Fichter [13] and Shi et al. [15] (which are the only two relevant studies available in the literature)—the rotation angle of membrane θ is assumed to be small so that “sinθ = tanθ” can be used in place of “sinθ = 1/(1 + 1/tan²θ)^1/2”—is given up, which makes the resulting nonlinear differential equation that governs the out-of-plane equilibrium more difficult to deal with analytically. The power series method is employed to analytically solve the resulting governing equations, and a new and more refined closed-form solution for the reformulated problem is finally presented. Due to giving up the small-rotation-angle assumption of membrane, i.e., using “sinθ = 1/(1 + 1/tan²θ)^1/2” rather than using “sinθ = tanθ” as Fichter [13] or Shi et al. [15] did, the closed-form solution presented here can be suitable for the larger rotation angle of membrane, in comparison with the only two relevant closed-form solutions presented by Shi et al. [15] and Fichter [13]. In Section 3, the validity of the closed-form solution obtained in Section 2 is proved firstly from the point of view that it can satisfy the boundary condition that is not used during its derivation. The convergence of the closed-form solution obtained in Section 2 is numerically investigated due to the complexity of coefficient expressions arising from power series method, showing that the special solutions of stress and deflection converge very well. It is also numerically shown that the closed-form solutions presented in this paper and the one presented in Shi et al. [15] or in Fichter [13] agree quite closely for lightly loaded small-rotation-angle membranes and gradually diverge slowly as the rotation angle of membrane or the loads applied intensifies. Finally, a confirmatory experiment is used to show that the closed-form solutions presented in this paper is indeed improved in accuracy and adaptability to the rotation angle of membrane, compared to the only two existing solutions presented by Fichter [13] and Shi et al. [15]. Concluding remarks are given in Section 4.

2. Membrane Equation and Its Solution

A linearly elastic, initially flat, stress-free circular membrane with thickness h, Poisson’s ratio v, and a Young’s modulus of elasticity E was fixed at the edge of radius a, and then a gas pressure q was applied to one side of the initially flat, peripherally fixed circular membrane, resulting in the deflection to the other side of the membrane, as shown in Figure 1, where a cylindrical coordinate system (r, φ, w) was introduced, whose coordinate origin o was placed in the centroid of the geometric intermediate plane of the initially flat circular membrane, the polar coordinate plane (r, φ) was located in the plane in which the geometric intermediate plane was located, r denoted the radial coordinate, φ denoted the angle coordinate but is not shown in Figure 1, w denoted the axial coordinate which is consistent with the deflecting direction of the circular membrane. Let us take out a free body from the central portion of the whole deflected circular membrane, a piece of circular membrane with radius r (0 ≤ r ≤ a), with a view of studying the static problem of equilibrium of the free body under the joint actions of the membrane force σ_rh at the boundary of the free body and the gas pressure q, as shown in Figure 2, where σ_r is the radial stress, h is the membrane thickness, and θ is the rotation angle of the deflected circular membrane, which varies with radial coordinate r.

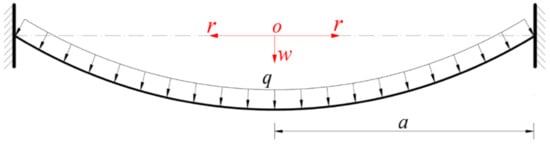
Figure 1. Sketch of the circular membrane under gas pressure q.

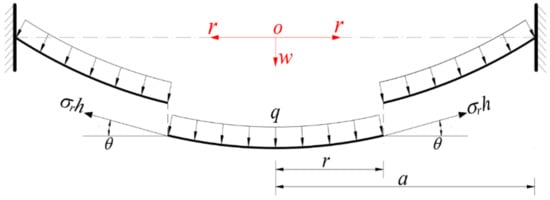
Figure 2. Free body diagram of the deflected circular membrane with radius 0 ≤ r ≤ a.

In the vertical direction perpendicular to the polar coordinate plane (r, φ), there are two vertical (transverse) forces, i.e., the vertical external force πr²q (0 ≤ r ≤ a) produced by the gas pressure q and the vertical component 2πrσ_rhsinθ of the membrane force σ_rh. Therefore, it can be found, from the condition of the resultant force being zero at the vertical direction, that the usually so-called out-of-plane equilibrium equation is

$$2\pi r{\sigma }_{r}h\sin \theta =\pi r^{2}q,$$

(1)

where

$$\sin \theta =1/\sqrt{1+1/{\tan }^2\theta }=1/\sqrt{1+1/{(-\mathrm{d}w/\mathrm{d}r)}^2}.$$

(2)

Substituting Equations (2) into (1) yields.

$$\frac{1}{2}rq\sqrt{1+1/{(-\mathrm{d}w/\mathrm{d}r)}^2}={\sigma }_{r}h.$$

(3)

It may be seen, by comparing Equation (2) in this paper with Equation (2) in Shi et al. [15], that the so-called small-rotation-angle assumption of membrane has been given up in the out-of-plane equilibrium equation, Equation (3). We still use the in-plane equilibrium equation derived originally by Fichter [13].

$${\sigma }_{t}h=\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-qr\frac{\mathrm{d}w}{\mathrm{d}r},$$

(4)

where σ_t denotes the circumferential stress. Suppose that the radial strain is denoted by e_r, the circumferential strain is denoted by e_t, the radial displacement at r is denoted by u(r) and the transversal displacement at r is denoted by w(r). Then the relations of the strain and displacement, i.e., the so-called geometric equations, may be written as

$$e_r=\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2$$

(5)

and

$$e_t=\frac{u}{r}.$$

(6)

The relations of the stress and strain are still assumed to satisfy the generalized Hooke’s law (the linearly elastic membrane), then the so-called physical equations are

$${\sigma }_r=\frac{E}{1-{\nu }^2}(e_r+\nu e_t)$$

(7)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}(e_t+\nu e_r).$$

(8)

Eliminating e_r and e_t from Equations (5) through (8) yields.

$${\sigma }_r=\frac{E}{1-{\nu }^2}[\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2+\nu \frac{u}{r}]$$

(9)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}[\frac{u}{r}+\nu \frac{\mathrm{d}u}{\mathrm{d}r}+\frac{\nu }{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2].$$

(10)

By means of Equations (4), (9), and (10), one attains.

$$\frac{u}{r}=\frac{1}{Eh}\left({\sigma }_{t}h-\nu {\sigma }_{r}h\right)=\frac{1}{Eh}\left[\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-\nu {\sigma }_{r}h-qr\frac{\mathrm{d}w}{\mathrm{d}r}\right].$$

(11)

Substituting the u in Equation (11) into Equation (9) yields.

$$3r\frac{\mathrm{d}}{\mathrm{d}r}\left({\sigma }_{r}h\right)+r^2\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}\left({\sigma }_{r}h\right)+\frac{Eh}{2}{\left(\frac{\mathrm{d}w}{\mathrm{d}r}\right)}^2-\left[r\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{r}^2}+\left(\nu +2\right)\frac{\mathrm{d}w}{\mathrm{d}r}\right]qr=0.$$

(12)

Equation (12) is commonly known as the consistency equation.

Equations (3), (4), and (12) are three differential equations concerning σ_r, σ_t, and w, and the boundary conditions for determining the special solutions of σ_r, σ_t, and w are

$$\frac{\mathrm{d}w}{\mathrm{d}r}=0 \mathrm{at} r=0,$$

(13)

$$\frac{u}{r}=\frac{1}{Eh}\left[\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-\nu {\sigma }_{r}h-qr\frac{\mathrm{d}w}{\mathrm{d}r}\right]=0 \mathrm{at} r=a$$

(14)

and

$$w=0 \mathrm{at} r=a.$$

(15)

Let us proceed to the following nondimensionalization.

$$Q=\frac{aq}{hE},W=\frac{w}{a},S_r=\frac{{\sigma }_r}{E},S_t=\frac{{\sigma }_t}{E},x=\frac{r}{a}$$

(16)

and transform Equations (3), (4), and (12)–(15) into

$$(4S_r^2-x^2{Q}^2){(-\frac{\mathrm{d}W}{\mathrm{d}x})}^2-x^2{Q}^2=0,$$

(17)

$$\frac{\mathrm{d}}{\mathrm{d}x}(x{S}_r)-S_t-xQ\frac{\mathrm{d}W}{\mathrm{d}x}=0,$$

(18)

$$3x\frac{\mathrm{d}}{\mathrm{d}x}(S_r)+x^2\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}(S_r)+\frac{1}{2}{(\frac{\mathrm{d}W}{\mathrm{d}x})}^2-Qx\left[x\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}(W)+(\nu +2)\frac{\mathrm{d}W}{\mathrm{d}x}\right]=0,$$

(19)

$$\frac{\mathrm{d}W}{\mathrm{d}x}=0 \mathrm{at} x=0,$$

(20)

$$\frac{\mathrm{d}}{\mathrm{d}x}\left(x{S}_r\right)-\nu S_r-Qx\frac{\mathrm{d}W}{\mathrm{d}x}=0 \mathrm{at} x=1$$

(21)

and

$$W=0 \mathrm{at} x=1.$$

(22)

S_r and W can be expanded into the power series in the x, due to the fact that the stress and deflection are both finite at x = 0 (i.e., at r = 0).

$$S_r(x)={\displaystyle \sum _{i=0}^{\infty }{c}_i{x}^i}$$

(23)

and

$$W(x)={\displaystyle \sum _{i=0}^{\infty }{d}_i{x}^i}.$$

(24)

The recursive relations between c_i or d_i can be determined by substituting Equations (23) and (24) into Equations (17) and (19), which results in that when i is odd c_i ≡ 0 and d_i ≡ 0, and when i is even the coefficients c_i and d_i can be expressed into the polynomial function in the coefficient c₀, see Appendix A (for c_i) and Appendix B (for d_i).

The remaining two coefficients c₀ and d₀ are commonly known as the undetermined constants and can be determined by using the boundary conditions Equations (21) and (22). From Equations (23) and (24), the boundary condition Equation (21) yields.

$$(1-\nu ){\displaystyle \sum _{i=0}^{\infty }{c}_i}+{\displaystyle \sum _{i=1}^{\infty }i{c}_i}-Q{\displaystyle \sum _{i=1}^{\infty }i{d}_i}=0.$$

(25)

Obviously, the substitution of c_i and d_i (in Appendix A and Appendix B) into Equation (25) give rise to a univariate equation for c₀, and the solution to this univariate equation determines the specific value of the undetermined constant c₀. As a result, the expression of S_r can be determined with the known c₀. Further, the boundary condition Equation (22) gives, from Equation (24).

$$d_0=-{\displaystyle \sum _{i=1}^{\infty }{d}_i}.$$

(26)

Therefore, the value of the undetermined constant d₀ can be determined by Equation (26) with the known c₀, because d_i is identically equal to zero when i is odd and is the functions of b₀ when i is even (see Appendix B). The expression of W can thus be determined with the known c₀ and d₀.

3. Results and Discussions

The boundary condition from Equation (13) or (20), which has not been used yet during the derivation above, can be used to exam the validity of the closed-form solution obtained in Section 2. From Equation (24), the first derivative of the W versus the x is

$$\frac{\mathrm{d}W}{\mathrm{dx}}={\displaystyle \sum _{i=1}^{\infty }i{d}_i{x}^{i-1}}.$$

(27)

It may be seen from Equation (27) that dW/dx ≡ d₁ when x = 0. However, from the derivation in Section 2, we know that d₁ ≡ 0 because d_i ≡ 0 when i is odd. Therefore, it may be concluded that dW/dx ≡ 0 at x = 0. This indicates that the boundary condition Equation (20) or Equation (13) can be naturally met by the closed-form solution obtained in Section 2. This to some extent indicates that the derivation in Section 2 is reliable.

The convergence of the power series solution obtained in Section 2 is usually of concern, but due to the complexity of the coefficient expressions (see Appendix A and Appendix B) it can only be discussed numerically rather than analytically. To this end, a numerical example is considered, where a peripherally fixed stress-free circular membrane with Poisson’s ratio v = 0.45, Young’s modulus of elasticity E = 7.84 MPa, thickness h = 0.2 mm, and radius a = 70 mm is subjected to a gas pressure q = 0.003 MPa. For convenience, the infinite power series in Equations (25) and (26) have to be truncated to n terms, that is

$$(1-\nu ){\displaystyle \sum _{i=0}^n{c}_i}+{\displaystyle \sum _{i=1}^{n}i{c}_i}-\frac{aq}{hE}{\displaystyle \sum _{i=1}^{n}i{d}_i}=0$$

(28)

and

$$d_0=-{\displaystyle \sum _{i=1}^n{d}_i}.$$

(29)

Given a specific value of the parameter n in Equations (28) and (29), the corresponding numerical value of the undetermined constant c₀ can be determined by using Equation (28), and with this known c₀ the corresponding numerical value of the undetermined constant d₀ can further be determined by using Equation (29). We start calculating the numerical values of the undetermined constants c₀ and d₀ from n = 2. The results of calculation of c₀ and d₀ are listed in Table 1, and the variation of c₀ and d₀ with n are shown in Figure 3 and Figure 4.

Table 1. Numerical values of c₀ and d₀ at different n when gas pressure q = 0.003 MPa.

n	c0	d0
2	0.114085	0.293485
4	0.131655	0.314756
6	0.138463	0.317106
8	0.141845	0.316443
10	0.143768	0.315326
12	0.144958	0.314283
14	0.145739	0.313412
16	0.146275	0.312708
18	0.146655	0.312145
20	0.146931	0.311695
22	0.147136	0.311335
24	0.147291	0.311044
26	0.147410	0.310809
28	0.147502	0.310618
30	0.147575	0.310462
32	0.147632	0.310335
34	0.147677	0.31023
36	0.147714	0.310143
38	0.147736	0.310083
40	0.147752	0.310041
42	0.147760	0.310022
44	0.147766	0.310013
46	0.147768	0.310006
48	0.147769	0.310003

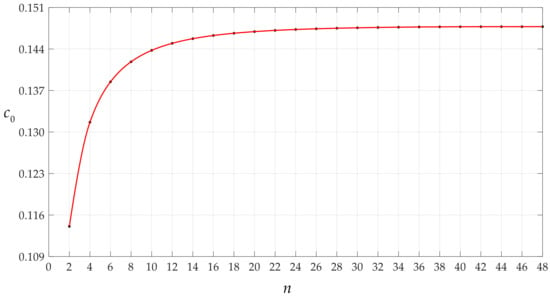
Figure 3. Variation of c₀ with n when q takes 0.003 MPa.

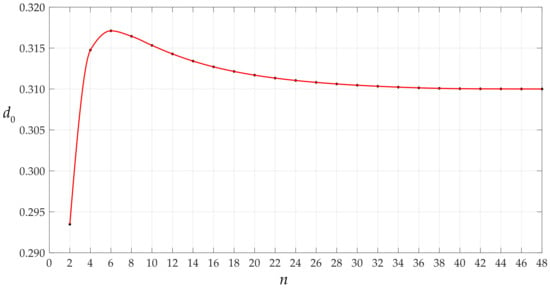
Figure 4. Variations of d₀ with n when q takes 0.003 MPa.

It may be seen from Figure 3 and Figure 4 that the data sequences of c₀ and d₀ already converge very well when n = 40. Therefore, only the expressions of c_i and d_i for i ≤ 40 are listed in Appendix A and Appendix B, and the undetermined constants c₀ and d₀ can finally take 0.147769 and 0.310003 (the values at n = 48, see Table 1), respectively.

For examining the convergence of the special solutions of stress and deflection at x = 1 (at r = a = 70 mm), the numerical values of c_i and d_i are calculated with c₀ = 0.147769 and d₀ = 0.310003, which are listed in Table 2. The variations of c_i and d_i with i are shown in Figure 5 and Figure 6, showing that the special solutions of stress and deflection also converge very well.

Table 2. Numerical values of c_i and d_i at different i when q = 0.003 MPa, c₀ = 0.147769 and d₀ = 0.310003.

i	ci	di
0	0.147769	0.310003
2	−0.039009	−0.226584
4	−0.008191	−0.041540
6	−0.003332	−0.016786
8	−0.001707	−0.008712
10	−0.000988	−0.005132
12	−0.000618	−0.003264
14	−0.000408	−0.002187
16	−0.000280	−0.001521
18	−0.000197	−0.001088
20	−0.000143	−0.000796
22	−0.000105	−0.000592
24	−0.000079	−0.000448
26	−0.000060	−0.000342
28	−0.000046	−0.000264
30	−0.000036	−0.000206
32	−0.000028	−0.000164
34	−0.000022	−0.000130
36	−0.000017	−0.000103
38	−0.000014	−0.000082
40	−0.000011	−0.000067
42	−0.000009	−0.000054
44	−0.000007	−0.000044
46	−0.000006	−0.000035
48	−0.000005	−0.000029

Figure 5. Variations of c_i with i when q = 0.003 MPa and c₀ = 0.147769.

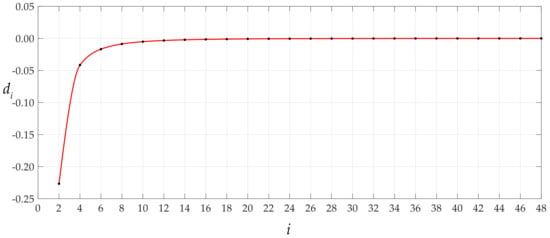
Figure 6. Variations of d_i with i when q = 0.003 MPa, c₀ = 0.147769 and d₀ = 0.310003.

It is worth mentioning that the magnitude of the rotation angle of membrane or the loads applied has an effect on the convergence rate of the data sequences of c₀ and d₀ or c_i and d_i. Let us consider the cases of the above circular membrane under the action of q = 0.0004 MPa and q = 0.0105 MPa. Figure 7, Figure 8, Figure 9 and Figure 10 show the variation of c₀ and d₀ with n and c_i and d_i with I for the case of q = 0.0004 MPa. Figure 11, Figure 12, Figure 13 and Figure 14 show the variation of c₀ and d₀ with n and c_i and d_i with i for the case of q = 0.0105 MPa. It can be seen from the comparison between Figure 3, Figure 7, and Figure 11, or Figure 4, Figure 8, and Figure 12, or Figure 5, Figure 9, and Figure 13, or Figure 6, Figure 10, and Figure 14 that the convergence rate of the data sequences of c₀ or d₀ or c_i or d_i slows down as the rotation angle of membrane or the loads applied intensifies.

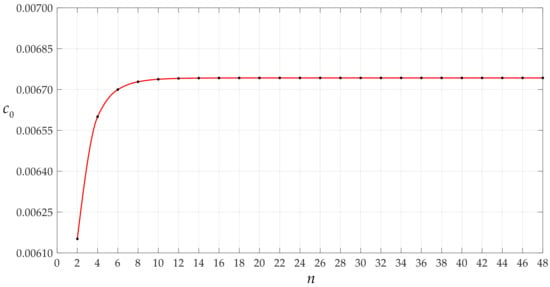
Figure 7. Variations of c₀ with n when q takes 0.00004 MPa.

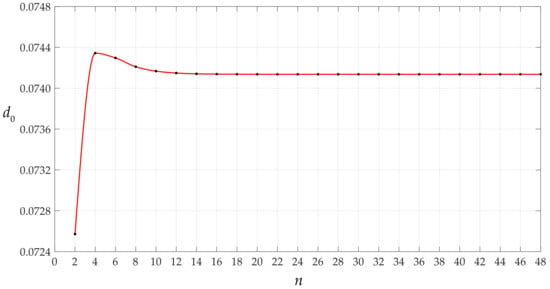
Figure 8. Variations of d₀ with n when q takes 0.00004 MPa.

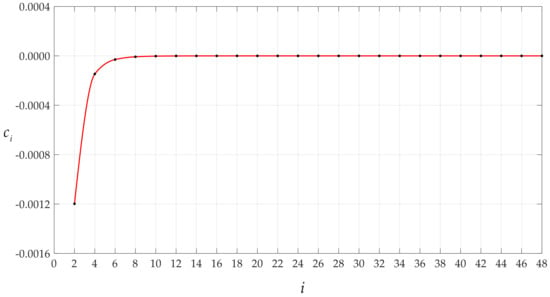
Figure 9. Variations of c_i with i when q takes 0.00004 MPa.

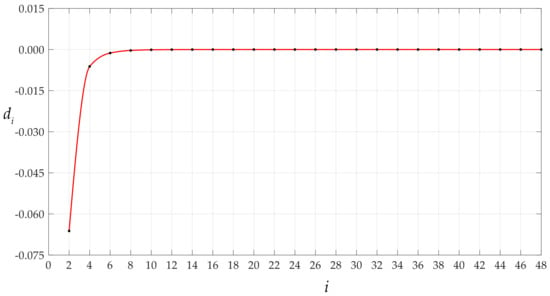
Figure 10. Variations of d_i with i when q takes 0.00004 MPa.

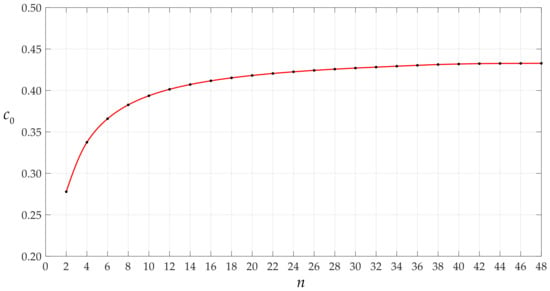
Figure 11. Variations of c₀ with n when q takes 0.0105 MPa.

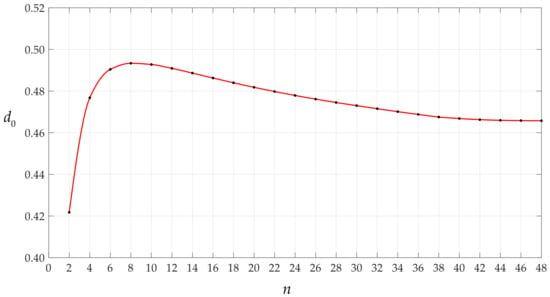
Figure 12. Variations of d₀ with n when q takes 0.0105 MPa.

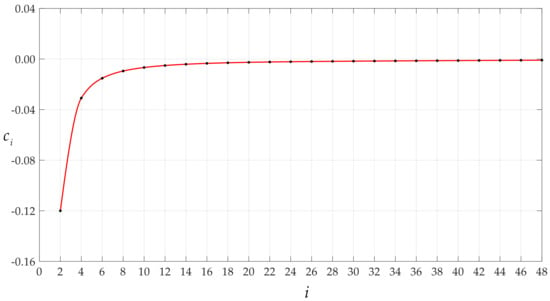
Figure 13. Variations of c_i with i when q takes 0.0105 MPa.

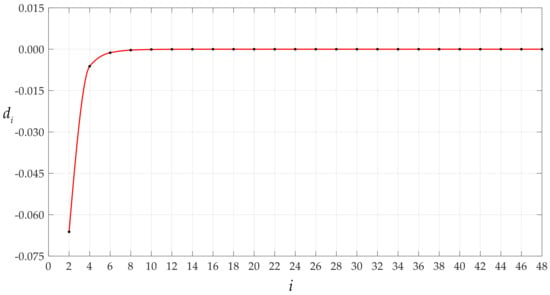
Figure 14. Variations of d_i with i when q takes 0.0105 MPa.

Now, let us show the improved effect of the closed-form solution presented in Section 2, the difference between the solution presented in Section 2, and the solution presented in Shi et al. [15] or in Fichter [13]. Figure 15 and Figure 16 show the deflection w(r) and radial stress σ_r(r) when a peripherally fixed stress-free circular membrane with Poisson’s ratio v = 0.45, Young’s modulus of elasticity E = 7.84 MPa, thickness h = 0.2 mm, and radius a = 70 mm is respectively subjected to q = 0.00004, q = 0.003, and q = 0.0105 MPa, where solution 1 refers to the solution presented in this paper and solution 2 refers to the solution presented in Shi et al. [15] or in Fichter [13].

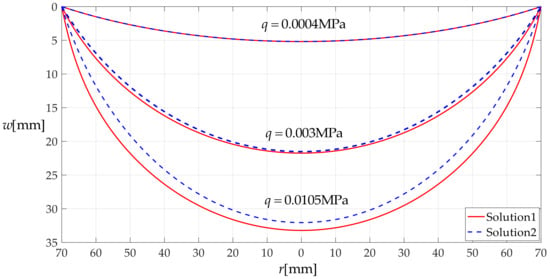
Figure 15. Variation of w with r when q takes 0.0004, 0.003, and 0.0105 MPa, respectively.

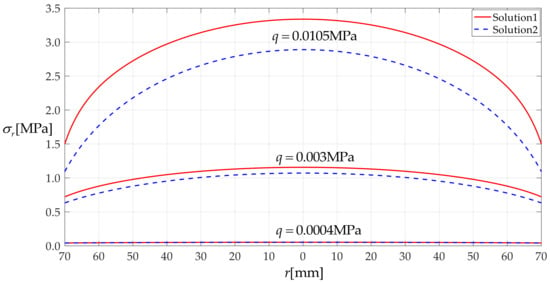
Figure 16. Variation of σ_r with r when q takes 0.0004, 0.003, and 0.0105 MPa, respectively.

It may be seen from Figure 7 and Figure 8 that the difference between the two solutions becomes more and more obvious as the loads q increase. This is because the rotation angle of the circular membrane θ increases accordingly with the increase of the loads q. Therefore, with the increase of the rotation angle of the circular membrane θ, the small-rotation-angle assumption of membrane which is adopted in Fichter [13] or in Shi et al. [15], i.e., the application of substituting “sinθ = tanθ” for “sinθ = 1/(1 + 1/tan²θ)^1/2”, will aggravate the loss of calculation accuracy of the closed-form solutions for deflection and stress.

Shi et al. [15] conducted a confirmatory experiment to show the calculation accuracy of their closed-form solution. We here still use their experimental results of an initially flat stress-free circular natural latex thin film with Young’s modulus of elasticity E = 0.941 MPa, Poisson’s ratio v = 0.43, thickness h = 0.8 mm, radius a = 70 mm, and subjected to the action of gas pressure q = 0.008 MPa, as a reference to make a comparison between the closed-form solution presented in this paper and the closed-form solution presented in Shi et al. [15] or Fichter [13], as shown in Figure 17, where solution 1 refers to the closed-form solution presented in this paper and solution 2 refers to the closed-form solution presented in Shi et al. [15] or Fichter [13]. Table 3 shows the error of the theoretical results relative to the experimental results. From Figure 17 and Table 3 it can be concluded that the closed-form solution presented here, due to giving up the small-rotation-angle assumption of membrane, has a higher calculation accuracy and is suitable for the case of larger rotation angle of membrane, in comparison with the only two relevant closed-form solutions presented in Shi et al. [15] and Fichter [13].

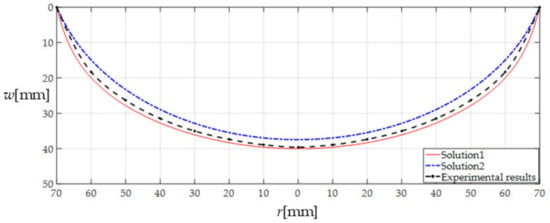
Figure 17. Membrane deflection along a diameter, experimental, and theoretical results.

Table 3. The measured and calculated results of membrane deflection and their relative errors.

r (mm)	Measured Results (mm)	Calculated Results by Solution 1 and Errors Relative to Measured Results		Calculated Results by Solution 2 and Errors Relative to Measured Results
		Results (mm)	Error	Results (mm)	Error
0	39.52	40.03	1.29%	37.85	4.22%
10	38.94	39.61	1.72%	36.98	5.02%
20	37.39	38.34	2.54%	35.48	5.11%
30	35.03	36.12	3.11%	32.86	6.20%
40	31.49	32.76	4.03%	28.94	8.09%
50	26.43	27.84	5.33%	23.42	11.39%
60	18.32	20.00	9.17%	15.12	17.47%

4. Concluding Remarks

In this study, the problem of large deflection of a peripherally fixed, initially flat, stress-free circular membrane subjected to gas pressure loading is reformulated under the condition of giving up the small-rotation-angle assumption of membrane—the rotation angle θ of membrane is assumed to be small so that “sinθ = 1/(1 + 1/tan²θ)^1/2” can be approximated by “sinθ = tanθ”, wherein a new and more refined closed-form solution without small-rotation-angle assumption is, for the first time, given in power series form, and relevant numerical and experimental studies are also carried out.

It is worth mentioning first that the correct determination of the undetermined constants c₀ and d₀ is often difficult and requires some auxiliary means to accomplish it, which is not mentioned above. As stated above, the undetermined constants c₀ and d₀ can be determined by Equations (28) and (29) for a given value of n, but actually this also results in some higher order equations for c₀ and d₀. It is well known that higher order equations may have multiple roots, but due to lack of judgement criterion, we do not know which of these roots is what we want, that is, which one is the true value of c₀ or d₀ that corresponds to the given n. This difficulty is overcome by auxiliary plotting in this study, that is, all the real roots are plotted into a so-called scatter plot, in which the points that can form smooth connecting lines are the true values of c₀ or d₀ that correspond to all values of n. Figure 3, Figure 4, Figure 7, Figure 8, Figure 11, and Figure 12 are the final results that delete the points that cannot form smooth connecting lines, and leave only the points that can form smooth connecting lines, i.e., the true values of c₀ or d₀ that correspond to all values of n. We have no way to explain this phenomenon, only guess that it might have something to do with the use of power series method, but the numerical and experimental studies above show that it is feasible to do so.

In addition, the following conclusions can be drawn from this study.

The closed-form solution with small-rotation-angle assumption, which is presented in previous studies, will lose more and more calculation accuracy gradually as the rotation angle of membrane or the loads applied intensifies, and thus it is not suitable for heavily loaded membranes with large rotation angle.

The closed-form solution without small-rotation-angle assumption, which is presented in this paper, can be used for heavily loaded membranes with large rotation angle due to giving up the small-rotation-angle assumption, and the confirmatory experiment conducted shows that it is reliable.

Although the closed-form solution without small-rotation-angle assumption has good convergence, its convergence rate depends on the magnitude of the rotation angle of membrane, or the magnitude of the loads applied. This means that the number of terms in the power series in Equations (28) and (29), n, should take a larger value for heavily loaded membranes with large rotation angle, in comparison with lightly loaded membranes with large rotation angle.

Since thin films, which are characterized based on pressured bulge or blister tests, usually show very large rotation angles, the use of the closed-form solution with small-rotation-angle assumption in this case is bound to bring a large characterization error. Therefore, in this sense, the closed-form solution without small-rotation-angle assumption presented in this paper fills in the gap in technical applications such as characterization of mechanical properties for freestanding thin films or thin-film/substrate systems based on pressured bulge or blister tests.