Extreme Value Analysis for Mixture Models with Heavy-Tailed Impurity

Abstract

This paper deals with the extreme value analysis for the triangular arrays which appear when some parameters of the mixture model vary as the number of observations grows. When the mixing parameter is small, it is natural to associate one of the components with “an impurity” (in the case of regularly varying distribution, “heavy-tailed impurity”), which “pollutes” another component. We show that the set of possible limit distributions is much more diverse than in the classical Fisher–Tippett–Gnedenko theorem, and provide the numerical examples showing the efficiency of the proposed model for studying the maximal values of the stock returns.

1. Introduction

Consider the mixture model

$$\begin{array}{c}\hfill F(x;\epsilon ,\overrightarrow{\theta })=(1-\epsilon )F^{\left(1\right)}(x;{\overrightarrow{\theta }}^{\left(1\right)})+\epsilon F^{\left(2\right)}(x,{\overrightarrow{\theta }}^{\left(2\right)}),\end{array}$$

(1)

where $\epsilon \in (0,1)$ is a mixture parameter, $F^{\left(1\right)}(x;{\overrightarrow{\theta }}^{\left(1\right)})$ and $F^{\left(2\right)}(x;{\overrightarrow{\theta }}^{\left(2\right)})$ are cumulative distribution functions (CDFs) of two distributions parametrised by vectors ${\overrightarrow{\theta }}^{\left(1\right)},{\overrightarrow{\theta }}^{\left(2\right)}$ correspondingly, and $\overrightarrow{\theta }=({\overrightarrow{\theta }}^{\left(1\right)},{\overrightarrow{\theta }}^{\left(2\right)})$. In this paper we focus on the case when the second component in this mixture corresponds to some heavy-tailed distribution, while the first one can be either light or heavy tailed. When $\epsilon$ is small, the second component can be referred to as the heavy-tailed impurity (the term “heavy-tailed impurity” is known in the context of percolation theory, see [1]. Here we use it in a more general set-up, following [2]). Some applications of this approach are described by Grabchak and Molchanov (2015) [2]. For instance, in population dynamics, this approach can be used for modelling the migration of species: The distance of migration of most species can be modelled by light-tailed distribution, but there is a small number of species with “very active” behaviour.

It would be worth mentioning that the parameters $\epsilon$ and $\overrightarrow{\theta }$ may depend on the number of available observations, denoted below by n. For instance, in the aforementioned example from population dynamics, the proportion of “very active” species decays when the total number of species grows. In this context, the distribution of the resulting variable changes with n, and this model can be considered as the infinitesimal triangular array—a collection of real random variables $\{X_{nj},j=1,\cdots ,k_n\},$$k_n\to \infty$ as $n\to \infty ,$ such that $X_{n1},\cdots ,X_{n{k}_n}$ are independent for each n. The classical limit theorems for this class of models are well known in the literature, see, e.g., monographs by Petrov (2012) [3], Meerschaert and Scheffler (2001) [4]. For instance, it is known that the class of possible non-degenerate limit laws of the sums $X_{n1}+\cdots +X_{n{k}_n}-c_n$ with deterministic $c_n$ and triangular array $\{X_{nj},j=1,\cdots ,k_n\}$ satisfying the assumption of infinite smallness,

$$\begin{array}{c}\hfill \forall \delta >0:{\displaystyle \underset{j=1,\cdots ,k_n}{sup}}\mathbb{P}\left\{\left|X_{nj}\right|>\delta \right\}\to 0,n\to \infty ,\end{array}$$

coincides with the class of infinitely divisible distributions.

Surprisingly, there are very few papers dealing with the extreme value analysis for this model. To the best of our knowledge, there exist no general statements describing the class of non-degenerate limits of

$$\begin{array}{c}\hfill (\underset{j=1,\cdots ,k_n}{max}{X}_{nj}-c_n)/s_n,n\to \infty ,\end{array}$$

(2)

with deterministic $c_n,s_n$. Clearly, the convergence to types theorem is applicable to this situation and guarantees that the limit law is determined up to the change of location and scale. Nevertheless, unlike the well-known Fisher–Tippett–Gnedenko theorem, the class of limit distributions in (2) includes not only the Gumbel, Fréchet and max-Weibull laws. Some conditions guaranteeing the convergence of the triangular array to some limit are given by Freitas and Hüsler (2003) [5], but their results essentially employ the assumption that the limit distribution is twice differentiable, which is violated in the examples of the model (1) provided below. Let us mention here that other known papers on this topic are concentrated on some particular examples yielding convergence to the classical extreme value distributions, such as the Gumbel law, and those related to them, see Anderson, Coles and Hüsler (1997) [6], Dkengne, Eckert and Naveau (2016) [7].

In the first part of the paper (Section 2) we consider the particular case of (1), when the first component has the Weibull distribution (and therefore it is in the maximum domain of attraction (MDA) of the Gumbel law), while the heavy-tailed impurity is modelled by the regularly varying distribution (MDA of the Fréchet law). Note that in the classical setting, when the parameters $\epsilon$ and $\overrightarrow{\theta }$ are fixed, the limit behaviour of the sum is determined by the second component, and therefore the maximum under proper normalisation converges to the Fréchet law. Interestingly enough, even in the case when only one parameter (namely the mixing parameter $\epsilon$) varies, the set of possible limit distributions includes Gumbel and Fréchet distributions and also one discontinuous law. The exact statement is formulated in Theorem 1.

In Section 3 we turn towards a more complicated model, which appears when one uses the truncated regularly varying distribution for the second component, and the truncation level M grows with $n$. This part of our research is motivated by a discussion concerning the choice between truncated and non-truncated Pareto-type distributions, see Beirlant, Fraga Alves and Gomes (2016) [8]. The asymptotic behaviour depends on the rate of growth of M: As we show, the resulting conditions are related to the soft, hard and intermediate truncation regimes introduced by Chakrabarty and Samorodnitsky (2012) [9]. Note that in that paper it is shown that the softly truncated regularly varying distribution has heavy tails (understood in the sense of the non-Gaussian limit law for the sum), and therefore the term “heavy-tailed impurity” can be also used for models of this kind.

The main theoretical contribution of our research is formulated as Theorem 2, dealing with the case when both $\epsilon$ and M depend on $n$. It turns out that the set of possible limit laws in (2) includes six different distributions, and, for some sets of parameters, the maximal value diverges under any (also nonlinear) normalisation. Our theoretical findings are illustrated by the simulation study (Section 4).

The choice of the Weibull distribution for the first component in (1) is partially based on the great popularity of this distribution in applications, see, e.g., the overview by Laherrere and Sornette (1998) [10]. As we show in Section 5, our model with heavy-tailed impurity is more appropriate for modelling the stock returns as a “pure” model. In this context, our paper continues the discussion started in the paper by Malevergne, Pisarenko and Sornette (2005) [11], where it is shown that the tails of the empirical distribution of log-returns decay slower than the tails of the Weibull distribution but faster than the power law.

2. Weibull-RV Mixture

In this section, we focus on a particular case of the model (1), namely

$$F(x;\epsilon ,\overrightarrow{\theta })=(1-\epsilon )F_1(x;\lambda ,\tau )+\epsilon F_2(x;\alpha )$$

(3)

where $\overrightarrow{\theta }=(\lambda ,\tau ,\alpha )$, $F_1$ is the distribution function of the Weibull law,

$$F_1(x;\lambda ,\tau )=F_1\left(x\right)=1-e^{-\lambda x^{\tau }},x\ge 0,\lambda >0,\tau >0,$$

(4)

and $F_2$ corresponds to the regularly varying distribution on $[m,\infty )$,

$$F_2(x;\alpha )=F_2\left(x\right)=1-x^{-\alpha }L\left(x\right),\alpha >0,x\in [m,\infty ),$$

(5)

with $m=inf\left\{x>0:F_2\left(x\right)>0\right\}$ and a continuous slowly varying function $L(·)$. Let us recall that by definition,

$$\begin{array}{c}\hfill \underset{x\to \infty }{lim}L\left(tx\right)/L\left(x\right)=1,\forall t>0,\end{array}$$

and the term “slow variation” comes from the property

$$\begin{array}{c}\hfill x^{-ϵ}L\left(x\right)\to 0\mathrm{and}{x}^{ϵ}L\left(x\right)\to \infty \mathrm{as} x\to \infty \end{array}$$

(6)

for every $ϵ>0.$ The extensive overview of the properties of slowly varying functions is given in [12,13].

As we already mentioned in the introduction, the first component is in the MDA of the Gumbel law, while the second is in the MDA of the Fréchet law. In Appendix A, we show that the the mixture distribution function F is in the MDA of the Fréchet law, provided that the parameters $\epsilon$ and $\overrightarrow{\theta }$ are fixed.

In what follows we consider the case when the mixing parameter $\epsilon ={\epsilon }_n$ decays to zero as n grows. It is natural to slightly generalise the model to the form of row-wise independent triangular array

$$\begin{array}{c}\hfill X_{nj}\sim F(x;{\epsilon }_n,\overrightarrow{\theta }),n\ge 1,j=1,\cdots ,k_n,\end{array}$$

(7)

where $k_n$ is an unbounded increasing sequence, and for any n the random variables $X_{nj},j=1,\cdots ,k_n$ are independent. The set-up allowing various numbers of elements in different rows is standard both in studying the classical limit laws (see [3]) and in the extreme value theory (see [7]).

As we show in the next theorem, the asymptotic behaviour of the maximum in this model is determined by the rate of growth of $k_n$, the rate of decay of ${\epsilon }_n$ and the slowly varying function $L$. Note that the rates of $log{k}_n$ and $k_n{\epsilon }_n$ are compared in terms of the following three alternative conditions,

$$\exists \beta >\frac{\tau }{\alpha }:\underset{n\to \infty }{lim}\frac{log{k}_n}{{\left(k_n{\epsilon }_n\right)}^{\beta }}=\infty ,$$

(8)

$$\exists \beta \in (0,\frac{\tau }{\alpha }):\underset{n\to \infty }{lim}\frac{log{k}_n}{{\left(k_n{\epsilon }_n\right)}^{\beta }}=0,$$

(9)

$$\exists c>0:k_n{\epsilon }_n\sim c{(log{k}_n)}^{\frac{\alpha }{\tau }}.$$

(10)

Theorem 1. 

Consider the row-wise independent triangular array (7). Assume that ${lim}_{x\to \infty }L\left(x\right)\in [0,\infty ]$ (this assumption means that the slowly varying function $L\left(x\right)$ does not exhibit infinite oscillation. The counterexample to this condition is given in [14], Example 1.1.6). Then for any sequences $k_n\to \infty$, ${\epsilon }_n\to 0$ there exist deterministic sequences $c_n,s_n$ such that

$$\underset{n\to \infty }{lim}\mathbb{P}\left\{\underset{j=1,\dots ,k_n}{max}{X}_{nj}\le s_{n}x+c_n\right\}=H\left(x\right),\forall x\in \mathbb{R}$$

(11)

with some non-degenerate limit law $H\left(x\right).$ More precisely, $H\left(x\right)$ belongs to the type of the following three distribution functions (due to the convergence to types theorem (Theorem A1.5 from [15]), if $H\left(x\right)$ is the distribution function of the limit law in (11), then any other non-degenerate law appearing in (11) under another normalisation is of the form $H(ax+b)$ with some constants $a,b$):

• Gumbel distribution, $H\left(x\right)=e^{-e^{-x}}$, $x\in \mathbb{R}$, if and only if any of the following conditions is satisfied

  (a) 

  $k_n{\epsilon }_n\to const\in [0,\infty )$ as $n\to \infty$;

  (b) 

  $k_n{\epsilon }_n\to \infty$ as $n\to \infty$, and (8) holds;

  (c) 

  (10) holds, and $L\left(u\right)\to 0$ as $u\to \infty$.

  In all cases, possible choice of the normalising sequences is

  $$\begin{array}{c}\hfill s_n={\left(\lambda \tau \right)}^{-1}{({\lambda }^{-1}log{k}_n)}^{\frac{1}{\tau }-1}and{c}_n={({\lambda }^{-1}log{k}_n)}^{\frac{1}{\tau }}.\end{array}$$

  (12)
• Fréchet distribution with parameter α, $H\left(x\right)=e^{-x^{-\alpha }}$, $x\ge 0$, if and only if any of the following conditions is satisfied

  (a) 

  (9) holds;

  (b) 

  (10) holds, and $L\left(u\right)\to \infty$ as $u\to \infty$.

  In all cases, one can take

  $$\begin{array}{c}\hfill s_n=F_2^{\leftarrow }(1-{\left(k_n{\epsilon }_n\right)}^{-1}),and{c}_n=0,\end{array}$$

  (13)

  where $F_2^{\leftarrow }\left(y\right)=inf\{x\in \mathbb{R}:F_2\left(x\right)\ge y\}$ for $y\in [0,1].$
• Discontinuous distribution with cdf

  $$H\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<{\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ e^{-(1+x^{-\alpha })},\hfill & x={\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ e^{-x^{-\alpha }},\hfill & x>{\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \end{array}\right.$$

  if (10) holds, and $L\left(u\right)\to \tilde{c}$ for some $\tilde{c}>0$ as $u\to \infty$. The normalising sequences can be fixed in the form (13).

Proof. 

The proof is given in Appendix B. □

The graphical representation of this result is presented in Figure 1.

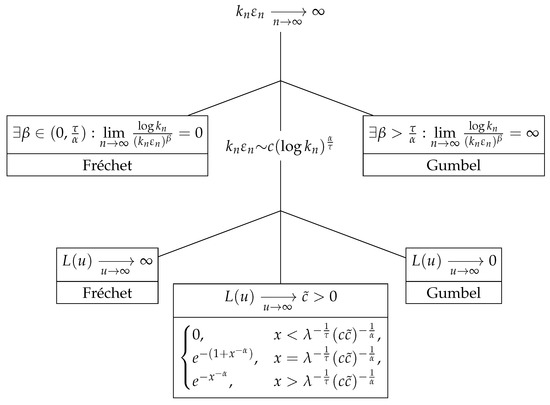
Figure 1. Possible limit distributions for maxima of the triangular array (3).

3. Weibull-Truncated RV Mixture

Now we consider one more complicated model, such that the distribution of the second component in (3) also changes as n grows. Consider the mixture distribution

$$F(x;\epsilon ,M,\overrightarrow{\theta })=(1-\epsilon )F_1(x;\lambda ,\tau )+\epsilon {\tilde{F}}_2(x;\alpha ,M),$$

(14)

whereas before, $\overrightarrow{\theta }=(\lambda ,\tau ,\alpha )$, $F_1$ is the distribution function of the Weibull law (see (4)), while ${\tilde{F}}_2$ is the upper-truncated regularly varying distribution,

$${\tilde{F}}_2(x;\alpha ,M)=\left\{\begin{array}{cc}\frac{F_2(x;\alpha )}{F_2(M;\alpha )},\hfill & \mathrm{if}x\in [m,M],\hfill \\ 1,\hfill & \mathrm{if}x>M\hfill \end{array}\right.$$

(15)

with $F_2(x;\alpha )$ corresponding to a regularly varying distribution (5).

It would be an interesting mentioning that the components in this model correspond to different maximum domains of attraction: the maximum for the first component under proper normalisation converges to the Gumbel law, while the second—to the max-Weibull law, see Appendix C.

By analogy with (7), we consider the triangular array

$$\begin{array}{c}\hfill X_{nj}\sim F(x;{\epsilon }_n,M_n,\overrightarrow{\theta }),n\ge 1,j=1,\cdots ,k_n,\end{array}$$

(16)

where $k_n,M_n$ are unbounded increasing sequences, and for any n the random variables $X_{nj},j=1,\cdots ,k_n$ are independent. Note that the classical limit laws for this model (law of large numbers and limit theorems for the sums) are essentially established in [16].

The next theorem reveals the asymptotic behaviour of the maximal value depending on the rates of ${\epsilon }_n,M_n,k_n$, and the properties of the slowly varying function $L$. An important difference from the model considered in Section 2 is that in some cases the limit distribution is degenerate for any (also non-linear) normalising sequence.

It turns out that if $k_n{\epsilon }_n$ tends to any finite constant, then the limit distribution is Gumbel. Our findings in the remaining case $k_n{\epsilon }_n\to \infty$ are presented in Table 1. The asymptotic behaviour of the maximum is determined by the asymptotic properties of the sequences $k_n,{\epsilon }_n$ in terms of (8)–(10), and the rate of growth of $M_n$ in terms of the following three alternating conditions:

$$\exists \gamma >\frac{1}{\alpha }:\underset{n\to \infty }{lim}\frac{M_n}{{\left(k_n{\epsilon }_n\right)}^{\gamma }}=\infty ,$$

(17)

$$\exists \gamma \in (0,\frac{1}{\alpha }):\underset{n\to \infty }{lim}\frac{M_n}{{\left(k_n{\epsilon }_n\right)}^{\gamma }}=0;$$

(18)

$$\exists \breve{c}>0:M_n\sim \breve{c}{\left(k_n{\epsilon }_n\right)}^{\frac{1}{\alpha }}.$$

(19)

Table 1. Possible limit distributions for maxima of the triangular array (16).

${\mathit{k}}_{\mathit{n}}{\mathit{\epsilon }}_{\mathit{n}}\underset{\mathit{n}\to \mathit{\infty }}{⟶}\mathit{\infty }$	(8)	(9)	(10)
(17)	Gumbel	Fréchet	Gumbel,
			if $L\left(u\right)\underset{u\to \infty }{⟶}0$
			Fréchet,
			if $L\left(u\right)\underset{u\to \infty }{⟶}\infty$
			Distribution I,
			if $L\left(u\right)\underset{u\to \infty }{⟶}\tilde{c}\in (0,\infty )$
(18)	Gumbel	Gumbel,	Gumbel
		if $k_n\gtrsim e^{\lambda M_n^{\tau }}$
		no limit,
		if $k_n\gtrsim e^{\lambda M_n^{\tau }}$ is not fulfilled
(19)	Gumbel	Fréchet,	Gumbel,
			if $L\left(u\right)\underset{u\to \infty }{⟶}0$
		if $L\left(u\right)\underset{u\to \infty }{⟶}0$	Gumbel,
			if $L\left(u\right)\underset{u\to \infty }{⟶}\tilde{c}\in (0,\infty ]$,
			and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}\in (0,1)$
		Distribution II,	Distribution III,
			if $L\left(u\right)\underset{u\to \infty }{⟶}\tilde{c}\in (0,\infty )$,
			and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}>1$
		if $L\left(u\right)\underset{u\to \infty }{⟶}\tilde{c}\in (0,\infty )$	Distribution IV,
			if $L\left(u\right)\underset{u\to \infty }{⟶}\tilde{c}\in (0,\infty )$,
			and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}=1$
		no limit,	no limit,
		if $L\left(u\right)\underset{u\to \infty }{⟶}\infty$	if $L\left(u\right)\underset{u\to \infty }{⟶}\infty$,
			and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}\ge 1$

The conditions (17)–(19) are related to the notion of hard and soft truncation. Following [9], we say that that a variable $\eta$ is truncated softly, if

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{k}_n\mathbb{P}\left\{\left|\eta \right|\ge M_n\right\}=0.\end{array}$$

(20)

For a regularly varying distribution of $\eta$, the condition (20) holds if there exists $\gamma >1/\alpha$ such that $M_n/k_n^{\gamma }\to \infty$. This fact follows from

$$\begin{array}{c}\hfill k_n\mathbb{P}\left\{\left|\eta \right|\ge M_n\right\}=k_n{M}_n^{-\alpha }L\left(M_n\right)\lesssim k_n{M}_n^{-\alpha +ϵ}={(M_n/k_n^{1/(\alpha -ϵ)})}^{(-\alpha +ϵ)}\end{array}$$

for any $ϵ>0$ (here and below we mean by $f_n\gtrsim g_n$ that $\underset{n\to \infty }{lim}(f_n/g_n)=\infty$). Analogously, $\eta$ is truncated hard, that is,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{k}_n\mathbb{P}\left\{\left|\eta \right|\ge M_n\right\}=\infty ,\end{array}$$

if there exists $\gamma \in (0,1/\alpha )$ such that $M_n/k_n^{\gamma }\to 0.$

The paper [9] deals with the asymptotic behaviour of the sums of random variables with truncated regularly varying distributions. It is demonstrated that the behaviour significantly depends on the truncation regime. This research was further extended by Paulauskas [17], who studied the convergence of sums of linear processes with softly and hardly tapered innovations.

Our results for the case (17) (see first raw in Table 1) coincide with the findings from [9]: “In the soft truncation regime, truncated power tails behave, in important respects, as if no truncation took place”. In fact, in our setup, the results are completely the same as for the non-truncated distribution considered in Theorem 1.

Our outcomes for (18) (second raw in Table 1) are quite close to another finding from [9], namely, “in the hard truncation regime much of “heavy tailedness” is lost”. Actually, we get that the behaviour is determined by the first component except the case (9) with ${lim}_{n\to \infty }{k}_n{e}^{-\lambda M_n^{\tau }}\ne \infty$.

Finally, the intermediate case (19) (third row in Table 1) is divided into various subcases. The comparison with [9] is not possible because the authors decide to “largely leave” this question “aside in this article, in order to keep its size manageable”. In our research, we provide the complete study of this case.

The exact result is formulated below.

Theorem 2. 

Consider the row-wise independent triangular array (16) under the assumption that ${\epsilon }_n\to 0,M_n\to \infty ,k_n\to \infty$ as $n\to \infty .$ Assume also that ${lim}_{x\to \infty }L\left(x\right)\in [0,\infty ].$

Then the non-degenerate limit law $H\left(x\right)$ for the properly normalised row-wise maximum $\underset{j=1,\dots ,k_n}{max}{X}_{nj}$ (see (11)) belongs to the type of the following distributions.

1. 

Gumbel distribution, $H\left(x\right)=e^{-e^{-x}}$, $x\in \mathbb{R}$, if and only if any of the following conditions is satisfied

1.1 

$k_n{\epsilon }_n\to const\in [0,\infty )$ as $n\to \infty$;

1.2 

$k_n{\epsilon }_n\to \infty$ as $n\to \infty$, and moreover

• (17) and (8) hold;
• (17) and (10) hold, and $L\left(u\right)\to 0$ as $u\to \infty ;$
• (18) and (8) hold;
• (18) and (9) hold, and $k_n\gtrsim e^{\lambda M_n^{\tau }};$
• (18) and (10) hold;
• (19) and (8) hold;
• (19) and (10) hold, and $L\left(u\right)\to 0$ as $u\to \infty ;$
• (19) and (10) hold, $L\left(u\right)\to \tilde{c}\in (0,\infty ]$ as $u\to \infty ,$ and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}\in (0,1)$.

In all cases, possible choice of the normalising sequences is given by (12).

2. 

Fréchet distribution with parameter α, $H\left(x\right)=e^{-x^{-\alpha }}$, $x\ge 0$, if and only if any of the following conditions is satisfied

• (17) and (9) hold;
• (17) and (10) hold, and $L\left(u\right)\to \infty$ as $u\to \infty ;$
• (19) and (9) hold, and $L\left(u\right)\to 0$ as $u\to \infty .$

In all cases, one can take $s_n,c_n$ in the form (13).

3. 

Special cases:

(I) 

$$\begin{array}{c}\hfill H\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<{\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ e^{-(1+x^{-\alpha })},\hfill & x={\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ e^{-x^{-\alpha }},\hfill & x>{\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \end{array}\right.\end{array}$$

provided (17) and (10) hold, and $L\left(u\right)\to \tilde{c}\in (0,\infty )$;

(II) 

$$H\left(x\right)=\left\{\begin{array}{cc}{e}^{\tilde{c}{\breve{c}}^{-\alpha }-x^{-\alpha }},\hfill & x\in (0,\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }}],\hfill \\ 1,\hfill & x>\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }},\hfill \end{array}\right.$$

provided (19) and (9) hold, $L\left(u\right)\to \tilde{c}\in (0,\infty )$;

(III) 

$$H\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<{\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ exp\left\{-1+\tilde{c}{\breve{c}}^{-\alpha }-{\lambda }^{\frac{\alpha }{\tau }}c\tilde{c}\right\},\hfill & x={\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\hfill \\ exp\left\{\tilde{c}{\breve{c}}^{-\alpha }-x^{-\alpha }\right\},\hfill & x\in ({\lambda }^{-\frac{1}{\tau }}{\left(c\tilde{c}\right)}^{-\frac{1}{\alpha }},\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }}],\hfill \\ 1,\hfill & x>\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }},\hfill \end{array}\right.$$

provided (19) and (10) hold, $L\left(u\right)\to \tilde{c}\in (0,\infty )$ as $u\to \infty ,$ and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}>1$;

(IV) 

$$H\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }},\hfill \\ e^{-1},\hfill & x=\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }},\hfill \\ 1,\hfill & x>\breve{c}{\tilde{c}}^{-\frac{1}{\alpha }},\hfill \end{array}\right.$$

provided (19) and (10) hold, $L\left(u\right)\to \tilde{c}\in (0,\infty )$ as $u\to \infty ,$ and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}=1$.

In all cases the normalising sequences can be chosen as in (13).

The limit distribution is degenerate for any sequences $s_n$ and $c_n$ in the following three cases:

• (18) and (9) hold, and the condition $k_n\gtrsim e^{\lambda M_n^{\tau }}$ is not fulfilled;
• (19) and (9) hold, and $L\left(u\right)\to \infty$ as $u\to \infty$;
• (19) and (10) hold, $L\left(u\right)\to \infty$ as $u\to \infty ,$ and ${\lambda }^{\frac{1}{\tau }}\breve{c}{c}^{\frac{1}{\alpha }}\ge 1$.

Moreover, in these cases the distribution of

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\mathbb{P}\left\{\underset{j=1,\dots ,k_n}{max}{X}_{nj}\le v_n\left(x\right)\right\}\end{array}$$

is degenerate for any increasing sequence $v_n\left(x\right),$ which is unbounded in n and $x.$

Proof. 

The proof is given in Appendix D. □

4. Simulation Study

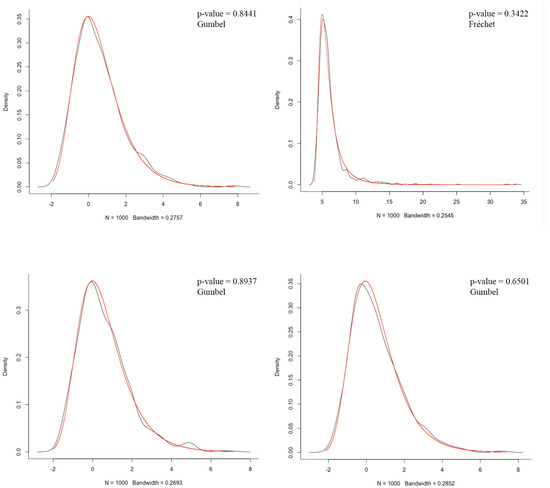
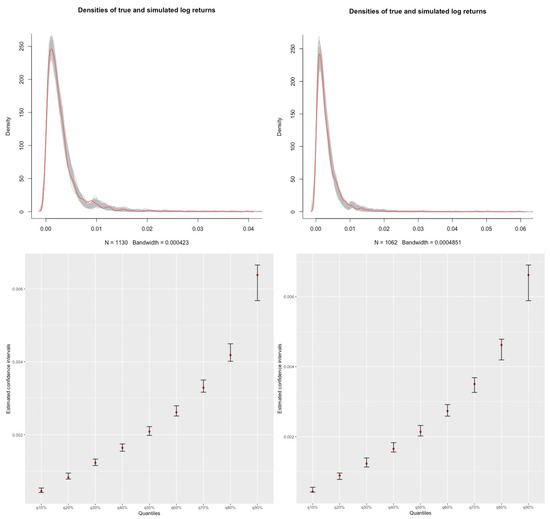
The aim of the current section is to illustrate the dependence of limit distribution for maxima in the model (16) on the rates of the mixing parameter ${\epsilon }_n$ and of the truncation level $M_n$. For this purpose we consider four triangular arrays (16) with $k_n=n$ having all permanent parameters the same, namely, $\overrightarrow{\theta }=(1,1,1.5)$, $L=1$ and $m=0.1$. The sequences ${\epsilon }_n$ and $M_n$ are chosen to satisfy the following pairs of conditions: (8)–(17), (9)–(17), (8)–(18) and (9)–(18). The exact form of mixing and truncation parameters are presented in Table 2.

Table 2. The values of ${\epsilon }_n$ and $M_n$ chosen for the numerical study.

	(8)	(9)
(17)	${\epsilon }_n=n^{-1}logn,$	${\epsilon }_n=n^{-1}{(logn)}^2,$
	$M_n=log(n+1)$	$M_n={(log(n+1))}^2$
(18)	${\epsilon }_n=n^{-1}logn,$	${\epsilon }_n=n^{-1}{(logn)}^2,$
	$M_n=\sqrt{log(n+1)}$	$M_n=\sqrt{log(n+1)}$

As previously, the primary separation is made due to the rates of $log{k}_n$ and $k_n{\epsilon }_n$: We fix ${\epsilon }_n=n^{-1}(logn)$ and ${\epsilon }_n=n^{-1}{(logn)}^2$, which imply conditions (8) and (9), respectively. Next, the models are divided according to the rate of growth of $M_n$ in the form $M_n={(log(n+1))}^a$ with $a=1/2,1,2.$ Recall that from Theorem 2, it follows that the limit distribution is Gumbel for the pairs (8)–(17), (8)–(18) and (9)–(18) (note that for the last two cases $k_n\gtrsim e^{\lambda M_n^{\tau }}$ under our choice), and Fréchet for the pair (9)–(17).

For each case we simulate 1000 samples of length 1000, and find the maximal value of each sample. The goodness-of-fit of the limit distributions of the maximal values suggested by Theorem 2 is tested by the Kolmogorov–Smirnov criterion. Figure 2 depicts the kernel density estimates of the densities of normalised maxima in each case superimposed with the limit distributions implied by Theorem 2. It can be seen that for all groups the density estimates are quite close to the theoretical densities, and the Kolmogorov–Smirnov test does not reject the null of the corresponding theoretical distributions (corresponding p-values are given on the same figure).

Figure 2. Densities of sample maxima for groups (8)–(17) (top left), (9)–(17) (top right), (8)–(18) (bottom left) and (9)–(18) (bottom right) superimposed with the theoretical limit distributions suggested by Theorem 2.

5. Modelling the Log-Returns of BMW Shares

Starting from the prominent paper by Mandelbrot [18], heavy-tailedness of distributions of price changes is a well-known stylised fact, leading to the frequent choice of power laws for the modelling, see, e.g., [19]. However, numerous papers admit that the tails of the distributions used for modelling the returns are though heavier than normal, yet lighter than of a power law. For instance, Laherrère and Sornette [10] demonstrate that daily price variations on the exchange market can be successfully described by the Weibull distribution with parameter smaller than one. Malevergne et al. [11] intently analyse financial returns on different time scales, ranging from daily to 5- and 1-minute data, and come to the conclusion that the Pareto distribution fits the highest 5% of the data, while the remaining 95% are most efficiently described by the Weibull law. Thus, it is reasonable to expect that the overall distribution of returns should be successfully described by the model which (in some sense) lies in between of these two distributions. This idea serves as a motivation of the application of the model (3) to modelling the log-returns.

In our study we consider hourly logarithmic returns of BMW shares in 2019. Following [11], we analyse positive and negative returns separately. The sample sizes are equal to 1130 and 1062, respectively. The plots for positive and negative log returns are presented in the first plot in Figure 3. In what follows, we assume that the log-returns are jointly independent. This assumption was checked by the chi-squared test resulting in p-values 0.234 and 0.111 for positive and negative returns, respectively.

Figure 3. First (second) row: The plot of data; p-values for Weibull fit for positive (absolute negative) log returns.

The analysis consists of four steps. Below we denote the positive log-returns by $X_1,\cdots ,X_{1130}$ and the negative log-returns by $Y_1,\cdots ,Y_{1062}$.

• Separation of components. For each $n=1,\cdots ,1130$, the sample $X_1,\cdots ,$$X_n$ is divided into two parts corresponding to the first and the second components in (14), where the slowly varying function L is equal to a constant. For such partition we assign all observations except the $\lfloor 1130·{\epsilon }_{1130}\rfloor$ greatest order statistics of the whole sample to the first component and test the goodness-of-fit for Weibull distribution by the Kolmogorov–Smirnov criterion. The values of ${\epsilon }_{1130}$ are taken on a grid from 0 to 0.5 with a step of 0.001. From the second plot in Figure 3 it can be seen that there is an evident peak in p-values, which corresponds to some value of the mixture parameter, which we denote by ${\widehat{\epsilon }}_{1130}$. The $\lfloor 1130·{\widehat{\epsilon }}_{1130}\rfloor$ upper order statistics are assumed to come from the heavy-tailed part.
  Next, let us show that the sequence ${\epsilon }_n$ vanishes as n grows. For all $n=1,\cdots ,1129$ the parameter ${\epsilon }_n$ is estimated as the proportion of elements corresponding to the second component. The same procedure is applied for each $n=1,\cdots ,1062$ to the sample $Y_1,\cdots ,Y_n$. The results are illustrated by Figure 4. The first plot in two rows indicates that in both cases ${\widehat{\epsilon }}_n$ declines with n, though in case of negative log returns the decrease is not so evident. From the second plot one can see that $k_n{\widehat{\epsilon }}_n$ with $k_n=n$ appear to tend to infinity. Therefore, as suggested by Theorems 1 and 2, we examine the asymptotic behaviour of the ratio $log{k}_n/{\left(k_n{\widehat{\epsilon }}_n\right)}^{\beta }$ for different values of $\beta >0$. For both positive and absolute values of negative log returns we get that for $\beta =0.45$ this ratio decreases rapidly.
  

  Figure 4. ${\widehat{\epsilon }}_n$ against n (left), $k_n{\widehat{\epsilon }}_n$ against n (middle), $log{k}_n{\left(k_n{\widehat{\epsilon }}_n\right)}^{-0.45}$ against n (right) for positive log returns of BMW (first row) and absolute values of negative log returns of BMW (second row).
• Model selection. Based on the partition obtained on the previous step, the decision between truncated and non-truncated distributions for the second component is made based on the test proposed by Aban, Meerschaert and Panorska [20]. From Figure 5 one observes that the null hypothesis of non-truncated law is not rejected for both positive and negative log returns since the p-values are significantly larger than 0.05. Thus, it can be concluded that the model (3) is more appropriate for the considered data. The Kolmogorov–Smirnov test does not reject the null of Pareto distribution for the observations assigned to the second component with p-values 0.971 and 0.925 for positive and negative log returns, respectively. It should be noted that in both cases the Pareto distribution does not fit the whole sample, since the p-values are smaller than ${10}^{-16}$.
  

  Figure 5. The p-values of the Aban’s test for positive (left) and absolute values of negative (right) log returns.
• Estimation of parameters. The parameters of the first and second components are estimated by the maximum-likelihood approach. The estimated values are presented in Table 3. Since $\widehat{\tau }/\widehat{\alpha }$ is equal to 0.483 for positive log returns and 0.484 for absolute values of negative, from Figure 4 we conclude that the assumption (9) is fulfilled with $\beta =0.45$, and therefore the limit distribution for maxima is the Fréchet distribution, see item 2 in Theorem 1.
  Table 3. Estimated values of the parameters of mixture distribution for positive and absolute values of negative log returns of BMW, 2019.

  Estimates	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\tau }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{m}}$	$\widehat{\mathit{\epsilon }}$
  Positive log returns	0.003	1.278	2.649	0.009	0.051
  Abs. negative log returns	0.003	1.246	2.573	0.01	0.04

  It is worth mentioning that for both positive and absolute values of negative log returns we get $\widehat{\alpha }>2$, which is completely coherent with general empirical results for financial returns and addresses the common critique against models with infinite variance, see [19].
• Validation of the model.Figure 6 depicts the true density of positive (top left) and absolute values of negative (top right) log returns superimposed with densities of 100 simulations from the mixture (3) with the corresponding parameter estimates. The constructed model is also verified by the empirical confidence intervals for the sample quantiles based on 100 simulations. The results are given in Table 4 and Table 5 and illustrated by Figure 6. These intervals are reasonably small and contain all true values of quantiles. Next, we apply the chi-squared test with the maximum likelihood estimates of parameters. Due to the known theory (see Section 4.4 from [21]), the statistics of this test converge to the chi-squared distribution with $K-1-D$ degrees of freedom, where K is the number of subintervals used for the chi-squared test, and D is the dimension of the parameter space (in our setting, $D=5$). Using $K=15$, we get the p-values 0.73 and 0.21 for positive and negative log returns, and therefore do not reject the null hypothesis. Finally, we arrive at the outcome that the model (3) is appropriate both for positive and absolute values of negative log returns of BMW at the considered time scale.
  

  Figure 6. Top left (right): Real (red) and simulated (grey) density of positive (negative) log returns; bottom left (right): Empirical quantiles of positive (negative) log returns and the corresponding confidence intervals.
  Table 4. Empirical quantiles of positive log returns of BMW, 2019, and the estimated confidence intervals.

  Quantiles $·{10}^3$	10%	20%	30%	40%	50%	60%	70%	80%	90%
  Lower CI	0.416	0.783	1.154	1.548	1.982	2.509	3.164	4.013	5.679
  Estimate	0.452	0.825	1.232	1.64	2.085	2.611	3.289	4.183	6.383
  Upper CI	0.537	0.946	1.33	1.747	2.223	2.79	3.498	4.493	6.657

  Table 5. Empirical quantiles of absolute values of negative log returns of BMW, 2019, and the estimated confidence intervals.

  Quantiles $·{10}^3$	10%	20%	30%	40%	50%	60%	70%	80%	90%
  Lower CI	0.417	0.778	1.134	1.562	2.021	2.583	3.262	4.191	5.884
  Estimate	0.431	0.892	1.231	1.654	2.14	2.73	3.501	4.619	6.62
  Upper CI	0.554	0.962	1.393	1.829	2.321	2.914	3.684	4.784	6.905

6. Conclusions

This paper contributes to the existing literature in the following respects.

• We model the heavy-tailed impurity via the mixture distribution with varying parameters and (following the ideas from [8,9]) consider the resulting model as a triangular array. The notion of heavy-tailed impurity is not new, but all previously known probabilistic results are concentrated only on the classical limit laws, see [2,16]. In this paper, we establish the limit laws for the maximum in these models.
• The paper delivers an example of the triangular array such that its row-wise maximum has (under proper normalisation) 6 different distributions, depending on the rates of the varying parameters. To the best of our knowledge, all previous articles on the extreme value analysis for triangular arrays deal with the convergence to the limit law having twice differentiable cdf ([5,7]) or closely related to the classical extreme value distributions ([6]), while some limits in our examples are discontinuous and very different from the classical laws.
• We show the difference between various types of truncation for the regularly varying distributions used for modelling the impurity. Our conditions (17)–(18) are close to soft and hard truncation regimes introduced in [9], leading to similar (but not completely the same) outcomes for our mixture model as for the model considered in [9]. Moreover, unlike previous papers, we study in details the case of intermediate truncation regime (19).
• For practical purposes we describe the four-step scheme for the application of this model to the asset price modelling. This approach can be considered as a possible development of the idea that the distribution of stock returns is in some sense between exponential and power law. A comprehensive discussion of this idea can be found in [11].