Study of the Boundary Value Problems for Nonlinear Wave Equations on Domains with a Complex Structure of the Boundary and Prehistory

Abstract

We study a boundary value problem for nonlinear partial differential equations of the hyperbolic type on the plain in a domain with a complex boundary. To find the missing data for the given boundary constraints, we solve a supplementary nonlinear problem. For the approximation of solutions, one constructive method is built.

1. Introduction

The study of processes of a different nature (e.g., gas sorption, drying by the air flow, pipes heating by a stream of hot water, etc.) often leads to boundary value problems (for short, BVPs) for nonlinear differential equations of the hyperbolic type on the plane, defined in the domains with a complex structure of the boundary. The general problem setting of such BVPs was first introduced by Collatz (see discussions in [1]). The author suggests splitting the given domain D by characteristics onto subdomains $D_i,i\in \mathbb{N}$ and the consecutive solution of the classical Cauchy, Darboux, and Gaursat problems on each of these subdomains. Since it is not possible to find the exact solution of the given nonlinear problem, every following BVP will contain errors in their outcome data. At the same time, it is unknown how these errors will influence the end result. This leads to the significant disadvantage of the approach, suggested by Collatz.

On the other hand, there are some recent results, devoted to constructive methods of investigation and approximate solution of such BVPs with continuous and discontinuous right-hand sides in the nonlinear differential equations (see discussions in [2,3,4,5,6]). In these papers, the studied problem is reduced to the equivalent system of nonlinear integral equations. It allows us to approximately solve the system by the constructed iterative methods, where at every iteration step, one gets a solution of the studied BVP in the given domain with a pre-defined precision. This eliminates the aforementioned disadvantage of Collatz’s approach.

Note that in [2,3,4,5,6], the authors studied problems where the initial data (i.e., the boundary conditions) are known. However, there are processes dependent on prehistory, which means that in the mathematical model, not all of the income data are defined. In this case, one has to investigate an additional BVP describing this prehistory. A classical example of such problems can be the mathematical model describing exploitation of the already used respirator. Even though the model of the previous usage of the respirator is given, the gas concentration in the sorbent (due to its exploitation) is unknown, and thus, is defined as a prehistory.

To our best knowledge, these types of problems are not studied in the literature. This explains the motivation of our research, of which results we present in the current paper.

2. Problem Setting

On the phase plain $xOt$, let us define a domain $D=D_1\cup D_2\cup D_3$ (see Figure 1), where

$$D_1=\left\{(t,x)\right|x\in (x_1,x_2],t\in (g_1\left(x\right),t_1]\},$$

$$D_2=\left\{(t,x)\right|x\in [x_0,x_1],t\in (g_2\left(x\right),t_2)\},$$

$$D_3=\left\{(t,x)\right|x\in (x_1,x_2],t\in (t_1,t_2]\},$$

$t=g_i\left(x\right)$ if $x=k_i\left(t\right)$, $i=1,2$ are the “free” curves and

$$g_1^{\prime }\left(x\right)>0,g_2^{\prime }\left(x\right)<0,$$

$$g_1\left(x_i\right)=t_{i-1},g_2\left(x_j\right)=t_{2-j},$$

for $j=0,1,x_0<x_1<x_2,t_0<t_1<t_2.$

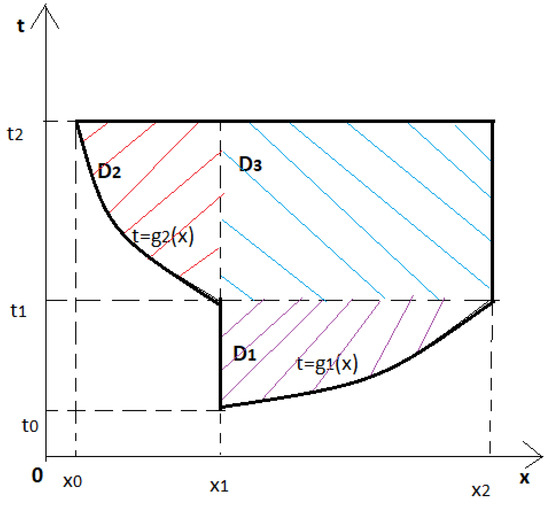
Figure 1. Domain $D=D_1\cup D_2\cup D_3$.

Problem 1.

In the space of functions

$$C^{*}({\overline{D}}_2\cup {\overline{D}}_3):=C^{\left(1.1\right)}(D_2\cup D_3)\cap C({\overline{D}}_2\cup {\overline{D}}_3)$$

find the solution of the wave equation

$$L_{a_i}^{\left(1.1\right)}u(t,x)=f(t,x,u(t,x)):=f\left[u(t,x)\right],$$

(1)

$$L_{a_i}^{\left(1.1\right)}u(t,x):=D^{\left(1.1\right)}u(t,x)+a_1(t,x)D^{\left(0.1\right)}u(t,x)+a_2(t,x)D^{\left(1.0\right)}u(t,x),$$

(2)

which satisfies the conditions:

$$u(g_2\left(x\right),x)={\psi }_2\left(x\right),u(t_2,x)=\phi \left(x\right),x\in [x_0,x_1],$$

(3)

$$u(t_1,x)=v(t_1,x),x\in [x_1,x_2].$$

(4)

Here, function $v(t,x)\in C^{*}\left({\overline{D}}_1\right)$ is a solution of the differential equation

$$L_{b_i}^{\left(1.1\right)}v(t,x)=\omega (t,x,v(t,x)):=\omega \left[v(t,x)\right],$$

(5)

satisfying constraints:

$$\begin{array}{c}v(t,x_1)=\mu \left(t\right),t\in [g_1\left(x\right),t_1],\\ v(g_1\left(x\right),x)={\psi }_1\left(x\right),x\in [x_1,x_2].\end{array}$$

(6)

Moreover, for the aforementioned problems conditions, we hold:

$${\psi }_2\left(x_0\right)=\phi \left(x_0\right),{\psi }_2\left(x_1\right)=\mu \left(t_1\right),\mu \left(t_0\right)={\psi }_1\left(x_1\right).$$

(7)

From here on, we assume that

$$f\left[u(t,x)\right]\in C\left({\overline{B}}_{2,2}\right),f:{\overline{B}}_{2,2}\to \mathbb{R},$$

$${\overline{B}}_{2,2}\subset {\mathbb{R}}^3,\Pi {\mathrm{p}}_{xOt}{\overline{B}}_{2,2}={\overline{D}}_2\cup {\overline{D}}_3:={\overline{D}}_4,$$

$$\omega \left[v(t,x)\right]\in C\left({\overline{B}}_{1,2}\right),\omega :{\overline{B}}_{1,2}\to \mathbb{R},$$

$${\overline{B}}_{1,2}\subset {\mathbb{R}}^3,\Pi {\mathrm{p}}_{xOt}{\overline{B}}_{1,2}={\overline{D}}_1,$$

$$a_1(t,x)\in C^{\left(0.1\right)}\left(D_4\right),a_2(t,x)\in C^{\left(1.0\right)}\left(D_4\right),$$

$$b_1(t,x)\in C^{\left(0.1\right)}\left(D_1\right),b_2(t,x)\in C^{\left(1.0\right)}\left(D_1\right).$$

In addition, let equalities

$$\begin{array}{c}{D}^{\left(0.1\right)}{a}_1(t,x)=D^{\left(1.0\right)}{a}_2(t,x),(t,x)\in D_4,\\ D^{\left(0.1\right)}{b}_1(t,x)=D^{\left(1.0\right)}{b}_2(t,x),(t,x)\in D_1,\end{array}$$

(8)

hold, and the given functions $\phi \left(x\right),{\psi }_2\left(x\right),{\psi }_1\left(x\right)$ and $\mu \left(t\right)$ are such that

$$\phi \left(x\right),{\psi }_2\left(x\right)\in C^1(x_0,x_1),$$

$${\psi }_1\left(x\right)\in C^1(x_1,x_2),$$

$$\mu \left(t\right)\in C^1(t_0,t_1).$$

Note that the solution of the BVP (1)–(4), (7) $u(t,x)=u_s(t,x)$, $(t,x)\in {\overline{D}}_s$, $s=2,3$, where $u_2(t,x)$ is a solution of the Darboux problem (1), (3) for $(t,x)\in {\overline{D}}_2$ and $u_3(t,x)$ is a solution of the Goursat problem for the differential Equation (1) with restrictions on the characteristics $t=t_1$ and $x=x_1$ given by

$$\begin{array}{c}{u}_3(t_1,x)=v(t_1,x),x\in [x_1,x_2],\\ u_3(t,x_1)=u_2(t,x_1),t\in [t_1,t_2].\end{array}$$

(9)

Furthermore, due to condition (7), an equality

$$v(t_1,x_1)=u_2(t_1,x_1)$$

is true.

3. Auxiliary Statements

It is easy to show that the lemma holds.

Lemma 1.

Let

$$f\left[u(t,x)\right]\in C\left({\overline{B}}_{2,2}\right),$$

$$\omega \left[v(t,x)\right]\in C\left({\overline{B}}_{1,2}\right),$$

$$a_1(t,x)\in C^{\left(0.1\right)}\left(D_4\right),a_2(t,x)\in C^{\left(1.0\right)}\left({\overline{D}}_4\right),$$

$$b_1(t,x)\in C^{\left(0.1\right)}\left(D_1\right),b_2(t,x)\in C^{\left(1.0\right)}\left(D_1\right)$$

and condition (8) hold.

Then, the BVP (1)–(7) is equivalent to the following system of integral equations

$$\begin{array}{c}{u}_s(t,x)={\Phi }_s(t,x)+{\epsilon }_s\left\{T_{1,3}{F}_1\left[u_1(\eta ,\xi )\right]+T_{2,3}{F}_2\left[u_2(\eta ,\xi )\right]\right\}\hfill \\ \hfill +T_s{F}_s\left[u_s(\eta ,\xi )\right],(t,x)\in {\overline{D}}_s,s=1,2,3,{\epsilon }_1={\epsilon }_2=0,{\epsilon }_3=1,\end{array}$$

(10)

where

$$v(t,x):=u_1(t,x),$$

$$F_1\left[u_1(t,x)\right]:=\omega \left[u_1(t,x)\right]+\left[D^{\left(1.0\right)}{b}_2(t,x)+b_1(t,x)b_2(t,x)\right]u_1(t,x),$$

$${\Phi }_1(t,x):=\mu \left(t\right)exp\left({\int }_x^{x_1}{b}_2(t,\xi )d\xi \right)$$

$$+\left[{\psi }_1\left(x\right)-\mu \left(g_1\left(x\right)\right)exp\left({\int }_x^{x_1}{b}_2(g_1\left(x\right),\xi )d\xi \right)\right]exp\left({\int }_t^{g_1\left(x\right)}{b}_1(\eta ,x)d\eta \right),$$

$$T_1{F}_1\left[u_1(\eta ,\xi )\right]:={\int }_{x_1}^x{\int }_{g_1\left(x\right)}^t{F}_1\left[u_1(\eta ,\xi )\right]K_1(x,t;\xi ,\eta )d\eta d\xi ,$$

$$K_1(x,t;\xi ,\eta ):=exp\left({\int }_t^{\eta }{b}_1(\tau ,x)d\tau +{\int }_x^{\xi }{b}_2(\eta ,\zeta )d\zeta \right),$$

$${\Phi }_2(t,x):=\phi \left(x\right)exp\left({\int }_t^{t_2}{a}_1(\eta ,x)d\eta \right)$$

$$+\left[{\psi }_2\left(k_2\left(t\right)\right)-\phi \left(k_2\left(t\right)\right)exp\left({\int }_t^{t_2}{a}_1(\eta ,k_2\left(t\right))d\eta \right)\right]exp\left({\int }_x^{k_2\left(t\right)}{a}_2(t,\xi )d\xi \right),$$

$$K(x,t;\xi ,\eta ):=exp\left({\int }_x^{\xi }{a}_2(\eta ,\zeta )d\zeta +{\int }_t^{\eta }{a}_1(\tau ,x)d\tau \right),$$

$$\begin{array}{c}{F}_s\left[u_s(t,x)\right]:=f\left[u_s(t,x)\right]+\left[D^{\left(0.1\right)}{a}_1(t,x)+a_1(t,x)a_2(t,x)\right]u_s(t,x),\\ (t,x)\in {\overline{D}}_s,s=2,3,\end{array}$$

$$T_2{F}_2\left[u_2(\eta ,\xi )\right]:={\int }_{t_2}^t{\int }_{k_2\left(t\right)}^{x}K(x,t;\xi ,\eta )F\left[u_2(\xi ,\eta )\right]d\xi d\eta ,$$

$${\Phi }_3(t,x):=\left[{\psi }_2\left(k_2\left(t\right)\right)-\phi \left(k_2\left(t\right)\right)exp\left({\int }_t^{t_2}{a}_1(\eta ,k_2\left(t\right))d\eta \right)\right]exp\left({\int }_x^{k_2\left(t\right)}{a}_2(t,\xi )d\xi \right)$$

$$+\left[\phi \left(x_1\right)exp\left({\int }_{t_1}^{t_2}{a}_1(\eta ,x_1)d\eta \right)-{\psi }_2\left(x_1\right)\right]K(x,t;x_1,t_1)$$

$$+\mu \left(t_1\right)exp\left({\int }_x^{x_1}{b}_2(t_1,\xi )d\xi +{\int }_t^{t_1}{a}_1(\eta ,x)d\eta \right)$$

$$+\left[{\psi }_1\left(x\right)-\mu \left(g_1\left(x\right)\right)exp\left({\int }_x^{x_1}{b}_2(g_1\left(x\right),\xi )d\xi \right)\right]exp\left({\int }_{t_1}^{g_1\left(x\right)}{b}_1(\eta ,x)d\eta +{\int }_t^{t_1}{a}_1(\eta ,x)d\eta \right),$$

$$T_3{F}_3\left[u_3(\eta ,\xi )\right]:={\int }_{t_1}^t{\int }_{x_1}^{x}K(x,t;\xi ,\eta )F_3\left[u_3(\eta ,\xi )\right]d\xi d\eta ,$$

$$T_{1,3}{F}_1\left[u_1(\eta ,\xi )\right]:={\int }_{x_1}^x{\int }_{g_1\left(x\right)}^{t_1}{F}_1\left[u_1(\eta ,\xi )\right]K_1(x,t_1;\xi ,\eta )d\eta d\xi exp\left({\int }_t^{t_1}{a}_1(\eta ,x)d\eta \right),$$

$$T_{2,3}{F}_2\left[u_2(\eta ,\xi )\right]:={\int }_{t_2}^t{\int }_{k_2\left(t\right)}^{x_1}K(x,t;\xi ,\eta )F_2\left[u_2(\eta ,\xi )\right]d\xi d\eta .$$

Note, that from conditions (9) follows that an inequality

$$D^{\left(1.0\right)}\left[u_2(t,x_1)-u_3(t,x_1)\right]=0$$

is true. But

$$\begin{array}{c}{D}^{\left(0.1\right)}\left[u_2(t,x_1)-u_3(t,x_1)\right]\hfill \\ \hfill =\left[D^{\left(0.1\right)}{u}_2(t_1,x_1)-u_1(t_1,x_1)\right]exp\left({\int }_t^{t_1}{a}_1(\eta ,x_1)d\eta \right):=\rho \left(t\right).\end{array}$$

(11)

Thus, a lemma holds.

Lemma 2.

Let conditions of Lemma 1 hold and the BVP (1)–(7) has a solution.

Then it is defined on the space $C^{*}\left({\overline{D}}_4\right)$ (i.e., it is regular), if

$$D^{\left(0.1\right)}\left[u_2(t_1,x_1)-u_1(t_1,x_1)\right]=0.$$

Otherwise, based on (11), $\rho \left(t\right)\ne 0$ and solution of the problem (1)–(7) is irregular.

4. Constructive Method of Investigation and Approximation of Solutions

Let us establish sufficient conditions of the existence and uniqueness of the solution of the system of integral Equation (10). For this purpose, let us introduce a space of functions $C_2\left({\overline{B}}_s\right)$.

Definition 1.

We say that functions

$$F_s\left[u_s(t,x)\right]\in C_2\left({\overline{B}}_s\right),F_s:{\overline{B}}_s\to \mathbb{R},$$

$${\overline{B}}_s\subset {\mathbb{R}}^3,\Pi {\mathrm{p}}_{xOt}{\overline{B}}_s={\overline{D}}_s,s=1,2,3,$$

if they satisfy conditions [7]:

1. 

$F_s\left[u_s(t,x)\right]\in C\left({\overline{B}}_s\right),s=1,2,3;$

2. 

in the space of functions $C\left({\overline{B}}_{s,1}\right),{\overline{B}}_{s,1}\subset {\mathbb{R}}^4$, $\Pi {\mathrm{p}}_{xOt}{\overline{B}}_{s,1}={\overline{D}}_s$, $s=1,2,3$ there exist functions $H_s(t,x,u_s(t,x);v_s(t,x))\equiv H_s[u_s(t,x);v_s(t,x)]$, such that:

• $H_s[u_s[t,x);u_s(t,x)]\equiv F_s\left[u_s(t,x)\right]$;
• for any pair of continuous functions $u_s(t,x),v_s(t,x)\in {\overline{B}}_{s,1}$ satisfying condition $u_s(t,x)\ge v_s(t,x)$, $(t,x)\in {\overline{D}}_s$, in the domain ${\overline{B}}_{s,1}$ the inequalities

  $$H_s[u_s[t,x);v_s(t,x)]-H_s[v_s[t,x);u_s(t,x)]\ge 0,$$

  (12)

  hold;
• functions $H_s[u_s[t,x);v_s(t,x)]$ in the domain ${\overline{B}}_{s,1}$ satisfy the Lipschitz condition, that is, for any two arbitrary pairs of continuous functions $u_{s,r}(t,x)$, $v_{s,r}(t,x)\in {\overline{B}}_{s,1}$, $r=1,2$ conditions are true:

  $$\begin{array}{c}\left|H_s[u_{s,1}(t,x);u_{s,2}(t,x)]-H_s[v_{s,1}(t,x);v_{s,2}(t,x)]\right|\\ \le L_s\left(|W_{s,1}(t,x)|+|W_{s,2}(t,x)|\right),\end{array}$$

  where $W_{s,r}(t,x)=u_{s,r}(t,x)-v_{s,r}(t,x)$, $r=1,2$ and $L_s$ are the Lipschitz constants, $s=1,2,3$.

Remark 1.

It is easy to prove that if functions $F_s\left[u_s(t,x)\right]\in C\left({\overline{B}}_s\right)$ have the bounded first-order partial derivatives with respect to $u_s(t,x)$, then they always belong to the space $C_2\left({\overline{B}}_s\right)$, $s=1,2,3$. An inverse statement is not true.

Assume that functions $z_{s,p}(t,x)$, $v_{s,p}(t,x)\in C\left({\overline{D}}_s\right)$ correspondingly belong to the domains ${\overline{B}}_{s,1}$, for all $s=1,2,3$ and $p\in {\mathbb{N}}_0:=\mathbb{N}\cup \left\{0\right\}$.

Additionally, let us introduce the following notations:

$$W_{s,p}(t,x):=z_{s,p}(t,x)-v_{s,p}(t,x),(t,x)\in {\overline{D}}_s,p\in {\mathbb{N}}_0,s=1,2,3,$$

$$\begin{array}{c}{f}_s^p(t,x):=H_s[z_{s,p}(t,x);v_{s,p}(t,x)],\\ f_{s,p}(t,x):=H_s[v_{s,p}(t,x);z_{s,p}(t,x)],\end{array}s=1,3,$$

$$\begin{array}{c}{f}_2^p(t,x):=H_2[v_{2,p}(t,x);z_{2,p}(t,x)],\\ f_{2,p}(t,x):=H_2[z_{2,p}(t,x);v_{2,p}(t,x)],\end{array}$$

$$\begin{array}{c}{R}_s^p(t,x):={\Phi }_s(t,x)+{\epsilon }_s\left\{T_{1,3}{f}_1^p(\eta ,\xi )+T_{2,3}{f}_2^p(\eta ,\xi )\right\}+T_s{f}_s^p(\eta ,\xi ),\\ R_{s,p}(t,x):={\Phi }_s(t,x)+{\epsilon }_s\left\{T_{1,3}{f}_{1,p}(\eta ,\xi )+T_{2,3}{f}_{2,p}(\eta ,\xi )\right\}+T_s{f}_{s,p}(\eta ,\xi ),\end{array}$$

$$\begin{array}{c}{\alpha }_{s,p}(t,x):=z_{s,p}(t,x)-R_s^p(t,x),\\ {\beta }_{s,p}(t,x):=v_{s,p}(t,x)-R_{s,p}(t,x),\end{array}$$

(13)

$$\begin{array}{c}{\overline{z}}_{s,p}(t,x):=z_{s,p}(t,x)-q_{s,p}(t,x)W_{s,p}(t,x),\\ {\overline{v}}_{s,p}(t,x):=v_{s,p}(t,x)+c_{s,p}(t,x)W_{s,p}(t,x),\end{array}p\in {\mathbb{N}}_0,$$

$$\begin{array}{c}{F}_s^p(t,x):=H_s[{\overline{z}}_{s,p}(t,x);{\overline{v}}_{s,p}(t,x)],\\ F_{s,p}(t,x):=H_s[{\overline{v}}_{s,p}(t,x);{\overline{z}}_{s,p}(t,x)],\end{array}s=1,3,$$

$$\begin{array}{c}{F}_2^p(t,x):=H_2[{\overline{v}}_{2,p}(t,x);{\overline{z}}_{2,p}(t,x)],\\ F_{2,p}(t,x):=H_2[{\overline{z}}_{2,p}(t,x);{\overline{v}}_{2,p}(t,x)],\end{array}$$

$$\begin{array}{c}{\overline{R}}_s^p(t,x):=R_s^p(t,x)\left|{}_{f_s^p(t,x)=F_s^p(t,x)}\right.,\\ {\overline{R}}_{s,p}(t,x):=R_{s,p}(t,x)\left|{}_{f_{s,p}(t,x)=F_{s,p}(t,x)}\right.,\end{array}$$

(14)

where $q_{s,p}(t,x)$ and $c_{s,p}(t,x)$ are arbitrary functions from the space $C\left({\overline{D}}_s\right)$ that satisfy conditions:

$$\begin{array}{c}0\le q_{s,p}(t,x)\le 0.5,\\ 0\le c_{s,p}(t,x)\le 0.5,\end{array}p\in {\mathbb{N}}_0,(t,x)\in {\overline{D}}_s.$$

(15)

Let us construct sequences of functions $\left\{z_{s,p}(t,x)\right\}$ and $\left\{v_{s,p}(t,x)\right\}$ in the form [7,8]:

$$\begin{array}{c}{z}_{s,p+1}(t,x)={\overline{R}}_s^p(t,x),\\ v_{s,p+1}(t,x)={\overline{R}}_{s,p}(t,x),\end{array}p\in {\mathbb{N}}_0,(t,x)\in {\overline{D}}_s,s=1,2,3.$$

(16)

As a zero approximation, we take arbitrary functions $z_{s,0}(t,x)$, $v_{s,0}(t,x)\in {\overline{B}}_{s,1}$ from the space $C\left({\overline{D}}_s\right)$, such that for $(t,x)\in {\overline{D}}_s$, the inequalities

$$W_{s,0}(t,x)\ge 0,{\alpha }_{s,0}(t,x)\ge 0,{\beta }_{s,0}(t,x)\le 0,(t,x)\in {\overline{D}}_s,s=1,2,3$$

(17)

hold.

Definition 2.

Functions $z_{s,0}(t,x)$, $v_{s,0}(t,x)\in C\left({\overline{D}}_s\right)$ that belong to the domain ${\overline{B}}_{s,1}$ and satisfy conditions (17) are called the comparison functions of the BVP (1)–(7).

From (13), (14), (16), we have:

$$\begin{array}{c}{z}_{s,p}(t,x)-z_{s,p+1}(t,x)={\alpha }_{s,p}(t,x)+R_s^p(t,x)-{\overline{R}}_s^p(t,x),\\ v_{s,p}(t,x)-v_{s,p+1}(t,x)={\beta }_{s,p}(t,x)+R_{s,p}(t,x)-{\overline{R}}_{s,p}(t,x),\end{array}$$

(18)

$$W_{s,p+1}(t,x)={\overline{R}}_s^p(t,x)-{\overline{R}}_{s,p}(t,x),p\in {\mathbb{N}}_0,(t,x)\in {\overline{D}}_s,s=1,2,3,$$

(19)

$$\begin{array}{c}{\alpha }_{s,p+1}(t,x)={\overline{R}}_s^p(t,x)-R_s^{p+1}(t,x),\\ {\beta }_{s,p+1}(t,x)={\overline{R}}_{s,p}(t,x)-R_{s,p+1}(t,x),(t,x)\in {\overline{D}}_s.\end{array}$$

(20)

Let us emphasize that due to (15), an estimate is true:

$$v_{s,0}(t,x)\le {\overline{v}}_{s,0}(t,x)\le {\overline{z}}_{s,0}(t,x)\le z_{s,0}(t,x),$$

i.e., ${\overline{z}}_{s,0}(t,x)$, ${\overline{v}}_{s,0}(t,x)\in {\overline{B}}_{s,1}$, if only $z_{s,0(t,x)}$, $v_{s,0}(t,x)\in {\overline{B}}_{s,1}$.

However, then from (18) and (19), taking into account (12), for $p=0$, we get the inequalities

$$W_{s,1}(t,x)\ge 0,z_{s,0}(t,x)\ge z_{s,1}(t,x),v_{s,0}(t,x)\le v_{s,1}(t,x),$$

or, in other words, relations

$$v_{s,0}(t,x)\le v_{s,1}(t,x)\le z_{s,1}(t,x)\le z_{s,0}(t,x),(t,x)\in {\overline{D}}_s,s=1,2,3,$$

hold. Thus, $z_{s,1}(t,x)$, $v_{s,1}(t,x)\in {\overline{B}}_{s,1}$.

Let us choose arbitrary functions $q_{s,0}(t,x)$ and $c_{s,0}(t,x)$ from the space of functions $C\left({\overline{D}}_s\right)$, which satisfy restrictions (15), in such a way that the inequalities

$$\begin{array}{c}{z}_{s,0}(t,x)-z_{s,1}(t,x)-q_{s,0}(t,x)W_{s,0}(t,x)\ge 0,\\ v_{s,0}(t,x)-v_{s,1}(t,x)+c_{s,0}(t,x)W_{s,0}(t,x)\le 0,\end{array}(t,x)\in {\overline{D}}_s$$

hold.

Then from (20) for $p=0$, we have that ${\alpha }_{s,1}(t,x)\ge 0$, ${\beta }_{s,1}(t,x)\le 0$, that is, the constructed functions $z_{s,1}(t,x)$ and $v_{s,1}(t,x)$ are the comparison functions of the problems (1)–(7).

Taking $z_{s,1}(t,x)$ and $v_{s,1}(t,x)$ as the income data and repeating the aforementioned arguments via the method of mathematical induction, we conclude that if, at every iteration step (16) continuous in ${\overline{D}}_s$ functions $q_{s,p}(t,x)$, $c_{s,p}(t,x)$ satisfying conditions (15) are chosen in a way that the inequalities

$$\begin{array}{c}{z}_{s,p}(t,x)-z_{s,p+1}(t,x)-q_{s,p}(t,x)W_{s,p}(t,x)\ge 0,\\ v_{s,p}(t,x)-v_{s,p+1}(t,x)+c_{s,p}(t,x)W_{s,p}(t,x)\le 0,\end{array}$$

(21)

where $p\in {\mathbb{N}}_0,(t,x)\in {\overline{D}}_s,s=1,2,3,$ are true, then for any $p\in \mathbb{N}$, we obtain

$$\begin{array}{c}{v}_{s,p}(t,x)\le v_{s,p+1}(t,x)\le z_{s,p+1}(t,x)\le z_{s,p}(t,x),\\ {\alpha }_{s,p}(t,x)\ge 0,{\beta }_{s,p}(t,x)\le 0,(t,x)\in {\overline{D}}_s,s=1,2,3.\end{array}$$

(22)

Let us show that the domain of functions $q_{s,p}(t,x)$ and $c_{s,p}(t,x)$, which satisfy conditions (15) and inequalities (21), is non–empty.

Theorem 1.

If $F_s\left[u_s(t,x)\right]\in C_2\left({\overline{B}}_s\right)$ and there exist comparison functions of the problem (1)–(7), then the set of functions $q_{s,p}(t,x)$, $c_{s,p}(t,x)$, which satisfy conditions (15), (21), is non–empty.

Proof. 

Let

$${\tau }_{s,p}(t,x):={\alpha }_{s,p}(t,x)-{\beta }_{s,p}(t,x)+W_{s,p}(t,x)$$

and let us put

$$\begin{array}{c}{q}_{s,p}(t,x)=\left\{\begin{array}{cc}{\alpha }_{s,p}(t,x){\left[{\tau }_{s,p}(t,x)\right]}^{-1},& W_{s,p}(t,x)\ne 0,\hfill \\ 0,& W_{s,p}(t,x)=0,\hfill \end{array}\right.\\ c_{s,p}(t,x)=\left\{\begin{array}{cc}-{\beta }_{s,p}(t,x){\left[{\tau }_{s,p}(t,x)\right]}^{-1},& W_{s,p}(t,x)\ne 0,\hfill \\ 0,& W_{s,p}(t,x)=0,\hfill \end{array}\right.\\ p\in {\mathbb{N}}_0,(t,x){\overline{D}}_s,s=1,2,3.\end{array}$$

(23)

Functions, defined according to (23), satisfy conditions (15) and

$$\begin{array}{c}{z}_{s,p}(t,x)-z_{s,p+1}(t,x)-q_{s,p}(t,x)W_{s,p}(t,x)\\ ={\alpha }_{s,p}(t,x)\left[1-W_{s,p}(t,x){\left({\tau }_{s,p}(t,x)\right)}^{-1}\right]+R_s^p(t,x)-{\overline{R}}_s^p(t,x)\ge 0,\end{array}$$

$$\begin{array}{c}{v}_{s,p}(t,x)-v_{s,p+1}(t,x)+c_{s,p}(t,x)W_{s,p}(t,x)\\ ={\beta }_{s,p}(t,x)\left[1-W_{s,p}(t,x){\left({\tau }_{s,p}(t,x)\right)}^{-1}\right]+R_{s,p}(t,x)-{\overline{R}}_{s,p}(t,x)\le 0,\end{array}$$

for all $p\in {\mathbb{N}}_0$ and $(t,x)\in {\overline{D}}_s$, $s=1,2,3$.

Thus, the theorem is proved.  □

5. Convergence Results

Let us show that the sequences of functions $\left\{z_{s,p}(t,x)\right\}$, $\left\{v_{s,p}(t,x)\right\}$, defined by (16), (21), converge uniformly for $(t,x)\in {\overline{D}}_s$ to the unique solution of the corresponding integral equation of the system (10).

Let us put

$$max\left\{\underset{{\overline{D}}_1\times {\overline{D}}_1}{sup}{K}_1(x,t;\xi ,\eta )exp\left({\int }_t^{t_1}{a}_1(\eta ,x)d\eta \right),\underset{{\overline{D}}_4\times {\overline{D}}_4}{sup}K(x,t;\xi ,\eta )\right\}=0.5K,$$

$$\underset{s}{max}\left\{\underset{{\overline{D}}_s}{sup}{W}_{s,0}(t,x)\right\}=d,$$

$$\mathcal{L}=\underset{s}{max}{L}_s,$$

$$\underset{s}{max}\left\{\underset{{\overline{D}}_s}{sup}\left(1-q_{s,p}(t,x)-c_{s,p}(t,x)\right)\right\}=q,$$

$$max\left\{1,x_2-x_0+t_2-t_0\right\}=\gamma .$$

Then, using the method of mathematical induction from (19), it is easy to conclude that for any $p\in \mathbb{N}$, $(t,x)\in {\overline{D}}_s$, the estimate

$$\underset{s}{max}\underset{{\overline{D}}_s}{sup}\left|W_{s,p}(t,x)\right|\le \frac{{\left[A(x-x_0+t_2-t_0)\right]}^p}{p!}d$$

(24)

is true, where $A=\mathcal{L}Kq\gamma$.

From the estimate (24), it follows that

$$\underset{p\to \infty }{lim}{W}_{s,p}(t,x)=0.$$

Thus, due to inequalities (22), we get

$$\underset{p\to \infty }{lim}{z}_{s,p}(t,x)=\underset{p\to \infty }{lim}{v}_{s,p}(t,x):=u_s(t,x),(t,x)\in {\overline{D}}_s,s=1,2,3.$$

Passing in (16) to the limit, when $p\to \infty$, we ensure that the limit functions $u_s(t,x)$ for $(t,x)\in {\overline{D}}_s$ are solutions of the corresponding integral equations of the system (10).

By contradiction, it is easy to show that if $F_s\left[u_s(t,x)\right]\in C_2\left({\overline{B}}_s\right)$ and conditions (18) hold, then the system (10) has a unique solution.

Theorem 2.

Let functions $F_s\left[u_s(t,x)\right]\in C_2\left({\overline{B}}_s\right)$, and there exist comparison functions of the BVP (1)–(7).

Then:

1. 

The system of integral Equation (10) has a solution, and it is unique for $(t,x)\in {\overline{D}}_s$, $s=1,2,3$;

2. 

Sequences of functions $\left\{z_{p,s}(t,x)\right\}$ and $\left\{v_{p,s}(t,x)\right\}$, constructed according to (16), (21), converge uniformly to the unique solution of the system of integral Equation (10) for $(t,x)\in {\overline{D}}_s$, where continuous functions $q_{s,p}(t,x)$, $c_{s,p}(t,x)$ satisfy conditions (15);

3. 

Estimate (24) holds;

4. 

For arbitrary $p\in \mathbb{N}$ and $(t,x)\in {\overline{D}}_s$, $s=1,2,3$, inequalities

$$v_{s,p}(t,x)\le v_{s,p+1}(t,x)\le u_s(t,x)\le z_{s,p+1}(t,x)\le z_{s,p}(t,x)$$

(25)

are true;

5. 

Convergence of the method (16), (21) is not slower than the convergence of the iterative method

$${\tilde{z}}_{s,p+1}(t,x)=R_s^p(t,x),{\tilde{v}}_{s,p+1}(t,x)=R_{s,p}(t,x).$$

(26)

Let us prove inequality (25). Suppose, that for some p at the point $(t_0,x_0)\in {\overline{D}}_s$,

$$z_{s,p}(t_0,x_0)<u_s(t_0,x_0).$$

Then, taking into account (22), at this point $\forall n\in \mathbb{N}$ we get

$$z_{s,p+n}(t_0,x_0)\le z_{s,p}(t_0,x_0)<u_s(t_0,x_0).$$

Hence, the sequence of functions $\left\{z_{s,p+n}(t_0,x_0)\right\}$ for $n\to \infty$ does not converge to $u_s(t_0,x_0)$. We came to a contradiction.

Analogically, we can prove that the inequality $v_{s,p}(t,x)\le u_s(t,x)$ is true.

If $z_{s,p}(t,x),v_{s,p}(t,x)$ are the comparison functions of the BVP (1)–(7), then from (16) and (25) follows:

$${\tilde{z}}_{s,p+1}(t,x)-z_{s,p+1}(t,x)=R_s^p(t,x)-{\overline{R}}_s^p(t,x)\ge 0,$$

$${\tilde{v}}_{s,p+1}(t,x)-v_{s,p+1}(t,x)=R_{s,p}(t,x)-{\overline{R}}_{s,p}(t,x)\le 0.$$

Consequently,

$${\tilde{v}}_{s,p+1}(t,x)\le v_{s,p+1}(t,x)\le z_{s,p+1}(t,x)\le {\tilde{z}}_{s,p+1}(t,x),(t,x)\in {\overline{D}}_s,s=1,2,3.$$

The last inequalities prove the fifth statement of the theorem.

6. Some Corollaries

Corollary 1.

Let conditions of Theorem 2 and conditions (8) hold.

Then the BVP (1)–(7) has a unique solution for $(t,x)\in {\overline{D}}_4$. Moreover, it is regular, if $D^{\left(0.1\right)}v(t_1,x_1)=D^{\left(0.1\right)}{u}_2(t_1,x_1)$. Otherwise, it is irregular.

Corollary 2.

Let

$$F_s\left[u_s(t,x)\right]\in C_2\left({\overline{B}}_s\right),$$

$$F_s\left[u_s(t,x)\right]\equiv H_s[u_s(t,x);0],s=1,3,$$

$$F_2\left[u_2(t,x)\right]\equiv H_s[0;u_2(t,x)],$$

conditions (8) hold and boundary constraints (3), (6) are homogeneous.

If $F_s\left[0\right]\ge (\le )0$, $s=1,3$, $F_2\left[0\right]\le (\ge )0$ in the domain ${\overline{B}}_s$, then the solution of the BVP (1)–(7) satisfies the inequalities:

$$u(t,x)\ge (\le )0,(t,x)\in {\overline{D}}_4.$$

Consider an equation of the form

$$L_{\left(1.1\right)}z(t,x)=f_1(t,x,z(t,x)):=f_1\left[z(t,x)\right],f_1:{\overline{B}}_{2,2}\to \mathbb{R},{\overline{B}}_{2,2}\subset {\mathbb{R}}^3.$$

(27)

Assume that the right-hand sides of the differential Equations (1) and (27) satisfy conditions:

• $F\left[u(t,x)\right]\in C_2\left({\overline{B}}_{2,2}\right)$;
• Function $f_1\left[z(t,x)\right]\in C\left({\overline{B}}_{2,2}\right)$, and in the domain, ${\overline{B}}_{2,2}$ has a bounded first-order derivative with respect to $z(t,x)$ that satisfies an inequality:

  $$\frac{\partial f_1\left[z(t,x)\right]}{\partial z(t,x)}+D^{\left(0.1\right)}{a}_1(t,x)+a_1(t,x)a_2(t,x)\ge 0,(t,x)\in {\overline{D}}_4;$$

  (28)
• For any function $v(t,x)\in {\overline{B}}_{2,2}$ from the space $C^{*}\left({\overline{D}}_4\right)$, the inequalities

  $$\begin{array}{c}{f}_1\left[v(t,x)\right]\ge (\le )f\left[v(t,x)\right],(t,x)\in {\overline{D}}_3,\\ f_1\left[v(t,x)\right]\le (\ge )f\left[v(t,x)\right],(t,x)\in {\overline{D}}_2\end{array}$$

  (29)

  hold.

Theorem 3

(comparison theorem). Let $a_i(t,x)$, $i=1,2$ in the domain ${\overline{D}}_4$ satisfy conditions (8). Let, for the right-hand sides $f\left[u\right(t,x\left)\right]$ and $f_1\left[z(t,x)\right]$ of Equations (1) and (27), the aforementioned conditions (1)–(3) hold, and in the domain ${\overline{B}}_{s,1}$ there exist the comparison functions of the problems (1)–(7) and (27), (3)–(7).

Then, solutions of these problems satisfy conditions:

$$u(t,x)\le (\ge )z(t,x),(t,x)\in {\overline{D}}_4.$$

(30)

Proof. 

According to Theorem 2 and Corollary 2, solutions of the problems (1)–(7) and (27), (3)–(7) exist, and are unique (regular or irregular). Hence, putting $W(t,x):=z(t,x)-u(t,x)$ and using the Mean Value Theorem, we get:

$$L_{\left(1.1\right)}W(t,x)=b(t,x)W(t,x)+f_1\left[u(t,x)\right]-f\left[u(t,x)\right],$$

where $b(t,x):=\frac{\partial {\tilde{f}}_1\left[z(t,x)\right]}{\partial z(t,x)}$ is a derivative, evaluated at some fixed value $z(t,x)\in {\overline{B}}_{2,2}$, $(t,x)\in {\overline{D}}_4$.

Obviously, function $W(t,x)$ satisfies the homogeneous conditions (3), (6) and $u(t_1,x)=v(t_1,x)=z(t_1,x)\Rightarrow W(t_1,x)=0$, $x\in [x_1,x_2]$. Moreover,

$$\begin{array}{c}{F}_4\left[W(t,x)\right]:=\left[b(t,x)+D^{\left(0.1\right)}{a}_1(t,x)+a_1(t,x)a_2(t,x)\right]W(t,x)\\ +f_1\left[u(t,x)\right]-f\left[u(t,x)\right],\end{array}$$

that is, due to (28), (29) we get:

$$F_4\left[W(t,x)\right]\in C_2\left({\overline{B}}_{2,2}\right)$$

and

$$F_4\left[W(t,x)\right]\equiv H[W(t,x);0],\mathrm{for}(t,x)\in {\overline{D}}_3,$$

$$F_4\left[W(t,x)\right]\equiv H[0;W(t,x)],\mathrm{for}(t,x)\in {\overline{D}}_2,$$

$$F_4\left[0\right]\ge (\le )0\mathrm{in} \mathrm{the} \mathrm{domain}{\overline{B}}_3,$$

$$F_4\left[0\right]\le (\ge )0\mathrm{in}{\overline{B}}_2.$$

On the basis of the Corollary 2

$$W(t,x)\ge (\le )0,\mathrm{for}(t,x)\in {\overline{D}}_4,$$

that is, the inequalities (30) hold.  □

Remark 2.

To speed-up convergence of the two-sided approximations to the solution of the problem (1)–(7), functions $z_{s,p}(t,x)$ and $v_{s,p}(t,x)$ can be constructed according to formulas:

$$\begin{array}{c}{z}_{s,p+1}(t,x)={\Phi }_s(t,x)+{\epsilon }_s\left\{T_{1,3}{f}_1^{p+1}(\eta ,\xi )+T_{2,3}{f}_2^{p+1}(\eta ,\xi )\right\}+T_s{F}_s^p(\eta ,\xi ),\\ v_{s,p+1}(t,x)={\Phi }_s(t,x)+{\epsilon }_s\left\{T_{1,3}{f}_{1,p+1}(\eta ,\xi )+T_{2,3}{f}_{2,p+1}(\eta ,\xi )\right\}+T_s{F}_{s,p}(\eta ,\xi )\end{array}.$$

(31)

One can show that the iterative method (31) converges not slower than the method (16), (21).

7. Discussion

To summarize, in the current paper, we have presented our recent results in the study of one boundary value problem for a nonlinear partial differential equation of the hyperbolic type on the plane in a domain with a complex boundary and a prehistory. To find the missing data for the given boundary constraints, we solved a supplementary nonlinear problem. In addition, we have built a two-sided constructive method to approximate solutions of the studied problems, and proved appropriate convergence properties.

As it was already mentioned in the Introduction, these problems have a wide spectrum of applications in applied sciences. Thus, the obtained results can be further broadened to study the mathematical models of real physical processes.