Three Solutions for a Partial Discrete Dirichlet Problem Involving the Mean Curvature Operator

Abstract

Partial difference equations have received more and more attention in recent years due to their extensive applications in diverse areas. In this paper, we consider a Dirichlet boundary value problem of the partial difference equation involving the mean curvature operator. By applying critical point theory, the existence of at least three solutions is obtained. Furthermore, under some appropriate assumptions on the nonlinearity, we respectively show that this problem admits at least two or three positive solutions by means of a strong maximum principle. Finally, we present two concrete examples and combine with images to illustrate our main results.

1. Introduction

Throughout this article, we denote by $\mathbb{R}$ and $\mathbb{Z}$ the sets of real numbers and integers, respectively. For $a,b\in \mathbb{Z}$ satisfying $a\le b$, define $\mathbb{Z}(a,b)=\{a,a+1,\cdots ,b\}$.

Consider the following partial discrete Dirichlet boundary value problem, denoted ($D_{\lambda }^{f,q}$):

$$\begin{array}{cc}\hfill -{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)& =\lambda f\left(\right(i,j),x(i,j\left)\right),\hfill \\ & (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n),\hfill \end{array}$$

with boundary conditions

$$\begin{array}{cc}\hfill & x(i,0)=x(i,n+1)=0,i\in \mathbb{Z}(0,m+1),\hfill \\ \hfill & x(0,j)=x(m+1,j)=0,j\in \mathbb{Z}(0,n+1).\hfill \end{array}$$

(1)

Here m and n are given positive integers, ${\Delta }_1$ and ${\Delta }_2$ are the forward difference operators, i.e., ${\Delta }_{1}x(i,j)=x(i+1,j)-x(i,j)$ and ${\Delta }_{2}x(i,j)=x(i,j+1)-x(i,j)$, ${\Delta }_1^{2}x(i,j)={\Delta }_1\left({\Delta }_{1}x(i,j)\right)$ and ${\Delta }_2^{2}x(i,j)={\Delta }_2\left({\Delta }_{2}x(i,j)\right)$, ${\varphi }_c$ denotes the mean curvature operator [1] defined by ${\varphi }_c\left(s\right)=\frac{s}{\sqrt{1+s^2}}$ for $s\in \mathbb{R}$, $q(i,j)\ge 0$ for each $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, $\lambda$ is a real parameter, and $f\left(\right(i,j),·)\in C(\mathbb{R},\mathbb{R})$ for all $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$.

As we all know, the theory of difference equations has been used extensively to study discrete mathematical models appearing in computer science, ecology, neural networks, economics and other fields [2,3,4,5]. During recent decades, many excellent results on the existence and multiplicity of solutions for difference equations have been acquired, which included results on boundary value problems [6,7,8,9,10,11], periodic and subharmonic solutions [12,13,14,15,16], homoclinic solutions [17,18,19,20,21,22,23,24,25,26] and heteroclinic solutions [27,28], etc.

Only one discrete variable is involved in the above difference equations, in fact that partial difference equations involving two or more discrete variables have also the numerous practical applications in many fields. For instance, Shi and Chua [29] established the following partial difference equation in image processing

$$(4+\lambda )v_{m,n}-v_{m-1,n}-v_{m+1,n}-v_{m,n-1}-v_{m,n+1}=\lambda d_{m,n},(m,n)\in \mathbb{Z}(0,M-1)\times \mathbb{Z}(0,N-1),$$

where $d_{m,n}$ is proportional to the intensity of the input image at the associated pixel, $v_{m,n}$ denotes the nodal voltage waveform of the resistive array, and the parameter $\lambda$ controls the amount of smoothing. In [30], to modelling the temperature distribution of a “very long” rod, Cheng introduced the nonlinear reaction diffusion equation

$$u_m^{(n+1)}-u_m^{\left(n\right)}-r\left(u_{m-1}^{\left(n\right)}-2u_m^{\left(n\right)}+u_{m+1}^{\left(n\right)}\right)=f\left(u_m^{\left(n\right)}\right),(m,n)\in \mathbb{Z}\times \mathbb{N},$$

where f is a real function defined on $\mathbb{R}$. Of course, these applications have greatly promoted the theoretical study of partial difference equations.

In [31,32,33], the authors considered the problem ($E_{\lambda }^f$):

$$\left\{\begin{array}{c}-{\Delta }_1^{2}u(i-1,j)-{\Delta }_2^{2}u(i,j-1)=\lambda f((i,j),u(i,j)),(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n),\hfill \\ u(i,0)=u(i,n+1)=0,i\in \mathbb{Z}(1,m),\hfill \\ u(0,j)=u(m+1,j)=0,j\in \mathbb{Z}(1,n).\hfill \end{array}\right.$$

Following the ideas from [34], the authors first investigated the nonlinear algebraic system associated with ($E_{\lambda }^f$) and further obtained several different results on the existence and multiplicity of solutions for problem ($E_{\lambda }^f$) by means of critical point theory.

In 2020, Du and Zhou [35] considered the partial discrete Dirichlet problem ($S_{\lambda }^f$):

$${\Delta }_1\left({\varphi }_p\left({\Delta }_{1}x(i-1,j)\right)\right)+{\Delta }_2\left({\varphi }_p\left({\Delta }_{2}x(i,j-1)\right)\right)+\lambda f((i,j),x(i,j))=0,(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$$

with boundary conditions (1). By directly establishing the variational structure corresponding to ($S_{\lambda }^f$) and applying critical point theory, the authors acquired a series of the existence results.

Lately, Wang and Zhou [36] discussed a more general problem ($S_{\lambda }^{f,q}$):

$$\begin{array}{cc}\hfill -{\Delta }_1\left[{\varphi }_p\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_p\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j)& {\varphi }_p\left(x(i,j)\right)=\lambda f((i,j),x(i,j)),\hfill \\ \hfill & (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\hfill \end{array}$$

with boundary conditions (1). Using critical point theory, the authors determined the intervals of parameter $\lambda$ in which problem ($S_{\lambda }^{f,q}$) admits at least three solutions.

Compared with the partial difference equations with ${\varphi }_p$-Laplacian, there is less work on the partial difference equations involving ${\varphi }_c$-Laplacian, which is mainly because the latter is more complex to deal with. In fact, ${\varphi }_c$-Laplacian has very important theoretical significance and application value [37,38].

Recently, Du and Zhou [39] studied the partial discrete Dirichlet problem ($D_{\lambda }^{f,0}$), namely problem ($D_{\lambda }^{f,q}$) when $q(i,j)=0$ for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$. The authors obtained the existence of multiple solutions for problem ($D_{\lambda }^{f,0}$) via critical point theory.

Owing to the reasons above, we will investigate the existence of at least three solutions for problem ($D_{\lambda }^{f,q}$) in this paper. Please note that Lemma 4 plays an important role in the proof of our results, which is more complex than [39]. In addition, different from the main tools of proof in [39], the existence of at least three solutions is obtained using another three critical points theorem. Based on a strong maximum principle, we further obtain the existence of at least two and three positive solutions when the nonlinearity f satisfies appropriate hypotheses, respectively.

First of all, we recall a critical lemma (see Theorem 2.1 of [40]).

Lemma 1.

Let X be a separable and reflexive real Banach space. $\mathsf{\Phi }:X\to \mathbb{R}$ is a nonnegative continuously Gâteaux differentiable and sequentially weakly lower semicontinuous functional whose Gâteaux derivative admits a continuous inverse on $X^{*}$. $J:X\to \mathbb{R}$ is a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact. Assume that there exists $x_0\in X$ such that $\mathsf{\Phi }\left(x_0\right)=J\left(x_0\right)=0$ and that

$\left(i\right)$

${lim}_{\parallel x\parallel \to +\infty }\left[\mathsf{\Phi }\left(x\right)-\lambda J\left(x\right)\right]=+\infty$ for all $\lambda \in [0,+\infty )$;

Furthermore, assume that there are $r>0$, $x_1\in X$ such that

$\left(ii\right)$

$r<\mathsf{\Phi }\left(x_1\right)$;

$\left(iii\right)$

$\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)<\frac{r}{r+\mathsf{\Phi }\left(x_1\right)}J\left(x_1\right)$.

Then, for each

$$\lambda \in {\Lambda }_1=\left(\frac{\mathsf{\Phi }\left(x_1\right)}{J\left(x_1\right)-\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)},\frac{r}{\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)}\right),$$

the equation

$${\mathsf{\Phi }}^{\prime }\left(x\right)-\lambda J^{\prime }\left(x\right)=0$$

(2)

has at least three solutions in X and, moreover, for each $h>1$, there exist an open interval

$${\Lambda }_2\subseteq \left[0,\frac{hr}{\frac{rJ\left(x_1\right)}{\mathsf{\Phi }\left(x_1\right)}-\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)}\right]$$

and a positive real number σ such that for each $\lambda \in {\Lambda }_2$, the Equation (2) has at least three solutions in X whose norms are less than σ.

The rest of this article is organized as follows. In Section 2, we introduce the variational framework corresponding to problem ($D_{\lambda }^{f,q}$) and show some basic lemmas. Our main results are presented in Section 3. In particular, when the nonlinearity f satisfies appropriate hypotheses, we respectively acquire the existence of at least two or three positive solutions for problem ($D_{\lambda }^{f,q}$) by applying the established strong maximum principle. In Section 4, we give two concrete examples and simulate the partial solutions by two images to illustrate our main results.

2. Preliminaries

Consider the space

$$\begin{array}{cc}\hfill X=\{x:& \mathbb{Z}(0,m+1)\times \mathbb{Z}(0,n+1)\to \mathbb{R}\mathrm{such}\mathrm{that}x(i,0)=x(i,n+1)=0,\hfill \\ \hfill & i\in \mathbb{Z}(0,m+1)\mathrm{and}x(0,j)=x(m+1,j)=0,j\in \mathbb{Z}(0,n+1)\}\hfill \end{array}$$

endowed with the norm

$$\parallel x\parallel ={\left(\sum _{j=1}^n\sum _{i=1}^{m+1}{\left({\Delta }_{1}x(i-1,j)\right)}^2+\sum _{i=1}^m\sum _{j=1}^{n+1}{\left({\Delta }_{2}x(i,j-1)\right)}^2\right)}^{\frac{1}{2}},\forall x\in X.$$

Then X is a separable and reflexive real Banach space and dim$\left(X\right)=mn$.

For any $x\in X$, we define

$$\begin{array}{cc}\hfill \mathsf{\Phi }\left(x\right)=& \sum _{j=1}^n\sum _{i=1}^{m+1}\left[\sqrt{1+{\left({\Delta }_{1}x(i-1,j)\right)}^2}-1\right]+\sum _{i=1}^m\sum _{j=1}^{n+1}\left[\sqrt{1+{\left({\Delta }_{2}x(i,j-1)\right)}^2}-1\right]\hfill \\ \hfill & +\sum _{j=1}^n\sum _{i=1}^{m}q(i,j)\left[\sqrt{1+{\left(x(i,j)\right)}^2}-1\right],\hfill \end{array}$$

(3)

$$J\left(x\right)=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),x(i,j)),$$

where

$${\displaystyle F((i,j),\xi )={\int }_0^{\xi }f((i,j),\tau )d\tau ,\forall ((i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times \mathbb{R}.}$$

It is easy to verify that $\mathsf{\Phi },J:X\to \mathbb{R}$ are two continuously Gâteaux differentiable functionals and for any $x,z\in X$,

$${\mathsf{\Phi }}^{\prime }\left(x\right)\left(z\right)=\sum _{j=1}^n\sum _{i=1}^m\{-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)\}z(i,j),$$

$$J^{\prime }\left(x\right)\left(z\right)=\sum _{j=1}^n\sum _{i=1}^{m}f((i,j),x(i,j))z(i,j).$$

Therefore, for any $x,z\in X$,

$$\begin{array}{cc}\hfill {(\mathsf{\Phi }-\lambda J)}^{\prime }\left(x\right)\left(z\right)=& \sum _{j=1}^n\sum _{i=1}^m\{-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)\hfill \\ \hfill & -\lambda f\left(\right(i,j),x(i,j\left)\right)\left\}z\right(i,j).\hfill \end{array}$$

Lemma 2.

Every critical point $x\in X$ of $\mathsf{\Phi }-\lambda J$ is just a solution of problem ($D_{\lambda }^{f,q}$).

Proof. 

Assume that $x\in X$ is a critical point of $\mathsf{\Phi }-\lambda J$, i.e., ${(\mathsf{\Phi }-\lambda J)}^{\prime }\left(x\right)=0$, then, for all $z\in X$,

$$\sum _{j=1}^n\sum _{i=1}^m\{-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)-\lambda f((i,j),x(i,j))\}z(i,j)=0.$$

(4)

For any $(h,k)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, define $z=z_{(h,k)}\in X$ by

$$z_{(h,k)}(i,j)=\left\{\begin{array}{c}1,(i,j)=(h,k),\hfill \\ 0,(i,j)\ne (h,k).\hfill \end{array}\right.$$

Substituting $z=z_{(h,k)}$ into (4), we have

$$-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(h-1,k)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(h,k-1)\right)\right]+q(h,k){\varphi }_c\left(x(h,k)\right)=\lambda f((h,k),x(h,k))$$

for each $(h,k)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$. Hence, x is a solution of problem ($D_{\lambda }^{f,q}$). □

Lemma 3.

For any $x\in X$, one has

$$\frac{4}{\sqrt{m+n+2}}{\parallel x\parallel }_{\infty }\le \parallel x\parallel \le 2\sqrt{2mn}{\parallel x\parallel }_{\infty },$$

(5)

where

$${\parallel x\parallel }_{\infty }=\underset{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}{max}\left\{\right|x(i,j)\left|\right\}.$$

Proof. 

On the one hand, from (2.1) of [39], for any $x\in X$, we have

$${\parallel x\parallel }_{\infty }=\underset{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}{max}\left\{\right|x(i,j)\left|\right\}\le \frac{\sqrt{m+n+2}}{4}\parallel x\parallel ,$$

which implies that

$$\frac{4}{\sqrt{m+n+2}}{\parallel x\parallel }_{\infty }\le \parallel x\parallel .$$

On the other hand, for each $(i,j)\in \mathbb{Z}(1,m+1)\times \mathbb{Z}(1,n)$, one has

$${\left({\Delta }_{1}x(i-1,j)\right)}^2\le \left(\right|x(i,j)|+{\left|x(i-1,j)\right|)}^2\le {2\left(\right|x(i,j)|}^2+{\left|x(i-1,j)\right|}^2).$$

Hence,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^{m+1}}{\left({\Delta }_{1}x(i-1,j)\right)}^2& \le 2\left({\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^{m+1}}{\left|x(i,j)\right|}^2+{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^{m+1}}{\left|x(i-1,j)\right|}^2\right)\hfill \\ & =2\left({\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}{\left|x(i,j)\right|}^2+{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}{\left|x(i,j)\right|}^2\right)\hfill \\ & =4{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}{\left|x(i,j)\right|}^2\hfill \\ & \le 4{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}{\left({\displaystyle \underset{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}{max}}\left\{\right|x(i,j)\left|\right\}\right)}^2\hfill \\ & ={4mn\parallel x\parallel }_{\infty }^2.\hfill \end{array}$$

Similarly, we infer

$$\sum _{i=1}^m\sum _{j=1}^{n+1}{\left({\Delta }_{2}x(i,j-1)\right)}^2\le 4mn{\parallel x\parallel }_{\infty }^2.$$

Therefore,

$$\parallel x\parallel ={\left(\sum _{j=1}^n\sum _{i=1}^{m+1}{\left({\Delta }_{1}x(i-1,j)\right)}^2+\sum _{i=1}^m\sum _{j=1}^{n+1}{\left({\Delta }_{2}x(i,j-1)\right)}^2\right)}^{\frac{1}{2}}\le 2\sqrt{2mn}{\parallel x\parallel }_{\infty }.$$

□

Remark 1.

Take $x\in X$, where

$$x(k,l)={(-1)}^{k+l},\forall (k,l)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n).$$

It is easy to verify that

$$\parallel x\parallel =\sqrt{8mn-2m-2n}\mathrm{and}{\parallel x\parallel }_{\infty }=1,$$

so,

$$\underset{m,n\to +\infty }{lim}\frac{\parallel x\parallel }{2\sqrt{2mn}{\parallel x\parallel }_{\infty }}=\underset{m,n\to +\infty }{lim}\frac{\sqrt{8mn-2m-2n}}{\sqrt{8mn}}=\underset{m,n\to +\infty }{lim}\sqrt{1-\frac{1}{4n}-\frac{1}{4m}}=1.$$

That is to say, $\parallel x\parallel$ and $2\sqrt{2mn}{\parallel x\parallel }_{\infty }$ are approximate when m and n are large enough.

Remark 2.

(5) implies that for any $x\in X$, ${\parallel x\parallel }_{\infty }\to +\infty$ as $\parallel x\parallel \to +\infty$.

Lemma 4.

Assume that Φ as defined in (3), then

$$\mathsf{\Phi }\left(x\right)\ge (1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right],\forall x\in X$$

(6)

holds, where $q_{*}=\underset{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}{min}\left\{q(i,j)\right\}$.

Proof. 

For convenience, denote $\mathsf{\Phi }\left(x\right)={\mathsf{\Phi }}_1\left(x\right)+{\mathsf{\Phi }}_2\left(x\right)$, where

$$\begin{array}{cc}\hfill & {\mathsf{\Phi }}_1\left(x\right)=\sum _{j=1}^n\sum _{i=1}^{m+1}\left[\sqrt{1+{\left({\Delta }_{1}x(i-1,j)\right)}^2}-1\right]+\sum _{i=1}^m\sum _{j=1}^{n+1}\left[\sqrt{1+{\left({\Delta }_{2}x(i,j-1)\right)}^2}-1\right],\hfill \\ \hfill & {\mathsf{\Phi }}_2\left(x\right)=\sum _{j=1}^n\sum _{i=1}^{m}q(i,j)\left[\sqrt{1+{\left(x(i,j)\right)}^2}-1\right].\hfill \end{array}$$

First, we discuss ${\mathsf{\Phi }}_1\left(x\right)$. Put

$$\begin{array}{cc}\hfill & v_1(i,j)=\sqrt{1+{\left({\Delta }_{1}x(i-1,j)\right)}^2}-1,(i,j)\in \mathbb{Z}(1,m+1)\times \mathbb{Z}(1,n),\hfill \\ \hfill & v_2(i,j)=\sqrt{1+{\left({\Delta }_{2}x(i,j-1)\right)}^2}-1,(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n+1).\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill \sum _{j=1}^n\sum _{i=1}^{m+1}{\left({\Delta }_{1}x(i-1,j)\right)}^2& =\sum _{j=1}^n\sum _{i=1}^{m+1}\left[{(v_1(i,j)+1)}^2-1\right]\hfill \\ & =\sum _{j=1}^n\sum _{i=1}^{m+1}{\left(v_1(i,j)\right)}^2+2\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)\hfill \\ & \le {\left[\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)\right]}^2+2\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j),\hfill \end{array}$$

and

$$\sum _{i=1}^m\sum _{j=1}^{n+1}{\left({\Delta }_{2}x(i,j-1)\right)}^2\le {\left[\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j)\right]}^2+2\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j).$$

Thus,

$$\begin{array}{cc}\hfill {\parallel x\parallel }^2& =\sum _{j=1}^n\sum _{i=1}^{m+1}{\left({\Delta }_{1}x(i-1,j)\right)}^2+\sum _{i=1}^m\sum _{j=1}^{n+1}{\left({\Delta }_{2}x(i,j-1)\right)}^2\hfill \\ & \le {\left[\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)\right]}^2+{\left[\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j)\right]}^2+2\left[\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)+\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j)\right]\hfill \\ & \le {\left[\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)+\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j)\right]}^2+2\left[\sum _{j=1}^n\sum _{i=1}^{m+1}{v}_1(i,j)+\sum _{i=1}^m\sum _{j=1}^{n+1}{v}_2(i,j)\right]\hfill \\ & ={\left({\mathsf{\Phi }}_1\left(x\right)\right)}^2+2{\mathsf{\Phi }}_1\left(x\right),\hfill \end{array}$$

which implies that

$${\mathsf{\Phi }}_1\left(x\right)\ge \sqrt{1+{\parallel x\parallel }^2}-1.$$

In view of (5), we obtain

$${\mathsf{\Phi }}_1\left(x\right)\ge \sqrt{1+\frac{16}{m+n+2}{\parallel x\parallel }_{\infty }^2}-1.$$

Next, we discuss ${\mathsf{\Phi }}_2\left(x\right)$. Please note that

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_2\left(x\right)& =\sum _{j=1}^n\sum _{i=1}^{m}q(i,j)\left[\sqrt{1+{\left(x(i,j)\right)}^2}-1\right]\hfill \\ & \ge q_{*}\sum _{j=1}^n\sum _{i=1}^m\left[\sqrt{1+{\left(x(i,j)\right)}^2}-1\right]\hfill \\ & \ge q_{*}\left[\sqrt{1+{\left({max}_{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}\left\{\right|x(i,j)\left|\right\}\right)}^2}-1\right]\hfill \\ & =q_{*}\left[\sqrt{1+{\parallel x\parallel }_{\infty }^2}-1\right].\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill \mathsf{\Phi }\left(x\right)& ={\mathsf{\Phi }}_1\left(x\right)+{\mathsf{\Phi }}_2\left(x\right)\hfill \\ & \ge \left[\sqrt{1+\frac{16}{m+n+2}{\parallel x\parallel }_{\infty }^2}-1\right]+q_{*}\left[\sqrt{1+{\parallel x\parallel }_{\infty }^2}-1\right]\hfill \\ & \ge \left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right]+q_{*}\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right]\hfill \\ & =(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right],\hfill \end{array}$$

which yields our conclusion. □

Finally, we establish the following strong maximum principle to acquire positive solutions of problem ($D_{\lambda }^{f,q}$).

Lemma 5.

Fix $x\in X$ such that for each $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, either

$$x(i,j)>0\mathrm{or}-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)\ge 0.$$

(7)

Then, either $x(i,j)>0$ for all $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$ or $x\equiv 0$.

Proof. 

Fix $x\in X$ satisfying (7). Let $\theta \in \mathbb{Z}(1,m)$, $\omega \in \mathbb{Z}(1,n)$ such that

$$x(\theta ,\omega )=min\left\{x(i,j):i\in \mathbb{Z}(1,m),j\in \mathbb{Z}(1,n)\right\}.$$

We consider two cases: $x(\theta ,\omega )>0$ and $x(\theta ,\omega )\le 0$.

Case (I): If $x(\theta ,\omega )>0$, so $x(i,j)>0$ for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, and the proof is complete.

Case (II): If $x(\theta ,\omega )\le 0$, so $x(\theta ,\omega )=min\left\{x(i,j):i\in \mathbb{Z}(0,m+1),j\in \mathbb{Z}(0,n+1)\right\}$. It is clear that ${\Delta }_{1}x(\theta -1,\omega )\le 0$ and ${\Delta }_{1}x(\theta ,\omega )\ge 0$. Please note that ${\varphi }_c\left(s\right)$ is increasing in s and ${\varphi }_c\left(0\right)=0$, we infer

$${\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\le 0\le {\varphi }_c\left({\Delta }_{1}x(\theta ,\omega )\right),$$

that is,

$${\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\right]\ge 0.$$

Analogously,

$${\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)\right]\ge 0.$$

Then,

$${\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\right]+{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)\right]\ge 0.$$

(8)

On the other hand, since $x(\theta ,\omega )\le 0$ and by virtue of (7), one has

$${\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\right]+{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)\right]\le q(\theta ,\omega ){\varphi }_c\left(x(\theta ,\omega )\right)\le 0.$$

(9)

By combining (8) with (9), we obtain

$${\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\right]+{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)\right]=0,$$

which implies that

$$\left\{\begin{array}{c}{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)\right]=0,\hfill \\ {\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)\right]=0,\hfill \end{array}\right.$$

namely

$$\left\{\begin{array}{c}{\varphi }_c\left({\Delta }_{1}x(\theta ,\omega )\right)={\varphi }_c\left({\Delta }_{1}x(\theta -1,\omega )\right)=0,\hfill \\ {\varphi }_c\left({\Delta }_{2}x(\theta ,\omega )\right)={\varphi }_c\left({\Delta }_{2}x(\theta ,\omega -1)\right)=0.\hfill \end{array}\right.$$

Hence,

$$\left\{\begin{array}{c}x(\theta +1,\omega )=x(\theta ,\omega )=x(\theta -1,\omega ),\hfill \\ x(\theta ,\omega +1)=x(\theta ,\omega )=x(\theta ,\omega -1).\hfill \end{array}\right.$$

If $\theta +1=m+1$, we have $x(\theta ,\omega )=0$. Otherwise, $\theta +1\in \mathbb{Z}(1,m)$. At this point, replacing $\theta$ by $\theta +1$, we have $x(\theta +2,\omega )=x(\theta +1,\omega )$. Repeating the reasoning we obtain $x(\theta ,\omega )=x(\theta +1,\omega )=x(\theta +2,\omega )=\cdots =x(m+1,\omega )=0$. Similarly, we acquire $x(\theta ,\omega )=x(\theta -1,\omega )=x(\theta -2,\omega )=\cdots =x(0,\omega )=0$. Thus, $x(i,\omega )=0$ for every $i\in \mathbb{Z}(1,m)$. We can prove that $x\equiv 0$ in the same manner, and the proof of Lemma 5 is complete. □

3. Main Results

For later convenience, put

$$Q=\sum _{j=1}^n\sum _{i=1}^{m}q(i,j),F_t=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),t).$$

Now, we state our main results.

Theorem 1.

Assume that there are positive constants $c,d,\mu ,\alpha$ satisfying $\alpha <1$ and

$$(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]>(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]$$

(10)

such that

(A₁)

$M_1<\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{mn\left\{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\right\}}$;

(A₂)

$F((i,j),\xi )\le \mu \left(1+{\left|\xi \right|}^{\alpha }\right),\forall ((i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times \mathbb{R}$.

Then, for every

$$\lambda \in {\Lambda }_1=\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{F_d-mn{M}_1},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{M}_1}\right),$$

problem ($D_{\lambda }^{f,q}$) has at least three solutions in X, where

$$M_1=\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [-c,c]}{max}F((i,j),\xi ).$$

Moreover, set

$$\begin{array}{cc}\hfill & a=(1+q_{*})(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right],\hfill \\ \hfill & b=(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d-mn(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]M_1.\hfill \end{array}$$

Then, for any $h>1$, there are an open interval ${\Lambda }_2\subseteq \left[0,\frac{a}{b}h\right]$ and a real number $\sigma >0$ such that for every $\lambda \in {\Lambda }_2$, problem ($D_{\lambda }^{f,q}$) has at least three solutions in X and their norms are less than σ.

Remark 3.

By virtue of the assumption $\left(A_1\right)$, it is easy to verify that the intervals ${\Lambda }_1$ and $\left[0,\frac{a}{b}h\right]$ are well-defined.

Remark 4.

For any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, if $f\left(\right(i,j),·):\mathbb{R}\to \mathbb{R}$ is a nonnegative continuous function, Lemma 5 ensures that every solution involved in Theorem 1 is either zero or positive.

Proof of Theorem 1.

Put X, $\mathsf{\Phi }$ and J as defined in Section 2, it is easy to see that X, $\mathsf{\Phi }$ and J satisfy all structure hypotheses requested in Lemma 1.

Take $x_0(i,j)=0$ for any $(i,j)\in \mathbb{Z}(0,m+1)\times \mathbb{Z}(0,n+1)$, so $x_0\in X$ and $\mathsf{\Phi }\left(x_0\right)=J\left(x_0\right)=0$.

For any $x\in X$, it follows from the assumption $\left(A_2\right)$ that

$$\begin{array}{cc}\hfill J\left(x\right)& =\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),x(i,j))\hfill \\ & \le \mu \sum _{j=1}^n\sum _{i=1}^m\left(1+{\left|x(i,j)\right|}^{\alpha }\right)\hfill \\ & \le \mu \sum _{j=1}^n\sum _{i=1}^{m}1+\mu \sum _{j=1}^n\sum _{i=1}^m{\left(\underset{\begin{array}{c}i\in \mathbb{Z}(1,m)\\ j\in \mathbb{Z}(1,n)\end{array}}{max}\left\{\right|x(i,j)\left|\right\}\right)}^{\alpha }\hfill \\ & =\mu mn+{\mu mn\parallel x\parallel }_{\infty }^{\alpha }.\hfill \end{array}$$

Combining with (6), for any $\lambda \ge 0$, one has

$$\begin{array}{cc}\hfill \mathsf{\Phi }\left(x\right)-\lambda J\left(x\right)& \ge (1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right]-\lambda \left(\mu mn+{\mu mn\parallel x\parallel }_{\infty }^{\alpha }\right)\hfill \\ & >(1+q_{*})\sqrt{min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-(1+q_{*})-\lambda \mu mn-\lambda \mu mn{\parallel x\parallel }_{\infty }^{\alpha }\hfill \\ & =(1+q_{*})min\left\{\frac{4}{\sqrt{m+n+2}},1\right\}{\parallel x\parallel }_{\infty }-\lambda \mu mn{\parallel x\parallel }_{\infty }^{\alpha }-(1+q_{*}+\lambda \mu mn).\hfill \end{array}$$

Taking into account that $\alpha <1$ and Remark 2, we have

$$\underset{\parallel x\parallel \to +\infty }{lim}\left[\mathsf{\Phi }\left(x\right)-\lambda J\left(x\right)\right]=+\infty ,\forall \lambda \in [0,+\infty ).$$

That is to say, the condition $\left(i\right)$ of Lemma 1 holds.

To verify the condition $\left(ii\right)$ of Lemma 1, set

$$r=(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right],$$

and

$$x_1(i,j)=\left\{\begin{array}{c}d,\mathrm{if}(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n),\hfill \\ 0,\mathrm{if}i=0,j\in \mathbb{Z}(0,n+1)\mathrm{or}i=m+1,j\in \mathbb{Z}(0,n+1),\hfill \\ 0,\mathrm{if}j=0,i\in \mathbb{Z}(0,m+1)\mathrm{or}j=n+1,i\in \mathbb{Z}(0,m+1).\hfill \end{array}\right.$$

Then $r>0$, $x_1\in X$ and

$$\mathsf{\Phi }\left(x_1\right)=(2m+2n+Q)\left[\sqrt{1+d^2}-1\right],$$

$$J\left(x_1\right)=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),d)=F_d.$$

We obtain $\mathsf{\Phi }\left(x_1\right)>r$ by (10), which yields the condition $\left(ii\right)$ of Lemma 1.

Now we only need to verify the condition $\left(iii\right)$ of Lemma 1. On the one hand, we infer

$$\frac{r}{r+\mathsf{\Phi }\left(x_1\right)}J\left(x_1\right)=\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}.$$

On the other hand, for any $x\in {\mathsf{\Phi }}^{-1}(-\infty ,r]$, it follows from (6) that

$$r\ge \mathsf{\Phi }\left(x\right)\ge (1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2}-1\right].$$

So,

$$min\left\{\frac{16}{m+n+2},1\right\}{\parallel x\parallel }_{\infty }^2\le {\left(\frac{r}{1+q_{*}}\right)}^2+\frac{2r}{1+q_{*}}.$$

Then, for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, one has

$${\left|x(i,j)\right|}^2\le {\parallel x\parallel }_{\infty }^2\le \left[{\left(\frac{r}{1+q_{*}}\right)}^2+\frac{2r}{1+q_{*}}\right]max\left\{\frac{m+n+2}{16},1\right\}=c^2,$$

i.e., $\left|x\right(i,j\left)\right|\le c$. Hence,

$${\mathsf{\Phi }}^{-1}(-\infty ,r]\subseteq \{x\in X:|x(i,j)|\le c,\forall (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\}.$$

In view of the assumption $\left(A_1\right)$, we deduce

$$\begin{array}{cc}\hfill \underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)& \le \underset{x\in \{x\in X:|x(i,j)|\le c,\forall (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n\left)\right\}}{sup}{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}F((i,j),x(i,j))\hfill \\ & \le {\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^m}\underset{\left|\xi \right|\le c}{max}F((i,j),\xi )\hfill \\ & \le mn\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [-c,c]}{max}F((i,j),\xi )\hfill \\ & <\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}\hfill \\ & =\frac{r}{r+\mathsf{\Phi }\left(x_1\right)}J\left(x_1\right),\hfill \end{array}$$

which means that the condition $\left(iii\right)$ of Lemma 1 is satisfied.

Please note that

$$\frac{\mathsf{\Phi }\left(x_1\right)}{J\left(x_1\right)-\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)}\le \frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{F_d-mn{M}_1}$$

and

$$\frac{r}{\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)}\ge \frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{M}_1}.$$

Therefore, Lemmas 1 and 2 guarantee that for any

$$\lambda \in {\Lambda }_1=\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{F_d-mn{M}_1},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{M}_1}\right),$$

problem ($D_{\lambda }^{f,q}$) has at least three solutions in X.

Moreover,

$$\frac{r}{\frac{rJ\left(x_1\right)}{\mathsf{\Phi }\left(x_1\right)}-\underset{x\in {\overline{{\mathsf{\Phi }}^{-1}(-\infty ,r)}}^w}{sup}J\left(x\right)}\le \frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}-mn{M}_1}=\frac{a}{b}.$$

Hence, Lemmas 1 and 2 ensure that for any $h>1$, there are an open interval ${\Lambda }_2\subseteq \left[0,\frac{a}{b}h\right]$ and a real number $\sigma >0$ such that for any $\lambda \in {\Lambda }_2$, problem ($D_{\lambda }^{f,q}$) has at least three solutions in X and their norms are less than $\sigma$. Theorem 1 is proved completely. □

Next, we verify the existence of at least two positive solutions for problem ($D_{\lambda }^{f,q}$) by means of Lemma 5.

Corollary 1.

Assume that $f\left(\right(i,j),0)\ge 0$ for every $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, and there are positive constants $c,d,\mu ,\alpha$ satisfying $\alpha <1$ and (10) such that

$\left(A_1^{*}\right)$

$M_2<\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{mn\left\{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\right\}}$;

$\left(A_2^{*}\right)$

$F((i,j),\xi )\le \mu \left(1+{\left|\xi \right|}^{\alpha }\right),\forall ((i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times (0,+\infty )$.

Then, for any

$$\lambda \in {\Lambda }_1=\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{F_d-mn{M}_2},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{M}_2}\right),$$

problem ($D_{\lambda }^{f,q}$) possesses at least two positive solutions in X, where

$$M_2=\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [0,c]}{max}F((i,j),\xi ).$$

Moreover, set

$$\begin{array}{cc}\hfill & a=(1+q_{*})(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right],\hfill \\ \hfill & b=(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d-mn(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]M_2.\hfill \end{array}$$

Then, for any $h>1$, there are an open interval ${\Lambda }_2\subseteq \left[0,\frac{a}{b}h\right]$ and a positive real number σ such that for any $\lambda \in {\Lambda }_2$, problem ($D_{\lambda }^{f,q}$) possesses at least two positive solutions in X whose norms are all less than σ.

Proof. 

For any $\left(\right(i,j),t)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times \mathbb{R}$, put

$$f^{*}((i,j),t)=\left\{\begin{array}{c}f\left(\right(i,j),t),t>0,\hfill \\ f\left(\right(i,j),0),t\le 0,\hfill \end{array}\right.$$

(11)

and

$${\displaystyle F^{*}((i,j),t)={\int }_0^t{f}^{*}((i,j),\tau )d\tau .}$$

(12)

So,

$${\displaystyle F^{*}((i,j),t)={\int }_0^t{f}^{*}((i,j),\tau )d\tau ={\int }_0^{t}f((i,j),\tau )d\tau =F((i,j),t),\forall t>0,}$$

$${\displaystyle F^{*}((i,j),t)={\int }_0^t{f}^{*}((i,j),\tau )d\tau ={\int }_0^{t}f((i,j),0)d\tau =f((i,j),0)t\le 0,\forall t\le 0.}$$

Hence,

$$\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [-c,c]}{max}{F}^{*}((i,j),\xi )=\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [0,c]}{max}F((i,j),\xi )=M_2,$$

and

$$\sum _{j=1}^n\sum _{i=1}^m{F}^{*}((i,j),d)=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),d)=F_d.$$

By virtue of the assumption $\left(A_1^{*}\right)$ and $\left(A_2^{*}\right)$, Theorem 1 ensures that problem ($D_{\lambda }^{f^{*},q}$) has at least three solutions when $\lambda$ belongs to intervals ${\Lambda }_1$ or ${\Lambda }_2$, respectively. Assume that x is one of the solutions of problem ($D_{\lambda }^{f^{*},q}$), then for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, either $x(i,j)>0$ or

$$-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)=\lambda f((i,j),0)\ge 0,$$

so either $x>0$ in $\mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$ or $x\equiv 0$ by Lemma 5. This indicates that problem ($D_{\lambda }^{f^{*},q}$) has at least two positive solutions in X, which are just positive solutions of problem ($D_{\lambda }^{f,q}$). The conclusion of Corollary 1 holds. □

Furthermore, we consider a special case of problem ($D_{\lambda }^{f,q}$), in which f has separated variables, namely ($D_{\lambda }^{\omega g,q}$):

$$\begin{array}{cc}\hfill -{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)& =\lambda \omega (i,j)g\left(x\right(i,j\left)\right),\hfill \\ & (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\hfill \end{array}$$

with Dirichlet boundary conditions (1). Here $\omega :\mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\to \mathbb{R}$ is nonnegative and non-zero, and $g:[0,+\infty )\to \mathbb{R}$ is a continuous function satisfying $g\left(0\right)\ge 0$.

For convenience, put

$${\displaystyle W=\sum _{j=1}^n\sum _{i=1}^m\omega (i,j),G\left(\xi \right)={\int }_0^{\xi }g\left(s\right)ds,{\omega }^{*}=\underset{(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)}{max}\omega (i,j).}$$

Corollary 2.

Assume that there are positive constants $c,d,\eta ,\alpha$ satisfying $\alpha <1$ and (10) such that

$\left(A_1^{\prime }\right)$

$\underset{\xi \in [0,c]}{max}G\left(\xi \right)<\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]WG\left(d\right)}{mn{\omega }^{*}\left\{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\right\}}$;

$\left(A_2^{\prime }\right)$

$G\left(\xi \right)\le \eta \left(1+{\left|\xi \right|}^{\alpha }\right),\forall \xi >0$.

Then, for any

$$\lambda \in {\Lambda }_1=\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{WG\left(d\right)-mn{\omega }^{*}\underset{\xi \in [0,c]}{max}G\left(\xi \right)},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{\omega }^{*}\underset{\xi \in [0,c]}{max}G\left(\xi \right)}\right),$$

problem ($D_{\lambda }^{\omega g,q}$) possesses at least two positive solutions in X.

Moreover, set

$$\begin{array}{cc}\hfill & a=(1+q_{*})(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right],\hfill \\ \hfill & \begin{array}{cc}\hfill b=& (1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]WG\left(d\right)\hfill \\ \hfill & -mn{\omega }^{*}(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\underset{\xi \in [0,c]}{max}G\left(\xi \right).\hfill \end{array}\hfill \end{array}$$

Then, for any $h>1$, there are an open interval ${\Lambda }_2\subseteq \left[0,\frac{a}{b}h\right]$ and a real number $\sigma >0$ such that for any $\lambda \in {\Lambda }_2$, problem ($D_{\lambda }^{\omega g,q}$) possesses at least two positive solutions in X whose norms are all less than σ.

Proof. 

For any $\left(\right(i,j),s)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times \mathbb{R}$, put

$$f((i,j),s)=\left\{\begin{array}{cc}\omega (i,j)g\left(s\right),\hfill & \hfill s\ge 0,\\ \omega (i,j)g\left(0\right),\hfill & \hfill s<0.\end{array}\right.$$

Note that

$$f\left(\right(i,j),0)=\omega (i,j)g\left(0\right)\ge 0,\forall (i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n),$$

and

$${\displaystyle F((i,j),\xi )={\int }_0^{\xi }f((i,j),s)ds={\int }_0^{\xi }\omega (i,j)g\left(s\right)ds=\omega (i,j)G\left(\xi \right),\forall \xi \ge 0,}$$

$${\displaystyle F((i,j),\xi )={\int }_0^{\xi }f((i,j),s)ds={\int }_0^{\xi }\omega (i,j)g\left(0\right)ds=\omega (i,j)g\left(0\right)\xi \le 0,\forall \xi <0.}$$

By direct computations, we have

$$F_d=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),d)=\sum _{j=1}^n\sum _{i=1}^m\omega (i,j)G\left(d\right)=WG\left(d\right),$$

and

$$M_2=\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [0,c]}{max}F((i,j),\xi )=\underset{\xi \in [0,c]}{max}G\left(\xi \right)\underset{(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)}{max}\omega (i,j)={\omega }^{*}\underset{\xi \in [0,c]}{max}G\left(\xi \right).$$

Moreover, we take

$$\mu =\eta {\omega }^{*}>0.$$

Taking into account $\left(A_1^{\prime }\right)$ and $\left(A_2^{\prime }\right)$, the conclusion of Corollary 2 holds with the help of Corollary 1. □

In fact, if $f\left(\right(i,j),0)>0$ for every $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, we can obtain the existence of at least three positive solutions for problem ($D_{\lambda }^{f,q}$) by means of Lemma 5.

Corollary 3.

For any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, if the assumption $f\left(\right(i,j),0)\ge 0$ in Corollary 1 is replaced by $f\left(\right(i,j),0)>0$ and other conditions remain unchanged, then for any $\lambda \in {\Lambda }_1$, problem ($D_{\lambda }^{f,q}$) admits at least three positive solutions in X. Moreover, for any $h>1$, there are an open interval ${\Lambda }_2\subseteq \left[0,\frac{a}{b}h\right]$ and a real number $\sigma >0$ such that for any $\lambda \in {\Lambda }_2$, problem ($D_{\lambda }^{f,q}$) admits at least three positive solutions in X whose norms are less than σ.

Proof. 

Put $f^{*}$ and $F^{*}$ as defined in (11) and (12). Similar to the proof of Corollary 1, we can establish that problem ($D_{\lambda }^{f^{*},q}$) admits at least three solutions when $\lambda$ belongs to intervals ${\Lambda }_1$ or ${\Lambda }_2$. Let x be an arbitrary solution of problem ($D_{\lambda }^{f^{*},q}$), then for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, either $x(i,j)>0$ or

$$-{\Delta }_1\left[{\varphi }_c\left({\Delta }_{1}x(i-1,j)\right)\right]-{\Delta }_2\left[{\varphi }_c\left({\Delta }_{2}x(i,j-1)\right)\right]+q(i,j){\varphi }_c\left(x(i,j)\right)=\lambda f((i,j),0)>0,$$

so either $x>0$ in $\mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$ or $x\equiv 0$ by Lemma 5. Please note that $x\equiv 0$ is not the solution of problem ($D_{\lambda }^{f^{*},q}$) due to $f\left(\right(i,j),0)>0$ for any $(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)$, which implies that x must be the positive solution of problem ($D_{\lambda }^{f^{*},q}$). So problem ($D_{\lambda }^{f^{*},q}$) admits at least three positive solutions in X, which are just positive solutions of problem ($D_{\lambda }^{f,q}$). Corollary 3 is proved. □

4. Examples

In this section, we present two concrete examples to illustrate our main results.

Example 1.

Consider the problem ($D_{\lambda }^{\omega g,q}$), where $m=n=2$, $c=2$, $d=9$, $\eta =e^7$, $\alpha =\frac{1}{2}$ and

$$q(i,j)=i+j,(i,j)\in \mathbb{Z}(1,2)\times \mathbb{Z}(1,2),$$

$$\omega (i,j)=ij,(i,j)\in \mathbb{Z}(1,2)\times \mathbb{Z}(1,2),$$

$$g\left(s\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{\sqrt{2}}{8}s{e}^{\frac{s}{2}},\hfill & 0\le s\le 8,\hfill \\ 4e^4{s}^{-\frac{1}{2}},\hfill & s>8.\hfill \end{array}\hfill \end{array}\right.$$

It is easy to see that $\omega :\mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\to \mathbb{R}$ is nonnegative and non-zero, and $g:[0,+\infty )\to \mathbb{R}$ is a continuous function satisfying $g\left(0\right)\ge 0$. Moreover, we infer that $Q=12$, $W=9$, $q_{*}=2$,

$${\omega }^{*}=\underset{(i,j)\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)}{max}\omega (i,j)=\underset{(i,j)\in \mathbb{Z}(1,2)\times \mathbb{Z}(1,2)}{max}ij=4,$$

and

$$G\left(\xi \right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{\sqrt{2}}{4}(\xi -2)e^{\frac{\xi }{2}}+\frac{\sqrt{2}}{2},\hfill & 0\le \xi \le 8,\hfill \\ 8e^4{\xi }^{\frac{1}{2}}-\frac{29\sqrt{2}}{2}{e}^4+\frac{\sqrt{2}}{2},\hfill & \xi >8.\hfill \end{array}\hfill \end{array}\right.$$

(13)

Then $G\left(d\right)=\frac{48-29\sqrt{2}}{2}{e}^4+\frac{\sqrt{2}}{2}$ and

$$\underset{\xi \in [0,c]}{max}G\left(\xi \right)=\underset{\xi \in [0,2]}{max}\left[\frac{\sqrt{2}}{4}(\xi -2)e^{\frac{\xi }{2}}+\frac{\sqrt{2}}{2}\right]=\frac{\sqrt{2}}{2}.$$

Note that

$$(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]=20\left(\sqrt{82}-1\right)\approx 161.108,$$

$$(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]=3\left(\sqrt{5}-1\right)\approx 3.708;$$

and

$$\begin{array}{cc}\hfill & \frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]WG\left(d\right)}{mn{\omega }^{*}\left\{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\right\}}\hfill \\ \hfill =& \frac{27\left(\sqrt{5}-1\right)\times \left[\left(48-29\sqrt{2}\right)e^4+\sqrt{2}\right]}{32\left(3\sqrt{5}+20\sqrt{82}-23\right)}\hfill \\ \hfill \approx & 2.423,\hfill \end{array}$$

which yield that (10) and $\left(A_1^{\prime }\right)$ in Corollary 2 are both true.

In view of (13), we deduce that if $0<\xi \le 8$, then

$$G\left(\xi \right)=\frac{\sqrt{2}}{4}(\xi -2)e^{\frac{\xi }{2}}+\frac{\sqrt{2}}{2}\le \frac{3\sqrt{2}}{2}{e}^4+\frac{\sqrt{2}}{2}<e^7<e^7\left(1+{\xi }^{\frac{1}{2}}\right)={\eta (1+|\xi |}^{\alpha });$$

if $\xi >8$, then

$$G\left(\xi \right)=8e^4{\xi }^{\frac{1}{2}}-\frac{29\sqrt{2}}{2}{e}^4+\frac{\sqrt{2}}{2}<8e^4{\xi }^{\frac{1}{2}}+\frac{\sqrt{2}}{2}<e^7{\xi }^{\frac{1}{2}}+e^7={\eta (1+|\xi |}^{\alpha }).$$

The above two cases show that

$$G\left(\xi \right)\le \eta (1+|\xi {|}^{\alpha }),\forall \xi >0,$$

and the condition $\left(A_2^{\prime }\right)$ in Corollary 2 holds.

Therefore, Corollary 2 ensures that for any

$$\begin{array}{cc}\hfill \lambda \in {\Lambda }_1& =\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{WG\left(d\right)-mn{\omega }^{*}\underset{\xi \in [0,c]}{max}G\left(\xi \right)},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{\omega }^{*}\underset{\xi \in [0,c]}{max}G\left(\xi \right)}\right)\hfill \\ & =\left(\frac{40\left(\sqrt{82}-1\right)}{9\times \left[\left(48-29\sqrt{2}\right)e^4+\sqrt{2}\right]-16\sqrt{2}},\frac{3\left(\sqrt{5}-1\right)}{8\sqrt{2}}\right)\hfill \\ & \approx (0.095,0.327),\hfill \end{array}$$

the problem considered admits at least two positive solutions in X.

In particular, take $\lambda =0.1\in {\Lambda }_1$, the problem considered can be simplified as

$$\begin{array}{cc}\hfill 4{\varphi }_c\left(x(1,1)\right)+& 5{\varphi }_c\left(x(1,2)\right)+5{\varphi }_c\left(x(2,1)\right)+6{\varphi }_c\left(x(2,2)\right)\hfill \\ & =\frac{1}{10}g\left(x(1,1)\right)+\frac{1}{5}g\left(x(1,2)\right)+\frac{1}{5}g\left(x(2,1)\right)+\frac{2}{5}g\left(x(2,2)\right).\hfill \end{array}$$

(14)

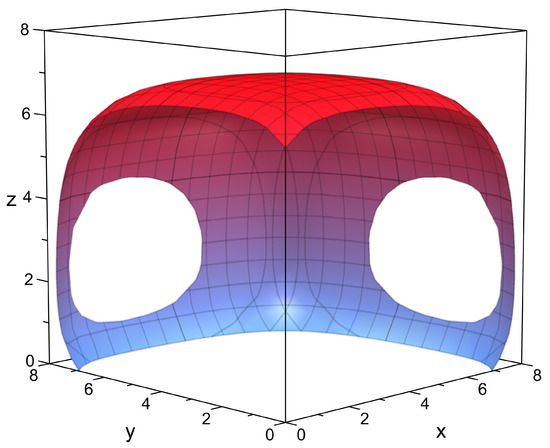
Put $x(1,1)=1$ and assume that $x(1,2)$, $x(2,1)$ and $x(2,2)$ belong to interval $(0,8]$, so Figure 1 shows the components $x(1,2)$, $x(2,1)$ and $x(2,2)$ of the solutions for (14) (for convenience, denote x = $x(1,2)$, y = $x(2,1)$ and z = $x(2,2)$). Clearly, the problem considered admits at least two positive solutions in X.

Figure 1. The image of components x, y, z of the solutions for (14).

Example 2.

Consider the problem ($D_{\lambda }^{f,q}$), where $m=n=2$, $c=1$, $d=8$, $\mu =2910$, $\alpha =\frac{1}{2}$ and

$$q(i,j)=i+j,(i,j)\in \mathbb{Z}(1,2)\times \mathbb{Z}(1,2),$$

$$f((i,j),s)=f\left(s\right)=\left\{\begin{array}{c}\begin{array}{cc}{s}^3+2,\hfill & s\le 8,\hfill \\ 1028\sqrt{2}{s}^{-\frac{1}{2}},\hfill & s>8.\hfill \end{array}\hfill \end{array}\right.$$

Obviously, f is a continuous function and $f\left(0\right)=2>0$, $Q=12$, $q_{*}=2$, and

$$F((i,j),\xi )=F\left(\xi \right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{1}{4}{\xi }^4+2\xi ,\hfill & \xi \le 8,\hfill \\ 2056\sqrt{2}{\xi }^{\frac{1}{2}}-7184,\hfill & \xi >8.\hfill \end{array}\hfill \end{array}\right.$$

So,

$$F_d=\sum _{j=1}^n\sum _{i=1}^{m}F((i,j),d)=\sum _{j=1}^2\sum _{i=1}^2\left(\frac{1}{4}\times 8^4+2\times 8\right)=4160,$$

and

$$M_2=\underset{\left(\right(i,j),\xi )\in \mathbb{Z}(1,m)\times \mathbb{Z}(1,n)\times [0,c]}{max}F((i,j),\xi )=\underset{\xi \in [0,1]}{max}\left(\frac{1}{4}{\xi }^4+2\xi \right)=\frac{9}{4}.$$

Moreover,

$$(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]=20\left(\sqrt{65}-1\right)\approx 141.245,$$

$$(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]=3\left(\sqrt{2}-1\right)\approx 1.243;$$

$$\begin{array}{cc}\hfill & \frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]F_d}{mn\left\{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]+(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]\right\}}\hfill \\ \hfill =& \frac{3120\left(\sqrt{2}-1\right)}{3\left(\sqrt{2}-1\right)+20\left(\sqrt{65}-1\right)}\hfill \\ \hfill \approx & 9.070;\hfill \end{array}$$

and

$$F((i,j),\xi )=\frac{1}{4}{\xi }^4+2\xi \le 1040<2910\times \left(1+{\xi }^{\frac{1}{2}}\right)={\mu (1+|\xi |}^{\alpha }),\forall 0<\xi \le 8,$$

$$F((i,j),\xi )=2056\sqrt{2}{\xi }^{\frac{1}{2}}-7184<2910{\xi }^{\frac{1}{2}}+2910={\mu (1+|\xi |}^{\alpha }),\forall \xi >8.$$

They indicate that the conditions (10), $\left(A_1^{*}\right)$ and $\left(A_2^{*}\right)$ in Corollary 3 hold, respectively. According to Corollary 3, for any

$$\begin{array}{cc}\hfill \lambda \in {\Lambda }_1& =\left(\frac{(2m+2n+Q)\left[\sqrt{1+d^2}-1\right]}{F_d-mn{M}_2},\frac{(1+q_{*})\left[\sqrt{1+min\left\{\frac{16}{m+n+2},1\right\}{c}^2}-1\right]}{mn{M}_2}\right)\hfill \\ & =\left(\frac{20\left(\sqrt{65}-1\right)}{4151},\frac{\sqrt{2}-1}{3}\right)\hfill \\ & \approx (0.035,0.138),\hfill \end{array}$$

the problem considered admits at least three positive solutions in X.

In particular, take $\lambda =0.1\in {\Lambda }_1$, the problem considered can be rewritten as

$$\begin{array}{cc}\hfill 40{\varphi }_c\left(x(1,1)\right)+50{\varphi }_c\left(x(1,2)\right)& +50{\varphi }_c\left(x(2,1)\right)+60{\varphi }_c\left(x(2,2)\right)\hfill \\ & =f\left(x\right(1,1\left)\right)+f\left(x\right(1,2\left)\right)+f\left(x\right(2,1\left)\right)+f\left(x\right(2,2\left)\right).\hfill \end{array}$$

(15)

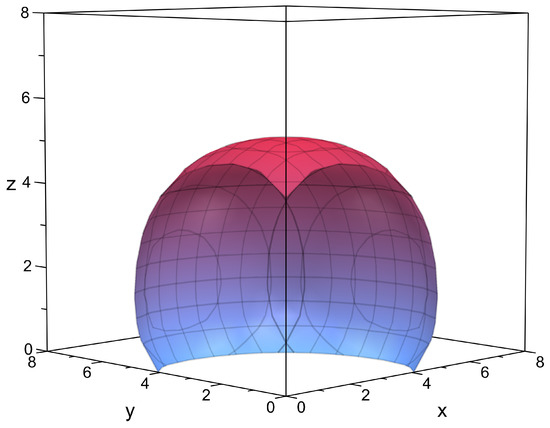
Set $x(1,1)=1$ and assume that $x(1,2)$, $x(2,1)$ and $x(2,2)$ belong to interval $(0,8]$, so Figure 2 shows the components $x(1,2)$, $x(2,1)$ and $x(2,2)$ of the solutions satisfying (15) (for convenience, denote x = $x(1,2)$, y = $x(2,1)$ and z = $x(2,2)$). Obviously, the problem considered admits at least three positive solutions in X.

Figure 2. The image of components x, y, z of the solutions for (15).

5. Conclusions

Mathematical models concerned with partial difference equations play important roles in many fields. In this article, the partial discrete problem ($D_{\lambda }^{f,q}$) involving the mean curvature operator is considered. In contrast to [39], by employing Theorem 2.1 in [40], some new sufficient conditions are established to ensure that problem ($D_{\lambda }^{f,q}$) admits at least three solutions, as shown in Theorem 1. Furthermore, under suitable assumptions on the nonlinearity f, we prove the existence of at least two positive solutions using the established strong maximum principle, as shown in Corollaries 1 and 2. Please note that Corollary 2 is an improvement of Corollary 3.3 in [36]. Additionally, we show that problem ($D_{\lambda }^{f,q}$) has at least three positive solutions in Corollary 3. Compared with [39], we prove the inequality about $\mathsf{\Phi }$ in Lemma 4 to obtain the coercivity of the functional $\mathsf{\Phi }-\lambda J$, which is more complex than [39]. The ingenious definition of norm $\parallel ·\parallel$ makes the proof of Lemma 4 simpler. On the other hand, to demonstrate the applicability of our results, we not only give two concrete examples, but also illustrate the existence of multiple solutions by images, which is more intuitive. How to obtain the existence and multiplicity of periodic or homoclinic solutions for the partial difference equations is a very worthy subject. This will be our future work.