Matching-Type Image-Labelings of Trees

Abstract

A variety of labelings on trees have emerged in order to attack the Graceful Tree Conjecture, but lack showing the connections between two labelings. In this paper, we propose two new labelings: vertex image-labeling and edge image-labeling, and combine new labelings to form matching-type image-labeling with multiple restrictions. The research starts from the set-ordered graceful labeling of the trees, and we give several generation methods and relationships for well-known labelings and two new labelings on trees.

1. Introduction and Preliminary

1.1. A Simple Introduction

A graph labeling is an assignment of non-negative integers to the vertices and edges of a graph subject to certain conditions. The problem of graph labeling can be traced to a well-known Ringel–Kotzig Decomposition Conjecture in popularization [1]: “A complete graph $K_{2n+1}$ can be decomposed into $2n+1$ subgraphs that are all isomorphic with a given tree of n edges”. This conjecture is explained and traced by Kotzig to the series of attacks intent on proving that trees are graceful. Labeling as a technique is applied to X-ray crystallography [2], communication network addressing [3], information encryption [4], radio channel assignment [5] and so on. In the past fifty years, starting from different practical problems, many types of new labelings have emerged. Gallian, in [6], distributes a survey on graph labeling. The famous conjecture is as follows.

Conjecture 1 

([7]). Every tree is graceful (Graceful Tree Conjecture, GTC).

GTC has aroused interest in graph labelings, and people have put forward a lot of labelings according to different practical problems. The odd-graceful labeling was introduced by Gnanajothi in 1991, and she conjectured:

Conjecture 2 

([8]). All trees admit odd-graceful labellings (OGTC).

Zhou et al. have shown that “Every lobster is odd-graceful” [9]. In 1981, Chang, Hsu, and Rogers [10] defined an elegant labeling f of a graph G with q edges as an injective function from the vertices of G to the set $\{0,1,2,\cdots ,q\}$ such that each edge $xy$ is assigned the label $f\left(x\right)+f\left(y\right)mod(q+1)$, and the resulting edge labels are nonzero and distinct. Then, the odd-elegant labeling was developed on the basis of this labeling. In 1970, Kotzig and Rosa defined the magic labeling of graphs. Inspired by Kotzig-Rosa notion, Enomoto, Lladó, Nakamigawa and Ringel [11] called a graph G with an edge-magic total labeling that has the additional property that the vertex labels from 1 to $\left|V\right|$ are super edge-magic total labeling [12]. Acharya and Hegde [13] have generalized sequential labelings to $(k,d)$-arithmetic total labeling and $(k,d)$-graceful labeling with positive integers k and d.

The algorithmic research on the labeling of graphs is interesting [14]. Among them, the research results on special graphs are the most significant. Gao et al. [15] showed relevant conclusions on the antimagic orientation of lobsters, and Sethuraman et al. [16] proved that any acyclic graph can be embedded in a unicyclic graceful graph. In this paper, inspired by graphical passwords, we put forward the concepts of new image-labelings: vertex image-labeling and edge image-labeling. We show the relationships between labelings on trees by producing several image-labelings from the set-ordered graceful labeling. Such results can be applied to molecular structures [17] and asymmetric cryptosystem [18], therefore, the theoretical research on labeling is meaningful.

1.2. Preliminary

Graphs mentioned here are simple and undirected. Let $G=(V,E)$ be a graph with vertex set V and edge set E, if the vertex set V can be divided into two disjoint subsets $V_1$ and $V_2$, such that the two end-vertices $v_1$ and $v_2$ of an edge $v_1{v}_2$ belong to two different vertex sets, that is $v_1\in V_1$ and $v_2\in V_2$, then G is called a bipartite graph. A $(p,q)$-graph is a graph with p vertices and q edges.

The number of elements in a set X is written as $\left|X\right|$. We will use an integer set $S_{k,d}=\{k,k+d,k+2d,\cdots ,k+(q-1)d\}$ for integers $k\ge 0$ and $d\ge 1$, and use $[x,y]$ to stand for an integer set $\{x,x+1,\cdots ,y\}$ with two integers $x,y$ subject to $0\le x<y$, as well as use ${[s,t]}^o$ to indicate an integer set $\{s,s+2,\cdots ,t\}$ for two odd integers $s,t$ holding $1\le s<t$. All numbers are integers, and other notations and terminologies not introduced here can be referred to [19].

Suppose that a $(p,q)$-graph G admits a mapping $f:S\to [a,b]$ with $S\subseteq V\left(G\right)\cup E\left(G\right)$, we write the label set $\left\{f\right(u):u\in S\}$ by $f\left(S\right)$, and we restate several well-known labelings as follows:

Definition 1

([20]). If the mapping θ holds $\theta \left(V\right(G\left)\right)\subseteq [0,q]$ with $min\theta \left(V\right(G\left)\right)=0$, $\theta \left(u\right)\ne \theta \left(v\right)$ for distinct $u,v\in V\left(G\right)$, and $\theta \left(E\right(G\left)\right)=\left\{\theta \right(uv)=|\theta \left(u\right)-\theta \left(v\right)|:uv\in E(G\left)\right\}=[1,q]$, then we call θ a graceful labeling of G.

If the $(p,q)$-graph G is a bipartite graph with vertex partition $(X,Y)$, and a graceful labeling θ holds $max\left\{\theta \right(u):u\in X\}<min\left\{\theta \right(v):v\in Y\}$ (abbreviated as $max\theta \left(X\right)<min\theta \left(Y\right)$), we call θ a set-ordered graceful labeling.

Definition 2

([6]). A $(p,q)$-graph G admits a mapping α holding $\alpha \left(V\right(G\left)\right)=\left\{f\right(u):u\in V(G\left)\right\}\subseteq [0,2q-1]$ and $min\alpha \left(V\right(G\left)\right)=0$, $\alpha \left(u\right)\ne \alpha \left(v\right)$ for distinct vertices $u,v\in V\left(G\right)$, $\alpha \left(E\left(G\right)\right)=\{\alpha \left(uv\right)=|\alpha \left(u\right)-\alpha \left(v\right)|:uv\in E\left(G\right)\}={[1,2q-1]}^o$, then α is called an odd-graceful labeling of graph G.

Definition 3

([6]). If a $(p,q)$-graph G has a function β holds $\beta \left(V\right(G\left)\right)\subseteq [0,2q-1]$, as well as $\beta \left(u\right)\ne \beta \left(v\right)$ for distinct vertices $u,v\in V\left(G\right)$, and $\beta \left(E\left(G\right)\right)=\{\beta \left(uv\right)=\beta \left(u\right)+\beta \left(v\right)(mod2q):uv\in E\left(G\right)\}={[1,2q-1]}^o$, we call β an odd-elegant labeling of graph G.

Definition 4

([13]). If there is a labeling δ of a $(p,q)$-graph G holding $\delta \left(V\right(G\left)\right)\subseteq [0,k+(q-1\left)d\right]$ such that $\delta \left(u\right)\ne \delta \left(v\right)$ for distinct $u,v\in V\left(G\right)$, $\delta \left(E\right(G\left)\right)=\left\{\delta \right(uv)=|\delta \left(u\right)-\delta \left(v\right)|:uv\in E(G\left)\right\}=\{k,k+d,k+2d,\cdots ,k+(q-1\left)d\right\}$, then we call δ a $(k,d)$-graceful labeling of graph G, where k and d are positive integers.

Definition 5

([6]). Let k and d be positive integers. A labeling γ of a $(p,q)$-graph G is said to be $(k,d)$-arithmetic total labeling if $\gamma \left(V\right(G\left)\right)\subseteq [0,k+(q-1\left)d\right]$, $\gamma \left(u\right)\ne \gamma \left(v\right)$ for distinct vertices $u,v\in V\left(G\right)$, and $\left\{\gamma \right(u)+\gamma (v):uv\in E(G\left)\right\}=\{k,k+d,k+2d,\cdots ,k+(q-1\left)d\right\}$ holds.

Definition 6

([6]). If the mapping σ holds $\sigma \left(V\right(G\left)\right)\cup \sigma \left(E\right(G\left)\right)=[1,p+q]$, and $\sigma \left(u\right)+\sigma \left(v\right)+\sigma \left(uv\right)=C$ for each edge $uv\in E\left(G\right)$, where C is a magic constant, then we call σ an edge-magic total labeling of G; moreover, σ is called a super edge-magic total labeling if $\sigma \left(V\right(G\left)\right)=[1,p]$.

Next, we define the following new labelings to explore the relationships between several known labelings introduced here.

Definition 7.

Let $f:V\left(G\right)\cup E\left(G\right)\to [a,b]$ and $g:V\left(G\right)\cup E\left(G\right)\to [a^{\prime },b^{\prime }]$ be two labelings of a $(p,q)$-graph G, integers $a,b,a^{\prime },b^{\prime }$ satisfy $0\le a<b$ and $0\le a^{\prime }<b^{\prime }$.

(1) An equation $f\left(v\right)+g\left(v\right)=k^{\prime }$ holds true for each vertex $v\in V\left(G\right)$, where $k^{\prime }$ is a positive constant and it is called vertex-image coefficient, then f and g are called a matching of vertex image-labelings (abbreviated as v-image-labelings);

(2) An equation $f\left(uv\right)+g\left(uv\right)=k{}^{″}$ holds true for every edge $uv\in E\left(G\right)$, and $k$ is a positive constant, called edge-image coefficient, then both labelings f and g are called a matching of edge image-labelings (abbreviated as e-image-labelings).

If labelings f and g are the same labeling functions, then they are called a matching of W-type v-image-labelings, or a matching of W-type e-image-labelings, where “W-type” $\in$ {graceful, odd-graceful, odd-elegant, $(k,d)$-graceful, $(k,d)$-arithmetic total, super edge-magic total}. See an example in Figure 1, $f_1$ and $g_1$ are a matching of set-ordered graceful v-image-labelings, $f_1$ and $h_1$ are a matching of set-ordered graceful e-image-labelings.

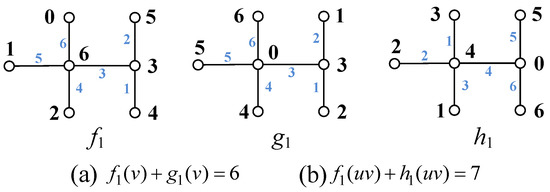
Figure 1. A tree T admits: (a) a matching of set-ordered graceful v-image-labelings $f_1$ and $g_1$, (b) a matching of set-ordered graceful e-image-labelings $f_1$ and $h_1$.

2. Main Results and Proofs

Theorem 1.

Let T be a tree with p vertices and q edges, $(X,Y)$ is the bipartition of vertices of T with $\left|X\right|=s$, $\left|Y\right|=t$ and $p=s+t$. If the tree T admits a set-ordered graceful labeling, then it admits a matching of graceful v-image-labelings and a matching of graceful e-image-labelings.

Proof. 

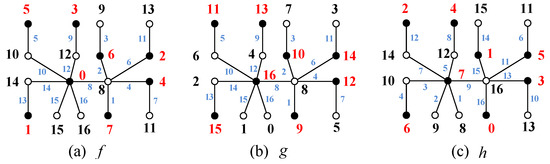
Since any tree is bipartite, and $(X,Y)$ is the bipartition of vertices of a tree T, where $X=\{x_i:i\in [1,s]\}$ and $Y=\{y_j:j\in [1,t]\}$ holding $s+t=\left|V\right(T\left)\right|=p$. Clearly, $x_i\in X$ and $y_j\in Y$ for each edge $x_i{y}_j$ of T. By the hypothesis of the theorem, the tree T admits a set-ordered graceful labeling f, without loss of generality, we have $f\left(x_i\right)=i-1$ with $i\in [1,s]$, $f\left(y_j\right)=s+j-1$ with $j\in [1,t]$ and $f\left(x_i{y}_j\right)=f\left(y_j\right)-f\left(x_i\right)=s+j-i$ for every edge $x_i{y}_j\in E\left(T\right)$, obviously, condition $maxf\left(X\right)<minf\left(Y\right)$ is satisfied. We define another set-ordered graceful labeling g of T as follows: $g\left(x_i\right)=s+t-1-f\left(x_i\right)$ with $i\in [1,s]$, $g\left(y_j\right)=s+t-1-f\left(y_j\right)$ with $j\in [1,t]$, and $g\left(x_i{y}_j\right)=f\left(x_i{y}_j\right)$ for every edge $x_i{y}_j\in E\left(T\right)$. Therefore, we have $f\left(v\right)+g\left(v\right)=s+t-1=p-1$ for every vertex $v\in V\left(T\right)$. According to Definition 1, f and g are a matching of graceful v-image-labelings with vertex-image coefficient $k^{\prime }=p-1$.

There is another labeling h of T defined as: $h\left(x_i\right)=s-1-f\left(x_i\right)=s-i$ with $i\in [1,s]$, $h\left(y_j\right)=t+2s-1-f\left(y_j\right)=t+s-j$ with $j\in [1,t]$, since $0\le s-i\le s-1$ and $s\le t+s-j\le p-1=q$, then $maxh\left(X\right)=s-1<s=minh\left(Y\right)$ and the vertex label set $h\left(V\right(T\left)\right)=[0,q]$, in addition, $h\left(x_i{y}_j\right)=|h\left(x_i\right)-h\left(y_j\right)|=h\left(y_j\right)-h\left(x_i\right)=t+i-j$ for each edge $x_i{y}_j\in E\left(T\right)$ with $1\le t+i-j\le q$, so the edge label set $h\left(E\right(T\left)\right)=[1,q]$, which shows that the labeling h is just a set-ordered graceful labeling of T. In addition, we find

$$\begin{array}{cc}\hfill h\left(x_i{y}_j\right)& =h\left(y_j\right)-h\left(x_i\right)=t+2s-1-f\left(y_j\right)-[s-1-f\left(x_i\right)]\hfill \\ \hfill & =t+s-[f\left(y_j\right)-f\left(x_i\right)]=t+s-f\left(x_i{y}_j\right)\hfill \end{array}$$

(1)

for each edge $x_i{y}_j\in E\left(T\right)$, immediately, we get $f\left(x_i{y}_j\right)+h\left(x_i{y}_j\right)=t+s=q+1$ for edge-image coefficient $k{}^{″}=q+1$, see Figure 2.

Figure 2. (a) A set-ordered graceful labeling f of a tree T; (b) A set-ordered graceful labeling g of T holding $f\left(v\right)+g\left(v\right)=p-1=16$; (c) A set-ordered graceful labeling h of T holding $f\left(uv\right)+h\left(uv\right)=q+1=17$.

The proof of the Theorem 1 is complete. □

Theorem 2.

If a tree T admits set-ordered graceful labeling, then T holds the following assertions:

$\left(1\right)$ T admits a matching of odd-graceful v-image-labelings and a matching of odd-graceful e-image-labelings.

$\left(2\right)$ T admits a matching of odd-elegant v-image-labelings and a matching of odd-elegant e-image-labelings.

$\left(3\right)$ T admits a matching of $(k,d)$-graceful v-image-labelings, and a matching of $(k,d)$-graceful e-image-labelings.

$\left(4\right)$ T admits a $(k,2)$-arithmetic total labeling and a $(k+2,2)$-arithmetic total labeling are a matching of v-image-labelings; T admits a matching of $(k,2)$-arithmetic total e-image-labelings.

$\left(5\right)$ T admits a matching of super edge-magic total v-image-labelings and a matching of super edge-magic total e-image-labelings.

Proof. 

(1) We define a matching of odd-graceful v-image-labelings $f_1$ and $g_1$ from the set-ordered graceful v-image-labelings f and g. Letting $f_1\left(x_i\right)=2f\left(x_i\right)=2i-2$ with $i\in [1,s]$, $f_1\left(y_j\right)=2f\left(y_j\right)-1=2s+2j-3$ with $j\in [1,t]$, and $f_1\left(x_i{y}_j\right)=f_1\left(y_j\right)-f_1\left(x_i\right)=2(s-i+j)-1$ for each edge $x_i{y}_j\in E\left(T\right)$. Since $f\left(V\right(T\left)\right)=[0,q]$ holds true, then the set of vertex labels of T under the labeling $f_1$ is a subset of $[0,2q-1]$, and

$$f_1\left(x_i{y}_j\right)=|f_1\left(x_i\right)-f_1\left(y_j\right)|=|2f\left(x_i\right)-(2f\left(y_j\right)-1)|=2f\left(x_i{y}_j\right)-1\in {[1,2q-1]}^o.$$

For any two vertices $u,v\in V\left(T\right)$, $f_1\left(u\right)\ne f_1\left(v\right)$ since $f\left(u\right)\ne f\left(v\right)$, we claim that $f_1$ is an odd-graceful labeling. Then, we define another odd-graceful labeling $g_1$ by setting $g_1\left(x_i\right)=2(s+t-1)-1-f_1\left(x_i\right)=2(p-i)-1$ with $i\in [1,s]$, $g_1\left(y_j\right)=2(s+t-1)-1-f_1\left(y_j\right)=2(t-j)$ with $j\in [1,t]$, and $g_1\left(x_i{y}_j\right)=g_1\left(x_i\right)-g_1\left(y_j\right)=2(s-i+j)-1$ for each edge $x_i{y}_j\in E\left(T\right)$. Immediately, the vertex label set $g_1\left(V\left(T\right)\right)\subseteq [0,2q-1]$, and the vertex label set is the union of an odd numbers set and an even numbers set, so

$$g_1\left(x_i{y}_j\right)=|g_1\left(x_i\right)-g_1\left(y_j\right)|,g_1\left(E\left(T\right)\right)={[1,2q-1]}^o,$$

we get $f_1\left(v\right)+g_1\left(v\right)=2(s+t-1)-1=2p-3$ for each vertex $v\in V\left(T\right)$ and claim that $f_1$ and $g_1$ are a matching of odd-graceful v-image-labelings with $k^{\prime }=2p-3$.

We also define another odd-graceful labeling $h_1$ by setting $h_1\left(x_i\right)=2(s-1)-f_1\left(x_i\right)=2(s-i)\le 2(s-1)$ with $i\in [1,s]$, $2s-1\le h_1\left(y_j\right)=2(p+s-2)-f_1\left(y_j\right)=2(p-j)-1$ with $j\in [1,t]$, so $h_1\left(V\left(T\right)\right)\subseteq [0,2q-1]$, $h_1\left(x_i{y}_j\right)=h_1\left(y_j\right)-h_1\left(x_i\right)=2t+2i-2j-1$ for each edge $x_i{y}_j\in E\left(T\right)$. In addition, $h_1\left(x_i{y}_j\right)=|h_1\left(x_i\right)-h_1\left(y_j\right)|=2q-f_2\left(x_i{y}_j\right)$, because $f_1\left(x_i{y}_j\right)\in {[1,2q-1]}^o$, so $h_1\left(E\left(T\right)\right)={[1,2q-1]}^o$, $h_1\left(u\right)\ne h_1\left(v\right)$ for distinct $u,v\in V\left(T\right)$. Therefore, $h_1$ is also an odd-graceful labeling, there is $f_1\left(x_i{y}_j\right)+h_1\left(x_i{y}_j\right)=2q$ for each edge $x_i{y}_j\in E\left(T\right)$, so $f_1$ and $h_1$ are a matching of set-ordered odd-graceful e-image-labelings with edge-image coefficient $k{}^{″}=2q$. The assertion $\left(1\right)$ has been proven.

(2) Setting $f_2\left(x_i\right)=2f\left(x_i\right)=2i-2$ with $i\in [1,s]$, $f_2\left(y_j\right)=(s+p-1)-f\left(y_j\right)-j+2=p-2j+2$ with $j\in [1,t]$, since $f_2\left(x_i\right)\le 2(s-1)$ and $f_2\left(y_j\right)\le p$, so $f_2\left(V\left(T\right)\right)\subseteq [0,2q-1]$. We set $f_2\left(x_i{y}_j\right)=f_2\left(x_i\right)+f_2\left(y_j\right)(mod2q)=p+2i-2j(mod2q)$ for each edge $x_i{y}_j\in E\left(T\right)$, we can find $f_2\left(y_j\right)$ is odd, and $f_2\left(x_i\right)$ is even, so $f_2\left(x_i{y}_j\right)$ is odd, thus $f_2\left(E\left(T\right)\right)={[1,2q-1]}^o$, so $f_2$ is an odd-elegant labeling. There is another odd-elegant labeling $g_2$ by setting $g_2\left(x_i\right)=p-f_2\left(x_i\right)=p-2i+2$ with $i\in [1,s]$, and $g_2\left(y_j\right)=p-f_2\left(y_j\right)=2j-2$ with $j\in [1,t]$, we can see $0\le g_2\left(x_i\right)$, $g_2\left(y_j\right)\le p$ and $g_2\left(V\left(T\right)\right)\subseteq [0,2q-1]$. In addition, $g_2\left(x_i{y}_j\right)=g_2\left(x_i\right)+g_2\left(y_j\right)(mod2q)=p-2i+2j(mod2q)$ for each edge $x_i{y}_j\in E\left(T\right)$, because the parity of $g_2\left(x_i\right)$ and $g_2\left(y_j\right)$ is opposite, so $g_2\left(x_i{y}_j\right)$ is odd, then we get $g_2\left(E\left(T\right)\right)={[1,2q-1]}^o$, we also get $f_2\left(v\right)+g_2\left(v\right)=p$ for $v\in V\left(T\right)$, which indicate that $f_2$ and $g_2$ are a matching of odd-elegant v-image-labelings with $k^{\prime }=p$.

An odd-elegant labeling $h_2$ of T can be obtained from $f_2$ in the following way: $h_2\left(x_i\right)=2(s-1)-f_2\left(x_i\right)=2(s-i)$ with $i\in [1,s]$, $h_2\left(y_j\right)=2t-f_2\left(y_j\right)=2t-p+2j-2$ with $j\in [1,t]$, thus, the vertex label set $h_2\left(V\left(G\right)\right)\subseteq [0,2q-1]$; since $h_2\left(x_i{y}_j\right)=h_2\left(x_i\right)+h_2\left(y_j\right)(mod2q)=p-2i+2j-2(mod2q)$ for each edge $x_i{y}_j\in E\left(T\right)$, we get the edge label set $h_2\left(E\left(T\right)\right)={[1,2q-1]}^o$. Additionally, it is not hard to compute $f_2\left(x_i{y}_j\right)+h_2\left(x_i{y}_j\right)=2p-2=2q$ for $x_i{y}_j\in E\left(T\right)$, thus $f_2$ and $h_2$ are a matching of odd-elegant e-image-labelings with $k{}^{″}=2q$. The assertion $\left(2\right)$ has been proven.

(3) For integers $k\ge 0$ and $d\ge 1$, we define a labeling $f_3$ as: $f_3\left(x_i\right)=df\left(x_i\right)=d(i-1)$ with $i\in [1,s]$, $f_3\left(y_j\right)=d[f\left(y_j\right)-1]+k=d(s+j-2)+k$ with $j\in [1,t]$. Since $f_3\left(x_i\right)\le d(s-1)$ and $s+j-2\le s+t-2=q-1$, we can get $f_3\left(y_j\right)\le k+d(q-1)$, and the vertex label set under $f_3$ is a subset of $[0,k+(q-1\left)d\right]$. Moreover,

$$f_3\left(x_i{y}_j\right)=|f_3\left(x_i\right)-f_3\left(y_j\right)|=f_3\left(y_j\right)-f_3\left(x_i\right)=k+d(s+j-i-1)\in S_{k,d},$$

which shows that $f_3$ is a $(k,d)$-graceful labeling of T. There is another $(k,d)$-graceful labeling $g_3$ defined as: $g_3\left(x_i\right)=k+(q-1)d-f_3\left(x_i\right)=k+d(q-i)\le k+(q-1)d$ with $i\in [1,s]$, $g_3\left(y_j\right)=k+(q-1)d-f_3\left(y_j\right)=d(q-s-j+1)$ with $j\in [1,t]$, and $g_3\left(x_i{y}_j\right)=|g_3\left(x_i\right)-g_3\left(y_j\right)|=g_3\left(x_i\right)-g_3\left(y_j\right)=k+d(s-i+j-1)$ for every edge $x_i{y}_j\in E\left(T\right)$. We obtain the vertex label set $g_3\left(V\left(T\right)\right)\subseteq [0,k+(q-1)d]$, and the edge label set $g_3\left(E\left(T\right)\right)=S_{k,d}$, moreover, $f_3\left(v\right)+g_3\left(v\right)=k+(q-1)d$ holds true for $v\in V\left(T\right)$, so we claim that $f_3$ and $g_3$ are a matching of $(k,d)$-graceful v-image-labelings with $k^{\prime }=k+(q-1)d$.

Another $(k,d)$-graceful labeling $h_3$ defined as: $h_3\left(x_i\right)=d(s-1)-f_3\left(x_i\right)=d(s-i)$ with $i\in [1,s]$, $h_3\left(y_j\right)=2k+d(2s+t-3)-f_3\left(y_j\right)=k+d(p-j-1)$ with $j\in [1,t]$, $h_3\left(x_i{y}_j\right)=h_3\left(y_j\right)-h_3\left(x_i\right)=k+d(t+i-j-1)$ for every edge $x_i{y}_j\in E\left(T\right)$, $h_3\left(V\left(T\right)\right)\le [0,k+(q-1)d]$, so

$$h_3\left(E\left(T\right)\right)=\{h_3\left(x_i{y}_j\right)=|f_3\left(x_i\right)-f_3\left(y_j\right)|:x_i{y}_j\in E\left(T\right)\}=S_{k,d}.$$

We can get $k{}^{″}=f_3\left(x_i{y}_j\right)+h_3\left(x_i{y}_j\right)=2k+(q-1)d$, which shows that $f_3$ and $h_3$ are a matching of $(k,d)$-graceful e-image-labelings with edge-image coefficient $k{}^{″}=2k+(q-1)d$. We have shown the assertion $\left(3\right)$.

(4) We, by defining a new labeling $f_4$, set a transformation: $f_4\left(x_i\right)=2f\left(x_i\right)=2(i-1)\le 2(s-1)$ with $i\in [1,s]$, $f_4\left(y_j\right)=k+2[f\left(y_j\right)-2j+2]=k+2(t-j)$ with $j\in [1,t]$, then $k\le f_4\left(y_j\right)\le k+2(t-1)$, so $f_4\left(u\right)\ne f_4\left(v\right)$ for distinct $u,v\in V\left(T\right)$, and $f_4\left(V\left(T\right)\right)\subseteq [0,k+2(q-1)]$, on the other hand, $f_4\left(x_i{y}_j\right)=k+2(t-j+i-1)$ for each edge $x_i{y}_j\in E\left(T\right)$, we calculate the set $\{f_4\left(x_i{y}_j\right)=f_4\left(x_i\right)+f_4\left(y_i\right):x_i{y}_j\in E\left(T\right)\}=S_{k,2}$, which means that the labeling $f_4$ is a $(k,2)$-arithmetic total labeling of T. Another labeling $g_4$ differing from $f_4$ is defined as: $g_4\left(x_i\right)=k+2(t-1)-f_4\left(x_i\right)=k+2t-2i$ with $i\in [1,s]$, $g_4\left(y_j\right)=k+2(t-1)-f_4\left(y_j\right)=2j-2$ with $j\in [1,t]$, and $g_4\left(x_i{y}_j\right)=k+2t-2i+2j-2$ for each edge $x_i{y}_j\in E\left(T\right)$, furthermore, the vertex label set $g_4\left(V\left(T\right)\right)\subseteq [0,k+2(q-1)]$, and

$$\{g_4\left(x_i{y}_j\right)=g_4\left(x_i\right)+g_4\left(y_j\right):x_i{y}_j\in E\left(T\right)\}=\{k+2,k+4,k+6,\cdots ,k+2q\}.$$

So, $g_4$ is a $(k+2,2)$-arithmetic total labeling, in addition, $f_4\left(v\right)+g_4\left(v\right)=k+2(t-1)$ for each vertex $v\in V\left(T\right)$, this means that $f_4$ and $g_4$ are a matching of v-image-labelings with $k^{\prime }=k+2(t-1)$.

We come to define a $(k,2)$-arithmetic total labeling $h_4$ of T as follows: $h_4\left(x_i\right)=f\left(x_i\right)+2s-3i+1=2(s-i)$ with $i\in [1,s]$, $h_4\left(y_j\right)=f\left(y_j\right)+j-s+2=2j+1$ with $j\in [1,t]$, $h_4\left(x_i{y}_j\right)=2(s-i+j)+1$ for each edge $x_i{y}_j\in E\left(T\right)$, the vertex label set $h_4\left(V\left(G\right)\right)\subseteq [0,k+2(q-1)]$, and moreover

$$\{h_4\left(x_i{y}_j\right)=h_4\left(x_i\right)+h_4\left(y_j\right):x_i{y}_j\in E\left(T\right)\}=S_{k,2}.$$

Then, we considering $f_4\left(x_i{y}_j\right)+h_4\left(x_i{y}_j\right)=k+2(t-j+i-1)+2(s-i+j)+1=k+2q+1$, so labelings $f_4$ and $h_4$ are a matching of $(k,2)$-arithmetic total e-image-labelings with edge-image coefficient $k{}^{″}=k+2q+1$. The assertion $\left(4\right)$ holds true.

(5) There is a labeling $f_5$ defined in the following way: $f_5\left(x_i\right)=f\left(x_i\right)+1=i$ with $i\in [1,s]$, and $f_5\left(y_j\right)=f\left(y_j\right)+t-2j+2=p-j+1$ with $j\in [1,t]$, and we set $f_5\left(x_i{y}_j\right)=p+s-i+j$ for each edge $x_i{y}_j\in E\left(T\right)$. It is not difficult to compute $f_5\left(x_i\right)+f_5\left(y_j\right)+f_5\left(x_i{y}_j\right)=2p+s+1$, since $1\le f_5\left(x_i\right)\le s$, $s+1\le f_5\left(y_j\right)\le p$ and $p+1\le f_5\left(x_i{y}_j\right)\le 2p-1=p+q$, we have $f_5\left(V\left(G\right)\right)\cup f_5\left(E\left(G\right)\right)=[1,p+q]$, so $f_5$ is a super edge-magic total labeling with magic coefficient $2p+s+1$ by definition. We come to define an edge-magic total labeling $g_5$ in the way: $p-s+1\le g_5\left(x_i\right)=p+1-f_5\left(x_i\right)=p-i+1\le p$ with $i\in [1,s]$, $1\le g_5\left(y_j\right)=p+1-f_5\left(y_j\right)=j\le t$ with $j\in [1,t]$, $g_5\left(x_i{y}_j\right)=2p+q+1-f_5\left(x_i{y}_j\right)=t+q+i-j+1$ for each edge $x_i{y}_j\in E\left(T\right)$, notice that $p+1\le f_5\left(x_i{y}_j\right)\le p+q$, so condition $g_5\left(V\left(T\right)\right)\cup g_5\left(E\left(T\right)\right)=[1,p+q]$ is true, and

$$\begin{array}{cc}\hfill g_5\left(x_i\right)+g_5\left(y_j\right)+g_5\left(x_i{y}_j\right)& =p+1-f_5\left(x_i\right)+p+1-f_5\left(y_j\right)+2p+q+1-f_5\left(x_i{y}_j\right)\hfill \\ \hfill & =2p-s+q+2\hfill \end{array}$$

(2)

to be a constant. Hence, $g_5$ is a super edge-magic total labeling, moreover, $f_5\left(v\right)+g_5\left(v\right)=p+1$ for each $v\in V\left(T\right)$ holds true, immediately, both labelings $f_5$ and $g_5$ are a matching of super edge-magic total v-image-labelings with $k^{\prime }=p+1$.

Another set-ordered edge-magic total labeling $h_5$ with magic coefficient $C=s+2p+1$ is defined as: $h_5\left(x_i\right)=s+1-f_5\left(x_i\right)=s-i+1$ with $i\in [1,s]$, $h_5\left(y_j\right)=2s+t+1-f_5\left(y_j\right)=s+j$ with $j\in [1,t]$, $h_5\left(x_i{y}_j\right)=2p+i-j-s$ for each edge $x_i{y}_j\in E\left(T\right)$. We also obtain $h_5\left(x_i\right)+h_5\left(x_i{y}_j\right)+h_5\left(y_j\right)=s+2p+1=C$. In addition, there is $k{}^{″}=f_5\left(x_i{y}_j\right)+h_5\left(x_i{y}_j\right)=3p=3(q+1)$ for each edge $x_i{y}_j\in E\left(T\right)$, which means that $f_5$ and $h_5$ are a matching of super set-ordered edge-magic total e-image-labelings with edge-image coefficient $k{}^{″}=3(q+1)$. This is the proof of the assertion $\left(5\right)$. □

For understanding the proof of Theorem 2, see the several matching-type image-labelings of a tree shown in Figure 3. If the two labelings f and l constituting the image-labelings are not the same type, we get a result as follows:

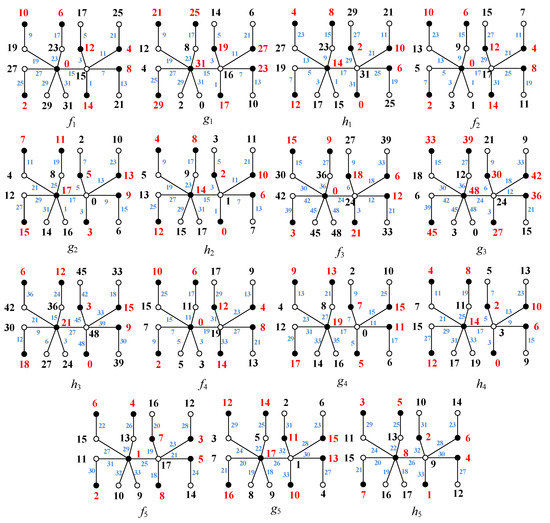
Figure 3. The examples for illustrating the conversions between image-labelings $f_s$, $f_s$, $h_s$ with $s=1,2,3,4,5$ in the proofs of Theorem 2.

Corollary 1.

If a tree T admits a set-ordered graceful labeling f, then it admits an edge-magic total labeling l, so that f and l are a matching of e-image-labelings with $k{}^{″}=p+q+1$.

Proof. 

Let $(X,Y)$ be the bipartition of vertices of a tree T, where $X=\{x_i:i\in [1,s]\}$ and $Y=\{y_j:j\in [1,t]\}$ holding $s+t=\left|V\right(T\left)\right|=p$. By the hypothesis of the theorem, T admits a graceful labeling f such that $f\left(x_i\right)=i-1$ with $i\in [1,s]$, $f\left(y_j\right)=s+j-1$ with $j\in [1,t]$ and $f\left(x_i{y}_j\right)=f\left(y_j\right)-f\left(x_i\right)=s+j-i$ for each edge $x_i{y}_j\in E\left(T\right)$, as well as $f\left(V\right(T\left)\right)=[0,q]$ and $f\left(E\right(T\left)\right)=[1,q]$, again, $maxf\left(X\right)=s-1<minf\left(Y\right)=s$, so f is a set-ordered graceful labeling. Next, we define an edge-magic total labeling l: $l\left(x_i\right)=p-f\left(x_i\right)=p-i+1$ with $i\in [1,s]$, $l\left(y_j\right)=p-f\left(y_{t-j+1}\right)=j$ with $j\in [1,t]$, and $l\left(x_i{y}_j\right)=q+t+i-j+1$ for every edge $x_i{y}_j\in E\left(T\right)$, as well as $l\left(V\right(T\left)\right)\cup l\left(E\right(T\left)\right)=[1,p+q]$, and we have $l\left(x_i\right)+l\left(x_i{y}_j\right)+l\left(y_j\right)=p+q+t+2=2p+t+1=C$ is a positive constant, thus l is called an edge-magic total labeling. In addition, we can see $f\left(x_i{y}_j\right)+l\left(x_i{y}_j\right)=s-i+j+q+t+i-j+1=p+q+1$ is a constant, so f and l are a matching of e-image-labelings with $k{}^{″}=p+q+1$. □

3. Conclusions

Inspired by public and private keys in graphical passwords, we propose two new labelings in this paper, called vertex image-labelings and edge image-labelings respectively. We combine the new labelings with the known labelings to form compound labelings to find the relationships between the two compound labelings. Starting from the set-ordered graceful labeling f of the tree, we first prove that two different set-ordered graceful labelings match them to form a matching of vertex image-labeling and a matching of edge image-labelings. Then, according to labeling f, the odd-graceful image-labelings, odd-elegant image-labelings, $(k,d)$-graceful image-labelings, $(k,d)$-arithmetic total image-labelings, super edge-magic total image-labelings of the tree are derived in turn. The new image-labelings can connect two labelings of the same type. This paper draws a conclusion: the above-mentioned matching-type image-labelings of the tree can be transformed into each other, knowing one of the labelings of a tree, we can quickly get the other labelings of the tree.