Abstract
A variety of labelings on trees have emerged in order to attack the Graceful Tree Conjecture, but lack showing the connections between two labelings. In this paper, we propose two new labelings: vertex image-labeling and edge image-labeling, and combine new labelings to form matching-type image-labeling with multiple restrictions. The research starts from the set-ordered graceful labeling of the trees, and we give several generation methods and relationships for well-known labelings and two new labelings on trees.
1. Introduction and Preliminary
1.1. A Simple Introduction
A graph labeling is an assignment of non-negative integers to the vertices and edges of a graph subject to certain conditions. The problem of graph labeling can be traced to a well-known Ringel–Kotzig Decomposition Conjecture in popularization [1]: “A complete graph can be decomposed into subgraphs that are all isomorphic with a given tree of n edges”. This conjecture is explained and traced by Kotzig to the series of attacks intent on proving that trees are graceful. Labeling as a technique is applied to X-ray crystallography [2], communication network addressing [3], information encryption [4], radio channel assignment [5] and so on. In the past fifty years, starting from different practical problems, many types of new labelings have emerged. Gallian, in [6], distributes a survey on graph labeling. The famous conjecture is as follows.
Conjecture 1
([7]). Every tree is graceful (Graceful Tree Conjecture, GTC).
GTC has aroused interest in graph labelings, and people have put forward a lot of labelings according to different practical problems. The odd-graceful labeling was introduced by Gnanajothi in 1991, and she conjectured:
Conjecture 2
([8]). All trees admit odd-graceful labellings (OGTC).
Zhou et al. have shown that “Every lobster is odd-graceful” [9]. In 1981, Chang, Hsu, and Rogers [10] defined an elegant labeling f of a graph G with q edges as an injective function from the vertices of G to the set such that each edge is assigned the label , and the resulting edge labels are nonzero and distinct. Then, the odd-elegant labeling was developed on the basis of this labeling. In 1970, Kotzig and Rosa defined the magic labeling of graphs. Inspired by Kotzig-Rosa notion, Enomoto, Lladó, Nakamigawa and Ringel [11] called a graph G with an edge-magic total labeling that has the additional property that the vertex labels from 1 to are super edge-magic total labeling [12]. Acharya and Hegde [13] have generalized sequential labelings to -arithmetic total labeling and -graceful labeling with positive integers k and d.
The algorithmic research on the labeling of graphs is interesting [14]. Among them, the research results on special graphs are the most significant. Gao et al. [15] showed relevant conclusions on the antimagic orientation of lobsters, and Sethuraman et al. [16] proved that any acyclic graph can be embedded in a unicyclic graceful graph. In this paper, inspired by graphical passwords, we put forward the concepts of new image-labelings: vertex image-labeling and edge image-labeling. We show the relationships between labelings on trees by producing several image-labelings from the set-ordered graceful labeling. Such results can be applied to molecular structures [17] and asymmetric cryptosystem [18], therefore, the theoretical research on labeling is meaningful.
1.2. Preliminary
Graphs mentioned here are simple and undirected. Let be a graph with vertex set V and edge set E, if the vertex set V can be divided into two disjoint subsets and , such that the two end-vertices and of an edge belong to two different vertex sets, that is and , then G is called a bipartite graph. A -graph is a graph with p vertices and q edges.
The number of elements in a set X is written as . We will use an integer set for integers and , and use to stand for an integer set with two integers subject to , as well as use to indicate an integer set for two odd integers holding . All numbers are integers, and other notations and terminologies not introduced here can be referred to [19].
Suppose that a -graph G admits a mapping with , we write the label set by , and we restate several well-known labelings as follows:
Definition 1
([20]). If the mapping θ holds with , for distinct , and , then we call θ a graceful labeling of G.
If the -graph G is a bipartite graph with vertex partition , and a graceful labeling θ holds (abbreviated as ), we call θ a set-ordered graceful labeling.
Definition 2
([6]). A -graph G admits a mapping α holding and , for distinct vertices , , then α is called an odd-graceful labeling of graph G.
Definition 3
([6]). If a -graph G has a function β holds , as well as for distinct vertices , and , we call β an odd-elegant labeling of graph G.
Definition 4
([13]). If there is a labeling δ of a -graph G holding such that for distinct , , then we call δ a -graceful labeling of graph G, where k and d are positive integers.
Definition 5
([6]). Let k and d be positive integers. A labeling γ of a -graph G is said to be -arithmetic total labeling if , for distinct vertices , and holds.
Definition 6
([6]). If the mapping σ holds , and for each edge , where C is a magic constant, then we call σ an edge-magic total labeling of G; moreover, σ is called a super edge-magic total labeling if .
Next, we define the following new labelings to explore the relationships between several known labelings introduced here.
Definition 7.
Let and be two labelings of a -graph G, integers satisfy and .
(1) An equation holds true for each vertex , where is a positive constant and it is called vertex-image coefficient, then f and g are called a matching of vertex image-labelings (abbreviated as v-image-labelings);
(2) An equation holds true for every edge , and is a positive constant, called edge-image coefficient, then both labelings f and g are called a matching of edge image-labelings (abbreviated as e-image-labelings).
If labelings f and g are the same labeling functions, then they are called a matching of W-type v-image-labelings, or a matching of W-type e-image-labelings, where “W-type” {graceful, odd-graceful, odd-elegant, -graceful, -arithmetic total, super edge-magic total}. See an example in Figure 1, and are a matching of set-ordered graceful v-image-labelings, and are a matching of set-ordered graceful e-image-labelings.
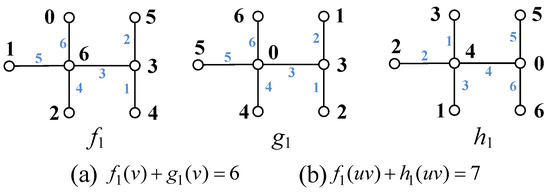
Figure 1.
A tree T admits: (a) a matching of set-ordered graceful v-image-labelings and , (b) a matching of set-ordered graceful e-image-labelings and .
2. Main Results and Proofs
Theorem 1.
Let T be a tree with p vertices and q edges, is the bipartition of vertices of T with , and . If the tree T admits a set-ordered graceful labeling, then it admits a matching of graceful v-image-labelings and a matching of graceful e-image-labelings.
Proof.
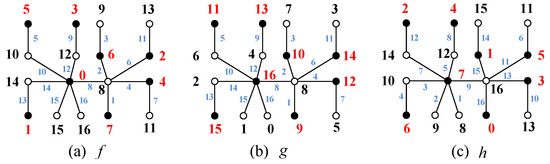
Since any tree is bipartite, and is the bipartition of vertices of a tree T, where and holding . Clearly, and for each edge of T. By the hypothesis of the theorem, the tree T admits a set-ordered graceful labeling f, without loss of generality, we have with , with and for every edge , obviously, condition is satisfied. We define another set-ordered graceful labeling g of T as follows: with , with , and for every edge . Therefore, we have for every vertex . According to Definition 1, f and g are a matching of graceful v-image-labelings with vertex-image coefficient .
There is another labeling h of T defined as: with , with , since and , then and the vertex label set , in addition, for each edge with , so the edge label set , which shows that the labeling h is just a set-ordered graceful labeling of T. In addition, we find
for each edge , immediately, we get for edge-image coefficient , see Figure 2.

Figure 2.
(a) A set-ordered graceful labeling f of a tree T; (b) A set-ordered graceful labeling g of T holding ; (c) A set-ordered graceful labeling h of T holding .
The proof of the Theorem 1 is complete. □
Theorem 2.
If a tree T admits set-ordered graceful labeling, then T holds the following assertions:
T admits a matching of odd-graceful v-image-labelings and a matching of odd-graceful e-image-labelings.
T admits a matching of odd-elegant v-image-labelings and a matching of odd-elegant e-image-labelings.
T admits a matching of -graceful v-image-labelings, and a matching of -graceful e-image-labelings.
T admits a -arithmetic total labeling and a -arithmetic total labeling are a matching of v-image-labelings; T admits a matching of -arithmetic total e-image-labelings.
T admits a matching of super edge-magic total v-image-labelings and a matching of super edge-magic total e-image-labelings.
Proof.
(1) We define a matching of odd-graceful v-image-labelings and from the set-ordered graceful v-image-labelings f and g. Letting with , with , and for each edge . Since holds true, then the set of vertex labels of T under the labeling is a subset of , and
For any two vertices , since , we claim that is an odd-graceful labeling. Then, we define another odd-graceful labeling by setting with , with , and for each edge . Immediately, the vertex label set , and the vertex label set is the union of an odd numbers set and an even numbers set, so
we get for each vertex and claim that and are a matching of odd-graceful v-image-labelings with .
We also define another odd-graceful labeling by setting with , with , so , for each edge . In addition, , because , so , for distinct . Therefore, is also an odd-graceful labeling, there is for each edge , so and are a matching of set-ordered odd-graceful e-image-labelings with edge-image coefficient . The assertion has been proven.
(2) Setting with , with , since and , so . We set for each edge , we can find is odd, and is even, so is odd, thus , so is an odd-elegant labeling. There is another odd-elegant labeling by setting with , and with , we can see , and . In addition, for each edge , because the parity of and is opposite, so is odd, then we get , we also get for , which indicate that and are a matching of odd-elegant v-image-labelings with .
An odd-elegant labeling of T can be obtained from in the following way: with , with , thus, the vertex label set ; since for each edge , we get the edge label set . Additionally, it is not hard to compute for , thus and are a matching of odd-elegant e-image-labelings with . The assertion has been proven.
(3) For integers and , we define a labeling as: with , with . Since and , we can get , and the vertex label set under is a subset of . Moreover,
which shows that is a -graceful labeling of T. There is another -graceful labeling defined as: with , with , and for every edge . We obtain the vertex label set , and the edge label set , moreover, holds true for , so we claim that and are a matching of -graceful v-image-labelings with .
Another -graceful labeling defined as: with , with , for every edge , , so
We can get , which shows that and are a matching of -graceful e-image-labelings with edge-image coefficient . We have shown the assertion .
(4) We, by defining a new labeling , set a transformation: with , with , then , so for distinct , and , on the other hand, for each edge , we calculate the set , which means that the labeling is a -arithmetic total labeling of T. Another labeling differing from is defined as: with , with , and for each edge , furthermore, the vertex label set , and
So, is a -arithmetic total labeling, in addition, for each vertex , this means that and are a matching of v-image-labelings with .
We come to define a -arithmetic total labeling of T as follows: with , with , for each edge , the vertex label set , and moreover
Then, we considering , so labelings and are a matching of -arithmetic total e-image-labelings with edge-image coefficient . The assertion holds true.
(5) There is a labeling defined in the following way: with , and with , and we set for each edge . It is not difficult to compute , since , and , we have , so is a super edge-magic total labeling with magic coefficient by definition. We come to define an edge-magic total labeling in the way: with , with , for each edge , notice that , so condition is true, and
to be a constant. Hence, is a super edge-magic total labeling, moreover, for each holds true, immediately, both labelings and are a matching of super edge-magic total v-image-labelings with .
Another set-ordered edge-magic total labeling with magic coefficient is defined as: with , with , for each edge . We also obtain . In addition, there is for each edge , which means that and are a matching of super set-ordered edge-magic total e-image-labelings with edge-image coefficient . This is the proof of the assertion . □
For understanding the proof of Theorem 2, see the several matching-type image-labelings of a tree shown in Figure 3. If the two labelings f and l constituting the image-labelings are not the same type, we get a result as follows:
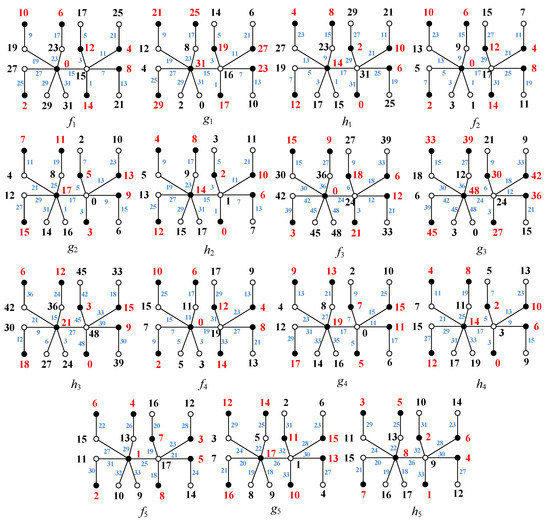
Figure 3.
The examples for illustrating the conversions between image-labelings , , with in the proofs of Theorem 2.
Corollary 1.
If a tree T admits a set-ordered graceful labeling f, then it admits an edge-magic total labeling l, so that f and l are a matching of e-image-labelings with .
Proof.
Let be the bipartition of vertices of a tree T, where and holding . By the hypothesis of the theorem, T admits a graceful labeling f such that with , with and for each edge , as well as and , again, , so f is a set-ordered graceful labeling. Next, we define an edge-magic total labeling l: with , with , and for every edge , as well as , and we have is a positive constant, thus l is called an edge-magic total labeling. In addition, we can see is a constant, so f and l are a matching of e-image-labelings with . □
3. Conclusions
Inspired by public and private keys in graphical passwords, we propose two new labelings in this paper, called vertex image-labelings and edge image-labelings respectively. We combine the new labelings with the known labelings to form compound labelings to find the relationships between the two compound labelings. Starting from the set-ordered graceful labeling f of the tree, we first prove that two different set-ordered graceful labelings match them to form a matching of vertex image-labeling and a matching of edge image-labelings. Then, according to labeling f, the odd-graceful image-labelings, odd-elegant image-labelings, -graceful image-labelings, -arithmetic total image-labelings, super edge-magic total image-labelings of the tree are derived in turn. The new image-labelings can connect two labelings of the same type. This paper draws a conclusion: the above-mentioned matching-type image-labelings of the tree can be transformed into each other, knowing one of the labelings of a tree, we can quickly get the other labelings of the tree.
Author Contributions
Create and conceptualize the idea, B.Y. and J.S.; writing—original draft preparation, J.S. and H.W.; writing—review and editing, J.S. and B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China under grants No. 61363060, No. 61662066, No. 61902005, and China Postdoctoral Science Foundation Grants No. 2019T120020 and No. 2018M641087.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ringel, G. Problem 25 in theory of graphs and its applications. Proc. Symp. Smolenice 1963, 162. [Google Scholar]
- Kumar, A.; Vats, A.K. Application of graph labeling in crystallography. Mater. Today Proc. 2020, 3. [Google Scholar] [CrossRef]
- Prasanna, N.L.; Sravanthi, K.; Sudhakar, N. Applications of graph labeling in communication networks. Orient. J. Comput. Sci. Technol. 2014, 7, 139–145. [Google Scholar]
- Tian, Y.; Li, L.; Peng, H.; Yang, Y. Achieving Flatness: Graph labeling can generate graphical honeywords. Comput. Secur. 2021, 5, 102212. [Google Scholar] [CrossRef]
- Van, D.; Leese, R.A.; Shepherd, M.A. Graph labeling and radio channel assignment. J. Graph. Theory 2015, 29, 263–283. [Google Scholar]
- Gallian, J.A. A dynamic survey of graph labeling. Electron. J. Comb. 2014, 17, 60–62. [Google Scholar]
- Rosa, A. On Certain Valuations of the Vertices of a Graph. In Theory of Graphs: International Symposium, Rome, Italy, July 1966; Gordon and Breach: New York, NY, USA, 1967; pp. 349–355. [Google Scholar]
- Gnanajothi, R.B. Topics in Graph Theory. Ph.D. Thesis, Madurai Kamaraj University, Tamil Nadu, India, 1991. [Google Scholar]
- Zhou, X.Q.; Yao, B.; Chen, X.E.; Tao, H.X. A proof to the odd-gracefulness of all lobsters. Ars Comb. 2012, 103, 13–18. [Google Scholar]
- Chang, G.J.; Hsu, D.F.; Rogers, D.G. Additive variations on a graceful theme: Some results on harmonious and other related graphs. Congr. Numer. 1981, 32, 181–197. [Google Scholar]
- Ringel, G.; Llado, A.S. Another tree conjecture. Bull. ICA 1996, 18, 83–85. [Google Scholar]
- Enomoto, H.; Llado, A.S.; Nakamigawa, T.; Ringel, G. Super Edge-magic Graphs. Sut J. Math. 1998, 2, 105–109. [Google Scholar]
- Acharya, B.D.; Hegde, S.M.J. Graph theory. Arith. Graphs 1990, 14, 275–299. [Google Scholar]
- Dinnen, M.J.; Ke, N.; Khosravani, M. Arithmetic progression graphs. Univ. J. Appl. Math. 2014, 2, 290–297. [Google Scholar] [CrossRef]
- Gao, Y.P.; Shan, S.L. Antimagic orientation of lobsters. Discret. Apllied Math. 2020, 287, 21–26. [Google Scholar] [CrossRef]
- Sethuraman, G.; Murugan, V. Generating graceful unicyclic graphs from a given forest. AKCE Int. J. Graphs Comb. 2020, 17, 592–605. [Google Scholar] [CrossRef]
- Sabirov, D.; Tukhbatullina, A.; Shepelevich, I. Information entropy of regular dendrimer aggregates and irregular intermediate structures. Liquids 2021, 1, 25–35. [Google Scholar] [CrossRef]
- Wang, H.Y.; Xu, J.; Ma, M.Y.; Zhang, H.Y. A new type of graphical passwords based on odd-elegant labelled graphs. Secur. Commun. Netw. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Golomb, S.W. How to Number a Graph. In Graph Theory and Computing; Read, R.C., Ed.; Academic Press: Cambridge, MA, USA, 1972; pp. 23–37. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).