Optimality Conditions for Group Sparse Constrained Optimization Problems

Abstract

In this paper, optimality conditions for the group sparse constrained optimization (GSCO) problems are studied. Firstly, the equivalent characterizations of Bouligand tangent cone, Clarke tangent cone and their corresponding normal cones of the group sparse set are derived. Secondly, by using tangent cones and normal cones, four types of stationary points for GSCO problems are given: $T^B$-stationary point, $N^B$-stationary point, $T^C$-stationary point and $N^C$-stationary point, which are used to characterize first-order optimality conditions for GSCO problems. Furthermore, both the relationship among the four types of stationary points and the relationship between stationary points and local minimizers are discussed. Finally, second-order necessary and sufficient optimality conditions for GSCO problems are provided.

1. Introduction

The sparsity of a vector means that few entries of the vector are non-zero, while the group sparsity of a vector means that non-zero entries or zero entries in the vector may have some group structures, that is, they appear in blocks in certain areas. A vector can be grouped according to the prior information of the group structure among the entries, and then each group is examined to see if they are zeros entirely. For example, genes of the same biological path can be regarded as a group in gene expression analysis, so when they are described by a vector, the vector has group sparsity. Since it was first proposed by Yuan and Lin [1] in 2006, the group sparse optimization has attracted much attention of researchers [2,3,4,5]. The aim of group sparse optimization is to seek a solution of group sparsity for a system. It is now known that group sparse optimization has broad applications in bioinformatics, pattern recognition, image restoration, neuroimaging and other fields [1,6,7,8]. For instance, we can restore the signal by use of group sparse optimization according to the prior information of its group sparse structure. Moreover, the stability of the recovery can be improved in the presence of noise while the accuracy of the recovery can be improved in the absence of noise [2]. In practical problems, it is more targeted to adopt the corresponding group sparse optimization model for problems with group sparse structure [9].

The general sparse constrained optimization has been researched by many authors and achieved a lot. Here we mention few of them. In [10], the authors proposed both concepts of restricted strong convexity and restricted strong smoothness to ensure the existence of unique solution for the sparse constrained optimization, and obtained the corresponding error bounds. In [11], the authors defined $N^B$-stationary point and $N^C$-stationary point for the sparse constrained optimization. Beck and Eldar [12] put forward three types of first-order necessary optimality conditions for sparse constraints optimization. One of them is the basic feasibility which is a generation of the necessary optimality condition for zero gradient in unconstrained optimization. Another one of them is the L-stationary point which is based on the fixed point condition and can be used to derive the iterative hard thresholding algorithm for solving sparse constrained optimization problems. As we all know, Calamai and Moŕe [13] introduced $T^B$-stationary points and $T^C$-stationary points to describe the optimal conditions for general constrained optimization problems. Although N-stationary points, L-stationary points and T-stationary points are equivalent for convex optimization problems, they are not equivalent for sparse constrained optimization problems because of the non-convexity. In [14], the authors provided a description of the tangent cone and the normal cone of the sparse set, and then used to describe the first-order optimality condition and the second-order optimality condition, furthermore, they extended the results to the optimization problems subjected to sparse constraints and non-negative constraints. Chen, Pan, and Xiu [15] characterized the solutions of three kinds of sparse optimization problems and investigated the relationship among them. Recently, Bian and Chen [16] gave an exact continuous relaxation problem for the sparsity penalty optimization problem, and proposed a smoothing proximal gradient for the relaxation problem.

However, the above works are mainly for general sparse optimization problems. Due to the complexity of the group sparse structure, there still lacks of research on group sparse constrained optimization problems. If the group sparsity is a penalty in the objective function, Peng and Chen [17] studied the first-order and second-order optimality conditions for the relaxation problems for group sparse optimization problems, while Pan and Chen [18] used a capped folded concave function to approximate the group sparsity function and showed that the solution set of the continuous approximation problem and the set of group sparse solutions are same.

This paper focuses on the following group sparse constrained optimization (GSCO) problem, that is,

$$\begin{array}{c}\hfill \underset{\mathbf{x}\in {\mathbb{R}}^n}{min}f\left(\mathbf{x}\right)s.t.{\parallel \mathbf{x}\parallel }_{2,0}\le k,\end{array}$$

(1)

where $f:{\mathbb{R}}^n\to \mathbb{R}$ is a continuously differentiable function or a twice continuously differentiable function, $\mathbf{x}\in {\mathbb{R}}^n$ is divided into m disjoint groups, denoted by $\mathbf{x}={({\mathbf{x}}_1^{\top },\cdots ,{\mathbf{x}}_m^{\top })}^{\top }$ with ${\mathbf{x}}_i={(x_{i\left(1\right)},\cdots ,x_{i\left(n_i\right)})}^{\top }\in {\mathbb{R}}^{n_i}$, $i=1,\cdots ,m$ and ${\sum }_{i=1}^m{n}_i=n,n_i\ge 1$, ${\parallel \mathbf{x}\parallel }_{2,0}:={\sum }_{i=1}^m♯\{\parallel {\mathbf{x}}_i{\parallel }_2\ne 0\}$ counts the number of non-zero groups in $\mathbf{x}$, where $\parallel {\mathbf{x}}_i{\parallel }_2$ is the ${\ell }_2$ vector norm of the ith group ${\mathbf{x}}_i$. Throughout this paper, for simplicity, $\parallel ·\parallel$ denotes the ${\ell }_2$ vector norm. Let k be a positive integer with $k\le m\le n$, and $S:=\{\mathbf{x}:\parallel \mathbf{x}{\parallel }_{2,0}\le k\}$ be a group sparse set.

Problem (1) is called GSCO due to the group structure in its entries. When $m=n$ and $n_i=1,i=1,\cdots ,m$, Problem (1) reduces to the standard sparse constrained optimization.

Problem (1) is non-convex, non-smooth, and non-Lipschitz, for which the optimality conditions are of the theoretical importance. It is the basis of analyzing and solving the problem. The optimality conditions for constrained optimization are closely related to tangent cones and normal cones of the constraint set. We will use Boligand tangent cone, Clarke tangent cone and the corresponding normal cones of the group sparse set to describe optimality conditions for Problem (1).

This paper is organized as follows. In Section 2, some basic notations and definitions are introduced. In Section 3, the equivalent expressions of Boligand tangent cone, Clarke tangent cone, and the corresponding normal cones of the group sparse constraint set S are given. In Section 4, first-order optimality conditions for Problem (1) based on the tangent cones and normal cones of S are provided. The relationship between stationary points and local minimizers of Problem (1) is also discussed. In Section 5, second-order necessary and sufficient optimality conditions for Problem (1) are given. At last, a brief concluding remark is given in Section 6.

2. Notations and Definitions

In this section, we introduce some notations and preliminaries including the definitions of Boligand tangent cone, Clarke tangent cone and their corresponding normal cones.

For any $\mathbf{x}={({\mathbf{x}}_1^{\top },{\mathbf{x}}_2^{\top },\cdots ,{\mathbf{x}}_m^{\top })}^{\top }\in {\mathbb{R}}^n$ with ${\mathbf{x}}_i\in {\mathbb{R}}^{n_i}$, the group support set of $\mathbf{x}$ is denoted by

$$\Gamma \left(\mathbf{x}\right):=\{i\in \{1,\cdots ,m\}:{\mathbf{x}}_i\ne \mathbf{0}\},$$

$|\Gamma (\mathbf{x}\left)\right|$ is the cardinality of the set $\Gamma \left(\mathbf{x}\right)$, then ${\parallel \mathbf{x}\parallel }_{2,0}=|\Gamma \left(\mathbf{x}\right)|$, which means ${\parallel \mathbf{x}\parallel }_{2,0}$ is the number of groups in $\mathbf{x}$ that have nonzero ${\ell }_2$-norm.

For the n-dimensional real number space ${\mathbb{R}}^n$, ${\mathbb{R}}_{x_i}$ denotes the $x_i$ coordinate axis, and ${\mathbb{R}}_{x_i{x}_j}^2$ denotes the $x_{i}O{x}_j$ coordinate plane. Let $e_i\in {\mathbb{R}}^n$ denote the n-dimensional vector in which the entries in ith group are all ones and the other entries are all zeros. Let $e_{ij}(i=1,\cdots ,m,j=1,\cdots ,n_i)$ denote the n-dimensional vector in which the jth entry of the ith group is one and the other entries are all zeros.

For a smooth function $f:{\mathbb{R}}^n\to \mathbb{R}$, let

$${[\nabla f\left(\mathbf{x}\right)]}_i:={({[\nabla f\left(\mathbf{x}\right)]}_{i\left(1\right)},\cdots ,{[\nabla f\left(\mathbf{x}\right)]}_{i\left(n_i\right)})}^{\top },\nabla f\left(\mathbf{x}\right):={({[\nabla f\left(\mathbf{x}\right)]}_1^{\top },\cdots ,{[\nabla f\left(\mathbf{x}\right)]}_m^{\top })}^{\top },$$

where $x_{i\left(j\right)}\in \mathbb{R}$ denotes the jth entry in ${\mathbf{x}}_i$ and ${[\nabla f\left(\mathbf{x}\right)]}_{i\left(j\right)}$ denotes the jth entry in ${[\nabla f\left(\mathbf{x}\right)]}_i$.

The following example shows that the group sparse structure is different from the sparse structure.

Example 1.

Let $\mathbf{x}={(x_1,x_2,x_3)}^{\top }$ be a 3-dimensional vector. We show the different ways of grouping and the corresponding group sparsity of $\mathbf{x}$ as follows.

(1)

When $\mathbf{x}={(x_1,x_2,x_3)}^{\top },n_1=n_2=n_3=1,$

if ${\parallel \mathbf{x}\parallel }_{2,0}=0,$ then $\mathbf{x}=\mathbf{0}$;

if ${\parallel \mathbf{x}\parallel }_{2,0}=1,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|x_1\in \mathbb{R}\backslash \left\{0\right\},x_2=x_3=0\}\bigcup \{\mathbf{x}|x_2\in \mathbb{R}\backslash \left\{0\right\},x_1=x_3=0\}\bigcup \{\mathbf{x}|x_3\in \mathbb{R}\backslash \left\{0\right\},x_1=x_2=0\}$;

if ${\parallel \mathbf{x}\parallel }_{2,0}=2,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|x_1,x_2\in \mathbb{R}\backslash \left\{0\right\},x_3=0\}\bigcup \{\mathbf{x}|x_1,x_3\in \mathbb{R}\backslash \left\{0\right\},x_2=0\}\bigcup \{\mathbf{x}|x_2,$$x_3\in \mathbb{R}\backslash \left\{0\right\},x_1=0\}$;

if ${\parallel \mathbf{x}\parallel }_{2,0}=3,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|x_1,x_2,x_3\in \mathbb{R}\backslash \left\{0\right\}\}$.

(2)

When $\mathbf{x}={(x_1,(x_2,x_3))}^{\top },n_1=1,n_2=2$,

if ${\parallel \mathbf{x}\parallel }_{2,0}=0,$ then $\mathbf{x}=\mathbf{0}$;

if ${\parallel \mathbf{x}\parallel }_{2,0}=1,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|x_1\in \mathbb{R}\backslash \left\{0\right\},x_2=x_3=0\}\bigcup \{\mathbf{x}|x_1=0,{(x_2,x_3)}^{\top }\in {\mathbb{R}}^2\backslash \left\{\mathbf{0}\right\}\}$;

if ${\parallel \mathbf{x}\parallel }_{2,0}=2,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|x_1\in \mathbb{R}\backslash \left\{0\right\},{(x_2,x_3)}^{\top }\in {\mathbb{R}}^2\backslash \left\{\mathbf{0}\right\}\}$.

(3)

When $\mathbf{x}={\left((x_1,x_2,x_3)\right)}^{\top }$, $n_1=3$,

if ${\parallel \mathbf{x}\parallel }_{2,0}=0,$ then $\mathbf{x}=\mathbf{0};$

if ${\parallel \mathbf{x}\parallel }_{2,0}=1,$ then $\mathbf{x}\in \left\{\mathbf{x}\right|{(x_1,x_2,x_3)}^{\top }\ne \mathbf{0}\}$.

In the end of this section, we will introduce the definition of Bouligand tangent cone, Clarke tangent cone and their corresponding normal cones [19].

Definition 1

([19]). Let $\Omega \subseteq {\mathbb{R}}^n$ be an arbitrary nonemepty set. The Bouligand tangent cone $T_{\Omega }^B\left(\widehat{\mathbf{x}}\right)$, the Clarke tangent cone $T_{\Omega }^C\left(\widehat{\mathbf{x}}\right)$ and their corresponding normal cone $N_{\Omega }^B\left(\widehat{\mathbf{x}}\right)$ and $N_{\Omega }^C\left(\widehat{\mathbf{x}}\right)$ to the set Ω at the point $\widehat{\mathbf{x}}\in \Omega$ are defined as follows.

(1)

Bouligand tangent cone:

$$T_{\Omega }^B\left(\widehat{\mathbf{x}}\right):=\left\{\mathbf{d}\in {\mathbb{R}}^n:\exists \left\{{\mathbf{x}}^t\right\}\subset \Omega ,\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}},\exists {\lambda }_t\ge 0,t\in \mathbb{N},s.t.\underset{t\to \infty }{lim}{\lambda }_t({\mathbf{x}}^t-\widehat{\mathbf{x}})=\mathbf{d}\right\};$$

(2)

Fréchet normal cone:

$$N_{\Omega }^B\left(\widehat{\mathbf{x}}\right):={\left[T_{\Omega }^B\left(\widehat{\mathbf{x}}\right)\right]}^{\circ }=\left\{\mathbf{u}\in {\mathbb{R}}^n:⟨\mathbf{u},\mathbf{z}⟩\le 0,\forall \mathbf{z}\in T_{\Omega }^B\left(\widehat{\mathbf{x}}\right)\right\};$$

(3)

Clarke tangent cone:

$$T_{\Omega }^C\left(\widehat{\mathbf{x}}\right):=\left\{\mathbf{d}\in {\mathbb{R}}^n:\begin{array}{c}\forall \left\{{\mathbf{x}}^t\right\}\subset \Omega ,\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}},\forall \left\{{\lambda }_t\right\}\subset {\mathbb{R}}_{+},\underset{t\to \infty }{lim}{\lambda }_t=0,\exists \left\{{\mathbf{d}}^t\right\}\subset {\mathbb{R}}^n,\\ s.t.\underset{t\to \infty }{lim}{\mathbf{d}}^t=\mathbf{d}\mathrm{and}{\mathbf{x}}^t+{\lambda }_t{\mathbf{d}}^t\in \Omega ,t\in \mathbb{N}\end{array}\right\};$$

(4)

Clarke normal cone:

$$N_{\Omega }^C\left(\widehat{\mathbf{x}}\right):={\left[T_{\Omega }^C\left(\widehat{\mathbf{x}}\right)\right]}^{\circ }=\left\{\mathbf{u}\in {\mathbb{R}}^n:⟨\mathbf{u},\mathbf{z}⟩\le 0,\forall \mathbf{z}\in T_{\Omega }^C\left(\widehat{\mathbf{x}}\right)\right\}.$$

3. Tangent Cones and Normal Cones of the Group Sparse Set $\mathit{S}$

Tangent cones and normal cones are widely used to describe optimality conditions for constrained optimization problems [19]. The following two theorems give the equivalent characterizations of Bouligand tangent cone, Clarke tangent cone and their corresponding normal cones to the group sparse constraint set S.

Theorem 1.

For any $\widehat{\mathbf{x}}\in S$, the Boligand tangent cone $T_S^B\left(\widehat{\mathbf{x}}\right)$ and Fréchet normal cone $N_S^B\left(\widehat{\mathbf{x}}\right)$ to the group sparse set S at the point $\widehat{\mathbf{x}}$ has the following equivalent expressions:

$$\begin{array}{ccc}\hfill T_S^B\left(\widehat{\mathbf{x}}\right)& =& \{\mathbf{d}\in {\mathbb{R}}^n:\parallel \mathbf{d}{\parallel }_{2,0}\le k,\parallel \widehat{\mathbf{x}}+\gamma \mathbf{d}{\parallel }_{2,0}\le k,\forall \gamma \in \mathbb{R}\}\hfill \\ & =& \bigcup _{J\in \Theta \left(\widehat{\mathbf{x}}\right)}\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin J\}\hfill \\ & =& \bigcup _{J\in \Theta \left(\widehat{\mathbf{x}}\right)}\mathrm{span}\{e_{ij},i\in J,j=1,\cdots ,n_i\};\hfill \end{array}$$

$$N_S^B\left(\widehat{\mathbf{x}}\right)=\left\{\begin{array}{cc}\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)\}=\mathrm{span}\{e_{ij},i\notin \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\},\hfill & \parallel \widehat{\mathbf{x}}{\parallel }_{2,0}=k,\hfill \\ \left\{\mathbf{0}\right\},\hfill & \parallel \widehat{\mathbf{x}}{\parallel }_{2,0}<k,\hfill \end{array}\right.$$

where $\Gamma \left(\widehat{\mathbf{x}}\right)=\{i\in \{1,\cdots ,m\}:{\widehat{\mathbf{x}}}_i\ne \mathbf{0}\}$, $\Theta \left(\widehat{\mathbf{x}}\right)=\{J\subseteq \{1,\cdots ,m\}:\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq J,\left|J\right|=k\}$, ${\mathbf{d}}_i\in {\mathbb{R}}^{n_i}$ is the ith group of $\mathbf{d}\in {\mathbb{R}}^n$, ${\mathbf{u}}_i\in {\mathbb{R}}^{n_i}$ is the ith group of $\mathbf{u}\in {\mathbb{R}}^n$.

Proof. 

(i) According to the definition of Bouligand tangent cone, we have

$$\begin{array}{c}\hfill T_S^B\left(\widehat{\mathbf{x}}\right)=\{\mathbf{d}\in {\mathbb{R}}^n:\exists \left\{{\mathbf{x}}^t\right\}\subseteq S,\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}},\exists {\lambda }_t\ge 0,t\in \mathbb{N},s.t.\underset{t\to \infty }{lim}{\lambda }_t({\mathbf{x}}^t-\widehat{\mathbf{x}})=\mathbf{d}\}.\end{array}$$

Firstly, we prove that $T_S^B\left(\widehat{\mathbf{x}}\right)=H\left(\widehat{\mathbf{x}}\right):=\{\mathbf{d}\in {\mathbb{R}}^n{:\parallel \mathbf{d}\parallel }_{2,0}\le k,\parallel \widehat{\mathbf{x}}+\gamma \mathbf{d}{\parallel }_{2,0}\le k,\forall \gamma \in \mathbb{R}\}.$

For any $\mathbf{d}\in T_S^B\left(\widehat{\mathbf{x}}\right)$, there exists $\left\{{\mathbf{x}}^t\right\}\subseteq S$ such that $\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}},$ then

$$\begin{array}{c}\hfill \Gamma \left(\widehat{\mathbf{x}}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)\mathrm{and}|\Gamma \left(\widehat{\mathbf{x}}\right)|\le |\Gamma \left({\mathbf{x}}^t\right)|\end{array}$$

for any sufficiently large t. It follows from ${\mathbf{x}}^t\in S$ that

$$\begin{array}{c}\hfill |\Gamma \left({\mathbf{x}}^t\right)|=\parallel {\mathbf{x}}^t{\parallel }_{2,0}\le k.\end{array}$$

Since $\mathbf{d}=\underset{t\to \infty }{lim}{\lambda }_t({\mathbf{x}}^t-\widehat{\mathbf{x}})$ with ${\lambda }_t\ge 0$, then $\Gamma \left(\mathbf{d}\right)\subseteq \Gamma ({\mathbf{x}}^t-\widehat{\mathbf{x}})$. Due to $\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$, we obtain

$$\begin{array}{c}\hfill \Gamma \left(\mathbf{d}\right)\subseteq \Gamma ({\mathbf{x}}^t-\widehat{\mathbf{x}})\subseteq \Gamma \left({\mathbf{x}}^t\right).\end{array}$$

Therefore,

$$\begin{array}{c}\hfill {\parallel \mathbf{d}\parallel }_{2,0}=|\Gamma \left(\mathbf{d}\right)|\le |\Gamma \left({\mathbf{x}}^t\right)|\le k.\end{array}$$

(2)

According to $\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$ and $\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$, then $\Gamma (\widehat{\mathbf{x}}+\gamma \mathbf{d})\subseteq \Gamma \left({\mathbf{x}}^t\right)$ for any $\gamma \in \mathbb{R}$. Hence we get

$$\begin{array}{c}\hfill \parallel \widehat{\mathbf{x}}{+\gamma \mathbf{d}\parallel }_{2,0}=|\Gamma (\widehat{\mathbf{x}}+\gamma \mathbf{d})|\le |\Gamma \left({\mathbf{x}}^t\right)|\le k.\end{array}$$

(3)

Combining (2) with (3), we get $T_S^B\left(\widehat{\mathbf{x}}\right)\subseteq H\left(\widehat{\mathbf{x}}\right)$.

Conversely, for any $\mathbf{d}\in H\left(\widehat{\mathbf{x}}\right)$, take any sequence $\left\{{\lambda }_t\right\}$ such that ${\lambda }_t>0$ and ${\lambda }_t\to \infty$, let ${\mathbf{x}}^t=\widehat{\mathbf{x}}+\frac{\mathbf{d}}{{\lambda }_t}$, then $\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}}$. Since $\parallel \widehat{\mathbf{x}}{+\gamma \mathbf{d}\parallel }_{2,0}\le k$ for any $\gamma \in \mathbb{R}$, we get

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}^t{\parallel }_{2,0}={\parallel \widehat{\mathbf{x}}+\frac{\mathbf{d}}{{\lambda }_t}\parallel }_{2,0}\le k,\end{array}$$

which means $\left\{{\mathbf{x}}^t\right\}\subseteq S$. It follows from $\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}}$ that $\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$. Hence we obtain

$$\begin{array}{c}\hfill \parallel \widehat{\mathbf{x}}{\parallel }_{2,0}=|\Gamma \left(\widehat{\mathbf{x}}\right)|\le |\Gamma \left({\mathbf{x}}^t\right)|=\parallel {\mathbf{x}}^t{\parallel }_{2,0}\le k.\end{array}$$

From ${\mathbf{x}}^t=\widehat{\mathbf{x}}+\frac{\mathbf{d}}{{\lambda }_t}$, we get

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{\lambda }_t({\mathbf{x}}^t-\widehat{\mathbf{x}})=\mathbf{d}.\end{array}$$

Hence we have $\mathbf{d}\in T_S^B\left(\widehat{\mathbf{x}}\right)$, which means $T_S^B\left(\widehat{\mathbf{x}}\right)\supseteq H\left(\widehat{\mathbf{x}}\right)$.

The above proof yields $T_S^B\left(\widehat{\mathbf{x}}\right)=H\left(\widehat{\mathbf{x}}\right)$.

It is easy to prove that

$$\begin{array}{c}\hfill H\left(\widehat{\mathbf{x}}\right)=\bigcup _{J\in \Theta \left(\widehat{\mathbf{x}}\right)}\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin J\}=\bigcup _{J\in \Theta \left(\widehat{\mathbf{x}}\right)}\mathrm{span}\{e_{ij},i\in J,j=1,\cdots ,n_i\}.\end{array}$$

(ii) According to the definition of Fréchet normal cone,

$$\begin{array}{ccc}\hfill N_S^B\left(\widehat{\mathbf{x}}\right)={\left[T_S^B\left(\widehat{\mathbf{x}}\right)\right]}^{\circ }& =& \{\mathbf{u}\in {\mathbb{R}}^n:⟨\mathbf{u},\mathbf{d}⟩\le 0,\forall \mathbf{d}\in T_S^B\left(\widehat{\mathbf{x}}\right)\}.\hfill \end{array}$$

For any $\mathbf{u}\in N_S^B\left(\widehat{\mathbf{x}}\right)$ and any $\mathbf{d}\in T_S^B\left(\widehat{\mathbf{x}}\right)$, it must hold $⟨\mathbf{u},\mathbf{d}⟩\le 0$.

If $\parallel \widehat{\mathbf{x}}{\parallel }_{2,0}=k$, we have

$$\begin{array}{c}\hfill ⟨\mathbf{u},\mathbf{d}⟩=\sum _{i\in \Gamma \left(\widehat{\mathbf{x}}\right)}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩+\sum _{i\notin \Gamma \left(\widehat{\mathbf{x}}\right)}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩.\end{array}$$

Since $\mathbf{d}\in T_S^B\left(\widehat{\mathbf{x}}\right)={\bigcup }_{J\in \Theta \left(\widehat{\mathbf{x}}\right)}\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin J\}$, for any $J\in \Theta \left(\widehat{\mathbf{x}}\right)$, we have $\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq J$ and ${\mathbf{d}}_i=\mathbf{0},i\notin J$. Thus we have ${\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)$, ${\displaystyle \sum _{i\notin \Gamma \left(\widehat{\mathbf{x}}\right)}}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩=0$, and then

$$\begin{array}{c}\hfill ⟨\mathbf{u},\mathbf{d}⟩={\displaystyle \sum _{i\in \Gamma \left(\widehat{\mathbf{x}}\right)}}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩\le 0,\end{array}$$

which, together with the arbitrariness of ${\mathbf{d}}_i\in {\mathbb{R}}^{n_i}$ for $i\in \Gamma \left(\widehat{\mathbf{x}}\right)$, implies ${\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)$. Therefore, $N_S^B\left(\widehat{\mathbf{x}}\right)=\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)\}$. It is easy to prove that $\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)\}=\mathrm{span}\{e_{ij},i\notin \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\}$.

If $\parallel \widehat{\mathbf{x}}{\parallel }_{2,0}<k$, for any $J\in \Theta \left(\widehat{\mathbf{x}}\right)$, it holds

$$\begin{array}{c}\hfill ⟨\mathbf{u},\mathbf{d}⟩=\sum _{i\in J}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩+\sum _{i\notin J}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩.\end{array}$$

We also have $⟨\mathbf{u},\mathbf{d}⟩={\displaystyle \sum _{i\in J}}⟨{\mathbf{u}}_i,{\mathbf{d}}_i⟩\le 0$, which also implies ${\mathbf{u}}_i=\mathbf{0},i\in J$. Due to $\parallel \widehat{\mathbf{x}}{\parallel }_{2,0}<k$, $\Gamma \left(\widehat{\mathbf{x}}\right)\subseteq J$ and $\left|J\right|=k$, it must hold ${\displaystyle \bigcup _{J\in \Theta \left(\widehat{\mathbf{x}}\right)}}J=\{1,2,\cdots ,m\}$, and then $N_S^B\left(\widehat{\mathbf{x}}\right)=\left\{\mathbf{0}\right\}$. □

Next, we give the equivalent characterizations of Clarke tangent cone and Clarke normal cone of the group sparse constraint set S.

Theorem 2.

For any $\widehat{\mathbf{x}}\in S$, the Clarke tangent cone and the Clarke normal cone of the group sparse set S at $\widehat{\mathbf{x}}$ have the following equivalent expressions:

$$\begin{array}{ccc}\hfill T_S^C\left(\widehat{\mathbf{x}}\right)& =& \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}\hfill \\ & =& \{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)\}\hfill \\ & =& \mathrm{span}\{e_{ij},i\in \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\};\hfill \end{array}$$

$$\begin{array}{ccc}\hfill N_S^C\left(\widehat{\mathbf{x}}\right)& =& \{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)\}\hfill \\ & =& \mathrm{span}\{e_{ij},i\notin \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\}.\hfill \end{array}$$

Proof. 

(i) According to the definition of Clarke tangent cone, we have

$$\begin{array}{c}\hfill T_S^C\left(\widehat{\mathbf{x}}\right)=\left\{\mathbf{d}\in {\mathbb{R}}^n:\begin{array}{cc}\forall \left\{{\mathbf{x}}^t\right\}\subseteq S,\hfill & \underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}},\forall \left\{{\lambda }_t\right\}\subset {\mathbb{R}}_{+},\underset{t\to \infty }{lim}{\lambda }_t=0,\exists \left\{{\mathbf{y}}^t\right\}\subset {\mathbb{R}}^n,\hfill \\ & s.t.\underset{t\to \infty }{lim}{\mathbf{y}}^t=\mathbf{d},{\parallel {\mathbf{x}}^t+{\lambda }_t{\mathbf{y}}^t\parallel }_{2,0}\le k,\forall t\in \mathbb{N}\hfill \end{array}\right\}.\end{array}$$

We first prove $T_S^C\left(\widehat{\mathbf{x}}\right)=\{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$.

To prove $T_S^C\left(\widehat{\mathbf{x}}\right)\subseteq \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$, we assume, on the contrary, that there exists $\mathbf{d}\in T_S^C\left(\widehat{\mathbf{x}}\right)$, but $\Gamma \left(\mathbf{d}\right)⊈\Gamma \left(\widehat{\mathbf{x}}\right)$. Then there exists $i_0\in \Gamma \left(\mathbf{d}\right)$ but $i_0\notin \Gamma \left(\widehat{\mathbf{x}}\right)$, which implies that ${\widehat{\mathbf{x}}}_{i_0}=\mathbf{0}$ but ${\mathbf{d}}_{i_0}\ne \mathbf{0}$.

Note that $|\Gamma (\widehat{\mathbf{x}}\left)\right|\le k$. For any $t\in \mathbb{N}$, take ${\Gamma }_t\subseteq \{1,2,\cdots ,m\}\backslash \{\Gamma \left(\widehat{\mathbf{x}}\right)\bigcup \left\{i_0\right\}\}$ such that

$$|\Gamma \left(\widehat{\mathbf{x}}\right)|+|{\Gamma }_t|=k.$$

Let ${\lambda }_t=\frac{1}{t^2}\downarrow 0$ and

$$\begin{array}{c}\hfill {\mathbf{x}}_i^t=\left\{\begin{array}{cc}{\mathbf{x}}_i,\hfill & i\in \Gamma \left(\widehat{\mathbf{x}}\right)\hfill \\ \frac{1}{t}{\mathbf{1}}_{n_i},\hfill & i\in {\Gamma }_t,\hfill \\ \mathbf{0},\hfill & i\in \{1,2,\cdots ,m\}\backslash \{{\Gamma }_t\bigcup \Gamma \left(\widehat{\mathbf{x}}\right)\}.\hfill \end{array}\right.\end{array}$$

where ${\mathbf{1}}_{n_i}$ is an $n_i$-dimensional vector of all ones. Then

$$\begin{array}{c}\hfill \Gamma \left({\mathbf{x}}^t\right)=\Gamma \left(\widehat{\mathbf{x}}\right)\bigcup {\Gamma }_t,\parallel {\mathbf{x}}^t{\parallel }_{2,0}=|\Gamma \left(\widehat{\mathbf{x}}\right)|+|{\Gamma }_t|=k,\end{array}$$

and thus $\left\{{\mathbf{x}}^t\right\}\subseteq S$, ${\mathbf{x}}_{i_0}^t=\mathbf{0}$, and $\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}}$. For any ${\mathbf{y}}^t\to \mathbf{d}$, we have

$$\begin{array}{c}\hfill {\mathbf{x}}_i^t+{\lambda }_t{\mathbf{y}}_i^t=\left\{\begin{array}{cc}{\mathbf{x}}_i^t+\frac{1}{t^2}{\mathbf{y}}_i^t\to {\widehat{\mathbf{x}}}_i,\hfill & i\in \Gamma \left(\widehat{\mathbf{x}}\right),\hfill \\ \frac{1}{t}{\mathbf{1}}_{n_i}+\frac{1}{t^2}{\mathbf{y}}_i^t\to \mathbf{0},\hfill & i\in {\Gamma }_t,\hfill \\ \mathbf{0}+\frac{1}{t^2}{\mathbf{y}}_{i_0}^t\to \mathbf{0},\hfill & i=i_0,\hfill \\ \mathbf{0}+\frac{1}{t^2}{\mathbf{y}}_i^t\to \mathbf{0},\hfill & i\in \{1,2,\cdots ,m\}\backslash \{{\Gamma }_t\bigcup \Gamma \left(\widehat{\mathbf{x}}\right)\bigcup \left\{i_0\right\}\}.\hfill \end{array}\right.\end{array}$$

Since ${\mathbf{y}}_{i_0}^t\to {\mathbf{d}}_{i_0}\ne \mathbf{0}$, for any sufficiently large t, we have

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}^t+{\lambda }_t{\mathbf{y}}^t{\parallel }_{2,0}\ge |\Gamma \left(\widehat{\mathbf{x}}\right)\bigcup {\Gamma }_t\bigcup \left\{i_0\right\}|=k+1,\end{array}$$

Therefore, ${\mathbf{x}}^t+{\lambda }_t{\mathbf{y}}^t\notin S$ for any sufficiently large t, which means $\mathbf{d}\notin T_S^C\left(\widehat{\mathbf{x}}\right)$ according to the definition of $T_S^C\left(\widehat{\mathbf{x}}\right)$. This contradiction shows that $T_S^C\left(\widehat{\mathbf{x}}\right)\subseteq \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$.

To prove $\{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}\subseteq T_S^C\left(\widehat{\mathbf{x}}\right)$, let $\mathbf{d}\in \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$. For any $\left\{{\mathbf{x}}^t\right\}\subseteq S$, with $\underset{t\to \infty }{lim}{\mathbf{x}}^t=\widehat{\mathbf{x}}$ and any $\left\{{\lambda }_t\right\}\subset {\mathbb{R}}_{+}$ with ${lim}_{t\to \infty }{\lambda }_t=0$, we have

$$\begin{array}{c}\hfill \Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right).\end{array}$$

(4)

Let ${\mathbf{y}}^t={\mathbf{x}}^t-\widehat{\mathbf{x}}+\mathbf{d}$, then from (4), we get $\Gamma \left({\mathbf{y}}^t\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$ and

$$\parallel {\mathbf{x}}^t+{\lambda }_t{\mathbf{y}}^t{\parallel }_{2,0}=|\Gamma ({\mathbf{x}}^t+{\lambda }_t{\mathbf{y}}^t)|\le |\Gamma \left({\mathbf{x}}^t\right)|\le k.$$

In addition, $\underset{t\to \infty }{lim}{\mathbf{y}}^t=\underset{t\to \infty }{lim}({\mathbf{x}}^t-\widehat{\mathbf{x}}+\mathbf{d})=\mathbf{d}$. It is easy to know that $\mathbf{d}\in T_S^C\left(\widehat{\mathbf{x}}\right)$ according to the definition of $T_S^C\left(\widehat{\mathbf{x}}\right)$. From the arbitrariness of $\mathbf{d}\in \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$, we have

$$\begin{array}{c}\hfill \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}\subseteq T_S^C\left(\widehat{\mathbf{x}}\right).\end{array}$$

Therefore, we have proved that $T_S^C\left(\widehat{\mathbf{x}}\right)=\{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$.

Since ${\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\mathbf{d}\right)$ and $\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)$ for any $\mathbf{d}\in \{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}$, it must hold ${\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)$. Hence we get

$$\begin{array}{c}\hfill T_S^C\left(\widehat{\mathbf{x}}\right)=\{\mathbf{d}\in {\mathbb{R}}^n:\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left(\widehat{\mathbf{x}}\right)\}=\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)\}.\end{array}$$

(5)

It is easy to prove that $\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)\}=\mathrm{span}\{e_{ij}:i\in \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\}$, then

$$\begin{array}{c}\hfill T_S^C\left(\widehat{\mathbf{x}}\right)=\mathrm{span}\{e_{ij}:i\in \Gamma \left(\widehat{\mathbf{x}}\right),j=1,\cdots ,n_i\}.\end{array}$$

(6)

(ii) According to the definition of Clarke normal cone, we have

$$\begin{array}{c}\hfill N_S^C\left(\widehat{\mathbf{x}}\right)={\left[T_S^C\left(\widehat{\mathbf{x}}\right)\right]}^{\circ }=\{\mathbf{u}\in {\mathbb{R}}^n:⟨\mathbf{d},\mathbf{u}⟩\le 0,\forall \mathbf{d}\in T_S^C\left(\widehat{\mathbf{x}}\right)\}.\end{array}$$

For any $\mathbf{d}\in T_S^C\left(\widehat{\mathbf{x}}\right)$ and any $\mathbf{u}\in N_S^C\left(\widehat{\mathbf{x}}\right)$, we have

$$\begin{array}{c}\hfill ⟨\mathbf{d},\mathbf{u}⟩=\sum _{i\in \Gamma \left(\widehat{\mathbf{x}}\right)}⟨{\mathbf{d}}_i,{\mathbf{u}}_i⟩+\sum _{i\notin \Gamma \left(\widehat{\mathbf{x}}\right)}⟨{\mathbf{d}}_i,{\mathbf{u}}_i⟩\le 0.\end{array}$$

From (5), ${\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left(\widehat{\mathbf{x}}\right)$, then we get ${\displaystyle \sum _{i\notin \Gamma \left(\widehat{\mathbf{x}}\right)}}⟨{\mathbf{d}}_i,{\mathbf{u}}_i⟩=0$, and thus

$$\begin{array}{c}\hfill ⟨\mathbf{d},\mathbf{u}⟩=\sum _{i\in \Gamma \left(\widehat{\mathbf{x}}\right)}⟨{\mathbf{d}}_i,{\mathbf{u}}_i⟩\le 0.\end{array}$$

which means ${\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)$ due to the arbitrariness of ${\mathbf{d}}_i\in {\mathbb{R}}^{n_i}$. Therefore, $N_S^C\left(\widehat{\mathbf{x}}\right)=\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left(\widehat{\mathbf{x}}\right)\}$. □

Obviously, the following relationship holds for Boligand tangent cone, Clarke normal cone and the corresponding normal cones of the group sparse set S at any point $\widehat{\mathbf{x}}\in S$:

$$T_S^C\left(\widehat{\mathbf{x}}\right)\subseteq T_S^B\left(\widehat{\mathbf{x}}\right),N_S^B\left(\widehat{\mathbf{x}}\right)\subseteq N_S^C\left(\widehat{\mathbf{x}}\right).$$

Remark 1.

In [14], the authors gave the expressions of tangent cone and normal cone to the sparse set $\{\mathbf{x}\in {\mathbb{R}}^n:\parallel \mathbf{x}{\parallel }_0\le k\}$. Theorems 1 and 2 in this paper are the extension of their results.

In the end of this section, we give an example of the tangent cones of S in ${\mathbb{R}}^3$.

Example 2.

Consider the group sparse set

$$S=\{\mathbf{x}={(x_1,(x_2,x_3))}^{\top }\in {\mathbb{R}}^3:\parallel \mathbf{x}{\parallel }_{2,0}\le 1\},$$

where $x_1$ is the first group, and ${(x_2,x_3)}^{\top }$ is the second group. Consider its Bouligand tangent cone and Clarke tangent cone at three points: ${\mathbf{x}}^1={(0,(1,1))}^{\top },{\mathbf{x}}^2={(0,(1,0))}^{\top }$ and ${\mathbf{x}}^3={(1,(0,0))}^{\top }$. It is easy to get the following statements: $\Gamma \left({\mathbf{x}}^1\right)=\left\{2\right\}$, $\Gamma \left({\mathbf{x}}^2\right)=\left\{2\right\}$, $\Gamma \left({\mathbf{x}}^3\right)=\left\{1\right\}$; $\Theta \left({\mathbf{x}}^1\right)=\left\{2\right\}$, $\Theta \left({\mathbf{x}}^2\right)=\left\{2\right\}$, $\Theta \left({\mathbf{x}}^3\right)=\left\{1\right\}$;

$T_S^B\left({\mathbf{x}}^1\right)=\{\mathbf{x}\in {\mathbb{R}}^3:{\mathbf{x}}_1=0\}={\mathbb{R}}_{x_2{x}_3}^2$; $T_S^C\left({\mathbf{x}}^1\right)=\{\mathbf{x}\in {\mathbb{R}}^3:{\mathbf{x}}_1=0\}={\mathbb{R}}_{x_2{x}_3}^2$;

$T_S^B\left({\mathbf{x}}^2\right)=\{\mathbf{x}\in {\mathbb{R}}^3:{\mathbf{x}}_1=0\}={\mathbb{R}}_{x_2{x}_3}^2$; $T_S^C\left({\mathbf{x}}^2\right)=\{\mathbf{x}\in {\mathbb{R}}^3:{\mathbf{x}}_1=0\}={\mathbb{R}}_{x_2{x}_3}^2$;

$T_S^B\left({\mathbf{x}}^3\right)=\{\mathbf{x}\in {\mathbb{R}}^3:x_2=x_3=0\}={\mathbb{R}}_{x_1}$; $T_S^C\left({\mathbf{x}}^3\right)=\{\mathbf{x}\in {\mathbb{R}}^3:x_2=x_3=0\}={\mathbb{R}}_{x_1}$.

Therefore, $T_S^B\left({\mathbf{x}}^1\right)=T_S^C\left({\mathbf{x}}^1\right)=T_S^B\left({\mathbf{x}}^2\right)=T_S^C\left({\mathbf{x}}^2\right)={\mathbb{R}}_{x_2{x}_3}^2$, $T_S^B\left({\mathbf{x}}^3\right)=T_S^C\left({\mathbf{x}}^3\right)={\mathbb{R}}_{x_1}$.

Figure 1 provides the figures of the above Bouligand tangent cones and Clarke tangent cones.

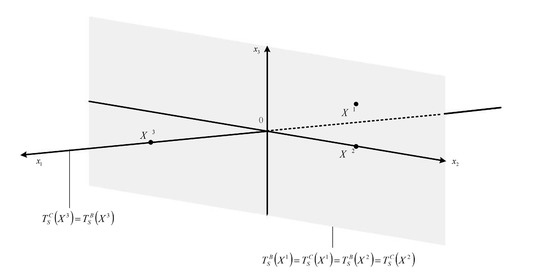
Figure 1. Bouligand tangent cones and Clarke tangent cones of S in ${\mathbb{R}}^3$, where $S=\{\mathbf{x}\in {\mathbb{R}}^3:\parallel \mathbf{x}{\parallel }_{2,0}\le 1\}$, ${\mathbf{x}}^1=(0,1,1),{\mathbf{x}}^2=(0,1,0)$ and ${\mathbf{x}}^3=(1,0,0)$.

From example 3.1, we can see that the key of group sparsity is to survey whether each group as a whole is zero instead of checking whether each entry is zero.

4. First-Order Optimality Conditions for Problem (1)

The optimality conditions for optimization problems are usually closely related to their stationary points. In this section, we use Bouligand tangent cones, Clarke tangent cones and their corresponding normal cones to specifically describe the N-stationary points and T-stationary points of Problem (1), then based on the descriptions, we investigate the relationship among the stationary points and the relationship between stationary points and local minimizers.

Definition 2.

${\mathbf{x}}^{*}\in S$ is called an $N^{♯}$-stationary point or $T^{♯}$-stationary point of Problem (1) if it meets the following conditions respectively:

(i) 

$N^{♯}$-stationary point: $\mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^{♯}\left({\mathbf{x}}^{*}\right);$

(ii) 

$T^{♯}$-stationary point: $0=\parallel {\nabla }_S^{♯}f\left({\mathbf{x}}^{*}\right)\parallel ;$

where $♯\in \{B,C\}$ stands for the sense of Bouligand or Clarke, and

$${\nabla }_S^{♯}f\left({\mathbf{x}}^{*}\right)=argmin\left\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\mathbf{d}\in T_S^{♯}\left({\mathbf{x}}^{*}\right)\right\}$$

is the projection gradient on Bouligand tangent cone or Clarke tangent cone.

Next, we will study the link between $N^B$-stationary point and $T^B$-stationary point of Problem (1).

Theorem 3.

Suppose ${\mathbf{x}}^{*}\in S$, then the following statements hold for Problem (1):

(i) 

If $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$, then ${\mathbf{x}}^{*}$ is an $N^B$-stationary point ⇔${\mathbf{x}}^{*}$ is a $T^B$-stationary point;

(ii) 

If $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, then ${\mathbf{x}}^{*}$ is an $N^B$-stationary point ⇔$\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}\iff$ ${\mathbf{x}}^{*}$ is a $T^B$-stationary point.

Proof. 

(i) Let $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$.

On one hand, suppose ${\mathbf{x}}^{*}\in S$ is an $N^B$-stationary point of Problem (1), then

$$\begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right),\end{array}$$

that is, $-\nabla f\left({\mathbf{x}}^{*}\right)\in N_S^B\left({\mathbf{x}}^{*}\right)$. By Theorem 2, $N_S^B\left({\mathbf{x}}^{*}\right)=\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left({\mathbf{x}}^{*}\right)\}$, then we have

$$\begin{array}{c}\hfill -\nabla f\left({\mathbf{x}}^{*}\right)\in \{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left({\mathbf{x}}^{*}\right)\},\end{array}$$

i.e.,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

It is easy to check that the converse is also true. That is, when $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$, it holds that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right)\iff {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

(7)

On the other hand, suppose ${\mathbf{x}}^{*}\in S$ is a $T^B$-stationary point of Problem (1), then

$$\begin{array}{c}\hfill 0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel .\end{array}$$

By Theorem 1, $T_S^B\left({\mathbf{x}}^{*}\right)=\{\mathbf{d}\in {\mathbb{R}}^n{:\parallel \mathbf{d}\parallel }_{2,0}\le k,\parallel {\mathbf{x}}^{*}+\gamma \mathbf{d}{\parallel }_{2,0}\le k,\forall \gamma \in \mathbb{R}\}$. Hence, in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$, we have

$$\begin{array}{c}\hfill \mathbf{d}\in T_S^B\left({\mathbf{x}}^{*}\right)\iff \Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left({\mathbf{x}}^{*}\right).\end{array}$$

Accordingly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)& =argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\mathbf{d}\in T_S^B\left({\mathbf{x}}^{*}\right)\}\hfill \\ & =argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\Gamma \left(\mathbf{d}\right)\subseteq \Gamma \left({\mathbf{x}}^{*}\right)\}.\hfill \end{array}\end{array}$$

For $i\notin \Gamma \left({\mathbf{x}}^{*}\right)$, ${\mathbf{d}}_i=\mathbf{0}$, then $\mathbf{0}={\left({\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\right)}_i$; For $i\in \Gamma \left({\mathbf{x}}^{*}\right)$, obviously, ${\left({\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\right)}_i=-{(\nabla f\left({\mathbf{x}}^{*}\right))}_i$. Hence we get

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\left({\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\right)}_i=\left\{\begin{array}{cc}\mathbf{0},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ -{(\nabla f\left({\mathbf{x}}^{*}\right))}_i,\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \end{array}\right.\end{array}\end{array}$$

According to $0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel$, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

It is easy to check that the converse is also true. That is, in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$, the following equivalence holds

$$\begin{array}{c}\hfill \begin{array}{c}\hfill 0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel \iff {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

(8)

Combining (7) with (8), we can conclude that, when $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$, ${\mathbf{x}}^{*}$ is an $N^B$-stationary point of Problem (1) if and only if it is a $T^B$-stationary point of Problem (1).

(ii) In the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, we first prove the equivalent relationship between $N^B$-stationary point of Problem (1) and $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$.

On one hand, suppose ${\mathbf{x}}^{*}\in S$ is an $N^B$-stationary point of Problem (1), then

$$\begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right),\end{array}$$

that is, $-\nabla f\left({\mathbf{x}}^{*}\right)\in N_S^B\left({\mathbf{x}}^{*}\right)$. It follows from $N_S^B\left({\mathbf{x}}^{*}\right)=\left\{\mathbf{0}\right\}$ that $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$. Hence the following implication holds

$$\begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right)\Rightarrow \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}.\end{array}$$

(9)

On the other hand, suppose $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$. In the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, by theorem 1, $N_S^B\left({\mathbf{x}}^{*}\right)=\mathbf{0}$. Therefore

$$\begin{array}{c}\hfill -\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}\in N_S^B\left({\mathbf{x}}^{*}\right),\end{array}$$

i.e., $\mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right)$. Hence the following implication holds

$$\begin{array}{c}\hfill \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}\Rightarrow \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right).\end{array}$$

(10)

From (9) and (10), we get the following equivalent relationship

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^B\left({\mathbf{x}}^{*}\right)\iff \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0},\end{array}\end{array}$$

(11)

that is, in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, ${\mathbf{x}}^{*}$ is an $N^B$-stationary point if and only if $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$.

In the following part, we prove the equivalent relationship between $T^B$-stationary point of Problem (1) and $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$ in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$.

Suppose ${\mathbf{x}}^{*}\in S$ satisfies $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$, then by Theorem 1,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)& =argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\mathbf{d}\in T_S^B\left({\mathbf{x}}^{*}\right)\}\hfill \\ & =argmin\{\parallel \mathbf{d}\parallel :\parallel \mathbf{d}{\parallel }_{2,0}\le k,\parallel {\mathbf{x}}^{*}+\gamma \mathbf{d}{\parallel }_{2,0}\le k,\forall \gamma \in \mathbb{R}\}\hfill \\ & =\mathbf{0}.\hfill \end{array}\end{array}$$

That is,

$$\begin{array}{c}\hfill \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}\Rightarrow 0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel .\end{array}$$

(12)

Conversely, suppose ${\mathbf{x}}^{*}$ is a $T^B$-stationary point of Problem (1), i.e.,

$$\begin{array}{c}\hfill 0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel ,\end{array}$$

then by Theorem 1,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbf{0}={\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)& =argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\mathbf{d}\in T_S^B\left({\mathbf{x}}^{*}\right)\}\hfill \\ & =argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\parallel \mathbf{d}{\parallel }_{2,0}\le k,\parallel {\mathbf{x}}^{*}+\gamma \mathbf{d}{\parallel }_{2,0}\le k,\forall \gamma \in \mathbb{R}\}.\hfill \end{array}\end{array}$$

Hence we get that $\parallel \nabla f\left({\mathbf{x}}^{*}\right)\parallel =\parallel \mathbf{0}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel \le \parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel$ for any $\mathbf{d}\in {\mathbb{R}}^n$ satisfying ${\parallel \mathbf{d}\parallel }_{2,0}\le k$, $\parallel {\mathbf{x}}^{*}{+\gamma \mathbf{d}\parallel }_{2,0}\le k$, $\forall \gamma \in \mathbb{R}$.

For any $i_0\in \{1,2,\cdots ,m\}$, take $\widehat{\mathbf{d}}\in {\mathbb{R}}^n$ such that $\Gamma \left(\widehat{\mathbf{d}}\right)=\left\{i_0\right\}$ and ${\widehat{\mathbf{d}}}_{i_0}=-{(\nabla f\left({\mathbf{x}}^{*}\right))}_{i_0}$. Following from $|\Gamma \left({\mathbf{x}}^{*}\right)|=\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \parallel {\mathbf{x}}^{*}+\gamma \widehat{\mathbf{d}}{\parallel }_{2,0}=|\Gamma \left({\mathbf{x}}^{*}\right)\cup \left\{i_0\right\}|\le |\Gamma \left({\mathbf{x}}^{*}\right)|+1\le k.\end{array}\end{array}$$

From $\parallel \nabla f\left({\mathbf{x}}^{*}\right)\parallel \le \parallel \widehat{\mathbf{d}}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel$, we obtain $\parallel {(\nabla f\left({\mathbf{x}}^{*}\right))}_{i_0}\parallel \le \parallel -{(\nabla f\left({\mathbf{x}}^{*}\right))}_{i_0}+{(\nabla f\left({\mathbf{x}}^{*}\right))}_{i_0}\parallel$, and then

$$\begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_{i_0}=\mathbf{0}.\end{array}$$

According to the arbitrariness of $i_0$, we get $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$. That is,

$$\begin{array}{c}\hfill \mathbf{0}=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel \Rightarrow \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0},\end{array}$$

(13)

Combining (12) with (13), in the case of $\parallel {\mathbf{x}}^{*}\parallel <k$, the following equivalent relationship holds

$$\begin{array}{c}\hfill 0=\parallel {\nabla }_S^{B}f\left({\mathbf{x}}^{*}\right)\parallel \iff \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}.\end{array}$$

The proof is thus finished. □

Furthermore, for Problem (1), its $N^C$-stationary point and $T^C$-stationary point have the following equivalent relationship.

Theorem 4.

For Problem (1), let ${\mathbf{x}}^{*}\in S$, then ${\mathbf{x}}^{*}$ is an $N^C$-stationary point if and only if it is a $T^C$-stationary point.

Proof. 

On one hand, by Theorem 2, $N_S^C\left({\mathbf{x}}^{*}\right)=\{\mathbf{u}\in {\mathbb{R}}^n:{\mathbf{u}}_i=\mathbf{0},i\in \Gamma \left({\mathbf{x}}^{*}\right)\}$. Then we have the following equivalences:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{x}}^{*}\mathrm{is} \mathrm{an}{N}^C‑\mathrm{stationary} \mathrm{point} \mathrm{of} \mathrm{Problem}\left(1\right)\hfill \\ \iff \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^C\left({\mathbf{x}}^{*}\right)\hfill \\ \iff -\nabla f\left({\mathbf{x}}^{*}\right)\in N_S^C\left({\mathbf{x}}^{*}\right)\hfill \\ \iff {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(14)

On the other hand, by Theorem 2, $T_S^C\left({\mathbf{x}}^{*}\right)=\{\mathbf{d}\in {\mathbb{R}}^n:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\}$. Then according to the definition of ${\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)$, we have that

$$\begin{array}{ccc}\hfill {\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)& =& argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)\}\hfill \\ & =& argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right)\parallel :{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\}\hfill \\ & =& argmin\{\parallel \mathbf{d}+\nabla f\left({\mathbf{x}}^{*}\right){\parallel }^2:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\}\hfill \\ & =& argmin\left\{\left(\sum _{i\in \Gamma \left({\mathbf{x}}^{*}\right)}+\sum _{i\notin \Gamma \left({\mathbf{x}}^{*}\right)}\right){\parallel {\mathbf{d}}_i+{(\nabla f\left({\mathbf{x}}^{*}\right))}_i\parallel }^2:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\right\}\hfill \\ & =& argmin\left\{\sum _{i\in \Gamma \left({\mathbf{x}}^{*}\right)}\parallel {\mathbf{d}}_i+{(\nabla f\left({\mathbf{x}}^{*}\right))}_i{\parallel }^2+\sum _{i\notin \Gamma \left({\mathbf{x}}^{*}\right)}{\parallel {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\parallel }^2:{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\right\}\hfill \\ & =& argmin\left\{\sum _{i\in \Gamma \left({\mathbf{x}}^{*}\right)}{\parallel {\mathbf{d}}_i+{(\nabla f\left({\mathbf{x}}^{*}\right))}_i\parallel }^2:{\mathbf{d}}_i\in {\mathbb{R}}^{n_i},i\in \Gamma \left({\mathbf{x}}^{*}\right);{\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right)\right\}.\hfill \end{array}$$

Thus by directly computing, ${\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)$ satisfies

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\left({\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)\right)}_i=\left\{\begin{array}{cc}-{(\nabla f\left({\mathbf{x}}^{*}\right))}_i,\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \mathbf{0},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

Therefore, the following equivalent relationships hold:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{x}}^{*}\mathrm{is} T^C‑\mathrm{stationary} \mathrm{point} \mathrm{of} \mathrm{Problem} \left(1\right)\hfill \\ \iff \mathbf{0}={\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)\hfill \\ \iff -{(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(15)

Combine (14) and (15), then we get the following equivalent relationships:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{0}\in \nabla f\left({\mathbf{x}}^{*}\right)+N_S^C\left({\mathbf{x}}^{*}\right)\iff {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right),\hfill \end{array}\right.\iff \parallel {\nabla }_S^{C}f\left({\mathbf{x}}^{*}\right)\parallel =0.\end{array}\end{array}$$

The proof is thus complete. □

Next, we investigate the relationship among the four types of stationary points of Problem (1).

Theorem 5.

Let ${\mathbf{x}}^{*}\in S$, then the following statements hold for Problem (1):

(i) 

If ${\mathbf{x}}^{*}$ is an $N^B$-stationary point, then it must be an $N^C$-stationary point;

(ii) 

If ${\mathbf{x}}^{*}$ is a $T^B$-stationary point, then it must be a $T^C$-stationary point.

Proof. 

(i) Let ${\mathbf{x}}^{*}$ is an $N^B$-stationary point of Problem (1). There are two cases: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$ and $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$.

Case 1: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$. In this case, by (7), $x^{*}$ is an $N^B$-stationary point if and only if

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right),\hfill \end{array}\right.\end{array}\end{array}$$

which, by (14), is equivalent to that ${\mathbf{x}}^{*}$ is an $N^C$-stationary point of Problem (1). Thus we obtain that $N^B$-stationary point and $N^C$-stationary point are equivalent in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$.

Case 2: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$. By (11), in this case, ${\mathbf{x}}^{*}$ is an $N^B$-stationary point of Problem (1) if and only if

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}.\end{array}\end{array}$$

By (14), ${\mathbf{x}}^{*}$ is an $N^C$-stationary point of Problem (1) if and only if

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

Clearly, in the case of $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$, if ${\mathbf{x}}^{*}$ is an $N^B$-stationary point of Problem (1), it must be an $N^C$-stationary point (the converse is not true). That is,

$$\begin{array}{c}\hfill N^B-\mathrm{stationary}\mathrm{point}\Rightarrow {\mathrm{N}}^{\mathrm{C}}-\mathrm{stationary}\mathrm{point}.\end{array}$$

(16)

(ii) According to Theorems 3 and 4, the $N^B$-stationary point of Problem (1) is equivalent to its $T^B$-stationary point, and the $N^C$-stationary point of Problem (1) is equivalent to its $T^C$-stationary point, this is,

$$N^B-\mathrm{stationary}\mathrm{point}\iff T^B-\mathrm{stationary}\mathrm{point};$$

$$N^C-\mathrm{stationary}\mathrm{point}\iff T^C-\mathrm{stationary}\mathrm{point}.$$

Moreover, from (16),

$$N^B-\mathrm{stationary}\mathrm{point}\Rightarrow N^C-\mathrm{stationary}\mathrm{point}.$$

Therefore,

$$T^B-\mathrm{stationary}\mathrm{point}\Rightarrow T^C-\mathrm{stationary}\mathrm{point}.$$

The proof is finished. □

To have a clear presentation, based on the proofs of Theorems 3 and 4, we use Table 1 to display the characterizations of the four types of stationary points of Problem (1).

Table 1. The characterizations of $T^B$-, $N^B$-, $T^C$-, $N^C$- stationary point for Problem (1).

Stationary Point	$\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=\mathit{k}$	$\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<\mathit{k}$
$T^B$-stationary point	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$	$\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$
$N^B$-stationary point	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$	$\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$
$T^C$-stationary point	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$
$N^C$-stationary point	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$	${(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right)\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right)\hfill \end{array}\right.$

In the end of this section, we discuss the relationship between the local minimizers of Problem (1) and its stationary points.

Theorem 6.

Let ${\mathbf{x}}^{*}\in S$ be a local minimizer of Problem (1), then the following two statements hold:

(i) 

${\mathbf{x}}^{*}$ is an $N^B$-stationary point and hence an $N^C$-stationary point;

(ii) 

${\mathbf{x}}^{*}$ is a $T^B$-stationary point and hence a $T^C$-stationary point.

Proof. 

Since ${\mathbf{x}}^{*}$ is a local minimizer of Problem (1), for sufficiently small $\alpha >0$, it holds that

$$\begin{array}{c}\hfill f\left({\mathbf{x}}^{*}\right)\le f({\mathbf{x}}^{*}+\alpha e_{ij}),\forall i\in J\supseteq \Gamma \left(x^{*}\right),\left|J\right|=k;j=1,\cdots ,n_i,\end{array}$$

and then

$$\begin{array}{c}\hfill 0\in argmin\{h_{ij}\left(\alpha \right)\triangleq f({\mathbf{x}}^{*}+\alpha e_{ij}):\alpha \ge 0\},\forall i\in J\supseteq \Gamma \left(x^{*}\right),\left|J\right|=k;j=1,\cdots ,n_i.\end{array}$$

Due to ${\mathbf{x}}^{*}\in S$, there are two cases: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$ and $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$.

Case 1: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}<k$. In this case, ${\bigcup }_{J\supseteq \Gamma \left(x^{*}\right),\left|J\right|=k}J=\{1,\cdots ,m\}$, then

$$\begin{array}{c}\hfill 0\in argmin\{h_{ij}\left(\alpha \right)=f({\mathbf{x}}^{*}+\alpha e_{ij}):\alpha \ge 0\},\forall i=1,\cdots ,m;\forall j=1,\cdots ,n_i.\end{array}$$

By the optimality conditions for the above problems, we have

$$\begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_{ij}=h_{ij}^{\prime }\left(0\right)=0,\forall i=1,\cdots ,m;\forall j=1,\cdots ,n_i.\end{array}$$

That is, $\nabla f\left({\mathbf{x}}^{*}\right)=\mathbf{0}$.

Case 2: $\parallel {\mathbf{x}}^{*}{\parallel }_{2,0}=k$. In this case,

$$\begin{array}{c}\hfill 0\in argmin\{h_{ij}\left(\alpha \right)=f({\mathbf{x}}^{*}+\alpha e_{ij}):\alpha \ge 0\},\forall i\in \Gamma \left({\mathbf{x}}^{*}\right);\forall j=1,\cdots ,n_i.\end{array}$$

It can be derived that ${(\nabla f\left({\mathbf{x}}^{*}\right))}_{ij}=0$, $\forall i\in \Gamma \left({\mathbf{x}}^{*}\right),\forall j=1,\cdots ,n_i$. That is, ${(\nabla f\left({\mathbf{x}}^{*}\right))}_i=\mathbf{0}$, $\forall i\in \Gamma \left({\mathbf{x}}^{*}\right).$

Combining the above two cases with (7) and (11), we know that ${\mathbf{x}}^{*}$ is an $N^B$-stationary point of Problem (1). From Theorem 5, ${\mathbf{x}}^{*}$ is also an $N^C$-stationary point of Problem (1).

(ii) From (i), ${\mathbf{x}}^{*}$ is both $N^B$-stationary point and $N^C$-stationary point. According to Theorems 3 and 4, ${\mathbf{x}}^{*}$ is both $T^B$-stationary point and $T^C$-stationary point. The proof is complete. □

As a summary of this section, we conclude the relationship among local minimizers and the four stationary points of Problem (1) as follows:

$$\begin{array}{ccc}\hfill \mathrm{local} \mathrm{minimizer}\Rightarrow & N^B‑\mathrm{stationary} \mathrm{point}& \iff T^B‑\mathrm{stationary} \mathrm{point}\hfill \\ & \Downarrow & \Downarrow \hfill \\ & N^C‑\mathrm{stationary} \mathrm{point}& \iff T^C‑\mathrm{stationary} \mathrm{point}.\hfill \end{array}$$

5. Second-Order Optimality Conditions for Problem (1)

In this section, we provide some second-order necessary or sufficient optimality conditions for Problem (1) by use of Clarke tangent cone.

Theorem 7

(Second-order necessary condition). Let ${\mathbf{x}}^{*}\in S$ be a local minimizer of Problem (1), then for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$, it must hold that ${\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)=0$ and

$${\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}\ge 0,$$

where ${\nabla }^{2}f\left({\mathbf{x}}^{*}\right)$ is the Hessian matrix of f at ${\mathbf{x}}^{*}$.

Proof. 

Since ${\mathbf{x}}^{*}\in S$ is a local minimizer of Problem (1), by Theorem 6, ${\mathbf{x}}^{*}$ is also an $N^C$-stationary point. By (14),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

According to (5), for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$,

$$\begin{array}{c}\hfill {\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right).\end{array}$$

Thus, for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$, it holds

$$\begin{array}{c}\hfill {\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)=0.\end{array}$$

(17)

In addition, since ${\mathbf{x}}^{*}$ is a local minimizer of Problem (1), for sufficiently small $\alpha >0$ and any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f\left({\mathbf{x}}^{*}\right)\le f({\mathbf{x}}^{*}+\alpha \mathbf{d}).\end{array}\end{array}$$

(18)

By Taylor’s Theorem,

$$\begin{array}{c}\hfill f({\mathbf{x}}^{*}+\alpha \mathbf{d})=f\left({\mathbf{x}}^{*}\right)+\alpha {\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right).\end{array}$$

(19)

Combine (17)–(19), then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f\left({\mathbf{x}}^{*}\right)\le & f\left({\mathbf{x}}^{*}\right)+\alpha {\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right)\hfill \\ \hfill =& f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right).\hfill \end{array}\end{array}$$

Hence,

$$\begin{array}{c}\hfill 0\le \frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right),\end{array}$$

which implies ${\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}\ge 0$, $\forall \mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$. The desired result is derived. □

Finally, we give a second-order sufficient condition for the optimality of Problem (1).

Theorem 8

(Second-order sufficient condition). Let ${\mathbf{x}}^{*}\in S$ be an $N^C$-stationary point of Problem (1), if for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\}$, it holds ${\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}>0$, then the following two statements hold:

(i) 

${\mathbf{x}}^{*}\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n$ is a strictly local minimizer of Problem (1);

(ii) 

${\mathbf{x}}^{*}$ satisfies the second-order growth condition, that is, there are $\omega >0$ and $\delta >0$ such that for any $\mathbf{x}\in B({\mathbf{x}}^{*},\delta )\bigcap {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n$,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f\left(\mathbf{x}\right)\ge f\left({\mathbf{x}}^{*}\right)+\omega {\parallel \mathbf{x}-{\mathbf{x}}^{*}\parallel }^2.\end{array}\end{array}$$

where ${\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n=\mathrm{span}\{e_{ij},i\in \Gamma \left({\mathbf{x}}^{*}\right),j=1,\cdots ,n_i\}$.

Proof. 

(i) Since ${\mathbf{x}}^{*}$ is an $N^C$-stationary point of Problem (1), from Theorem 2, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {(\nabla f\left({\mathbf{x}}^{*}\right))}_i\left\{\begin{array}{cc}=\mathbf{0},\hfill & i\in \Gamma \left({\mathbf{x}}^{*}\right),\hfill \\ \in {\mathbb{R}}^{n_i},\hfill & i\notin \Gamma \left({\mathbf{x}}^{*}\right).\hfill \end{array}\right.\end{array}\end{array}$$

For any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)$, by (5),

$$\begin{array}{c}\hfill {\mathbf{d}}_i=\mathbf{0},i\notin \Gamma \left({\mathbf{x}}^{*}\right).\end{array}$$

Then for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\}$, it holds

$$\begin{array}{c}\hfill {\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)=0.\end{array}$$

By Taylor’s Theorem, for any sufficiently small $\alpha >0$,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f({\mathbf{x}}^{*}+\alpha \mathbf{d})=& f\left({\mathbf{x}}^{*}\right)+\alpha {\mathbf{d}}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right)\hfill \\ \hfill =& f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right).\hfill \end{array}\end{array}$$

Since ${\mathbf{d}}^T{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}>0,\forall \mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\}$, then for any sufficiently small $\alpha >0$,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f({\mathbf{x}}^{*}+\alpha \mathbf{d})=f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{\alpha }^2{\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}+o\left({\alpha }^2\right)>f\left({\mathbf{x}}^{*}\right).\end{array}\end{array}$$

Therefore, ${\mathbf{x}}^{*}$ is a strictly local minimizer of Problem (1).

(ii) Assume, on the contrary, that the second-order growth condition does not hold at ${\mathbf{x}}^{*}$, then there is a sequence ${\left\{{\mathbf{x}}^t\right\}}_{t\in \mathbb{N}}\subset {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n$ such that ${\left\{{\mathbf{x}}^t\right\}}_{t\in \mathbb{N}}\to {\mathbf{x}}^{*}$ but

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f\left({\mathbf{x}}^t\right)<f\left({\mathbf{x}}^{*}\right)+\frac{1}{t}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }^2.\end{array}\end{array}$$

Let ${\mathbf{z}}^t=\frac{{\mathbf{x}}^t-{\mathbf{x}}^{*}}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }$, then $\parallel {\mathbf{z}}^t\parallel =1$. Since ${\{\frac{{\mathbf{x}}^t-{\mathbf{x}}^{*}}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }\}}_{t\in \mathbb{N}}$ is bounded, without loss of generality, suppose ${\mathbf{z}}^t\to \mathbf{z}$, then $\parallel \mathbf{z}\parallel =1$.

It follows ${\mathbf{x}}^t\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n$ that $\Gamma \left({\mathbf{x}}^t\right)\subseteq \Gamma \left({\mathbf{x}}^{*}\right)$. Due to $\underset{t\to \infty }{lim}{\mathbf{x}}^t={\mathbf{x}}^{*}$, we have $\Gamma \left({\mathbf{x}}^{*}\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)$, then

$$\Gamma \left({\mathbf{x}}^t\right)=\Gamma \left({\mathbf{x}}^{*}\right)$$

for any sufficiently large t. From ${\mathbf{z}}^t=\frac{{\mathbf{x}}^t-{\mathbf{x}}^{*}}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }$, we get

$$\Gamma \left({\mathbf{z}}^t\right)\subseteq \Gamma \left({\mathbf{x}}^t\right)=\Gamma \left({\mathbf{x}}^{*}\right)\mathrm{and}{\mathbf{z}}^t\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n\backslash \left\{\mathbf{0}\right\}.$$

Moreover, from $\underset{t\to \infty }{lim}{\mathbf{z}}^t=\mathbf{z}$, it follows

$$\Gamma \left(\mathbf{z}\right)\subseteq \Gamma \left({\mathbf{z}}^t\right)\subseteq \Gamma \left({\mathbf{x}}^{*}\right)\mathrm{and}\mathbf{z}\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n\backslash \left\{\mathbf{0}\right\}$$

for any sufficiently large t. According to (6), it holds

$$\begin{array}{c}\hfill {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n=\mathrm{span}\{e_{ij},i\in \Gamma \left({\mathbf{x}}^{*}\right),j=1,\cdots ,n_i\}=T_S^C\left({\mathbf{x}}^{*}\right).\end{array}$$

Hence, for any ${\mathbf{z}}^t\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n\backslash \left\{\mathbf{0}\right\}$, we have ${\mathbf{z}}^t\in T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\}$, which together with (5) yields

$$\begin{array}{c}\hfill {\left({\mathbf{z}}^t\right)}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)=0.\end{array}$$

By Taylor’s Theorem,

$$\begin{array}{c}\hfill f\left({\mathbf{x}}^t\right)-f\left({\mathbf{x}}^{*}\right)={({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)({\mathbf{x}}^t-{\mathbf{x}}^{*})+o(\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2).\end{array}$$

Since $\frac{{({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }\nabla f\left({\mathbf{x}}^{*}\right)={\left({\mathbf{z}}^t\right)}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)=0$, we have

$$\begin{array}{ccc}\hfill \frac{f\left({\mathbf{x}}^t\right)-f\left({\mathbf{x}}^{*}\right)}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2}& =& \frac{1}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2}({({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }\nabla f\left({\mathbf{x}}^{*}\right)+\frac{1}{2}{({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)({\mathbf{x}}^t-{\mathbf{x}}^{*})\hfill \\ & & +o(\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2))\hfill \\ & =& \frac{\frac{1}{2}{({\mathbf{x}}^t-{\mathbf{x}}^{*})}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)({\mathbf{x}}^t-{\mathbf{x}}^{*})}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2}+o\left(1\right)\hfill \\ & =& \frac{1}{2}{\left({\mathbf{z}}^t\right)}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right){\mathbf{z}}^t+o\left(1\right).\hfill \end{array}$$

Under the assumption that $f\left({\mathbf{x}}^t\right)<f\left({\mathbf{x}}^{*}\right)+\frac{1}{t}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}\parallel }^2$, we obtain

$$\begin{array}{c}\hfill \frac{1}{t}>\frac{f\left({\mathbf{x}}^t\right)-f\left({\mathbf{x}}^{*}\right)}{\parallel {\mathbf{x}}^t-{\mathbf{x}}^{*}{\parallel }^2}=\frac{1}{2}{\left({\mathbf{z}}^t\right)}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right){\mathbf{z}}^t+o\left(1\right).\end{array}$$

Letting $t\to \infty$, we get

$${\mathbf{z}}^T{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{z}\le 0,\mathrm{where}\mathbf{z}\in {\mathbb{R}}_{\Gamma \left({\mathbf{x}}^{*}\right)}^n\backslash \left\{\mathbf{0}\right\}=T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\},$$

which contradicts the condition that ${\mathbf{d}}^{\top }{\nabla }^{2}f\left({\mathbf{x}}^{*}\right)\mathbf{d}>0$ holds for any $\mathbf{d}\in T_S^C\left({\mathbf{x}}^{*}\right)\backslash \left\{\mathbf{0}\right\}$. Therefore, the second-order growth condition must hold at ${\mathbf{x}}^{*}$. □

6. Concluding Remarks

In this paper, the first-order optimality conditions are built for group sparsity constrained optimization problems by use of Bouligand tangent cone, Clarke tangent and their corresponding normal cones, and the relationship among the local minimizers and the four types of stationary points of Problem (1) is investigated. Furthermore, the second-order sufficient and second-order necessary optimality conditions for group sparsity constrained optimization problems are provided. The results show that $N^C$-stationary points of Problem (1) may be strictly local minimizers, and even can fulfill the second-order growth condition under some mild conditions. The results provide the theoretical basis for analyzing or solving the group sparsity constrained optimization problems. In the future, we will use the optimality conditions to design algorithms for solving the problems.