Abstract
Difficulties in the curricular units (CU) of the mathematical science area, particularly those related to differential and integral calculus (DIC), are often found among students of engineering degrees, leading to high failure rates. A research work was developed with the objective of finding the reasons that lead the students to fail in the CU of DIC (CU-DIC) taught in the 1st year of the engineering undergraduate degrees at the Coimbra Engineering Institute (ISEC), in Portugal. Applying a case study methodology, this article will present a current diagnosis with the objective to establish relationships between teaching methods and students’ learning strategies, and besides, we propose to build learning environments that lead to higher success. The analysis of collected data allows us to conclude that the CU-DIC in the ISEC maintain an identical distribution in the hourly load in several engineering degrees, where contents are adjusted to each context taking into account the CUs of each degree. The data analysis found better results in the academic year that includes two examination moments without any relationship between class attendance, dropout and pass rates. We propose some different teaching/learning strategies in CU-DIC and new learning environments that enhance freshmen students’ engagement and participation in their own learning process.
1. Introduction
Curricular units of differential and integral calculus are the best way to acquire the theoretical basis necessary for engineering students’ professional futures, and for this, they are present in most of the undergraduate degrees taught in several higher education institutions (HEI).
However, despite its obvious importance, it has been noticed over the years that this basic science is the cause of high failure rates in engineering undergraduate degrees, resulting in several problems, such as absenteeism and, consequently, dropping out of university studies.
The failure and dropout rates in CU-DIC have evidenced the need to question what methodologies and teaching approaches are applied, which learning environments are developed that best allow students to be co-responsible in their educational process, and which assessment practices are related to their school success and lead to significant learning [1,2,3].
These issues related to mathematics failure in teaching engineering students have frequently appeared in national and international discussions being addressed in several published works, which have received well deserved mention by the international specialized literature. In 1991, American Mathematical Monthly presented data showed that 45% of students enrolled in a course of engineering calculus obtained a level equal or higher than C (marks goes from A to E, with A being the best one and E the worst one).
David Tall, for example, has been a lead researcher in the field of advanced mathematical thinking, whose questions revolve around the difficulties encountered in learning basic concepts of calculus, with cognitive psychology as a background for their epistemological analysis [4,5].
Another international example of this concern was the movement to reform the teaching of calculus, which began in the 1980s and was known as the “calculus reform”. This movement had as a starting point a controversial document of the mathematician Peter Lax, who attacked the courses of calculus at the time. According to its precursors, the “calculus reform” had as basic characteristics the use of technology, that is, computational software and graphing calculators, both for the learning of concepts and theorems and for problem solving [6,7,8,9,10,11,12].
There has also been a growing debate about the relationship between skills development emerging from upper secondary education and failure in the teaching of mathematics in engineering [13]. Recently, with the general objective of highlighting the changes produced in the teaching of engineering in European studies, within the scope of the RULES_MATH project, some examples were presented from the University of Salamanca (Spain) and the University of Gazi (Turkey). In this study, technological tools were used for teaching and learning calculus, from training in calculation strategies to reasoning processes in the application of contents in engineering situations [14].
Also, the acquisition of basic and elementary knowledge, essential to the full integration of students in DIC, has been one of the main reasons for failure in higher education. This discussion has led to the definition of multiple strategies that aim to overcome the difficulties detected and a consequent analysis of the impact of the implementation of these measures [15,16,17,18,19,20,21,22,23].
An analysis of student’s mistakes in examination tests also allowed to identify and to categorize different difficulties that appeared in the learning of basic contents strategies where established to overcome these mistakes later on [24,25,26].
Abdulwahed et al. summarized the innovative methods used in response to the necessary reform of mathematics education [27]. The trends observed in the proposed changes in learning and teaching, many of which are rooted in constructivist ideology, were categorized into six groups:
- The use of learner-centred methods.
- Contextualization of mathematics using real-world examples.
- Development of strategies to overcome gaps in basic and elementary knowledge.
- Applying face-to face classes and student conversation.
- Improvement of students’ motivation, involvement and self-efficiency.
- Different learning styles approaches.
Ni Fhloinn & Carr presented a diversity of formative assessment types for mathematical engineering, including classroom exercises, homework, mock exam questions, desk quizzes, presentations, critical analysis of statistical articles, peer-to-peer teaching, and on-line assessments and electronic voting systems [28]. They provided practical tips for implementing such assessments, with a particular focus on time or resource constraints in case of large classes, as well as effective feedback methods. They also considered the benefits of such formative assessments for students and staff.
Technology is evidenced as a facilitator in the innovative approaches applied in mathematics teaching, not only in software packages use for mathematical analysis of specific domain but also in the general use of learning technologies and online tools [29,30,31,32].
Computers can contribute to the learning process. Its use may influence curriculum, teaching, assessment, motivation, socialization, etc. [33,34,35,36,37,38,39,40].
There are no perfect solutions, but the identification of constraints to the implementation of new approaches in teaching mathematics will allow the necessary adaptation to the contexts and will consequently lead to eventual behavioural changes of the educational agents.
For this study, we considered that, in general, in the mathematical community, there are several options to construct a curriculum [41]. Cardella proposed the use of mathematical thinking identified by Schoenfeld, extending the horizon to be reached by the teaching of mathematics in engineering degrees. Schoenfeld argued that in addition to learning contents, there are strategies for problem solving; metacognitive processes in the use of mathematical resources, goals and practices that together make up mathematical thinking [42,43,44]. Since understanding a concept does not happen in the same way for different individuals, genetic decomposition serves as support in the elaboration of teaching instructions that consider the possible cognitive paths that students use in the process of acquiring a concept. Similarly, Asiala et al. presented in broad sense the meaning of “learn and know something in mathematics”:
“An individual’s mathematical knowledge is her or his tendency to respond to perceived mathematical problem situations by reflecting on problems and their solutions in a social context and by constructing or reconstructing mathematical actions, processes, and objects by organizing these in schemas to use in dealing with situations”.[45] (p. 5)
In 2004, the Committee on the Undergraduate Program in Mathematics (CUPM) of the American Mathematical Association wrote a curriculum guide containing recommendations that followed the same strategic line [46]. This report was based on workshops where professors from a broad range of partners’ disciplines presented their understanding of the necessary qualifications for success in mathematics curricular units.
Finally, the Danish KOM project led by Niss organized a detailed and systematic description of what is achieved with mathematics teaching using the concept of competence that influenced the description of learning objectives reflected in the OECD-PISA studies [47]:
“Mathematical competence means the ability to understand, judge, make and use mathematics in a variety of intra and extra mathematical contexts in situations in which mathematics plays or can play a role. Necessary, but certainly not sufficient, prerequisites for mathematical competence are lots of factual knowledge and technical skills in the same way as vocabulary, orthography, and grammar are necessary but not sufficient prerequisites for literacy”.[48] (pp. 6–7)
The KOM project has identified eight mathematical competencies which, while overlapping in some respects, emphasize others. These competencies are:
- Thinking mathematically (C1), reasoning mathematically (C2), posing and solving mathematical problems (C3), and modelling mathematically (C4), which make up the ability to ask and answer questions in and with mathematics.
- Representing mathematical entities (C5), handling mathematical symbols and formalism (C6), communicating in, with, and about mathematics (C7), and making use of aids and tools (C8) are concerned with “the ability to deal with and manage mathematical language and tools” [48].
It is clearly accepted that these eight competencies cannot be acquired just by attending classes, so appropriate forms of student involvement and co-responsibility must be implemented.
There is a lot of research that tries to explain the failure in the UC-DIC but there is some lack of scientific production that proposes an integrated and sustained intervention. It will be important to articulate, to describe and to analyze a practice of teaching and assessment, implemented in classroom context, which can be relate to the learning and the academic success of the students [49].
2. Portuguese Context in the Access to Engineering Studies
In Portugal, compulsory education is until the age of 18 and consists of two levels: basic (nine years) and secondary (three years). The access to higher education is through the application to the national contest organized by the General Directorate for Higher Education (GDHE). This competition is held each year at the end of upper secondary education and is organized in three phases, according to a previously defined calendar. The National Commission for Access to Higher Education is responsible for defining rules for fixing admission tests for each academic year (specific tests are required for each undergraduate degree).
Although they may take other forms, entrance exams are currently implemented in final national examinations, which are held at two different times through of secondary compulsory education. The final mark obtained in these examinations will include the weighted average together with the final internal classification obtained by the students during the three years of secondary education. For each degree, candidates will get a score that will be serialized according to the existing candidates.
The definition of specific tests is made according to the requirements of each undergraduate degree in the conditions of admission and intends to prove the capacity of students to attend higher education.
The entrance exams that are required for each course are fixed by each institution, and cannot, in general, be more than two.
The policies for entering into higher education and the current relationship between training and demand intend to be a democratic process, with a clear deficit in demand in 2013. Since 2014 the offer tends to stabilize and there is an inversion of the situation (https://www.dges.gov.pt/estatisticasacesso/2018/).
Portuguese higher education includes university and polytechnic system. The difference between the conceptions regarding the two subsystems has marked the students’ choices in the access to higher education and generates some doubts to students.
The university education, traditionally related to knowing how to think and currently, largely due to Anglo-Saxon influence, linked to scientific research, is composed by 55% of students who access higher education. On the other hand, polytechnic education, traditionally linked to know-how and to knowledge applicability, is followed by the remaining 45%.
In the last five years, this proportion did not have significant variability. This asymmetry may be explained by the absence of real different offers, since both systems confer identical degrees (graduations and masters degrees), with doctorates (still) being reserved for universities. To increase the confusion of the candidates, the offer of the type of courses is often identical, and in most cases, there are no different pedagogies in both systems of education.
Democratization in the access to higher education also reveals asymmetries in the offer/demand of the various courses, noting that engineering areas have been deprecated in recent years. The number of engineering courses (HEE) corresponds to 20% of the offer of higher education (HE). This percentage is distributed by the university system (USE) with 56% of the undergraduate engineering degrees, and by polytechnic (PSE) with the remaining degrees (http://www.dges.gov.pt).
The available data on the GDHE website shows an increasing demand for engineering degrees with a percentage of vacancies filled, on average, by 90.11% in the USE and by 94.91% of the candidates in the PSE. Civil engineering degrees have the lowest demand and computer engineering the highest one.
The low offer/demand for engineering studies could be explained by the fact that in 2012, mathematics and physics were introduced as compulsory subjects in entrance exams to access to most engineering courses. Higher education teachers certified this measure as an essential one considering the requirement of theoretical bases in crucial areas of knowledge. However, the inability to generate the preference and vocation for those disciplines leads to disinterest in those areas. This abandonment necessarily implies the lack of preparation in mathematics and physics of the majority of students at the end of the secondary cycle, provoking, cumulatively, a lack of interest in engineering. This deficit in demand has forced HEIs to change the number of vacancies due to the positions obtained in previous years, implying the closure and/or creation of new degrees.
Coimbra Engineering Institute is an organic unit of the Polytechnic Institute of Coimbra that offers engineering undergraduate degrees, such as: industrial management (EGI), bioengineering (BioE), mechanics (EM), electromechanics (EEM), electrotechnology (normal-EE and post-work regime-EE (PL)), informatics (normal-EI, post-work regime-EI (PL) and European course-EI (CE)), biomedical (EBiom) and civil (EC). In the 2018/19 academic year, and in order to meet the weak demand for EC, ISEC created a new engineering degree in sustainable cities management (GSC) which was presented with a curricular plan focused on economic, environmental and social sustainability of learning methodologies that allow students to develop professional skills.
The available data, on the GDHE website, for occupation rates (occupied/vacancies) in the ISEC for the last four years (from 2015 to 2018), are summarized in Figure 1.
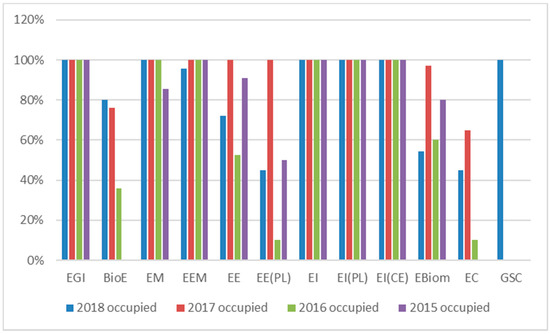
Figure 1.
Occupation rate distribution in ISEC, for the three phases of the competition.
The most sought-after degrees are EI and EM, filling all the vacancies during the 1st phase of the competition. In 2015 EC had not any candidate and only in 2017 obtained a placement rate of 65%, for 20 available positions. Regarding the general occupation rate, the ISEC reached for the years 2015, 2016, 2017, and 2018, respectively, the values 86%, 79%, 97%, and 88%. To adjust the offer to demand, there was a reduction in the number of vacancies in EBiom, EE and EEM, an increase in EM and the creation of new BioE and GSC degrees.
The distribution of offer/demand rate in ISEC is thus dependent on the number of students interested in engineering degrees whose variation can be explained by the results obtained in the examinations of the specific entrance exams: Mathematics A and Physics-Chemistry A (secondary school subjects considered essential for entry into engineering degrees). However, since this list of exams is not applied to engineering specialty, for example, EI does not require physics as a specific exam for access, it may be appropriate to make an analysis of the averages of the entrance grades in the exams of those two disciplines.
According to data from 2018, published by the National Jury of Examinations, about Mathematics A, 32,401 inmates (students who are enrolled in the regular system of education) reached an average of 10.9 (over 20). However, the 13,032 self-proposed ones (students who do not attend any educational institution and who underwent the tests) did not go beyond 6.1, a lower score than the previous year (6.8). It should be noticed that self-proposed students represent 28.68% of the total number of students who passed Mathematics A test, and the number of students who did this test decreased by 8% about 2017. Despite the improvements in grades, Mathematics A continues to be among the disciplines where there is more failure: 14% of the inmates do not pass (compared to 13% in 2017) and 78% of the self-proposed also had negative marks (compared to 72% in 2017). It should also be noticed that the average scores obtained by the internal students in the entrance exams fall drastically concerning the results obtained at the end of secondary education, from 14.0 to 10.9 (over 20 values).
Also, Mathematics A is among the disciplines with the highest number of tests carried out in the 1st phase, which present distribution of the means of the exam classifications with greater dispersion of the data and consequently with higher value of the coefficient of variation. It should be noted that in the second phase this test shows the same behaviour in terms of the characteristics of the respective distributions.
These values indicate that the distributions of the classifications in these disciplines have a significant number of extreme values, which have a great influence on the average values of the classifications. Thus, the study of these distributions should also consider other measures of central tendency, namely the median and the fashion.
Physics-Chemistry A averages increased in relation to the results of 2017: from 9.9 to 10.6 for the internal students and from 8.0 to 9.5 for the self-proposed students. This rise in the marks of Physics-Chemistry resumes the behaviour of three consecutive years of rises after a drastic fall in 2017 when the discipline took the last place of the table.
Self-proposed students represent 38.41% of the total number of students who underwent a Physical-Chemistry exam. The number of students who participated in this test has decreased by 8% in relation to 2017. The failure rate, although considerable, has decreased compared to the previous year: 10% of the internal students failed (compared to 14% in 2017) and 52% of the self-proposed also had negative results (compared to 64% in 2017). It should be noticed that in an analogous way that in Mathematics A, the scores obtained in Physics-Chemistry A by the internal students in the entrance exams fell drastically in relation to the results obtained at the end of the secondary school, from 14.2 to 10.9.
Because of the poor results and the fluctuation of the marks obtained in these tests, which are key disciplines to accessing engineering degrees, students naturally tend to avoid engineering and look for alternatives in other areas.
Against this background, the Polytechnic Higher Education schools are attempting to fill the decrease in demand for engineering degrees by making use of other access modalities allowed by law, such as access over 23 years of age, holders of upper or middle courses, diplomas of technological specialization, specials, etc. It is, however, an audience with diverse personal, motivational and cognitive characteristics, with consequent heterogeneity in basic and elementary knowledge, essential for integration in engineering courses, especially in the area of mathematics. Although this alternative may benefit the financing of higher education, more attention will inevitably be devoted to the definition of alternative means to complement the training of some of the admitted profiles [23].
In this context, it is a priority that mathematics teachers in engineering degrees, especially those who teach in the first year, seek changes in their pedagogical practices. It is important to adapt educational strategies to the characteristics of students, their modes of communication, difficulties and learning styles. This practice becomes a permanent challenge for teachers of higher education and makes them to debate some important issues, namely as regards the relation of the students’ success with their motivation and way of learning as well as the way teachers do their assessment practices.
3. Differential and Integral Calculus in ISEC
Teachers in ISEC have proven, during several years of teaching, what the literature presents, realizing the great difficulties of the students, in particular with CU-DIC, in the 1st semester of the 1st year in all of undergraduate engineering degrees. The curricula of the engineering degrees are sequentially constructed and all the UC contents are taught in an articulated form, so it is very important that the students acquire the essential and elementary mathematics concepts to integrate CU-DIC.
Indeed, these courses lead to high failure rates and therefore to a demotivation of all those involved in the educational process, placing teachers in constant self-reflection. Engineering teachers should develop appropriate strategies to adapt, as best as possible, to the ever-increasing heterogeneity in the knowledge and skills acquired by students in secondary education [21,23,50].
Aware of the difficulties in accessing to higher education, ISEC’s Department of Physics and Mathematics (DFM) has developed several activities that allow students the opportunity to bridge gaps in mathematics. One of the measures found by the DFM was to offer CU-DIC in a sliding regime. This extraordinary regime arises from the attempt to overcome the failure detected over the years, in the CU of Mathematics, taught in the 1st year/1st semester of engineering studies. In fact, in the academic year 2002/2003, the Scientific Committee (CC) of the Scientific Area of Mathematics (ACM) of ISEC implemented the pedagogical experience “sliding disciplines” which, after analysis and corrections introduced to optimize resources and improvement of results, began to integrate the distribution of teaching service. These CUs are conducted in alternative semesters, complementing the curricular program of the degrees. This operation also allows students over 23 years to access ISEC, with prior preparation during the first semester to acquire the basic essential knowledge to the integration in the curricular units of DIC.
Notwithstanding all this effort, we have verified that students did not meet the expectations, showing low pass rates and high dropout rates (both in classes and examination moments).
Reversing these trends in students’ performance is an unequivocal purpose associated with teaching practice. An exploratory study was carried out, to allow a diagnosis of the situation regarding the teaching of the DIC in the CUs in engineering degrees at ISEC in general, and in particular in the CU whose head is one of this study’s authors. The analysis of these data may subsequently lead to the need for a research that seeks to design, develop, and evaluate an intervention at the level of teaching and assessment practices of the CU-DIC that leads to better learning and increased success rates.
4. The Study
4.1. Methodology
This exploratory study follows a methodology of quantitative research, considering the observation and analysis of collected data. Taking into account that the analysis may allow us to understand and explain the factors that affect students’ failure in CU-DIC integrated into the curricular plan of engineering degrees, the approach of this case study will be done according to an interpretative paradigm. Therefore, it is intended, without any kind of control over the situation, to obtain explanations that allow the establishment of relations between the operation of the various CU-DICs taught at ISEC and their respective pass rates. The conclusions may lead to the implementation of teaching, learning and assessment strategies that contribute to the promotion of success in those CUs. The data treatment had a descriptive statistical approach.
4.2. Instruments
From the academic year 2010/2011, CC-ACM requested CU managers from several disciplinary groups (groups of teachers who teach CU in the same mathematical area: analysis, algebra, statistics, and applied mathematics) the characterization records of each CU (called FCU), which integrate the respective programmed contents, the assessment methodologies and the skills to be developed. Other important documents are systematization of information reports (RCU) that include class attendance, dropout and pass rates. These records and reports (FCU and RCU) are completed semi-annually by the professors responsible for each CU-DIC and constitute the data collection to be evaluated in order to carry out a continuous analysis of the results obtained in the CU-CDI.
These instruments refer to the period from 2011/2012 to 2017/2018, corresponding to 7 academic years, associated with 11 CU-DIC, and integrated into the disciplinary group of analysis.
Considering the context and the objective of the study that was proposed, we collected the following relevant information:
- Contents taught in the CU-DIC of each degree of engineering at ISEC.
- Assessment methodologies.
- Students’ competencies that will be acquired.
- Type of classes integrated by each CU (theoretical, theoretical-practical, or tutorial orientation).
- The number of hours of on-site classes with students and unaccompanied work.
- Attendance classes’ rate, considering only the highest lowest rate found with an indication of the week in which each occurrence was confirmed.
- Attendance rate in examination moments are given by the ratio between the number of students participating in the assessment (P) and the number of enrolled students in the CU (I), i.e., P/I;
- Dropout rate in the examination moments given by the ratio between the number of evaluated students (A) and the number of students participating in the assessment (P), i.e., A/P.
- Pass rate in examination moments are given by the ratio between the number of students approved (Ap) and the number of evaluated students (A), i.e., Ap/A.
The analysis of these assessment rates corresponds to the exam (Ex) and distributed evaluation (AD), which includes 2 or more mid-term examination moments. The study was conducted in different forms of assessment in order to understand which strategy has the best final results.
However, since the RCUs integrate final information elaborated in a systematized form by the teachers responsible for each CU-DIC, they do not allow to draw more specific conclusions on the relation of the pass rates with the alternative assessment methods. Consequently, a complementary study was carried out in the degrees of EI and EBiom.
For this purpose, the assessment guidelines were analysed in these 7 years under review, and which integrate the data of the pass rate in AD, Ex and the final pass rate (T). It should be noted that, similar to the RCU, these pass rates are calculated in relation to the number of students evaluated, thus excluding dropouts.
4.3. Sample
As mentioned above, the results presented here come from the analysis over a period of 7 years, between the academic year 2011/2012 and 2017/2018. UC-DIC’s records and evaluation reports (FCU and RCU) of 11 engineering degrees were analysed, for the 1st semester (EGI, BioE, EM, EEM, EE, EI, EBiom, EC, GSC and Chemical (EQ) and Biological Engineering (EBiol) which became extinct in 2015) and 4 of these UC-DIC (EM, EEM, EE and EI) taught in the 2nd semester, under the CU sliding regime.
In total, 126 records and reports were analysed: 51 characterization records (FCU) and 75 information of systematization reports (RCU). From these 75 reports of each curricular unit, 51 were from the first semester, and 24 were from the second semester and refer to the CU sliding regime.
5. Results
The research developed has the objective of finding the reasons that lead the students to fail in the CU-DIC taught in the 1st year of the engineering undergraduate degrees in ISEC. A diagnosis to establish relationships between teaching methods and students’ learning strategies was performed. Table 1 summarizes the main results, which are detailed in subsequent sections.

Table 1.
Main results.
5.1. General Scope
From the observation of the FCU, the hours of on-site classes of the different CUs are currently distributed by theoretical, practical and theoretical-practical classes and are shown in Figure 2. From the analysis, we conclude that EC and GSC only have theoretical-practical classes in a total of 77 h (5.5 h/week) and 49 h (3.5 h/week), respectively. The remaining UCs have 28 h of theoretical classes (2 h/week) and 28 h of theoretical-practical classes (2 h/week), except EBiol that registers 30 h and EBiom that contemplates 42 h theoretical-practical (3 h/week). EM and EI also have 14 h (1 h/week) of practical classes and EE 14 h (1 h/week) of tutorial orientation classes.

Figure 2.
On-site classes distribution of the different CUs at ISEC.
Regarding the contents contemplated in the FCU, these were grouped into the following categories: Real functions of real variables: exponential and logarithmic (RF); limits and continuity (LC); derivation (D); hyperbolic functions (HF); trigonometric and inverse functions (TF); primitivation (P); applications of integral calculus (AIC); improper integral (II); differential equations (DE); theory of errors—Taylor’s polynomial (TE); non-linear equations—numerical methods (NLE); numerical integration (NI); differential equations—numerical methods (DEN); numerical series (NS); matrices (M); determinants (Dt).
We found some items that are common to all CU-DICs under study, namely, basics concepts of differential and integral calculus (Figure 3) such as trigonometric and inverse functions, primitivation and applications of integral calculus, although the curricular plans integrate other more specific topics according to the degree they are referring to (numerical calculus, differential equations, numerical series and basic concepts of algebra). Matrices and determinants are subjects covered in UC-DIC when the undergraduate curriculum does not contain an algebra unit.
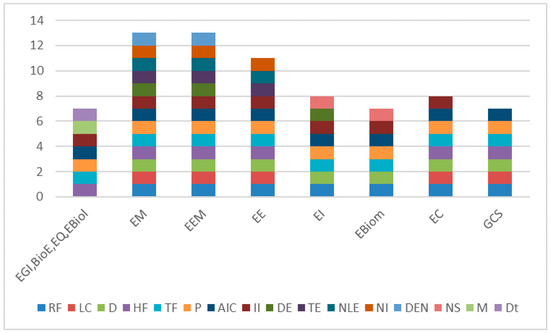
Figure 3.
Programmed content distribution.
The analysis of the competencies to be acquired by students, defined in the KOM project was based on the description made by the teachers in the FCU. These competencies are distributed in the different degrees as is presented in Figure 4. Reasoning mathematically competence is the only one common to all degrees. It should be stressed that some competencies mentioned in the KOM project are not explicitly included in some degrees. This will not mean that teachers do not consider them at the time of the present study.

Figure 4.
KOM competences distribution.
Regarding attendance classes rate, it was found that there was a significant decrease in all CUs during both semesters.
Of the 75 RCUs analysed, 50 reported that the attendance rate is less than 50% and 21 show a rate between 50% and 75%. EBiom degree registered the highest attendance rate (above 80%). However, it should be noted that the degrees with the lowest attendance rate (less than 30%) are reported in the sliding CU (in 18 of the 24 RCUs). The values ranged from 10.5% (EEM in 2014/2015) and 73.7% (EE in 2011/2012) with an average of 27.97%, in the seven academic years. This result is easily justified by the fact that these sliding regimes work in addition to the curricular program of the degree, thus burdening the teaching component in the second semester.
Overall, about the dropout rate, it is observed that only nine CU have percentages below 75% and 50% of the RCU refer to values above 90%. Also, in this approach, the lowest values are achieved in the CUs that operate in a sliding regime.
The pass rates in the seven years under analysis are summarized in Figure 5 and Figure 6. Note that the values corresponding to the EQ, EGI, BioE, and EBiol degrees were only broken down in the academic year 2017/2018. The data in the RCU for the first semester concludes that EBiom presents the best results with a mean of 73.10% (between 62.5% and 88.2%), with EE showing lower results than the other undergraduate degrees (between 27.9% and 52.1%), presenting an average of 42.24%.
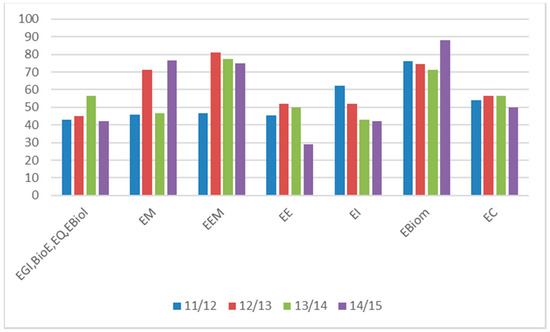
Figure 5.
Pass rate distribution for the 1st semester of the academic years 2011/2012 to 2014/2015 and all undergraduate degrees in ISEC.
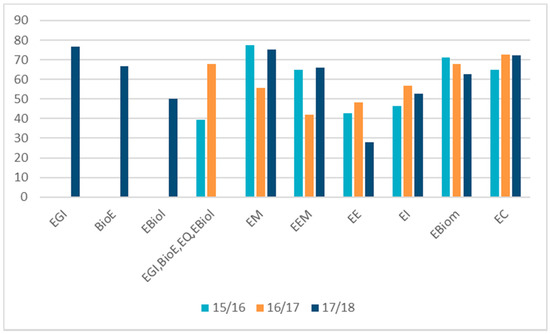
Figure 6.
Pass rate distribution for the 1st semester of the academic years 2015/2016 to 2016/2017 and all undergraduate degrees in ISEC.
It is also verified that the overall average of the pass rate in the first half of the year is 58.40%, with a standard deviation of 14.34% and an average deviation of 12.4%.
Note that, in the academic year 2017/2018, the values corresponding to the EGI, BioE, and EBiol degrees were only broken down and EQ ceased to be taught.
Regarding the second semester, the results evidenced in the RCU were summarized in Figure 7. It should be noted that in the 2011/2012 and 2012/2013 academic years the results of the EEM and EM degrees were gathered in a single RCU, so that they could not be extracted the partial pass rate. In addition, in the academic year 2015/2016, EE did not work due to the reduced number of entries in the scope of access to higher education.

Figure 7.
Pass rates distribution (2nd semester).
From the collected data, it can be evidenced that EM is the degree that has the highest pass rates, with an average of 66.32%, followed by EE with 52.26%, and IE with 50.07%. For EEM, the frequency rate is between 10.5% and 17.5%, so we can conclude that the pass rates are not very significant.
It is also verified that, the overall average of the pass rate in the 2nd semester of the year is 57.36%, with a standard deviation of 17.39% and an average deviation of 12.96%.
The pass rates in the second semester (average 57.36%) were compared with the values registered in the 1st semester in the CU that is conducted in a sliding regime (average 55.44%). We can affirm that the difference does not reflect the application of a concerted learning investment strategy but only that option is considered, by the students, as another opportunity to achieve success. It should be noted that in 2015, the creation of an optional curricular plan (OCP) produced a change. The OCP aimed at students with poor knowledge in mathematics. The course director of each engineering degree should prepare that plan, with the distribution of CUs for two years. The selecting students to join the OCP would be done through the application of the diagnostic test, based on the following three assumptions:
- Complementary course related to essential knowledge in mathematics (CU pre-calculus frequency).
- Attendance of CU-DIC in sliding regime.
- Integration in OCP, taking into account compulsory frequency in pre-calculus unit.
This proposal would allow a reinforcement of the basic and elementary knowledge essential to the integration in the CU-DIC, which are fundamental in the teaching of engineering.
5.2. Private Sector—Biomedical and Informatics
In the analysis of the assessment guidelines of CU-DIC, we can infer from the EBiom results that the attendance rate at the examinations is high (except the year 2014/2015 which registers a lower rate even though higher than that found in other undergraduate degrees). As for the pass rate, the AD is the students’ preferred modality; although in 2016/2017 there was a reversal of the situation (Figure 8). The AD pass rates are between 83.33% and 100%, while Ex varies between 25% and 66.67%. Total pass rates are between 71.79% and 88.24%, with an average of 78.82%.
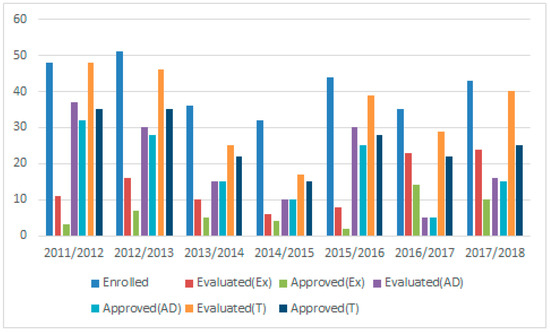
Figure 8.
Pass rates distribution (AD, Ex, T): Biomedical.
With regards to informatics, the CU-DIC works in the first semester and in a sliding regime (2nd semester). The data show a low rate of attendance to the examinations, obtaining an average of 40.51% in the first semester. Regarding the pass rates in the first half, the Ex ratio is between 13.30% and 38.60%, while in the AD there are pass rates between 67.27% and 81.25% (Figure 9). Total pass rates range from 41.15% to 57%, with an average of 48.02%.
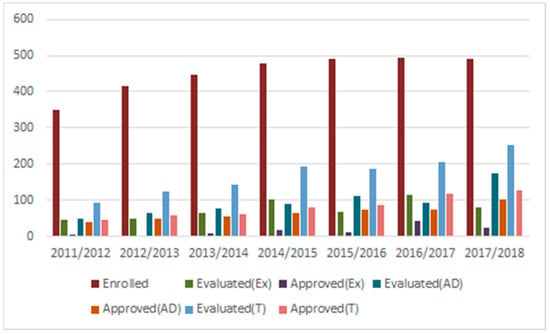
Figure 9.
Pass rates distribution (AD, Ex, T): Informatics—1st semester.
Concerning the second semester, the attendance rate at the examinations was 26.4%, a result that is not surprising since this semester the CU works in addition to the curricular program of the degree, which is observed in the remaining CUs that operate in a sliding regime. Regarding the pass rates in the second half of the year, the Ex ratio is between 20% and 32.84%, while in the AD there are pass rates between 47.50% and 86.11% (Figure 10). It should be noted that the worst percentages in AD were in the years 2011, 2012 and 2016, which integrated a component distributed by 4 moments of mid-term examinations. Total pass rates range from 40.23% to 51.09%, with an average of 44.69%.

Figure 10.
Pass rates distribution (AD, Ex, T): Informatics—2nd semester.
In summary, we can conclude that the pass rates obtained by AD induce this to be a strategy leading to the success in CU-DIC taught in EBiom and EI degrees (Table 2). It should also be noted that the difference in performance between the students of both degrees can be explained by the ease of integration of EBiom students in the CU-DIC. This corroborates the study carried out which concludes that, in terms of the median, EBiom students perform better on the diagnostic test, applied to the entrance of higher education in ISEC, while EI students present the worst classifications [51].

Table 2.
Pass rates measures: Ex and AD.
6. Conclusions and Future Work
The demand in the two Portuguese higher education subsystems (university-55% and polytechnic-45%) shows an asymmetry that can be explained by the nonexistence of real differentiation of offerings. Only 22% of higher education candidates chose one of 218 engineering degrees. This small percentage can be explained by the requirement for mathematics and physics as entrance exams for most engineering courses.
At ISEC the most required engineering degrees are Informatics and Mechanics Engineering. Civil Engineering continues to register the lowest percentage of interest. It is also evident that the variation of offer/demand in ISEC depends on the results obtained in the exams of specific tests of Mathematics A and Physics-Chemistry A with national averages, respectively of 10.9 and 10.6. These averages are three points below the national averages of students’ internal grades in upper secondary education.
In the study carried out in the curricular unit of differential and integral calculus at ISEC, to make a diagnosis of the situation regarding the teaching/learning of those CUs in engineering degrees, the following conclusions were found:
- The time for on-side classes of the different CU-DIC taught in engineering degrees at the ISEC is distributed by theoretical, practical, and theoretical-practical classes, except EC and GSC that only consider theoretical-practical classes. EM and EI consider practical classes and EE includes tutorial guidance classes.
- The common contents to all CU-DICs under study are trigonometric functions, primitivation, definite integral, and improper integrals, which constitute the core of the mathematical knowledge that teachers understand as essential.
- We can also infer that the competencies defined in the FCU do not seem to influence the success of mathematics in the engineering courses since the pass rates do not have significant deviations between degrees.
- We can also conclude that the CU-DIC in the various degrees in engineering of the ISEC register very variable assessment attendance rates. Although there is no relationship between the attendance rates at the examinations and the pass rates, it should be noted that fewer and fewer students attend classes and exams—a fact that will influence the final pass rate, which is found to be low.
In the degrees that run on a sliding regime, there is lower average participation in the examinations. This result is easily justified by the fact that these CUs work in addition to the curricular program of the degree, overloading the academic component.
The pass rates of the CUs that run on a sliding regime do not differ between the two semesters. Therefore, it is possible to infer the need to review the functioning of these CUs. It will be important to apply a concerted strategy of investment in the learning carried out by the student, that it can’t be considered only one extra opportunity for success. In the particular context of EBiom and EI it is concluded, after analyzing the data that students obtain better results in the processes that include distributed evaluation, preferably the one that integrates two mid-term examination moments. For the seven school years analyzed, EBiom has a high attendance rate and an average pass rate of 78.82%. EI shows a low attendance rate, especially in the 2nd semester, with an average pass rate of 48.02% in the 1st semester and 44.69% in the 2nd semester. In future work, we could analyze the student’s profile in higher education that leads to better attendance and passing rates.
As already mentioned, the teaching of CU-DIC has been evidenced in many studies, namely about difficulties demonstrated by students in basic and elementary contents, essential to their full integration in that subject. This inevitably leads to an adaptation of the curricular organization and the definition of actions that allow modifying the situation. Since 2015, ISEC has been implementing a mathematics support center that aims to help students overcome gaps in essential math concepts. Another solution may be the introduction of teaching strategies that allow students to adapt their learning styles to the desired learning outcomes.
The low participation of the students in the curricular assessment process together with the pass rate obtained in the distributed evaluation can lead us to enunciate a set of questions that are related to:
- Student’s profile attending and participating in different examination models proposed by teachers.
- Relationship between the attendance rates (at the classes and examinations) and economic, social, cultural, technology development conditions.
- Teaching/learning strategies to be applied, aimed at reaching students who do not carry out the examination and understand the consequent reasons that led them to dropout.
- The set of basic and elementary level knowledge that students need to master upon entering higher education.
- Mistakes made in basic and elementary knowledge that allow the definition of a structured intervention in overcoming gaps.
- Environments that lead to meaningful learning and involve all actors (teachers and students) in the educational process.
The answer to these and other questions that may be related shall form the basis for future work.
Author Contributions
Investigation, M.E.B.d.A., A.Q.-D. and M.J.C.; Methodology, M.E.B.d.A., A.Q.-D. and M.J.C.; Supervision, A.Q.-D.; Writing—original draft, M.E.B.d.A.; Writing—review & editing, A.Q.-D. and M.J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project “New Rules for Assessing Mathematical Competencies (RULES-MATH)” and the Coimbra Engineering Institute, ISEC.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
This research was partially supported by the project “New Rules for Assessing Mathematical Competencies (RULES-MATH)” (2017-1-ESO1-KA203-038491), financed by Erasmus+ program, “Análisis de tareas matemáticas planteadas por estudiantes para maestro a partir de procesos reflexivos.” (SA050G19) financed by Ministry of Education of the Junta de Castilla y Léon, Spain. Any opinions, findings, conclusions, or recommendations expressed in the material are those of the authors and do not necessarily reflect those of funding agencies. This research work is made within University of Salamanca PhD Programme on Education in the Knowledge Society scope.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barbosa, M.A. O Insucesso no Ensino e Aprendizagem na Disciplina de Cálculo Diferencial e Integral. Master’s Thesis, Pontifícia Universidade Católica do Paraná, Curitiba, Brazil, 2004. [Google Scholar]
- Rezende, W.M. O Ensino de Cálculo: Dificuldades de Natureza Epistemológica. Ph.D. Thesis, Faculdade de Educação, Universidade de São Paulo, USP, Sao Paulo, Brazil, 2003. [Google Scholar]
- Rosa, O.S. Aspectos Motivacionais do Cálculo Diferencial e Integral. Post-Graduate Program. Master’s Thesis, Universidade de Severino Sombra, Vassouras, Brazil, 2011. [Google Scholar]
- Tall, D. Advanced Mathematical Thinking; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Tall, D. The Transition to Advanced Mathematical Thinking: Functions, Limits, Infinity and Proof. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 495–511. [Google Scholar]
- Arts, J.A.R.; Gijselaers, W.H.; Segers, M.S.R. Enhancing Problem-Solving Expertise by Means of an Authentic, Collaborative, Computer Supported and Problem-Based Course. Eur. J. Psychol. Educ. 2006, 21, 71–90. [Google Scholar] [CrossRef]
- Baldino, R.R.; Cabral, T.C.B. Revivendo o Cálculo Infinitesimal com uso de Tecnologia do Ponto de Vista da Educação Matemática; Departamento de Matemática, IGCE, UNESP: Rio Claro, Brazil, 2000. [Google Scholar]
- Berman, A.; Verner, I.M.; Aroshas, S. The Teaching Calculus with Applications Experiment Succeeded-Why and What Else? In Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education, CERME 5, Larnaca, Cyprus, 22–26 February 2007; Pitta-Pantazi, D., Philippou, G., Eds.; University of Cyprus and ERME: Lanarca, Cyprus, 2007; pp. 2060–2069. [Google Scholar]
- Domenico, L.C.A. Aprendizagem de Cálculo Diferencial e Integral por Meio de Tecnologias de Informação e Comunicação. Master’s Thesis, Pontifícia Universidade Católica do Paraná, Curitiba, Brazil, 2006. [Google Scholar]
- Hallett, D.H. What Have We Learned from Calculus Reform? The Road to Conceptual Understanding. MAA Notes 2006, 69, 43. [Google Scholar]
- Skouras, A.S. Coordinating Formal and Informal Aspect of Mathematics in a Computer Based Learning Environment. Int. J. Math. Educ. Sci. Technol. 2006, 37, 947–964. [Google Scholar] [CrossRef]
- Gomes, G.; Frant, J.; Powell, A. O Pensamento Matemático Dos Estudantes de Engenharia: Um Estudo de Caso do Projeto de Final de Curso. In Proceedings of the XIII CIAEM-IACME, Recife, Brazil, 26–30 June 2011. [Google Scholar]
- Silius, K.; Pohjolainen, S.; Kangas, J.; Joutsenlahti, J. What Can Be Done to Bridge the Competency Gap between Upper-Secondary School and University Mathematics? In Proceedings of the 2011 IEEE Global Engineering Education Conference (EDUCON), Amman, Jordan, 4–6 April 2011; pp. 428–436. [Google Scholar]
- Martín-Vaquero, J.; Cáceres, M.J.; Rodríguez, G.; Queiruga-Dios, A.; Yilmaz, F. Basic Mathematics Assessment in Engineering Degrees: Case Study. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Canary Islands, Spain, 18–20 April 2018; pp. 1639–1644. [Google Scholar]
- Koch, D.; Herrin, G.D. Intervention Strategy for Improving Success Rates in Calculus. In Proceedings of the 2006 ASEE Annual Conference and Exposition, Chicago, IL, USA, 18 June 2006; Volume 775. [Google Scholar]
- Gill, O.; O’Donoghue, J. Justifying the Existence of Mathematics Learning Supports Measuring the Effectiveness of a Mathematics Learning Centre. In Proceedings of the ALM, Rotterdam, The Netherlands, 2–5 July 2017. [Google Scholar]
- Gill, O.; O’Donoghue, J. The Mathematical Deficiencies of Students Entering Third Level: An Item by Item Analysis of Student Diagnostic Tests. In Proceedings of the Second National Conference on Research in Mathematics Education (MEI2), St. Patrick’s College, Dublin, Ireland, 14–15 September 2007; pp. 228–239. [Google Scholar]
- O’Sullivan, C.; Bhaird, C.; Fitzmaurice, O.; Fhloinn, E. An Irish Mathematics Learning Support Network (IMLSN) Report on Student Evaluation of Mathematics Learning Support: Insights from a Large Scale Multi-Institutional Survey; National Centre for Excellence in Mathematics and Science Teaching and Learning (NCEMSTL): Limerick, Ireland, 2014. [Google Scholar]
- Hieb, J.; Lyle, K.; Ralston, P.; Chariker, J. Predicting Performance in a First Engineering Calculus Course: Implications for Interventions. Int. J. Math. Educ. Sci. Technol. 2015, 46, 40–55. [Google Scholar] [CrossRef]
- Nite, S.B.; Capraro, R.M.; Capraro, M.M.; Allen, G.D.; Pilant, M.; Morgan, J. A Bridge to Engineering: A Personalized Precalculus (Bridge) Program. In Proceedings of the 2015 IEEE Frontiers in Education Conference (FIE), El Paso, TX, USA, 21–24 October 2015; pp. 1–6. [Google Scholar]
- Fidalgo, C.; Bigotte, E.; Rasteiro, D. Understanding the Difficulties in Mathematics of Engineering Students in the Transition from Second to Third Level Education. In Proceedings of the 4th ATEE Winter Conference, Lisbon, Portugal, 2–4 April 2012; pp. 477–487. [Google Scholar]
- Bigotte, E.; Gomes, A.; Branco, J.R.; Pessoa, T. The Influence of Educational Learning Paths in Academic Success of Mathematics in Engineering Undergraduate. In Proceedings of the 2016 IEEE Frontiers in Education Conference (FIE), Eire, PA, USA, 12–15 October 2016; pp. 1–6. [Google Scholar]
- Carr, M.; Fidalgo, C.; Bigotte, E.; Branco, J.R.; Santos, V.; Murphy, E.; Ni Fhloinn, E. Mathematics Diagnostic Test in Engineering: An International Comparison between Ireland and Portugal. Eur. J. Eng. Educ. 2015, 40, 546–556. [Google Scholar] [CrossRef]
- Borasi, R. Exploring Mathematics Through the Analysis of Errors. Learn. Math. 1987, 7, 2–8. [Google Scholar]
- Cury, H. Análise de Erros em Disciplinas Matemáticas de Cursos Superiores. In Proceedings of the III Seminário Internacional de Pesquisa em Educação Matemática, Águas de Lindóia, São Paulo, Brazil, 10–14 October 2006. [Google Scholar]
- Bigotte, E.; Fidalgo, C.; Rasteiro, D. The Teaching of Mathematics in Engineering: The ACAM-Assessment of Competencies/Improvement Actions Project. In Proceedings of the 16th Seminar Mathematical Education of Engineers SEFI, Salamanca, Spain, 28–30 June 2012. [Google Scholar]
- Abdulwahed, M.; Jaworski, B.; Crawford, A. Innovative Approaches to Teaching Mathematics in Higher Education: A Review and Critique. Nordic Stud. Math Educ. 2012, 17, 49–68. [Google Scholar]
- Ni Fhloinn, E.; Carr, M. Formative Assessment in Mathematics for Engineering Students. Eur. J. Eng. Educ. 2017, 42, 458–470. [Google Scholar] [CrossRef]
- Kaput, J. The Representational Roles of Technology in Connecting Mathematics with Authentic Experience. In Didactics of Mathematics as a Scientific Discipline; Biehler, R., Scholz, R.W., Sträßer, R., Winkelmann, B., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 379–397. [Google Scholar]
- Teodoro, V.D. Modellus: Learning Physics with Mathematical Modelling; Universidade Nova de Lisboa: Lisbon, Portugal, 2002. [Google Scholar]
- Blackwell, L.S.; Trzesniewski, K.H.; Dweck, C.S. Implicit Theories of Intelligence Predict Achievement across an Adolescent Transition: A Longitudinal Study and an Intervention. Child Dev. 2007, 78, 246–263. [Google Scholar] [CrossRef] [PubMed]
- Martins, S.I.C.G. An Approach to Teach Calculus/Mathematical Analysis (for Engineering Students) Using Computers and Active Learning—Its Conception, Development of Materials and Evaluation. Ph.D. Thesis, Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa, Lisbon, Portugal, 2013. [Google Scholar]
- Tall, D.; Smith, D.; Piez, C. Technology and Calculus. In Research on Technology and the Teaching and Learning of Mathematics; Volume I: Research Syntheses; Heid, M.K., Blume, G.M., Eds.; IAP: Charlotte, NC, USA, 2008; pp. 207–258. [Google Scholar]
- Rasteiro, D.; Bigotte, E.; Fidalgo, C. Contributions of B-Learning in the Teaching of Mathematics in Engineering: An Effective Shared Responsibility of Students. In Proceedings of the Atas do II Congresso Internacional TIC e Educação (TICEduca2012), Lisbon, Portugal, 24 April 2012; pp. 3164–3183. [Google Scholar]
- Sevimli, E. Do Calculus Students Demand Technology Integration Into Learning Environment? Case of Instructional Differences. Int. J. Educ. Technol. High. Educ. 2016, 13, 37. [Google Scholar] [CrossRef]
- Firmino, G.L.; Siqueira, A.M.O. A Matemática No Ensino de Engenharia. J. Eng. Exact Sci. 2017, 3, 331–334. [Google Scholar] [CrossRef]
- Mendezabal, M.; Tindowen, D. Improving Students’ Attitude, Conceptual Understanding and Procedural Skills in Differential Calculus Through Microsoft Mathematics. J. Technol. Sci. Educ. 2018, 8, 385–397. [Google Scholar] [CrossRef]
- Almendra, M. Competency-Based Learning for Motivation and Academic Performance in a Pre-calculus Course. Am. J. Educ. Res. 2019, 7, 58–63. [Google Scholar]
- Kinnari-Korpela, H. Enhancing Learning in Engineering Mathematics Education Utilising Educational Technology and Promoting Active Learning. Ph.D. Thesis, Tampere University, Tampere, Finland, 2019. [Google Scholar]
- Davis, M.; Hunter, G.; Thalaal, L.; Tran Ba, V.; Wooding-Olajorin, A. Developing “Smart” Tutorial Tools to Assist Students Learn Calculus, Taking Account of Their Changing Preferred Approaches to Learning. In Intelligent Environments 2019. Workshop Proceedings of the 15th International Conference on Intelligent Environments, Rabat, Morocco, 24–27 June 2019; IOS Press: Amsterdam, The Netherlands, 2019; Volume 26, p. 227. [Google Scholar]
- Alpers, B.A.; Demlova, M.; Fant, C.H.; Gustafsson, T.; Lawson, D.; Mustoe, L.; Olsson-Lehtonen, B.; Robinson, C.; Velichova, D. A Framework for Mathematics Curricula in Engineering Education: A Report of the Mathematics Working Group; Loughborough University: Loughborough, UK, 2013. [Google Scholar]
- Cardella, M. Which Mathematics Should We Teach Engineering Students? An Empirically Grounded Case for a Broad Notion of Mathematical Thinking. Teach. Math. Its Appl. Int. J. IMA 2008, 27, 150–159. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense-Making in Mathematics. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 334–370. [Google Scholar]
- Schoenfeld, A.H. Reflections on Doing and Teaching Mathematics. In Mathematical Thinking and Problem Solving; LEA: Hillsdale NJ, USA, 1994; pp. 53–75. [Google Scholar]
- Asiala, M.; Brown, A.; DeVries, D.J.; Dubinsky, E.; Mathews, D.; Thomas, K. A Framework for Research and Curriculum Development in Undergraduate Mathematics Education. Res. Coll. Math. Educ. 1996, 2, 1–32. [Google Scholar]
- Barker, W.; Bressoud, D.; Epp, S.; Ganter, S.; Haver, B.; Pollatsek, H. Undergraduate Programs and Courses in Mathematical Sciences. CUPM Curriculum Guide 2004; The Mathematical Association of America: Washington, DC, USA, 2004. [Google Scholar]
- Schleicher, A.; Zimmer, K.; Evans, J.; Clements, N. PISA 2009 Assessment Framework: Key Competencies in Reading, Mathematics and Science; OECD Publishing (NJ1): Paris, France, 2010. [Google Scholar]
- Niss, M. Mathematical Competencies and the Learning of Mathematics: The Danish KOM Project. In Proceedings of the 3rd Mediterranean Conference on Mathematics Education, Athens, Greece, 3–5 January 2003; Gagatsis, A., Papastravidis, S., Eds.; Hellenic Mathematical Society and Cyprus Mathematical Society: Athens, Greece, 2003; pp. 115–124. [Google Scholar]
- Rasmussen, C.; Ellis, J.; Zazkis, D. Features of Successful Calculus Programs at Five Doctoral Degree Granting Institutions. In Proceedings of the Joint Meeting of PME 38 and PME-NA 36, Vancouver, BC, Canada, 15–20 July 2014; Nicol, C., Oesterle, S., Liljedahl, P., Allan, D., Eds.; PME: Vancouver, BC, Canada, 2014; Volume 5, pp. 33–40. [Google Scholar]
- Bigotte, E.; Branco, J.R. A Program to Promote Mathematical Knowledge for Students’ Integration in Engineering Degrees: CeAMatE. In Proceedings of the CISPEE 2018—International Conference of the Portuguese Society for Engineering Education, Aveiro, Portugal, 27–29 June 2018; pp. 1–6. [Google Scholar]
- Bigotte, E.; Correia, A.; Fidalgo, C.; Caridade, C.R.M.; Rasteiro, D.M.L.D.; Amorim, M.C.; Baeta, N.M.S.; Rosa, P.; Silva, P.M.; Silva, P.; et al. Projeto “ACAM-Avaliação de Competências/Ações de Melhoria”. In Proceedings of the Actas XIX Colóquio da Secção Portuguesa da AFIRSE: Revisitar os Estudos Curriculares. Onde Estamos e Para Onde Vamos? EDUCA/Secção Portuguesa da AFIRSE, Lisbon, Portugal, 2–4 February 2012; pp. 1546–1559. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).