Abstract
In this paper, we consider the digital cohomology modules of a digital image consisting of a bounded and finite subset of and an adjacency relation. We construct a contravariant functor from the category of digital images and digital continuous functions to the category of unitary R-modules and R-module homomorphisms via the category of cochain complexes of R-modules and cochain maps, where R is a commutative ring with identity . We also examine the digital primitive cohomology classes based on digital images and find the relationship between R-module homomorphisms of digital cohomology modules induced by the digital convolutions and digital continuous functions.
Keywords:
pointed digital homotopy; digital cohomology module; digital convolution; digital primitive cohomology class MSC:
Primary 68U03; Secondary 18F99; 16W50; 68U10; 55N91; 57T25
1. Introduction
1.1. Cohomology and Hopf Space
A cohomology group is a general mathematical term for a (positive integer graded or representation ring graded) sequence of -modules associated with a topological space (or a spectrum) usually defined from a usual cochain complex by taking a Homfunctor on a chain complex, where is the ring of integers. A cohomology group may be viewed as another method of assigning richer algebraic and topological invariants to a topological space than a homology group. Some versions of a cohomology group arise by dualizing the construction of a homology group. As usual, the singular (or simplicial) cochains are group homomorphisms (or, equivalently, -module homomorphisms) from the free Abelian group to an Abelian group G in classical homology and cohomology theories; that is, is a group homomorphism, where is the n-th singular chain group of a topological space X.
The classical (equivariant) homology and cohomology modules are important algebraic tools to give answers to a large number of difficult problems in mathematics and are in practice the fundamental algebraic gadgets. As an application, the digital versions of classical homology and cohomology groups (or -modules) may be important algebraic tools to classify (pointed) digital images from the digital homotopy theoretic point of view. In particular, the formal and informal definitions of many terms in homotopy and simplicial (co)homology theory based on a digital image on or were nicely described in [1,2,3,4].
A (pointed) topological space is said to be a (pointed) Hopf space if there is a (base point preserving or pointed) continuous map:
for which the unique constant map:
at is a two-sided identity up to homotopy in the classical sense; that is,
and:
where is the diagonal function and is the identity function on . The (base point preserving or pointed) continuous map:
above is said to be a homotopy multiplication (or multiplication) of .
The (pointed) Hopf spaces have been a direct and natural generalization of Lie groups in classical homotopy theory as nicely presented in [5,6,7]. The multiplicative structure of a Hopf space creates many interesting structures to its classical homology and cohomology groups. For example, the classical cohomology ring of a zero-connected Hopf space with finitely generated free cohomology groups with some multiplications and comultiplications becomes a Hopf algebra; see ([8] (III Theorem 7.15)). Furthermore, we can consider the Pontryagin algebra derived from the multiplication structure of a Hopf space on the homology level as one of the advantages in classical homology theory.
1.2. Motivation and Goal
The digital topology is highly related to the combinatorial topology, and it concerns the features and properties of the digital images in , especially the two-dimensional or three-dimensional digital images corresponding to the topological features and properties of objects in the category of topological spaces and continuous functions. Historically, the digital topology was first studied in the late 1960s by A. Rosenfeld. Digital surfaces and digital manifolds were also developed in the early 1980s and in 1990s, respectively.
There are many standard approaches for the consideration of a digital counterpart of the standard topology on such as the axiomatic approach, the imbedding approach, and the graph-theoretic approach [9]. Moreover, it is well known that the notion of a (pointed) Hopf space is one of the Eckmann–Hilton dual concepts of a (pointed) co-Hopf space. These spaces were introduced in [10] and were used to characterize when a pointed CW-space has the homotopy type of a suspension ([11] (Theorem A)); see also [12]. The author investigated the co-Hopf structures on a wedge of (localized) spheres [13,14,15,16,17,18] and a suspension with the standard comultiplication in the sense of same n-types [19,20,21,22,23]; see also [24,25] for the topics that are related to the fundamental concepts of those spaces.
The above statements force us to investigate another approach to study digital topology out of classical homotopy theory and digital counterparts of those ideas in classical homology and cohomology theories. In the current paper, we introduce another consideration of the so-called algebraic approach from the classical homology and cohomology groups. More precisely, the present study deals with the algebraic invariants and their important properties of digital cohomology modules over a commutative ring with the identity of a digital image with an adjacency relation originated from the classical cohomology groups with coefficients in an additive Abelian group of a topological space in cohomology theory. The main purposes of this paper are to investigate a contravariant functor from the category of digital images and digital continuous functions to the category of unitary R-modules and R-module homomorphisms (Theorem 1) and the digital primitive cohomology classes (Theorem 2) and to examine the relationship between R-module homomorphisms of digital cohomology modules induced by the digital convolutions and digital continuous functions (Theorem 3).
1.3. Organization
We now give a short overview of the structure of this paper. In the current study, we denote a commutative ring with identity by R. In Section 2, we introduce the basic notions of digital images with -adjacency relations and consider the category of (pointed) digital images and (base point preserving or pointed) digital continuous functions. In Section 3, we develop the digital homology and cohomology modules over a commutative ring R with identity based on digital images with adjacency relations. We construct a contravariant functor from the category of digital images and digital continuous functions to the category of unitary R-modules and R-module homomorphisms. In Section 4, we consider a pointed digital Hopf space together with a digital homotopy multiplication. We investigate the important properties of digital primitive cohomology classes in digital Hopf spaces as digital images and find the relationship between R-module homomorphisms of digital cohomology R-modules induced by the digital convolutions and digital continuous functions.
2. Preliminaries
Let be the set of all integers, and let:
be the set of all functions:
such that:
for each ; that is, the set of all lattice points in the n-dimensional Euclidean space for , where for . We note that the above function:
can be identified with the lattice point by defining:
to be:
for each .
For a positive integer u with , we define an adjacency relation as follows.
Definition 1
([26]). The two different functions or the two different points and in are said to be -adjacent if:
- there are at most u distinct indices i with the property ; and
- for all indices j, if , then .
Example 1.
- (1)
- The set of -adjacent points of zero in is the set consisting of and one.
- (2)
- The set of -adjacent points of in is the set consisting of , , , and .
- (3)
- The set of -adjacent points of in is the set consisting of , , , , , , , and .
A -adjacency relation on may be considered as the cardinality of the set of lattice points that have the -adjacency relations centered at in . From this point of view, we define the following.
Definition 2.
The -adjacent points of are said to be two-adjacent.
Convention: We sometimes denote the -adjacency relation on a digital image X by the -adjacency relation for short unless we specifically state otherwise.
A digital image consists of a bounded and finite subset X of and an adjacency relation on X. A digital image in is said to be -connected ([27,28]) if for each set consisting of two distinct points x and y, there exists a subset:
consisting of distinct points such that:
- ; and
- and are -adjacent for .
Example 2.
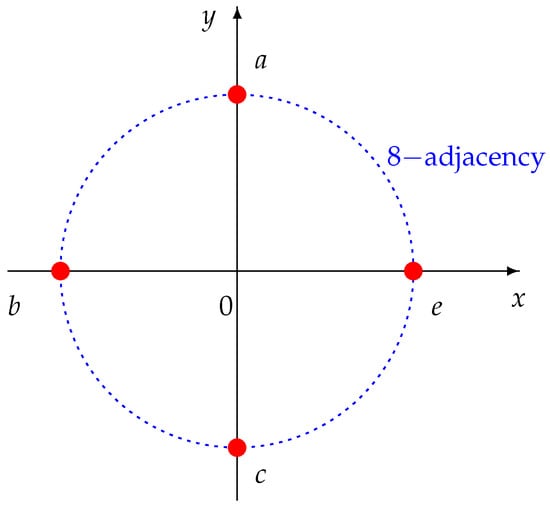
Let be a subset of , where:
- ;
- ;
- and
- .
Then, X is a digital image with eight-adjacent relation in ; see Figure 1.

Figure 1.
A digital image with the eight-adjacency relation.
Definition 3
([29]). Let and be the digital images with -adjacency and -adjacency relations, respectively. A function:
of digital images is said to be a -continuous function if the image of every -connected subset of the digital image under f is a -connected subset of ; see also ([28] (Definition 2.3)).
Let a and b be elements of , considered as a simply ordered set, with . The bounded and finite set:
considered as a digital image with the two-adjacency relation in is said to be a digital interval; see [27,30]. A triple consisting of a digital image X with a -adjacency relation and an element of X is said to be a pointed digital image [31]. Here, is called a base point of just like a base point of a pointed topological space. A -continuous function of pointed digital images:
such that:
is called a base point preserving digital continuous function (or a pointed digital continuous function).
Definition 4
([26,28,32]). Let and be pointed digital images with -adjacency and -adjacency relations, respectively, and let:
be the base point preserving -continuous functions. Assume that there is a function:
such that:
- and for all ;
- the function defined by for all is -continuous;
- the function defined by for all is -continuous; and
- for all ,
where is a digital interval. Then, F is called a pointed digital -homotopy between f and g, usually written as:
and f and g are called pointed digital -homotopic in Y.
As usual, we denote the pointed digital homotopy class by as the equivalence class of a base point preserving -continuous function .
Remark 1.
We note that if , , and are pointed digital images and if is a -continuous function and is a -continuous function, then it can be shown that the composite is also a -continuous function. Therefore, it is possible for us to consider the pointed digital category whose object classes are pointed digital images and whose morphism classes are base point preserving digital continuous functions. By ignoring the base points once in a while, we can also construct the category whose object classes are digital images and whose morphism classes are digital continuous functions.
3. Digital Homology and Cohomology Modules
A module is one of the pivotal algebraic structures in algebra and algebraic topology. A module over a ring is a generalization of the notion of a vector space over a field, wherein the corresponding scalars are the elements of an arbitrary given ring (with identity).
Historically, classical cohomology modules were not defined until long after homology modules because cohomology modules are much less natural than homology modules geometrically. The mathematical term “homology” was first used in a topological sense by H. Poincaré in 1897.
In this section, we explore the digital homology and cohomology modules of digital images and construct a contravariant functor from the category of digital images and digital continuous functions to the category of unitary R-modules and R-module homomorphisms, where R is a commutative ring with identity .
Let , , …, and be the elements of , and let be a finite subset of consisting of all of these elements; that is,
Similarly, as described earlier, we denote the -adjacency relation in the digital image as a finite subset of by for our notational convenience.
For a digital image with a -adjacency relation, a -continuous function:
is called a digital n-simplex in . We note that for every so that the set is a -connected subset of , either:
or is a -connected subset of .
Let R be a commutative ring with identity , and let be a digital image with a -adjacency relation. For each , we denote by the non-negatively graded free R-module with the basis consisting of all digital n-simplexes in and define the so-called digital boundary operator:
by
where is the i-th face function; see [33,34]. It can be shown that:
for all , and thus, is automatically an R-submodule of for each . The n-th digital homology module over R of a digital image with a -adjacency relation is defined by:
for each [33]; see also [2,35].
We observe that if the commutative ring R with identity is equal to the ring of integers, then the non-negatively graded free -module (or free Abelian group) is denoted by for short, and similarly for the n-th digital homology module.
We now explore the digital cohomology modules over a commutative ring R with identity as follows.
Definition 5.
The module of n-cochains of a digital image , with coefficients in a commutative ring R with identity , is defined to be the R-module:
whose scalar multiplication:
is given by:
where:
- ;
- ;
- ; and
- ⋄ is the ring multiplication in the commutative ring R with identity considered as the R-module over itself.
Definition 6.
The digital coboundary operator is defined as the dual of the digital boundary operator that is,
for each .
Remark 2.
We note that if R is a commutative ring with identity , then is a unitary R-module. Indeed, we have:
for all ; that is,
for all .
Definition 7.
The kernel of:
is said to be the module of digital n-cocycles in and is denoted by for all .
Definition 8.
The image of:
is said to be the module of digital n-coboundaries in and is denoted by for all .
From Definitions 7 and 8, we can see that:
- and are R-submodules of ;
- for all ; and
- is an R-submodule of .
Therefore, we can define the following.
Definition 9.
The n-th digital cohomology module over R of a digital image is defined to be the corresponding cohomology module over R of the cochain complex obtained by the dual R-modules along with the dual R-module homomorphisms, i.e.,
for all .
Indeed, as a quotient R-module, has the unitary R-module structure because R is a commutative ring with identity; see below.
Remark 3.
If K is a simplicial complex, then the classical simplicial homology of K is isomorphic to the singular homology of the polytope of ([36] (Theorem 34.3)), and similarly for cohomology groups from the universal coefficient theorem for cohomology. In the context of digital images, on the other hand, there is a small difference between the n-th simplicial cohomology group ([4] (Definition 3.2)) and the n-th digital cohomology module in that the n-th digital cohomology module does not require dividing a digital image into n-simplexes. However, it is well known in mathematics that the smooth compact surfaces can be triangulated.
Let A and B be R-modules. A function is said to be an R-module homomorphism if the following diagrams:
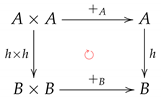 and:
and:
 are strictly commutative, where:
are strictly commutative, where:


- and are the binary operations on A and B, respectively;
- the bullets • in blue are the scalar multiplications on the R-modules A and B with the same notation; and
- is the identity function on the commutative ring R with identity.
We note that if:
is a digital n-simplex in and if:
is a -continuous function, then it can be shown that:
is a digital n-simplex in . Therefore, by using the linear property, we have an R-module homomorphism of R-modules:
defined by:
where is an element of the commutative ring R with identity, and the bullets • in blue are the scalar multiplications on the R-modules and with the same notation.
Moreover, we have the following.
Remark 4.
The following diagram:
 strictly commutes for every , where is the digital boundary operator of a digital image .
strictly commutes for every , where is the digital boundary operator of a digital image .

Let and be categories. We recall that a contravariant functor:
consists of an object function, which assigns to every object X of an object of and a morphism function that assigns to every morphism of a morphism of such that:
and:
where:
- is the identity morphism in ;
- is the identity morphism in ;
- is a morphism class in ; and
- is a morphism class in .
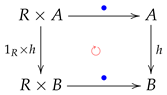
As usual, we define a map:
by:
for every ; that is, the following triangle:
 is strictly commutative, where is the ring of integers.
is strictly commutative, where is the ring of integers.

For any element r of R and any element of , it can be seen that the map:
preserves the addition and the scalar multiplication. Indeed, we have:
for all , where the bullets • in blue are the scalar multiplications on the R-module structures of or . Therefore, we have the following.
Lemma 1.
Let R be a commutative ring with identity . Then, any -continuous function:
induces an R-module homomorphism of unitary R-modules:
Proof.
See ([37] (Proposition 2.5)) for more details. □
We note that the following diagram:
 is strictly commutative, where and are digital coboundary operators of the digital images and , respectively, for all .
is strictly commutative, where and are digital coboundary operators of the digital images and , respectively, for all .

It can be seen that, for each digital image , is a unitary R-module whose scalar multiplication:
is given by:
where:
- ;
- with ; and
- the bullet “•” in blue is the scalar multiplication on as an R-submodule of .
Indeed, by Remark 2, we have:
for all , where is the (multiplicative) identity in R.
Lemma 2.
Let be a -continuous function. Then, the map:
given by:
is an R-module homomorphism, where with .
Proof.
If is any element of , then:
and thus:
that is,
Therefore, we have:
for each . Similarly, if is any element of , then:
for some , and:
Therefore, we obtain:
for each .
If is an element of , then:
that is, the definition of is independent of the choice of representatives. Thus, the map:
is well defined.
We now show that:
is an R-module homomorphism for each . Let:
and:
be the elements of . Then, we have:
that is, preserves the addition.
We note that has the R-module structure for each digital image and that:
is an R-module homomorphism by Lemma 1; that is, the following diagram:
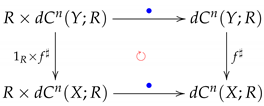 is strictly commutative. Therefore, for all and , we also obtain:
where ⋄ is the ring multiplication in the commutative ring R with identity considered as the R-module over itself as in Definition 5; that is, preserves the scalar multiplication, as required. □
is strictly commutative. Therefore, for all and , we also obtain:
where ⋄ is the ring multiplication in the commutative ring R with identity considered as the R-module over itself as in Definition 5; that is, preserves the scalar multiplication, as required. □

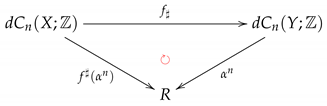
Let be the category of digital images and digital continuous functions as mentioned earlier in Remark 1, and let be the category of unitary R-modules and R-module homomorphisms. Then, we have the following theorem.
Theorem 1.
Let R be a commutative ring with identity . Then, the functor:
given by:
is a contravariant functor for each .
Proof.
If is the identity morphism in and if is any digital n-cocycle, i.e.,
then we have:
that is, , the identity automorphism on for each .
If is a digitally -continuous function and is a digitally -continuous function, then, by Lemmas 1 and 2, we obtain:
for any , . Therefore, we have:
for each , as required. □
Remark 5.
The above results assert that for a digital image X, the assignment is a contravariant functor F from the category of digital images and digital continuous functions to the category of cochain complexes of R-modules and cochain maps. Similarly, the assignment is a covariant functor ; see ([37] (Proposition 6.8)). We note that the following triangle:
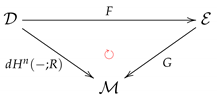 is commutative.
is commutative.

4. Digital Primitive Cohomology Classes
In algebra, a primitive element of a co-algebra C over an element g is an element x that satisfies:
where is the so-called algebraic comultiplication and g is an element of C that maps to the multiplicative identity of the base field (or commutative ring with identity ) under the counit; see ([38] (page 510)).
In this section, we define a digital primitive cohomology class and find out the relationship between R-module homomorphisms of digital cohomology R-modules induced by the digital convolutions and digital continuous functions based on the digital Hopf spaces with digital homotopy multiplications (compare with [39,40]) as the immediate application of a Hopf space in algebraic topology; see also [8,41].
Let be a constant function at , and let:
be the identity function on .
Definition 10
([31,42]). A pointed digital Hopf space consists of a pointed digital image with an adjacency relation and a -continuous function , which is called a digital homotopy multiplication (or digital multiplication for short) such that the following diagrams:
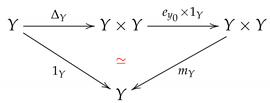 and:
and:
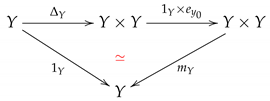 commutate up to pointed digital homotopy, where is the diagonal function.
commutate up to pointed digital homotopy, where is the diagonal function.


Example 3

([42], Example 3.8). Let be a digital image with the eight-adjacent relation, where and as in Example 2. If we define a binary operation by the rule of Table 1, then it can be shown that the pointed digital image is a digital Hopf space with the digital multiplication:
where and and is digital homotopy associative and commutative. There exists also a digital homotopy inverse:
so that becomes a digital commutative Hopf group. Indeed, it is a pointed digital Hopf space.

Table 1.
A binary operation .
One of the reasons for considering a Hopf space with a digital homotopy multiplication is to define the digital version of the usual convolution in mathematics as follows.
Definition 11
([31,42]). If is a digital Hopf space with a digital homotopy multiplication and if:
are the base point preserving -continuous functions, then a digital convolution of and is defined by the digital homotopy class of the composition:
that is,
where is the diagonal function.
Let be the first and second projections onto Y, respectively.
Definition 12.
Let be a digital Hopf space with a digital homotopy multiplication . Then, an element is said to be a digital primitive cohomology class if:
where:
are the R-module homomorphisms of digital cohomology modules induced by the first and second projections respectively; see ([38] (page 804)) and ([8] (page 143)) in the sense of coalgebra and homotopy theory, respectively.
Definition 13
([31,34]). Let and be pointed digital Hopf spaces with digital multiplications and , respectively. A base point preserving -continuous function:
is said to be a digital Hopf function if and are pointed digital -homotopic in ; that is,
Remark 6.
One of the Eilenberg–Steenrod axioms is the homotopy axiom in (generalized) homology and cohomology theories, K-theory, bordism and cobordism theories, Brown–Peterson cohomology theory, and so on; that is, they are invariant under homotopy equivalences. More precisely, homotopic maps induce the same morphism in those theories, i.e., if , then , where C is the covariant (or contravariant) functor inducing those theories (compare with [4]). In our case, it can be seen that if:
then:
Indeed, if:
is a digital -homotopy between f and g; that is, , and if:
is a -continuous function given by:
for all , then there exists an R-module homomorphism:
such that:
that is, plays the role of a chain homotopy between and , where:
- is a digital boundary operator; and
- are R-module homomorphisms (as chain maps) induced by and , respectively.
Since:
and:
we have:
at the level of digital homology modules. By applying the contravariant functor to the above chain homotopy with a little more work, we have the result of Remark 6; see ([43] (Theorems 4.23 and 12.4)) for more details.
Let be the R-submodule of consisting of all the digital primitive cohomology classes. Then, we have the following theorem.
Theorem 2.
Let and be digital Hopf spaces with digital multiplications and , respectively, and let be a digital Hopf function of digital Hopf spaces. Then, we obtain:
where:
is an R-module homomorphism of digital cohomology modules induced by the -continuous functions f.
Proof.
Let be the first and second projections, respectively, onto W, where or Y. Then, by the contravariant functorial property of the digital cohomology R-modules in Theorem 1, the following commutative diagram:
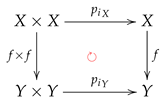 induces a commutative diagram:
induces a commutative diagram:
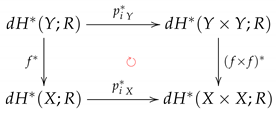 for each .
for each .


Since is a digital Hopf function, by using the digital homotopy relation (2) and Remark 6, we see that the following diagram:
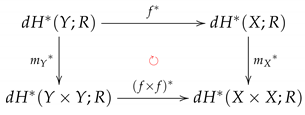 is also strictly commutative.
is also strictly commutative.
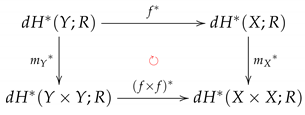
If y is any digital primitive cohomology class in the digital cohomology module with coefficients in a commutative ring R with identity, that is , then we obtain:
Therefore, the image of the R-submodule of under the R-module homomorphism:
is also an R-submodule of , as required. □
We now find the relationship between R-module homomorphisms of digital cohomology R-modules induced by the digital convolutions and digital continuous functions.
Theorem 3.
Let be a digital Hopf space with a digital multiplication , and let:
be -continuous functions. If is any digital primitive cohomology class; that is, , then:
where:
are R-module homomorphisms of digital cohomology modules induced by the -continuous functions f and g, respectively, and similarly for .
Proof.
Once again, we let be the first and second projections, respectively, onto W, where or Y. The contravariant functorial property in Theorem 1 asserts that the following commutative triangle:
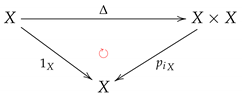 induces a strictly commutative diagram of digital cohomology R-modules:
induces a strictly commutative diagram of digital cohomology R-modules:
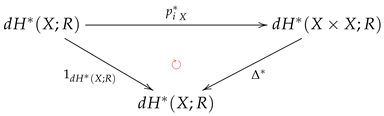 for each , where:
for each , where:


- is the diagonal function;
- is the identity function; and
- is the identity automorphism on .
Similarly, the commutative rectangles:
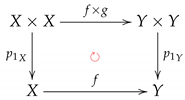 and:
and:
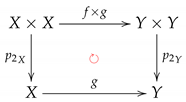 induce the strictly commutative diagrams of digital cohomology R-modules:
induce the strictly commutative diagrams of digital cohomology R-modules:
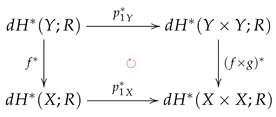 and:
and:
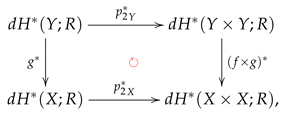 respectively. The digital convolution of and says that:
respectively. The digital convolution of and says that:


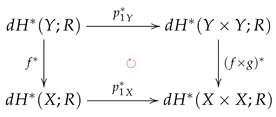
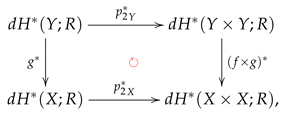
Therefore, if , then we have:
for all and . We note that the third equality above is guaranteed by the fact that y is a digital primitive cohomology class, and the fifth equality comes from the R-module homomorphism:
induced by the diagonal function , as required. □
Remark 7.
The hypothesis of the digital primitive cohomology class in Theorem 3 is absolutely necessary. In general, if y is an element of , which is not necessarily digital primitive, and if:
where is the sum of decomposable digital cohomology classes, then it can be seen that:
5. Conclusions and Further Prospects
Hopf spaces and their Eckmann–Hilton dual notions play an important role in classical (equivariant) homotopy theory in algebraic topology. The digital topology concerns features and properties of the digital images in , especially the two-dimensional or three-dimensional digital images corresponding to the topological features and properties of objects.
In this paper, we investigated some fundamental properties of the digital cohomology modules and the primitive cohomology classes of digital images. More specifically, this study focused on constructing the contravariant functor from the category of (pointed) digital images and (base point preserving) digital continuous functions to the category of unitary R-modules and R-module homomorphisms, where R is a commutative ring with identity . By using the contravariant functorial property in digital cohomology modules, we also examined the digital primitive cohomology classes and developed the relationship between R-module homomorphisms of digital cohomology R-modules induced by the digital convolutions and digital continuous functions.
We hope that our methods will be used to study the advantages of coalgebras along with the Hopf algebras, which will be studied in the near future as a subsequent paper. We also hope that the results will be applied to the concepts of various (algebra) comultiplications with many kinds of perturbations on the (algebraic) objects in many areas of algebra, the algebraic topology, and computer sciences.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2018R1A2B6004407).
Conflicts of Interest
The author declares no conflict of interest.
References
- Arslan, H.; Karaca, I.; Öztel, A. Homology groups of n-dimensinal images. In Proceedings of the XXI Turkish National Mathematics Symposium, Bolu, Turkey, 27 November 2008; p. B1-13. [Google Scholar]
- Boxer, L.; Karaca, I.; Öztel, A. Topological invariants in digital images. J. Math. Sci. Adv. Appl. 2011, 11, 109–140. [Google Scholar]
- Ege, O.; Karaca, I. Digital homotopy fixed point theory. C. R. Acad. Sci. Paris Ser. I 2015, 353, 1029–1033. [Google Scholar] [CrossRef]
- Ege, O.; Karaca, I. Cohomology theory for digital images. Rom. J. Inf. Sci. Technol. 2013, 16, 10–28. [Google Scholar]
- James, I.M. On H-spaces and their homotopy groups. Quart. J. Math. 1960, 11, 161–179. [Google Scholar] [CrossRef]
- Arkowitz, M.; Curjel, C.R. On maps of H-spaces. Topology 1967, 6, 137–148. [Google Scholar] [CrossRef][Green Version]
- Arkowitz, M.; Lupton, G. Loop-theoretic properties of H-spaces. Math. Proc. Camb. Philos. Soc. 1991, 110, 121–136. [Google Scholar] [CrossRef]
- Whitehead, G.W. Elements of Homotopy Theory; Graduate Texts in Math 61; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Eckhardt, U.; Latecki, L. Digital topology. In Current Topics in Pattern Recognition Research, (Research Trends); Council of Scientific Information: Trivandrum, India, 1995. [Google Scholar]
- Hilton, P. Homotopy Theory and Duality; Gordon and Breach Science Publishers: New York, NY, USA; London, UK; Paris, France, 1965. [Google Scholar]
- Berstein, I.; Hilton, P.J. On suspensions and comultiplications. Topology 1963, 2, 73–82. [Google Scholar] [CrossRef]
- Ganea, T. Cogroups and suspensions. Invent. Math. 1970, 9, 185–197. [Google Scholar] [CrossRef]
- Lee, D.-W. Phantom maps and the Gray index. Topol. Appl. 2004, 138, 265–275. [Google Scholar] [CrossRef]
- Arkowitz, M.; Lee, D.-W. Properties of comultiplications on a wedge of spheres. Topol. Appl. 2010, 157, 1607–1621. [Google Scholar] [CrossRef]
- Arkowitz, M.; Lee, D.-W. Comultiplications on a wedge of two spheres. Sci. China Math. 2011, 54, 9–22. [Google Scholar] [CrossRef]
- Lee, D.-W. Comultiplication structures for a wedge of spheres. Filomat 2016, 30, 3525–3546. [Google Scholar] [CrossRef]
- Lee, D.-W. On the digitally quasi comultiplications of digital images. Filomat 2017, 31, 1875–1892. [Google Scholar] [CrossRef]
- Lee, D.-W. Comultiplications on the localized spheres and Moore spaces. Mathematics 2020, 8, 86. [Google Scholar] [CrossRef]
- Lee, D.-W. On the same n-type conjecture for the suspension of the infinite complex projective space. Proc. Am. Math. Soc. 2009, 137, 1161–1168. [Google Scholar] [CrossRef]
- Lee, D.-W. On the same n-type structure for the suspension of the Eilenberg-MacLane spaces. J. Pure Appl. Algebra 2010, 214, 2027–2032. [Google Scholar] [CrossRef]
- Lee, D.-W. On the same n-type of the suspension of the infinite quaternionic projective space. J. Pure Appl. Algebra 2013, 217, 1325–1334. [Google Scholar] [CrossRef]
- Lee, D.-W. On the generalized same N-type conjecture. Math. Proc. Camb. Phil. Soc. 2014, 157, 329–344. [Google Scholar] [CrossRef]
- Lee, D.-W. On the same N-types for the wedges of the Eilenberg-MacLane spaces. Chin. Ann. Math. Ser. B 2016, 37, 951–962. [Google Scholar] [CrossRef]
- Lee, D.-W. Algebraic loop structures on algebra comultiplications. Open Math. 2019, 17, 742–757. [Google Scholar] [CrossRef]
- Lee, D.-W.; Lee, S. Homotopy comultiplications on the k-fold wedge of spheres. Topol. Appl. 2019, 254, 145–170. [Google Scholar] [CrossRef]
- Boxer, L. Homotopy properties of sphere-like digital images. J. Math. Imaging Vis. 2006, 24, 167–175. [Google Scholar] [CrossRef]
- Boxer, L. Digitally continuous functions. Pattern Recognit. Lett. 1994, 15, 833–839. [Google Scholar] [CrossRef]
- Boxer, L. A classical construction for the digital fundamental group. J. Math. Imaging Vis. 1999, 10, 51–62. [Google Scholar] [CrossRef]
- Rosenfeld, A. Continuous functions on digital pictures. Pattern Recognit. Lett. 1986, 4, 177–184. [Google Scholar] [CrossRef]
- Boxer, L. Properties of digital homotopy. J. Math. Imaging Vis. 2005, 22, 19–26. [Google Scholar] [CrossRef]
- Lee, D.-W. Digital H-spaces and actions in the pointed digital homotopy category. Appl. Algebra Engrg. Comm. Comput. 2020, 31, 149–169. [Google Scholar] [CrossRef]
- Khalimsky, E. Motion, deformation, and homotopy in finite spaces. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Alexandria, VA, USA, 20 October 1987; pp. 227–234. [Google Scholar]
- Lee, D.-W. Digital singular homology groups of digital images. Far East J. Math. Sci. (FJMS) 2014, 71, 39–63. [Google Scholar]
- Lee, S.; Kim, Y.; Lim, J.-E.; Lee, D.-W. On the Digital Pontryagin Algebras. Symmetry 2020, 12, 875. [Google Scholar] [CrossRef]
- Vergili, T.; Karaca, I. Some properties of homology groups of Khalimsky spaces. Math. Sci. Lett. 2015, 4, 131–140. [Google Scholar]
- Munkres, J.R. Elements of Algebraic Topology; Addison-Wesley Publishing Company: Menlo Park, CA, USA, 1984. [Google Scholar]
- Rotman, J.J. An Introduction to Homological Algebra, 2nd ed.; Universitext; Springer: New York, NY, USA, 2009. [Google Scholar]
- Strom, J. Modern Classical Homotopy Theory; Graduate Studies in Mathematics, 127; American Mathematical Society: Providence, RI, USA, 2011. [Google Scholar]
- Ege, O.; Karaca, I. Digital H-spaces. In Proceedings of the 3rd International Symposium on Computing in Science and Engineering, ISCSE, Kusadasi, Aydin, Turkey, 24–25 October 2013; pp. 133–138. [Google Scholar]
- Ege, O.; Karaca, I. Some properties of digital H-spaces. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1930–1941. [Google Scholar] [CrossRef]
- Spanier, E. Algebraic Topology; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Lee, D.-W. Near-rings on digital Hopf groups. Appl. Algebra Engrg. Comm. Comput. 2018, 29, 261–282. [Google Scholar] [CrossRef]
- Rotman, J.J. An Introduction to Algebraic Topology; Graduate Texts in Mathematics, 119; Springer: New York, NY, USA, 1988. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).