Dual Associate Null Scrolls with Generalized 1-Type Gauss Maps

Abstract

In this work, a pair of dual associate null scrolls are defined from the Cartan Frenet frame of a null curve in Minkowski 3-space. The fundamental geometric properties of the dual associate null scrolls are investigated and they are related in terms of their Gauss maps, especially the generalized 1-type Gauss maps. At the same time, some representative examples are given and their graphs are plotted by the aid of a software programme.

1. Introduction

In differential geometry, the associate curves and associate surfaces such as the Bertrand curve, the Mannheim curve, evolute-involute pair, the parallel surfaces and the focal surfaces etc. compose a large class of fascinating subjects in the curve and surface theory not only in Euclidean space but also in pseudo-Euclidean space, such as Minkowski space [1,2,3,4]. However, due to the difference of metric between Euclidean space and Minkowski space, there are cases where there are differences. For example, the Bertrand curve could be involved by the directional associated curve of a space curve due to the causal character of vectors in Minkowski space [5].

As the simplest foliated submanifolds, ruled surfaces are divided into five types according to the causal character of the base curve and the ruling flow [6]. Among of them, for the ruled surfaces with lightlike rulings, the base curves can be null curves or non-null curves obviously. It is worth noting that the ruled surfaces with non-null base curves are equivalent to the ones with null base curves via the appropriate transformation as stated in [7]. Without loss of generality, we always can choose a null curve as the base curve of a ruled surface with lightlike ruling and the normalization condition is satisfied at the same time, which is said to be a null scroll [7,8,9,10]. Furthermore, the null scroll under Cartan Frenet frame is called a B-scroll [11].

Considering the normalization condition of a null scroll and the Frenet frame of a null curve, in the present work, a pair of null scrolls satisfying the same normalization condition are constructed, i.e., the tangent vector field of the base curve of the first null scroll is set as the ruling flow of the second null scroll and the tangent vector field of the base curve of the second null scroll is set as the ruling flow of the first null scroll. Since the 1970’s, many research works about the classification of submanifolds respect to the Laplacian of Gauss maps have been done in Euclidean space and Minkowski space, which are very useful tools in investigating and characterizing many important submanifolds [12,13,14,15]. Based on the fundamental geometric properties of the null scroll pair, we aim at the Laplacian of the Gauss maps of the dual associate null scrolls according to the current progress for the classifications of submanifolds respect to the Gauss maps proposed in [16], i.e., the generalized 1-type Gauss map, which can be regarded as a generalization of both 1-type Gauss map and pointwise 1-type Gauss map. The Gauss map $\mathbb{G}$ of a submanifold $\mathbb{M}$ is of generalized 1-type if the Gauss map $\mathbb{G}$ of $\mathbb{M}$ satisfies

$$\Delta \mathbb{G}=f\mathbb{G}+gC$$

(1)

for some non-zero functions $(f,g)$ on $\mathbb{M}$ and a constant vector C, where $\Delta$ denotes the Laplacian defined on $\mathbb{M}$, which is given by

$$\Delta =-\frac{1}{\sqrt{\left|\mathcal{G}\right|}}\sum _{i,j}\frac{\partial }{\partial x^i}\left(\sqrt{\left|\mathcal{G}\right|}{g}^{ij}\frac{\partial }{\partial x^j}\right),$$

(2)

where $(x_1,\dots ,x_n)$ is a local coordinate system of $\mathbb{M}$, $g^{ij}$ the components of the inverse matrix of the first fundamental form of $\mathbb{M}$ and $\mathcal{G}$ the determinant of the first fundamental form of $\mathbb{M}$ [17]. Especially, if both f and g are non-zero constants, (1) can be written by $\Delta \mathbb{G}=\mu (\mathbb{G}+C)$, $(\mu \in \mathbb{R}-\{0\left\}\right)$. In this case, the Gauss map is just of 1-type in the usual sense. If the function f is equal to g, (1) can be expressed by $\Delta \mathbb{G}=f(\mathbb{G}+C)$. The Gauss map is said to be of pointwise 1-type. More precisely, the pointwise 1-type Gauss map is said to be of the first kind when $C=0$, or else the second kind. If f and g vanish identically, then $\mathbb{G}$ is said to be harmonic.

The paper is organized as follows. In Section 2, some basic facts including the Frenet formula and the structure function of null curves are reviewed, then a pair of associate curves on lightlike cone and a dual associate null scrolls are defined. In Section 3, the geometric properties such as the Gaussian curvatures, mean curvatures and the Laplacians of the Gauss maps are shown and the generalized 1-type Gauss maps are discussed, respectively. The relationships between the dual associate null scrolls are explored and summarized.

Throughout this paper, all the geometric objects under consideration are smooth and all surfaces are connected unless otherwise stated.

2. Preliminaries

Let ${\mathbb{E}}_1^3$ be the Minkowski 3-space with natural Lorentzian metric

$$⟨·,·⟩=d{x}_1^2+d{x}_2^2-d{x}_3^2$$

in terms of the natural coordinate system $(x_1,x_2,x_3)$. A vector v in ${\mathbb{E}}_1^3$ is said to be spacelike, timelike and lightlike (null) if $⟨v,v⟩>0$ or $v=0$, $⟨v,v⟩<0$ and $⟨v,v⟩=0$$(v\ne 0)$, respectively. The norm of a vector v is defined by $\parallel v\parallel =\sqrt{|⟨v,v⟩|}$. An arbitrary curve r is spacelike, timelike or lightlike if its tangent vector $r^{\prime }$ is spacelike, timelike or lightlike, correspondingly. At the same time, a surface is said to be timelike, spacelike or lightlike if its normal vector is spacelike, timelike or lightlike, respectively.

Proposition 1

([5]). Let $r\left(s\right)$ be a null curve parameterized by the null arc length s (i.e., $\parallel r^{″}\left(s\right)\parallel =1$)in ${\mathbb{E}}_1^3$. Then there exists a unique Cartan frame $\{r^{\prime }\left(s\right)=T\left(s\right),N\left(s\right),B\left(s\right)\}$ such that

$$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)=N\left(s\right),\hfill \\ N^{\prime }\left(s\right)=\kappa \left(s\right)T\left(s\right)-B\left(s\right),\hfill \\ B^{\prime }\left(s\right)=-\kappa \left(s\right)N\left(s\right),\hfill \end{array}\right.$$

(3)

where $⟨T\left(s\right),T\left(s\right)⟩=⟨B\left(s\right),B\left(s\right)⟩=⟨T\left(s\right),N\left(s\right)⟩=⟨B\left(s\right),N\left(s\right)⟩=0,⟨T\left(s\right),B\left(s\right)⟩=⟨N\left(s\right),N\left(s\right)⟩=1$ and $T\left(s\right)=N\left(s\right)\times T\left(s\right),N\left(s\right)=T\left(s\right)\times B\left(s\right),-B\left(s\right)=N\left(s\right)\times B\left(s\right).$

In the sequence, $T\left(s\right),N\left(s\right)$ and $B\left(s\right)$ is called the tangent, principal normal and binormal vector field of $r\left(s\right)$, respectively. From (3), it is easy to know that $\kappa \left(s\right)=-\frac{1}{2}⟨r^{‴}\left(s\right),r^{‴}\left(s\right)⟩$. The function $\kappa \left(s\right)$ is called the null curvature of $r\left(s\right)$, which is an invariant under Lorentzian transformations [18].

Considering the relationship between the tangent vector field $T\left(s\right)$ and the binormal vector field $B\left(s\right)$ of a null curve $r\left(s\right)$, i.e., $⟨T\left(s\right),B\left(s\right)⟩=1$, we could define a pair of associate curves on lightlike cone as follows:

Definition 1.

Let $r\left(s\right)$ be a null curve framed by $\left\{T\right(s),N(s),B(s\left)\right\}$ in ${\mathbb{E}}_1^3$. Then $b_1\left(s\right)=\lambda \left(s\right)T\left(s\right)$, $b_2\left(s\right)=\frac{1}{\lambda \left(s\right)}B\left(s\right)$ is called a generalized T-associate curve and a generalized B-associate curve of $r\left(s\right)$ for some non-zero smooth function $\lambda \left(s\right)$, respectively. $b_1\left(s\right)$ and $b_2\left(s\right)$ are called dual associate curves of $r\left(s\right)$ on lightlike cone.

In [5], the authors introduced the structure function and the representation formula of a null curve. Namely,

Proposition 2

([5]). Let $r\left(s\right):I\to {\mathbb{E}}_1^3$ be a null curve. Then $r\left(s\right)$ can be written as

$$r\left(s\right)=\int \frac{1}{2f^{\prime }}(f^2-1,2f,f^2+1)ds,(f^{\prime }=\frac{df}{ds}),$$

(4)

where $f=f\left(s\right)$ is called the structure function of $r\left(s\right)$. And the null curvature $\kappa \left(s\right)$ of $r\left(s\right)$ can be expressed by

$$\kappa \left(s\right)=\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{(log{f}^{\prime })}^{″}.$$

(5)

Definition 2

([6]). Let $a\left(s\right):{\mathrm{I}}_1\to {\mathbb{E}}_1^3$ be a null curve parameterized by null arc length and $b\left(s\right)$ a transversal null vector field along $a\left(s\right)$. Then the immersion

$$X(s,t)=a\left(s\right)+tb\left(s\right),(t\in {\mathrm{I}}_2\subset \mathbb{R})$$

is called a null scroll which satisfies $⟨a^{\prime }\left(s\right),a^{\prime }\left(s\right)⟩=0$, $⟨b\left(s\right),b\left(s\right)⟩=0$ and the normalization condition $⟨a^{\prime }\left(s\right),b\left(s\right)⟩=1$.

According to the definitions of generalized T-associate curve, generalized B-associate curve of a null curve and the definition of null scrolls, we want to construct a pair of null scrolls which satisfy the same normalization condition. This idea motivate the following definition.

Definition 3.

Let $r\left(s\right)$ be a null curve framed by $\left\{T\right(s),N(s),B(s\left)\right\}$ in ${\mathbb{E}}_1^3$, $b_1\left(s\right)$ and $b_2\left(s\right)$ dual associate curves of $r\left(s\right)$. Then

$$X_1(s,t_1)=\int b_2\left(s\right)ds+t_1{b}_1\left(s\right)$$

(6)

is called a null scroll with generalized T-lightlike ruling;

$$X_2(s,t_2)=\int b_1\left(s\right)ds+t_2{b}_2\left(s\right)$$

(7)

is called a null scroll with generalized B-lightlike ruling. The null scrolls $X_1(s,t_1)$ and $X_2(s,t_2)$ are called dual associate null scrolls.

As the straightforward conclusion of Proposition 2, Definitions 1 and 3, we have

Proposition 3.

Let $r\left(s\right)$ be a null curve with structure function $f=f\left(s\right)$ in ${\mathbb{E}}_1^3$. Then

• the dual associate curves $b_i\left(s\right)$$(i=1,2)$ of $r\left(s\right)$ can be expressed by

  $$\left\{\begin{array}{c}\begin{array}{cc}\hfill b_1\left(s\right)=& \frac{\lambda }{2f^{\prime }}(f^2-1,2f,f^2+1),\hfill \\ \hfill b_2\left(s\right)=& \frac{1}{\lambda }(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1));\hfill \end{array}\hfill \end{array}\right.$$
• the dual associate null scrolls $X_i\left(s\right)$$(i=1,2)$ can be expressed by

  $$\left\{\begin{array}{c}\begin{array}{c}\hfill X_1(s,t_1)=\int \frac{1}{\lambda }(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1))ds+t_1\frac{\lambda }{2f^{\prime }}(f^2-1,2f,f^2+1),\\ \hfill X_2(s,t_2)=\int \frac{\lambda }{2f^{\prime }}(f^2-1,2f,f^2+1)ds+t_2\frac{1}{\lambda }(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1)).\end{array}\hfill \end{array}\right.$$

Obviously, the dual associate curves and the dual associate null scrolls are decided by the function $\lambda \left(s\right)$ and the structure function $f\left(s\right)$, completely. The following example can explain the construction of the defined dual associate null scrolls.

Example 1.

Consider a null curve $r\left(s\right)$ with null curvature $\kappa \left(s\right)=4s^{-2}$. From Proposition 2, we have

$$\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{(log{f}^{\prime })}^{″}=4s^{-2}.$$

Solving the above differential equation, we have $f\left(s\right)=s^3$ or $f\left(s\right)=s^{-3}$. From Proposition 3, we have

• when $\lambda \left(s\right)=\frac{1}{3},$ the dual associate curves and the dual associate null scrolls can be written as (see Figure 1 and Figure 2)

  $$\left\{\begin{array}{c}{b}_1\left(s\right)=\frac{s}{18}(s^3-s^{-3},2,s^3+s^{-3}),\hfill \\ b_2\left(s\right)=(-4s^2+s^{-4},4s^{-1},-4s^2-s^{-4})\hfill \end{array}\right.$$

  and

  $$\left\{\begin{array}{c}{X}_1(s,t_1)=\frac{1}{3}(-4s^3-s^{-3},12logs,-4s^3+s^{-3})+\frac{t_{1}s}{18}(s^3-s^{-3},2,s^3+s^{-3}),\hfill \\ X_2(s,t_2)=\frac{1}{18}(\frac{s^5}{5}+s^{-1},s^2,\frac{s^5}{5}-s^{-1})+t_2(-4s^2+s^{-4},4s^{-1},-4s^2-s^{-4});\hfill \end{array}\right.$$
  

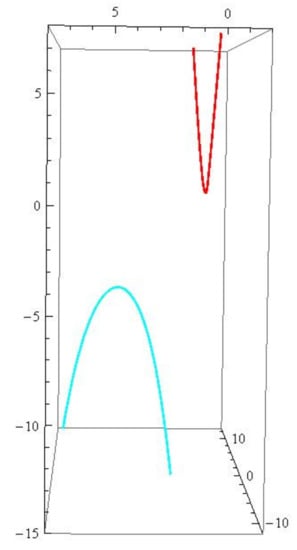  Figure 1. The red (blue) curve is the generalized $T\left(B\right)$-associate curve $b_1\left(b_2\right)$ of r.
  

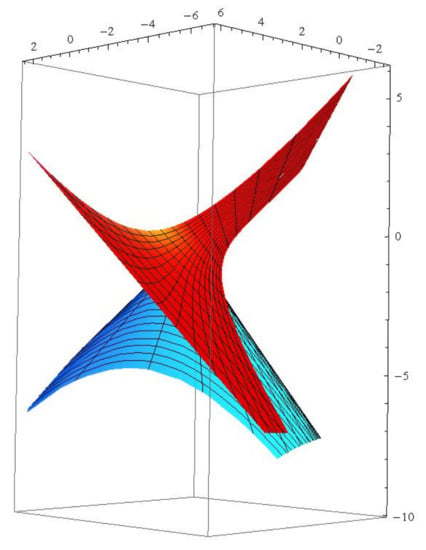  Figure 2. The red (blue) surface is the null scroll with generalized $T\left(B\right)$-lightlike ruling $X_1\left(X_2\right)$.
• when $\lambda \left(s\right)=s,$ the dual associate curves and the dual associate null scrolls can be written as (see Figure 3 and Figure 4)

  $$\left\{\begin{array}{c}{b}_1\left(s\right)=\frac{s^2}{6}(s^3-s^{-3},2,s^3+s^{-3}),\hfill \\ b_2\left(s\right)=\frac{1}{3s}(-4s^2+s^{-4},4s^{-1},-4s^2-s^{-4})\hfill \end{array}\right.$$

  and

  $$\left\{\begin{array}{c}{X}_1(s,t_1)=\frac{1}{3}(-2s^2-\frac{1}{4}{s}^{-4},-4s^{-1},-2s^2+\frac{1}{4}{s}^{-4})+\frac{t_1{s}^2}{6}(s^3-s^{-3},2,s^3+s^{-3}),\hfill \\ X_2(s,t_2)=\frac{1}{36}(s^6-6logs,4s^3,s^6+6logs)+\frac{t_2}{3s}(-4s^2+s^{-4},4s^{-1},-4s^2-s^{-4}).\hfill \end{array}\right.$$
  

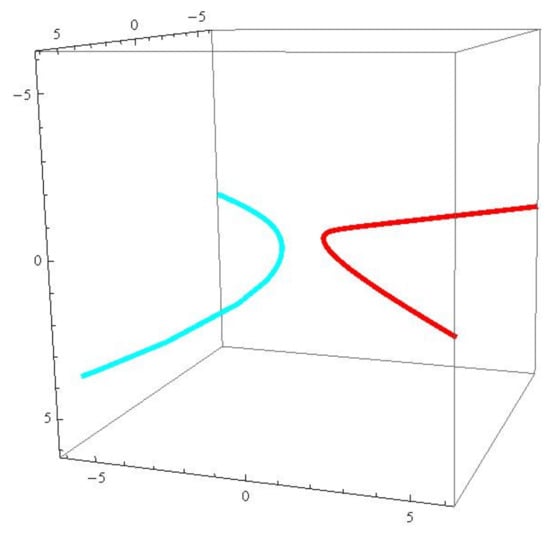  Figure 3. The red (blue) curve is the generalized $T\left(B\right)$-associate curve $b_1\left(b_2\right)$ of r.
  

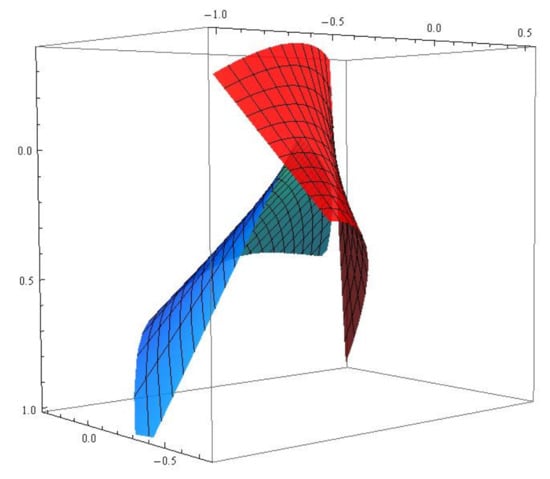  Figure 4. The red (blue) surface is the null scroll with generalized $T\left(B\right)$-lightlike ruling $X_1\left(X_2\right)$.

3. Main Result

We will discuss the geometric properties of the dual associate null scrolls and the Laplacians of their Gauss maps.

3.1. The Null Scroll with Generalized T-Lightlike Ruling

To meet the requirements of discussion, we prepare some basic elements of $X_1(s,t_1)$. Initially, from (6) and Proposition 1, we have

$$X_{1s}=t_1{\lambda }^{\prime }T+t_1\lambda N+\frac{1}{\lambda }B,X_{1t_1}=\lambda T.$$

Based on above equations, the components of the first fundamental form $g_{ij}(i,j=1,2)$ are

$$\begin{array}{cc}\hfill g_{11}=& ⟨X_{1s},X_{1s}⟩=t_1^2{\lambda }^2+\frac{2t_1{\lambda }^{\prime }}{\lambda },\hfill \\ \hfill g_{12}=& ⟨X_{1s},X_{1t_1}⟩=1,\hfill \\ \hfill g_{22}=& ⟨X_{1t_1},X_{1t_1}⟩=0,\hfill \end{array}$$

(8)

then, we have $g_{11}{g}_{22}-g_{12}^2=-1.$ Meanwhile, the Gauss map ${\mathbb{G}}_1$ of $X_1$ is given by

$${\mathbb{G}}_1=\frac{X_{1s}\times X_{1t_1}}{\parallel X_{1s}\times X_{1t_1}\parallel }=t_1{\lambda }^{2}T-N$$

(9)

which satisfies $⟨{\mathbb{G}}_1,{\mathbb{G}}_1⟩=1.$ Furthermore, by (9), we have

$$\begin{array}{cc}\hfill & {\mathbb{G}}_{1s}=(2t_1\lambda {\lambda }^{\prime }-\kappa )T+t_1{\lambda }^{2}N+B,\hfill \\ \hfill & {\mathbb{G}}_{1t_1}={\lambda }^{2}T.\hfill \end{array}$$

(10)

Then, the components of the second fundamental form $h_{ij}(i,j=1,2)$ are

$$\begin{array}{cc}\hfill h_{11}=& -⟨X_{1s},{\mathbb{G}}_{1s}⟩=\frac{\kappa }{\lambda }-3t_1{\lambda }^{\prime }-t_1^2{\lambda }^3,\hfill \\ \hfill h_{12}=& -⟨X_{1t_1},{\mathbb{G}}_{1s}⟩=-\lambda ,\hfill \\ \hfill h_{22}=& -⟨X_{1t_1},{\mathbb{G}}_{1t_1}⟩=0.\hfill \end{array}$$

(11)

By (8) and (11), the Gaussian curvature $K_1$ and the mean curvature $H_1$ of $X_1$ are given by, respectively

$$K_1=\frac{h_{11}{h}_{22}-h_{12}^2}{g_{11}{g}_{22}-g_{12}^2}={\lambda }^2,$$

(12)

$$H_1=\frac{g_{11}{h}_{22}-2g_{12}{h}_{12}+g_{22}{h}_{11}}{2(g_{11}{g}_{22}-g_{12}^2)}=-\lambda .$$

(13)

Obviously, the Gaussian curvature $K_1$ and the mean curvature $H_1$ of $X_1$ satisfy

$$H_1^2=K_1={\lambda }^2.$$

(14)

From now on, we compute the Laplacian of Gauss map ${\mathbb{G}}_1$ and discuss the null scroll $X_1$ with generalized 1-type Gauss map.

By (2), the Laplacian ${\Delta }_1$ of the null scroll $X_1$ is obtained by

$${\Delta }_1=-2\frac{\partial }{\partial s}\frac{\partial }{\partial t_1}+2({\lambda }^2{t}_1+\frac{{\lambda }^{\prime }}{\lambda })\frac{\partial }{\partial t_1}+({\lambda }^2{t}_1^2+2\frac{{\lambda }^{\prime }{t}_1}{\lambda })\frac{{\partial }^2}{\partial t_1^2}.$$

(15)

Substituting (9) into (15), we get

$${\Delta }_1{\mathbb{G}}_1=(2{\lambda }^4{t}_1-2\lambda {\lambda }^{\prime })T-2{\lambda }^{2}N=(2K_1^2{t}_1-K_1^{\prime })T-2K_{1}N.$$

(16)

Suppose that $X_1$ has generalized 1-type Gauss map, i.e., ${\Delta }_1{\mathbb{G}}_1=f_1{\mathbb{G}}_1+g_1{C}_1$. Without loss of generality, we may decompose the constant vector $C_1$ via the Cartan frame $\{T,N,B\}$ of the null curve $r\left(s\right)$ as

$$C_1=C_{11}T+C_{12}N+C_{13}B,$$

(17)

where $C_{11}=⟨C_1,B⟩,C_{12}=⟨C_1,N⟩,C_{13}=⟨C_1,T⟩$.

Substituting (9), (16) and (17) into ${\Delta }_1{\mathbb{G}}_1=f_1{\mathbb{G}}_1+g_1{C}_1$, we obtain the following equation system

$$\left\{\begin{array}{c}2{\lambda }^4{t}_1-2\lambda {\lambda }^{\prime }={\lambda }^2{t}_1{f}_1+g_1{C}_{11},\hfill \\ -2{\lambda }^2=g_1{C}_{12}-f_1,\hfill \\ g_1{C}_{13}=0.\hfill \end{array}\right.$$

(18)

Since $g_1$ is a non-zero smooth function, then $C_{13}=0$ from the last equation of (18). Furthermore, by the first two equations of (18), we have

$$\left\{\begin{array}{c}{f}_1(s,t_1)=\frac{C_{12}(2{\lambda }^4{t}_1-2\lambda {\lambda }^{\prime })+2{\lambda }^2{C}_{11}}{C_{12}{\lambda }^2{t}_1+C_{11}}=\frac{C_{12}(2K_1^2{t}_1-K_1^{\prime })+2K_1{C}_{11}}{C_{12}{K}_1{t}_1+C_{11}},\hfill \\ g_1(s,t_1)=-\frac{2\lambda {\lambda }^{\prime }}{C_{12}{\lambda }^2{t}_1+C_{11}}=-\frac{K_1^{\prime }}{C_{12}{K}_1{t}_1+C_{11}},\hfill \end{array}\right.$$

(19)

where $C_{11}^2+C_{12}^2\ne 0.$ Meanwhile, $\lambda$ is a non-constant function since $g_1$ is a non-zero smooth function.

Conversely, if we use the above information with the given functions $(f_1,g_1)$ in (19) and the constant vector $C_1$, then the null scroll $X_1$ satisfies ${\Delta }_1{\mathbb{G}}_1=f_1{\mathbb{G}}_1+g_1{C}_1$.

Theorem 1.

Let $X_1$ be a null scroll with generalized T-lightlike ruling in ${\mathbb{E}}_1^3$. Then $X_1$ has generalized 1-type Gauss map if and only if the Gauss map ${\mathbb{G}}_1$ of $X_1$ satisfies

$${\Delta }_1{\mathbb{G}}_1=f_1{\mathbb{G}}_1+g_1{C}_1$$

for some non-zero smooth functions $(f_1,g_1)$ as

$$\left\{\begin{array}{c}{f}_1=f_1(s,t_1)=\frac{C_{12}(2{\lambda }^4{t}_1-2\lambda {\lambda }^{\prime })+2{\lambda }^2{C}_{11}}{C_{12}{\lambda }^2{t}_1+C_{11}}=\frac{C_{12}(2K_1^2{t}_1-K_1^{\prime })+2K_1{C}_{11}}{C_{12}{K}_1{t}_1+C_{11}},\hfill \\ g_1=g_1(s,t_1)=-\frac{2\lambda {\lambda }^{\prime }}{C_{12}{\lambda }^2{t}_1+C_{11}}=-\frac{K_1^{\prime }}{C_{12}{K}_1{t}_1+C_{11}}\hfill \end{array}\right.$$

and a constant vector $C_1=(C_{11},C_{12},0)$. Where $C_{11}^2+C_{12}^2\ne 0$, $\lambda =\lambda \left(s\right)$ is a non-constant smooth function.

Remark 1.

Particularly, when $C_1=(C_{11},0,0)$, ($C_{11}\ne 0$), the functions $(f_1,g_1)$ only depend on s, i.e.,

$$\left\{\begin{array}{c}{f}_1=f_1\left(s\right)=2{\lambda }^2=2K_1,\hfill \\ g_1=g_1\left(s\right)=-\frac{2\lambda {\lambda }^{\prime }}{C_{11}}=-\frac{K_1^{\prime }}{C_{11}}.\hfill \end{array}\right.$$

Corollary 1.

Let $X_1$ be a null scroll with generalized T-lightlike ruling in ${\mathbb{E}}_1^3$. Then $X_1$ has pointwise 1-type Gauss map of the second kind if and only if the Gauss map ${\mathbb{G}}_1$ of $X_1$ satisfies

$${\Delta }_1{\mathbb{G}}_1=f_1({\mathbb{G}}_1+C_1)$$

for some non-zero smooth function $f_1$ as

$$f_1=f_1\left(s\right)=2{\lambda }^2=C_0^2{e}^{-2C_{11}s},(C_0\in \mathbb{R}-\left\{0\right\})$$

and a constant vector $C_1=(C_{11},0,0)$, ($C_{11}\ne 0$).

Proof of Corollary 1.

Suppose that the null scroll $X_1$ has pointwise 1-type Gauss map of the second kind. It means that $f_1=g_1$ in Theorem 1. Thus, we have

$${\lambda }^4{C}_{12}{t}_1-\lambda {\lambda }^{\prime }{C}_{12}+\lambda {\lambda }^{\prime }=-{\lambda }^2{C}_{11}.$$

(20)

From (20), we can get the following equation system

$$\left\{\begin{array}{c}{\lambda }^4{C}_{12}{t}_1=0,\hfill \\ -\lambda {\lambda }^{\prime }{C}_{12}+\lambda {\lambda }^{\prime }=-{\lambda }^2{C}_{11}.\hfill \end{array}\right.$$

(21)

Since $\lambda$ is a non-zero smooth function, $C_{12}=0$ is concluded from the first equation of (21). By the second equation of (21), we get differential equation $\lambda {\lambda }^{\prime }=-{\lambda }^2{C}_{11}.$ Solving this equation, we have

$$\lambda =\frac{C_0}{\sqrt{2}}{e}^{-C_{11}s}(C_0\in \mathbb{R}-\left\{0\right\}).$$

By Remark 1, $f_1=2{\lambda }^2=C_0^2{e}^{-2C_{11}s}$, ($C_{11}\ne 0$). Conversely, if we use the above information with the given function $f_1$ and constant vector $C_1$, the null scroll $X_1$ satisfies ${\Delta }_1{\mathbb{G}}_1=f_1({\mathbb{G}}_1+C_1)$.  □

Corollary 2.

There does not exist the null scroll with generalized T-lightlike ruling in ${\mathbb{E}}_1^3$ which has 1-type Gauss map of the second kind.

Proof of Corollary 2.

Suppose that the null scroll $X_1$ has 1-type Gauss map of the second kind, i.e., ${\Delta }_1{\mathbb{G}}_1=\mu ({\mathbb{G}}_1+C_1),(\mu \in \mathbb{R}-\left\{0\right\})$. It means that $f_1=\mu$, then $C_{11}=0$ which contradicts with $C_{11}\ne 0$ in Corollary 1.  □

Corollary 3.

Let $X_1$ be a null scroll with generalized T-lightlike ruling in ${\mathbb{E}}_1^3$. Then $X_1$ has pointwise 1-type Gauss map of the first kind if and only if one of the following statements holds:

• $X_1$ has 1-type Gauss map of the first kind;
• $X_1$ has non-zero constant Gaussian curvature or non-zero constant mean curvature.

Proof of Corollary 3

Suppose that the null scroll $X_1$ has pointwise 1-type Gauss map of the first kind, i.e., ${\Delta }_1{\mathbb{G}}_1=f_1{\mathbb{G}}_1$. From Corollary 1, we can get $C_{11}=0$ and $f_1=2{\lambda }^2=C_0^2.$ Therefore, $X_1$ has 1-type Gauss map of the first kind since ${\Delta }_1{\mathbb{G}}_1=C_0^2{\mathbb{G}}_1,(C_0\in \mathbb{R}-\left\{0\right\})$. By (12) and (13), the Gaussian curvature $K_1$ and the mean curvature $H_1$ are non-zero constant. Conversely, if one of the statements holds, it follows that $\lambda$ is a non-zero constant. This completes the proof.  □

Corollary 4.

There does not exist the null scroll with generalized T-lightlike ruling in ${\mathbb{E}}_1^3$ which has harmonic Gauss map.

Proof of Corollary 4

Suppose that the null scroll $X_1$ has harmonic Gauss map, i.e., ${\Delta }_1{\mathbb{G}}_1=0$. Then, we have $\lambda =0$ and it is impossible.  □

3.2. The Null Scroll with Generalized B-Lightlike Ruling

To meet the requirements of discussion, we prepare some basic elements of $X_2$. Initially, from (7) and Proposition 1, we have

$$X_{2s}=\lambda T-\frac{t_2\kappa }{\lambda }N-\frac{t_2{\lambda }^{\prime }}{{\lambda }^2}B,X_{2t_2}=\frac{1}{\lambda }B.$$

Based on above equations, the components of the first fundamental form $g_{ij}(i,j=1,2)$ are

$$\begin{array}{cc}\hfill g_{11}=& ⟨X_{2s},X_{2s}⟩=\frac{t_2^2{\kappa }^2}{{\lambda }^2}-\frac{2t_2{\lambda }^{\prime }}{\lambda },\hfill \\ \hfill g_{12}=& ⟨X_{2s},X_{2t_2}⟩=1,\hfill \\ \hfill g_{22}=& ⟨X_{2t_2},X_{2t_2}⟩=0,\hfill \end{array}$$

(22)

then, we have $g_{11}{g}_{22}-g_{12}^2=-1.$ Meanwhile, the Gauss map ${\mathbb{G}}_2$ of $X_2$ is given by

$${\mathbb{G}}_2=\frac{X_{2s}\times X_{2t_2}}{\parallel X_{2s}\times X_{2t_2}\parallel }=N+\frac{t_2\kappa }{{\lambda }^2}B$$

(23)

which satisfies $⟨{\mathbb{G}}_2,{\mathbb{G}}_2⟩=1.$ Furthermore, by (23), we have

$$\begin{array}{cc}\hfill & {\mathbb{G}}_{2s}=\kappa T-\frac{t_2{\kappa }^2}{{\lambda }^2}N+(t_2{\left(\frac{\kappa }{{\lambda }^2}\right)}^{\prime }-1)B,\hfill \\ \hfill & {\mathbb{G}}_{2t_2}=\frac{\kappa }{{\lambda }^2}B.\hfill \end{array}$$

(24)

Then, the components of the second fundamental form $h_{ij}(i,j=1,2)$ are

$$\begin{array}{cc}\hfill h_{11}=& -⟨X_{2s},{\mathbb{G}}_{2s}⟩=\lambda (1-t_2{\left(\frac{\kappa }{{\lambda }^2}\right)}^{\prime })-\frac{t_2^2{\kappa }^3}{{\lambda }^3}+\frac{t_2\kappa {\lambda }^{\prime }}{{\lambda }^2},\hfill \\ \hfill h_{12}=& -⟨X_{2t_2},{\mathbb{G}}_{2s}⟩=-\frac{\kappa }{\lambda },\hfill \\ \hfill h_{22}=& -⟨X_{2t_2},{\mathbb{G}}_{2t_2}⟩=0.\hfill \end{array}$$

(25)

By (22) and (25), the Gaussian curvature $K_2$ and the mean curvature $H_2$ of $X_2$ are given by, respectively

$$K_2=\frac{h_{11}{h}_{22}-h_{12}^2}{g_{11}{g}_{22}-g_{12}^2}=\frac{{\kappa }^2}{{\lambda }^2},$$

(26)

$$H_2=\frac{g_{11}{h}_{22}-2g_{12}{h}_{12}+g_{22}{h}_{11}}{2(g_{11}{g}_{22}-g_{12}^2)}=-\frac{\kappa }{\lambda }.$$

(27)

It is evident that the Gaussian curvature $K_2$ and the mean curvature $H_2$ of $X_2$ satisfy

$$H_2^2=K_2=\frac{{\kappa }^2}{{\lambda }^2}.$$

(28)

From now on, we compute the Laplacian of Gauss map ${\mathbb{G}}_2$ and discuss the null scroll $X_2$ with generalized 1-type Gauss map.

By (2), the Laplacian ${\Delta }_2$ of the null scroll $X_2$ is obtained by

$${\Delta }_2=-2\frac{\partial }{\partial s}\frac{\partial }{\partial t_2}+2(\frac{{\kappa }^2{t}_2}{{\lambda }^2}-\frac{{\lambda }^{\prime }}{\lambda })\frac{\partial }{\partial t_2}+(\frac{{\kappa }^2{t}_2^2}{{\lambda }^2}-\frac{2{\lambda }^{\prime }{t}_2}{\lambda })\frac{{\partial }^2}{\partial t_2^2}.$$

(29)

Substituting (23) into (29), we get

$${\Delta }_2{\mathbb{G}}_2=\frac{2{\kappa }^2}{{\lambda }^2}N+(\frac{2\kappa {\lambda }^{\prime }}{{\lambda }^3}+\frac{2{\kappa }^3{t}_2}{{\lambda }^4}-\frac{2{\kappa }^{\prime }}{{\lambda }^2})B=2K_{2}N+\frac{2K_2^2{t}_2-K_2^{\prime }}{\kappa }B.$$

(30)

Suppose that $X_2$ has generalized 1-type Gauss map, i.e., ${\Delta }_2{\mathbb{G}}_2=f_2{\mathbb{G}}_2+g_2{C}_2$. Without loss of generality, we may decompose the constant vector $C_2$ via the Cartan frame $\{T,N,B\}$ of $r\left(s\right)$ as

$$C_2=C_{21}T+C_{22}N+C_{23}B,$$

(31)

where $C_{21}=⟨C_2,B⟩,C_{22}=⟨C_2,N⟩,C_{23}=⟨C_2,T⟩$.

Substituting (23), (30) and (31) into ${\Delta }_2{\mathbb{G}}_2=f_2{\mathbb{G}}_2+g_2{C}_2$, we obtain the following equation system

$$\left\{\begin{array}{c}{g}_2{C}_{21}=0,\hfill \\ f_2+g_2{C}_{22}=\frac{2{\kappa }^2}{{\lambda }^2},\hfill \\ f_2\frac{\kappa t_2}{{\lambda }^2}+g_2{C}_{23}=\frac{2\kappa {\lambda }^{\prime }}{{\lambda }^3}+\frac{2{\kappa }^3{t}_2}{{\lambda }^4}-\frac{2{\kappa }^{\prime }}{{\lambda }^2}.\hfill \end{array}\right.$$

(32)

Since $g_2$ is a non-zero smooth function, from the first equation of (32), we conclude $C_{21}=0$. By the last two equations of (32), we have

$$\left\{\begin{array}{c}{f}_2(s,t_2)=\frac{C_{22}(2\kappa \lambda {\lambda }^{\prime }+2{\kappa }^3{t}_2-2{\kappa }^{\prime }{\lambda }^2)-2C_{23}{\kappa }^2{\lambda }^2}{{\lambda }^2(C_{22}\kappa t_2-C_{23}{\lambda }^2)}=\frac{C_{22}(2K_2^2{t}_2-K_2^{\prime })-2C_{23}\kappa K_2}{C_{22}{K}_2{t}_2-C_{23}\kappa },\hfill \\ g_2(s,t_2)=\frac{2\lambda {\left(\frac{\kappa }{\lambda }\right)}^{\prime }}{C_{22}\kappa t_2-C_{23}{\lambda }^2}=\frac{K_2^{\prime }}{C_{22}{K}_2{t}_2-C_{23}\kappa },\hfill \end{array}\right.$$

(33)

where $C_{22}^2+C_{23}^2\ne 0$. Meanwhile, $\frac{\kappa }{\lambda }$ is a non-constant function since $g_2$ is a non-zero smooth function.

Conversely, if we use the above information with the given functions $(f_2,g_2)$ in (33) and the constant vector $C_2$, the null scroll $X_2$ satisfies ${\Delta }_2{\mathbb{G}}_2=f_2{\mathbb{G}}_2+g_2{C}_2$.

Theorem 2.

Let $X_2$ be a null scroll with generalized B-lightlike ruling in ${\mathbb{E}}_1^3$. Then $X_2$ has generalized 1-type Gauss map if and only if the Gauss map ${\mathbb{G}}_2$ of $X_2$ satisfies

$${\Delta }_2{\mathbb{G}}_2=f_2{\mathbb{G}}_2+g_2{C}_2$$

for some non-zero smooth functions $(f_2,g_2)$ as

$$\left\{\begin{array}{c}{f}_2=f_2(s,t_2)=\frac{C_{22}(2\kappa \lambda {\lambda }^{\prime }+2{\kappa }^3{t}_2-2{\kappa }^{\prime }{\lambda }^2)-2C_{23}{\kappa }^2{\lambda }^2}{{\lambda }^2(C_{22}\kappa t_2-C_{23}{\lambda }^2)}=\frac{C_{22}(2K_2^2{t}_2-K_2^{\prime })-2C_{23}\kappa K_2}{C_{22}{K}_2{t}_2-C_{23}\kappa },\hfill \\ g_2=g_2(s,t_2)=\frac{2\lambda {\left(\frac{\kappa }{\lambda }\right)}^{\prime }}{C_{22}\kappa t_2-C_{23}{\lambda }^2}=\frac{K_2^{\prime }}{C_{22}{K}_2{t}_2-C_{23}\kappa }\hfill \end{array}\right.$$

and a constant vector $C_2=(0,C_{22},C_{23})$. Where $C_{22}^2+C_{23}^2\ne 0$ and $\frac{\kappa }{\lambda }$ is a non-constant smooth function.

Remark 2.

In particular, when $C_2=(0,0,C_{23})$, ($C_{23}\ne 0$), the functions $(f_2,g_2)$ only depend on s, i.e.,

$$\left\{\begin{array}{c}{f}_2=f_2\left(s\right)=\frac{2{\kappa }^2}{{\lambda }^2}=2K_2,\hfill \\ g_2=g_2\left(s\right)=\frac{2(\kappa {\lambda }^{\prime }-{\kappa }^{\prime }\lambda )}{C_{23}{\lambda }^3}=-\frac{K_2^{\prime }}{C_{23}\kappa }.\hfill \end{array}\right.$$

Corollary 5.

Let $X_2$ be a null scroll with generalized B-lightlike ruling in ${\mathbb{E}}_1^3$. Then $X_2$ has pointwise 1-type Gauss map of the second kind if and only if the Gauss map ${\mathbb{G}}_2$ of $X_2$ satisfies

$${\Delta }_2{\mathbb{G}}_2=f_2({\mathbb{G}}_2+C_2)$$

for some non-zero smooth functions $f_2$ as

$$f_2=\frac{2{\kappa }^2}{{\lambda }^2}=2K_2,$$

and a constant vector $C_2=(0,0,C_{23})$, ($C_{23}\ne 0$).

Proof Corollary 5

Suppose that the null scroll $X_2$ has pointwise 1-type Gauss map of the second kind, i.e., ${\Delta }_2{\mathbb{G}}_2=f_2({\mathbb{G}}_2+C_2)$. It means that $f_2=g_2$ in Theorem 2. Thus, we get $2{\kappa }^3{C}_{22}=0$. Since $f_2$ is a non-zero smooth function, then $\kappa \ne 0$ and $C_{22}=0.$ Therefore,

$$f_2=\frac{2{\kappa }^2}{{\lambda }^2}=2K_2.$$

Conversely, if we use the above information with the given function $f_2$ and constant vector $C_2$, the null scroll $X_2$ satisfies ${\Delta }_2{\mathbb{G}}_2=f_2({\mathbb{G}}_2+C_2)$.  □

Corollary 6.

There does not exist the null scroll with generalized B-lightlike ruling in ${\mathbb{E}}_1^3$ which has 1-type Gauss map of the second kind.

Proof Corollary 6

Suppose that the null scroll $X_2$ has 1-type Gauss map of the second kind, i.e., ${\Delta }_2{\mathbb{G}}_2=\mu ({\mathbb{G}}_2+C_2),(\mu \in \mathbb{R}-\left\{0\right\})$. It means that $f_2=\frac{2{\kappa }^2}{{\lambda }^2}=\mu .$ Obviously, $H_2$ is a non-zero constant. By (32), we get $C_{22}=0$ and $C_{23}=\frac{-H_2^{\prime }}{\kappa H_2}=0$ which contradicts with $C_{23}\ne 0$ in Corollary 5.  □

Corollary 7.

Let $X_2$ be a null scroll with generalized B-lightlike ruling in ${\mathbb{E}}_1^3$. The $X_2$ has pointwise 1-type Gauss map of the first kind if and only if one of the following statements holds:

• $X_2$ has 1-type Gauss map of the first kind;
• $X_2$ has non-zero constant Gaussian curvature or non-zero constant mean curvature.

Proof Corollary 7

Suppose that the null scroll $X_2$ has pointwise 1-type Gauss map of the first kind, i.e., ${\Delta }_2{\mathbb{G}}_2=f_2{\mathbb{G}}_2$. From the last two equations of (32), we have $f_2=\frac{2{\kappa }^2}{{\lambda }^2}$ and ${\left(\frac{\kappa }{\lambda }\right)}^{\prime }=0$. Then the function $f_2$ is a non-zero constant function, i.e., $X_2$ has 1-type Gauss map of the first kind. By (26) and (27), the Gaussian curvature $K_2$ and the mean curvature $H_2$ are non-zero constant. Conversely, if one of the statements holds, then $\frac{\kappa }{\lambda }$ is a non-zero constant. This completes the proof.  □

Corollary 8.

Let $X_2$ be a null scroll with generalized B-lightlike ruling in ${\mathbb{E}}_1^3$. The $X_2$ has harmonic Gauss map if and only if the Gaussian curvature or the mean curvature of $X_2$ vanishes.

Proof Corollary 8

Suppose that the null scroll $X_2$ has harmonic Gauss map, i.e., ${\Delta }_2{\mathbb{G}}_2=0.$ Then we have $\kappa =0$ and the Gaussian curvature $K_2$ and the mean curvature $H_2$ are equal to zero by (26) and (27). The converse is obvious.  □

3.3. The Relationship between the Dual Associate Null Scrolls

In this section, we summarize and investigate the relations between the dual associate null scrolls. Meanwhile, the representations of some dual associate null scrolls are obtained according to their Gauss maps.

By (14) and (28), we have the following conclusion readily.

Theorem 3.

The Gaussian curvatures $K_i(i=1,2)$ and the mean curvatures $H_i(i=1,2)$ of the dual associate null scrolls $X_i(i=1,2)$ in ${\mathbb{E}}_1^3$ are related by

$$H_1^2{H}_2^2=K_1{K}_2={\kappa }^2.$$

From (16) and (30), we get

Theorem 4.

The Laplacians of Gauss maps ${\Delta }_i{\mathbb{G}}_i(i=1,2)$ of the dual associate null scrolls $X_i(i=1,2)$ in ${\mathbb{E}}_1^3$ are related by

$$⟨{\Delta }_1{\mathbb{G}}_1,{\Delta }_1{\mathbb{G}}_1⟩⟨{\Delta }_2{\mathbb{G}}_2,{\Delta }_2{\mathbb{G}}_2⟩=16K_1^2{K}_2^2=16{\kappa }^4.$$

From Proposition 3 and Corollary 1, we can get the following result.

Corollary 9.

Let $X_1$ be a null scroll with generalized T-lightlike ruling which has pointwise 1-type Gauss map of the second kind in ${\mathbb{E}}_1^3$. Then the dual associate null scrolls can be expressed as

$$\left\{\begin{array}{c}\begin{array}{c}\hfill X_1=\int \frac{\sqrt{2}{e}^{C_{11}s}}{C_0}(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1))ds+t_1\frac{\sqrt{2}{C}_0}{4f^{\prime }{e}^{C_{11}s}}(f^2-1,2f,f^2+1),\\ \hfill X_2=\int \frac{\sqrt{2}{C}_0}{4f^{\prime }{e}^{C_{11}s}}(f^2-1,2f,f^2+1)ds+t_2\frac{\sqrt{2}{e}^{C_{11}s}}{C_0}(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1)),\end{array}\hfill \end{array}\right.$$

where $C_0\in \mathbb{R}-\left\{0\right\}$ and $C_{11}\ne 0$.

By the proof of Corollary 3, the following conclusion is obtained easily.

Corollary 10.

Let $X_1$ be a null scroll with generalized T-lightlike ruling which has pointwise 1-type Gauss map of the first kind in ${\mathbb{E}}_1^3$. Then the dual associate null scrolls can be expressed by

$$\left\{\begin{array}{c}\begin{array}{c}\hfill X_1=\int \frac{1}{c}(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1))ds+t_1\frac{c}{2f^{\prime }}(f^2-1,2f,f^2+1),\\ \hfill X_2=\int \frac{c}{2f^{\prime }}(f^2-1,2f,f^2+1)ds+t_2\frac{1}{c}(-\frac{f^{″2}}{4f^{\prime 3}}(f^2-1,2f,f^2+1)+\frac{f^{″}}{f^{\prime }}(f,1,f)-f^{\prime }(1,0,1)),\end{array}\hfill \end{array}\right.$$

where $c\in \mathbb{R}-\left\{0\right\}.$

Theorem 5.

Let $X_2$ be a null scroll with generalized B-lightlike ruling which has harmonic Gauss map in ${\mathbb{E}}_1^3$. Then the dual associate null scrolls can be expressed by

$$\left\{\begin{array}{c}{X}_1(s,t_1)=\int \frac{1}{\lambda }(\frac{1}{a},0,-\frac{1}{a})ds+t_1\lambda (\frac{a}{2}-\frac{s^2}{2a},-s,\frac{a}{2}+\frac{s^2}{2a}),\hfill \\ X_2(s,t_2)=\int \lambda (\frac{a}{2}-\frac{s^2}{2a},-s,\frac{a}{2}+\frac{s^2}{2a})ds+t_2\frac{1}{\lambda }(\frac{1}{a},0,-\frac{1}{a}).\hfill \end{array}\right.$$

where $a\in \mathbb{R}-\left\{0\right\}.$

Proof of Theorem 5

By the proof of Corollary 8, we have $\kappa =0$. From (5), we have

$$\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{(log{f}^{\prime })}^{″}=0.$$

Solving the above equation, the structure function $f\left(s\right)$ of $r\left(s\right)$ is given by

$$f\left(s\right)=-\frac{a}{s},(a\in \mathbb{R}-\left\{0\right\}).$$

By Proposition 3, the dual associate null scrolls can be expressed by

$$\left\{\begin{array}{c}{X}_1(s,t_1)=\int \frac{1}{\lambda }(\frac{1}{a},0,-\frac{1}{a})ds+t_1\lambda (\frac{a}{2}-\frac{s^2}{2a},-s,\frac{a}{2}+\frac{s^2}{2a}),\hfill \\ X_2(s,t_2)=\int \lambda (\frac{a}{2}-\frac{s^2}{2a},-s,\frac{a}{2}+\frac{s^2}{2a})ds+t_2\frac{1}{\lambda }(\frac{1}{a},0,-\frac{1}{a}).\hfill \end{array}\right.$$

 □

Example 2.

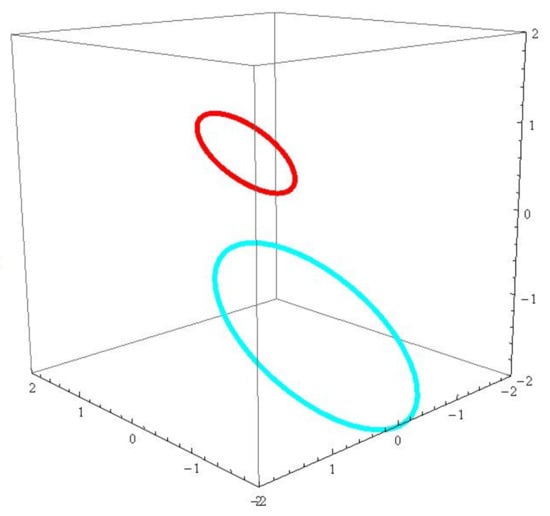
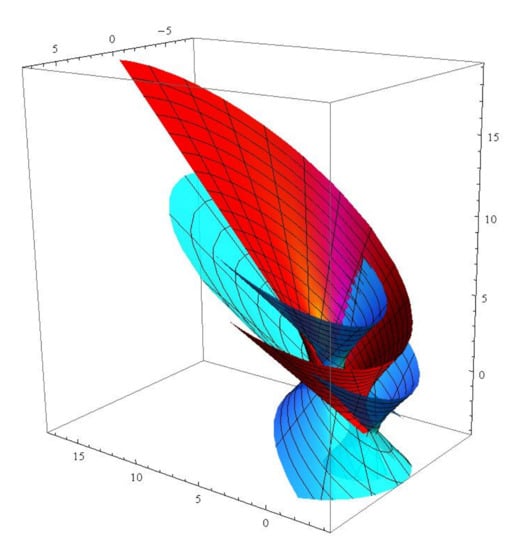
Consider a null curve $r\left(s\right)$ with $\kappa =-\frac{1}{2}$. From Proposition 2, we have

$$\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{(log{f}^{\prime })}^{″}=-\frac{1}{2}.$$

Solving the above differential equation, we have $f\left(s\right)=2tan\frac{s}{2}$. From Proposition 3, when $\lambda \left(s\right)=\frac{1}{2},$ the dual associate curves and the dual associate null scrolls can be written as (see Figure 5 and Figure 6)

$$\left\{\begin{array}{c}{b}_1\left(s\right)=({sin}^2\frac{s}{2}-\frac{1}{4}{cos}^2\frac{s}{2},\frac{1}{2}sins,{sin}^2\frac{s}{2}+\frac{1}{4}{cos}^2\frac{s}{2}),\hfill \\ b_2\left(s\right)=(\frac{1}{2}{sin}^2\frac{s}{2}-2{cos}^2\frac{s}{2},sins,-\frac{1}{2}{sin}^2\frac{s}{2}-2{cos}^2\frac{s}{2})\hfill \end{array}\right.$$

and

$$\left\{\begin{array}{c}{X}_1(s,t_1)=(-\frac{3}{4}s-\frac{5}{4}sins,-coss,-\frac{5}{4}s-\frac{3}{4}sins)+t_1({sin}^2\frac{s}{2}-\frac{1}{4}{cos}^2\frac{s}{2},\frac{1}{2}sins,{sin}^2\frac{s}{2}+\frac{1}{4}{cos}^2\frac{s}{2}),\hfill \\ X_2(s,t_2)=(\frac{3}{8}s-\frac{5}{8}sins,-\frac{1}{2}coss,\frac{5}{8}s-\frac{3}{8}sins)+t_2(\frac{1}{2}{sin}^2\frac{s}{2}-2{cos}^2\frac{s}{2},sins,-\frac{1}{2}{sin}^2\frac{s}{2}-2{cos}^2\frac{s}{2}).\hfill \end{array}\right.$$

Figure 5. The red (blue) curve is the generalized $T\left(B\right)$-associate curve $b_1\left(b_2\right)$ of r.

Figure 6. The red (blue) surface is the null scroll with generalized $T\left(B\right)$-lightlike ruling $X_1\left(X_2\right)$.

Example 3.

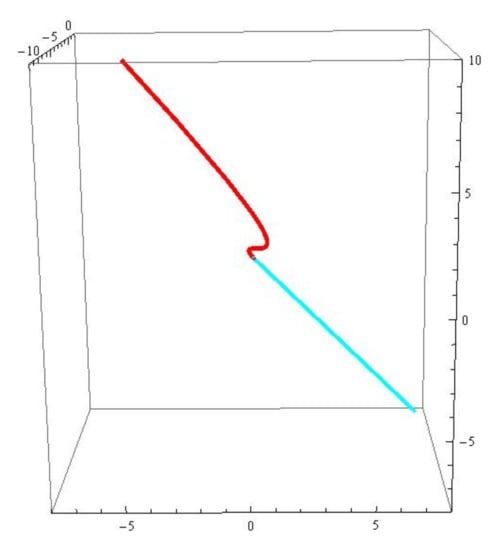
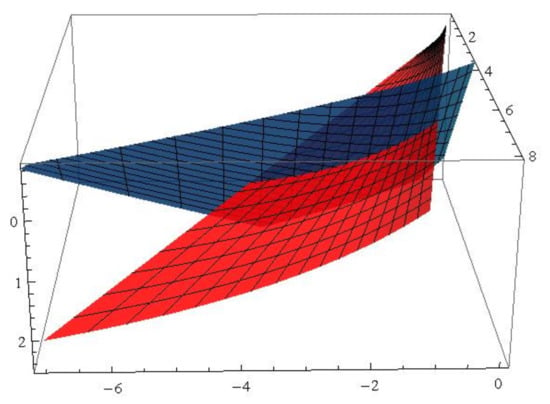
In Theorem 5, supposing $a=1$ and the function $\lambda \left(s\right)=e^s$, then the dual associate curves and the dual associate null scrolls can be written as (see Figure 7 and Figure 8).

$$\left\{\begin{array}{c}{b}_1\left(s\right)=e^s(\frac{1}{2}-\frac{s^2}{2},-s,\frac{1}{2}+\frac{s^2}{2}),\hfill \\ b_2\left(s\right)=e^{-s}(1,0,-1)\hfill \end{array}\right.$$

and

$$\left\{\begin{array}{c}{X}_1(s,t_1)=(-e^{-s},0,e^{-s})+t_1{e}^s(\frac{1}{2}-\frac{s^2}{2},-s,\frac{1}{2}+\frac{s^2}{2}),\hfill \\ X_2(s,t_2)=(-\frac{1}{2}{e}^s{(s-1)}^2,e^s(1-s),\frac{1}{2}{e}^s({(s-1)}^2+2))+t_2{e}^{-s}(1,0,-1).\hfill \end{array}\right.$$

Figure 7. The red (blue) curve is the generalized $T\left(B\right)$-associate curve $b_1\left(b_2\right)$ of r.

Figure 8. The red (blue) surface is the null scroll with generalized $T\left(B\right)$-lightlike ruling $X_1\left(X_2\right)$.

Remark 3.

In Example 2, the dual associate null scrolls have pointwise 1-type Gauss map of the first kind; in Example 3, the null scroll $X_1$ has pointwise 1-type Gauss map of the second kind and the null scroll $X_2$ has harmonic Gauss map, respectively.