Independent Rainbow Domination Numbers of Generalized Petersen Graphs P(n,2) and P(n,3)

Abstract

We obtain new results on independent 2- and 3-rainbow domination numbers of generalized Petersen graphs $P(n,k)$ for certain values of $n,k\in \mathbb{N}$. By suitably adjusting and applying a well established technique of tropical algebra (path algebra) we obtain exact 2-independent rainbow domination numbers of generalized Petersen graphs $P(n,2)$ and $P(n,3)$ thus confirming a conjecture proposed by Shao et al. In addition, we compute exact 3-independent rainbow domination numbers of generalized Petersen graphs $P(n,2)$. The method used here is developed for rainbow domination and for Petersen graphs. However, with some natural modifications, the method used can be applied to other domination type invariants, and to many other classes of graphs including grids and tori.

1. Introduction

As a combinatorial optimization problem, ordinary domination consists of determining the minimum number of places in which to keep a resource such that every place either has a resource or is adjacent to the place in which the resource exists. In practical applications, some additional constraints or desires must usually be taken into account. The following practical example is given in [1]. Consider a large computer network which consists of some clients and servers with t distinct resources $s_1,s_2,\cdots ,s_t$, and look for the minimum number of servers each one possessing a non-empty subset of these resources in order that any client can be connected directly to a subset of servers that together have each resource $s_i$ ($1\le i\le t$). If all the resources have an identical cost, the goal is to find the minimum value of the number of copies of such t resources. This application naturally can be modeled by the concept of t-rainbow domination. If we have an additional constraint that prevents any pair of servers from occupying adjacent locations, then we have the independent t-rainbow domination problem.

In this article we obtain new results on exact values of independent 2-rainbow domination number of generalized Petersen graphs $P(n,2)$ and $P(n,3)$. We confirm a conjecture from [2] (remark after Theorems 6 and 7), where it was conjectured that the upper bounds (obtained in [2] (Theorems 6 and 7)) for the independent 2-rainbow domination number of generalized Petersen graphs $P(n,2)$ and $P(n,3)$ are the exact values. We confirm this by suitably adjusting and applying a well known tropical (path) algebra technique for polygraphs (see e.g., [3,4,5,6]). Moreover, by applying this technique we obtain also the exact formula for the independent 3-rainbow domination number of generalized Petersen graphs $P(n,2)$. Some of the results were announced in the extended abstract of the talk at the conference SOR19 [7], where only the main ideas without detailed proofs were pointed out.

The article is organized as follows. In Section 2 we recall some graph theoretical and tropical algebra preliminaries that we will use in our proofs. In Section 3 we provide the theoretical framework on polygraphs needed for our purposes. Then we apply these theoretical results to generalized Petersen graphs $P(n,2)$ and $P(n,3)$ in Section 4. In Section 5 we prove the exact formulas for independent 2-rainbow domination numbers of generalized Petersen graphs $P(n,2)$ and $P(n,3)$ and for independent 3-rainbow domination numbers of generalized Petersen graphs $P(n,2)$. In the concluding section we discuss the potential of the method to be generalized to other domination type invariants and to other classes of graphs.

2. Preliminaries

2.1. Graphs and Independent Rainbow Domination

For a graph F, $S\subseteq V\left(F\right)$ and $w\in V\left(F\right)$, let $N_S\left(w\right)$ denote the open neighborhood of w in S, i.e., $\left\{u\right|uw\in E\left(F\right),u\in S\}$, and let $N_S\left[w\right]$ denote the closed neighborhood of w, i.e., $N_S\left[w\right]=\left\{w\right\}\cup N_S\left(w\right)$. If $S=V\left(F\right)$ and no confusion can occur, $N_S\left(w\right)$ and $N_S\left[w\right]$ will be denoted shortly by $N\left(w\right)$ and $N\left[w\right]$, respectively. If $S^{\prime }\subseteq V\left(F\right)$, then the definition $N\left(S^{\prime }\right)={\cup }_{x\in S^{\prime }}N\left(x\right)$ is applied. The degree of a vertex w is the total number of edges incident to w. The interval of natural numbers is denoted by $[i,j]=\{k\in \mathbb{N}|i\le k\le j\}$.

Inspired by several facility location problems, Brešar, Henning and Rall [8,9,10] initiated the study of the k-rainbow domination problem. The problem is proved to be NP-complete even if the input graph is a chordal graph or a bipartite graph (see Chang [11]). This problem has already attracted considerable attention and many other types of domination are widely applied to real-world scenarios, see for example [12,13,14]. The independent k-rainbow domination problem was studied in [2], where it was proved that also this domination problem is NP-complete, even if the input graph is a bipartite or planar graph. Note that a different but related notion of k-rainbow independent domination was studied in [15].

An independent set S of a graph F is a subset of $V\left(F\right)$ for which vertices are pairwise non-adjacent. Given a graph F and a positive integer t, the goal is to assign a subset of the color set $\{1,2,\cdots ,t\}$ to every vertex of F such that every vertex with the empty set assigned has all t colors in its neighborhood. Such an assignment is called a t-rainbow dominating function ($tRDF$) of the graph F. If in addition, the vertices assigned nonempty sets are pairwise non-adjacent, then a $tRDF$ is called independent t-rainbow dominating function ($ItRDF$). The weight of g, an $ItRDF$ (or a $tRDF$) of a graph F, is the value $w\left(g\right)={\sum }_{v\in V\left(F\right)}\left|g\left(v\right)\right|$. If H is a vertex induced subgraph of $V\left(F\right)$, the weight restricted to H is $w_H\left(g\right)={\sum }_{v\in v\left(H\right)}\left|g\left(v\right)\right|$. The independent t-rainbow domination number$i_{rt}\left(F\right)$ is the minimum weight over all $ItRDF$s in F. Let H be a subgraph of F and f a function that assigns subsets of $\{1,2,\cdots ,t\}$ to vertices $V\left(F\right)$. We say f is a partial $ItRDF$ for H if it satisfies the following three conditions: (1) f assigns subsets of $\{1,\cdots ,t\}$ to vertices of F, (2) the set of vertices assigned nonempty sets is independent set, and (3) for any vertex of H with $f\left(v\right)=\varnothing$ it holds that ${\cup }_{x\in N\left(v\right)}f\left(x\right)=\{1,\cdots ,t\}$, i.e., all colors appear in the neighborhood of v.

Note that a $tRDF$f can alternatively be given by an ordered $(t+1)$-tuple of sets $(f_0,f_1,\cdots ,f_t)$ where ($v\in f_i\iff i\in f\left(v\right)$ for $i=1,2,\cdots ,t$) and ($v\in f_0\iff f\left(v\right)=\varnothing$). We simply write $f=(f_0,f_1,\cdots ,f_t)$. If, in addition, the set ${\cup }_{i=1}^t{f}_i$ is independent, then f is an $ItRDF$. Note that in this setting, the weight of f is the sum of cardinalities, $w\left(f\right)={\sum }_{i\ne 0}\left|f_i\right|$, of course excluding $f_0$.

2.2. Polygraphs and Generalized Petersen Graphs

Let $G_1,\dots ,G_n$ be arbitrary mutually disjoint graphs and $X_1,\dots ,X_n$ a sequence of sets of edges such that an edge of $X_i$ joins a vertex of $V\left(G_i\right)$ with a vertex of $V\left(G_{i+1}\right)$ ($X_i\subseteq V\left(G_i\right)\times V\left(G_{i+1}\right)$ for $i\in [1,n]$). A polygraph ${\Omega }_n={\Omega }_n(G_1,\dots G_n;X_1,\dots X_n)$ over monographs $G_1,\dots ,G_n$ has the vertex set $V\left({\Omega }_n\right)=V\left(G_1\right)\cup \dots \cup V\left(G_n\right),$ and the edge set $E\left({\Omega }_n\right)=E\left(G_1\right)\cup X_1\cup \dots \cup E\left(G_n\right)\cup X_n.$ For convenience, we set $G_0=G_n$ and $G_{n+1}=G_1$. Thus, $X_0=X_n$, so we can write, for example, $X_n\subseteq V\left(G_n\right)\times V\left(G_{n+1}\right)=V\left(G_n\right)\times V\left(G_1\right)$, or $X_0\subseteq V\left(G_0\right)\times V\left(G_1\right)=V\left(G_n\right)\times V\left(G_1\right)$.

If all graphs $G_i$ are isomorphic to a fixed graph G (i.e., there exists an isomorphism ${\phi }_i:V\left(G_i\right)⟶V\left(G\right)$ for $i=0,1,\dots ,n+1$, and ${\phi }_0={\phi }_n$ and ${\phi }_{n+1}={\phi }_1$) and all sets $X_i$ are equal to a fixed set $X\subseteq V\left(G\right)\times V\left(G\right)$ (i.e., $(u,v)\in X⟺\left({\phi }_i^{-1}\left(u\right),{\phi }_{i+1}^{-1}\left(v\right)\right)\in X_i$ for all i), we call such a graph rotagraph, ${\omega }_n(G;X)$. A polygraph is called nearly rotagraph, if $n-1$ of its monographs are isomorphic to a fixed graph G and consequently at most two consecutive sets $X_i$ are not equal to the fixed set of edges X.

For positive integers $n\ge 3$ and k, $1\le k<\frac{n}{2}$, the generalized Petersen graph $P(n,k)$ is defined to be the graph with the vertex set $\{h_i^1,h_i^2|i\in \{0,1,\cdots ,n-1\}\}$ and the edge set $\{h_i^1{h}_i^2,h_i^1{h}_{i+k}^1,h_i^2{h}_{i+1}^2|i\in \{0,1,\cdots ,n-1\}\}$, in which the subscripts are computed modulo n (see [2,16]).

The following results were proved in [2] (Theorems 5, 6, and 7).

Theorem 1. 

(i) If $n\ge 4$, then

$$i_{r2}\left(P(n,1)\right)=\left\{\begin{array}{cc}n,\hfill & ifn\equiv 0(mod2)\hfill \\ n+1,\hfill & ifn\equiv 1(mod2)\hfill \end{array}\right.$$

(ii) If $n\ge 7$, then

$$i_{r2}\left(P(n,2)\right)\le \left\{\begin{array}{cc}⌈\frac{4n}{5}⌉,\hfill & n\equiv 0mod10\hfill \\ ⌈\frac{4n}{5}⌉+1,\hfill & n\equiv 9mod10\hfill \\ ⌈\frac{4n}{5}⌉+2,\hfill & n\equiv 2,3,4,5,7,8mod10\hfill \\ ⌈\frac{4n}{5}⌉+3,\hfill & n\equiv 1,6mod10\hfill \end{array}\right.$$

and

$$i_{r2}\left(P(n,3)\right)\le \left\{\begin{array}{cc}⌈\frac{7n}{8}⌉,\hfill & n\equiv 0,2,4,14mod16\hfill \\ ⌈\frac{7n}{8}⌉+1,\hfill & n\equiv 5,7,8,10,12,13,15mod16\hfill \\ ⌈\frac{7n}{8}⌉+2,\hfill & n\equiv 1,3,6,9,11mod16\hfill \end{array}\right.$$

It was conjectured in [2] that the inequalities in Theorem 1(ii) are actually equalities. We confirm this conjecture in Theorems 4 and 5 by applying a well established tropical (path) algebra technique. An important observation for the application of this technique is that $P(n,k)$ are in fact polygraphs. Recall that for a monograph G of $P(n,k)$ (for details see Section 4), f is a partial $ItRDF$ for G if all vertices of G that are assigned the empty set have all missing colors in their open neighbourhood in $P(n,k)$, which implies that the possibly missing colors must be supplied by vertices of the neighboring monographs. In particular, this means that it is enough to consider three consecutive monographs in order to establish the set of all partial $ItRDF$ functions for G.

2.3. Tropical Algebra

Tropical algebra (min-plus algebra) is an algebra (in fact, a semialgebra) over the ordered, idempotent semiring (in fact, semifield) $\mathbb{R}\cup \{\infty \}$, equipped with the operations of addition $a\oplus b=min(a,b)$ and multiplication $a\odot b=a+b$, with the unit elements ∞ (for addition ⊕) and 0 (for multiplication ⊙). The operations of addition and multiplication are (as in standard arithmetic) associative and commutative, and multiplication is distributive over addition. Matrix and polynomial operations can naturally be defined similarly to their standard counterparts, with the min-plus operations replacing the standard operations. In particular, for two $n\times n$ matrices $A,B$ with entries from $\mathbb{R}\cup \{\infty \}$ we define the product $AB$ by

$${\left(AB\right)}_{ij}=\underset{l=1,\dots ,n}{min}(a_{il}+b_{lj})$$

for all $i,j=1,\dots ,n$. The mth tropical power of A is denoted by $A^m$. More precisely,

$$A_{ij}^m=\underset{i_1,\dots ,i_{m-1}\in \{1,\dots ,n\}}{min}(a_{i{i}_1}+a_{i_1{i}_2}+\cdots +a_{i_{m-1}j})$$

for all $i,j=1,\dots ,n$. In fact, in our application we will consider matrices over idempotent subsemiring $\mathbb{N}\cup \left\{0\right\}\cup \{\infty \}$ equipped with the above operations (sometimes called path algebra, see e.g., [3,4,5,6]). For a later reference observe that the trace of a matrix in min-plus algebra is the minimum over the diagonal elements, i.e.,

$$tr\left(A\right)=\underset{i}{min}{A}_{ii}.$$

For a later reference, we recall a useful property of trace in $(min,+)$ algebra and we include its short proof for the sake of completeness.

Lemma 1.

Let $A,B\in {(\mathbb{R}\cup \{\infty \})}^{n\times n}$. Then $tr\left(AB\right)=tr\left(BA\right).$

Proof. 

We have ${\left(AB\right)}_{ii}={min}_{k=1,\dots ,n}(a_{ik}+b_{ki})$ for each $i=1,\dots ,n$ and ${\left(BA\right)}_{kk}={min}_{i=1,\dots ,n}(b_{ki}+a_{ik})$ for each $k=1,\dots ,n$. Therefore $tr\left(AB\right)={min}_i{\left(AB\right)}_{ii}={min}_k{\left(BA\right)}_{kk}=tr\left(BA\right)$, which completes the proof. □

For more information on tropical algebra we refer to the monograph of Butkovič [17]. Min-plus algebra is isomorphic to max-plus algebra, which is the semifield $\mathbb{R}\cup \{-\infty \}$, where addition is replaced by maximum and multiplication by addition (see e.g., [17,18] and the references there), and also to max-times algebra ${\mathbb{R}}_{+}$, where addition is replaced by maximum and multiplication is the same as in standard arithmetic (see e.g., [19] and the references there). Tropical algebra is a part of a broader branch of mathematics, called “idempotent mathematics”, which was developed mainly by Maslov and his collaborators (see e.g., [20,21]).

3. Theoretical Framework

We proceed by providing a formal definition of the weighted digraph which can be associated with the given polygraph that allows application of the algebraic approach. Intuitively, we are going to construct a directed graph in which vertices correspond to restrictions of $ItRDF$ functions to pairs of consecutive monographs and arcs correspond to pairs of vertices which both are a restriction of the same $ItRDF$ on one monograph. Note that the construction and the results below are not equivalent to the idea proposed in [3] elaborated in [6], and applied in c.f. [4,5,22]. The main reason to introduce a new construction is due to the fact that in the case of t-rainbow domination, a vertex with neighbors in both neighboring monographs can only be evaluated when all neighbors have known colors. One possible method would be to consider larger monographs. Another alternative that is used here is to define the associated digraph based on ordered pairs of monographs. Rougly speaking, the associated digraph defined here can be seen as a line graph of the associated graph as defined in [3,4,5,6,22].

Given a polygraph G, we define an auxiliary associated digraph $\mathcal{G}$ as follows. The vertices of $\mathcal{G}$ are ordered tuples of subsets of vertices $(D_0,D_1,D_2,\cdots ,D_t)$ such that $D_0\cup D_1\cup D_2\cup \cdots \cup D_t=V\left(G_i\right)\cup V\left(G_{i+1}\right)$ for some $i\in [1,n]$ and there is a partial $ItRDF$$f=(f_0,f_1,f_2,\cdots ,f_t)$, for the subgraph induced on $V\left(G_i\right)\cup V\left(G_{i+1}\right)$, defined (at least) on $V\left(G_{i-1}\right)\cup V\left(G_i\right)\cup V\left(G_{i+1}\right)\cup V\left(G_{i+2}\right)$, such that $D_0=f_0\cap (V\left(G_i\right)\cup V\left(G_{i+1}\right))$, $D_1=f_1\cap (V\left(G_i\right)\cup V\left(G_{i+1}\right))$, … , $D_t=f_t\cap (V\left(G_i\right)\cup V\left(G_{i+1}\right))$. We denote by $\mathcal{V}{\left(\mathcal{G}\right)}_{i,i+1}$ the set of vertices that are partial $ItRDF$ for $V\left(G_i\right)\cup V\left(G_{i+1}\right)$. Obviously, $\mathcal{V}\left(\mathcal{G}\right)={\cup }_{i=1}^n\mathcal{V}{\left(\mathcal{G}\right)}_{i,i+1}$.

The weight of vertex $D=(D_0,D_1,D_2,\dots ,D_t)$ is, by definition,

$$w\left(D\right)=\frac{1}{2}\left(\right|D_1|+|D_2|+\cdots +|D_t\left|\right).$$

For a later reference we introduce some more convenient notations. A vertex of $\mathcal{G}$ is an ordered tuple of sets that meet some monographs, so the restriction of D to monograph $G_i$ is denoted by

$$D^i=D\cap G_i.$$

More precisely, this means $D^i=(D_0^i,D_1^i,D_2^i,\dots ,D_t^i)$, where $D_0^i=D_0\cap V\left(G_i\right)$, $D_1^i=D_1\cap V\left(G_i\right)$, … , $D_t^i=D_t\cap V\left(G_i\right)$.

In words, vertices of $\mathcal{G}$ are partial $ItRDF$ of two consecutive monographs. Two vertices of $\mathcal{G}$ are connected when they exactly match on the common monograph. As the edge sets $X_i$ and $X_{i+1}$ meet on the monograph $G_{i+1}$, the two partial $ItRDF$ are both defined on vertices of $G_{i+1}$, and they can either match or differ on these vertices.

More formally, two vertices u, v of $\mathcal{G}$ are connected by an arc $(u,v)$ if, (1) for some i, $u\in \mathcal{V}{\left(\mathcal{G}\right)}_{i-1,i}$, $v\in \mathcal{V}{\left(\mathcal{G}\right)}_{i,i+1}$, and (2) u and v match on $V\left(G_i\right)$. More precisely, $u_0^i=v_0^i$, $u_1^i=v_1^i$, … , $u_t^i=v_t^i$. Clearly, $u\cap v$ is a partial $ItRDF$ for $G_i$. (We use a brief notation for the intersection of triples, i.e., $u\cap v=(u_0,u_1,u_2,\dots ,u_t)\cap (v_0,v_1,v_2,\dots ,v_t)=(u_0\cap v_0,u_1\cap v_1,u_2\cap v_2,\dots ,u_t\cap v_t)$. The weight of the arc $(u,v)$ is, naturally, defined as the sum of weights of u and v, hence

$$w(u,v)=w\left(u\right)+w\left(v\right).$$

Note that $w(u,v)=w\left(u\right)+w\left(v\right)=w\left(u^{i-1}\right)+w\left(u^i\right)+w\left(v^i\right)+w\left(v^{i+1}\right)=w\left(u^{i-1}\right)+2w\left(u^i\right)+w\left(v^{i+1}\right)=\frac{1}{2}\left(\right|u_1^{i-1}|+|u_2^{i-1}|+\cdots +|u_t^{i-1}\left|\right)+|u_1^i|+|u_2^i|+\cdots +|u_t^i|+\frac{1}{2}\left(\right|v_1^{i+1}|+|v_2^{i+1}|+\cdots +|v_t^{i+1}\left|\right)=w\left(u_{i-1}\right)+2w\left(u_i\right)+w\left(u_{i+1}\right).$ By induction, a walk given by consecutive arcs $(u_1,u_2),(u_2,u_3)\cdots (u_{\ell -1},u_{\ell })$, has weight $w\left(u_1\right)+2w\left(u_2\right)+\cdots +2w\left(u_{\ell -1}\right)+w\left(u_{\ell }\right)$. In words, a walk meets some consecutive monographs. By definition, it gives rise to a partial $ItRDF$ on the union of monographs that the walk crosses, i.e., are related to the inner vertices of the walk. The weight of the walk is the sum of cardinalities over all inner monographs, plus half of the cardinalities of the first and last vertex on the walk.

Now we prove that the independent t-rainbow domination number is closely related to certain walks in the associated graph $\mathcal{G}$.

Theorem 2.

The independent t-rainbow domination number $i_{rt}\left({\Omega }_n\right(G_1,G_2,\cdots ,G_n;$$X_1,X_2,$$\cdots ,$$X_n\left)\right)$ of the polygraph ${\Omega }_n(G_1,G_2,\cdots ,G_n;X_1,X_2,\cdots ,X_n)$ equals the minimum weight of a closed walk of length n in $\mathcal{G}$.

Proof. 

Observe that any closed walk must meet each of the monographs (i.e., meets a vertex of $\mathcal{V}{\left(\mathcal{G}\right)}_{i,i+1}$ for all $i\in [1,n]$). Hence, if a walk is of length n, then it meets each $\mathcal{V}{\left(\mathcal{G}\right)}_{i,i+1}$ exactly once. In the sequel we show how such a walk defines an $ItRDF$.

Assume there is a closed walk $v^{1,2},v^{2,3},...,v^{n,1},v^{1,2}$ of length n in $\mathcal{G}$. Without loss of generality, $v^{1,2}\in \mathcal{V}{\left(\mathcal{G}\right)}_{1,2}$. By definition, $v^{1,2}$ and $v^{2,3}$ restricted to $G_2$ define a partial $ItRDF$ on $G_2$. In general, for any $i\in [1,n]$, $v^{i,i+1}$ and $v^{i+1,i+2}$ restricted to $G_{i+1}$ define a partial $ItRDF$ on $G_{i+1}$. Thus we can set $f_j={\cup }_{i=1}^n{\left(v^{i,i+1}\right)}_j$, $j=0,1,2,\dots ,t$, and observe that $f=(f_0,f_1,f_2,\dots ,f_t)$ is an $ItRDF$ of ${\Omega }_n(G_1,G_2,\cdots ,G_n;X_1,X_2,\cdots ,X_n)$. Finally, the weight of the closed walk $v^{1,2},v^{2,3},...,v^{n,1},v^{1,2}$ is the sum of weights of its vertices

$$\sum _{i=1}^{n}w\left(v^{i,i+1}\right)=\sum _{i=1}^n\frac{1}{2}\left(\right|{\left(v^{i,i+1}\right)}^i|+|{\left(v^{i,i+1}\right)}^{i+1}\left|\right)=\sum _{i=1}^n\left(\right|f_1^i|+|f_2^i|+\cdots +|f_t^i\left|\right)=|f_1|+|f_2|+\cdots +|f_t|.$$

So we have seen that any closed walk on n vertices gives rise to an $ItRDF$. On the other hand, it is trivial to observe that any $ItRDF$f provides arcs of a closed walk. Hence the minimal weight of a closed walk equals to the minimum weight of an $ItRDF$. □

Consider two consecutive monographs $G_k$ and $G_{k+1}$ and the corresponding vertices in $\mathcal{V}{\left(\mathcal{G}\right)}_{k,k+1}$. Let $L=\left\{u^k\right|u\in \mathcal{V}{\left(\mathcal{G}\right)}_{k,k+1}\}$ and $R=\left\{u^{k+1}\right|u\in \mathcal{V}{\left(\mathcal{G}\right)}_{k,k+1}\}$ be the sets of all restrictions of arcs to the two monographs. Let $A(k,k+1)$ be the matrix with elements $a_{ij}$, for $i\in L$ and $j\in R$, where the value of $a_{ij}$ is

$$a_{ij}=\left\{\begin{array}{cc}w\left(u\right)\hfill & \mathrm{if}(i,j)=u\in \mathcal{V}{\left(\mathcal{G}\right)}_{k,k+1}\hfill \\ \infty \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

Let us compute the product $P=A(k-1,k)A(k,k+1)$,

$$P_{ij}=min\{w(i,x)+w(x,j)\},$$

where x runs over all ordered tuples of subsets of $V\left(G_k\right)$ such that both $(i,x)\in \mathcal{V}{\left(\mathcal{G}\right)}_{k-1,k}$ and $(x,j)\in \mathcal{V}{\left(\mathcal{G}\right)}_{k,k+1}$. In words, the product is the weight of a path that starts at $V\left(G_{k-1}\right)$ and ends at $V\left(G_{k+1}\right)$, such that the two intersections are, respectively, the ordered tuples i and j, and has minimum weight. Therefore, by induction, the mimimum weight of a closed walk of length n on polygraph with n monographs will appear as a diagonal element of the corresponding product of matrices. The conclusion can be stated formally as

Theorem 3.

For $k=1,2,\cdots ,n$, let $A(k,k+1)$ be the matrices defined by (1). Then the independent t-rainbow domination number of polygraph ${\Omega }_n(G_1,G_2,\cdots ,G_n;X_1,X_2,\cdots ,X_n)$ equals

$$i_{rt}\left({\Omega }_n(G_1,G_2,\cdots ,G_n;X_1,X_2,\cdots ,X_n)\right)=tr(A(1,2)A(2,3)\cdots A(n,n+1))$$

Now consider the special case when the polygraph is a rotagraph. Observe that in this case the matrices $A(k,k+1)$ are independent of k. Thus we can define a matrix $A=A(1,2)$ with elements $a_{ij}=w(i,j)$, $(i,j)\in \mathcal{V}{\left(\mathcal{G}\right)}_{1,2}$ and write

Corollary 1.

The independent t-rainbow domination number of rotagraph ${\omega }_n(G;X)$ is

$$i_{rt}\left({\omega }_n(G;X)\right)=tr\left(A^n\right).$$

Finally, we will need a version of this result for the case when the polygraph is an almost rotagraph. Recall that a polygraph is an almost rotagraph, if all monographs but one are isomorphic: $G_2\simeq G_3\simeq \cdots \simeq G_n$. Consequently, also $X_1$ and $X_n$ may differ from other $X_i=X$.

Corollary 2.

Let polygraph ${\Omega }_n(G_1,G_2,\cdots ,G_n;X_1,X_2,\cdots ,X_n)$ be an almost rotagraph, that is $G_2=G_3=\cdots =G_n=G$ and $X_2=X_3=\cdots =X_{n-1}=X$. Then $i_{rt}\left({\Omega }_n\right(G_1,G,\cdots ,G;$$X_1,X,$$\cdots ,$X, $X_n\left)\right)$ equals

$$tr\left(A(1,2)A^{n-2}A(n,1)\right)=tr\left(A(n,1)A(1,2)A^{n-2}\right)=tr\left(A^{k}A(n,1)A(1,2)A^{n-2-k}\right)$$

for any $k\in [1,n-2]$, where $A=A(2,3)$.

Proof. 

Clearly, using Theorem 1 we have $i_{rt}\left({\Omega }_n\right(G_1,G,\cdots ,G;$$X_1,X,$$\cdots ,$X, $X_n\left)\right)=$ $tr\left(A\right(1,2)$$A^{n-2}A(n,1))$. The other statements can be easily seen by shifting the indices of the monographs, or by applying Lemma 1. □

4. Application to Petersen Graphs

In this section, we apply the above path algebra technique to obtain exact values $i_{r2}\left(P(n,2)\right)$, $i_{r2}\left(P(n,3)\right)$ and $i_{r3}\left(P(n,2)\right)$.

Let $n\ge 1$ and $k<\frac{n}{2}$. For $m<\frac{n}{2}$, we define the non-cyclical version of the Petersen graph $\overline{P}(m,k)$ to be the subgraph of $P(n,k)$, induced on vertices $\{h_i^1,h_i^2\mid i\in [1,m]\}$. See examples in Figure 1.

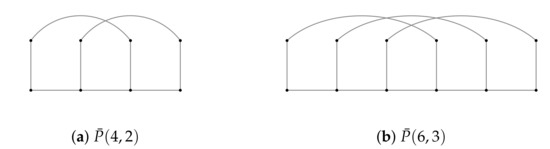
Figure 1. Non-cyclical versions of $P(n,k)$.

Observe that Petersen graphs of the form $P(2n,2)$ are rotagraphs ${\omega }_n(\overline{P}(2,2);X)$, where X denotes the set of edges as depicted in Figure 2. Similarly, Petersen graphs of the form $P(2n+1,2)$ are nearly rotagraphs ${\Omega }_n(\overline{P}(3,2),\overline{P}(2,2),\cdots ,\overline{P}(2,2);X^{\prime },X,\cdots ,X,X^{\prime \prime })$, where $X^{\prime }$, X and $X^{\prime \prime }$ denote the sets of edges as depicted in Figure 3. Furthermore, $P(3n,3)$ are rotagraphs ${\omega }_n(\overline{P}(3,3);Y)$ (Figure 4) and $P(3n+m,3)$ are nearly rotagraphs ${\Omega }_n(\overline{P}(3+m,3),\overline{P}(3,3),\cdots ,\overline{P}(3,3);Y^{\prime },Y,\cdots ,Y,Y^{\prime \prime })$ for $m\in \{1,2\}$, where $Y^{\prime }$, Y and $Y^{\prime \prime }$ denote the sets of edges as depicted in Figure 5.

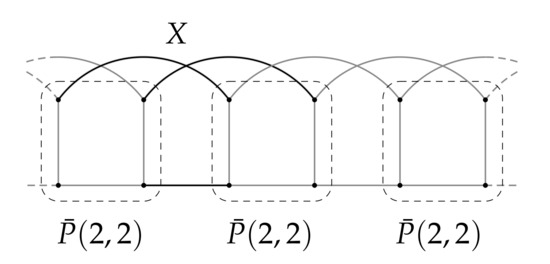
Figure 2. $P(2n,2)$ as a rotagraph.

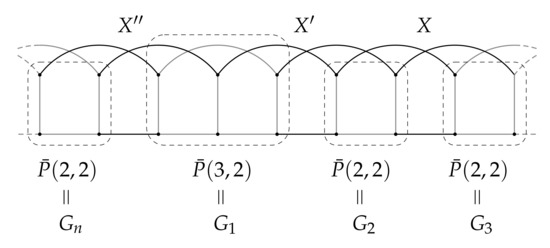
Figure 3. $P(2n+1,2)$ as a nearly rotagraph.

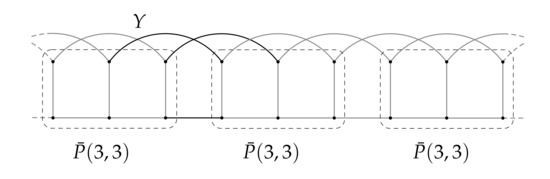
Figure 4. $P(3n,3)$ as a rotagraph.

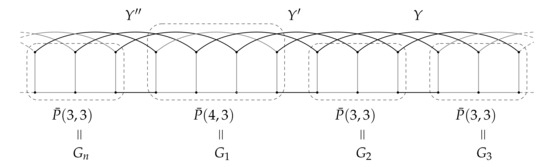
Figure 5. $P(3n+m,3)$ as nearly rotagraph for $m=1$. Graphs for $m=2$ are obtained similarly.

First consider rotagraphs $P(2n,2)={\omega }_n(\overline{P}(2,2);X)$. Let $C=\{\varnothing ,\{1\},\{2\},\{1,2\left\}\right\}$ be the set of all possible colors of a vertex and $C^8$ the set of colorings of $\overline{P}(4,2)$ (with ordered vertices). We denote by S the lexicographically ordered set of colorings from $C^8$ that define a partial $I2RDF$ of $\overline{P}(4,2)$. By checking which of all possible colorings define a partial $I2RDF$ (the code is available at [23]), we compute that there are exactly 165 partial $I2RDF$-s (out of the possible $4^8$ colorings). Note that these colorings are exactly the vertices of the graph $\mathcal{G}$ that is associated to ${\omega }_n(\overline{P}(2,2);X)$ by construction explained in the previous section. Hence we can apply Corollary 1 and obtain

$$i_{r2}\left(P(2n,2)\right)=tr\left(A^n\right).$$

Let us continue with $P(2n+1,2)$. Set $G_1=\overline{P}(3,2)$ and $G_i=\overline{P}(2,2)$ for all $i\ne 1$. Also, let $X_2=X_3=\cdots =X_{n-1}$ be X and $X_1=X^{\prime }$, $X_n=X^{\prime \prime }$ as defined above and depicted in Figure 5. Consequently, all the matrices $A(k,k+1)$, for $k\in [2,n-1]$, are equal to the matrix A that was used for $P(2n,2)$ above. For further use we denote $A_0=A^2$.

Instead of writing up $A(1,2)$ and $A(n,1)$ explicitly, we will directly compute the product $A(n,1)A(1,2)$. Consider the subgraph induced on $V\left(G_n\right)\cup V\left(G_1\right)\cup V\left(G_2\right)=\overline{P}(7,2)$. Let u and v be any partial $I2RDF$ on $V\left(G_n\right)\cup V\left(G_1\right)$ and $V\left(G_1\right)\cup V\left(G_2\right)$, respectively, such that (1) u and v match on $G_1$, i.e, $u_1=v_1$ (2) $u\cap G_n=u_n$ and (3) $v\cap G_2=v_2$. Observe that for the matrix $A_1$ with elements

$$w_1(u_n,v_2)=\underset{u_1=v_1}{min}\left\{\frac{1}{2}w\left(u\right)+\frac{1}{2}w\left(v\right)\right\}=\underset{T=u_1=v_1}{min}\left\{\frac{1}{2}w\left(u_n\right)+w\left(T\right)+\frac{1}{2}w\left(v_2\right)\right\}.$$

we have

Lemma 2.

$A_1=A(n,1)A(1,2)$.

By Corollary 2, it follows $i_{r2}\left(P(2n+1,2)\right)=tr\left(A_1{A}^{n-2}\right).$

We repeat an analogue procedure for $P(n,3)$. First we consider rotagraphs $P(3n,3)={\omega }_n(\overline{P}(3,3);Y)$. Straightforward computations show that in this case, there are 4494 partial $I2RDF$ colorings for the subgraphs $\overline{P}(3,3)$ ([23]). Therefore, we form a $4494\times 4494$ matrix $B={(u_i,v_j)}_{i,j}$ and denote also $B_0=B^2$.

For the nearly rotagraphs $P(3n+m,3)$, $m=1,2$, we define the first monograph as $G_1=\overline{P}(3+m,3)$, and set all other $G_i=\overline{P}(3,3)$. As in the previous case, we can obtain the matrices $B_m={\left(w_m(u_i,v_j)\right)}_{i,j}$, $m=1,2$, directly, instead of computing the products $A(n,1)A(1,2)$. Again, Corollaries 1 and 2 are implying that

$$i_{r2}\left(P(3\ell ,3)\right)=tr\left(B^{\ell }\right)$$

and

$$i_{r2}\left(P(3\ell +m,3)\right)=tr\left(B_m{B}^{\ell -2}\right)\mathrm{for}m=1,2.$$

Similarly we calculate $i_{r3}\left(P(n,2)\right)$. Let C and $C_m$, $m=0,1$, be the associated matrices (of size $903\times 903$) for $P(n,2)$, defined exactly in the same way as A and $A_m$, respectively, except taking $t=3$ (i.e., three colors).

It is well known that the tropical powers of appropriate matrices have a cyclic behaviour (see e.g., [3,5,17]). In our case, we get

$$\begin{array}{ccc}\hfill A^{13}& =A^8\hfill & +{\left[8\right]}_{i,j=1}^{165,}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill B^{27}& =B^{11}\hfill & +{\left[42\right]}_{i,j=1}^{4494},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill C^{15}& =C^{10}\hfill & +{\left[12\right]}_{i,j=1}^{903}.\hfill \end{array}$$

(4)

Consequently,

$$\begin{array}{cccc}\hfill A^{\ell +5}& =A^{\ell }\hfill & +{\left[8\right]}_{i,j=1}^{165}\hfill & \mathrm{for}l\ge 8,\hfill \end{array}$$

(5)

$$\begin{array}{cccc}\hfill B^{\ell +16}& =B^{\ell }\hfill & +{\left[42\right]}_{i,j=1}^{4494}\hfill & \mathrm{for}l\ge 11,\hfill \end{array}$$

(6)

$$\begin{array}{cccc}\hfill C^{\ell +5}& =C^{\ell }\hfill & +{\left[12\right]}_{i,j=1}^{903}\hfill & \mathrm{for}l\ge 10,\hfill \end{array}$$

(7)

In addition, we compute the traces for smaller powers and present the results in Table 1, Table 2 and Table 3. The source code of the Python program can be found in [23].

Table 1. $i_{r2}$ values for generalized Petersen graphs $P(n,2)$.

Graph	$\mathit{P}(5,2)$	$\mathit{P}(6,2)$	$\mathit{P}(7,2)$	$\mathit{P}(8,2)$	⋯	$\mathit{P}(28,2)$	$\mathit{P}(29,2)$
$i_{r2}$	6	7	9	9	⋯	25	25
Obtained as	$tr\left(A_1\right)$	$tr\left(A_{0}A\right)$	$tr\left(A_{1}A\right)$	$tr\left(A_0{A}^2\right)$	⋯	$tr\left(A_0{A}^{12}\right)$	$tr\left(A_1{A}^{12}\right)$

Table 2. $i_{r2}$ values for generalized Petersen graphs $P(n,3)$.

Graph	$\mathit{P}(7,3)$	$\mathit{P}(8,3)$	$\mathit{P}(9,3)$	$\mathit{P}(10,3)$	⋯	$\mathit{P}(88,3)$	$\mathit{P}(89,3)$
$i_{r2}$	8	8	10	10	⋯	78	80
Obtained as	$tr\left(B_1\right)$	$tr\left(B_2\right)$	$tr\left(B_{0}B\right)$	$tr\left(B_{1}B\right)$	⋯	$tr\left(B_1{B}^{27}\right)$	$tr\left(B_2{B}^{27}\right)$

Table 3. $i_{r3}$ values for generalized Petersen graphs $P(n,2)$.

Graph	$\mathit{P}(5,2)$	$\mathit{P}(6,2)$	$\mathit{P}(7,2)$	$\mathit{P}(8,2)$	⋯	$\mathit{P}(32,2)$	$\mathit{P}(33,2)$
$i_{r3}$	9	10	11	13	⋯	42	44
Obtained as	$tr\left(C_1\right)$	$tr\left(C_{0}C\right)$	$tr\left(C_{1}C\right)$	$tr\left(C_0{C}^2\right)$	⋯	$tr\left(C_0{C}^{14}\right)$	$tr\left(C_1{C}^{14}\right)$

5. Exact Values of Independent 2- and 3-Rainbow Domination Numbers

Application of the path algebra approach described in the previous section makes it possible to write closed expressions for exact values of independent 2- and 3-rainbow domination numbers. We prove the following

Theorem 4.

Let $n\ge 7$.

$$i_{r2}\left(P(n,2)\right)=\left\{\begin{array}{cc}⌈\frac{4n}{5}⌉,\hfill & n\equiv 0mod10\hfill \\ ⌈\frac{4n}{5}⌉+1,\hfill & n\equiv 9mod10\hfill \\ ⌈\frac{4n}{5}⌉+2,\hfill & n\equiv 2,3,4,5,7,8mod10\hfill \\ ⌈\frac{4n}{5}⌉+3,\hfill & n\equiv 1,6mod10\hfill \end{array}\right.$$

Furthermore, $i_{r2}\left(P(5,2)\right)=6$ and $i_{r2}\left(P(6,2)\right)=7$.

Proof. 

We set $A_0=A^2$. From the fact that $A_m{A}^{\ell +5}=A_m{A}^{\ell }+{\left[8\right]}_{i,j=1}^{165}$ for $\ell \ge {\ell }_0=8$ and $i_{r2}\left(P(2\ell +4+m,2)\right)=tr\left(A_m{A}^{\ell }\right)$ for $m=0,1$ and the fact that the monographs contain 4 vertices, it follows for $\ell \ge {\ell }_0=8$, or equivalently, $n>2{\ell }_0+4=20$, that

$$i_{r2}\left(P(n,2)\right)=i_{r2}\left(P(n+5·2,2)\right)+8.$$

The statement of the theorem holds since $⌈\frac{4(n+5·2)}{5}⌉=⌈\frac{4n}{5}⌉+8$ and the fact that the formula holds for $n=7,8,\dots 29$, which was verified by computing the traces (see the results in Table 1).

Hence the upper bounds given in [2] are indeed the exact values.

From Table 1 we also have $i_{r2}\left(P(5,2)\right)=6$ and $i_{r2}\left(P(6,2)\right)=7$. □

Theorem 5.

Let $n\ge 7$.

$$i_{r2}\left(P(n,3)\right)=\left\{\begin{array}{cc}⌈\frac{7n}{8}⌉,\hfill & n\equiv 0,2,4,14mod16\hfill \\ ⌈\frac{7n}{8}⌉+1,\hfill & n\equiv 5,7,8,10,12,13,15mod16\hfill \\ ⌈\frac{7n}{8}⌉+2,\hfill & n\equiv 1,3,6,9,11mod16\hfill \end{array}\right.$$

Proof. 

The proof is analogous to that of Theorem 4. We compute that the formula holds for $n=7,8,\dots ,89$ (see Table 2). From the fact that $B_m{B}^{\ell +16}=B_m{B}^{\ell }+{\left[42\right]}_{i,j=1}^{4494}$ for $\ell \ge {\ell }_0=11$ and $i_{r2}\left(P(3\ell +6+m,3)\right)=tr\left(B_m{B}^{\ell }\right)$ for $m=0,1,2$ (here we again take $B_0=B^2$), it follows for $\ell \ge {\ell }_0=11$, or equivalently, $n\ge 3{\ell }_0+6=90$, that

$$i_{r2}\left(P(n,3)\right)=i_{r2}\left(P(n+16·3,3)\right)+42.$$

The statement of the theorem holds, since $⌈\frac{7(n+16·3)}{8}⌉=⌈\frac{7n}{8}⌉+42.$ □

Theorem 6.

Let $n\ge 7$.

$$i_{r3}\left(P(n,2)\right)=\left\{\begin{array}{cc}⌈\frac{6n}{5}⌉,\hfill & n\equiv 0mod10\hfill \\ ⌈\frac{6n}{5}⌉+2,\hfill & n\equiv 7,9mod10\hfill \\ ⌈\frac{6n}{5}⌉+3,\hfill & n\equiv 2,3,5,6,8mod10\hfill \\ ⌈\frac{6n}{5}⌉+4,\hfill & n\equiv 1,4mod10\hfill \end{array}\right.$$

Furthermore, $i_{r3}\left(P(5,2)\right)=9$ and $i_{r3}\left(P(6,2)\right)=10$.

Proof. 

We again set $C_0=C^2$. It holds $C_m{C}^{\ell +5}=C_m{C}^{\ell }+{\left[12\right]}_{i,j=1}^{165}$ for $\ell \ge {\ell }_0=10$ and $i_{r3}\left(P(2\ell +4+m,2)\right)=tr\left(C_m{C}^{\ell }\right)$ for $m=0,1$. Since the monographs have 4 vertices, it follows for $\ell \ge {\ell }_0=10$, or equivalently, $n>2{\ell }_0+4+m=24$ that

$$i_{r3}\left(P(n,2)\right)=i_{r3}\left(P(n+5·2,2)\right)+12.$$

The statement of the theorem holds since $⌈\frac{6(n+5·2)}{5}⌉=⌈\frac{6n}{5}⌉+12$ and the fact that the formula holds for $n=7,8,\dots 34$ (see the results in Table 3). To complete the proof, $i_{r3}\left(P(5,2)\right)=9$ and $i_{r3}\left(P(6,2)\right)=10$ is also evident from Table 3. □

Since it is known (see e.g., [2]) that $P(2k+1,k+1)\cong P(2k+1,2)$ and $P(3k+2,k+1)\cong P(3k+2,3)$ for all $k\ge 2$ we obtain also the following consequences.

Corollary 3.

Let $k\ge 2$.

$$i_{r2}\left(P(2k+1,k+1)\right)=\left\{\begin{array}{cc}⌈\frac{8k+4}{5}⌉+1,\hfill & k\equiv 4mod5\hfill \\ ⌈\frac{8k+4}{5}⌉+2,\hfill & k\equiv 1,2,3mod5\hfill \\ ⌈\frac{8k+4}{5}⌉+3,\hfill & k\equiv 0mod5\hfill \end{array}\right.$$

Corollary 4.

Let $k\ge 2$.

$$i_{r2}\left(P(3k+2,k+1)\right)=\left\{\begin{array}{cc}⌈\frac{21k+14}{8}⌉,\hfill & k\equiv 0,4,6,10mod16\hfill \\ ⌈\frac{21k+14}{8}⌉+1,\hfill & k\equiv 1,2,7,8,9,14,15mod16\hfill \\ ⌈\frac{21k+14}{8}⌉+2,\hfill & k\equiv 3,5,11,12,13mod16\hfill \end{array}\right.$$

Corollary 5.

Let $k\ge 2$.

$$i_{r3}\left(P(2k+1,k+1)\right)=\left\{\begin{array}{cc}⌈\frac{12k+6}{5}⌉+2,\hfill & k\equiv 3,4mod5\hfill \\ ⌈\frac{12k+6}{5}⌉+3,\hfill & k\equiv 1,2mod5\hfill \\ ⌈\frac{12k+6}{5}⌉+4,\hfill & k\equiv 0mod5\hfill \end{array}\right.$$

6. Conclusions and Future Work

In this article we have studied the t-independent rainbow domination number $i_{rt}$ of polygraphs. For a polygraph that is formed by n monographs we have established that its t-independent rainbow domination number equals the minimum weight of a closed walk of length n of a suitably associated graph. Consequently, by applying the formalism of tropical (min-plus) algebra the $i_{rt}$ of a polygraph equals the trace of product of suitably associated n matrices, all calculated in tropical algebra.

As the generalized Petersen graphs $P(n,k)$ are almost rotagraphs, it is shown that the calculation of $i_{rt}\left(P(n,k)\right)$ mainly depends on efficient calculation of tropical powers of a single relatively large matrix. It is well known that the tropical powers of a large class of matrices possess’ a nice cyclic behaviour, which enables to explicitly calculate all tropical powers. In other words, in time constant in n we can provide closed expressions valid for all n. In this paper we successfully established the explicit formulas for $i_{r2}\left(P(n,2)\right)$, $i_{r2}\left(P(n,3)\right)$ and $i_{r3}\left(P(n,2)\right)$ that were not known before.

In conclusion, we wish to emphasize that the contribution of this paper goes much further. First, the same approach can in principle be applied to other domination type problems (see c.f. [5,24] for a general definition covering a number of domination type problems that can be handled by a unified algebraic approach). For example, a slight adaptation of our computer code based on a modification of the corresponding matrices would give results for another version of independent rainbow domination [15]. Second, the implementation code of the method for our experiment was not optimized, and it is a reasonable challenge to investigate the potential of the method when implemented on a parallel supercomputer with optimized code. Next we plan calculation of t-independent rainbow domination numbers of generalized Petersen graphs $P(n,k)$ for other t and k. Finally, generalized Petersen graphs are only one example of nearly rotagraphs. Popular examples of rotagraphs and fasciagraphs include grid graphs and tori that are Cartesian products of paths and cycles (see c.f. [4,5,25]). Further examples include other graph products, not to mention molecular graphs that are studied in mathematical chemistry and provide a thesaurus of fasciagraphs, rotagraphs, nearly rotagraphs and nearly fasciagraphs that are practically relevant classes of graphs.