Squeezed Hybrid Nanofluid Flow Over a Permeable Sensor Surface

Abstract

This paper examines the squeezed hybrid nanofluid flow over a permeable sensor surface with magnetohydrodynamics (MHD) and radiation effects. The alumina (Al₂O₃) and copper (Cu) are considered as the hybrid nanoparticles, while water is the base fluid. The governing equations are reduced to the similarity equations, using the similarity transformation. The resulting equations are programmed in Matlab software through the bvp4c solver to obtain the numerical solutions. It was found that the heat transfer rate was greater for the hybrid nanofluid, compared to the regular nanofluid. It was observed that dual solutions exist for some values of the permeable parameter S. The upper branch solutions of the skin friction coefficient (${\mathit{Re}}_x^{1/2}{C}_f$) and the heat transfer rate at the surface (${\mathit{Re}}_x^{-1/2}N{u}_x$) enhance with the added Cu nanoparticle (${\phi }_2$) and for larger magnetic strength ($M$). Moreover, the values of ${\mathit{Re}}_x^{1/2}{C}_f$ decrease, whereas the values of ${\mathit{Re}}_x^{-1/2}N{u}_x$ increase for both branches, with the rise of the squeeze flow index ($b$). Besides, an increment of the heat transfer rate at the sensor surface for both branches was observed in the presence of radiation ($R$). Temporal stability analysis was employed to determine the stability of the dual solutions, and it was discovered that only one of them was stable and physically reliable as time evolves.

1. Introduction

Nowadays, the problem of heat transfer in industrial processes has become the main topic of interest to the researchers. Previously, fluids like water, oil, and ethylene glycol were regularly considered as cooling liquids in those processes, but their heat transfer rates are limited. In 1995, Choi and Eastman [1] introduced fluid called “nanofluid” to replace the use of regular fluids in industrial processes. Nanofluid was composed by dispersing one type of nanoparticle in the aforementioned fluids to enhance their thermal conductivity. However, the researchers found that the thermal properties of the nanofluid could be improved with the addition of more than a single nanoparticle in the base fluid and named it as ‘hybrid nanofluid’. Experimental studies that consider the hybrid nanocomposite particles were conducted by several researchers, for example, Turcu et al. [2] and Jana et al. [3]. Besides, Suresh et al. [4] synthesized the Al₂O₃–Cu nanocomposite powder by using a thermochemical method. From the experimental data, it was revealed that the added hybrid nanoparticles enhanced the thermal conductivity of the fluid.

Apart from that, the numerical studies of hybrid nanofluid were extended to the boundary layer flow problem. For instance, the flow over a stretching surface with Al₂O₃–Cu hybrid nanoparticles was studied by Devi and Devi [5]. They found that the enhancement in the heat transfer occurs at higher values of the nanoparticle volume concentrations. Besides, Waini et al. [6,7,8,9,10,11,12,13], in a series of papers, extended the hybrid nanofluid flow problem to different surfaces, considering the dual nature behaviour of the solutions. Additionally, the problem of hybrid nanofluid flow with different physical parameters was also considered by several authors [14,15,16,17,18,19,20]. For further reading, one can refer to the review papers of nanofluid [21,22,23] and hybrid nanofluid [24,25,26,27,28,29]. Besides, the use of hybrid nanofluid can improve the heat transfer rate due to the synergistic effects as discussed by Sarkar et al. [24]. Due to its capability to improve the heat transfer rate, most of the applications that involve heat transfer, such as coolant in machining and electronic and transformer cooling, are considering hybrid nanofluid as heat transfer fluid.

Squeezed flow over a sensor surface with heat transfer has significant applications in industrial, chemical, and biomedical processes. The sensing element that is commonly used in these processes is microcantilever [30]. This is due to its capability in diagnosing several terminal diseases and also its rapid respond to biowarfare or hazardous agents. Besides, the microcantilever sensor also has high sensitivity, the finest procedure characteristics, actual time sense, and lower cost [31]. Therefore, the study on a sensor surface has gained a lot of consideration by scientists, engineers, and researchers. In this respect, Khaled and Vafai [32] initially studied the flow over a sensor surface placed in a squeezed channel with magnetohydrodynamics (MHD) effects. They found that the rising of the squeezing free stream velocity tended to enhance the local Nusselt number and local wall shear stress. Then, Mahmood et al. [33] investigated a similar problem, but they employed three different methods to solve the locally non-similar momentum and energy equations. Since that, the topic of flow over a sensor surface was vigorously investigated by researchers considering various type of fluids. For example, Hayat et al. [34] examined the squeezed flow in a second-grade fluid. Furthermore, Khan et al. [35] and Salahuddin et al. [36] considered the Carreau and Carreau–Yasuda fluids, respectively. Besides, Ganesh Kumar et al. [37] studied the unsteady squeezed flow of a tangent hyperbolic fluid. Apart from that, the nanofluid flow over a sensor surface was considered by several authors with different aspects, such as Ul Haq et al. [38], Hamzah et al. [39], Akbar and Khan [40], Kandasamy et al. [41], and Nayak et al. [42].

Thus, the objective of this paper is to examine the permeability effects on the hybrid nanofluid flow over a sensor surface with the magnetic field and radiation by employing Tiwari and Das [43] model. Here, we consider water as the base fluid, and copper (Cu) and alumina (Al₂O₃) as the hybrid nanoparticles. The results are obtained for several physical parameters and presented graphically through tables. Additionally, the comparison results for limiting cases are done with previously published data. Besides, the theoretical analysis from this study is beneficial to other researchers or engineers to further investigate the heat transfer problem that arises in the modern industry.

2. Mathematical Formulation

Consider an unsteady squeezed flow over a permeable sensor surface in a hybrid nanofluid, as illustrated in Figure 1. Here, the x- and y-axes are the Cartesian coordinates, where x is assigned along the sensor surface, and y is orthogonal from the surface. The sensor surface (having a length (L)) is placed in a squeezed channel where the height of the channel ($h\left(t\right)$) is much larger than the thickness of the boundary layer. Here, we assume that the squeezing in the free stream starts from the tip of the surface, where the lower plate is fixed while the upper plate is squeezed. The surface permeable velocity ($v_w\left(t\right)$) through the sensor surface is considered. It was also assumed that a magnetic field strength ($B\left(t\right)$) was applied normal to the flow. Therefore, the equations that govern the hybrid nanofluid flow are (Khaled and Vafai [32]):

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\rho }_{hnf}}\frac{\partial p}{\partial x}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^{2}u,$$

(2)

$$\frac{\partial U}{\partial t}+U\frac{\partial U}{\partial x}=-\frac{1}{{\rho }_{hnf}}\frac{\partial p}{\partial x}-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^{2}U,$$

(3)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{(\rho C_p)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{{(\rho C_p)}_{hnf}}\frac{\partial q_r}{\partial y},$$

(4)

where $u$ and $v$ represent the velocity components along the $x$- and $y$-axes, while $p,q_r, T, t,$ and $U$ represent the pressure, the radiative heat flux, the hybrid nanofluid temperature, time, and the axial free stream velocity, respectively. Now, by substituting the pressure gradient term from Equation (3), Equation (2) is transformed into the following form:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{\partial U}{\partial t}+U\frac{\partial U}{\partial x}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^2\left(U-u\right).$$

(5)

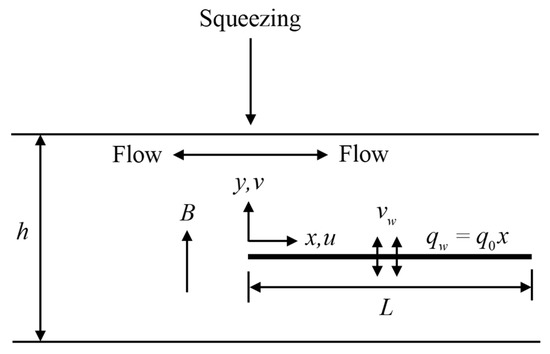
Figure 1. Physical model.

The radiative heat flux is given as (see Rosseland [44], Cortell [45]):

$$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y},$$

(6)

where $k^{*}$ and ${\sigma }^{*}$ denote the mean absorption coefficient and the Stefan–Boltzmann constant, respectively. Using Taylor series, $T^4$ is expanded about $T_{\infty }$; and ignoring the higher-order terms, we have $T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4$. Thus, Equation (4) becomes (see Waini et al. [8]; Cortell [45]):

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{{(\rho C_p)}_{hnf}}\left[k_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}\right]\frac{{\partial }^{2}T}{\partial y^2}$$

(7)

subject to:

$$\begin{gathered} u\left(x,0,t\right)=0,v\left(x,0,t\right)=v_w\left(t\right),-k_{hnf}\frac{\partial T\left(x,0,t\right)}{\partial y}=q_w\left(x\right) \\ u\left(x,\infty ,t\right)=U\left(x,t\right),T\left(x,\infty ,t\right)=T_{\infty }, \end{gathered}$$

(8)

where $U\left(x,t\right)$, $q_w\left(x\right)$, and $T_{\infty }$ represent the free stream velocity, the wall heat flux, and the free stream temperature, respectively. Meanwhile, the thermophysical correlations of hybrid nanofluid are given in Table 1 (see [5,46]). Besides, the physical properties of Al₂O₃, Cu, and water are provided in Table 2 (see [46,47]). Here, Al₂O₃ and Cu volume fractions are given by ${\phi }_1$ and ${\phi }_2$, and the subscripts $n1$ and $n2$ correspond to their solid components, respectively. Additionally, we employed the uniform size of the spherical nanoparticles of Al₂O₃ and Cu. Besides, the fluid, nanofluid, and hybrid nanofluid were designated by the subscripts $f, nf$, and $hnf$, respectively.

Table 1. Thermophysical properties of nanofluid and hybrid nanofluid.

Thermophysical Properties	Nanofluid	Hybrid Nanofluid
Density	${\rho }_{nf}=\left(1-{\phi }_1\right){\rho }_f+{\phi }_1{\rho }_{n1}$	${\rho }_{hnf}=\left(1-{\phi }_2\right)\left[\left(1-{\phi }_1\right){\rho }_f+{\phi }_1{\rho }_{n1}\right]+{\phi }_2{\rho }_{n2}$
Heat capacity	${(\rho C_p)}_{nf}=\left(1-{\phi }_1\right){(\rho C_p)}_f+{\phi }_1{(\rho C_p)}_{n1}$	${(\rho C_p)}_{hnf}=\left(1-{\phi }_2\right)[\left(1-{\phi }_1\right){(\rho C_p)}_f+{\phi }_1\left(\rho C_p{)}_{n1}\right]+{\phi }_2{(\rho C_p)}_{n2}$
Dynamic viscosity	${\mu }_{nf}=\frac{{\mu }_f}{{(1-{\phi }_1)}^{2.5}}$	${\mu }_{hnf}=\frac{{\mu }_f}{{(1-{\phi }_1)}^{2.5}{(1-{\phi }_2)}^{2.5}}$
Thermal conductivity	$k_{nf}=\frac{k_{n1}+2k_f-2{\phi }_1\left(k_f-k_{n1}\right)}{k_{n1}+2k_f+{\phi }_1\left(k_f-k_{n1}\right)}\times \left(k_f\right)$	$k_{hnf}=\frac{k_{n2}+2k_{nf}-2{\phi }_2\left(k_{nf}-k_{n2}\right)}{k_{n2}+2k_{nf}+{\phi }_2\left(k_{nf}-k_{n2}\right)}\times \left(k_{nf}\right)$ where $k_{nf}=\frac{k_{n1}+2k_f-2{\phi }_1\left(k_f-k_{n1}\right)}{k_{n1}+2k_f+{\phi }_1\left(k_f-k_{n1}\right)}\times \left(k_f\right)$
Electrical conductivity	${\sigma }_{nf}=1+\frac{3\left(\frac{{\sigma }_{n1}}{{\sigma }_f}-1\right){\phi }_1}{2+\frac{{\sigma }_{n1}}{{\sigma }_f}-\left(\frac{{\sigma }_{n1}}{{\sigma }_f}-1\right){\phi }_1}\times \left({\sigma }_f\right)$	${\sigma }_{hnf}=\frac{{\sigma }_{n2}+2{\sigma }_{nf}-2{\phi }_2\left({\sigma }_{nf}-{\sigma }_{n2}\right)}{{\sigma }_{n2}+2{\sigma }_{nf}+{\phi }_2\left({\sigma }_{nf}-{\sigma }_{n2}\right)}\times \left({\sigma }_{nf}\right)$ where ${\sigma }_{nf}=\frac{{\sigma }_{n1}+2{\sigma }_f-2{\phi }_1\left({\sigma }_f-{\sigma }_{n1}\right)}{{\sigma }_{n1}+2{\sigma }_f+{\phi }_1\left({\sigma }_f-{\sigma }_{n1}\right)}\times \left({\sigma }_f\right)$

Table 2. Thermophysical properties of Al₂O₃, Cu, and water.

Thermophysical Properties	Al2O3	Cu	Water
$\rho \left(kg/m^3\right)$	3970	8933	997.1
$C_p\left(J/kgK\right)$	765	385	4179
$k\left(W/mK\right)$	40	400	0.613
$\sigma \left(S/m\right)$	3.69 × 107	5.96 × 107	0.05
Prandtl number, $\mathit{Pr}$			6.2

Referring to Khaled and Vafai [32], the following form of the free stream velocity, the surface permeable velocity, the magnetic field, and the surface heat flux were considered:

$$U\left(x,t\right)=ax,v_w\left(t\right)=v_0\sqrt{a},B\left(t\right)=B_0\sqrt{a},q_w\left(x\right)=q_{0}x,$$

(9)

where $v_0$ is the reference surface permeable velocity, $B_0$ is the reference magnetic field strength, and $q_0$ is the reference heat flux. An appropriate transformation is introduced as:

$$\psi =\sqrt{a{v}_f}xf\left(\eta \right),\eta =y\sqrt{a/v_f},\theta \left(\eta \right)=\frac{T-T_{\infty }}{\left(q_{0}x/k_f\right)\sqrt{v_f/a}},a=\frac{1}{s+bt},$$

(10)

where $\psi$ denotes the stream function with $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$ so that Equation (1) is identically fulfilled. Here, a is the squeeze flow strength with s as a constant, and b is the squeeze flow index. According to Khaled and Vafai [32], the channel’s height movement is described by the following condition: $h\left(t\right)=h_0{e}^{-st}$ for $b=0$; and $h\left(t\right)=h_0/{\left(s+bt\right)}^{\left(1/b\right)}$ for $b>0$, where $h_0$ is a constant. Employing these definitions, we get

$$u=ax{f}^{\prime }\left(\eta \right),v=-\sqrt{a{v}_f}f\left(\eta \right).$$

(11)

Thus, Equations (5) and (7) become:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{f}^{‴}+\left(f+\frac{b\eta }{2}\right)f^{″}-{f^{\prime }}^2+b\left(f^{\prime }-1\right)+\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M\left(1-f^{\prime }\right)+1=0,$$

(12)

$$\frac{1}{Pr}\frac{1}{{(\rho C_p)}_{hnf}/{(\rho C_p)}_f}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right){\theta }^{″}+\left(f+\frac{b\eta }{2}\right){\theta }^{\prime }-\left(f^{\prime }+\frac{b}{2}\right)\theta =0,$$

(13)

subject to:

$$\begin{gathered} f\left(0\right)=-S,f^{\prime }\left(0\right)=0,{\theta }^{\prime }\left(0\right)=-\frac{k_f}{k_{hnf}}, \\ {f}^{\prime }(\infty )=1,\theta (\infty )=0, \end{gathered}$$

(14)

where the notation (′) means the differentiation with respect to $\eta$, $M$ represents the magnetic parameter, $R$ represents the radiation parameter, $\mathit{Pr}$ represents the Prandtl number, and $S$ represents the permeability parameter; with $S<0$ for suction and $S>0$ for injection. These parameters are defined as:

$$M=\frac{{\sigma }_f{B}_0^2}{{\rho }_f},R=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k^{*}{k}_f},\mathit{Pr}=\frac{{(\mu C_p)}_f}{k_f},S=\frac{v_0}{\sqrt{{\nu }_f}}.$$

(15)

The skin friction coefficient ($C_f$) and the local Nusselt number ($N{u}_x$) are defined as:

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}^2},N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)},$$

(16)

where ${\tau }_w$ and $q_w$ symbolized the shear stress and the heat flux from the surface defined as (see Waini et al. [8]; Cortell [45]):

$${\tau }_w={\mu }_{hnf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k_{hnf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}+{\left(q_r\right)}_{y=0}.$$

(17)

Using (10), (16), and (17), one gets:

$${\mathit{Re}}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),{\mathit{Re}}_x^{-1/2}N{u}_x=\left(1+\frac{k_f}{k_{hnf}}\frac{4}{3}R\right)\frac{1}{\theta \left(0\right)},$$

(18)

where ${\mathit{Re}}_x=Ux/{\nu }_f$ denotes the local Reynolds number.

3. Stability Analysis

It was found that dual solutions exist for some values of the physical parameters, so analysis to determine the real solution was required. Therefore, the stability analysis introduced by Merkin [48] and Weidman et al. [49] was considered for this purpose. The analysis was initiated by introducing the new variables based on Equation (10) and given as follows:

$$\psi =\sqrt{a{v}_f}xf\left(\eta ,\tau \right),\eta =y\sqrt{a/v_f},\theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{\left(q_{0}x/k_f\right)\sqrt{v_f/a}},\tau =at,a=\frac{1}{s+bt}.$$

(19)

Using (19) and following the same procedure as the previous section, we have:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}f}{\partial {\eta }^3}+\left(f+\frac{b\eta }{2}\right)\frac{{\partial }^{2}f}{\partial {\eta }^2}-{\left(\frac{\partial f}{\partial \eta }\right)}^2+b\left(\frac{\partial f}{\partial \eta }-1\right)+\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M\left(1-\frac{\partial f}{\partial \eta }\right)+1-\left(1-b\tau \right)\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0,$$

(20)

$$\frac{1}{Pr}\frac{1}{{(\rho C_p)}_{hnf}/{(\rho C_p)}_f}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right)\frac{{\partial }^2\theta }{\partial {\eta }^2}+\left(f+\frac{b\eta }{2}\right)\frac{\partial \theta }{\partial \eta }-\left(\frac{\partial f}{\partial \eta }+\frac{b}{2}\right)\theta -\left(1-b\tau \right)\frac{\partial \theta }{\partial \tau }=0,$$

(21)

subject to:

$$\begin{gathered} f\left(0,\tau \right)=-S,\frac{\partial f}{\partial \eta }\left(0,\tau \right)=0,\frac{\partial \theta }{\partial \eta }\left(0,\tau \right)=-\frac{k_f}{k_{hnf}}, \\ \frac{\partial f}{\partial \eta }\left(\infty ,\tau \right)=1,\theta \left(\infty ,\tau \right)=0. \end{gathered}$$

(22)

According to Weidman et al. [49], the relations given in Equation (23) were employed to examine the stability of the steady solution, $f=f_0\left(\eta \right)$, and $\theta ={\theta }_0\left(\eta \right)$ of Equations (12) to (14).

$$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta \right),\theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\gamma \tau }G\left(\eta \right),$$

(23)

where $\gamma$ indicates the unknown eigenvalue that determines the stability of the solutions, whereas $F\left(\eta \right)$ and $G\left(\eta \right)$ are small compared to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$. The stability of the steady flow, $f_0\left(\eta \right)$, and ${\theta }_0\left(\eta \right)$ are investigated by setting $\tau =0$ in Equations (20) and (21). By inserting Equation (23) into Equations (20) to (22), one obtains:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{F}^{‴}+\left(f_0+\frac{b\eta }{2}\right)F^{″}+f_0^{″}F-2f_0^{\prime }{F}^{\prime }+b{F}^{\prime }-\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M{F}^{\prime }+\gamma F^{\prime }=0,$$

(24)

$$\frac{1}{Pr}\frac{1}{{(\rho C_p)}_{hnf}/{(\rho C_p)}_f}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right)G^{″}+\left(f_0+\frac{b\eta }{2}\right)G^{\prime }+{\theta }_0^{\prime }F-\left(f_0^{\prime }+\frac{b}{2}\right)G-{\theta }_0{F}^{\prime }+\gamma G=0,$$

(25)

subject to:

$$\begin{gathered} F\left(0\right)=0,F^{\prime }\left(0\right)=0,G^{\prime }\left(0\right)=0, \\ {F}^{\prime }(\infty )=0, G(\infty )=0. \end{gathered}$$

(26)

Without loss of generality, the values of $\gamma$ from Equations (24) to (26) were obtained for the case of $F^{″}\left(1\right)=1$, as proposed by Harris et al. [50].

4. Results and Discussion

Equations (12) to (14) are solved in Matlab software by bvp4c solver that employed the 3-stage Lobatto IIIa formula (see Shampine et al. [51]). A suitable selection of the boundary layer thickness, ${\eta }_{\infty }$, and the initial guess are required to obtain the solutions. Moreover, several researchers [52,53,54,55,56] also employed this solver for solving the boundary layer flow problems. Here, we considered that volume fractions of Cu varied from 0 to 0.04 $\left(0\le {\phi }_2\le 0.04\right)$, while Al₂O₃ was kept fixed at ${\phi }_1=0.1$, and water was used as the base fluid.

Table 3 provides the comparison values of $f^{″}\left(0\right)$ under different values of $M$ and $S$ for regular fluid (${\phi }_1={\phi }_2=0$) when $b=0$, with Sparrow et al. [57], and Yih [58]. It was observed that the comparison was in excellent agreement with Sparrow et al. [57], and Yih [58], which supports the validity of the present numerical procedure. Additionally, Table 4 displays the comparison values of $f^{″}\left(0\right)$ and $1/\theta \left(0\right)$ with those obtained by Ul Haq et al. [38] for different values of $b$ and $S$ when ${\phi }_1={\phi }_2=0$ (regular fluid), $\mathit{Pr}=6.2$, $R=0$, and $M=0.5$. From the computation, we found that the comparison showed good agreement with Ul Haq et al. [38]. Besides, the values of ${\mathit{Re}}_x^{1/2}{C}_f$ and when $\mathit{Pr}=6.2$ with different physical parameters are presented in Table 5. It was found that the values of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ increased with the rise of ${\phi }_2$ and M, whereas these physical quantities decreased with the rise of $S$. Moreover, the rise of b and R lead to an increase the local Nusselt number, ${\mathit{Re}}_x^{-1/2}N{u}_x$, whereas the skin friction coefficient, ${\mathit{Re}}_x^{1/2}{C}_f$, decreased with the increase of b; but, as expected, remained unchanged with variation of R. Additionally, the heat transfer rate of Al₂O₃-Cu/water hybrid nanofluid was intensified if compared to Cu/water nanofluid. This finding shows that the heat transfer rate was higher in the hybrid nanofluid than in the regular nanofluid.

Table 3. Values of the skin friction coefficient $f^{″}\left(0\right)$ under different values of the magnetic parameter $M$ and the permeability parameter $S$ for regular fluid (${\phi }_1={\phi }_2=0$) when $b=0$.

$\mathit{M}$	$\mathit{S}$	Sparrow et al. [57]	Yih [58]	Present Results
0	1	0.7605	0.756575	0.756575
	0	1.231	1.232588	1.232588
	−1		1.889314	1.889314
1	1	1.124	1.116421	1.116421
	0	1.584	1.585331	1.585331
	−1		2.202940	2.202940

Table 4. Values of the skin friction coefficient $f^{″}\left(0\right)$ and the local Nusselt number $1/\theta \left(0\right)$ under different values of $b$ and $S$ for regular fluid (${\phi }_1={\phi }_2=0$) when $\mathit{Pr}=6.2$, $R=0$, and $M=0.5$.

$\mathit{b}$	$\mathit{S}$	Ul Haq et al. [38]		Present Results
		${\mathit{f}}^{″}\left(0\right)$	$1/\mathit{\theta }\left(0\right)$	${\mathit{f}}^{″}\left(0\right)$	$1/\mathit{\theta }\left(0\right)$
0	−0.5			1.718541	3.840316
	0.5	1.162236	0.46815	1.162236	0.468150
1	−0.5	1.481134	4.696999	1.481134	4.696999
	0.5	0.866523	1.208932	0.866523	1.208932
2	−0.5			1.222208	5.380508
	0.5			0.506833	1.839583

Table 5. Values of the skin friction coefficient ${\mathit{Re}}_x^{1/2}{C}_f$ and the local Nusselt number ${\mathit{Re}}_x^{-1/2}N{u}_x$ under different physical parameters when $\mathit{Pr}=6.2$.

${\mathit{\phi }}_2$	$\mathit{b}$	$\mathit{M}$	$\mathit{R}$	$\mathit{S}$	$\mathbf{Cu}/\mathbf{Water}({\mathit{\phi }}_1=0)$		$\mathbf{Cu}-{\mathbf{Al}}_2{\mathbf{O}}_3/\mathbf{Water}({\mathit{\phi }}_1=0.1)$
					${\mathit{Re}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	${\mathit{Re}}_{\mathit{x}}^{-1/2}\mathit{N}{\mathit{u}}_{\mathit{x}}$	${\mathit{Re}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	${\mathit{Re}}_{\mathit{x}}^{-1/2}\mathit{N}{\mathit{u}}_{\mathit{x}}$
0	0	0	0	0	1.232588	1.573433	1.602057	1.860326
0.02					1.361008	1.655977	1.737286	1.947250
0.04					1.489346	1.736260	1.874379	2.033031
0.04	0.5				1.310038	2.261957	1.648715	2.611603
	1				1.115515	2.712764	1.403904	3.110646
	2				0.668444	3.469936	0.841253	3.952873
	2	0.2			0.801908	3.489410	1.024317	3.978345
		0.4			0.922159	3.506375	1.187917	4.000253
		0.6			1.032259	3.521447	1.336850	4.019529
		0.2	0.2		0.801908	3.903484	1.024317	4.342731
			0.4		0.801908	4.282869	1.024317	4.682781
			0.6		0.801908	4.635574	1.024317	5.003124
			0.2	−0.2	1.012031	4.672733	1.278661	5.091581
				0	0.801908	3.903484	1.024317	4.342731
				0.2	0.596024	3.214263	0.775292	3.661256

On the other hand, the variations of the velocity profiles ($f^{\prime }\left(\eta \right)$) and the temperature profiles ($\theta \left(\eta \right)$) when ${\phi }_1={\phi }_2=0$ (regular fluid), $S=M=R=0$, and $\mathit{Pr}=6.7$ for $b=0.5,1,1.5,2$ are displayed in Figure 2a and Figure 3a, respectively. The results exhibited qualitatively similarly to those obtained by Khaled and Vafai [32]. It was observed that $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ decreased with the rising values of b (the decrease of the channel’s height) for the first solutions. Interestingly, we found that the second solutions exist for this problem, which are displayed in Figure 2b and Figure 3b. From these figures, all profiles asymptotically satisfy the free stream conditions (14), thus supporting the validity of the numerical solutions. These behaviours reveal that the second solution was not physically stable, and thus has no physical sense. Although such solutions are deprived of physical significance, they are nevertheless of interest so far as the differential equations are concerned [59,60].

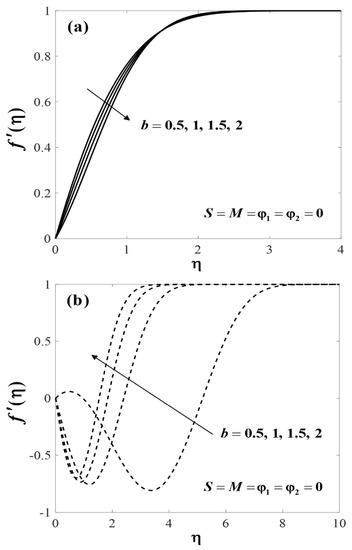
Figure 2. Impact of $b$ on $f\prime \left(\eta \right)$ for (a) first solutions, and (b) second solutions.

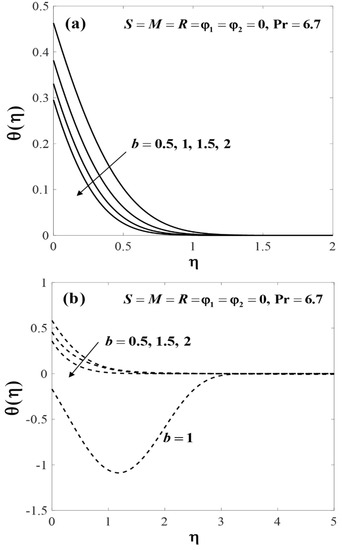
Figure 3. Impact of $b$ on $\theta \left(\eta \right)$ for (a) first solutions, and (b) second solutions.

The non-uniqueness of the solutions of Equations (12) to (14) are observed for $S<S_c$, and no similarity solution was obtained when $S>S_c$, as shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Separately, the effects of $S$ and ${\phi }_2$ on ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ when $\mathit{Pr}=6.2,$ $b=2$, $M=R=0.2$, and ${\phi }_1=0.1$ are given in Figure 4 and Figure 5. The dual solutions exist for the permeability parameter $S\le S_c$, where $S_{c1}=1.1824$, $S_{c2}=1.1300$, and $S_{c3}=1.0902$ for ${\phi }_2=0, 0.02$ and $0.04$, respectively. Moreover, for fixed values of $S$, the upper branch solution of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ was slightly enhanced with the rise of ${\phi }_2$. These observations were consistent with Sarkar et al. [24], which stated that the addition of hybrid nanoparticles tends to improve the heat transfer due to the synergistic effects. Furthermore, Figure 6 and Figure 7 illustrate the variations of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x\mathrm{against}S$ when $\mathit{Pr}=6.2$, $M=R=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$ for various values of $b$. It was discovered that the increase of b tends to decrease the skin friction coefficient, ${\mathit{Re}}_x^{1/2}{C}_f$, whereas the local Nusselt number, ${\mathit{Re}}_x^{-1/2}N{u}_x$, increases for both branches. This implied that the reduction of the skin friction coefficient and the enhancement of the heat transfer rate at the sensor surface were observed when the channel’s height decreases. It was shown that the critical values for $b=2,2.5,$ and $3$ are $S_{c1}=1.0902$, $S_{c2}=0.7676$, and $S_{c3}=0.5464$, respectively. The plots of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ against S for various values of M when $\mathit{Pr}=6.2$, $b=2$, $R=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$ are depicted in Figure 8 and Figure 9. The rise of M contributes to the increment of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ for the upper branch, whereas for the lower branch, the opposite trends are observed. Here, we found that the presence of magnetic strength increases the range of S for which the solutions are in existence, where $S_{c1}=0.8217$, $S_{c2}=1.0902$, and $S_{c3}=1.4120$ are the critical values for $M=0, 0.2,$ and $0.4$, respectively.

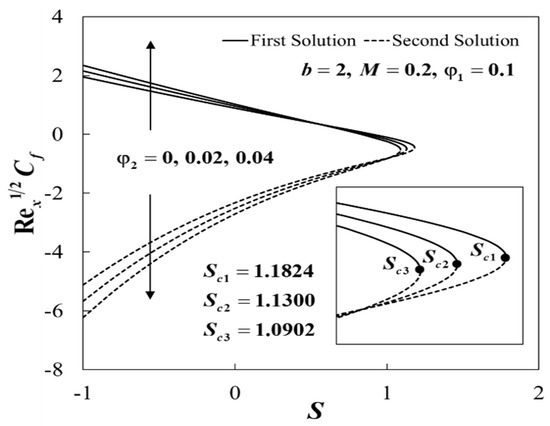
Figure 4. Impact of ${\phi }_2$ and $S$ on ${\mathit{Re}}_x^{1/2}{C}_f$.

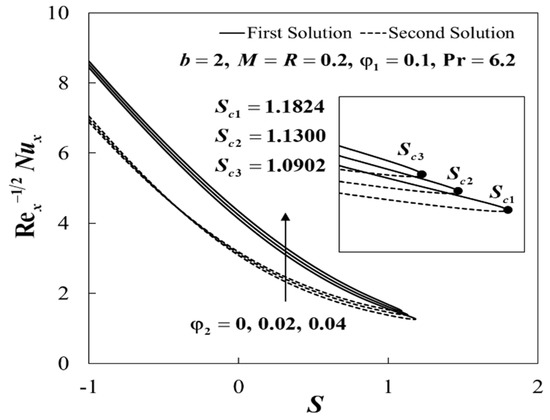
Figure 5. Impact of ${\phi }_2$ and $S$ on ${\mathit{Re}}_x^{-1/2}N{u}_x$.

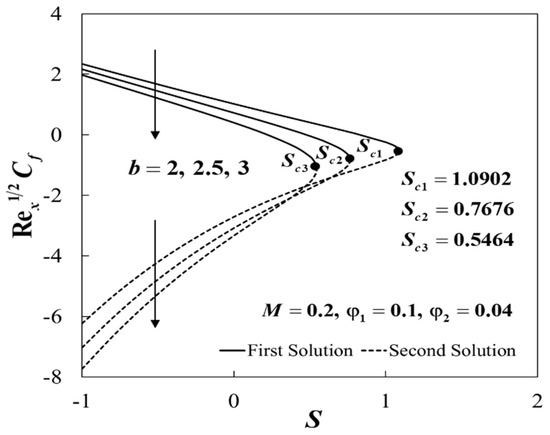
Figure 6. Impact of $b$ and $S$ on ${\mathit{Re}}_x^{1/2}{C}_f$.

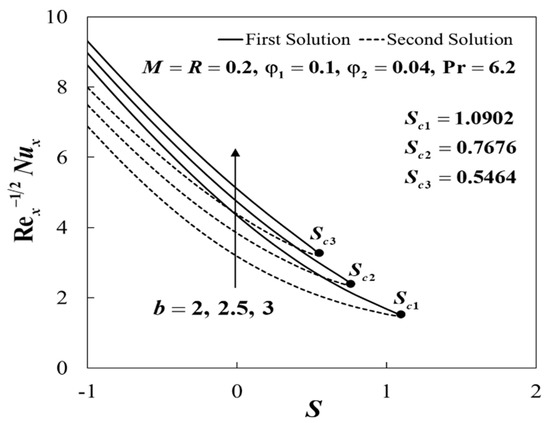
Figure 7. Impact of $b$ and $S$ on ${\mathit{Re}}_x^{-1/2}N{u}_x$.

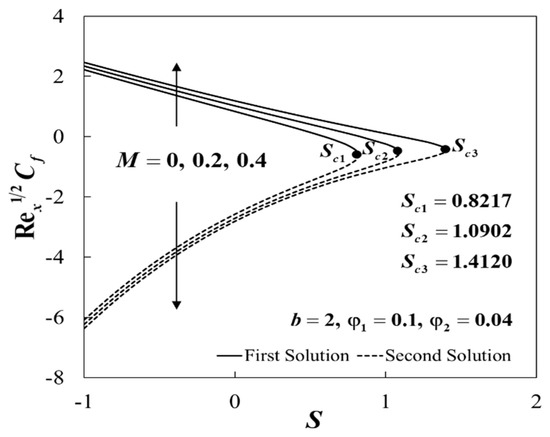
Figure 8. Impact of $M$ and $S$ on ${\mathit{Re}}_x^{1/2}{C}_f$.

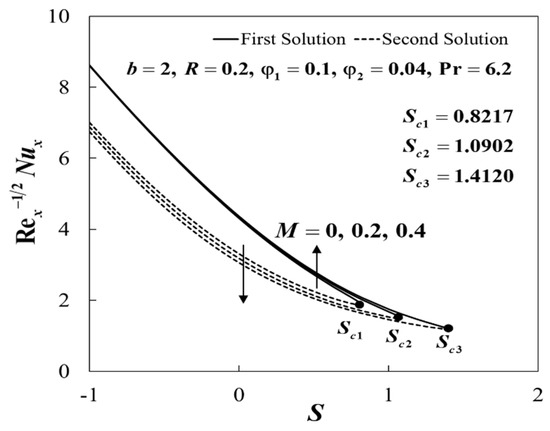
Figure 9. Impact of $M$ and $S$ on ${\mathit{Re}}_x^{-1/2}N{u}_x$.

Further, the profiles of $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ for several values of ${\phi }_2$ when $\mathit{Pr}=6.2$, $b=2$, $S=M=R=0.2$, and ${\phi }_1=0.1$ are plotted in Figure 10 and Figure 11. The increasing behaviour for both branch solutions of $f\prime \left(\eta \right)$ were observed with the increase of ${\phi }_2$, but the observation was reversed for $\theta \left(\eta \right)$. Meanwhile, Figure 12 and Figure 13 display the impact of M on $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ when $\mathit{Pr}=6.2$, $b=2$, $S=R=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$. Note that, $f^{\prime }\left(\eta \right)$ increases whereas $\theta \left(\eta \right)$ decreases for the first solution with the increase of M, however, the observation is reversed for the second solution. Theoretically, a magnetic field induces a drag or Lorentz force which decelerates the fluid flow. However, when the flow is squeezed, the magnetic parameter (M) will act oppositely and consequently leads to an increase in the fluid velocity. These observations are consistent with the results obtained by Khaled and Vafai [32]. In addition, an increase in the velocity ($f^{\prime }\left(\eta \right)$) was noticed for the second solution, and it decreased for the first solution with increased values of S. Meanwhile, the temperature ($\theta \left(\eta \right)$) increases for both branches when $\mathit{Pr}=6.2$, $b=2$, $M=R=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$, as displayed in Figure 14 and Figure 15.

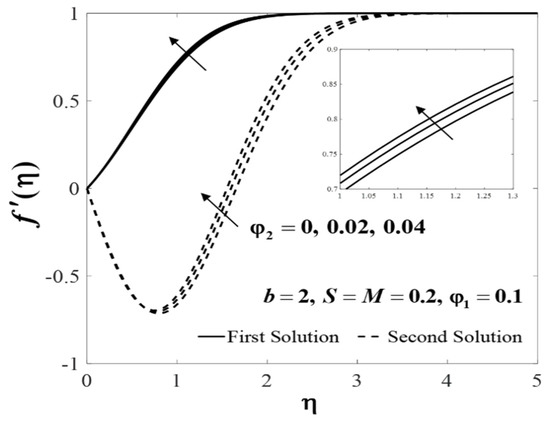
Figure 10. Impact of ${\phi }_2$ on $f\prime \left(\eta \right)$.

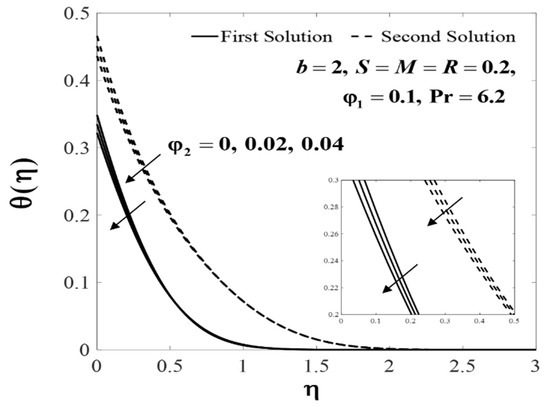
Figure 11. Impact of ${\phi }_2$ on $\theta \left(\eta \right)$.

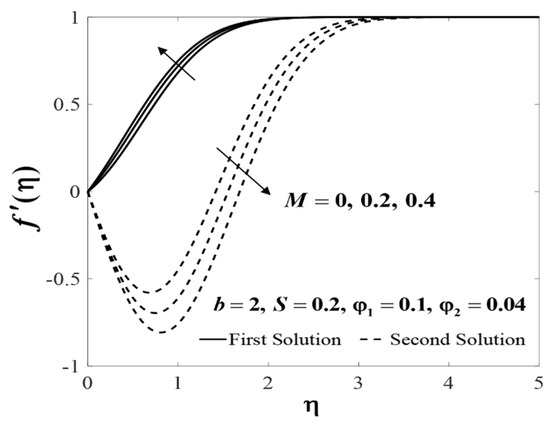
Figure 12. Impact of $M$ on $f^{\prime }\left(\eta \right)$.

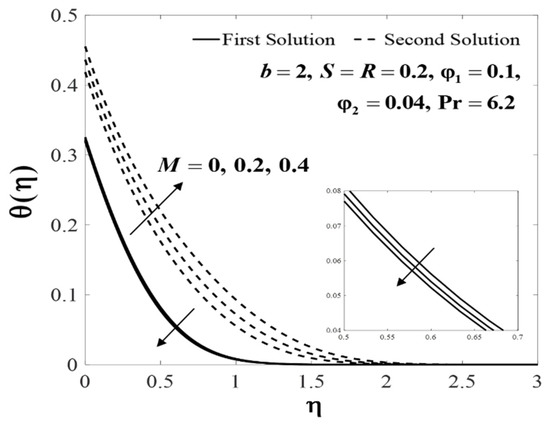
Figure 13. Impact of $M$ on $\theta \left(\eta \right)$.

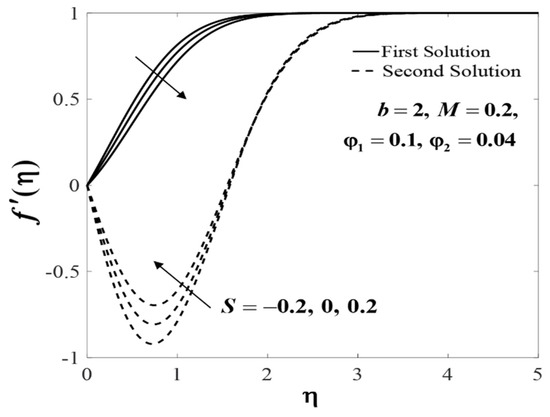
Figure 14. Impact of $S$ on $f^{\prime }\left(\eta \right)$.

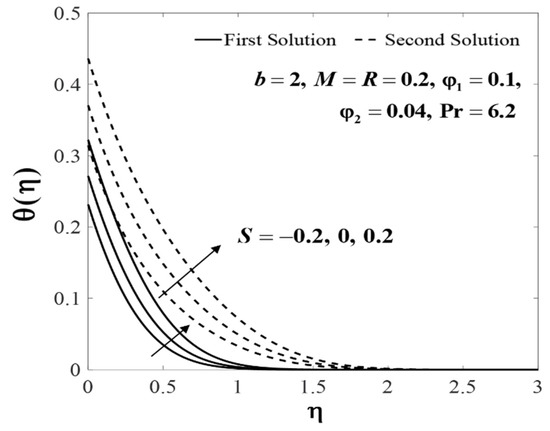
Figure 15. Impact of $S$ on $\theta \left(\eta \right)$.

The effects of $R$ and $S$ on ${\mathit{Re}}_x^{-1/2}N{u}_x$ when $\mathit{Pr}=6.2$, $b=2$, $M=0.2$, ${\phi }_1=0.1$ and ${\phi }_2=0.04$ are displayed in Figure 16. We found that ${\mathit{Re}}_x^{-1/2}N{u}_x$ increased in the presence of radiation. Moreover, Figure 17 portrays the velocity profiles $\theta \left(\eta \right)$ for various values of $R$ when $\mathit{Pr}=6.2$, $b=2$, $M=S=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$. Physically, larger values of $R$ enhance the radiative heat energy in the boundary layer. From the definition $R=4 {\sigma }^{*}{T}_{\infty }^3/k^{*}{k}_f$, it was noticed that $R$ was related to Stephan number, which measures the relative importance of thermal radiation heat transfer to the conduction heat transfer. Therefore, for larger values of $R$, radiation is dominant over conduction that causes a rise in the fluid temperature. We note that for all values of $R$, the critical value was $S_c=1.0902$.

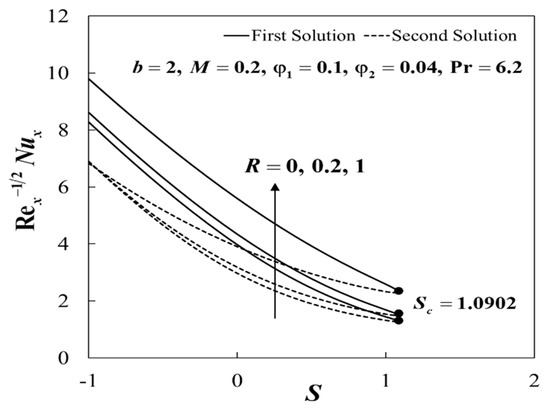
Figure 16. Impact of $R$ and $S$ on ${\mathit{Re}}_x^{-1/2}N{u}_x$.

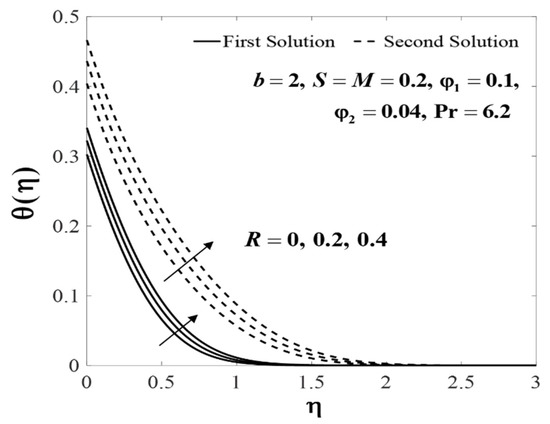
Figure 17. Impact of $R$ on $\theta \left(\eta \right)$.

The variations of $\gamma$ against S when $b=2$, $M=0.2$, ${\phi }_1=0.1$, and ${\phi }_2=0.04$ are portrayed in Figure 18. It was noticed that the sign of $\gamma$ for the first solution was positive, while it was negative for the second solution. By the definition in Equation (23), as time evolves $\left(\tau \to \infty \right)$, $e^{-\gamma \tau }\to 0$ for the positive value of $\gamma$ and $e^{-\gamma \tau }\to \infty$ for the negative value of $\gamma$. Thus, this implies that the first solution is the real solution and stable, whereas the other is unstable and not physically relevant in the long run.

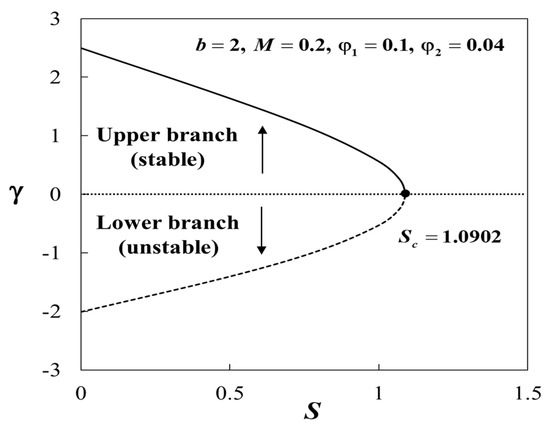
Figure 18. Plot of $\gamma$ against $S$.

5. Conclusions

In the present paper, the squeezed hybrid nanofluid flow over a permeable sensor surface with heat transfer was accomplished. Results validation was done for limiting cases, where the present results are comparable with the existing results. The rate of heat transfer for the hybrid nanofluid was greater than that of the regular nanofluid. Based on our computations, there exist two solutions for squeezed flow problems, due to an external free stream created by the squeezing strength. On the other hand, the numerical results revealed that the solutions were not unique for $S<S_c$, and no similarity solutions were obtained when $S>S_c$. The values of ${\mathit{Re}}_x^{1/2}{C}_f$ and ${\mathit{Re}}_x^{-1/2}N{u}_x$ increased with the rise in values of ${\phi }_2$ and M. Besides, the values of ${\mathit{Re}}_x^{1/2}{C}_f$ decreased, whereas the values of ${\mathit{Re}}_x^{-1/2}N{u}_x$ increased, with the increase of b. Additionally, the values of ${\mathit{Re}}_x^{-1/2}N{u}_x$ were enhanced in the presence of radiation (R). The upsurge of ${\phi }_2$ contributed to the increment in $f^{\prime }\left(\eta \right)$ for both branches, but the observation was reversed for $\theta \left(\eta \right)$. Additionally, $f^{\prime }\left(\eta \right)$ increased whereas $\theta \left(\eta \right)$ decreased for the first solution with the increase of M, but the behavior was reversed for the second solution. The temporal stability analysis showed, that between the two solutions, only one was stable and reliable in the long run, while the other was unstable. The outcome from this study provides the theoretical analysis of the flow and heat transfer in a hybrid nanofluid that is beneficial to other researchers or engineers in choosing suitable parameters for heat transfer optimization in modern industry.