Abstract
This paper examines the squeezed hybrid nanofluid flow over a permeable sensor surface with magnetohydrodynamics (MHD) and radiation effects. The alumina (Al2O3) and copper (Cu) are considered as the hybrid nanoparticles, while water is the base fluid. The governing equations are reduced to the similarity equations, using the similarity transformation. The resulting equations are programmed in Matlab software through the bvp4c solver to obtain the numerical solutions. It was found that the heat transfer rate was greater for the hybrid nanofluid, compared to the regular nanofluid. It was observed that dual solutions exist for some values of the permeable parameter S. The upper branch solutions of the skin friction coefficient () and the heat transfer rate at the surface () enhance with the added Cu nanoparticle () and for larger magnetic strength (). Moreover, the values of decrease, whereas the values of increase for both branches, with the rise of the squeeze flow index (). Besides, an increment of the heat transfer rate at the sensor surface for both branches was observed in the presence of radiation (). Temporal stability analysis was employed to determine the stability of the dual solutions, and it was discovered that only one of them was stable and physically reliable as time evolves.
1. Introduction
Nowadays, the problem of heat transfer in industrial processes has become the main topic of interest to the researchers. Previously, fluids like water, oil, and ethylene glycol were regularly considered as cooling liquids in those processes, but their heat transfer rates are limited. In 1995, Choi and Eastman [1] introduced fluid called “nanofluid” to replace the use of regular fluids in industrial processes. Nanofluid was composed by dispersing one type of nanoparticle in the aforementioned fluids to enhance their thermal conductivity. However, the researchers found that the thermal properties of the nanofluid could be improved with the addition of more than a single nanoparticle in the base fluid and named it as ‘hybrid nanofluid’. Experimental studies that consider the hybrid nanocomposite particles were conducted by several researchers, for example, Turcu et al. [2] and Jana et al. [3]. Besides, Suresh et al. [4] synthesized the Al2O3–Cu nanocomposite powder by using a thermochemical method. From the experimental data, it was revealed that the added hybrid nanoparticles enhanced the thermal conductivity of the fluid.
Apart from that, the numerical studies of hybrid nanofluid were extended to the boundary layer flow problem. For instance, the flow over a stretching surface with Al2O3–Cu hybrid nanoparticles was studied by Devi and Devi [5]. They found that the enhancement in the heat transfer occurs at higher values of the nanoparticle volume concentrations. Besides, Waini et al. [6,7,8,9,10,11,12,13], in a series of papers, extended the hybrid nanofluid flow problem to different surfaces, considering the dual nature behaviour of the solutions. Additionally, the problem of hybrid nanofluid flow with different physical parameters was also considered by several authors [14,15,16,17,18,19,20]. For further reading, one can refer to the review papers of nanofluid [21,22,23] and hybrid nanofluid [24,25,26,27,28,29]. Besides, the use of hybrid nanofluid can improve the heat transfer rate due to the synergistic effects as discussed by Sarkar et al. [24]. Due to its capability to improve the heat transfer rate, most of the applications that involve heat transfer, such as coolant in machining and electronic and transformer cooling, are considering hybrid nanofluid as heat transfer fluid.
Squeezed flow over a sensor surface with heat transfer has significant applications in industrial, chemical, and biomedical processes. The sensing element that is commonly used in these processes is microcantilever [30]. This is due to its capability in diagnosing several terminal diseases and also its rapid respond to biowarfare or hazardous agents. Besides, the microcantilever sensor also has high sensitivity, the finest procedure characteristics, actual time sense, and lower cost [31]. Therefore, the study on a sensor surface has gained a lot of consideration by scientists, engineers, and researchers. In this respect, Khaled and Vafai [32] initially studied the flow over a sensor surface placed in a squeezed channel with magnetohydrodynamics (MHD) effects. They found that the rising of the squeezing free stream velocity tended to enhance the local Nusselt number and local wall shear stress. Then, Mahmood et al. [33] investigated a similar problem, but they employed three different methods to solve the locally non-similar momentum and energy equations. Since that, the topic of flow over a sensor surface was vigorously investigated by researchers considering various type of fluids. For example, Hayat et al. [34] examined the squeezed flow in a second-grade fluid. Furthermore, Khan et al. [35] and Salahuddin et al. [36] considered the Carreau and Carreau–Yasuda fluids, respectively. Besides, Ganesh Kumar et al. [37] studied the unsteady squeezed flow of a tangent hyperbolic fluid. Apart from that, the nanofluid flow over a sensor surface was considered by several authors with different aspects, such as Ul Haq et al. [38], Hamzah et al. [39], Akbar and Khan [40], Kandasamy et al. [41], and Nayak et al. [42].
Thus, the objective of this paper is to examine the permeability effects on the hybrid nanofluid flow over a sensor surface with the magnetic field and radiation by employing Tiwari and Das [43] model. Here, we consider water as the base fluid, and copper (Cu) and alumina (Al2O3) as the hybrid nanoparticles. The results are obtained for several physical parameters and presented graphically through tables. Additionally, the comparison results for limiting cases are done with previously published data. Besides, the theoretical analysis from this study is beneficial to other researchers or engineers to further investigate the heat transfer problem that arises in the modern industry.
2. Mathematical Formulation
Consider an unsteady squeezed flow over a permeable sensor surface in a hybrid nanofluid, as illustrated in Figure 1. Here, the x- and y-axes are the Cartesian coordinates, where x is assigned along the sensor surface, and y is orthogonal from the surface. The sensor surface (having a length (L)) is placed in a squeezed channel where the height of the channel () is much larger than the thickness of the boundary layer. Here, we assume that the squeezing in the free stream starts from the tip of the surface, where the lower plate is fixed while the upper plate is squeezed. The surface permeable velocity () through the sensor surface is considered. It was also assumed that a magnetic field strength () was applied normal to the flow. Therefore, the equations that govern the hybrid nanofluid flow are (Khaled and Vafai [32]):
where and represent the velocity components along the - and -axes, while and represent the pressure, the radiative heat flux, the hybrid nanofluid temperature, time, and the axial free stream velocity, respectively. Now, by substituting the pressure gradient term from Equation (3), Equation (2) is transformed into the following form:
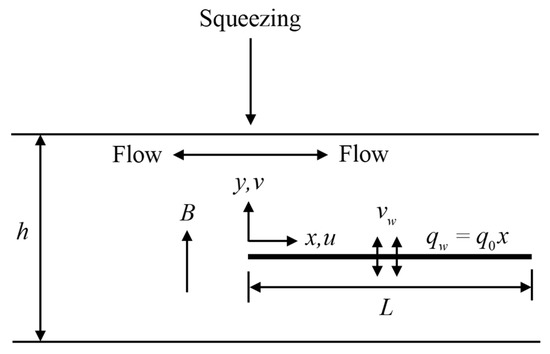
Figure 1.
Physical model.
The radiative heat flux is given as (see Rosseland [44], Cortell [45]):
where and denote the mean absorption coefficient and the Stefan–Boltzmann constant, respectively. Using Taylor series, is expanded about ; and ignoring the higher-order terms, we have . Thus, Equation (4) becomes (see Waini et al. [8]; Cortell [45]):
subject to:
where , , and represent the free stream velocity, the wall heat flux, and the free stream temperature, respectively. Meanwhile, the thermophysical correlations of hybrid nanofluid are given in Table 1 (see [5,46]). Besides, the physical properties of Al2O3, Cu, and water are provided in Table 2 (see [46,47]). Here, Al2O3 and Cu volume fractions are given by and , and the subscripts and correspond to their solid components, respectively. Additionally, we employed the uniform size of the spherical nanoparticles of Al2O3 and Cu. Besides, the fluid, nanofluid, and hybrid nanofluid were designated by the subscripts , and , respectively.

Table 1.
Thermophysical properties of nanofluid and hybrid nanofluid.

Table 2.
Thermophysical properties of Al2O3, Cu, and water.
Referring to Khaled and Vafai [32], the following form of the free stream velocity, the surface permeable velocity, the magnetic field, and the surface heat flux were considered:
where is the reference surface permeable velocity, is the reference magnetic field strength, and is the reference heat flux. An appropriate transformation is introduced as:
where denotes the stream function with and so that Equation (1) is identically fulfilled. Here, a is the squeeze flow strength with s as a constant, and b is the squeeze flow index. According to Khaled and Vafai [32], the channel’s height movement is described by the following condition: for ; and for , where is a constant. Employing these definitions, we get
Thus, Equations (5) and (7) become:
subject to:
where the notation (′) means the differentiation with respect to , represents the magnetic parameter, represents the radiation parameter, represents the Prandtl number, and represents the permeability parameter; with for suction and for injection. These parameters are defined as:
The skin friction coefficient () and the local Nusselt number () are defined as:
where and symbolized the shear stress and the heat flux from the surface defined as (see Waini et al. [8]; Cortell [45]):
Using (10), (16), and (17), one gets:
where denotes the local Reynolds number.
3. Stability Analysis
It was found that dual solutions exist for some values of the physical parameters, so analysis to determine the real solution was required. Therefore, the stability analysis introduced by Merkin [48] and Weidman et al. [49] was considered for this purpose. The analysis was initiated by introducing the new variables based on Equation (10) and given as follows:
Using (19) and following the same procedure as the previous section, we have:
subject to:
According to Weidman et al. [49], the relations given in Equation (23) were employed to examine the stability of the steady solution, , and of Equations (12) to (14).
where indicates the unknown eigenvalue that determines the stability of the solutions, whereas and are small compared to and . The stability of the steady flow, , and are investigated by setting in Equations (20) and (21). By inserting Equation (23) into Equations (20) to (22), one obtains:
subject to:
Without loss of generality, the values of from Equations (24) to (26) were obtained for the case of , as proposed by Harris et al. [50].
4. Results and Discussion
Equations (12) to (14) are solved in Matlab software by bvp4c solver that employed the 3-stage Lobatto IIIa formula (see Shampine et al. [51]). A suitable selection of the boundary layer thickness, , and the initial guess are required to obtain the solutions. Moreover, several researchers [52,53,54,55,56] also employed this solver for solving the boundary layer flow problems. Here, we considered that volume fractions of Cu varied from 0 to 0.04 , while Al2O3 was kept fixed at , and water was used as the base fluid.
Table 3 provides the comparison values of under different values of and for regular fluid () when , with Sparrow et al. [57], and Yih [58]. It was observed that the comparison was in excellent agreement with Sparrow et al. [57], and Yih [58], which supports the validity of the present numerical procedure. Additionally, Table 4 displays the comparison values of and with those obtained by Ul Haq et al. [38] for different values of and when (regular fluid), , , and . From the computation, we found that the comparison showed good agreement with Ul Haq et al. [38]. Besides, the values of and when with different physical parameters are presented in Table 5. It was found that the values of and increased with the rise of and M, whereas these physical quantities decreased with the rise of . Moreover, the rise of b and R lead to an increase the local Nusselt number, , whereas the skin friction coefficient, , decreased with the increase of b; but, as expected, remained unchanged with variation of R. Additionally, the heat transfer rate of Al2O3-Cu/water hybrid nanofluid was intensified if compared to Cu/water nanofluid. This finding shows that the heat transfer rate was higher in the hybrid nanofluid than in the regular nanofluid.

Table 3.
Values of the skin friction coefficient under different values of the magnetic parameter and the permeability parameter for regular fluid () when .

Table 4.
Values of the skin friction coefficient and the local Nusselt number under different values of and for regular fluid () when , , and .

Table 5.
Values of the skin friction coefficient and the local Nusselt number under different physical parameters when .
On the other hand, the variations of the velocity profiles () and the temperature profiles () when (regular fluid), , and for are displayed in Figure 2a and Figure 3a, respectively. The results exhibited qualitatively similarly to those obtained by Khaled and Vafai [32]. It was observed that and decreased with the rising values of b (the decrease of the channel’s height) for the first solutions. Interestingly, we found that the second solutions exist for this problem, which are displayed in Figure 2b and Figure 3b. From these figures, all profiles asymptotically satisfy the free stream conditions (14), thus supporting the validity of the numerical solutions. These behaviours reveal that the second solution was not physically stable, and thus has no physical sense. Although such solutions are deprived of physical significance, they are nevertheless of interest so far as the differential equations are concerned [59,60].
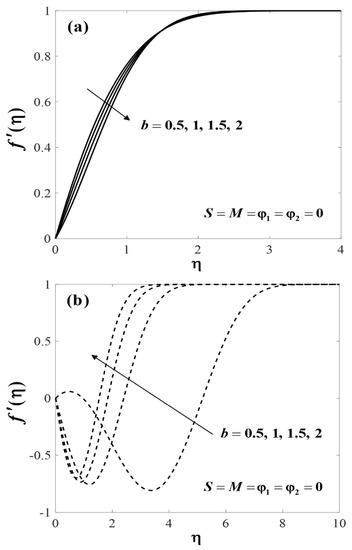
Figure 2.
Impact of on for (a) first solutions, and (b) second solutions.
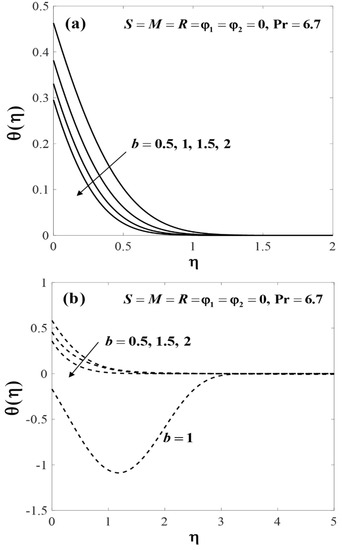
Figure 3.
Impact of on for (a) first solutions, and (b) second solutions.
The non-uniqueness of the solutions of Equations (12) to (14) are observed for , and no similarity solution was obtained when , as shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Separately, the effects of and on and when , , and are given in Figure 4 and Figure 5. The dual solutions exist for the permeability parameter , where , , and for and , respectively. Moreover, for fixed values of , the upper branch solution of and was slightly enhanced with the rise of . These observations were consistent with Sarkar et al. [24], which stated that the addition of hybrid nanoparticles tends to improve the heat transfer due to the synergistic effects. Furthermore, Figure 6 and Figure 7 illustrate the variations of and when , , , and for various values of . It was discovered that the increase of b tends to decrease the skin friction coefficient, , whereas the local Nusselt number, , increases for both branches. This implied that the reduction of the skin friction coefficient and the enhancement of the heat transfer rate at the sensor surface were observed when the channel’s height decreases. It was shown that the critical values for and are , , and , respectively. The plots of and against S for various values of M when , , , , and are depicted in Figure 8 and Figure 9. The rise of M contributes to the increment of and for the upper branch, whereas for the lower branch, the opposite trends are observed. Here, we found that the presence of magnetic strength increases the range of S for which the solutions are in existence, where , , and are the critical values for and , respectively.
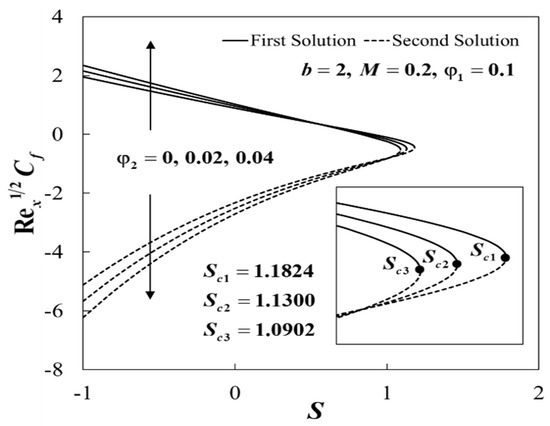
Figure 4.
Impact of and on .
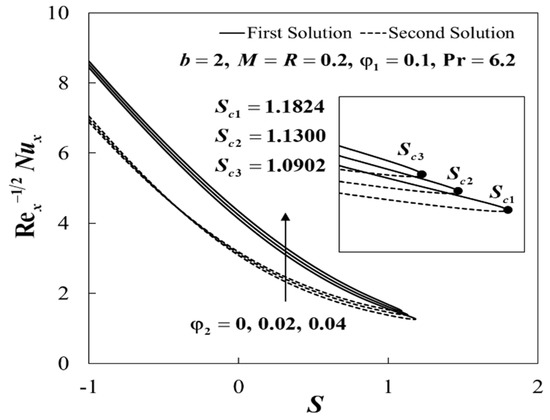
Figure 5.
Impact of and on .
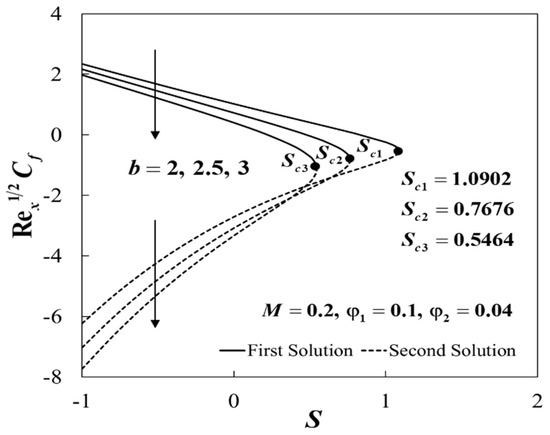
Figure 6.
Impact of and on .
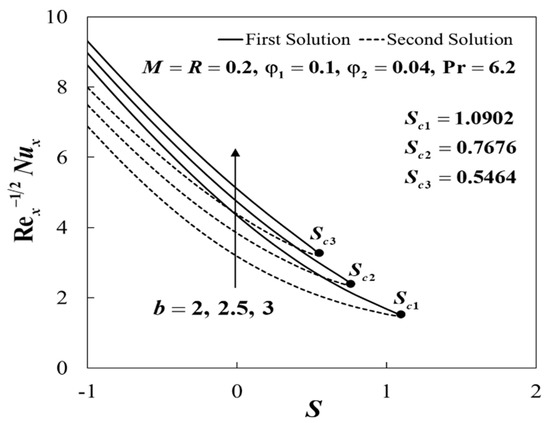
Figure 7.
Impact of and on .
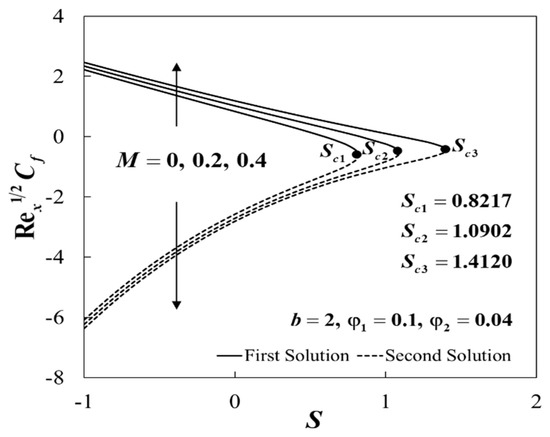
Figure 8.
Impact of and on .
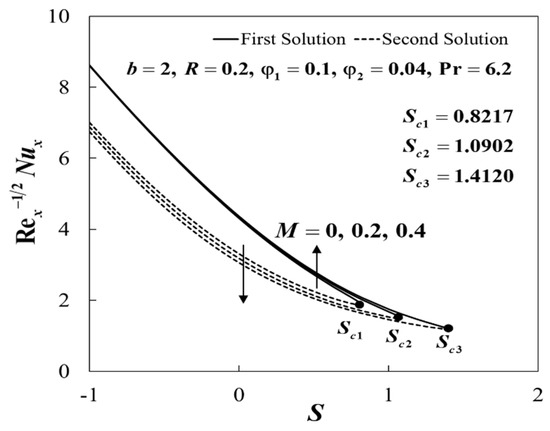
Figure 9.
Impact of and on .
Further, the profiles of and for several values of when , , , and are plotted in Figure 10 and Figure 11. The increasing behaviour for both branch solutions of were observed with the increase of , but the observation was reversed for . Meanwhile, Figure 12 and Figure 13 display the impact of M on and when , , , , and . Note that, increases whereas decreases for the first solution with the increase of M, however, the observation is reversed for the second solution. Theoretically, a magnetic field induces a drag or Lorentz force which decelerates the fluid flow. However, when the flow is squeezed, the magnetic parameter (M) will act oppositely and consequently leads to an increase in the fluid velocity. These observations are consistent with the results obtained by Khaled and Vafai [32]. In addition, an increase in the velocity () was noticed for the second solution, and it decreased for the first solution with increased values of S. Meanwhile, the temperature () increases for both branches when , , , , and , as displayed in Figure 14 and Figure 15.
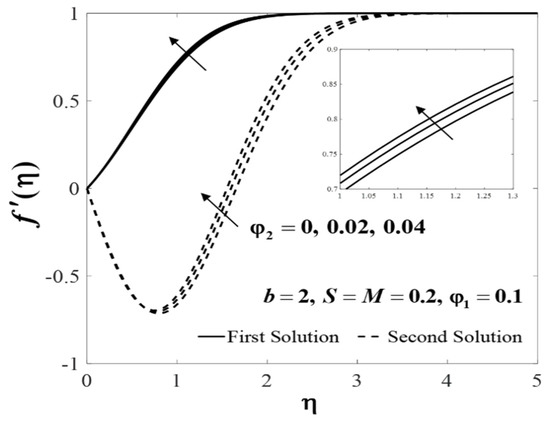
Figure 10.
Impact of on .
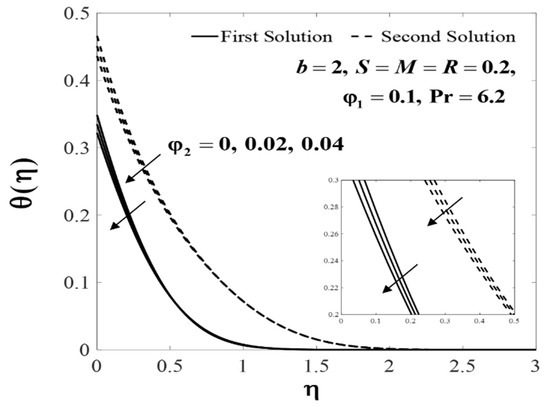
Figure 11.
Impact of on .
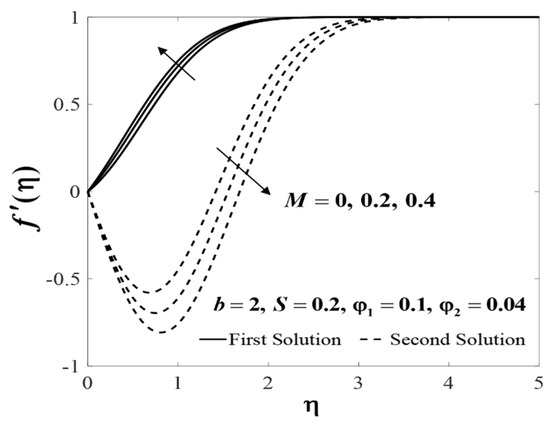
Figure 12.
Impact of on .
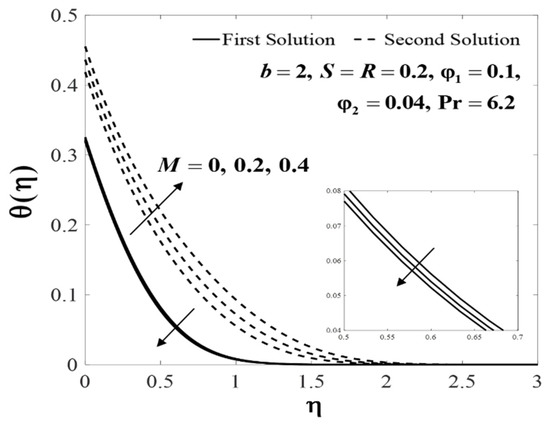
Figure 13.
Impact of on .
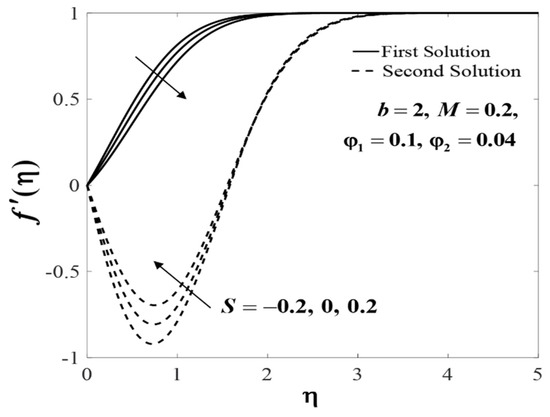
Figure 14.
Impact of on .
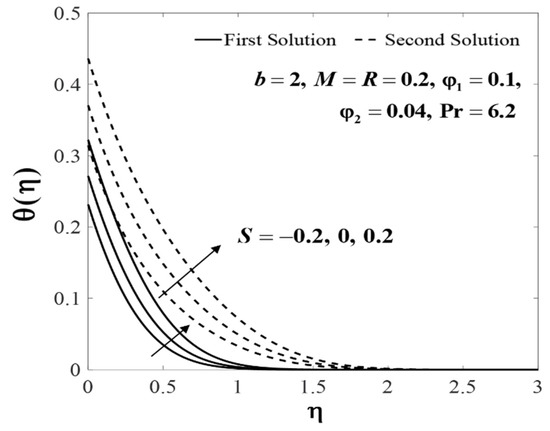
Figure 15.
Impact of on .
The effects of and on when , , , and are displayed in Figure 16. We found that increased in the presence of radiation. Moreover, Figure 17 portrays the velocity profiles for various values of when , , , , and . Physically, larger values of enhance the radiative heat energy in the boundary layer. From the definition , it was noticed that was related to Stephan number, which measures the relative importance of thermal radiation heat transfer to the conduction heat transfer. Therefore, for larger values of , radiation is dominant over conduction that causes a rise in the fluid temperature. We note that for all values of , the critical value was .
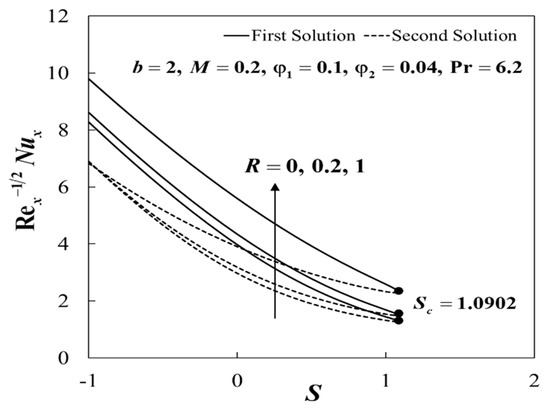
Figure 16.
Impact of and on .
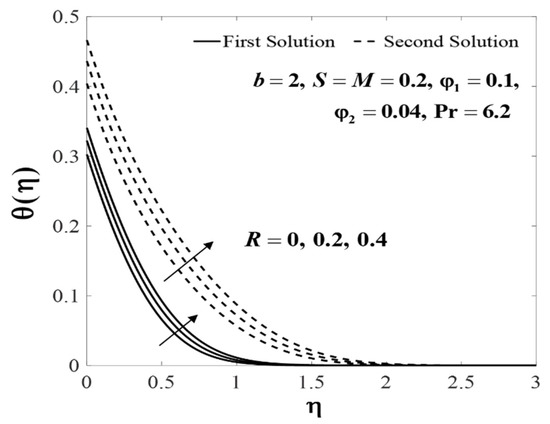
Figure 17.
Impact of on .
The variations of against S when , , , and are portrayed in Figure 18. It was noticed that the sign of for the first solution was positive, while it was negative for the second solution. By the definition in Equation (23), as time evolves , for the positive value of and for the negative value of . Thus, this implies that the first solution is the real solution and stable, whereas the other is unstable and not physically relevant in the long run.
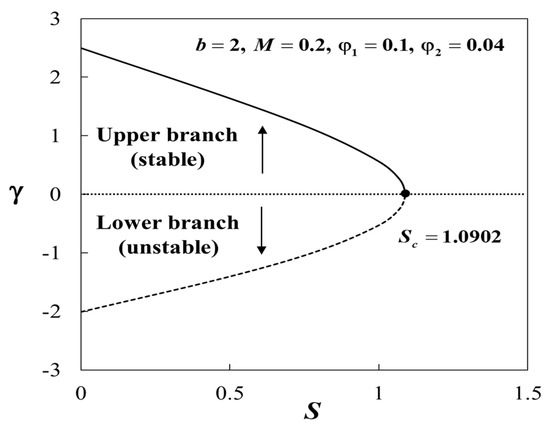
Figure 18.
Plot of against .
5. Conclusions
In the present paper, the squeezed hybrid nanofluid flow over a permeable sensor surface with heat transfer was accomplished. Results validation was done for limiting cases, where the present results are comparable with the existing results. The rate of heat transfer for the hybrid nanofluid was greater than that of the regular nanofluid. Based on our computations, there exist two solutions for squeezed flow problems, due to an external free stream created by the squeezing strength. On the other hand, the numerical results revealed that the solutions were not unique for , and no similarity solutions were obtained when . The values of and increased with the rise in values of and M. Besides, the values of decreased, whereas the values of increased, with the increase of b. Additionally, the values of were enhanced in the presence of radiation (R). The upsurge of contributed to the increment in for both branches, but the observation was reversed for . Additionally, increased whereas decreased for the first solution with the increase of M, but the behavior was reversed for the second solution. The temporal stability analysis showed, that between the two solutions, only one was stable and reliable in the long run, while the other was unstable. The outcome from this study provides the theoretical analysis of the flow and heat transfer in a hybrid nanofluid that is beneficial to other researchers or engineers in choosing suitable parameters for heat transfer optimization in modern industry.
Author Contributions
Conceptualization, I.P.; funding acquisition, A.I.; methodology, I.W.; Project administration, A.I.; supervision, A.I. and I.P.; validation, I.P.; writing—original draft, I.W.; writing—review and editing, A.I. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by a grant from Ministry of Education Malaysia, grant number is FRGS/1/2019/STG06/UKM/01/4.
Acknowledgments
The financial support received from the Ministry of Education Malaysia (Project Code: FRGS/1/2019/STG06/UKM/01/4) and the Universiti Teknikal Malaysia Melaka is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| constant | |
| squeeze flow strength | |
| squeeze flow index | |
| magnetic field | |
| reference magnetic field strength | |
| skin friction coefficient | |
| specific heat at constant pressure | |
| heat capacitance of the fluid | |
| dimensionless stream function | |
| height of the channel | |
| thermal conductivity of the fluid | |
| Rosseland mean absorption coefficient | |
| sensor surface length | |
| local Nusselt number | |
| magnetic parameter | |
| Prandtl number | |
| pressure | |
| reference heat flux | |
| radiative heat flux in y direction | |
| surface heat flux | |
| radiation parameter | |
| local Reynolds number | |
| permeable parameter | |
| time | |
| fluid temperature | |
| surface temperature | |
| ambient temperature | |
| velocity component in the x- and y- directions | |
| free stream velocity | |
| reference surface permeable velocity | |
| surface permeable velocity | |
| Cartesian coordinates | |
| Greek symbols | |
| eigenvalue | |
| similarity variable | |
| dimensionless temperature | |
| dynamic viscosity of the fluid | |
| kinematic viscosity of the fluid | |
| density of the fluid | |
| electrical conductivity of the fluid | |
| Stefan–Boltzmann constant | |
| dimensionless time variable | |
| wall shear stress | |
| nanoparticle volume fractions for Al2O3 (alumina) | |
| nanoparticle volume fractions for Cu (copper) | |
| stream function | |
| Subscripts | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| Superscript | |
| ′ | differentiation with respect to |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L.; Pana, O.; Soran, M.L.; Koos, A.A.; et al. New polypyrrole-multiwall carbon nanotubes hybrid materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Jana, S.; Salehi-Khojin, A.; Zhong, W.H. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu- Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer along a permeable stretching/shrinking curved surface in a hybrid nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer past a vertical thin needle with prescribed surface heat flux. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4875–4894. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alexandria Eng. J. 2020, 59, 91–99. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge. Appl. Math. Mech. 2020, 41, 507–520. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Groşan, T.; Pop, I. Mixed convection of a hybrid nanofluid flow along a vertical surface embedded in a porous medium. Int. Commun. Heat Mass Transf. 2020, 114, 104565. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Khan, A.U. Rotating flow of Ag-CuO/H2O hybrid nanofluid with radiation and partial slip boundary effects. Eur. Phys. J. E 2018, 41, 75. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, M.; Dinarvand, S.; Eftekhari Yazdi, M.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Rostami, M.N.; Dinarvand, S.; Pop, I. Dual solutions for mixed convective stagnation-point flow of an aqueous silica–alumina hybrid nanofluid. Chinese J. Phys. 2018, 56, 2465–2478. [Google Scholar] [CrossRef]
- Subhani, M.; Nadeem, S. Numerical analysis of micropolar hybrid nanofluid. Appl. Nanosci. 2019, 9, 447–459. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Magnetohydrodynamics (MHD) axisymmetric flow and heat transfer of a hybrid nanofluid past a radially permeable stretching/shrinking sheet with Joule heating. Chinese J. Phys. 2020, 64, 251–263. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Raza, J.; Khan, I. Magnetohydrodynamic flow of Cu–Fe3O4/H2O hybrid nanofluid with effect of viscous dissipation: Dual similarity solutions. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid convective heat transfer using semi analytical and numerical approaches: A review. J. Taiwan Inst. Chem. Eng. 2016, 65, 43–77. [Google Scholar] [CrossRef]
- Myers, T.G.; Ribera, H.; Cregan, V. Does mathematics contribute to the nanofluid debate? Int. J. Heat Mass Transf. 2017, 111, 279–288. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. Applications of nanofluids in porous medium A critical review. J. Therm. Anal. Calorim. 2019, 135, 1479–1492. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor–A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications–A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mirlohi, A.; Alhuyi Nazari, M.; Ghasempour, R. A review of thermal conductivity of various nanofluids. J. Mol. Liq. 2018, 265, 181–188. [Google Scholar] [CrossRef]
- Datskos, P.G.; Oden, P.I.; Thundat, T.; Wachter, E.A.; Warmack, R.J.; Hunter, S.R. Remote infrared radiation detection using piezoresistive microcantilevers. Appl. Phys. Lett. 1996, 69, 2986–2988. [Google Scholar] [CrossRef]
- Hussain, A.; Zetoon, R.; Ali, S.; Nadeem, S. Magnetically driven flow of pseudoplastic fluid across a sensor surface. J. Brazilian Soc. Mech. Sci. Eng. 2019, 41, 185. [Google Scholar] [CrossRef]
- Khaled, A.R.A.; Vafai, K. Hydromagnetic squeezed flow and heat transfer over a sensor surface. Int. J. Eng. Sci. 2004, 42, 509–519. [Google Scholar] [CrossRef]
- Mahmood, M.; Asghar, S.; Hossain, M.A. Squeezed flow and heat transfer over a porous surface for viscous fluid. Heat Mass Transf. 2007, 44, 165–173. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, M.; Nadeem, S.; Alsaedi, A.; Obaidat, S. Squeezed flow and heat transfer in a second grade fluid over a sensor surface. Therm. Sci. 2014, 18, 357–364. [Google Scholar] [CrossRef]
- Khan, M.; Malik, M.Y.; Salahuddin, T.; Khan, I. Heat transfer squeezed flow of Carreau fluid over a sensor surface with variable thermal conductivity: A numerical study. Results Phys. 2016, 6, 940–945. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M.; Khan, I. MHD squeezed flow of Carreau-Yasuda fluid over a sensor surface. Alexandria Eng. J. 2017, 56, 27–34. [Google Scholar] [CrossRef]
- Ganesh Kumar, K.; Gireesha, B.J.; Krishanamurthy, M.R.; Rudraswamy, N.G. An unsteady squeezed flow of a tangent hyperbolic fluid over a sensor surface in the presence of variable thermal conductivity. Results Phys. 2017, 7, 3031–3036. [Google Scholar] [CrossRef]
- Ul Haq, R.; Nadeem, S.; Khan, Z.H.; Noor, N.F.M. MHD squeezed flow of water functionalized metallic nanoparticles over a sensor surface. Phys. E 2015, 73, 45–53. [Google Scholar] [CrossRef]
- Hamzah, N.S.A.; Kandasamy, R.; Muhammad, R. Thermal radiation energy on squeezed MHD flow of Cu, Al2O3 and CNTs-nanofluid over a sensor surface. Alexandria Eng. J. 2016, 55, 2405–2421. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H. Variable fluid properties analysis with water based CNT nanofluid over a sensor sheet: Numerical solution. J. Mol. Liq. 2017, 232, 471–477. [Google Scholar] [CrossRef]
- Kandasamy, R.; Mohammad, R.; Zailani, N.A.B.M.; Jaafar, N.F.B. Nanoparticle shapes on squeezed MHD nanofluid flow over a porous sensor surface. J. Mol. Liq. 2017, 233, 156–165. [Google Scholar] [CrossRef]
- Nayak, M.K.; Bhatti, M.M.; Makinde, O.D.; Akbar, N.S. Transient magneto-squeezing flow of NaCl-CNP nanofluid over a sensor surface inspired by temperature dependent viscosity. Defect Diffus. Forum 2018, 387, 600–614. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik und Atom-Theoretische Grundlagen; Springer: Berlin, Germany, 1931; ISBN 9783662245330. [Google Scholar]
- Cortell, R. Heat and fluid flow due to non-linearly stretching surfaces. Appl. Math. Comput. 2011, 217, 7564–7572. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.; Omar, Z. Numerical investigation of copper-water (Cu-water) nanofluid with different shapes of nanoparticles in a channel with stretching wall: Slip effects. Math. Comput. Appl. 2016, 21, 43. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521824040. [Google Scholar]
- Soid, S.K.; Ishak, A.; Pop, I. MHD stagnation-point flow over a stretching/shrinking sheet in a micropolar fluid with a slip boundary. Sains Malays 2018, 47, 2907–2916. [Google Scholar] [CrossRef]
- Kamal, F.; Zaimi, K.; Ishak, A.; Pop, I. Stability analysis of MHD Stagnation-point flow towards a permeable stretching/shrinking sheet in a nanofluid with chemical reactions effect. Sains Malays 2019, 48, 243–250. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. J. Heat Transfer 2019, 141, 012406. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. On the stability of the flow and heat transfer over a moving thin needle with prescribed surface heat flux. Chinese J. Phys. 2019, 60, 651–658. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. A stability analysis for magnetohydrodynamics stagnation point flow with zero nanoparticles flux condition and anisotropic slip. Energies 2019, 12, 1268. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Eckert, E.R.G.; Minkowycz, W.J. Transpiration cooling in a magneto-hydrodynamic stagnation-point flow. Appl. Sci. Res. 1963, 11, 125–147. [Google Scholar] [CrossRef]
- Yih, K.A. The effect of uniform suction/blowing on heat transfer of magnetohydrodynamic Hiemenz flow through porous media. Acta Mech. 1998, 130, 147–158. [Google Scholar] [CrossRef]
- Ridha, A. Aiding flows non-unique similarity solutions of mixed-convection boundary-layer equations. Zeitschrift fur Angew. Math. Phys. 1996, 47, 341–352. [Google Scholar] [CrossRef]
- Ishak, A.; Merkin, J.H.; Nazar, R.; Pop, I. Mixed convection boundary layer flow over a permeable vertical surface with prescribed wall heat flux. Zeitschrift fur Angew. Math. Phys. 2008, 59, 100–123. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).