Abstract
A set of vertices of a graph G is a total dominating set if every vertex of G is adjacent to at least one vertex in such a set. We say that a total dominating set D is a total outer k-independent dominating set of G if the maximum degree of the subgraph induced by the vertices that are not in D is less or equal to . The minimum cardinality among all total outer k-independent dominating sets is the total outer k-independent domination number of G. In this article, we introduce this parameter and begin with the study of its combinatorial and computational properties. For instance, we give several closed relationships between this novel parameter and other ones related to domination and independence in graphs. In addition, we give several Nordhaus–Gaddum type results. Finally, we prove that computing the total outer k-independent domination number of a graph G is an NP-hard problem.
1. Introduction
Theory of domination in graphs is one of the most important topics in graph theory. In the last few decades, the interest in this area has increased, due to its applications to different fields of science, such as linear algebra, communication networks, social sciences, computational complexity, algorithm design, complex ecosystems, optimization problems, among others (for example, see [1,2]). In this sense, in this important area, a very high number of variants of domination parameters have been developed, which are combinations of two or more parameters. In this article, we center our attention on the study of a new parameter, which is a combination between the following well-known parameters: total domination and k-independence in graphs. In addition, we focus the investigation some computational and combinatorial properties of it.
Throughout this article, we consider simple graphs G. Given a set , and a vertex , denotes the set of neighbors of v in D, that is, and . In addition, let . The parameter denotes the degree of v in G. For short, we will often use and instead of and , respectively. The minimum and maximum degrees of G will be denoted by and , respectively. A leaf vertex of G is a vertex of degree one, and a support vertex of G is a vertex adjacent to a leaf vertex. The set of leaves and support vertices will be denoted by and , respectively. The subgraph induced by will be denoted by . Given two sets , denotes the set of all edges of G that join a vertex of X and a vertex of Y.
A set of vertices of a graph G is independent if the subgraph induced by it is isomorphic to an empty graph. The independence number of G is the maximum cardinality among all independent sets of G and is denoted by .
A set is a dominating set of G if every vertex in is adjacent to at least one vertex in D. The domination number of G is the minimum cardinality among all dominating sets of G, and it is denoted by .
In [3,4], Fink and Jacobson generalized the concepts of dominating and independent sets. For an integer , we say that a set is k-independent if the maximum degree of the subgraph induced by the vertices of X is less than or equal to , that is, . The k-independence number of G is the maximum cardinality among all k-independent sets of G and is denoted by . A -set is a k-independent set of cardinality . Thus, when , the 1-independence number is the classical independence number. Moreover, we say that a set is k-dominating if every vertex in has at least k neighbors in D. The k-domination number of G is the minimum cardinality among all k-dominating sets of G and is denoted by . A k-dominating set of cardinality is called a -set. For more information on k-independence and k-domination, we suggest the relatively recent survey [5].
A dominating set is a total dominating set of G if the subgraph induced by the vertices of D has no isolated vertex. The total domination number of G is the minimum cardinality among all total dominating sets of G and is denoted by . A total dominating set of cardinality is called -set. For more information on total domination, we suggest the survey [6] and the book [7].
A total outer k-independent dominating set (or TOkID set, for short) is a total dominating set such that is a k-independent set. The minimum cardinality among all TOkID sets is the total outer k-independent domination number of G and is denoted by . A TOkID set of cardinality is a -set. When , a TOkID set is a total outer-independent dominating set, that is, a total dominating set D such that the subgraph induced by is isomorphic to an empty graph. This last concept was introduced in [8] and also barely looked at in [9] under the name of total co-independent domination number. Recently, it was analyzed in [10,11,12].
Given a graph G with no isolated vertex, in order to have a TOkID set D of G, any vertex of must have at least one neighbor in D and must have at most neighbors in . Hence, .
Moreover, we observe that, if , , …, with are the components of a non-connected graph H with no isolated vertex, then any TOkID set of H is formed by a TOkID set in each component , for . In the following remark, we expose the quotation above, and, as a consequence, in the paper, we only study the TOkID sets of nontrivial connected graphs.
Remark 1.
Let H be a non-connected graph with no isolated vertex. If , , …, with , are the components of H, then
The remainder of this article is structured as follows. Section 2 introduces primary combinatorial and computational results. For instance, we show that the problem of finding the total outer k-independent domination number of a graph is NP-hard. In addition, we give the exact value of this parameter for some specific families of graphs, and we expose general bounds and discuss the extreme cases. Finally, Section 3 is dedicated to giving several Nordhaus–Gaddum type results concerning the parameter .
2. Primary Combinatorial and Computational Results
It is natural to think that, due to the concept of “TOkID set", the total outer k-independent domination number is related to the total domination number and the k-independence number. This simple quotation leads to the following result.
Theorem 1.
If G is a connected graph of order n, then
Moreover, it is not difficult to see that, for any nontrivial connected graph G, any TOID set is a TOkID set, where . Therefore, the following inequality chain holds.
Proposition 1.
If G is a connected graph of order n and maximum degree Δ, then
The following remark is an immediate consequence of the proposition above.
Remark 2.
Let G be any connected graph. If , then for every .
Next, we give a theoretical characterization of the graphs that have equal TOkID and TOID numbers. For this, we need some extra terminology and notation. For any -set D, let be the set of vertices defined as follows:
Lemma 1.
Let G be a nontrivial connected graph. For any -set D with ,
Proof.
Let D be any -set. Notice that is a TOID set of G. Thus, . □
Theorem 2.
Let G be a connected graph. For an integer , if and only if for some -set D.
Proof.
Suppose that and let D be a -set. Thus, . Since every TOID set is a TOkID set, it follows that D is also a TOkID set of G of cardinality . Hence, D is also a -set and satisfies that . Conversely, if there exists a -set D such that , then, by Proposition 1 and Lemma 1, the result follows. □
Now, we give an example of a subfamily of graphs given by Cabrera et al. in [13], in which the lower bound of Theorem 1 is achieved for the graphs of this family, and also the equivalence of Theorem 2 is satisfied. To this end, we need to introduce the family of graphs . Before this, we shall need the following operations for vertices or induced paths of a graph G. Note that these operations were already presented in [12].
Addition oftpendant vertices: Given a vertex x, add t new vertices and the edges for every .
Inflation of sizeq: Given an induced path of G, in which , remove the vertex v and the two incident edges, and replace them with q vertices and edges for every .
From the cycle , we obtain a graph by making the following sequence of operations.
- (i)
- Apply the operation “Addition of pendant vertices”, and , to all vertices of a -set , respectively.
- (ii)
- Apply the operation “Inflation of size ” with and to the three possible paths of order three between .
Figure 1 shows an example of a graph belonging to the family . Next, we expose a result which relates and for graphs .
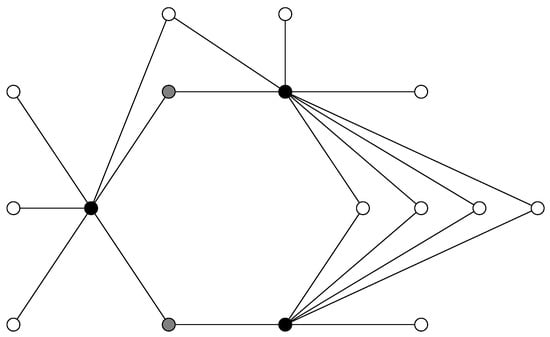
Figure 1.
A graph where the three black-colored vertices form a -set and the two gray-colored vertices form a possible set to be added to the black-colored vertices to get a -set.
Remark 3.
If , then .
According to the remark above, we can easily check that, for any graph , . Since every TOkID set is also a total dominating set and by equality chain above, we have that every -set is also a -set too. Hence, if , then for every -set D.
Now, we consider the decision problem associated with total outer k-independent domination number of graphs.
| TOTAL OUTER k-INDEPENDENT DOMINATION PROBLEM (TOkID PROBLEM) INSTANCE: A nontrivial connected graph G and a positive integer r PROBLEM: Deciding whether is less than r |
We will show that the TOkID PROBLEM is NP-Complete by making a reduction from a known decision problem concerning the k-independence number of graphs, which was solved in 1989 by Jacobson and Peters [14]. In this article, the authors showed that the problem of determining the number for an arbitrary graph G is NP-Complete.
Next, we define a family of graphs, which we will need to make the reduction. Fixing a positive integer k, the graph is obtained from a path , by adding four copies of , and joining with an edge each vertex of with all the vertices from two of such copies. (see Figure 2I). Let G be a connected graph with and let be n graphs isomorphic to the graph . We construct the graph by adding edges between the -vertex of G and one vertex of maximum degree of the -graph . See Figure 2II for an example.
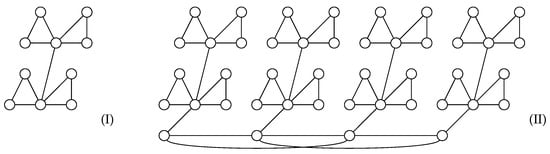
Figure 2.
The graph (I) and a graph (II) where G is a complete graph minus one edge.
Lemma 2.
If G is a connected graph of order n and any positive integer , then
Proof.
Let G be a nontrivial connected graph such that and let be the graph described above (). We define as the two vertices of maximum degree in the copy of the graph used to construct and let A be a -set. Notice that is a k-independent set of . Hence,
On the other hand, let S be a -set. It is straightforward to see that for every and that . Therefore,
which completes the proof. □
The following theorem shows the NP-completeness of the TOkID PROBLEM.
Theorem 3.
TOkID PROBLEM is NP-complete.
Proof.
The TOkID PROBLEM belongs to NP, since we can check in polynomial time that a given set has cardinality at most r and is a TOkID set. Let and be the graph and the vertices described in the lemma above, respectively. Now, we will prove that .
Let A be a -set and let . Notice that D is a total dominating set of and is a k-independent set. Thus, D is a TOkID set of and, as a consequence,
Moreover, by Theorem 1 and Lemma 2, we obtain that . Therefore, .
Now, for , it is readily seen that if and only if , which completes the reduction. Hence, TOkID PROBLEM is NP-complete. □
The next result is an immediate consequence of the previous theorem.
Corollary 1.
The problem of computing the total outer k-independent domination number of a nontrivial connected graph is NP-hard.
According to the complexity results above, it is desirable to bound the total outer k-independent domination number or compute its exact value for several families of graphs. We next center our attention on this second goal. We will use the notation , , , , , and for path graphs, cycle graphs, complete graphs, star graphs, double star graphs, empty graphs and wheel graphs of order n, respectively. In addition, we use the notation for the bipartite complete graph and, without loss of generality, we always assume that .
Remark 4
([7]). For any integer , .
Proposition 2.
The following equalities hold for any integer .
- (i)
- and .
- (ii)
- and .
- (iii)
- (iv)
- .
- (v)
- (vi)
Proof.
The equalities and are given in [8]. From Proposition 1 and Remark 4, we deduce (i) and (ii). The equalities (iii)–(v) are straightforward. Now, we proceed to prove (vi). Let be the bipartite complete graph with partite sets and of cardinality r and s, respectively. Let . Notice that is a TOkID set of . Hence, . If , then we are done. Thus, we assume that . Next, we analyze two cases.
Case 1. . Let such that and . Notice that X is a TOkID set of . Hence, . Now, let D be a -set. Since , and , we have that and . Thus, . Therefore, .
Case 2. . Let such that and . Notice that X is a TOkID set of . Hence, . Now, let D be a -set. Since , and , we have that and . Thus, . Therefore, . □
Let G and H be two graphs of order and , respectively. The corona product graph is defined as the graph obtained from G and H, by taking one copy of G and copies of H and joining by an edge every vertex from the -copy of H with the -vertex of G. For every , will denote the copy of H in associated with x.
Next, we study the total outer k-independent domination number of corona product graphs. Before, we shall need the following useful lemmas.
Lemma 3.
If G and H are two graphs with no isolated vertex, then, for any positive integer ,
Proof.
Let S be a -set. For any , let be the copy of S associated with . Since is a k-independent set of , we have that . Now, we suppose that and let D be a -set. Thus, there exists a vertex such that . This can only happen if , which implies that , contradicting the fact that since . Therefore, , which completes the proof. □
Lemma 4.
If G and H are two graphs with no isolated vertex, then
Proof.
Notice that is a total dominating set of . Hence, . Moreover, we observe that each copy of H contains at least one vertex in any total dominating set of . Thus, , which completes the proof. □
Theorem 4.
If G is a graph with no isolated vertex, then, for every graph H with no isolated vertex,
Proof.
If , then it is straightforward to see that is a TOkID set of . Hence, by Lemma 4 and the statement above, we have that . Therefore, Theorem 1 leads to .
From now on, we assume that . Let S be a -set. For any , let be the copy of S associated with . Since is a k-independent set of , by Lemma 3, we deduce that R is a -set. Moreover, we observe that is a total dominating set of . Thus, is a TOkID set of and so . The proof is completed by Theorem 1. □
Now, we continue the article giving relationships between the total outer k-independent domination number and other parameters of a graph.
Theorem 5
([15]). If G is a connected graph of order and maximum degree , then .
Theorem 6.
If G is a connected graph of order n and size m, then
Furthermore, if and only if .
Proof.
Let D be a -set. Since D is also a total dominating set of G, each vertex in is adjacent to at least one vertex in D. Hence, . In addition, as is a k-independent set, we have that . Since , we obtain
which is equivalent to . Therefore, , which completes the proof of the lower bound.
In order to prove the upper bound, we first suppose that . Let v be a vertex of maximum degree and let be a set of k vertices adjacent to v. Clearly, the set is k-independent. If is a total dominating set, then D is a TOkID set. Hence, . Now, we assume that D is not a total dominating set of G. Since G is connected, it can only happen when . Let and consider the set . Observe that is a total dominating set of G of cardinality at most and is k-independent. Hence, is a TOkID set of G and so, .
Now, we suppose that . Hence, by Proposition 1 and Theorem 5, we have that .
Finally, we assume that . Thus, and again, by Proposition 1, it follows that . Conversely, if , then, by previous cases ( and ), we deduce that , which completes the proof. □
The lower bound above is tight. For instance, it is achieved for the cycle with , where, by Proposition 2(ii), we obtain .
The following result is a direct consequence of Theorems 1 and 6.
Corollary 2.
Let G be a nontrivial connected graph of order n. Let k be an integer such that . If or , then .
Next, we give an upper bound for the total outer k-independent domination number of a graph.
Theorem 7.
If G is a connected graph of order n, then for any positive integer ,
Proof.
Let S be a -set. Since S is k-independent, then is a -dominating set of G. Now, we fix a vertex and let A be the set of isolated vertices of . Let be a subset of S of minimum cardinality such that for every . Clearly, . Moreover, notice that the set is a TOkID set of G. Hence,
which completes the proof. □
We remark that the upper bound given in Theorem 7 is tight. For example, it is achieved for the graph , where is an integer. It is easy to check that , , and . The graph , for example, is illustrated in Figure 3.
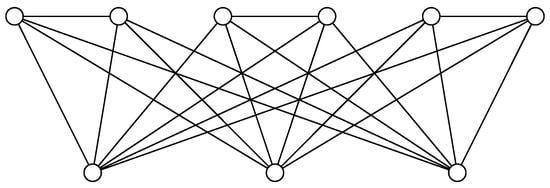
Figure 3.
The graph .
Our next result provides a lower bound for the total outer k-independent domination number in terms of the order, minimum degree, and the maximum degree of a graph.
Theorem 8.
If G is a connected graph of order n, then for any positive integer ,
Furthermore, if , then , where is a graph with no isolated vertex of order and is a -regular graph of order .
Proof.
Let D be a -set. If , then, by Theorem 13(iii), we have that and . Hence, the bound is satisfied. Now, we assume that . Since every vertex in has at least neighbors in D, we obtain that . In addition, since every vertex in D has at most neighbors in , we deduce that
which implies that the bound is satisfied.
Now, we assume that . Since D is also a total dominating set of G, we have that is a graph with no isolated vertex of order . Let . If , then as is k-independent, which is a contradiction. Hence, for every vertex , it satisfies that and, consequently, . Thus, is a -regular graph of order and , which completes the proof. □
For any integer , let be the family of -regular graphs of order , and let , where . Observe that , where . Hence, by Theorem 13(i), we have that . In addition, one can check that , , and , concluding that the lower bound given in the previous theorem is tight, and it is achieved for the graph G. Recall that, for any integer , the family is not empty. Next, we give an example of a graph . Let be the graph with vertex set and edge set , where the subscripts are taken modulo k. It is not difficult to see that the graph is a -regular graph of order , as desired. The graph , for example, is illustrated in Figure 4.
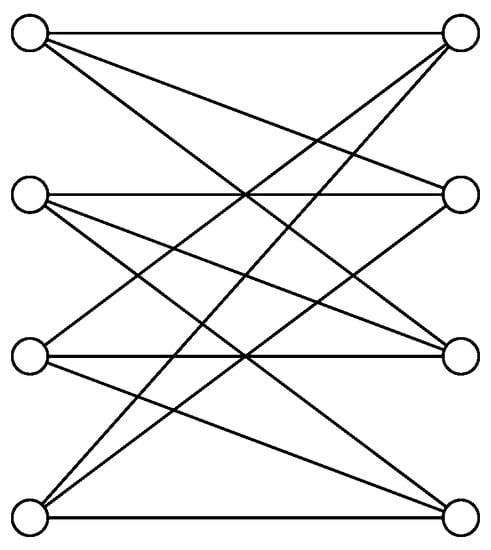
Figure 4.
The graph .
In order to derive another results, we need to state the following results.
Theorem 9.
Let G be a graph.
- (i)
- [16]If , then
- (ii)
- [3]If , then
The following result is a direct consequence of combining Theorems 1 and 9(i).
Theorem 10.
If G is a connected graph, then for any positive integer ,
We remark that the lower bound given in the theorem above is sharp. For example, it is achieved for any complete graph with and .
From Theorems 10 and 9(ii), we immediately have the next theorem.
Theorem 11.
If G is a connected graph, then for any positive integer ,
To conclude this section, we proceed to characterize all graphs achieving the extreme values given in Proposition 1. Before this, we shall need the following result and notation.
Theorem 12
([8]). Let G be a graph of order n. Then, if and only if or G is a complete graph with at least three vertices.
We define the k-join operation between two graphs G and H, and denoted by , as the disjoint union of G and H by joining each vertex of G to k or vertices of H. For each integer positive k and any graphs G and H, the family of all graphs obtained by the operation above is denoted by .
Theorem 13.
Let G be a connected graph of order n. Then, the following statement holds.
- (i)
- if and only if , where F is some graph with .
- (ii)
- For , we have that if and only if either and or and .
- (iii)
- if and only if and G is the path .
Proof.
We first proceed to prove (i). Suppose that and let D be a -set. Clearly, D induces a path . Moreover, is a k-independent set, which implies that the subgraph induced by , namely F, has maximum degree . In addition, as D is a total dominating set, every vertex in is adjacent to one or two vertices in D, i.e., for every . Therefore, , where F is some graph with . The necessary condition is straightforward and so the proof of (i) holds.
We now proceed to prove (ii). If either and or and , then it is easy to see that . Hence, we assume that G is a connected graph satisfying . By Theorem 6, we obtain that and, if , then . If , then, by Theorem 12, we give that . Moreover, if , then and . Hence, G is either or , which completes the proof of (ii).
Finally, we proceed to prove (iii). If and , then it is straightforward that . Conversely, if G is a connected graph such that , then, by Theorem 6, we obtain that and . Hence, G is the path , which completes the proof. □
3. Nordhaus–Gaddum Type Inequalities
In 1956, Nordhaus and Gaddum published an article [17], where it gave lower and upper bounds on the sum and product of the chromatic numbers of a graph and its complement. From this research idea, these types of inequalities was defined as Nordhaus–Gaddum type inequalities, and have been well studied for several domination parameters. We suggest a recent survey [18]. In the present section, we initiate the study of Nordhaus–Gaddum type inequalities for the total outer k-independence domination number.
We first establish a lower and upper bounds on the sum of the total outer k-independence domination numbers of a graph and its complement. Before this, we remark that in this section we involve the study of not connected graphs. However, it is necessary to assume that both G and have no isolated vertices. This last condition implies that . In addition, we assume that .
Lemma 5.
For any integer ,
Proof.
Let u and v be two adjacent vertices of . Notice that is a TO1ID set of . Hence, . Now, suppose that and let D be a -set. Observe that and any three vertices in contain a path , which is a contradiction since is an independent set. Therefore, , which completes the proof. □
Theorem 14.
For any graph G of order such that neither G nor contains isolated vertices,
Furthermore,
- (i)
- if and only if .
- (ii)
- if and only if and .
- (iii)
- if and only if and , with .
Proof.
First, we prove the lower bound. Since for any graph G without isolated vertices, the trivial lower bound follows and also (i) is straightforward. Now, let D and be a -set and a -set, respectively. As and are k-independent in G and , respectively, we have that and for every . Hence, , and, as a consequence,
which implies that , as desired.
Next, we prove the upper bound. Suppose that . Notice that either G or is connected. By symmetry, we assume that G is connected. Since and , by Theorem 6, we have that . This implies that , which is a contradiction. Therefore, the upper bound follows.
Now, we proceed to prove (ii). If and , then it is straightforward to observe that . Conversely, we assume that . Since G is connected, Theorem 6 leads to and . Hence, by Theorem 13(iii), it follows that consists of disjoint copies of . Since , we have that k can only take the value 1 and so . This implies, by Theorem 13(ii), that . Therefore, and , which completes the proof of (ii).
Finally, we proceed to prove (iii). First, we suppose that . Again, as G is connected, we have that or . Hence, we analyze these two cases.
Case 1. . If , then by Theorem 13(ii), we have that ( and is isomorphic to , where ) or ( and is isomorphic to , where ). In both cases, we can construct a TOkID set of G of cardinality , which contradicts the condition .
Case 2. . If , then by Theorem 13(iii) we have that and is isomorphic to , with . Moreover, Lemma 5 leads to , as desired.
On the other hand, we suppose that and , with . By symmetry, we consider that . Theorem 13(iii) and Lemma 5 lead to . Hence, , which completes the proof. □
Next, we show that the upper bounds in Theorem 14 can be improved if we assume that both G and are connected graphs.
Theorem 15.
If G is a graph of order such that both G and are connected, then
Proof.
Notice that, if both G and are connected, then , and by Theorem 6 we have that . Hence, □
Next, we give Nordhaus–Gaddum type inequalities for the product of the TOkID numbers of a graph and its complement.
Theorem 16.
If G is a graph of order such that neither G nor contains isolated vertices, then
Furthermore,
- (i)
- if and only if .
- (ii)
- if and only if and .
Proof.
We first prove the upper bound. Since either G or is connected (by symmetry, we assume that G is connected) and , we deduce by Theorem 6 that . Therefore, .
Suppose now that there exists a graph G of order n for which . Without loss of generality, we assume that and . Thus, by Theorem 13(iii), we have that and consists of disjoint copies of , which is a contradiction with the equality above by Lemma 5.
As a consequence, , which implies
as desired.
Now, we suppose that the equality in the inequality (1) holds. Hence, either or . Without loss of generality, we may assume that . By Theorem 13(ii), we have that either ( and , where ) or ( and , where ). In both cases, if , then we can construct a TOkID set of G of cardinality , which contradicts the condition . Since , we obtain that and . The other hand is straightforward to see, which completes the proof of statement (ii).
In order to prove the lower bound, by Theorem 14, we have
Now, we minimize subject to . If , then, by Theorem 14(i), we obtain the equivalence with the condition . Therefore, and statement (i) holds. On the other hand, if , then we obtain either or . Therefore, , which completes the proof. □
4. Conclusions and Open Problems
In this paper, we have introduced and studied the total outer k-independent domination number of graphs. Among the main contributions, we emphasize the following.
- We have shown the close relationship that exists between the total outer k-independent domination number and other domination parameters such as domination number, total domination number, k-domination number, and k-independence number.
- We have obtained general bounds for the parameter and discussed the sharpness of them.
- In a specific section of the article, we focused on the study of Nordhaus–Gaddum type inequalities for the total outer k-independence domination number.
- We have shown that the problem of finding the total outer k-independent domination number of a graph is NP-hard.
In order to continue with this new line of research, we propose some open problems, which we consider to be interesting.
- (a)
- Characterize the graphs G of order n such that and .
- (b)
- Since the problem of finding is NP-hard, is there a polynomial-time algorithm for finding for any tree T?
- (c)
- To find possible practical applications to the parameter studied.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported in part by two grants from the Ministerio de Economía y Competitividad, Agencia Estatal de Investigacioìn (AEI) and Fondo Europeo de Desarrollo Regional (FEDER) (MTM2016-78227-C2-1-P and MTM2015-69323-REDT), Spain.
Acknowledgments
We would like to thank the referees for their careful reading of the manuscript and several useful comments that have helped us to improve the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farber, M.R. Applications of Linear Programming Duality to Problems Involving Independence and Domination; Simon Fraser University, Computing Science: Burnaby, BC, Canada, 1981. [Google Scholar]
- Gupta, P. Domination in Graph with Application. Indian J. Res. 2013, 2, 115–117. [Google Scholar]
- Fink, J.F.; Jacobson, M.S. n-Domination in Graphs. In Graph Theory with Applications to Algorithms and Computer Science; John Wiley and Sons: New York, NY, USA, 1985; pp. 283–300. [Google Scholar]
- Fink, J.F.; Jacobson, M.S. n-Domination and Forbidden Subgraphs. In Graph Theory with Applications to Algorithms and Computer Science; John Wiley and Sons: New York, NY, USA, 1985; pp. 301–311. [Google Scholar]
- Chellali, M.; Favaron, O.; Hansberg, A.; Volkmann, L. k-Domination and k-Independence in Graphs: A Survey. Graphs Comb. 2012, 28, 1–55. [Google Scholar] [CrossRef]
- Henning, M.A. A survey of selected recent results on total domination in graphs. Discret. Math. 2009, 309, 32–63. [Google Scholar] [CrossRef]
- Henning, M.A.; Yeo, A. Total Domination in Graphs. Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Krzywkowski, M. Total Outer-Independent Domination in Graphs. Manuscript. 2014. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.704.9143&rep=rep1&type=pdf (accessed on 22 January 2020).
- Soner, N.D.; Murthy, B.V.D.; Deepak, G. Total co-independent domination in graphs. Appl. Math. Sci. 2012, 6, 6545–6551. [Google Scholar]
- Cabrera Martínez, A.; Cabrera García, S.; Peterin, I.; Yero, I.G. Total co-independent domination number of some graph operations. 2019. submitted. [Google Scholar]
- Cabrera Martínez, A.; Hernández Mira, F.A.; Sigarreta, J.M.; Yero, I.G. A note on total co-independent domination in trees. 2017. submitted. [Google Scholar]
- Cabrera Martínez, A.; Hernández Mira, F.A.; Sigarreta, J.M.; Yero, I.G. On computational and combinatorial properties of the total co-independent domination number of graphs. Comput. J. 2019, 62, 97–108. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Kuziak, D.; Yero, I.G. Outer-independent total Roman domination in graphs. Discret. Appl. Math. 2019, 269, 107–119. [Google Scholar] [CrossRef]
- Jacobson, M.S.; Peters, K. Complexity questions for n-domination and related parameters. Congr. Numer. 1989, 68, 7–22. [Google Scholar]
- Cockayne, E.J.; Dawes, R.M.; Hedetniemi, S.T. Total domination in graphs. Networks 1980, 10, 211–219. [Google Scholar] [CrossRef]
- Jacobson, M.S.; Peters, K.; Rall, D.F. On n-irredundance and n-domination. Ars Combin. 1990, 29B, 151–160. [Google Scholar]
- Nordhaus, E.A.; Gaddum, J. On complementary graphs. Am. Math. Mon. 1956, 63, 175–177. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. A survey of Nordhaus–Gaddum type relations. Discret. Appl. Math. 2013, 161, 466–546. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).