New High Accuracy Analysis of a Double Set Parameter Nonconforming Element for the Clamped Kirchhoff Plate Unilaterally Constrained by an Elastic Obstacle

Abstract

In this paper, a non-$C^0$ double set parameter finite element method is presented for the clamped Kirchhoff plate with an elastic unilateral obstacle. A new high accuracy error estimate with order $O(h^2)$ in the broken energy norm is derived by use of a series of novel approaches, including some special features of the element and an incomplete biquadratic interpolation operator. At the same time, some experimental results are provided to verify the theoretical analysis.

1. Introduction

Let $\mathsf{\Omega }\subset {\mathbf{R}}^2$ be a bounded convex polygonal domain with a Lipschitz continuous boundary $\mathsf{\Gamma }$. We consider a thin flat plate $\mathsf{\Omega }\times (-d/2,d/2)$ clamped on its lateral boundary $\mathsf{\Gamma }\times (-d/2,d/2)$, where $d>0$ is the thickness of the plate and assumed to be small. Assume that the plate is subject to a load $f\in L^2(\mathsf{\Omega }), f\le 0 a.e. \mathrm{in} \mathsf{\Omega }$ and constrained unilaterally by an elastic obstacle $\psi \in L^2(\mathsf{\Omega })$, then displacement function u can be obtained by solving the weak formulation (cf. [1]):

$$\mathrm{Find} u\in V, \mathrm{such} \mathrm{that} a(u,v)+\ell (u,v)=(f,v), \forall v\in V,$$

(1)

where $V=H_0^2(\mathsf{\Omega }),a(w,v)={\int }_{\mathsf{\Omega }}[\Delta w\Delta v+(1-\nu )(2w_{xy}{v}_{xy}-w_{xx}{v}_{yy}-w_{yy}{v}_{xx})]dxdy,$ $\ell (u,v)={\int }_{\mathsf{\Omega }}\kappa {(u-\psi )}_{-}vdxdy, t_{-}=min\{t,0\},(f,v)={\int }_{\mathsf{\Omega }}fvdxdy,$ $\nu \in (0,1/2)$ is Poisson’s ratio and $\kappa \ge {\kappa }_0>0$ describes the stiffness of the obstacle.

It was shown in [1] that the displacement function u can also be derived by the minimization problem:

$$\mathrm{Find} u\in V, \mathrm{such} \mathrm{that} \forall v\in V J(u)\le J(v)$$

(2)

with the total energy $J(v)=\frac{1}{2}a(v,v)+\frac{1}{2}{\int }_{\mathsf{\Omega }}\kappa {[{(v-\psi )}_{-}]}^{2}dxdy-(f,v).$ Furthermore, the problem (2) is equivalent to the following fourth-order variational inequality of the second kind:

$$\left\{\begin{array}{c}\mathrm{Find} u\in V, \mathrm{such} \mathrm{that}\hfill \\ {\displaystyle a(u,v-u)+{\int }_{\mathsf{\Omega }}\frac{\kappa }{2}{[{(v-\psi )}_{-}]}^{2}dxdy-{\int }_{\mathsf{\Omega }}\frac{\kappa }{2}{[{(u-\psi )}_{-}]}^{2}dxdy\ge (f,v-u),\forall v\in V.}\hfill \end{array}\right.$$

(3)

In particular, in the limit $\kappa \to \infty$, the obstacle becomes rigid, and the problem reduces to the constrained minimization:

$$\left\{\begin{array}{c}\mathrm{Find} u\in K^{*}, \mathrm{such} \mathrm{that}\hfill \\ {\displaystyle u=arg\underset{v\in K^{*}}{min}[\frac{1}{2}a(v,v)-(f,v)]}\hfill \end{array}\right.$$

(4)

with $K^{*}=\{v\in V:v\ge \psi \mathrm{in} \mathsf{\Omega }\}$, which is the classical displacement obstacle problem of the clamped Kirchhoff plate (cf. [2]) and is equivalent to the following fourth-order variational inequality of the first kind:

$$\left\{\begin{array}{c}\mathrm{Find} u\in K^{*}, \mathrm{such} \mathrm{that}\hfill \\ a(u,v-u)\ge (f,v-u), \forall v\in K^{*}.\hfill \end{array}\right.$$

(5)

It is well known that nonconforming finite element methods (FEMs) are an attractive option for solving high order differential equations since the smoothness requirement on finite element functions is weakened. As we know, nonconforming FEMs for the problem (4), the plate obstacle problem with a rigid obstacle, have achieved fruitful results [3,4,5,6,7,8,9], but very few for the elastic obstacle problem (2), except [10]. Compared with the conforming FEMs studied in [1,11], $C^0$ continuous and discontinuous nonconforming (i.e., $C^0$ and non-$C^0$ nonconforming) FEMs were discussed in [10], and convergence analyses were established. On the other hand, the high accuracy analysis of nonconforming FEMs has been an active research area in practical computations, and many high accuracy results have been derived for variational inequalities and the boundary value problem [12,13,14,15,16,17,18,19,20]. However, for the plate obstacle problem (4) with a rigid obstacle, the exact solution u only belongs to $H^3(\mathsf{\Omega })\cap C^2(\mathsf{\Omega })$ instead of $H_{loc}^4(\mathsf{\Omega })$ [21,22]; thus, the lack of $H^4$ regularity makes it impossible to develop high accuracy analysis. Fortunately, it was shown in [10] that the solution is more regular if the obstacle is elastic. In fact, the solution of the problem (2) belongs to $H^4(\mathsf{\Omega })$ when the largest interior angles of the domain $\mathsf{\Omega }$ are smaller than $126.283696\dots °$, and thus, the high accuracy analysis of FEMs for the problem (2) is possible and worth exploring.

In this paper, we attempt to present a high accuracy analysis of nonconforming double set parameter FEMs for the obstacle problem (2). The double set parameter method presented in [23,24] is a useful method to construct unconventional elements, and it involves two sets of parameters. The first set is chosen to meet the convergence requirements according to the generalized patch test [25] or F-E-M-test [26], while the second set is selected to be simple so that the total number of unknowns in the resulting discrete system is small. Up to now, several nonconforming double set parameter plate elements have been successfully applied to deal with the two-sided displacement obstacle problem of the clamped plate [8], plate bending problems [16,27], the linear elasticity problem [28], the fourth-order elliptic singular perturbation problem [29,30,31] and so on. In this paper, a non-$C^0$ nonconforming double set parameter plate element is employed for the elastic obstacle problem (2). We develop a series of novel approaches including some special features of the element and an incomplete biquadratic interpolation operator so as to get the high accuracy result with order $O(h^2)$ in the broken energy norm. Furthermore, we carry out a numerical experiment to show the performance of the proposed method.

2. A Twelve Parameter Double Set Parameter Element and Its Typical Properties

In the beginning, we introduce a twelve parameter double set parameter element briefly. The readers are referred to [27] for details.

Assume that $T_h$ is a regular rectangular decomposition of $\mathsf{\Omega }$. For a given $K\in T_h$, let its center be $(x_K,y_K)$, four vertices be $a_i(x_i,y_i)$, four edges be $F_i=\overline{a_i{a}_{i+1}} (i=1,2,3,4(mod4))$, and the edge length be $2h_x$ and $2h_y$, respectively. Moreover, we denote $h={max}_{K\in T_h}\{h_x,h_y\}$. Besides, assume that $\widehat{K}=[-1,1]\times [-1,1]$ is the reference element on the $\xi -\eta$ plane with a center point $(0,0)$, four vertices ${\widehat{a}}_1=(-1,-1),{\widehat{a}}_2=(1,-1),{\widehat{a}}_3=(1,1)$, and ${\widehat{a}}_4=(-1,1)$, and four edges ${\widehat{F}}_1=\overline{{\widehat{a}}_1{\widehat{a}}_2}$, ${\widehat{F}}_2=\overline{{\widehat{a}}_2{\widehat{a}}_3}$, ${\widehat{F}}_3=\overline{{\widehat{a}}_3{\widehat{a}}_4}$, and ${\widehat{F}}_4=\overline{{\widehat{a}}_4{\widehat{a}}_1}$. Then, there exists an affine mapping $J:\widehat{K}⟶K$:

$$\left\{\begin{array}{c}x=x_K+h_x\xi \\ y=y_K+h_y\eta \end{array}\right.$$

(6)

satisfying $J(\widehat{K})=K,v(x,y)=\widehat{v}(\xi ,\eta ).$

The shape function space on the element K is taken as:

$$P(K)=P_3(K)\cup \{x^4,y^4\}=Span\{p_1,\dots ,p_{12}\},$$

(7)

where ${\displaystyle p_1=\frac{1}{4}(1-\xi )(1-\eta ), p_2=\frac{1}{4}(1+\xi )(1-\eta ), p_3=\frac{1}{4}(1+\xi )(1+\eta ), p_4=\frac{1}{4}(1-\xi )(1+\eta ), p_5=(1-{\xi }^2), p_6=(1-{\eta }^2), p_7=(1-{\xi }^2)\eta , p_8=(1-{\eta }^2)\xi , p_9=(1-{\xi }^2)\xi , p_{10}=(1-{\eta }^2)\eta ,p_{11}=(1-{\xi }^2){\xi }^2, p_{12}=(1-{\eta }^2){\eta }^2,}$ and $P_m(K)$ denotes the space consisting of piecewise polynomials of degree m on element K.

The degrees of freedom are selected as:

$$D(v)={(d_1(v),d_2(v),\dots ,d_{12}(v))}^{\prime },$$

(8)

where:

$$d_i(v)=v(a_i),i=1,2,3,4,$$

$$d_5(v)={\frac{1}{h}}_x{\int }_{F_1}vds={\int }_{-1}^1\widehat{v}(\xi ,-1)d\xi , d_6(v)={\frac{1}{h}}_y{\int }_{F_2}vds={\int }_{-1}^1\widehat{v}(1,\eta )d\eta ,$$

$$d_7(v)=-{\frac{1}{h}}_x{\int }_{F_3}vds={\int }_{-1}^1\widehat{v}(\xi ,1)d\xi , d_8(v)=-{\frac{1}{h}}_y{\int }_{F_4}vds={\int }_{-1}^1\widehat{v}(-1,\eta )d\eta ,$$

$$d_9(v)=-\frac{h_y}{h_x}{\int }_{F_1}\frac{\partial v}{\partial n}ds={\int }_{-1}^1\frac{\partial \widehat{v}}{\partial \eta }(\xi ,-1)d\xi , d_{10}(v)=\frac{h_x}{h_y}{\int }_{F_2}\frac{\partial v}{\partial n}ds={\int }_{-1}^1\frac{\partial \widehat{v}}{\partial \xi }(1,\eta )d\eta ,$$

$$d_{11}(v)=-\frac{h_y}{h_x}{\int }_{F_3}\frac{\partial v}{\partial n}ds={\int }_{-1}^1\frac{\partial \widehat{v}}{\partial \eta }(\xi ,1)d\xi , d_{12}(v)=\frac{h_x}{h_y}{\int }_{F_4}\frac{\partial v}{\partial n}ds={\int }_{-1}^1\frac{\partial \widehat{v}}{\partial \xi }(-1,\eta )d\eta .$$

For $v\in P(K)$, let:

$${\displaystyle v=\sum _{i=1}^{12}{\beta }_i{p}_i=(P,b),}$$

(9)

where $b={({\beta }_1,{\beta }_2,···,{\beta }_{12})}^{\prime }\in {\mathbb{R}}^{12},P={(p_1,p_2,···,p_{12})}^{\prime }.$

Substituting (9) into (8), we get:

$$D(v)=Mb$$

(10)

with:

$$\begin{array}{c}\hfill M=\left(\begin{array}{cccccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 1& 0& 0& \frac{4}{3}& 0& -\frac{4}{3}& 0& 0& 0& \frac{4}{15}& 0\\ 0& 1& 1& 0& 0& \frac{4}{3}& 0& \frac{4}{3}& 0& 0& 0& \frac{4}{15}\\ 0& 0& 1& 1& \frac{4}{3}& 0& \frac{4}{3}& 0& 0& 0& \frac{4}{15}& 0\\ 1& 0& 0& 1& 0& \frac{4}{3}& 0& -\frac{4}{3}& 0& 0& 0& \frac{4}{15}\\ -\frac{1}{2}& -\frac{1}{2}& \frac{1}{2}& \frac{1}{2}& 0& 4& \frac{4}{3}& 0& 0& -4& 0& 4\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{2}& -\frac{1}{2}& -4& 0& 0& \frac{4}{3}& -4& 0& -4& 0\\ -\frac{1}{2}& -\frac{1}{2}& \frac{1}{2}& \frac{1}{2}& 0& -4& \frac{4}{3}& 0& 0& -4& 0& -4\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{2}& -\frac{1}{2}& 4& 0& 0& \frac{4}{3}& -4& 0& 4& 0\end{array}\right).\end{array}$$

(11)

It is easy to check that $|M|=\frac{2^{24}}{3^4*5^2}\ne 0$; thus $b=M^{-1}D(v)$, i.e., it holds that:

$$\forall v\in P(K), v=(P,M^{-1}D(v)).$$

(12)

Next, we take nodal parameters as:

$$Q(v)={(v_1,v_{1x},v_{1y},v_2,v_{2x},v_{2y},v_3,v_{3x},v_{3y},v_4,v_{4x},v_{4y})}^{\prime },$$

(13)

where $v_i,v_{ix},v_{iy}$ are the function values of v and its first derivatives at vertices $a_i$, respectively.

Then, approximating $D(v)$ by a linear combination of the nodal parameters $Q(v)$ as follows:

$$d_i(v)=v_i, (i=1,2,3,4),$$

for $d_i(v) (i=5,6,7,8)$, the numerical integrating values of cubic Hermite interpolation polynomials on the corresponding sides result in:

$$\left\{\begin{array}{c}{d}_5(v)=v_1+v_2+\frac{h_x}{3}(v_{1x}-v_{2x})+O(h^4{|v|}_{4,K,\infty }),\hfill \\ d_6(v)=v_2+v_3+\frac{h_y}{3}(v_{2y}-v_{3y})+O(h^4{|v|}_{4,K,\infty }),\hfill \\ d_7(v)=v_3+v_4+\frac{h_x}{3}(v_{4x}-v_{3x})+O(h^4{|v|}_{4,K,\infty }),\hfill \\ d_8(v)=v_1+v_4+\frac{h_y}{3}(v_{1y}-v_{4y})+O(h^4{|v|}_{4,K,\infty }),\hfill \end{array}\right.$$

(14)

for $d_i(v) (i=9,10,11,12)$, the trapezoidal rule of numerical integration giving:

$$\left\{\begin{array}{c}{d}_9(v)=h_y(v_{1y}+v_{2y})+O(h^3{|v|}_{3,K,\infty }),\hfill \\ d_{10}(v)=h_x(v_{2x}+v_{3x})+O(h^3{|v|}_{3,K,\infty }),\hfill \\ d_{11}(v)=h_y(v_{3y}+v_{4y})+O(h^3{|v|}_{3,K,\infty }),\hfill \\ d_{12}(v)=h_x(v_{1x}+v_{4x})+O(h^3{|v|}_{3,K,\infty }).\hfill \end{array}\right.$$

(15)

The above discretizations can be rewritten in matrix form as:

$$D(v)=GQ(v)+E(v),$$

(16)

where:

$$\begin{array}{c}\hfill G=\left(\begin{array}{cccccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 1& \frac{h_x}{3}& 0& 1& -\frac{h_x}{3}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& \frac{h_y}{3}& 1& 0& -\frac{h_y}{3}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& -\frac{h_x}{3}& 0& 1& \frac{h_x}{3}& 0\\ 1& 0& \frac{h_y}{3}& 0& 0& 0& 0& 0& 0& 1& 0& -\frac{h_y}{3}\\ 0& 0& h_y& 0& 0& h_y& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& h_x& 0& 0& h_x& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& h_y& 0& 0& h_y\\ 0& h_x& 0& 0& 0& 0& 0& 0& 0& 0& h_x& 0\end{array}\right).\end{array}$$

(17)

and:

$$E(v)={(0,0,0,0,{\epsilon }_1(v),{\epsilon }_1(v),{\epsilon }_1(v),{\epsilon }_1(v),{\epsilon }_2(v),{\epsilon }_2(v),{\epsilon }_2(v),{\epsilon }_2(v))}^{\prime }$$

(18)

with ${\epsilon }_1(v)=O(h^4{|v|}_{4,K,\infty }),{\epsilon }_2(v)=O(h^3{|v|}_{3,K,\infty })$. From (18), it is obvious that the term $E(v)$ does not affect the convergence properties, and we neglect it and introduce a new set of parameters:

$$\overline{Q}(v)={(q_1(v),q_2(v),···,q_{12}(v))}^{\prime }$$

such that:

$$D(v)=G\overline{Q}(v),$$

(19)

where $q_1(v)=v(a_1), q_4(v)=v(a_2), q_7(v)=v(a_3), q_{10}(v)=v(a_4), q_2(v)={\overline{v}}_x(a_1), q_5(v)={\overline{v}}_x(a_2),q_8(v)={\overline{v}}_x(a_3), q_{11}(v)={\overline{v}}_x(a_4), q_3(v)={\overline{v}}_y(a_1), q_6(v)={\overline{v}}_y(a_2), q_9(v)={\overline{v}}_y(a_3), q_{12}(v)={\overline{v}}_y(a_4),$ and ${\overline{v}}_x(a)$ and ${\overline{v}}_y(a)$ have perturbations on $v_x(a)$ and $v_y(a)$, respectively. The readers are referred to [23,24] for details.

Then, using (10) and (19), we obtain:

$$b=M^{-1}G\overline{Q}(v),$$

(20)

which in conjunction with (9) leads to the real shape function v. Thus, the unknowns of the discrete system are $\overline{Q}(v)$, and the real shape function space $\overline{P}(K)$ is a subspace of $P(K)$:

$$\overline{P}(K)=\{v\in P(K);v=(P,M^{-1}Gq),\forall q\in {\mathbb{R}}^{12}\}.$$

(21)

It is easy to check that $rank(G)=10$, i.e., the dimension of $\overline{P}(K)$ is 10, and $v\in \overline{P}(K)$ can be expressed as ${\displaystyle v=\sum _{i=1}^{12}{\beta }_i{p}_i,}$ where:

$$\left\{\begin{array}{c}{\beta }_1=q_1,{\beta }_2=q_4,{\beta }_3=q_7,{\beta }_4=q_{10},\hfill \\ {\beta }_5=\frac{h_x}{8}(q_2-q_5-q_8+q_{11}),{\beta }_6=\frac{h_y}{8}(q_3+q_6-q_9-q_{12}),\hfill \\ {\beta }_7=\frac{h_x}{8}(-q_2+q_5-q_8+q_{11}),{\beta }_8=\frac{h_y}{8}(-q_3+q_6-q_9+q_{12}),\hfill \\ {\beta }_9=\frac{1}{8}(-q_1+q_4+q_7-q_{10})+\frac{h_x}{8}(-q_2-q_5-q_8-q_{11})+\frac{h_y}{24}(-q_3+q_6-q_9+q_{12}),\hfill \\ {\beta }_{10}=\frac{1}{8}(-q_1-q_4+q_7+q_{10})+\frac{h_x}{24}(-q_2+q_5-q_8+q_{11})+\frac{h_y}{8}(-q_3-q_6-q_9-q_{12}),\hfill \\ {\beta }_{11}=0,{\beta }_{12}=0.\hfill \end{array}\right.$$

(22)

Obviously, $v\in \overline{P}(K)$ is a cubic polynomial. In other words, $\overline{P}(K)$ is a completely cubic polynomial space. We denote the corresponding FE space by $V_h$:

$$V_h=\{v;v{|}_K=(P,M^{-1}Gq),\forall q\in {\mathbb{R}}^{12},K\in T_h,v(a)={\overline{v}}_x(a)={\overline{v}}_y(a)=0,\mathrm{for} \mathrm{any} \mathrm{nodes} a\in \mathsf{\Gamma }\}.$$

(23)

Lemma 1.

For any $v_h\in V_h$, the following properties hold:

$(R1)$$v_h$ is continuous at the vertices of elements and is zero at the vertices on Γ.

$(R2)$${\int }_F{v}_{h}ds$ is continuous across the element edge F and is zero on $F\subset \mathsf{\Gamma }$.

$(R3)$$\forall p(s)\in P_1(F)$, i.e., $p(s)$ is a linear polynomial function defined on the element edge F, and ${\int }_{F}p(s)\frac{\partial v_h}{\partial n}ds$ is continuous across the element edge F and is zero on $F\subset \mathsf{\Gamma }$.

$(R4)$${\Vert ·\Vert }_h$ is a norm over $V_h$, where ${\Vert ·\Vert }_h={({\sum }_{K\in T_h}{|·|}_{2,K}^2)}^{\frac{1}{2}}$.

Proof. 

From (8) and (19), we know that $D(v_h)$ is continuous between elements and:

$$\left\{\begin{array}{c}{d}_1=q_1,d_2=q_4,d_3=q_7,d_4=q_{10},\hfill \\ d_5=q_1+q_4+\frac{h_x}{3}(q_2-q_5),d_6=q_4+q_7+\frac{h_y}{3}(q_6-q_9),\hfill \\ d_7=q_7+q_{10}+\frac{h_x}{3}(q_{11}-q_8),d_8=q_1+q_{10}+\frac{h_y}{3}(q_3-q_{12}),\hfill \\ d_9=h_y(q_3+q_6),d_{10}=h_x(q_5+q_8),d_{11}=h_y(q_9+q_{12}),d_{12}=h_x(q_2+q_{11}).\hfill \end{array}\right.$$

(24)

Furthermore, it follows from (22) that:

$${\displaystyle \begin{array}{c}{\displaystyle {\int }_{F_1}s\frac{\partial v_h}{\partial n}ds=\frac{h_x}{3}(q_3-q_6),{\int }_{F_2}s\frac{\partial v_h}{\partial n}ds=\frac{h_y}{3}(q_8-q_5),}\hfill \\ {\displaystyle {\int }_{F_3}s\frac{\partial v_h}{\partial n}ds=\frac{h_x}{3}(q_9-q_{12}),{\int }_{F_4}s\frac{\partial v_h}{\partial n}ds=\frac{h_y}{3}(q_2-q_{11}),}\hfill \end{array}}$$

(25)

which together with (24) and the definition of $d_i (i=1,2,\dots ,12)$ yields $(R1)$, $(R2)$, and $(R3)$.

At the same time, suppose $\Vert v_h{\Vert }_h=0$, then for any $K\in T_h$, it holds that $v_h{\mid }_K\in P_1(K)$. From $(R1)$ and $(R2)$, we can immediately get $v_h\equiv 0$; thus, $(R4)$ holds true.  □

3. High Accuracy Analysis

We consider the discrete approximation form of the variational inequality (3) as:

$$\left\{\begin{array}{c}\mathrm{Find} u_h\in V_h, \mathrm{such} \mathrm{that} \forall v_h\in V_h\hfill \\ {\displaystyle a(u_h,v_h-u_h)+\sum _{K\in T_h}{\int }_K\frac{\kappa }{2}{[{(v_h-\psi )}_{-}]}^{2}dxdy-\sum _{K\in T_h}{\int }_K\frac{\kappa }{2}{[{(u_h-\psi )}_{-}]}^{2}dxdy\ge (f,v_h-u_h),}\hfill \end{array}\right.$$

(26)

where $a_h(w_h,v_h)=\sum _{K\in T_h}{\int }_K[\Delta w_h\Delta v_h+(1-\nu )(2w_{hxy}{v}_{hxy}-w_{hxx}{v}_{hyy}-w_{hyy}{v}_{hxx})]dxdy.$

It was shown in [1] that the problem (26) is equivalent to the discrete approximation of the plate problem:

$$\left\{\begin{array}{c}\mathrm{Find} u_h\in V_h, \mathrm{such} \mathrm{that} \forall v_h\in V_h,\hfill \\ {\displaystyle a_h(u_h,v_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{v}_{h}dxdy=(f,v_h).}\hfill \end{array}\right.$$

(27)

which is also equivalent to the minimization problem:

$$\mathrm{Find} u_h\in V_h, \mathrm{such} \mathrm{that} \forall v_h\in V_h J_h(u_h)\le J_h(v_h)$$

(28)

where the energy functional $J_h(v_h)=\frac{1}{2}{a}_h(v_h,v_h)+\frac{1}{2}\sum _{K\in T_h}{\int }_K\kappa {[{(v_h-\psi )}_{-}]}^{2}dxdy-(f,v_h).$ Since $a_h(·,·)$ is coercive on $V_h$, we can get the lower bound for $J_h(v_h)$ and $J_h(v_h)\to \infty$ (as $\parallel v_h{\parallel }_h\to \infty$). Then, using the elementary inequality $(t_{-}-s_{-})(t-s)\ge 0$ and an argument similar to that used in [10], we have:

Theorem 1.

The problem (26) has a unique solution $u_h$. Moreover, $\parallel u_h{\parallel }_h$ and $\parallel {(u_h-\psi )}_{-}{\parallel }_0$ are uniformly bounded independently of h.

In what follows, we will give error estimates for (26).

Theorem 2.

Assume that u and $u_h$ are the solutions of (3) and (26), respectively, and the largest internal angle of Ω is $\omega <126.283696\dots °$. Then, we have:

$${∥u-u_h∥}_h\le C{h}^2{(\parallel u\parallel }_4+{\Vert f\Vert }_0{+\Vert (u-\psi )}_{-}{\Vert }_0).$$

(29)

Here and later, positive constant C is independent of h and may be different at each appearance.

Proof. 

Employing the triangle inequality yields:

$${∥u-u_h∥}_h\le {∥u-{\mathrm{\Pi }}_{h}u∥}_h+{∥{\mathrm{\Pi }}_{h}u-u_h∥}_h,$$

(30)

where ${\mathrm{\Pi }}_h$ is the associated interpolation operator on $V_h$. Let $w_h={\mathrm{\Pi }}_{h}u-u_h$. We have by (27) that:

$$\begin{array}{cc}\hfill {∥w_h∥}_h^2& \le C{a}_h(w_h,w_h)=C\left[a_h({\mathrm{\Pi }}_{h}u-u,w_h)+a_h(u,w_h)-a_h(u_h,w_h)\right]\hfill \\ \hfill & \le C{∥{\mathrm{\Pi }}_{h}u-u∥}_h{∥w_h∥}_h+C\left[a_h(u,w_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy-(f,w_h)\right].\hfill \end{array}$$

(31)

Now, we focus on the estimate of the second term on the right-hand side of (31). Obviously,

$$\begin{array}{c}{\displaystyle a_h(u,w_h)-(f,w_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy}\hfill \\ {\displaystyle =\sum _{K\in T_h}{\int }_{\partial K}M(u)\frac{\partial w_h}{\partial \mathbf{n}}ds+ϵ\sum _{K\in T_h}{\int }_{\partial K}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}}\frac{\partial w_h}{\partial \mathbf{s}}ds}\hfill \\ {\displaystyle -\sum _{K\in T_h}{\int }_K\nabla (\Delta u)·\nabla w_{h}dxdy-(f,w_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy,}\hfill \end{array}$$

(32)

where $M(u)=\Delta u-(1-\nu )\frac{{\partial }^{2}u}{\partial {\mathbf{s}}^2}$ and $ϵ=(1-\nu )$. In order to estimate (32), we notice that the solution u of the problem (3) satisfies (see [10]):

$$-{\int }_{\mathsf{\Omega }}\nabla \Delta u·\nabla vdxdy+{\int }_{\mathsf{\Omega }}\kappa {(u-\psi )}_{-}vdxdy=(f,v), \forall v\in H_0^1(\mathsf{\Omega }).$$

(33)

However, from the construction of the element and $(R1)$–$(R3)$ in Lemma 1, we know that $w_h⊈H^1(\mathsf{\Omega })$. In this situation, we need to introduce a piecewise interpolation polynomial of $w_h$ as follows:

$$w_h^I{\mid }_K\in P_2(K)\cup \{x^{2}y,x{y}^2\}, w_h^I{\mid }_K(a_i)=w_h(a_i),{\int }_F{w}_h^{I}ds={\int }_F{w}_{h}ds, \forall F\subset \partial K.$$

(34)

Then, from $(R1)$ and $(R2)$ in Lemma 1, we have $w_h^I\in H_0^1(\mathsf{\Omega })$, which in conjunction with (32) and (33) yields:

$$\begin{array}{c}{\displaystyle a_h(u,w_h)-(f,w_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy}\hfill \\ {\displaystyle =\sum _{K\in T_h}{\int }_{\partial K}M(u)\frac{\partial w_h}{\partial \mathbf{n}}ds+ϵ\sum _{K\in T_h}{\int }_{\partial K}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}}\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds-\sum _{K\in T_h}{\int }_K\nabla (\Delta u)·\nabla (w_h-w_h^I)dxdy}\hfill \\ {\displaystyle -\sum _{K\in T_h}{\int }_K\nabla (\Delta u)·\nabla w_h^{I}dxdy-(f,w_h)+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy}\hfill \\ {\displaystyle =\sum _{K\in T_h}{\int }_{\partial K}M(u)\frac{\partial w_h}{\partial \mathbf{n}}ds+ϵ\sum _{K\in T_h}{\int }_{\partial K}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}}\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds-\sum _{K\in T_h}{\int }_K\nabla (\Delta u)·\nabla (w_h-w_h^I)dxdy}\hfill \\ {\displaystyle +(f,w_h^I-w_h)-{\int }_{\mathsf{\Omega }}\kappa {(u-\psi )}_{-}{w}_h^{I}dxdy+\sum _{K\in T_h}{\int }_K\kappa {(u_h-\psi )}_{-}{w}_{h}dxdy}\hfill \\ {\displaystyle =\sum _{K\in T_h}{\int }_{\partial K}M(u)\frac{\partial w_h}{\partial \mathbf{n}}ds+ϵ\sum _{K\in T_h}{\int }_{\partial K}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}}\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds-\sum _{K\in T_h}{\int }_K\nabla (\Delta u)·\nabla (w_h-w_h^I)dxdy}\hfill \\ {\displaystyle +(f,w_h^I-w_h)-\sum _{K\in T_h}{\int }_K\kappa {(u-\psi )}_{-}(w_h^I-w_h)dxdy+\sum _{K\in T_h}{\int }_K\kappa [{(u_h-\psi )}_{-}-{(u-\psi )}_{-}]w_{h}dxdy}\hfill \\ {\displaystyle \triangleq \sum _{j=1}^6{(Er)}_j.}\hfill \end{array}$$

(35)

Now, we start to estimate ${(Er)}_j$ one by one for $j=1,2,\dots ,6.$

Firstly, for $\varphi \in C^0(\mathsf{\Omega })$, let $P_1^F\varphi$ be the piecewise linear Lagrange interpolation on edge F and $P_0^F\frac{\partial w_h}{\partial \mathbf{n}}=\frac{1}{\mid F\mid }{\int }_F\frac{\partial w_h}{\partial \mathbf{n}}ds$ with $\mid F\mid ={\int }_{F}1ds,$ then the corresponding remainders are:

$$R_1^F\varphi =\varphi -P_1^F\varphi , R_0^F\frac{\partial w_h}{\partial \mathbf{n}}=\frac{\partial w_h}{\partial \mathbf{n}}-P_0^F\frac{\partial w_h}{\partial \mathbf{n}}.$$

Applying $(R3)$ in Lemma 1 leads to:

$$\sum _{K\in T_h}\sum _{F\subset \partial K}{\int }_F(P_1^{F}M(u))\frac{\partial w_h}{\partial \mathbf{n}}ds=0,$$

$$\sum _{K\in T_h}\sum _{F\subset \partial K}{\int }_F(P_1^{F}M(u))(P_0^F\frac{\partial w_h}{\partial \mathbf{n}})ds=0, \sum _{K\in T_h}\sum _{F\subset \partial K}{\int }_{F}M(u)(P_0^F\frac{\partial w_h}{\partial \mathbf{n}})ds=0,$$

which follows from:

$$\begin{array}{ccc}{|(Er)}_1|\hfill & =\hfill & {\displaystyle |\sum _{K\in T_h}\sum _{F\subset \partial K}{\int }_F(R_1^{F}M(u))(R_0^F\frac{\partial w_h}{\partial \mathbf{n}})ds|}\hfill \\ \hfill & \le \hfill & {\displaystyle |\sum _{K\in T_h}\sum _{F\subset \partial K}{({\int }_F{(R_1^{F}M(u))}^{2}ds)}^{\frac{1}{2}}{({\int }_F{(R_0^F\frac{\partial w_h}{\partial \mathbf{n}})}^{2}ds)}^{\frac{1}{2}}|\le C{h}^2{\parallel u\parallel }_4{\Vert w_h\Vert }_h.}\hfill \end{array}$$

(36)

Here, the Cauchy–Schwarz inequality and interpolation theorem [32,33] are used.

Secondly, for $K\in T_h$, we have:

$$\begin{array}{c}{\displaystyle \sum _{F\subset \partial K}{\int }_F(P_1^F\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds}\hfill \\ {\displaystyle ={\int }_{F_1}(P_1^{F_1}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x,y_K-h_y)\frac{\partial (w_h-w_h^I)}{\partial x}dx-{\int }_{F_3}(P_1^{F_3}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x,y_K+h_y)\frac{\partial (w_h-w_h^I)}{\partial x}dx}\hfill \\ {\displaystyle +{\int }_{F_2}(P_1^{F_2}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x_K+h_x,y)\frac{\partial (w_h-w_h^I)}{\partial y}dy-{\int }_{F_4}(P_1^{F_4}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x_K-h_x,y)\frac{\partial (w_h-w_h^I)}{\partial y}dy.}\hfill \end{array}$$

(37)

Employing integration by parts and (34), the first term of (37) can be estimated as:

$$\begin{array}{c}{\displaystyle {\int }_{F_1}(P_1^{F_1}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x,y_K-h_y)\frac{\partial (w_h-w_h^I)}{\partial x}dx}\hfill \\ {\displaystyle =(P_1^{F_1}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(w_h-w_h^I){|}_{a_2}^{a_1}-{\int }_{F_1}\frac{d(P_1^{F_1}\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})(x,y_K-h_y)}{dx}(w_h-w_h^I)dx=0.}\hfill \end{array}$$

(38)

Similarly, it holds that:

$$\begin{array}{c}{\displaystyle \sum _{F\subset \partial K}{\int }_F(P_1^F\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds=0,}\hfill \end{array}$$

(39)

which together with interpolation theorem yields:

$$\begin{array}{cc}\hfill {\displaystyle {|(Er)}_2|}& =|ϵ\sum _{K\in T_h}\sum _{F\subset \partial K}{\int }_F(\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}}-P_1^F\frac{{\partial }^{2}u}{\partial \mathbf{n}\partial \mathbf{s}})\frac{\partial (w_h-w_h^I)}{\partial \mathbf{s}}ds|\le C{h}^2{\parallel u\parallel }_4{\Vert w_h\Vert }_h.\hfill \end{array}$$

(40)

Thirdly, it follows from the definition of $w_h^I$ in (34) that:

$${\int }_K\nabla (w_h-w_h^I)dxdy=\sum _{F\subset \partial K}{\int }_F(w_h-w_h^I)ds=0.$$

(41)

Then, let $P_0^K\nabla (\Delta u)=\frac{1}{\mid K\mid }{\int }_K\nabla (\Delta u)dxdy$ and $\mid K\mid ={\int }_{K}1dxdy$. With a similar argument as ${(Er)}_1$ and ${(Er)}_2$, we obtain:

$$\begin{array}{c}\hfill {\displaystyle {|(Er)}_3|=|\sum _{K\in T_h}{\int }_K(\nabla (\Delta u)-P_0^K\nabla (\Delta u))·\nabla (w_h-w_h^I)dxdy|\le C{h}^2{\parallel u\parallel }_4{\Vert w_h\Vert }_h.}\end{array}$$

(42)

As for ${(Er)}_4$ and ${(Er)}_5$, from the Cauchy–Schwarz inequality and interpolation theorem, it holds that:

$${|(Er)}_4|=|f(w_h^I-w_h){|\le \Vert f\Vert }_0\parallel w_h-w_h^I{\parallel }_0\le C{h}^2{\Vert f\Vert }_0{\Vert w_h\Vert }_h$$

(43)

and:

$$\begin{array}{ccc}{|(Er)}_5|\hfill & \le \hfill & {\kappa \Vert (u-\psi )}_{-}{\Vert }_0{\parallel w_h-w_h^I\parallel }_0\hfill \\ & \le \hfill & C{h}^2{\Vert (u-\psi )}_{-}{\Vert }_0{\Vert w_h\Vert }_h.\hfill \end{array}$$

(44)

Finally, employing the elementary inequality $(t_{-}-s_{-})(t-s)\ge 0$ and Theorem 1, we have:

$$\begin{array}{ccc}{(Er)}_6\hfill & =\hfill & {\displaystyle \sum _{K\in T_h}{\int }_K\kappa [{(u_h-\psi )}_{-}-{(u-\psi )}_{-}]({\mathrm{\Pi }}_{h}u-u+u-u_h)dxdy}\hfill \\ \hfill & \le \hfill & {\displaystyle \sum _{K\in T_h}{\int }_K\kappa [{(u_h-\psi )}_{-}-{(u-\psi )}_{-}]({\mathrm{\Pi }}_{h}u-u)dxdy}\hfill \\ \hfill & \le \hfill & C(\Vert {(u_h-\psi )}_{-}{\Vert }_0+\Vert {(u-\psi )}_{-}{\Vert }_0)\parallel {\mathrm{\Pi }}_h{u-u\parallel }_0\le C\Vert {(u-\psi )}_{-}{\Vert }_0{\parallel {\mathrm{\Pi }}_{h}u-u\parallel }_0.\hfill \end{array}$$

(45)

Combining (31), (35), and the above bounds of ${(Er)}_1$–${(Er)}_6$ results in:

$$\begin{array}{c}\hfill \begin{array}{ccc}{∥{\mathrm{\Pi }}_{h}u-u_h∥}_h^2\hfill & \le \hfill & C{h}^4{(\parallel u\parallel }_4^2+{\Vert f\Vert }_0^2{+\Vert (u-\psi )}_{-}{\Vert }_0^2)\hfill \\ & +\hfill & C(\parallel {\mathrm{\Pi }}_{h}u-u{\parallel }_h^2+\Vert {(u-\psi )}_{-}{\Vert }_0\parallel {\mathrm{\Pi }}_{h}u-u{\parallel }_0).\hfill \end{array}\end{array}$$

(46)

Therefore, the desired result (29) follows from (30), (46) and the interpolation theorem immediately.  □

Remark 1.

$w_h^I$ plays a key role in the estimations of ${(Er)}_2$ and ${(Er)}_3$ in Theorem 2. If using the error estimate method in [10], we can only obtain the convergence result with the order of $O(h)$. In addition, it should be pointed out that the analysis presented herein is also valid for the elastic obstacle problem with $j(v)={\int }_{\mathsf{\Omega }}\kappa {[{(v-\psi )}_{+}]}^{2}dxdy$, $t_{+}=max\{t,0\}$, and $f\in L^2(\mathsf{\Omega }), f\ge 0 a.e. in \mathsf{\Omega }$.

Remark 2.

Compared with the work in [10], we obtain the same high accuracy result $O(h^2)$ with a non-$C^0$ nonconforming element instead of the $C^0$ nonconforming ACM’s rectangular element. Therefore, our work is an extension of [10], and the requirement for the nonconforming plate element’s smoothness from $C^0$ continuity to mean $C^1$ continuity is further reduced ($(R1)$–$(R3)$ implies that the element discussed in this paper is of the mean $C^1$ type). It can be checked that the high accuracy result in Theorem 2 is no longer true for many classical non-$C^0$ nonconforming plate elements, such as the Morley triangle element, the Veubeke triangle element, and so on.

4. Numerical Experiment

In this section, we consider the elastic obstacle problem (2) with $\mathsf{\Omega }={[0,1]}^2$, $f=-10, \nu =0.25$, and an elastic obstacle defined by the function $\psi =\left\{\begin{array}{c}0 \mathrm{if} (x,y)\in {[0.3;0.7]}^2,\hfill \\ -1 \mathrm{otherwise}.\hfill \end{array}\right.$ Since the exact solution is unknown, we refer the numerical solution on rectangles with $h=1/128$ as the exact solution to show the errors. The domain $\mathsf{\Omega }$ is divided into $N\times N$ rectangles, and the cases $\kappa ={10}^j, j=0,1,3,4$ with $N=8,16,32,64$ are computed, respectively. The numerical results are given in the following Table 1. Moreover, Figure 1, Figure 2 and Figure 3 illustrate the numerical solution $u_h$ with $N=64$, and Figure 4 presents the errors in the logarithm scales. It is obvious that the errors in the energy norm are convergent at order $O(h^2)$, which coincides with the theoretical analysis in Theorem 2.

Table 1. Errors of $\Vert u-u_h{\Vert }_h$ and the CPU time.

$\mathit{\kappa }\setminus \mathit{N}\times \mathit{N}$	$4\times 4$	$8\times 8$	$16\times 16$	$32\times 32$	$64\times 64$
$\kappa$ = ${10}^0$	13.50099036072611	3.60334964063092	0.88702928335453	0.20887990183367	0.04536489180482
$time(s)$	0.048482	0.073726	0.207029	0.667169	51.440274
$\kappa$ = ${10}^1$	13.48345125601387	3.59535482262866	0.88451602203801	0.20828947880233	0.04523833745855
$time(s)$	0.108480	0.394770	2.421881	10.936272	50.397260
$\kappa$ = ${10}^3$	11.44582259361440	2.88258835869155	0.69885436205702	0.16610400089376	0.03616945545106
$time(s)$	5.307547	28.444150	187.683438	793.338376	3411.901540
$\kappa$ = ${10}^4$	11.241262037642660	2.87323216390585	0.62499932334938	0.15026200240187	0.03545375844482
$time(s)$	17.876946	99.593113	919.972509	5191.457737	19,710.033405

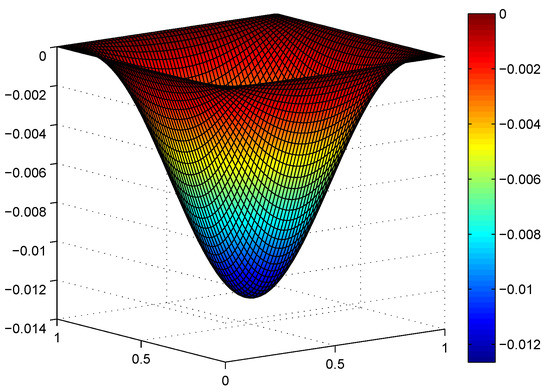
Figure 1. The numerical solution $u_h$ with $\kappa =10$.

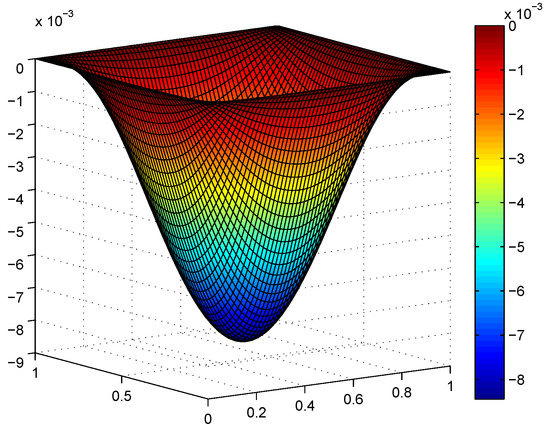
Figure 2. The numerical solution $u_h$ with $\kappa ={10}^3$.

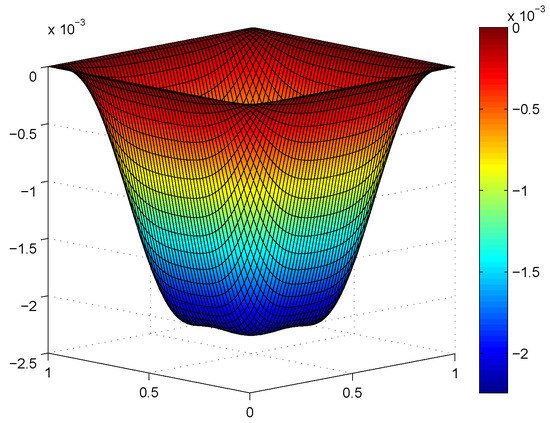
Figure 3. The numerical solution $u_h$ with $\kappa ={10}^4$.

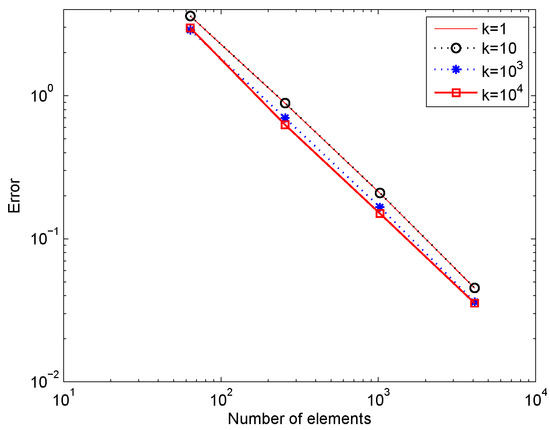
Figure 4. Errors in the energy norm with different k.