Spurious OLS Estimators of Detrending Method by Adding a Linear Trend in Difference-Stationary Processes—A Mathematical Proof and Its Verification by Simulation

Abstract

Adding a linear trend in regressions is a frequent detrending method in economic literatures. The traditional literatures pointed out that if the variable considered is a difference-stationary process, then it will artificially create pseudo-periodicity in the residuals. In this paper, we further show that the real problem might be more serious. As the Ordinary Least Squares (OLS) estimators themselves are of such a detrending method is spurious. The first part provides a mathematical proof with Chebyshev’s inequality and Sims–Stock–Watson’s algorithm to show that the OLS estimator of trend converges toward zero in probability, and the other OLS estimator diverges when the sample size tends to infinity. The second part designs Monte Carlo simulations with a sample size of 1,000,000 as an approximation of infinity. The seed values used are the true random numbers generated by a hardware random number generator in order to avoid the pseudo-randomness of random numbers given by software. This paper repeats the experiment 100 times, and gets consistent results with mathematical proof. The last part provides a brief discussion of detrending strategies.

1. Introducing the Problematic

The traditional time-series models focused on stationary processes. As a matter of fact, Wold’s (1954) [1] famous decomposition theorem indicated that any covariance-stationary process could be formulated as the sum of infinite white noises. Thanks to this stationary process’ property, the Autoregressive moving average model (ARMA) models applying the method proposed by Box and Jenkins (1970) [2] gradually became the main modeling in time-series analysis. However, what happens when the series are not stationary?

By simulating two distinct random walks and regressing one to another, Granger and Newbold (1974) [3] revealed the “spurious regression problem.” The OLS estimators of the correlation between these two independent random walks should be zero, but the Monte Carlo simulations performed by the econometricians indicated OLS estimators significantly different from zero, along with very high R². They put forward the idea that such a regression is “spurious,” because it makes no sense, even when it exhibits very high R². Other authors, such as Phillips (1986) [4] or Davidson and McKinnon (1993) [5], revealed similar results, leading to the following conclusions: (i) If the dependent variable is integrated of order 1, that is to say, I(1), then under null hypothesis, the residuals of the regression would also be I(1). However, as the usual statistical tests of the OLS estimators (Fisher or Student tests) are based on a hypothesis of residuals as white noise, these tests are no longer effective if such an assumption is not maintained. (ii) Some asymptotic properties are no longer valid, such as those of the ADF statistics, because they did not obey the same laws in the case of stationary processes. (iii) As the residuals are also I(1), the previsions are not efficient—except when a cointegration relationship between variables exists.

Here, we only examine time-series nonstationarity on average, to be distinguished from that in variance. Since Nelson and Plosser’s (1982) [6] contribution, nonstationarity on average can itself be classified into two categories: the first one is related to trend-stationary (TS) processes which present nonstationarity because of the deterministic trends characterizing their structure; the second category is linked to difference-stationary (DS) processes which contain a stochastic structure, or unit root. The processes considered can be made stationary by adding or removing the deterministic trends in the regressions in the case of TS processes, or, alternatively, in the case of DS processes, through difference operators, going from ARMA to Autoregressive Integrated Moving Average model (ARIMA).

Unit root tests are generally used to identify the nature of a nonstationary process, whether deterministic or stochastic. For DS, in particular, a solution is offered within ARIMA models through difference operators or the cointegration methods respectively proposed by Engle and Granger (1987) [7] in a univariate approach, and by Johansen (1991) [8] in a multivariate approach. Meanwhile, Stock (1987) [9] has demonstrated that, within such frameworks, the OLS estimators converge toward the real values if the variables are cointegrated, and the speed of convergence is faster than that of the usual case (that is, 1/T instead of 1/$\surd T$, where T is the sample size).

The cointegration theory achieved great success, but it has several inconveniences. It requires that all the variables must be integrated in the same order; otherwise, the cointegration models cannot be applied. However, it is difficult to make sure that all series have the same order of integration in the economic model which is tested. For example, GDP growth rates are often I(0), while some price indices can be I(2). Moreover, a supplementary difficulty in using difference operators destined to stabilize a DS process comes from the fact that variables in various orders of difference may not match the theoretical models which are employed.

It follows that the detrending method consisting of adding a linear trend into the regression has become common in empirical studies, due to its simplicity and its compatibility with a wide range of models. Many authors have chosen to add a linear trend in their regressions when they considered their dependent variables as nonstationary. Thus, detrending methods are often used in TS processes despite the nonstationary nature of the latter. Nevertheless, TS detrending methods cause specific problems when the series is in fact a DS process.

2. Literature Review

Studying the implications of treating TS processes as DS processes with the application of a difference operator, Chan, Hayya and Ord (1977) [10] found that the difference operator creates an artificial disturbance in the differentiated series. Indeed, the autocorrelation function equals to −1/2 when lag = $\pm 1$. Later, Nelson and Kang (1981) [11] examined the reverse case, in other words, the effects of treating DS processes as TS processes by adding a linear trend into the regression, and stated that, when a detrending method is used, the covariance of the residuals depends on the size of the sample and on time. By simulation, they showed that adding a linear trend into the regressions for TS processes generates a strong artificial autocorrelation of the residuals for the first lags, and thus induces a pseudo-periodicity—the corresponding spectral density function exhibiting a single peak at a period equal to 0.83 of the sample size. More precisely, treating TS processes as DS processes by difference operator artificially creates a “short-run” cyclical movement in the series, while, conversely, a “long-run” cyclical movement is artificially generated when treating DS processes as TS processes (we speak about “short-run,” since the disturbance happens when lag = $\pm 1$, and “long-run,” because the problem appears when the period corresponds to 0.83 of the sample size, or almost the same importance than the latter).

These fundamental studies have shown the importance of distinguishing between TS and DS processes, but remained concentrated on artificial correlations of the residuals. None of them focused on the OLS estimators themselves. In addition, the samples which are used are relative small. Following Nelson and Kang’s (1981) [11] research line, we shall mathematically demonstrate that the OLS estimators of detrending method by adding a linear trend in DS processes can be considered as spurious. As we shall see, the OLS estimator of the trend tends to zero when the sample size tends to infinity, while the other OLS estimator (intercept) is divergent in the same situation. After this, we shall design a simulation series to be experimented on by a sample of a million observations. The seed values are given by Rand Corporation (2001) [12]. As the dataset of simulation contains more than 100 million points, we shall present the program built by SAS with the seed values table in the Appendix A, so that readers will be in a position to reproduce the simulations with the same codifications.

3. A Mathematical Proof

We suppose that $y_t$ is a DS; for example, the random walk:

$$y_t=y_{t-1}+v_t$$

where $v_t$ is a white noise—and considering a weak form of stationarity, or of the second order.

Let us apply a time detrending method by adding a linear trend into the regression; that is to say, we have the model:

$$y_t=\alpha +\beta t+{\epsilon }_t$$

where $\alpha$ and $\beta$ are coefficients to be estimated, and t is the time variable: t = 1,2,3…T, with T the sample size, or number of observations. ${\epsilon }_t$ is the innovation.

Suppose: $X_t=\left(\begin{array}{c}1\\ t\end{array}\right)$, $\gamma =\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)$, and $b_T$ is the OLS estimators of $\gamma$ based on a sample of size T.

We get:

$$b_T=\left(\begin{array}{c}\widehat{{\alpha }_T}\\ \widehat{{\beta }_T}\end{array}\right)={\left({\displaystyle \sum }_{t=1}^T{X}_t{X}_t^{\prime }\right)}^{-1}\left({\displaystyle \sum }_{t=1}^T{X}_t{y}_t\right)$$

For the term:

$$\left({\displaystyle \sum }_{t=1}^T{X}_t{X}_t^{\prime }\right)=\left(\begin{array}{cc}{{\displaystyle \sum }}^{ }1& {{\displaystyle \sum }}^{ }t\\ {{\displaystyle \sum }}^{ }t& {{\displaystyle \sum }}^{ }{t}^2\end{array}\right)=\left(\begin{array}{cc}T& T\left(T+1\right)/2\\ T\left(T+1\right)/2& T\left(T+1\right)\left(2T+1\right)/6\end{array}\right)$$

As

$${\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)}^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$$

Then:

$$\begin{gathered} {\left({\displaystyle \sum }_{t=1}^T{X}_t{X}_t^{\prime }\right)}^{-1}=\frac{1}{T^2\left(T+1\right)\left(2T+1\right)/6-T^2{\left(T+1\right)}^2/4}\left(\begin{array}{cc}T\left(T+1\right)\left(2T+1\right)/6& -T\left(T+1\right)/2\\ -T\left(T+1\right)/2& T\end{array}\right) \\ =\frac{12}{T^2\left(T+1\right)\left(T-1\right)}\left(\begin{array}{cc}\frac{T\left(T+1\right)\left(2T+1\right)}{6}& -\frac{T\left(T+1\right)}{2}\\ -\frac{T\left(T+1\right)}{2}& T\end{array}\right) \\ =\frac{2}{T\left(T-1\right)}\left(\begin{array}{cc}2T+1& -3\\ -3& 6/\left(T+1\right)\end{array}\right) \end{gathered}$$

Additionally, for the term:

$$\left({\displaystyle \sum }_{t=1}^T{X}_t{y}_t\right)=\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{t=1}^T}{y}_t\\ {\displaystyle {\displaystyle \sum }_{t=1}^T}t{y}_t\end{array}\right)$$

So:

$$\begin{array}{cc}\hfill \left(\begin{array}{c}\widehat{{\alpha }_T}\\ \widehat{{\beta }_T}\end{array}\right)=& \frac{2}{T\left(T-1\right)}\left(\begin{array}{cc}2T+1& -3\\ -3& 6/\left(T+1\right)\end{array}\right)\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{t=1}^T}{y}_t\\ {\displaystyle {\displaystyle \sum }_{t=1}^T}t{y}_t\end{array}\right)\hfill \\ \hfill =& \frac{2}{T\left(T-1\right)}\left(\begin{array}{c}\left(2T+1\right){{\displaystyle \sum }}^{ }{y}_t-3{{\displaystyle \sum }}^{ }t{y}_t\\ -3{{\displaystyle \sum }}^{ }{y}_t+\frac{6}{T+1}{{\displaystyle \sum }}^{ }t{y}_t\end{array}\right)\hfill \end{array}$$

Thus, we have, respectively:

$$\{\begin{array}{c}\widehat{{\alpha }_T}=\frac{2}{T\left(T-1\right)}\left(\left(2T+1\right){{\displaystyle \sum }}^{ }{y}_t-3{{\displaystyle \sum }}^{ }t{y}_t\right)\\ \widehat{{\beta }_T}=\frac{6}{T\left(T-1\right)}\left(-{{\displaystyle \sum }}^{ }{y}_t+\frac{2}{T+1}{{\displaystyle \sum }}^{ }t{y}_t\right)\end{array}\left(A\right)$$

However, initially we have seen that:

$$y_t=y_{t-1}+v_t$$

Additionally

$$v_t~WN$$

That is:

$$y_t=y_0+{\displaystyle \sum }_{j=1}^t{v}_j$$

Therefore:

$$\begin{gathered} {\displaystyle \sum }_{t=1}^T{y}_t={\displaystyle \sum }_{t=1}^T\left(y_0+{\displaystyle \sum }_{j=1}^t{v}_j\right)=T{y}_0+T{v}_1+\left(t-1\right)v_2+\cdots +2v_{T-2}+v_T \\ =T{y}_0+{\displaystyle \sum }_{t=1}^T\left(T+1-t\right)v_t=T{y}_0+\left(T+1\right){\displaystyle \sum }_{t=1}^T{v}_t-{\displaystyle \sum }_{t=1}^{T}t{v}_t \end{gathered}$$

Additionally:

$$\begin{gathered} {\displaystyle \sum }_{t=1}^{T}t{y}_t={\displaystyle \sum }_{t=1}^{T}t\left(y_0+{\displaystyle \sum }_{j=1}^t{v}_j\right)=y_0{\displaystyle \sum }_{t=1}^{T}t+{\displaystyle \sum }_{t=1}^{T}t\left({\displaystyle \sum }_{j=1}^t{v}_j\right) \\ =y_0\frac{\left(T+1\right)T}{2}+\left(1+\cdots +T\right)v_1+\left(2+\cdots +T\right)v_2+\cdots +\left(T-1+T\right)v_{T-2}+T{v}_T \\ =y_0\frac{\left(T+1\right)T}{2}+{\displaystyle \sum }_{t=1}^T\frac{\left(t+T\right)\left(T-t+1\right)}{2} =y_0\frac{\left(T+1\right)T}{2}+\frac{T\left(T+1\right)}{2}{\displaystyle \sum }_{t=1}^T{v}_t-\frac{1}{2}{\displaystyle \sum }_{t=1}^T{t}^2{v}_t+\frac{1}{2}{\displaystyle \sum }_{t=1}^{T}t{v}_t \end{gathered}$$

It becomes:

$$\widehat{{\alpha }_T}=y_0+\frac{\left(T+1\right)\left(T+2\right)}{\left(T-1\right)T}{\displaystyle \sum }_{t=1}^T{v}_t-\frac{4T+5}{T-1}{\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t+\frac{3T}{T-1}{\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t$$

Additionally

$$\widehat{{\beta }_T}=-\frac{6}{\left(T+1\right)}·\frac{1}{T}{\displaystyle \sum }_{t=1}^T{v}_t-\frac{6T^2}{\left(T+1\right)\left(T-1\right)}·\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t+\frac{6T\left(T+2\right)}{\left(T+1\right)\left(T-1\right)}·\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t$$

When $T\to +\infty$, we respectively get:

$$\begin{gathered} \frac{\left(T+1\right)\left(T+2\right)}{\left(T-1\right)T}\to 1, -\frac{4T+5}{T-1}\to -4, \frac{3T}{T-1}\to 3, -\frac{6}{\left(T+1\right)}\to 0, -\frac{6T^2}{\left(T+1\right)\left(T-1\right)}\to -6, \\ \mathrm{and} \frac{6T\left(T+2\right)}{\left(T+1\right)\left(T-1\right)}\to 6. \end{gathered}$$

Thus, we need to determine the convergence of the six terms: ${\displaystyle \sum }_{t=1}^T{v}_t$, ${\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t$, ${\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t$, $\frac{1}{T}{\displaystyle \sum }_{t=1}^T{v}_t$, $\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t$ and $\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t$. Intuitively, they seem to tend toward zero when $T\to +\infty$.

Both ${\displaystyle \sum }_{t=1}^T{v}_t$ and $\frac{1}{T}{\displaystyle \sum }_{t=1}^T{v}_t$ converge to zero; as $v_t$ is a white noise, its expectation is zero. However, for the other terms, that multiply a coefficient situated between 0 and 1, the symmetry of white noises in infinity is not valid. So, $\frac{t}{T}{v}_t$ or $\frac{t^2}{T^2}{v}_t$ cannot be cancelled by each other. Additionally, as $v_t$ may be positive, negative or zero, the inequality $0<\frac{t}{T}{v}_t<v_t$ (or $0<\frac{t^2}{T^2}{v}_t<v_t$) does not hold true; however, we cannot use the squeeze theorem to prove that the limits of the remaining four terms exist and that they are equal to zero.

Consequently, we turn now to the Chebyshev’s inequality (see here, among many others: Fischer (2010) [13], Knuth (1997) [14] and originally, Chebyshev (1867) [15]). If X is a random variable, $E\left(X\right)=\mu$, $\mathrm{V}\left(X\right)={\sigma }^2$ for $\forall k\in R$ and $k>0$, and then:

$$\mathrm{Pr}\left(\left|X-\mu \right|\ge k\sigma \right)\le \frac{1}{k^2}$$

Here, it is clear that, if we could demonstrate that the variances of the four terms are bounded, the convergence in probability of the four terms is also proven. Let us note:

$$\begin{gathered} A=\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t B={\displaystyle \sum }_{t=1}^T\frac{t}{T}{v}_t \\ C=\frac{1}{T}{\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t D={\displaystyle \sum }_{t=1}^T\frac{t^2}{T^2}{v}_t \end{gathered}$$

We first study the convergences of A and B, then, symmetrically, we shall get the conclusions for C and D.

As $v_t$ is a white noise, that is, $E(v_t)=0$, so $V(v_t)={\sigma }^2$ is constant over time and, for $\forall i\ne j$, $Cov(v_i,v_j)=0$. Obviously, $E\left(A\right)=0$ and $E\left(B\right)=0$:

$$V\left(B\right)=\frac{1^2}{T^2}V\left(v_1\right)+\frac{2^2}{T^2}V\left(v_2\right)+\cdots +\frac{T^2}{T^2}V\left(v_T\right)+{\displaystyle \sum }_{i\ne j}^{T}Cov(\frac{i}{T}{v}_i,\frac{j}{T}{v}_j)$$

As $Cov(v_i,v_j)=0$ for $\forall i\ne j$, then: $Cov(\frac{i}{T}{v}_i,\frac{j}{T}{v}_j)=0$ and $V(v_t)={\sigma }^2$ for any t. We have:

$$V\left(B\right)={\sigma }_B^2=\frac{{\sigma }^2}{T^2}\left(1^2+2^2+\cdots +T^2\right)=\frac{{\sigma }^2}{T^2}\frac{1}{6}T\left(T+1\right)\left(2T+1\right)=\frac{\left(T+1\right)\left(2T+1\right)}{6T}{\sigma }^2$$

Additionally,

$$V\left(A\right)={\sigma }_A^2=\frac{1}{T^2} V\left(B\right)=\frac{\left(T+1\right)\left(2T+1\right)}{6T^3}{\sigma }^2$$

According to the general version of the Chebyshev’s inequality, we know that, for variable A:

$$\begin{gathered} \mathrm{Pr}\left(\left|A-E\left(A\right)\right|\ge k{\sigma }_A\right)\le \frac{1}{k^2} \\ \mathrm{Pr}\left(\left|A-0\right|\ge k{\sigma }_A\right)\le \frac{1}{k^2} \\ 1-\mathrm{Pr}\left(\left|A\right|\ge k{\sigma }_A\right)\ge 1-\frac{1}{k^2} \end{gathered}$$

As

$$\begin{gathered} 1-\mathrm{Pr}\left(\left|A\right|\ge k{\sigma }_A\right)=\mathrm{Pr}\left(\left|A\right|\le k{\sigma }_A\right) \\ \mathrm{Pr}\left(\left|A\right|\le k{\sigma }_A\right)\ge 1-\frac{1}{k^2} \end{gathered}$$

When $T\to +\infty$,

$${\sigma }_A=\sqrt{V\left(A\right)}=\sqrt{\frac{\left(T+1\right)\left(2T+1\right)}{6T^3}{\sigma }^2}=0$$

So:

$$\underset{T\to +\infty }{\lim }\mathrm{Pr}\left(\left|A\right|\le k{\sigma }_A\right)=\mathrm{Pr}\left(\left|A\right|\le 0\right)\ge 1-\frac{1}{k^2}$$

For any $k>0$, when $k\to +\infty$, $\mathrm{Pr}\left(\left|A\right|\le 0\right)\ge 1$. Obviously: $\mathrm{Pr}\left(\left|A\right|=0\right)=1$. Consequently, we can infer that, when $T\to +\infty$, then: $A\stackrel{P}{\to }$0.

Nevertheless, regarding B, as its variance tends to infinity when $T\to +\infty$, so B is divergent.

Symmetrically, we can demonstrate that, when $T\to +\infty$, $C\stackrel{P}{\to }$0 and D are divergent, because:

$$V\left(D\right)=\frac{T\left(T+1\right)\left(2T+1\right)\left(3T^2+3T-1\right)}{30T^4}{\sigma }^2$$

Additionally,

$$V\left(C\right)=\frac{T\left(T+1\right)\left(2T+1\right)\left(3T^2+3T-1\right)}{30T^6}{\sigma }^2$$

When $T\to +\infty$,$V\left(C\right)\to 0$ and $V\left(D\right)\to +\infty$.

Turning back to the OLS estimator $b_T$, we see that, when $T\to +\infty$, $\widehat{{\alpha }_T}$ is not convergent, and $\widehat{{\beta }_T}$ converges to zero in probability. So, when the sample size grows to infinity, the coefficient of the trend will tend to zero. This means that this trend is useless. We are indeed still regressing from a random walk to another one. The high R² of the regressions observed in the literature might just be caused by the similarity between a trend and a random walk in the short run, as seen in the simulations performed by Newbold and Granger (1974) [3]. In other words, adding a linear trend in the regressions for DS processes would not play any significant role; and it would even involve “new” spurious regressions in the sense of Granger and Newbold (1974) [3].

As Box and Draper (1987) [16] pertinently wrote it: “Essentially, all models are wrong, but some are useful” (p. 424).

4. Verification by Simulation

In order to verify this mathematical proof, let us simulate the model by SAS through Monte Carlo simulation. The Monte Carlo simulations are widely used computational methods that rely on repeated random sampling to obtain numerical results. It is now more and more popular, in the research of economics based on the use of randomness, to solve deterministic problems (for a more introductive presentation of Monte Carlo simulations, see Rubinstein and Kroese (2016) [17]). The Monte Carlo simulations have the following advantages in economic fields (for a survey on the application of Monte Carlo simulations in economics, see Creal (2012) [18]): (1) some economic models are too complicated to find analytical solutions in short time, or even impossible, as in this situation, Monte Carlo simulations are efficient methods to find numerical solutions (for example, see Kourtellos et al. (2016) [19]). (2) For some economic models, it is difficult to find practical examples in the real world that strictly meet the conditions of the theoretical models (Lux (2018) [20]). For instance, the sample size of macro variables are relatively short, it is difficult to meet the statistical credibility. However, in this situation, Monte Carlo simulations provide the possibility of large samples to verify some economic theories. (3) Due to the methods of data collection, the endogenous problems and identification problems sometimes exists in economic modeling (see the critical of Romer (2016) [21]). As a consequence, the estimated statistical relationships are no longer reliable. Monte Carlo simulations provide an effective way to explore the relationships between economic variables (for example, Reed and Zhu (2017) [22]).

The Monte Carlo simulations also have their disadvantages: (1) Monte Carlo simulations cannot replace the strict mathematical proof, but only provide approximate calculations based on probability when the analytic solutions cannot be provided or cannot be provided temporarily. That is to say it is just a non-deterministic algorithm opposite to the deterministic algorithm. This is why in the first section we also provide a strict mathematical proof. (2) Monte Carlo simulations only provide a possibility of exploring the problems, but the results of experiments may depend on the scientificity of the experimental design. For instance, this paper underlines the importance of true randomness in the experimental design.

The aim of the Monte Carlo simulations in this research is to reveal that, when the considered variable is a DS process, what kinds of problems will appear if we treat it as a TS process. So we need three basic assumptions: (1) the variable is DS, to strictly guarantee this point, the experimental design chooses the simplest and most common DS process, namely, random walk. (2) Infinite sample size; the mathematical proof based on asymptotic consistent theory requires an infinite sample size. Additionally, Monte Carlo simulations are probabilistic methods, which also need a large enough sample size. Thus, one million is chosen as the approximation of infinity. (3) True randomness. To avoid false conclusions caused by pseudo-random numbers, the experimental design takes a two-step strategy to ensure the true randomness of generated random numbers. That is to say, in the first step, we generate true random numbers by hardware random number generator as seed values; in the second step, we use the true random numbers as seed values to generate the samples of 1 million size.

That is to say, to do that, we shall follow four successive steps:

• Step 1: We generate a white noise, $v_t$, with a sample size of T = 1,000,000. Here, we set the white noise as Gaussian. The seed values (see Table A1) employed for the simulations at this step are provided by the Rand Corporation (2001) [12] with a hardware random number generator to make sure that the simulations effectively use true random numbers, because the random number generated by software is in fact a “pseudorandom.”
• Step 2: We generate a random walk, $y_t$, in our original equation by setting $y_0=0$:

  $$y_t=y_{t-1}+v_t$$

  $y_t$ also having a million observations.
• Step 3: We then regress the DS, $y_t$, to a linear trend with an intercept.
• Step 4: We repeat this experiment 100 times successively, and each time we use a different true random number as a seed value.

The simulation results appear to be consistent with the mathematical proof. The details of $\widehat{{\alpha }_T}$, $\widehat{{\beta }_T}$ and R² are summarized in Table 1 and in Table A2 of Appendix C. The simulation program by SAS is provided in Appendix B, the reader could reproduce our work with the same codes. Besides, Figure 1 and Figure 2 (presenting only the first 10 simulations to make them concise) show the evolutions of $\widehat{{\alpha }_T}$ and $\widehat{{\beta }_T}$ when the sample size grows from 100 up to 1,000,000 points, while the simulations of $\widehat{{\alpha }_T}$, $\widehat{{\beta }_T}$, $\widehat{t_{\widehat{{\alpha }_T}}}$ and $\widehat{t_{\widehat{{\beta }_T}}}$ generated by various seed values with a true random number are shown in Figure 3 and Figure 4.

Table 1. Summary of the simulation results, with a sample size of T = 1,000,000.

	$\widehat{{\mathit{\alpha }}_{\mathit{T}}}$	$\widehat{{\mathit{t}}_{\widehat{{\mathit{\alpha }}_{\mathit{T}}}}}$	$\widehat{{\mathit{\beta }}_{\mathit{T}}}$	$\widehat{{\mathit{t}}_{\widehat{{\mathit{\beta }}_{\mathit{T}}}}}$	${\mathit{R}}^2$
Mean	6.11764361	6.14650186	0.00002174	60.0860629	0.45983
Variance	143,633.942	554,191.079	1.57763 × 10−6	2,744,822.52	0.10287
Standard Deviation	378.990689	744.440111	0.00125604	1656.75059	0.32073
Max	867.64848	1707.15789	0.00307578	5799.95595	0.97113
Min	−743.23667	−1501.88113	−0.00245505	−3604.89913	1.15357 × 10−5
P-value of null test	0	-	0	-	-

Note: The location tests of $\widehat{{\alpha }_T}$ and $\widehat{{\beta }_T}$ cannot be the judgments of convergence to zero because the convergence means that the latter occurs within the sample when T tends to infinity.

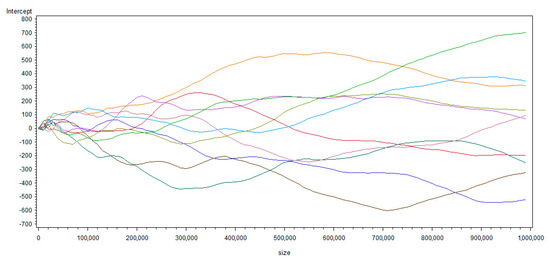
Figure 1. Evolutions of $\widehat{{\alpha }_T}$ when the sample size increases from 100 up to 1,000,000.

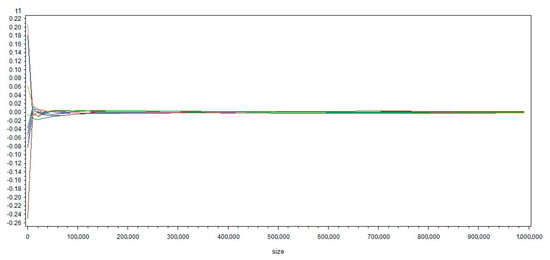
Figure 2. Evolutions of $\widehat{{\beta }_T}$ when the sample size increases from 100 up to 1,000,000.

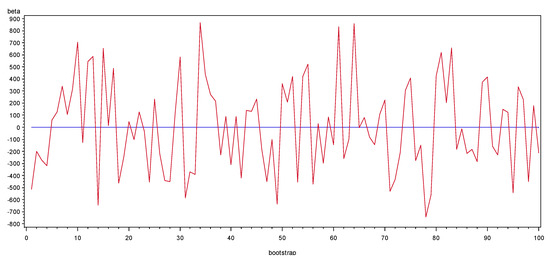
Figure 3. Simulations of $\widehat{{\alpha }_T}$ (in red) and $\widehat{{\beta }_T}$ (in blue).

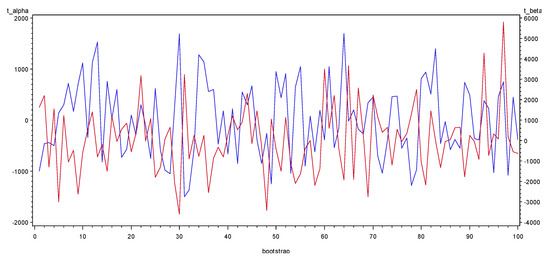
Figure 4. Simulations of $\widehat{t_{\widehat{{\alpha }_T}}}$ (in red) and $\widehat{t_{\widehat{{\beta }_T}}}$ (in blue).

At this point in the reasoning, several important results must be underlined:

(1)

From Figure 1 and Figure 2, we can observe that $\widehat{{\alpha }_T}$ is divergent, with its variance increasing when the sample size grows, while $\widehat{{\beta }_T}$ converges to zero. The simulation results therefore confirm the mathematical proof previously provided. In addition, from Figure 2, we see that the sample size should be greater than at least 1000 to get a conclusion of convergence becoming clear. That is, the size of the samples simulated by Granger and Newbold (1974) [3] or Nelson and Kang (1981) [11] seem to not be big enough to support their conclusions; even if the latter are right, and can be confirmed and re-obtained by our own simulations mobilizing 1,000,000 observations as an approximation of infinity (the sample size was 50 for Granger and Newbold (1974) [3] and 101 (in order to calculate a sample autocorrelation function of 100 lags) for Nelson and Kang (1981). This is probably because computers’ calculation capacities were much less powerful in the 1970s than today. Thanks to the progress in computing science, we can reinforce the statistical credibility of their findings).

(2)

From Figure 3, we observe that, as expected, when $T\to +\infty$, $\widehat{{\beta }_T}$ converges to zero (the magnitude level of $\widehat{{\beta }_T}$ is 10⁻⁵ considering that the decimal precision of the 32-bit computer used is 10⁻⁷, which is almost not-different from zero) and $\widehat{{\alpha }_T}$ is divergent even if the seed values are modified. For 100 different simulations, the conclusions still hold, which indicates that there is no problem of pseudo-randomness in our simulations (even if their conclusions are correct, the simulations by Granger and Newbold (1974) [3] as well as by Nelson and Kang (1981) [11] did not pay attention to the pseudo-randomness, nor specify how the random numbers are obtained). By performing them, as we set all $y_0$ equal to zero, if $\widehat{{\alpha }_T}$ is convergent, then it must converge to $y_0$, in other words, to zero. However, $\widehat{{\alpha }_T}$ seriously deviates from its mathematical expectation zero for different simulations. Thus, the regressions are spurious because the OLS estimator of the trend converges to zero and the other OLS estimator diverges when the sample size tends to infinity.

(3)

From the last column of Table 1, we see that, sometimes, these regressions get a very high R² (the highest being 0.97, with an average of 0.45 for the 100 experiments). This is a classic result associated to spurious regressions, already pointed out by Granger and Newbold (1974) [3].

(4)

From Table 1 and Figure 4, we see that the t-statistics of the OLS estimators are very high, and that all the p-values of $H_0: \widehat{t_{\widehat{{\alpha }_T}}}=0$ and $H_0: \widehat{t_{\widehat{{\beta }_T}}}=0$ are zero. Thus, the OLS estimators are definitely significant when the sample size tends to infinity. This is also a well-known result associated to spurious regressions, since the residuals are not white noises (as indicated above, and studied by Nelson and Kang (1981) [11], we did not test the correlation of the residuals here). In these conditions, we understand that the usual and fundamental Fisher or Student tests of the OLS estimators are no longer valid, precisely because they are based on the assumption of residuals as white noises. If we use such a detrending method in DS processes, we will indeed get wrong conclusions of significance of the explicative variables.

We understand that our results call for a re-examination of the robustness of the classic findings in macroeconomics. To give an example, in a famous paper, Mankiw, Romer and Weil (1990) [23] identified a significant and positive contribution of education to the per capita GDP growth rate. In a theoretical framework close to a Solowian model, their approach consisted in augmenting a production function with constant returns to scale and decreasing marginal factorial returns, by including a variable of human capital in order to regress, in logarithms, per capita GDP to the investment rates of physical capital and of schooling. Their conclusion is probably accurate; but, as they added a linear trend as a detrending method, whatever the input variable that is selected, it will be found statistically significant as long as the size of their sample is sufficiently large. Our own study has described, in an original manner, the behavior of OLS estimators themselves when the sample size tends to infinity. By comparison, the samples used for simulation by Chan, Hayya and Ord (1977) [10], or Nelson and Kang (1981) [11], are relatively small—even if, obviously, they were extremely useful.

5. Concluding Remarks

The introduction of a linear trend generally aimed at avoiding spurious regressions. However, Nelson and Kang (1981) [11], following Chan, Hayya and Ord (1977) [10], had showed that, in OLS estimates, the assimilation of a difference-stationary process (DS)—the most probable process for GDP, with that of unit root, according to Nelson and Plosser (1982)—to a trend-stationary process (TS), (as did Chow and Li (2002) [24], among others, while the log of China’s GDP may present a unit root) can lead to a situation where the covariance of the residuals depends on the size of the sample, which artificially induces an autocorrelation of the residuals for the lags, and, by generating a pseudo-periodicity in the latter, generates a cyclical movement into the series. However, their analyses mainly focused on the residuals, and their simulated sample size remained small. Here, following Nelson and Kang’s (1981) research line, and using the Chebyshev’s inequality, we have given a strict mathematical proof of the fact that the OLS estimators of a detrending method by adding a linear trend in DS processes are spurious. When the sample size tends to infinity, the OLS estimator of the trend converges toward zero in probability, while the other OLS estimator is divergent. The empirical verification attempted by designing a series through the Monte Carlo method and by performing simulations on a sample of a million observations as an approximation of infinity and true random numbers as seed values has finally provided results consistent with the mathematical proof.

Thus, in the context of what has been specified here, our main conclusion according to which the OLS estimators themselves are spurious when the sample size increases also implies that identifying the nature of time series becomes extremely important. For example, it is crucial to decide whether GDP series are to be treated as TS or DS processes—in a short-run context in which random walks usually look like TS processes (on the basis of many macroeconomic series, Nelson and Plosser (1982) [6] have stated that GDP series would be DS rather than TS processes. More recent studies, such as that by Darné (2009) [25], have reexamined GNP series with new unit root tests, and shown that the US GNP expressed in real terms seems to be a stochastic trend). Even if their effectiveness is questioned, especially because of the sensitivity of the choice of the truncation parameters, we recommend using unit root tests to reduce the risk of inappropriately selecting the detrending method, but by regressing the variables of the models used in the first differences of the logarithm forms when such tests show that they contain unit roots (such an advice has been applied in a recent study on China’s long-run growth using a new time-series database of capital stocks from 1952 to 2014 built through an original methodology. See Long and Herrera (2015, 2016) [26,27]). From a theoretical point of view, regressions in the first differences of the logarithm forms are acceptable both by neoclassic and Keynesian modeling, in which they can easily be interpreted in terms of growth-rate dynamics; and from an econometric point of view, logarithms might be useful when a problem of heteroscedasticity appears, while difference operators can help to avoid spurious regressions if there are unit roots. To avoid the over-differencing problem, we finally recommend using inverse autocorrelation functions (IACFs) to determine the order of integration, along with unit root tests and correlogram (See Cleveland (1972) [28], Chatfield (1979) [29] and Priestey (1981) [30]). That is to say, we suggest the following modeling strategy: (i) if the unit roots tests and correlogram indicate that the variables are stationary in the first differences of the logarithm forms; we stay in traditional time series regressions. (ii) If the variables contain unit roots in the first differences of the logarithm forms, we could pass to cointegration framework or effectuate a second difference operation. (iii) If unit root tests and correlogram both indicate that the series seem be stationary but IACF indicates that the series might be over-differenced (in this case, Autoregressive Function (ACF) and Partial Autoregressive Function (PACF) present characteristics of stationary process (or decrease hyperbolically) while IACF presents characteristics of nonstationary process) that implies an integer order of integration is not sufficient, the true order of integration might be between 0 and 1. That is to say, we might need to pass from traditional time series models to fractal theory (Hosking (1981) [31]) such as AutoRegressive Fractionally Integrated Moving Average (ARFIMA) models or fractional cointegration.