Type II Topp Leone Power Lomax Distribution with Applications

Abstract

In many areas of applied sciences, the last step of a study often consists in analyzing in depth the collected data. Among all the kinds of data, the lifetime data are well-known to convey a great deal of information whose capture is necessary to identify one or more key phenomena. In this regards, numerous mathematical models have been proposed, including those based on lifetime distributions. In this paper, we introduce a new four-parameter lifetime distribution based on the type II Topp-Leone-G family and the power Lomax distribution. In comparison to the existing distributions, the new one is characterized by very flexible probability functions: increasing, decreasing, J, and reverse J shapes are observed for the probability density and hazard rate functions, giving first signs on the potential of adaptability of the related model. With this idea in mind, the new distribution is studied in detail, from both the theoretical and applied sides. After showing its main mathematical properties, the related model is investigated with estimation of the parameters by the maximum likelihood method. We applied it to two practical datasets, including the well-know aircraft windshield data. We show that the new model performs better than several modern adversary models, motivating its use in an applied setting.

1. Introduction

1.1. From the Lomax Distribution to the Power Lomax Distribution

Over the last decades, the so-called Lomax distribution (introduced in [1]) was revealed to be a goldest distribution for a plethora of applications in applied sciences. We refer the reader to the works of [2] for applications in life testing, [3] for applications in queue service discipline, [4] for applications in personal wealth, and [5] for applications in internet traffic, to name a few. The use of the Lomax distribution is often motivated by its heavy tailed nature and the simplicity of the related probability functions, providing an interesting polynomial alternative to the exponential-type distributions (exponential, Rayleigh, Weibull, etc.) (see [6]). Indeed, the mathematical definition of the Lomax distribution is based on the following cumulative distribution function (cdf):

$$\begin{array}{c}\hfill G_{*}(x;\alpha ,\lambda )=1-{\left(1+\frac{x}{\lambda }\right)}^{-\alpha },x>0,\end{array}$$

(1)

with $\alpha ,\lambda >0$. Thus, $\alpha$ is a shape parameter and $\lambda$ is a scale parameter. The corresponding probability function (pdf) is given by

$$\begin{array}{c}\hfill g_{*}(x;\alpha ,\lambda )=\frac{\alpha }{\lambda }{\left(1+\frac{x}{\lambda }\right)}^{-\alpha -1},x>0.\end{array}$$

(2)

In view of this pdf, we can notice that the Lomax distribution naturally appears as a special case of other well-known distributions, such as the Pareto type II, Pareto type IV, Feller-Pareto, Fisher and beta of the second kind distributions.

However, the Lomax distribution has some limitations: beyond the data showing heavy tailed features, the related model can lack of flexibility and be useless for a thorough analysis. For this reason, numerous efforts have been launched to generalized these distributions in the best way possible. Among these generalizations, we would like to mention the Marshall-Olkin extended Lomax distribution by [7], the exponentiated Lomax distribution by [8], the McDonald Lomax distribution by [9], the Poisson Lomax distribution by [10], the gamma Lomax distribution by [11], the exponential Lomax distribution by [12], the transmuted Lomax distribution by [13], the weighted Lomax distribution by [14], the Weibull Lomax distribution by [15], the Gompertz Lomax distribution by [16], the Transformed-Transformer Lomax distribution by [17], and the power Lomax (PL) distribution by [18].

For the purposes of this paper, let us now discuss the PL distribution. First, it is defined by the following cdf:

$$\begin{array}{c}\hfill G_o(x;\alpha ,\beta ,\lambda )=G_{*}(x^{\beta };\alpha ,\lambda )=1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha },x>0,\end{array}$$

(3)

with $\alpha ,\beta ,\lambda >0$. Thus, $\alpha$ and $\beta$ are two shape parameters and $\lambda$ is a scale parameter. The corresponding pdf is given by

$$\begin{array}{c}\hfill g_o(x;\alpha ,\beta ,\lambda )=\frac{\alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1},x>0.\end{array}$$

(4)

The additional parameter $\beta$ has a significant effect on the flexibility on the pdf. In particular, one can show that $g_o(x;\alpha ,\beta ,\lambda )$ is increasing if $\beta >1$ and decreasing if $\beta \le 1$. This generalization thus reaches of new level of flexibility in term of modeling by keeping a relative simplicity for the expressions of the corresponding probability functions.

1.2. On the Extensions of the PL Distribution through the Use of General Families of Distributions

In the recent literature, some recent extensions of the PL distribution have seen the light through the use of general families of distributions. We refer to the exponentiated PL distribution introduced by [19], the odds generalized exponential PL distribution proposed by [20], and the transmuted PL distribution studied by [21]. The first one is a member of the exponentiated-G family by [22], the second one is member of the odds generalized exponential-G family by [23], and the third one is a member of the transmuted-G family by [24], all defined with the PL distribution as baseline distribution.

The main idea of these three extensions is to exploit the parameter(s) of the considered general family as tuning parameter(s) to increase the desirable properties of the former PL distribution, including more possibilities for the values of the mean, variance, mode, skewness and kurtosis. The practical gain is flagrant, with better fits for various datasets in comparison to the former PL distribution. Thus, the consideration of new powerful families of distributions can give desirable extensions of the PL distributions, with possible new perspectives.

With this idea in mind, let us now briefly present an emergent family of distributions: the type II Topp-Leone-G (TIITL-G) family introduced by [25], known to be a suitable alternative to the exponentiated-G, odds generalized exponential-G and transmuted-G families (among others). For the mathematical backgrounds, the cdf of the TIITL-G family is given by

$$\begin{array}{c}\hfill F(x;\theta ,\xi )=1-{[1-G{(x;\xi )}^2]}^{\theta },x\in \mathbb{R},\end{array}$$

(5)

where $\theta$ is a positive shape parameter and $G(x;\xi )$ is a cdf of a baseline continuous distribution which may depend on a parameter vector $\xi$. The corresponding pdf is given by

$$\begin{array}{c}\hfill f(x;\theta ,\xi )=2\theta g(x;\xi )G(x;\xi ){[1-G{(x;\xi )}^2]}^{\theta -1},x\in \mathbb{R},\end{array}$$

(6)

where $g(x;\xi )$ is the pdf corresponding to $G(x;\xi )$. One can remark that the TIITL-G family is a simplified version of the Kumaraswamy-G family by [26]. The role of the parameter $\theta$ is to create new possible levels of skewness and tail weights from the cdf $G(x;\xi )$. Therefore, the TIITL-G family was naturally used to extend several well-known distributions, with applications. For instance, we refer the reader to the works of [27,28] for extension of the inverse and generalized inverse Rayleigh distributions and [29] for extension of the inverted Kumaraswamy distribution.

In this paper, a similar methodology is adopted but with a focus on the PL distribution. Indeed, we extend the PL distribution through the TIITL-G family; the special member of the TIITL-G family defined with the PL distribution as baseline distribution is considered.

1.3. Novelty and Contributions

Thus, we create a new four-parameter lifetime distribution, called the type II Topp-Leone power Lomax (TIITLPL). The main contributions of this study are the followings:

• To improve the characteristics and flexibility of the PL distribution by using the TIITL-G family (as motivated above). In particular, increasing, decreasing, J, and reverse J shapes are observed for the probability density and hazard rate functions, illustrating this claim.
• To introduce an extended version of the PL distribution whose quantile function has a closed-form.
• To study important statistical properties of the TIITLPL distribution, including the skewness, kurtosis, and various kinds of moments and order statistics.
• To explore the inferential features of the TIITLPL distribution through the use of the maximum likelihood method, providing a comprehensive methodology for the practitioner.
• To provide better fits than the competing modified models. In this study, an exhaustive list of such competitor models are considered (including those described in [11,19,21,30,31,32,33], to name a few), with favorable results for the TIITLPL model.

All these points are developed in detail through the study, with discussions and comparisons to the existing works.

1.4. Paper Organization

In Section 2, we define the TIITLPL distribution and present its main functions of interest. Some mathematical properties of the distribution are investigated in Section 3. Section 4 focuses on the inference of the TIITLPL model, with estimation of the unknown parameters by the method of maximum likelihood. In Section 5, we illustrate the importance of the TIITLPL model by means of two practical datasets: the well-known aircraft windshield and cancer patient datasets. A conclusion is proposed in Section 6.

2. The TIITLPL Distribution

This section is devoted to the presentation of the TIITLPL distribution, including its main probability functions with analytical and graphical studies.

2.1. Definition

As developed in the Introduction, the cdf of the TIITLPL distribution is obtained by compounding the cdf given by Equation (5) with the one given by Equation (3). Thus, it is given by

$$\begin{array}{c}\hfill F(x;\theta ,\alpha ,\beta ,\lambda )=1-{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta },x>0,\end{array}$$

(7)

with $\theta ,\alpha ,\beta ,\lambda >0$. In addition, by Equations (6) and (4), the corresponding pdf follows:

$$\begin{array}{cc}\hfill & f(x;\theta ,\alpha ,\beta ,\lambda )=\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta -1},\hfill \\ \hfill & x>0.\hfill \end{array}$$

(8)

Remark 1.

The common brace term of the cdf and pdf can also be expressed as

$$1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2={\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\left[2-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right].$$

Thus, for instance, the pdf can be expressed as

$$\begin{array}{cc}\hfill & f(x;\theta ,\alpha ,\beta ,\lambda )=\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\theta \alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left[2-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^{\theta -1},\hfill \\ \hfill & x>0.\hfill \end{array}$$

Let us now study some analytical properties of $f(x;\theta ,\alpha ,\beta ,\lambda )$. When $x\to 0$, by using standard limited developments, we get $f(x;\theta ,\alpha ,\beta ,\lambda )\sim (2\theta {\alpha }^2\beta /{\lambda }^2)x^{2\beta -1}$. Hence, if $\beta \in (0,1/2)$, we have ${lim}_{x\to 0}f(x;\theta ,\alpha ,\beta ,\lambda )=+\infty$; if $\beta =1/2$, we have ${lim}_{x\to 0}f(x;\theta ,\alpha ,\beta ,\lambda )=\theta {\alpha }^2/{\lambda }^2$; and, $if \beta >1/2$, we have ${lim}_{x\to 0}f(x;\theta ,\alpha ,\beta ,\lambda )=0$.

In addition, when $x\to +\infty$, we have $f(x;\theta ,\alpha ,\beta ,\lambda )\sim 2^{\theta }\theta \alpha \beta {\lambda }^{\alpha \theta }{x}^{-\alpha \theta \beta -1}$. That is, for all the values of the parameters, we have ${lim}_{x\to +\infty }f(x;\theta ,\alpha ,\beta ,\lambda )=0$.

The critical points of $f(x;\theta ,\alpha ,\beta ,\lambda )$ can be described analytically. Indeed, a critical point of $f(x;\theta ,\alpha ,\beta ,\lambda )$, say $x_c$, satisfies the non-linear equation given by ${\{log\left[f(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{\prime }{\mid }_{x=x_c}=0$ (where the differentiation is according to x), with

$$\begin{array}{cc}\hfill & {\{log\left[f(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{\prime }=(\beta -1)\frac{1}{x}-(\alpha +1)\beta \frac{x^{\beta -1}}{\lambda +x^{\beta }}+\frac{\alpha \beta }{\lambda }\frac{x^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}}{1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }}\hfill \\ \hfill & -\frac{2(\theta -1)\alpha \beta }{\lambda }\frac{x^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2}.\hfill \end{array}$$

Then, the nature of $x_c$ can be determined by investigating the sign of the real number ${\eta }_c={\{log\left[f(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{″}{\mid }_{x=x_c}$. In view of the complexity of the equation above, there is no closed-form for $x_c$, but numerical solutions exist via the use of any mathematical software. To handle the flexibility of $f(x;\theta ,\alpha ,\beta ,\lambda )$, Figure 1 shows some plots of this function for selected values of $\theta$, $\alpha$, $\beta$, and $\lambda$. We observe that $f(x;\theta ,\alpha ,\beta ,\lambda )$ is left skewed, right skewed, J, reverse J, and near symmetrical shaped.

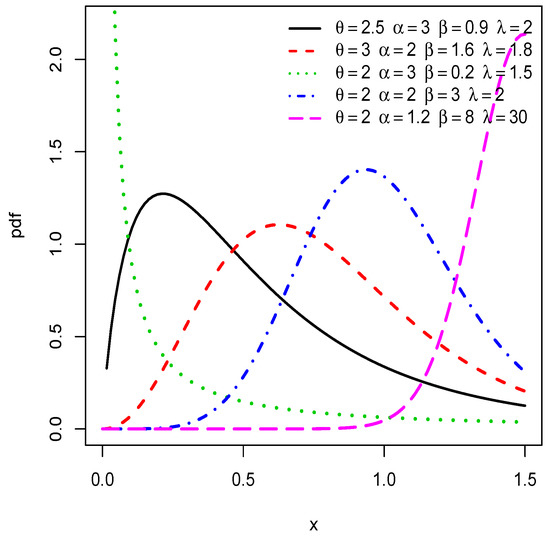
Figure 1. Plots of the pdf of the TIITLPL distribution for selected values of the parameters.

2.2. Common Reliability Functions

The survival function (sf), hazard rate function (hrf), reversed hazard rate function, and cumulative hazard rate function of the TIITLPL distribution are given, respectively, by

$$\begin{array}{c}\hfill S(x;\theta ,\alpha ,\beta ,\lambda )={\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta },x>0,\end{array}$$

(9)

$$\begin{array}{cc}\hfill & h(x;\theta ,\alpha ,\beta ,\lambda )=\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{-1},\hfill \\ \hfill & x>0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & r(x;\theta ,\alpha ,\beta ,\lambda )=\frac{2\theta \alpha \beta }{\lambda }\frac{x^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta -1}}{1-{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta }},\hfill \\ \hfill & x>0\hfill \end{array}$$

and

$$\begin{array}{c}\hfill C(x;\theta ,\alpha ,\beta ,\lambda )=-\theta log\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\},x>0.\end{array}$$

Among them, the most informative function remains the hrf. Let us now study it analytically.

When $x\to 0$, we obtain $h(x;\theta ,\alpha ,\beta ,\lambda )\sim (2\theta {\alpha }^2\beta /{\lambda }^2)x^{2\beta -1}$. Hence, if $\beta \in (0,1/2)$, we have ${lim}_{x\to 0}h(x;\theta ,\alpha ,\beta ,\lambda )=+\infty$; if $\beta =1/2$, we have ${lim}_{x\to 0}h(x;\theta ,\alpha ,\beta ,\lambda )=\theta {\alpha }^2/{\lambda }^2$; and, $if \beta >1/2$, we have ${lim}_{x\to 0}h(x;\theta ,\alpha ,\beta ,\lambda )=0$.

In addition, when $x\to +\infty$, we get $h(x;\theta ,\alpha ,\beta ,\lambda )\sim \theta \alpha \beta x^{-1}$. Thus, for all the values of the parameters, we have ${lim}_{x\to +\infty }h(x;\theta ,\alpha ,\beta ,\lambda )=0$. We see that the parameters have no effect on the rate of convergence of $h(x;\theta ,\alpha ,\beta ,\lambda )$, contrary to $f(x;\theta ,\alpha ,\beta ,\lambda )$.

Furthermore, the critical points of $h(x;\theta ,\alpha ,\beta ,\lambda )$ can be described analytically. Then, a critical point of $h(x;\theta ,\alpha ,\beta ,\lambda )$, say $x_{cc}$, satisfies the non-linear equation given by ${\{log\left[h(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{\prime }{\mid }_{x=x_{cc}}=0$, with

$$\begin{array}{cc}\hfill & {\{log\left[h(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{\prime }=(\beta -1)\frac{1}{x}-(\alpha +1)\beta \frac{x^{\beta -1}}{\lambda +x^{\beta }}+\frac{\alpha \beta }{\lambda }\frac{x^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}}{1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }}\hfill \\ \hfill & -\frac{2(\theta -1)\alpha \beta }{\lambda }\frac{x^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2}\hfill \\ \hfill & +\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{-1}.\hfill \end{array}$$

Then, the sign of the real number ${\eta }_{cc}={\{log\left[h(x;\theta ,\alpha ,\beta ,\lambda )\right]\}}^{″}{\mid }_{x=x_{cc}}$ can inform us on the nature of $x_{cc}$. Again, no closed-form for $x_{cc}$ exist, but we can evaluate it numerically at least. The flexibility of $h(x;\theta ,\alpha ,\beta ,\lambda )$ is illustrated in Figure 2 for selected values of $\theta$, $\alpha$, $\beta$, and $\lambda$. In particular, we observe that $h(x;\theta ,\alpha ,\beta ,\lambda )$ is increasing, decreasing, upside-down bathtub, and constant shaped.

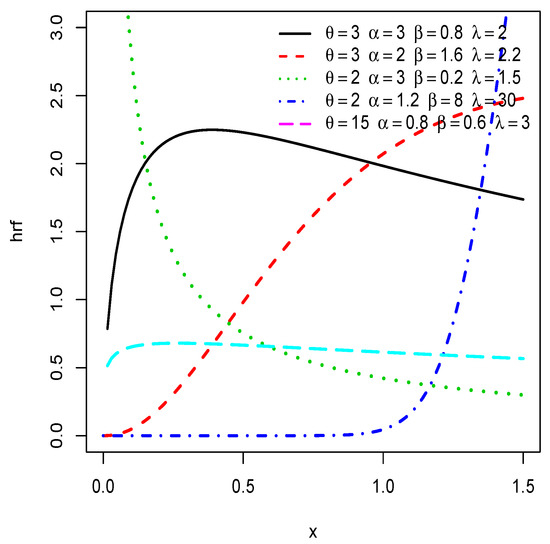
Figure 2. Plots of the hrf of the TIITLPL distribution for selected values of the parameters.

3. Mathematical Properties

The main mathematical properties of the TIITLPL distribution are discussed in this section.

3.1. Quantile Function and Applications

The quantile function of a distribution is useful to described important properties of the distribution. Here, we present the quantile function of the TIITLPL distribution, as well as related properties, applications, and functions.

3.1.1. Definition

The quantile function of the TIITLPL distribution is defined by $Q(u;\theta ,\alpha ,\beta ,\lambda )=F^{-1}(u;\theta ,\alpha ,\beta ,\lambda )$, $u\in (0,1)$. After some algebraic manipulations, we get

$$Q(u;\theta ,\alpha ,\beta ,\lambda )={\lambda }^{1/\beta }{\left\{{\left[1-\sqrt{1-{(1-u)}^{1/\theta }}\right]}^{-1/\alpha }-1\right\}}^{1/\beta },u\in (0,1).$$

In particular, the quartiles of the TIITLPL distribution can be expressed. Here, we just mention the median (second quartile) given by

$$M=Q(0.5;\theta ,\alpha ,\beta ,\lambda )={\lambda }^{1/\beta }{\left\{{\left[1-\sqrt{1-{0.5}^{1/\theta }}\right]}^{-1/\alpha }-1\right\}}^{1/\beta }.$$

Table 1 presents the numerical values of the median of the TIITLPL distribution for some values of the parameters. We see that various values can be obtained, i.e., $M\in (0,1801)$, showing the flexibility of the central tendency of the distribution.

Table 1. The numerical values of the median of the TIITLPL distribution for some values of the parameters.

$(\mathit{\theta },\mathit{\alpha },\mathit{\beta },\mathit{\lambda })$	M
$(0.5,0.5,0.5,0.5)$	540.1999
$(5.0,0.5,0.5,0.5)$	54019.99
$(5.0,1.0,0.5,0.5)$	1800.6660
$(5.0,2.0,0.5,0.5)$	232.4650
$(5.0,2.5,0.5,0.5)$	141.8530
$(5.0,0.5,1.0,0.5)$	1206.2180
$(5.0,2.0,1.0,0.5)$	26.97185
$(5.0,2.0,2.0,0.5)$	7.6697
$(5.0,2.0,5.0,0.5)$	2.8015
$(5.0,2.0,0.5,1.0)$	9.6382
$(5.0,2.0,0.5,5.0)$	0.0358
$(5.0,2.0,5.0,5.0)$	0.0282
$(5.0,5.0,5.0,5.0)$	0.0077

3.1.2. Generated Values

The following result holds in our setting: For a random variable U following the uniform distribution on $(0,1)$, the random variable $X=Q(U;\theta ,\alpha ,\beta ,\lambda )$ follows the TIITLPL distribution. Hence, generated values from the TIITLPL distribution are obtained as follows. Let $u_1,\dots ,u_n$ be n independent realizations from U. Then, n values from the TIITLPL distribution are given by $x_1,\dots ,x_n$, where $x_i=Q(u_i;\theta ,\alpha ,\beta ,\lambda )$ for $i=1,\dots ,n$.

3.1.3. Some Related Functions

Important functions can be derived from the quantile function. For instance, upon differentiation of $Q(u;\theta ,\alpha ,\beta ,\lambda )$ according to u, the quantile density function is given by

$$\begin{array}{cc}\hfill & q(u;\theta ,\alpha ,\beta ,\lambda )=\frac{{\lambda }^{1/\beta }}{2\alpha \beta \theta }\frac{{(1-u)}^{1/\theta -1}{\left[1-\sqrt{1-{(1-u)}^{1/\theta }}\right]}^{-1/\alpha -1}{\left\{{\left[1-\sqrt{1-{(1-u)}^{1/\theta }}\right]}^{-1/\alpha }-1\right\}}^{1/\beta -1}}{\sqrt{1-{(1-u)}^{1/\theta }}},\hfill \\ \hfill & u\in (0,1).\hfill \end{array}$$

In addition, the hazard quantile function is defined by $H(u;\theta ,\alpha ,\beta ,\lambda )={\left[(1-u)q(u;\theta ,\alpha ,\beta ,\lambda )\right]}^{-1}$, i.e.,

$$\begin{array}{cc}\hfill & H(u;\theta ,\alpha ,\beta ,\lambda )=\frac{2\alpha \beta \theta }{{\lambda }^{1/\beta }}\frac{\theta \sqrt{1-{(1-u)}^{1/\theta }}}{{(1-u)}^{1/\theta }{\left[1-\sqrt{1-{(1-u)}^{1/\theta }}\right]}^{-1/\alpha -1}{\left\{{\left[1-\sqrt{1-{(1-u)}^{1/\theta }}\right]}^{-1/\alpha }-1\right\}}^{1/\beta -1}},\hfill \\ \hfill & u\in (0,1).\hfill \end{array}$$

These functions are useful in reliability. In particular, $H(u;\theta ,\alpha ,\beta ,\lambda )$ can be interpreted as a certain the conditional probability involving the $100(1-u)\%$ point of distribution. In addition, the quantile function is uniquely determined as the following integral expression:

$$Q(u;\theta ,\alpha ,\beta ,\lambda )={\int }_0^u\frac{1}{(1-x)H(x;\theta ,\alpha ,\beta ,\lambda )}dx.$$

We refer the reader to [34,35].

3.1.4. Skewness and Kurtosis Based on the Quantile Function

A common approach to measure the skewness and kurtosis of a distribution is to consider measures defined with moments. However, these moments do not always exist. This is particularly true for heavy-tailed distributions such as the Lomax or PL distribution. For this reason, some alternatives are given by the use of the quantile function. In particular, to measure the skewness, we can use the Galton skewness coefficient defined by

$$S=\frac{Q(1/4;\theta ,\alpha ,\beta ,\lambda )+Q(3/4;\theta ,\alpha ,\beta ,\lambda )-2Q(1/2;\theta ,\alpha ,\beta ,\lambda )}{Q(3/4;\theta ,\alpha ,\beta ,\lambda )-Q(1/4;\theta ,\alpha ,\beta ,\lambda )}.$$

To evaluate the kurtosis, we can use the Moors kurtosis coefficient defined by

$$K=\frac{Q(7/8;\theta ,\alpha ,\beta ,\lambda )-Q(5/8;\theta ,\alpha ,\beta ,\lambda )+Q(3/8;\theta ,\alpha ,\beta ,\lambda )-Q(1/8;\theta ,\alpha ,\beta ,\lambda )}{Q(6/8;\theta ,\alpha ,\beta ,\lambda )-Q(2/8;\theta ,\alpha ,\beta ,\lambda )}.$$

The sign of S is informative on the direction of the skewness of the distribution: $S>0$ for right skewed, $S=0$ for symmetric, and $S<0$ for left skewed. The value of K measures the tail-heaviness of the distribution; in general, the bigger is the value of K is, the heavier is the tail of the distribution. We refer the reader to [36,37] for further details on these measures.

Three-dimensional plots for S and K are proposed in Figure 3 and Figure 4. We see smooth variations for the three-dimensional surface corresponding to these measures (in green), with possible high variations according to the values of the parameters, showing the flexibility of the distribution on these aspects.

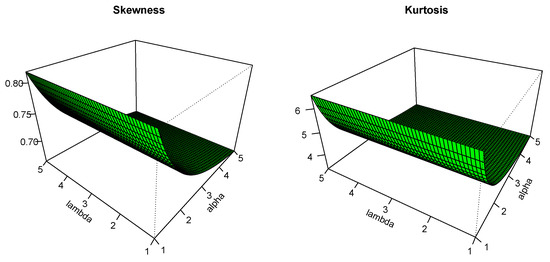
Figure 3. Plots for S and K for $\alpha ,\lambda \in (1,5)$, $\beta =0.5$, and $\theta =5$.

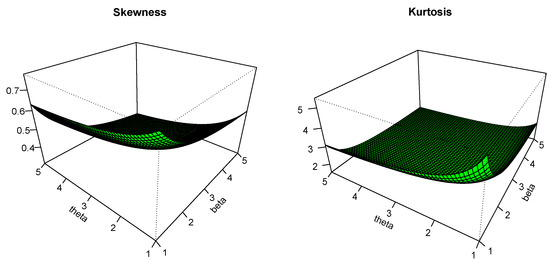
Figure 4. Plots for S and K for $\beta ,\theta \in (1,5)$, $\alpha =0.5$, and $\lambda =5$.

3.2. Useful Expansions

The following result proposes a series expansion for the pdf of the TIITLPL distribution.

Theorem 1.

For any $x>0$, we have

$$\begin{array}{c}\hfill f(x;\theta ,\alpha ,\beta ,\lambda )=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{a}_{k,\ell }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell -1},\end{array}$$

where

$$\begin{array}{c}\hfill a_{k,\ell }=\frac{\alpha \beta }{\lambda }\left(\genfrac{}{}{0pt}{}{\theta }{k}\right)\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right){(-1)}^{k+\ell }\ell ,\end{array}$$

(10)

with $\left(\genfrac{}{}{0pt}{}{b}{k}\right)=b(b-1)\dots (b-k+1)/k!$.

Proof. 

Owing to Equation (7), by applying the generalized binomial and standard binomial formulas in a row, we get

$$\begin{array}{cc}\hfill F(x;\theta ,\alpha ,\beta ,\lambda )& =1-\sum _{k=0}^{+\infty }\left(\genfrac{}{}{0pt}{}{\theta }{k}\right){(-1)}^k{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^{2k}\hfill \\ \hfill & =1-\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k}\left(\genfrac{}{}{0pt}{}{\theta }{k}\right)\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right){(-1)}^{k+\ell }{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell }.\hfill \end{array}$$

By differentiating the (left and right) functions above according to x, we get the desired result. This ends the proof of Theorem 1. □

A generalization of this result is given below.

Theorem 2.

Let υ be a positive integer. For any $x>0$, we have

$$\begin{array}{c}\hfill S{(x;\theta ,\alpha ,\beta ,\lambda )}^{\upsilon }f(x;\theta ,\alpha ,\beta ,\lambda )=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{a}_{k,\ell }^{\left[\upsilon \right]}{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell -1},\end{array}$$

where

$$\begin{array}{c}\hfill a_{k,\ell }^{\left[\upsilon \right]}=\frac{\alpha \beta }{\lambda (\upsilon +1)}\left(\genfrac{}{}{0pt}{}{\theta (\upsilon +1)}{k}\right)\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right){(-1)}^{k+\ell }\ell .\end{array}$$

(11)

Proof. 

We start the proof by expanding the function $S{(x;\theta ,\alpha ,\beta ,\lambda )}^{\upsilon +1}$. Owing to Equation (9) and the generalized binomial and standard binomial formulas, we obtain

$$\begin{array}{cc}\hfill S{(x;\theta ,\alpha ,\beta ,\lambda )}^{\upsilon +1}& =\sum _{k=0}^{+\infty }\left(\genfrac{}{}{0pt}{}{\theta (\upsilon +1)}{k}\right){(-1)}^k{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^{2k}\hfill \\ \hfill & =\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k}\left(\genfrac{}{}{0pt}{}{\theta (\upsilon +1)}{k}\right)\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right){(-1)}^{k+\ell }{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell }.\hfill \end{array}$$

By differentiating the functions above according to x and noticing that

$${\left[S{(x;\theta ,\alpha ,\beta ,\lambda )}^{\upsilon +1}\right]}^{\prime }=-(\upsilon +1)S{(x;\theta ,\alpha ,\beta ,\lambda )}^{\upsilon }f(x;\theta ,\alpha ,\beta ,\lambda ),$$

we establish the desired result. This ends the proof of Theorem 2. □

One can remark that $a_{k,\ell }^{\left[0\right]}=a_{k,\ell }^{\left[\upsilon \right]}$.

Theorems 1 and 2 are useful for determining sums expressions of important statistical measures. Some of them are presented in the next.

3.3. Moments

Two kinds of moments for the TIITLPL distribution are now investigated, with discussions.

3.3.1. Ordinary moments

Let X be a random variable following the TIITLPL distribution. Then, if it exists, the sth ordinary moment of X is given by

$$\begin{array}{cc}\hfill {\mu }_s^{\prime }& =E\left(X^s\right)={\int }_{-\infty }^{+\infty }{x}^{s}f(x;\theta ,\alpha ,\beta ,\lambda )dx\hfill \\ \hfill & ={\int }_0^{+\infty }{x}^s\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta -1}dx.\hfill \end{array}$$

Since, when $x\to +\infty$, we have $f(x;\theta ,\alpha ,\beta ,\lambda )\sim 2^{\theta }\theta \alpha \beta {\lambda }^{\alpha \theta }{x}^{-\alpha \theta \beta -1}$, this integral exists if and only if $s<\alpha \theta \beta$ (there is no problem of existence when $x\to 0$). If the parameters s, $\theta$, $\alpha$, $\beta$, and $\lambda$ are fixed, we can evaluate the numerical values of ${\mu }_s^{\prime }$ by using a mathematical software such as R, Matlab, and Mathematica.

A sum expression of ${\mu }_s^{\prime }$ can be derived to Theorem 1, as presented below.

Proposition 1.

Let us suppose that $s<\alpha \beta min(\theta ,1)$. Then, we have

$$\begin{array}{c}\hfill {\mu }_s^{\prime }=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{b}_{k,\ell ,s}B(s/\beta +1,\alpha \ell -s/\beta ),\end{array}$$

where

$$\begin{array}{c}\hfill b_{k,\ell ,s}={\lambda }^{s/\beta }\alpha \left(\genfrac{}{}{0pt}{}{\theta }{k}\right)\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right){(-1)}^{k+\ell }\ell \end{array}$$

(12)

and $B(x,y)$ denotes the standard beta function defined by $B(x,y)={\int }_0^1{t}^{x-1}{(1-t)}^{y-1}dt$.

Proof. 

It follows from Theorem 1 that

$$\begin{array}{c}\hfill {\mu }_s^{\prime }={\int }_{-\infty }^{+\infty }{x}^{s}f(x;\theta ,\alpha ,\beta ,\lambda )dx=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{a}_{k,\ell }{I}_{\ell ,s},\end{array}$$

where $a_{k,\ell }$ is given by Equation (10) and

$$I_{\ell ,s}={\int }_0^{+\infty }{x}^{s+\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell -1}dx.$$

Now, by applying the two changes of variables $x={\left(\lambda y\right)}^{1/\beta }$ and $y=u/(1-u)=-1+1/(1-u)$ in a row, we get

$$\begin{array}{cc}\hfill I_{\ell ,s}& =\frac{1}{\beta }{\lambda }^{s/\beta +1}{\int }_0^{+\infty }{y}^{s/\beta }{\left(1+y\right)}^{-\alpha \ell -1}dy=\frac{1}{\beta }{\lambda }^{s/\beta +1}{\int }_0^1{u}^{s/\beta }{\left(1-u\right)}^{\alpha \ell -s/\beta -1}du\hfill \\ \hfill & =\frac{1}{\beta }{\lambda }^{s/\beta +1}B(s/\beta +1,\alpha \ell -s/\beta ).\hfill \end{array}$$

By putting the above equalities together and noticing that $({\lambda }^{s/\beta +1}/\beta )a_{k,\ell }=b_{k,\ell ,s}$, we end the proof of Proposition 1. □

By taking $s=1$, we obtain the mean of X, i.e., $\mu ={\mu }_1^{\prime }$. The variance of X is obtained by ${\sigma }^2=E[{(X-\mu )}^2]={\mu }_2^{\prime }-{\mu }^2$. Further, one can determine the sth central moment and sth cumulant of X defined by, respectively,

$${\mu }_s=E\left[{(X-\mu )}^s\right]=\sum _{k=0}^s\left(\genfrac{}{}{0pt}{}{s}{k}\right){\mu }_{s-k}^{\prime }{(-1)}^k{\mu }^k,{\kappa }_s={\mu }_s^{\prime }-\sum _{k=1}^{s-1}\left(\genfrac{}{}{0pt}{}{s-1}{k-1}\right){\kappa }_k{\mu }_{s-k}^{\prime },$$

with ${\kappa }_1=\mu$. One can also express several measures of skewness and kurtosis based on the central moments (or cumulants).

3.3.2. Incomplete Moments

Let X be a random variable following the TIITLPL distribution and, for any $t\ge 0$, let $X_t$ be the random variable such that $X_t=X$ if $X\le t$ and 0 otherwise. Then, the sth incomplete moment of X is given by

$$\begin{array}{cc}\hfill {\mu }_s^{\prime }\left(t\right)& =E\left(X_t^s\right)={\int }_{-\infty }^t{x}^{s}f(x;\theta ,\alpha ,\beta ,\lambda )dx\hfill \\ \hfill & ={\int }_0^t{x}^s\frac{2\theta \alpha \beta }{\lambda }{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta -1}dx.\hfill \end{array}$$

Note that ${\mu }_s^{\prime }\left(t\right)$ always exists. As for the ordinary moments, if the parameters s, t, $\theta$, $\alpha$, $\beta$, and $\lambda$ are fixed, a numerical calculation of ${\mu }_s^{\prime }\left(t\right)$ is always possible by any mathematical software.

In this regards, by using the R software, Table 2 collects the numerical values of the first four incomplete moments of the TIITLPL distribution with $t=100$ for some values of the parameters. We observe that the parameters of the distribution have a high impact on these values.

Table 2. The numerical values of the first four incomplete moments of the TIITLPL distribution with $t=100$ for some values of the parameters.

$(\mathit{\theta },\mathit{\alpha },\mathit{\beta },\mathit{\lambda })$	${\mathit{\mu }}_1^{\prime }\left(100\right)$	${\mathit{\mu }}_2^{\prime }\left(100\right)$	${\mathit{\mu }}_3^{\prime }\left(100\right)$	${\mathit{\mu }}_4^{\prime }\left(100\right)$
$(0.5,0.5,0.5,0.5)$	6.5310	329.8982	21948	1642994
$(5.0,0.5,0.5,0.5)$	3.0469	83.6055	4496.53	304584
$(5.0,1.0,0.5,0.5)$	0.2716	0.8662	18.6814	905.1954
$(5.0,2.0,0.5,0.5)$	0.03667	0.0061	0.0038	0.0111
$(5.0,2.5,0.5,0.5)$	0.0210	0.0017	0.0004	0.0003
$(5.0,0.5,1.0,0.5)$	1.2956	6.6656	141.9529	6614.0360
$(5.0,2.0,1.0,0.5)$	0.1528	0.03667	0.0126	0.0061
$(5.0,2.0,2.0,0.5)$	0.3661	0.1528	0.0712	0.03667
$(5.0,2.0,5.0,0.5)$	0.6575	0.4426	0.3044	0.2139
$(5.0,2.0,0.5,1.0)$	0.1467	0.0980	0.2437	2.3221
$(5.0,2.0,0.5,5.0)$	3.6090	51.7157	1679.7620	84843.84
$(5.0,2.0,5.0,5.0)$	1.0420	1.1118	1.2121	1.3482
$(5.0,5.0,5.0,5.0)$	0.8527	0.7423	0.6583	0.5939

From the analytical point of view, a sum expression of ${\mu }_s^{\prime }\left(t\right)$ is presented below.

Proposition 2.

We have

$$\begin{array}{c}\hfill {\mu }_s^{\prime }\left(t\right)=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{b}_{k,\ell ,s}{B}_{t^{\beta }/(t^{\beta }+\lambda )}(s/\beta +1,\alpha \ell -s/\beta ),\end{array}$$

where $b_{k,\ell ,s}$ is given by Equation (12) and $B_w(x,y)$ denotes the lower incomplete beta function defined by $B_w(x,y)={\int }_0^w{t}^{x-1}{(1-t)}^{y-1}dt$.

Proof. 

The proof is similar to the one of Proposition 1, only the upper bound of the integral term must be adjusted. Thus, Theorem 1 gives

$$\begin{array}{c}\hfill {\mu }_s^{\prime }\left(t\right)={\int }_{-\infty }^t{x}^{s}f(x;\theta ,\alpha ,\beta ,\lambda )dx=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{a}_{k,\ell }{I}_{\ell ,s}\left(t\right),\end{array}$$

where $a_{k,\ell }$ is given by Equation (10) and

$$I_{\ell ,s}\left(t\right)={\int }_0^t{x}^{s+\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell -1}dx.$$

Now, by applying the two changes of variables $x={\left(\lambda y\right)}^{1/\beta }$ and $y=u/(1-u)=-1+1/(1-u)$, i.e., $u=y/(1+y)$, in a row, we get

$$\begin{array}{cc}\hfill I_{\ell ,s}\left(t\right)& =\frac{1}{\beta }{\lambda }^{s/\beta +1}{\int }_0^{t^{\beta }/\lambda }{y}^{s/\beta }{\left(1+y\right)}^{-\alpha \ell -1}dy=\frac{1}{\beta }{\lambda }^{s/\beta +1}{\int }_0^{t^{\beta }/(t^{\beta }+\lambda )}{u}^{s/\beta }{\left(1-u\right)}^{\alpha \ell -s/\beta -1}du\hfill \\ \hfill & =\frac{1}{\beta }{\lambda }^{s/\beta +1}{B}_{t^{\beta }/(t^{\beta }+\lambda )}(s/\beta +1,\alpha \ell -s/\beta ).\hfill \end{array}$$

Since $({\lambda }^{s/\beta +1}/\beta )a_{k,\ell }=b_{k,\ell ,s}$, by combining the above equalities, we end the proof of Proposition 2. □

From the incomplete moments of X, one can define important quantities and functions. For instance, one can express the mean deviations of X about the mean $\mu$ and the median M by, respectively,

$${\delta }_1=E\left(\right|X-\mu \left|\right)=2\mu F(\mu ;\theta ,\alpha ,\beta ,\lambda )-2{\mu }_1^{\prime }\left(\mu \right),{\delta }_2=E\left(\right|X-M\left|\right)=\mu -2{\mu }_1^{\prime }\left(M\right).$$

Other quantities can be defined in a similar manner. Well-known functions defined with the s-incomplete moment include the sth lower and upper conditional moments of X defined by, respectively,

$$\begin{array}{c}\hfill {\mu }_s^{\nabla }\left(t\right)=E(X^s\mid X\le t)=\frac{1}{F(t;\theta ,\alpha ,\beta ,\lambda )}{\mu }_s^{\prime }\left(t\right),t\ge 0\end{array}$$

and

$$\begin{array}{c}\hfill {\mu }_s^{▵}\left(t\right)=E(X^s\mid X>t)=\frac{1}{S(t;\theta ,\alpha ,\beta ,\lambda )}[{\mu }_s^{\prime }-{\mu }_s^{\prime }\left(t\right)],t\ge 0.\end{array}$$

3.4. Order Statistics

Let X be a random variable following the TIITLPL distribution and, for a random sample of size n from X, say $X_1,\dots ,X_n$, let $X_{i:n}$ be the ith order statistic such that $X_{1:n}\le X_{2:n}\le \dots \le X_{n:n}$, where $X_{u:n}\in \{X_1,\dots ,X_n\}$ for $u=1,\dots ,n$. In full generality, the study of the order statistics is of importance since they naturally appear in various applications, mainly those involving systems composed of several components that can fail independently of each other. Here, some distributional properties of $X_{i:n}$ are presented. First, the pdf of $X_{i:n}$ is given by

$$f_{i:n}(x;\theta ,\alpha ,\beta ,\lambda )=\frac{n!}{(i-1)!(n-i)!}F{(x;\theta ,\alpha ,\beta ,\lambda )}^{i-1}S{(x;\theta ,\alpha ,\beta ,\lambda )}^{n-i}f(x;\theta ,\alpha ,\beta ,\lambda ),x>0.$$

It follows from the binomial formula that

$$f_{i:n}(x;\theta ,\alpha ,\beta ,\lambda )=\frac{n!}{(i-1)!(n-i)!}\sum _{j=0}^{i-1}\left(\genfrac{}{}{0pt}{}{i-1}{j}\right){(-1)}^{j}S{(x;\theta ,\alpha ,\beta ,\lambda )}^{j+n-i}f(x;\theta ,\alpha ,\beta ,\lambda ),x>0.$$

An immediate application of Theorem 2 gives us the following series expansion:

$$f_{i:n}(x;\theta ,\alpha ,\beta ,\lambda )=\sum _{j=0}^{i-1}\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{b}_{k,\ell }^{[j+n-i]}{x}^{\beta -1}{\left(1+\frac{x^{\beta }}{\lambda }\right)}^{-\alpha \ell -1},x>0,$$

where

$$\begin{array}{c}\hfill b_{k,\ell }^{[j+n-i]}=\frac{n!}{(i-1)!(n-i)!}\left(\genfrac{}{}{0pt}{}{i-1}{j}\right){(-1)}^j{a}_{k,\ell }^{[j+n-i]}\end{array}$$

and $a_{k,\ell }^{[j+n-i]}$ is defined by Equation (11) with $\upsilon =j+n-i$.

From this series expansion, structural properties of the distribution of $X_{s:n}$ can be determined, as several kinds of moments. For instance, after some algebraic manipulations, the sth moment of $X_{s:n}$ is given by

$$\begin{array}{c}\hfill {\mu }_{i:n,s}^{\prime }=E\left(X_{i:n}^s\right)=\sum _{j=0}^{i-1}\sum _{k=0}^{+\infty }\sum _{\ell =1}^{2k}{c}_{k,\ell }^{[j+n-i]}B(s/\beta +1,\alpha \ell -s/\beta ),\end{array}$$

where $c_{k,\ell }^{[j+n-i]}=({\lambda }^{s/\beta +1}/\beta )b_{k,\ell }^{[j+n-i]}$.

Let us now focus on the extreme order statistics defined by $X_{1:n}=inf(X_1,\dots ,X_n)$ and $X_{n:n}=sup(X_1,\dots ,X_n)$, having the pdfs given by, respectively,

$$f_{1:n}(x;\theta ,\alpha ,\beta ,\lambda )=nS{(x;\theta ,\alpha ,\beta ,\lambda )}^{n-1}f(x;\theta ,\alpha ,\beta ,\lambda ),x>0$$

and

$$f_{n:n}(x;\theta ,\alpha ,\beta ,\lambda )=nF{(x;\theta ,\alpha ,\beta ,\lambda )}^{n-1}f(x;\theta ,\alpha ,\beta ,\lambda ),x>0.$$

The following result concerns the limiting distributions of $X_{1:n}$ and $X_{n:n}$, involving the well-known Weibull and Fréchet distributions.

Theorem 3. 

• The limiting distribution of ${\left(X_{1:n}\right)}_{n\in {\mathbb{N}}^{*}}$ is the Weibull distribution with the following cdf: $F_{*}(x;\beta )=1-e^{-x^{2\beta }}$, $x>0$, i.e., there exist ${\left(a_n\right)}_{n\in {\mathbb{N}}^{*}}$ and ${\left(b_n\right)}_{n\in {\mathbb{N}}^{*}}$ such that

  $$\underset{n\to +\infty }{lim}P\left(b_n(X_{1:n}-a_n)\le x\right)=F_{*}(x;\beta ).$$
• The limiting distribution of ${\left(X_{n:n}\right)}_{n\in {\mathbb{N}}^{*}}$ is the Fréchet distribution with the following cdf: $F_{**}(x;\theta ,\alpha ,\beta )=e^{-x^{-\alpha \theta \beta }}$, $x>0$, i.e., there exist ${\left(a_n\right)}_{n\in {\mathbb{N}}^{*}}$ and ${\left(b_n\right)}_{n\in {\mathbb{N}}^{*}}$ such that

  $$\underset{n\to +\infty }{lim}P\left(b_n(X_{n:n}-a_n)\le x\right)=F_{**}(x;\theta ,\alpha ,\beta ).$$

Proof. 

• Let us recall that, when $x\to 0$, we have $f(x;\theta ,\alpha ,\beta ,\lambda )\sim (2\theta {\alpha }^2\beta /{\lambda }^2)x^{2\beta -1}$ and $Q(0;\theta ,\alpha ,\beta ,\lambda )=0$. Hence, owing to l’Hospital’s rule, we have

  $$\begin{array}{cc}\hfill & \underset{ϵ\to 0}{lim}\frac{F\left(Q\right(0;\theta ,\alpha ,\beta ,\lambda )+ϵx;\theta ,\alpha ,\beta ,\lambda )}{F\left(Q\right(0;\theta ,\alpha ,\beta ,\lambda )+ϵ;\theta ,\alpha ,\beta ,\lambda )}=\underset{ϵ\to 0}{lim}\frac{F(ϵx;\theta ,\alpha ,\beta ,\lambda )}{F(ϵ;\theta ,\alpha ,\beta ,\lambda )}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\frac{xf(ϵx;\theta ,\alpha ,\beta ,\lambda )}{f(ϵ;\theta ,\alpha ,\beta ,\lambda )}=x^{2\beta }.\hfill \end{array}$$
  It follows from ([38] Theorem 8.3.6) the desired result.
• Let us recall that, when $x\to +\infty$, we have $f(x;\theta ,\alpha ,\beta ,\lambda )\sim 2^{\theta }\theta \alpha \beta {\lambda }^{\alpha \theta }{x}^{-\alpha \theta \beta -1}$. Thus, by applying l’Hospital’s rule, we have

  $$\begin{array}{c}\hfill \underset{t\to +\infty }{lim}\frac{1-F(tx;\theta ,\alpha ,\beta ,\lambda )}{1-F(t;\theta ,\alpha ,\beta ,\lambda )}=\underset{t\to +\infty }{lim}\frac{xf(tx;\theta ,\alpha ,\beta ,\lambda )}{f(t;\theta ,\alpha ,\beta ,\lambda )}=x^{-\alpha \theta \beta }.\end{array}$$
  The desired result follows from ([39] Theorem 1.6.2 and Corollary 1.6.3).

The proof of Theorem 3 is completed. □

4. Inference

We now investigate the inferential aspect of the TIITLPL model. The unknown parameters are estimated by the well-established maximum likelihood estimation method.

4.1. Maximum Likelihood Estimation Method

The maximum likelihood estimation method consists in determining the parameters that maximize the likelihood function of the sample data, called the maximum likelihood estimates (MLEs). For the purpose of this paper, from an observed sample $x_1,\dots ,x_n$ from the TIITLPL distribution, the corresponding likelihood function is given by

$$\begin{array}{cc}\hfill & L(\theta ,\alpha ,\beta ,\lambda )=\prod _{i=1}^{n}f(x_i;\theta ,\alpha ,\beta ,\lambda )\hfill \\ \hfill & =\prod _{i=1}^n\left[\frac{2\theta \alpha \beta }{\lambda }{x}_i^{\beta -1}{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]{\left\{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}}^{\theta -1}\right].\hfill \end{array}$$

The MLEs of $\theta$, $\alpha$, $\beta$, and $\lambda$ are denoted by $\widehat{\theta }$, $\widehat{\alpha }$, $\widehat{\beta }$, and $\widehat{\lambda }$, respectively. They can also be obtained by maximization of a more tractable function: the log-likelihood function is given by

$$\begin{array}{cc}\hfill & \ell (\theta ,\alpha ,\beta ,\lambda )=log\left[L\right(\theta ,\alpha ,\beta ,\lambda \left)\right]=nlog\left(2\right)+nlog\left(\theta \right)+nlog\left(\alpha \right)+nlog\left(\beta \right)-nlog\left(\lambda \right)\hfill \\ \hfill & +(\beta -1)\sum _{i=1}^{n}log\left(x_i\right)-(\alpha +1)\sum _{i=1}^{n}log\left(1+\frac{x_i^{\beta }}{\lambda }\right)+\sum _{i=1}^{n}log\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]\hfill \\ \hfill & +(\theta -1)\sum _{i=1}^{n}log\left\{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\}.\hfill \end{array}$$

Thus, $\widehat{\theta }$, $\widehat{\alpha }$, $\widehat{\beta }$, and $\widehat{\lambda }$ are the simultaneous solutions of the following non-linear equations: $\partial \ell (\theta ,\alpha ,\beta ,\lambda )/\partial \theta =0$, $\partial \ell (\theta ,\alpha ,\beta ,\lambda )/\partial \alpha =0$, $\partial \ell (\theta ,\alpha ,\beta ,\lambda )/\partial \beta =0$ and $\partial \ell (\theta ,\alpha ,\beta ,\lambda )/\partial \lambda =0$, according to the parameters. Here, these partial derivatives are of complexed form, i.e.,

$$\begin{array}{c}\hfill \frac{\partial \ell (\theta ,\alpha ,\beta ,\lambda )}{\partial \theta }=\frac{n}{\theta }+\sum _{i=1}^{n}log\left\{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2\right\},\end{array}$$

(13)

$$\begin{array}{cc}\hfill \frac{\partial \ell (\theta ,\alpha ,\beta ,\lambda )}{\partial \alpha }& =\frac{n}{\alpha }-\sum _{i=1}^{n}log\left(1+\frac{x_i^{\beta }}{\lambda }\right)+\sum _{i=1}^n\frac{{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }log\left(1+\frac{x_i^{\beta }}{\lambda }\right)}{1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }}\hfill \\ \hfill & -2(\theta -1)\sum _{i=1}^n\frac{{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]log\left(1+\frac{x_i^{\beta }}{\lambda }\right)}{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \frac{\partial \ell (\theta ,\alpha ,\beta ,\lambda )}{\partial \beta }& =\frac{n}{\beta }+\sum _{i=1}^{n}log\left(x_i\right)-(\alpha +1)\sum _{i=1}^n\frac{x_i^{\beta }log\left(x_i\right)}{\lambda +x_i^{\beta }}+\frac{\alpha }{\lambda }\sum _{i=1}^n\frac{x_i^{\beta }log\left(x_i\right){\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha -1}}{1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }}\hfill \\ \hfill & -\frac{2\alpha (\theta -1)}{\lambda }\sum _{i=1}^n\frac{x_i^{\beta }log\left(x_i\right){\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \frac{\partial \ell (\theta ,\alpha ,\beta ,\lambda )}{\partial \lambda }& =-\frac{n}{\lambda }+\frac{\alpha +1}{{\lambda }^2}\sum _{i=1}^n\frac{x_i^{\beta }}{1+\frac{x_i^{\beta }}{\lambda }}-\frac{\alpha }{{\lambda }^2}\sum _{i=1}^n\frac{x_i^{\beta }{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha -1}}{1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }}\hfill \\ \hfill & +\frac{2\alpha (\theta -1)}{{\lambda }^2}\sum _{i=1}^n\frac{x_i^{\beta }{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha -1}\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}{1-{\left[1-{\left(1+\frac{x_i^{\beta }}{\lambda }\right)}^{-\alpha }\right]}^2}.\hfill \end{array}$$

Let us just mention that, owing to Equation (13), the MLEs satisfy the following simple relation:

$$\begin{array}{c}\hfill \widehat{\theta }={\left\{-\frac{1}{n}\sum _{i=1}^{n}log\left\{1-{\left[1-{\left(1+\frac{x_i^{\widehat{\beta }}}{\widehat{\lambda }}\right)}^{-\widehat{\alpha }}\right]}^2\right\}\right\}}^{-1}.\end{array}$$

However, we have no closed-forms for the MLEs. Numerical maximization algorithms are useful in this regards; most of the statistical softwares can be used to provide numerical evaluations of the MLEs. Finally, the choice of the MLEs in our context is motivated as usual: theoretical results ensure that, under some (abstract regularity) conditions, the subjacent random versions of the MLEs converge (in some senses) to the real value of the unknown parameters, which is a very desirable property for practical purposes. In addition, thanks to the existing theory on the MLEs, one can provide asymptotic confidence sets and likelihood tests involving $\theta$, $\alpha$, $\beta$, and $\lambda$, which is, however, out the scope of this study.

4.2. Simulation

Thus, mathematical guarantees justify the use of the MLEs in our setting. We now illustrate this fact through a complete numerical study. We proceed as follows:

• One thousand random samples of size $n=50$, 100, 200, and 500 are generated from the TIITLPL distribution by the use of the quantile function (see Section 3.1.2).
• Eight different sets of values of true parameters $\alpha$, $\lambda$, $\beta$, and $\theta$ in order, are taken as
  Set 1 $=(0.5,0.5,0.5,0.5)$, Set 2 $=(0.5,0.5,1.5,0.5)$, Set 3 $=(0.5,1.5,0.8,1.5)$,
  Set 4 $=(0.5,1.5,1.5,1.2)$, Set 5 $=(0.5,0.5,2,0.5)$, Set 6 $=(1,0.5,2,0.5)$,
  Set 7 $=(0.5,1,1.2,1.5)$, Set 8 $=(0.8,0.5,1.5,1.5)$.
• The mean of the obtained MLEs (Estimates) and the mean squared errors (MSEs) for the selected sets of parameters are calculated.
• Numerical outcomes are listed in Table 3 and Table 4.
  Table 3. Estimates and MSEs of TIITLPL distribution for MLEs by using different parameter values.

  	Set 1		Set 2		Set 3		Set 4
  n	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
  50	0.471	0.090	0.602	0.091	0.587	0.058	0.554	0.128
  	0.537	0.238	0.663	0.223	2.145	2.429	1.614	1.138
  	0.735	0.223	1.758	0.587	0.920	0.250	2.122	1.636
  	0.771	0.431	0.662	0.344	1.790	1.041	1.650	1.552
  100	0.504	0.084	0.644	0.053	0.574	0.033	0.609	0.083
  	0.428	0.085	0.669	0.128	1.747	0.446	1.739	0.510
  	0.660	0.122	1.633	0.258	0.865	0.115	1.665	0.239
  	0.656	0.245	0.474	0.088	1.479	0.284	1.310	1.088
  200	0.525	0.081	0.617	0.046	0.577	0.017	0.642	0.058
  	0.546	0.075	0.585	0.041	1.623	0.141	1.719	0.199
  	0.558	0.045	1.561	0.124	0.832	0.025	1.548	0.085
  	0.685	0.233	0.475	0.071	1.309	0.149	1.066	0.293
  500	0.504	0.061	0.647	0.035	0.592	0.013	0.660	0.051
  	0.477	0.051	0.612	0.027	1.620	0.058	1.729	0.137
  	0.539	0.013	1.449	0.035	0.815	5.258 *	1.515	0.023
  	0.636	0.169	0.419	0.018	1.226	0.106	0.942	0.141

  * indicates that the value multiply ${10}^{-3}$.
  Table 4. Estimates and MSEs of TIITLPL distribution for MLEs by using different parameter values.

  	Set 5		Set 6		Set 7		Set 8
  n	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
  50	0.651	0.147	0.773	0.210	0.699	0.206	1.268	0.48
  	0.613	0.303	0.486	0.228	1.464	4.786	1.143	3.391
  	2.442	1.194	2.549	1.534	1.588	0.918	1.603	0.247
  	0.746	0.758	1.058	1.221	1.752	2.663	1.432	1.103
  100	0.667	0.133	0.806	0.147	0.767	0.161	1.199	0.248
  	0.621	0.156	0.437	0.074	1.326	0.386	0.774	0.895
  	2.296	0.714	2.310	0.440	1.247	0.115	1.592	0.123
  	0.652	0.484	0.845	0.612	1.286	0.630	1.148	0.600
  200	0.735	0.109	0.828	0.109	0.750	0.102	1.197	0.168
  	0.647	0.078	0.456	0.039	1.247	0.177	0.703	0.093
  	2.064	0.121	2.099	0.169	1.253	0.061	1.468	0.033
  	0.478	0.222	0.819	0.594	1.115	0.582	1.098	0.222
  500	0.725	0.07	0.898	0.036	0.768	0.090	1.167	0.140
  	0.680	0.056	0.483	0.017	1.269	0.139	0.639	0.043
  	1.880	0.073	2.043	0.048	1.195	0.013	1.484	0.016
  	0.406	0.043	0.612	0.121	1.004	0.314	1.054	0.221

The calculations were performed via Mathematica 9. We observe that the MSEs converge to zero when the sample size is increased, which is consistent with the well-known theoretical convergence properties of the MLEs.

5. Applications

In this section, the highly effectiveness of TIITLPL distribution is proved by the use of two well-known practical datasets: the aircraft windshield dataset and the cancer patient data, presented in more detail below.

We also make comparisons with other distributions by providing a formative evaluation of the goodness of fit of the models. The following goodness of fit measures are considered: the Akaike information criterion (AIC), consistent AIC (CAIC), Hannan–Quinn information criterion (HQIC), Anderson–Darling (A${}^{*}$), and Cramér–von Mises (W${}^{*}$). In general, the smaller the values of these statistics is, the better the fit to the data is.

5.1. Aircraft Windshield Data

The first dataset was studied by [40], which represents the failure times for a particular windshield device. A brief statistical description of them is given in Table 5.

Table 5. Descriptive statistics for the aircraft windshield data.

n	Mean	Median	Standard Deviation	Skewness	Kurtosis
84	2.56	2.35	1.12	0.10	−0.71

In particular, we see that the data are platykurtosis. More informative descriptive illustrations are given in Figure 5.

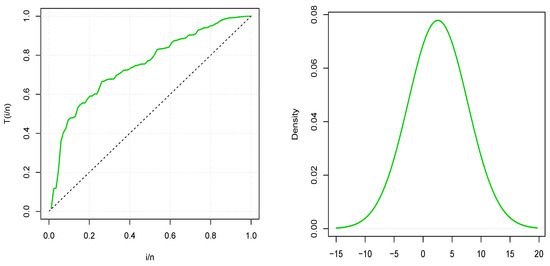
Figure 5. Plots TTT and kernel density plot for the aircraft windshield data.

The total time on test (TTT) plot in Figure 5 shows a concave TTT-transform, indicating that the hrf is possibly increasing. Moreover, the basic kernel density estimator is nearly symmetrical (unimodal). Hence, the TIITLPL model could be appropriate for fitting this dataset.

Thus, for the aircraft windshield data, we compare the fit of the TIITLPL distribution with the following distributions: the gamma Lomax (GL) distribution by [11], beta Lomax (BL) distribution by [30], transmuted Weibull Lomax (TWL) distribution by [33], Kumaraswamy Weibull (KwW) distribution by [41], McDonald Weibull (McW) distribution by [42], beta Weibull (BW) distribution by [43], transmuted log-logistic (TLL) distribution by [44], and (standard) log-logistic (LL) distribution and transmuted Marshall-Olkin Fréchet (TMOFr) distribution by [45].

The MLEs of the parameters of these distributions and the corresponding standard errors (SEs) for windshield data are provided in Table 6. The statistics AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ are listed in Table 7.

Table 6. MLEs and SEs (in parentheses) for the aircraft windshield data.

Distributions	MLEs and SEs
TIITLPL($\mathbf{\theta }$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	213.2225 (8.0985)	3.6880 (0.7192)	1.2282 (0.1149)	186.8420 (7.6076)	-
BL($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$)	3.6036 (0.6187)	32.6387 (13.7145)	4.8307 (9.2382)	119.0374 (42.9269)	-
KwW($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$)	34.6604 (17.5270)	81.8464 (52.0142)	14.4338 (27.0952)	0.2040 (0.0423)	-
McW($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathit{c}$)	17.6864 (6.2220)	33.6392 (19.9941)	1.9406 (1.0111)	0.3062 (0.0454)	16.7211 (9.6221)
BW($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$)	34.1808 (14.8389)	11.4968 (6.7300)	1.3609 (1.0020)	0.2982 (0.0603)	-
TMOFr($\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\sigma }$, $\mathbf{\lambda }$)	200.7472 (87.2751)	1.9524 (0.1252)	0.1022 (0.0173)	−0.8692 (0.1012)	-
$\mathbf{TLL}$($\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	2.0589 (0.2759)	3.1025 (0.3408)	−0.4839 (0.3853)	-	-
$\mathbf{LL}$($\mathbf{\alpha }$, $\mathbf{\beta }$)	2.3911 (0.1369)	3.2235 (0.2971)	-	-	-

Table 7. The AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ statistics for the aircraft windshield data.

Distributions	AIC	CAIC	HQIC	A${}^{*}$	W${}^{*}$
$\mathbf{TIITLPL}$	269.0398	269.5461	272.9485	0.6245	0.0621
$\mathbf{BL}$	285.4354	285.9355	289.3650	1.4080	0.1684
$\mathbf{KwW}$	281.4345	281.9411	291.1585	1.5062	0.1851
$\mathbf{McW}$	283.8993	284.6692	296.0532	1.5917	0.1992
BW	305.0283	305.5343	314.7519	3.2277	0.4655
$\mathbf{TMOFr}$	309.4725	309.9785	319.1953	2.4042	0.3209
$\mathbf{TLL}$	284.7719	285.0719	287.7034	1.4922	0.1842
$\mathbf{LL}$	283.1625	283.3106	285.1168	1.5203	0.1866

We note from the results in Table 7 that the TIITLPL model gives the smallest values of AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ as compared to the other competitive models. Therefore, the TIITLPL distribution provides the best fit for the aircraft windshield data. To illustrate and complete these numerical results, Figure 6 plots the histogram and the estimated pdf of the TIITLPL distribution, the Probability-Probability (P-P) plot showing a nice line adjustment of the scatter plot, and the estimated cdf and sf over the empirical cdf and sf, respectively.

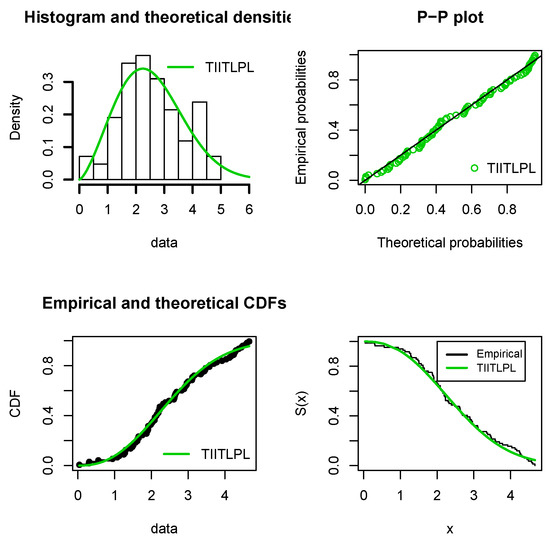
Figure 6. Several kinds of fits of the TIITLPL distribution for the aircraft windshield data.

In addition, we would like to mention that, for this dataset, the TIITLPL distribution outperforms the EPL distribution by [19] presented in the Introduction; if we compare Table 7 and ([19] Table 5), the AIC, CAIC, A${}^{*}$, and $W^{*}$ are favorable for the TIITLPL distribution.

5.2. Cancer Patient Data

The cancer patient dataset describes the remission times (in months) of a random sample of 128 bladder cancer patients studied by [46]. A brief statistical description of them is given in Table 8.

Table 8. Descriptive statistics for the cancer patient data.

n	Mean	Median	Standard Deviation	Skewness	Kurtosis
128	9.37	6.39	10.51	3.25	15.20

We can remark that the data are right skewed with a high kurtosis showing the heavy tailed nature of the data. More informations are given in Figure 7 with the consideration of a TTT plot and a basic kernel estimation of the unknown subjacent pdf.

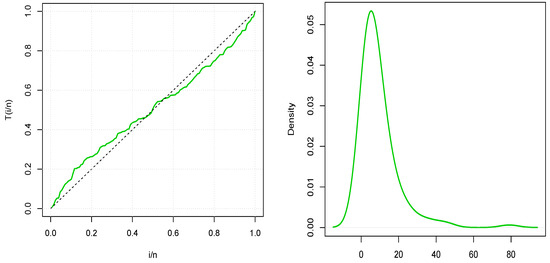
Figure 7. Plots TTT and kernel density plot for the cancer patient data.

The TTT-plot in Figure 7 shows that the TTT-transform is first concave then convex giving an indication of bathtub shape of the hrf. Furthermore, the kernel density estimator is heavy right skewed (unimodal). Hence, the TIITLPL model could be appropriate model for fitting the cancer patient dataset.

For these data, we thus compare the fit of the TIITLPL distribution with some other distributions: the transmuted modified Weibull (TMW) distribution by [47], transmuted additive Weibull (TAW) distribution by [31], generalized inverse gamma (GIG) distribution by [32], beta exponentiated Burr XII (BEBXII) distribution by [48], beta Fréchet (BFr) distribution by [49], Kumaraswamy log-logistic (KwLL) distribution by [50], transmuted complementary Weibull geometric (TCWG) distribution by [51], Kumaraswamy exponentiated Burr XII (KwEBXII) distribution by [52], generalized transmuted Weibull (GTW) distribution by [53], and the exponentiated transmuted generalized Rayleigh (ETGR) distribution by [54].

The MLEs of the parameters of these distributions and the corresponding SEs for the cancer patient data are provided in Table 9. The statistics AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ are listed in Table 10.

Table 9. MLEs and SEs (in parentheses) for the cancer patient data.

Distribution	MLEs and SEs
$\mathbf{TIITLPL}$($\mathbf{\theta }$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	3.7264 (0.1187)	1.8637 (0.2335)	0.8039 (0.1253)	13.3937 (1.2256)	-
$\mathbf{KwLL}$($\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathit{a}$, $\mathit{b}$)	4.6580 (13.1634)	0.2984 (0.1675)	7.8661 (4.4933)	113.0181 (23.364)	-
$\mathbf{TCWG}$($\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$, $\mathbf{\gamma }$)	106.0695 (124.8000)	1.7124 (0.0992)	0.2173 (0.6104)	0.0090 (0.0070)	-
$\mathbf{KwEBXII}$($\mathit{a}$, $\mathit{b}$, $\mathit{c}$, $\mathbf{\beta }$, $\mathit{k}$)	2.7805 (44.5102)	67.636 (104.728)	0.3380 (0.3857)	3.0833 (49.3534)	0.8398 (1.7235)
$\mathbf{BEBXII}$($\mathit{a}$, $\mathit{b}$, $\mathit{c}$, $\mathbf{\beta }$, $\mathit{k}$)	22.1869 (21.9561)	20.2778 (17.2968)	0.2243 (0.1446)	1.7804 (1.0763)	1.3067 (1.0794)
$\mathbf{GIG}$($\mathit{a}$, $\mathit{b}$, $\mathit{c}$, $\mathbf{\beta }$, $\mathit{k}$)	2.3272 (0.3698)	0.0002 (0.0002)	17.9315 (7.3857)	0.5430 (0.0420)	0.0010 (0.0003)
$\mathbf{BFr}$($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$)	12.5268 (24.4699)	33.342 (36.348)	27.7533 (71.5078)	0.1690 (0.1040)	-
$\mathbf{ETGR}$($\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$, $\mathbf{\delta }$)	7.3765 (5.3893)	0.0473 (0.0042)	0.1182 (0.2600)	0.0491 (0.0362)	-
$\mathbf{TMW}$($\mathit{a}$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	0.0002 (0.0114)	0.1208 (0.0240)	0.8955 (0.6260)	0.4075 (0.4070)	-
$\mathbf{TAW}$($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	0.00003 (0.0061)	1.0065 (0.0353)	0.1139 (0.0322)	0.9722 (0.125)	−0.1630 (0.2803)
$\mathbf{GTW}$($\mathit{a}$, $\mathit{b}$, $\mathbf{\alpha }$, $\mathbf{\beta }$, $\mathbf{\lambda }$)	2.7965 (1.117)	0.0128 (7.214)	0.2991 (0.1512)	0.6542 (0.1216)	0.0020 (1.7691)

Table 10. The AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ statistics for the cancer patient data.

Distributions	AIC	CAIC	HQIC	A${}^{*}$	W${}^{*}$
$\mathbf{TIITLPL}$	828.1981	828.5239	832.8331	0.2043	0.0340
$\mathbf{KwLL}$	829.5312	829.8570	834.1672	0.3173	0.0494
$\mathbf{TCWG}$	829.9953	830.3201	834.6335	0.3064	0.0435
$\mathbf{KwEBXII}$	831.6514	832.1432	837.4453	0.3244	0.0485
$\mathbf{BEBXII}$	841.2684	841.7644	855.5283	0.9515	0.1345
$\mathbf{GIG}$	839.8243	840.3163	854.0853	2.6188	0.4100
$\mathbf{BFr}$	842.9651	843.2924	854.3735	1.1218	0.1689
$\mathbf{ETGR}$	866.3500	866.6755	877.7588	2.3617	0.3980
$\mathbf{TMW}$	836.4555	836.7759	847.8586	0.1259	0.7609
$\mathbf{TAW}$	838.47833	838.9777	852.7390	0.1130	0.7030
$\mathbf{GTW}$	831.3475	831.8395	837.1411	0.3058	0.0469

We note from the results in Table 10 that the TIITLPL model gives the smallest values of AIC, CAIC, HQIC, A${}^{*}$, and W${}^{*}$ as compared to the other competitive models. Therefore, TIITLPL distribution provides the best fit for the cancer patient data.

Figure 8 plots the histogram and the estimated pdf of the TIITLPL distribution, the probability-probability (P-P) plot, and the estimated cdf and sf over the empirical cdf and sf, respectively, all showing nice fits for the TIITLPL distribution.

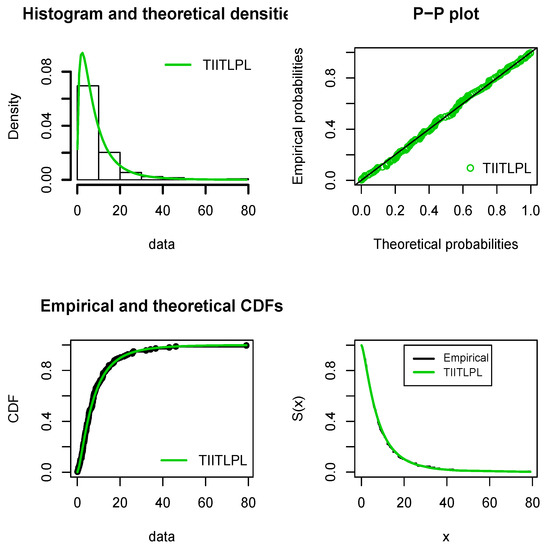
Figure 8. Several kinds of fits of the TIITLPL distribution for the cancer patient data.

As a last remark, for this dataset, we observe that the TIITLPL distribution outperforms the TPL distribution by [21] presented in the Introduction; if we compare Table 10 with ([21] Table 2), the AIC, CAIC, and HQIC are favorable for the TIITLPL distribution.

6. Final Remarks

Motivated by the high demand of data analysis in applied sciences, we introduce a new four-parameter lifetime distribution, called the TIITLPL distribution, having desirable properties in this regards. We study its main mathematical aspects, proving comprehensible results of independent interest. Then, the related model is explored by the use of the maximum likelihood method. Two concrete datasets are then analyzed, including the well-known aircraft windshield data. Fair comparisons are performed with modern and well-established adversary models, with favorable issues for the TIITLPL model. Thanks to its potentiality, we hope that the TIITLPL distribution will give satisfaction to researchers in various applied areas wishing a depth analysis of their lifetime data.