Hybrid Control Scheme for Projective Lag Synchronization of Riemann–Liouville Sense Fractional Order Memristive BAM NeuralNetworks with Mixed Delays

Abstract

This sequel is concerned with the analysis of projective lag synchronization of Riemann–Liouville sense fractional order memristive BAM neural networks (FOMBNNs) with mixed time delays via hybrid controller. Firstly, a new type of hybrid control scheme, which is the combination of open loop control and adaptive state feedback control is designed to guarantee the global projective lag synchronization of the addressed FOMBNNs model. Secondly, by using a Lyapunov–Krasovskii functional and Barbalet’s lemma, a new brand of sufficient criterion is proposed to ensure the projective lag synchronization of the FOMBNNs model considered. Moreover, as special cases by using a hybrid control scheme, some sufficient conditions are derived to ensure the global projective synchronization, global complete synchronization and global anti-synchronization for the FOMBNNs model considered. Finally, numerical simulations are provided to check the accuracy and validity of our obtained synchronization results.

1. Introduction

Differential equation and dynamic system modeling have become important research topics in natural science and engineering technology [1,2,3,4,5,6,7,8,9,10,11,12]. In 1695, the foundation of non-integer order calculus, which is a generalization integer order differential and integrals, was first of all discussed through Guillaume de Leibnitz and Gottfried Wilhelm Leibnitz, and its development were very gradual for long period [13,14,15,16]. However, during the last two decades, the study of fractional differential equations has been widely applicable to many real world problems. In fact, they have already been successfully applied in many fields of engineering including but not restricted to market dynamics [17], neural networks [18] and polarization [19]. In reality, many real-world objects need to be described with the aid of fractional order models due to the fact that dynamics of fractional-order models are more correct than integer-order models. From the application point of view, for the electronic implementation of bidirectional associative memory (BAM) neural network model, many of the researchers attempted to update the normal capacitor by fractional capacitor; then, it creates the fractional order BAM neural network (FOBNNs) models [20,21,22,23,24]. In addition to that, time delays can impose complexity and restrictions in neural networks and the existence may lead to instability, chaos, and oscillation [25,26,27,28,29,30,31,32,33,34]. At present, a huge amount of research works on the dynamic FOBNNs with time delays have been discussed. For example, in [20], the authors pointed out the global asymptotical stability criteria of fuzzy FOBNNs with delays and impulsive effects by Riemann–Liouville derivative, employing contraction mapping principle and fuzzy theory. In [21], the authors illustrate the global asymptotic stability issues of FOBNNs with delays and impulses via fractional order Barbalat’s lemma and Lyapunov-like function. Otherwise, during a particular period, the signal propagation is distributed because the variety of axon sizes and lengths are too large. In this manner, the attention of distributed delays is significant in fractional order neural networks (FONNs) dynamical systems, and there is a huge amount of research works on FONNs with distributed delay—see, for instance, [35,36]. In [20], the existence and Lyapunov-stability of impulsive hybrid FOBNNs with mixed delays were discussed by Zhang et al. and the sufficient conditions are derived to assure the stability condition of Hybrid FOBNNs with mixed time-delays via contraction mapping principle, integer order Lyapunov functional and periodically intermittent control.

In pattern recognition, optimization, and associative memory, memristors have the most crucial probable applications, which are introduced by Leon Chua in 1971 [37]. Chua’s paper in IEEE Transactions on Circuit theory in 1971 is considered to be the pioneering work in the corresponding subject of studies, after almost 40 years, for memristors to change from a definitely theoretic idea into workable usage. The Hewlett-Packard laboratory established the practically working memristor in 2008 [38]. In [39], Kim et al. successfully proposed memristor bridge synapse architecture and resolved the difficulty of the problem of nonvolatile synaptic weight garage and put in force recently proposed hardware learning techniques. After this, the memristor has discovered numerous applications in various interdisciplinary areas. The resistor is used to simulate the biological synapses of neural networks circuit implementation, and these biological synapses have the same characteristics as those of a memristor. Then, by replacing the resistor with a memristor in fractional order neural networks circuit implementation, the fractional order memristive neural networks (FOMNNs) can be formulated. Still now, via different approaches, many novel results on the dynamical analysis of FOMNNs time delays have been reported in [40,41,42,43].

The basic idea of chaos synchronization with different initial conditions was initially introduced by Pecora and Carroll in [44], and it has attracted great attention due to their successful applications such as artificial intelligence, image processing automatic control, associative memories, and secure communication. A few coupled structures can synchronize by themselves. However, others can’t attain synchronization by themselves. On this circumstance, we have applied some suitable controllers to practical fractional order neural networks system to make certain the corresponding asymptotic behavior and enhance system performance. During the recent years, various kinds of control techniques have been developed by many researchers, for instance, [34,45,46,47,48,49,50]. In [34], by using the adaptive control and linear delayed feedback control technique, the author discussed the synchronization of delayed FOMNNs with different orders. In [48], Wu et al. presented some new conditions on the projective synchronization in finite time of nonidentical neural networks with fractional order derivative by using sliding mode control theory. In [49], the sufficient conditions are derived to ensure the finite-time Mittag–Leffler synchronization of delayed FOMNNs with different orders by applying the Lyapunov-stability theory and a state feedback control. In Ref. [50], the authors addressed the lag synchronization for FOMNNs on the basis of period intermittent control, properties of Mittag–Leffler function and fractional inequality technique. Nevertheless, the synchronization of FOMBNNs via a hybrid control approach has not yet been investigated. Motivated by the above arguments, the main novelty of this research work is outlined in detail as follows:

• Based on the theory of differential inclusions and set valued map analysis, the drive-response synchronization error system is formulated.
• A novel hybrid controller, which is the combination of open loop control and adaptive state feedback control are designed to ensure the projective lag synchronization criteria for FOMBNNs with mixed time delays.
• Based on the designed hybrid controller and Barbalats lemma, the projective lag synchronization criteria for the drive-response models of the considered FOMBNNs are studied demonstrably.
• As a special case of complete synchronization, anti-synchronization and projective synchronization of FMNNs is also investigated. Hence, Corollary 3 is new and these results has not been seen in any of the literature.
• In contrast to the existing results in the literature, the hybrid control BAM type neural networks and mixed time delays have not taken into consideration; however, our proposed results make it up.

2. Preliminaries and Problem Statement

Notations. In this work, N signifies the space of natural numbers from 1 to n, $R^n$ stands for the space of n-D Euclidean space, respectively. $R^{m\times n}$ stands for the set of all $m\times n$ real matrices. For $z\left(t\right)={(z_1\left(t\right),\dots ,z_n\left(t\right))}^T\in R^n$, we denote

$$\begin{array}{c}\hfill \parallel z\left(t\right)\parallel =\sum _{i=1}^n\mathrm{\left|}{z}_i\left(t\right)\mathrm{\right|}.\end{array}$$

The sign function $sign\left(z\right)$ is described by

$$\begin{array}{c}\hfill sign\left(z\right)=\left\{\begin{array}{c}1,z>0,\hfill \\ 0,z=0,\hfill \\ -1,z<0.\hfill \end{array}\right.\end{array}$$

Let $C\left([-\omega ,0],R^n\right)$ describe the family of Banach space, which consists of 1-order continuous function maps from $[-\omega ,0]$ into $R^n$. $D^q$ denotes the Riemann–Liouville derivative operator with $0<q<1$. $\mathcal{K}\left[L\right]$ signifies the closure of the convex hull of set L.

In this section, we will first recall some basic definitions and important properties in fractional order calculus.

Definition 1.

The Riemann–Liouville fractional integral of $z\left(t\right)$ is described as [15]:

$$\begin{array}{c}\hfill D^{-q}z\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(q\right)}{\int }_0^t{(t-\gamma )}^{q-1}z\left(\gamma \right)\mathrm{d}\gamma ,\end{array}$$

where $q\in R^{+}$.

Definition 2.

The Caputo-type fractional derivative of $z\left(t\right)$ is described as [15]:

$$\begin{array}{c}{D}^{q}z\left(t\right)=\left\{\begin{array}{cc}{D}^{-(n-q)}\left(\frac{d^n}{d{t}^n}z\left(t\right)\right),\hfill & ifq\in (n-1,n),\hfill \\ \left(\frac{d^n}{d{t}^n}z\left(t\right)\right),\hfill & ifq=n,\hfill \end{array}\right.\hfill \end{array}$$

where $q\in R^{+},n\in Z^{+}$.

Definition 3.

The Riemann–Liouville fractional derivative of $z\left(t\right)$ is described as [15]:

$$\begin{array}{ccc}{D}^{q}z\left(t\right)\hfill & =& \frac{d^n}{d{t}^n}[D^{(n-q)}z\left(t\right)]\hfill \\ & =& \frac{1}{\mathsf{\Gamma }(n-\alpha )}\frac{d^n}{d{t}^n}{\int }_0^t{(t-\gamma )}^{n-1-\alpha }z\left(\gamma \right)d\gamma ,\hfill \end{array}$$

where $0\le n-1\le q<n,n\in Z^{+}$.

Lemma 1.

Let $p>0,q>0,$ and $x\left(t\right),z\left(t\right)\in C^1[0,b].$ The following properties hold [15]:

(1) 

$D^p{D}^{-q}x\left(t\right)=D^{p-q}x\left(t\right)$;

(2) 

$D^p{D}^{-p}x\left(t\right)=x\left(t\right)$;

(3) 

$D^p(x\left(t\right)\pm z\left(t\right))=D^{p}x\left(t\right)\pm D^{p}z\left(t\right)$.

Lemma 2.

Function $\xi \left(t\right)$ is defined on the interval $[0,+\infty )$, if function $\xi \left(t\right)$ is uniformly continuous and ${\int }_0^{+\infty }\xi \left(\tau \right)d\tau$ exists and is bounded, then ${lim}_{t\to +\infty }\xi \left(t\right)=0$ [51].

Motivated by the descriptions in the section above, in this work, we will firstly establish the model of FOMBNNs that can be represented as below:

$$\begin{array}{ccc}{D}^q{y}_i\left(t\right)\hfill & =& -a_i{y}_i\left(t\right)+\sum _{j=1}^m\left[b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j\left(t\right)\right)+\sum _{j=1}^m\left[c_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{j=1}^m\left[d_{ji}\left(y_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds+J_i,t\ge 0,\hfill \\ \hfill D^q{z}_j\left(t\right)& =& -u_j{z}_j\left(t\right)+\sum _{i=1}^n\left[v_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i\left(t\right)\right)+\sum _{i=1}^n\left[w_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{i=1}^n\left[x_{ij}\left(z_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds+H_j,t\ge 0,\hfill \end{array}$$

(1)

where $i\in \{1,2,\dots ,n\}$ and $j\in \{1,2,\dots ,m\}$. Let $y\left(t\right)={(y_1\left(t\right),y_2\left(t\right),\dots ,y_n\left(t\right))}^T\in R^n$ and $z\left(t\right)={(z_1\left(t\right),z_2\left(t\right),\dots ,z_m\left(t\right))}^T\in R^m$ stands for the neural state vector at time t. $a_i>0$ and $u_j>0$ signifies the weight of self feedback connection. $f\left(z\left(t\right)\right)=\left(\right(f_1\left(z_1\left(t\right)\right),\dots ,{\left(f_m\left(z_m\left(t\right)\right)\right)}^T\in R^m$ and $g\left(y\left(t\right)\right)=\left(\right(g_1\left(y_1\left(t\right)\right),\dots ,{\left(g_n\left(y_n\left(t\right)\right)\right)}^T\in R^n$ represents the activation function of the neurons. $J_i$ and $H_j$ denotes external inputs outside the system and $\rho \left(t\right)>0$ corresponds to the transmission discrete delays and satisfies $0<\rho \left(t\right)\le \rho$, $\dot{\rho }\left(t\right)\le \sigma <1$, $\rho$ is constant, while $r\left(t\right)$ signifies the distributed time-varying delays, which is continuous function and satisfies $0<r\left(t\right)\le r$, r is positive constant. The memristor connection weights are defined by

$$\begin{array}{c}\hfill b_{ji}\left(y_i\left(t\right)\right)=\left\{\begin{array}{c}{b}_{ji}^{\star },\mathrm{\left|}{y}_i\left(t\right)\mathrm{\right|}\le T_i\hfill \\ b_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.c_{ji}\left(y_i\left(t\right)\right)=\left\{\begin{array}{c}{c}_{ji}^{\star },{\left|}{y}_i\left(t\right){\right|}\le T_i\hfill \\ c_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill d_{ji}\left(y_i\left(t\right)\right)=\left\{\begin{array}{c}{d}_{ji}^{\star },{\left|}{y}_i\left(t\right){\right|}\le T_i\hfill \\ d_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.v_{ij}\left(z_j\left(t\right)\right)=\left\{\begin{array}{c}{v}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ v_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}{w}_{ij}\left(z_j\left(t\right)\right)=\left\{\begin{array}{c}{w}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ w_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.x_{ij}\left(z_j\left(t\right)\right)=\left\{\begin{array}{c}{x}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ x_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\hfill \end{array}$$

in which switching jumps $T_i$, ${\tilde{T}}_j>0,b_{ji}^{\star },c_{ji}^{\star },d_{ji}^{\star },v_{ij}^{\star },w_{ij}^{\star },x_{ij}^{\star },b_{ji}^{\star \star },c_{ji}^{\star \star },d_{ji}^{\star \star },v_{ij}^{\star \star },w_{ij}^{\star \star }$ and $x_{ij}^{\star \star }$ are known positive constants.

According to set-valued map theory and differential inclusion analysis [52,53], FOMBNNs (1) can be written as follows:

$$\begin{array}{ccc}{D}^q{y}_i\left(t\right)\hfill & \in & -a_i{y}_i\left(t\right)+\sum _{j=1}^m\left[\mathcal{K}\left(b_{ji}\left(y_i\left(t\right)\right)\right)\right]f_j\left(z_j\left(t\right)\right)+\sum _{j=1}^m\left[\mathcal{K}\left(c_{ji}\left(y_i\left(t\right)\right)\right)\right]f_j\left(z_j(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{j=1}^m\left[\mathcal{K}\left(d_{ji}\left(y_i\left(t\right)\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds+J_i,t\ge 0\hfill \\ D^q{z}_j\left(t\right)\hfill & \in & -u_j{z}_j\left(t\right)+\sum _{i=1}^n\left[\mathcal{K}\left(v_{ij}\left(z_j\left(t\right)\right)\right)\right]g_i\left(y_i\left(t\right)\right)+\sum _{i=1}^n\left[\mathcal{K}\left(w_{ij}\left(z_j\left(t\right)\right)\right)\right]g_i\left(y_i(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{i=1}^n\left[\mathcal{K}\left(x_{ij}\left(z_j\left(t\right)\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds+H_j,t\ge 0.\hfill \end{array}$$

(2)

We define

$$\begin{array}{c}\mathcal{K}\left[b_{ji}\left(y_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{b}_{ji}^{\star },{\left|}{y}_i\left(t\right){\right|}\le T_i\hfill \\ [{\underline{b}}_{ji},{\overline{b}}_{ji}],{\left|}{y}_i\left(t\right){\right|}=T_i\hfill \\ b_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.\mathcal{K}\left[c_{ji}\left(y_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{c}_{ji}^{\star },{\left|}{y}_i\left(t\right){\right|}\le T_i\hfill \\ [{\underline{c}}_{ji},{\overline{c}}_{ji}],{\left|}{y}_i\left(t\right){\right|}=T_i\hfill \\ c_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}\mathcal{K}\left[d_{ji}\left(y_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{d}_{ji}^{\star },{\left|}{y}_i\left(t\right){\right|}\le T_i\hfill \\ [{\underline{d}}_{ji},{\overline{d}}_{ji}],{\left|}{y}_i\left(t\right){\right|}=T_i\hfill \\ d_{ji}^{\star \star },{\left|}{y}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.\mathcal{K}\left[v_{ij}\left(z_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{v}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{v}}_{ij},{\overline{v}}_{ij}],{\left|}{z}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ v_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}\mathcal{K}\left[w_{ij}\left(z_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{w}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{w}}_{ij},{\overline{w}}_{ij}],{\left|}{z}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ w_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\mathcal{K}\left[x_{ij}\left(z_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{x}_{ij}^{\star },{\left|}{z}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{x}}_{ij},{\overline{x}}_{ij}],{\left|}{z}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ x_{ij}^{\star \star },{\left|}{z}_j\left(t\right){\right|}>{\tilde{T}}_j.\hfill \end{array}\right.\hfill \end{array}$$

In this work, we define ${\underline{b}}_{ji}=min\{b_{ji}^{\star },b_{ji}^{\star \star }\},{\overline{b}}_{ji}=max\{b_{ji}^{\star },b_{ji}^{\star \star }\},{\underline{c}}_{ji}=min\{c_{ji}^{\star },c_{ji}^{\star \star }\},{\overline{c}}_{ji}=max\{c_{ji}^{\star },c_{ji}^{\star \star }\},{\underline{d}}_{ji}=min\{d_{ji}^{\star },d_{ji}^{\star \star }\},{\overline{d}}_{ji}=max\{d_{ji}^{\star },d_{ji}^{\star \star }\},{\underline{v}}_{ij}=min\{v_{ij}^{\star },v_{ij}^{\star \star }\},{\overline{v}}_{ij}=max\{v_{ij}^{\star },v_{ij}^{\star \star }\},{\underline{w}}_{ij}=min\{w_{ij}^{\star },w_{ij}^{\star \star }\},{\overline{w}}_{ij}=max\{w_{ij}^{\star },w_{ij}^{\star \star }\},{\overline{x}}_{ij}=max\{x_{ij}^{\star },x_{ij}^{\star \star }\},{\underline{x}}_{ij}=min\{x_{ij}^{\star },x_{ij}^{\star \star }\}.$

Then, there exist ${\widehat{b}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(b_{ji}\left(y_i\left(t\right)\right)\right)\right]$, ${\widehat{c}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(c_{ji}\left(y_i\left(t\right)\right)\right)\right],$ ${\widehat{d}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(d_{ji}\left(y_i\left(t\right)\right)\right)\right]$, ${\widehat{v}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(v_{ij}\left(z_j\left(t\right)\right)\right)\right]$, ${\widehat{w}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(w_{ij}\left(z_j\left(t\right)\right)\right)\right]$ and ${\widehat{x}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(x_{ij}\left(z_j\left(t\right)\right)\right)\right]$, the measurable function such that

$$\begin{array}{ccc}{D}^q{y}_i\left(t\right)\hfill & =& -a_i{y}_i\left(t\right)+\sum _{j=1}^m{\widehat{b}}_{ji}\left(t\right)f_j\left(z_j\left(t\right)\right)+\sum _{j=1}^m{\widehat{c}}_{ji}\left(t\right)f_j\left(z_j(t-\rho \left(t\right))\right)+\sum _{j=1}^m{\widehat{d}}_{ji}\left(t\right){\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds\hfill \\ & & +J_i,t\ge 0\hfill \\ D^q{z}_j\left(t\right)\hfill & =& -u_j{z}_j\left(t\right)+\sum _{i=1}^n{\widehat{v}}_{ij}\left(t\right)g_i\left(y_i\left(t\right)\right)+\sum _{i=1}^n{\widehat{w}}_{ij}\left(t\right)g_i\left(y_i(t-\rho \left(t\right))\right)+\sum _{i=1}^n{\widehat{x}}_{ij}\left(t\right){\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds\hfill \\ & & +H_j,t\ge 0.\hfill \end{array}$$

(3)

Consider FOMBNNs (1) as a drive system, the response system is given by

$$\begin{array}{ccc}{D}^q{\tilde{y}}_i\left(t\right)\hfill & =& -a_i{\tilde{y}}_i\left(t\right)+\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]f_j\left({\tilde{z}}_j\left(t\right)\right)+\sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]f_j\left({\tilde{z}}_j(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left({\tilde{z}}_j\left(s\right)\right)ds+J_i+{\zeta }_i\left(t\right),t\ge 0\hfill \\ D^q{\tilde{z}}_j\left(t\right)\hfill & =& -u_j{\tilde{z}}_j\left(t\right)+\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]g_i\left({\tilde{y}}_i\left(t\right)\right)+\sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]g_i\left({\tilde{y}}_i(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left({\tilde{y}}_i\left(s\right)\right)ds+H_j+{\varsigma }_j\left(t\right)t\ge 0.\hfill \end{array}$$

(4)

for $i\in \{1,2,\dots ,n\}$ and $j\in \{1,2,\dots ,m\}$, where ${\zeta }_i\left(t\right)$ and ${\varsigma }_j\left(t\right)$ denotes the hybrid control. Let $\tilde{y}\left(t\right)={({\tilde{y}}_1\left(t\right),{\tilde{y}}_2\left(t\right),\dots ,{\tilde{y}}_n\left(t\right))}^T\in R^n$ and $\tilde{z}\left(t\right)={({\tilde{z}}_1\left(t\right),{\tilde{z}}_2\left(t\right),\dots ,{\tilde{z}}_m\left(t\right))}^T\in R^m$ is the neuron state vector of the response system (4), the parameters can be defined as

$$\begin{array}{c}{b}_{ji}\left({\tilde{y}}_i\left(t\right)\right)=\left\{\begin{array}{c}{b}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le T_i\hfill \\ b_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.c_{ji}\left({\tilde{y}}_i\left(t\right)\right)=\left\{\begin{array}{c}{c}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le T_i\hfill \\ c_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}{d}_{ji}\left({\tilde{y}}_i\left(t\right)\right)=\left\{\begin{array}{c}{d}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le T_i\hfill \\ d_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>T_i,\hfill \end{array}\right.v_{ij}\left({\tilde{z}}_j\left(t\right)\right)=\left\{\begin{array}{c}{v}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ v_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}{w}_{ij}\left({\tilde{z}}_j\left(t\right)\right)=\left\{\begin{array}{c}{w}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ w_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.x_{ij}\left({\tilde{z}}_j\left(t\right)\right)=\left\{\begin{array}{c}{x}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ x_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j.\hfill \end{array}\right.\hfill \end{array}$$

By using differential inclusion of response system FOMBNNs (5), in the sense of Filippov, it follows that

$$\begin{array}{ccc}{D}^q{\tilde{y}}_i\left(t\right)\hfill & \in & -a_i{\tilde{y}}_i\left(t\right)+\sum _{j=1}^m\left[\mathcal{K}\left(b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right]f_j\left({\tilde{z}}_j\left(t\right)\right)+\sum _{j=1}^m\left[\mathcal{K}\left(c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right]f_j\left({\tilde{z}}_j(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{j=1}^m\left[\mathcal{K}\left(d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left({\tilde{z}}_j\left(s\right)\right)ds+J_i+{\zeta }_i\left(t\right),t\ge 0\hfill \end{array}$$

$$\begin{array}{ccc}{D}^q{\tilde{z}}_j\left(t\right)\hfill & \in & -u_j{\tilde{z}}_j\left(t\right)+\sum _{i=1}^n\left[\mathcal{K}\left(v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right]g_i\left({\tilde{y}}_i\left(t\right)\right)+\sum _{i=1}^n\left[\mathcal{K}\left(w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right]g_i\left({\tilde{y}}_i(t-\rho \left(t\right))\right)\hfill \\ & & +\sum _{i=1}^n\left[\mathcal{K}\left(x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left({\tilde{y}}_i\left(s\right)\right)ds+H_j+{\varsigma }_j\left(t\right),t\ge 0.\hfill \end{array}$$

(5)

We define

$$\begin{array}{c}\mathcal{K}\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{b}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{b}}_{ji},{\overline{b}}_{ji}],{\left|}{\tilde{y}}_i\left(t\right){\right|}={\tilde{T}}_j\hfill \\ b_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\mathcal{K}\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{c}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{c}}_{ji},{\overline{c}}_{ji}],{\left|}{\tilde{y}}_i\left(t\right){\right|}={\tilde{T}}_j\hfill \\ c_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}\mathcal{K}\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]=\left\{\begin{array}{c}{d}_{ji}^{\star },{\left|}{\tilde{y}}_i\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{d}}_{ji},{\overline{d}}_{ji}],{\left|}{\tilde{y}}_i\left(t\right){\right|}={\tilde{T}}_j\hfill \\ d_{ji}^{\star \star },{\left|}{\tilde{y}}_i\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\mathcal{K}\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{v}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{v}}_{ij},{\overline{v}}_{ij}],{\left|}{\tilde{z}}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ v_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{c}\mathcal{K}\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{w}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{w}}_{ij},{\overline{w}}_{ij}],{\left|}{\tilde{z}}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ w_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j,\hfill \end{array}\right.\mathcal{K}\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]=\left\{\begin{array}{c}{x}_{ij}^{\star },{\left|}{\tilde{z}}_j\left(t\right){\right|}\le {\tilde{T}}_j\hfill \\ [{\underline{x}}_{ij},{\overline{x}}_{ij}],{\left|}{\tilde{z}}_j\left(t\right){\right|}={\tilde{T}}_j\hfill \\ x_{ij}^{\star \star },{\left|}{\tilde{z}}_j\left(t\right){\right|}>{\tilde{T}}_j.\hfill \end{array}\right.\hfill \end{array}$$

Then, there exist ${\check{b}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right]$, ${\check{c}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right]$ ${\check{d}}_{ji}\left(t\right)\in \left[\mathcal{K}\left(d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right)\right],$${\check{v}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right]$, ${\check{w}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right],$ and ${\check{x}}_{ij}\left(t\right)\in \left[\mathcal{K}\left(x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right)\right]$ the measurable function such that

$$\begin{array}{ccc}{D}^q{\tilde{y}}_i\left(t\right)\hfill & =& -a_i{\tilde{y}}_i\left(t\right)+\sum _{j=1}^m{\check{b}}_{ji}\left(t\right)f_j\left({\tilde{z}}_j\left(t\right)\right)+\sum _{j=1}^m{\check{c}}_{ji}\left(t\right)f_j\left({\tilde{z}}_j(t-\rho \left(t\right))\right)+\sum _{j=1}^m{\check{d}}_{ji}\left(t\right){\int }_{t-r\left(t\right)}^t{f}_j\left({\tilde{z}}_j\left(s\right)\right)ds\hfill \\ & & +J_i+{\zeta }_i\left(t\right),t\ge 0,\hfill \\ D^q{\tilde{z}}_j\left(t\right)\hfill & =& -u_j{\tilde{z}}_j\left(t\right)+\sum _{i=1}^n{\check{v}}_{ij}\left(t\right)g_i\left({\tilde{y}}_i\left(t\right)\right)+\sum _{i=1}^n{\check{w}}_{ij}\left(t\right)g_i\left({\tilde{y}}_i(t-\rho \left(t\right))\right)+\sum _{i=1}^n{\check{x}}_{ij}\left(t\right){\int }_{t-r\left(t\right)}^t{g}_i\left({\tilde{y}}_i\left(s\right)\right)ds\hfill \\ & & +H_j+{\varsigma }_j\left(t\right),t\ge 0.\hfill \end{array}$$

(6)

The initial values of drive-response systems are defined as follows $y_i\left(s\right)={\widehat{\sigma }}_i\left(s\right),z_j\left(s\right)={\widehat{\varrho }}_j\left(s\right),{\tilde{y}}_i\left(s\right)={\tilde{\sigma }}_i\left(s\right),{\tilde{z}}_j\left(s\right)={\tilde{\varrho }}_j\left(s\right),$ respectively, $s\in [-\omega ,0],{\widehat{\sigma }}_i\left(s\right),{\widehat{\varrho }}_j\left(s\right),{\tilde{\sigma }}_i\left(s\right),{\tilde{\varrho }}_j\left(s\right)\in C\left([-\omega ,0],R\right)$, where $\omega =max\{\rho ,r\}fori=1,2,\dots ,n,j=1,2,\dots ,m.$

Before ending this section, we introduce projective lag synchronization definition, which will play important roles in the proof of our main theorem below.

Definition 4.

If there exists a positive constants $\lambda ,\tau \in R$, such that for any solutions of FOMBNNs (1) and (4) with different initial values, one can obtain

$$\begin{array}{c}\underset{t\to \infty }{lim}\sum _{i=1}^n{|}{\tilde{y}}_i\left(t\right)-\lambda y_i(t-\tau ){|}+\underset{t\to \infty }{lim}\sum _{j=1}^m\left|{\right|}{\tilde{z}}_j\left(t\right)-\lambda z_j(t-\tau ){|}=0,\hfill \end{array}$$

then (1) and (4) can realize global projective lag synchronization, where λ is the projective coefficient and τ is the projective transmittal delay.

Remark 1.

If $\tau =0$, systems (1) and (4) can realize global projective synchronization. If $\tau =0,\lambda =1$, the (1) and (4) can realize global complete asymptotical synchronization. if $\tau =0,\lambda =-1$, systems (1) and (4) can realize anti-synchronization.

Remark 2.

If $\lambda =0$, the inequality in above Definition 4 is reduced into the following form:

$$\begin{array}{c}\underset{t\to \infty }{lim}\sum _{i=1}^n{\left|}{\tilde{y}}_i\left(t\right){\right|}+\underset{t\to \infty }{lim}\sum _{j=1}^m{\left|}{\tilde{z}}_j\left(t\right){\right|}=0.\hfill \end{array}$$

In this situation, the FOMBNNs (1) is said to be global asymptotical stabilized to the origin.

$\mathbf{Assumption}\left(\mathcal{H}\right).$ The nonlinear activation function $f_j$ and $g_i$ satisfies the Lipschitz-continuous if there exists constants $L_i>0$ and ${\tilde{L}}_j>0$ such that

$$\begin{array}{ccc}{|}{g}_i\left(\tilde{y}\right)-g_i\left(y\right){|}\hfill & \le & L_i{|}\tilde{y}-y{|}\hfill \\ {|}{f}_j\left(\tilde{z}\right)-f_j\left(z\right){|}\hfill & \le & {\tilde{L}}_j{|}\tilde{z}-z{|},\hfill \end{array}$$

for all $y,z,\tilde{y},\tilde{z}\in R$ and $i=1,2,\dots ,n,j=1,2,\dots ,m.$

3. Main Results

In this section, by using the suitable Lyapunov-function, some sufficient conditions are derived to ensure the global projective lag synchronization via hybrid control schemes, and we will derive to guarantee the several synchronization criteria for things such as drive-response systems.

Let ${\alpha }_i\left(t\right)={\tilde{y}}_i\left(t\right)-\lambda y_i(t-\tau )$, ${\beta }_j\left(t\right)={\tilde{z}}_j\left(t\right)-\lambda z_j(t-\tau )$ and a hybrid controller is designed as

$$\begin{array}{c}{\zeta }_i\left(t\right)={\widehat{\zeta }}_i\left(t\right)+{\check{\zeta }}_i\left(t\right)and{\varsigma }_j\left(t\right)={\widehat{\varsigma }}_j\left(t\right)+{\check{\varsigma }}_j\left(t\right),\hfill \end{array}$$

(7)

where

$$\begin{array}{ccc}{\widehat{\zeta }}_i\left(t\right)\hfill & =& -\lambda \sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)-b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\tau )\right)-\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[(f_j\left(\lambda z_j(t-\tau )\right)-\lambda \left(f_j{z}_j(t-\tau )\right)\right]\hfill \\ & & -\lambda \sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)-c_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\tau -\rho (t-\tau ))\right)-\sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right][f_j\left(\lambda z_j\right(t-\tau \hfill \\ & & -\rho (t-\tau )\left)\right)-\lambda \left(f_j\left(z_j(t-\tau -\rho (t-\tau ))\right)\right)]-\lambda \sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)-d_{ji}\left(y_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left(z_j(s-\tau )\right)ds\hfill \\ & & -\sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t\left[f_j(\lambda z_j(s-\tau )-\lambda \left(f_j{z}_j(s-\tau )\right)\right]ds+(\lambda -1)J_i,\hfill \\ {\check{\zeta }}_i\left(t\right)\hfill & =& -{\eta }_i\left(t\right){\alpha }_i\left(t\right),{\dot{\eta }}_i\left(t\right)=\frac{-{\kappa }_i{\theta }_i{\left|}{\alpha }_i\left(t\right){\right|}}{{\eta }_i\left(t\right)}+{\kappa }_i{\left|}{\alpha }_i\left(t\right){\right|}\hfill \end{array}$$

and

$$\begin{array}{ccc}{\widehat{\varsigma }}_j\left(t\right)\hfill & =& -\lambda \sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)-v_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\tau )\right)-\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i(t-\tau )\right)-\lambda \left(g_i{y}_i(t-\tau )\right)\right]\hfill \\ & & -\lambda \sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)-w_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\tau -\rho (t-\tau ))\right)-\sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right][g_i\left(\lambda y_i\right(t-\tau \hfill \\ & & -\rho (t-\tau )\left)\right)-\lambda \left(g_i\left(y_i(t-\tau -\rho (t-\tau ))\right)\right)]-\lambda \sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)-x_{ij}\left(z_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left(y_i(s-\tau )\right)ds\hfill \\ & & -\sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t\left[g_i\left(\lambda y_i(s-\tau )\right)-\lambda \left(g_i{y}_i(s-\tau )\right)\right]ds+(\lambda -1)H_j,\hfill \\ {\check{\varsigma }}_j\left(t\right)\hfill & =& -{\mu }_j\left(t\right){\beta }_j\left(t\right),{\dot{\mu }}_j\left(t\right)=\frac{-{\iota }_j{\delta }_j{\left|}{\beta }_j\left(t\right){\right|}}{{\mu }_j\left(t\right)}+{\iota }_j{\left|}{\beta }_j\left(t\right){\right|},\hfill \end{array}$$

where ${\kappa }_i,{\theta }_i,{\xi }_i,{\iota }_j,{\delta }_j$ and ${\gamma }_j$ are the positive constants, ${\eta }_i\left(t\right)$ and ${\mu }_j\left(t\right)$ stands for the adaptive coupling strengths. Based on the hybrid controller scheme (7), combining Equations (2) and (5), then the synchronization error system can be obtained as follows:

$$\begin{array}{ccc}{D}^q{\alpha }_i\left(t\right)\hfill & \in & -a_i{\alpha }_i\left(t\right)+\sum _{j=1}^m\mathcal{K}\left[b_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]\left[f_j({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))-f_j\left(\lambda z_j(t-\tau )\right)\right]\hfill \\ & & +\sum _{j=1}^m\mathcal{K}\left[c_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right][f_j({\beta }_j(t-\rho \left(t\right))+\lambda z_j(t-\tau -\rho (t-\tau )))-f_j\left(\lambda z_j\right(t-\tau \hfill \\ & & -\rho (t-\tau )\left)\right)]+\sum _{j=1}^m\mathcal{K}\left[d_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]{\int }_{t-r\left(t\right)}^t[f_j({\beta }_j\left(s\right)+\lambda z_j(s-\tau ))\hfill \\ & & -f_j\left(\lambda z_j(s-\tau )\right)]ds-{\eta }_i\left(t\right){\alpha }_i\left(t\right),t\ge 0,\hfill \\ D^q{\beta }_j\left(t\right)\hfill & \in & -u_j{\tilde{z}}_j\left(t\right)+\sum _{i=1}^n\mathcal{K}\left[v_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]\left[g_i({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))-g_i\left(\lambda y_i(t-\tau )\right)\right]\hfill \\ & & +\sum _{i=1}^n\mathcal{K}\left[w_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right][g_i({\alpha }_i(t-\rho \left(t\right))+\lambda y_i(t-\tau -\rho (t-\tau )))-g_i\left(\lambda y_i\right(t-\tau \hfill \\ & & -\rho (t-\tau )\left)\right)]+\sum _{i=1}^n\mathcal{K}\left[x_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]{\int }_{t-r\left(t\right)}^t[g_i({\alpha }_i\left(s\right)+\lambda y_i(s-\tau ))\hfill \\ & & -g_i\left(\lambda y_i(s-\tau )\right)]ds-{\mu }_j\left(t\right){\beta }_j\left(t\right),t\ge 0.\hfill \end{array}$$

or ${\check{b}}_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\in \mathcal{K}\left[b_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]$, ${\check{c}}_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\in \mathcal{K}\left[c_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]$, ${\check{d}}_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\in \mathcal{K}\left[d_{ji}({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]$, ${\check{v}}_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\in \mathcal{K}\left[v_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]$, ${\check{w}}_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\in \mathcal{K}\left[w_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]$ and ${\check{x}}_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\in \mathcal{K}\left[x_{ij}({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]$ exist such that

$$\begin{array}{ccc}{D}^q{\alpha }_i\left(t\right)\hfill & =& -(a_i+{\eta }_i\left(t\right)){\alpha }_i\left(t\right)+\sum _{j=1}^m{\check{b}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]\left[f_j({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))-f_j\left(\lambda z_j(t-\tau )\right)\right]\hfill \\ & & +\sum _{j=1}^m{\check{c}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right][f_j({\beta }_j(t-\rho \left(t\right))+\lambda z_j(t-\tau -\rho (t-\tau )))-f_j(\lambda z_j(t-\tau -\rho (t\hfill \\ & & -\tau \left)\right)\left)\right]+\sum _{j=1}^m{\check{d}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]{\int }_{t-r\left(t\right)}^t\left[f_j({\beta }_j\left(s\right)+\lambda z_j(s-\tau ))-f_j\left(\lambda z_j(s-\tau )\right)\right]ds\hfill \end{array}$$

(8)

and

$$\begin{array}{ccc}{D}^q{\beta }_j\left(t\right)\hfill & =& -(u_j+{\mu }_j\left(t\right)){\beta }_j\left(t\right)+\sum _{i=1}^n{\check{v}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]\left[g_i({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))-g_i\left(\lambda y_i(t-\tau )\right)\right]\hfill \\ & & +\sum _{i=1}^n{\check{w}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right][g_i({\alpha }_i(t-\rho \left(t\right))+\lambda y_i(t-\tau -\rho (t-\tau )))-g_i(\lambda y_i(t-\tau -\rho (t\hfill \\ & & -\tau \left)\right)\left)\right]+\sum _{i=1}^n{\check{x}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]{\int }_{t-r\left(t\right)}^t\left[g_i({\alpha }_i\left(s\right)+\lambda y_i(s-\tau ))-g_i\left(\lambda y_i(s-\tau )\right)\right]ds.\hfill \end{array}$$

(9)

Theorem 1.

Suppose that Assumptions $\left[\mathcal{H}\right]$ hold, then drive system (1) and response system (4) are globally projective lag synchronized via hybrid controller (7) if the following conditions hold:

$$\begin{array}{cc}{\Omega }_1=\hfill & \underset{1\le i\le n}{min}\left\{a_i+{\theta }_i-\sum _{j=1}^m\left({\mathbb{V}}_{ij}+\frac{{\mathbb{W}}_{ij}}{1-\sigma }+\rho {\mathbb{X}}_{ij}\right)L_i\right\}>0,\\ {\mathsf{\Theta }}_2=\hfill & \underset{1\le j\le m}{min}\left\{u_j+{\delta }_j-\sum _{i=1}^n\left({\mathbb{B}}_{ji}+\frac{{\mathbb{C}}_{ji}}{1-\sigma }+\rho {\mathbb{D}}_{ji}\right){\tilde{L}}_j\right\}>0.\end{array}$$

Here, ${\mathbb{B}}_{ji}=max\left\{{\right|}{b}_{ji}^{\star }{|},{|}{b}_{ji}^{\star \star }{\left|}\right\},{\mathbb{C}}_{ji}=max\left\{{\right|}{c}_{ji}^{\star }{|},{|}{c}_{ji}^{\star \star }{\left|}\right\},{\mathbb{D}}_{ji}=max\left\{{\right|}{d}_{ji}^{\star }{|},{|}{d}_{ji}^{\star \star }{\left|}\right\},{\mathbb{V}}_{ij}=max\left\{{\right|}{v}_{ij}^{\star }{|},{|}{v}_{ij}^{\star \star }{\left|}\right\},{\mathbb{W}}_{ij}=max\left\{{\right|}{w}_{ij}^{\star }{|},{|}{w}_{ij}^{\star \star }{\left|}\right\}$ and ${\mathbb{X}}_{ij}=max\left\{{\right|}{x}_{ij}^{\star }{|},{|}{x}_{ij}^{\star \star }{\left|}\right\},$ while ${\theta }_i>0$ and ${\delta }_j>0$ denote constants.

Proof. 

Consider the following Lyapunov-like functional

$$\begin{array}{c}V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right),\hfill \end{array}$$

(10)

where

$$\begin{array}{ccc}{V}_1\left(t\right)\hfill & =& D^{-(1-q)}\left(\sum _{i=1}^n|{\alpha }_i\left(t\right)|+\sum _{j=1}^m|{\beta }_j\left(t\right)|\right),\hfill \\ V_2\left(t\right)\hfill & =& \sum _{i=1}^n\frac{1}{2{\kappa }_i}{\eta }_i{\left(t\right)}^2+\sum _{j=1}^m\frac{1}{2{\iota }_j}{\mu }_j{\left(t\right)}^2,\hfill \\ V_3\left(t\right)\hfill & =& \sum _{j=1}^m\sum _{i=1}^n{\mathbb{C}}_{ji}{\tilde{L}}_j{\int }_{t-\tau \left(t\right)}^t|{\beta }_j\left(s\right)|\mathrm{d}s+\sum _{j=1}^m\sum _{i=1}^n{\mathbb{D}}_{ji}{\tilde{L}}_j{\int }_{-\rho \left(t\right)}^0{\int }_{t+s}^t|{\beta }_j\left(s\right)|\mathrm{d}s\hfill \\ & & +\sum _{i=1}^n\sum _{j=1}^m{\mathbb{W}}_{ij}{L}_i{\int }_{t-\tau \left(t\right)}^t|{\alpha }_i\left(s\right)|\mathrm{d}s+\sum _{i=1}^n\sum _{j=1}^m{\mathbb{X}}_{ij}{L}_i{\int }_{-\rho \left(t\right)}^0{\int }_{t+s}^t|{\alpha }_i\left(s\right)|\mathrm{d}s.\hfill \end{array}$$

Then, by applying the Riemann–Liouville derivative for Lyapunov functional (10), one has

$$\begin{array}{c}\dot{V}\left(t\right)={\dot{V}}_1\left(t\right)+{\dot{V}}_2\left(t\right)+{\dot{V}}_3\left(t\right),\hfill \end{array}$$

(11)

where

$$\begin{array}{ccc}{\dot{V}}_1\left(t\right)\hfill & =& D^q\left[\sum _{i=1}^n|{\alpha }_i\left(t\right)|+\sum _{j=1}^m|{\beta }_j\left(t\right)|\right]\hfill \\ & \le & \sum _{i=1}^{n}sgn\left({\alpha }_i\left(t\right)\right)D^q{\alpha }_i\left(t\right)+\sum _{j=1}^{m}sgn\left({\beta }_j\left(t\right)\right)D^q{\beta }_j\left(t\right)\hfill \\ & \le & \sum _{i=1}^{n}sgn\left({\alpha }_i\left(t\right)\right)\{-(a_i+{\eta }_i\left(t\right)){\alpha }_i\left(t\right)+\sum _{j=1}^m{\check{b}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right][f_j({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\hfill \\ & & -f_j\left(\lambda z_j(t-\tau )\right)]+\sum _{j=1}^m{\check{c}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right][f_j({\beta }_j(t-\rho \left(t\right))+\lambda z_j(t-\tau -\rho (t-\tau )))\hfill \\ & & -f_j\left(\lambda z_j(t-\tau -\rho (t-\tau ))\right)]+\sum _{j=1}^m{\check{d}}_{ji}\left[({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))\right]{\int }_{t-r\left(t\right)}^t[f_j({\beta }_j\left(s\right)+\lambda z_j(s-\tau ))\hfill \\ & & -f_j\left(\lambda z_j(s-\tau )\right)\left]ds\right\}+\sum _{j=1}^{m}sgn\left({\beta }_j\left(t\right)\right)\{-(u_j+{\mu }_j\left(t\right)){\beta }_j\left(t\right)+\sum _{i=1}^n{\check{v}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]\hfill \\ & & \left[g_i({\alpha }_i\left(t\right)+\lambda y_i(t-\tau ))-g_i\left(\lambda y_i(t-\tau )\right)\right]+\sum _{i=1}^n{\check{w}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right][g_i({\alpha }_i(t-\rho \left(t\right))\hfill \\ & & +\lambda y_i(t-\tau -\rho (t-\tau )))-g_i\left(\lambda y_i(t-\tau -\rho (t-\tau ))\right)]+\sum _{i=1}^n{\check{x}}_{ij}\left[({\beta }_j\left(t\right)+\lambda z_j(t-\tau ))\right]\hfill \end{array}$$

$$\begin{array}{cc}& {\int }_{t-r\left(t\right)}^t\left[g_i({\alpha }_i\left(s\right)+\lambda y_i(s-\tau ))-g_i\left(\lambda y_i(s-\tau )\right)\right]ds\}\hfill \\ \le & \sum _{i=1}^n\{-(a_i+{\eta }_i\left(t\right))|{\alpha }_i\left(t\right)|+\sum _{j=1}^m{\mathbb{B}}_{ji}{\tilde{L}}_j|{\beta }_j\left(t\right)|+\sum _{j=1}^m{\mathbb{C}}_{ji}{\tilde{L}}_j|{\beta }_j(t-\rho \left(t\right))|\hfill \\ & +\sum _{j=1}^m{\mathbb{D}}_{ji}{\tilde{L}}_j{\int }_{t-r\left(t\right)}^t|{\beta }_j\left(s\right)|ds\}+\sum _{j=1}^m\{-(u_j+{\mu }_j\left(t\right))|{\beta }_j\left(t\right)|+\sum _{i=1}^n{\mathbb{V}}_{ij}{L}_i|{\alpha }_i\left(t\right)|\hfill \\ & +\sum _{i=1}^n{\mathbb{W}}_{ij}{L}_i|{\alpha }_i(t-\rho \left(t\right))|+\sum _{i=1}^n{\mathbb{X}}_{ij}{L}_i{\int }_{t-r\left(t\right)}^t|{\alpha }_i\left(s\right)|ds\}\hfill \end{array}$$

$$\begin{array}{ccc}{\dot{V}}_2\left(t\right)\hfill & =& \sum _{i=1}^n\frac{2{\eta }_i\left(t\right){\dot{\eta }}_i\left(t\right)}{2{\kappa }_i}+\sum _{j=1}^m\frac{2{\mu }_j\left(t\right){\dot{\mu }}_j\left(t\right)}{2{\iota }_j}\hfill \\ & =& \sum _{i=1}^n\frac{{\eta }_i\left(t\right)}{{\kappa }_i}\left[\frac{-{\kappa }_i{\theta }_i|{\alpha }_i\left(t\right)|}{{\eta }_i\left(t\right)}+{\kappa }_i|{\alpha }_i\left(t\right)|\right]+\sum _{j=1}^m\frac{{\mu }_j\left(t\right)}{{\iota }_j}\left[\frac{-{\iota }_j{\delta }_j|{\beta }_j\left(t\right)|}{{\mu }_j\left(t\right)}+{\iota }_j|{\beta }_j\left(t\right)|\right]\hfill \\ & =& \sum _{i=1}^n\left[-{\theta }_i|{\alpha }_i\left(t\right)|+{\eta }_i\left(t\right)|{\alpha }_i\left(t\right)|\right]+\sum _{j=1}^m\left[-{\delta }_j|{\beta }_j\left(t\right)|+{\mu }_j\left(t\right)|{\beta }_j\left(t\right)|\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}{\dot{V}}_3\left(t\right)\hfill & =& -\frac{1}{1-\sigma }\sum _{i=1}^n\sum _{j=1}^m{\mathbb{W}}_{ij}{L}_i\left[(1-\dot{\rho }\left(t\right))|{\alpha }_i(t-\rho \left(t\right))|-|{\alpha }_i\left(t\right)|\right]+\sum _{i=1}^n\sum _{j=1}^m{\mathbb{X}}_{ij}{L}_i{\int }_{-r\left(t\right)}^0[|{\alpha }_i\left(t\right)|\hfill \\ & & -|{\alpha }_i(t+s)|]ds-\frac{1}{1-\sigma }\sum _{j=1}^m\sum _{i=1}^n{\mathbb{C}}_{ji}{\tilde{L}}_j\left[(1-\dot{\rho }\left(t\right))|{\beta }_j(t-\rho \left(t\right))|-|{\beta }_j\left(t\right)|\right]\hfill \\ & & +\sum _{j=1}^m\sum _{i=1}^n{\mathbb{D}}_{ji}{\tilde{L}}_j{\int }_{-r\left(t\right)}^0\left[|{\beta }_j\left(t\right)|-|{\beta }_j(t+s)|\right]ds\hfill \\ & \le & -\sum _{i=1}^n\sum _{j=1}^m{\mathbb{W}}_{ij}{L}_i|{\alpha }_i(t-\rho \left(t\right))|+\frac{1}{1-\sigma }\sum _{i=1}^n\sum _{j=1}^m{\mathbb{W}}_{ij}{L}_i|{\alpha }_i\left(t\right)|+\sum _{i=1}^n\sum _{j=1}^m{\mathbb{X}}_{ij}{L}_{i}r|{\alpha }_i\left(t\right)|\hfill \\ & & -\sum _{i=1}^n\sum _{j=1}^m{\mathbb{X}}_{ij}{L}_i{\int }_{t-r\left(t\right)}^t|{\alpha }_i\left(s\right)|ds-\sum _{j=1}^m\sum _{i=1}^n{\mathbb{C}}_{ji}{\tilde{L}}_j|{\beta }_j(t-\rho \left(t\right))|+\frac{1}{1-\sigma }\sum _{j=1}^m\sum _{i=1}^n{\mathbb{C}}_{ji}{\tilde{L}}_j|{\beta }_j\left(t\right)|\hfill \\ & & +\sum _{j=1}^m\sum _{i=1}^n{\mathbb{D}}_{ji}{\tilde{L}}_{j}r|{\beta }_j\left(t\right)|-\sum _{j=1}^m\sum _{i=1}^n{\mathbb{D}}_{ji}{\tilde{L}}_j{\int }_{t-r\left(t\right)}^t|{\beta }_j\left(s\right)|ds.\hfill \end{array}$$

From Equation (11), it follows that

$$\begin{array}{ccc}\dot{V}\left(t\right)\hfill & \le & -\sum _{i=1}^n\left\{a_i+{\theta }_i-\sum _{j=1}^m\left({\mathbb{V}}_{ij}+\frac{{\mathbb{W}}_{ij}}{1-\sigma }+r{\mathbb{X}}_{ij}\right)L_i\right\}|{\alpha }_i\left(t\right)|\hfill \\ & & -\sum _{j=1}^m\left\{u_j+{\delta }_j-\sum _{i=1}^n\left({\mathbb{B}}_{ji}+\frac{{\mathbb{C}}_{ji}}{1-\sigma }+r{\mathbb{D}}_{ji}\right){\tilde{L}}_j\right\}|{\beta }_j\left(t\right)|.\hfill \end{array}$$

We can choose the appropriate positive scalars ${\Omega }_1,{\mathsf{\Theta }}_1$ such that

$$\begin{array}{ccc}\dot{V}\left(t\right)\hfill & \le & -{\Omega }_1\sum _{i=1}^n|{\alpha }_i\left(t\right)|-{\mathsf{\Theta }}_1\sum _{j=1}^m|{\beta }_j\left(t\right)|\hfill \\ & \le & -{\rm Y}\left[\sum _{i=1}^n|{\alpha }_i\left(t\right)|+\sum _{j=1}^m|{\beta }_j\left(t\right)|\right]\hfill \\ & \le & -{\rm Y}\Psi \left(t\right),\hfill \end{array}$$

where $\mathsf{\Psi }\left(t\right)={\sum }_{i=1}^n|{\alpha }_i\left(t\right)|+{\sum }_{j=1}^m|{\beta }_j\left(t\right)|$ and ${\rm Y}=min\{{\Omega }_1,{\mathsf{\Theta }}_1\}.$ We can get $V\left(0\right)\ge V\left(t\right)+\mathsf{{\rm Y}}{\int }_0^t\mathsf{\Psi }\left(\gamma \right)d\gamma$; it is simple to get ${\int }_0^t\mathsf{\Psi }\left(\gamma \right)d\gamma$ has a finite limit and $\mathsf{\Psi }\left(\gamma \right)$ bounded that is ${\alpha }_i\left(t\right)$ and ${\beta }_j\left(t\right)$ is bounded. Therefore, there exist a constant $\varpi >0$ such that $D^q|\mathsf{\Psi }\left(t\right)|\le \varpi$, $t\ge 0$ is bounded. Based on the Barbalet’s Lemma 2, we show that $\mathsf{\Psi }\left(t\right)$ is uniformly continuous. For $0\le t_1<t_2$

$$\begin{array}{ccc}|\mathsf{\Psi }\left(t_1\right)-\mathsf{\Psi }\left(t_2\right))|\hfill & =& |\left(\mathsf{\Psi }\left(t_1\right)-\mathsf{\Psi }\left(0\right)\right)-\left(\mathsf{\Psi }\left(t_2\right)-\mathsf{\Psi }\left(0\right)\right)|\hfill \\ & =& |D^{-q}{D}^q\left(\mathsf{\Psi }\left(t_1\right)\right)-D^{-q}{D}^q\left(\mathsf{\Psi }\left(t_2\right)\right)|\hfill \\ & =& \frac{1}{\mathsf{\Gamma }\left(q\right)}|{\int }_0^{t_1}{(t_1-\gamma )}^{q-1}{D}^q\left(\mathsf{\Psi }\left(\gamma \right)\right)d\gamma -{\int }_0^{t_2}{(t_2-\gamma )}^{q-1}{D}^q\left(\mathsf{\Psi }\left(\gamma \right)\right)d\gamma |\hfill \\ & \le & \frac{1}{\mathsf{\Gamma }\left(q\right)}[|{\int }_0^{t_1}[{(t_1-\gamma )}^{q-1}-{(t_2-\gamma )}^{q-1}]D^q\left(\mathsf{\Psi }\left(\gamma \right)\right)d\gamma |\hfill \\ & & +|{\int }_{t_1}^{t_2}{(t_2-\gamma )}^{q-1}{D}^q\left(\mathsf{\Psi }\left(\gamma \right)\right)d\gamma |]\hfill \\ & \le & \frac{\varpi }{\mathsf{\Gamma }\left(q\right)}\left[|{\int }_0^{t_1}[{(t_1-\gamma )}^{q-1}-{(t_2-\gamma )}^{q-1}]d\gamma |+|{\int }_{t_1}^{t_2}{(t_2-\gamma )}^{q-1}d\gamma |\right]\hfill \\ & \le & \frac{2\varpi }{q\mathsf{\Gamma }\left(q\right)}\left[t_1^q-t_2^q+2{(t_2-t_1)}^q\right]\hfill \\ & \le & \frac{2\varpi }{\mathsf{\Gamma }(q+1)}{\left(t_2-t_1\right)}^q<\epsilon ,\hfill \end{array}$$

where $|t_2-t_1|<\epsilon \left(\iota \right)=\sqrt[q]{\frac{\iota \mathsf{\Gamma }(q+1)}{2\varpi }}$. Thus, $\mathsf{\Psi }\left(t\right)$ is uniformly continuous, by Lemma 2, we have

$$\begin{array}{c}\underset{t\to +\infty }{lim}\sum _{i=1}^n|{\alpha }_i\left(t\right)|=0\hfill \end{array}$$

and

$$\begin{array}{c}\underset{t\to +\infty }{lim}\sum _{j=1}^m|{\beta }_j\left(t\right)|=0.\hfill \end{array}$$

Therefore, based on Definition 4, systems (1) and (4) are globally projective lag synchronized via hybrid controller (7). The proof is completed.

Suppose the systems (1) and (4) are without distributed delay, then we have to select the following hybrid controller in a response system such as

$$\begin{array}{c}{\zeta }_i\left(t\right)={\widehat{\zeta }}_i\left(t\right)+{\check{\zeta }}_i\left(t\right)and{\varsigma }_j\left(t\right)={\widehat{\varsigma }}_j\left(t\right)+{\check{\varsigma }}_j\left(t\right),\hfill \end{array}$$

(12)

where

$$\begin{array}{ccc}{\widehat{\zeta }}_i\left(t\right)\hfill & =& -\lambda \sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)-b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\tau )\right)-\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[(f_j\left(\lambda z_j(t-\tau )\right)-\lambda \left(f_j\left(z_j(t-\tau )\right)\right)\right]\hfill \\ & & -\lambda \sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)-c_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\tau -\rho (t-\tau ))\right)\hfill \\ & & -\sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[f_j\left(\lambda z_j(t-\tau -\rho (t-\tau ))\right)-\lambda (f_j\left(z_j(t-\tau -\rho (t-\tau ))\right)\right]+(\lambda -1)J_i\hfill \\ {\check{\zeta }}_i\left(t\right)\hfill & =& -{\eta }_i\left(t\right){\alpha }_i\left(t\right),{\dot{\eta }}_i\left(t\right)=\frac{-{\kappa }_i{\theta }_i|{\alpha }_i\left(t\right)|}{{\eta }_i\left(t\right)}+{\kappa }_i|{\alpha }_i\left(t\right)|\hfill \end{array}$$

and

$$\begin{array}{ccc}{\widehat{\varsigma }}_j\left(t\right)\hfill & =& -\lambda \sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)-v_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\tau )\right)-\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i(t-\tau )\right)-\lambda (g_i\left(y_i(t-\tau )\right)\right]\hfill \\ & & -\lambda \sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)-w_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\tau -\rho (t-\tau ))\right)\hfill \\ & & -\sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i(t-\tau -\rho (t-\tau ))\right)-\lambda (g_i\left(y_i(t-\tau -\rho (t-\tau ))\right)\right]+(\lambda -1)H_j\hfill \\ {\check{\varsigma }}_j\left(t\right)\hfill & =& -{\mu }_j\left(t\right){\beta }_j\left(t\right),{\dot{\mu }}_j\left(t\right)=\frac{-{\iota }_j{\delta }_j|{\beta }_j\left(t\right)|}{{\mu }_j\left(t\right)}+{\iota }_j|{\beta }_j\left(t\right)|.\hfill \end{array}$$

These corollaries are directly obtained from our main Theorem 3. □

Corollary 1.

Suppose that Assumptions $\left[\mathcal{H}\right]$ hold, then drive system (1) and response system (4) without distributed delay are globally projective lag synchronized via hybrid controller (12), if the following conditions hold:

$$\begin{array}{ccc}{\Omega }_1\hfill & =& \underset{1\le i\le n}{min}\left\{a_i+{\theta }_i-\sum _{j=1}^m\left({\mathbb{V}}_{ij}+\frac{{\mathbb{W}}_{ij}}{1-\sigma }\right)L_i\right\}>0,\hfill \\ {\mathsf{\Theta }}_2\hfill & =& \underset{1\le j\le m}{min}\left\{u_j+{\delta }_j-\sum _{i=1}^n\left({\mathbb{B}}_{ji}+\frac{{\mathbb{C}}_{ij}}{1-\sigma }\right){\tilde{L}}_j\right\}>0,\hfill \end{array}$$

where ${\mathbb{B}}_{ji}=max\{|b_{ji}^{\star }|,|b_{ji}^{\star \star }|\},{\mathbb{C}}_{ji}=max\{|c_{ji}^{\star }|,|c_{ji}^{\star \star }|\},{\mathbb{V}}_{ij}=max\{|v_{ij}^{\star }|,|v_{ij}^{\star \star }|\}$ and ${\mathbb{W}}_{ij}=max\{|w_{ij}^{\star }|,|w_{ij}^{\star \star }|\},$ ${\theta }_i,{\xi }_i,{\delta }_j$ and ${\gamma }_j$ denotes the appropriate positive constants.

Proof. 

The proof is repeated to Theorem 3. Hence, the proof is omitted here. □

Supposing the drive-response systems are without discrete and distributed delay, then we have to select the following hybrid controller in a response system such as

$$\begin{array}{c}{\zeta }_i\left(t\right)={\widehat{\zeta }}_i\left(t\right)+{\check{\zeta }}_i\left(t\right)and{\varsigma }_j\left(t\right)={\widehat{\varsigma }}_j\left(t\right)+{\check{\varsigma }}_j\left(t\right),\hfill \end{array}$$

(13)

where

$$\begin{array}{ccc}{\widehat{\zeta }}_i\left(t\right)\hfill & =& -\lambda \sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)-b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j\left(t\right)\right)-\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[(f_j\left(\lambda z_j\left(t\right)\right)-\lambda \left(f_j{z}_j\left(t\right)\right)\right]+(\lambda -1)J_i\hfill \\ {\check{\zeta }}_i\left(t\right)\hfill & =& -{\eta }_i\left(t\right){\alpha }_i\left(t\right),{\dot{\eta }}_i\left(t\right)=\frac{-{\kappa }_i{\theta }_i|{\alpha }_i\left(t\right)|}{{\eta }_i\left(t\right)}+{\kappa }_i|{\alpha }_i\left(t\right)|,\hfill \end{array}$$

$$\begin{array}{ccc}{\widehat{\varsigma }}_j\left(t\right)\hfill & =& -\lambda \sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)-v_{ij}\left(z_j\left(t\right)\right)\left(t\right)\right]g_i\left(y_i\left(t\right)\right)-\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i\left(t\right)\right)-\lambda \left(g_i{y}_i\left(t\right)\right)\right]+(\lambda -1)H_j,\hfill \\ {\check{\varsigma }}_j\left(t\right)\hfill & =& -{\mu }_j\left(t\right){\beta }_j\left(t\right),{\dot{\mu }}_j\left(t\right)=\frac{-{\iota }_j{\delta }_j|{\beta }_j\left(t\right)|}{{\mu }_j\left(t\right)}+{\iota }_j|{\beta }_j\left(t\right)|.\hfill \end{array}$$

These corollaries are directly obtained from our main Theorem 3.

Corollary 2.

Suppose that Assumptions $\left[\mathcal{H}\right]$ hold, then systems (1) and (4) are without discrete and distributed delay are globally projective lag synchronized via hybrid controller (13) if the following conditions hold:

$$\begin{array}{ccc}{\Omega }_1\hfill & =& \underset{1\le i\le n}{min}\left\{a_i+{\theta }_i-\sum _{j=1}^m{\mathbb{V}}_{ij}{L}_i\right\}>0,\hfill \\ {\mathsf{\Theta }}_2\hfill & =& \underset{1\le j\le m}{min}\left\{u_j+{\delta }_j-\sum _{i=1}^n{\mathbb{B}}_{ji}{\tilde{L}}_j\right\}>0.\hfill \end{array}$$

where ${\mathbb{B}}_{ji}=max\{|b_{ji}^{\star }|,|b_{ji}^{\star \star }|\}$ and ${\mathbb{V}}_{ij}=max\{|v_{ij}^{\star }|,|v_{ij}^{\star \star }|\},$ ${\theta }_i$ and ${\delta }_j$ denotes the appropriate positive constants.

Proof. 

The proof is similar to the proof of Theorem 3. Hence, the proof is omitted here. □

Let ${\alpha }_i\left(t\right)={\tilde{y}}_i\left(t\right)-\lambda y_i\left(t\right)$ and ${\beta }_j\left(t\right)={\tilde{z}}_j\left(t\right)-\lambda z_j\left(t\right).$ If $\tau =0$, the control input (7) can be reduced into the following form:

$$\begin{array}{ccc}{\zeta }_i\left(t\right)\hfill & =& -\lambda \sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)-b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j\left(t\right)\right)-\lambda \sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)-c_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\rho \left(t\right))\right)\hfill \\ & & -\lambda \sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)-d_{ji}\left(y_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds-\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[(f_j\left(\lambda z_j\left(t\right)\right)-\lambda (f_j\left(z_j\left(t\right)\right)\right]\hfill \\ & & -\sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]\left[f_j\left(\lambda z_j(t-\rho \left(t\right))\right)-\lambda (f_j\left(z_j(t-\rho \left(t\right))\right)\right]-\sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t[f_j(\lambda z_j\left(s\right)\hfill \\ & & -\lambda \left(f_j{z}_j\left(s\right)\right)]ds+(\lambda -1)J_i-{\eta }_i\left(t\right){\alpha }_i\left(t\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}{\varsigma }_j\left(t\right)\hfill & =& -\lambda \sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)-v_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i\left(t\right)\right)-\lambda \sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)-w_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\rho \left(t\right))\right)\hfill \\ & & -\lambda \sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)-x_{ij}\left(z_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds-\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i\left(t\right)\right)-\lambda \left(g_i\left(y_i\left(t\right)\right)\right)\right]\hfill \\ & & -\sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]\left[g_i\left(\lambda y_i(t-\rho \left(t\right))\right)-\lambda \left(g_i\left(y_i(t-\rho \left(t\right))\right)\right)\right]-\sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t[g_i\left(\lambda y_i\left(s\right)\right)\hfill \\ & & -\lambda \left(g_i{y}_i\left(s\right)\right)]ds+(\lambda -1)H_j-{\mu }_j\left(t\right){\beta }_j\left(t\right).\hfill \end{array}$$

(15)

Let ${\alpha }_i\left(t\right)={\tilde{y}}_i\left(t\right)-y_i\left(t\right)$ and ${\beta }_j\left(t\right)={\tilde{z}}_j\left(t\right)-z_j\left(t\right).$ If $\tau =0$ and $\lambda =1$, the control input (7) can be reduced into the following form:

$$\begin{array}{ccc}{\zeta }_i\left(t\right)\hfill & =& -\sum _{j=1}^m\left[b_{ji}\left({\tilde{y}}_i\left(t\right)\right)-b_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j\left(t\right)\right)-\sum _{j=1}^m\left[c_{ji}\left({\tilde{y}}_i\left(t\right)\right)-c_{ji}\left(y_i\left(t\right)\right)\right]f_j\left(z_j(t-\rho \left(t\right))\right)\hfill \\ & & -\sum _{j=1}^m\left[d_{ji}\left({\tilde{y}}_i\left(t\right)\right)-d_{ji}\left(y_i\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds-{\eta }_i\left(t\right){\alpha }_i\left(t\right),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}{\varsigma }_j\left(t\right)\hfill & =& -\sum _{i=1}^n\left[v_{ij}\left({\tilde{z}}_j\left(t\right)\right)-v_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i\left(t\right)\right)-\sum _{i=1}^n\left[w_{ij}\left({\tilde{z}}_j\left(t\right)\right)-w_{ij}\left(z_j\left(t\right)\right)\right]g_i\left(y_i(t-\rho \left(t\right))\right)\hfill \\ & & -\sum _{i=1}^n\left[x_{ij}\left({\tilde{z}}_j\left(t\right)\right)-x_{ij}\left(z_j\left(t\right)\right)\right]{\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds-{\mu }_j\left(t\right){\beta }_j\left(t\right).\hfill \end{array}$$

(17)

Let ${\alpha }_i\left(t\right)={\tilde{y}}_i\left(t\right)+y_i\left(t\right)$ and ${\beta }_j\left(t\right)={\tilde{z}}_j\left(t\right)+z_j\left(t\right).$ If $\tau =0$ and $\lambda =-1$, the control input (7) can be reduced into the following form:

$$\begin{array}{ccc}{\zeta }_i\left(t\right)\hfill & =& -\sum _{j=1}^m{b}_{ji}\left(y_i\left(t\right)\right)f_j\left(z_j\left(t\right)\right)-\sum _{j=1}^m{c}_{ji}\left(y_i\left(t\right)\right)f_j\left(z_j(t-\rho \left(t\right))\right)-\sum _{j=1}^m{d}_{ji}\left(y_i\left(t\right)\right){\int }_{t-r\left(t\right)}^t{f}_j\left(z_j\left(s\right)\right)ds\hfill \\ & & -\sum _{j=1}^m{b}_{ji}\left({\tilde{y}}_i\left(t\right)\right)f_j(-z_j\left(t\right))-\sum _{j=1}^m{c}_{ji}\left({\tilde{y}}_i\left(t\right)\right)f_j(-z_j(t-\rho \left(t\right)))\hfill \\ & & -\sum _{j=1}^m{d}_{ji}\left({\tilde{y}}_i\left(t\right)\right){\int }_{t-r\left(t\right)}^t{f}_j(-z_j\left(s\right))ds-2J_i-{\eta }_i\left(t\right){\alpha }_i\left(t\right),\hfill \end{array}$$

(18)

$$\begin{array}{ccc}{\varsigma }_j\left(t\right)\hfill & =& -\sum _{i=1}^n{v}_{ij}\left(z_j\left(t\right)\right)g_i\left(y_i\left(t\right)\right)-\sum _{i=1}^n{w}_{ij}\left(z_j\left(t\right)\right)g_i\left(y_i(t-\rho \left(t\right))\right)-\sum _{i=1}^n{x}_{ij}\left(z_j\left(t\right)\right){\int }_{t-r\left(t\right)}^t{g}_i\left(y_i\left(s\right)\right)ds\hfill \\ & & -\sum _{i=1}^n{v}_{ij}\left({\tilde{z}}_j\left(t\right)\right)g_i(-y_i\left(t\right))-\sum _{i=1}^n{w}_{ij}\left({\tilde{z}}_j\left(t\right)\right)g_i(-y_i(t-\rho \left(t\right)))\hfill \\ & & -\sum _{i=1}^n{x}_{ij}\left({\tilde{z}}_j\left(t\right)\right){\int }_{t-r\left(t\right)}^t{g}_i(-y_i\left(s\right))ds-2H_j-{\mu }_j\left(t\right){\beta }_j\left(t\right).\hfill \end{array}$$

(19)

Corollary 3.

Supposing that Assumptions $\left[\mathcal{H}\right]$ hold and conditions of Theorem 3 hold, then systems (1) and (4) are globally projective synchronized, globally complete synchronized, globally anti-synchronized based on the hybrid controller (14) and (15), (16), (17) and (18), (19) when ${\dot{\eta }}_i\left(t\right),{\dot{\mu }}_j\left(t\right)$ designs as follows:

$$\begin{array}{c}{\dot{\eta }}_i\left(t\right)=\frac{-{\kappa }_i{\theta }_i|{\alpha }_i\left(t\right)|}{{\eta }_i\left(t\right)}+{\kappa }_i|{\alpha }_i\left(t\right)|,{\dot{\mu }}_j\left(t\right)=\frac{-{\iota }_j{\delta }_j|{\beta }_j\left(t\right)|}{{\mu }_j\left(t\right)}+{\iota }_j|{\beta }_j\left(t\right)|,\hfill \end{array}$$

where ${\kappa }_i,{\theta }_i,{\xi }_i,{\iota }_j,{\delta }_j$ and ${\gamma }_j$ denote the positive constants, ${\eta }_i\left(t\right)$ and ${\mu }_j\left(t\right)$ denotes the adaptive constants.

Proof. 

The proof of Corollary 3 is similar to the proof of Theorem 3. Hence, the proof is omitted here. □

Remark 3.

In [54], the author considers lag-synchronization error systems as $\tilde{g}\left(e(t-\rho \left(t\right))\right)=g\left(y(t-\rho \left(t\right))\right)-g\left(x(t-\sigma -\rho \left(t\right))\right)$, where σ is lag transmittal delay. However, the author of [46] argues that the above synchronization error systems are not valid—thus corrected lag synchronization error systems such as $\tilde{g}\left(e(t-\rho \left(t\right))\right)=g\left(y(t-\rho \left(t\right))\right)-g\left(x(t-\sigma -\rho (t-\sigma ))\right)$. In addition, the above consideration affects the validity of obtained proposed results. Here, evidently, we can choose the corrected lag synchronization errors with a projective sense. Thus, our error models are more valid and reasonable.

Remark 4.

Suppose memristive connection weights satisfy these conditions $b_{ji}^{\star }=b_{ji}^{\star \star },c_{ji}^{\star }=c_{ji}^{\star \star },d_{ji}^{\star }=d_{ji}^{\star \star },v_{ij}^{\star }=v_{ij}^{\star \star },w_{ij}^{\star }=w_{ij}^{\star \star }$ and $z_{ij}^{\star }=z_{ij}^{\star \star }$. Our problems turn up to the hybrid control for a general class of global projective lag synchronization of Riemann–Liouville type FOMBNNs with mixed time delays. In fact, we can easily derive from Theorem 3 to lag projective synchronization criteria for considered network models by employing the hybrid control method. When $q=1$, our result is still true for an integer order case.

Remark 5.

In order to portray how to tune the control gains to achieve the projective lag synchronization goal for considered FOMBNNs, we take Theorem 3 and present some rules, which are listed below:

1. 

Based on the hybrid control, we choose the values of $\tau ,\rho ,\sigma ,a_i,u_j,v_{ij}^{\star },w_j^{\star },x_{ij}^{\star },b_{ji}^{\star },c_{ji}^{\star },d_{ji}^{\star },L_i$ and $L_j$ according to assumptions and system parameters.

2. 

Next, justify whether

$$\begin{array}{cc}{\theta }_i>\hfill & \left[\sum _{j=1}^m\left({\mathbb{V}}_{ij}+\frac{{\mathbb{W}}_{ij}}{1-\sigma }+r{\mathbb{X}}_{ij}\right)L_i-a_i\right],\hfill \\ {\delta }_j>\hfill & \left[\sum _{i=1}^n\left({\mathbb{B}}_{ji}+\frac{{\mathbb{C}}_{ji}}{1-\sigma }+\rho {\mathbb{D}}_{ji}\right){\tilde{L}}_j-u_j\right].\hfill \end{array}$$

When we adjust the above parameters of the system, then the control gains of the hybrid controller (7) can be tuned slightly to realize a projective synchronization goal.

3. 

Next, we choose a time lag $\vartheta =2$ and projective coefficient $\lambda =3$.

4. 

Then, by using the dedicated simulation software tools and also selecting the simulation step size $h=0.01$, the output trajectories confirm that the tuned control gains converge gradually to some positive constants.

Remark 6.

Basically, the Lyapunov method provides a very effective tool to realize synchronization analysis of a nonlinear system. However, it is very complicated to calculate the fractional order derivative of an auxiliary function. In order to avoid this complication, we design the integer order auxiliary function including fractional order derivative and integral terms and it helps to calculate its first-order derivative of an auxiliary function, which is guaranteed by the Definition of R-L fractional order differentiation and integration. The main advantage of our proposed method is that we can avoid calculating the fractional-order derivatives of the Lyapunov functional.

4. Numerical Example

Consider a vector form of two-state FOMBNNs as follows:

$$\begin{array}{ccc}{D}^{q}y\left(t\right)\hfill & =& -Ay\left(t\right)+B\left(y\left(t\right)\right)f\left(z\left(t\right)\right)+C\left(y\left(t\right)\right)f\left(z(t-\rho \left(t\right))\right)+D\left(y\left(t\right)\right){\int }_{t-r\left(t\right)}^{t}f\left(z\left(s\right)\right)ds+J,\hfill \\ D^{q}z\left(t\right)\hfill & =& -Uz\left(t\right)+V\left(z\left(t\right)\right)g\left(y\left(t\right)\right)+W\left(z\left(t\right)\right)g\left(y(t-\rho \left(t\right))\right)+X\left(z\left(t\right)\right){\int }_{t-r\left(t\right)}^{t}g\left(y\left(s\right)\right)ds+H,\hfill \end{array}$$

(20)

where $q=0.97,y\left(t\right)={(y_1\left(t\right),y_2\left(t\right))}^T,z\left(t\right)={(z_1\left(t\right),z_2\left(t\right))}^T,f\left(z\right)={(f_1\left(z_1\right),f_2\left(z_2\right))}^T,g\left(y\right)={(g_1\left(y_1\right),g_2\left(y_2\right))}^T,f_j\left(z_j\right)=tanh\left(z_j\right),g_i\left(y_i\right)=tanh\left(y_i\right),\rho \left(t\right)=\frac{0.8e^t}{1+e^t},r\left(t\right)=0.5cost+1,\sigma =0.2<1,r=1,\rho =2,J={\left(00\right)}^T,H={\left(00\right)}^T,a_1=a_2=4,u_1=u_2=5,$ and

$$\begin{array}{ccc}B\left(y\right(t\left)\right)\hfill & =& \left(\begin{array}{cc}{b}_{11}\left(y_1\right)& -3\\ 2& b_{22}\left(y_2\right)\end{array}\right),C\left(y\left(t\right)\right)=\left(\begin{array}{cc}{c}_{11}\left(y_1\right)& 1\\ -5& c_{22}\left(y_2\right)\end{array}\right),D\left(y\left(t\right)\right)=\left(\begin{array}{cc}{d}_{11}\left(y_1\right)& 3\\ -2& d_{22}\left(y_2\right)\end{array}\right),\hfill \\ V\left(z\right(t\left)\right)\hfill & =& \left(\begin{array}{cc}{v}_{11}\left(z_1\right)& -1.8\\ -2.5& v_{22}\left(z_2\right)\end{array}\right),W\left(z\left(t\right)\right)=\left(\begin{array}{cc}{w}_{11}\left(z_1\right)& -2.8\\ 4.5& w_{22}\left(z_2\right)\end{array}\right),X\left(z\left(t\right)\right)=\left(\begin{array}{cc}{x}_{11}\left(z_1\right)& -3.8\\ 2& x_{22}\left(z_2\right)\end{array}\right),\hfill \end{array}$$

$$\begin{array}{ccc}{b}_{11}\left(y_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}2.31,|y_1\left(t\right)|\le 1\hfill \\ -2.31,|y_1\left(t\right)|>1,\hfill \end{array}\right.b_{22}\left(y_2\left(t\right)\right)=\left\{\begin{array}{c}2,|y_2\left(t\right)|\le 1\hfill \\ -2,|y_2\left(t\right)|>1,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}{c}_{11}\left(y_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}1.62,|y_1\left(t\right)|\le 1\hfill \\ -1.62,|y_1\left(t\right)|>1,\hfill \end{array}\right.c_{22}\left(y_2\left(t\right)\right)=\left\{\begin{array}{c}2.5,|y_2\left(t\right)|\le 1\hfill \\ -2.5,|y_2\left(t\right)|>1,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}{d}_{11}\left(y_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}1.3,|y_1\left(t\right)|\le 1\hfill \\ -1.3,|y_1\left(t\right)|>1,\hfill \end{array}\right.d_{22}\left(y_2\left(t\right)\right)=\left\{\begin{array}{c}1.72,|y_2\left(t\right)|\le 1\hfill \\ -1.72,|y_2\left(t\right)|>1.\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}{v}_{11}\left(z_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}0.81,|z_1\left(t\right)|\le 1\hfill \\ -0.81,|z_1\left(t\right)|>1,\hfill \end{array}\right.v_{22}\left(z_2\left(t\right)\right)=\left\{\begin{array}{c}0.88,|z_2\left(t\right)|\le 1\hfill \\ -0.88,|z_2\left(t\right)|>1,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}{w}_{11}\left(z_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}1.37,|z_1\left(t\right)|\le 1\hfill \\ -1.37,|z_1\left(t\right)|>1,\hfill \end{array}\right.w_{22}\left(z_2\left(t\right)\right)=\left\{\begin{array}{c}1.03,|z_2\left(t\right)|\le 1\hfill \\ -1.03,|z_2\left(t\right)|>1,\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}{x}_{11}\left(z_1\left(t\right)\right)\hfill & =& \left\{\begin{array}{c}1.21,|z_1\left(t\right)|\le 1\hfill \\ -1.21,|z_1\left(t\right)|>1,\hfill \end{array}\right.x_{22}\left(z_2\left(t\right)\right)=\left\{\begin{array}{c}0.42,|z_2\left(t\right)|\le 1\hfill \\ -0.42,|z_2\left(t\right)|>1.\hfill \end{array}\right.\hfill \end{array}$$

The response system is given by

$$\begin{array}{ccc}{D}^q\tilde{y}\left(t\right)\hfill & =& -A\tilde{y}\left(t\right)+B\left(\tilde{y}\left(t\right)\right)f\left(\tilde{z}\left(t\right)\right)+C\left(\tilde{y}\left(t\right)\right)f\left(\tilde{z}(t-\rho \left(t\right))\right)+D\left(\tilde{y}\left(t\right)\right){\int }_{t-r\left(t\right)}^{t}f\left(\tilde{z}\left(s\right)\right)ds+J+\zeta \left(t\right),\hfill \\ D^q\tilde{z}\left(t\right)\hfill & =& -U\tilde{z}\left(t\right)+V\left(\tilde{z}\left(t\right)\right)g\left(\tilde{y}\left(t\right)\right)+W\left(\tilde{z}\left(t\right)\right)g\left(\tilde{y}(t-\rho \left(t\right))\right)+X\left(\tilde{z}\left(t\right)\right){\int }_{t-r\left(t\right)}^{t}g\left(\tilde{y}\left(s\right)\right)ds+H+\varsigma \left(t\right),\hfill \end{array}$$

(21)

where $\zeta \left(t\right)={({\zeta }_1\left(t\right),{\zeta }_2\left(t\right))}^T$ and $\varsigma \left(t\right)={({\varsigma }_1\left(t\right),{\varsigma }_2\left(t\right))}^T$. All other parameters are similar to that defined in a drive system. In hybrid control scheme (7), we can choose ${\eta }_i\left(0\right)={\mu }_j\left(0\right)=0.01,{\kappa }_i={\theta }_i=0.1,{\iota }_j={\delta }_i=0.1$ for $i,j=1,2.$${\theta }_1=11.6,{\theta }_2=11.5,{\delta }_1=7,{\delta }_2=7.5$ and $\lambda =3,,L_1=L_2=0.8,{\tilde{L}}_1=0.5,$${\tilde{L}}_2=0.4.$ It is easy to check the following inequities hold

$$\begin{array}{c}\underset{i}{min}\left\{a_i+{\theta }_i-\sum _{j=1}^m\left({\mathbb{V}}_{ij}+\frac{{\mathbb{W}}_{ij}}{1-\sigma }+r{\mathbb{X}}_{ij}\right)L_i\right\}>0,\hfill \\ \underset{j}{min}\left\{u_j+{\delta }_j-\sum _{i=1}^n\left({\mathbb{B}}_{ji}+\frac{{\mathbb{C}}_{ji}}{1-\sigma }+r{\mathbb{D}}_{ji}\right){\tilde{L}}_j\right\}>0\hfill \end{array}$$

for $i,j=1,2$. Based on Theorem 3, the drive-response systems (20) and (21) are globally projective lag synchronized via hybrid controller (7). Next, we select the initial values of FOMBNNs (20) and (21) as $\left(y\right(t),z(t\left)\right)=(1.8,-1.5,-1.9,-0.5)$ and $(\tilde{y}\left(t\right),\tilde{z}\left(t\right))=(-1.2,1.1,-1.1,-1.2)$. The projective lag synchronization error evolution for state variables are depicted in Figure 1 and Figure 2, which shows that synchronization of projective error dynamical systems converges to origin, while the adaptive control gains are provided in Figure 3 and Figure 4, which confirms that the adaptive control gains converge to some positive constants.

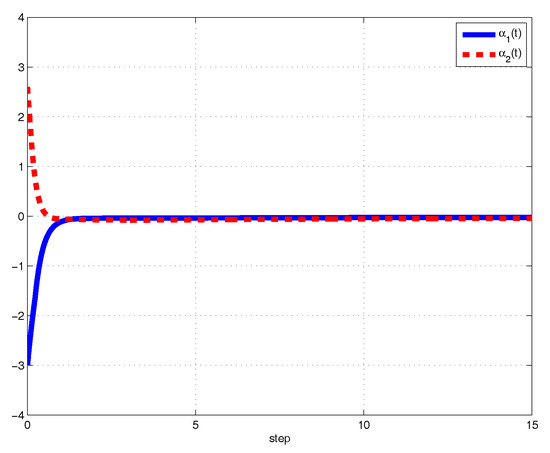
Figure 1. The error state trajectory of $r_i\left(t\right)$ and ${\tilde{r}}_j\left(t\right)$.

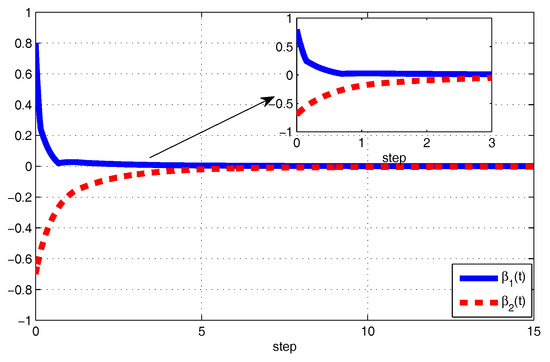
Figure 2. The error state trajectory of $r_i\left(t\right)$ and ${\tilde{r}}_j\left(t\right)$.

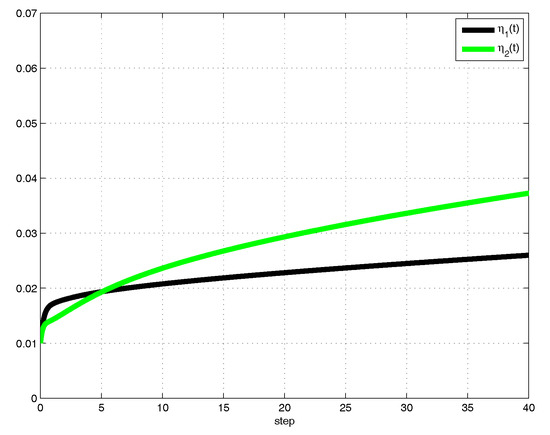
Figure 3. The control gains of controller $\left(7\right)$.

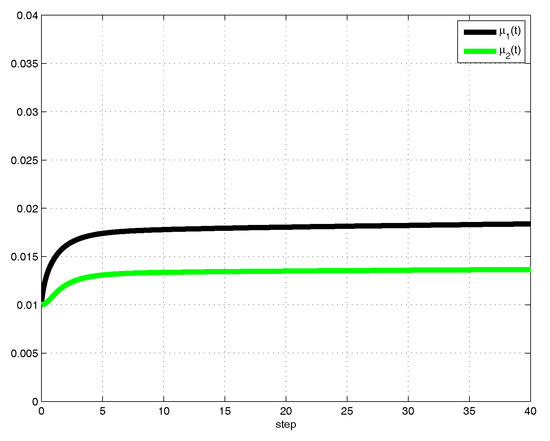
Figure 4. The control gains of controller $\left(7\right)$.

5. Conclusions

In this research work, a hybrid control scheme for projective lag synchronization of FOMBNNs with mixed delays is investigated. On the one hand, by a key role of Lyapunov theory, differential inclusion theory and fractional order Barbalet’s lemma, some novel sufficient conditions have been established to assure the projective lag synchronization of the designed fractional order neural network model. On the other hand, as a special case of complete synchronization, anti-synchronization and projective synchronization of FOMBNNs are also investigated, and these results have not been seen yet. Lastly, we give some computer simulations to delineate the correctness of the proposed main consequences.

In [50,54,55], the authors discussed lag synchronization of integer and fractional order memristive neural networks with switching jump mismatch, based on different control approaches including a state feedback control, period intermittent control. In [56,57], authors proposed the projective synchronization with (or without) memristive neural networks via hybrid control schemes in the Caputo sense. Inspired by [21], the author derived asymptotic stability conditions of delayed FOMBNNs via fractional Barbalat’s Lemma and R-L derivative properties. However, the hybrid control for projective lag synchronization with the combination of the Riemann–Liouville sense fractional order memristive BAM neural networks model is discussed for the first time in this work. Moreover, the presented hybrid control can be applied for solving projective lag synchronization of Riemann–Liouville sense fractional order Cohen–Grossberg coupled neural networks with mixed delays, and we will consider this interesting issue for future work.