A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities
Abstract
1. Introduction
2. Mathematical Formulation
3. The Solution Method
3.1. Spatial Discretization
3.2. Temporal Discretization
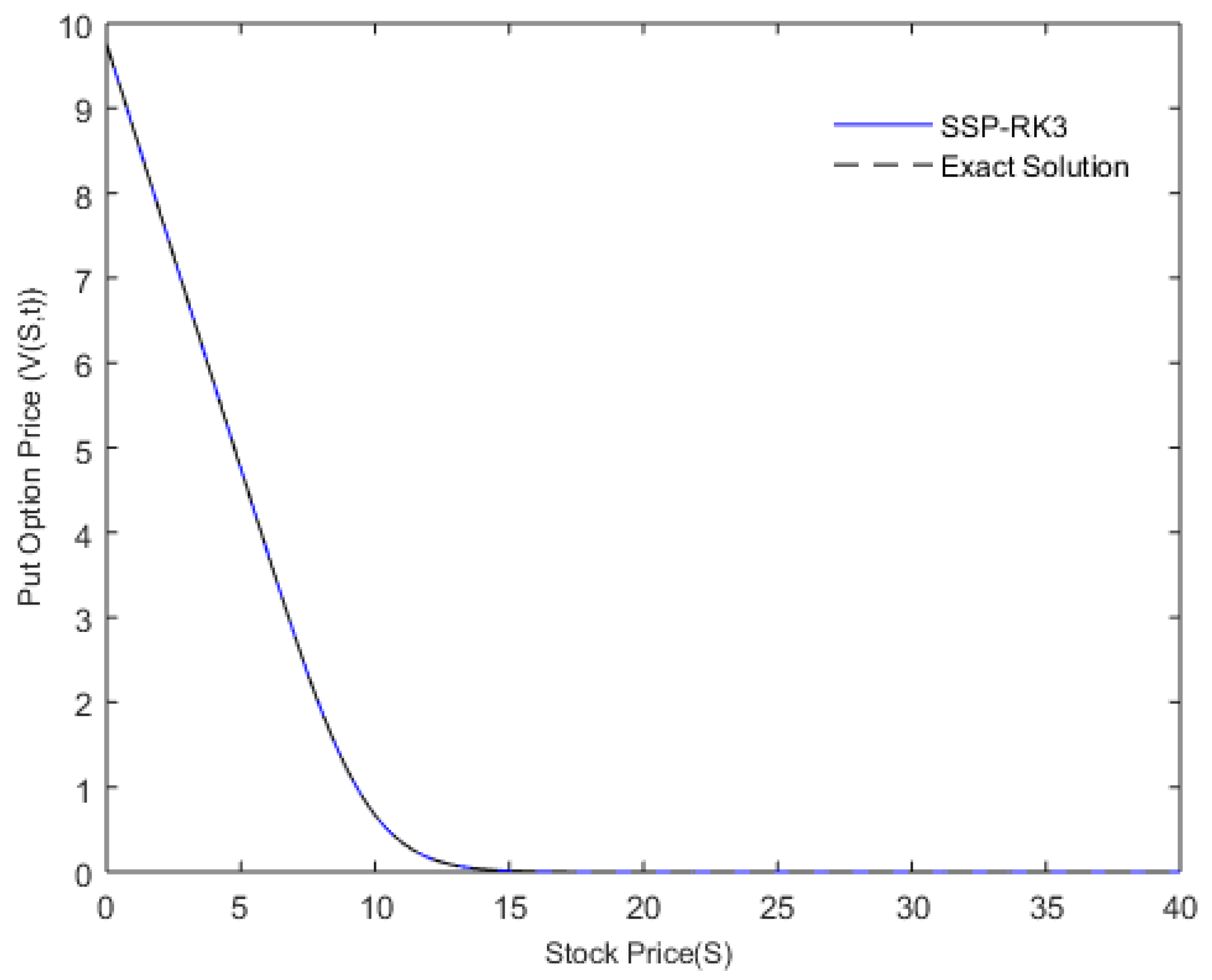
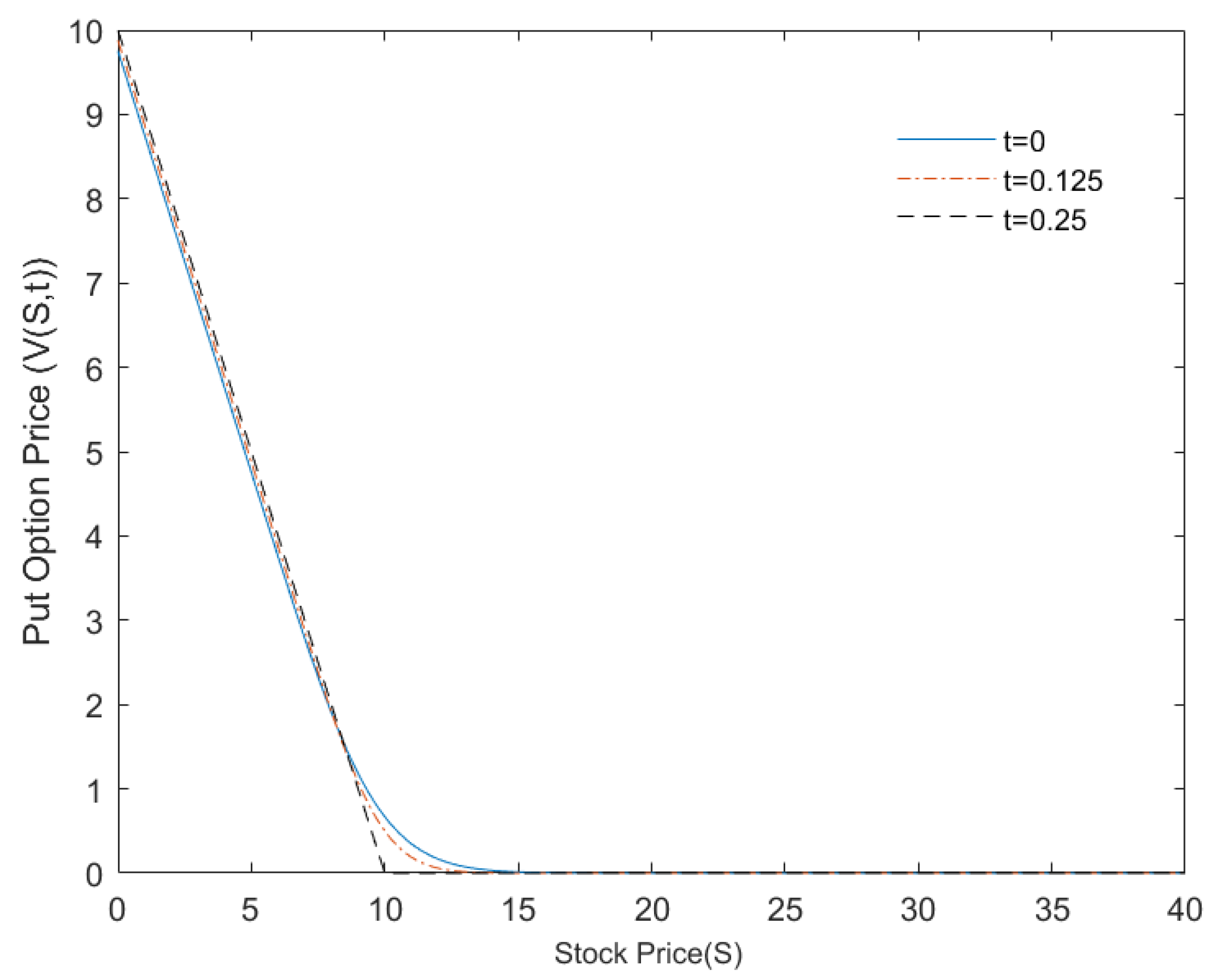
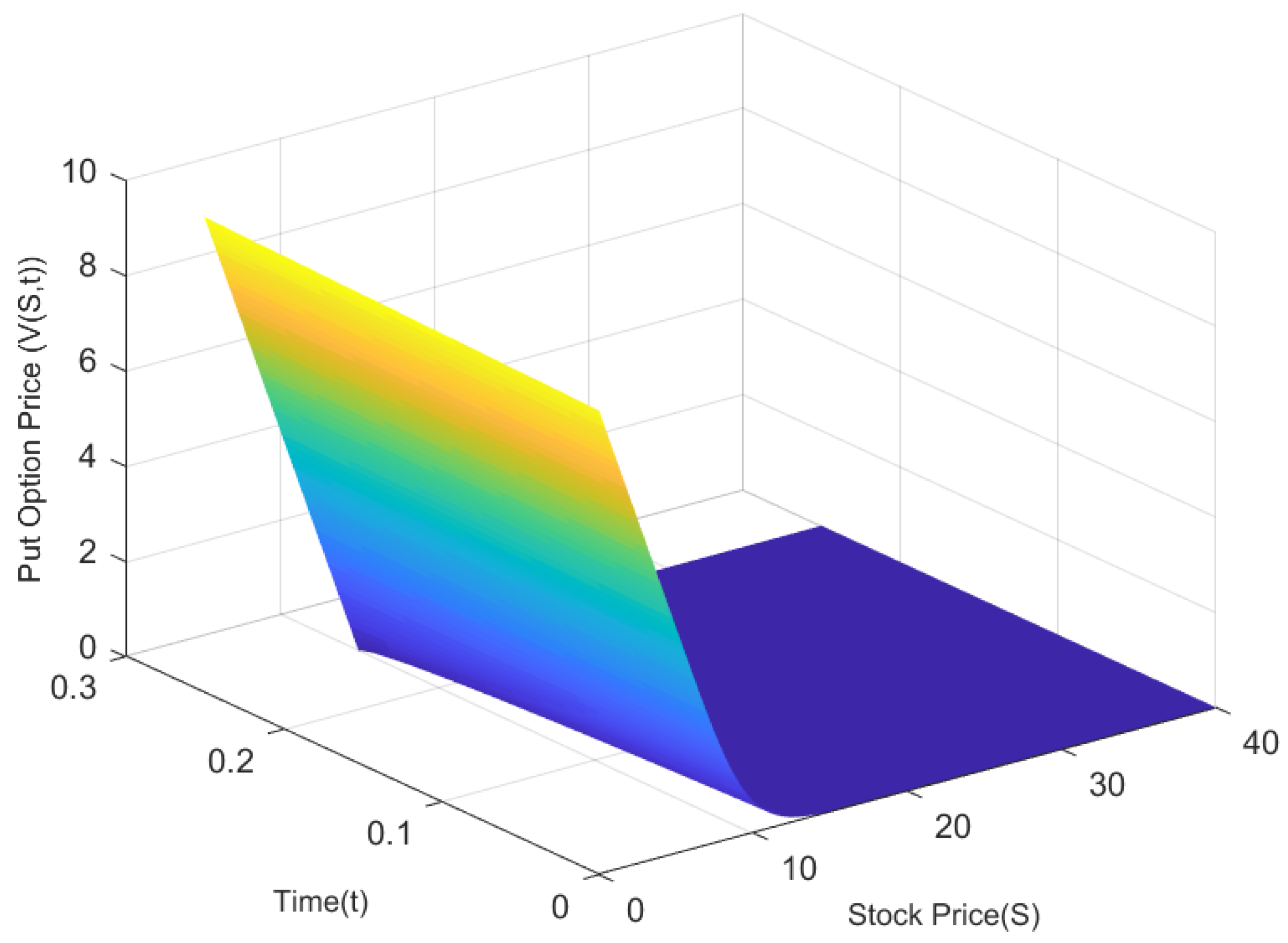
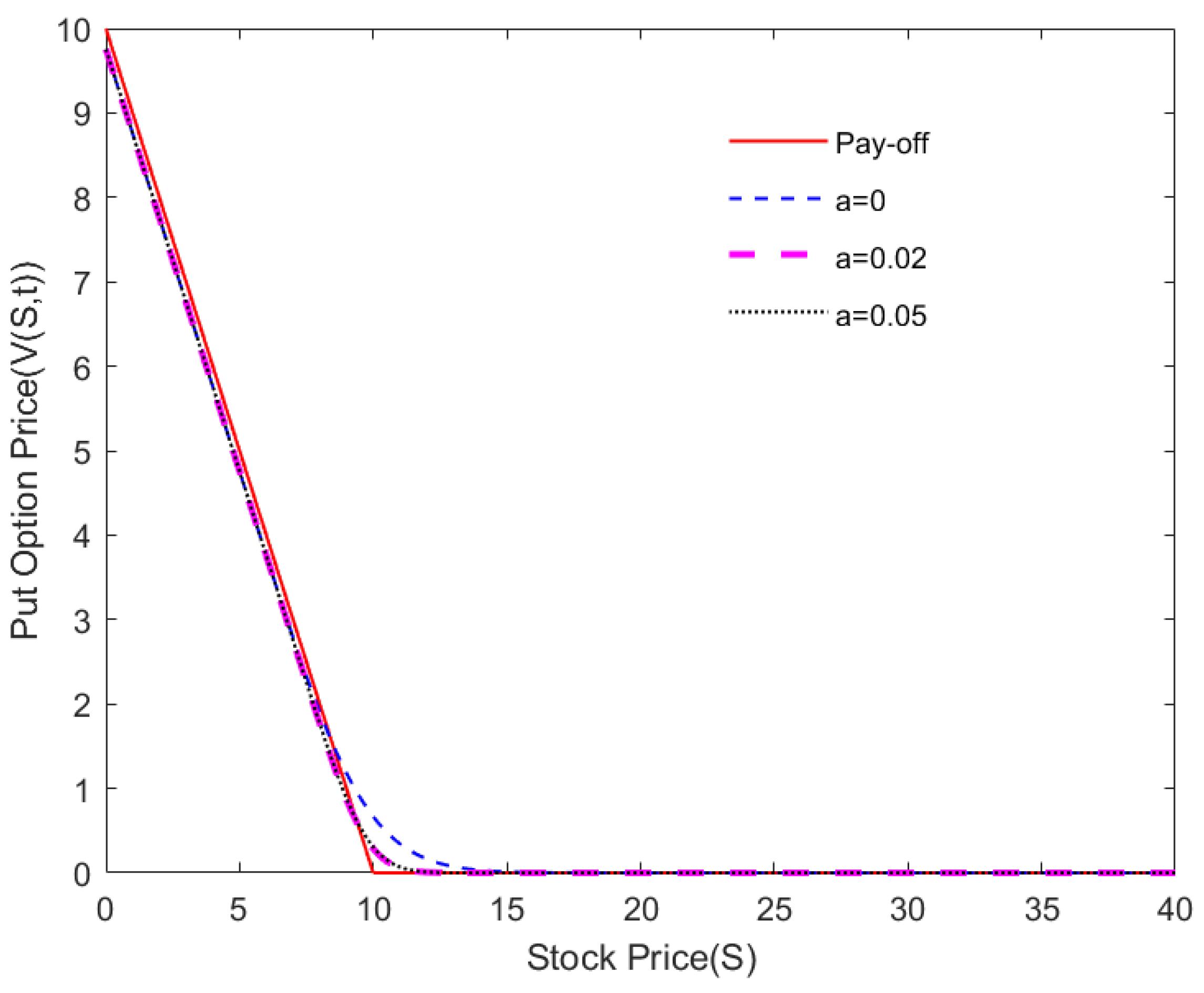
4. Numerical Results and Analysis
5. Conclusions and Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, J.; Davidson, M.; Corless, R.M. Compact finite difference method for American option pricing. J. Comput. Appl. Math. 2007, 206, 306–321. [Google Scholar] [CrossRef]
- Lesmana, D.C.; Wang, S. An upwind finite difference method for a nonlinear Black–Scholes equation governing European option valuation under transaction cost. Appl. Math. Comput. 2013, 219, 8811–8828. [Google Scholar] [CrossRef]
- Rad, J.A.; Parand, K.; Abbasbandy, S. Local week form meshles techniques based on the radial point interpolation (RPI) method and local boundary integral equation (LBIE) method to evaluate European and American options. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1178–1200. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and other corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Yildirim, T. Various Finite Difference Solutions of Option Pricing Models. Master’s Thesis, Yildiz Tecnical University, Istanbul, Turkey, 2016. [Google Scholar]
- Widdicks, M.; Duck, P.W.; Andricopoulos, A.D.; Newton, D.P. The Black-Scholes equation revisited: Asymptotic expansions and singular perturbations. Math. Financ. 2005, 15, 373–391. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of optional option pricing. Bell J. Econ. Manag. Sci. 1973, 1, 141–183. [Google Scholar] [CrossRef]
- Leland, H.E. Option pricing and replication with transaction cost. J. Financ. 1985, 40, 1283–1301. [Google Scholar] [CrossRef]
- Boyle, P.P.; Vorst, T. Option replication in dicrete time with transaction cost. J. Financ. 1992, 47, 271–293. [Google Scholar] [CrossRef]
- Kusuoka, S. Limit theorem on option replication with transaction costs. Ann. Appl. Probab. 1995, 5, 198–221. [Google Scholar] [CrossRef]
- Barles, G.; Soner, H.M. Option pricing with transaction costs and nonlinear Black–Scholes equation. Financ. Stoch. 1998, 2, 799–812. [Google Scholar] [CrossRef]
- Cox, C.; Ross, S.A. The valuation of options for alternative stochastic process. J. Financ. Econ. 1976, 3, 145–146. [Google Scholar] [CrossRef]
- Tangman, D.Y.; Gopaul, A.; Bhuruth, M. Numerical pricing of options using high order compact finite difference schemes. J. Comput. Appl. Math. 2008, 218, 270–280. [Google Scholar] [CrossRef]
- McCartin, B.J.; Labadie, S.M. Accurate and efficient pricing of vanilla stock options via the Crandall-Douglas scheme. Appl. Math. Comput. 2003, 143, 39–60. [Google Scholar] [CrossRef]
- Ankudinova, J.; Ehrdardt, M. On the numerical solution of nonlinear Black–Scholes equations. Comput. Math. Appl. 2008, 56, 799–812. [Google Scholar] [CrossRef]
- Company, R.; Jodar, L. A numerical method for European option pricing with transaction costs nonlinear equation. Math. Comput. Model. 2009, 50, 910–920. [Google Scholar] [CrossRef]
- Jeong, D.; Yoo, M.; Kim, J. Finite difference method for the Black–Scholes equation without boundary conditions. Comput. Econ. 2018, 51, 961–972. [Google Scholar] [CrossRef]
- Koleva, M.N.; Mudzimbabwe, W.; Vulkov, L.G. Fourth-order conmpact finite schemes for a parabolic ordinary system of European option pricing liquidity shock model. Numer. Algorithms 2017, 74, 59–75. [Google Scholar] [CrossRef]
- Rao, S.C. Numerical solution of generalized Black–Scholes model. Appl. Math. Comput. 2018, 321, 401–421. [Google Scholar]
- Sari, M.; Balacescu, A. Discrete algorithms for Black Scholes option pricing economic model. In Business and Applied Economics Book of Abstracts; Institute of Economic Sciences: Belgrade, Serbia, 2018; pp. 152–155. [Google Scholar]
- Mashayekhi, S.; Hugger, J. Finite difference schemes for a nonlinear Black–Scholes Model with transaction cost and volatility risk. Acta Math. Univ. Comen. 2015, 84, 255–266. [Google Scholar]
- Hout, K.; Valkov, R. Numerical solution of a two-asset option valuation PDE by ADI finite difference discretization. AIP Conf. Proc. 2015, 1648, 1648. [Google Scholar]
- Hendrick, C.; Heuer, C.; Ehrhardt, M.; Günther, M. High-order ADI finite difference schemes for parabolic equations in the combination technique with application in finance. J. Comput. Appl. Math. 2017, 316, 175–194. [Google Scholar] [CrossRef]
- Markolefas, S. Standard Galerkin formulation with high order Langrange finite elements for option markets pricing. Appl. Math. Comput. 2008, 195, 707–720. [Google Scholar]
- Lin, S.B.; Chen, C.D. Applying the Model Order Reduction method to a European option pricing model. Econ. Model. 2013, 33, 533–536. [Google Scholar] [CrossRef]
- Falloon, W.; Turner, D. The Evaluation of a Market, Managing Energy Price Risk; Risk Books: London, UK, 1999. [Google Scholar]
- Kumar, A.; Tripathi, L.P.; Kadalbajoob, M.K. A numerical study of Asian option with radial basis functions based finite differences method. Eng. Anal. Bound. Elem. 2015, 50, 1–7. [Google Scholar] [CrossRef]
- Rad, J.A.; Parand, K.; Ballestra, L.C. Pricing European and American options by radial basis point interpolation. Appl. Math. Comput. 2015, 251, 363–377. [Google Scholar] [CrossRef]
- Vecer, J. Black–Scholes representation for Asian option. Math. Financ. 2014, 24, 598–626. [Google Scholar] [CrossRef]
- Bayraktar, E.; Xing, H. Pricing Asian options for jump diffusion. Math. Financ. 2011, 21, 117–143. [Google Scholar] [CrossRef]
- Sin, K. Numerical Methods for Derivative Pricing with Applications to Barrier Options. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2010. [Google Scholar]
- Moon, K.S. Efficient Monte-Carlo algorithm for pricing barrier options. Commun. Korean Math. Soc. 2008, 2, 285–294. [Google Scholar] [CrossRef]
- Zeng, X.C.; Guo, I.; Zhu, S.P. Pricing European Options Regime-Switching Assets: A comparative study of Monte Carlo and finite difference approaches. ANZIAM J. 2017, 2, 183–199. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. On splitting-based numerical methods for nonlinear models of European options. Int. J. Comput. Math. 2016, 93, 781–796. [Google Scholar] [CrossRef]
- Hozman, J.; Tichy, T. On the impact of various formulations of the boundary condition within numerical option valuation by DG method. Filomat 2016, 30, 4253–4263. [Google Scholar] [CrossRef]
- Anwar, M.N.; Andallah, L.S. A study on numerical solution of Black–Scholes model. J Math. Financ. 2018, 8, 372–381. [Google Scholar] [CrossRef]
- Appadu, A.R. Comparison of some finite difference methods for the Black–Scholes equation. AIP Conf. Proc. 2018, 1978, 470098. [Google Scholar]
- Jeong, D.; Yoo, M.; Yoo, C.; Kim, J. A hybrid Monte Carlo and finite difference method for option pricing. Comput. Econ. 2019, 53, 111–124. [Google Scholar] [CrossRef]
- Cen, Z.; Chen, W. A HODIE finite difference scheme for pricing American options. Adv. Differ. Equ. 2019, 2019, 67. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W.; Tadmor, E. Strong stability-preserving high-order time discretization methods. SIAM Rev. 2001, 43, 89–112. [Google Scholar] [CrossRef]
- Dura, G.; Moşneagu, A.M. Numerical approximation of Black–Scholes equation. Analele Ştiintifice Ale Universitătii Al.I. Cuza Din Iai (S.N) Matematică 2010, 5, 39–64. [Google Scholar] [CrossRef]
- Leentvaar, C.C. Numerical Solution of the Black–Scholes Equation with a Small Number of Grid Points. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Sari, M.; Gurarslan, G.; Zeytinoglu, A. High-order finite difference schemes for the solution of the generalized Burgers-Fisher equation. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1296–1308. [Google Scholar] [CrossRef]
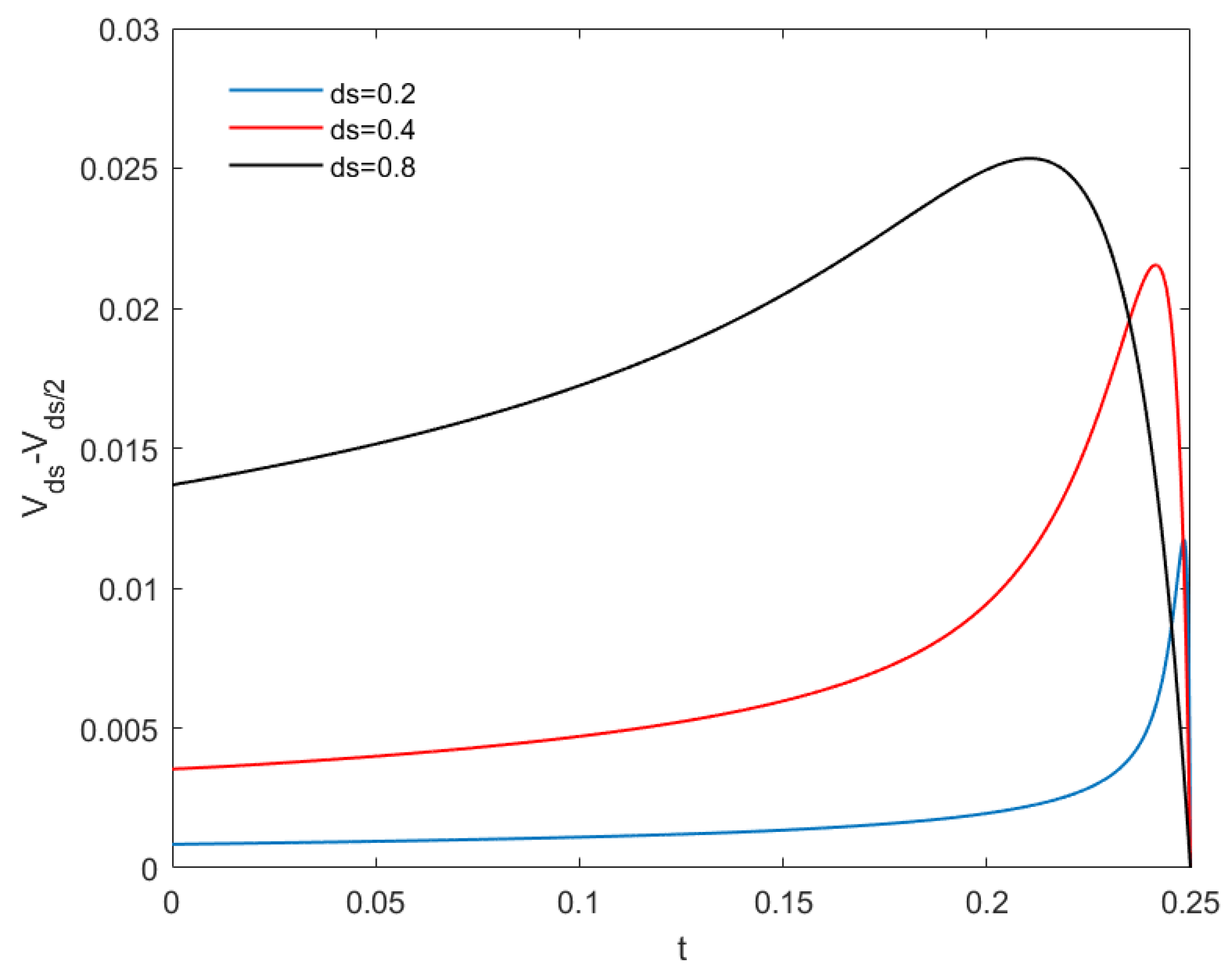
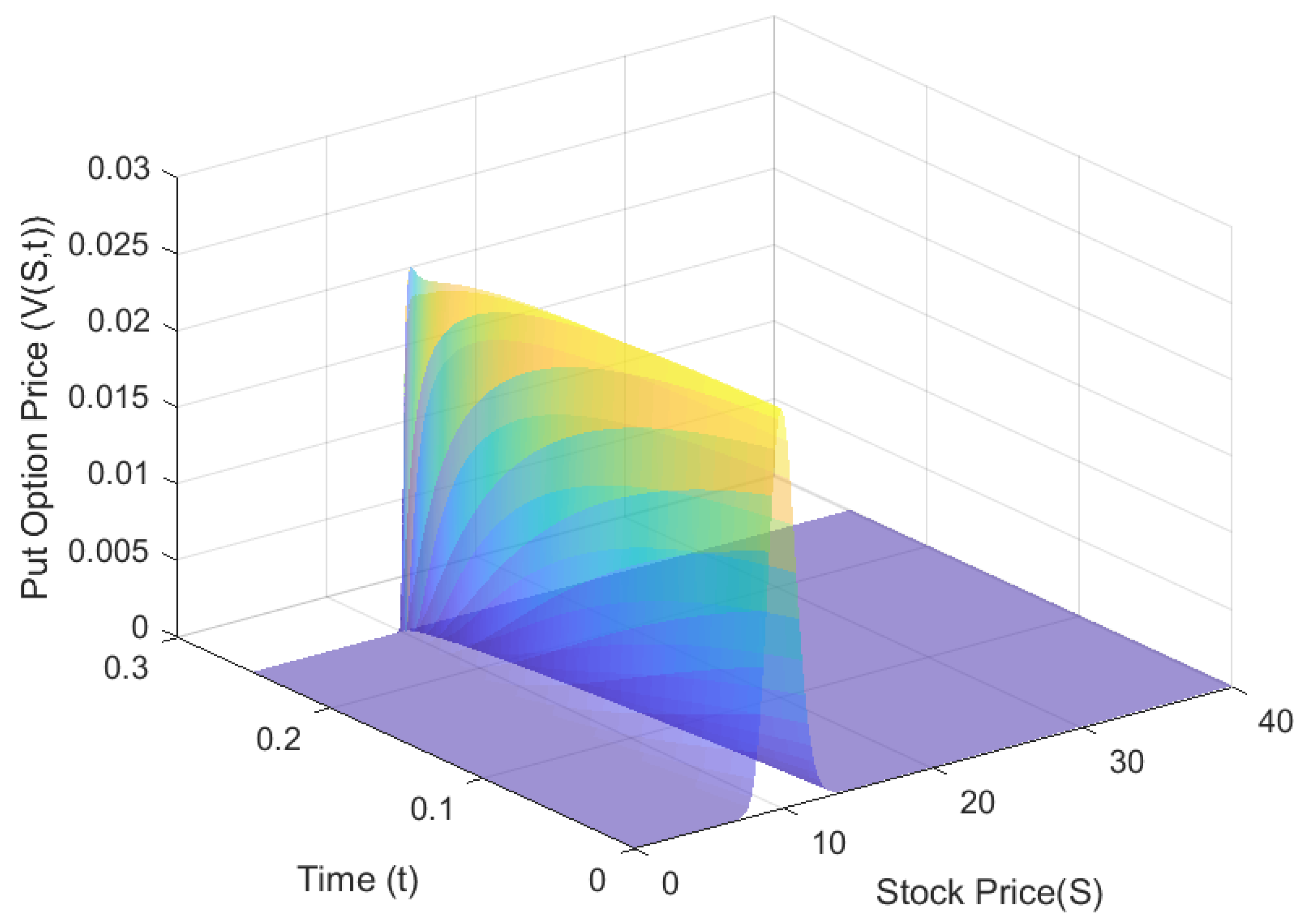
| S | SSP-RK3 + FD6 | Dura and Moşneagu [41] | Exact | ||
|---|---|---|---|---|---|
| Linear Model | Nonlinear Model | Solution | |||
| a = 0.02 | a = 0.05 | (Linear Model) | |||
| 4.0 | 5.753096 | 5.753096 | 5.753096 | 5.753102 | 5.753100 |
| 8.0 | 1.902102 | 1.904440 | 1.915559 | 1.902102 | 1.902434 |
| 10.0 | 0.668906 | 0.673788 | 0.696650 | 0.668360 | 0.669390 |
| 16.0 | 0.005324 | 0.005498 | 0.006353 | 0.005419 | 0.005386 |
| 20.0 | 1.091776 × 10 | 1.139578 × 10 | 1.375594 × 10 | 1.170806 × 10 | 1.129336 × 10 |
| N | M | Ratio | Ratio | ||
|---|---|---|---|---|---|
| 51 | 101 | 0.018822 | 0.007153 | ||
| 101 | 1001 | 0.018035 | 1.043695 | 0.002887 | 2.477658 |
| 201 | 2001 | 0.002668 | 6.759370 | 6.547562 × 10 | 4.409275 |
| 401 | 4001 | 4.036584 × 10 | 6.609549 | 1.392947 × 10 | 4.700510 |
| N | M | Error (Linear Model) | Error (Nonlinear Model) |
|---|---|---|---|
| 51 | 101 | 0.013100 | 0.012081 |
| 101 | 1001 | 0.004132 | 0.003932 |
| 201 | 2001 | 8.054754 × 10 | 9.081600 × 10 |
| N | M | CPU (Linear Model) | CPU (Nonlinear Model) | CPU (Nonlinear Model) |
|---|---|---|---|---|
| a = 0.02 | a = 0.05 | |||
| 51 | 101 | 0.136891 | 0.166548 | 0.171630 |
| 101 | 2001 | 3.223077 | 3.807224 | 3.830958 |
| 201 | 4001 | 12.112536 | 14.122904 | 14.242410 |
| 401 | 8001 | 63.284679 | 72.833058 | 72.978609 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulen, S.; Popescu, C.; Sari, M. A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities. Mathematics 2019, 7, 760. https://doi.org/10.3390/math7080760
Gulen S, Popescu C, Sari M. A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities. Mathematics. 2019; 7(8):760. https://doi.org/10.3390/math7080760
Chicago/Turabian StyleGulen, Seda, Catalin Popescu, and Murat Sari. 2019. "A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities" Mathematics 7, no. 8: 760. https://doi.org/10.3390/math7080760
APA StyleGulen, S., Popescu, C., & Sari, M. (2019). A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities. Mathematics, 7(8), 760. https://doi.org/10.3390/math7080760






