Characterization of Graphs Associated with Numerical Semigroups

Abstract

Let $\mathsf{\Gamma }$ be a numerical semigroup. We associate an undirected graph $G\left(\mathsf{\Gamma }\right)$ with a numerical semigroup $\mathsf{\Gamma }$ with vertex set $\{v_i:i\in \mathbb{N}\backslash \mathsf{\Gamma }\}$ and edge set $\{v_i{v}_j\iff i+j\in \mathsf{\Gamma }\}$. In this article, we discuss the connectedness, diameter, girth, and some other related properties of the graph $G\left(\mathsf{\Gamma }\right)$.

1. Introduction

In the last couple of decades, researchers have been assigning graphs to various kinds of algebraic structures, which opens new horizons to study algebraic structures with the help of graph theoretic properties and vice versa. In the recent past, various families of graphs associated with algebraic structures have been studied by a number of researchers (see [1,2,3,4,5,6,7,8]). The theory of the numerical semigroup is quite useful in the study of non-negative integer solutions of a linear equation in several variables with coefficients in $\mathbb{N}$ [9,10,11,12,13]. Applications of the numerical semigroup can be found in the study of the parameters of algebraic geometry codes [14,15,16].

Algebraic combinatorics employs algebraic methods to solve combinatorial problems and vice versa. The main feature of this subject is any useful interaction between algebra and combinatorics. One of the research areas in this field is associating a graph with an algebraic structure and has attracted considerable attention. It aims at exposing the relationship between algebra and graph theory and applications of one to the other. In [17], recently, a new combinatorial problem associated with the numerical semigroup was studied. A subset $\mathsf{\Gamma }\subseteq \mathbb{N}$ of nonnegative integers is known as the numerical semigroup if it satisfies the following condition:

• $a+b\in \mathsf{\Gamma }$$\forall a,b\in \mathsf{\Gamma },$
• $0\in \mathsf{\Gamma }$,
• $\mathbb{N}\backslash \mathsf{\Gamma }$ is finite.

The least positive integer in $\mathsf{\Gamma }$, denoted by $m\left(\mathsf{\Gamma }\right)$, is known as the multiplicity of the numerical semigroup. The elements of $\mathbb{N}\backslash \mathsf{\Gamma }$ are called the gaps of $\mathsf{\Gamma }$, and the largest of these gaps is known as the Frobenius number, denoted by $F\left(\mathsf{\Gamma }\right)$. A numerical semigroup $\mathsf{\Gamma }$ is symmetric if and only if $x\in \mathbb{Z}\backslash \mathsf{\Gamma }$ implies $F-x\in \mathsf{\Gamma }$, while it is known as pseudo symmetric if and only if $x\in \mathbb{Z}\backslash \mathsf{\Gamma }$ implies $F-x\in \mathsf{\Gamma }$ or $x=\frac{F}{2}$. It is well known that every numerical semigroup is finitely generated, that is there exist $a_1,\cdots ,a_t$ such that $\mathsf{\Gamma }=<a_1,\cdots ,a_t>=\{n_1{a}_1+\cdots n_t{a}_t:n_1,\cdots n_t\in \mathbb{N}\}$. Moreover, every numerical semigroup has a unique minimal system of generators. The cardinality of a minimal system of generators is called the embedding dimension of numerical semigroup $\mathsf{\Gamma }$, denoted by $e\left(\mathsf{\Gamma }\right)$. This is also well known that $e\left(\mathsf{\Gamma }\right)\le m\left(\mathsf{\Gamma }\right)$. For more details on e numerical semigroup, see [18].

A graph G is a pair of two sets V and E, where V is the set of vertices and E is the set of edges. The order $\left|V\right|$ of a set V is known as the order of the graph, while the order $\left|E\right|$ of the set E is known as the size of the graph. The distance between any two vertices p and q of a graph G is the length of the shortest path between them, denoted by $d(p,q)$, while the maximum distance between any two vertices of the graph G is known as the diameter, denoted by $\mathrm{diam}\left(G\right)$. The length of a shortest cycle in the graph is referred to as the girth of the graph. An alternate sequence of vertices and edges $v_1{e}_1{v}_2{e}_2{v}_3{e}_3{v}_4\cdots v_{n-1}{e}_{n-1}{v}_n$ is known as a path, denoted by $P_n$. A graph G is said to be complete if their is an edge between every pair of edges, and it is doted by $K_n$. Any vertex p of a connected graph G is referred to as a cut vertex, whose removal leaves the graph disconnected. A connected graph without cut vertices is referred to as a non-separable graph. Let $\mathsf{\Gamma }$ be a numerical semigroup. We define an undirected graph $G\left(\mathsf{\Gamma }\right)$ with vertex set $\{v_i:i\in g\left(\mathsf{\Gamma }\right)=\mathbb{N}\backslash \mathsf{\Gamma }\}$ and edge set $\{v_i{v}_j\iff i+j\in \mathsf{\Gamma }\}$.

The layout of this paper is as follows. Section 2 consist of four parts. We briefly describe the concept of connectedness and completeness of $G\left(\mathsf{\Gamma }\right)$ in Section 2.1. In Section 2.2, we present some results regarding the diameter and girth of $G\left(\mathsf{\Gamma }\right)$. In Section 2.3, we discuss the concept of the cut-point and connectivity of $G\left(\mathsf{\Gamma }\right)$, and in Section 2.4, we classify $G\left(\mathsf{\Gamma }\right)$ for some cases. Finally Section 3 concludes the article.

2. Results and Discussions

This section has been divided into four major parts: In this first part, the connectedness and completeness of $G\left(\mathsf{\Gamma }\right)$ are discussed. The second part consists of the diameter and girth of $G\left(\mathsf{\Gamma }\right)$. The third part is about the cut-point and separability of $G\left(\mathsf{\Gamma }\right)$, while in the fourth part, the classification of $G\left(\mathsf{\Gamma }\right)$ is presented.

2.1. Connectedness and Completeness of $G\left(\mathsf{\Gamma }\right)$

In this section, we show that $G\left(\mathsf{\Gamma }\right)$ is always a connected graph. Moreover, we provide the sufficient and necessary condition for $G\left(\mathsf{\Gamma }\right)$ to be complete.

Proposition 1.

Let Γ be a numerical semigroup of multiplicity $m\left(\mathsf{\Gamma }\right)$ and Frobenius number $F\left(\mathsf{\Gamma }\right)$. Then, $G\left(\mathsf{\Gamma }\right)$ is a connected graph with order at least $m\left(\mathsf{\Gamma }\right)-1$.

Proof. 

This is obvious, because $m\left(\mathsf{\Gamma }\right)$ is the smallest positive integer belonging to $\mathsf{\Gamma }$ and $F\left(\mathsf{\Gamma }\right)$ is the largest gap of $\mathsf{\Gamma }$. □

Proposition 2.

Let $n\ge 1$ be an integer. Then, there is a numerical semigroup Γ of multiplicity two such that $K^n\simeq G\left(\mathsf{\Gamma }\right)$.

Proof. 

For an integer $n\ge 1$, consider a numerical semigroup $\mathsf{\Gamma }=<2,2n+1>$. Then, clearly, $\mathsf{\Gamma }$ is symmetric and $g\left(\mathsf{\Gamma }\right)=\{1,3,5,\cdots ,2n-1\}.$ As all positive even integers are in $\mathsf{\Gamma }$ and the sum of two odd integers is an even integer, therefore, for all $i,j\in g\left(\mathsf{\Gamma }\right),$$i\ne j$ gives $i+j\in \mathsf{\Gamma }$. This implies that every two vertices of $G\left(\mathsf{\Gamma }\right)$ has an edge, and therefore, $G\left(\mathsf{\Gamma }\right)$ is isomorphic to a complete graph of order n. □

Theorem 1.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ. Then, $G\left(\mathsf{\Gamma }\right)$ is complete if and only if Γ is one of the semigroups given in Table 1.

Table 1. List of Numerical semigroups Γ for which $G(\mathsf{\Gamma }$) is complete.

$\mathbf{\Gamma }$	$\mathit{e}\left(\mathbf{\Gamma }\right)$
$<2,2n+1>,n\ge 1$	2
$<3,4>$	2
$<3,4,5>$	3
$<3,5>$	2
$<3,5,7>$	3

Proof. 

If $G\left(\mathsf{\Gamma }\right)$ is complete, then $m\left(\mathsf{\Gamma }\right)\ge 4$ is not possible because if $m\left(\mathsf{\Gamma }\right)\ge 4$, then there exist $1,2\in g\left(\mathsf{\Gamma }\right)$ such that there is no edge between $v_1$ and $v_2$. Therefore, the only possibilities remaining are either $m\left(\mathsf{\Gamma }\right)=2$ or $m\left(\mathsf{\Gamma }\right)=3$. If $m\left(\mathsf{\Gamma }\right)=2$, then the only possibility is that $\mathsf{\Gamma }=<2,2n+1>,n\ge 1$, and if $m\left(\mathsf{\Gamma }\right)=3$, then either $\mathsf{\Gamma }=<3,v_0>$ or $\mathsf{\Gamma }=<3,v_0,v_1>$, as $G\left(\mathsf{\Gamma }\right)$ is complete; therefore, $v_0$ must be four or five, because if $v_0\ge 7$, then there exist $1,4\in g\left(\mathsf{\Gamma }\right)$ such that there is no edge between $v_1$ and $v_4$. Now, if $v_0=4$, then $\mathsf{\Gamma }=<3,4>$ or $\mathsf{\Gamma }=<3,4,5>$, and if $v_0=5$, then, $\mathsf{\Gamma }=<3,5>$ or $\mathsf{\Gamma }=<3,5,7>$. The other implication is obvious. □

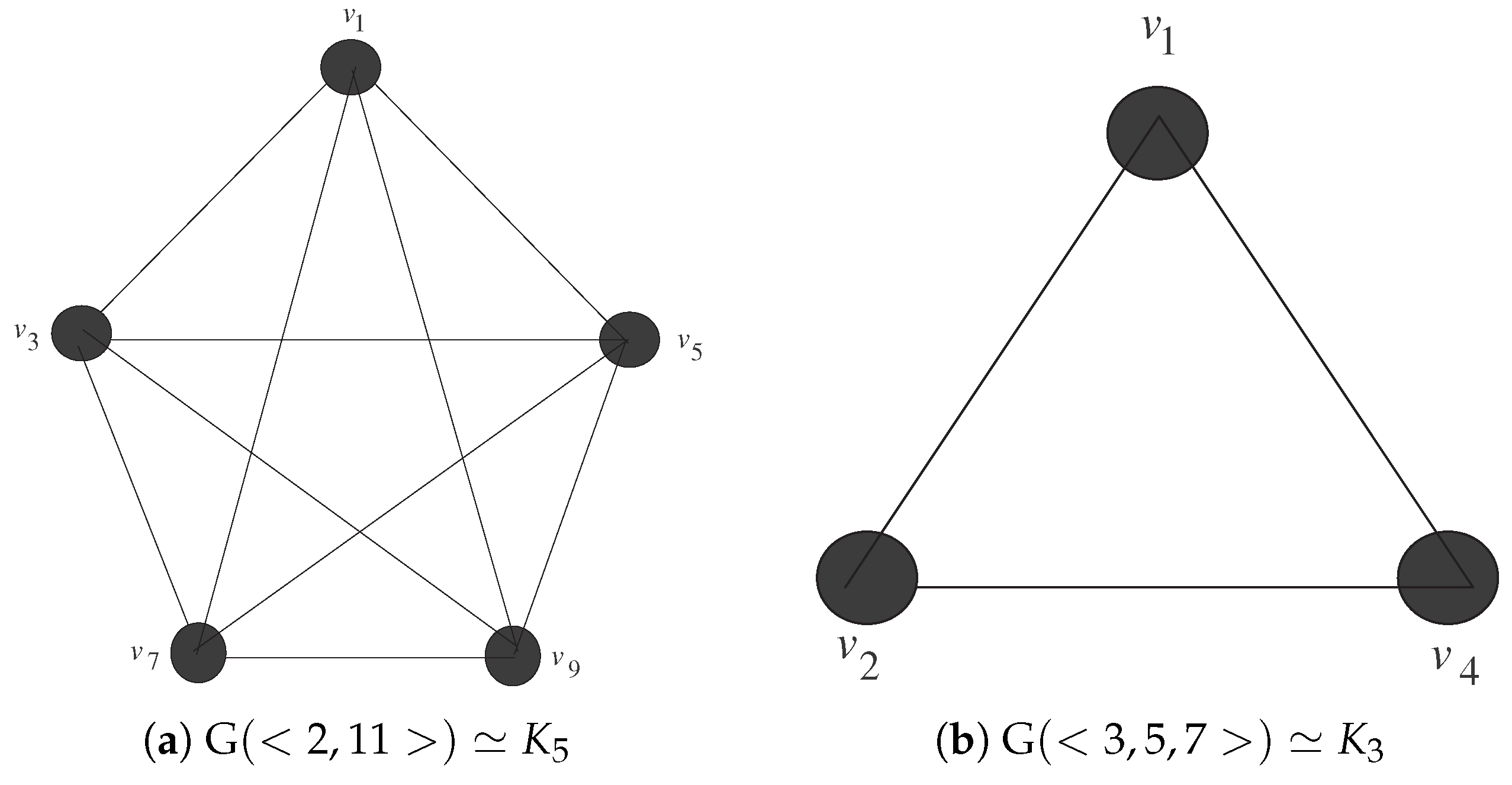
In Figure 1, we provide two examples of complete graphs corresponding to the numerical semigroups $<2,11>$ and $<3,5,7>$.

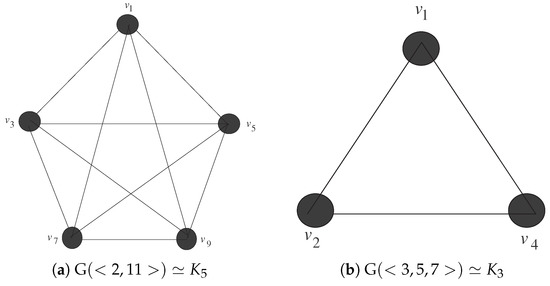
Figure 1. Two examples, when $G\left(\mathsf{\Gamma }\right)$ is complete.

2.2. Diameter and Girth of $G\left(\mathsf{\Gamma }\right)$

In this section, we present our results on the diameter and girth of $G\left(\mathsf{\Gamma }\right)$.

Proposition 3.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ. Then, diam$\left(G\right(\mathsf{\Gamma }\left)\right)\le 2$. Furthermore, if $G\left(\mathsf{\Gamma }\right)$ contains a cycle, then gr$\left(G\right(\mathsf{\Gamma }\left)\right)\le 5$.

Proof. 

As $F\left(\mathsf{\Gamma }\right)\in g\left(\mathsf{\Gamma }\right)$ is the largest gap, therefore $F\left(\mathsf{\Gamma }\right)+k\in \mathsf{\Gamma }$ for all $k\in g\left(\mathsf{\Gamma }\right)$ and $k\ne F\left(\mathsf{\Gamma }\right)$. This implies that $v_{F\left(\mathsf{\Gamma }\right)}$ has an edge with every vertex $v_k$, and therefore, $d(v_{F\left(\mathsf{\Gamma }\right)},v_k)=1$. Now, for any two vertices $v_i$ and $v_j,$$i\ne j$, we have:

$$d(v_i,v_j)\le d(v_i,v_{F\left(\mathsf{\Gamma }\right)})+d(v_{F\left(\mathsf{\Gamma }\right)},v_j)\le 2;$$

this implies:

$$\mathrm{diam}\left(G\right(\mathsf{\Gamma }\left)\right)\le 2.$$

Moreover, if any undirected graph G has a cycle, then gr$\left(G\right)\le 2$diam$\left(G\right)+1$ (see [19], Proposition 1.3.2). Therefore, gr$\left(G\right(\mathsf{\Gamma }\left)\right)\le 5$. □

Proposition 4.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ. If the order of $G\left(\mathsf{\Gamma }\right)\ge 4,$ then $G\left(\mathsf{\Gamma }\right)$ must contain a cycle of length three.

Proof. 

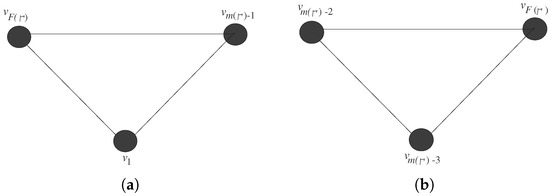
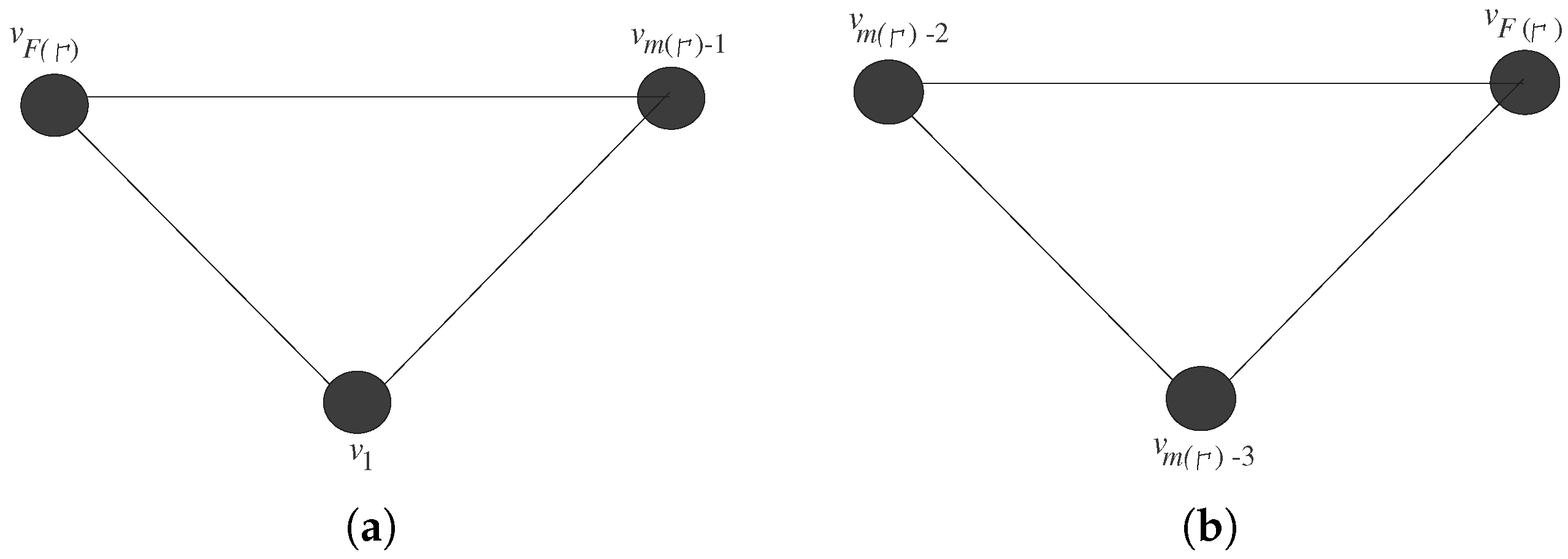
If $G\left(\mathsf{\Gamma }\right)$ is complete, then trivially, it contains a cycle of length three, and if $G\left(\mathsf{\Gamma }\right)$ is not a complete graph, then $m\left(\mathsf{\Gamma }\right)\ge 3$ (see Theorem 1). Note that, if $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)-1$, then $1,m\left(\mathsf{\Gamma }\right)-1,F\left(\mathsf{\Gamma }\right)$ are distinct and must belong to $g\left(\mathsf{\Gamma }\right)$. Since $F\left(\mathsf{\Gamma }\right)\in g\left(\mathsf{\Gamma }\right)$ is the largest gap, therefore $v_{F\left(\mathsf{\Gamma }\right)}$ has an edge with vertices $v_1$ and $v_{m\left(\mathsf{\Gamma }\right)-1}$. Furthermore, $v_1$ and $v_{m\left(\mathsf{\Gamma }\right)-1}$ are connected by an edge because $1+m\left(\mathsf{\Gamma }\right)-1=m\left(\mathsf{\Gamma }\right)\in \mathsf{\Gamma }$. This gives that vertices $v_1$, $v_{m\left(\mathsf{\Gamma }\right)-1}$ and $v_{F\left(\mathsf{\Gamma }\right)}$ form a cycle of length three (see Figure 2a). Now, if $F\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)-1$, then $m\left(\mathsf{\Gamma }\right)\ge 5$ because the order of $G\left(\mathsf{\Gamma }\right)\ge 4$. In this case, $m\left(\mathsf{\Gamma }\right)-3,m\left(\mathsf{\Gamma }\right)-2,F\left(\mathsf{\Gamma }\right)$ are distinct and must belong to $g\left(\mathsf{\Gamma }\right)$. Note that

$$m\left(\mathsf{\Gamma }\right)-3+m\left(\mathsf{\Gamma }\right)-2=\left(m\right(\mathsf{\Gamma })-1)+\left(m\right(\mathsf{\Gamma })-4)=F\left(\mathsf{\Gamma }\right)+\left(m\right(\mathsf{\Gamma })-4).$$

Figure 2. Induced subgraphs of $g\left(\mathsf{\Gamma }\right)$ for the cases (a) $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)-1$ and (b) $F\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)-1$.

This gives that $v_{m\left(\mathsf{\Gamma }\right)-2}$ and $v_{m\left(\mathsf{\Gamma }\right)-3}$ are connected by an edge, and therefore, $v_{m\left(\mathsf{\Gamma }\right)-3}$, $v_{m\left(\mathsf{\Gamma }\right)-2}$, and $v_{F\left(\mathsf{\Gamma }\right)}$ form a cycle of length three (see Figure 2b). □

Corollary 1.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ such that the order of $G\left(\mathsf{\Gamma }\right)\ge 4$. Then, $G\left(\mathsf{\Gamma }\right)$ is not a bipartite graph.

Corollary 2.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ such that the order of $G\left(\mathsf{\Gamma }\right)\ge 4$. Then, gr$\left(G\right(\mathsf{\Gamma }\left)\right)=3$.

2.3. Cut-Point and Separability of $G\left(\mathsf{\Gamma }\right)$

In this section, we investigate the case when $G\left(\mathsf{\Gamma }\right)$ has a cut-point. Moreover, we show that if $\mathsf{\Gamma }$ is an irreducible numerical semi-group, then $G\left(\mathsf{\Gamma }\right)$ has no cut-point.

Proposition 5.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semi-group Γ such that the order of $G\left(\mathsf{\Gamma }\right)\ge 3$. If $F\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)-1$, then $v_{F\left(\mathsf{\Gamma }\right)}$ is the only cut-point of $G\left(\mathsf{\Gamma }\right)$.

Proof. 

If $F\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)-1$, then $g\left(\mathsf{\Gamma }\right)=\{1,2,\cdots ,m(\mathsf{\Gamma })-1\}$. This gives that $v_1$ is connected only with $v_{m\left(\mathsf{\Gamma }\right)-1}$; therefore, $G\left(\mathsf{\Gamma }\right)-\left\{v_F\right\}$ has at least two disconnected components. This implies that $v_F$ is a cut-point. Moreover, for all $i\in g\left(\mathsf{\Gamma }\right)-\left\{F\right(\mathsf{\Gamma }\left)\right\},$$v_i$ is connected by $v_{F\left(\mathsf{\Gamma }\right)}$ by an edge. Therefore, $G\left(\mathsf{\Gamma }\right)-\left\{v_i\right\}$ is always a connected graph. □

Remark 1.

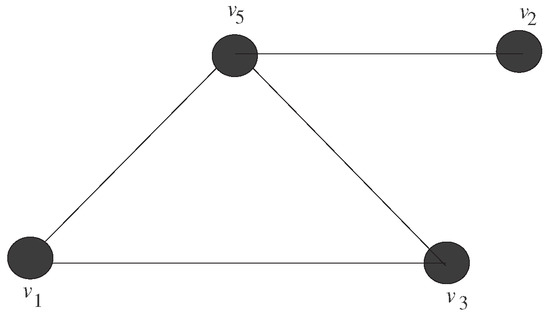
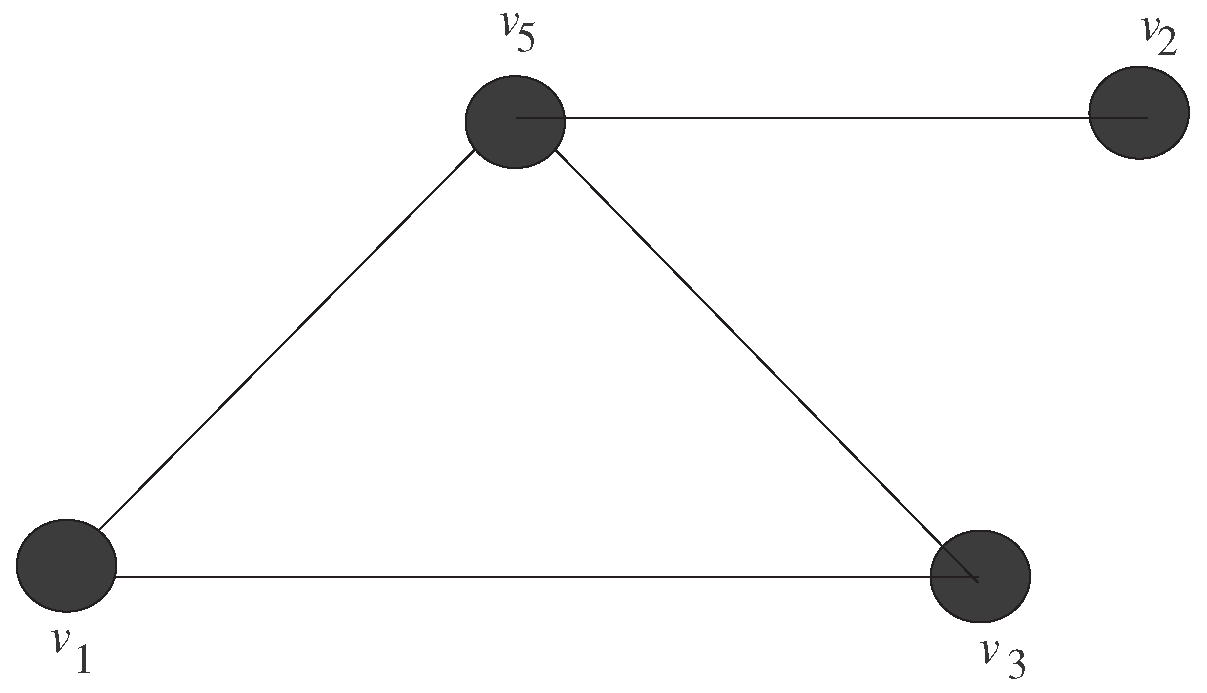
Note that even in the case of $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)-1,$$G\left(\mathsf{\Gamma }\right)$ can have the cut-point. For example if $\mathsf{\Gamma }=<4,6,7,9>$, then $F\left(\mathsf{\Gamma }\right)=5>4=m\left(\mathsf{\Gamma }\right)$, and $G\left(\mathsf{\Gamma }\right)$ is given in the following Figure 3.

Figure 3. $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)-1,$ but $G\left(\mathsf{\Gamma }\right)$ has a cut-point.

Proposition 6.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a symmetric or pseudo-symmetric numerical semigroup. If $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right),$ then $G\left(\mathsf{\Gamma }\right)$ has no cut-point.

Proof. 

As $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)$ and $m\left(\mathsf{\Gamma }\right)\in \mathsf{\Gamma }$, therefore $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)\in g\left(\mathsf{\Gamma }\right)$.

If $\mathsf{\Gamma }$ is symmetric, then for any $i\in g\left(\mathsf{\Gamma }\right)$ and $i\ne F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right),$ we have:

$$F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i=F\left(\mathsf{\Gamma }\right)-\left(m\right(\mathsf{\Gamma })-i).$$

If $m\left(\mathsf{\Gamma }\right)-i<0$, then clearly $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i\in \mathsf{\Gamma }$, and if $m\left(\mathsf{\Gamma }\right)-i>0$, then $m\left(\mathsf{\Gamma }\right)-i\in g\left(\mathsf{\Gamma }\right)$ and $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i\in \mathsf{\Gamma },$ because $\mathsf{\Gamma }$ is symmetric. Note that $m\left(\mathsf{\Gamma }\right)-i\ne F,$ because $F\left(\mathsf{\Gamma }\right)>m\left(\mathsf{\Gamma }\right)$. This gives that for any $i,j\in g\left(\mathsf{\Gamma }\right),i,j\ne F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right),F\left(\mathsf{\Gamma }\right),$ vertices $v_i$, $v_j$ must have two different paths of length two, $v_i-v_{F\left(\mathsf{\Gamma }\right)}-v_j$ and $v_i-v_{F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)}-v_j$.

Now, if $\mathsf{\Gamma }$ is pseudo-symmetric, then $\frac{F\left(\mathsf{\Gamma }\right)}{2}\in g\left(\mathsf{\Gamma }\right)$. If $\frac{F\left(\mathsf{\Gamma }\right)}{2}<F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)$, then for any $i\in g\left(\mathsf{\Gamma }\right)$ and $i\ne F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right),$ we write:

$$F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i=F\left(\mathsf{\Gamma }\right)-\left(m\right(\mathsf{\Gamma })-i).$$

If $m\left(\mathsf{\Gamma }\right)-i<0$, then clearly $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i\in \mathsf{\Gamma }$, and if $m\left(\mathsf{\Gamma }\right)-i>0$, then $m\left(\mathsf{\Gamma }\right)-i\in g\left(\mathsf{\Gamma }\right)$. Assume $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i\in g\left(\mathsf{\Gamma }\right)$, then either $m\left(\mathsf{\Gamma }\right)-i\in \mathsf{\Gamma }$ or $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i=\frac{F\left(\mathsf{\Gamma }\right)}{2}$. Note that $m\left(\mathsf{\Gamma }\right)-i\in \mathsf{\Gamma }$ is not possible because $m\left(\mathsf{\Gamma }\right)-i\in g\left(\mathsf{\Gamma }\right)$ and $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i=\frac{F\left(\mathsf{\Gamma }\right)}{2}$ is also not possible because $\frac{F\left(\mathsf{\Gamma }\right)}{2}<F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)$. Therefore, the only possibility is $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)+i\in \mathsf{\Gamma }$. This gives that for any $i,j\in g\left(\mathsf{\Gamma }\right),i,j\ne F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right),F\left(\mathsf{\Gamma }\right),$ vertices $v_i$, $v_j$ must have two different paths of length two, $v_i-v_{F\left(\mathsf{\Gamma }\right)}-v_j$ and $v_i-v_{F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)}-v_j$.

Now, if $\frac{F\left(\mathsf{\Gamma }\right)}{2}>F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)$, then for any $i\in g\left(\mathsf{\Gamma }\right)$ and $i\ne \frac{F\left(\mathsf{\Gamma }\right)}{2},$ consider $\frac{F\left(\mathsf{\Gamma }\right)}{2}+i\in g\left(\mathsf{\Gamma }\right).$ As $F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right)<\frac{F\left(\mathsf{\Gamma }\right)}{2}<\frac{F\left(\mathsf{\Gamma }\right)}{2}+i<F\left(\mathsf{\Gamma }\right),$ therefore there exist some $j\in g\left(\mathsf{\Gamma }\right),j<m\left(\mathsf{\Gamma }\right),j\ne \frac{F\left(\mathsf{\Gamma }\right)}{2}$ such that $F\left(\mathsf{\Gamma }\right)-j=\frac{F\left(\mathsf{\Gamma }\right)}{2}+i.$ Then, either $j\in \mathsf{\Gamma }$ or $F\left(\mathsf{\Gamma }\right)-j=\frac{F\left(\mathsf{\Gamma }\right)}{2}$. Clearly, $j\in \mathsf{\Gamma }$ is not possible because $j\in g\left(\mathsf{\Gamma }\right)$, and also, $F\left(\mathsf{\Gamma }\right)-j=\frac{F\left(\mathsf{\Gamma }\right)}{2}$ is not possible because $j\ne \frac{F\left(\mathsf{\Gamma }\right)}{2}$. Therefore, the only possibility is $\frac{F\left(\mathsf{\Gamma }\right)}{2}+i\in \mathsf{\Gamma }$. This gives that for any $i,j\in g\left(\mathsf{\Gamma }\right),i,j\ne F\left(\mathsf{\Gamma }\right)-m\left(\mathsf{\Gamma }\right),F\left(\mathsf{\Gamma }\right),$ vertices $v_i$, $v_j$ must have two different paths of length two, $v_i-v_{F\left(\mathsf{\Gamma }\right)}-v_j$ and $v_i-v_{\frac{F\left(\mathsf{\Gamma }\right)}{2}}-v_j$. □

Corollary 3.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a symmetric or pseudo-symmetric numerical semigroup. Then, $G\left(\mathsf{\Gamma }\right)$ is not separable.

2.4. Classification of $G\left(\mathsf{\Gamma }\right)$

In this section, we provide the sufficient and necessary condition of $G\left(\mathsf{\Gamma }\right)$ to be a path graph on three vertices. Moreover, we classify all graphs for the cases when the order of $G\left(\mathsf{\Gamma }\right)$ is equal to $m\left(\mathsf{\Gamma }\right)$ or $m\left(\mathsf{\Gamma }\right)+1$.

Theorem 2.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ. Then, $G\left(\mathsf{\Gamma }\right)\simeq P_3$ if and only if $m\left(\mathsf{\Gamma }\right)=4$ and $F\left(\mathsf{\Gamma }\right)=3$.

Proof. 

If $G\left(\mathsf{\Gamma }\right)\simeq P_3$, then $\mid g\left(\mathsf{\Gamma }\right)\mid =3$, and there are two vertices of degree one and one vertex of degree two. Note that $m\left(\mathsf{\Gamma }\right)=2$ and 3 is not possible, because if $m\left(\mathsf{\Gamma }\right)=2$, then $G\left(\mathsf{\Gamma }\right)\simeq K_3$, and if $m\left(\mathsf{\Gamma }\right)=3$, then $g\left(\mathsf{\Gamma }\right)=\{1,2,F\},$ where $F>3$; therefore, $G\left(\mathsf{\Gamma }\right)\simeq K_3$. Furthermore, $m\left(\mathsf{\Gamma }\right)\ge 5$ is not possible, because the order of $G\left(\mathsf{\Gamma }\right)=3$. This implies that the only possibility is $m\left(\mathsf{\Gamma }\right)=4$ and $F\left(\mathsf{\Gamma }\right)=3$. The other implication is obvious. □

Corollary 4.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a numerical semigroup Γ. If the order of $G\left(\mathsf{\Gamma }\right)=3$, then either $G\left(\mathsf{\Gamma }\right)\simeq K_3$ or $G\left(\mathsf{\Gamma }\right)\simeq P_3$.

Lemma 1.

Let Γ be a pseudo-symmetric numerical semigroup. Then, there is no $G\left(\mathsf{\Gamma }\right)$ of order $m\left(\mathsf{\Gamma }\right)+1$.

Proof. 

If $\mathsf{\Gamma }$ is pseudo-symmetric and the order of $G\left(\mathsf{\Gamma }\right)$ is $m\left(\mathsf{\Gamma }\right)+1$, then $m\left(\mathsf{\Gamma }\right)+1=\frac{F\left(\mathsf{\Gamma }\right)+2}{2}$. This gives $F\left(\mathsf{\Gamma }\right)=2m\left(\mathsf{\Gamma }\right),$ which is not possible. □

In the following proposition, $[v_i:v_1,v_2,\cdots ,v_k]$ denote that the vertices $v_1,v_2,\cdots ,v_k$ are adjacent to the vertex $v_i$, and we call this the adjacency vector of vertex $v_i$.

Proposition 7.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a symmetric or pseudo-symmetric numerical semigroup. If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)$ or $m\left(\mathsf{\Gamma }\right)+1$, then $G\left(\mathsf{\Gamma }\right)$ can be computed as follows:

Proof. 

$\mathbf{Case}\mathbf{1}$: If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)$, then $g\left(\mathsf{\Gamma }\right)=\{1,2,\cdots ,m(\mathsf{\Gamma })-1,F(\mathsf{\Gamma }\left)\right\},$ where $F\left(\mathsf{\Gamma }\right)=2m\left(\mathsf{\Gamma }\right)-1$, if $\mathsf{\Gamma }$ is symmetric, and $F\left(\mathsf{\Gamma }\right)=2m\left(\mathsf{\Gamma }\right)-2$, if $\mathsf{\Gamma }$ is pseudo-symmetric. Now, if $m\left(\mathsf{\Gamma }\right)$ is odd, then the adjacency vectors for the vertices of graph $G\left(\mathsf{\Gamma }\right)$ are $[v_i:v_{m\left(\mathsf{\Gamma }\right)-i},v_{m\left(\mathsf{\Gamma }\right)-i+1},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{F\left(\mathsf{\Gamma }\right)}],$ for $1\le i\le \frac{m\left(\mathsf{\Gamma }\right)-1}{2}$ and $[v_i:v_{i+1},v_{i+2},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{F\left(\mathsf{\Gamma }\right)}],$ and for $\frac{m\left(\mathsf{\Gamma }\right)-1}{2}<i<m\left(\mathsf{\Gamma }\right)-1$ and $[v_{m\left(\mathsf{\Gamma }\right)-1}:v_{F\left(\mathsf{\Gamma }\right)}]$. If $m\left(\mathsf{\Gamma }\right)$ is even, then the adjacency vectors for the vertices of graph $G\left(\mathsf{\Gamma }\right)$ are $[v_i:v_{m\left(\mathsf{\Gamma }\right)-i},v_{m\left(\mathsf{\Gamma }\right)-i+1},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{F\left(\mathsf{\Gamma }\right)}],$ for $1\le i<\frac{m\left(\mathsf{\Gamma }\right)}{2}$ and $[v_i:v_{i+1},v_{i+2},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{F\left(\mathsf{\Gamma }\right)}],$ and for $\frac{m\left(\mathsf{\Gamma }\right)}{2}\le i<m\left(\mathsf{\Gamma }\right)-1$ and $[v_{m\left(\mathsf{\Gamma }\right)-1}:v_{F\left(\mathsf{\Gamma }\right)}]$.

$\mathbf{Case}\mathbf{2}$: If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)$, then there is no $G\left(\mathsf{\Gamma }\right),$ if $\mathsf{\Gamma }$ is pseudo-symmetric (see Lemma 1), so the only possibility is that $\mathsf{\Gamma }$ is symmetric; therefore, $g\left(\mathsf{\Gamma }\right)=\{1,2,\cdots ,m(\mathsf{\Gamma })-1,m(\mathsf{\Gamma })+1,F(\mathsf{\Gamma }\left)\right\},$ where $F\left(\mathsf{\Gamma }\right)=2m\left(\mathsf{\Gamma }\right)+1$. If $m\left(\mathsf{\Gamma }\right)$ is odd, then the adjacency vectors for the vertices of graph $G\left(\mathsf{\Gamma }\right)$ are $[v_i:v_{m\left(\mathsf{\Gamma }\right)-i},v_{m\left(\mathsf{\Gamma }\right)-i+1},\cdots ,\widehat{v_{m\left(\mathsf{\Gamma }\right)-j}},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{m\left(\mathsf{\Gamma }\right)+1},v_{F\left(\mathsf{\Gamma }\right)}]$, for $1\le i\le \frac{m\left(\mathsf{\Gamma }\right)-1}{2}$, where $\widehat{v_{m\left(\mathsf{\Gamma }\right)-j}}$ is a vertex excluded from the adjacency vector, if $i-j=1$ and $[v_i:v_{i+1},v_{i+2},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{m\left(\mathsf{\Gamma }\right)+1},v_{F\left(\mathsf{\Gamma }\right)}],$ and for $\frac{m\left(\mathsf{\Gamma }\right)-1}{2}<i\le m-1$ and $[v_{m\left(\mathsf{\Gamma }\right)+1}:v_{F\left(\mathsf{\Gamma }\right)}]$. Now, if $m\left(\mathsf{\Gamma }\right)$ is even, then the adjacency vectors for the vertices of graph $G\left(\mathsf{\Gamma }\right)$ are $[v_i:v_{m\left(\mathsf{\Gamma }\right)-i},v_{m\left(\mathsf{\Gamma }\right)-i+1},\cdots ,\widehat{v_{m\left(\mathsf{\Gamma }\right)-j}},\cdots ,v_{m\left(\mathsf{\Gamma }\right)-1},v_{m\left(\mathsf{\Gamma }\right)+1},v_{F\left(\mathsf{\Gamma }\right)}],$ for $1\le i<\frac{m\left(\mathsf{\Gamma }\right)}{2}$, where $\widehat{v_{m\left(\mathsf{\Gamma }\right)-j}}$ is a vertex excluded from the adjacency vector, if $i-j=1$ and $[v_i:v_{i+1},v_{i+2},\cdots ,\widehat{v_{i+j}},v_{m\left(\mathsf{\Gamma }\right)-1},v_{m\left(\mathsf{\Gamma }\right)+1},v_{F\left(\mathsf{\Gamma }\right)}],$ for $\frac{m\left(\mathsf{\Gamma }\right)}{2}\le i\le m\left(\mathsf{\Gamma }\right)-1$, where $\widehat{v_{i+j}}$ is a vertex excluded from the adjacency vector, and if $2i+j-1=m\left(\mathsf{\Gamma }\right)$ and $[v_{m\left(\mathsf{\Gamma }\right)+1}:v_{F\left(\mathsf{\Gamma }\right)}]$. □

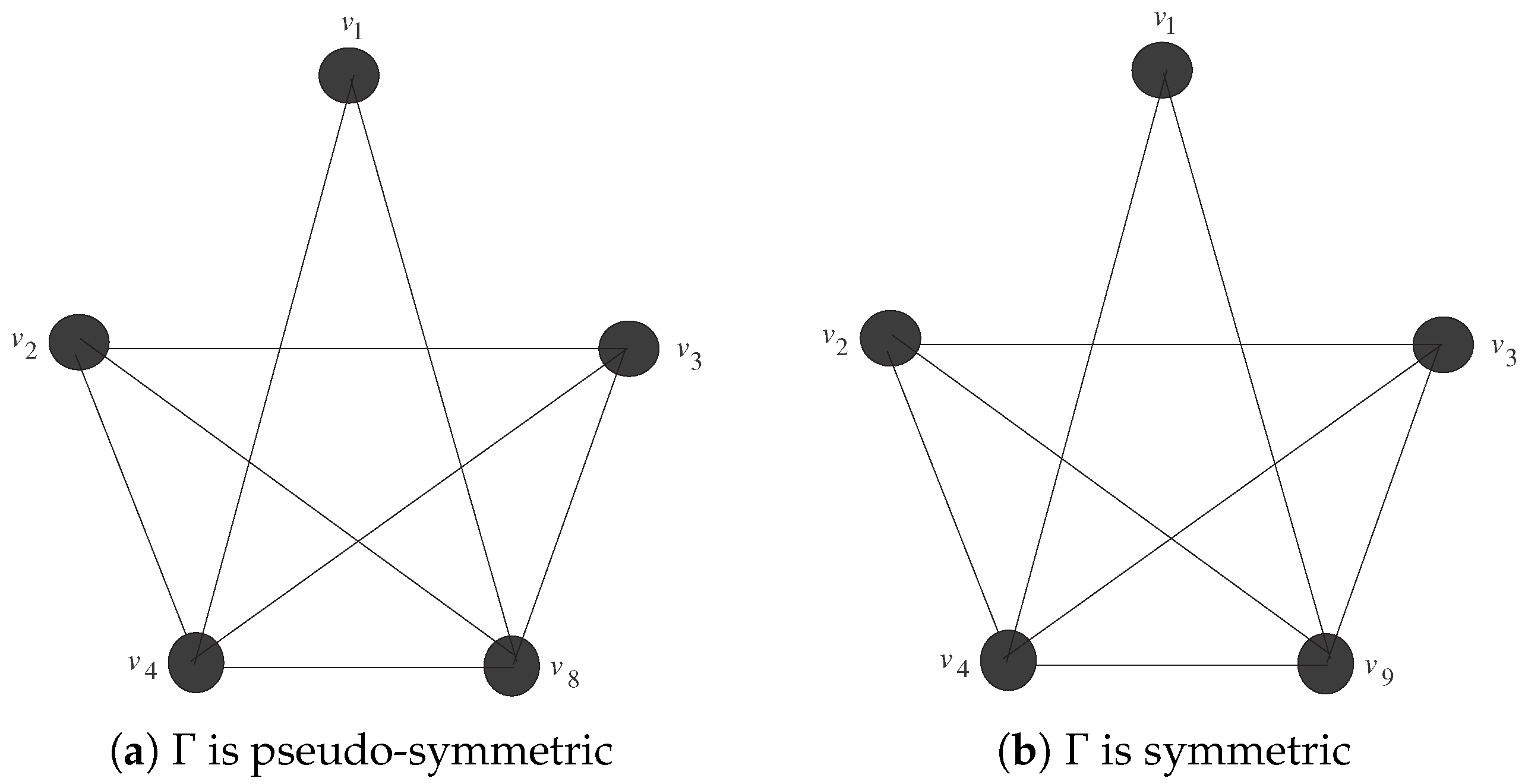
In Figure 4, we give the classification of graphs for $\mid g\left(\mathsf{\Gamma }\right)\mid =m\left(\mathsf{\Gamma }\right)=5$ by using Proposition 7.

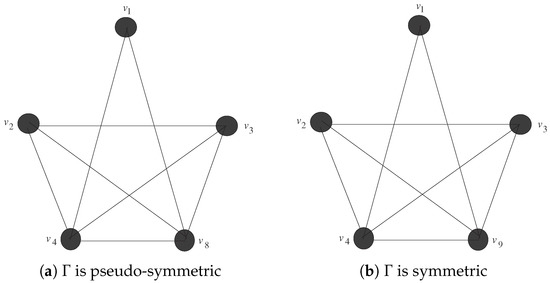
Figure 4. $\mid g\left(\mathsf{\Gamma }\right)\mid =m\left(\mathsf{\Gamma }\right)=5$.

Corollary 5.

Let $G\left(\mathsf{\Gamma }\right)$ be a graph associated with a symmetric or pseudo-symmetric numerical semigroup. If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)$ or $m\left(\mathsf{\Gamma }\right)+1$, then ${\kappa }_v\left(G\left(\mathsf{\Gamma }\right)\right)$, and the connectivity of $G\left(\mathsf{\Gamma }\right)$ is two or three.

Proof. 

If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)$, then from Proposition 7, it follows that deg$\left(v_1\right)=2,$ which is minimum. Therefore, ${\kappa }_v\left(G\left(\mathsf{\Gamma }\right)\right)\le 2$, but from Proposition 6, it follows that ${\kappa }_v\left(G\left(\mathsf{\Gamma }\right)\right)=2.$

If the order of $G\left(\mathsf{\Gamma }\right)=m\left(\mathsf{\Gamma }\right)+1$, then deg$\left(v_1\right)=3,$ which is minimum, if $m\left(\mathsf{\Gamma }\right)\ne 4$ and deg$\left(v_2\right)=2,$ which is minimum, and if $m\left(\mathsf{\Gamma }\right)=4$. Therefore, ${\kappa }_v\left(G\left(\mathsf{\Gamma }\right)\right)=2$ or 3. □

3. Conclusions

In this article, graphs associated with a numerical semigroup have been studied, and it was proven that these graphs are connected. We also studied some properties like girth, diameter, cut-point, etc., of these graphs. A necessary and sufficient condition has been given for a graph associated with the numerical semigroup to be complete. Furthermore, we presented the classification of these graphs for some special cases.