Abstract
In the present article, fractional-order partial differential equations with proportional delay, including generalized Burger equations with proportional delay are solved by using Natural transform decomposition method. Natural transform decomposition method solutions for both fractional and integer orders are obtained in series form, showing higher convergence of the proposed method. Illustrative examples are considered to confirm the validity of the present method. Therefore, Natural transform decomposition method is considered to be one of the best analytical technique, to solve fractional-order linear and non-linear Partial deferential equations particularly fractional-order partial differential equations with proportional delay.
1. Introduction
A delay differential equations (DDE’s) is one in which the derivative of the unknown function at a specific time is given as far as the values of function at the pastime. In the mathematical evaluation of a physical procedure, we commonly assume that, the characteristic of idea taken into account depends only on the present situation, a hypothesis which established for a dynamical system. However, there are a lot of physical situations which are not feasible under such hypothesis and may lead poor execution. In this circumstance it is smarter to think about that, the system conduct also relies upon the previous state. These schemes are called time-delay schemes [1,2].
Many physical procedure both natural and artificial, in economics, physics, chemistry, biology, medicine, and engineering involves time delay. A more realistic model must contain some past history of the system. Infect time delay occurs in almost every physical situation, responsible for results very closed to reality. Introduction of delay in the model, builds up its elements, and allows a detail investigation of this present reality wonders [3]. DDE’s are considered to be very useful in biological as well as physical sciences for which the evaluation of the model does not depend only on the current situation with the scheme, yet in addition on the previous history, such as delayed epidemic model, delay modeling in psychology, exothermic and endothermic chemical reactions in chemical industry [4].
Generally it is tough experience in order to find an exact result of a wide range of differential equations. Nevertheless, numerous effective techniques has been developed to find the approximate result of partial differential equations (PDE’s) with proportional delay, such as functional constraint’s method [5], iterated pseudo spectral method [6], reduce differential transform method (RDTM) for PDE’s by Abazari and Ganji [7], homotopy perturbation method for time fractional PDE’s by Sakar et al. and F. Shakeri [4,8], variational iteration method (VIM) [9], predictor-corrector algorithm [10], Adams-Bashforth-Moulton algorithm [11], a numerical method for delayed differential equations in fractional order: based on the definition of GL [12], an extended predictor-corrector algorithm for differential equations in variable-order fractional delay [13], Optimal Periodic-Gain fractional delayed state feedback control for linear periodic time-delayed systems [14], spectral collocation methods [15], group analysis method for Burgers equation due to Tanthanuch [16], andthe two-dimensional differential transform method the solution of specific class of PDE’s [17].
Natural transform and Adomian decomposition method are two powerful methods that have been used to have developed Natural transform decomposition method. Many physical phenomena which are modeled by PDE’s and fractional PDE’s are solved by using NTDM, such as the analytical solution of couple system of non-linear PDE’s are suggested in [18], the solution non-linear ODE,s are successfully presented in [19], non-linear PDE’s [20], fractional unsteady flow of a poly tropic gas model [21], fractional telegraph equations [22], fractional Fokker-Plank equation and Schrodinger equation [23]. The rest of the article is structured as: In Section 2, we recall several basic properties and definition form Natural transform and fractional calculus. In Section 3, the idea of Natural transform decomposition method. In Section 4, we explain many problems to maintenance the accuracy and efficiency of the present method, while the last section is devoted conclusion.
2. Preliminaries
Definition 1.
The natural transform of is define as [24,25]:
where s and u are the transform variables.
Definition 2.
The inverse natural transform of a function is defined by
where s and u are the Natural transform variables and p is a real constant and the integral is taken along in the complex plane .
Definition 3.
Natural Transform of nth Derivative
If is the nth derivative of function is given by,
Theorem 1.
If , are the transform function respectively and is given by;
where is convolution of two functions h and l.
Definition 4.
Riemann–Liouville fractional integral [26]
where Γ denotes the gamma function define by,
Definition 5.
The Caputo operator of order γ for a fractional derivative is given by the following mathematical expression for , , , [27,28].
Definition 6.
The Mittag-Leffler function for is defined by the following subsequent series,
Theorem 2.
Here, we will study the convergence analysis as same manner in [29] of the NTDM applied to the fractional partial differential equations with proportional delay. Let us consider the Hilbert space H which may define by the set of applications:
Now we consider the fractional partial differential equations with proportional delay in the above assumptions and let us denote
then the fractional partial differential equations with proportional delay becomes, in an operator form
The NTDM is convergence, if the following two hypotheses are satisfied:
whatever may be, there exist a constantsuch that forwith, we havefor every.
3. Idea of Fractional Natural Transform Decomposition Method
In this section, the NTDM to find the general solution FPDE’s with proportional delay.
where the Caputo Operator , where L and N are linear and non-linear functions, q is the origin function.
The initial condition is
Applying the Natural transform to Equation (1), we have
and using the differentiation property of Natural transform, we get
The NTDM solution is represented by the following infinite series
and the non-linear terms (if any) in problem are define by the infinite series of Adomian polynomials,
substitution Equation (5) and Equation (6) in Equation (4), we get
Applying the linearity of the Natural transform,
Generally, we can write
4. Results
Example 1.
Consider the proportional delay of generalized Burgers equation as given by [8]:
with initial condition
Taking Natural transform of Equation (11),
Applying inverse Natural transform
Using ADM procedure, we get
for
The subsequent terms are
The NTDM solution for example 1 is
when , then NTDM solution is
This result is calculated to the exact solution of Equation (11);
The NTDM solution for and 1 are reported in Table 1. The surface solution behavior of for different values of 1, , and are depicted in Figure 1, and the plots of the solution for at different time intervals is depicted in Figure 1. The error plot of Example 1 show in Figure 2.

Table 1.
Numerical results of Example 1 at , 1 and Absolute Error.
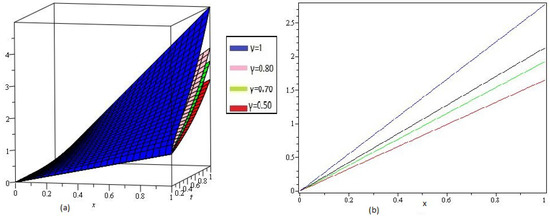
Figure 1.
Numerical results of Example 1, for different value of γ and .
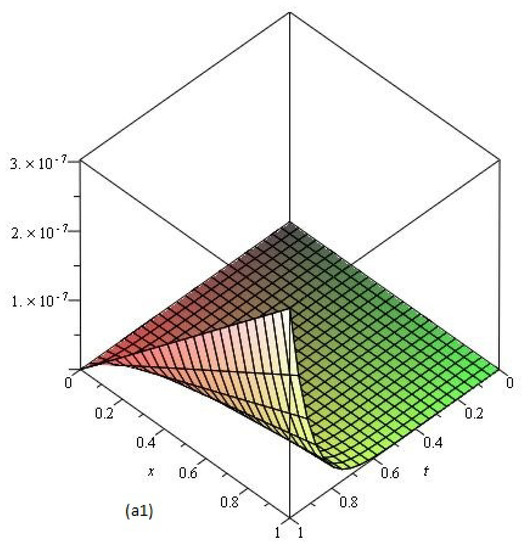
Figure 2.
The error plot of Example 1, at .
Example 2.
Consider the FPDE’s with proportional delay as given in [8]:
with the initial condition is
Taking Natural transform of Equation (17),
Applying inverse Natural transform
Using ADM procedure, we get
for
The subsequent terms are
The NTDM solution for Example 2 is
when , then NTDM solution is
This result is calculated to the exact solution of Equation (17);
The NTDM solution for and 1 are reported in Table 2. The surface solution behavior of for different values of 1, , and are depicted in Figure 3, and the plots of the solution for at different time intervals is depicted in Figure 3. The error plot of Example 2 show in Figure 4.

Table 2.
Numerical results of Example 2 at and .
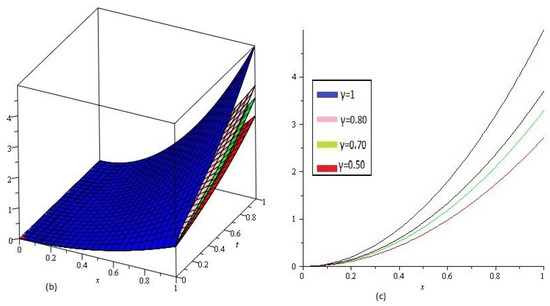
Figure 3.
Numerical results of for Example 2, for different value of γ and .
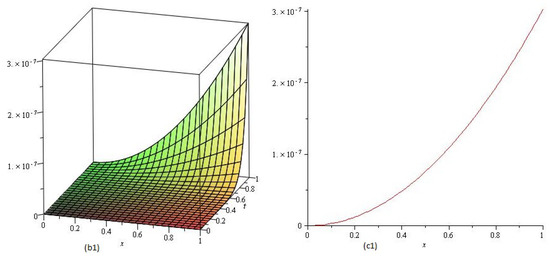
Figure 4.
The error plot of Example 2, at and .
Example 3.
Consider the TFPDE with proportional delay as given by [8]:
with the initial condition is
Taking Natural transform of Equation (23),
Applying inverse Natural transform
Using ADM procedure, we get
for
The subsequent terms are
The NTDM solution for example 3 is
when , then NTDM solution is
This result is calculated to the exact solution of Equation (23);
The NTDM solution for and 1 are reported in Table 3. The surface solution behavior of for different values of 1, , and are depicted in Figure 5, and the plot of the solution for at different time intervals is depicted in Figure 5. The error plot of Example 3 show in Figure 6.

Table 3.
Numerical results of Example 3 at and .
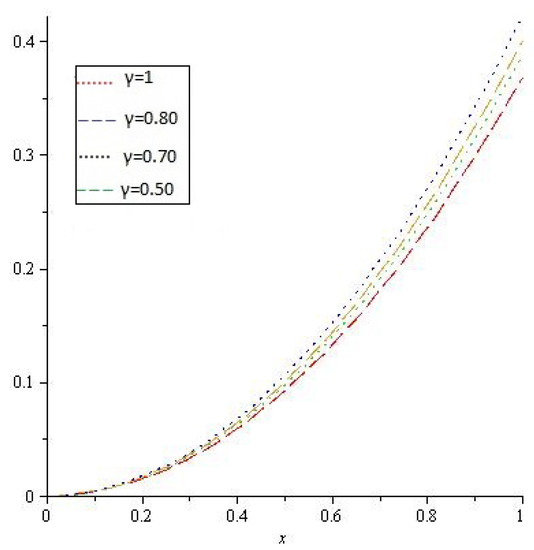
Figure 5.
Numerical results of for Example 3, for different value of γ.
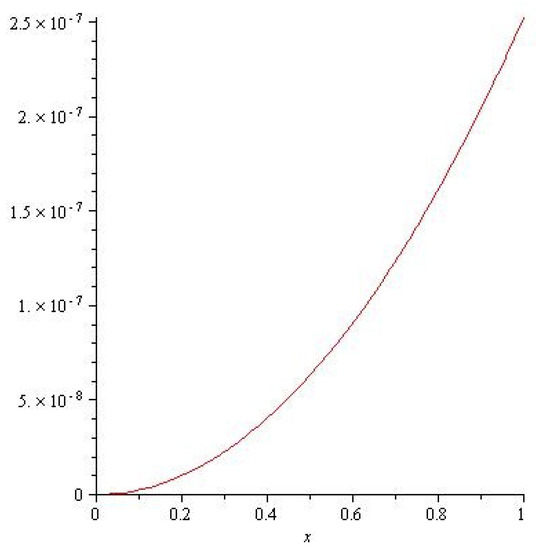
Figure 6.
The error plot of Example 3, at .
5. Conclusions
In this paper, the analytical solutions of fractional-order partial differential equations with Proportional delays are determined, using NTDM. The NDTM solutions are determined for both integer and fractional order problems. The proposed solutions agreed excellently with homotopy perturbation method (HPM) [8], homotopy perturbation transform method (HPTM) [30] and reduced differential transform method (RDTM) [7]. The NTDM solutions have shown the highest concurrence with the exact solutions of the problems. Moreover, the validity and applicability of the proposed method is confirmed with the help of some numerical examples. On the basis of NTDM solutions, it is observed that the solutions at different fractional-order, is approaches to integer-order solution of the problems. On the basis of the above narration, NTDM can be used to find the analytical solution of other non-linear FPDEs, which are frequently used in science and engineering. NTDM, solutions for fractional-order problems, will prove the better understanding of the real world problems represented by FPDEs.
Author Contributions
Conceptualization, R.S. and H.K.; Methodology, M.A.; Software, R.S.; Validation, P.K. and M.A.; Formal Analysis, R.S.; Investigation, R.S. and P.K.; Resources, H.K. and P.K.; Data Curation, R.S.; Writing—Original Draft Preparation, R.S.; Writing—Review and Editing, H.K., M.A. and P.K.; Visualization, M.A.; Supervision, M.A., P.K.; Project Administration, P.K.; Funding Acquisition, P.K.
Funding
Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Acknowledgments
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computationaland Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflicts of Interest
The authors have no conflict of interest.
References
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Dugard, L.; Verriest, E.I. Stability and control of time-delay systems. In Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 1997; Volume 228. [Google Scholar]
- Fridman, E.; Fridman, L.; Shustin, E. Steady modes in relay control systems with time delay and periodic disturbances. J. Dyn. Syst. Measur. Control 2000, 122, 732–737. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Solution of delay differential equations via a homotopy perturbation method. Math. Comput. Model. 2008, 48, 486–498. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Functional constraints method for constructing exact solutions to delay reaction-diffusion equations and more complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 417–430. [Google Scholar] [CrossRef]
- Mead, J.; Zubik-Kowal, B. An iterated pseudospectral method for delay partial differential equations. Appl. Numer. Math. 2005, 55, 227–250. [Google Scholar] [CrossRef]
- Abazari, A. Kilicman, Application of differential transform method on nonlinear integro-differential equations with proportional delay. Neural Comput. Appl. 2014, 24, 391–397. [Google Scholar] [CrossRef]
- Sakar, M.G.; Uludag, F.; Erdogan, F. Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 2016, 40, 6639–6649. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L. The variational iteration method for solving a neutral functional-differential equation with proportional delays. Comput. Math. Appl. 2010, 59, 2696–2702. [Google Scholar] [CrossRef]
- Bhalekar, S.A.C.H.I.N.; Daftardar-Gejji, V.A.R.S.H.A. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calcul. Appl. 2011, 5, 1–9. [Google Scholar]
- Wang, Z. A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Zhou, J. A numerical method for delayed fractional-order differential equations: Based on GL definition. Appl. Math. Inf. Sci. 2013, 7, 525–529. [Google Scholar]
- Moghaddam, B.P.; Yaghoobi, S.; Machado, J.T. An extended predictor–corrector algorithm for variable-order fractional delay differential equations. J. Comput. Nonlinear Dyn. 2016, 11, 061001. [Google Scholar]
- Dabiri, A.; Butcher, E.A.; Poursina, M.; Nazari, M. Optimal periodic-gain fractional delayed state feedback control for linear fractional periodic time-delayed systems. IEEE Trans. Autom. Control 2017, 63, 989–1002. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl. Math. Model. 2018, 56, 424–448. [Google Scholar] [CrossRef]
- Tanthanuch, J. Symmetry analysis of the nonhomogeneous inviscid burgers equation with delay. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4978–4987. [Google Scholar] [CrossRef]
- Abazari, R.; Masoud, G. Extended two-dimensional DTM and its application on nonlinear PDEs with proportional delay. Int. J. Comp. Math. 2011, 88, 1749–1762. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 2014, 92, 757–776. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Silambarasan, R. November. Advances in the natural transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Science Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus AND Fractional Differential Equations, 1st ed.; Wiley: London, UK, 1993; p. 384. [Google Scholar]
- Naghipour, A.; Manafian, J. Application of the Laplace Adomian decomposition and implicit methods for solving Burgers’ equation. TWMS J. Pure Appl. Math. 2015, 6, 68–77. [Google Scholar]
- Singh, B.K.; Pramod, K. Homotopy perturbation transform method for solving fractional partial differential equations with proportional delay. SeMA J. 2018, 75, 111–125. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).