Abstract
This paper has the objective to empirically test Harrod’s explanations of economic dynamics addressing both growth and business cycles. In particular we test Harrod’s speculation that opening the economy to foreign trade could lead to a reduction of cyclical instability. The main variables determining the dynamic behaviour are wealth, savings, competitiveness and, therefore, balance of trade. The behaviour of the model under scrutiny is highly non-linear and the conclusion is that stable cycles are possible only under particular conditions. In fact, this empirical test shows a stable long-run pattern for those specific parameters.
1. Introduction
As mentioned by Salvadori (2003) [1] “economic growth was central in classical political economy from Adam Smith to David Ricardo, and then in its ‘critique’ by Karl Marx, but moved to the periphery during the so-called ‘marginal revolution’. John von Neumann’s growth model and Roy Harrod’s attempt to generalise Keynesian principle of effective demand to the long-run re-ignited interest in growth theory. Following the publication of papers by Robert Solow and Nicholas Kaldor in the mid-1950s, growth theory became one of the central topics of the economics profession until well into the early 1970s. After a decade of dormancy, since the mid-1980s, economic growth has once again become a central topic in economic theorising. The recent theory is called ‘endogenous growth theory’, since according to it the growth rate is determined from within the model and is not given as an exogenous variable”.
While Kaldor’s theory influenced the academic debate on business cycles, Harrod inspired Solow’s who, with his seminal paper “A Contribution to the Theory of Economic Growth” (1956) [2], set the basis of modern growth theory. However, recent research based on a thorough reading of Harrod’s theory [3,4], challenges Solow’s interpretation “which ultimately dominated the profession’s view of Harrod” [4]. The idea the Harrod’s model “implied a tendency toward progressive collapse of the economy” and that he invoked a fixed-coefficients production function has “little to do with the problem of long-run growth as Solow understood it, but instead addressed medium-run fluctuations, the “inherent instability” of economies” [4].
There are several reasons why we are dealing with Harrod’s model. First of all, Harrod, through Solow’s interpretation, has contributed to the foundation of modern growth theory. Secondly, the Harrod model provides a dynamic framework and some guidelines to policy-makers in terms of supply-side policies (see Figure 1). In fact they should consider the combination of investment, technological change, population growth, unemployment and aggregate demand. Another reason is that, in his framework, the warranted rate of growth is not a single moving equilibrium, but a “highly unstable” one. This is called Harrod’s knife-edge instability or the instability principle (see Figure 2 ). Therefore the idea of dynamically unstable multiple equilibria or the alternative Harrod’s suggestion of a Leijonhufvud’s “corridor stability” in our opinion is worth being explored. Whereas in the 1970s and the 1980s unemployment and stagflation discarded those theories, in the 20th century “in the leading Western economies there have been prolonged periods when more saving would have been beneficial, and others with every appearance of inadequate effective demand” [5]. As Harrod’s model is one of the few able to predict that, “it still deserves serious attention” [5]. For reasons given above, the objective of this paper is to empirically test Harrod’s explanations of economic dynamics by checking a specific model on a open economy. Our conclusion is that the model behaves as expected only for some specific values of parameters.
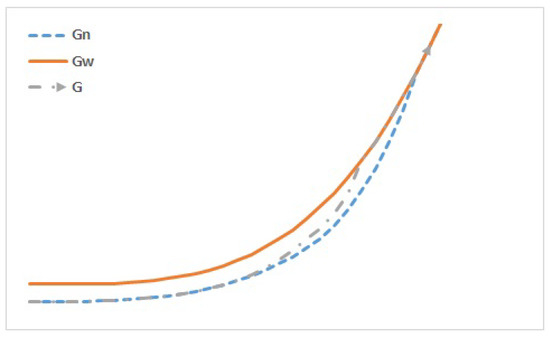
Figure 1.
Supply side policy (i.e., a policy aimed at increasing the aggregate supply through investments, deregulation, liberalization, privatization, etc.) to raise the natural growth path. When there is a permanent unemployment equilibrium. Policy-makers may employ supply side policies in order to increase both: the actual growth and G and the natural growth .
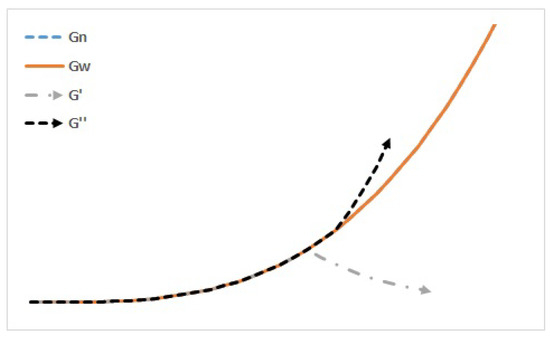
Figure 2.
The Harrod knife-edge or unstable equilibrium. When there is sustainable full employment. A departure from that may lead to recession () or booming periods ().
This paper is organized as follows. Section 2 provides an overview on the existing literature. Section 3 provides some background and discloses the data we used. Section 4 describes Harrod’s model. Section 5 shows the results of our calibration. Some concluding remarks and hints for future research are in last section.
2. Literature Review
The renewed interest in Harrod’s though is, also, due to an epistemological work that has Besomi among its main contributors: “plunging into the original texts soon made it obvious that the subject of Harrod’s dynamics was more intricate than the portrait given in textbook rendition” [3] and that many interpretations were erroneous. Baumol [6], for instance, asserts that “the main achievement of his [Harrod’s] model lies in the ideas it inspired in those who did not fully understand it”. In fact Harrod himself “claimed that his dynamics was essentially different from, and indeed more fundamental than, the mainstream interpretation of it (an interpretation which, of course, reflected the notion of dynamics which gained almost universal acceptance after the war)” [3].
The so-called Harrod’s Dynamics is the result of a number of works resumed in “The Making of Harrod’s Dynamics” by Besomi (1999) [3] and of which the most significant are “Towards a Dynamic Economics” (1948) [7] and “Economic Essays” (1972) [8]. This happened because Harrod “returned several times on the topic of his essays in correspondence with Keynes, who sometimes managed to force him to re-formulate his propositions” [3].
In summary, Harrod identified two stages in explaining economic dynamics: the first was the determination of the rate of growth at the equilibrium (given a certain ratio of saving over income and investment per unit increase of output), the second was related to the changes of those ratios (changes that would lead to different equilibria and would be responsible for cycles).
Because of different formulations Harrod’s theory was subject to several interpretations. For example according to Tinbergen (1937) [9] the model was a combination of multiplier and accelerator that could not give rise to cyclical behaviour, but could only lead to an explosive growth or to an equilibrium. Samuelson (1939) [10], (1943) [11], in a different formulation with lagged variables, found out that for a range of the multiplier and accelerator coefficients there was a cyclical behaviour.
On the other hand the so-called ‘Harrod-Domar model’ was extensively used to explain growth as the result of the optimal combination of saving and investment. This led to a debate on other factors determining the growth as well as around the multiplicity of equilibria and their instability. For example according to Solow (1956) [2] relaxing the Harrod’s assumption of a constant capital/output ratio the system would have drifted towards the full employment. Moreover, while Harrod set a stress on the so called “principle of instability” to describe the adjustments between effective accumulation of capital and warranted accumulation, Solow interpretation solved the puzzle by assuming that the warranted rate of growth () was constant and that technology was flexible (even though Harrod insisted on the fact that the did depend on time and cycle). Therefore, when Axel Leijonhufvud [12] sketched the idea of a corridor, Harrod in Economic Dynamics [13] convened that it was an appropriate approach to what he was thinking about failures of effective demand.
Robinson (1970) [14] summarized a long debate on the post-Keynesian front that showed how multiple equilibria could be attained if were considered the different propensities to save existent between social classes. Last but not least Kalecki (1933–1939) [15] and Kaldor (1960) [16] focused on the technical progress, on the non-linearities of the investment and savings functions and on the determinants of investment decisions. This inspired a disparate number of works from multiple attractors and global bifurcations [17] to homoclinic tangles [18], from the global existence of periodic solutions [19] to the existence of chaotic behaviour not for a single specific value but within a reasonable interval for each parameter [20,21]. Shaikh (2009) [22] explains key differences between Harrodian and Keynesian theories and policies, proves the stability of the Harrodian warranted path and shows that the Keynesian paradox of thrift is transient. Moudud (2009) [23] shows how to combine taxation with public investments in order to raise the warranted growth rate (which, according to Harrod, is otherwise reduced by an increase in the budged deficit/GDP ratio). Serrano et al. (2019) [24] claim that Harrod’s instability is an instance of what Hicks calls “static instability” and they show that the Sraffian Supermultiplier [25] model overcomes the Harrodian instability. Skott (2019) [26] contends that there is no need to introduce autonomous demand as the “driver of long-run economic growth and as a stabilizing force”, but it suffice to model “the supply side (the labor market) and/or economic policy” to obtain those results.
Apart from the aforementioned models, and to have a deeper insight into cycles and financial bubbles, it is worth mentioning that recurrence quantification analysis (RQA) has been introduced by a number of authors. For example Fabretti and Ausloos (2005) [27] found cases on financial markets where RQA could detect a difference in state and recognize the critical regime such as a warning before a crash. Along this line Addo et al. (2013) [28] who claims “the usefulness of recurrence plots in identifying, dating and explaining financial bubbles and crisis” and that recurrence plots show “that these plots are robust to extreme values, non stationarity and to the sample; are replicable and transparent; are adaptive to different time series and finally, can provide better chronology of financial cycles since it avoids revision of crisis dates through time”. Orlando and Zimatore (2017–2019) [29,30,31] investigated the potential explanatory capability of RQA to show the structural characteristics of economic time series and on RQA anticipating signals.
Finally Yoshida (1999) [32] and Sportelli (2001) [33,34], from the 1990s Harrod’s Dynamics offered a theoretical framework to explain jointly economic growth and business cycles through the Harrod’s “instability principle”. However for Yoshida the instability derives from a putty-clay technology in conjunction with flexibility of prices, while for Sportelli the instability derives from the gaps between Harrod’s rates of growth: actual, warranted and natural. Further, it has been shown that in that framework [34] opening to foreign trade can lead to reducing cyclical instability of the economy as Harrod suggested.
3. Material and Mmethods
3.1. Cycles
Cyclical fluctuations in economy, Figure 3, correspond to the duration or the amplitude between a high/peak and the succeeding low/trough [35]. The so-called peak-trough-peak (PTP) cycle affects the whole economy (e.g., wages, demand, prices, credit, etc.). Seasonal swings are typically short-term, but cyclical fluctuations could last for years. A depression is a prolonged and deep recession. As mentioned by Eckstein (1986) [36] when “financial distress produces sharp discontinuities in flows of funds and spending and when the financial strains include tight monetary policy, much lessened availability of money and credit, sharp rises of interest rates, and deteriorating balance sheets for households, businesses, and financial institutions”.
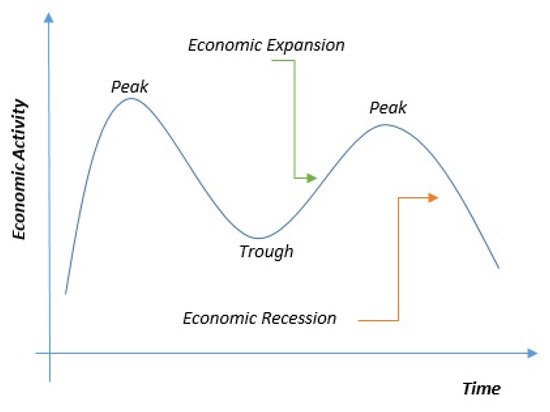
Figure 3.
The business cycle can be classified into four stages: (1) expansion when economic activity grows steadily; (2) boom when the aggregate demand grows more than the aggregate output which overheats the economy; (3) recession phase when the aggregate output cool down after a peak; (4) recovery after a through. The so-called “specific cycle amplitude” corresponds to the vertical distance between the peak and the trough.
3.2. USA Recessions
In the following Figure 4 we display the path of USA investments alongside recessions as reckoned by FRED (Table 1).
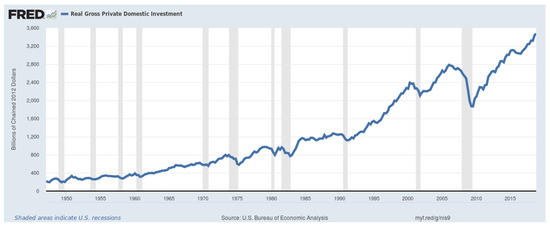
Figure 4.
USA real gross private domestic investment ( GPDIC1 ), billions of chained 2012 dollars, seasonally adjusted annual rate. Source: FRED, Federal Reserve Bank of St. Louis; https://fred.stlouisfed.org/series/GPDIC1, 16 March 2019. Greyed areas correspond to periods of economic recessions (Table 1).

Table 1.
USA recessions.
3.3. Groundwork on Growth and Cycle Theories
As already mentioned, Kaldor and Harrod laid down the basis for modern theory on growth and cycles. In particular, Kaldor suggested that growth depends on income distribution and that the shifts between wages and profits determine the savings ratio. Therefore equilibrium is achieved when (the rate of growth required for a full employment) equates (the warranted rate of growth). Keynes argued that in the short run, through the multiplier, more demand (e.g., investments, public spending, exports) translates into an increase in output. Harrod shares the same view with regard to the short run but “notes that investment not only induces production through the multiplier, but also simultaneously expands capacity. On this basis he shows that investment is sustainable only if it is self-consistent, and for this to hold it must follow a particular growth path which he calls the warranted path” [22]. In other terms, in Harrod’s view, instead, it is the discrepancy between the natural rate of growth (), the warranted rate of growth () and the actual one (G), that generates instability. This instability could be lessened when the economy is open to foreign trades. In fact, “for a country in which is tending to exceed and there is by consequence a chronic tendency to depression (because G cannot exceed ), a positive value of the balance of trade expressed as a fraction of income (i.e., the net export rate) may be beneficial” [7]. Therefore, Harrod “predicts that incompatibilities between long-term saving and investment opportunity are all but certain to cause prolonged unemployment (which will be structural where exceeds and demand deficient where exceeds ) with persistent inflation in addition wherever long-term saving is inadequate for the natural rate of growth” [5]. In terms of public policy “the difficulties may be too great to be dealt with by a mere anti-cycle policy” [8] hence government should increase public investment when > or, conversely, seek to generate more long term savings when < .
3.4. The Dataset
Data is taken from several sources such as the Maddison Project, the World Bank, IMF (International Monetary Fund) and BEA (U.S. Bureau of Economic Analysis). Time series are retrieved from their original dataset or from FRED as detailed in the following.
3.4.1. World GDP Data
Annual world GDP estimate has been retrieved from the Maddison-Penn world table [38,39], (from 1946 to 1961). This has been linked up with World Bank (https://data.worldbank.org/indicator/NY.GDP.MKTP.KD.ZG) and IMF (https://www.imf.org/external/datamapper/NGDP_RPCH@WEO/OEMDC/ADVEC/WEOWORLD) data (available from 1961 to 2018). Annual data has been changed into quarterly via the compounding law.
3.4.2. BEA Data
In the following table (Table 2) we list the time series considered for our analysis as retrieved from FRED.

Table 2.
BEA time series.
4. A Mathematical Specification of the Harrod’s Model
The model we are testing shows that Harrod’s speculation holds true only for a specific set of parameters and with positive net exports coupled with competitiveness in foreign markets. In those specific conditions regular cycles in the long period can be achieved.
From now onwards the notation we are going to use is:
As in [34] we assume that:
- (A)
- The desired capital is an increasing function of the difference between the current and the expected change of demand i.e.,such that . So that, ex post, at the equilibrium , , , (or equivalently ). Denoted as a reaction parameter representing how sensitive are firms to discrepancies between actual and warranted relative changes of demand, the linearisation of (1) can be expressed as
- (B)
- According to Alexander [40], changes in the growth rate of income depends on the difference between ex ante and ex post investments, that isso that dividing by Y and considering that , we haveTherefore can be expressed as a function F of u with if and if we assume F to be linear we obtainwith because investments changes in the productive capacity makes investment sticky.
- (C)
- Saving rate varies over time depending on unforeseen differences between technical progress and rate of growth and on income fluctuations:where the parameters and represent the sensitivities and the variable describes the economic cycle.
- (D)
- Changes in the ratio of the trade balance depend on , and G as followsAs usual we can assume that the mapping is linear and by denoting the sensitivities of the balance of trade to foreign rate of growth, technical progress and domestic growth rate, Equation (2) can be rewritten aswhere implies that i.e., a constant domestic production without technical progress has a negative effect on the balance of trade or, equivalently, .
- (E)
- The expected rate of change of aggregate demand is linear with to the difference between G and i.e.,where denotes how quick the expected rate of growth adjusts to the actual growth.
- (F)
- The dynamic of technological progress is described by a continuous, increasing non-linear function of share of income saved and devoted to investments
5. Results and Analysis
To empirically test the Harrod’s model we evaluated the average distance between the historical data series presented in Section 3.4 and the orbit produced by Equation (6) that starts at time 0 at the same initial point of the data series and best fits the data series. This orbit can be found by suitably calibrating the parameters in Equation (6) through a numerical optimization. The aim of the optimization was thus to minimize the square error between the historical time series and the orbit produced by Equation (6) that starts at time 0 at the same initial point of the data series. In formula, we want to compute the quantity:
where is the vector that stacks the data of the rate of growth of domestic income, the expected rate of growth of aggregate demand, the share of income saved, and the net export rate for the quarter t ( is the first quarter of 1947, is the second quarter of 2018). Similarly, P is the vector of the 13 parameters of the model (reported in Table 3), and stacks the four variables that solve the differential Equation (6) with parameters set in P starting at : the integral between t and allows us to compute the average value of the (continuous) signal over the quarter of interest, to be compared with the data. Note that an additional dummy parameter has been added. This parameter permits us to rescale the time of the signal produced by the model, in order to best fit with the time-scale of the data. The optimization variables are the 13 + 1 parameters: since they have physical meaning only when positive, this adds a set of constrains to be satisfied. Formally speaking, in order to find the best fitting solution, we solve the following constrained optimization problem:

Table 3.
Harrod model parameters.
This problem is solved using the interior point method [41,42] implemented in the Matlab fmincon routine. Since the problem is not convex, the optimization algorithm may converge to a local optimal solution. To better explore the space of the optimal solutions, we introduce a multi-start algorithm: the optimization is then run several times starting from a randomly perturbed sample draft from a distribution centred in the parameter setting provided in [34].
Since the aim of this work is to evaluate the Harrod’s model, we report in Table 3 the parameters for both the original model and three calibrations we have obtained that present qualitatively different behaviours (together with the value of their distance D—for calibration 2, D is computed with ). The model, calibrated with real data, may display convergence to a long-run equilibrium (calibration 1, Figure 5), divergence (calibration 2, Figure 6) as well as a lightly damped oscillatory behaviour (calibration 3, Figure 7). It is worth saying that the global optimum is obtained with calibration 1. However, with calibrations 2 and 3, we displayed sub-optimal results to provide a context for our results. In fact, qualitatively, we obtain similar values to the ones in [34]. Moreover we concur with this conclusion “when the value of is large enough, the long period dynamics of the saving rate is such that it can generate an irregular cycle in the system only if the net export rate is very low. On the contrary, starting from positive and meaningful values of the net export rate, the system may simply generate a limit cycle (or at most a double cycle) if a higher works together with adequate competitiveness on the foreign markets. This is the only formal result consistent with Harrod’s intuition that a more moderate cyclical instability can emerge in an open economy compared to a closed one”.
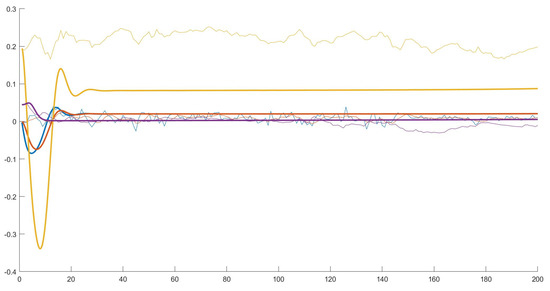
Figure 5.
Time series obtained with parameters of calibration 1, that displays convergence to the long-run equilibrium. Legend: blue = rate of growth, red = expected rate of growth, yellow = share of saved income, violet: trade to income ratio. Thick line: model, normal line: data.
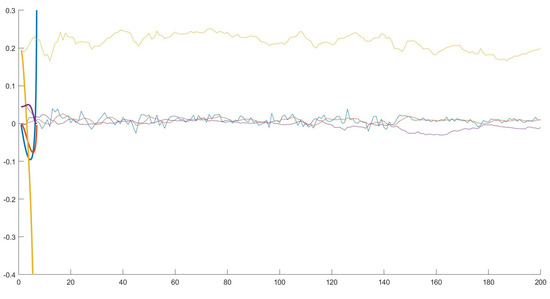
Figure 6.
Time series obtained with parameters of calibration 2, that displays divergence from the long-run equilibrium. Legend: blue = rate of growth, red = expected rate of growth, yellow = share of saved income, violet: trade to income ratio. Thick line: model, normal line: data.
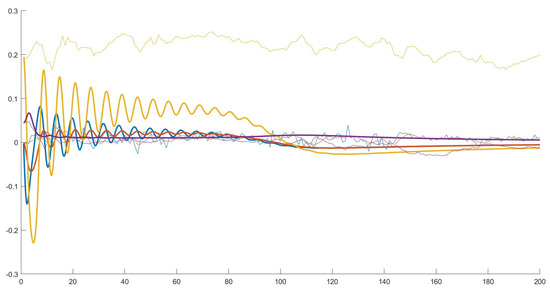
Figure 7.
Time series obtained with parameters of calibration 3, that displays lightly damped oscillatory behaviour around the long-run equilibrium. Legend: blue = rate of growth, red = expected rate of growth, yellow = share of saved income, violet: trade to income ratio. Thick line: model, normal line: data.
6. Conclusions
The Harrod’s model has the merit of rearranging Keynes’s ideas into a dynamic framework with some additional specification on the supply side. In fact “where the warranted growth rate represents an economy’s growth path on which aggregate demand and supply remain in balance, the model’s natural growth rate reflects the supply of productive resources and the level of technology, the long-run limit to real output growth. The interaction between the warranted and natural growth rates provides a useful perspective for policymaking in today’s environmentally-constrained global economy. Also, since the growth of the labor force is built into the natural growth path, the model also helps to clarify policy choices in an economy impacted by immigration” [43]. Therefore “supply-side policies must be developed along with the standard Keynesian demand side policies, and the interactions between the two require disaggregated policies to address specific types of investment, technological change, and demand. That is, it is not generally possible to solve the unemployment problem by simply expanding aggregate demand” [43]. Harrod’s theory, thus, may be seen as the link between classical economy (that stressed on the importance of investment for growth) and Keynesian approach “primarily concerned with the demand and income generating effect of investment” [44]. In real life this theory was put in practice in India. In fact, the Indian fifth five year plan (1974–1979) was based on a mix of Harrod macroeconomic model and Leontief inter-industry model and it was aimed at achieving both self-reliance and growth. Main priorities on the industrial sectors were the developments of: (i) core industry, (ii) industry for export and diversification, (iii) mass consumption production, (iv) small industry and ancillary industry feeders of large industries. The target growth rate was 4.4% and, as a result, the actual growth rate was 4.8% [44].
Having said that, to remind the importance of the model, this paper shows (for a specific set of parameters) that it is possible to find a match between Harrod’s suggestions and reality. Next research will focus on the Yoshida model [32] for a comparison and, possibly, for a calibration on real data.
Author Contributions
Conceptualization, G.O.; methodology, F.D.R.; software, F.D.R.; validation, G.O. and F.D.R. formal analysis, G.O. and F.D.R.; investigation, G.O. and F.D.R.; resources, G.O.; data curation, G.O.; writing—orignal, G.O.; writing—review and editing, G.O. and F.D.R.; visualization, G.O. and F.D.R. supervision, G.O.; project administration, G.O.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salvadori, N. The Theory of Economic Growth: A ‘Classical’ Perspective; Edward Elgar: Cheltenham, UK, 2003. [Google Scholar]
- Solow, R.M. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Besomi, D. The Making of Harrod’s Dynamics; St. Martin’s Press: New York, NY, USA, 1999. [Google Scholar]
- Halsmayer, V.; Hoover, K.D. Solow’s Harrod: Transforming macroeconomic dynamics into a model of long-run growth. Eur. J. Hist. Econ. Thought 2016, 23, 561–596. [Google Scholar] [CrossRef]
- Eltis, W. Harrod Domar Growth Model; Palgrave Macmillan: London, UK, 1987; pp. 1–5. [Google Scholar] [CrossRef]
- Baumol, W.J. Review: Daniele Besomi, the making of harrod’s dynamics. Hist. Political Econ. 2000, 32, 1037–1039. [Google Scholar] [CrossRef]
- Harrod, R.F. Towards a Dynamic Economics: Some Recent Developments of Economic Theory and Their Application to Policy; MacMillan and Company: London, UK, 1948. [Google Scholar]
- Harrod, R.F.S. Economic Essays, 2nd ed.; Macmillan Publisher: London, UK, 1972. [Google Scholar]
- Tinbergen, J.; Harrod, R.F. The Trade Cycle. An Essay; Springer: Heidelberg, Germany, 1937; pp. 89–91, Weltwirtschaftliches Archiv. [Google Scholar]
- Samuelson, P.A. A synthesis of the principle of acceleration and the multiplier. J. Political Econ. 1939, 47, 786–797. [Google Scholar] [CrossRef]
- Samuelson, P.A. Dynamics, statics, and the stationary state. Rev. Econ. Stat. 1943, 25, 58–68. [Google Scholar] [CrossRef]
- Leijonhufvud, A. Effective demand failures. Swed. J. Econ. 1973, 75, 7–48. [Google Scholar] [CrossRef]
- Harrod, R. Economic Dynamics; Palgrave Macmillan: Basingstoke, UK, 1973. [Google Scholar]
- Robinson, J. Harrod after twenty-one years. Econ. J. 1970, 731–737. [Google Scholar] [CrossRef]
- Kalecki, M. Studies in the Theory of Business Cycles, 1933–1939; A.M. Kelley: New York, NY, USA, 1966. [Google Scholar]
- Kaldor, N. Essays on Economic Stability and Growth; Duckworth: London, UK, 1960; Volume 1. [Google Scholar]
- Bischi, G.I.; Dieci, R.; Rodano, G.; Saltari, E. Multiple attractors and global bifurcations in a Kaldor-type business cycle model. J. Evol. Econ. 2001, 11, 527–554. [Google Scholar] [CrossRef]
- Agliari, A.; Dieci, R.; Gardin, L. Homoclinic tangles in a Kaldor-like business cycle model. J. Econ. Behav. Organ. 2007, 62, 324–347. [Google Scholar] [CrossRef]
- Kaddar, A.; Alaoui, H.T. Global existence of periodic solutions in a delayed Kaldor-Kalecki model. Nonlinear Anal. Model. Control 2009, 14, 463–472. [Google Scholar]
- Orlando, G. A discrete mathematical model for chaotic dynamics in economics: Kaldor’s model on business cycle. Math. Comput. Simul. 2016, 125, 83–98. [Google Scholar] [CrossRef]
- Orlando, G. Chaotic business sycles within a Kaldor-Kalecki framework. In Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors; Pham, V.T., Vaidyanathan, S., Volos, C., Kapitaniak, T., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 133–161. [Google Scholar] [CrossRef]
- Shaikh, A. Economic policy in a growth context: A classical synthesis of Keynes and Harrod. Metroeconomica 2009, 60, 455–494. [Google Scholar] [CrossRef]
- Moudud, J.K. The role of the state and Harrod’s economic dynamics: Toward a new policy agenda? Int. J. Political Econ. 2009, 38, 35–57. [Google Scholar] [CrossRef]
- Serrano, F.; Freitas, F.; Bhering, G. The Trouble with Harrod: The fundamental instability of the warranted rate in the light of the Sraffian Supermultiplier. Metroeconomica 2019, 70, 263–287. [Google Scholar] [CrossRef]
- Nikiforos, M. Some Comments on the Sraffian Supermultiplier Approach to Growth and Distribution. Levy Econ. Inst. 2018. [Google Scholar] [CrossRef]
- Skott, P. Autonomous demand, Harrodian instability and the supply side. Metroeconomica 2019, 70, 233–246. [Google Scholar] [CrossRef]
- Fabretti, A.; Ausloos, M. Recurrence plot and recurrence quantification analysis techniques for detecting a critical regime. Examples from financial market indices. Int. J. Modern Phys. C 2005, 16, 671–706. [Google Scholar] [CrossRef]
- Addo, P.M.; Billio, M.; Guegan, D. Nonlinear dynamics and recurrence plots for detecting financial crisis. N. Am. J. Econ. Financ. 2013, 26, 416–435. [Google Scholar] [CrossRef]
- Orlando, G.; Zimatore, G. RQA correlations on real business cycles time series. In Indian Academy of Sciences Conference Series; Proceedings of the Conference on Perspectives in Nonlinear Dynamics (2016); Springer: Cham, Switzerland, 2017; Volume 1, pp. 35–41. [Google Scholar] [CrossRef]
- Orlando, G.; Zimatore, G. Recurrence quantification analysis of business cycles. Chaos Solitons Fractals 2018, 110, 82–94. [Google Scholar] [CrossRef]
- Orlando, G.; Zimatore, G. RQA correlations on business cycles: A comparison between real and simulated data. In Advances on Nonlinear Dynamics of Electronic Systems; World Scientific: Singapore, 2019; pp. 62–68. [Google Scholar] [CrossRef]
- Yoshida, H. Harrod’s ’knife-edge’ reconsidered: An application of the Hopf bifurcation theorem and numerical simulations. J. Macroecon. 1999, 21, 537–562. [Google Scholar] [CrossRef]
- Sportelli, M.C. Dynamic complexity in a Keynesian growth-cycle model involving Harrod’s instability. J. Econ. 2000, 71, 167–198. [Google Scholar] [CrossRef]
- Sportelli, M.; Celi, G. A mathematical approach to Harrod’s open economy dynamics. Metroeconomica 2011, 62, 459–493. [Google Scholar] [CrossRef]
- Bry, G.; Boschan, C. Standard business cycle analysis of economic time series. In Cyclical Analysis of Time Series: Selected Procedures and Computer Programs; NBEr: Cambridge, MA, USA, 1971; pp. 64–150. [Google Scholar]
- Eckstein, O.; Sinai, A. The mechanisms of the business cycle in the postwar era. In The American Business Cycle: Continuity and Change; University of Chicago Press: Chicago, IL, USA, 1986; pp. 39–122. [Google Scholar]
- BEA. USA Recessions, Gross Domestic Product [A191RP1Q027SBEA]—US. Bureau of Economic Analysis, 2016; Retrieved from FRED, Federal Reserve Bank of St. Louis. 10 November 2016. Available online: https://fred.stlouisfed.org/series/A191RP1Q027SBEA (accessed on 8 May 2019).
- Bolt, J.; van Zanden, J.L. The Maddison Project: Collaborative research on historical national accounts. Econ. Hist. Rev. 2014, 67, 627–651. [Google Scholar] [CrossRef]
- Feenstra, R.C.; Inklaar, R.; Timmer, M.P. The next generation of the Penn World Table. Am. Econ. Rev. 2015, 105, 3150–3182. [Google Scholar] [CrossRef]
- Alexander, S.S. Mr. Harrod’s dynamic model. Econ. J. 1950, 60, 724–739. [Google Scholar] [CrossRef]
- Biggs, M. Constrained minimization using recursive quadratic programming. In Towards Global Optimization; Dixon, L., Szergo, G., Eds.; North-Holland: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Vandenberg, H.; Rosete, A.R.M. Extending the Harrod-Domar model: Warranted growth with immigration, natural environmental constraints, and technological change. Am. Rev. Political Econ. 2019, 3. Available online: https://www.arpejournal.com/archived-issues/volume-13-issue-1-papers-and-proceedings-of-the-2018-icape-conference/extending-the-harrod-domar-model-warranted-growth-with-immigration-natural-environmental-constraints-and-technological-change/ (accessed on 8 May 2019).
- Dash, L.N. World Bank and Economic Development of India; APH Publishing: Louisville, KY, USA, 2000. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).