Abstract
Shift scheduling problems (SSPs) are advanced NP-hard problems which are generally evaluated with integer programming. This study presents an applicable shift schedule of workers in a large-scale natural gas combined cycle power plant (NGCCPP), which realize 35.17% of the total electricity generation in Turkey alone, as at of the end of 2018. This study included 80 workers who worked three shifts in the selected NGCCPP for 30 days. The proposed scheduling model was solved according to the skills of the workers, and there were nine criteria by which the workers were evaluated for their abilities. Analytic network process (ANP) is a method used for obtaining the weights of workers’ abilities in a particular skill. These weights are used in the proposed scheduling model as concepts in goal programming (GP). The SSP–ANP–GP model sees employees’ everyday preferences as their main feature, bringing high-performance to the highest level, and bringing an objective functionality, and lowering the lowest success of daily choice. At the same time, the model introduced large-scale and soft constraints that reflect the nature of the shift requirements of this program by specifying the most appropriate program. The required data were obtained from the selected NGCCPP and the model solutions were approved by the plant experts. The SSP–ANP–GP model was resolved at a reasonable time. Monthly acquisition time was significantly reduced, and the satisfaction of the employees was significantly increased by using the obtained program. When past studies were examined, it was determined that a shift scheduling problem of this size in the energy sector had not previously been studied.
1. Introduction
Personnel efficiency and productivity is one of the basic objectives of many companies and organizations. While trying to find all the existing elements that can affect efficiency and productivity, personnel scheduling is an important problem that must be attentively steered. Personnel scheduling problems can be even more complicated by shifts in plans for industries in which shift personnel work seven days a week, and specific personnel have to work non-routine working hours. Some service providers must continuously operate, such as power plants, hospitals, and security and safety-related units while serving mostly the common good, and scheduling problems such as the above are further complicated.
Electricity generation in power plants and maintenance or repair work require complex structured, specialized, and labor-intensive activities. When considering the high impact and indispensability of electrical energy in daily human life, the process of assigning suitable employees to such specialized work and improving the performance of these employees comes to the fore with the impact on society, in addition to the economic value added. Power plants are continuous generation facilities with the main purpose of achieving uninterrupted, reliable, efficient, economical, and environmentally-friendly energy generation called sustainable energy supply, therefore, it is an indispensable requirement to manage the generation, manpower, material, and maintenance processes within this system by operating the plants in accordance with the operating rules in the direction of this five-legged comprehensive target. In other words, maximizing employee performance related to personnel management through balanced work distribution, appointment of the appropriate employees for the appropriate jobs, etc. has critical importance in terms of sustainable energy supply. With today’s constantly developing technology, power plants are operated by shift personnel from a main control center or supervisory control and data acquisition (SCADA) system, which distributes control to the power plant (DCS) remotely. Throughout the world, as in Turkey, although not with the SCADA system currently, personnel-operated power plants are still existing. Compared to advanced technology, the number of shift personnel working in these old plants is naturally higher than that of modern plants, and the probability of operator errors from shift personnel is higher than that of SCADA. Put differently, shift personnel may experience faulty operations due to fatigue, lack of concentration, experience, fair working order, and thus lack of motivation in these power plants. As a result, long-term failures and thus millions of kWh of energy and income loss may occur. In addition, a negative social impact may occur due to the lack of sustainable energy supply. From this point of view, it can be said that personnel scheduling models used for fair and appropriate assignments have critical importance in electricity generation facilities.
In spite of the various models proposed and resolved in SSPs, shift scheduling studies involving personnel in power plants or other related areas are still insufficient. Previous works on SSPs have mainly focused on factory or security personnel, health personnel (i.e., doctors and nurses), teachers, and police officers. For this reason, this study is a new application of models for shift scheduling problems (SSPs) and will be relevant to solving SSPs.
When the distribution of resources used in electricity generation in the world is examined, it is seen that the most widely-used resource for electricity generation is coal, after which natural gas is the second most common resource. When we look at the resources with the largest share of electrical energy generation in the countries with the largest economies, coal is predominantly used in the United States, China, India, and Germany, natural gas in Russia, nuclear energy in France, and renewable energy resources in Canada. Natural gas is the number one resource to generate electricity in Turkey, and this has not changed in the last 10 years. Over the last 10 years in Turkey, power was generated on average of 40% due to natural gas, and the share of this resource in Turkey’s energy mix was 35.17% as at of the end of 2018. According to these data, natural gas is the most widely used resource in electricity generation in Turkey [1]. Although there is no resource availability in Turkey for natural gas, NGCCPPs are the most widely used power plants, because these large-scale facilities have important advantages such as having high capacities, low setup times, low installation costs, low environmental impacts, short run times, high yields, ease of operation and maintenance, and long economic lifespans, compared to other fossil-fueled-based power plants. The high share of natural gas in Turkey’s total electricity generation with the above-mentioned advantages of the NGCCPPs and the importance of the personnel scheduling in the power plants are taken into consideration together, and the objective of the study is to schedule the shift personnel fairly and according to their capabilities in the large-scale NGCCPP in Turkey.
NGCCPPs consist of generation blocks, and each combined cycle generation block includes two gas turbines, two compressors, two gas turbine generators, two waste heat boilers, two condenser units, one steam turbine and one steam turbine generator. In addition to these, dry-type or sea water-cooled wet type cooling towers, water treatment plant, switchgear, and control and control systems are located in the plant.
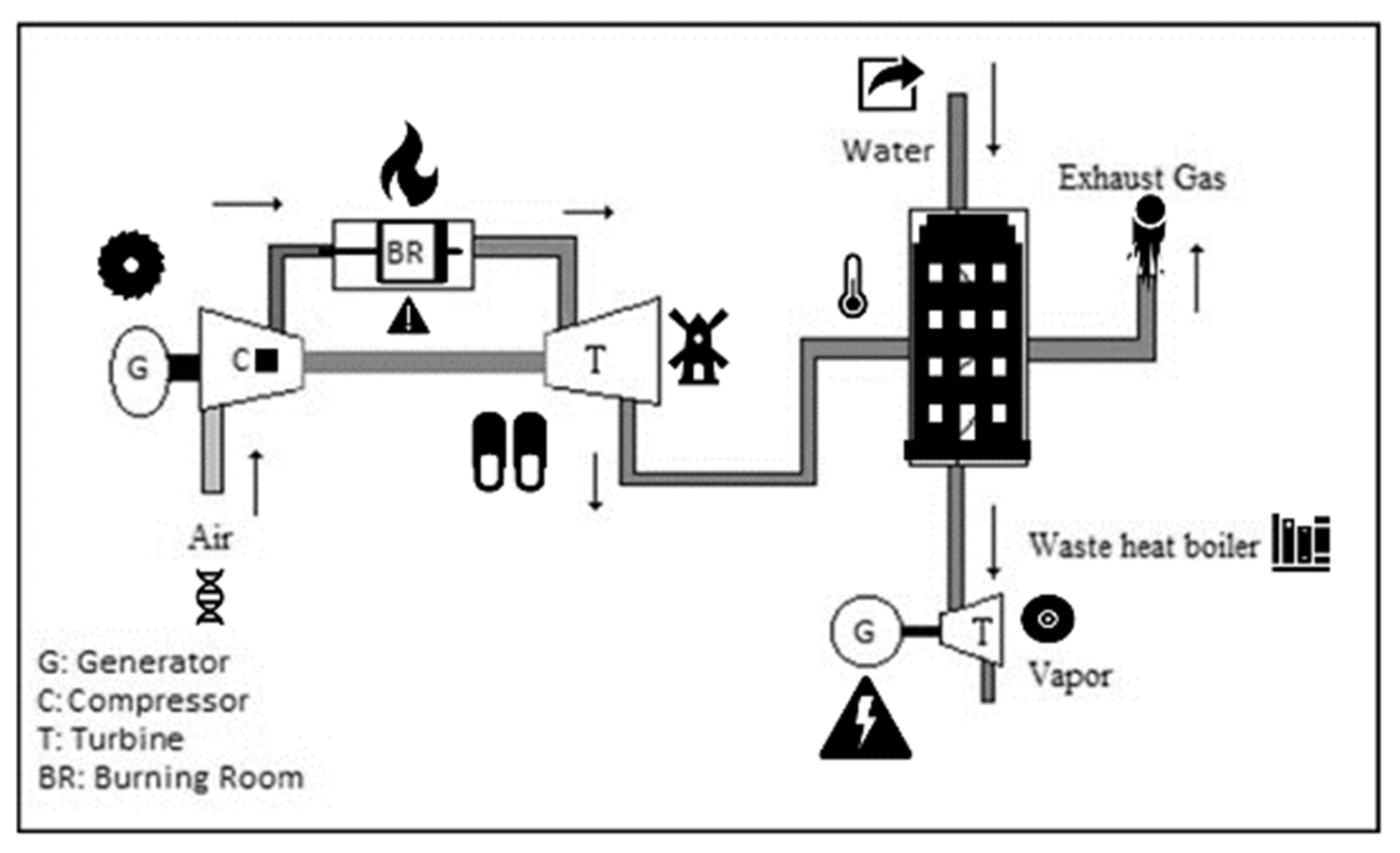
Generation blocks operate independently of each other in NGCCPPs. However, blocks use some facilities that are in common. Electricity generation in these plants is carried out in two different stages, as shown in Figure 1. The natural gas is mixed with air and it is been burned in gas turbines. Burned gas turns the gas turbine on the same shaft as a generator and generates electricity in the first stage. Simultaneously, the hot gases generated from this combustion are sent to the waste heat boiler, and steam is generated by this heat. Steam reaching the required pressure and temperature is sent to the steam turbine and the turbine is rotated to generate the second stage electricity by the generator means located on the same shaft as the steam turbine. Steam from the steam turbine is condensed in the condensers with the cooling water from the cooling towers and converted into water. The condensation water, which accumulates in the lower part of the condensers, is sent to the waste heat boilers for reheating. Steam produced in the boiler is sent to the steam turbine and the cycle is completed. There are three different pressure levels (low, medium, high pressure) in the boilers, which is produced by steam force in order to keep the efficiency at maximum level. Thus, the hot gases in the boilers are utilized as much as possible [2].
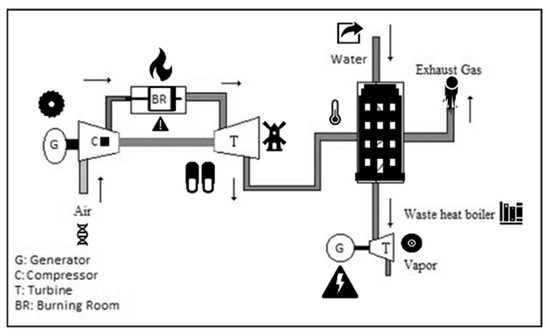
Figure 1.
Schematic representation of the working principle of the combined cycle power plant.
Turbines are the most important of the systems mentioned in NGCCPPs. This is, as the basic reasons explain, that electricity is produced in gas-turbine steam turbines. If the turbines are deactivated, the corresponding block disables the unit (each gas turbine is called a unit) and the system stops. On the other hand, some NGCCPPs have by-pass lines, and the hot gas from an accidental gas turbine, which is formed in the waste heat boilers of the steam turbine, can be directly discharged to the atmosphere by means of a by-pass chute and only electricity generation can be continued in gas turbines (single operation). In addition, these systems are structurally more complex than other systems in the plant.
When previous studies were examined, SSP with this size (30 days for 80 personnel) within the energy sector has not been studied before. The problem of the scheduling of worker’s shift known as SSP can be complicated, especially in the case of multiple shifts and multiple employees with many employees and skills, due to the sophisticated constraints and solution alternatives. Preparing the schedules of staffs manually is thus infertile and time consuming. Therefore, a methodical approximation for initiating a useful schedule is required within a short period of time. Currently, the scheduling of the operation of the shifts of the NGCCPP is carried out manually. This paper deals with the formulation of a model for the shift scheduling problem for NGCCPP employees working with newly defined constraints that define the structure of the industry, organizational policies, and shift schedules, and the requirements that determine the daily preferences of workers. The model seeks to produce the most appropriate monthly shift plan that maximizes employees’ job satisfaction. In this way, stoppages caused by operator error are reduced from 53 hours to 4 hours, and both financial gain is achieved, and the target of sustainable energy supply is reached at this power plant. Furthermore, with this study which provides multi-objective scheduling on the basis of the capabilities of a large group of 80 employees working in NGCCPP for the first time in the literature, a shortcoming in the SSP literature is eliminated.
The paper is shaped as follows: After a brief introduction, the next section gives a literature overview around the problems of shift scheduling. The next section gives information about the perspectives and applications of the study. The last section gives related discussions of the computational results and the conclusion of the study.
2. Shift Scheduling Problem (SSP)
Coordination of workload plans and assignment of personnel and staff planning and personnel scheduling in order to meet the demand for resources that change with time. These problems occur in service industries, such as police officers, call center operators, hospital nurses, transportation personnel (aircraft crews, bus drivers) and so on. It is a very important topic for personnel scheduling. These environments are often prolonged and unsteady, and personnel needs undulate over time. Schedules typically include equipment requirements, trade union rules, etc. It is the subject of various restrictions dictated by inherent features of personnel scheduling problems. The problems that arise tend to be combinatorically difficult. For personnel scheduling problems, Baker proposed one of the first classification methods [3]. In the study of Baker [3] and Pinedo [4] SSP is a brand of the personnel scheduling problem. Personnel scheduling problem’s structure can be divided into several categories. General solution method is with integer programming. This method contains a large class of personnel scheduling problem solutions. Besides, there is a specific category of integer programming problems, namely cyclical personnel problems. This problem can be used in terms of class and a combinatorial viewpoint. Apart from these, crew and operator scheduling problems have a different model structure. In the personnel scheduling problem, there are assignment models. In spite of the fact that every assignment mold belongs to a financial reason, it is a reason why the cost is relatively easy. A cycle structure is thinking of a beforehand. With annotative adjustments, the cycle can be a single day, another week or a few weeks. Part of the previous episode is limited to a loop.
In general, the SSP deals with the assignments of employees to each shift determining the number and criteria. Each shift is getting shaped to specific start and finish times. The number and placement of moats time or the long and the short lengths of the shifts are limiting with legal and business rules. The main goal of scheduling shifts is to optimize employee allocations. Besides, it also helps to minimize the total cost. This requires that each shift be precisely assigned to personnel, qualified by several constraints that must be satisfied. SSP is key to ensuring that services continuously operate without any timeframes in specific service sectors, as well as hospitals, police stations, seizure centers, railway stations and airports [5].
One of the main difficulties of shift scheduling concerns with requirements and limitations of existing personnel while a work pattern of each shifts depending on the number of certain regulations. This planning is getting more difficult when multiple shifts and break or idle times and/or lots of skilled and variable shifts are involved, where every shift needs a combination of these to fulfill the request for that shift. When highly skilled employees can accomplish many different activities during the same shift, the problem becomes more difficult. The shift programming problem’s mathematical models are formulated to solve, subject to several constraints such as one shift per day, number of permits per day, shift order, gap between shifts, rest day after day and night shifts, consecutive days, and working consecutive night regulations, fixed hours for shifts, restricted working hours, number of workers based on skill or skill, etc. Restrictions taken into account in the SSP may include the ordering or preference of consecutive shifts or preferred shifts to be followed, forbidden shift sequences, constraints on demand, and minimum rest periods between shift changes. For this reason, various SSP variations can be found depending on the restrictions applied. A type of SSP is the Day-off SSP (D-SSP) that focuses on determining the most suitable rest days for an employee’s planning horizon. This problem is that the cost of closed molds on different days is different and the goal is to minimize the total labor cost. In this study, model formulation is considered preferences of the workers presented through its objective function and constraints.
In this paper, the SSP is formulated as Analytic Network Process (ANP) and Goal Programming (GP) model for personnel of power plant, referred to as the SSP-ANP-GP model. However, the recommended goal programming model is different from other models for scheduling shift personnel described above because of the different goals. The objective of the SSP-ANP-GP model is to maximize the personnel’s needs, which is determined with four goals in the proposed model.
Mathematical programming models for the SSP can be solved using precise algorithms, intuitive approaches, and top-level information. Our model gives an optimal solution, but in the case of large-scale problems, it is hard to apply in terms of operation time and complexity. Because of that reason, metaheuristics and intuitive approaches are more hopeful options for these situations. It is much better in big-size problems when an intuitive, optimization is sufficient as a solution and has optimal solutions in reasonable time. Approximate optimization algorithm frameworks are meta-analyses that can be defined as a primary strategy or a general algorithmic framework that can be applied to a variety of problems with only a few changes. They are commonly used when they are confronted with a complex problem that cannot be resolved by certain algorithms [6]. The SSP-ANP-GP model of our paper is solved using the integer linear programming algorithm of IBM ILOG optimization tool (IBM, Armonk, New York, NY, USA), which employs the heuristics and exact approaches.
In our paper, a different SSP approach is used for the literature review in shift scheduling studies apart from other studies. It shows that our SSP application area is different from other data and application areas. The energy sector is a new sector for the SSP problems. According to the results of the investigated papers, shift scheduling studies are done for the main production or service personnel. In other words, there is a gap in scheduling of people working in auxiliary and complementary processes in the energy sector for personnel scheduling literature.
On the other hand, these processes may directly affect the quality levels of output of production and service systems, customer satisfaction levels, even sectoral positions of enterprises and social welfare level. The most important examples of this are continuous production systems such as electricity generation, petrochemical and cement production, telecommunication, and health services. However, personnel performing auxiliary and complementary processes may be partly or entirely engaged in the same work with the shift team directly involved in the main processes. The most important example in this situation is the power generation plants. Personnel operating and maintaining these facilities, especially those with electrical and electronic origins, can be operated as both shift and maintenance personnel. This provides significant advantages in terms of productivity, quality, uninterrupted production, and costs in terms of the establishment that owns the plant. Because of that reason, shift scheduling studies are very important in the energy sector, and above all, in power generation facilities.
3. Related Works
According to the observations on personnel scheduling, most studies focused on creating appropriate shift schedules or work programs for workers, considering a deterministic workload. The research process of this paper started with an investigation of the review articles [7,8]. After that point, the cited paper was investigated, which were given in the review articles. The whole reference list was checked and completed in related articles. Search phrase combinations were stated: Workforce scheduling, personnel scheduling and staffing.
Personnel scheduling literature showed a variety of investigation methodologies that brought together a specific analytical approach with a solution or evaluation technique. A number of studies, mathematical programming categories such as goal programming, linear programming, dynamic programming, and integer programming or optimization were classified as intuitive. Queuing, constraint programming and simulation were other categories for solution technique.
In general, scheduling has an important role in the production and service sector [9]. Most popular studies are done in the shift scheduling area. Shift scheduling is a widely studied area, which is a process that plays an important role in manufacturing and service industries. SSPs can be very complicated, especially in the case of multiple shifts with a large number of employees due to multiple constraints and skill-based works. Shift scheduling problem is a complex NP-hard integer programming problem. There are some examples about large-scale scheduling problems in the literature. As a literature observation, the SSP study in the energy sector has not been encountered in previous studies before. The SSP can be complex, especially in the case of several shifts, with many employees and skills, due to complex constraints and solution alternatives. Especially in most of the shift scheduling studies, the application results were not given. At this point, our study reveals its difference from other studies. Considering all of these, it is thought that shift scheduling studies on energy facilities are a new area waiting to be explored.
In Figure 2, a general literature overview is shown. Those studies are the most related studies to this paper. As is shown in Figure 2, solution methods and objectives/criteria are investigated. Generally; heuristic methods [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], integer programming [25,26,27,28,29,30,31,32,33,34,35,36,37,38] and goal programming [39,40,41,42,43,44,45,46,47,48,49] are the most used techniques for solving SSP. Within the scope of all the studies in Figure 2, some studies which were thought to be most similar to the model structure of our study were selected and explained in detail below.

Figure 2.
Literature Overview.
Aickelin et. al. [10] have studied a heuristic technique which is called Improved Squeaky Wheel Optimization (ISWO) for scheduling problems of the drivers in their work. This method develops the main Squeaky Wheel Optimization (SWO) method.
Aickelin et al. [11] developed a solution to two different staff scheduling problems by discussing and analyzing a heuristic method. The new model improves the effectiveness and execution speed. The results are presented on two different areas of staff scheduling. These are: Bus and train driver shift schedules and nurse shift schedules.
Yunes et. al. [13] have dealt with the issue of shift scheduling for a firm using hybrid algorithms and integer programming methods in their work. In this article, the general team management problem has been discussed, which derives from the daily operation of an urban transit bus company serving the public area. They divided the problem into two distinct subproblems: Shift scheduling and crew rostering. They studied each of these problems using constraint logic programming and mathematical programming approaches. Moreover, hybrid column generation algorithms are developed for solving problems, with combining constraint logic programming methods and mathematical programming.
Akjiratikarl et al. [14], the problem of scheduling home caregivers was solved by the Particle-based Swarm Optimization (PSO), the meta-intuitive technique for population. The proposed methodology is applied, tested and compared with existing solutions on various real problem examples. With these aspects of the study revealed, it showed the difference between the others.
Abbink et. al. [24] have successfully implemented a complex SSP model in their work. The authors described the corresponding analysis methods for scheduling the personnel. The authors have developed an alternative heuristic model that satisfies personnel. New schedules produced according to the alternative production model have reduced personnel costs.
In Alfares [27]’s study, a four day-off scheduling problem for three weeks were resolved. A mathematical model of this problem has been formulated and solved efficiently by setting a limit on the workforce dimension.
Trilling et al. [28] have studied the SSP of the nurses at the hospital in their work. Their study focuses two methods to solve the staff scheduling problem based on constraint and integer programming. Maximization of the fairness of the schedule is the main objective. They tested two techniques in order to be compared.
Lezaun et al. [29] studied the shift scheduling of railroad drivers. They presented a practical study on how to provide a more equitable annual work allocation for Metro Bilbao. The proposed model is solved as a series of four types of integer programming problems. The main benefit of this paper is to combine part-time allocation with a workload unevenly distributed on the days of the week and a planning time frame divided into five periods of three different types.
In Alfares [32]’s paper, the Information Technology help desk operators described personnel shift schedules for a large petrochemical company. The aim of the author was to reduce the cost of labor by setting the best staff level and employee weekly tour schedules needed to cover the changing workload during the 24-hour work period. An integer programming model has been formulated and solved to determine tour scheduling assignments. Selected tour scheduling offers better service at a lower cost and for fewer employees.
In another study Lezaun et al. [33], presented a case study commissioned by the Spanish railway carrier for the annual rostering of shift schedules for the station personnel. A mixed rostering process was used in their research. These problems were resolved using the computer software LINGO package. The model of the study was similar to our model structure.
Corominas et al. [34] aimed at eliminating the issue of production planning by making shift schedules of production workers in their work. They proposed a mixed-integer linear program model. The model helped to solve the problem of scheduling the production and the working hours of an expert team which runs in a multi-product process.
Bard et al. [35] investigated the tour scheduling problem in the United States Postal Service for their work. The study suggested a model to tour scheduling problem for decreasing the size of the personnel scheduling, targeted with several scenarios with integer linear programing. The whole mathematical model included not only full-time but also part-time workers, in addition the specific constraints described by the union contract. They solved the problem faster and in a more cost-efficient way.
Corominas et al. [36] have studied problems such as labor balancing and regulation, using a mixed integer programming model in their work. Their study presented the scheduling problem of annual working hours for any employee, where weekly working hours belong to a pre-set finite set and day-off weeks are the same for all employees. The problem is modeled and solved as a mixed integer linear program.
Bağ et al. [39] investigated the SSP of nurses using a 0–1 goal programming and analytic network process in their work. The analytical networking process (ANP) was used to determine the weights of the goal program. The model was implemented in a state hospital.
Hung-Tso et al. [40] investigated the problem of staff scheduling with the goal programming technique in their work. A linear goal programming model is proposed, and three management goals are considered simultaneously for generating a roster.
Li et al. [41], Kassa and Tizazu [42], Louly [43], Labadi et al. [44] and Todovic et al. [45] studied shift scheduling by using goal programming method and intuitive methods together.
Shuib and Kamarudin [46], studied an SSP of the workers at the largest power plant in Malaysia. Their study aimed to define the basic criteria and conditions of the shift planning problem at the power plant in order to formulate the goal programming model for the shift programming problem, which optimized the daytime preferences of the workers and determined the optimal scheduling for the model-based workers. The study focused on three legs which were shift scheduling, day-off scheduling, and scheduling with demands. The study involved scheduling 43 personnel in a specific department of the power plant for 28 days where personnel work in three shifts (morning, evening, and night shifts) and with day-offs.
Ernst et al. [50] conducted a bibliographic study that contributed significantly to the literature on personnel SSPs in their work. They do not review the software packages in their work. Rather, they review scheduling problems in specific areas of application and the models and algorithms reported in the literature for the solutions. They also search for commonly used methods to solve staff problems.
Azaies and Al-Sharif [51] have solved the SSPs of the nurses by using a 0–1 goal programming method in their studies. This study is an example of an NP-hard integer programming problem. The model of the study is similar to our model structure. The constructed model calculates as well as some of the policies proposed in the literature regarding both the hospital targets and the preferences of the nurses. Hospital objectives include providing uninterrupted service with unnecessary nursing skills and staff size and avoiding additional costs for unnecessary overtime.
Topaloğlu [52] studied the problem of shift scheduling health-care personnel with goal programming method. The author suggested a goal programming (GP) model that includes both hard and soft constraints for a monthly planning period. Hard constraints must be strictly observed but may be violated if soft constraints are required. The relative significance values of soft constraints were calculated by the analytic hierarchy process (AHP) used as deviation coefficients from the soft constraints in the objective function. Their models were tested in the emergency room of a large local university hospital. The main results of the study are that realistic problems can be solved quickly, and the schedules created have very high qualifications according to the schedules prepared manually.
In Alfares [53]’s study, a simulation approach was presented for workers’ permission schedules when daily labor demands were random variables. The author created a simulation model and stated that the proposed approach is a case study application. The model stated that the employees had a limited number of jobs, included variable workload, and that employees had policy restrictions on the selection of work programs. The shift scheduling model also offered an alternative for leave days, reducing average production times for maintenance work orders by 25% without increasing the number of employees or cost.
Alfieri et al. [54] have defined an intuitive procedure with an intuitive branch-price algorithm based on a dynamic programming algorithm to find a suitable solution for pricing. They tested the results on the timetable of train lines.
Chu [55] solved the SSP of airport staff using the goal programming technique in his work. Chu proposed an integrated crew duty assignment for the luggage department staff at Hong Kong International Airport. The results could be adopted as a good crew schedule. The result showed that it was both feasible and the model satisfied various work conditions and minimized idle shifts.
In Thompson and Pullman’s [56] study, the SSP of the staff were solved. The study focused on workforce schedules breaks or reliefs of the workers.
Sinreich and Jabali [57] used a linear programming model and simulation tools to solve the SSP in their work. In their study, they used a linear optimization model (S-model) and a heuristic iterative simulation-based algorithm (SWSSA) for scheduling the resources’ work shifts, one resource at a time. Their algorithm was tested using data that was gathered from emergency departments of five general hospital. By using this model, they were able to achieve a reduction in patient’s “length of stay” minutes.
The other paper of Al-Yakoob and Sherali [58] concerns the issue of assigning employees to a range of work centers, taking into account the preferences expressed for specific shifts, days and business centers by using a heuristic method. Computational results have shown that the proposed approach can facilitate the creation of good quality scheduling even for large-scale problematic cases at a reasonable time. De Matta and Peters [59] used branch and price; Tsai and Li [60] used genetic algorithm and Lezaun et al. [61] used binary programming for solving scheduling problems.
Rönnberg and Larsson [62] studied the problem of appointing nurses shift scheduling in the Swedish healthcare sector. The authors present a pilot study that aims to determine if it is possible to create an optimization tool that presents a program that is automatically available based on the charts recommended by nurses. The study was conducted in a typical Swedish nursing ward, where we developed a mathematical model and presented timetables. The results of this study are highly encouraging and suggest ongoing studies. Zolfaghari et al. [63] used genetic algorithm and Alsheddy and Tsang [64] used linear programming for solving scheduling problem.
Fırat and Hurkens [65] performed personnel shift schedules with mixed integer programming. The authors assigned technicians to tasks with multi-level skills requirements. The study deals with the scheduling of complex tasks with a non-homogeneous resource set. They created programs by repetitively applying a flexible matching model that selects the tasks to be processed and which creates technician groups assigned to task combinations. The underlying mixed integer programming model is capable of reviewing technician-task distributions and performs very well, especially in the case of rare skills. Asensio-Cuesta et al. [66] used genetic algorithm for solving scheduling problem.
4. Methods
In this study, two different methods were used. One of them was goal programming. The other one was the analytic network process. These two techniques will be briefly summarized below.
4.1. Goal Programming (GP)
Goal programming is a kind of multi-criteria decision-making model. The model is established using both soft constraints and hard constraints. Soft constraints are used to model situations where deviations are acceptable to a desired goal value. Thus, more than one desired situation is provided approximately or fully. Goal programming is a mathematical programming method aiming at minimizing deviations from the goal values determined by turning aims to goals and ranking goals by importance ratings, or weighting each of them. In linear programming, while a single objective function is used, it is aimed to achieve the same goal by targeting multiple goals differently in the goal programming. In 1955, Charnes and his colleagues first worked on goal programming [67]. Later in 1961 and 1977, Charnes and Cooper developed this model [68,69]. Ignizio [70] describes goal programming as follows: Minimize the deviations in the aim thus that each target reaches as far as possible the given goals. The goal programming mathematical representation is as follows [71]:
g = 1…e s = 1…y, g: Number of goals s: Number of decision variables
4.2. Analytic Network Process (ANP)
Analytical Networking (ANP) is a multi-criteria decision-making technique developed by Thomas L. Saaty as a more general approach than the Analytic Hierarchy Process (AHP) method and works with the dual comparative logic like AHP. The Analytical Networking Process can be used to model decision problems that need to take account of the relationships between factors and to achieve more effective results. In the ANP method, factors affecting a goal and a target are grouped according to their effects on each other and a suitable network is modeled [72]. The ANP differs from the AHP in that it uses a hierarchical structure (network / network form) instead of a hierarchical structure from top to bottom [73]. Furthermore, an important problem encountered in the AHP method is rank reversal. Order change; the alternative priorities determined by a particular set of factors change when a new alternative is added or removed [74]. This problem has been reduced by the ANP method [72]. Steps of the ANP method is like that [75]:
Step 1: Determining the Decision-Making Problem
Step 2: Determining Relationships: Interactions between criteria and sub criteria are identified.
Step 3: Performing Criteria Binary Comparisons
Step 4: Calculating of Consistency: The consistency ratio (CR) of each binary comparison matrix is calculated. For consistency, CR < 0.1.
Step 5: Creating Super Matrices in Order:
- Unweighted Super Matrix: A square matristor consisting of super matrices, vectors that take into account all interactions between the problem criterion, sub criterion, and alternatives. - Weighted Super Matrix: The unweighted super matrix is equal to 1 column sum.
- Limit Super Matrix: The weighted super matrix is formed by taking the strength of the lines until they are not changed.
Step 6: Determination of the Best Alternative: Alternative priorities are obtained by selecting the highest alternative among these values by finding the limit super matrix and criterion weights.
5. Case Study
This study was carried out on a large-scale shift scheduling optimization with the sustainability of the electricity generation of a NGCCPP for 80 workers at their place of destination directly acting considering programming model for 30 days in Turkey. The application area and the magnitude of the problem have been realized by the combination of the methods mentioned for the first time in the literature. The implementation steps of the work are given in Figure 3. Our study was conducted with four levels. The First Level was getting shaped in the name of the data collection and model development. The second stage was generated as ANP calculations and analysis of the result. The third level was generated as a model computation and analysis step. The fourth level was the validation and verification of the model. In the first level, all data were taken from the technical management and human resource department of the power plant.

Figure 3.
Schematic representation of the study.
In this study, scheduling focuses on three steps. These are demand modeling, scheduling of shifts, and scheduling of the days-off. This paper deals with SSP of the personnel who are in working for generation of the electricity to the power plant. The goal programming method is used for its advantages in many shifts and many employees of many workers.
5.1. Determining the Workers’ Skill Weights with Analytic Network Process (ANP)
Analytic Network Process includes decision-maker’s judgments value. It can also provide a decision-making process included in the model. Besides significant tangible or intangible factors to be correct, the decision must be examined. ANP gives solution that can accommodate within the complex structure and this method is capable of easy calculation. As mentioned in the first phase of the work, there are a number of situations that stop electricity production if it is checked and not intervened at the required times. The ability of each worker working in the natural gas combined cycle line to intervene in these situations is different. As it seen in Figure 4, ANP steps are applied in order. Schematic representation of the network structure can be seen in Figure 5.
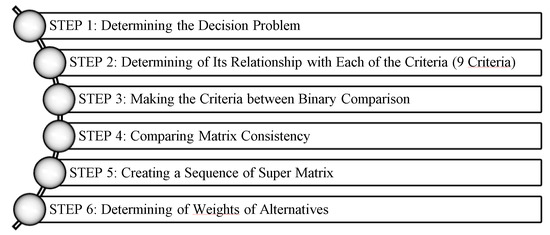
Figure 4.
Schematic representation of the analytic network process (ANP) steps.
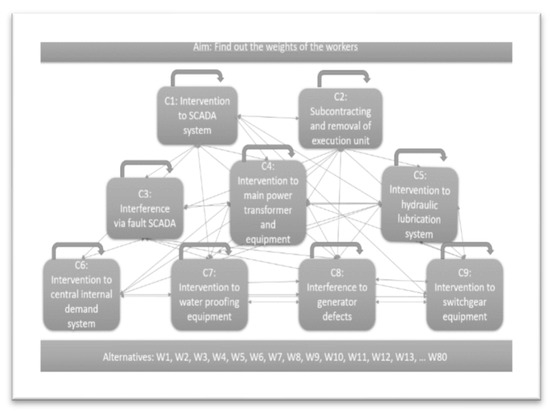
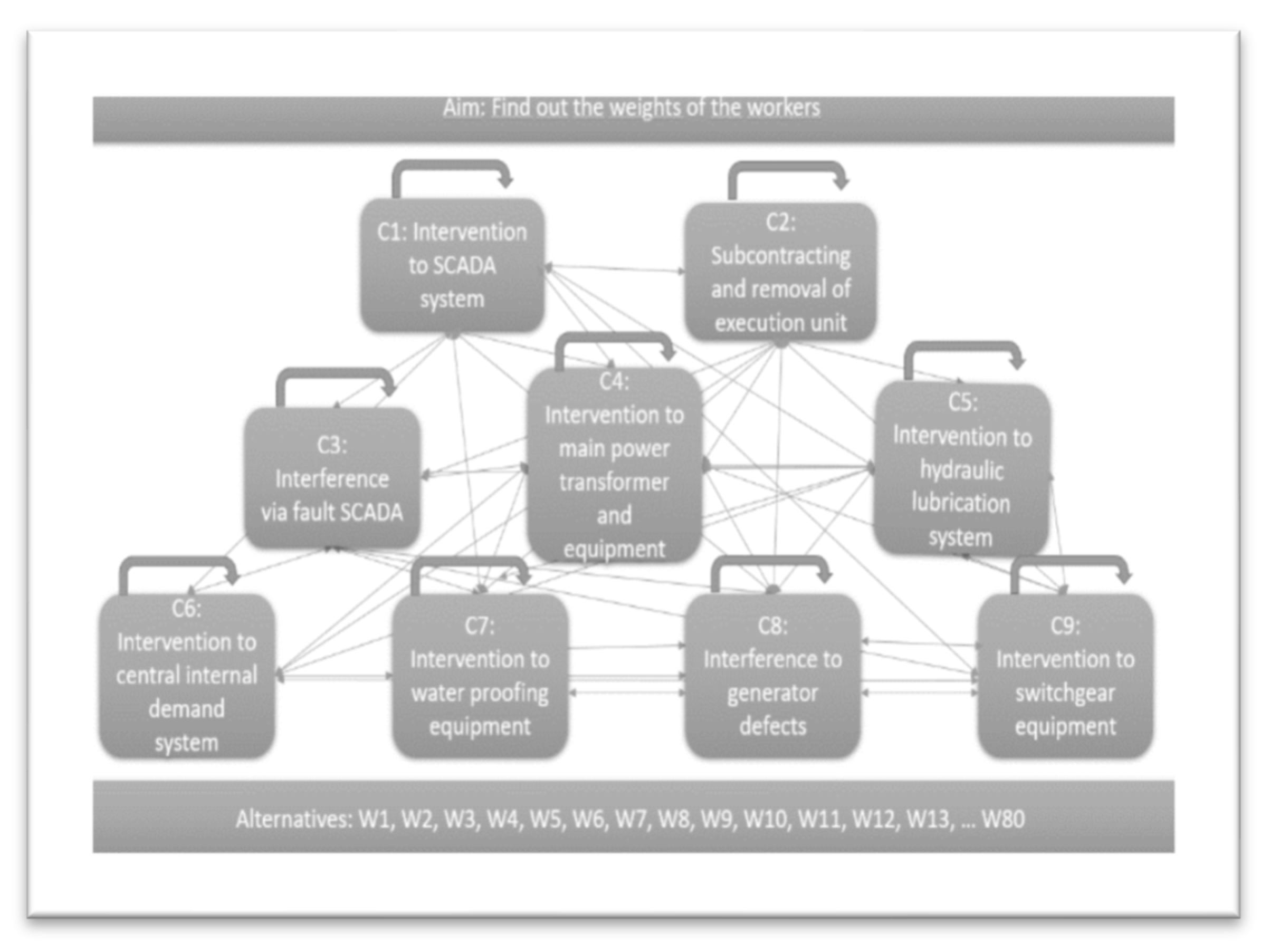
Figure 5.
Schematic representation of the network structure.
There are nine criteria of the skills of the workers. Each criterion is determined with the expert of the power plant. The network structure was established based on the internal and external dependencies among the criteria in the hierarchical structure. According to these nine criteria, each personnel’s skill weight is determined. These criteria are given in Table 1.

Table 1.
Criteria about personnel skills (C1, C2, …, C9).
Consistency ratios (CR) of the binary comparison matrix prepared with the central experts were found to be less than 0.10. This means that the matrices were consistent. Three types of super matrix calculations are made in ANP. These are the unweighted supermatrix, weighted supermatrix and limit supermatrix. On a lean quilt; matrices obtained as a result of initial effects. The relative weight vectors obtained from the ANP charts are placed on the columns and rows of this matrix.
After transferring the data to the super decisions 3.0 package program, the weighted sequence of the alternatives is reached by obtaining the non-weighted super matrix, the weighted super matrix and the limit super matrix, respectively. Limit super matrix of the ANP calculations is given in Appendix A as Figure A1, Figure A2 and Figure A3.
After all calculations, each worker’s score is determined with the help of the nine criteria. In Table 2, ANP weights of each worker are given.

Table 2.
ANP Weights (ti) of the workers (P1, P2, P3, … P80).
In this model, a seniority-based calculation was made in order to incorporate the skill basics into the model, and a separate mean value was calculated for each level of seniority level. In calculating these average values, the number of seniorities (4 different levels) and the individual weight values (obtained in ANP calculations) were used. Therefore, the weights are included in the model. According to this, the average values for the shift supervisor, foreman, expert and assistant are given in Table 3 respectively.

Table 3.
Seniority-based ANP weights (ti) of the workers.
The values which are observed in Table 3 will be used in the goal constraints.
5.2. Proposed Goal Programming Model
Satisfying every goal specified by the decision-makers may not always be possible to completely provide. Therefore, goal programming is often referred to as a sequence of procedure in which the multiple goals are satisfied in their priority order [71]. The shift scheduling model will also attempt to satisfy several goals like establishing fairness among personnel. Because of that reason, a unique goal programming model is an excellent approach to solve this problem.
5.2.1. Notations
The workers (P1, P2, P3, … P80) (i) in this department were divided into three shifts (k); Morning (S1) shift 8 a.m. to 4 p.m., Evening (S2) shift—4 p.m. to 12 a.m., and Night (S3) shift—12 a.m. to 8 a.m. Scheduling horizon is 30 days (j). Workers in the power plant have four different seniority level. These are:
- (1st Seniority-Shift Supervisor, 2nd Seniority-Foreman, 3rd Seniority-Expert, 4th Seniority-Assistant)
- There are 80 People in the department (4 Shift Supervisors, 12 Foremen, 24 Experts, 40 Assistants)
- 3 Shifts (Morning, Evening and Night Shifts)
There are some hard and weak constraints about our mathematical model. There are 10 sets of constraints, six of them correspond to the hard constraints (Constraint 1–Constraint 6 under 5.2.4 Constraints subsection) and the four corresponds to weak constraints (Goal 1–Goal 4 under 5.2.5 Goal Constraints subsection):
Constraint 1: Number of personnel needed for each shift every day. (3 shifts 20 people) Number of personnel assigned to their seniority in each shift.
- At least 1 Shift Supervisor must be present in each shift. (1st Seniority Level)
- There must be at least 3 in each shift from the Foremen. (2nd Seniority Level)
- There must be at least 6 in each shift from the Experts. (3rd Seniority Level)
- There must be at least 10 in each shift from the Assistants. (4th Seniority Level)
Constraint 2: A staff working any day at night shift should not work in the morning and evening shifts the next day.
Constraint 3: A person working on any day of the evening shift should not work the next day in the morning.
Constraint 4: This constraint indicates that every staff member should take one day day-off (at least) in a week. In other words, every staff member should not work more than 6 days in a week:
Constraint 5: Every staff member should not work on his/her the day off.
Constraint 6: In the evening shift, the staff cannot be operated more than 9 days.
Decision variables to be used are Xijk and hij, here notation of i, j and k are the indices for 80 workers, 30 days and three shifts, respectively. Variable Xijk indicates worker i is assigned to work on day j for shift k and hij, indicate the assignment of worker i to be in day-off, respectively, on day j.
The complete formulation of the SSP-GP model is as follows:
5.2.2. Parameters: All Parameters Are Given in the Model Below
i: Personnel index, i = 1,2,…,l
j: Day index, j = 1,2,…,m
k: Shift index, k = 1,2,…,n
g: Goal index, g = 1,2,…,z
l: Number of Personnel, l = 80
m: Number of Day, m = 30
n: Number of Shifts, n = 3
ti: Weights of the skills of each personnel, i = 1,2,…,l
hij: Decision variable for day-off of ith personnel, jth day i = 1,2,…,l j = 1…m
5.2.3. Decision Variables: There Are Two Decision Variables on the Model. Those Are and
5.2.4. Constraints
Constraint 1: The constraint that indicating the number of personnel assigned to each grade in accordance with their seniority:
Constraint 2: The constraint that indicating if a staff working any day at night shift should not work in the morning and evening shifts the next day:
Constraint 3: The constraint that indicating if a person working on any day of the evening should not work the next day in the morning:
Constraint 4: This constraint indicates that every staff member should take one day day-off (at least) in a week. In other words, every staff member should not work more than 6 days in a week:
Constraint 5: The constraint that indicating every staff member should not work on his/her the day off:
Constraint 6: The constraint that indicating in the night shift, the staff cannot be operated more than 9 days:
5.2.5. Goal Constraints
The total number of shifts assigned to each staff by their seniority should be as equal as possible.
Goal 1: Constraints for Shift Supervisors
Goal 2: Constraints for Foremen
Goal 3: Constraints for Experts
Goal 4: Constraints for Assistants
5.2.6. Objective Function
5.3. Analysis of The Result
All goals have the same weight. Solving of the model is used with the features computer which processor "Intel (R) Core (TM) i7-2800 CPU@2.00 GH", 16 GB of memory and Windows 10 operating system. The proposed model, ILOG CPLEX Studio IDE is written in the program and is solved with the CPLEX solvent. The proposed schedule is created after running the ILOG CPLEX Studio IDE Solver at a reasonable time.
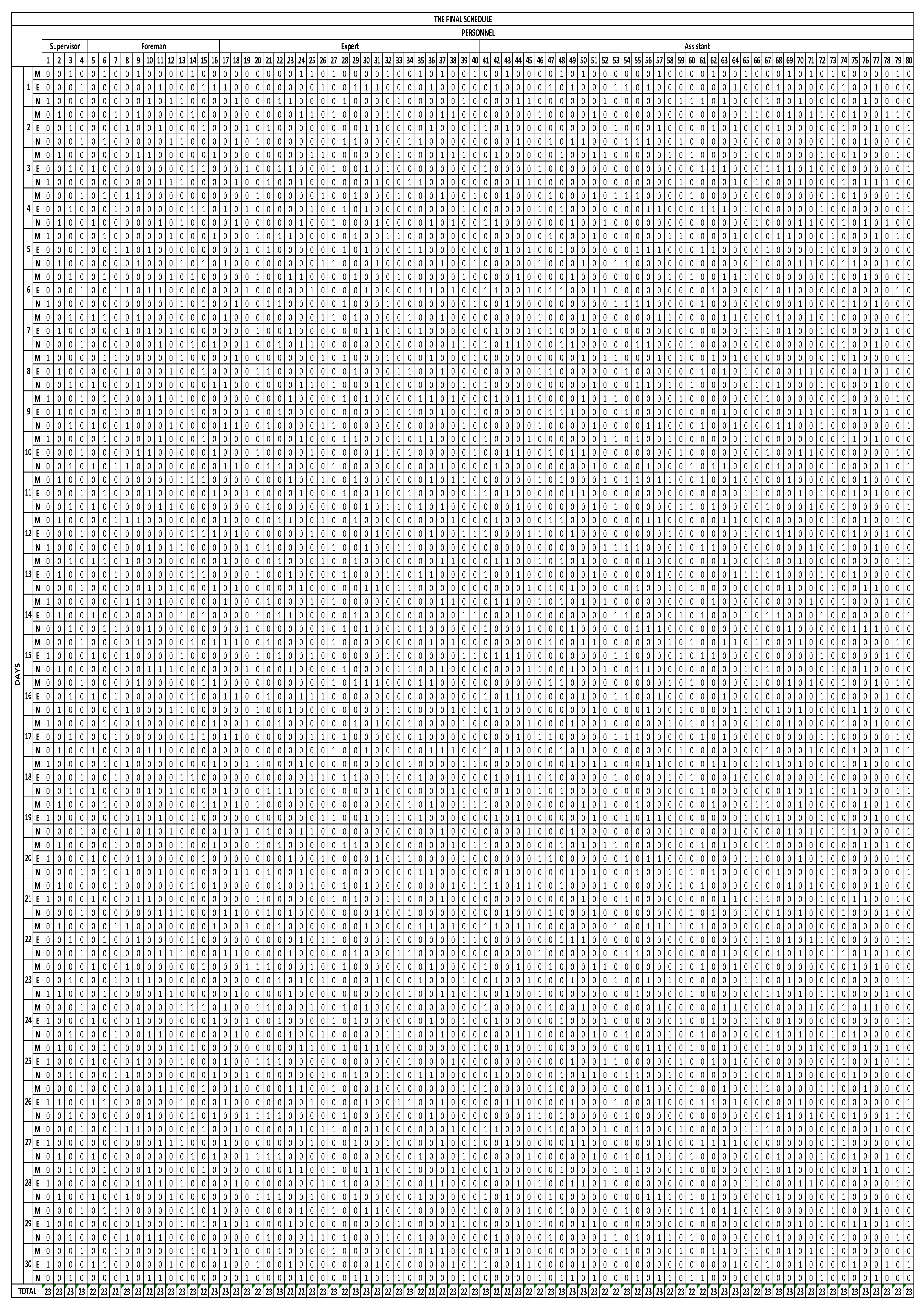
The complete assignment results can be seen in Figure 6. In order to examine the results in detail, the amount of deviation or not, if any, was calculated. The results show that a 1.56% positive deviation was observed from the second goal. A 0.48% negative deviation was observed to the fourth goal. There was no deviation from the first and third goals. As can be seen here, the deviation rates are very low, and the model has yielded positive and efficient results.

Figure 6.
The final schedule.
The model of this study increases the balanced assignments of the workers and that the program needs to adapt these workers on shift scheduling. Thus, it will increase the satisfaction of workers in terms of considering their shift schedule. As it seen from the Table 4, workloads of the personnel are unstable and irregular when the schedules are done in the manual. It has been determined that staff assignments are made by ignoring the hard and soft constraints.

Table 4.
Workloads of each personnel with manual scheduling.
In the Table 5, the workloads of each personnel can be seen after scheduling is done with a mathematical model. All hard constraints are satisfied and many of the soft constraints are satisfied. Worker’s preferences are not ignored.

Table 5.
Workloads of each personnel after scheduling is done with mathematical model.
Computational results are given in Table 6. When the results are examined, the ratio of the demands that are met before the work is done and the rates after the work are done are different from each other. According to gathering results, fair scheduling requests were met, and fairness was provided from shift schedules. The preferences mentioned in the study constitute the entire hard and soft constraints. In the previous manual scheduling, 4 of 10 constraints, some hard, some soft, were not available. After the solution of the proposed mathematical model, all hard and weak constraints were met. 24 of the total 80 employees work 22 days and 56 of them work 23 days in a month for proposed scheduling mathematical model.

Table 6.
Computational result.
This scheduling study, together with shift scheduling issues, has made very high contributions to reducing costs. In order to express the contributions of this work in decreasing costs, it is more appropriate to first explain the calculation over the capacity of the plant. We can say that if the power plant runs at 100% capacity, installed capacity of the power plant is 1000 MW. According to this, the monthly capacity can be calculated as 720 hours (24 hours × 30 days). 1 MW electricity is selling by 17.1 Kuruş (One Turkish Lira (₺) is equal to 100 Turkish Kuruş) from the Energy Market Inspection Agency (EPDK, Ankara, Turkey). This value is the wholesale electricity sales price for 2018 in Turkey. We can find the monthly 100% total generation capacity of the NGCCPP as 720.000 MW (1000 MW × 24 Hours × 30 Days).
There are some shutdown problems of the power plant also included, which arise from doing shift scheduling manually. When the shift scheduling is done manually, on average 53 hours were lost because of SSP. Due to the faults from shift scheduling, 53 hours shutdown caused 90.630.000 ₺ expenses to the NGCCPP (53 Hours × 1000 MW × 17,1 Krş × 100). After the proposed schedule was applied in six months in the power plant, some results were gathered and calculated from the engineering department. According to this, 53 hours loss has been decreased to 4 hours loss after the proposed model of shift scheduling was done. After our implementation of the new schedule, only 4 hours shutdown were seen in the NGCCPP because of the faults from shift scheduling errors. 4 hours shutdown cause 6.840.000 ₺ expenses to the NGCCPP (4 Hours × 1000 MW × 17,1 Krş × 100). According to this calculations, 83.790.000 ₺ total profit (90.630.000 ₺ – 6.840.000 ₺) is gathering from proposed model of shift scheduling. For this reason, this article differs from other studies in the literature in the context of giving the results of application.
6. Conclusions
NGCCPPs have significant advantages such as having high capacities, low setup times, low installation costs, low environmental impacts, short run times, high yields, ease of operation and maintenance, and a long economic lifespan compared to the other types of power plants, which are especially fossil fueled and providing base load requirements. Despite the lack of resource availability, because of these advantages, these power plants are located in first place with a third of Turkey’s energy mix as at of the end of 2018.
The main purpose of NGCCPPs, as in all others, is to provide a sustainable energy supply and one of the most important and problematic pillars of this comprehensive goal is the uninterruptedness. Because, many factors such as operating the power plants without considering the operation and maintenance directives, fuel quality, grid failure, atmospheric conditions, and lack of water cause the NGCCPs’ shutdowns. In addition to this, in NGCCPPs without a SCADA system, the power plant is operated from a main control room or in place by intervening on the equipment spread over the power plant. In this context, the continuity of generation is directly related to the operators, or in other words, to their attention. Because fatigue, unwillingness, and a lack of motivation may cause the operators not to perform the necessary interventions on time. This may lead to longer shutdowns in the power plant. An important way to increase operator motivation in power plants is to establish a fair work distribution and to make competency-based assignments. Therefore, in this study, talent based SSP is handled in one of the large-scale NGCCPP in Turkey and a monthly shift schedule is obtained by solving the proposed multi-objective goal programming model supported with ANP, which is used for calculating the operators’ competencies for decreasing the generation shutdowns due to operator errors.
The power plant has previously been operated by schedules which were unplanned, arbitrary, and without considering the operator qualifications. Therefore, the motivation and work requests of the operators had been lost, and their attention levels decreased considerably. Thus, the power plant had to interrupt generation for 53 hours due to operator error. This loss means millions of kWh of energy; equaling to a significant monetary magnitude. The shift schedule produced by the proposed model within this study has maximized the operator motivation on the basis of fair work distribution and capabilities. Thus, a 92.5% improvement was achieved in operator-centered generation downtimes and millions of TL losses were prevented.
Two of the most important reasons for operators’ motivation loss are that operators are assigned to the shifts without a fair and balanced distribution and without regard to their level of expertise, regardless of their seniority. This fact is agreed upon by all managers and operators at the power plant where this study was carried out. The impact of their level of expertise on motivation is related to each operator’s feeling safe. As mentioned above, the fact that the generation carried out in the power plant is removed from sustainability can cause significant financial losses and social problems. In addition, each shift is a team of four seniority levels, and team members think that a balanced distribution of expertise levels will ensure that sustainable energy supply will not be interrupted. This is consistent with the 92.5% improvement in the proposed model’s generation downtimes. From this point of view, it can be interpreted that operator motivation is increased by taking the working competencies of the proposed model into consideration in the shift schedules produced in NGCCPPs.
The model was solved by using IBM ILOG Optimization Tool in a reasonable time by considering the complexity of the model and the use of precise and intuitive algorithms rather than metaheuristic approaches. However, the SSP-ANP-GP model significantly reduces the time it takes to obtain a monthly schedule based on the current manual scheduling. On the basis of the 30-day program obtained with the SSP-ANP-GP model, the satisfaction of the workers for their day-off preferences increased significantly compared to the current schedule. In addition, according to the current schedule and practice, each worker has to work with a fixed group of people throughout the year. By contrast, in addition to having preferred leisure time choices, the workers have the opportunity to work with a variety of people for their shifts. It has been shown that optimal results that maximizes the day-off preferences can be obtained using the formulated SSP-ANP-GP model.
The proposed SSP-ANP-GP model has the potential to be adapted to the other power plants by changing some possible constraints such as holidays, operator groups, shift number etc. In other words, all types of power plants have specific conditions, requirements, or constraints based on their technology, and the proposed model can be directly applied to the NGCCPPs without a DCS system. However, computational results consistent with real life power plant management of the proposed model show that this study comes to the fore from other studies in the literature.
The examination of the results of the study and the possibility of long-term implementation are important for the contribution to the literature. In practice, SSPs tend to be intertwined with other factory programming problems. For example, the reservation date etc. (it is not possible to change). In the literature, these more general problems (the integration of machine planning and personnel planning) have not been addressed yet. However, there are a number of programming systems on the market at this time. Regarding the solution method, we can see that the literature has multiplied the mathematical programming approaches and metaheuristic approaches.
In spite of the significant increase in productivity of complete algorithms in order to solve integer programming problems in recent years, they are often not applicable to solve practical problems in the medium and large size due to excessive working times and memory requirements. For this reason, for the future application of the SSP-ANP-GP model in the electricity generation of workers’ shift schedules, heuristics can be considered to obtain a complete or approximate solution for shorter calculation times. Other proposals for future work to expand or investigate the SSP for future applications may include strategically reducing the number of decision variables and constraints to make it more practical in the field of application for overtime. In a different point of view, researchers may create a user-friendly interface for using the mathematical model and knowledge based on the solutions obtained by the users to solve SSPs quickly.
Author Contributions
The analyses were carried out by E.H.Ö. This paper was written by E.H.Ö., E.Ö. and T.E. supervised the conducted the research, reviewed and revised the paper. T.E. and E.Ö. reviewed, revised, and improved the paper.
Funding
This research received no external funding.
Conflicts of Interest
“The authors declare no conflict of interest.” “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results”.
Appendix A

Figure A1.
Limit super matrix of the ANP calculations.
Figure A1.
Limit super matrix of the ANP calculations.


Figure A2.
Limit super matrix of the ANP calculations (cont.).
Figure A2.
Limit super matrix of the ANP calculations (cont.).

Figure A3.
Limit super matrix of the ANP calculations (cont.).
Figure A3.
Limit super matrix of the ANP calculations (cont.).

References
- Electricity Generation Company of Turkey; Yearly Activity Report; EUAS: Ankara, Turkey, 2018.
- Oocities Internet Source: Gas Turbines with Steam Injection. Available online: http://www.oocities.org/siliconvalley/platform/6647/kojenen2.htm (accessed on 11 April 2018).
- Baker, K.R. Workforce allocation in cyclical scheduling problems: A survey. Oper. Res. Q. 1976, 27, 155–167. [Google Scholar] [CrossRef]
- Pinedo, M. Planning and Scheduling in Manufacturing and Services; Springer: New York, NY, USA, 2005. [Google Scholar]
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley Series on Parallel and Distributed Computing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Morton, T.E.; Pentico, D.W. Heuristic Scheduling Systems: With Applications to Production Systems and Project Management; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Brucker, P.; Qu, R.; Burke, E. Personnel scheduling: Models and complexity. Eur. J. Oper. Res. 2011, 210, 467–473. [Google Scholar] [CrossRef]
- Bergh, J.V.; Beliën, J.; Bruecker, P.; Demeulemeester, E.; Boeck, L. Personnel scheduling: A literature review. Eur. J. Oper. Res. 2013, 226, 367–385. [Google Scholar] [CrossRef]
- Gür, Ş.; Eren, T. Scheduling and Planning in Service Systems with Goal Programming: Literature Review. Mathematics 2018, 6, 265. [Google Scholar] [CrossRef]
- Aickelin, U.; Burke, E.K.; Li, J.P. Improved squeaky wheel optimisation for driver scheduling, Parallel Problem Solving from Nature—Ppsn Ix. Lect. Notes Comput. Sci. 2006, 4193, 182–191. [Google Scholar] [CrossRef]
- Aickelin, U.; Burke, E.K.; Li, J.P. An evolutionary squeaky wheel optimization approach to personnel scheduling. IEEE Trans. Evol. Comput. 2009, 13, 433–443. [Google Scholar] [CrossRef]
- Aickelin, U.; Dowsland, K.A. An indirect genetic algorithm for a nurse scheduling problem. Comput. Oper. Res. 2004, 31, 761–778. [Google Scholar] [CrossRef]
- Yunes, T.H.; Moura, A.V.; De Souza, C.C. Hybrid column generation approaches for urban transit crew management problems. Transp. Sci. 2005, 39, 273–288. [Google Scholar] [CrossRef]
- Akjiratikarl, C.; Yenradee, P.; Drake, P.R. PSO-based algorithm for home care worker scheduling in the UK. Comput. Ind. Eng. 2007, 53, 55–583. [Google Scholar] [CrossRef]
- Ásgeirsson, E. Bridging the gap between self-schedules and feasible schedules in staff scheduling. Ann. Oper. Res. 2014. [Google Scholar] [CrossRef]
- Lei, L.; Pinedo, M.; Qi, L.; Wang, S.; Yang, J. Personnel scheduling and supplies provisioning in emergency relief operations. Ann. Oper. Res. 2015, 235, 487–515. [Google Scholar] [CrossRef]
- Smet, P.; Wauters, T.; Mihaylov, M.; Vanden Berghe, G. The shift minimisation personnel task scheduling problem: A new hybrid approach and computational insights. Omega 2014, 46, 64–73. [Google Scholar] [CrossRef]
- Mısır, M.; Smet, P.; Vanden Berghe, G. An analysis of generalised heuristics for vehicle routing and personnel rostering problems. J. Oper. Res. Soc. 2015, 66, 858–870. [Google Scholar] [CrossRef]
- Mısır, M.; Smet, P.; Verbeeck, K.; Vanden Berghe, G. Security personnel routing and rostering: A hyper-heuristic approach. In Proceedings of the 3rd International Conference on Applied Operational Research, İstanbul, Turkey, 3 August 2011. [Google Scholar]
- Smet, P.; Vanden Berghe, G. A matheuristic approach to the shift minimisation personnel task scheduling problem. In Proceedings of the 9th International Conference on the Practice and Theory of Automated Timetabling, Son, Norway, 28–31 August 2012; pp. 145–160. [Google Scholar]
- Lee, C.Y.; Lei, L.; Pinedo, M. Current trends in deterministic scheduling. Ann. Oper. Res. 1997, 70, 1–41. [Google Scholar] [CrossRef]
- Veen, E.; Hans, E.W.; Post, G.F.; Veltman, B.; Dumitrescu, S. Shift rostering using decomposition: Assign weekend shifts first. J. Sched. 2015, 18, 29–43. [Google Scholar] [CrossRef]
- Smet, P.; Bilgin, B.; De Causmaecker, P.; Vanden Berghe, G. Modelling and evaluation issues in nurse rostering. Ann. Oper. Res. 2014, 218, 303–326. [Google Scholar] [CrossRef]
- Abbink, E.; Fischetti, M.; Kroon, L.; Timmer, G.; Vromans, M. Reinventing crew scheduling at Netherlands railways. Interfaces 2005, 35, 393–401. [Google Scholar] [CrossRef]
- Aickelin, U.; White, P. Building better nurse scheduling algorithms. Ann. Oper. Res. 2004, 128, 159–177. [Google Scholar] [CrossRef]
- Alfares, H.K. Survey, categorization, and comparison of recent tour scheduling literature. Ann. Oper. Res. 2004, 127, 145–175. [Google Scholar] [CrossRef]
- Alfares, H.K. Compressed workweek scheduling with days-off consecutivity weekend-off frequency and work stretch constraints. Informatics 2006, 44, 175–189. [Google Scholar] [CrossRef]
- Trilling, L.; Guinet, A.; Le Magny, D. Nurse scheduling using integer linear programming and constraint programming. In Proceedings of the 12th IFAC International Symposium, Saint-Etienne, France, 17–19 May 2006; Elsevier: Amsterdam, The Netherlands, 2006; Volume 3, pp. 651–656. [Google Scholar] [CrossRef]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Crew rostering problem in a public transport company. J. Oper. Res. Soc. 2006, 57, 1173–1179. [Google Scholar] [CrossRef]
- Al-Yakoob, S.M.; Sherali, H.D. Mixed-integer programming models for an employee scheduling problem with multiple shifts and work locations. Ann. Oper. Res. 2007, 155, 119–142. [Google Scholar] [CrossRef]
- Al-Yakoob, S.M.; Sherali, H.D. Multiple shift scheduling of hierarchical workforce with multiple work centers. Informatics 2007, 18, 325–342. [Google Scholar]
- Alfares, H.K. Operator staffing and scheduling for an IT-help call centre. Eur. J. Ind. Eng. 2007, 1, 414–430. [Google Scholar] [CrossRef]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Staff rostering for the station personnel of a railway company. J. Sched. 2007, 10, 245–254. [Google Scholar] [CrossRef]
- Corominas, A.; Lusa, A.; Pastor, R. Using a MILP model to establish a framework for an annualised hours agreement. Eur. J. Oper. Res. 2007, 177, 1495–1506. [Google Scholar] [CrossRef]
- Bard, J.F.; Binici, C.; De Silva, A.H. Staff scheduling at the United States Postal Service. Comput. Oper. Res. 2003, 30, 745–771. [Google Scholar] [CrossRef]
- Corominas, A.; Lusa, A.; Pastor, R. Planning annualised hours with a finite set of weekly working hours and joint holidays. Ann. Oper. Res. 2004, 128, 217–233. [Google Scholar] [CrossRef]
- Henao, C.A.; Muñoz, J.C.; Ferrer, J.C. The impact of multi-skilling on personnel scheduling in the service sector: A retail industry case. J. Oper. Res. Soc. 2015, 66, 1949–1959. [Google Scholar] [CrossRef]
- Veldhoven, S.; Post, G.; van der Veen, E.; Curtois, T. An assessment of a days off decomposition approach to personnel shift scheduling. Ann. Oper. Res. 2016, 239, 207–223. [Google Scholar] [CrossRef]
- Bağ, N.; Özdemir, M.; Eren, T. 0-1 Hedef Programlama ve ANP Yöntemi ile Hemşire Çizelgeleme Problemi Çözümü. Int. J. Eng. Res. Dev. 2012, 1, 2–6. [Google Scholar]
- Hung-Tso, L.; Yen-Ting, C.; Tsung-Yu, C.; Yi-Chun, L. Crew rostering with multiple goals: An empirical study. Comput. Ind. Eng. 2012, 63, 483–493. [Google Scholar] [CrossRef]
- Li, J.; Burke, E.K.; Curtois, T.; Petrovic, S.; Rong, Q. The falling tide algorithm: A new multi-objective approach for complex workforce scheduling. Omega 2012, 40, 283–293. [Google Scholar] [CrossRef]
- Kassa, B.A.; Tizazu, A.E. Personnel scheduling using an integer programming model- an application at Avanti Blue-Nile Hotels. SpringerPlus 2013, 2, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Louly, M.A. A goal programming model for staff scheduling at a telecommunications center. J. Math. Model. Algorithms Oper. Res. 2013, 12, 167–178. [Google Scholar] [CrossRef]
- Labidi, M.; Mrad, M.; Gharbi, A.; Louly, M.A. Scheduling IT Staff at a Bank: A Mathematical Programming Approach. Sci. World J. 2014, 1, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Todovic, D.; Makajic-Nikolic, D.; Kostic-Stankovic, M.; Martic, M. Police officer scheduling using goal programming. Polic. Int. J. Police Strateg. Manag. 2015, 38, 295–313. [Google Scholar] [CrossRef]
- Shuib, A.; Kamarudin, F.I. Solving shift scheduling problem with days-off preference for power station workers using binary integer goal programming model. Ann. Oper. Res. 2019, 272, 355–372. [Google Scholar] [CrossRef]
- Özder, E.H.; Varlı, E.; Eren, T. A Model Suggestion for Cleaning Staff Scheduling Problem with Goal Programming Approach. Black Sea J. Sci. 2017, 7, 114–127. [Google Scholar] [CrossRef]
- Varlı, E.; Alağaş, H.; Eren, T.; Özder, E.H. Goal Programming Solution of the Examiner Assignment Problem. Bilge Int. J. Sci. Technol. Res. 2017, 1, 105–118. [Google Scholar]
- Akbari, M.; Zandieh, M.; Dorri, B. Scheduling part-time and mixed-skilled workers to maximize employee satisfaction. Int. J. Adv. Manuf. Technol. 2013, 64, 1017–1027. [Google Scholar] [CrossRef]
- Ernst, A.T.; Jiang, H.; Krishnamoorthy, M.; Sier, D. Staff scheduling and rostering: A review of applications, methods and models. Eur. J. Oper. Res. 2004, 153, 3–27. [Google Scholar] [CrossRef]
- Azaiez, M.N.; Al-Sharif, S.S. A 0–1 goal programming model for nurse scheduling. Comput. Oper. Res. 2005, 32, 491–507. [Google Scholar] [CrossRef]
- Topaloğlu, S.A. multi-objective programming model for scheduling emergency medicine residents. Comput. Ind. Eng. 2006, 51, 375–388. [Google Scholar] [CrossRef]
- Alfares, H.K. A simulation approach for stochastic employee days-off scheduling. Int. J. Model. Simul. 2007, 27, 9–15. [Google Scholar] [CrossRef]
- Alfieri, A.; Kroon, L.; Van de Velde, S. Personnel scheduling in a complex logistic system: A railway application case. J. Intell. Manuf. 2007, 18, 223–232. [Google Scholar] [CrossRef]
- Chu, S.C.K. Generating, scheduling and rostering of shift crew-duties: Applications at the Hong Kong International Airport. Eur. J. Oper. Res. 2007, 177, 1764–1778. [Google Scholar] [CrossRef]
- Thompson, G.M.; Pullman, M.E. Scheduling workforce relief breaks in advance versus in real-time. Eur. J. Oper. Res. 2007, 181, 139–155. [Google Scholar] [CrossRef]
- Sinreich, D.; Jabali, O. Staggered workshifts: A way to downsize and restructure an emergency department workforce yet maintain current operational performance. Health Care Manag. Sci. 2007, 10, 293–308. [Google Scholar] [CrossRef]
- Al-Yakoob, S.M.; Sherali, H.D. A column generation approach for an employee scheduling problem with multiple shifts and work locations. J. Oper. Res. Soc. 2008, 59, 34–43. [Google Scholar] [CrossRef]
- De Matta, R.; Peters, E. Developing work schedules for an inter-city transit system with multiple driver types and fleet types. Eur. J. Oper. Res. 2009, 192, 852–865. [Google Scholar] [CrossRef]
- Tsai, C.C.; Li, S.H.A. A two-stage modeling with genetic algorithms for the nurse scheduling problem. Expert Syst. Appl. 2009, 36, 9506–9512. [Google Scholar] [CrossRef]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Rostering in a rail passenger carrier. J. Sched. 2007, 10, 245–254. [Google Scholar] [CrossRef]
- Rönnberg, E.; Larsson, T. Automating the self-scheduling process of nurses in Swedish healthcare: A pilot study. Health Care Manag. Sci. 2010, 13, 35–53. [Google Scholar] [CrossRef] [PubMed]
- Zolfaghari, S.; Quan, V.; El-Bouri, A.; Khashayardoust, M. Application of a genetic algorithm to staff scheduling in retail sector. Int. J. Ind. Syst. Eng. 2010, 5, 20–47. [Google Scholar] [CrossRef]
- Alsheddy, A.; Tsang, E.P.K. Empowerment scheduling for a field workforce. J. Sched. 2011, 14, 639–654. [Google Scholar] [CrossRef]
- Fırat, M.; Hurkens, C.A.J. An improved MIP-based approach for a multi-skill workforce scheduling problem. J. Sched. 2011, 15, 363–380. [Google Scholar] [CrossRef]
- Asensio-Cuesta, S.; Diego-Mas, J.A.; Canos-Daros, L.; Andres-Romano, C. A genetic algorithm for the design of job rotation schedules considering ergonomic and competence criteria. Int. J. Adv. Manuf. Technol. 2012, 60, 1161–1174. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Ferguson, R. Optimal Estimation of Executive Compensation by Linear Programming. Manag. Sci. 1955, 1, 138–151. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Management Models and Industrial Applications of Linear Programming; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Charnes, A.; Cooper, W.W. Goal programming and multiple objective optimizations. Eur. J. Oper. Res. 1977, 1, 39–54. [Google Scholar] [CrossRef]
- Ignizio, J. Introduction to Goal Programming; Sage Publications Inc.: Beverley Hills, CA, USA, 1985. [Google Scholar]
- Lee, S.M. Goal Programming for Decision Analysis of Multiple Objectives; Auerback: Philadelphia, PA, USA, 1972. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Veen, E.; Veltman, B. Rostering from Staffing Levels: A Branch-And-Price Approach. Int. J. Health Manag. Inf. 2011, 2, 41–52. [Google Scholar]
- Hamurcu, M.; Eren, T. Raylı Sistem Projeleri Kararında Ahs-Hp ve Aas-Hp Kombinasyonu. Gazi Mühendislik Bilimleri Derg. 2017, 3, 1–13. [Google Scholar]
- Hamurcu, M.; Gür, Ş.; Özder, E.H.; Eren, T. A Multicriteria Decision Making for Monorail Projects with Analytic Network Process and 0–1 Goal Programming. Int. J. Adv. Electron. Comput. Sci. 2016, 3, 8–12. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).