A Novel Bat Algorithm with Multiple Strategies Coupling for Numerical Optimization

Abstract

A bat algorithm (BA) is a heuristic algorithm that operates by imitating the echolocation behavior of bats to perform global optimization. The BA is widely used in various optimization problems because of its excellent performance. In the bat algorithm, the global search capability is determined by the parameter loudness and frequency. However, experiments show that each operator in the algorithm can only improve the performance of the algorithm at a certain time. In this paper, a novel bat algorithm with multiple strategies coupling (mixBA) is proposed to solve this problem. To prove the effectiveness of the algorithm, we compared it with CEC2013 benchmarks test suits. Furthermore, the Wilcoxon and Friedman tests were conducted to distinguish the differences between it and other algorithms. The results prove that the proposed algorithm is significantly superior to others on the majority of benchmark functions.

1. Introduction

In the past ten years, many heuristic optimization algorithms, such as particle swarm optimization (PSO) [1,2,3], ant colony optimization (ACO) [4,5], bat algorithm (BA) with triangle-flipping strategy [6], fly algorithm (FA) [7,8,9], cuckoo search [10,11,12,13], pigeon-inspired optimization algorithm, and genetic algorithm (GA) [14], have been developed to solve complex computational problems. It became popular because of its superior ability, which deals with a variety of complex issues. Moreover, it has been proven that there is no heuristic algorithm that can perform generally enough to solve all optimization problems [15]. Therefore, scholars have tried to solve these problems with different bionic algorithms.

BA [16,17,18,19] is a novel heuristic optimization algorithm, inspired by the echolocation behavior of bats. This algorithm carries out the search process using artificial bats as search agents mimicking the natural pulse loudness and emission rate of real bats. To improve the performance of BA, different strategies have been proposed. We will elaborate in the following three research situations.

(I) Parameter adjustment

For the standard BA algorithm, four main parameters are required: frequency, emission, constants, and emission rate. The frequency is used to balance the impact of the historical optimal position on the current position. The bat individual will search far from the group historical position when the search range of frequency is large, and vice versa. In general, the choice of frequency range is determined by different issues. Hasançebi [20] set the pulse frequency range to [0–1]. Gandomi and Yang [21] sets the frequency range to [0–2] in the chaotic bat algorithm. Fister et al. [22] sets the frequency to [0–5] in their algorithm. Ali [23] sets the frequency to [0–100] in the power system. Xie et al. [24] proposed an adaptive adjustment strategy for frequency. Pérez et al. [25] designed a fuzzy controller to dynamically adjust the range of pulse frequencies, while Liu [26] replaced the frequency with a Lévy distribution. To improve the local search capability, Yilmaz and Kucuksille [27] added a random item with two randomly selected bats to explore more search space. Cai [28] introduced a linear decreasing function into the bat algorithm to enhance the global search capability.

(II) Formula adjustment

In terms of global search, the step size of the standard BA algorithm decreases with the increase of iterations, which causes the algorithm to be sensitive to local optimum. Focusing on this problem, Bahmani-Firouzi and Azizipanah-Abarghooee [29] proposed four different velocity updating strategies to keep a balance between exploitation and exploration. Inspired by PSO, Yilmaz and Kucuksille [30] put the inertia weight into the velocity update equation. Xie et al [24] use random parts associated with Lévy distributions instead of avoidance. To improve the local search capability, four differential evolutionary strategies were employed to replace the original local search pattern in the standard BA [31]. Xie et al. [32] also incorporated the Lévy flight in the velocity update equation, but four randomly selected bats were used to guide the search pattern. Zhu et al. [33] replace the swarm historical best position with the mean best position to enhance the convergence speed.

(III) Application

BA has been widely applied to various areas, including classification, wireless sensor [34], and data mining. Yang and Gandomi [35] proposed a bat algorithm to solve multi-objective problems; Bora et al. [36] proposed a bat-inspired optimization approach to solve the brushless direct current (DC) wheel motor problem; Sambariya and Prasad [37] proposed a metaheuristic bat algorithm for solving robust turning of power system stabilizer for small signal stability enhancement; Sathya and Ansari [38] highlighted the load frequency control using dual mode bat algorithm based scheduling of PI controllers for interconnected power systems; Sun and Xu [39] proposed node localization of wireless sensor networks based on a hybrid bat-quasi-newton algorithm; Cao et al. [40] improved low energy adaptive clustering hierarchy protocol based on a local centroid bat algorithm.

Furthermore, there are many applications in big data and machine learning [41,42], such as Hamidzadeh et al. [43], who proposed a novel method called chaotic bat algorithm for support vector data description (SVDD) (CBA-SVDD) to design effective descriptions of data. Alsalibi [44] proposed a novel membrane-inspired binary bat algorithm for facial feature selection. Furthermore, it outperforms recent state-of-the-art face recognition methods on three benchmark databases. Therefore, the bat algorithm has a wide range of applications. In addition, the bat algorithm has been proposed to optimize support vector machine (SVM) parameters that reduce the classification error [45]. Notably, increasing SVM prediction accuracy and avoiding local optimal trap using the bat algorithm has been very helpful in biomedical research [46,47].

The rest of this paper is organized as follows. Section 2 provides a brief description of the standard BA. In Section 3, we listed eight improvement strategies and proposed a novel bat algorithm with multiple strategy coupling. Numerical experiments on the CEC2013 benchmark set are conducted in Section 4. Finally, the discussion and future work are given in Section 5.

2. Bat Algorithm

The bat algorithm [48] was proposed by Xin-She Yang, based on the echolocation of microbats. Bats usually use echolocation to find food. During removal, bats usually send out short pulses, however, when they encounter food, their pulse send out rates increase and the frequency goes up. The increase in frequency means frequency-tuning, which shortens the echolocations’ time and increases the location accuracy. In the standard bat algorithm, each individual $i$ has a defined position $x_i(t)$ and velocity $v_i(t)$ in the search space, which will be updated as the number of iterations increases. The new positions $x_i(t)$ and velocities $v_i(t)$ can be calculated as follows:

$$x_i(t+1)=x_i(t)+v_i(t+1)$$

(1)

$$v_i(t+1)=v_i(t)+(x_i(t)-p(t))\cdot f_i$$

(2)

$$f_i=f_{\min }+(f_{\max }-f_{\min })\cdot \beta$$

(3)

where $\beta$ is a random vector with uniform distribution, the range of which is [0, 1]. $p(t)$ is the current global optimal solution and $f_{\min }=0$, $f_{\max }=1$.

As we also know, whether BA has global and local search capabilities depends on its parameters; therefore, it is necessary to achieve a balance between global search and local search capabilities by adopting adaptive parameters. The formula for the local search strategy is as follows:

$$x_i(t+1)=\overrightarrow{p}(t)+\epsilon \overline{A}(t)$$

(4)

where $\epsilon$ is a random number from [−1, 1], $\overline{A}(t)$ is the average loudness of population.

In addition, it achieves global search by controlling loudness $A_i(t+1)$ and pulse rate $r_i(t+1)$.

$$A_i(t+1)=\alpha A_i(t)$$

(5)

$$r_i(t+1)=r_i(0)[1-\exp (-\gamma t)]$$

(6)

where $\alpha$ and $\gamma$ are constants and $\alpha >0,\gamma >0$. $A_i(0)$ and $r_i(0)$ are initial values of loudness and pulse rate, respectively.

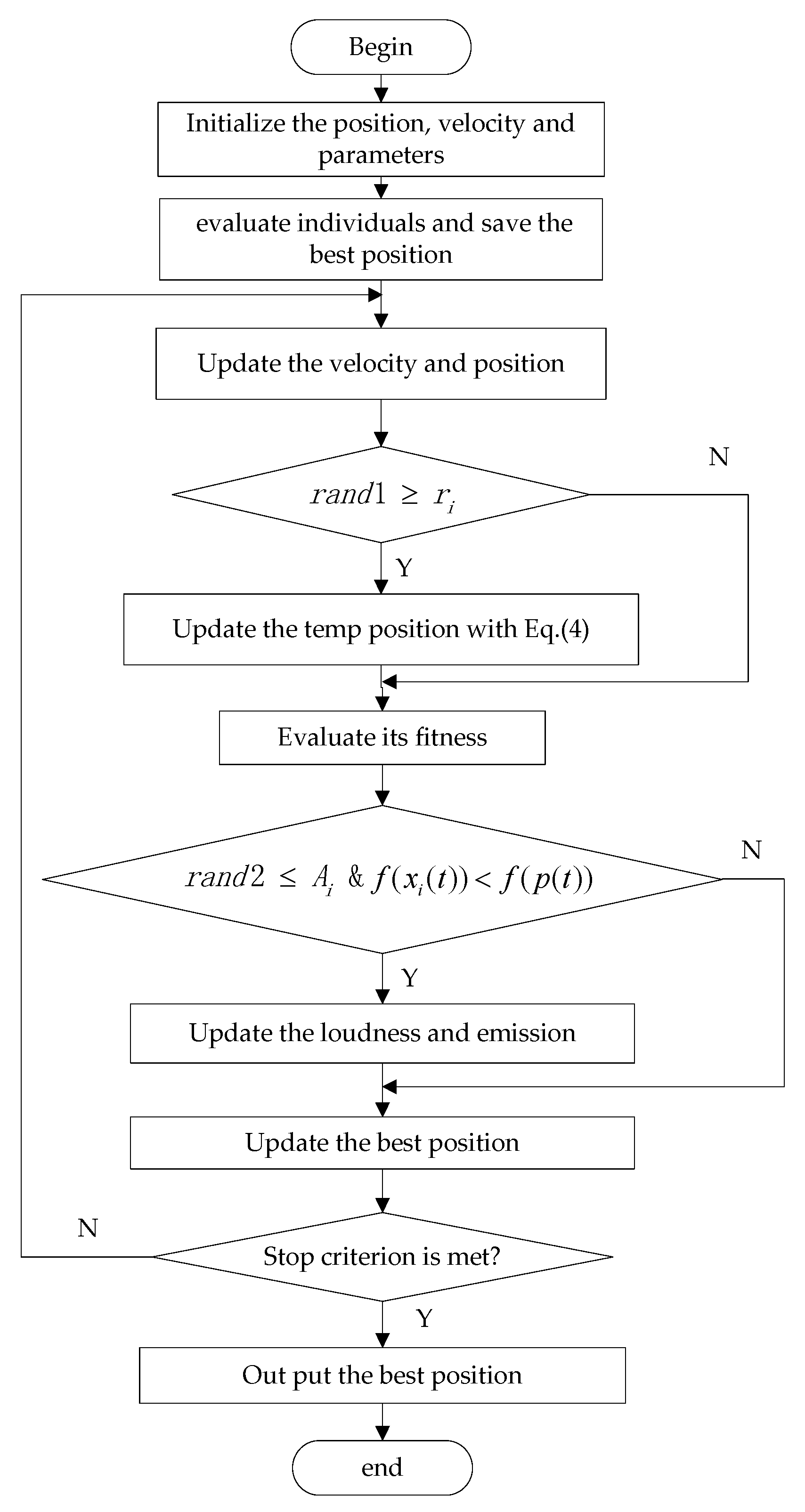
The following describes the execution steps of the standard bat algorithm.

Step 1: 

For each bat, initialize the position, velocity, and parameters and randomly generate the frequency with Equation (3).

Step 2: 

Update the position and velocity of each bat with Equations (1) and (2).

Step 3: 

For each bat, generate a random number ($0<rand1<1$). Update the temp position and calculate the fitness value for corresponding bat with Equation (4) if $rand1<r_i(t)$.

Step 4: 

For each bat, generate a random number ($0<rand2<1$). Update $A_i(t)$ and $r_i(t)$ with Equations (5) and (6), respectively, if $rand2<A_i(t)$ and $f(x_i(t))<f(p(t))$.

Step 5: 

Sort each individual based on fitness values and save the best position.

Step 6: 

The algorithm is finished if the condition is met, otherwise, move on to Step 2.

Detailed steps about the standard bat algorithm are presented in Figure 1.

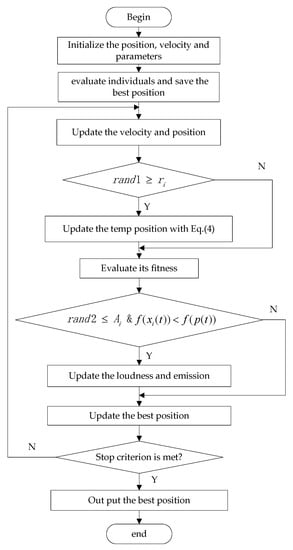
Figure 1. The flowchart of the standard bat algorithm (BA).

3. Bat Algorithm with Multiple Strategy Coupling

Through a large number of experimental studies, we found that different operators play an important role in the convergence ability of the algorithm. When the development operator increases, the global convergence ability of the algorithm becomes weaker; when the exploration operator increases, the convergence accuracy will be insufficient. Therefore, in this paper, we propose a multiple strategy autonomous selection strategy. The main idea is that different individuals choose which strategy to update the position according to the quality of fitness. In this paper, the bat algorithm with multiple strategy coupling (mixBA) formed will adopt the following eight strategies.

• (1) The velocity and position formula of the original algorithm are adopted [42]:

  $$x_{ik}(t+1)=x_{ik}(t)+v_{ik}(t+1)$$

  (7)

  $$v_{ik}(t+1)=v_{ik}(t)+(x_{ik}(t)-p_k(t))\cdot f_i$$

  (8)
• (2) The velocity and position formula of the improved algorithm are adopted [29]:

  $$x_{ik}(t+1)=x_{ik}(t)+v_{ik}(t+1)$$

  (9)

  $$v_{ik}(t+1)=v_{ik}(t)+(x_{ik}(t)-w_k(t))\cdot f_i$$

  (10)

  where $w_k$ is the position of the worst individual.
• (3) The position and velocity formula of Levy flight was adopted by Xie et al. [24]:

  $$f_i^t=((f_{\max }-f_{\min })\frac{t}{n_t}+f_{\min })\beta$$

  (11)

  $$v_i^t=({\widehat{x}}_i-x^{\ast })f_i^t$$

  (12)

  $$x_i^t={\widehat{x}}_i+usign[rand(1)-\frac{1}{2}]\oplus L\mathrm{e}vy(\lambda )$$

  (13)

  where $\beta$ is a random constant, $n_t$ is a constant, ${\widehat{x}}_i$ is the best position of the $i\mathrm{th}$ bat, and $x^{\ast }$ is the best position of those found so far. $L\mathrm{e}vy(\lambda )$ ($1<\lambda \le 3$) is step length of the Levy flight and $\oplus$ stands for dot product.
• (4) The position and velocity formula of Levy flight was adopted by Liu [26]:

  $$x_i^{t+1}=x_i^t+Lévy(\lambda )\otimes (x_i^t-x^{\ast })$$

  (14)
  ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}$ and ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}+1}$ are $i\mathrm{th}$ the position of $t$ bat in generation and $t+1$ generation, respectively.
• (5) The position and velocity formula with the idea of genetic algorithms was adopted:

  $$x_i(t+1)=D{x}_i(t)+(1-D)x_i^{\ast }(t)$$

  (15)
  The formula is a two-point crossover operator in simulation genetic algorithm.
• (6) The position and velocity formula with the idea of PSO was adopted:

  $$v_{ik}(t+1)=v_{ik}(t)+r_1{(x_{ik}(t)-p_{gk}(t))}_i+r_2(x_{ik}(t)-p_{ik}(t))$$

  (16)

  $$x_{ik}(t+1)=x_{ik}(t)+v_{ik}(t+1)$$

  (17)

  where $r_1$ and $r_2$ are random constants and $p_{gk}$ is the best position by the entire swarm.
• (7) A local disturbance strategy based on inertial parameters is adopted:

  $$x_i(t+1)=x_i^{\ast }(t)+wr$$

  (18)

  $$w=w_{\max }-(w_{\max }-w_{\min })\cdot t/T_{\max }$$

  (19)

  where $w_{\max }$ and $w_{\min }$ are the maximum and minimum values, respectively, of inertia weight and $T_{\max }$ is the maximum number of iterations.
• (8) The local search strategy of flight to optimal position is adopted.

  $$x_i(t+1)=x_i^{\ast }(t)+r\cdot (p_{gk}(t)-x_{ik}(t))$$

  (20)

  where $p_{gk}$ is the best position by the entire swarm and $r$ is a random constant.

The above strategies are chosen by the form of probability. Therefore, the number of bat individuals of choosing different strategies varies from generation to generation. Each strategy adjusts the probability of it being selected according to evaluation results. When the fitness value is better, the probability of the strategy will be adjusted by Equation (21).

$$P(n+1)=P(n)+(1-\lambda )\cdot P(n)$$

(21)

Otherwise, it is calculated as follows:

$$P(n+1)=\lambda \cdot P(n)$$

(22)

where $\lambda =0.75$, which is a parameter used to adjust the rate of probability change. The larger $\lambda$ is, the slower the rate of probability reduction will be. To ensure the diversity of the population, we define the probability lower bound for each strategy as 0.01. The procedure of the bat algorithm with multiple strategy coupling is shown in Table 1.

Table 1. The procedure of the bat algorithm (BA) with multiple strategy coupling.

Algorithm 1: Bat algorithm with multiple strategy coupling

Begin  For each bat, initialize the position, velocity, parameters and probability table;  While (stop criterion is met)   Randomly generate the frequency for each bat with Equation 3;   Evaluate its fitness; Switch num = 8   Case 1 (rand < p1)   Update the velocity and position with strategy1.   Case 2 (p1 < rand < p2)   Update the velocity and position with strategy2   Case 3 (p2 < rand < p3)   Update the velocity and position with strategy3.   Case 4 (p3 < rand < p4)   Update the velocity and position with strategy4.   Case 5 (p4 < rand < p5)   Update the velocity and position with strategy5.   Case 6 (p5 < rand < p6)   Update the velocity and position with strategy6.   Case 7 (p6 < rand < p7)   Update the velocity and position with strategy7.   Case 8 (p7 < rand < p8)   Update the velocity and position with strategy8.  Evaluate its fitness;  If the position is update  Update the loudness and emission rate;  Update the probability table;   If pi < 0   Pi = 0.001;   End  End  Rank the bats and save the best position; End Output the best position; End

4. Experimental Result

4.1. Text Functions and Parameter

The algorithm is tested on the CEC2013 benchmark set [43]. The test set can be divided into three groups, as shown in Table 2.

Table 2. The CEC2013 benchmark set.

F1–F5 belongs to uni-modal functions

F6–F20 belongs to multi-modal functions

F21–F28 belongs to composition functions

The experiment is tested on Matlab 2016a environment (2016a, MathWorks, Natick, MA, USA). For details of parameter settings for the bat algorithm with multiple strategies coupling (mixBA), please refer to Table 3. It is worth emphasizing that the parameters of the adopted strategy are not optimized in this paper. In our algorithm, we used the following indicators to evaluate the experimental results.

$$mean\hspace{1em}error=\left|\frac{{\displaystyle \sum _{j=1}^{51}{f}_j}}{51}-f_{true}\right|$$

(23)

where $f_{true}$ is the actual solution set of the test set.

Table 3. The CEC2013 benchmark set.

Pop size	100
Run	51
Frequency	[0, 5]
$A(0)$	0.95
$r(0)$	0.9
$\alpha$	0.99
$\gamma$	0.9
Search Domain	[−100, 100]D

4.2. Comparison of MixBA with State-of-the-Art Algorithms

In this section, we will compare mixBA with six other algorithms. The algorithms involved are presented in Table 4.

Table 4. The involved algorithm.

Bat algorithm with multiple strategy coupling (mixBA);

Standard bat algorithm (SBA);

Self-adaptive heterogeneous particle swarm optimization (PSO) [49];

Bat algorithm with Lévy distribution (LBA1) [26];

Bat algorithm with Lévy distribution (LBA2) [32];

Bat algorithm with arithmetic centroid strategy (ACBA) [40]

Oriented cuckoo search (OCS) [34]

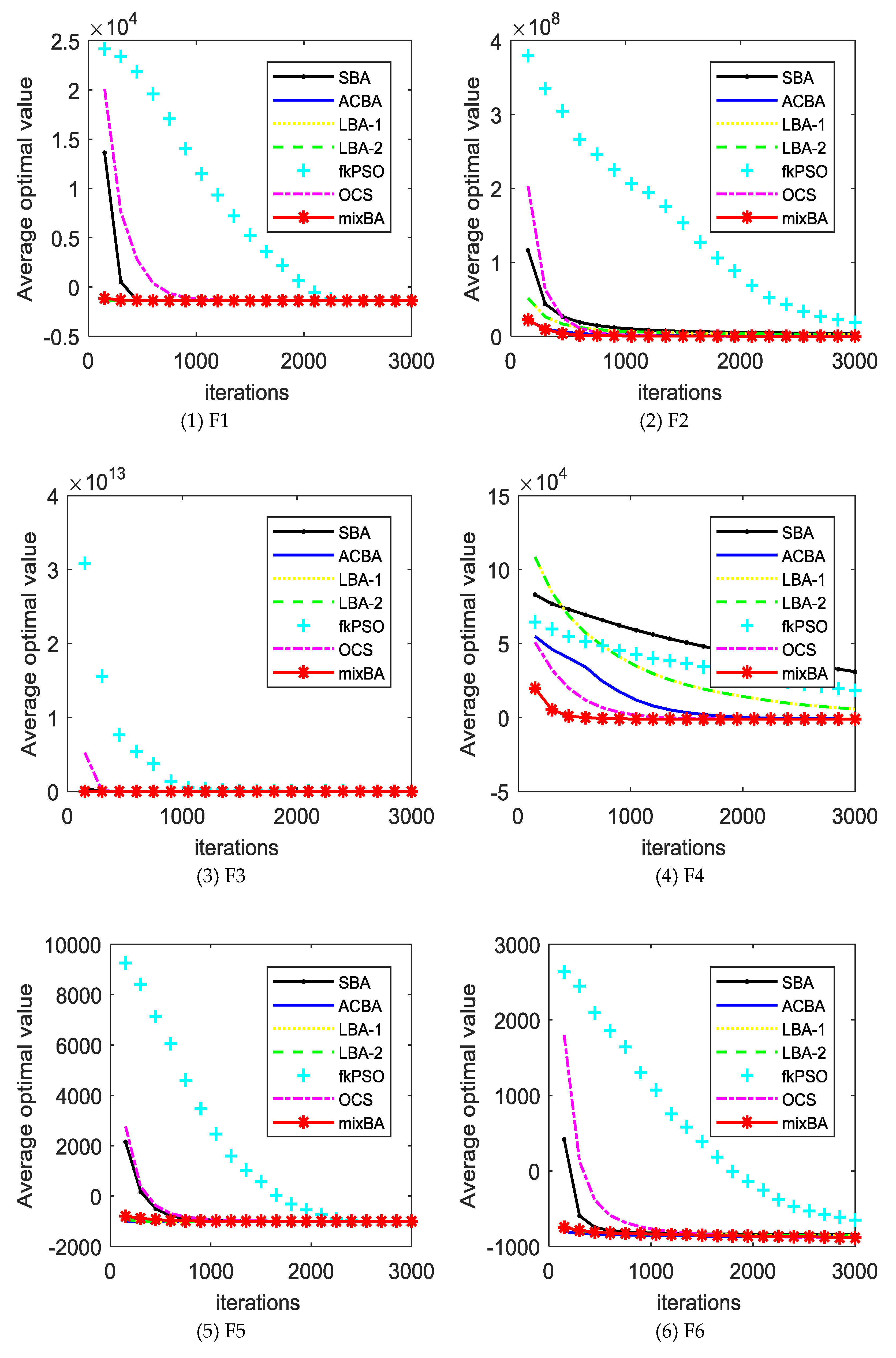
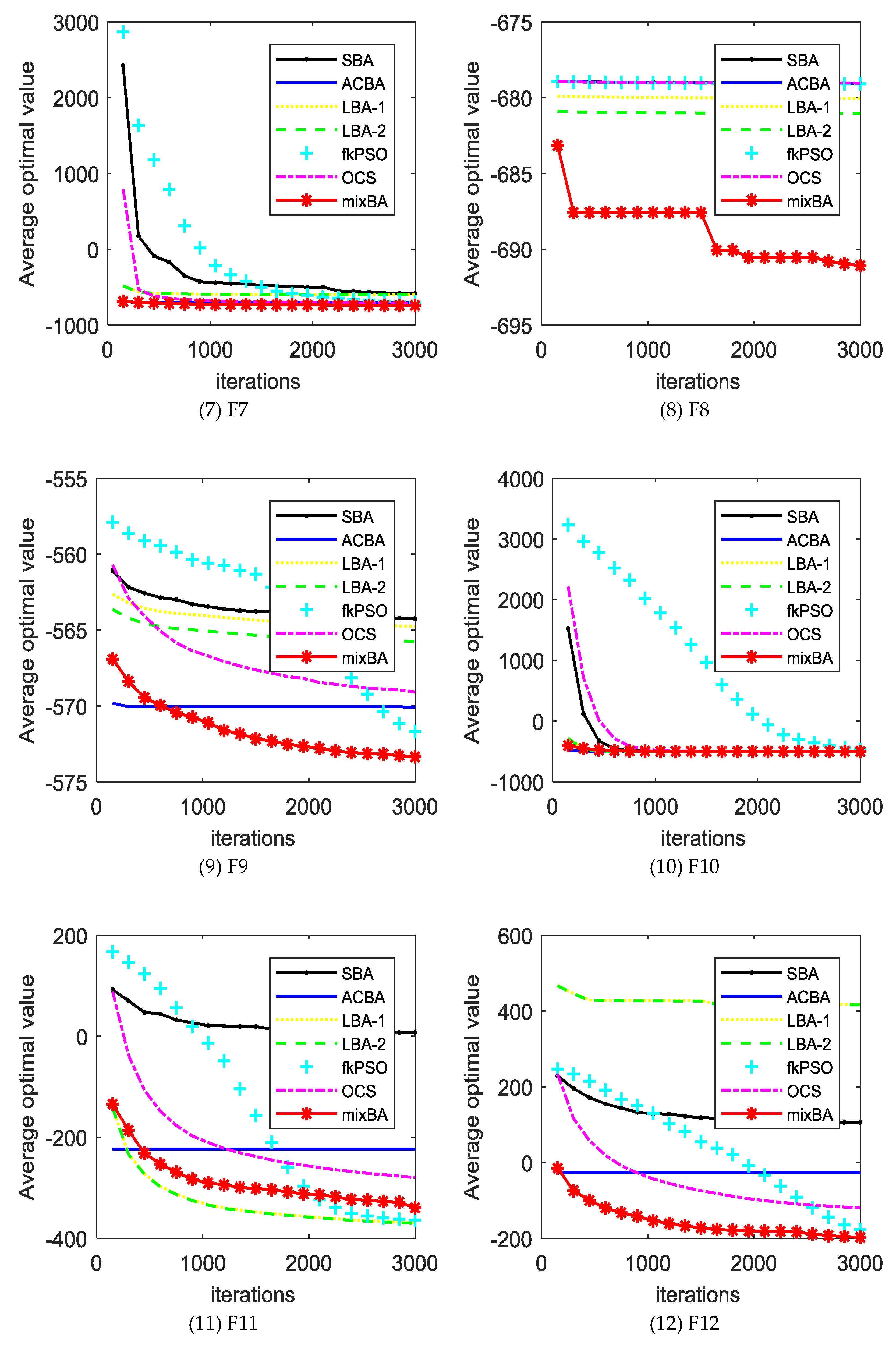
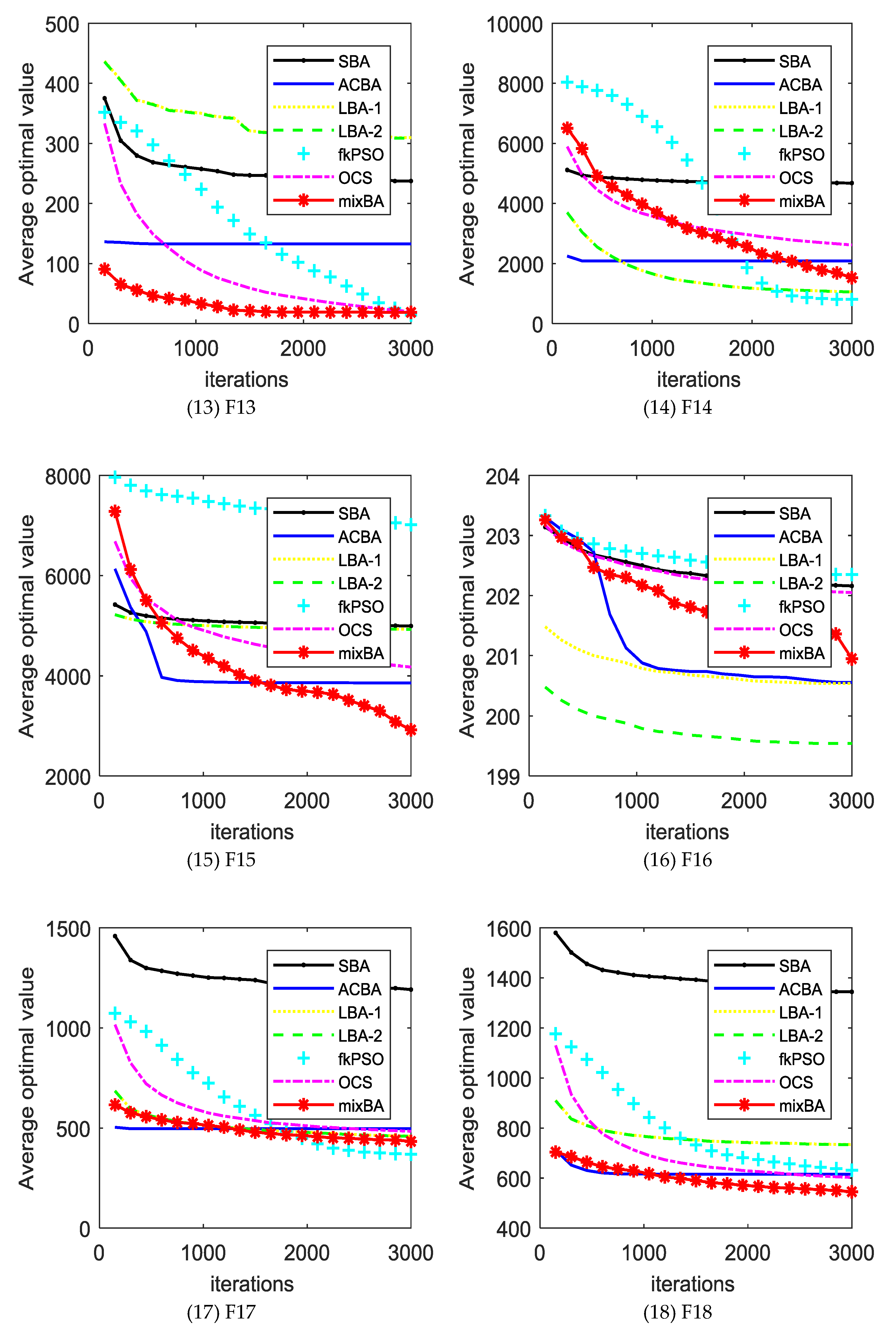
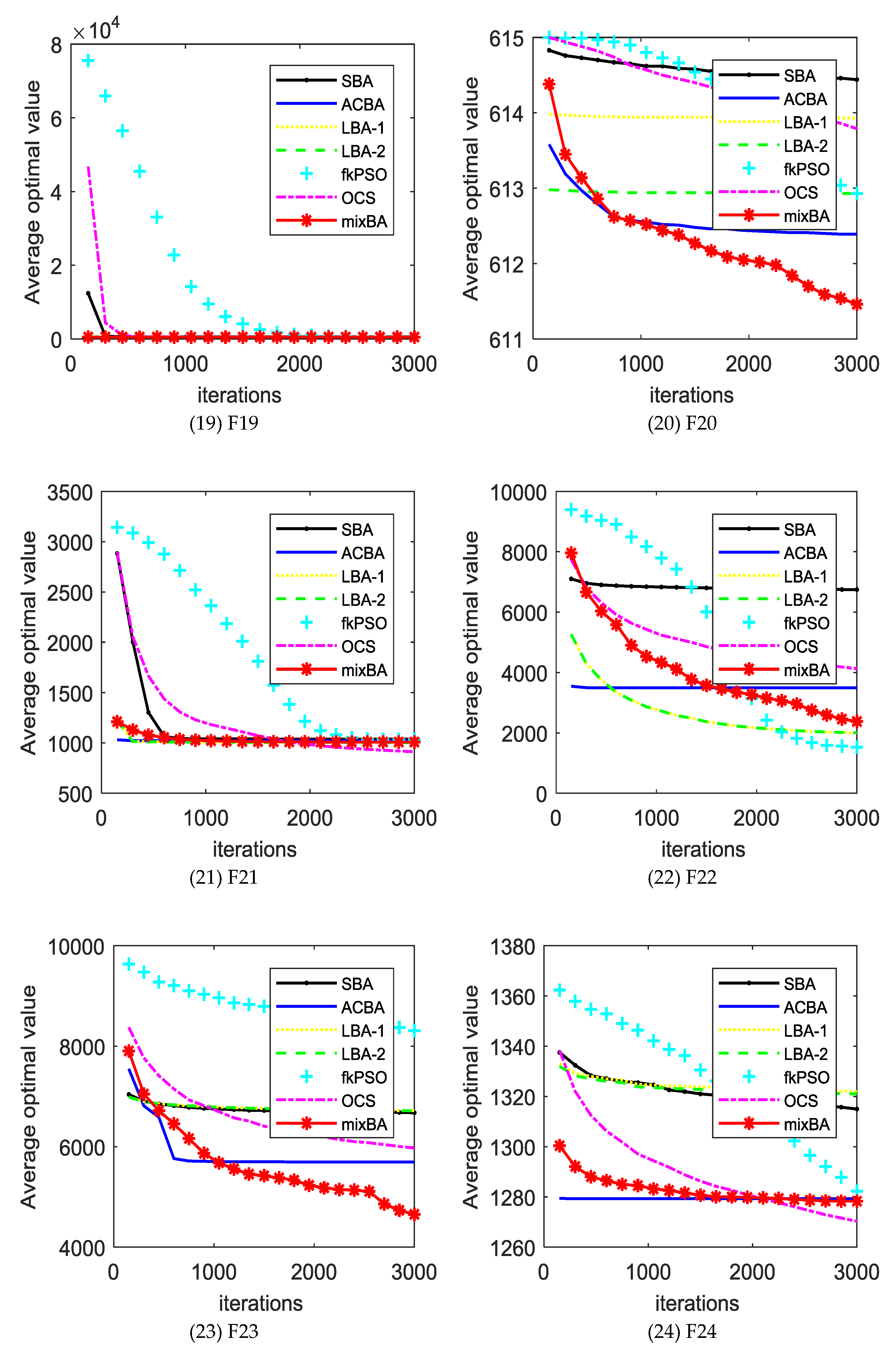
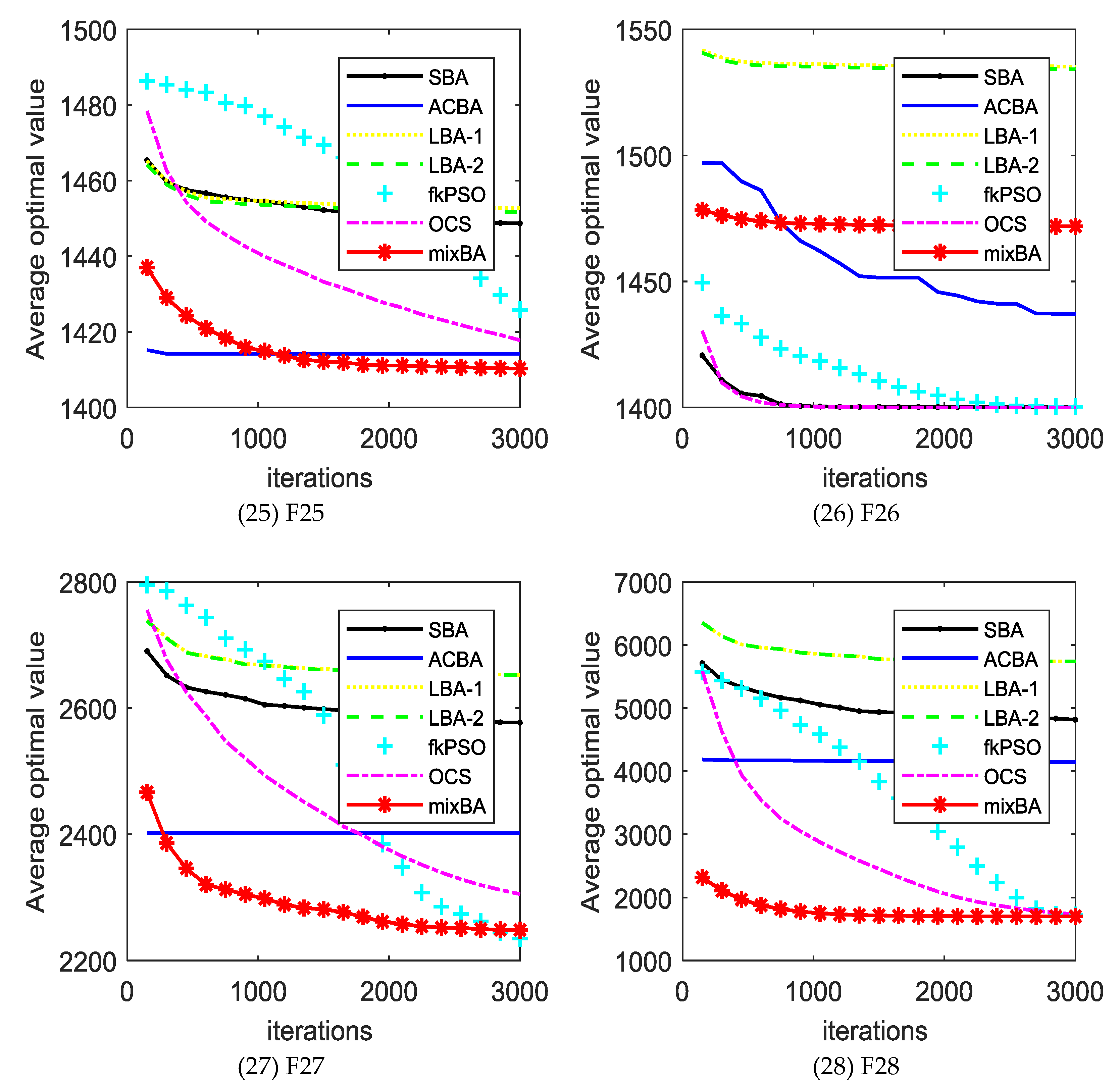
The experimental results will be compared with the standard bat algorithm (SBA), PSO, bat algorithm with Lévy distribution LBA1, LBA2, bat algorithm with arithmetic centroid strategy (ACBA), and oriented cuckoo search (OCS) algorithms. Table A1 (in Appendix A) shows the average error obtained by different algorithms in different test functions. In the last line of the table, w refers to the number of mixBA algorithms superior to other algorithms in the test function, t indicates the number of performances similar to other algorithms, and L refers to the number of mixBA algorithms inferior to other algorithms. The dynamic comparison can be viewed in Figure 2.

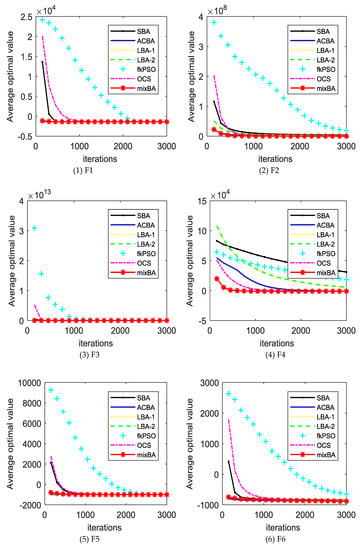
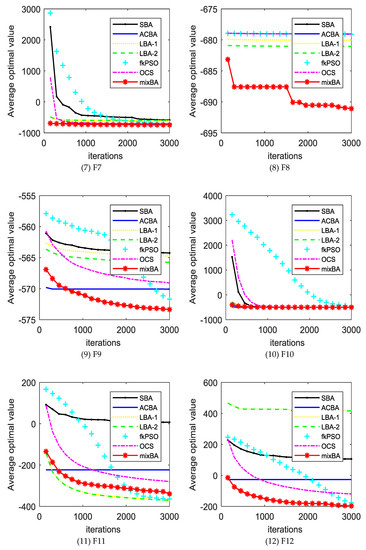
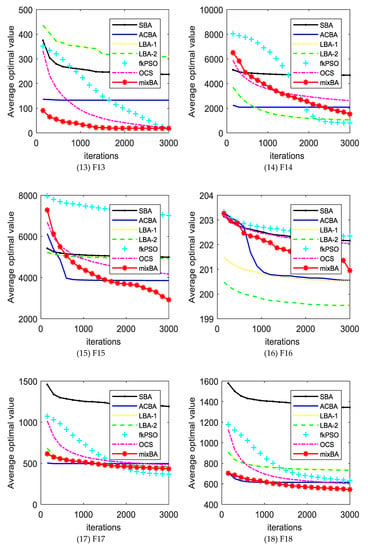
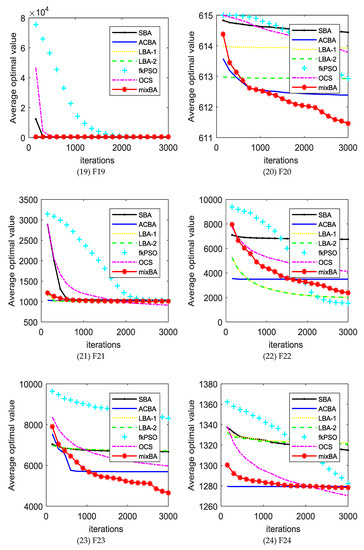
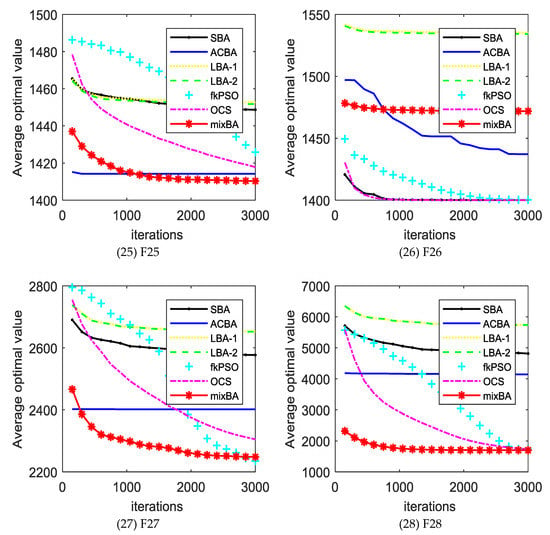
Figure 2. The convergence curves of different algorithms on the benchmark set. SBA—standard bat algorithm; ACBA—bat algorithm with arithmetic centroid strategy; LBA—bat algorithm with Lévy distribution; PSO—particle swarm optimization; OCS—oriented cuckoo search.

From Table A1, mixBA won 27 functions, 28 functions, and 26 functions compared with SBA, LBA1, and LBA2, respectively. Compared with the mixBA algorithm, the PSO and OCS algorithm has seven functions and six functions, respectively, that are good.

For most of the test functions, the SBA does not find the global optimal solution. For ACBA and PSO, it only finds optimal solutions on function F1 and F5. LBA1 and LBA2 showed excellent searching ability on functions F11, F14, and F17. OCS obtains good solutions on functions F1, F4, and F5. MixBA can find reasonable solutions on the most of the functions.

Table 5 presents the statistical results obtained by Friedman tests [30,50]. The smaller the ranking value, the better the performance of the algorithm. From the results, we can get the ranks of seven algorithms as follows: SBA, LBA1, LBA2, ACBA, PSO, OCS, mixBA. The highest ranking shows that mixBA is the best algorithm among the seven algorithms.

Table 5. Friedman test for the seven algorithms. SBA—standard bat algorithm; ACBA—bat algorithm with arithmetic centroid strategy; LBA—bat algorithm with Lévy distribution; PSO—particle swarm optimization; OCS—oriented cuckoo search.

Algorithm	Rankings
SBA	5.86
ACBA	3.59
LBA1	5.61
LBA2	5.05
FK-PSO	3.09
OCS	2.86
mixBA	1.95

Table 6 shows the results of the Wilcoxon test [51]. For SBA, ACBA, LBA1, LBA2 and PSO algorithm,$p<0.05$. The results of this experiment show that the performance of mixBA is far superior to that of other algorithms. For OCS, the p-value is approximately equal to the 0.05 significance level.

Table 6. Wilcoxon test for the seven algorithms.

mixBA vs	p-Value
SBA	0
ACBA	0
LBA1	0
LBA2	0
FK-PSO	0.04
OCS	0.068

Figure 2 shows the convergence of different algorithms in different test functions. In most cases, our proposed algorithm has better results. However, it is undeniable that in a few cases, our proposed algorithm shows poor performance compared with other algorithms, such as in F11, F14, F16, F17, F22, F24, and F26. This is because the magnitude of the probability adjustment of the strategy is large, which leads to the algorithm prematurely selecting a certain strategy to make the algorithm fall into the local optimal. In addition, Table A2 shows the runtime of each algorithm on the CEC2013 benchmark set. It is obvious that the running time of the mixBA algorithm is slightly higher than that of SBA on F1 and F2, but significantly smaller than other algorithms in other test functions.

5. Conclusions

Bio-inspired computation is a collection for stochastic optimization algorithms inspired by biological phenomenon. BA is novel bio-inspired algorithm inspired by bat behaviors, and has been used to solve engineering optimization problems. However, with a single optimization strategy, it shows weakness in solving various complex optimization problems. To tackle this issue, this paper proposes a bat algorithm with multiple strategy coupling (mixBA) to improve the performance of BA. The simulation results show that the performance of the mixBA is superior to that of other algorithms. This is because of the adoption of adaptive multi-strategies coupling rules. The algorithm can adjust the probabilities of different strategies based on the evaluation index. In most cases, this manner guarantees the global convergence and local exploration ability of the algorithm. However, in some cases, this treatment causes other strategies to be ignored early and fall into the local optimum. This is the reason that the proposed algorithm performs worse than the other ones in some test functions, such as F11, F14, F16, F17, F22, F24, and F26. Therefore, we will continue to explore the impact of the probability change of the strategies on optimization performance in subsequent studies and seek better solutions.