Abstract
We study the singularity on principal normal and binormal surfaces generated by smooth curves with singular points in the Euclidean 3-space. We discover the existence of singular points on such binormal surfaces and study these singularities by the method of singularity theory. By using structure functions, we can characterize the ruled surface generated by special curves.
1. Introduction
As the easiest parameterized surfaces, ruled surfaces are widely used in project practices, architecture, and computer-aided design [1,2]. However, on the ruled surfaces there may exist singular points. For that reason, many people study the classification of different types of singularities of a ruled surface. Taking advantage of Gauss curvature, ruled surfaces can be classified either as developable surfaces or as non-developable surfaces. From [3,4,5,6,7], we know that the generic singularities of a developable surface are the cuspidal edge, the swallowtail, and the cuspidal cross-cap. We also know that the cross-cap is the only singular point of existence on the principal normal surface of regular space curves (see [8,9]). Meanwhile, on the binormal surface of regular space curves, there are no singular points. However, for singular curves, the situation is different, and we will study the character of the singular points on such a binormal surface.
In [10], Müller gave the definition of two integral invariants, which are the pitch and the angle of pitch of a closed ruled surface in (three-dimensional Euclidean space). For a general ruled surface, the base curve is not unique. In order to solve the uncertainty of a base curve on the ruled surface, Liu and Yuan used the uniqueness of the striction line on the general ruled surface. Since the derivative of the base curve does not identically vanish, this surface is a non-developable ruled surface. In [11], they extended the definition of pitch to non-developable ruled surfaces. In [12], Liu et al. defined structure functions, which are invariants of non-developable surfaces. They used these functions to characterize the properties of surfaces. Meanwhile, they gave the relationship between these invariants and the pitch function, the angle function of pitch of the ruled surface (see [12,13,14]).
In this paper, we regard the singular curve as the Frenet-type framed base curve. In Section 3 and Section 4, we give the notations of the principal normal and binormal surfaces of a Frenet-type framed base curve in Euclidean 3-space and investigate the character of singular points on these surfaces. In Section 5, we give a standard equation of a non-developable ruled surface and then study its structure functions. Moreover, we give the kinematic meanings at singular points. In Section 6, we use an example to state the singular points on these non-developable surfaces.
Throughout this article, all manifolds and maps are smooth.
2. Preliminaries
In this section, we study the ruled surface generated by Frenet-type framed base curves (see [15,16,17]). Since there exist singular points on these surfaces, in general, we cannot construct the normal vector of these surfaces. Therefore, we regard them as framed base surfaces that are smooth surfaces with a moving frame (see [15]).
Definition 1.
We call a framed surface if and for all , where , and .
If there exists such that is a framed surface, then we call a framed base surface. We define , then is a moving frame along . Thus, we have
where are smooth functions. These functions are called the basic invariants of . By the integrability conditions of the framed surface [15], we have . We call a curvature of the framed surface if
We suppose that is the framed surface and . The surface f is a front around p if and only if . More details are available from [15].
Next, we study the first special non-developable ruled surface, that is, the principal normal surface.
3. Principal Normal Surface along Frenet-Type Framed Base Curves
If there exists a regular unit speed curve and a function satisfies for all , then we call a Frenet -type framed base curve (FTFB curve). We call an orthonormal frame along in , where and . More details are available from [16]. The FTFB curve is one special kind of framed base curve [15,16]. As we want to intuitively observe the properties at singular points on the ruled surface, we choose this kind curve that is similar to the Frenet curve. A principal normal surface M is a map given by . By direct calculations, singular points of surface M construct the set . We can divide them into two classes and , where
From above, we know the points of are located on the .
Next, we consider the characters of singular points of surfaces.
Theorem 1.
We suppose that is an FTFB curve and is the principal normal surface of .
- (1)
- If and , then is a cross-cap at the point .
- (2)
- If and , then is a cross-cap at the point .
Proof.
Taking the derivative of f, we can compute that
We have the second-order derivation of f as follows:
Then we obtain
We have known that the union of and are the set of singular points of surface M. Thus, if , then . And if , then From [9], this completes the proof. □
Since the Bertrand curve and Bertrand mate can be regard as curves on the principal normal surface, then we consider the singular point located on such curves.
Corollary 1.
Let be the space Bertrand curve of an FTFB curve and be the principal normal surface of .
- (1)
- If is the ordinary cusp singularity of , then is a cross-cap at the point .
- (2)
- If is the ordinary cusp singularity of the Bertrand mate of , then is a cross-cap at the point .
Proof.
By the definition of ordinary cusp singularity [18], we know the ordinary cusp singularity of satisfying and . From [17,19], is a space Bertrand curve of an FTFB curve if and only if there exist two constants and such that and . Reasoning for all , then we obtain .
Suppose is the Bertrand mate of ,
where A is a non-zero constant. By differentiating and using the Frenet equation, we obtain
If is the ordinary cusp singularity of , then and . □
Because the principal normal surface has singular points, then we regard it as the framed base surface. Next, we analyze singular points of this surface by using the criterion about a framed surface (see [15]).
For a principal normal surface , if there exist two smooth functions satisfying , where and then we have the framed surface . We denote . Then is a moving frame along .
Because of the integrability condition, we have
By direct calculations, we know that and . Let be the singular point of the principal normal surface f. Because of
the null vector field can be written as . If , then we obtain
By the criterion of the singular point on the framed surface [15], we can get that the surface is a cuspidal edge at a singular point if
- (i)
- , , or
- (ii)
- , , .
The surface is a swallowtail at a singular point if
- (iii)
- , , , or
- (iv)
- , , , .
The surface is a cuspidal cross-cap at a singular point if
- (v)
- , , , or
- (vi)
- , , , .
By the derivative of , any above case no exists. Therefore, we get the conclusion.
Theorem 2.
Let M be the principal normal surface of the FTFB curve . If M is a framed base surface, then the singular points of M are non-degenerate. But the surface M at a singular point cannot be the cuspidal edge, swallowtail, or cuspidal cross-cap.
4. Binormal Surface along Frenet-Type Framed Base Curves
Let be an FTFB curve and be an orthonormal frame along in . A binormal surface M is a map given by
By straightforward calculations, singular points of surface M construct the set
We can divide it into two classes and , where
From above, we know the points of are located on the and the points of construct a ruling of f. By direct calculations, we have
Therefore, we get the following conclusions.
Theorem 3.
Let be the binormal surface of the FTFB curve . If and , then is a cross-cap at the singular point .
When is a Mannheim mate of an FTFB curve, we know for all (see [19]). Therefore, the singular points of the binormal surface of are only located on . Next, we consider the characters of these singular points.
Corollary 2.
Let be the Mannheim mate of an FTFB curve and be the binormal surface of . If is the ordinary cusp singularity of , then is a cross-cap at a singular point of the surface.
If there exist singular points on the binormal surface of the FTFB curve, then we assume that the binormal surface is a framed base surface.
For a binormal surface, if there exist two smooth functions such that , where and . Then we get the framed surface , where . The integrability condition is
By calculations, the curvature of the surface is , where
By using the criterion of the type of singular points of a framed surface in [15], we obtain the following conclusions.
Theorem 4.
Let f be the binormal surface of an FTFB curve . We assume that is a framed surface.
(A) Suppose that is a singular point of with , then is a cuspidal edge at if and only if
- (1)
- , or
- (2)
- , , , .
(B) Suppose that is a singular point of with , , then is a cuspidal cross-cap at if and only if
- (3)
- , or
- (4)
- , , , .
Proof.
Since , the null vector field is . Suppose is a non-degenerate singular point of . Since , then should satisfy one of the following conditions:
- (a)
- and or
- (b)
- , and .
At first, we consider case (a). Because of , then , that is, . Hence, the singular curve is given by the form , where y is a function with . By a straightforward calculation,
and . Thus, we have the assertion (1), (3). Next, we consider the case (b). By the above conditions, we know that . Hence, the singular curve can also be given by . Therefore, we get and . Thus, we have the assertion (2), (4). □
Suppose is the non-degenerate singular point of . Since the integrability condition , then satisfies one of the following conditions:
- (c)
- and ,
- (d)
- and .
From the case (c), we know that the singular point also belongs to Thus, we omit it. In the case (d), because of , then . Hence, the surface cannot be the cuspidal edge, swallowtail, or cuspidal cross-cap at such a singular point .
5. Ruled Invariant of Ruled Surface
In [10], Müller introduced two integral invariants that are the pitch and angle of pitch of a closed ruled surface in In [11], Liu and Yuan wanted to generalize these conceptions to the general ruled surface. They wanted to use the directrix line and orthogonal trajectory of the ruling to define the pitch of a general ruled surface. But the directrix line is not unique. To solve this uncertainty, they assumed that the directrix line is the striction line of the surface. In [12,13,14], Liu et al. defined structure functions of a non-developable ruled surface in . Then they verified any non-developable ruled surface for which the directrix line is the striction line of the surface and the direction of ruling can be determined by the orthonormal transformations. They gave the geometric description of the structure functions.
In this paper, we focus on the principal normal and binormal surfaces generated by FTFB curves in . They are non-developable ruled surfaces. We want to investigate the structure functions of these surfaces and observe the geometric characterization of structure functions at singular points.
Firstly, let us introduce structure functions of the non-developable ruled surface. Let
be an FTFB curve and be a regular unit speed curve. We call the spherical Frenet frame of the spherical curve in , where the tangent vector and normal vector are and , respectively. Then we get the following equation:
where is the spherical curvature function of in .
Under the above notations, if is a striction line of , we call
the standard equation of the (non-developable) ruled surface in . Because is the striction line, we have with two smooth functions and . We call , , and structure functions of the (non-developable) ruled surface in . These functions {, , } can determine the ruled surface under a transformation in .
Let be the orthogonal trajectory of the ruling on the surface passing through , then can be expressed as
We call
the pitch of the (non-developable) ruled surface at , and the pitch function of the (non-developable) ruled surface .
From the definition, we have and . If for any , then we call the non-pitched ruled surface.
Next, we will use {, , } to characterize the surface generated by special framed base curves and describe the singular points.
Theorem 5.
Let be a non-pitched ruled surface with a structure equation. If structure functions satisfy equation with constant , then is the binormal surface of a Mannheim mate of an FTFB curve.
Proof.
Because , then is the binormal surface of . By direct calculations, we obtain , , . From [19], the necessary and sufficient condition about which an FTFB curve is a Mannheim mate is
then we know . □
By the above assumptions, if is the singular point of Mannheim mate of an FTFB curve, then . This means that is the -singularity of .
Theorem 6.
Let be a non-developable ruled surface and be a striction line of such that . If the structure functions of satisfy the situations
- 1.
- 2.
- ,
- 3.
- , and
- 4.
- ,
where are constants, then is the principal normal surface of a Bertrand curve of an FTFB curve.
Proof.
The derivative of has the form
Put , then
Continue taking the derivative of , and we get
Therefore, is the principal normal surface of .
Put , then . Since the cross-product of and is , then we have
Then Hence, the condition
is equal to
Then we complete the proof. □
From the proof, we know that if is the singular point of a Bertrand curve of an FTFB curve, then and . Using the same method, we can describe the binormal surface of the Mannheim curve by using {, , }.
Theorem 7.
Let be a non-pitched ruled surface with a structure equation. If structure functions satisfy
then is the binormal surface of a Mannheim curve of an FTFB curve.
Therefore, we know that if , then is the singular point of the Mannheim mate of .
6. Example
We give an example of the principal normal and binormal surface of an FTFB curve in Euclidean 3-space. Then we can observe the singularity type on these ruled surfaces.
Example 1.
Let be
where
By straighting calculations, we have , , and
Let and be the principal normal and binormal surfaces of the FTFB curve , respectively. Then the sets of singularities of and are
By Theorem 1, has the cross-cap singularity at (Figure 1). By Theorems 3 and 4, has the cross-cap singularity at and has cuspidal edge singularities at (Figure 2).
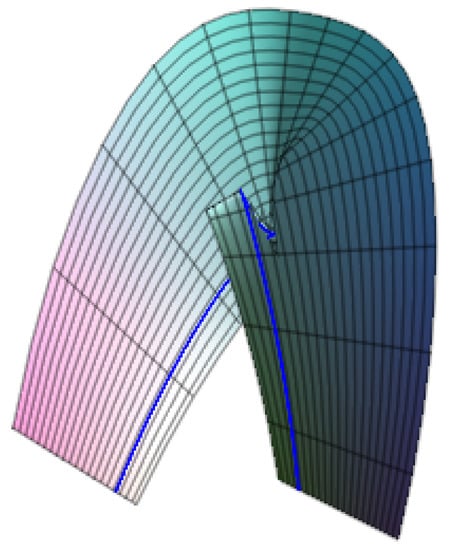
Figure 1.
and .
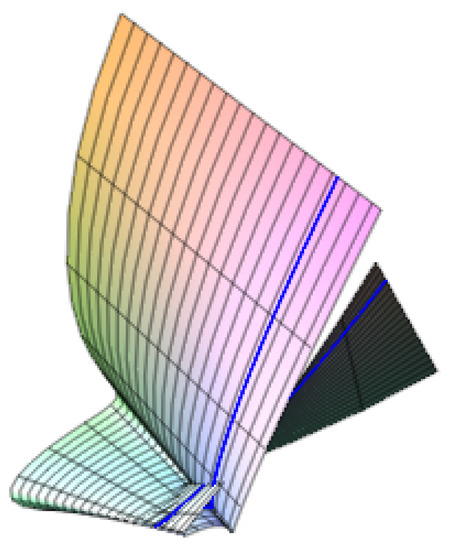
Figure 2.
and .
Author Contributions
Conceptualization, J.H. and D.P.; Writing—Original Draft Preparation, J.H.; Writing—Review and Editing, D.P.; Funding Acquisition, D.P.
Funding
This research was funded by the National Natural Science Foundation of China grant number 11671070.
Acknowledgments
We would like to thank the anonymous reviewers for their very careful reading and valuable comments/suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Papaioannou, S.G.; Kiritsis, D. An application of Bertrand curves and surfaces to CAD/CAM. Comput. Aided Des. 1985, 17, 348–352. [Google Scholar] [CrossRef]
- Ravani, B.; Ku, T.S. Bertrand offsets of ruled and developable surfaces. Comput. Aided Des. 1991, 23, 145–152. [Google Scholar] [CrossRef]
- Cleave, J.P. The form of the tangent-developable at points of zero torsion on space curves. Math. Proc. Camb. Philos. Soc. 1980, 88, 403–407. [Google Scholar] [CrossRef]
- Ishikawa, G. Determinacy of the envelope of the osculating hyperplanes to a curve. Bull. Lond. Math. Soc. 1993, 25, 603–610. [Google Scholar] [CrossRef]
- Hananoi, S.; Izumiya, S. Normal developable surfaces of surfaces along curves. Proc. R. Soc. Edinb. Sect. A 2017, 147, 177–203. [Google Scholar] [CrossRef]
- Tanaka, J.; Ohmoto, T. Geometric algebra and singularities of ruled and developable surfaces. arXiv 2018, arXiv:1808.10587. [Google Scholar]
- Zhao, Q.; Pei, D.; Wang, Y. Singularities for One-Parameter Developable Surfaces of Curves. Symmetry 2019, 11, 108. [Google Scholar] [CrossRef]
- Izumiya, S.; Takeuchi, N. Singularities of ruled surfaces in R3. Math. Proc. Camb. Philos. Soc. 2001, 130, 1–11. [Google Scholar] [CrossRef]
- Izumiya, S.; Takeuchi, N. Geometry of ruled surfaces. In Applicable Mathematics in the Golden Age; Misra, J.C., Ed.; Narosa Publishing House: New Delhi, India, 2003; pp. 305–338. [Google Scholar]
- Müller, H.R. Über geschlossene Bewegungsvorgänge. Monatsh. Math. 1951, 55, 206–214. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, Y. Pitch functions of ruled surfaces and B-scrolls in Minkowski 3-space. J. Geom. Phys. 2012, 62, 47–52. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Y.; Jung, S.D. Invariants of non-developable ruled surfaces in Euclidean 3-space. Beitr. Algebra Geom. 2014, 55, 189–199. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.; Jung, S.D. Structure and characterization of ruled surfaces in Euclidean 3-space. Appl. Math. Comput. 2014, 233, 252–259. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Jung, S.D. Ruled invariants and associated ruled surfaces of a space curve. Appl. Math. Comput. 2019, 348, 479–486. [Google Scholar] [CrossRef]
- Fukunaga, T.; Takahashi, M. Framed surfaces in the Euclidean space. Bull. Braz. Math. Soc. New Ser. 2019, 50, 37–65. [Google Scholar] [CrossRef]
- Honda, S. Rectifying developable surfaces of framed base curves and framed helices. Adv. Stud. Pure Math. 2018, 78, 273–292. [Google Scholar]
- Huang, J.; Pei, D. Singularities of special curves in 3-space forms. 2019. In Preprint. [Google Scholar]
- Izumiya, S.; Romero Fuster, M.C.; Ruas, M.A.S.; Tari, F. Differential Geometry from a Singularity Theory Viewpoint; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2016; pp. 15–21. [Google Scholar]
- Huang, J.; Chen, L.; Izumiya, S.; Pei, D. Geometry of special curves and surfaces in 3-space form. J. Geom. Phys. 2019, 136, 31–38. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).