Abstract
In recent works, exact and nonstandard finite difference schemes for scalar first order linear delay differential equations have been proposed. The aim of the present work is to extend these previous results to systems of coupled delay differential equations where X is a vector, and A and B are commuting real matrices, in general not simultaneously diagonalizable. Based on a constructive expression for the exact solution of the vector equation, an exact scheme is obtained, and different nonstandard numerical schemes of increasing order are proposed. Dynamic consistency properties of the new nonstandard schemes are illustrated with numerical examples, and proved for a class of methods.
1. Introduction
Due to the presence of time lags in the dynamics of most real systems, delay differential equations (DDE) have become basic instruments in the mathematical modelling of a wide range of problems in science and engineering, such as in population biology, physiology, epidemiology, economics, and control problems (see, e.g., [1,2,3,4,5], and references therein), and special methods have been developed to compute numerical solutions for DDE [6]. In the case of differential problems without delay, exact schemes have been defined for different particular problems, and the use of nonstandard finite difference (NSFD) numerical schemes has gained increasing interest in the last years [7,8,9]. The NSFD numerical schemes can be competitive in terms of accuracy while providing dynamically consistent solutions, i.e., they can provide numerical discrete solutions that inherit the structural properties defining the dynamical behaviour of the original continuous equation [10]. The possibility of defining NSFD schemes that reproduce the qualitative behaviour of the continuous solutions has made them specially attractive for population and epidemiology models (e.g., [11,12,13,14,15]), and they have also been proposed for some problems with delay [16,17,18,19,20,21]. However, for DDE models the construction of exact schemes, and consequently of NSFD methods derived from them, has not been much developed.
In [22], a NSFD method was proposed for the scalar first order linear delay problem
where , , and is a continuous function. The method of [22] was exact in the initial time interval , and then switched to a NSFD method of second order at most. More recently [23], an exact scheme for problem (1)–(2) was constructed, valid in the whole domain of definition, and a family of increasing order NSFD schemes was defined. The NSFD methods presented in [22,23] were shown to be consistent with different dynamical properties of the continuous problem (1)–(2).
In the present work, we consider the coupled linear delay system
satisfying the initial condition
where and are d-dimensional real vector functions, and A and B are commuting real matrices, in general not simultaneously diagonalizable.
The usefulness of nonstandard schemes for scalar linear delay problems and their possible advantages over alternative numerical methods have been discussed in [22,23]. Particularly, the family of schemes proposed in [23] allows the computation of numerical solutions for scalar linear delay problems with the required degree of accuracy and with comparatively low computational complexity. Moreover, the numerical approximations obtained with these nonstandard schemes reproduce dynamical properties of the exact continuous solutions, such as asymptotic stability, positivity, and oscillation behaviour.
The aim, and main contribution, of the present work is to make available, for a wide class of coupled linear delay differential systems, NSFD methods that possess analogous advantages to those in the scalar setting, exhibiting similar properties in terms of accuracy and dynamic consistency. It is to be remarked that for a class of the new NSFD schemes proposed in this work, the schemes as defined in Theorem 3, it is rigorously proved that they preserve delay dependent stability. This is a property that usual alternative methods, such as natural Runge-Kutta methods, do not possess, and that is challenging to prove for numerical methods for linear delay systems [6] (p. 356).
There are two main difficulties when dealing with problem (3)–(4), compared with the corresponding scalar problem (1)–(2). Firstly, the obtention of an exact constructive solution that would allow deriving an exact scheme. Secondly, once the new NSFD schemes are defined, the process of proving dynamical properties, which is much more complex than in the scalar case. To overcome these difficulties, the key point is to assume commutativity of the coupled coefficient matrices, a property also considered in other problems involving delay systems [24]. With this assumption, a compact expression for the exact solution of problem (3)–(4), analogous to the scalar case, can be obtained. Also, for commuting matrices, a common Schur basis exists and both matrix coefficients in (3), A and B, can be simultaneously reduced to triangular form, which facilitates analyzing the dynamical properties of the new proposed NSFD schemes.
This paper is structured as follows. In the next section, based on a constructive expression for the exact solution of the initial value vector problem (3)–(4), an exact scheme that is valid in the whole domain of definition is obtained. In Section 3, a family of new nonstandard schemes of increasing order of accuracy are proposed. Next, in Section 4, dynamic consistency properties of the new nonstandard schemes are illustrated with numerical examples and proved for a class of methods. In the final section, the results are summarized and discussed.
2. Exact Numerical Scheme
In our next theorem we present an explicit expression for the solution of problem (3)–(4), derived by using the method of steps [25] (pp. 45–47) and an integral convolution [26] (p. 67), in a similar way as was done in [27] for the scalar problem (1)–(2).
Theorem 1.
Proof.
From the exact solution given in Theorem 1, an exact numerical difference scheme can be obtained, in a similar way as done in [23] for the scalar case, as shown in the next theorem.
Theorem 2.
Proof.
Write , corresponding to the three terms in expression (5). Then, expanding the binomial terms and rearranging and renaming indices, one has
Remark 1.
The expressions given in Theorems 1 and 2 are also valid when , i.e., for the particular case of the pure delay problem
If A and B are diagonal, or in the case where they are simultaneously diagonalizable after the usual change of variables, problem (3)–(4) consists of d independent scalar problems, and the expressions given by Theorems 1 and 2 for each component of coincide with those given in [23] for the corresponding scalar problems.
Example 1.
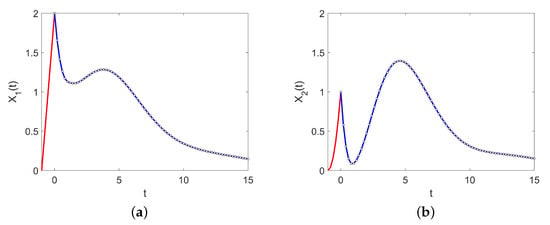
Figure 1 presents a numerical example of application of the results of this section, showing the continuous solution given by Theorem 1 (lines) and the exact numerical solution of Theorem 2 with (points), for the problem (3)–(4) with parameters and

Figure 1.
Exact solutions (lines) and numerical solutions provided by the exact scheme (points) for the two components of Example 1. (a) First component, . (b) Second component, .
3. Nonstandard Finite Difference Methods of Increasing Orders
The exact numerical solution given by Theorem 2 has the drawback of the integral term in (6), as an exact expression could be obtained for certain initial functions , but in general a numerical approximation would be needed. A class of methods could be derived by approximating this integral term, either by using some numerical integration algorithm or by approximating the initial function with some family of functions that allowed the explicit computation of the integral. Instead, as proposed in [23] for the scalar problem, a family of nonstandard methods of increasing orders can be derived by computing the exact solution in the first M intervals and then discarding the integral term, as shown in the next theorem. We define two classes of methods of order M, and methods, depending on whether the full sum in (6) is kept or a truncated sum is used.
Theorem 3.
Let and . For a given , assume that the values of , for , are computed using the exact scheme of Theorem 2. Define F and T schemes to compute successive values for any by the expressions
Then, both numerical schemes, and , have local error and order M.
Proof.
Let be any vector norm and a compatible norm for matrices, and consider the scheme . Assume that for , which is the case for . Then, for and , using (6), one gets
Let , and such that and for . Then, by the induction hypothesis, the first term in (10) is and the second term is bounded by
Similar arguments result in the same bounds holding for the scheme . □
Remark 2.
The results of Theorem 3 also hold if the values for in the first intervals are computed using any numerical method of order at least , instead of using the exact scheme. Although both types of schemes, and , have the same order, more general dynamic consistency properties can be proved for the class of schemes, as shown in the next section.
The error analysis of the methods provided by Theorem 3 is illustrated in the next two figures. Errors of numerical solutions for Example 1, computed using schemes of three different orders, are shown in Figure 2 (top). The corresponding errors relative to the expected order, i.e., errors divided by , are shown in Figure 2 (bottom), with results in agreement with the expected orders given by Theorem 3.
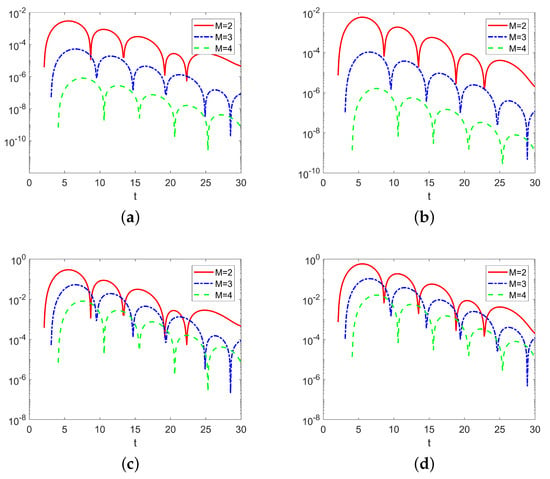
Figure 2.
Absolute errors (log-scale) of numerical solutions for Example 1, computed using three different schemes of increasing orders, with . (a,b) Absolute errors for the first and second component, respectively. (c,d) Errors divided by .
Figure 3 presents the errors in relation with the size of the mesh for numerical solutions of Example 1 computed using , the truncated method with . Errors overlap when divided by , clearly showing that the method is of order three, as established in Theorem 3.
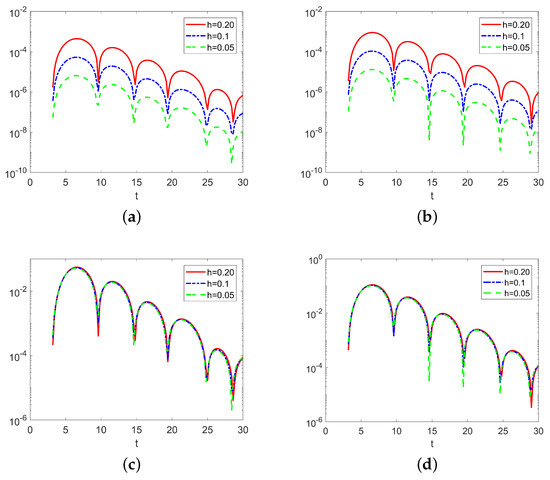
Figure 3.
Errors (log-scale) of numerical solutions for Example 1, computed with the method using three different mesh sizes. (a,b) Absolute errors for the first and second component, respectively. (c,d) Errors divided by .
4. Dynamic Consistency Properties
In this section we analyse the consistency between dynamic properties of the numerical solutions resulting from applying the and schemes defined in Theorem 3 and the continuous solutions of problem (3)–(4).
4.1. Asymptotic Stability
First we will show that the schemes defined in Theorem 3 preserve delay-dependent stability, i.e., that they are -stable [28].
It is well known that for the trivial solution of (3)–(4) to be asymptotically stable it is necessary and sufficient that all the roots of the characteristic equation
where I is the identity matrix, have negative real parts, . This condition, involving a transcendental equation with an infinite number of roots, is difficult to verify in general. However, when A and B commute, there is a common Schur basis for them, and they can be simultaneously reduced to triangular form, with elements in the diagonal corresponding to the eigenvalues of each matrix [29]. Thus, in this case, condition (11) is equivalent to
where are pairs of eigenvalues of A and B, as they appear in the i diagonal position in the common triangular form. Hence, writing for any of these pairs, it follows that if the trivial solution of (3)–(4) is asymptotically stable then
implies .
Consider now the difference equations system (8) defining the scheme. For any n such that , the integer part of is . Thus, we can write (8) in the form of a Volterra difference system of convolution type,
by setting , the d-dimensional zero matrix, when , and
when , for integer k. Thus, using the Z-transform method, it holds that the system (14) is asymptotically stable if all roots of the characteristic equation
satisfy [30] (Theorem 5.21), where is the Z transform of B. In this case,
Now we have the basis to prove our next theorem.
Theorem 4
Proof.
From the common triangular decompositions of A and B, it follows that every root of (16) must satisfy, for some pair of ordered eigenvalues ,
Remark 3.
For the class of schemes, a general and unconditional result similar to Theorem 4 is not to be expected, as shown by considering the simple case where , , and , so that the scheme reduces to
Delay Independent Stability
Our next theorem shows that the class of schemes do preserve absolute or delay independent stability, i.e., that they are P-stable [6] (p. 296). This is also trivially the case for schemes, as P-stability is a weaker condition than -stability.
Theorem 5
Proof.
Using the common triangular forms of A and B, and considering a pair of ordered eigenvalues , a necessary condition for the trivial solution of (3)–(4) to be delay-independent asymptotically stable is [31,32]
The stability analysis provided by Theorems 4 and 5 assures that, for a fixed delay, the region of asymptotic stability for (3)–(4) is contained in the region of asymptotic stability of schemes, while for schemes it can only be assured that the region of asymptotic stability of (3)–(4) for all delays is contained in the corresponding region for the numerical solution. However, schemes usually perform much better than can be guaranteed, as shown in the next example.
Example 2.
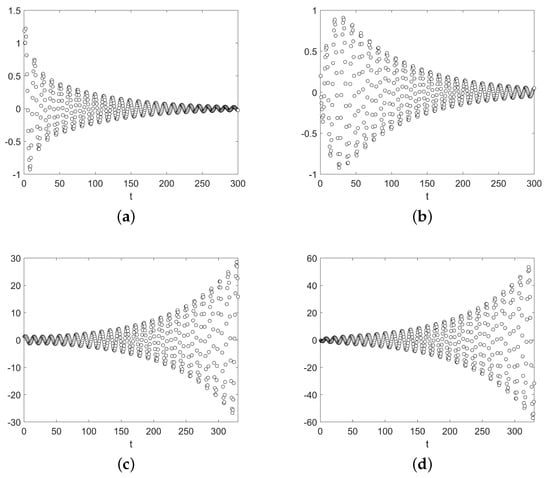
Figure 4 shows the numerical solutions computed with the method , with , for the pure delay problem (7) with parameters
and two different values of delay, and .

Figure 4.
Numerical solutions computed with the method for Example 2 with two different values of delay, showing stable and unstable behaviours. (a,b) First and second component, respectively, with delay . (c,d) First and second component, respectively, with delay .
Matrix B has real eigenvalues, and . Hence, in this case the trivial solution of (7) is asymptotically stable if all the eigenvalues β of B satisfy [6] (p. 289), i.e., for . As shown in Figure 4, the numerical solutions present the correct behaviour, even for values of τ close to the limit of stability. For both components, the solution approach zero as t increases for , inside the region of stability (Figure 4, top), while they diverge for , outside the region of stability (Figure 4, bottom).
4.2. Oscillation and Positivity
Our next theorem shows that schemes also preserve the oscillation properties of exact solutions for problem (3)–(4).
We recall that a solution of (3) is said to oscillate if every component of the solution has arbitrary large zeros; otherwise it is called non-oscillatory [33] (Definition 5.0.1). It is known that every solution of the delay differential system (3) oscillates if and only if the characteristic Equation (11) has no real roots [33] (Theorem 5.1.1).
Theorem 6
We will use the result of the following lemma, whose proof is similar to that of Theorem 7.1.1 in [33].
Lemma 1.
Proof of Theorem 6.
Using common triangular decompositions of A and B, if every solution of (3)–(4) oscillates then, for any pair of ordered eigenvalues , Equation (13), or equivalently Equation (19), has no real roots. If we assume that there is a non-oscillatory solution of (8) we get a contradiction, since, from Lemma 1, there would be a positive z satisfying
and writing , we would get Equation (19) with a real root. □
Remark 4.
For the class of schemes, a general result similar to Theorem 6 seems difficult, although particular cases could be dealt with, as shown in our next proposition.
Proposition 1.
If every solution of the pure delay problem (7) oscillates, then the numerical solutions computed using the scheme also oscillate.
Proof.
For the pure delay problem (7), an equivalent condition for every solution to oscillate is that B has no real eigenvalues in the interval [33] (Theorem 5.2.2). The characteristic equation for the system of difference equations (9) defining the scheme, i.e., Equation (22) with and , reads
and every solution oscillates if (26) has no positive roots [33] (Theorem 7.1.1). But z is a root of (26) if for an eigenvalue of B it holds that
Thus, if every solution of (7) oscillates, so that any possible real eigenvalue of B satisfies , and we assume that there is a positive root of (27), we get a contradiction. From (27), if z is positive, then is real and . Hence, it follows that and
But for , the maximum value of is attained when , so that
□
Example 3.
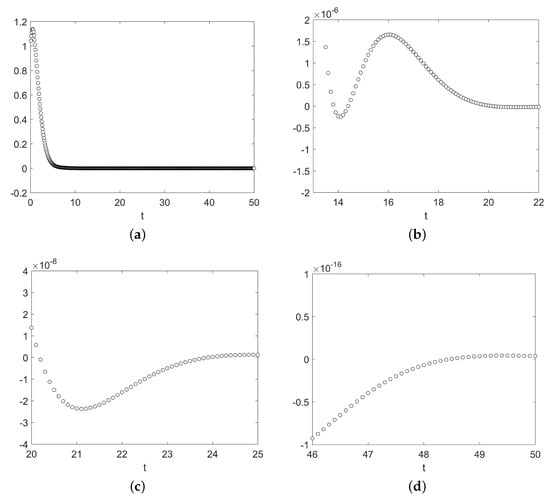
Figure 5 shows the numerical solution computed with the method , with , for the first component of the pure delay problem (7) with parameters and B and as in Example 2. In this case, every solution oscillates if all the eigenvalues β of B satisfy . As shown in Figure 4, the numerical solutions preserve the correct behaviour, even for a value of τ very close to the limit of oscillation.

Figure 5.
Numerical solution for the first component of Example 1 and zoom-views in different intervals. (a) . (b) . (c) . (d) .
Positivity
Conditions for the solution of a DDE system to preserve positivity, in the sense that for any component-wise positive initial function the solution always remains positive, are necessarily very restrictive.
Consider the pure delay problem (7). If element-wise, i.e., , then it is clear from the expression of the exact solution given in (5) that for any component-wise positive initial function all components of the solution remain positive for all . In this case, it is also clear from the expressions of and schemes given in Theorem 3 that the numerical solutions computed with both methods also remain positive for all .
If B is only non-negative, i.e., element-wise, then the exact as well as the numerical solutions remain non-negative for any non-negative initial function and all . The condition of all elements of B being non-negative is also necessary to preserve positivity, for if there is an element of B, say negative, then it is possible to find an initial function, component-wise positive, for which some component of becomes negative, already in the first interval . To see this, take with components and , and choose such that
Taking into account that, from (5), for one gets where the components of are and , with , it follows that the first component of becomes negative,
since for
For the general linear problem (3)–(4), if and also element-wise, then it is also immediate that positivity is preserved both in the exact solution and in the numerical solutions computed using the and schemes. For , non-negativity of the solutions, both exact and numerical, is preserved if A is Metzler, i.e., with non-negative off-diagonal elements, as then is non-negative for any .
5. Conclusions
Despite the growing interest in NSFD methods, including their application to some problems with delay, the scheme presented in Theorem 2 is possibly the first example of an exact scheme for a system of delay differential equations, generalising to systems of linear DDE with commuting matrix coefficients the results presented in [23] for scalar linear DDE problems.
The families of and schemes defined in Theorem 3 allow the computation of numerical solutions for problem (3)–(4) with high accuracy and low computational costs for extended time intervals, showing good dynamic consistency properties. In particular, schemes have been proved to preserve delay-dependent asymptotic stability of the continuous solution, i.e., they are -stable difference methods, while schemes have been proved to preserve delay-independent asymptotic stability, i.e., they are P-stable methods. Also, schemes preserve the oscillation behaviour of the exact solution, which has also been proved for the scheme when applied to the pure delay problem (7). Both types of scheme also provide numerical solutions that remain positive, or non-negative, when the original problem satisfy conditions assuring the corresponding property.
Several problems and lines of research are open from the results presented in this work. Proving dynamic consistency properties similar to those of schemes for some particular schemes, either in general or when applied to some type of problems or under certain conditions, could deserve further attention, as schemes offer the same accuracy than schemes with reduced computational needs. Applying the new schemes to low order systems, e.g., with coefficients being or matrices, might allow to express the systems of difference equations defining the schemes in the more usual form of a NSFD method, with derivatives for each component being approximated by the corresponding increments divided by a scalar function , as has been done for some examples of systems without delay [34,35]. This could also be the case when considering problems where the matrix coefficients A and B posses some special structure.
Author Contributions
Conceptualization, M.Á.C. and F.R.; methodology and formal analysis, all authors; writing—original draft preparation, F.R.; writing—review and editing, all authors.
Funding
This research was funded by Ministerio de Economía y Competitividad grant number CGL2017-89804-R.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kuang, Y. Delay Differential Equations. With Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Kolmanovskii, V.; Myshkis, A. Introduction to the Theory and Applications of Functional Differential Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wu, M.; He, Y.; She, J.-H. Stability Analysis and Robust Control of Time-Delay Systems; Science Press: Beijing, China; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Chalishajar, D.N.; Kumar, A. Total controllability of the second order semi-linear differential equation with infinite delay and non-instantaneous impulses. Math. Comput. Appl. 2018, 23, 32. [Google Scholar] [CrossRef]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Mickens, R.E. (Ed.) Advances on Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2005. [Google Scholar]
- Patidar, K.C. Nonstandard finite difference methods: Recent trends and further developments. J. Differ. Equ. Appl. 2016, 22, 817–849. [Google Scholar] [CrossRef]
- Stuart, A.M.; Humphries, A.R. Dynamical Systems and Numerical Analysis; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
- Arenas, A.J.; Moraño, J.A.; Cortés, J.C. Non-standard numerical method for a mathematical model of RSV epidemiological transmission. Comput. Math. Appl. 2008, 56, 670–678. [Google Scholar] [CrossRef]
- Arenas, A.J.; González-Parra, G.; Chen-Charpentier, B.M. A nonstandard numerical scheme of predictor–corrector type for epidemic models. Comput. Math. Appl. 2010, 59, 3740–3749. [Google Scholar] [CrossRef]
- Mickens, R.E.; Washington, T.M. NSFD discretizations of interacting population models satisfying conservation laws. Comput. Math. Appl. 2013, 66, 2307–2316. [Google Scholar] [CrossRef]
- Guerrero, F.; González-Parra, G.; Arenas, A.J. A nonstandard finite difference numerical scheme applied to a mathematical model of the prevalence of smoking in Spain: A case study. Comput. Appl. Math. 2014, 33, 13–25. [Google Scholar] [CrossRef]
- Sekiguchi, M.; Ishiwata, E. Global dynamics of a discretized SIRS epidemic model with time delay. J. Math. Anal. Appl. 2010, 371, 195–202. [Google Scholar] [CrossRef]
- Wang, Y. Dynamics of a nonstandard finite-difference scheme for delay differential equations with unimodal feedback. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3967–3978. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Ding, X. Numerical dynamics of a nonstandard finite difference method for a class of delay differential equations. J. Math. Anal. Appl. 2013, 400, 25–34. [Google Scholar] [CrossRef]
- Xu, J.; Geng, Y. Stability preserving NSFD scheme for a delayed viral infection model with cell-to-cell transmission and general nonlinear incidence. J. Differ. Equ. Appl. 2017, 23, 893–916. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, Y. Global dynamics of a discrete viral infection model with time delay, virus-to-cell and cell-to-cell transmissions. J. Differ. Equ. Appl. 2017, 23, 1853–1868. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Lyapunov direct method for investigating stability of nonstandard finite difference schemes for metapopulation models. J. Differ. Equ. Appl. 2018, 24, 15–47. [Google Scholar] [CrossRef]
- Garba, S.M.; Gumel, A.B.; Hassan, A.S.; Lubuma, J.M.-S. Switching from exact scheme to nonstandard finite difference scheme for linear delay differential equation. Appl. Math. Comput. 2015, 258, 388–403. [Google Scholar] [CrossRef]
- García, M.A.; Castro, M.A.; Martín, J.A.; Rodríguez, F. Exact and nonstandard numerical schemes for linear delay differential models. Appl. Math. Comput. 2018, 338, 337–345. [Google Scholar] [CrossRef]
- Pospíšil, M. Representation and stability of solutions of systems of functional differential equations with multiple delays. Electron. J. Qual. Theory 2012, 54, 1–30. [Google Scholar] [CrossRef]
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- El’sgol’ts, L.E.; Norkin, S.B. Introduction to the Theory and Application of Differential Equations with Deviating Arguments; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Martín, J.A.; Rodríguez, F.; Company, R. Analytic solution of mixed problems for the generalized diffusion equation with delay. Math. Comput. Model. 2004, 40, 361–369. [Google Scholar] [CrossRef]
- Guglielmi, N. On the asymptotic stability properties of Runge–Kutta methods for delay differential equations. Numer. Math. 1997, 77, 467–485. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Elaydi, S.N. An Introduction to Difference Equations; Springer: New York, NY, USA, 1996. [Google Scholar]
- Čermák, J.; Jánský, J.; Nechvátal, L. Exact versus discretized stability regions for a linear delay differential equation. Appl. Math. Comput. 2019, 347, 712–722. [Google Scholar] [CrossRef]
- Nishiguchi, J. On parameter dependence of exponential stability of equilibrium solutions in differential equations with a single constant delay. Discrete Contin. Dyn. Syst. 2016, 36, 5657–5679. [Google Scholar] [CrossRef]
- Györi, I.; Ladas, G. Oscillation Theory of Delay Differential Equations; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Roeger, L.-I.W. Exact finite-difference schemes for two-dimensional linear systems with constant coefficients. J. Comput. Appl. Math. 2008, 219, 102–109. [Google Scholar] [CrossRef]
- Quang, A.D.; Tuan, H.M. Exact finite difference schemes for three-dimensional linear systems with constant coefficients. J. Vietnam J. Math. 2018, 46, 471–492. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).