Modified Halpern Iterative Method for Solving Hierarchical Problem and Split Combination of Variational Inclusion Problem in Hilbert Space

Abstract

The purpose of this paper is to introduce the split combination of variational inclusion problem which combines the concept of the modified variational inclusion problem introduced by Khuangsatung and Kangtunyakarn and the split variational inclusion problem introduced by Moudafi. Using a modified Halpern iterative method, we prove the strong convergence theorem for finding a common solution for the hierarchical fixed point problem and the split combination of variational inclusion problem. The result presented in this paper demonstrates the corresponding result for the split zero point problem and the split combination of variation inequality problem. Moreover, we discuss a numerical example for supporting our result and the numerical example shows that our result is not true if some conditions fail.

1. Introduction

Throughout this article, we let H be a real Hilbert spaces with inner products $⟨·,·⟩$ and norms $\parallel ·\parallel$ and let C be a nonempty closed convex subset of a real Hilbert spaces H.

Definition 1.

Let C be a nonempty subset of a real Hilbert spaces H and $Z:C\to C$ be a self mapping. Z is called a nonexpansive mapping if

$$\parallel Zx-Zy\parallel \le \parallel x-y\parallel ,\mathit{for}\mathit{all}x,y\in C.$$

Z is called a firmly nonexpansive mapping if

$${\parallel Zx-Zy\parallel }^2\le ⟨x-y,Zx-Zy⟩,\mathit{for}\mathit{all}x,y\in C.$$

A mapping $W:C\to H$ is called α-inverse strongly monotone [1], if there exists a positive real number $\alpha$ such that

$$⟨x-y,Wx-Wy⟩\ge {\alpha \parallel Wx-Wy\parallel }^2,\forall x,y\in C.$$

(1)

If $W:C\to H$ is $\alpha$-inverse strongly monotone, then W is monotone mapping, that is,

$$⟨Wx-Wy,x-y⟩\ge 0,\forall x,y\in H.$$

Remark 1.

(i) If $\alpha =1$ in Equation (1), then W is firmly nonexpansive mapping.

For $i=1,2,\dots ,N$, let $A_i:H\to H$ be a single-valued mapping and $M:H\to 2^H$ be a multi-valued mapping, from the concept of variational inclusion problems, Khuangsatung and Kangtunyakarn [2] introduced the problem of finding $x\in H$ such that

$$\theta \in {\mathsf{\Sigma }}_{i=1}^N{a}_i{A}_{i}x+Mx,$$

(2)

for all $a_i\in (0,1)$ with ${\sum }_{i=1}^N{a}_i=1$ and $\theta$ is a zero vector. This problem is called the modified variational inclusion. The set of solutions of Equation (2) is denoted by $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)$. If we set $A_i=B$ for $i=1,2,\dots ,N$ then Equation (2) reduces to $\theta \in Bx+Mx$, which is the variational inclusion problem. The set of solution of variational inclusion problem is denoted by $VI(H,B,M)$.

The variational inclusion problems are extensively studied in mathematical programming, optimal control, mathematical economics, etc. In recent years, considerable interest has been shown in developing various extensions and generalization of the variational inclusion problem; for instance [3,4] and reference therein.

The operator M is called a maximal monotone [5], if M is monotone, i.e., $⟨u-v,x-y⟩\ge 0$, wherever $u\in M(x),v\in M(y)$ and the graph $G(M)$ of M (that is, $G(M):=\{(x,u)\in H\times H:u\in M(x)\}$) is not property contained in the graph of any other monotone operator.

Let resolvent operator $J_{\lambda }^M:H\to H$ be defined by $J_{\lambda }^M(x)={(I+\lambda M)}^{-1}(x)$, for all $x\in H$, where M is a multi-valued maximal monotone mapping, $\lambda >0$ and I is an identity mapping.

Let $T:C\to C$ be a mapping. A point $x\in C$ is called a fixed point of T if $Tx=x$. The set of fixed points of T is denoted $Fix(T)=\{x\in C:Tx=x\}$. Fixed point problem is an important area of mathematical analysis. This problem applies about the solution in many problem in Hilbert space such as nonlinear operator equation, variational inclusion problem, etc.; for instance [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

Khuangsatung and Kangtunyakarn [2] proposed the following iterative algorithm:

$$\left\{\begin{array}{l}{w}_1,\mu \in H,\hfill \\ \sum _{i=1}^N{b}_i{\mathsf{\Psi }}_i(z_n,y)+\frac{1}{r_n}⟨y-z_n,z_n-w_n⟩\ge 0,\forall y\in C,\hfill \\ w_{n+1}={\alpha }_n\mu +{\beta }_n{w}_n+{\gamma }_n{J}_{\lambda }^M(I-\lambda \sum _{i=1}^N{a}_i{A}_i)w_n+{\eta }_n(I-{\rho }_n(I-S))w_n+{\delta }_n{z}_n,\forall n\ge 1,\hfill \end{array}\right.$$

where $S:H\to H$ is a $\kappa$-strictly pseudononspreading mapping (i.e., if there exists $\kappa \in [0,1)$ such that ${\parallel Su-Sv\parallel }^2\le {\parallel u-v\parallel }^2+\kappa {\parallel (I-S)u-(I-S)v\parallel }^2+2⟨u-Su,v-Sv⟩$, $\forall u,v\in H$) and under certain assumptions of ${\mathsf{\Psi }}_i:C\times C\to \mathbb{R}$ is a bifunction for all $i=1,2,\dots ,N$, they proved strong convergence theorem for solving the modified variational inclusion problem under some suitable conditions of $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}$, $\left\{{\eta }_n\right\}$, $\left\{{\delta }_n\right\}$ and $\left\{{\rho }_n\right\}$.

Over the decades, there are many mathematicians interested in studying the variational inequality problem, which is one of the important problems. The methods used to solve this problem can be applied for other solutions such as physics, economics, finance, optimization, network analysis, medical images, water resourced and structural analysis. The set of solution of the variational inequality problem is denoted by

$$VI(C,A)=\{u\in C:⟨v-u,Au⟩\ge 0\},$$

for all $v\in C$ and $A:C\to H$ is a mapping.

Many iterative methods have been developed for solving variational inequality problem, see, for instance [7,8].

By using the concept of the variational inequality problem, Moudafi and Mainge [9] firstly introduced hierarchical fixed point problem for a nonexpansive mapping T with respect to another nonexpansive mapping S on H: Find $x^{\ast }\in Fix(T)$ such that

$$⟨S{x}^{\ast }-x^{\ast },x-x^{\ast }⟩\le 0,\forall x\in Fix(T),$$

(3)

where $S:H\to H$ is a nonexpansive mapping. It is easy to see that Equation (3) is equivalent to the following fixed point problem: Find $x^{\ast }\in H$ such that

$$x^{\ast }=P_{Fix(T)}\circ S{x}^{\ast },$$

(4)

where $P_{Fix(T)}$ is the metric projection of H onto $Fix(T)$. The solution set of Equation (3) is denoted by $\mathsf{\Phi }=\{x^{\ast }\in H:⟨S{x}^{\ast }-x^{\ast },x-x^{\ast }⟩\le 0,\forall x\in Fix(T)\}$. It is obvious that $\mathsf{\Phi }=VI(Fix(T),I-S)$. Note that Equation (3) covers monotone variational inequality on fixed point sets, minimization problem, etc. Many iterative methods have been developed for solving the hierarchical fixed point problem in Equation (3), see example [9,10,11].

By using the concept of Krasnoselski–Mann iterative algorithm, Moudafi [10] introduced iterative scheme (5) for nonexpansive mapping $S,T$ on a subset C of Hilbert space:

$$\left\{\begin{array}{l}{x}_0\in C,\hfill \\ x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}P{x}_n+(1-{\sigma }_n)T{x}_n),\forall n\ge 0.\hfill \end{array}\right.$$

(5)

He proved the weak convergence theorem of the sequence $\left\{x_n\right\}$, where $\left\{{\alpha }_n\right\}$, $\left\{{\sigma }_n\right\}\subset (0,1)$ satisfies

(i)

${\sum }_{n=0}^{+\infty }{\sigma }_n<+\infty$,

(ii)

${\sum }_{n=0}^{+\infty }{\alpha }_n(1-{\alpha }_n)=+\infty$,

(iii)

${lim}_{n\to +\infty }\frac{\parallel x_{n+1}-x_n\parallel }{(1-{\alpha }_n){\sigma }_n}=0$.

Let $H_1$ and $H_2$ be two real Hilbert spaces and C, Q be a nonempty closed convex subset of a real Hilbert spaces $H_1$ and $H_2$, respectively. Let $A:H_1\to H_2$ be a bounded linear operator. Censor and Elfving [14] introduced the split feasibility problem $(SEP)$ which is to find a point $x\in C$ and $Ax\in Q$. Many authors have studied this concept of SEP to modified their problem, see example [12,13,14,15].

In 2010, Censor, Gibali and Reich [13] introduced the split variational inequality problem which relies on the split feasibility problem and thus created the iterative algorithm for solving a strong convergence theorem of the split variational inclusion problem; more detail [13].

The split monotone variational inclusion problem, which consists of special cases, which is being used in practice as a model in the intensity-modulated radiation therapy treatment planning, the modeling of many inverse problems, and other problems; see for instance [11,12,13,14,15].

For every $i=1,2,\dots ,N$. Let $A_i:H_1\to H_1$, $B_i:H_2\to H_2$ be mappings and $M_A:H_1\to 2^{H_1}$ and $M_B:H_2\to 2^{H_2}$ be multi-value mappings. Inspired and motivated by Moudafi [12] and Khuangsatung and Kangtunyakarn [2], we define the split combination of the variational inclusion problem (SCVIP) which is find $x^{\ast }\in H_1$ such that

$${\theta }_{H_1}\in \sum _{i=1}^N{a}_i{A}_i{x}^{\ast }+M_A{x}^{\ast },$$

(6)

and

$$y^{\ast }=A{x}^{\ast }\mathrm{such}\mathrm{that}{\theta }_{H_2}\in \sum _{i=1}^N{b}_i{B}_i{y}^{\ast }+M_B{y}^{\ast },$$

(7)

where $A:H_1\to H_2$ is a bounded linear operator and ${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$.

The set of all the solutions for Equations (6) and (7) are denoted by $\mathsf{\Omega }=\{x\in VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i,M_A):Ax\in VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i,M_B)\}$.

If we set $A_i=A$ and $B_i=B$ for all $i=1,2,\dots ,N$ then SCVIP reduces to the split monotone variational inclusion problem (SMVI), which is,

$$\mathrm{find}{x}^{\ast }\in H_1\mathrm{such}\mathrm{that}0\in A(x^{\ast })+M_A(x^{\ast }),$$

(8)

and such that

$$y^{\ast }=A{x}^{\ast }\in H_2\mathrm{solves}0\in B(y^{\ast })+M_B(y^{\ast }),$$

(9)

introduced by Moudafi [12]. The set of all these solutions for Equations (8) and (9) are denoted by $\Theta =\{x^{\ast }\in VI(H_1,f,B_2):A{x}^{\ast }\in VI(H_2,g,B_2)\}$.

Very recently, Kazmi et al. [11] proved the strong convergence theorem under suitable condition of parameters for solving the hierarchical fixed point problem and SMVI by using hybrid iterative method as follows:

$$\left\{\begin{array}{l}{x}_0\in C,C_0=C;\hfill \\ u_n=(1-{\alpha }_n)x_n+{\alpha }_n{P}_C({\sigma }_{n}S{x}_n+(1-{\sigma }_n)W_n{x}_n);\hfill \\ z_n=J_{\lambda }^{M_1}(I-\lambda f)(u_n);\hfill \\ w_n=J_{\lambda }^{M_2}(I-\lambda g)(A{z}_n);\hfill \\ y_n=z_n+\gamma A^{\ast }(w_n-A{z}_n);\hfill \\ C_n=\{z\in C:\parallel y_n{-z\parallel }^2\le (1-{\alpha }_n{\sigma }_n)\parallel x_n{-z\parallel }^2+{\alpha }_n{\sigma }_n\parallel S{x}_n-z{\parallel }^2\};\hfill \\ Q_n\{z\in C:⟨x_n-z,x_0-x_n⟩\ge 0\};\hfill \\ x_{n+1}=P_{C_n\bigcap Q_n}{x}_0,n\ge 0.\hfill \end{array}\right.$$

(10)

where $M_1:H_1\to 2^{H_1}$, $M_2:H_2\to 2^{H_2}$ are multi-valued maximal monotone operators, $f:C\to H_1$ is ${\theta }_1$-inverse strongly monotone mapping, $g:Q\to H_2$ is ${\theta }_2$-inverse strongly monotone mapping, ${\left\{T_i\right\}}_{i=1}^N:C\to C$ is a finite family of nonexpansive mappings and $W_n$ is a W-mapping generated by $T_1,T_2,\dots ,T_N$ and ${\lambda }_{n,1},{\lambda }_{n,2},\dots ,{\lambda }_{n,N}$ for all $n\in \mathbb{N}\cup \left\{0\right\}$.

Based on the results mentioned above, we give our theorem for SCVIP and some important results as follows:

(i)

We first establish Lemma 8 which shows the equivalence between SCVIP and fixed point problem of nonexpansive mapping under suitable conditions on our parameters. Further, we give some example to support Lemma 8 and the example shows that Lemma 8 is not true if some condition fails.

(ii)

We establish a strong convergence theorem of the sequences generated by the modified Halpern iterative method for finding a common solution of hierarchical fixed point problem for a nonexpansive mapping and SCVIP.

(iii)

We apply our main result to obtain a strong convergence theorem of the sequences generated by the modified Halpern iterative method for finding a common solution of hierarchical fixed point problem for a nonexpansive mapping and split combination of variational inequality problem and a strong convergence theorem for finding a common solution of hierarchical fixed point problem for nonexpansive mapping and split zero point problem.

(iv)

We give some illustrative numerical examples to support our main result and our examples show that our main result is not true if some conditions fail.

2. Preliminaries

In this paper, we denote weak and strong convergence by the notations ’⇀’ and ’→’, respectively. We recall some concepts and results needed in the sequel.

Let H be a real Hilbert space and let C be a nonempty closed convex subset of H. Then for any $x\in H$, there exists a unique nearest point in C, denoted by $P_{C}x$, such that

$$\parallel x-P_{C}x\parallel \le \parallel x-y\parallel ,\forall y\in C.$$

(11)

The mapping $P_C$ is called the matric projection of H onto C. It is well known that $P_C$ is nonexpansive and satisfies

$$⟨x-y,P_{C}x-P_{C}y⟩\ge {\parallel P_{C}x-P_{C}y\parallel }^2,\forall x\in H.$$

(12)

Moreover, $P_{C}x$ is characterized by the fact $P_{C}x\in C$ and

$$⟨x-P_{C}x,y-P_{C}x⟩\le 0,\forall y\in C,$$

(13)

which implies that

$${\parallel x-y\parallel }^2 \ge \parallel x-P_C{x\parallel }^2+{\parallel y-P_{C}x\parallel }^2,\forall x\in H,y\in C.$$

(14)

Lemma 1

([4]). Let $\left\{a_n\right\},\left\{c_n\right\}\subset {\mathbb{R}}^{+}$, $\left\{{\alpha }_n\right\}\subset (0,1)$ and $\left\{b_n\right\}\subset \mathbb{R}$ be sequences such that

$$a_{n+1}=(1-{\alpha }_n)a_n+b_n+c_n,\mathit{for}\mathit{all}n\ge 0.$$

Assume ${\sum }_{n=0}^{\infty }{c}_n<\infty$. Then the following results hold:

(i) 

if $b_n\le {\alpha }_{n}C$ where $C\ge 0$, then $\left\{a_n\right\}$ is a bounded sequence,

(ii) 

if ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$ and ${lim\; sup}_{n\to \infty }\frac{b_n}{{\alpha }_n}\le 0$, then ${lim}_{n\to \infty }{a}_n=0$.

Lemma 2

([19]). Let E be a uniformly convex Banach space, C a nonempty closed convex subset of E, and $S:C\to C$ a nonexpansive mapping with $Fix(S)\ne \varnothing$. Then $I-S$ is demiclosed at zero.

Lemma 3

([4]). Let $u\in H$ be a solution of variational inclusion if and only if $u=J_{\lambda }^M(u-\lambda Bu),\forall \lambda >0$, i.e.,

$$VI(H,B,M)=Fix(J_{\lambda }^M(I-\lambda B)),\forall \lambda >0.$$

where $B:H\to H$ is a single-valued mapping. Further, if $\lambda \in (0,2\alpha ]$, then $VI(H,B,M)$ is a closed convex subset in H.

Lemma 4

([4]). The resolvent operator $J_{\lambda }^M$ associated with M is single-valued, nonexpansive for all $\lambda >0$ and 1-inverse strongly monotone.

Lemma 5

([2]). Let H be a real Hilbert space and let $M:H\to 2^H$ be a multi-valued maximal monotone mapping. For every $i=1,2,\dots ,N$, let $A_i:H\to H$ be ${\alpha }_i$-inverse strongly monotone mapping with $\eta ={min}_{i=1,2,\dots ,N}\left\{{\alpha }_i\right\}$ and ${\bigcap }_{i=1}^{N}VI(H,A_i,M)\ne \varnothing$. Then

$$VI\left(H,\sum _{i=1}^N{a}_i{A}_i,M\right)=\bigcap _{i=1}^{N}VI(H,A_i,M),$$

where ${\sum }_{i=1}^N{a}_i=1$ and $0<a_i<1$ for every $i=1,2,\dots ,N$. Moreover, $J_{\lambda }^M(I-\lambda {\sum }_{i=1}^N{a}_i{A}_i)$ is a nonexpansive mapping, for all $0<\lambda <2\eta$.

Example 1.

Let $H=\mathbb{R}$. For every $i=1,2,\dots ,N$, let $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{ix}{4}+(i+1)$ for all $x\in H$ and $M:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $Mx=\left\{\frac{x}{4}\right\}$ for all $x\in \mathbb{R}$. Let $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$ for all $i=1,2,\dots ,N$. Then $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)={\bigcap }_{i=1}^{N}VI(H,A_i,M)$.

Proof of Solution.

Since $A_{i}x=\frac{ix}{4}+(i+1)$, we have $A_i$ is $\frac{4}{i}$-inverse strongly monotone mapping. By definition of $a_i$ and $A_i$, we have

$$\sum _{i=1}^N{a}_i{A}_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})A_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})(\frac{ix}{4}+(i+1)).$$

From Lemma 5, we have $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)={\bigcap }_{i=1}^{N}VI(H,A_i,M)=\{-4\}$. □

Example 2.

Let $H=\mathbb{R}$. For every $i=1,2,\dots ,N$, let $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{ix}{4}+(i+1)$ for all $x\in H$ and $M:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $Mx=\left\{\frac{x}{4}\right\}$ for all $x\in \mathbb{R}$. Let $a_i=\frac{3}{4^i}+\frac{1}{N}(\frac{1}{4^N}+1)$ for all $i=1,2,\dots ,N$. Then $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)\ne {\bigcap }_{i=1}^{N}VI(H,A_i,M)$.

Proof of Solution.

Since $A_{i}x=\frac{ix}{4}+(i+1)$, we have $A_i$ is $\frac{4}{i}$-inverse strongly monotone mapping. By definition of $a_i$ and $A_i$, we have

$$\sum _{i=1}^N{a}_i{A}_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N}(\frac{1}{4^N}+1))A_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N}(\frac{1}{4^N}+1))(\frac{ix}{4}+(i+1)).$$

Then ${\bigcap }_{i=1}^{N}VI(H,A_i,M)=\{-4\}$ and $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)\ne \{-4\}$. It implies that $VI(H,{\sum }_{i=1}^N{a}_i{A}_i,M)\ne {\bigcap }_{i=1}^{N}VI(H,A_i,M)$ because ${\sum }_{i=1}^N{a}_i=2$. □

Remark 2.

Example 1 shows that Lemma 5 is true where ${\sum }_{i=1}^N{a}_i=1$ and Example 2 shows that Lemma 5 is not true if a condition fails, that is ${\sum }_{i=1}^N{a}_i\ne 1$.

Lemma 6

([17]). Let $C\subseteq H$ be a nonempty closed and convex set and let $T:C\to H$ be a nonexpansive mapping. Then $Fix(T)$ is closed and convex.

Lemma 7.

Let $H_1$ and $H_2$ be Hilbert spaces. Let $M_A:H_1\to 2^{H_1}$ be a multi-valued maximal monotone mapping and $M_B:H_2\to 2^{H_2}$ be a multi-valued maximal monotone mapping. Let $A:H_1\to H_2$ be a bounded linear operator. For every $i=1,2,\dots ,N$, let $A_i:H_1\to H_1$ be ${\alpha }_i$-inverse strongly monotone with ${\eta }_A={min}_{i=1,2,\dots ,N}\left\{{\alpha }_i\right\}$ and $B_i:H_2\to H_2$ be ${\beta }_i$-inverse strongly monotone with ${\eta }_B={min}_{i=1,2,\dots ,N}\left\{{\beta }_i\right\}$. For each $x,y\in H_1$, then

$$\begin{array}{c}\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax)\hfill \\ -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(y-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay){\parallel }^2\hfill \\ \le {\parallel x-y\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2,\hfill \end{array}$$

where ${\lambda }_A\in (0,2{\eta }_A)$, ${\lambda }_B\in (0,2{\eta }_B)$, ${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$ and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $A^{\ast }A$.

Proof. 

Let $x,y\in H_1$. Consider

$$\begin{array}{c}\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax)\hfill \\ -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(y-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay){\parallel }^2\hfill \\ \le \parallel (x-y)-\gamma (A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay){\parallel }^2\hfill \\ ={\parallel x-y\parallel }^2-2\gamma ⟨x-y,A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay⟩\hfill \\ +{\gamma }^2\parallel A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ \le {\parallel x-y\parallel }^2+2\gamma ⟨Ay-Ax,(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay⟩\hfill \\ +{\gamma }^{2}L\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ ={\parallel x-y\parallel }^2+2\gamma ⟨Ay-Ax+J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ax-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ax\hfill \\ +J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ay-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ay,(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax\hfill \\ -(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay⟩\hfill \\ +{\gamma }^{2}L\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ ={\parallel x-y\parallel }^2+2\gamma [⟨J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ay-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)Ax,\hfill \\ (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay⟩\hfill \\ -⟨(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay,\hfill \\ (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay⟩]\hfill \\ +{\gamma }^{2}L\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ \le {\parallel x-y\parallel }^2+2\gamma [\frac{1}{2}\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ -\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)){Ay\parallel }^2]\hfill \\ +{\gamma }^{2}L\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2\hfill \\ ={\parallel x-y\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay{\parallel }^2.\hfill \end{array}$$

Hence

$$\begin{array}{c}\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ax)\hfill \\ -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(y-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ay){\parallel }^2\hfill \\ \le {\parallel x-y\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))Ax-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))Ay{\parallel }^2.\hfill \end{array}$$

 □

We introduce Lemma 8 which shows an association between the SCVIP and the fixed point problem of nonexpansive mapping under suitable conditions on our parameters. Furthermore, we give examples for supporting Lemma 8 and the examples shows that Lemma 8 is not true if parameters are not satisfied.

Lemma 8.

Let $H_1$ and $H_2$ be Hilbert spaces. Let $M_A:H_1\to 2^{H_1}$ be a multi-valued maximal monotone mapping and $M_B:H_2\to 2^{H_2}$ be a multi-valued maximal monotone mapping. Let $A:H_1\to H_2$ be a bounded linear operator. For every $i=1,2,\dots ,N$, let $A_i:H_1\to H_1$ be ${\alpha }_i$-inverse strongly monotone with ${\eta }_A={min}_{i=1,2,\dots ,N}\left\{{\alpha }_i\right\}$ and $B_i:H_2\to H_2$ be ${\beta }_i$-inverse strongly monotone with ${\eta }_B={min}_{i=1,2,\dots ,N}\left\{{\beta }_i\right\}$. Suppose that $\mathsf{\Omega }\ne \varnothing$. Then the following are equivalent:

(i) 

$x^{\ast }\in \mathsf{\Omega }$

(ii) 

$x^{\ast }=J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })$,

where ${\lambda }_A\in (0,2{\eta }_A)$, ${\lambda }_B\in (0,2{\eta }_B)$, ${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$ and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $A^{\ast }A$.

Proof. 

Let the condition holds.

$(i)\Rightarrow (ii)$ Let $x^{\ast }\in \mathsf{\Omega }$, we have $x^{\ast }\in VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i,M_A)$ and $A{x}^{\ast }\in VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i,M_B)$.

From Lemma 3, we have $x^{\ast }\in Fix(J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i))$ and $A{x}^{\ast }\in Fix(J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))$, which implies that $x^{\ast }=J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)x^{\ast }$ and $A{x}^{\ast }=J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)A{x}^{\ast }$.

By $x^{\ast }=J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)x^{\ast }$ and $A{x}^{\ast }=J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)A{x}^{\ast }$, we have

$$\begin{array}{cc}\hfill J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }& -\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast })\hfill \\ & =J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(A{x}^{\ast }-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)A{x}^{\ast })\hfill \\ & =J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)x^{\ast }\hfill \\ & =x^{\ast }.\hfill \end{array}$$

It implies that

$$J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast })=x^{\ast }.$$

(15)

$(ii)\Rightarrow (i)$ Let $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })=x^{\ast }$ and let $w\in \mathsf{\Omega }$.

We will show that $I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i$ and $I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i$ are nonexpansive, for all $i=1,2,\dots ,N$.

Since $A_i:C\to H$ be ${\alpha }_i$-inverse strongly monotone mapping with ${\eta }_A={min}_{i=1,2,\dots ,N}\left\{{\alpha }_i\right\}$ and ${\lambda }_A\in (0,2{\eta }_A)$, we have

$$\begin{array}{cc}\hfill \parallel (I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)x& -(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i){y\parallel }^2\hfill \\ & ={\parallel x-y\parallel }^2-2{\lambda }_A\sum _{i=1}^N{a}_i⟨x-y,A_{i}x-A_{i}y⟩+{\lambda }_A^2\sum _{i=1}^N{a}_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2-2{\lambda }_A\sum _{i=1}^N{a}_i{\alpha }_i\parallel A_{i}x-A_i{y\parallel }^2+{\lambda }_A^2\sum _{i=1}^N{a}_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2-2{\lambda }_A{\eta }_A\sum _{i=1}^N{a}_i\parallel A_{i}x-A_i{y\parallel }^2+{\lambda }_A^2\sum _{i=1}^N{a}_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & ={\parallel x-y\parallel }^2+{\lambda }_A\sum _{i=1}^N{a}_i({\lambda }_A-2{\eta }_A){\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2.\hfill \end{array}$$

Thus $I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i$ is a nonexpansive mapping, for all $i=1,2,\dots ,N$. By using the same proof, we obtain that $I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i$, for all $i=1,2,\dots ,N$ is a nonexpansive mapping and $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)$ is nonexpansive mapping.

From $w\in \mathsf{\Omega }$ and $(i)\Rightarrow (ii)$, we have $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)Aw=Aw$ and $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(w-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))Aw)=w$.

From Lemma 7 and $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)Aw=w$, we have

$$\begin{array}{cc}\hfill \parallel x^{\ast }{-w\parallel }^2& =\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast })\hfill \\ & -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(w-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Aw){\parallel }^2\hfill \\ & \le \parallel x^{\ast }-w{\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }\hfill \\ & -(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)){Aw\parallel }^2\hfill \\ & =\parallel x^{\ast }{-w\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }{\parallel }^2.\hfill \end{array}$$

(16)

Applying Equation (16), we have

$$A{x}^{\ast }\in Fix(J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i)).$$

(17)

From Lemma 5, we have

$$A{x}^{\ast }\in VI\left(H_1,\sum _{i=1}^N{b}_i{B}_i,M_B\right).$$

(18)

From the definition of $x^{\ast }$ and Equation (17), we have

$$\begin{array}{cc}\hfill x^{\ast }& =J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast })\hfill \\ & =J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)x^{\ast }.\hfill \end{array}$$

From Lemma 5, we have

$$x^{\ast }\in VI\left(H_2,\sum _{i=1}^N{a}_i{A}_i,M_A\right).$$

(19)

From Equations (18) and (19), we have $x^{\ast }\in \mathsf{\Omega }$. □

Example 3.

Let $H_1=H_2=\mathbb{R}$. For every $i=1,2,\dots ,N$, let $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{ix}{4}+(i+1)$ for all $x\in H_1$ and $B_i:\mathbb{R}\to \mathbb{R}$ define by $B_{i}y=\frac{iy}{2}+(i+1)$ for all $y\in H_2$. Let $M_A:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_{A}x=\left\{\frac{x}{4}\right\}$ for all $x\in \mathbb{R}$ and $M_B:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_{B}x=\left\{\frac{y}{2}\right\}$ for all $y\in \mathbb{R}$. Let $Ax=x$, for all $x\in \mathbb{R}$. Let $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$ and $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$ for all $i=1,2,\dots ,N$. Then $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })=-4$.

Proof of Solution

It is easy to observe $A_i$ is $\frac{4}{i}$-inverse strongly monotone mapping and $B_i$ is $\frac{2}{i}$-inverse strongly monotone mapping. By definition of $A_i$, $B_i$ and $a_i$, $b_i$, we have

$$\sum _{i=1}^N{a}_i{A}_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})A_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})(\frac{ix}{4}+(i+1)),$$

and

$$\sum _{i=1}^N{b}_i{B}_{i}y=\sum _{i=1}^N(\frac{2}{3^i}+\frac{1}{N{3}^N})B_{i}y=\sum _{i=1}^N(\frac{2}{3^i}+\frac{1}{N{3}^N})(\frac{iy}{2}+(i+1)).$$

Then $\mathsf{\Omega }=\{-4\}$. From definition of A, we have $L=1$. Choose ${\lambda }_A=\frac{1}{N}$, ${\lambda }_B=\frac{1}{N}$ and $\gamma =\frac{1}{10}$. From Lemma 8, we have $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })=-4$. □

Example 4.

Let $H_1=H_2=\mathbb{R}$. For every $i=1,2,\dots ,N$, let $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{ix}{4}+(i+1)$ for all $x\in H_1$ and $B_i:\mathbb{R}\to \mathbb{R}$ define by $B_{i}y=\frac{iy}{2}+(i+1)$ for all $y\in H_2$. Let $M_A:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_{A}x=\left\{\frac{x}{4}\right\}$ for all $x\in \mathbb{R}$ and $M_B:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_{B}x=\left\{\frac{y}{2}\right\}$ for all $y\in \mathbb{R}$. Let $Ax=x$, for all $x\in \mathbb{R}$. Let $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$ and $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$ for all $i=1,2,\dots ,N$. Then $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })=x^{\ast }$ for all $x^{\ast }\in \mathbb{R}$.

Proof of Solution

It is easy to observe $A_i$ is $\frac{4}{i}$-inverse strongly monotone mapping and $B_i$ is $\frac{2}{i}$-inverse strongly monotone mapping. By definition of $A_i$, $B_i$ and $a_i$, $b_i$, we have

$$\sum _{i=1}^N{a}_i{A}_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})A_{i}x=\sum _{i=1}^N(\frac{3}{4^i}+\frac{1}{N{4}^N})(\frac{ix}{4}+(i+1)),$$

and

$$\sum _{i=1}^N{b}_i{B}_{i}y=\sum _{i=1}^N(\frac{2}{3^i}+\frac{1}{N{3}^N})B_{i}y=\sum _{i=1}^N(\frac{2}{3^i}+\frac{1}{N{3}^N})(\frac{iy}{2}+(i+1)).$$

Then $\mathsf{\Omega }=\{-4\}$. From definition of A, we have $L=1$. Choose ${\lambda }_A=0$, ${\lambda }_B=0$ and $\gamma =\frac{1}{10}$, we have $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })=x^{\ast }$ for all $x^{\ast }\in \mathbb{R}$.

So Example 4 shows that Lemma 8 is not true because ${\lambda }_A=0$ and ${\lambda }_B=0$. □

3. Main Result

We prove a strong convergence theorem to approximate a common solution of SCVIP and hierarchical fixed point problem of nonexpansive mapping.

Theorem 1.

Let $H_1,H_2$ be real Hilbert spaces. Let $M_A:H_1\to 2^{H_1}$ be a multi-valued maximal monotone mapping and $M_B:H_2\to 2^{H_2}$ be a multi-valued maximal monotone mapping. Let $A:H_1\to H_2$ be a bounded linear operator with its adjoint operator $A^{\ast }$. Let $A_i:H_1\to H_1$ be ${\alpha }_i$-inverse strongly monotone with ${\eta }_A={min}_{i=1}\left\{{\alpha }_i\right\}$ and $B_i:H_2\to H_2$ be ${\beta }_i$-inverse strongly monotone with ${\eta }_B={min}_{i=1}\left\{{\beta }_i\right\}$. Let $S,T:H_1\to H_1$ be two nonexpansive mappings. Assume that $\mathbb{F}=\mathsf{\Phi }\cap \mathsf{\Omega }\ne \varnothing$. Let the sequence $\left\{x_n\right\}$ generated by $u,x_1\in H_1$ and

$$\left\{\begin{array}{l}{u}_n=J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_n-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n),\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n),\hfill \\ x_{n+1}={\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n,\hfill \end{array}\right.$$

(20)

where $\left\{{\mu }_n\right\},\left\{{\phi }_n\right\},\left\{{\theta }_n\right\},\left\{{\alpha }_n\right\},\left\{{\sigma }_n\right\}\subseteq [0,1]$ with ${\mu }_n+{\phi }_n+{\theta }_n=1$ for all $n\ge 1$, ${\lambda }_A\in (0,2{\eta }_A)$, ${\lambda }_B\in (0,2{\eta }_B)$ and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $A^{\ast }A$. Suppose the following conditions hold:

(i) 

${lim}_{n\to \infty }{\mu }_n=0$, ${\sum }_{n=1}^{\infty }{\mu }_n=\infty$,

(ii) 

$0<c\le {\phi }_n,{\theta }_n\le d<1$, $\exists c,d>0$,

(iii) 

${\sum }_{n=1}^{\infty }|{\mu }_{n+1}-{\mu }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\phi }_{n+1}-{\phi }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\theta }_{n+1}-{\theta }_n|<\infty$

(iv) 

${lim}_{n\to \infty }{\sigma }_n=0$, ${\sum }_{n=1}^{\infty }{\sigma }_n<\infty$,

(v) 

${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$,

(vi) 

${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$, $a_i>0$ and $b_i>0$ for all $i=1,2,\dots ,N$.

Then $\left\{x_n\right\}$ converges strongly to $z_0\in \mathbb{F}$, where $z_0=P_{\mathbb{F}}u$.

Proof. 

Step1. First, we prove that $\left\{x_n\right\}$, $\left\{y_n\right\}$ and $\left\{u_n\right\}$ are bounded.

We will show that $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)$ and $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)$ are nonexpansive mapping. Since $A_i$ is ${\alpha }_i$-inverse strongly monotone with ${\eta }_A={min}_{i=1}\left\{{\alpha }_i\right\}$, we have

$$\begin{array}{cc}\hfill {∥(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)x-(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)y∥}^2& ={∥(x-y)-{\lambda }_A(\sum _{i=1}^N{a}_i{A}_{i}x-\sum _{i=1}^N{a}_i{A}_{i}y)∥}^2\hfill \\ & \le {\parallel x-y\parallel }^2-2{\lambda }_A\sum _{i=1}^N{a}_i⟨x-y,A_{i}x-A_{i}y⟩\hfill \\ & +{\lambda }_A^2\sum _{i=1}^N{a}_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2-2{\lambda }_A\sum _{i=1}^N{a}_i{\alpha }_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & +{\lambda }_A^2\sum _{i=1}^N{a}_i{\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2+{\lambda }_A\sum _{i=1}^N{a}_i({\lambda }_n-2{\eta }_A){\parallel A_{i}x-A_{i}y\parallel }^2\hfill \\ & \le {\parallel x-y\parallel }^2.\hfill \end{array}$$

Thus $I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i$ is a nonexpansive mapping, for all $i=1,2,\dots ,N$. By using the same proof, we obtain that $I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i$ is a nonexpansive mapping. Since $J_{{\lambda }_A}^{M_A}$ and $J_{{\lambda }_B}^{M_B}$ are nonexpnsive mapping, we have $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)$ and $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)$ are nonexpansive mapping.

Let $p\in \mathbb{F}$ then $p\in H_1$ and $p\in \mathsf{\Phi }$ which $Tp=p$. Now, we estimate

$$\begin{array}{cc}\hfill \parallel y_n{-p\parallel }^2& =\parallel (1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n){-p\parallel }^2\hfill \\ & =\parallel (1-{\alpha }_n)(x_n-p)+{\alpha }_n({\sigma }_n(S{x}_n-p)+(1-{\sigma }_n)(T{x}_n-p)){\parallel }^2\hfill \\ & \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\parallel ({\sigma }_n(S{x}_n-p)+(1-{\sigma }_n)(T{x}_n-p))\parallel }^2\hfill \\ & \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\sigma }_n\parallel S{x}_n{-p\parallel }^2+{\alpha }_n(1-{\sigma }_n){\parallel T{x}_n-p\parallel }^2\hfill \\ & \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\sigma }_n\parallel S{x}_n{-p\parallel }^2+{\alpha }_n(1-{\sigma }_n){\parallel x_n-p\parallel }^2\hfill \\ & =(1-{\alpha }_n{\sigma }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\sigma }_n{\parallel S{x}_n-p\parallel }^2.\hfill \end{array}$$

(21)

Since $p\in \mathbb{F}$, then $p\in \mathsf{\Omega }$ and $J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)p=p$ and $J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i)Ap=Ap$. By Lemma 8, we have

$$J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(p-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ap)=p.$$

By Lemma 7, we have

$$\begin{array}{cc}\hfill \parallel u_n& {-p\parallel }^2\hfill \\ & =\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_n-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n)\hfill \\ & -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(p-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ap){\parallel }^2\hfill \\ & \le \parallel x_n{-p\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))Ap{\parallel }^2\hfill \\ & \le \parallel x_n{-p\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n{\parallel }^2\hfill \\ & \le \parallel x_n{-p\parallel }^2.\hfill \end{array}$$

(22)

By Equations (21) and (22), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& =\parallel {\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n{-p\parallel }^2\hfill \\ & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\parallel y_n{-p\parallel }^2+{\theta }_n{\parallel u_n-p\parallel }^2\hfill \\ & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\left[(1-{\alpha }_n{\sigma }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\sigma }_n{\parallel S{x}_n-p\parallel }^2\right]+{\theta }_n{\parallel x_n-p\parallel }^2\hfill \\ & ={\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\parallel x_n{-p\parallel }^2-{\phi }_n{\alpha }_n{\sigma }_n\parallel x_n{-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_n\parallel S{x}_n{-p\parallel }^2+{\theta }_n{\parallel x_n-p\parallel }^2\hfill \\ & ={\mu }_n{\parallel u-p\parallel }^2+(1-{\mu }_n)\parallel x_n{-p\parallel }^2-{\phi }_n{\alpha }_n{\sigma }_n\parallel x_n{-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_n{\parallel S{x}_n-p\parallel }^2\hfill \\ & \le (1-{\mu }_n)\parallel x_n{-p\parallel }^2+{\mu }_n{\parallel u-p\parallel }^2+{\mu }_n{\alpha }_n{\sigma }_n{\parallel S{x}_n-p\parallel }^2.\hfill \end{array}$$

(23)

From Lemma 1(i), therefore $\left\{x_n\right\}$ is bounded. So are $\left\{u_n\right\}$, $\left\{y_n\right\}$.

Step2. Show that ${lim}_{n\to \infty }\parallel x_{n+1}-x_n\parallel =0$, ${lim}_{n\to \infty }\parallel x_n-u_n\parallel =0$ and ${lim}_{n\to \infty }\parallel x_n-y_n\parallel =0$.

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & =\parallel {\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n-{\mu }_{n-1}u-{\phi }_{n-1}{y}_{n-1}-{\theta }_{n-1}{u}_{n-1}\parallel \hfill \\ \hfill & =\parallel ({\mu }_n-{\mu }_{n-1})u+({\phi }_n-{\phi }_{n-1})y_{n-1}+{\phi }_n(y_n-y_{n-1})\hfill \\ \hfill & +({\theta }_n-{\theta }_{n-1})u_{n-1}+{\theta }_n(u_n-u_{n-1})\parallel \hfill \\ \hfill & \le |{\mu }_n-{\mu }_{n-1}|\parallel u\parallel +|{\phi }_n-{\phi }_{n-1}|\parallel y_{n-1}\parallel +{\phi }_n\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & +|{\theta }_n-{\theta }_{n-1}|\parallel u_{n-1}\parallel +{\theta }_n\parallel u_n-u_{n-1}\parallel .\hfill \end{array}$$

(24)

From definition of $u_n$, Lemma 7 and $\gamma \in (0,\frac{1}{L})$, we have

$$\begin{array}{cc}\hfill \parallel u_n-u_{n-1}{\parallel }^2& =\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_n-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n)\hfill \\ \hfill & -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_{n-1}-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n-1}){\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x_{n-1}{\parallel }^2-\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n\hfill \\ \hfill & -(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n-1}{\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x_{n-1}{\parallel }^2.\hfill \end{array}$$

It implies that

$$\parallel u_n-u_{n-1}\parallel \le \parallel x_n-x_{n-1}\parallel .$$

(25)

From definition of $y_n$, we have

$$\begin{array}{cc}\hfill \parallel y_n-y_{n-1}\parallel & =\parallel (1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n)\hfill \\ \hfill & -[(1-{\alpha }_{n-1})x_{n-1}+{\alpha }_{n-1}({\sigma }_{n-1}S{x}_{n-1}+(1-{\sigma }_{n-1})T{x}_{n-1})]\parallel \hfill \\ \hfill & =\parallel (x_n-x_{n-1})-{\alpha }_n{x}_n+{\alpha }_{n-1}{x}_{n-1}+{\alpha }_n{x}_{n-1}-{\alpha }_n{x}_{n-1}\hfill \\ \hfill & +{\alpha }_n{\sigma }_{n}S{x}_n-{\alpha }_{n-1}{\sigma }_{n-1}S{x}_{n-1}+{\alpha }_n{\sigma }_{n}S{x}_{n-1}-{\alpha }_n{\sigma }_{n}S{x}_{n-1}\hfill \\ \hfill & +{\alpha }_{n}T{x}_n-{\alpha }_{n-1}T{x}_{n-1}+{\alpha }_{n}T{x}_{n-1}-{\alpha }_{n}T{x}_{n-1}\hfill \\ \hfill & -{\alpha }_n{\sigma }_{n}T{x}_n+{\alpha }_{n-1}{\sigma }_{n-1}T{x}_{n-1}+{\alpha }_n{\sigma }_{n}T{x}_{n-1}-{\alpha }_n{\sigma }_{n}T{x}_{n-1}\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_n)(x_n-x_{n-1})+({\alpha }_{n-1}-{\alpha }_n)x_{n-1}\hfill \\ \hfill & +({\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1})S{x}_{n-1}+{\alpha }_n{\sigma }_n(S{x}_n-S{x}_{n-1})\hfill \\ \hfill & +{\alpha }_n(1-{\sigma }_n)(T{x}_n-T{x}_{n-1})+({\alpha }_n-{\alpha }_{n-1})T{x}_{n-1}\hfill \\ \hfill & +({\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n)T{x}_{n-1}\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-x_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel +{\alpha }_n{\sigma }_n\parallel S{x}_n-S{x}_{n-1}\parallel \hfill \\ \hfill & +{\alpha }_n(1-{\sigma }_n)\parallel T{x}_n-T{x}_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-x_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel +{\alpha }_n{\sigma }_n\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +{\alpha }_n(1-{\sigma }_n)\parallel x_n-x_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & =\parallel x_n-x_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel .\hfill \end{array}$$

(26)

From Equations (24)–(26), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & \le |{\mu }_n-{\mu }_{n-1}|\parallel u\parallel +|{\phi }_n-{\phi }_{n-1}|\parallel y_{n-1}\parallel +{\phi }_n\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & +|{\theta }_n-{\theta }_{n-1}|\parallel u_{n-1}\parallel +{\theta }_n\parallel u_n-u_{n-1}\parallel \hfill \\ \hfill & \le |{\mu }_n-{\mu }_{n-1}|\parallel u\parallel +|{\phi }_n-{\phi }_{n-1}|\parallel y_{n-1}\parallel \hfill \\ \hfill & +{\phi }_n[\parallel x_n-x_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel ]\hfill \\ \hfill & +|{\theta }_n-{\theta }_{n-1}|\parallel u_{n-1}\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & =({\phi }_n+{\theta }_n)\parallel x_n-x_{n-1}\parallel +|{\mu }_n-{\mu }_{n-1}|\parallel u\parallel +|{\phi }_n-{\phi }_{n-1}|\parallel y_{n-1}\parallel \hfill \\ \hfill & +{\phi }_n|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel +{\phi }_n|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel \hfill \\ \hfill & +{\phi }_n|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel +{\phi }_n|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\theta }_n-{\theta }_{n-1}|\parallel u_{n-1}\parallel \hfill \\ \hfill & \le (1-{\mu }_n)\parallel x_n-x_{n-1}\parallel +|{\mu }_n-{\mu }_{n-1}|\parallel u\parallel +|{\phi }_n-{\phi }_{n-1}|\parallel y_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_{n-1}-{\alpha }_n|\parallel x_{n-1}\parallel +|{\alpha }_n{\sigma }_n-{\alpha }_{n-1}{\sigma }_{n-1}|\parallel S{x}_{n-1}\parallel \hfill \\ \hfill & +|{\alpha }_n-{\alpha }_{n-1}|\parallel T{x}_{n-1}\parallel +|{\alpha }_{n-1}{\sigma }_{n-1}-{\alpha }_n{\sigma }_n|\parallel T{x}_{n-1}\parallel \hfill \\ \hfill & +|{\theta }_n-{\theta }_{n-1}|\parallel u_{n-1}\parallel .\hfill \end{array}$$

By Lemma 1(i), conditions (i) and (iii), we have

$$\underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(27)

From definition of $u_n$, we have

$$\begin{array}{cc}\hfill x_{n+1}-u_n& ={\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n-u_n\hfill \\ \hfill & ={\mu }_n(u-u_n)+{\phi }_n(y_n-u_n).\hfill \end{array}$$

(28)

From Equations (21) and (22), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& =\parallel {\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n{-p\parallel }^2\hfill \\ \hfill & ={\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\parallel y_n{-p\parallel }^2+{\theta }_n{\parallel u_n-p\parallel }^2\hfill \\ \hfill & -{\mu }_n{\phi }_n\parallel u-y_n{\parallel }^2-{\mu }_n{\theta }_n\parallel u-u_n{\parallel }^2-{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\parallel y_n{-p\parallel }^2+{\theta }_n\parallel u_n{-p\parallel }^2-{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n[(1-{\alpha }_n{\sigma }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{\sigma }_n\parallel S{x}_n-p{\parallel }^2]\hfill \\ \hfill & +{\theta }_n\parallel x_n{-p\parallel }^2-{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2\hfill \\ \hfill & ={\mu }_n{\parallel u-p\parallel }^2+{\phi }_n\parallel x_n{-p\parallel }^2-{\phi }_n{\alpha }_n{\sigma }_n{\parallel x_n-p\parallel }^2\hfill \\ \hfill & +{\phi }_n{\alpha }_n{\sigma }_n\parallel S{x}_n{-p\parallel }^2+{\theta }_n\parallel x_n{-p\parallel }^2-{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+(1-{\mu }_n)\parallel x_n{-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_n{\parallel S{x}_n-p\parallel }^2\hfill \\ \hfill & -{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+\parallel x_n{-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_{n}K-{\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2,\hfill \end{array}$$

where $K={sup}_n\{\parallel S{x}_n-p{\parallel }^2\}$. It follow that

$$\begin{array}{cc}\hfill {\phi }_n{\theta }_n{\parallel y_n-u_n\parallel }^2& \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_{n}K+\parallel x_n{-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_{n}K+\parallel x_n-x_{n+1}\parallel (\parallel x_n-p\parallel +\parallel x_{n+1}-p\parallel )\hfill \\ \hfill & \le {\mu }_n{\parallel u-p\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_{n}K+\parallel x_n-x_{n+1}\parallel L_1,\hfill \end{array}$$

where $L_1={sup}_n\{\parallel x_n-p\parallel +\parallel x_{n+1}-p\parallel \}$. From Equation (27), conditions (i), (ii) and (v), we have

$$\underset{n\to \infty }{lim}\parallel y_n-u_n\parallel =0.$$

(29)

From Equations (28) and (29), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-u_n\parallel & =\parallel {\mu }_n(u-u_n)+{\phi }_n(y_n-u_n)\parallel \hfill \\ \hfill & \le {\mu }_n\parallel u-u_n\parallel +{\phi }_n\parallel y_n-u_n\parallel .\hfill \end{array}$$

From Equation (29) and a condition (i), we have

$$\underset{n\to \infty }{lim}\parallel x_{n+1}-u_n\parallel =0.$$

(30)

Since

$$\begin{array}{cc}\hfill \parallel x_n-u_n& =\parallel x_n-x_{n+1}+x_{n+1}-u_n\parallel \hfill \\ \hfill & \le \parallel x_n-x_{n-1}\parallel +\parallel x_{n+1}-u_n\parallel .\hfill \end{array}$$

From Equations (28) and (30), we have

$$\underset{n\to \infty }{lim}\parallel x_n-u_n\parallel =0.$$

(31)

Since

$$\begin{array}{cc}\hfill \parallel x_n-y_n& =\parallel x_n-u_n+u_n-y_n\parallel \hfill \\ \hfill & \le \parallel x_n-u_n\parallel +\parallel u_n-y_n\parallel .\hfill \end{array}$$

From Equations (29) and (31), we have

$$\underset{n\to \infty }{lim}\parallel x_n-y_n\parallel =0.$$

(32)

Step3. ${lim}_{n\to \infty }\parallel x_n-T{x}_n\parallel =0$.

We have

$$\parallel x_n-T{x}_n\parallel \le \parallel x_n-y_n\parallel +\parallel y_n-T{x}_n\parallel .$$

(33)

Since $\left\{x_n\right\}$ is bounded and the mappings $S,T$ are nonexpansive then there exists a $K_1>0$ such that $\parallel S{x}_n-T{x}_n\parallel \le K_1$, for all $n\ge 0$. Now, we estimate

$$\begin{array}{cc}\hfill \parallel y_n-T{x}_n\parallel & =\parallel (1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n)-T{x}_n\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_n)(x_n-T{x}_n)+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n-T{x}_n)\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_n)(x_n-T{x}_n)+{\alpha }_n({\sigma }_{n}S{x}_n-{\sigma }_{n}T{x}_n)\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-T{x}_n\parallel +{\alpha }_n{\sigma }_n\parallel S{x}_n-T{x}_n\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\left[\parallel x_n-y_n\parallel +\parallel y_n-T{x}_n\parallel \right]+{\alpha }_n{\sigma }_n\parallel S{x}_n-T{x}_n\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-u_n\parallel +(1-{\alpha }_n)\parallel y_n-T{x}_n\parallel +{\alpha }_n{\sigma }_n\parallel S{x}_n-T{x}_n\parallel ,\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill {\alpha }_n\parallel y_n-T{x}_n\parallel & \le (1-{\alpha }_n)\parallel x_n-y_n\parallel +{\alpha }_n{\sigma }_n\parallel S{x}_n-T{x}_n\parallel \hfill \\ \hfill & \le \parallel x_n-y_n\parallel +{\alpha }_n{\sigma }_n{K}_1.\hfill \end{array}$$

It follow that

$$\parallel y_n-T{x}_n\parallel \le \frac{\parallel x_n-y_n\parallel }{{\alpha }_n}+{\sigma }_n{K}_1.$$

(34)

Since ${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$, we have ${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n}={lim}_{n\to \infty }{\sigma }_n·\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$.

From ${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n}=0$, Equation (34) and a condition (v), we have

$$\underset{n\to \infty }{lim}\parallel y_n-T{x}_n\parallel =0.$$

(35)

Thus, it follows from Equations (32), (33) and (35), we have

$$\underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.$$

(36)

Step4. $x^{\ast }\in \mathbb{F}$

Since $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_k}\right\}$ which converges weakly to $x^{\ast }$. We may assume that

$$\underset{n\to \infty }{lim\; inf}⟨-x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩=\underset{k\to \infty }{lim}⟨-x_{n_k},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩,$$

and

$$\underset{n\to \infty }{lim\; inf}⟨S{x}_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩=\underset{k\to \infty }{lim}⟨S{x}_{n_k},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩.$$

We will show that $x^{\ast }\in Fix(T)$. Assume that $x^{\ast }\notin Fix(T)$, then $x^{\ast }\ne T{x}^{\ast }$ and using Opial’s property of Hilbert space and Equation (35), we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-x^{\ast }\parallel & <\underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-T{x}^{\ast }\parallel \hfill \\ \hfill & \le \underset{k\to \infty }{lim\; inf}\left(\parallel x_{n_k}-T{x}_{n_k}\parallel +\parallel T{x}_{n_k}-T{x}^{\ast }\parallel \right)\hfill \\ \hfill & \le \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-x^{\ast }\parallel ,\hfill \end{array}$$

which is a contradiction. Therefore, $x^{\ast }\in Fix(T)$.

Next, we show that $x^{\ast }\in \mathsf{\Phi }$. Consider

$$\begin{array}{cc}\hfill y_n-x_n& =(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n)-x_n\hfill \\ \hfill & ={\alpha }_n{\sigma }_n(S{x}_n-x_n)+{\alpha }_n(1-{\sigma }_n)(T{x}_n-x_n),\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill S{x}_n-x_n& =\frac{y_n-x_n}{{\alpha }_n{\sigma }_n}-\frac{{\alpha }_n(1-{\sigma }_n)(T{x}_n-x_n)}{{\alpha }_n{\sigma }_n}\hfill \\ \hfill & =\frac{y_n-x_n}{{\alpha }_n{\sigma }_n}+\frac{(1-{\sigma }_n)(I-T)x_n}{{\sigma }_n}.\hfill \end{array}$$

It follows that

$$S{x}_n-x_n-\frac{y_n-x_n}{{\alpha }_n{\sigma }_n}=\frac{(1-{\sigma }_n)(I-T)x_n}{{\sigma }_n}.$$

Since T is nonexpansive, we have $I-T$ is monotone. Let $x\in Fix(T)$, we have

$$\begin{array}{cc}\hfill ⟨S{x}_n-x_n& -\frac{y_n-x_n}{{\alpha }_n{\sigma }_n},x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & =\frac{(1-{\sigma }_n)}{{\sigma }_n}⟨(I-T)x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & =\frac{(1-{\sigma }_n)}{{\sigma }_n}⟨(I-T)x_n-(I-T)(x-\frac{y_n-x_n}{{\alpha }_n})+(I-T)(x-\frac{y_n-x_n}{{\alpha }_n}),\hfill \\ \hfill & x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & =\frac{(1-{\sigma }_n)}{{\sigma }_n}[⟨(I-T)x_n-(I-T)(x-\frac{y_n-x_n}{{\alpha }_n}),x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & +⟨(I-T)(x-\frac{y_n-x_n}{{\alpha }_n}),x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩]\hfill \\ \hfill & \le \frac{(1-{\sigma }_n)}{{\sigma }_n}⟨(I-T)(x-\frac{y_n-x_n}{{\alpha }_n}),x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & \le \frac{(1-{\sigma }_n)}{{\sigma }_n}\parallel (I-T)(x-\frac{y_n-x_n}{{\alpha }_n})\parallel \parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel \hfill \\ \hfill & =\frac{(1-{\sigma }_n)}{{\sigma }_n}\parallel (I-T)(x-\frac{y_n-x_n}{{\alpha }_n})-(I-T)x\parallel \parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel \hfill \\ \hfill & \le 2(1-{\sigma }_n)\frac{\parallel y_n-x_n\parallel }{{\alpha }_n{\sigma }_n}\parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel ,\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill ⟨S{x}_n-x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩& \le 2(1-{\sigma }_n)\frac{\parallel y_n-x_n\parallel }{{\alpha }_n{\sigma }_n}\parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel \hfill \\ \hfill & +⟨\frac{y_n-x_n}{{\alpha }_n{\sigma }_n},x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & \le 3\frac{\parallel y_n-x_n\parallel }{{\alpha }_n{\sigma }_n}\parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel .\hfill \end{array}$$

(37)

Since ${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n}=0$, we have

$$\underset{k\to \infty }{lim}⟨\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩=0.$$

(38)

From Equation (38) and $\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}+x_{n_k}\rightharpoonup x^{\ast }$, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; inf}⟨& -x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & =\underset{k\to \infty }{lim}⟨-x_{n_k},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩\hfill \\ \hfill & =\underset{k\to \infty }{lim}⟨-x_{n_k}-(x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}})+(x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}),x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩\hfill \\ \hfill & =\underset{k\to \infty }{lim}[⟨x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩\hfill \\ \hfill & -⟨x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩]\hfill \\ \hfill & =\underset{k\to \infty }{lim}[⟨x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩-⟨x,x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩\hfill \\ \hfill & +⟨\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}},x-\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩]\hfill \\ \hfill & =\parallel x-x^{\ast }{\parallel }^2-⟨x,x-x^{\ast }⟩.\hfill \end{array}$$

(39)

Since S is weakly continuous and $\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}+x_{n_k}\rightharpoonup x^{\ast }$, we obtain

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; inf}⟨S{x}_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩=\underset{k\to \infty }{lim}⟨S{x}_{n_k},x& -\frac{y_{n_k}-x_{n_k}}{{\alpha }_{n_k}}-x_{n_k}⟩=⟨S{x}^{\ast },x-x^{\ast }⟩.\hfill \end{array}$$

(40)

From Equations (37), (39) and (40), we have

$$\begin{array}{cc}\hfill ⟨S{x}^{\ast }-x^{\ast },x-x^{\ast }⟩& =⟨S{x}^{\ast },x-x^{\ast }⟩-⟨x^{\ast },x-x^{\ast }⟩\hfill \\ \hfill & =⟨S{x}^{\ast },x-x^{\ast }⟩+{\parallel x-x^{\ast }\parallel }^2-⟨x,x-x^{\ast }⟩\hfill \\ \hfill & =\underset{n\to \infty }{lim\; inf}\left[⟨S{x}_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩-⟨x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\right]\hfill \\ \hfill & =\underset{n\to \infty }{lim\; inf}⟨S{x}_n-x_n,x-\frac{y_n-x_n}{{\alpha }_n}-x_n⟩\hfill \\ \hfill & \le \underset{n\to \infty }{lim\; inf}3\frac{\parallel y_n-x_n\parallel }{{\alpha }_n{\sigma }_n}\parallel x-\frac{y_n-x_n}{{\alpha }_n}-x_n\parallel \hfill \\ \hfill & \le 0.\hfill \end{array}$$

Hence $x^{\ast }$ solve Hierarchical fixed point problem, i.e., $x^{\ast }\in \mathsf{\Phi }$.

Next, we show that $x^{\ast }\in \mathsf{\Omega }$. Assume that $x^{\ast }\ne J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast })$. Applying the Opial’s property, Equation (31) and Lemma 7, we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; inf}& \parallel x_{n_k}-x^{\ast }\parallel \hfill \\ \hfill & <\underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }\parallel \hfill \\ \hfill & =\underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_{n_k}-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n_k}\hfill \\ \hfill & +J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_{n_k}-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n_k}\hfill \\ \hfill & -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }\parallel \hfill \\ \hfill & \le \underset{k\to \infty }{lim\; inf}[\parallel x_{n_k}-J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_{n_k}-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n_k}\parallel \hfill \\ \hfill & +\parallel J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_{n_k}-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n_k}\hfill \\ \hfill & -J_{{\lambda }_A}^{M_A}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }\parallel ]\hfill \\ \hfill & \le \underset{k\to \infty }{lim\; inf}[\parallel x_{n_k}-u_{n_k}\parallel +\parallel x_{n_k}-x^{\ast }\parallel \hfill \\ \hfill & -\gamma (1-\gamma L)\parallel (I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_{n_k}-(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}^{\ast }\parallel ]\hfill \\ \hfill & \le \underset{k\to \infty }{lim\; inf}\left[\parallel x_{n_k}-u_{n_k}\parallel +\parallel x_{n_k}-x^{\ast }\parallel \right]\hfill \\ \hfill & =\underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-x^{\ast }\parallel .\hfill \end{array}$$

This is a contradiction. Then $x^{\ast }=J_{{\lambda }_A}^{M_A}(I-{\lambda }_A{\sum }_{i=1}^N{a}_i{A}_i)(x^{\ast }-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_B{\sum }_{i=1}^N{b}_i{B}_i))A{x}^{\ast }$. From Lemma 8, we have $x^{\ast }\in \mathsf{\Omega }$. Therefore, $x^{\ast }\in \mathbb{F}$.

Step5. Finally, we will prove that $\left\{x_n\right\}$ converges strongly to $z_0=P_{\mathbb{F}}u$.

We show that ${lim\; sup}_{n\to \infty }⟨u-z_0,x_n-z_0⟩\le 0$, where $z_0=P_{\mathbb{F}}u$. We may assume the subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ with

$$\underset{n\to \infty }{lim\; sup}⟨u-z_0,x_n-z_0⟩=\underset{k\to \infty }{lim}⟨u-z_0,x_{n_k}-z_0⟩.$$

(41)

Since $x_{n_k}\rightharpoonup x^{\ast }$ as $k\to \infty$ and $x^{\ast }\in \mathbb{F}$. By Equations (13) and (41), we have

$$\underset{n\to \infty }{lim\; sup}⟨u-z_0,x_n-z_0⟩=\underset{k\to \infty }{lim}⟨u-z_0,x_{n_k}-z_0⟩\le 0$$

(42)

From Equations (21) and (22), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-z_0{\parallel }^2& =\parallel {\mu }_{n}u+{\phi }_n{y}_n+\theta u_n-z_0{\parallel }^2\hfill \\ \hfill & =\parallel {\mu }_n(u-z_0)+{\phi }_n(y_n-z_0)+\theta (u_n-z_0){\parallel }^2\hfill \\ \hfill & \le \parallel {\phi }_n(y_n-z_0)+\theta (u_n-z_0){\parallel }^2+2⟨{\mu }_n(u-z_0),x_{n+1}-z_0⟩\hfill \\ \hfill & \le {\phi }_n\parallel y_n-z_0{\parallel }^2+\theta {\parallel u_n-z_0\parallel }^2+2{\mu }_n⟨u-z_0,x_{n+1}-z_0⟩\hfill \\ \hfill & \le {\phi }_n[(1-{\alpha }_n{\sigma }_n)\parallel x_n-z_0{\parallel }^2+{\alpha }_n{\sigma }_n\parallel S{x}_n-z_0{\parallel }^2]\hfill \\ \hfill & +\theta \parallel x_n-z_0{\parallel }^2+2{\mu }_n⟨u-z_0,x_{n+1}-z_0⟩\hfill \\ \hfill & \le {\phi }_n\parallel x_n-z_0{\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_n{\parallel S{x}_n-z_0\parallel }^2\hfill \\ \hfill & +\theta \parallel x_n-z_0{\parallel }^2+2{\mu }_n⟨u-z_0,x_{n+1}-z_0⟩\hfill \\ \hfill & \le (1-{\mu }_n)\parallel x_n-z_0{\parallel }^2+{\phi }_n{\alpha }_n{\sigma }_n{\parallel S{x}_n-z_0\parallel }^2\hfill \\ \hfill & +2{\mu }_n⟨u-z_0,x_{n+1}-z_0⟩.\hfill \end{array}$$

Applying Lemma 1(ii), conditions (i), (iv) and Equation (42), we can conclude that the $\left\{x_n\right\}$ converges strongly to $z_0=P_{\mathbb{F}}u$. This completes the proof. □

Next, we have the following strong convergence to approximation a common element of solution the set of SMVI and hierarchical fixed point problem of nonexpansive mapping.

Corollary 1.

Let $H_1,H_2$ be real Hilbert spaces. Let $M_A:H_1\to 2^{H_1}$ be a multi-valued maximal monotone mapping and $M_B:H_2\to 2^{H_2}$ be a multi-valued maximal monotone mapping. Let $F:H_1\to H_2$ be a bounded linear operator with its adjoint operator $F^{\ast }$. Let $A:H_1\to H_1$ be α-inverse strongly monotone and $B:H_2\to H_2$ be β-inverse strongly monotone. Let $S,T:H_1\to H_1$ be two nonexpansive mappings. Assume that $\mathbb{F}=\mathsf{\Phi }\cap \Theta \ne \varnothing$. Let the sequence $\left\{x_n\right\}$ generated by $u,x_1\in H_1$ and

$$\left\{\begin{array}{l}{u}_n=J_{{\lambda }_A}^{M_A}(I-{\lambda }_{A}A)(x_n-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-{\lambda }_{B}B))F{x}_n),\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n),\hfill \\ x_{n+1}={\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n,\hfill \end{array}\right.$$

(43)

where $\left\{{\mu }_n\right\},\left\{{\phi }_n\right\},\left\{{\theta }_n\right\},\left\{{\alpha }_n\right\},\left\{{\sigma }_n\right\}\subseteq [0,1]$ with ${\mu }_n+{\phi }_n+{\theta }_n=1$ for all $n\ge 1$, ${\lambda }_A\in (0,2\alpha )$, ${\lambda }_B\in (0,2\beta )$ and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $F^{\ast }F$. Suppose the following conditions hold:

(i) 

${lim}_{n\to \infty }{\mu }_n=0$, ${\sum }_{n=1}^{\infty }{\mu }_n=\infty$,

(ii) 

$0<c\le {\phi }_n,{\theta }_n\le d<1$, $\exists c,d>0$,

(iii) 

${\sum }_{n=1}^{\infty }|{\mu }_{n+1}-{\mu }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\phi }_{n+1}-{\phi }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\theta }_{n+1}-{\theta }_n|<\infty$

(iv) 

${lim}_{n\to \infty }{\sigma }_n=0$, ${\sum }_{n=1}^{\infty }{\sigma }_n<\infty$,

(v) 

${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$,

Then $\left\{x_n\right\}$ converges strongly to $z_0\in \mathbb{F}$, where $z_0=P_{\mathbb{F}}u$.

Proof. 

Put $A_i\equiv A$ and $B_i\equiv B$ for all $i=1,2,\dots ,N$ in Theorem 1. From Theorem 1, we obtain the desired result. □

4. Application

4.1. Split Zero Point Problem

Let H be a real HIlbert space. Let $M:H\to 2^H$ be a maximal monotone operator. Then the zero point problem is to find $x^{\ast }\in H$ such that

$$0\in M{x}^{\ast },$$

(44)

such an $x^{\ast }\in H$ is called a zero point of M. The set of zero point of M is denoted by $M^{-1}(0)$.

Let $H_1$ and $H_2$ be two real Hilbert spaces. Setting $A_i\equiv 0$ and $B_i\equiv 0$ for all $i=1,2,..,N$ in SCVIP, then SCVIP reduce to the split zero point problem: Find $x^{\ast }\in H_1$ such that

$$0\in M_A{x}^{\ast },$$

(45)

and

$$y^{\ast }\in A{x}^{\ast }\mathrm{such}\mathrm{that}0\in M_B{y}^{\ast },$$

(46)

where $A:H_1\to H_2$ is bounded linear operator, $M_A:H_1\to 2^{H_1}$ and $M_B:H_2\to 2^{H_2}$ are multi-valued mapping. The set of all solution of this problem is denoted by ${\mathsf{\Omega }}_2=\{x\in M_A^{-1}(0):Ax\in M_B^{-1}(0)\}$.

The split zero point problem which consists of the special cases, split feasibility problem, variational inequalities, etc., which is used in practice as a model in machine learning, image processing and linear inverse problem.

Next, we give the strong convergence theorem for solving the split zero point problem and the hierarchical fixed point problem of nonexpansive mapping.

Corollary 2.

Let $H_1,H_2$ be real Hilbert spaces. Let $M_A:H_1\to 2^{H_1}$ be a multi-valued maximal monotone mapping and $M_B:H_2\to 2^{H_2}$ be a multi-valued maximal monotone mapping. Let $A:H_1\to H_2$ be a bounded linear operator with its adjoint operator $A^{\ast }$. Let $S,T:H_1\to H_1$ be two nonexpansive mappings. Assume that $\mathbb{F}=\mathsf{\Phi }\cap {\mathsf{\Omega }}_2\ne \varnothing$. Let the iterative sequence generated by hybrid iterative algorithm:

$$\left\{\begin{array}{l}{u}_n=J_{{\lambda }_A}^{M_A}(x_n-\gamma A^{\ast }{J}_{{\lambda }_B}^{M_B}A{x}_n),\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n),\hfill \\ x_{n+1}={\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n,\hfill \end{array}\right.$$

(47)

where $\left\{{\delta }_n\right\},\left\{{\phi }_n\right\},\left\{{\eta }_n\right\},\left\{{\alpha }_n\right\},\left\{{\sigma }_n\right\}\subseteq [0,1]$ with ${\delta }_n+{\phi }_n+{\eta }_n=1$ for all $n\ge 1$, and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $A^{\ast }A$. Suppose the following conditions hold:

(i) 

${lim}_{n\to \infty }{\mu }_n=0$, ${\sum }_{n=1}^{\infty }{\mu }_n=\infty$,

(ii) 

$0<c\le {\phi }_n,{\theta }_n\le d<1$, $\exists c,d>0$,

(iii) 

${\sum }_{n=1}^{\infty }|{\mu }_{n+1}-{\mu }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\phi }_{n+1}-{\phi }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\theta }_{n+1}-{\theta }_n|<\infty$

(iv) 

${lim}_{n\to \infty }{\sigma }_n=0$, ${\sum }_{n=1}^{\infty }{\sigma }_n<\infty$,

(v) 

${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$,

Then $\left\{x_n\right\}$ converges strongly to $z\in \mathbb{F}$, where $z=P_{\mathbb{F}}u$.

Proof. 

Put $A_i\equiv 0$ and $B_i\equiv 0$ for all $i=1,2,\dots ,N$ in Theorem 1. From Theorem 1, we obtain the desired conclusion. □

4.2. Split Combination of Variational Inequalities Problem

Let H be a real Hilbert space, let C be a nonempty closed convex subset of H and let h be a proper lower semicontinuous convex function of H into $(-\infty ,+\infty ]$. The subdifferential $\partial h$ of h is defined by

$$\partial h(x)=\{z\in H:h(x)+⟨z,u-x⟩\le h(u),\forall u\in H\},$$

for all $x\in H$. From Rockafellar [16], we get that $\partial h$ is a maximal monotone operator. Let $i_C$ be the indicator function of C, i.e.,

$$i_C=\left\{\begin{array}{l}0;ifx\in C,\hfill \\ +\infty ;ifx\notin C.\hfill \end{array}\right.$$

Then $i_C$ is a proper, lower semicontinuous and convex function on H and so the subdifferential $\partial i_C$ of $i_C$ is a maximal monotone operator. The resolvent operator $J_r^{\partial i_C}$ of $\partial i_C$ for $\lambda >0$ defined by $J_r^{\partial i_C}(x)={(I+\lambda \partial i_C)}^{-1}(x)$, $x\in H$, then we have $J_r^{\partial i_C}(x)=P_{C}x$ for all $x\in H$ and $\lambda >0$; see more detail [18]. Moreover, let $h:H\to H$ be a single valued operator, we have $x\in VI(H,h,\partial i_C)=VI(C,h)$.

Setting $M_A=\partial i_{H_1}$ and $M_B=\partial i_{H_2}$ in Equations (6) and (7), then SCVIP reduce to the split combination of variational inequality problem, that is find $x^{\ast }\in H_1$ such that

$$⟨\sum _{i=1}^N{a}_i{A}_i{x}^{\ast },x-x^{\ast }⟩\ge 0,\forall x\in H_1,$$

(48)

and

$$y^{\ast }=A{x}^{\ast }\in H_2\mathrm{such}\mathrm{that}⟨\sum _{i=1}^N{b}_i{B}_i{y}^{\ast },y-y^{\ast }⟩\ge 0,\forall y\in H_2,$$

(49)

where $A:H_1\to H_2$ is bounded linear operator and ${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$. The set of all this is denoted by ${\mathsf{\Omega }}_3=\{x\in VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i):Ax\in VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i)\}$.

Remark 3.

If $M_A=\partial i_{H_1}$ and $M_B=\partial i_{H_2}$, then we have Ω reduce to ${\mathsf{\Omega }}_3$.

Proof. 

We will show that $VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i,M_A)=VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i)$. We have for $x^{\ast }\in H_1$.

Consider,

$$\begin{array}{cc}\hfill x^{\ast }\in VI(H_1,\sum _{i=1}^N{a}_i{A}_i,M_A)& \iff {\theta }_{H_1}\in \sum _{i=1}^N{a}_i{A}_i{x}^{\ast }+M_A{x}^{\ast }\hfill \\ \hfill & \iff {\theta }_{H_1}\in \sum _{i=1}^N{a}_i{A}_i{x}^{\ast }+\partial i_{H_1}(x^{\ast })\hfill \\ \hfill & \iff -\sum _{i=1}^N{a}_i{A}_i{x}^{\ast }\in \partial i_{H_1}(x^{\ast })\hfill \\ \hfill & \iff ⟨\sum _{i=1}^N{a}_i{A}_i{x}^{\ast },x-x^{\ast }⟩\ge 0,\forall x\in H_1,\hfill \\ \hfill & \iff x^{\ast }\in VI(H_1,\sum _{i=1}^N{a}_i{A}_i).\hfill \end{array}$$

Similarly, we also have $VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i,M_B)=VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i)$. Then $\mathsf{\Omega }\equiv {\mathsf{\Omega }}_3$ where $M_A=\partial i_{H_1}$ and $M_B=\partial i_{H_2}$. □

The split combination of variational inequality problem has played an essential role for concrete problems in dynamic emission tomographic image reconstruction, signal recovery problems, beam-forming problems, power-control problems, bandwidth allocation problems and optimal control problems.

Next, we establish a strong convergence theorem for solving the split combination of variational inequality problem and hierarchical fixed point problem of nonexpansive mapping by using a modified Halpern iterative method as follows:

Theorem 2.

Let $H_1,H_2$ be real Hilbert spaces. Let $A:H_1\to H_2$ be a bounded linear operator with its adjoint operator $A^{\ast }$. Let $A_i:H_1\to H_1$ be ${\alpha }_i$-inverse strongly monotone with ${\eta }_A={min}_{i=1}\left\{{\alpha }_i\right\}$ and $B_i:H_2\to H_2$ be ${\beta }_i$-inverse strongly monotone with ${\eta }_B={min}_{i=1}\left\{{\beta }_i\right\}$. Let $S,T:H_1\to H_1$ be two nonexpansive mappings. Assume that $\mathbb{F}=\mathsf{\Phi }\cap {\mathsf{\Omega }}_3\ne \varnothing$. Let the sequence $\left\{x_n\right\}$ generated by $u,x_1\in H_1$ and

$$\left\{\begin{array}{l}{u}_n=P_{H_1}(I-{\lambda }_A\sum _{i=1}^N{a}_i{A}_i)(x_n-\gamma A^{\ast }(I-P_{H_2}(I-{\lambda }_B\sum _{i=1}^N{b}_i{B}_i))A{x}_n),\hfill \\ y_n=(1-{\alpha }_n)x_n+{\alpha }_n({\sigma }_{n}S{x}_n+(1-{\sigma }_n)T{x}_n),\hfill \\ x_{n+1}={\mu }_{n}u+{\phi }_n{y}_n+{\theta }_n{u}_n,\hfill \end{array}\right.$$

(50)

where $\left\{{\mu }_n\right\},\left\{{\phi }_n\right\},\left\{{\theta }_n\right\},\left\{{\alpha }_n\right\},\left\{{\sigma }_n\right\}\subseteq [0,1]$ with ${\mu }_n+{\phi }_n+{\theta }_n=1$ for all $n\ge 1$, ${\lambda }_A\in (0,2{\eta }_A)$, ${\lambda }_B\in (0,2{\eta }_B)$ and $\gamma \in (0,\frac{1}{L})$ with L is the spectral radius of $A^{\ast }A$. Suppose the following conditions hold:

(i) 

${lim}_{n\to \infty }{\mu }_n=0$, ${\sum }_{n=1}^{\infty }{\mu }_n=\infty$,

(ii) 

$0<c\le {\phi }_n,{\theta }_n\le d<1$, $\exists c,d>0$,

(iii) 

${\sum }_{n=1}^{\infty }|{\mu }_{n+1}-{\mu }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\phi }_{n+1}-{\phi }_n|<\infty$, ${\sum }_{n=1}^{\infty }|{\theta }_{n+1}-{\theta }_n|<\infty$

(iv) 

${lim}_{n\to \infty }{\sigma }_n=0$, ${\sum }_{n=1}^{\infty }{\sigma }_n<\infty$,

(v) 

${lim}_{n\to \infty }\frac{\parallel x_n-y_n\parallel }{{\alpha }_n{\sigma }_n}=0$,

(vi) 

${\sum }_{i=1}^N{a}_i={\sum }_{i=1}^N{b}_i=1$, $a_i>0$ and $b_i>0$ for all $i=1,2,\dots ,N$.

Then $\left\{x_n\right\}$ converges strongly to $z_0\in \mathbb{F}$, where $z_0=P_{\mathbb{F}}u$.

Proof. 

Put $M_A=\partial i_{H_1}$ and $M_B=\partial i_{H_2}$ in Theorem 1. Using the same method in Theorem 1, we have the desired conclusion. □

5. Numerical

The purpose of this section is to give a numerical example to support some of our. The following example given for supporting Theorem 1 and example show that Theorem 1 is not true if condition (iv) fails, but conditions (i), (ii), (iii), (v) and (vi) are satisfied.

Since Theorem 1 can solve hierarchical fixed point problem for a nonexpansive mapping and SCVIP which our problems can modify for concrete problem in signal processing, image reconstruction, intensity-modulated radiationtherapy treatment planning and sensor networks in computerized tomography. So, we give a numerical example as follows:

Example 5.

Let $H_1=H_2=\mathbb{R}$, the set of all real numbers, with the inner product defined by $⟨x,y⟩=xy$, for all $x,y\in \mathbb{R}$ and induced usual norm $|·|$. For every $i=1,2,..,N$, let the mapping $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{x}{4i}$ for all $x\in H_1$ and $B_i:\mathbb{R}\to \mathbb{R}$ define by $B_{i}y=\frac{y}{3i}$ for all $y\in H_2$, respectively, let $M_A,M_B:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_A(x)=\left\{2x\right\}$, for all $x\in \mathbb{R}$ and $M_B(y)=\left\{2y\right\}$, for all $y\in \mathbb{R}$. Let the mapping $A:\mathbb{R}\to \mathbb{R}$ be defined by $A(x)=-2x$, for all $x\in \mathbb{R}$ and let $\gamma \in (0,\frac{1}{4})$, so we choose $\gamma =\frac{1}{10}$. Let the mapping $T:\mathbb{R}\to \mathbb{R}$ be defined by $Tx=max\{0,-x\}$, for all $x\in \mathbb{R}$ and let the mapping $S:\mathbb{R}\to \mathbb{R}$ be defined by $Sx=min\{0,\frac{x}{2}\}$, for all $x\in \mathbb{R}$. Setting $\left\{{\mu }_n\right\}$ = $\left\{\frac{1}{5n}\right\}$, $\left\{{\phi }_n\right\}$ = $\left\{\frac{7n+1}{15n}\right\}$, $\left\{{\theta }_n\right\}$ = $\left\{\frac{8n-4}{15n}\right\}$, $\left\{{\alpha }_n\right\}$ = $\left\{\frac{1}{n}\right\}$ and $\left\{{\sigma }_n\right\}$ = $\left\{\frac{1}{4n^2}\right\}$, $\forall n\in \mathbb{N}$. For every $i=1,2,\dots ,N$, suppose that $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$ and $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$. Then $\left\{x_n\right\}$ converges strongly to a point $x^{\ast }=0\in \mathbb{F}$.

Proof of Solution.

It is easy to check that $a_i$ and $b_i$ satisfies all the conditions of Theorem 1 and $A_i$ is $\frac{1}{4i}$-inverse strongly monotone and $B_i$ is $\frac{1}{3i}$-inverse strongly monotone for all $i=1,2,\dots ,N$. We choose ${\lambda }_A=\frac{1}{4N}$, ${\lambda }_B=\frac{1}{3N}$. Since $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$, we obtain

$$\sum _{i=1}^N{a}_i{A}_{i}x=\sum _{i=1}^N\left(\frac{3}{4^i}+\frac{1}{N{4}^N}\right)\frac{x}{4i}.$$

Then $0\in VI(H_1,{\sum }_{i=1}^N{a}_i{A}_i,M_A)$. Since $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$, we have

$$\sum _{i=1}^N{b}_i{B}_{i}y=\sum _{i=1}^N\left(\frac{2}{3^i}+\frac{1}{N{3}^N}\right)\frac{y}{3i}.$$

Then $0\in VI(H_2,{\sum }_{i=1}^N{b}_i{B}_i,M_B)$. Thus $\left\{0\right\}=\mathsf{\Omega }$.

It is easy to observe that $T,S$ are nonexpansive mappings with $Fix(T)=\left\{0\right\}$, $Fix(S)=\left\{0\right\}$. Hence $\mathsf{\Phi }=\left\{0\right\}$. Therefore $\mathbb{F}=\mathsf{\Phi }\cap \mathsf{\Omega }=\left\{0\right\}$.

For every $n\in \mathbb{N}$, $\left\{{\mu }_n\right\}$ = $\left\{\frac{1}{5n}\right\}$, $\left\{{\phi }_n\right\}$ = $\left\{\frac{7n+1}{15n}\right\}$, $\left\{{\theta }_n\right\}$ = $\left\{\frac{8n-4}{15n}\right\}$, $\left\{{\alpha }_n\right\}$ = $\left\{\frac{1}{n}\right\}$ and $\left\{{\sigma }_n\right\}$ = $\left\{\frac{1}{4n^2}\right\}$, then the sequence $\left\{{\mu }_n\right\}$, $\left\{{\phi }_n\right\}$, $\left\{{\theta }_n\right\}$, $\left\{{\alpha }_n\right\}$ and $\left\{{\sigma }_n\right\}$ satisfy all the conditions of Theorem 1. We rewrite (20) as follows:

$$\left\{\begin{array}{l}{u}_n=J_{{\lambda }_A}^{M_A}(I-\frac{1}{4N}\sum _{i=1}^N{a}_i{A}_i)(x_n-\gamma A^{\ast }(I-J_{{\lambda }_B}^{M_B}(I-\frac{1}{3N}\sum _{i=1}^N{b}_i{B}_i))A{x}_n),\hfill \\ y_n=(1-\frac{1}{n})x_n+\frac{1}{0}(\frac{1}{4n^2}S{x}_n+(1-\frac{1}{4n^2})T{x}_n),\hfill \\ x_{n+1}=\frac{1}{5n}u+\frac{7n+1}{15n}{y}_n+\frac{8n-4}{15n}{u}_n,\hfill \end{array}\right.$$

(51)

Choose $u=-1$, $x_1=1$, $N=100$ and $n=100$. The numerical for the sequence $\left\{x_n\right\}$ are shown Table 1 and Figure 1. □

Table 1. The values of $\left\{x_n\right\}$ with $N=100,n=100$.

n	${\mathit{x}}_{\mathit{n}}$
1	1.0000
2	−0.0767
3	−0.1178
4	−0.1125
5	−0.1027
⋮	⋮
50	−0.0139
⋮	⋮
96	−0.0073
97	−0.0072
98	−0.0071
99	−0.0070
100	−0.0070

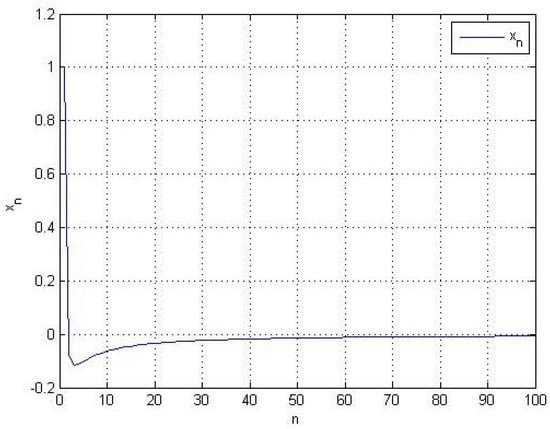
Figure 1. The sequence $\left\{x_n\right\}$ converges strongly to 0 with initial values $x_1=1$, $N=100$ and $n=100$.

Example 6.

Let $H_1=H_2=\mathbb{R}$, the set of all real numbers, with the inner product defined by $⟨x,y⟩=xy$, for all $x,y\in \mathbb{R}$ and induced usual norm $|·|$. For every $i=1,2,..,N$, let the mapping $A_i:\mathbb{R}\to \mathbb{R}$ define by $A_{i}x=\frac{x}{4i}$ for all $x\in H_1$ and $B_i:\mathbb{R}\to \mathbb{R}$ define by $B_{i}y=\frac{y}{3i}$ for all $y\in H_2$, respectively, let $M_A,M_B:\mathbb{R}\to 2^{\mathbb{R}}$ be defined by $M_A(x)=\left\{2x\right\}$, for all $x\in \mathbb{R}$ and $M_B(y)=\left\{2y\right\}$, for all $y\in \mathbb{R}$. Let the mapping $A:\mathbb{R}\to \mathbb{R}$ be defined by $A(x)=-2x$, for all $x\in \mathbb{R}$ and let $\gamma \in (0,\frac{1}{4})$, so we choose $\gamma =\frac{1}{10}$. Let the mapping $T:\mathbb{R}\to \mathbb{R}$ be defined by $Tx=max\{0,-x\}$, for all $x\in \mathbb{R}$ and let the mapping $S:\mathbb{R}\to \mathbb{R}$ be defined by $Sx=min\{0,\frac{x}{2}\}$, for all $x\in \mathbb{R}$. Setting $\left\{{\mu }_n\right\}$ = $\left\{\frac{1}{5n}\right\}$, $\left\{{\phi }_n\right\}$ = $\left\{\frac{7n+1}{15n}\right\}$, $\left\{{\theta }_n\right\}$ = $\left\{\frac{8n-4}{15n}\right\}$, $\left\{{\alpha }_n\right\}$ = $\left\{\frac{1}{n}\right\}$ and $\left\{{\sigma }_n\right\}$ = $\left\{n\right\}$, $\forall n\in \mathbb{N}$. For every $i=1,2,\dots ,N$, suppose that $a_i=\frac{3}{4^i}+\frac{1}{N{4}^N}$ and $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$. Then $\left\{x_n\right\}$ is divegence.

Proof of Solution.

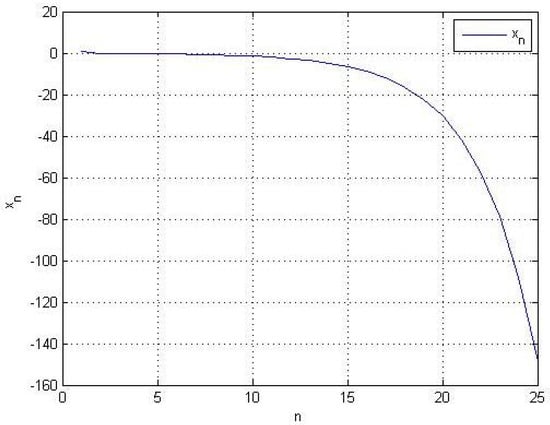
Note that the sequence $\left\{{\mu }_n\right\}$, $\left\{{\phi }_n\right\}$, $\left\{{\theta }_n\right\}$, $\left\{{\alpha }_n\right\}$, $a_i$ and $b_i$ satisfies the conditions (i), (ii), (iii), (v) and (vi) from Theorem 1, while assumption (iv) does not converge to 0 since

$$\underset{n\to \infty }{lim}n=\infty .$$

Choose $u=-1$, $x_1=1$, $N=100$ and $n=25$. The numerical for the sequence $\left\{x_n\right\}$ are shown in Table 2 and Figure 2. Therefore, $\left\{x_n\right\}$ does not converge to 0. □

Table 2. The values of $\left\{x_n\right\}$ with $N=100,n=25$.

n	${\mathit{x}}_{\mathit{n}}$
1	1.0000
2	−0.0767
3	−0.1717
4	−0.3525
5	−0.4736
⋮	⋮
17	−12.0108
⋮	⋮
21	−41.7292
22	−57.2056
23	−78.5297
24	−107.9388
25	−148.5342

Figure 2. The sequence $\left\{x_n\right\}$ is divergence with initial values $x_1=1$, $N=100$ and $n=25$.

Next, we give example to support out some result in a two dimensional space of real numbers.

Example 7.

Let $H_1=H_2={\mathbb{R}}^2$, with the inner product defined by $⟨x,y⟩=xy=x_1·y_1+x_2·y_2$, for all $x=(x_1,x_2),y=(y_1,y_2)\in {\mathbb{R}}^2$ and induced usual norm $\parallel ·\parallel$ defined by $\parallel x\parallel =\sqrt{x_1^2+x_2^2}$ for all $x=(x_1,x_2)\in {\mathbb{R}}^2$. For every $i=1,2,..,N$, let the mapping $A_i:{\mathbb{R}}^2\to {\mathbb{R}}^2$ define by $A_{i}x=\frac{x}{3i}$ for all $x=(x_1,x_2)\in H_1$ and $B_i:{\mathbb{R}}^2\to {\mathbb{R}}^2$ define by $B_{i}y=\frac{y}{4i}$ for all $y=(y_1,y_2)\in H_2$, respectively, let $M_A,M_B:{\mathbb{R}}^2\to 2^{{\mathbb{R}}^2}$ be defined by $M_A(x)=\left\{x\right\}$, for all $x=(x_1,x_2)\in {\mathbb{R}}^2$ and $M_B(y)=\left\{3y\right\}$, for all $y=(y_1,y_2)\in {\mathbb{R}}^2$. Let the mapping $A:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be defined by $A(x)=3x$, for all $x=(x_1,x_2)\in {\mathbb{R}}^2$ and let $\gamma \in (0,\frac{1}{9})$, so we choose $\gamma =\frac{1}{15}$. Let the mapping $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be defined by $Tx=\frac{x}{3}$, for all $x=(x_1,x_2)\in {\mathbb{R}}^2$ and let the mapping $S:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be defined by $Sx=min\{0,\frac{x}{5}\}$, for all $x=(x_1,x_2)\in {\mathbb{R}}^2$. Setting $\left\{{\mu }_n\right\}$ = $\left\{\frac{1}{4n}\right\}$, $\left\{{\phi }_n\right\}$ = $\left\{\frac{7n+1}{12n}\right\}$, $\left\{{\theta }_n\right\}$ = $\left\{\frac{5n-4}{12n}\right\}$, $\left\{{\alpha }_n\right\}$ = $\left\{\frac{1}{n}\right\}$ and $\left\{{\sigma }_n\right\}$ = $\left\{\frac{1}{4n^2}\right\}$, $\forall n\in \mathbb{N}$. For every $i=1,2,\dots ,N$, suppose that $a_i=\frac{9}{{10}^i}+\frac{1}{N{10}^N}$ and $b_i=\frac{2}{3^i}+\frac{1}{N{3}^N}$. Then $\left\{x_n\right\}$ converges strongly to a point $x^{\ast }=(0,0)\in \mathbb{F}$.

Proof of Solution.

It is easy to check that $a_i$ and $b_i$ satisfies all the conditions of Theorem 1 and $A_i$ is $\frac{1}{3i}$-inverse strongly monotone and $B_i$ is $\frac{1}{4i}$-inverse strongly monotone for all $i=1,2,\dots ,N$. We choose ${\lambda }_A=\frac{1}{5N}$, ${\lambda }_B=\frac{1}{7N}$. Thus $\{(0,0)\}=\mathsf{\Omega }$.

For definition of T and S, then T and S are nonexpansive mapping with $Fix(T)=\{(0,0)\}$. Hence $\mathsf{\Phi }=\{(0,0)\}$. Therefore $\mathbb{F}=\mathsf{\Phi }\cap \mathsf{\Omega }=\{(0,0)\}$.

For every $n\in \mathbb{N}$, $\left\{{\mu }_n\right\}$ = $\left\{\frac{1}{4n}\right\}$, $\left\{{\phi }_n\right\}$ = $\left\{\frac{7n+1}{12n}\right\}$, $\left\{{\theta }_n\right\}$ = $\left\{\frac{5n-4}{12n}\right\}$, $\left\{{\alpha }_n\right\}$ = $\left\{\frac{1}{n}\right\}$ and $\left\{{\sigma }_n\right\}$ = $\left\{\frac{1}{4n^2}\right\}$, then the sequence $\left\{{\mu }_n\right\}$, $\left\{{\phi }_n\right\}$, $\left\{{\theta }_n\right\}$, $\left\{{\alpha }_n\right\}$ and $\left\{{\sigma }_n\right\}$ satisfy all the conditions of Theorem 1.

From Theorem 1, we can conclude that the sequence $\left\{x_n\right\}$ converges to $(0,0)$. □

6. Conclusions

(i)

Table 1 and Figure 1 show that the sequence $\left\{x_n\right\}$ converges to 0, where $\left\{0\right\}=\mathsf{\Phi }\cap \mathsf{\Omega }$.

(ii)

Table 2 and Figure 2 show that the sequence $\left\{x_n\right\}$ diverge, where condition $(iv)$ is violated since ${lim}_{n\to \infty }{\sigma }_n\ne 0$.