Use of Enumerative Combinatorics for Proving the Applicability of an Asymptotic Stability Result on Discrete-Time SIS Epidemics in Complex Networks
Abstract
1. Introduction
2. Epidemics Spreading in Complex Networks
3. Control Problem Statement
4. Bifurcation Analysis
5. Selection of Nodes to Be Controlled
6. Simulations
- A scale-free network proposed according to the algorithm in [24], for homogeneous and non-homogeneous cases.
- A regular network for homogeneous and non-homogeneous cases.
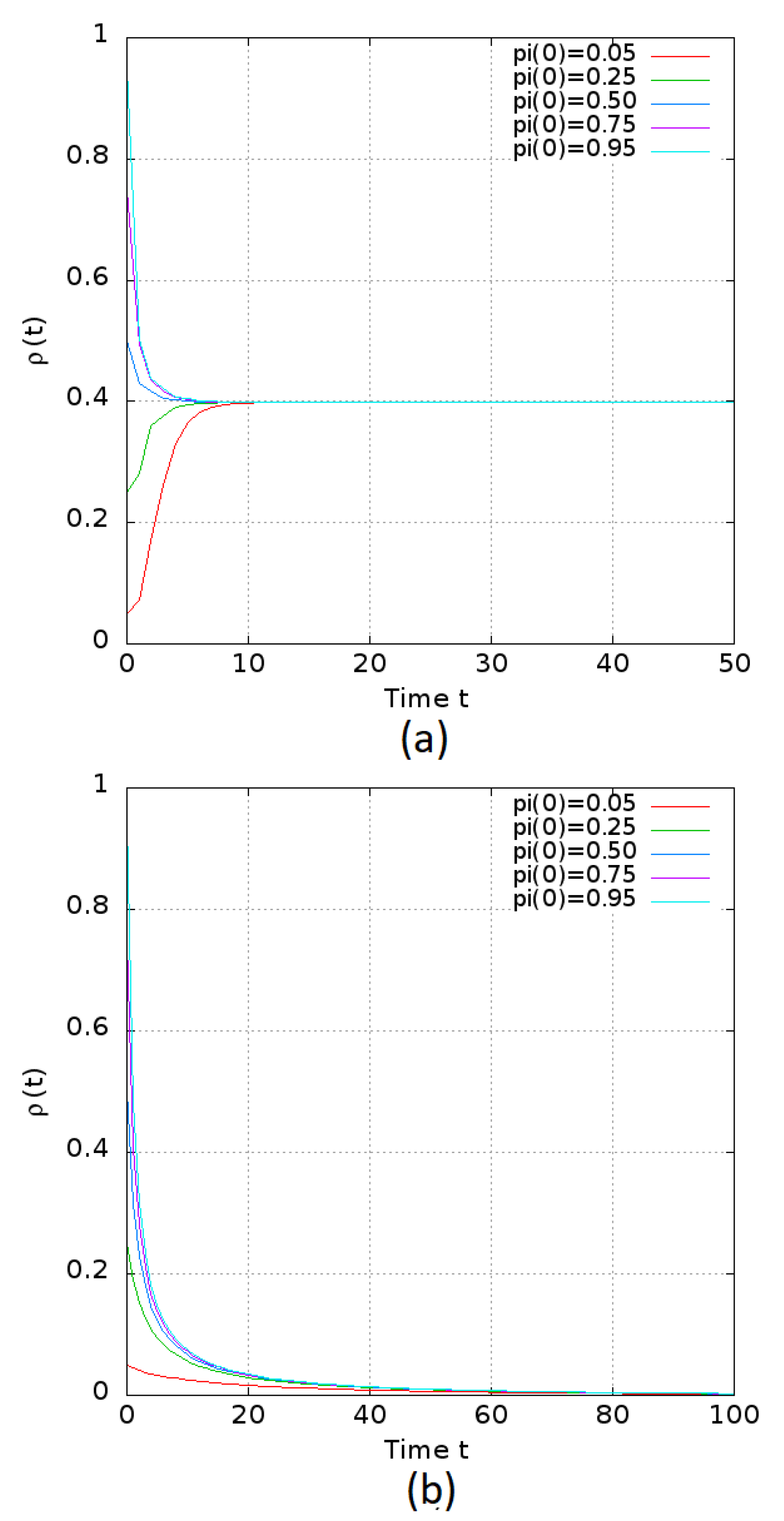
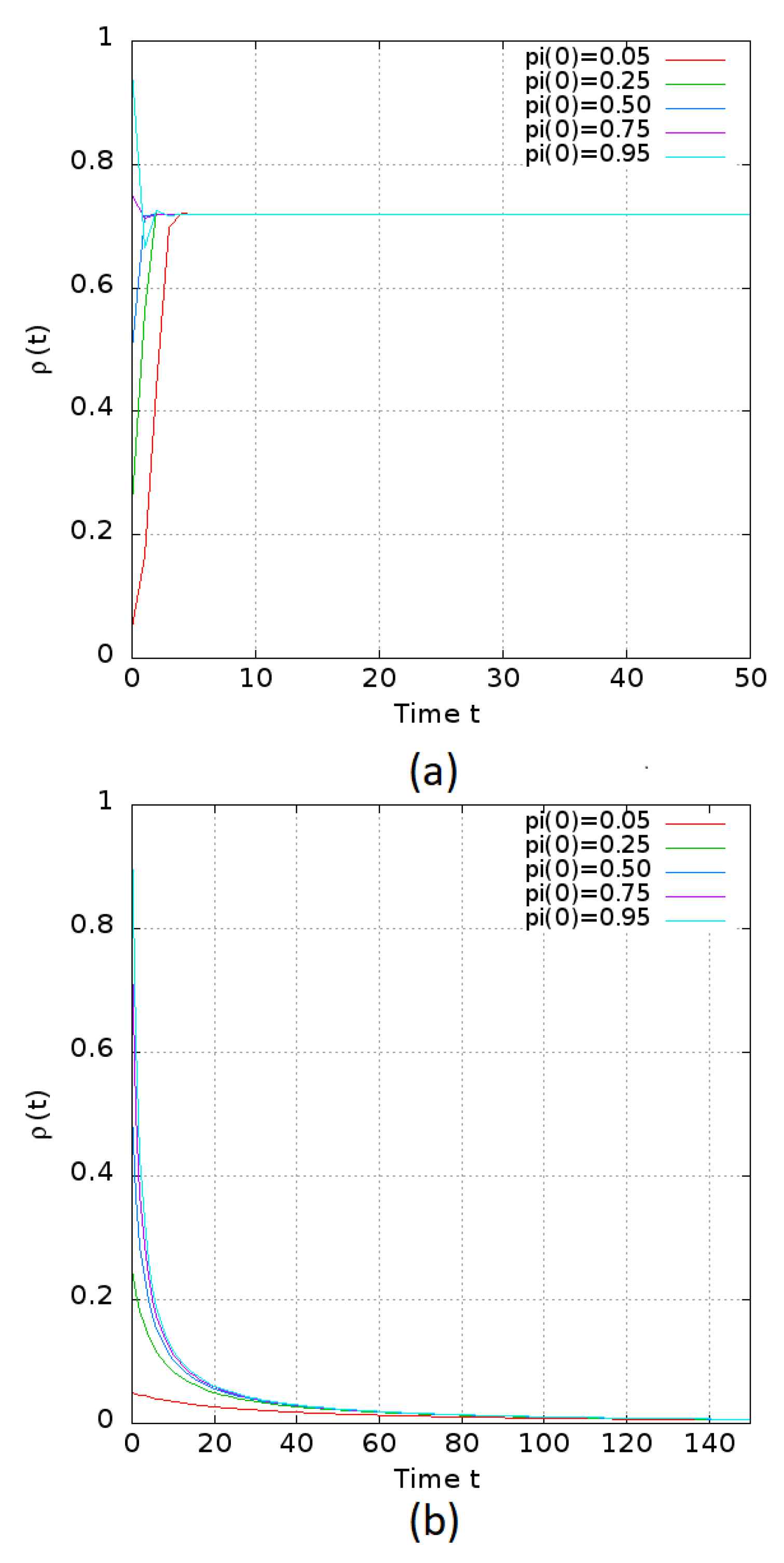
6.1. Non-Homogeneous Scale-Free Network
6.2. Homogeneous Scale-Free Network
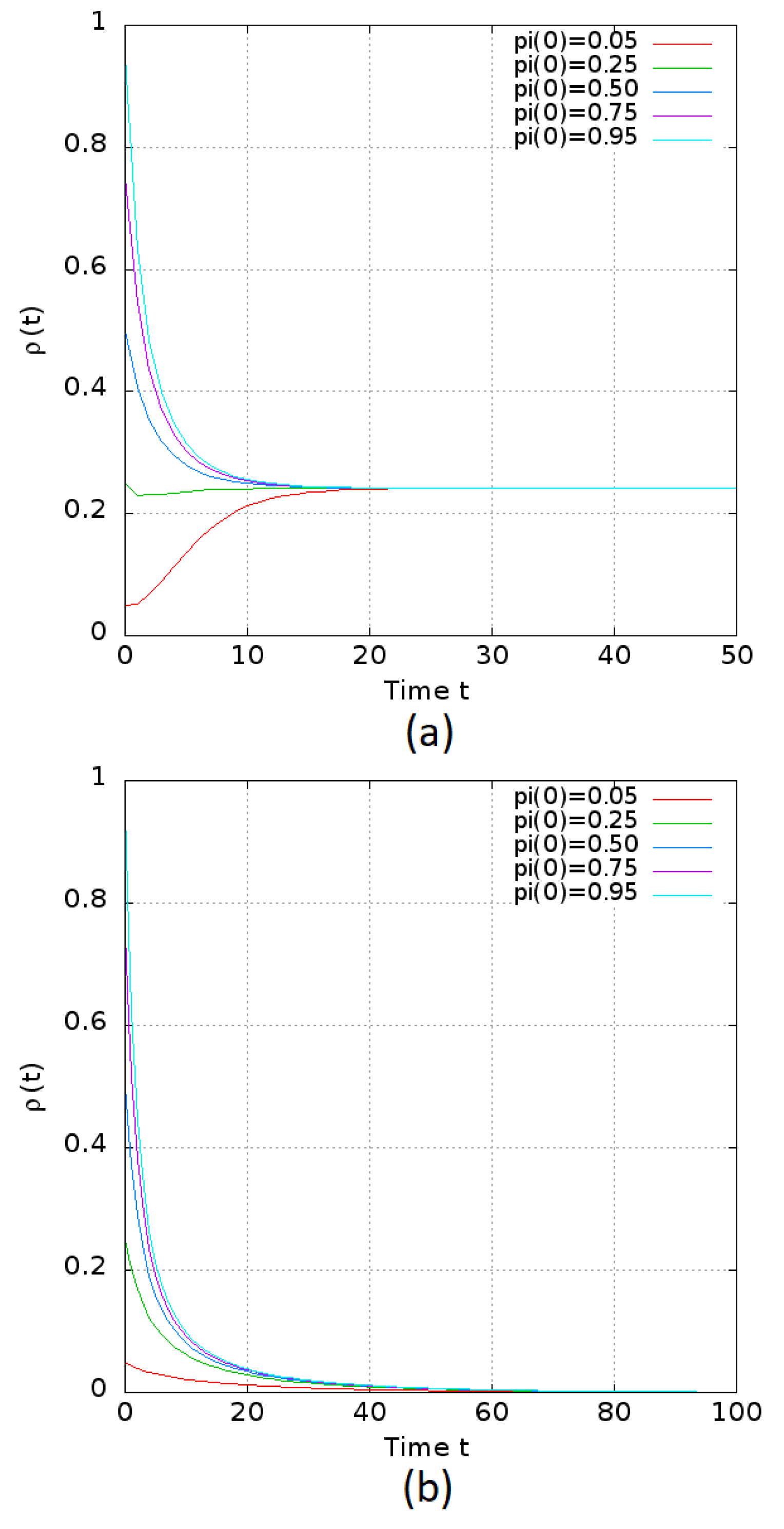
6.3. Non-Homogeneous Regular Network
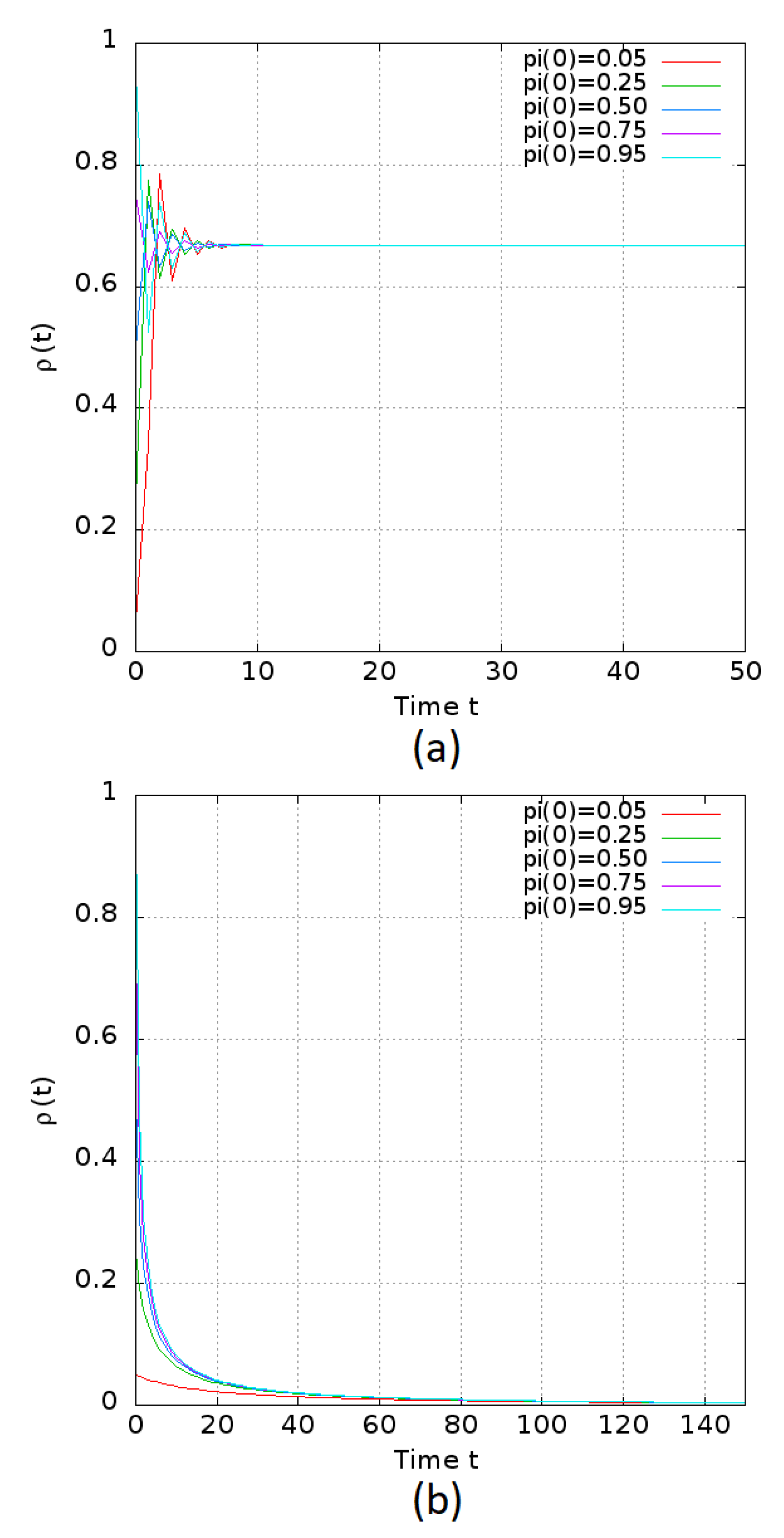
6.4. Homogeneous Regular Network
7. The Applicability of the Result
8. Enumeration and Generating Functions
- Labeled graphs problems,
- Unlabeled graphs problems.
9. Enumerating Regular Graphs
- (i)
- each row sum is specified and bounded,
- (ii)
- the entries are bounded,
- (iii)
- a specified sparse set of entries must be zero.
- (i)
- if ,
- (ii)
- .
10. Combinatorial Proof of Applicability of the Result on Control Node Selection
11. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
- (i)
- the size of an element is a nonnegative integer;
- (ii)
- the number of elements of any given size is finite.
- Sometimes it can be found an exact formula for the members of the sequence in a pleasant way. If it is not the case, when the sequence is complicated, a good approximation can be obtained.
- A recurrence formula can be obtained. Most often generating functions arise from recurrence formula. Sometimes, however, a new recurrence formula, from generating functions and new insights of the nature of the sequence can be obtained.
- Averages and other statistical properties of a sequence can be obtained.
- When the sequence is very difficult to deal with, asymptotic formulas can be obtained instead of an exact formula. For example, the n-th prime number is approximately when n is very big.
- Unimodality, convexity, etc. of a sequence can be proved.
- Some identities can be proved easily by using generating functions. For instance,
- Relationship between problems can be discovered from the stricking resemblance of the respective generating functions.
- Symbolic Methods that establish systematically relations discrete mathematics constructions and operations on generating functions that encode counting sequences.
- Complex Asymptotics that allow for extracting asymptotic counting information from the generating functions by the mapping to the complex plane mentioned above.
- Random structures concerning the probabilistic properties accomplished by large random structures.
- Labeled graphs problems,
- Unlabeled graphs problems.
| p | |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 4 |
| 4 | 38 |
| 5 | 728 |
| 6 | 26,704 |
| 7 | 1,866,256 |
| 8 | 251,548,592 |
| 9 | 66,296,291,072 |
| 10 | 34,496,488,594,816 |
| 11 | 35,641,657,548,953,344 |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 |
References
- Alarcón Ramos, L.A.; Bernal Jaquez, R.; Shaum, A. Output-Feedback Control for Discrete-Time Spreading Models in Complex Networks. Entropy 2018, 20, 204. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; 6th Printing with Corrections; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Erdös, P. Graph theory and Probability. Can. J. Math. 1959, 11, 34–38. [Google Scholar] [CrossRef]
- Alon, N.; Spencer, J.H. The Probabilistic Method, 2nd ed.; New York Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Chakrabarti, D.; Wang, Y.; Wang, C.; Leskovec, J.; Faloutsos, C. Epidemic thresholds in real networks. ACM Trans. Inf. Syst. Secur. 2008, 10, 1–26. [Google Scholar] [CrossRef]
- Galam, S. Rational Group Decision Making: A random field Ising model at T = 0. arXiv, 1997; arXiv:cond-mat/9702163v1. [Google Scholar]
- Galam, S. From 2000 Bush? Gore to 2006 Italian elections: Voting at fifty-fifty and the contrarian effect. Qual. Quant. 2007, 41, 579–589. [Google Scholar] [CrossRef]
- Galam, S. Social Paradoxes of Majority Rule Voting and Renormalization Group. J. Stat. Phys. 1990, 61, 943–951. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics: A review of Galam models. arXiv, 2008; arXiv:physics.soc-ph/0803.183v1. [Google Scholar]
- Gómez, S.; Gómez-Garde nes, J.; Moreno, Y.; Arenas, A. Non-perturbative heterogeneous mean-field approach to epidemic spreading in complex networks. Phys. Rev. E 2011, 84, 036105. [Google Scholar] [CrossRef]
- Axelrod, R. The Dissemination of Culture: A model with local convergence and global polarization. J. Confl. Resolut. 1997, 41, 203–226. [Google Scholar] [CrossRef]
- Gonzalez-Avella, J.C.; Eguiluz, V.M.; Cosenza, M.G.; Klemm, K.; Herrera, J.L.; San Miguel, M. Nonequilibrium transition induced by mass media in a model for social influence. Phys. Rev. E 2005, 72, 065102. [Google Scholar] [CrossRef]
- Gonzalez-Avella, J.C.; Cosenza, M.G.; Tucci, K. Local versus global interactions in nonequilibrium transitions: A model of social dynamics. Phys. Rev. E 2006, 73, 046119. [Google Scholar] [CrossRef]
- Klemm, K.; Eguiluz, M.; Toral, R.; San Miguel, M. Nonequilibrium transitions in complex networks: A model of social interaction. Phys. Rev. E 2003, 67, 026120. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Slotine, J.-J.; Barabási, A.-L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Nepusz, T.; Vicsek, T. Controlling edge dynamics in complex networks. Nat. Phys. 2012, 8, 568–573. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Zampieri, S.; Bullo, F. Controllability metrics, limitations and algorithms for complex networks. IEEE Trans. Control Netw. Syst. 2014, 1, 40–52. [Google Scholar] [CrossRef]
- Lombardi, A.; Hörnquist, M. Controllability analysis of networks. Phys. Rev. E 2007, 75, 056110. [Google Scholar] [CrossRef]
- Tanner, H.G. On the controllability of nearest neighbor interconnections. In Proceedings of the 2004 CDC—43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 3, p. 2467. [Google Scholar]
- Kalman, R.E. Mathematical description of linear dynamical systems. J. Soc. Ind. Appl. Math. Ser. A 1963, 1, 152–192. [Google Scholar] [CrossRef]
- Ahn, H.J.; Hassibi, B. Global dynamics of epidemic spread over complex networks. In Proceedings of the 2013 IEEE 52nd Annual Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 4579–4585. [Google Scholar]
- Cullen, C.G. Matrices and Linear Transformations, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1972. [Google Scholar]
- Gerschgorin, S. Über die Abgrenzung der Eigenwerte einer Matrix. Izv. Akad. Nauk. USSR Otd. Fiz.-Mat. Nauk. 1931, 6, 749–754. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Wang, W.; Tang, M.; Stanley, H.E.; Braunstein, L.A. Unification of theoretical approaches for epidemic spreading on complex networks. Rep. Prog. Phys. 2017, 80, 036603. [Google Scholar] [CrossRef]
- Prakash, B.A.; Chakrabarti, D.; Faloutsos, M.; Valler, N.; Faloutsos, C. Got the Flu (or Mumps)? Check the Eigenvalue! arXiv, 2010; arXiv:physics.soc-ph/1004.0060v1. [Google Scholar]
- Courcelle, B.; Makowsky, J.A.; Rotics, U. On the fixed parameter complexity of graph enumeration problems definable in monadic second order logic. Discret. Appl. Math. 2001, 108, 23–52. [Google Scholar] [CrossRef]
- Nijenhuis, A.; Wilf, H.S. The Enumeration of Connected Graphs and Linked Diagrams. J. Comb. Theory 1979, 27, 356–359. [Google Scholar] [CrossRef]
- Ronald, C. Read, Some unusual enumeration problems. Ann. N. Y. Acad. Sci. 1970, 175, 314–326. [Google Scholar]
- Mackay Brendan, D. Asymptotics for symmetric 0–1 matrices with preescribed row sums. Ars Comb. 1985, 19A, 15–25. [Google Scholar]
- Mackay Brendan, D.; Wormald Nicholas, C. Uniform generation of random regular graphs of moderate degree. J. Algorithms 1990, 11, 52–67. [Google Scholar] [CrossRef]
- Mackay Brendan, D.; Wormald Nicholas, C. Asymptotic enumeration by degree sequence of graphs of high degree. Eur. J. Comb. 1990, 11, 565–580. [Google Scholar] [CrossRef]
- Mackay Brendan, D.; Wormald Nicholas, C. Asymptotic Enumeration by Degree Sequence with Degrees O(). Combinatorica 1991, 11, 369–382. [Google Scholar] [CrossRef]
- Pólya, G. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Math. 1937, 68, 145–254. [Google Scholar] [CrossRef]
- Harary, F.; Palmer, E.M. Graph Enumeration; Academic Press: New York, NY, USA; London, UK, 1973. [Google Scholar]
- Wright, E.M. Graphs on unlabelled nodes with a given number of edges. Acta Math. 1971, 126, 1–9. [Google Scholar] [CrossRef]
- Bender, E.A.; Canfield, E.R. The asymptotic number of labeled graphs with given degree sequences. J. Comb. Theory 1978, 24, 296–307. [Google Scholar] [CrossRef]
- Bollobás, B. A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. Eur. J. Comb. 1980, 1, 311–316. [Google Scholar] [CrossRef]
- Bollobás, B. The asymptotic number of unlabelled regular graphs. J. Lond. Math. Soc. 1981, 1, 201–206. [Google Scholar] [CrossRef]
- Pei, S.; Morone, F.; Makse, H.A. Theories for influencer identification in complex networks. arXiv, 2018; arXiv:physics.soc-ph/1707.01594v2. [Google Scholar]
- Cha, M.; Haddadi, H.; Benevenuto, F.; Gummandi, P.K. Measuring user influence in Twitter: The million follower fallacy. In Proceedings of the 4th International AAAI Conference on Weblogs and Social Media, Washington, DC, USA, 23–26 May 2010; Volume 10, pp. 10–17. [Google Scholar]
- Watts, D.J.; Dodds, P.S. Influential networks and public opinion formation. J. Consum. Res. 2007, 34, 441–458. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Pei, S.; Makse, H.A. Spreading dynamics in complex networks. J. Stat. Mech. Theory Exp. 2013, 2013, P12002. [Google Scholar] [CrossRef]
- Min, B.; Morone, F.; Makse, H.A. Searching for influencers in big-data complex networks. In Diffusive Spreading in Nature, Technology and Society; Bunde, A., Caro, J., Karger, J., Vogl, G., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Leskovec, J.; Adamic, L.A.; Huberman, B.A. The dynamics of viral marketing. ACM Trans. Web 2007, 1, 5. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations; Simon and Schuster: New York, NY, USA, 2010. [Google Scholar]
- Sedgewick, R.; Flajolet, P. Analytic Combinatorics, Zeroth ed.; Fifth Printing; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Wilf, H.S. Generatingfunctionology, 3rd ed.; A K Peters Ltd.: Wellesley, MA, USA, 2006. [Google Scholar]
- Louis, C. Advanced Combinatorics: The Art of Finite and Infinite Expansions; D. Reidel Publishing Company: Dordrecht-Holland, The Netherlands; Boston, MA, USA, 1974. [Google Scholar]
- Sedgewick, R.; Flajolet, P. An Introduction to the Analysis of Algorithms; 2nd Printing; Addison-Wesley: Boston, MA, USA, 2001. [Google Scholar]
- Euler, L. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae; Holding Institution, American Museum of Natural History Library: New York, NY, USA, 1750–1776; Volume 7, pp. 13–14. Available online: https://www.biodiversitylibrary.org/bibliography/9527#/summary (accessed on 21 March 2018).
- Kirchhoff, G. Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme gefuhrt wird. Ann. Phys. Chem. 1847, 72, 497–508. [Google Scholar] [CrossRef]
- Cayley, A. A Theorem on trees. Q. J. Math. Oxf. Ser. Collect. Pap. Camb. 1897, 13, 26–28. [Google Scholar]
- Redfield, J.H. The theory of group-reduced distributions. Am. J. Math 1927, 49, 433–455. [Google Scholar] [CrossRef]
- Mallows, C.L.; Riordan, J. The inversion enumerator for labeled trees. Bull. Am. Math. Soc. 1968, 74, 92–94. [Google Scholar] [CrossRef]
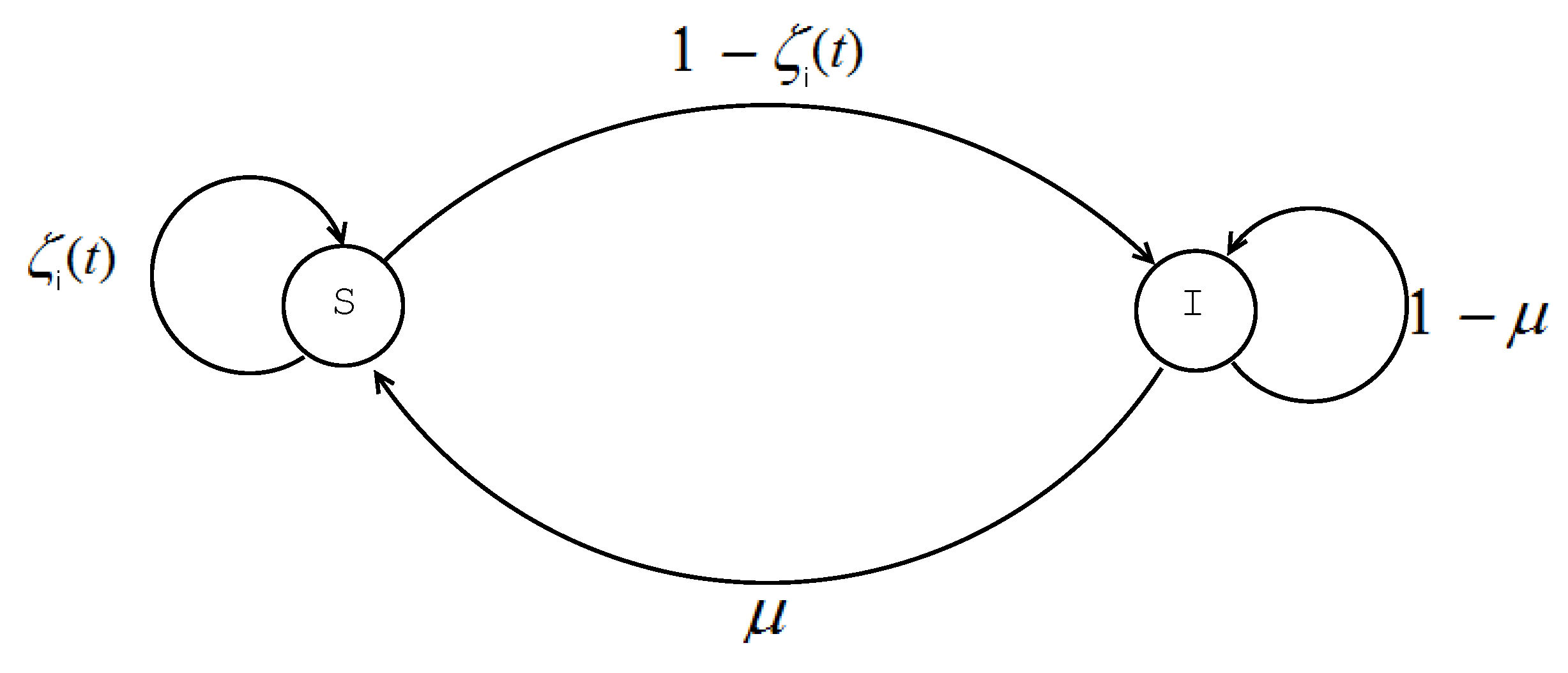
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez Lucatero, C.; Alarcón Ramos, L.A. Use of Enumerative Combinatorics for Proving the Applicability of an Asymptotic Stability Result on Discrete-Time SIS Epidemics in Complex Networks. Mathematics 2019, 7, 30. https://doi.org/10.3390/math7010030
Rodríguez Lucatero C, Alarcón Ramos LA. Use of Enumerative Combinatorics for Proving the Applicability of an Asymptotic Stability Result on Discrete-Time SIS Epidemics in Complex Networks. Mathematics. 2019; 7(1):30. https://doi.org/10.3390/math7010030
Chicago/Turabian StyleRodríguez Lucatero, Carlos, and Luis Angel Alarcón Ramos. 2019. "Use of Enumerative Combinatorics for Proving the Applicability of an Asymptotic Stability Result on Discrete-Time SIS Epidemics in Complex Networks" Mathematics 7, no. 1: 30. https://doi.org/10.3390/math7010030
APA StyleRodríguez Lucatero, C., & Alarcón Ramos, L. A. (2019). Use of Enumerative Combinatorics for Proving the Applicability of an Asymptotic Stability Result on Discrete-Time SIS Epidemics in Complex Networks. Mathematics, 7(1), 30. https://doi.org/10.3390/math7010030





