Hypersurfaces with Generalized 1-Type Gauss Maps

Abstract

In this paper, we study submanifolds in a Euclidean space with a generalized 1-type Gauss map. The Gauss map, G, of a submanifold in the n-dimensional Euclidean space, ${\mathbb{E}}^n$, is said to be of generalized 1-type if, for the Laplace operator, $\Delta$, on the submanifold, it satisfies $\Delta G=fG+gC$, where C is a constant vector and f and g are some functions. The notion of a generalized 1-type Gauss map is a generalization of both a 1-type Gauss map and a pointwise 1-type Gauss map. With the new definition, first of all, we classify conical surfaces with a generalized 1-type Gauss map in ${\mathbb{E}}^3$. Second, we show that the Gauss map of any cylindrical surface in ${\mathbb{E}}^3$ is of the generalized 1-type. Third, we prove that there are no tangent developable surfaces with generalized 1-type Gauss maps in ${\mathbb{E}}^3$, except planes. Finally, we show that cylindrical hypersurfaces in ${\mathbb{E}}^{n+2}$ always have generalized 1-type Gauss maps.

1. Introduction

The notion of finite type submanifolds in a Euclidean space or a pseudo-Euclidean space was introduced by Chen in the 1980s [1]. He also extended this notion to a general differential map, namely, the Gauss map, on the submanifolds. The notions of finite type immersion and finite type Gauss map are useful tools for investigating and characterizing many important submanifolds [1,2,3,4,5,6,7,8,9,10,11,12]. Moreover, Chen et al. dealed with the finite type Gauss map as an immersion and with its relation to the topology of some submanifolds [13,14].

The simplest type of finite type Gauss map is the 1-type. A submanifold, M, of a Euclidean space or a pseudo-Euclidean space has a 1-type Gauss map if the Gauss map, G, of M satisfies

$$\Delta G=\lambda (G+C)$$

(1)

for some $\lambda \in \mathbb{R}$ and has a constant vector, C, where $\Delta$ denotes the Laplace operator defined on M. Planes, circular cylinders and spheres in ${\mathbb{E}}^3$ are typical examples of surfaces with 1-type Gauss maps.

As a generalization of a 1-type Gauss map, the first and third authors introduced the notion of a pointwise 1-type Gauss map of submanifolds in reference [15]. A submanifold is said to have a pointwise 1-type Gauss map if the Laplacian of its Gauss map, G, takes the form

$$\Delta G=f(G+C)$$

(2)

for a non-zero smooth function, f, and a constant vector, C. More precisely, a pointwise 1-type Gauss map is said to be of the first kind if $C=0$ in (2); otherwise, it is said to be of the second kind. A helicoid, a catenoid and a right cone in ${\mathbb{E}}^3$ are typical examples of surfaces with pointwise 1-type Gauss maps. Many results of submanifolds with pointwise 1-type Gauss maps in ambient spaces were obtained in references [6,16,17,18,19,20,21,22,23,24,25,26,27]. On the other hand, it is well-known that a circular cylinder in ${\mathbb{E}}^3$ has a usual 1-type Gauss map. However, we consider the following cylindrical surface parameterized by

$$x(s,t)=\left(\frac{s}{2}cos(lns)+\frac{s}{2}sin(lns),-\frac{s}{2}cos(lns)+\frac{s}{2}sin(lns),t\right).$$

Then, the Gauss map, G, of the surface is given by

$$G=(-sin(lns),cos(lns),0).$$

We can easily show that the Gauss map, G, satisfies

$$\Delta G=\frac{1}{s^2}\left(1+cot(lns)\right)G-\frac{1}{s^2}csc(lns)(0,1,0),$$

which yields a Gauss map, G, that is neither of usual 1-type, nor of pointwise 1-type.

In this reason, we have the following definition:

Definition 1.

A submanifold, M, of a Euclidean space is said to have a generalized 1-type Gauss map if the Gauss map, G, on M satisfies the equation

$$\Delta G=fG+gC$$

(3)

for some smooth functions ($f,g$) and has a constant vector, C.

If both f and g are constant in (3), then M has a 1-type Gauss map. If $f=g$ in (3), then M has a pointwise 1-type Gauss map. Hence, the notion of a generalized 1-type Gauss map is a generalization of both a 1-type Gauss map and a pointwise 1-type Gauss map.

In [22], Dursun studied flat surfaces in ${\mathbb{E}}^3$ with a pointwise 1-type Gauss map and proved the following proposition.

Proposition 1.

Let M be a flat surface in ${\mathbb{E}}^3$. Then, M has a pointwise 1-type Gauss map of the second kind if and only if M is an open part of one of the following surfaces:

(1) 

A plane in ${\mathbb{E}}^3$,

(2) 

A right circular cone in ${\mathbb{E}}^3$,

(3) 

A cylinder, up to a rigid motion, parameterized by

$$x(s,t)=\gamma (s)+t\beta ,$$

where $\gamma =\gamma (s)$ is a unit speed planar base curve with curvature $k=k(s)$ satisfying the ordinary differential equation

$${(\frac{dk}{ds})}^2=k^4(s)\{a{k}^2(s)+2bk(s)-1\}$$

for some real numbers, a and $b(\ne 0)$, and the director vector $\beta =(0,0,1)$.

In this paper, we study developable surfaces in ${\mathbb{E}}^3$: cylindrical surfaces, conical surfaces and tangent developable surfaces. In Section 3, we completely classify developable surfaces with generalized a 1-type Gauss map and give some examples. In the last section, we prove that cylindrical hypersurfaces in ${\mathbb{E}}^{n+2}$ always have generalized 1-type Gauss maps.

Throughout this paper, we assume that all objects are smooth and all surfaces are connected unless mentioned.

2. Preliminaries

Let $x:M\to {\mathbb{E}}^m$ be an isometric immersion from an n-dimensional Riemannian manifold, M, into ${\mathbb{E}}^m.$ Denote the Levi–Civita connections of M and ${\mathbb{E}}^m$ by ∇ and $\tilde{\nabla }$, respectively. Let X and Y be vector fields tangent to M, and let $\xi$ be a unit normal vector field of M. Then, the Gauss and Weingarten formulas are given by

$${\tilde{\nabla }}_{X}Y={\nabla }_{X}Y+h(X,Y),$$

(4)

$${\tilde{\nabla }}_X\xi =-A_{\xi }X+D_X\xi ,$$

(5)

respectively. Here, h is the second fundamental form; D is the normal connection defined on the normal bundle; and $A_{\xi }$ is the shape operator (or the Weingarten operator) in the direction of $\xi$ on M. Note that the second fundamental form, h, and the shape operator, $A_{\xi }$, are related by

$$⟨h(X,Y),\xi ⟩=⟨A_{\xi }X,Y⟩.$$

(6)

The mean curvature vector field, $\overrightarrow{H}$, is defined by

$$\overrightarrow{H}=\frac{1}{n}\mathrm{tr}h,$$

(7)

where $\mathrm{tr}h$ is the trace of h. The mean curvature, H, of M is given by $H=\sqrt{⟨\overrightarrow{H},\overrightarrow{H}⟩}$.

Moreover, the Laplace operator, $\Delta$, acting on a scalar valued function, $\varphi$, is given by

$$\Delta \varphi =-\sum _{i=1}^n({\tilde{\nabla }}_{e_i}{\tilde{\nabla }}_{e_i}\varphi -{\tilde{\nabla }}_{{\nabla }_{e_i}{e}_i}\varphi ),$$

(8)

where $\{e_1,\cdots ,e_n\}$ is an orthonormal local tangent frame on M. Or, locally, it is expressed as

$$\Delta \varphi =-\frac{1}{\sqrt{g}}\sum _{i,j=1}^n\frac{\partial }{\partial x_i}(\sqrt{g}{g}^{ij}\frac{\partial \varphi }{\partial x_j}),$$

(9)

where $(g^{ij})$ and g denote the inverse matrix and the determinant of the matrix $(g_{ij})$, respectively, with the coefficients $g_{ij}$ of the Riemannian metric $⟨·,·⟩$ on M induced from that of ${\mathbb{E}}^m$.

3. Surfaces with Generalized 1-Type Gauss Maps

In this section, we completely classify developable surfaces in ${\mathbb{E}}^3$ with a generalized 1-type Gauss map.

A regular surface in ${\mathbb{E}}^3$ whose Gaussian curvature vanishes is called a developable surface, whose surface is a cylindrical surface, a conical surface or a tangent developable surface [28].

For a hypersurface in a Euclidean space, the next lemma plays an important role in our paper [21].

Lemma 1.

Let M be a hypersurface of ${\mathbb{E}}^{n+2}$. Then, the Laplacian of the Gauss map, G, is given by

$$\Delta G=\left|\right|A_G{\left|\right|}^{2}G+(n+1)\nabla H,$$

(10)

where $\nabla H$ is the gradient of the mean curvature, H; $A_G$ is the shape operator of M; and $\left|\right|A_G{\left|\right|}^2=tr(A_G^2)$.

Suppose that a developable surface in ${\mathbb{E}}^3$ has a generalized 1-type Gauss map, that is, the Gauss map G of the surface satisfies the condition

$$\Delta G=fG+gC$$

(11)

for some smooth functions, $f,g$, and a constant vector, C. It follows from (10) that M has generalized 1-type Gauss map with $C=0$, that is, M has a pointwise 1-type Gauss map of the first kind if and only if M has a constant mean curvature, H. If f and g are equal to each other with $C\ne 0$, then M has a pointwise 1-type Gauss map of the second kind and the results occur in [22]. Therefore, sometimes, in the proof of this paper, we assume that $f\ne g$ has non-zero functions and $C\ne 0$.

By combining (10) and (11) and taking the inner product with the orthonormal local frame $e_1,e_2$ and G, respectively, we have

$$\begin{array}{cc}\hfill 2e_1\left(H\right)& =g{C}_1,\hfill \\ \hfill 2e_2\left(H\right)& =g{C}_2,\hfill \\ \hfill \left|\right|A_G{\left|\right|}^2& =f+g{C}_3,\hfill \end{array}$$

(12)

where $C=C_1{e}_1+C_2{e}_2+C_{3}G$ with $C_1=⟨C,e_1⟩$, $C_2=⟨C,e_2⟩$ and $C_3=⟨C,G⟩$.

3.1. Conical Surfaces

A conical surface, M, in ${\mathbb{E}}^3$ can be parametrized by

$$x(s,t)={\alpha }_0+t\beta (s),s\in I,t>0,$$

such that $⟨\beta (s),\beta (s)⟩=⟨{\beta }^{\prime }(s),{\beta }^{\prime }(s)⟩=1$, where ${\alpha }_0$ is a constant vector. We take the orthonormal tangent frame, $\{e_1,e_2\}$, on M such that $e_1=\frac{1}{t}\frac{\partial }{\partial s}$ and $e_2=\frac{\partial }{\partial t}$. The Gauss map of M is given by $G=e_1\times e_2$. Through a direct calculation, we have

$$\begin{array}{c}{\tilde{\nabla }}_{e_1}{e}_1=-\frac{1}{t}{e}_2-\frac{{\kappa }_g(s)}{t}G,{\tilde{\nabla }}_{e_1}{e}_2=\frac{1}{t}{e}_1,\hfill \\ {\tilde{\nabla }}_{e_2}{e}_1={\tilde{\nabla }}_{e_2}{e}_2=0,{\tilde{\nabla }}_{e_1}G=\frac{{\kappa }_g}{t}{e}_1,{\tilde{\nabla }}_{e_2}G=0,\hfill \end{array}$$

(13)

where ${\kappa }_g(s)=⟨\beta (s),{\beta }^{\prime }(s)\times {\beta }^{″}(s)⟩$ denotes the geodesic curvature of $\beta$ in the unit sphere, ${\mathbb{S}}^2(1)$. We may assume that ${\kappa }_g(s)\ne 0,s\in I$; otherwise, the conical surface is an open part of a plane. Furthermore, by reversing the orientation of the spherical curve, $\beta$, we may assume that the geodesic curvature, ${\kappa }_g$, of $\beta$ is positive. It follows from (13) that the mean curvature, H, and the trace, $\left|\right|A_G{\left|\right|}^2$, of the square of the shape operator are given by

$$H=-\frac{{\kappa }_g(s)}{2t},\left|\right|A_G{\left|\right|}^2=\frac{{\kappa }_g^2(s)}{t^2}.$$

(14)

Suppose that M has a generalized 1-type Gauss map, that is, the Gauss map, G, of the conical surface satisfies (11). Then, since $C_1=⟨C,{\beta }^{\prime }⟩$, $C_2=⟨C,\beta ⟩$ and $C_3=⟨C,{\beta }^{\prime }\times \beta ⟩$, the components $C_i(i=1,2,3)$ of the constant vector, C, are functions of only s. Let us differentiate $C_1$, $C_2$ and $C_3$ with respect to $e_1$. Then, from (13), we have the following:

$$C_1^{\prime }(s)+C_2(s)+{\kappa }_g(s)C_3(s)=0,$$

(15)

$$C_2^{\prime }(s)-C_1(s)=0,$$

(16)

$$C_3^{\prime }(s)-{\kappa }_g(s)C_1(s)=0.$$

(17)

With the help of (14), (12) can be written as

$$-\frac{1}{t^2}{\kappa }_g^{\prime }(s)=g{C}_1,$$

(18)

$$\frac{{\kappa }_g(s)}{t^2}=g{C}_2,$$

(19)

$$\frac{{\kappa }_g^2(s)}{t^2}=f+g{C}_3.$$

(20)

By combining (18) and (19) and using (16), we have

$$g{\left({\kappa }_g(s)C_2\right)}^{\prime }=0.$$

Since $g\ne 0$, ${\kappa }_g(s)C_2$ is a non-zero constant, say c, we obtain

$$C_2=\frac{c}{{\kappa }_g(s)}.$$

(21)

Together with (19), this implies

$$g=\frac{{\kappa }_g^2(s)}{c{t}^2},$$

(22)

and hence, from (18), we get

$$C_1=-\frac{c{\kappa }_g^{\prime }(s)}{{\kappa }_g^2(s)}.$$

(23)

Thus, it follows from (15) that we have

$$C_3=\frac{c\left({\kappa }_g(s){\kappa }_g^{″}(s)-2{{\kappa }_g^{\prime }(s)}^2-{\kappa }_g^2(s)\right)}{{\kappa }_g^4(s)}.$$

(24)

Note that the function f is determined by (20), (22) and (24).

Now, we have $\phi (s)=1/{\kappa }_g(s)>0$. Then, (21) and (23) become, respectively,

$$C_2=c\phi$$

(25)

and

$$C_1=c{\phi }^{\prime }.$$

(26)

Furthermore, it follows from (17) and (24) that

$$C_3=-c(\phi {\phi }^{″}+{\phi }^2)$$

(27)

and

$$C_3^{\prime }=c\frac{{\phi }^{\prime }}{\phi }.$$

(28)

Thus, from (27) and (28) we see that the function $\phi$ must satisfy the following nonlinear differential equation of order 3:

$${\phi }^2{\phi }^{‴}+\phi {\phi }^{\prime }{\phi }^{″}+2{\phi }^2{\phi }^{\prime }+{\phi }^{\prime }=0.$$

(29)

In order to solve (29), first, we put $p=d\phi /ds$. Then the differential equation (29) becomes

$$p\left({\phi }^{2}p\frac{d^{2}p}{d{\phi }^2}+{\phi }^2{(\frac{dp}{d\phi })}^2+\phi p\frac{dp}{d\phi }+2{\phi }^2+1\right)=0,$$

which can be rewritten as

$$\phi p\left(\frac{d}{d\phi }(\phi p\frac{dp}{d\phi })+2\phi +\frac{1}{\phi }\right)=0.$$

(30)

Since $\phi >0$, we divide into two cases, as follows.

Case 1.$p=d\phi /ds=0$. The geodesic curvature, ${\kappa }_g$, is a nonzero constant, that is, the spherical curve, $\beta (s)$, is a small circle. Therefore, M is an open part of a right circular cone, and M has a pointwise 1-type Gauss map.

Case 2.$p=d\phi /ds\ne 0$.

From (30), we obtain

$$\frac{d}{d\phi }(\phi p\frac{dp}{d\phi })+2\phi +\frac{1}{\phi }=0,$$

(31)

which yields

$$\phi p\frac{dp}{d\phi }+{\phi }^2+ln\phi =\frac{a}{2}$$

(32)

for some constant, a. By integrating (32), we have

$$p^2=aln\phi +b-{\phi }^2-{(ln\phi )}^2$$

(33)

for some constant, b. Recalling $p=d\phi /ds$, from (33), one gets

$$\frac{d\phi }{ds}=\pm {\left(aln\phi +b-{\phi }^2-{(ln\phi )}^2\right)}^{\frac{1}{2}},$$

(34)

which is equivalent to

$$\frac{d\phi }{{\left(aln\phi +b-{\phi }^2-{(ln\phi )}^2\right)}^{\frac{1}{2}}}=\pm ds.$$

(35)

Hence, for an indefinite integral, $F(t)$, of the function $\psi (t)={\left(alnt+b-t^2-{(lnt)}^2\right)}^{-1/2}$, we see that

$$F(\phi )=\pm s,$$

(36)

where the signature is determined according to whether the derivative of $\phi$ is positive or not. Thus we get

$${\kappa }_g(s)=\frac{1}{\phi (s)}=\frac{1}{F^{-1}(\pm s)}.$$

(37)

Furthermore, it follows from (25)–(27) that C can be expressed as

$$C=c\left({\phi }^{\prime }{e}_1+\phi e_2-(\phi {\phi }^{″}+{\phi }^2)G\right),$$

(38)

or equivalently,

$$C=c\left(-\frac{{\kappa }_g^{\prime }}{{\kappa }_g^2}{e}_1+\frac{1}{{\kappa }_g}{e}_2+\frac{{\kappa }_g(s){\kappa }_g^{″}(s)-2{{\kappa }_g^{\prime }(s)}^2-{\kappa }_g^2(s)}{{\kappa }_g^4(s)}G\right).$$

(39)

Conversely, for some constants, a and b, such that the function

$$\psi (t)={\left(alnt+b-t^2-{(lnt)}^2\right)}^{-1/2}$$

(40)

is well-defined on some interval, $J\subset (0,\infty )$, we take an indefinite integral, $F(t)$, of the function $\psi (t)$. If we denote the image of the function, F, by I, then $F:J\to I$ is a strictly increasing function with $F^{\prime }(t)=\psi (t)$. Let us consider the function $\phi ={\phi }_{\pm }$, defined by ${\phi }_{\pm }(s)=F^{-1}(\pm s)$, which maps the interval, $\pm I$, onto J, respectively. Here $-I$ means the interval $\{-s|s\in I\}$. Then, the function $\phi ={\phi }_{\pm }$ is positive for the interval $I_{\pm }$ (say, I) and satisfies $F(\phi )=\pm s$.

For any unit speed spherical curve $\beta (s)$ in the unit sphere ${\mathbb{S}}^2(1)$ with the geodesic curvature ${\kappa }_g(s)=1/\phi (s)$, we consider a surface M in ${\mathbb{E}}^3$ to be parametrized by

$$x(s,t)={\alpha }_0+t\beta (s),s\in I,t>0,$$

(41)

where ${\alpha }_0$ is a constant vector. Given any non-zero constant, c, we put

$$f(s,t)=\frac{1}{t^2{\phi }^2(s)}\left(\phi (s){\phi }^{″}(s)+{\phi }^2(s)+1\right),g(s,t)=\frac{1}{c{t}^2{\phi }^2(s)}.$$

(42)

For the orthonormal tangent frame, $\{e_1,e_2\}$, on M, such that $e_1=\frac{1}{t}\frac{\partial }{\partial s}$ and $e_2=\frac{\partial }{\partial t}$ and the Gauss map of M given by $G=e_1\times e_2$, we put

$$C=c\{{\phi }^{\prime }(s)e_1+\phi (s)e_2-\left(\phi (s){\phi }^{″}(s)+{\phi }^2(s)\right)G\}.$$

(43)

Note that it follows from the definition of $\phi$ that the function $\phi$ satisfies (29). Hence, by using (13), it is straightforward to show that

$${\tilde{\nabla }}_{e_1}C={\tilde{\nabla }}_{e_2}C=0,$$

(44)

which implies that C is a constant vector. Furthermore, similar to the first part of this subsection, the Gauss map, G, of the conical surface, M, satisfies

$$\Delta G=fG+gC,$$

where $f,g$ and C are given in (42) and (43), respectively. This shows that M has a generalized 1-type Gauss map.

Thus, we have the following theorem 1:

Theorem 1.

A conical surface in ${\mathbb{E}}^3$ has a generalized 1-type Gauss map if and only if it is an open part of one of the following surfaces:

(1) 

A plane,

(2) 

A right circular cone,

(3) 

A conical surface parameterized by

$$x(s,t)={\alpha }_0+t\beta (s),$$

where ${\alpha }_0$ is a constant vector and $\beta (s)$ is a unit speed spherical curve in the unit sphere ${\mathbb{S}}^2(1)$ with a positive geodesic curvature, ${\kappa }_g$, which for some indefinite integral $F(t)$ of the function $\psi (t)={\left(alnt+b-t^2-{(lnt)}^2\right)}^{-1/2}$ with $a,b\in R$, is given by

$${\kappa }_g(s)=\frac{1}{F^{-1}(\pm s)}.$$

3.2. Cylindrical Surfaces

In this subsection, we prove the following theorem:

Theorem 2.

All cylindrical surfaces in ${\mathbb{E}}^3$ have a generalized 1-type Gauss map.

Proof. 

Let M be a cylindrical surface in ${\mathbb{E}}^3$ generated by a base curve, $\alpha (s)$, and a constant vector, $\beta$. Then, M can be parametrized by

$$x(s,t)=\alpha (s)+t\beta ,$$

such that $⟨{\alpha }^{\prime }(s),{\alpha }^{\prime }(s)⟩=1,⟨{\alpha }^{\prime }(s),\beta ⟩=0$ and $⟨\beta ,\beta ⟩=1$. Hence, the base curve, $\alpha (s)$, is a unit speed plane curve. Let us denote the curvature function of $\alpha (s)$ by $\kappa (s)$.

Consider an orthonormal frame $\{e_1,e_2\}$ on M such that $e_1=\frac{\partial }{\partial t}$ and $e_2=\frac{\partial }{\partial s}$. Then, the Gauss map, G, of M is given by $G=e_1\times e_2$. By direct calculation, we obtain

$$\begin{array}{c}{\tilde{\nabla }}_{e_1}{e}_1={\tilde{\nabla }}_{e_1}{e}_2={\tilde{\nabla }}_{e_2}{e}_1=0,{\tilde{\nabla }}_{e_2}{e}_2=\kappa (s)G,\hfill \\ {\tilde{\nabla }}_{e_1}G=0,{\tilde{\nabla }}_{e_2}G=-\kappa (s)e_2.\hfill \end{array}$$

(45)

It follows from (45) that the mean curvature, H, and the trace $\left|\right|A_G{\left|\right|}^2$ of the square of the shape operator are given by

$$\begin{array}{c}\hfill H=\frac{\kappa (s)}{2},\left|\right|A_G{\left|\right|}^2={\kappa }^2(s),\end{array}$$

(46)

which are functions of only s.

First, suppose that M has a generalized 1-type Gauss map. Together with (46), the first equation of (12) shows that $C_1=0$. Hence, (12) can be rewritten as

$$\begin{array}{cc}\hfill {\kappa }^2(s)& =f+g{C}_3,\hfill \\ \hfill {\kappa }^{\prime }(s)& =g{C}_2.\hfill \end{array}$$

(47)

Since $C_2=⟨C,{\alpha }^{\prime }(s)⟩$ and $C_3=⟨C,\beta \times {\alpha }^{\prime }(s)⟩$, $C_2$ and $C_3$ are functions of only s. By differentiating $C_2$ and $C_3$ with respect to $e_2$, the component functions of C satisfy the following equations:

$$\begin{array}{cc}\hfill C_2^{\prime }(s)-\kappa (s)C_3(s)& =0,\hfill \\ \hfill C_3^{\prime }(s)+\kappa (s)C_2(s)& =0,\hfill \end{array}$$

(48)

which yield $C_2^2(s)+C_3^2(s)=c^2$ for some non-zero constant, c. We may put

$$C_2(s)=csin\theta (s),C_3(s)=ccos\theta (s)$$

(49)

with ${\theta }^{\prime }(s)=\kappa (s)$. Therefore, the constant vector, C, becomes

$$C=csin\theta (s)e_2+ccos\theta (s)G.$$

(50)

By combining (47) and (49), one also gets

$$g=\frac{{\kappa }^{\prime }(s)}{csin\theta (s)},f={\kappa }^2(s)-{\kappa }^{\prime }(s)cot\theta (s).$$

(51)

Conversely, for any cylindrical surface, we choose a curve, $\alpha (s)$, and a unit vector, $\beta$, such that the cylindrical surface is parametrized by $x(s,t)=\alpha (s)+t\beta$ with $⟨{\alpha }^{\prime }(s),{\alpha }^{\prime }(s)⟩=1,⟨{\alpha }^{\prime }(s),\beta ⟩=0$. Then, for a non-zero constant, c, and an indefinite integral, $\theta (s)$, of the curvature function, $\kappa (s)$, of $\alpha$, we put

$$C=csin\theta (s)e_2+ccos\theta (s)G,$$

(52)

where $e_1=\frac{\partial }{\partial t}$, $e_2=\frac{\partial }{\partial s}$ and $G=e_1\times e_2$. It follows from (45) that ${\tilde{\nabla }}_{e_1}C=0$ and ${\tilde{\nabla }}_{e_2}C=0$, which shows that C is a constant vector. Furthermore, it is straightforward to show that the Gauss map, G, of the cylindrical surface satisfies

$$\Delta G=fG+gC,$$

where $f,g$ and C are given in (51) and (52), respectively. This shows that the cylindrical surface has a generalized 1-type Gauss map. ☐

Example 1.

We consider the surface to be parameterized by

$$x(s,t)=\left(2cos(\sqrt{s})+2\sqrt{s}sin(\sqrt{s}),2sin(\sqrt{s})-2\sqrt{s}cos(\sqrt{s}),t\right).$$

Then, the surface is cylindrical, generated by the plane curve with the curvature $\kappa (s)=\frac{1}{2\sqrt{s}}$, and its Gauss map G is given by

$$G=\left(sin(\sqrt{s}),-cos(\sqrt{s}),0\right).$$

From this, the Laplacian of G can be expressed as

$$\begin{array}{cc}\hfill \Delta G& =\left(\frac{1}{4s\sqrt{s}}cos(\sqrt{s})+\frac{1}{4s}sin(\sqrt{s}),\frac{1}{4s\sqrt{s}}sin(\sqrt{s})-\frac{1}{4s}cos(\sqrt{s}),0\right)\hfill \\ \hfill & =\frac{1}{4s}\left(1+\frac{cot(\sqrt{s})}{\sqrt{s}}\right)G+\frac{csc(\sqrt{s})}{4s\sqrt{s}}C,\hfill \end{array}$$

where $C=(0,1,0)$.

The plane curve and the cylindrical surface in Example 1 are shown in Figure 1 and Figure 2, respectively.

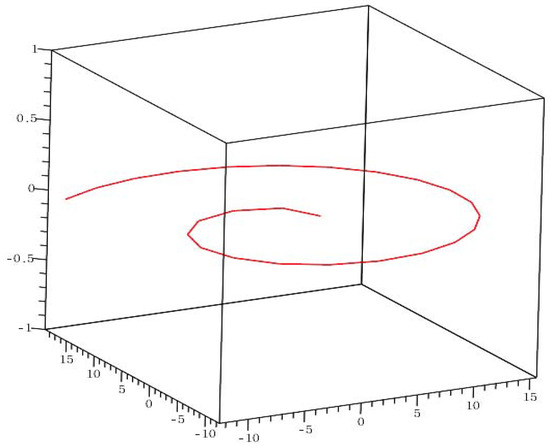
Figure 1. The plane curve in Example 1.

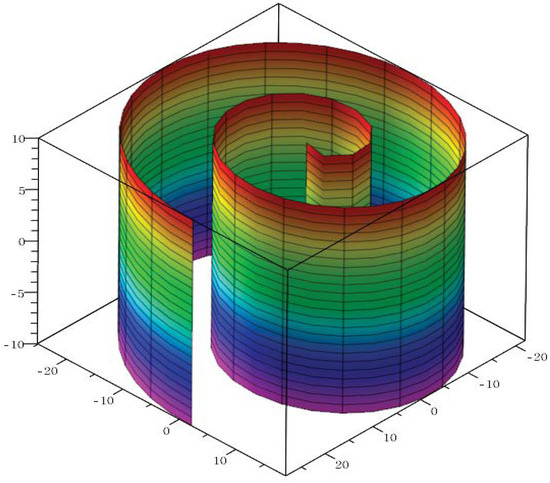
Figure 2. The cylindrical surface in Example 1.

3.3. Tangent Developable Surfaces

In this subsection, we prove the following theorem:

Theorem 3.

A tangent developable surface in ${\mathbb{E}}^3$ with a generalized 1-type Gauss map is an open part of a plane.

Proof. 

Let M be a tangent developable surface in ${\mathbb{E}}^3$. Then, M is locally parametrized by

$$x(s,t)=\alpha (s)+t{\alpha }^{\prime }(s),s\in I,t\ne 0,$$

where $\alpha (s)$ is a unit speed curve with non-zero curvature $\kappa (s)$ in ${\mathbb{E}}^3$. Let us denote the unit tangent vector, principal normal vector and binormal vector of $\alpha (s)$, by $T,N$ and B, respectively. The natural frames, $\{x_s,x_t\}$ of x, are given by

$$x_s=T+t\kappa (s)N,x_t={\alpha }^{\prime }(s)=T.$$

The parametrization x is regular whenever $t\kappa (s)\ne 0$. We take the orthonormal frame, $\{e_1,e_2\}$, on M such that

$$\begin{array}{cc}\hfill e_1& =\frac{\partial }{\partial t}=T,\hfill \\ \hfill e_2& =\frac{1}{t\kappa (s)}\left(\frac{\partial }{\partial s}-\frac{\partial }{\partial t}\right)=N.\hfill \end{array}$$

(53)

Then, the Gauss map, G, of M is given by $G=e_1\times e_2=T\times N=B$. By direct calculation, we obtain

$$\begin{array}{c}{\tilde{\nabla }}_{e_1}{e}_1={\tilde{\nabla }}_{e_1}{e}_2=0,{\tilde{\nabla }}_{e_2}{e}_1=\frac{1}{t}{e}_2,\hfill \\ {\tilde{\nabla }}_{e_2}{e}_2=-\frac{1}{t}{e}_1+\frac{\tau }{t\kappa }G,{\tilde{\nabla }}_{e_1}G=0,{\tilde{\nabla }}_{e_2}G=\frac{\tau }{t\kappa }{e}_2,\hfill \end{array}$$

(54)

which yields

$$H=\frac{\tau }{2t\kappa },\left|\right|A_G{\left|\right|}^2={\left(\frac{\tau }{t\kappa }\right)}^2.$$

(55)

Now, we suppose that the tangent developable surface, M, has a generalized 1-type Gauss map. Since $C_1=⟨C,T⟩$, $C_2=⟨C,N⟩$ and $C_3=⟨C,B⟩$, the components of C are functions of s only. Hence, it follows from (54) that the components of C satisfy the following:

$$C_1^{\prime }-\kappa C_2=0,$$

(56)

$$C_2^{\prime }+\kappa C_1-\tau C_3=0,$$

(57)

$$C_3^{\prime }+\tau C_2=0.$$

(58)

Due to (55), (12) can be rewritten as

$$-\frac{\tau }{t^2\kappa }=g{C}_1,$$

(59)

$$\frac{1}{t^2\kappa }\left({\left(\frac{\tau }{\kappa }\right)}^{\prime }+\frac{\tau }{t\kappa }\right)=g{C}_2,$$

(60)

$$\frac{{\tau }^2}{t^2{\kappa }^2}=f+g{C}_3.$$

(61)

By combining (59) and (14), one finds that

$$\tau C_2+\left({\left(\frac{\tau }{\kappa }\right)}^{\prime }+\frac{\tau }{t\kappa }\right)C_1=0,$$

(62)

or equivalently,

$$\left({\left(\frac{\tau }{\kappa }\right)}^{\prime }{C}_1+\tau C_2\right)t\kappa +\tau C_1=0.$$

(63)

Since the parameter $t(\ne 0)$ is arbitrary, from (63), we have

$$\begin{array}{cc}\hfill {\left(\frac{\tau }{\kappa }\right)}^{\prime }{C}_1+\tau C_2& =0,\hfill \\ \hfill \tau C_1& =0.\hfill \end{array}$$

(64)

Finally, we suppose that the torsion, $\tau (s)$, of the curve, $\alpha (s)$, does not vanish identically. Then, since the set $J=\{s\in I|\tau (s)\ne 0\}$ is non-empty, (64) shows that $C_1=0$ and $C_2=0$. From this and (57), we have $C_3=0$. In the long run, one gets $C=0$. It follows from (12) and (55) that the mean curvature, $H=\tau (s)/\left(2t\kappa (s)\right)$, is constant, which shows that $\tau$ must vanish identically. That is, $J=\{s\in I|\tau (s)\ne 0\}$ is empty, which leads a contradiction. This yields that $\alpha (s)$ is a plane curve, and hence, M is an open part of a plane. This completes the proof of Theorem 6. ☐

Note that a plane is a kind of cylindrical surface and also a kind of circular right cone. Thus, by summarizing all the results in this section, we established the following classification theorem for developable surfaces with generalized 1-type Gauss maps:

Theorem 4.

(Classification Theorem) A developable surface, M, in ${\mathbb{E}}^3$ has a generalized 1-type Gauss map if and only if it is an open part of one of the following:

(1) 

A cylindrical surface,

(2) 

A circular right cone,

(3) 

A conical surface parameterized by

$$x(s,t)={\alpha }_0+t\beta (s),$$

where ${\alpha }_0$ is a constant vector and $\beta (s)$ is a unit speed spherical curve in the unit sphere, ${\mathbb{S}}^2(1)$, with a positive geodesic curvature, ${\kappa }_g$, which is, for some indefinite integral, $F(t)$, of the function $\psi (t)={\left(alnt+b-t^2-{(lnt)}^2\right)}^{-1/2}$ with $a,b\in R$, given by

$${\kappa }_g(s)=\frac{1}{F^{-1}(\pm s)}.$$

4. Cylindrical Hypersurfaces with Generalized 1-Type Gauss Maps

In this section, we study cylindrical hypersurfaces with generalized 1-type Gauss maps in ${\mathbb{E}}^{n+2}$. Suppose that a hypersurface, M, in ${\mathbb{E}}^{n+2}$ has a generalized 1-type Gauss map, that is, the Gauss map, G, of the hypersurface satisfies the condition

$$\Delta G=fG+gC$$

(65)

for some non-zero smooth functions, $f,g$, and a non-zero constant vector, C. By combining (10) and (65) and taking the scalar product with the orthonormal local frame, $e_1,e_2,\dots ,e_{n+1}$ of M and the Gauss map, G, respectively, we obtain

$$\begin{array}{c}(n+1)e_i\left(H\right)=g{C}_i,i=1,2,\dots ,n+1\hfill \end{array}$$

(66)

and

$$\begin{array}{c}\left|\right|A_G{\left|\right|}^2=f+g{C}_{n+2},\hfill \end{array}$$

(67)

where, for $i=1,2,\dots ,n+1$, $C_i=⟨C,e_i⟩$ and $C_{n+2}=⟨C,G⟩$.

By extending Theorem 3.3, finally, we prove the following theorem:

Theorem 5.

A cylindrical hypersurface, M, in ${\mathbb{E}}^{n+2}$ has a generalized 1-type Gauss map.

Proof. 

Let M be a cylindrical hypersurface in the $(n+2)$-dimensional Euclidean space, ${\mathbb{E}}^{n+2}$. Then, M can be parametrized by

$$x\left(s,t_1,\dots ,t_n\right)=\alpha (s)+\sum _{i=1}^n{t}_i{\beta }_i$$

such that $⟨{\alpha }^{\prime },{\alpha }^{\prime }⟩=1$, $⟨{\alpha }^{\prime },{\beta }_i⟩=0$ and $⟨{\beta }_i,{\beta }_j⟩={\delta }_{ij},i,j=1,\dots ,n$. Then, the generator $\alpha$ is a plane curve with the Frenet frame $T,N$ and we have the orthonormal frame $\{e_1,e_2,\dots ,e_{n+1}\}$ on M, such that $e_i=\frac{\partial }{\partial t_i},i=1,\dots ,n$ and $e_{n+1}=\frac{\partial }{\partial s}=T$. Hence, by rearranging ${\beta }_i$, if necessary, we may assume that the Gauss map, G, of M is given by $G=e_1\times \cdots \times e_{n+1}=N$. By direct calculation, we get

$$\begin{array}{c}{\tilde{\nabla }}_{e_i}{e}_j={\tilde{\nabla }}_{e_{n+1}}{e}_j={\tilde{\nabla }}_{e_i}{e}_{n+1}=0,i,j=1,\dots n,\hfill \\ {\tilde{\nabla }}_{e_i}G=0,i=1,\dots n,{\tilde{\nabla }}_{e_{n+1}}{e}_{n+1}=\kappa G,{\tilde{\nabla }}_{e_{n+1}}G=-\kappa e_{n+1},\hfill \end{array}$$

(68)

where $\kappa$ is the curvature function of the generator, $\alpha$. (68) implies that

$$\begin{array}{c}\hfill H=\frac{\kappa }{n+1},\left|\right|A_G{\left|\right|}^2={\kappa }^2,\end{array}$$

(69)

which are the functions of only s.

Now, suppose that M has a generalized 1-type Gauss map. That is, G satisfies (65). Then, C in ${\mathbb{E}}^{n+2}$ can be expressed as $C={\sum }_{j=1}^{n+1}{C}_j{e}_j+C_{n+2}G$ in the frame $\{e_1,e_2,\dots ,e_{n+1},G\}$. Together with (69), (66) implies that $C_i=0$ because $e_i(H)=0$, but $g\ne 0$ for $i=1,\dots ,n$. Hence, we have

$$\begin{array}{c}\hfill C=C_{n+1}{e}_{n+1}+C_{n+2}G=C_{n+1}T+C_{n+2}N.\end{array}$$

(70)

By differentiating (70) with respect to $e_i$ for $i=1,\dots ,n$, (68) shows that

$$\begin{array}{c}\hfill e_i(C_{n+1})=e_i(C_{n+2})=0,i=1,\dots ,n.\end{array}$$

(71)

Hence, $C_{n+1}$ and $C_{n+2}$ are functions of s only. By differentiating (70) with respect to $e_{n+1}$, (68) also gives

$$\begin{array}{c}{e}_{n+1}\left(C_{n+1}\right)-\kappa (s)C_{n+2}=0,\hfill \\ e_{n+1}\left(C_{n+2}\right)+\kappa (s)C_{n+1}=0\hfill \end{array}$$

(72)

with $C_{n+1}^2(s)+C_{n+2}^2(s)=d^2$ for some non-zero constant, d. Hence, we may put

$$C_{n+1}(s)=dsin\theta (s),C_{n+2}(s)=dcos\theta (s),$$

(73)

where $\theta (s)$ is an indefinite integral of the curvature function $\kappa (s)$. Therefore, the constant vector, C, is given by

$$\begin{array}{c}\hfill C=dsin\theta (s)e_{n+1}+dcos\theta (s)G=dsin\theta (s)T+dcos\theta (s)N.\end{array}$$

(74)

Furthermore, it follows from (66), (67) and (69) that

$$\begin{array}{cc}\hfill f& ={\kappa }^2(s)-{\kappa }^{\prime }(s)cot\theta (s),\hfill \\ \hfill g& =\frac{{\kappa }^{\prime }}{dsin\theta (s)}.\hfill \end{array}$$

(75)

Conversely, for a cylindrical hypersurface, M, in ${\mathbb{E}}^{n+2}$, we may choose a curve, $\alpha (s)$, and n unit vectors ${\beta }_1,\dots ,{\beta }_n$ such that M is parametrized by

$$x\left(s,t_1,\dots ,t_n\right)=\alpha (s)+\sum _{i=1}^n{t}_i{\beta }_i$$

such that $⟨{\alpha }^{\prime },{\alpha }^{\prime }⟩=1$, $⟨{\alpha }^{\prime },{\beta }_i⟩=0$ and $⟨{\beta }_i,{\beta }_j⟩={\delta }_{ij},i,j=1,\dots ,n$. For a non-zero constant, d, and an indefinite integral, $\theta (s)$, of the curvature function $\kappa (s)$ of $\alpha$, we put

$$C=dsin\theta (s)e_{n+1}+dcos\theta (s)G,$$

(76)

where $e_i=\frac{\partial }{\partial t_i}$, $e_{n+1}=\frac{\partial }{\partial s}$ and $G=e_1\times e_2\times \cdots \times e_{n+1}$ for $i=1,\dots ,n$. It follows from (68) that ${\tilde{\nabla }}_{e_1}C=0$ and ${\tilde{\nabla }}_{e_2}C=0$, and hence, C is a constant vector. Furthermore, it is straightforward to show that the Gauss map of M satisfies

$$\Delta G=fG+gC,$$

where $f,g$ and C are given in (75) and (76), respectively. This shows that the cylindrical hypersurface has a generalized 1-type Gauss map. ☐

5. Conclusions

To find the best possible estimate of the total mean curvature of a compact submanifold of Euclidean space, Chen introduced the study of finite type submanifolds. Specifically, minimal submanifolds are characterized in a natural way. In our example, a cylindrical surface has neither a usual 1-type, nor a pointwise 1-type Gauss map. In this reason, we defined a new definiton, the generalized 1-type Gauss map. After that, we characterized developable surfaces with a generalized 1-type Gauss map in ${\mathbb{E}}^3$.