On the Most Extended Modal Operator of First Type over Interval-Valued Intuitionistic Fuzzy Sets

Krassimir Atanassov

doi:10.3390/math6070123

¹

Department of Bioinformatics and Mathematical Modelling, Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences, 105 Acad. G. Bonchev Str., 1113 Sofia, Bulgaria

²

Intelligent Systems Laboratory, Prof. Asen Zlatarov University, 8010 Bourgas, Bulgaria

Mathematics2018, 6(7), 123;https://doi.org/10.3390/math6070123

This article belongs to the Special Issue Fuzzy Mathematics

Version Notes

Order Reprints

Abstract

The definition of the most extended modal operator of first type over interval-valued intuitionistic fuzzy sets is given, and some of its basic properties are studied.

Keywords:

interval-valued intuitionistic fuzzy set; intuitionistic fuzzy set; modal operator

1. Introduction

Intuitionistic fuzzy sets (IFSs; see [1,2,3,4,5]) were introduced in 1983 as an extension of the fuzzy sets defined by Lotfi Zadeh (4.2.1921–6.9.2017) in [6]. In recent years, the IFSs have also been extended: intuitionistic L -fuzzy sets [7], IFSs of second [8] and nth [9,10,11,12] types, temporal IFSs [4,5,13], multidimensional IFSs [5,14], and others. Interval-valued intuitionistic fuzzy sets (IVIFSs) are the most detailed described extension of IFSs. They appeared in 1988, when Georgi Gargov (7.4.1947–9.11.1996) and the author read Gorzalczany’s paper [15] on the interval-valued fuzzy set (IVFS). The idea of IVIFS was announced in [16,17] and extended in [4,18], where the proof that IFSs and IVIFSs are equipollent generalizations of the notion of the fuzzy set is given.

Over IVIFS, many (more than the ones over IFSs) relations, operations, and operators are defined. Here, similar to the IFS case, the standard modal operators ☐ and ◇ have analogues, but their extensions—the intuitionistic fuzzy extended modal operators of the first type—already have two different forms. In the IFS case, there is an operator that includes as a partial case all other extended modal operators. In the present paper, we construct a similar operator for the case of IVIFSs and study its properties.

2. Preliminaries

Let us have a fixed universe E and its subset A. The set

A = {⟨ x, M_{A} (x), N_{A} (x) ⟩ ∣ x \in E},

where

M_{A} (x) \subset [0, 1] and N_{A} (x) \subset [0, 1]

are closed intervals and for all

x \in E

:

sup M_{A} (x) + sup N_{A} (x) \leq 1

(1)

is called IVIFS, and functions

M_{A} : E \to P ([0, 1])

and

N_{A} : E \to P ([0, 1])

represent the set of degrees of membership (validity, etc.) and the set of degrees of non-membership (non-validity, etc.) of element

x \in E

to a fixed set

A \subseteq E

, where

P (Z) = {Y | Y \subseteq Z}

for an arbitrary set

Z .

Obviously, both intervals have the representation:

M_{A} (x) = [inf M_{A} (x), sup M_{A} (x)],

N_{A} (x) = [inf N_{A} (x), sup N_{A} (x)] .

Therefore, when

inf M_{A} (x) = sup M_{A} (x) = μ_{A} (x) and inf N_{A} (x) = sup N_{A} (x) = ν_{A} (x),

the IVIFS A is transformed to an IFS.

We must mention that in [19,20] the second geometrical interpretation of the IFSs is given (see Figure 1).

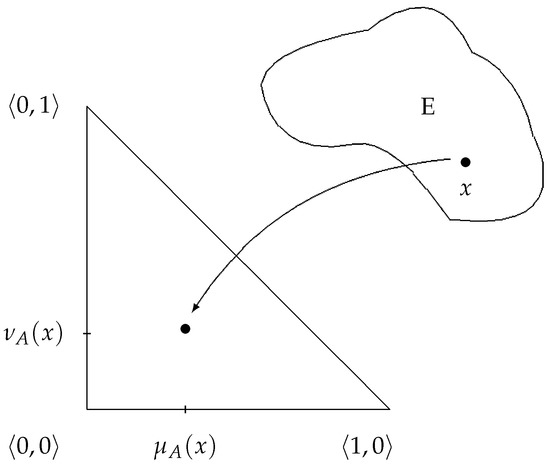
Figure 1. The second geometrical interpretation of an intuitionistic fuzzy set (IFS).

IVIFSs have geometrical interpretations similar to, but more complex than, those of the IFSs. For example, the analogue of the geometrical interpretation from Figure 1 is shown in Figure 2.

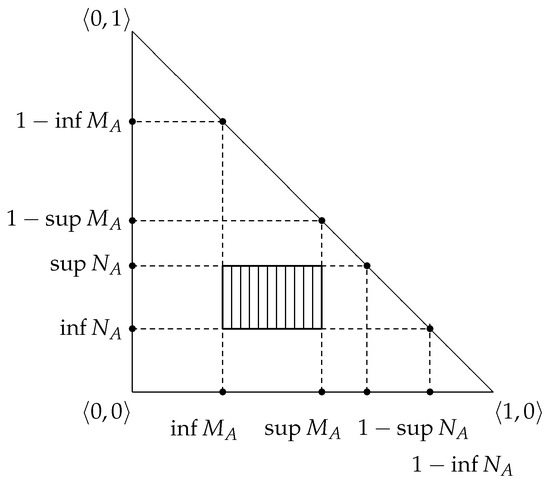
Figure 2. The second geometrical interpretation of an interval-valued intuitionistic fuzzy set (IVIFS).

Obviously, each IVFS A can be represented by an IVIFS as

A = {⟨ x, M_{A} (x), N_{A} (x) ⟩ ∣ x \in E}

= {⟨ x, M_{A} (x), [1 - sup M_{A} (x), 1 - inf M_{A} (x)] ⟩ ∣ x \in E} .

The geometrical interpretation of the IVFS A is shown in Figure 3. It has the form of a section lying on the triangle’s hypotenuse.

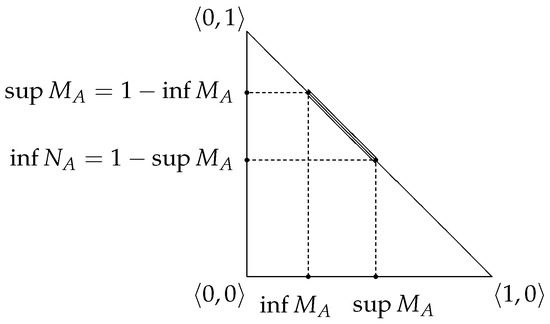
Figure 3. The second geometrical interpretation of an IVFS.

Modal-type operators are defined similarly to those defined for IFSs, but here they have two forms: shorter and longer. The shorter form is:

\begin{matrix} ☐ A = & {⟨ x, M_{A} (x), [inf N_{A} (x), 1 - sup M_{A} (x)] ⟩ ∣ x \in E}, \\ ◇ A = & {⟨ x, [inf M_{A} (x), 1 - sup N_{A} (x)], N_{A} (x) ⟩ ∣ x \in E}, \\ D_{α} (A) = & {⟨ x, [inf M_{A} (x), sup M_{A} (x) + α (1 - sup M_{A} (x) - sup N_{A} (x))], \\ [inf N_{A} (x), sup N_{A} (x) + (1 - α) (1 - sup M_{A} (x) - sup N_{A} (x))] ⟩ \\ ∣ x \in E}, \\ F_{α, β} (A) = & {⟨ x, [inf M_{A} (x), sup M_{A} (x) + α (1 - sup M_{A} (x) - sup N_{A} (x))], \\ [inf N_{A} (x), sup N_{A} (x) + β (1 - sup M_{A} (x) - sup N_{A} (x))] ⟩ \\ ∣ x \in E}, f o r α + β \leq 1, \\ G_{α, β} (A) = & {⟨ x, [α inf M_{A} (x), α sup M_{A} (x)], [β inf N_{A} (x), β sup N_{A} (x)] ⟩ \\ ∣ x \in E}, \\ H_{α, β} (A) = & {⟨ x, [α inf M (x), α sup M_{A} (x)], [inf N_{A} (x), sup N_{A} (x) \\ + β (1 - sup M_{A} (x) - sup N_{A} (x))] ⟩ ∣ x \in E}, \\ H_{α, β}^{*} (A) = & {⟨ x, [α inf M_{A} (x), α sup M_{A} (x)], [inf N_{A} (x), sup N_{A} (x) \\ + β (1 - α sup M_{A} (x) - sup N_{A} (x))] ⟩ ∣ x \in E}, \\ J_{α, β} (A) = & {⟨ x, [inf M_{A} (x), sup M_{A} (x) + α (1 - sup M_{A} (x) \\ - sup N_{A} (x))], [β inf N_{A} (x), β sup N_{A} (x)] ⟩ ∣ x \in E}, \\ J_{α, β}^{*} (A) = & {⟨ x, [inf M_{A} (x), sup M_{A} (x) + α (1 - sup M_{A} (x) \\ - β sup N_{A} (x))], [β inf N_{A} (x), β . sup N_{A} (x)] ⟩ ∣ x \in E}, \end{matrix}

where

α, β \in [0, 1] .

Obviously, as in the case of IFSs, the operator

D_{α}

is an extension of the intuitionistic fuzzy forms of (standard) modal logic operators ☐ and ◇, and it is a partial case of

F_{α, β}

.

The longer form of these operators (operators ☐, ◇, and D do not have two forms—only the one above) is (see [4]):

\begin{matrix} {\bar{F}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) = & {⟨ x, [inf M_{A} (x) + α (1 - sup M_{A} (x) - sup N_{A} (x)), \\ sup M_{A} (x) + β (1 - sup M_{A} (x) - sup N_{A} (x))], \\ [inf N_{A} (x) + γ (1 - sup M_{A} (x) - sup N_{A} (x)), \\ sup N_{A} (x) + δ (1 - sup M_{A} (x) - sup N_{A} (x))] ⟩ ∣ x \in E} \\ where β + δ \leq 1, \\ {\bar{G}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) = & {⟨ x, [α inf M_{A} (x), β sup M_{A} (x)], \\ [γ inf N_{A} (x), δ sup N_{A} (x)] ⟩ ∣ x \in E}, \\ {\bar{H}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) = & {⟨ x, [α inf M_{A} (x), β sup M_{A} (x)], \\ [inf N_{A} (x) + γ (1 - sup M_{A} (x) - sup N_{A} (x)), \\ sup N_{A} (x) + δ (1 - sup M_{A} (x) - sup N_{A} (x))] ⟩ ∣ x \in E}, \\ {\bar{H}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})}^{*} (A) = & {⟨ x, [α inf M_{A} (x), β sup M_{A} (x)], \\ [inf N_{A} (x) + γ (1 - β sup M_{A} (x) - sup N_{A} (x)), \\ sup N_{A} (x) + δ (1 - β sup M_{A} (x) - sup N_{A} (x))] ⟩ ∣ x \in E}, \\ {\bar{J}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} = & {⟨ x, [inf M_{A} (x) + α (1 - sup M_{A} (x) - sup N_{A} (x)), \\ sup M_{A} (x) + β (1 - sup M_{A} (x) - sup N_{A} (x))], \\ [γ inf N_{A} (x), δ sup N_{A} (x)] ⟩ ∣ x \in E}, \\ {\bar{J}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})}^{*} (A) = & {⟨ x, [inf M_{A} (x) + α (1 - δ sup M_{A} (x) - sup N_{A} (x)), \\ sup M_{A} (x) + β (1 - sup M_{A} (x) - δ sup N_{A} (x))], \\ [γ . inf N_{A} (x), δ . sup N_{A} (x)] ⟩ ∣ x \in E}, \end{matrix}

where

α, β, γ, δ \in [0, 1]

such that

α \leq β

and

γ \leq δ

.

Figure 4 shows to which region of the triangle the element

x \in E

(represented by the small rectangular region in the triangle) will be transformed by the operators

F, G, . . .,

irrespective of whether they have two or four indices.

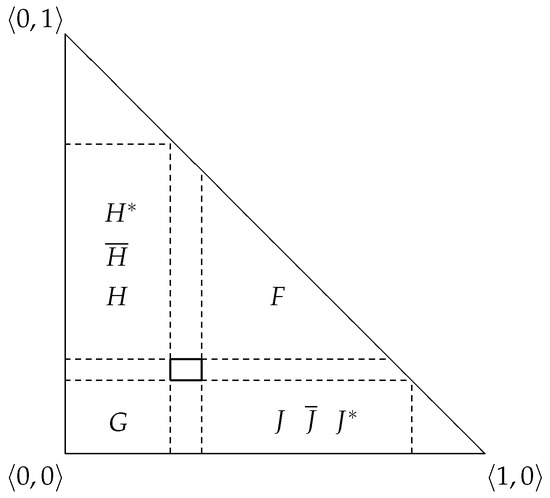
Figure 4. Region of transformation by the application of the operators.

3. Operator $X$

Now, we introduce the new operator

X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A)

= {⟨ x, [a_{1} inf M_{A} (x) + b_{1} (1 - inf M_{A} (x) - c_{1} inf N_{A} (x)),

a_{2} sup M_{A} (x) + b_{2} (1 - sup M_{A} (x) - c_{2} sup N_{A} (x))],

[d_{1} inf N_{A} (x) + e_{1} (1 - f_{1} inf M_{A} (x) - inf N_{A} (x)),

d_{2} sup N_{A} (x) + e_{2} (1 - f_{2} sup M_{A} (x) - sup N_{A} (x))] ⟩ | x \in E},

where

a_{1}, b_{1}, c_{1}, d_{1}, e_{1}, f_{1}, a_{2}, b_{2}, c_{2}, d_{2}, e_{2}, f_{2} \in [0, 1]

, the following three conditions are valid for

i = 1, 2

:

a_{i} + e_{i} - e_{i} f_{i} \leq 1,

(2)

b_{i} + d_{i} - b_{i} c_{i} \leq 1,

(3)

b_{i} + e_{i} \leq 1,

(4)

and

a_{1} \leq a_{2}, b_{1} \leq b_{2}, c_{1} \leq c_{2}, d_{1} \leq d_{2}, e_{1} \leq e_{2}, f_{1} \leq f_{2} .

(5)

Theorem 1.

For every IVIFS A and for every

a_{1}, b_{1}, c_{1}, d_{1}, e_{1}, f_{1}, a_{2}, b_{2}, c_{2}, d_{2}, e_{2}, f_{2}

\in [0, 1]

that satisfy (2)–(5),

X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A)

is an IVIFS.

Proof.

Let

a_{1}, b_{1}, c_{1}, d_{1}, e_{1}, f_{1}, a_{2}, b_{2}, c_{2}, d_{2}, e_{2}, f_{2} \in [0, 1]

satisfy (2)–(5) and let A be a fixed IVIFS. Then, from (5) it follows that

a_{1} inf M_{A} (x) + b_{1} (1 - inf M_{A} (x) - c_{1} inf N_{A} (x))

\leq a_{2} sup M_{A} (x) + b_{2} (1 - sup M_{A} (x) - c_{2} sup N_{A} (x))

and

d_{1} inf N_{A} (x) + e_{1} (1 - f_{1} inf M_{A} (x) - inf N_{A} (x))

\leq d_{2} sup N_{A} (x) + e_{2} (1 - f_{2} sup M_{A} (x) - sup N_{A} (x)) .

Now, from (5) it is clear that it will be enough to check that

X = a_{2} sup M_{A} (x) + b_{2} (1 - sup M_{A} (x) - c_{2} sup N_{A} (x))

+ d_{2} sup N_{A} (x) + e_{2} (1 - f_{2} sup M_{A} (x) - sup N_{A} (x))

= (a_{2} - b_{2} - e_{2} f_{2}) sup M_{A} (x) + (d_{2} - e_{2} - b_{2} c_{2}) sup N_{A} (x) + b_{2} + e_{2} \leq 1 .

In fact, from (2),

a_{2} - b_{2} - e_{2} f_{2} \leq 1 - b_{2} - e_{2}

and from (3):

d_{2} - e_{2} - b_{2} c_{2} \leq 1 - b_{2} - e_{2} .

Then, from (1),

X \leq (1 - b_{2} - e_{2}) (sup M_{A} (x) + sup N_{A} (x)) + b_{2} + e_{2}

\leq 1 - b_{2} - e_{2} + b_{2} + e_{2} = 1 .

Finally, when

sup M_{A} (x) = inf N_{A} (x) = 0

and from (4),

X = b_{2} (1 - 0 - 0) + e_{2} (1 - 0 - 0) = b_{2} + e_{2} \leq 1 .

Therefore, the definition of the IVIFS is correct. ☐

All of the operators described above can be represented by the operator

X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})}

at suitably chosen values of its parameters. These representations are the following:

\begin{matrix} ☐ A & = X_{(\begin{matrix} 1 & 0 & r_{1} & 1 & 0 & s_{1} \\ 1 & 0 & r_{2} & 1 & 1 & 1 \end{matrix})} (A), \\ ◇ A & = X_{(\begin{matrix} 1 & 0 & r_{1} & 1 & 0 & s_{1} \\ 1 & 1 & 1 & 1 & 0 & s_{2} \end{matrix})} (A), \\ D_{α} (A) & = X_{(\begin{matrix} 1 & 0 & r_{1} & 1 & α & 1 \\ 1 & 0 & r_{2} & 1 & 1 - α & 1 \end{matrix})} (A), \\ F_{α, β} (A) & = X_{(\begin{matrix} 1 & 0 & r_{1} & 1 & 0 & s_{1} \\ 1 & α & 1 & 1 & β & 1 \end{matrix})} (A), \\ G_{α, β} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & β & 0 & s_{1} \\ α & 0 & r_{2} & β & 0 & s_{2} \end{matrix})} (A), \\ H_{α, β} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & 1 & 0 & s_{1} \\ α & 0 & r_{2} & 1 & β & 1 \end{matrix})} (A), \\ H_{α, β}^{*} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & α & 0 & s_{1} \\ 1 & 0 & r_{2} & 1 & β & α \end{matrix})} (A), \\ J_{α, β} (A) & = X_{(\begin{matrix} 1 & 0 & r_{1} & β & 0 & s_{1} \\ 1 & α & 1 & β & 0 & s_{2} \end{matrix})} (A), \\ J_{α, β}^{*} (A) & = X_{(\begin{matrix} 1 & 0 & r_{1} & β & 0 & s_{1} \\ 1 & α & β & β & 0 & s_{2} \end{matrix})} (A), \\ {\bar{F}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) & = X_{(\begin{matrix} 1 & α & 1 & 1 & γ & 1 \\ 1 & β & 1 & 1 & δ & s_{1} \end{matrix})} (A), \end{matrix}

\begin{matrix} {\bar{G}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & β & 0 & s_{1} \\ γ & 0 & r_{2} & δ & 0 & s_{2} \end{matrix})} (A), \\ {\bar{H}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & 1 & γ & 1 \\ β & 0 & r_{2} & 1 & δ & 1 \end{matrix})} (A), \\ {\bar{H}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})}^{*} (A) & = X_{(\begin{matrix} α & 0 & r_{1} & 1 & γ & 1 \\ β & 0 & r_{2} & 1 & δ & β \end{matrix})} (A), \\ {\bar{J}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})} (A) & = X_{(\begin{matrix} 1 & α & 1 & γ & 0 & s_{1} \\ 1 & β & 1 & δ & 0 & s_{2} \end{matrix})} (A), \\ {\bar{J}}_{(\begin{matrix} α & γ \\ β & δ \end{matrix})}^{*} (A) & = X_{(\begin{matrix} 1 & α & δ & γ & 0 & s_{1} \\ 1 & β & δ & δ & 0 & s_{2} \end{matrix})} (A), \end{matrix}

where

r_{1}, r_{2}, s_{1}, s_{2}

are arbitrary real numbers in the interval

[0, 1]

.

Three of the operations, defined over two IVIFSs A and B, are the following:

\begin{matrix} \neg A & = & {⟨ x, N_{A} (x), M_{A} (x) ⟩ ∣ x \in E}, \\ A \cap B & = & {⟨ x, [min (inf M_{A} (x), inf M_{B} (x)), min (sup M_{A} (x), sup M_{B} (x))], \\ [max (inf N_{A} (x), inf N_{B} (x)), max (sup N_{A} (x), sup N_{B} (x))] ⟩ ∣ x \in E}, \\ A \cup B & = & {⟨ x, [max (inf M_{A} (x), inf M_{B} (x)), max (sup M_{A} (x), sup M_{B} (x))], \\ [min (inf N_{A} (x), inf N_{B} (x)), min (sup N_{A} (x), sup N_{B} (x))] ⟩ ∣ x \in E} . \end{matrix}

For any two IVIFSs A and B, the following relations hold:

\begin{matrix} A \subset B & iff & \forall x \in E, inf M_{A} (x) \leq inf M_{B} (x), inf N_{A} (x) \geq inf N_{B} (x), \\ sup M_{A} (x) \leq sup M_{B} (x) and sup N_{A} (x) \geq sup N_{B} (x)), \\ A \supset B & iff & B \subset A, \\ A = B & iff & A \subset B and B \subset A . \end{matrix}

Theorem 2.

For every two IVIFSs A and B and for every

a_{1}, b_{1}, c_{1}, d_{1}, e_{1}, f_{1}, a_{2}, b_{2},

c_{2}, d_{2}, e_{2}, f_{2}

\in [0, 1]

that satisfy (2)–(5),

(a): $\neg X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (\neg A) = X_{d, e, f, a, b, c} (A),$
(b): $X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A \cap B)$

$\subset X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A) \cap X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (B),$
(c): $X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A \cup B)$

$\supset X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A) \cup X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (B) .$

Proof.

(c) Let

a_{1}, b_{1}, c_{1}, d_{1}, e_{1}, f_{1}, a_{2}, b_{2}, c_{2}, d_{2}, e_{2}, f_{2} \in [0, 1]

satisfy (2)–(5) , and let A and B be fixed IVIFSs. First, we obtain:

Y = X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A \cup B)

= X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} ({⟨ x, [max (inf M_{A} (x), inf M_{B} (x)),

max (sup M_{A} (x), sup M_{B} (x))],

[min (inf N_{A} (x), inf N_{B} (x)), min (sup N_{A} (x), sup N_{B} (x))] ⟩ ∣ x \in E})

= {⟨ x, [a_{1} max (inf M_{A} (x), inf M_{B} (x)) + b_{1} (1 - max (inf M_{A} (x), inf M_{B} (x))

- c_{1} min (inf N_{A} (x), inf N_{B} (x))), a_{2} max (sup M_{A} (x) sup M_{B} (x))

+ b_{2} (1 - max (sup M_{A} (x) sup M_{B} (x)) - c_{2} min (sup N_{A} (x), sup N_{B} (x)))],

[d_{1} min (inf N_{A} (x), inf N_{B} (x)) + e_{1} (1 - f_{1} max (inf M_{A} (x), inf M_{B} (x))

- min (inf N_{A} (x), inf N_{B} (x))), d_{2} min (sup N_{A} (x), sup N_{B} (x))

+ e_{2} (1 - f_{2} max (sup M_{A} (x) sup M_{B} (x)) - min (sup N_{A} (x), sup N_{B} (x)))] ⟩ | x \in E} .

Second, we calculate:

Z = X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (A) \cup X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})} (B)

= {⟨ x, [a_{1} inf M_{A} (x) + b_{1} (1 - inf M_{A} (x) - c_{1} inf N_{A} (x)),

a_{2} sup M_{A} (x) + b_{2} (1 - sup M_{A} (x) - c_{2} sup N_{A} (x))],

[d_{1} inf N_{A} (x) + e_{1} (1 - f_{1} inf M_{A} (x) - inf N_{A} (x)),

d_{2} sup N_{A} (x) + e_{2} (1 - f_{2} sup M_{A} (x) - sup N_{A} (x))] ⟩ | x \in E}

\cup {⟨ x, [a_{1} inf M_{B} (x) + b_{1} (1 - inf M_{B} (x) - c_{1} inf N_{B} (x)),

a_{2} sup M_{B} (x) + b_{2} (1 - sup M_{B} (x) - c_{2} sup N_{B} (x))],

[d_{1} inf N_{B} (x) + e_{1} (1 - f_{1} inf M_{B} (x) - inf N_{B} (x)),

d_{2} sup N_{B} (x) + e_{2} (1 - f_{2} sup M_{B} (x) - sup N_{B} (x))] ⟩ | x \in E}

= {⟨ x, [max (a_{1} inf M_{A} (x) + b_{1} (1 - inf M_{A} (x) - c_{1} inf N_{A} (x)),

a_{1} inf M_{B} (x) + b_{1} (1 - inf M_{B} (x) - c_{1} inf N_{B} (x))),

max (a_{2} sup M_{A} (x) + b_{2} (1 - sup M_{A} (x) - c_{2} sup N_{A} (x)),

a_{2} sup M_{B} (x) + b_{2} (1 - sup M_{B} (x) - c_{2} sup N_{B} (x)))],

[min (d_{1} inf N_{A} (x) + e_{1} (1 - f_{1} inf M_{A} (x) - inf N_{A} (x)),

d_{1} inf N_{B} (x) + e_{1} (1 - f_{1} inf M_{B} (x) - inf N_{B} (x))),

min (d_{2} sup N_{A} (x) + e_{2} (1 - f_{2} sup M_{A} (x) - sup N_{A} (x)),

d_{2} sup N_{B} (x) + e_{2} (1 - f_{2} sup M_{B} (x) - sup N_{B} (x)))] ⟩ ∣ x \in E} .

Let

P = a_{1} max (inf M_{A} (x), inf M_{B} (x)) + b_{1} (1 - max (inf M_{A} (x), inf M_{B} (x))

- c_{1} min (inf N_{A} (x), inf N_{B} (x))) - max (a_{1} inf M_{A} (x) + b_{1} (1 - inf M_{A} (x) - c_{1} inf N_{A} (x)),

a_{1} inf M_{B} (x) + b_{1} (1 - inf M_{B} (x) - c_{1} inf N_{B} (x)))

= a_{1} max (inf M_{A} (x), inf M_{B} (x)) + b_{1} - b_{1} max (inf M_{A} (x), inf M_{B} (x))

- b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x))) - max ((a_{1} - b_{1}) inf M_{A} (x) + b_{1} - b_{1} c_{1} inf N_{A} (x),

(a_{1} - b_{1}) inf M_{B} (x) + b_{1} - b_{1} c_{1} inf N_{B} (x))

= a_{1} max (inf M_{A} (x), inf M_{B} (x)) - b_{1} max (inf M_{A} (x), inf M_{B} (x))

- b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) - max ((a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} inf N_{A} (x),

(a_{1} - b_{1}) inf M_{B} (x) - b_{1} c_{1} inf N_{B} (x)) .

Let

inf M_{A} (x) \geq inf M_{B} (x)

. Then

P = (a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) - max ((a_{1} - b_{1}) inf M_{A} (x)

- b_{1} c_{1} inf N_{A} (x), (a_{1} - b_{1}) inf M_{B} (x) - b_{1} c_{1} inf N_{B} (x)) .

Let

(a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} inf N_{A} (x) \geq (a_{1} - b_{1}) inf M_{B} (x) - b_{1} c_{1} inf N_{B} (x) .

Then

P = (a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) - (a_{1} - b_{1}) inf M_{A} (x)

+ b_{1} c_{1} inf N_{A} (x)

= b_{1} c_{1} inf N_{A} (x) - b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) \geq 0 .

If

(a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} inf N_{A} (x) < (a_{1} - b_{1}) inf M_{B} (x) - b_{1} c_{1} inf N_{B} (x) .

Then

P = (a_{1} - b_{1}) inf M_{A} (x) - b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) - (a_{1} - b_{1}) inf M_{B} (x)

+ b_{1} c_{1} inf N_{B} (x)) .

= b_{1} c_{1} inf N_{B} (x) - b_{1} c_{1} min (inf N_{A} (x), inf N_{B} (x)) \geq 0 .

Therefore, the

inf M_{A}

-component of IVIFS Y is higher than or equal to the

inf M_{A}

-component of IVIFS Z. In the same manner, it can be checked that the same inequality is valid for the

sup M_{A}

-components of these IVIFSs. On the other hand, we can check that that the

inf N_{A}

- and

sup N_{A}

-components of IVIFS Y are, respectively, lower than or equal to the

inf N_{A}

and

sup N_{A}

-components of IVIFS Z. Therefore, the inequality (c) is valid. ☐

4. Conclusions

In the near future, the author plans to study some other properties of the new operator

X_{(\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \end{matrix})}

.

In [21], it is shown that the IFSs are a suitable tool for the evaluation of data mining processes and objects. In the near future, we plan to discuss the possibilities of using IVIFSs as a similar tool.

Funding

This research was funded by the Bulgarian National Science Fund under Grant Ref. No. DN-02-10/2016.

Conflicts of Interest

The author declares no conflict of interest.

References

Atanassov, K. Intuitionistic Fuzzy Sets. 1983, VII ITKR Session. Deposed in Centr. Sci.-Techn. Library of the Bulg. Acad. of Sci., 1697/84. Available online: http://www.biomed.bas.bg/bioautomation/2016/vol_20.s1/files/20.s1_03.pdf (accessed on 13 July 2018).
Atanassov, K. Intuitionistic fuzzy sets. Int. J. Bioautom. 2016, 20, S1–S6. [Google Scholar]
Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
Atanassov, K. Intuitionistic Fuzzy Sets; Springer: Heidelberg, Germany, 1999. [Google Scholar]
Atanassov, K. On Intuitionistic Fuzzy Sets Theory; Springer: Berlin, Germany, 2012. [Google Scholar]
Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
Atanassov, K.; Stoeva, S. Intuitionistic L-fuzzy sets. In Cybernetics and Systems Research 2; Trappl, R., Ed.; Elsevier Sci. Publ.: Amsterdam, The Nertherlands, 1984; pp. 539–540. [Google Scholar]
Atanassov, K. A second type of intuitionistic fuzzy sets. BUSEFAL 1993, 56, 66–70. [Google Scholar]
Atanassov, K.; Szmidt, E.; Kacprzyk, J.; Vassilev, P. On intuitionistic fuzzy pairs of n-th type. Issues Intuit. Fuzzy Sets Gen. Nets 2017, 13, 136–142. [Google Scholar]
Atanassov, K.T.; Vassilev, P. On the Intuitionistic Fuzzy Sets of n-th Type. In Advances in Data Analysis with Computational Intelligence Methods; Studies in Computational Intelligence; Gawęda, A., Kacprzyk, J., Rutkowski, L., Yen, G., Eds.; Springer: Cham, Switzerland, 2018; Volume 738, pp. 265–274. [Google Scholar]
Parvathi, R.; Vassilev, P.; Atanassov, K. A note on the bijective correspondence between intuitionistic fuzzy sets and intuitionistic fuzzy sets of p-th type. In New Developments in Fuzzy Sets, Intuitionistic Fuzzy Sets, Generalized Nets and Related Topics; SRI PAS IBS PAN: Warsaw, Poland, 2012; Volume 1, pp. 143–147. [Google Scholar]
Vassilev, P.; Parvathi, R.; Atanassov, K. Note on intuitionistic fuzzy sets of p-th type. Issues Intuit. Fuzzy Sets Gen. Nets 2008, 6, 43–50. [Google Scholar]
Atanassov, K. Temporal Intuitionistic Fuzzy Sets; Comptes Rendus de l’Academie bulgare des Sciences; Bulgarian Academy of Sciences: Sofia, Bulgaria, 1991; pp. 5–7. [Google Scholar]
Atanassov, K.; Szmidt, E.; Kacprzyk, J. On intuitionistic fuzzy multi-dimensional sets. Issues Intuit. Fuzzy Sets Gen. Nets 2008, 7, 1–6. [Google Scholar]
Gorzalczany, M. Interval-valued fuzzy fuzzy inference method—Some basic properties. Fuzzy Sets Syst. 1989, 31, 243–251. [Google Scholar] [CrossRef]
Atanassov, K. Review and New Results on Intuitionistic Fuzzy Sets. 1988, IM-MFAIS-1-88, Mathematical Foundations of Artificial Intelligence Seminar. Available online: http://www.biomed.bas.bg/bioautomation/2016/vol_20.s1/files/20.s1_03.pdf (accessed on 13 July 2018 ).
Atanassov, K. Review and new results on intuitionistic fuzzy sets. Int. J. Bioautom. 2016, 20, S7–S16. [Google Scholar]
Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
Atanassov, K. Geometrical Interpretation of the Elements of the Intuitionistic Fuzzy Objects. 1989, IM-MFAIS-1-89, Mathematical Foundations of Artificial Intelligence Seminar. Available online: http://biomed.bas.bg/bioautomation/2016/vol_20.s1/files/20.s1_05.pdf (accessed on 13 July 2018).
Atanassov, K. Geometrical interpretation of the elements of the intuitionistic fuzzy objects. Int. J. Bioautom. 2016, 20, S27–S42. [Google Scholar]
Atanassov, K. Intuitionistic fuzzy logics as tools for evaluation of Data Mining processes. Knowl.-Based Syst. 2015, 80, 122–130. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

On the Most Extended Modal Operator of First Type over Interval-Valued Intuitionistic Fuzzy Sets

Abstract

1. Introduction

2. Preliminaries

3. Operator $X$

4. Conclusions

Funding

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics

On the Most Extended Modal Operator of First Type over Interval-Valued Intuitionistic Fuzzy Sets

Abstract

1. Introduction

2. Preliminaries

3. Operator X

4. Conclusions

Funding

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics

3. Operator $X$