Abstract
In this work, we propose a framework for economic model predictive control (EMPC) with zone tracking. A zone tracking stage cost is incorporated into the existing EMPC framework to form a multi-objective optimization problem. We provide sufficient conditions for asymptotic stability of the optimal steady state and characterize the exact penalty for the zone tracking cost which prioritizes zone tracking objective over economic objective. Moreover, an algorithm to modify the target zone based on the economic performance and reachability of the optimal steady state is proposed. The modified target zone effectively decouples the dynamic zone tracking and economic objectives and simplifies parameter tuning.
1. Introduction
Process control of chemical plants needs to address a number of objectives including safety, environmental regulations, product quality, energy efficiency, profitability, etc. Based on the emphasis of the control objectives in practice, three elements or three facets of control exist [1]: regulatory control, constraint control and maneuvering control. Regulatory control refers to the conventional setpoint tracking control which minimizes the variance of controlled variables to the setpoint. Constraint control, or zone control, prevents the system from violating its boundary and steers the system back into the zone whenever constraint violation happens. No control action is required if the system is (predicted to be) in the target zone. Maneuvering control moves the system from the current operating point to a new operating point, typically due to economic considerations or change of operating conditions. Generally speaking, a well designed control system necessarily integrates all three control types, although emphasis on the three facets of control may vary from application to application.
Model predictive control (MPC) has been the most widely applied advanced control technique. The ability to handle constraints and to incorporate economic considerations makes MPC an ideal platform for integrating different control objectives. The literature is rich with theories for conventional setpoint tracking MPC ([2]). The past decade has seen an increasing academic interest in economic model predictive control (EMPC) ([3,4,5,6]) which integrates economic objectives into regulatory setpoint tracking control. On the contrary, zone control has received less attention. In the MPC framework, zone control is usually dealt with by the so-called soft constraint technique ([7,8,9,10,11]). As its name suggests, soft constraint is often dismissed as a trick to avoid feasibility issue with hard constraint, and is discussed separately from set-point tracking and economic objectives. To the best of the authors’ knowledge, only a few MPC frameworks explicitly handle zone tracking objectives ([12,13,14]). A practical challenge for the design and implementation of an integrated control system is the difficulty in parameter tunning. How to tradeoff different control objectives via the tuning parameters to get the desired closed-loop performance is crucial to the successful implementation of any control framework.
In this work, we propose an EMPC framework with integrated zone control. A zone tracking stage cost which penalizes a weighted norm and squared norm distance to the target zone is incorporated into the EMPC framework to form a multi-objective optimization problem. We provide sufficient conditions for asymptotic stability of the optimal steady state and characterize the exact penalty for the zone tracking cost which prioritizes the zone tracking objective over the economic objective. Moreover, we propose an algorithm to modify the target zone based on the economic performance and reachability of the optimal steady state in the target zone. The modified target zone is constructed as an invariant subset of the original target zone in which closed-loop transient economic performance is guaranteed. EMPC with the modified target zone effectively decouples the zone tracking and economic objectives and enjoys a simplified and more transparent parameter tuning procedure. Finally, two numerical examples are investigated which reveal the intrinsic difficulties in parameter tunning for EMPC with zone tracking and demonstrate the efficacy of the proposed approach.
2. Problem Setup
2.1. Notation
Throughout this work, denotes the norm of the vector x such that . The operator denotes the norm or Euclidean norm of a scalar or a vector. The symbol denotes the set of integers . The symbol denotes the set of non-negative integers . The symbol denotes projection of the set onto its subspace . A function is said to be positive definite with respect to a set , if for all and otherwise.
2.2. System Description and Control Objective
We consider the following nonlinear discrete time system:
where , , , denote the state and input at time n, respectively. The vector function is continuous. The system is subject to coupled state and input constraint:
where , , are all compact sets. The primary control objective is to steer and maintain the system in a compact set . The distance to the target zone is measured by the function which is positive definite with respect to the target zone . There is also a secondary economic objective to minimize the operational cost characterized by the function . Both and are continuous functions. Since zone tracking objectives are usually associated with important process specifications concerning safety or product quality, an ideal control strategy should satisfy zone objectives whenever possible and allow zone tracking violation only for a short period of time. This leads to the following formal statement of the control objective as an infinite-horizon optimization problem:
The above optimization problem optimizes the economic performance over an infinite horizon and minimizes the zone tracking error for the first K time steps when the system is outside the target zone . When the system is steered into the target zone, the zone tracking error is zero. The duration of zone target violation K is also an explicit objective which ensures that the zone tracking objective is satisfied in finite time. The optimization of Equation (2) is essentially a multi-objective optimization problem in which the magnitude, duration of zone target violation, as well as the economic performance are traded off.
For simplicity of exposition, we assume that the optimization of Equation (2) is well defined. This implies that the system can be steered to the target zone in finite time without violating the constraint. Moreover, the infinite sum is bounded. This condition is satisfied for strictly dissipative systems if we assume without loss of generality that the economic performance at the optimal steady state is zero [6].
Let denote the economically optimal steady state in the target zone . That is:
We assume that uniquely solves the above steady-state optimization problem. Note that the economic cost function is not necessarily positive definite with respect to .
3. EMPC with Zone Tracking
In this section, we propose a general framework for EMPC with zone tracking to tackle the infinite-horizon optimization problem in Equation (2). The EMPC is formulated as a finite horizon optimization problem which is solved repeatedly in a receding horizon fashion to approximate the optimal solution to Equation (2). We provide sufficient conditions for asymptotic stability of the optimal steady state and discuss how zone tracking can be prioritized using exact penalty.
3.1. EMPC Formulation
At a sampling time n, the EMPC is formulated as the following finite-horizon optimization problem:
In the above optimization, the objective function Equation (4) minimizes the zone tracking error and economic performance over a finite horizon of N steps, Equation (5) is the system model, Equation (6) specifies the initial condition, Equation (7) sets the state and input constraints. The point-wise terminal constraint Equation (8) requires the terminal state to arrive at the optimal steady state after N steps. This implicitly imposes constraint on the duration of zone objective violation (K in Equation (2)).
Let , denote the optimal solution. The input injected to the system at time n is: . At the next sampling time , the optimization of Equation (4) is re-evaluated, generating an implicit feedback control law . We denote the feasibility region of the optimization problem of Equation (4) by . Due to the terminal constraint Equation (8), is forward invariant under the EMPC design. In other words, the EMPC design is recursively feasible. The zone tracking penalty is defined by the following function:
where and are positive scalars. The zone tracking penalty defined in Equation (9) is formulated implicitly as an optimization problem which minimizes weighted norm and squared norm distance from the point to the target zone . The distance to the target zone is evaluated by introducing artificial variables which are bounded in the target zone . It is easy to verify that defined in Equation (9) is positive definite with respect to the target zone . When the zone tracking penalty of Equation (9) is used, Equation (4) is equivalent to the following optimization problem:
Remark 1.
The incorporation of the norm penalty allows for the so-called exact penalty which will be discussed in Section 3.3. From a multi-objective optimization point of view, the combined use of the linear ( norm) penalty and quadratic (squared norm) penalty offers a way to trade off the magnitude and duration of zone tracking violation [7]. Larger linear penalty may, though not necessarily, result in more drastic control move with smaller duration of zone tracking violation. On the contrary, quadratic penalty generally leads to mild control action with smaller zone tracking violation but larger duration of violation. These results will be demonstrated in the simulation.
Remark 2.
A well-known technique to address the feasibility issues in MPC is to employ the so-called soft constraint where slack variables are introduced to relax hard (state) constraint. Interested readers may refer to [7,9] which provide comprehensive discussions on constraint relaxation of MPC using soft constraint. Let the target zone be characterized by where . When soft constraint is used, the penalty for constraint violation has the following form:
The function defined above is also positive definite with respect to the target zone . Note that the zone tracking penalty is different from in Equation (9). In the above example, implementing the soft-constraint penalty requires artificial variables whereas for the number is . The soft-constraint penalty may be better described as an output zone tracking penalty (considering as the system output) whereas in Equation (9) is a zone tracking penalty for system state and input. The pros and cons of state zone tracking against output zone tracking calls for further investigation. One advantage of using the state zone tracking penalty is that it allows set-theoretic method ([15]) in the EMPC design. In Section 4 an algorithm based on set-theoretic method will be proposed to modify the target zone.
3.2. Stability Analysis
In the following, we establish sufficient conditions for asymptotic stability of the optimal steady state .
Definition 1.
(Strictly dissipative systems) The system of Equation (1) is strictly dissipative with respect to the supply rate if there exists a continuous storage function and a function such that the following holds for all and :
Assumption A1.
(Strict dissipativity, [16]) The system of Equation (1) is strictly dissipative with respect to the supply rate
Assumption A2.
(weak controllability, ([17])) There exists a function such that for all , there exists a feasible solution to Equation (4) such that:
Theorem 1.
If Assumptions 1 and 2 hold, then the optimal steady state is asymptotically stable under the EMPC of Equation (4) with a region of attraction .
Proof.
To proceed, we define the rotated cost as:
From Assumption 1, the rotated cost satisfies
Substitute Equation (11) into the Equation (4), the optimization problem of Equation (4) can be equivalently written as follows:
The last three terms in the objective function of the above optimization are all constant and can be dropped (because of constraints Equations (6) and (8)). The above optimization is then reduced to:
where . Since is non-negative and taking into Equation (12), we have:
Moreover, Assumption 2 implies the existence of a function such that (see [17] Appendix):
Finally, the value function is strictly non-increasing and satisfies:
Remark 3.
If the optimal steady state lies in the interior of the target zone, then asymptotic stability of the optimal steady state implies finite-time convergence into the target zone. However, if the optimal steady state is on the boundary of the target zone, asymptotic stability of the optimal steady state does not imply finite-time convergence to the target zone. One way to still achieve nominal finite-time convergence to the target zone is to implement the whole predicted input sequence instead of only the first element. That is, for . At the sampling time , re-evaluate the optimization of Equation (4) based on the state measurement . Due to the terminal constraint, the nominal system will reach the optimal steady state in N steps. Another way is to employ sufficiently large norm zone tracking penalty (large ) which is known to result in deadbeat control policy ([18]).
3.3. Prioritized Zone Tracking
In practice, zone control objectives are usually associated with important or urgent objectives such as operation safety and product specification. Thus a natural question to ask is how to pick the zone tracking penalty such that the zone tracking is prioritized over the economic objective? In other words, how to ensure that the system stays in the target zone whenever possible? The answer has to do with the so-called exact penalty function. To proceed with the discussion, we introduce the concept of the dual norm:
Definition 2.
(dual norm) Consider the p norm of a vector u, , . We refer to as the dual norm of where is defined as follows:
It can be verified that is the dual norm of and vice versa. Consider the following constrained optimization problem:
The above hard-constraint optimization problem can be recast as the following soft-constraint optimization problem:
where c is a positive scalar. It is conceivable that if the penalty c is sufficiently large, then the solution to the Equation (17) will be identical to Equation (16). The following well-known result specifies how large is sufficiently large for c:
Theorem 2.
Consider the optimization of Equations (16) and (17). Assume that the solutions to both problems satisfy second-order sufficient conditions, and let λ denote the vector of the Lagrange multipliers of Equation (16). If where is the dual norm of , then the solutions to Equations (16) and (17) are identical.
Proof.
The proof can be found in [19] Theorem 14.3.1. ☐
Any penalty function satisfying the conditions in Theorem 2 is called the exact penalty function. When exact penalty is used, the soft-constraint optimization problem has the same solution as the original problem. This means that if we treat the feasibility region, , as the target zone and the penalty, , as the zone tracking penalty, the exact penalty prioritizes the zone tracking objective over the economic objective.
Remark 4.
The exact penalty function problem for Equation (16) is usually written in the following form:
The above formulation is equivalent to the problem of Equation (17). With slight abuse of language, we refer to the soft-constraint formulation in Equation (17) with as the exact penalty. Essentially what allows the exact penalty to be exact or to prioritize the constraint objective is the non-smoothness of the penalty function at . In the case of equality constraint, the same result applies since one can also treat as a set of inequality constraints and . In this case, the exact penalty function problem becomes:
In the light of Theorem 2, we can construct the following optimization problem in which zone tracking is made the hard constraint:
To make the statement of the final result more compact, we employ the definition of the N-step reachable set [20]:
Definition 3.
(N-step reachable set) We use to denote the set of states that can be steered to in N steps while satisfying the state and input constraints . That is,
Based on the above definition, the EMPC is capable of maintaining the system in the target zone only if . Now we are ready to state and prove the final result:
Theorem 3.
Proof.
Theorem 3 implies that if the norm penalty is sufficiently large, then the zone tracking objective is prioritized over the economic objective. Note that the constraints (18c)–(18e) can be combined by canceling the slack variables and into the compact form:
Thus the EMPC of Equation (18) yields the same solution to the following EMPC constrained by the target zone:
The constraint (6) is removed because . Therefore, sufficiently large norm penalty term in effect can convert the zone tracking objective into hard constraints whenever possible.
Remark 5.
Note that exact penalty cannot be achieved by the quadratic term unless can be made infinitely large [9]. Note also that to ensure for all and , the condition needs to be satisfied for Lagrange multipliers λ associated with all . Finding the exact lower bound for such is in general difficult. The task is possible for linear systems with quadratic tracking costs and polyhedral constraints ([8]).
4. Modified Target Zone
The EMPC with zone tracking framework discussed in Section 3 is applicable to a broad class of control systems with multiple objectives involving economic optimization, zone tracking or setpoint tracking. A challenging problem in practice that largely affects the performance of MPC is parameter tuning. Specifically, for the EMPC of Equation (10), how does one pick and such that the closed-loop system achieves the desired tradeoff between magnitude and duration of zone tracking violation as well as economic performance? As a rule of thumb, if the zone objective is more important than economic objective, one should pick sufficiently large such that it makes zone tracking the exact penalty, and tune relative to to tradeoff magnitude and duration of constraint violation. While this method suits most scenarios, for certain systems which we will show in the simulation, naive choice of a large zone tracking penalty may lead to arbitrarily poor transient economic performance.
Parameter tuning can be a challenging task for a number of reasons: (i) the number of tuning parameters can be large depending on the number of system states and inputs. In the EMPC formulation Equation (10), we have lumped all tuning parameters into two parameters, and , for simplicity of exposition. Note that in principle each element of the system state and input may be assigned a weight, for quadratic penalty a weighting matrix may be used; (ii) there is a lack of transparency in the relationship between closed-loop performance and tuning parameters; (iii) the difficulty may be intrinsic to the problem. That is, suitable tuning parameters may vary under different conditions or states. These will be illustrated in the simulation example.
Motivated by the above considerations, we propose an algorithm to modify the target zone. The idea is to construct a modified target zone which is an invariant subset of the original target zone in which closed-loop transient economic performance is guaranteed. In this way, EMPC tracking the modified target zone will have guaranteed economic performance once the system is in the modified target zone. Moreover, under exact zone tracking penalty, the closed-loop system will not leave the target zone once it enters. EMPC tracking the modified target zone allows the user to tradeoff magnitude and duration of zone tracking violation by tuning and without worrying about poor transient economic performance. The proposed algorithm is outlined below:
| Algorithm 1: Modified target zone. | |
| 1. | Choose some and |
| 2. | Set |
| 3. | for |
| Calculate with Equation. (20) | |
| end | |
| 4. | The modified target zone is |
The modified target zone , obtained by Algorithm 1 is a zone in which the system can be steered to the optimal steady state in M steps in the target zone while the economic performance of each step is upper bounded by . Once the modified target zone is obtained, the EMPC of Equation (10) may be implemented with the original target zone replaced by the modified target zone . The properties of the EMPC that tracks the modified target zone are summarized in the following theorem:
Theorem 4.
Consider the system of Equation (1) under the EMPC of Equation (10) with the target zone replaced with the modified target zone and .
- (i)
- If is an exact zone tracking penalty for for all , then the modified target zone is forward invariant under the closed-loop system. That is,
- (ii)
- If in addition Assumptions 1 and 2 hold, the transient economic performance in the modified target zone is upper bounded such that for any time instant K where , the following holds:
Proof.
(i) First, we prove that the sets , , defined in Equation (20) are nested such that for . We can start from . It is easy to verify that because the point satisfies the conditions in Equation (20) for . Thus we have . Then we can prove by induction. Suppose that for all . Consider in Equation (20) and , we have . Now consider in Equation (20) and . Since for any , is a subset of . This proves that the sets are nested for all . The nestedness of the set implies that whenever , there is a feasible sequence bounded in that reaches the optimal steady state in M steps. This further implies that the exact penalty for tracking the modified target zone will act as hard constraint and prevent the system from leaving the modified target zone .
(ii) Let the optimal solution at time instant n be denoted by and , . The corresponding terminal state is because of the terminal constraint Equation (8). A feasible solution at time instant can be constructed as follows: , with the corresponding state trajectory: . Let denote the optimal value function at time n, the value function is upper bounded by the above feasible solution, which yields:
Rearranging the above and replacing with , we have:
Summing both sides from to ∞:
If , from Algorithm 1 and Equation (20), there exist state and input trajectories which satisfy:
The above implies that
Moreover, under Assumptions 1 and 2, we know from Theorem 1 that . This means that the optimal solution as . Thus we have
Remark 6.
The tuning parameters M and α in Algorithm 1 may have significant impacts shaping the modified target zone. The parameter α can be thought of as the instantaneous acceptable performance loss and the total transient economic performance loss in the modified target zone. Under the same M, larger α may, but not necessarily, result in larger modified target zone. The parameter α is useful only if . Similarly, under the same α, larger M may result in larger modified target zone. It is possible that the modified target zone is finitely determined. That is, for some , for all . In this case Algorithm 1 may be stopped after K steps. In the extreme case where , the modified target zone is a singleton of the optimal steady state . The proposed approach becomes the conventional set-point tracking MPC. On the other hand if both M and α are sufficiently large then the modified target zone equals or approaches the maximal control invariant set in the target zone. We note that the modified target zone based on the tuning parameters M and α essentially provides a means to make parameter tuning of the original problem more transparent.
Remark 7.
Note that step (3) of Algorithm 1 involves set projection and set intersection operations. These operations could be computationally difficult for generic nonlinear systems. For linear systems with polyhedral target set and polyhedral performance level set , Equation (20) can be computed using Fourier–Motzkin elimination as well as the redundancy removal method in ([21]). Note also that large M or a large number of system states may result in complex representations of the modified target zone (a set characterized by many inequalities) in Algorithm 1. Therefore computation complexity of the modified EMPC also needs to be taken into consideration while choosing parameters M and α.
5. Simulation
5.1. Example 1
The first example is a linear scalar system:
With state and input constraints , respectively. The target set is = . The economic cost is which corresponds to an optimal steady state . Two different initial states: and are considered to indicate the asymmetric closed-loop performance. The control horizon is when not specified. The simulations and discussions are carried out as follows: first, we will simulate the EMPC in Section 3 which tracks the original target zone. Exact zone tracking penalty is used and special attention is paid to the difficulties in parameter tunning. Then we will simulate EMPC with modified target zone in Section 4 to demonstrate the advantage of the proposed approach.
5.1.1. EMPC Tracking the Original Target Zone
Figure 1 shows the closed-loop input trajectories of the EMPC of Equation (10) with and respectively. The corresponding economic performances are shown in Figure 2. It is seen that all closed-loop trajectories reach the target zone in finite steps and asymptotically converge to the optimal value . As the quadratic zone tracking penalty increases, the control action gets milder, the magnitude of zone tracking violation becomes smaller but it takes longer to reach the target zone.
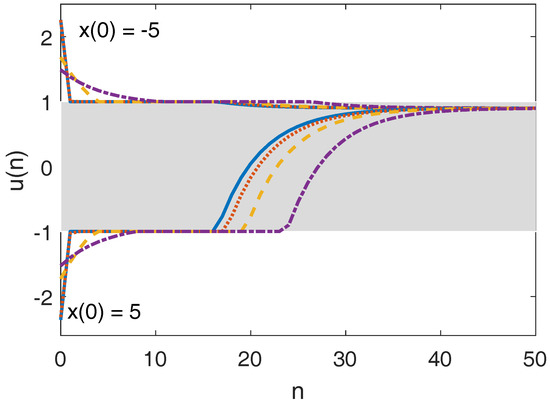
Figure 1.
Closed-loop input trajectories of EMPC of Equation (10) with and (solid), (dotted), (dashed), (dash dotted), respectively. Shaded area depicts the input target zone. The upper and lower part correspond to initial state and = 5, respectively.
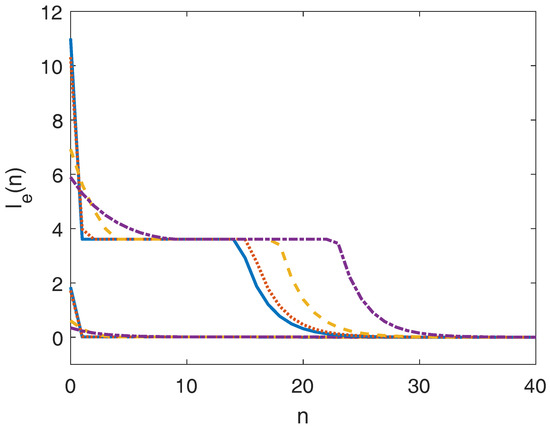
Figure 2.
Closed-loop economic performance of EMPC of Equation (10) with and (solid), (dotted), (dashed), (dash dotted), respectively. The upper and lower part correspond to initial state and , respectively.
Another interesting observation is the target boundary riding. That is, the closed-loop input trajectories reach the target zone and stay on the zone boundary (at or ) for some time before approaching the optimal steady state value. Similar phenomena of zone boundary riding due to norm penalty was observed in [7]. The occurrence of boundary riding is due to the exact zone tracking penalty and inconsistency between the zone tracking and economic objective (which also includes setpoint tracking).
Comparing the trajectories emitting from and with the same zone tracking penalty, we can see that they are (almost) symmetric outside or on the zone boundary, and asymmetric inside the target zone. Again, this is due to the large zone tracking penalty. The transient economic performance of different trajectories are summarized in Table 1. From Figure 2 and Table 1, we can see that economic performance is less of concern if the initial state is . In this case we may pick the zone tracking penalty regardless of the transient economic performance. If smaller zone tracking violation is desirable, a large quadratic penalty, , may be picked. However, if the initial state is , transient performance varies significantly under different quadratic penalties. In this case it might be desirable to pick smaller quadratic zone tracking penalty to achieve better transient economic performance. This shows that the difficulty of parameter tuning is intrinsic to the system.

Table 1.
Transient economic performance of EMPC of Equation (10).
Figure 3 shows the input trajectories under different control horizons . It is seen that with poor choices of the penalties and , increasing the control horizon N may result in longer duration of target boundary riding and deteriorated economic performance. This also indicates difficulty in parameter tuning and controller design since one would expect larger control horizon to result in better performance.
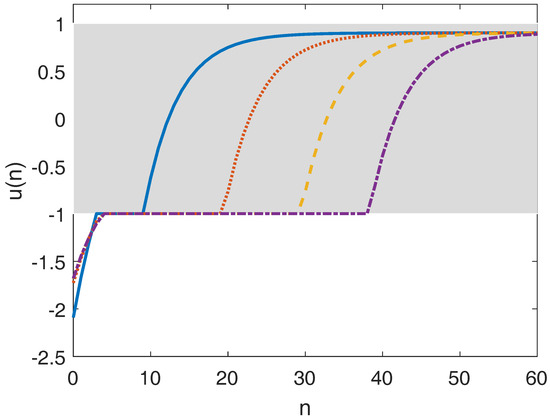
Figure 3.
Closed-loop input trajectories of EMPC in Equation (10) with , and , (solid), (dotted), (dashed), (dash dotted), respectively.
5.1.2. EMPC Tracking the Modified Target Zone
Apply Algorithm 1 to the example with and , the modified target zone is obtained as follows:
where , , . The constraint set , target zone and modified target zone are illustrated in Figure 4.
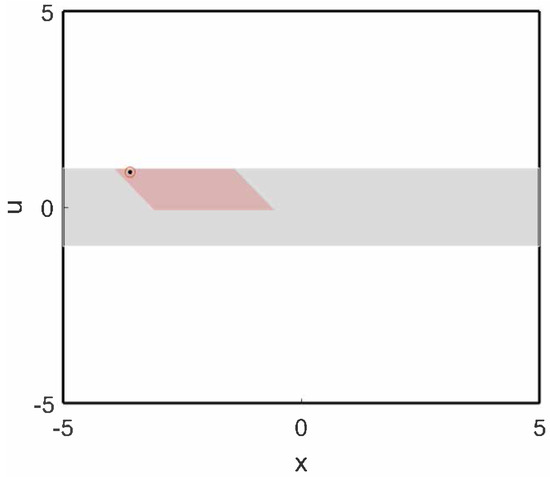
Figure 4.
The constraint set (box), target zone (shaded rectangle) and modified target zone (parallelogram). The circle indicates the optimal steady state .
Figure 5 and Figure 6 show the closed-loop input trajectories and economic performances of the EMPC tracking the modified target zone in Equation (24). Comparing Figure 5 and Figure 6 with Figure 1 and Figure 2, we can see that EMPC tracking the modified target zone leads to more balanced economic performance in the target zone while accomplishing fast zone tracking for the target zone . Boundary riding takes place at the boundary of the modified target zone which corresponds to the economic performance bound specified by . This makes a good tuning parameter.
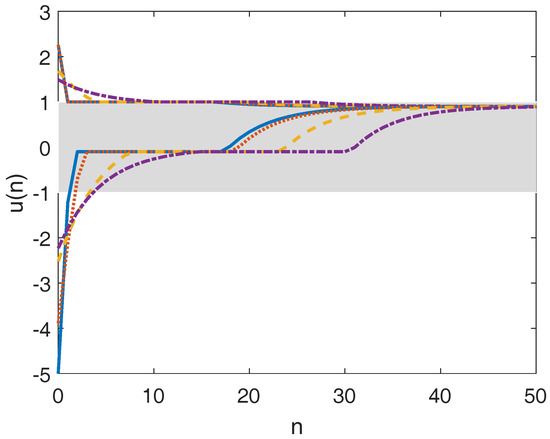
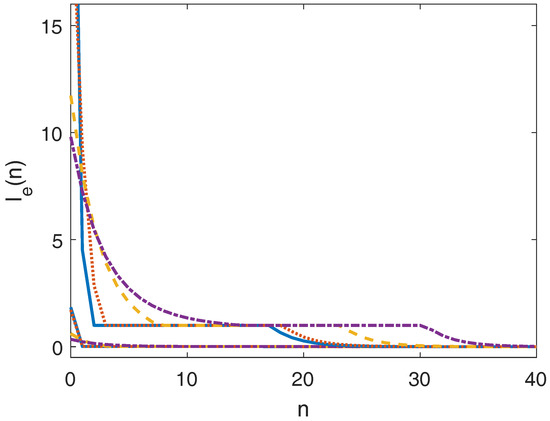
Table 2 compares the transient economic performance of the EMPC tracking the target zone and EMPC tracking the modified target zone . It is seen that both EMPCs achieve almost the same economic performance for the initial state . When , EMPC tracking the modified target zone results in improved transient economic performance with less variations under different tuning parameter . This implies that we can now use to tune for zone tracking (magnitude versus duration) and use and M associated with the modified target zone to tune for economic performance. Tracking the modified target zone effectively decomposes the zone tracking and economic objectives.

Table 2.
Comparison of the transient economic performance of EMPC tracking the target zone and EMPC tracking the modified zone .
5.2. Example 2
The second example is a building heating control system taken from [22]. The heating system is modeled as the following discrete-time linear system:
where , and are the state, input and disturbance vectors, respectively. The process variables are described in Table 3. The sampling time of the system is 0.5 h. The system matrices are

Table 3.
Building heating control system variable description.
The control objective is to keep the room temperature between 20 °C and 21 °C while reducing energy consumption from the heat pump compressor. The target zone is thus , the economic cost is where p is the electricity price. Without loss of generality in the simulation results, we assume that the electricity price USD/kW·h. We assume constant ambient temperature and solar radiation . The control input is subject to the constraint W. The optimal steady state which solves Equation (3) is: , .
In the simulation, we compare three different control schemes: (i) a set-point tracking MPC which tracks the optimal steady state with a stage cost where and ; (ii) the EMPC of Equation (10) with and which is equivalent to the EMPC in [22] with a large zone tracking penalty; and (iii) EMPC with modified target zone by Algorithm 1 with and . The initial state is . The control horizons of all controllers are (48 h). The room temperature and heat input profiles are shown in Figure 7, the phase space plot of the system is shown in Figure 8, transient economic performances or the additional electricity cost of the three control schemes are summarized in Table 4. It is seen that EMPC with prioritized zone tracking is able to reach the desired room temperature zone in the shortest period of time of 10 h but at a higher electricity cost of $411.1 with a significant overshoot. The conventional setpoint tracking MPC has the slowest response and reaches the desired temperature in 24 h with an additional electricity cost of $363.3. EMPC with the modified target zone yields a balanced solution which reaches the desired room temperature in 16 h with an additional electricity cost of $369.8.
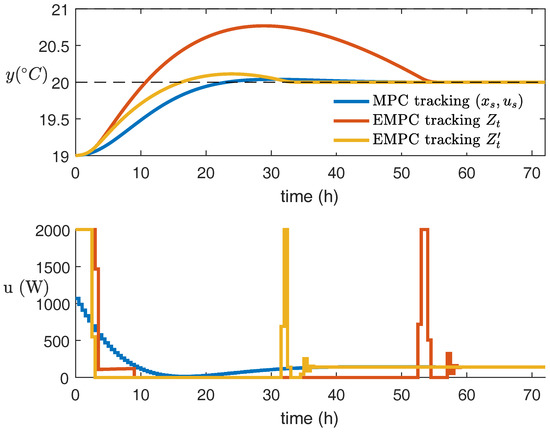
Figure 7.
Room temperature and heat input profiles under different control schemes.
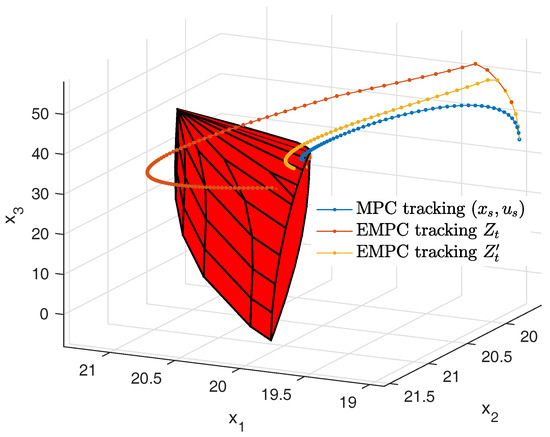
Figure 8.
Phase space plot of different control schemes. The polyhedron depicts the modified target zone .

Table 4.
Additional electricity cost of the three control schemes.
Moreover, we investigated the closed-loop performance of the EMPC with modified target zones under varying parameters and M in Algorithm 1. It was found that in this example, the closed-loop behavior is more sensitive to M than to . Figure 9 shows the room temperature and heat input profiles of EMPC with modified target zone by Algorithm 1 with and . It is seen that as M increases, the time to reach the desired room temperature deceases from 24 to 15 h, which suggests that M is a good tuning parameter.
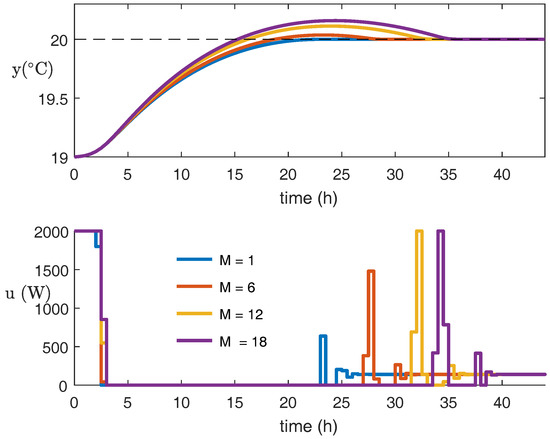
Figure 9.
Room temperature and heat input profiles of EMPC with modified target zone by Algorithm 1 with and .
6. Conclusions
In this work, we proposed an EMPC framework with integrated zone control. The proposed EMPC design is essentially a multi-objective optimization problem in which the magnitude and duration of zone objective violation as well as the economic performance are traded off. Asymptotic stability of the optimal steady state and prioritized zone tracking with exact penalty function were discussed. An algorithm to modify the target zone is proposed which simplifies the parameter tuning procedure and decouples the zone tracking and economic objective. Future research will consider the proposed approach for time-varying and uncertain systems.
Author Contributions
Su Liu and Jinfeng Liu conceived the idea of the proposed controller design. Su developed the theory, carried out the simulations and wrote the paper. Jinfeng Liu supervised the research findings and reviewed the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, J.Z. Challenging control problems and emerging technologies in enterprise optimization. Control Eng. Pract. 2003, 11, 847–858. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Angeli, D.; Bates, C.N. Fundamentals of economic model predictive control. In Proceedings of the 51th IEEE Conference on Decision and Control, Grand Wailea, HI, USA, 10–13 December 2012; pp. 3851–3861. [Google Scholar]
- Grüne, L. Economic receding horizon control without terminal constraints. Automatica 2013, 49, 725–734. [Google Scholar] [CrossRef]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Liu, S.; Liu, J. Economic model predictive control with extended horizon. Automatica 2016, 73, 180–192. [Google Scholar] [CrossRef]
- Scokaert, P.; Rawlings, J.B. Feasibility issues in linear model predictive control. AIChE J. 1999, 45, 1649–1659. [Google Scholar] [CrossRef]
- Kerrigan, E.C.; Maciejowski, J.M. Soft constraints and exact penalty functions in model predictive control. In Proceedings of the UKACC International Conference Control, Cambridge, UK, 4–7 October 2000. [Google Scholar]
- De Oliveira, N.M.C.; Biegler, L.T. Constraint handing and stability properties of model-predictive control. AIChE J. 1994, 40, 1138–1155. [Google Scholar] [CrossRef]
- Zeilinger, M.N.; Morari, M.; Jones, C.N. Soft Constrained Model Predictive Control With Robust Stability Guarantees. IEEE Trans. Autom. Control 2014, 59, 1190–1202. [Google Scholar] [CrossRef]
- Askari, M.; Moghavvemi, M.; Almurib, H.A.F.; Haidar, A.M.A. Stability of Soft-Constrained Finite Horizon Model Predictive Control. IEEE Trans. Ind. Appl. 2017, 53, 5883–5892. [Google Scholar] [CrossRef]
- Ferramosca, A.; Limon, D.; González, A.H.; Odloak, D.; Camacho, E. MPC for tracking zone regions. J. Process Control 2010, 20, 506–516. [Google Scholar] [CrossRef]
- Lez, A.H.G.; Marchetti, J.L.; Odloak, D. Robust model predictive control with zone control. IET Control Theory Appl. 2009, 3, 121–135. [Google Scholar]
- González, A.H.; Odloak, D. A stable MPC with zone control. J. Process Control 2009, 19, 110–122. [Google Scholar] [CrossRef]
- Blanchini, F. Set invariance in control. Automatica 1999, 35, 1747–1767. [Google Scholar] [CrossRef]
- Amrit, R.; Rawlings, J.B.; Angeli, D. Economic optimization using model predictive control with a terminal cost. Annu. Rev. Control 2011, 35, 178–186. [Google Scholar] [CrossRef]
- Diehl, M.; Amrit, R.; Rawlings, J.B. A Lyapunov function for economic optimizing model predictive control. IEEE Trans. Autom. Control 2011, 56, 703–707. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B. Linear programming and model predictive control. J. Process Control 2000, 10, 283–289. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Kerrigan, E.C.; Maciejowski, J.M. Invariant sets for constrained nonlinear discrete-time systems with application to feasibility in model predictive control. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 5, pp. 4951–4956. [Google Scholar]
- Keerthi, S.; Gilbert, E. Computation of minimum-time feedback control laws for discrete-time systems with state-control constraints. IEEE Trans. Autom. Control 1987, 32, 432–435. [Google Scholar] [CrossRef]
- Halvgaard, R.; Poulsen, N.K.; Madsen, H.; Jørgensen, J.B. Economic model predictive control for building climate control in a smart grid. In Proceedings of the IEEE Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).