Implicit Equations of the Henneberg-Type Minimal Surface in the Four-Dimensional Euclidean Space

Abstract

Considering the Weierstrass data as $(\psi ,f,g)=(2,1-z^{-m},z^n)$, we introduce a two-parameter family of Henneberg-type minimal surface that we call ${\mathfrak{H}}_{m,n}$ for positive integers $(m,n)$ by using the Weierstrass representation in the four-dimensional Euclidean space ${\mathbb{E}}^4$. We define ${\mathfrak{H}}_{m,n}$ in $(r,\theta )$ coordinates for positive integers $(m,n)$ with $m\ne 1,n\ne -1,-m+n\ne -1$, and also in $(u,v)$ coordinates, and then we obtain implicit algebraic equations of the Henneberg-type minimal surface of values $(4,2)$.

1. Introduction

The theory of surfaces has an important role in mathematics, physics, biology, architecture, see e.g., the classical books [1,2] and papers [3,4,5,6,7,8,9].

A minimal surface in the three-dimensional Euclidean space ${\mathbb{E}}^3$, also in higher dimensions, is a regular surface for which the mean curvature vanishes identically. See [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] for details. On the other hand, a Henneberg surface [4,5,6], also obtained by the Weierstrass representation [8,9] is well-known classical minimal surface in ${\mathbb{E}}^3$.

In the four-dimensional Euclidean space ${\mathbb{E}}^4$, a general definition of rotation surfaces was given by Moore in [28] as follows

$$X(u,t)=\left(\begin{array}{c}{x}_1(u)cos(at)-x_2(u)sin(at)\\ x_1(u)cos(at)+x_2(u)sin(at)\\ x_3(u)cos(bt)-x_4(u)sin(bt)\\ x_3(u)cos(bt)+x_4(u)sin(bt)\end{array}\right).$$

A more restricted case can be found in [29]:

$$W(u,t)=(x_1(u),x_2(u),r(u)cos(t),r(u)sin(t)).$$

It is a bit too general since the curve is not located in any subspace before rotation.

Güler and Kişi [30] studied the Weierstrass representation, the degree and the classes of surfaces in ${\mathbb{E}}^4$, see [31,32,33,34,35,36,37,38] for some previous work.

In this paper, we study a two-parameter family of Henneberg-type minimal surfaces using the Weierstrass representation in ${\mathbb{E}}^4$. We give the Weierstrass equations for a minimal surface in ${\mathbb{E}}^4$, and obtain two normals of the surface in Section 2.

In Section 3, we introduce complex form of the Henneberg-type minimal surface in 4-dimension, considering 3-dimension case. Then we define Henneberg-type minimal surface in the polar coordinates using real part for values $(m,n)$ called ${\mathfrak{H}}_{m,n}$, where m and n are positive integers with $m\ne 1$, $n\ne -1$, $-m+n\ne -1$. We also focus on Henneberg-type minimal surface ${\mathfrak{H}}_{4,2}$ using the Weierstrass representation in ${\mathbb{E}}^4$, and give explicit parametrizations for minimal Henneberg-type surface of values $(4,2)$.

Finally, we describe how we obtained the implicit algebraic equation of the Henneberg-type surface ${\mathfrak{H}}_{4,2}$, by using elimination techniques based on Groebner Basis in the software package Maple in Section 4.

2. Weierstrass Equations for a Minimal Surface in 𝔼⁴

We identify $\overrightarrow{x}$ and $\overrightarrow{x^t}$ without further comment. Let ${\mathbb{E}}^4=\left(\{\overrightarrow{x}={(x_1,x_2,x_3,x_4)}^t|x_i\in \mathbb{R}\},⟨·,·⟩\right)$ be the 4-dimensional Euclidean space with metric $⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_3{y}_3+x_4{y}_4$.

Hoffman and Osserman [12] gave the Weierstrass equations for a minimal surface in ${\mathbb{E}}^4$:

$$\Phi (z)=\frac{\psi }{2}\left[1+fg,i(1-fg),f-g,-i(f+g)\right].$$

(1)

Here, $\psi$ is analytic and the order of the zeros of $\psi$ must be greater than the order of the poles of f, g at each point.

$$\begin{array}{ccc}\hfill X_x-i{X}_y& =& \Phi (z)\hfill \\ & =& [(1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y,\hfill \\ & & \left(f_2{g}_1+f_1{g}_2\right)x-y+f_1{g}_{1}y-f_2{g}_{2}y,\hfill \\ & & \left(f_1-g_1\right)x+(-f_2+g_2)y,\left(f_2+g_2\right)x+(f_1+g_1)y]\hfill \\ & & -i[-y-f_1(g_{2}x+g_{1}y)+f_2(-g_{1}x+g_{2}y),\hfill \\ & & (-1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y,\hfill \\ & & +(-f_2+g_2)x+(-f_1+g_1)y,\hfill \\ & & \left(f_1+g_1\right)x-(f_2+g_2)y],\hfill \end{array}$$

where $\psi =2z$ and $f=f_1+i{f}_2$, $g=g_1+i{g}_2.$ We set

$$\begin{array}{ccc}\hfill w_1& =& [-(f_2{g}_{1}x+f_1{g}_{2}x-y+f_1{g}_{1}y-f_2{g}_{2}y),\hfill \\ & & (1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y,\hfill \\ & & -(\left(f_2+g_2\right)x+(f_1+g_1)y),\hfill \\ & & \left(f_1-g_1\right)x+(-f_2+g_2)y]\hfill \end{array}$$

which is perpendicular to $X_x,$ and

$$\begin{array}{ccc}\hfill w_2& =& [-((-1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y),\hfill \\ & & -y-f_1(g_{2}x+g_{1}y)+f_2(-g_{1}x+g_{2}y),\hfill \\ & & -(f_{1}x+g_{1}x-(f_2+g_2)y),\hfill \\ & & -f_{2}x+g_{2}x+(-f_1+g_1)y]\hfill \end{array}$$

which is perpendicular to $X_y$.

So far, we see that:

$$\begin{array}{ccc}\hfill b& =& ⟨X_x,w_2⟩\hfill \\ & =& -(-1+f_1^2+f_2^2)(1+g_1^2+g_2^2)(x^2+y^2)\hfill \\ & =& -⟨X_y,w_1⟩,\hfill \end{array}$$

while

$$\begin{array}{ccc}\hfill a& =& ⟨X_x,X_x⟩\hfill \\ & =& ⟨X_y,X_y⟩\hfill \\ & =& \left(1+f_1^2+f_2^2\right)(1+g_1^2+g_2^2)(x^2+y^2)\hfill \\ & =& ⟨w_j,w_j⟩.\hfill \end{array}$$

Next, we use Gram-Schmidt to find an orthonormal basis for the normal space. Let $e_1=X_x/\sqrt{a}$ and $e_2=X_y/\sqrt{a}.$

Then we get

$$n_1=\sqrt{\frac{a}{a^2-b^2}}\left(w_1+\frac{b}{a}{X}_y\right)$$

(2)

and

$$n_2=\sqrt{\frac{a}{a^2-b^2}}\left(w_2-\frac{b}{a}{X}_x\right),$$

(3)

where

$$\begin{array}{ccc}\hfill a^2-b^2& =& 4\left(f_1^2+f_2^2\right){\left(x^2+y^2\right)}^2{\left(g_1^2+g_2^2+1\right)}^2,\hfill \\ \hfill \sqrt{\frac{a}{a^2-b^2}}& =& \sqrt{\frac{1+f_1^2+f_2^2}{4\left(f_1^2+f_2^2\right)\left(x^2+y^2\right)\left(g_1^2+g_2^2+1\right)}},\hfill \\ \hfill \frac{b}{a}& =& -\frac{-1+f_1^2+f_2^2}{1+f_1^2+f_2^2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill w_1& =& \left(\begin{array}{c}-\left(f_1{g}_2+f_2{g}_1\right)x-\left(-1+f_1{g}_1-f_2{g}_2\right)y\\ (1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y\\ -\left(f_2+g_2\right)x-(f_1+g_1)y\\ \left(f_1-g_1\right)x+(-f_2+g_2)y\end{array}\right),\hfill \\ \hfill w_2& =& \left(\begin{array}{c}-((-1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y)\\ -y-f_1(g_{2}x+g_{1}y)+f_2(-g_{1}x+g_{2}y)\\ -(f_{1}x+g_{1}x-(f_2+g_2)y)\\ -f_{2}x+g_{2}x+(-f_1+g_1)y\end{array}\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill X_x& =& \left(\begin{array}{c}(1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y\\ f_2{g}_{1}x+f_1{g}_{2}x-y+f_1{g}_{1}y-f_2{g}_{2}y\\ f_{1}x-g_{1}x+(-f_2+g_2)y\\ f_{2}x+g_{2}x+(f_1+g_1)y\end{array}\right),\hfill \\ \hfill X_y& =& \left(\begin{array}{c}-\left(f_1{g}_2+f_2{g}_1\right)x+\left(-1-f_1{g}_1+f_2{g}_2\right)y\\ (-1+f_1{g}_1-f_2{g}_2)x-(f_2{g}_1+f_1{g}_2)y\\ \left(-f_2+g_2\right)x+(-f_1+g_1)y\\ \left(f_1+g_1\right)x-(f_2+g_2)y\end{array}\right).\hfill \end{array}$$

With $x=rcos(\theta )$, $y=rsin(\theta )$, $f_1=1-r^{-m}cos(m\theta )$, $f_2=-r^{-m}sin(m\theta )$, $g_1=r^{n}cos(n\theta )$, $g_2=r^{n}sin(n\theta )$ we have the following two normals:

$$n_1(r,\theta )=A\left(\begin{array}{c}Bsin\left(\theta \right)-r^{2m}{r}^{n}sin\left(\left(n+1\right)\theta \right)+r^m{r}^{n}sin\left(\left(m+n+1\right)\theta \right)\\ Bcos\left(\theta \right)+r^{2m}{r}^{n}cos\left(\left(n+1\right)\theta \right)-r^m{r}^{n}cos\left(\left(m+n+1\right)\theta \right)\\ -r^{2m}sin\left(\theta \right)+r^{m}sin\left(\left(m+1\right)\theta \right)-B{r}^{n}sin\left(\left(n+1\right)\theta \right)\\ r^{2m}cos\left(\theta \right)-r^{m}cos\left(\left(m+1\right)\theta \right)-B{r}^{n}cos\left(\left(n+1\right)\theta \right)\end{array}\right),$$

(4)

and

$$n_2(r,\theta )=A\left(\begin{array}{c}Bcos\left(\theta \right)-r^{2m}{r}^{n}cos\left(\left(n+1\right)\theta \right)+r^m{r}^{n}cos\left(\left(m+n+1\right)\theta \right)\\ -Bsin\left(\theta \right)-r^{2m}{r}^{n}sin\left(\left(n+1\right)\theta \right)+r^m{r}^{n}sin\left(\left(m+n+1\right)\theta \right)\\ -r^{2m}cos\left(\theta \right)+r^{m}cos\left(\left(m+1\right)\theta \right)-B{r}^{n}cos\left(\left(n+1\right)\theta \right)\\ -r^{2m}sin\left(\theta \right)+r^{m}sin\left(\left(m+1\right)\theta \right)+B{r}^{n}sin\left(\left(n+1\right)\theta \right)\end{array}\right),$$

(5)

where $A={\left[B\left(r^{2n}+1\right)\left(2r^{2m}-2r^{m}cos\left(m\theta \right)+1\right)\right]}^{-1/2},$ $B=r^{2m}-2r^{m}cos\left(m\theta \right)+1.$

When we check inner products of $n_1$ and $n_2$ with themselves, we get

$$\begin{array}{ccc}\hfill ⟨n_1,n_1⟩& =& ⟨n_2,n_2⟩\hfill \\ & =& A^2\left(r^{2n}+1\right)\left(r^{2m}+r^{4m}-2r^{3m}cos\left(m\theta \right)+B^2\right)\hfill \\ & =& 1.\hfill \end{array}$$

3. Henneberg Family of Surfaces ${\mathfrak{H}}_{m,n}$

In 3-space, the Weierstrass data of the Henneberg surface is known as $(f,g)=(1-1/z^4,z)$. In 4-space, we consider general case of it and choose $\psi =2$, $f=1-1/z^m$ and $g=z^n$ in (1). This gives

$$\Phi (z)=\left(1+z^n-z^{n-m},i(1-z^n+z^{n-m}),1-z^{-m}-z^n,-i(1-z^{-m}+z^n)\right).$$

(6)

We integrate (6) to get complex form of the family of Henneberg-type minimal surface:

$$\int \Phi (z)dz=\left(\begin{array}{c}z+{\displaystyle \frac{z^{n+1}}{n+1}}-{\displaystyle \frac{z^{-m+n+1}}{-m+n+1}}\\ i\left(z-{\displaystyle \frac{z^{n+1}}{n+1}}+{\displaystyle \frac{z^{-m+n+1}}{-m+n+1}}\right)\\ z-{\displaystyle \frac{z^{-m+1}}{-m+1}}-{\displaystyle \frac{z^{n+1}}{n+1}}\\ -i\left(z-\frac{z^{-m+1}}{-m+1}+{\displaystyle \frac{z^{n+1}}{n+1}}\right)\end{array}\right)$$

(7)

with $m\ne 1,n\ne -1,-m+n\ne -1.$ Therefore, we get following definition:

Definition 1.

Taking the real part of the (7), with $z=r{e}^{i\theta }$, we obtain family of Henneberg-type minimal surface ${\mathfrak{H}}_{m,n}$ as follows

$${\mathfrak{H}}_{m,n}(r,\theta )=\left(\begin{array}{c}rcos(\theta )+{\displaystyle \frac{r^{n+1}cos((n+1)\theta )}{n+1}}-{\displaystyle \frac{r^{-m+n+1}cos((-m+n+1)\theta )}{-m+n+1}}\\ -rsin(\theta )+{\displaystyle \frac{r^{n+1}sin((n+1)\theta )}{n+1}}-{\displaystyle \frac{r^{-m+n+1}sin((-m+n+1)\theta )}{-m+n+1}}\\ rcos(\theta )-{\displaystyle \frac{r^{-m+1}cos((-m+1)\theta )}{-m+1}}-{\displaystyle \frac{r^{n+1}cos((n+1)\theta )}{n+1}}\\ rsin(\theta )-{\displaystyle \frac{r^{-m+1}sin((-m+1)\theta )}{-m+1}}+{\displaystyle \frac{r^{n+1}sin((n+1)\theta )}{n+1}}\end{array}\right),$$

(8)

where $m\ne 1,n\ne -1,-m+n\ne -1.$

Algebraic Henneberg-Type Minimal Surface ${\mathfrak{H}}_{4,2}$

Next, we choose $(\psi ,f,g)=(2,1-1/z^4,z^2)$ in (1). This means $(m,n)=(4,2)$. Hence, we can define Henneberg-type surface ${\mathfrak{H}}_{4,2}$ in $(r,\theta )$ and $(u,v)$ coordinates in the four-dimensional Euclidean space.

Definition 2.

In $(r,\theta )$ coordinates, taking $m=4,$$n=2$ in (8), we have Henneberg-type minimal surface as follows:

$${\mathfrak{H}}_{4,2}(r,\theta )=\left(\begin{array}{c}{\displaystyle \frac{r^{3}cos(3\theta )}{3}}+rcos(\theta )+{\displaystyle \frac{cos(\theta )}{r}}\\ {\displaystyle \frac{r^{3}sin(3\theta )}{3}}-rsin(\theta )-{\displaystyle \frac{sin(\theta )}{r}}\\ -{\displaystyle \frac{r^{3}cos(3\theta )}{3}}+rcos(\theta )+{\displaystyle \frac{cos(3\theta )}{3r^3}}\\ {\displaystyle \frac{r^{3}sin(3\theta )}{3}}+rsin(\theta )-{\displaystyle \frac{sin(3\theta )}{3r^3}}\end{array}\right)=\left(\begin{array}{c}x(r,\theta )\\ y(r,\theta )\\ z(r,\theta )\\ w(r,\theta )\end{array}\right).$$

(9)

With the help of following equalities

$$\begin{array}{ccc}\hfill \frac{r^{3}cos(3\theta )}{3}& =& \frac{1}{3}{r}^3{cos}^3\theta -r^{3}cos\theta {sin}^2\theta ,\hfill \\ \hfill \frac{r^{3}sin(3\theta )}{3}& =& -\frac{1}{3}{r}^3{sin}^3\theta +r^3{cos}^2\theta sin\theta ,\hfill \\ \hfill \frac{cos(3\theta )}{3r^3}& =& \frac{1}{3r^3}{cos}^3\theta -\frac{1}{r^3}cos\theta {sin}^2\theta ,\hfill \\ \hfill \frac{sin(3\theta )}{3r^3}& =& -\frac{1}{3r^3}{sin}^3\theta +\frac{1}{r^3}{cos}^2\theta sin\theta ,\hfill \end{array}$$

and substituting

$$\frac{cos(\theta )}{r}=\frac{u}{u^2+v^2},\frac{sin(\theta )}{r}=\frac{v}{u^2+v^2},$$

into (9), we have following definition:

Definition 3.

Henneberg-type minimal surface in $(u,v)$ coordinates is defined by as follows:

$${\mathfrak{H}}_{4,2}(u,v)=\left(\begin{array}{c}{\displaystyle \frac{1}{3}}{u}^3-u{v}^2+u+{\displaystyle \frac{u}{u^2+v^2}}\\ -{\displaystyle \frac{1}{3}}{v}^3+u^{2}v-v-{\displaystyle \frac{v}{u^2+v^2}}\\ -{\displaystyle \frac{1}{3}}{u}^3+u{v}^2+u+{\displaystyle \frac{1}{3}}{\displaystyle \frac{u^3}{{\left(u^2+v^2\right)}^3}}-{\displaystyle \frac{u{v}^2}{{\left(u^2+v^2\right)}^3}}\\ -{\displaystyle \frac{1}{3}}{v}^3+u^{2}v+v+{\displaystyle \frac{1}{3}}{\displaystyle \frac{v^3}{{\left(u^2+v^2\right)}^3}}-{\displaystyle \frac{u^{2}v}{{\left(u^2+v^2\right)}^3}}\end{array}\right)=\left(\begin{array}{c}x(u,v)\\ y(u,v)\\ z(u,v)\\ w(u,v)\end{array}\right),$$

(10)

where $u:=rcos\theta ,$ $v:=rsin\theta .$

Next, we see algebraic surface and its degree:

Definition 4.

With ${\mathbb{R}}^4=\{(x,y,z,w)\mid x,y,z,w\in \mathbb{R}\},$ the set of roots of a polynomial $f(x,y,z,w)=0$ gives an algebraic surface. An algebraic surface is said to be of $degree$ n, when $n=deg(f).$

On the other hand, we meet following lemma about an algebraic minimal surface and an algebraic curve, obtained by Henneberg:

Lemma 1.

(Henneberg [5,7]) A plane intersects an algebraic minimal surface in an algebraic curve.

See also [16] for details.

Considering the above definition and lemma in 4-space, we obtain the following corollaries for the algebraic curves within the Henneberg-type minimal surface ${\mathfrak{H}}_{4,2}(u,v)$ in (10):

Corollary 1.

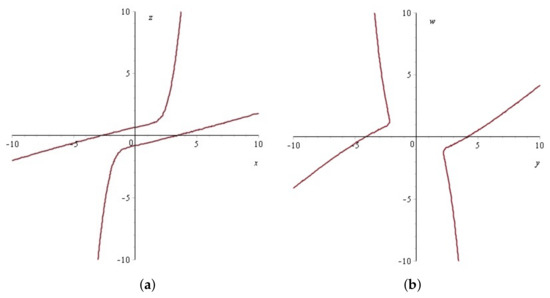
The implicit equation of the curve

$${\mathfrak{H}}_{4,2}(u,0)={\gamma }_{4,2}(u)=\left(\begin{array}{c}{\displaystyle \frac{1}{3}}{u}^3+u+{\displaystyle \frac{1}{u}}\\ 0\\ -{\displaystyle \frac{1}{3}}{u}^3+u+{\displaystyle \frac{1}{3u^3}}\\ 0\end{array}\right)$$

on the $xz$-plane, obtained by eliminating u and v, is as follows (see Figure 1a)

$$\begin{array}{ccc}\hfill {\gamma }_{4,2}(x,z)& =& -729x^6+6561x^{5}z-19683x^4{z}^2+19683x^3{z}^3+1458x^5-10935x^{4}z\hfill \\ & & +26244x^3{z}^2-19683x^2{z}^3+9720x^4-32076x^{3}z+65610x^2{z}^2+6561x{z}^3\hfill \\ & & -59049z^4-14040x^3+36936x^{2}z-49572x{z}^2-729z^3-38772x^2\hfill \\ & & +72576xz-116154z^2+29016x-27000z+83240.\hfill \end{array}$$

Figure 1. Henneberg algebraic curves. (a): ${\gamma }_{4,2}(x,z)=0$; (b): ${\gamma }_{4,2}(y,w)=0$.

Its degree is $deg({\gamma }_{4,2}(x,z))=6.$ Hence, the $xz$-plane intersects the algebraic minimal surface ${\mathfrak{H}}_{4,2}(u,v)$ in an algebraic curve ${\gamma }_{4,2}(u)$.

Corollary 2.

The implicit equation of the curve

$${\mathfrak{H}}_{4,2}(0,v)={\gamma }_{4,2}(v)=\left(\begin{array}{c}0\\ -{\displaystyle \frac{1}{3}}{v}^3-v-{\displaystyle \frac{1}{v}}\\ 0\\ -{\displaystyle \frac{1}{3}}{v}^3+v+{\displaystyle \frac{1}{3v^3}}\end{array}\right)$$

on the $yw$-plane, obtained by eliminating u and v, is as follows (see Figure 1b)

$$\begin{array}{ccc}\hfill {\gamma }_{4,2}(y,w)& =& 729w^3{y}^3-2187w^2{y}^4+2187w{y}^5-729y^6+2187w^4\hfill \\ & & -8748w^{3}y+12636w^2{y}^2-3402w{y}^3+14823y^4\hfill \\ & & +13365w^2+25623wy-41175y^2+39601,\hfill \end{array}$$

and we see that its degree is $deg({\gamma }_{4,2}(y,w))=6.$ Therefore, the $yw$-plane intersects the algebraic minimal surface ${\mathfrak{H}}_{4,2}(u,v)$ in an algebraic curve ${\gamma }_{4,2}(v)$.

Next, we will focus on the implicit equation of the algebraic surface $H_{4,2}(x,y,z,w)$ and on the degree of the Henneberg-type surface ${\mathfrak{H}}_{4,2}(u,v)$.

By eliminating u and v of ${\mathfrak{H}}_{4,2}(u,v)$ using Groebner Basis in the Maple software package (see Section 4), we obtain the irreducible implicit equations of $H_{4,2}\left(x,y,z,w\right)=0$ in the cartesian coordinates $x,y,z,w$. The degrees of the 125 implicit equations vary from 12 to 15. Next, we show only the leading term of one of the degree 15 implicit equations:

$$\begin{array}{ccc}\hfill H_{4,2}(x,y,z,w)& =& -200357529114010966392986849696173135384400160212306238814\hfill \\ & & 6921798341947018263352974811247016293579407850833661779885\hfill \\ & & 3866925524317171303746574348380455005752233355972467214402\hfill \\ & & 70054850560x{y}^{2}z{w}^{11}+729\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}.\hfill \end{array}$$

Since $deg\left(H_{4,2}\right)=15$, we have that $H_{4,2}(x,y,z,w)=0$ is an implicit algebraic Henneberg-type minimal surface in 4-space.

4. Maple Codes and Figures for Algebraic Henneberg Surface in 𝔼⁴

To compute the implicit equation of the Henneberg surface in ${\mathbb{E}}^4$ we have tried a series of standard techniques in elimination theory: projective (Macaulay) and sparse multivariate resultants implemented in the Maple package multires (The package can be found at http://www-sop.inria.fr/galaad/software/multires/multires), Maple’s native implicitization command Implicitize, and implicitization based on Maples’ native implementation of Groebner Basis. For the latter we implemented in Maple the method in [39] (Chapter 3, p. 128).

All the above methods failed to give the implicit equations in reasonable time. In particular, for the resultant methods, the bottleneck was the computation of the determinant of the huge resultant matrix.

The final and successful method we have tried was to compute the equations defining the elimination ideal using the Groebner Basis package FGb [40]. The package can be found at: https://www-polsys.lip6.fr/ jcf/FGb/index.html.

The time required to output the 125 polynomials defining the elimination ideal was under 20 s. See Figure 2 and Figure 3 for the projections in ${\mathbb{R}}^3$ of the surface defined by one of these polynomials.

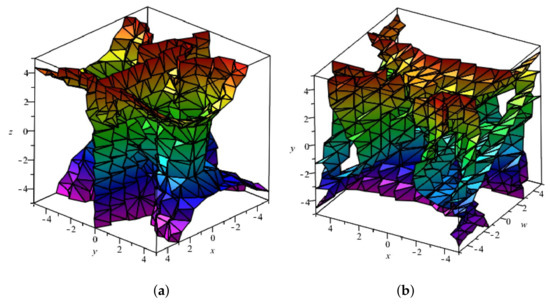
Figure 2. Projection in ${\mathbb{R}}^3$ of a Henneberg algebraic surface. (a): $H_{4,2}(x,y,z)=0$; (b): $H_{4,2}(x,y,w)=0$.

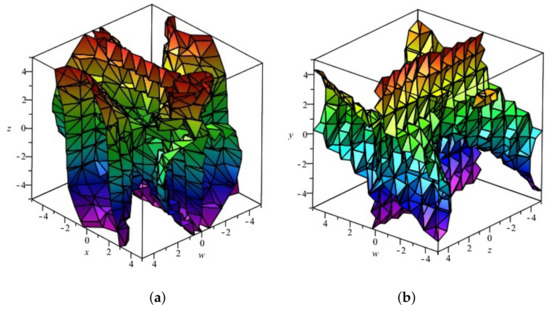
Figure 3. Projection in ${\mathbb{R}}^3$ of a Henneberg algebraic surface. (a): $H_{4,2}(x,z,w)=0$; (b): $H_{4,2}(y,z,w)=0$.