Abstract
The contribution of this article is quadruple. It (1) unifies various schemes of premodels/models including situations such as presheaves/sheaves, sheaves/flabby sheaves, prespectra/-spectra, simplicial topological spaces/(complete) Segal spaces, pre-localised rings/localised rings, functors in categories/strong stacks and, to some extent, functors from a limit sketch to a model category versus the homotopical models for the limit sketch; (2) provides a general construction from the premodels to the models; (3) proposes technics that allow one to assess the nature of the universal properties associated with this construction; (4) shows that the obtained localisation admits a particular presentation, which organises the structural and relational information into bundles of data. This presentation is obtained via a process called an elimination of quotients and its aim is to facilitate the handling of the relational information appearing in the construction of higher dimensional objects such as weak -categories, weak -groupoids and higher moduli stacks.
1. Introduction
1.1. Motivation 1
There is an abundant literature on how to construct an algebraic object from one of its presentations [1,2,3,4,5]—this process will be referred to as a localisation. It is also well-known that the category of algebraic objects will satisfy strict universal properties if the objects themselves can be distinguished from their presentations by strict properties and, similarly, the category will usually satisfy weak universal properties if the objects can be distinguished from their presentations by weak properties, but little is known about how to derive strict universal properties for the category when the algebraic objects are only characterised by weak properties. One of the goals of the present paper is to address this lack.
If we think of an algebraic object as a model for a limit sketch [1], then algebraic objects can usually be distinguished from their presentations by lifting properties. Specifically, in the case of a limit sketch D, the presentations are given by the functors while the models are given by those presentations that preserve the chosen limits of D; as shown in [3], this type of property can be expressed in terms of a lifting property in the functor category . On the other hand, the localisation of a presentation X into a model is endowed with a reflection property, which equips X with a map such that for every arrow where M is a model, there exists an arrow making the following diagram commute.
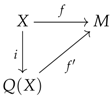
If the lifting properties characterising the models are strict, then one is able to show that the reflection is strict, that is to say that the arrow is unique for any given . For instance, in [3], one starts by characterising the models via strict lifting properties and the strictness of these is naturally carried over to the reflection property. This is the same idea in [4] where the author is able to construct a (strict) reflection from the strict lifting properties inherently associated with well-pointed endofunctors.
On the other hand, if the lifting properties are weak, then one is usually only able to show that the reflection is weak, in which case the arrow is only proven to exist. For instance, in [6], the small object argument (recall that this argument comes from Homotopy Theory, which mostly, if not only, deals with weak lifting properties; see [7,8]) is used to construct weak reflections for subcategories of injective objects.Similarly, in Garner’s framework [9,10], the small object argument is generalised to construct weak homomorphisms of ∞-categories à la Batanin [11] while the possibility to construct ∞-categories is assumed: the reason being that ∞-categories are objects that can be characterised by strict lifting properties [12] (Corollary 1.19) while weak homomorphisms between these do not require such a strictness.
However, to the best of my knowledge, there has not been any published work explaining how to obtain strict reflection properties from weak lifting constructions such as the small object argument. In fact, it is not even clear how to obtain strict universal properties from weak characterisations in general. For instance, in [13], essential weak factorisation systems were introduced to study injective and projective hulls, which are meant to capture canonical envelops of injective and projective objects, with the goal of strengthening the lifting properties associated with the usual associated replacements (see intro. ibid.), but it is not said if these hulls can satisfy strict universal properties; in fact [14] gives a hint that this is unlikely and states that only an almost reflection property can be shown. The paper even emphasises the need of methods to pass from a weak setting to a strict one in its last section [14] (Section 4), in which it is asked if it is possible to know when strict universal properties, such as naturality and functoriality, can be shown to be satisfied by a given weak reflection.
In an area of Mathematics in which the weakening of definitions and theories (e.g., ∞-topos theory, univalent homotopy type theory, devired algebraic geometry, etc.) have now taken more and more importance, but whose language—Category Theory—also takes advantage of strict universal properties, it is, indeed, of interest to know if there are theorems that allow one to determine whether a set of weak lifting properties defining a type of algebraic object can provide the associated category with a strict universal property—at least stricter than the expected one.
The present paper is an effort to provide a set of technics and theorems showing that such a scheme is possible. Precisely, one of the main contributions of this paper is to propose a language (or context) in which it is possible to say if a category of algebraic objects that are characterised by weak lifting properties can be shown to possess a strict universal property (see Section 1.3). We will even show that the proposed argument is a generalisation of Quillen’s small object argument (see Corollary 2) and will thus answer one of our earlier questions. The theorems given herein are meant to be generalised in future work (in which the boundary between strictness and weakness will become blurrier), the purpose being to pave the way for the construction of models taking their values in higher categorical structures.
1.2. Motivation 2
The second matter that motivates the present paper is the so-called elimination of quotients mentioned in the title, which basically comes down to conclude that the way we encode an object is as important as its inherent properties. For instance, it is this same type of ideas that motivated
- ▹
- the introduction of the elimination of imaginaries, in Shelah’s Model Theory [15,16], in which quotients are eliminated in the form of definable quotient maps by using the various sorts available from the ambient (multi-sorted) theory;
- ▹
- the development of the concept of covering space, in Algebraic Topology [17], that provides ways to blow up the quotients acting on a space and to bring out its homotopical properties by studying the automorphisms acting on the resulting quotient maps;
- ▹
- the definition of stack, in Algebraic Geometry [18], due to the existence of non-trivial automorphisms that may occur because of the different ways a moduli space can be represented.
To really understand how the coding of objects, and, even that of sets, matters from the point of view of their algebraic structures, let us consider an example. Take a set X and consider the coproduct encoded by the following logical specification:
If one takes R to be the binary relation on that identifies with for every , then the quotient is obviously isomorphic to X. However, in much the same way as it is fundamental to not confuse an isomorphism with an identity, it is, here, important to understand that is not same as X. From the point of view of the present paper, the difference between X and lies in the implicit algebraic structure with which is equipped. This object can indeed be seen as a surjection equipped with two sections whose cospan structure defines a universal cocone, and this structure is noticeable even thought is isomorphic to a mere set. In other words, the quotient can be seen as living way beyond the category of sets, for the simple reason that isomorphisms are not the same as identities.
All this shows that the way we construct algebraic objects matters quite substantially, mainly because the algebraic properties coming along with their representations can turn out to be either very useful or extremely cumbersome (e.g., X versus ).
The goal of our so-called ‘elimination of quotients’ will be to eliminate the cumbersome quotients that may occur in the representation of algebraic objects and organise, in the form of quotient maps, the useful ones. Here, I feel important to mention that such a re-organisation is possible because our objects are characterised by weak lifting properties, which allow more freedom than strict ones.
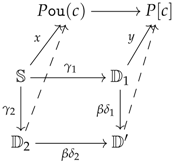
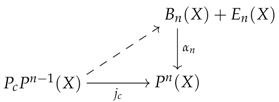
If we look at how Kelly [4] (Theorem 10.2) constructs algebraic objects, and to be more specific, models for some limit sketch , where K denotes the set of limit cones associated with D, we see that he isolates each cone and constructs, for each of these and every presentation , a well-pointed endofunctor where the object completes the presentation X with operations required by the sub-theory of . To complete X with respect to the operations required by the whole theory , he pushes out the wide span made of the arrows , for all , to obtain a well-pointed endofunctor . In particular, each cone is equipped with a factorisation as follows:
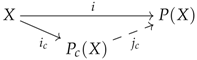
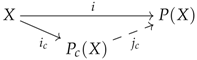
Finally, the reflector associated with the theory is computed through a transfinite composition of the following form:
Isolating each cone c in K and proceeding to a pushout of the well-pointed endofunctors is a necessity if one wants to use the very neat and compact formalism of well-pointed endofunctors. However, this pushout procedure, as elegant as it may be, adds more cumbersome quotients than useful ones. Precisely, the wide pushout of the objects looks more like the type because it mostly identifies all the copies of X living in each through the maps .
As we can imagine, these cumbersome quotients become much more abundant when enriching our algebraic objects to other categories than and it would not be imaginable to be willing to do combinatorics with representations that repeat and contract the same information over and over. Not only do the results proposed in the present article avoid these cumbersome quotients, but they also bring out the hidden algebraic structure of the useful ones, where, here, the term ‘algebraic structure’ is used in the sense previously discussed for the quotient .
In fact, our results go in the direction of Lawvere’s work [5], in which the concept of congruence is used to construct a reflector from the category of presentations to that of models by showing how the quotients act on the free algebra functor applied on the presentations [5] (Theorem 5.1). It is worth noting that the concept of congruence has given rise to a very rich theory regarding the characterisation of congruence lattices for varieties of algebras [19,20]. Our results can therefore be seen as a refined extension of Lawvere’s work. This refinement is presented in the form of a formal language that could be seen as suitable for a generalisation of Congruence Lattice Theory to more general objects than those proposed by Lawvere.
1.3. Results for Motivation 1
In the same fashion as there are categories of models for a theory [1], or categories of fibrants objects [21] or even systems of fibrant objects [22], it is, here, proposed the definition of system of premodels (see Definition 3), which gathers in the same structure a category of presentations together with maps along which the models are defined via weak lifting properties. An interesting feature of this structure is that it encompasses many examples that are meant to be captured operibus citatis; particular examples can also be found in [23,24,25,26]. There is also a novelty in the fact that the maps along which the weak lifting properties are defined are not maps in the category of values or that of presentations, but in a category whose level of definition allows one to verify whether the subcategory of the resulting models possesses a strict reflection property. For instance, this allows us to retrieve and explain the strict reflection property associated with the models for a limit sketch.
If we restrict ourselves to algebraic objects defined by limit-preserving functors, say valued in a category in which choices of colimits are obvious, a system of premodels is given by:
- (1)
- a limit sketch ;
- (2)
- a category with enough limits and pushouts, if not all;
- (3)
- a subcategory ;
- (4)
- for every cone , a set of commutative squares in , say as follows:
Before giving the definition of a model for this structure, we need to recall that a cone c in K is a natural transformation where is an object in D, is a small category, is the obvious constant functor picking out the object in D and is some functor . Now, a model for the previous structure is a functor in such that for every , the canonical arrow:
for which we shall prefer the more compact notation , is orthogonal in the arrow category to every commutative square in (as shown below):

In the case of limits sketches, we retrieve the usual definition of model by taking, for every cone , the following pair of commutative squares in ; the leftmost one encodes the surjectiveness of the map while the other one encodes its injectiveness:
One of the very advantages of this language is to allow the specification of more general arrows than bijections such as weak equivalences (see characterisation in [27] (Lemma 7.5.1)). This explains why this language is expected to be generalised to higher categorical structures in the future.
Now, our main result, given in Theorems 8 and 9, can be simplified in terms of Theorem 1, in which items (i) and (ii) are in fact redundant. The statement makes use of the arrow , which denotes, for every commutative square contained in and every , the universal arrow induced by the pair of arows and under the pushout (denoted by ) of the arrows and .
Theorem 1.
Suppose that is an identity. For every object A in , there exists an arrow in (Theorem 9) such that for every arrow in where X is a model for the system of premodels, if
- (i)
- the map β is an epimorphism for every square in and every ;
- (ii)
- the arrow is a monomorphism in ;
- (iii)
- the arrow is an epimorphism for every square in and every ,
then there exists a unique arrow making the following diagram commute (Theorems 8 and 9):
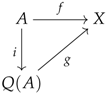
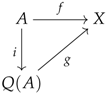
As one can see, the previous theorem explains, in the language of systems of premodels, why one can expect a strict reflection property in the case of set-valued models for a limit sketch.
In Theorem 1, the assumption that the inclusion is an identity will be replaced, in Theorems 8 and 9, with the notion of effectiveness, which translates a variation of the concept of definability in (notice the parallelism with the concept of elimination of imaginaries given in Section 1.2). As will be shown in Theorem 7, this concept of definability becomes trivial if is taken to be equal to .
1.4. Results for Motivation 2
From the point of view of motivation 2, the present paper mainly focus on models for limit sketches in , so that we will mostly state our results from the perspective of these objects. This will nevertheless give an idea of what our theorems look like when generalised to other categories. The proof of the results stated below will be recapitulated in the conclusion of the present paper (Section 9).
We now consider a limit sketch , where, for simplicity only, K is supposed to be a finite set of finite-limit cones. The proposition given below states that it is possible to construct the reflector of any presentation in a very specific way, which is not visible from Kelly’s construction [4].
Proposition 1.
For every presentation X in and ordinal , there exist a pair of objects and and an epimorphism such that the reflector of X for the theory is given by the transfinite composition of the following sequence of arrows in :
In addition, the mappings and are functorial and the arrow is natural in X.
Of course, one could argue that the map coming from Kelly’s construction can be factorised into an epimorphism and a monomorphism , so that we might recover the previous form, but it is not obvious whether can be decomposed into a functorial sum in , mainly because the quotients that acts on might prevent from doing so. In fact, there is a much stronger way to assess the difference between Kelly’s construction and the previous one, which is given below.
Proposition 2.
For every presentation X in , there exist a sequence of epimorphism , as given in Proposition 1, for which there is a natural transformation of transfinite sequences:
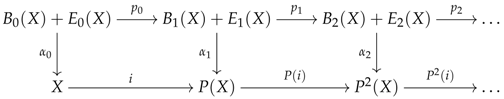 for which is the identity on X and if there exists a dashed arrow making the following triangle commute, then it must factorise through the canonical map and the object is a model for the limit sketch whenever :
for which is the identity on X and if there exists a dashed arrow making the following triangle commute, then it must factorise through the canonical map and the object is a model for the limit sketch whenever :
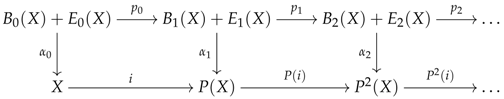

In other words, Kelly’s construction has too many quotients to be non-trivially lifted to the elimination of quotients, and if a lift exists, then it cannot be in the free part , which means that, at rank n, the free operations added to satisfy the theory are superfluous.
Even though the natural transformation is to identify free operations between each other, note that it cannot identify too much information either as the universal property of a reflector implies that the transfinite colimit of provides an isomorphism between the two underlying reflectors of X:
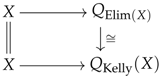

In fact, we will show that, in the case of models for a limit sketch, the so-called elimination of quotients takes the form given in Theorem 2, in which every cone c in K is again viewed as a natural transformation where is an object in D, is a small category, is the obvious constant functor picking out in D and is some functor .
Theorem 2.
For every presentation X in , there exist a sequence of epimorphisms as given in Proposition 2, for which we will denote the coproduct object as a functor , such that:
- -
- and ;
- -
- is the left Kan extension of the functor:along the functor , where K is seen as a discrete small category;
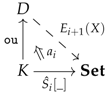
- -
- the epimorphism is the quotient map making the following identifications:
- (1)
- for every object d in D, it identifies a pair if there exists a cone and an arrow in D for which the pushout of the canonical arrow along maps x and y to the same element;
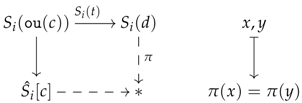
- (2)
- for every object d in D, it identifies a pair where and if there exists a cone , an object z in the diagram of c and a morphism in D such that x and y can be lifted to a common element in via the span made of the following composites.
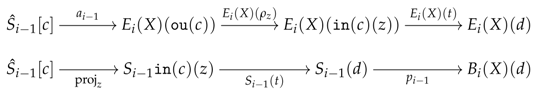
Even though we have only discussed the finite-limit case, all of the previous propositions hold for non-finite limit-sketches. In this case, the ordinal becomes the cardinality of the limit-sketch (see the end of Section 4.1) and the transfinite sequence of arrows needs to be defined such that is the transfinite colimits of all the arrows preceding the rank .
1.5. Road Map
The main results of the paper start to be developed from Section 4, while Section 2 and Section 3 give an account of various notations, conventions and technicalities. Specifically, Section 2 introduces a set of conventions meant to facilitate our notations while Section 7 focuses on a notion of smallness that will only be used in Section 7.
Even if Section 2 does not sound so attractive, the reader might want to skim through this section to get used to specific notations such as (Section 2.1); (Section 2.3); as well as (Section 2.5) and (Section 2.14).
Section 3 defines a notion of smallness that generalises the usual one. Recall that one usually says that an object D in some category is small if for any functor (or, sometimes, any functor belonging to a certain classes of functors. This restriction generally arises in non-accessible categories such as in the category of topological spaces). Defined from the ordinal category to , say , the following canonical map is a bijection:
On the other hand, the smallness condition defined in Section 3 would be more of the following type. The property is now centred on the functor F and not on the object D any more; we then consider a set of objects G in and say that a functor is G-convergent if the following canonical map is a bijection for every object :
The reason for this change is that the image will not always be a colimit of the form .
Then comes Section 4, in which is defined the notion of system of premodels. The difference with the simplified version given in Section 1.3 and that of Section 4 is that the canonical map is now constructed from various parts of the system of premodel structure, so that it is now of the form where R is a right adjoint endofunctor on . This right adjoint R will often be an identity functor in this paper, save for -spectra, in which case it will be equal to the loop space functor . In the future, the functor R will however take multiple forms.
Section 5 and Section 6 work together to formalise the idea of algebraic structure associated with a quotient. Recall that completing a presentation with operations usually requires the adding of free operations along with certain quotients. In our case, the free structure will be added to the presentations, but the quotient structure will be resolved in a separate object (see Section 6.7). The term resolved here refers to the concept of resolution developed in [28], which should be viewed as a way of passing from what looks like a set to a higher dimensional structure, such as category or a quotient map .
The purpose of Section 5, alone, is to give a theoritical generalisation of Quillen’s small object argument [8] while Section 6 focuses on applying the formalism of Section 5 to systems of premodels.
The difference between our argument and Quillen’s one is that one does no longer consider strict pushouts at every step and the lifts meant to be produced by these pushouts only commutes in the subsequent steps. These differences arise for two reasons. The first one is the desired elimination of quotients and the second one is due to the fact that the pushouts used in the usual argument do not necessarily commute with the right adjoints (including the limits) involved in the construction of the object .
To be able to formalise the previous ideas, we will introduce the concept of tome, whose goal is to gather all the squares that one would like to force to admit a lift through the small object argument. This will take the form of a functor , where h is an object in the arrow category . Note that this tool will mainly find its use in the way the category is encoded.
Specifically, in Section 6, this category will be discrete and will take the form of a coproduct of what could look like two left Kan extensions:
The left-hand sum will allow us to parameterise all those squares that are to force the adding of the structural information to the presentations while the right-hand sum will allow us to handle all of the quotients that the adding of this information is supposed to generate. Note that the rightmost sum of is only meant to quotient out what has been added at a previous step, leaving free the information added by the current leftmost sum and thus producing the elimination of quotients discussed in Section 1.4. All the data needed to talk about an elimination of quotients such as , , , , , (and some more) will be gathered into the notion of constructor (see Section 6.4). Remarks 11 and 13 might be helpful in seeing what all those left Kan extension-like constructions actually parameterise.
Finally, the small object argument is carried out in Section 7 where the smallness condition is used to prove the usual lifting properties. The universal property satisfied by our construction is discussed in Section 8 via Theorems 9 (existential part) and 8 (uniqueness). The latter mainly focus on the properties required to prove Theorem 2, whose proof is recapitulated in the conclusion (see Section 9.2).
1.6. Acknowledgments
I would like to thank Steve Lack and the referees for comments that allowed the improvement of the earlier versions of this text. I would also like to thank the members of the Australian Category Seminar for various remarks regarding the content of this paper.
2. Background, Notations and Conventions
2.1. Ordinals
Any ordinal will be identified with the preorder category it induces. For every ordinal , the inclusion functor will be denoted by . For convenience, the preorder category of one and two objects will be denoted by and , respectively. We shall also use the notation to denote the least infinite ordinal.
2.2. Wide Subcategories
Let be a category. A subcategory will be said to be wide if the inclusion functor is surjective on objects. Put simply, this means that contains all the objects of .
2.3. Limits and Colimits
For every category and small category D, the obvious functor mapping an object to the pre-composition of with the canonical functor will be denoted by . For convenience, the category will often be identified with the category . If they exist, the left and right adjoints of will be denoted by and , respectively. Recall that the images of these two functors are understood as the colimits and limits of over D, respectively. As usual, in the case where the functor exists, the category will be said to be complete over D. Similarly, the category will be said to be cocomplete over D when the functor exists.
Proposition 3.
If a category is complete (resp. cocomplete), then so is for any small category D where the limits (resp. colimits) are defined objectwise in .
Proof.
Suppose that is complete. For every object d in D, the restriction functor mapping X to has a right adjoint whose images are given by the Right Kan extensions along the functor picking out d [29]. This implies that commutes with limits. By duality, the other statement regarding colimits follows. ☐
2.4. Cardinality
Let A be an object in . The cardinality of A is the least ordinal such that there is a bijection between A and . In ZFC, the axiom of choice ensures that the cardinality of a set A always exists, which will be denoted by .
For any small category D, the cardinality of D is the cardinality of the following coproduct of sets, where is the set of objects of D:
The cardinality of D will be denoted by . Below is given a well-known result on the commutativity of limits and colimits.
Proposition 4.
For every small category D and limit ordinal , the canonical natural transformation valued in over is an isomorphism.
Proof.
See Appendix A. ☐
Similarly, for every complete category and small category D, the functor commutes with colimits (see Proposition 3). In fact, it follows from Proposition 4 that the unit of the adjuncion commutes with colimits in as stated in the next proposition.
Proposition 5.
For every small category D and limit ordinal , denote by the letter η the units of the two adjunctions in and . The following diagram of canonical arrows in commutes for any functor :
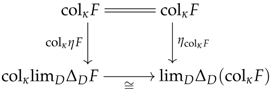
Proof.
See Appendix A. ☐
2.5. Universal Shiftings
Let be a functor between small categories. The pre-composition with i induces an obvious functor . Mostly for convenience, the composition of this functor with the colimit functor will later be denoted by . The obvious canonical natural transformation will be called the universal shifting along i. Similarly, the composition of the functor with the limit functor will be denoted by .
2.6. Right Lifting Property
Let be a category and be a class of arrows in . The class of arrows of that have the right lifting property (abbrev. rlp) with respect to the arrows of will be denoted by .
2.7. Sequential Functors
Let be some ordinal and be a category. A functor will be said to be sequential if for any limit ordinal in , the object may be identified with the colimit of the functor such that, for every ordinal in , the morphism corresponds to the arrow of the universal cocone of associated with .
Proposition 6.
If a morphism has the rlp with respect to every arrow for every , then f belongs to .
Proof.
It is straightforward to show that if a morphism f has the rlp with respect to two composable arrows i and j, then it has the rlp with respect to the composition . A direct generalisation to the transfinite case shows the proposition. ☐
2.8. Limit Sketches
A limit sketch is a small category equipped with a subset Q of its cones (Recall that these are, by definition, natural transformations of the form in where A is a small category, U is a functor and d an object in , called the peak). The cones in Q will be said to be chosen. A model for a limit sketch in a category is a functor that sends the chosen cones in Q to universal cones (‘Universal’ here means that the cone, say , defines a limit of the functor ) in . The models of a limit sketch in define the objects of a category whose morphisms are natural transformations in over . For any limit sketch , the category of models for in will be denoted by .
Example 1 (Limit sketc for monoids).
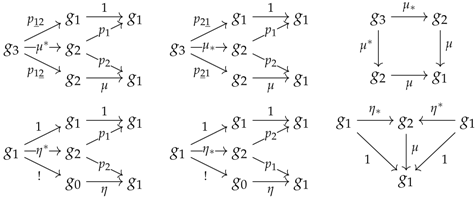
The category of monoids in may be defined as a category of models for a certain limit sketch . The underlying small category of is freely generated over a set of arrows and quotiented by commutativity relations. Specifically, the category has four objects , , and , where is called the underlying object of the sketch, and a set of arrows as follows, where the identities have been forgotten:
The commutativity relations are given by the diagrams:
 while the chosen cones are given by the trivial cone, of peak , defined over the empty category and the following spans:
while the chosen cones are given by the trivial cone, of peak , defined over the empty category and the following spans:

The astute reader might have noticed that μ and η stand for the multiplication and unit of the monoid structure. It will come in handy to denote the preceding limit sketch by . Note that other limit sketches can give rise to the same models, so that the previous limit sketch is only an example among other possible presentations of the theory of monoids.
Example 2 (Limit sketch for commutative monoids).
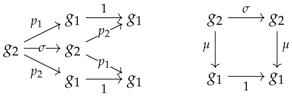
It is possible to add one more arrow and two diagrams to the limit sketch so that the category of models associated with the resulting limit sketch, say , is that of commutative monoids. Precisely, this would imply the adding of an arrow that makes the following diagrams commute:

Example 3 (Limit sketch for abelian groups).
It is also possible to add three more arrows and two diagrams to the limit sketch so that the category of models associated with the resulting limit sketch, which will later be denoted by for the notations given below, is that of abelian groups. Precisely, this would imply the adding of three arrows , and that makes the following diagrams commute:
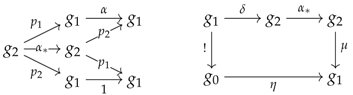

Example 4 (Limit sketch for rings).
By definition, the subcategory of generated by , , , ⋯, and ! is also included in . The pushout of and along these underlying inclusions provides a certain limit sketch that contains five objects and all the arrows and cones appearing in and ; the associated limit sketch combines the structure of a monoid with the structure of a commutative monoid. One thus recovers the theory of rings if one adds an object , a chosen cone and the following arrows and commutativity relations to :
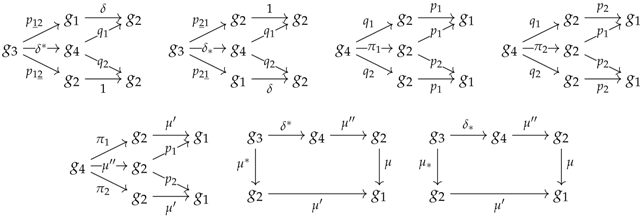

The resulting limit sketch then defines a sketch for which the models are rings. The limit sketch to which the identity morphism is added to the set of chosen cones—when seen as a trivial cone—will later be denoted by .
2.9. Subfunctors
Let D be a small category and be a functor. A subfunctor of F is a functor such that (1) for every object d in D, the inclusion holds and (2) for every morphism in D, the function is the restriction of along the respective inclusions of the domain and codomain.
2.10. Overcategories
Let be a category and X be an object in . The obvious functor mapping an arrow in to the object A in will be denoted by ∂.
Remark 1.
Let be a small category. Any functor may be seen as a natural transformation in over of the form . The converse is also true.
Let now be a functor. It will come in handy to denote by the obvious functor on satisfying the following mapping rule on the objects:
2.11. Covering Families
Let D be a small category and d be an object in D. A covering family on d is a collection of arrows in D. For every morphism in D, we shall speak of the pullback of S along f to refer to a collection of arrows where the arrow is a pullback of along f. Also, note that every morphism gives rise to a family . This last operation is used to define a more complex operation on S as follows. For every , take a covering family on . We will denote by the covering family on d obtained by the disjoint union of families for every .
2.12. Grothendieck Pretopologies
Let D be a small category. A Grothendieck pretopology on D consists, for every object d in D, of a collection of covering families S on d such that:
- (1)
- (Stability) for every arrow in D, the pullback exists in ;
- (2)
- (Locality) for every and in , the covering family is in ;
- (3)
- (Identity) for every object d in D, the singleton is in .
Such a collection will usually be denoted by J. A category D equipped with a Grothendieck pretopology J on D will be called a site.
Remark 2.
Every covering family on an object d in may be seen as a functor if A is seen as a discrete category. It follows from the stability and locality axioms that this functor extends to a product-preserving functor where is the completion of A under products. This functor will be called the stabilisation of S.
2.13. Families
For any category , the notation will be used to denote the category whose objects are pairs where S is a discrete category and F is a functor and whose morphisms are given by pairs where a is a functor and is a natural transformation .
2.14. Bounded Diagrams
Let D be a small category, d be an object in D and be a category. We will denote by the category whose objects are triples where P and Q are functors and e is an arrow in and whose morphisms, say , are given by pairs of natural transformations of respective forms and making the following square commute:
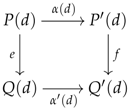
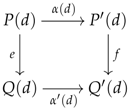
Note that is also a functor category where is the smallest subcategory of consisting of the two copies of D and the arrow linking the two copies of d.
3. Convergent Functors
This section aims to define the notion of convergent functor, which is to replace the notion of “small object” that is usually used in transfinite constructions.
3.1. Emulations
Let and be two small categories and be a category. A pair of functors and will be called an -emulation in if it is equipped with a natural isomorphism as follows:
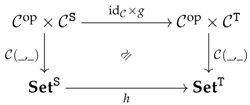

In terms of an equation, the previous diagram means that is equipped with a natural isomorphism (in the variables , and ) as follows:
Example 5.
Let be a small category and be a category. Take g to be the identity functor and h to be the identity functor . By definition, the pair is a -emulation.
Example 6.
Let be a functor between small categories and be a category. Take g to be the pre-composition functor induced by U and h to be the equivalent version of g in . It suffices a few lines of calculation to show that the following isomorphism holds, which implies that the pair defines an -emulation:
Example 7.
Let be a small category and be a category. Take g to be the functor and h to be the functor . It follows from Example 6 that the pair is a -emulation:
Example 8.
Let be a small category and be a category complete over . Take g to be the limit functor and h to be the limit functor . It is a well-known fact following from Yoneda’s Lemma that the pair is an -emulation.
Example 9.
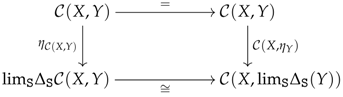
Let be a small category and be a category complete over . We will denote by η the unit of the adjunction valued in any category. Now, take g to be the obvious functor mapping an object X in to the arrow in and h to be the equivalent version of g in the category (which is complete over ). It follows from Yoneda’s Lemma that the following diagram commutes, which implies that the pair is an -emulation:

Example 10.
Let be a small category. For this example, we shall additionally need a small category A together a cone in . Let now denote a complete category over A. The unit of the adjunction in will be denoted by η. Now, to define our emulation, take g to be the obvious functor mapping a functor to the arrow:
in and h to be the equivalent version of g in the category . It follows from Yoneda’s Lemma that the pair is an -emulation. Specifically, the isomorphism associated with the pair may be deduced from the isomorphisms involved in Examples 6, 8 and 9.
Example 11.
Let be a small category. For this example, we shall need a small category A together a cone in . Let now denote a complete category over A. The unit of the adjunction in will be denoted by η. Now, to define our emulation, take g to be the obvious functor mapping an object in to the arrow:
in and h to be the equivalent version of g in the category . It follows from the isomorphisms involved in Examples 7, 8 and 10 that the pair is an -emulation.
3.2. Cocontinuous Emulations
Let and be two small categories, be a category and be a limit ordinal. An -emulation in will be said to be κ-cocontinuous, if for every object , the functor preserves colimits over .
Example 12.
Since identity functors preverse colimits, the pair of Example 5 is a κ-cocontinuous -emulation for every limit ordinal κ.
Example 13.
Consider the same context as that used in Example 6. Since is cocomplete over any small category D, the colimits of are componentwise colimits, which means that for every functor , the following isomorphism holds for every :
This directly implies that the functor preserves colimits, which shows that the -emulation is κ-cocontinuous for every limit ordinal κ.
Example 14.
It follows from Example 13 that the -emulation of Example 7 is κ-cocontinuous for every limit ordinal κ.
Example 15.
Consider the same context as that used in Example 8 and suppose to be given a limit ordinal κ satisfying the inequality . It directly follows from Proposition 4 that the functor preserves colimits over κ. This shows that the -emulation is κ-cocontinuous.
Example 16.
Consider the same context as that used in Example 9 and suppose to be given an limit ordinal κ satisfying the inequality . It follows from Proposition 5 that the functor preserves colimits over κ. This shows that the -emulation is κ-cocontinuous.
Example 17.
By using the cocontinuity involved in Examples 15 and 16, we may show that the -emulation is κ-cocontinuous for any limit ordinal κ satisfying the inequality .
Example 18.
By using the cocontinuity involved in Examples 13, 15 and 16, Example we may show that the -emulation is κ-cocontinuous for any limit ordinal κ satisfying the inequality .
3.3. Convergent Functors
For any class of objects of , a functor will be said to be -convergent in if for every object in , the following canonical function (obtained by homing) is an isomorphism in :
If the class turns out to be a singleton , the functor will more explicitly be said to be -convergent.
Remark 3.
One of the useful implications of the previous definition is that if a functor is -convergent in , then for every object and morphism in , there exist an ordinal and a morphism making the following diagram commute in :
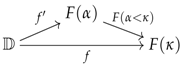
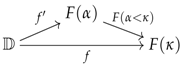
Let now and denote two small categories and be a functor. A functor will be said to be unimorly G-convergent in if for every object s in and object t in , the following canonical function is an isomorphism in :
In other words, the evaluation of F at an object s in is -convergent.
Lemma 1.
Let and be two small categories such that and be a category. Let be a functor and consider a uniformly G-convergent functor in . For every cocontinuous -emulation , the composite functor is G-convergent in .
Proof.
The following series of natural isomorphisms proves the statement:
This last isomorphism shows that is G-convergent in . ☐
Example 19.
Applying Lemma 1 to the -emulation of Example 5 implies that if a functor is uniformly G-convergent in and the inequality holds, then the functor is G-convergent in .
Example 20.
Applying Lemma 1 to the -emulation of Example 18 implies that if a functor is uniformly G-convergent in for some functor and the inequality holds, then the functor mapping an ordinal n in to the following composite arrow in is G-convergent in :
Remark 4.
It follows from Lemma 1 that if a functor is uniformly G-convergent in , then is -convergent in . Specifically, this follows from the fact that commutes with hom-sets (see Example 14) and the following series of isomorphisms:
4. Models for a Croquis
This section defines the notions of premodel and model for which we want to construct the localisation. We start with the type of theory on which the models are defined.
4.1. Croquis
Let D be a small category. Recall that a cone in D over a small category A consists of two functors and and a natural transformation . When such a cone is called c, the functor will be denoted by , the functor will be denoted by and the small category A will be referred to as the elementary shape of c and denoted by .
Definition 1.
A croquis category (or croquis) in D consists of a set K of cones in D and a functor (where K is seen as a discrete category) called the regular output.
A croquis as above will be denoted by a triple and sometimes shortened to the pair when the ambient category D is obvious.
Convention 1.
For every croquis , the operation induces a function from K to . Alternatively, this may be seen as a functor . If the functor is equal to , then the croquis will be denoted by or K and the functor will be said to be trivial.
Example 21 (Arrow categories).
Let D be a small category, be a subcategory of D and be some given functor. The set of arrows of defines an obvious set of cones of elementary shape in . However, because is a subcategory of D, we shall in fact see as a set of cones specifically in D. The croquis (in D) made of and the regular output mapping any arrow in to the object will later be denoted by .
Example 22 (Spectra).
Let denote the wide discrete subcategory of the ordinal category ω and denote the full subcategory of restricted to positive ordinals. Let be the predecessor operation . The croquis defined by will later be used to characterise Ω-spectra.
Example 23 (Sketches).
Any limit sketch defines an obvious croquis where K stands for the set of chosen cones and where the associated regular output is the trivial one.
Example 24 (Grothendieck’s pretopologies).
Let J denote a Grothendieck pretopology on a small (opposite) category . A covering family in may be seen as a cone of the form in D over A. If one denotes by the stabilisation of C (see Remark 2), this cone gives rise to another cone over . Equipping D with the set of these latest cones, say , gives rise to an obvious croquis .
Example 25 (Flabby pretopologies).
Let J denote a Grothendieck pretopology on a small (opposite) category . The croquis that will later give rise to flabby sheaves and the Godement resolution is the union of the two croquis and . Precisely, this croquis consists of the union of the two sets of cones and and the trivial regular output.
Example 26 (Segal croquis).
Let Δ denote the category of non-zero finite ordinals and preserving-order functions, which is known as the simplex category. Denote by the wide subcategory of Δ whose arrows are injective functions and, for every object , denote by the composition of the functor (see Section 2.10) with the obvious inclusion . The Segal croquis of is of the form (for a trivial regular output) where:
- (i)
- contains, for every object , the cone , defined over , that stems from the dual transformation described in Remark 1 for the inclusion functor ;
- (ii)
- contains, for every object , the cone given below (expressed in Δ as a cocone), where, if one denotes , and :
- (1)
- is the function with the mapping rules and ;
- (2)
- is the function with the mapping rule ;
- (3)
- is the function with the mapping rule .
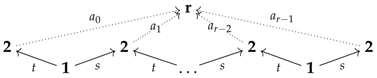
This croquis will be denoted by .
Example 27 (Complete Segal croquis).
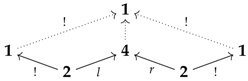
Let Δ be the simplex category. The complete Segal croquis of is given by its Segal croquis to which is added the unique cone whose peak is the ordinal and whose diagram in Δ is given, below, underlying the cocone of dotted arrows, where, if one denotes and :
- (1)
- is the function with the mapping rules and ;
- (2)
- is the function with the mapping rules and ;

The induced cone in will be denoted by as it is meant to describe the set of isomorphism structures relative to the natural categorical (or nerval) structure of . The resulting croquis will be denoted by .
We shall speak of an elementary shape of a croquis to refer to the elementary shape of one of its cones. Because K is a small category, the class of elementary shapes of is a set, which will be denoted by . The cardinality of a croquis is then given by the cardinal of the coproduct of every small category in :
4.2. Premodels
Let be a croquis and be a category. For any endofunctor , denote by the category whose objects are triples where (1) P is a functor , (2) S is a functor (To not say a ‘function valued in a category’. Such a simplification will be common later on) and (3) e denotes a collection of arrows in for every and and whose morphisms, say of the form , are pairs where f and a are two natural transformations of respective forms and making the following diagram commute for every and :
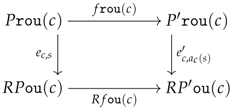

The objects of will be called the R-premodels for . For convenience, the category will sometimes be denoted as when is trivial and as when R is also an identity.
Example 28 (Premodels).
The category of premodels for a sketch to a category corresponds to the full subcategory of whose objects are such that the images of S are equal to and the morphism is an identity for every . This subcategory is isomorphic to .
Example 29 (Presheaves).
The category of presheaves over a site corresponds to the full subcategory of whose objects are such that the images of S are equal to and the morphism is an identity for every . This subcategory is isomorphic to .
Example 30 (Prespectra).
If denotes the loop space functor on the category of pointed topological spaces and denotes the predecessor operation on , then the category of prespectra is the full subcategory of whose objects are such that the images of S are equal to . This subcategory will be denoted by .
Example 31 (Pre-localised rings).
Let denote the category of sets and be the limit sketch defined in Example 4. The category of ‘pre-localised rings’ is defined as the full subcategory of the category whose objects are such that (1) is a model for ; (2) the image of above the cone is equal to a subset of while its images above all the other cones are equal to and (3) the morphism is given by:
- -
- the right multiplication map for every if ;
- -
- the identity morphism otherwise.
This subcategory will be denoted by .
Example 32 (Pre-Segal spaces).
Let denote the category of topological spaces and continuous functions. The category of pre-Segal spaces is the category of simplical topological spaces; it is given as the full subcategory of whose objects are such that the images of the functor S are equal to and the morphism is an identity for every . Thecategory of pre-complete Segal spaces is defined similarly by replacing with .
Definition 2.
Let D be a small category and be a category. For any given endofunctor , a category of R-premodels is a subcategory of the category .
Example 33.
Premodels for a sketch, presheaves on a site, prespectra, pre-localised rings and pre-Segal spaces are examples of such categories (see the previous examples).
4.3. Models
Let D be a small category, be a croquis in D and be a complete category over the elementary shapes of K. Suppose to be given a right adjoint . The first goal of this section is to define a functor for every cone . In this respect, for every cone c in K of the form , for which we shorten the notation to the symbol r, the functor maps any premodel to the family taking any to the following composite arrow in :
For every morphism of R-premodel of the form , the image morphism is given, for every , by the following morphism in :
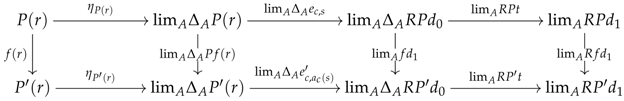
Definition 3 (System of premodels).
A system of R-premodels consists of (1) a croquis ; (2) a category that is complete on the elementary shapes of K and admits a terminal object; (3) a category of R-premodels where R is a right adjoint and (4), for every cone , a set of commutative squares in , called the diskads (see left diagram, below) equipped with a pushout in (see right diagram, below):


The collection consisting of all the sets will usually be denoted by . A system of R-premodels will be denoted as a 4-tuple and said to be defined over D in . The diagrams used in Definition 3 can more efficiently be described as a colimit sketch in (i.e. diagram equipped with colimits) of the following form:

This type of colimit sketch will be called a vertebra and denoted by the symbols . For such a vertebra, it will come in handy to refer to the arrows , , and as the seed, coseed, stem and trivial stem, respectively. Finally, the left adjoint of will conventionally be denoted by L.
Definition 4 (Model).
An R-premodel in a system of R-premodels will be said to be anR-model if, for every cone , every component of the arrow in has the right lifting property with respect to all the diskads of when these are seen as arrows in with respect to the notations of Equation (3):

Example 34 (Models for a sketch).
For every limit sketch , define the system of premodels consiting of the croquis K (see Example 23); the associated category of premodels and, for every cone c in K, the set made of the following vertebrae in :
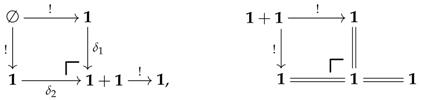
The -models of such a system correspond to the models for the sketch .
Example 35 (Sheaves).
For every site , define the system of premodels consiting of the croquis (see Example 29); the associated category of premodels and, for every cone c in , the set made of the vertebrae given in Equation (4). The -models of such a system correspond to the sheaves over .
Example 36 (Flabby sheaves).
For every site , define the system of premodels consiting of the croquis defined in Example 25; the functor category and:
- (i)
- for every cone c in , the set made of the vertebrae given in Equation (4);
- (ii)
- for every cone c in , the set made of the leftmost vertebra of Equation (4) only.
The -models of such a system correspond to the sheaves over whose morphisms over any arrow in D are surjective, namely the flabby sheaves over .
Example 37 (Sheaves in categories).

For every site , define the system of premodels consiting of the croquis (see Example 29); the associated category of premodels and, for every cone c in , the set made of the following vertebrae for the obvious choices of morphisms, where:
- (1)
- is a terminal category;
- (2)
- is the free living isomorphism category (i.e., two objects, one isomorphism);
- (3)
- is the free living arrow category (i.e., two objects, one arrow);
- (4)
- is category made of two objects and two parallel arrows between them.

The -models of such a system correspond to those ‘sheaves’ for which the sheaf condition is not a bijection but an equivalence of categories.
Example 38 (Strong stacks).
For every site , define the system of premodels consiting of the croquis defined in Example 25; the functor category and:
- (i)
- for every cone c in , the set made of the leftmost vertebra of Equation (4) when seen in (instead of ) and the rightmost two vertebrae of Equation (5);
- (ii)
- for every cone c in , the set made of the leftmost vertebra of Equation (5) only.
The -models of such a system correspond to the strong stack (see [23]). The strong stacks completion constructed in ibid corresponds to a special case of the general construction given in this paper.
Example 39 (Strong stacks up to homotopy).
For every site , define the system of premodels consiting of the croquis defined in Example 25; the functor category and:
- (i)
- for every cone c in , the set made of the vertebrae given in Equation (5);
- (ii)
- for every cone c in , the set made of the leftmost vertebra of Equation (5) only.
The -models of such a system may be identified to the strong stacks of [23] up to the notion of homotopy defined thereof.
Example 40 (Segal spaces).
Define the system of premodels consisting of the croquis defined in Example 26; the category of pre-Segal spaces , which is included in and:
- (i)
- for every cone c in , the set of obvious vertebrae induced by the diskads given in Equation (6), where:
- -
- n runs over the natural numbers;
- -
- the object is the topological n-disc;
- -
- the map is the obvious hemisphere inclusion;
- (ii)
- for every cone c in , the set of Vertebrae (7), where n runs over the positive integers and:
- -
- the object is the topological -sphere;
- -
- the maps between the different objects are induced by the obvious inclusions;
The -models of such a system correspond to the Segal spaces in (see [25] for a definition enriched in simplicial sets).
Example 41 (Complete Segal spaces).
Define the system of premodels consisting of the croquis defined in Example 27; the category of pre-complete Segal spaces , which is included in , and:
- (1)
- for every cone c in that is in fact in , the same set of vertebrae defined in Example 40;
- (2)
- for the cone (see Example 27), the set of vertebrae of the form (7) for every positive integer n.
The -models of such a system correspond to the complete Segal spaces in (see [25] for a definition enriched in simplicial sets).
Example 42 (Spectra).
For the loop space functor , define the system of Ω-premodels consiting of the croquis defined in Example 22; the category of prespectra and, for every cone c in , the set of vertebrae of pointed spaces defined in Diagram (8), where n is a positive number and:
- -
- where the object is the quotient of the -sphere by itself (i.e., a point);
- -
- where the object is the quotient of the n-disc by its boundary;
- -
- where the object is the quotient of the n-sphere by its equator;
- -
- where the object is the quotient of the -disc by its equator;
- -
- where the object is the quotient of the -disc by one of its hemispheres;
- -
- where the object is the quotient of the -disc by its boundary;
- -
- where the maps between the different objects are the obvious inclusions:

The Ω-models of such a system correspond to the Ω-spectra.
Example 43 (Localisation of rings).
Consider the system of premodels consisting of the croquis (see Example 31), the subcategory and, for the cone c in , the set made of the vertebrae given in Equation (4). The -models of such a system correspond to the rings P for which the map is invertible for every , or in other words those rings that are localised at their associated subset of elements S. Fields are particular examples.
Remark 5.
Many other examples could have been provided. Recall that it is common fact (see [27] (Lemma 7.5.1), [30] or [31] (Proposition 8)) that, in some nice model category , the notion of weak equivalence may be characterised via the type of right lifting property expressed in Example 4. For instance, Examples 40 and 41 on Segal spaces could have been extended to any nice cofibrantly generated model category, which need not be simplicial (contrary to usual practice). In fact, it is worth noting that the type of localisation described in the present article is an alternative to the usual simplicial Bousfield Localisation process (see [7]). On could also look at the type of localisation discussed in [32] (Corollary 8.8), which could be comprised in a more technical generalisation of the present work. Future work will also aim at generalising Example 37 to weaker functors in order to charactise the notions of -stack and strong -stack.
5. Narratives and the Small Object Argument
This section aims to introduce the small object argument that will be used for the construction of the localisation. The difference from that given below and the one defined by Quillen [8] is the notion of ‘degree’ coming along with the concept of narrative (see below). The degree is the key ingredient that allows us to obtain our so-called elimination of quotients.
| Notions | Descriptions | |
| Tome | A collection of commutative squares whose rightmost vertical arrows are all equal: this can be visualised as a ‘book’ whose pages are glued along a spine. The pages can satisfy certain compatibility relations. |  |
| Morphisms of tomes | Regular: relate the spine and the pages of two ‘books’ together. | |
| Loose: only relate the spines. | ||
| Oeuvre | An ordered collection of tomes related via loose morphisms; the theme is the common object towards which the spines of the books go to. | |
| Narrative of degree | An oeuvre that is equipped with sub-diagrams of its tomes, called the events, and choices of lifts for these sub-diagrams, called the viewpoints These lifts only ‘commute’ from the k-th book to the -th book. | |
5.1. Numbered Categories and Compatibility
In the sequel, the term numbered category will denominate any pair where is a category and is a limit ordinal. A small category will be said to be compatible with if (1) the category admits colimits over and (2) the inequality holds. By extension, a functor will be said to be compatible with a numbered category if its domain is compatible with .
5.2. Lifting Systems
Let us now define in formal terms what will later be seen as a set of generating cofibrations for our small object argument. Let be an numbered category. A lifting system in is a set J of objects of that are compatible with as functors.
5.3. Right Lifting Property
Let be an numbered category and J be a lifting system in . For every functor in J, the image of an object s in via will usually be denoted by . A morphism in will be said to have the right lifting property with respect to the system J if for any functor in J, the morphism has the rlp with respect to the arrow in . In the sequel, the class of morphisms of that have the right lifting property with respect to a lifting system J will be denoted by .
Example 44.
If J is a set of functors of the form picking out some objects of , then the preceding right lifting property corresponds to the usual one.
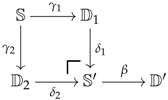
5.4. Tomes
Let be a category. A tome in is a triple consisting of a morhism in , a small category on which admits all colimits and a functor . According to Remark 1 applied to the arrow category , a way of seeing a tome in is in the form of a cocone in over the functor . Because has all colimits over , the earlier cocone provides an arrow in after applying the adjunction property of on it. This latest arrow will be referred to as the content of . Note that for any functor , we may pre-compose the universal shifting induced by i (see Section 2.5) with the content of as follows:
The resulting arrow will later play a central role and be referred to as the content of along .
5.5. Morphisms of Tomes
Let be a category. A loose morphism of tomes from to is given by a morphism in . A regular morphism of tomes is given by a morphism in and a functor making the next right diagram commute:
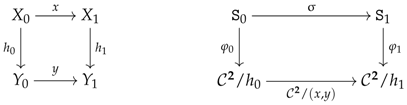

The arrow symbol associated with loose morphisms will be denoted as . The category whose objects are tomes in and whose arrows are regular (resp. loose) morphisms of tomes will be denoted by (resp. ). For a fixed object Q in , the wide subcategory of that is restricted to the loose morphisms whose components are identities on Q will be denoted by .
5.6. Oeuvres and Narratives
Let be a numbered category and Q be an object in . An oeuvre of theme Q in is a functor lifting (This lifting is formal and is mostly justified by the definition of the morphisms given in Section 5.9) to along the obvious inclusion .
Convention 2.
In the sequel, the image of an inequality in via an oeuvre will be denoted by . For convenience, when l is successor of k in , the notations will be shortened to . For every object k in , the morphism will be denoted as an arrow while the image of the composite functor at an object s in will be denoted as .
For every finite ordinal , a narrative of theme Q and degree δ in is an oeuvre of theme Q equipped with:
(1) (events) for every ordinal , a set , called the set of events at rank k, consisting of objects of that are compatible with as functors;
(2) (viewpoint) for every functor in the set , a lift for the commutative square (living in ) resulting from the pre-composition of the content of along with the arrow ; the square is therefore of the form in . The lift will later be referred to as the viewpoint at rank k along i.
Remark 6.
It follows from Convention 2 that the viewpoint at rank k along i mentioned in item (2) must be of the form .
Convention 3.
The functor induced by the sequence of arrows for every inequality in will be denoted by G and called the context functor.
Observe that any oeuvre and, a fortiori, any narrative as defined above provides a factorisation in as given below. This factorisation is that used for our small object argument:

Also, notice that the set of events induces an obvious lifting system , which will be denoted by .
5.7. Small Object Argument
Let be a numbered category, Q be an object in and be a narrative of theme Q and degree . A lifting system J in will be said to agree with the narrative if for every ordinal and functor in J admiting a lift of along ∂ (see left diagram below), there exists a functor in whose composite with gives the lift (see right diagram below):


Proposition 7 (Small Object Argument).
Let J be a lifting system in agreeing with the narrative . If the context functor is uniformly -convergent in for every , then the morphism appearing in Equation (9) is in .
Proof.
The goal of the proof is to show that the morphism is in . To do so, let be a functor in J and consider any arrow . The proposition will be proven if the commutative square encoded by this arrow admits a lift. By assumption, the functor is uniformly -convergent in . It follows from Remark 4, taken from the viewpoint of Remark 3, and the fact that is limit (Recall that if is limit, then for every ordinal , the successor is also in for every ) that there exist an ordinal and an arrow factorising as follows:
Note that an application of the universal property of the adjunction on the leftmost arrow of Equation (11) provides an arrow in as follows (where the leftmost arrow, given below, is the unit of ):
According to Remark 1, Arrow (12) induces a functor , which makes the leftmost diagram of Equation (10) commute. Because the lifting system J agrees with the narrative , there must exist a functor making the right diagram of Equation (10) commute. This means, after re-applying the adjunction , that Equation (11) is in fact of the following form, where the leftmost arrow is precisely the content of the tome along :
It follows from the viewpoint axiom (see Section 5.6) satisfied by that the Composite admits a lift. This implies that the whole composite (13) admits a lift, which, a fortiori, implies that the arrow admits a lift. ☐
5.8. Strict Narratives
Let be a numbered category and Q be an object in . For any narrative of theme Q, recall that the set of events gives a collection of functors that induces a cocone under the category (see Section 5.6). A narrative of theme Q and degree will be said to be strict in if:
- (1)
- for every ordinal , the cocone induced by the elements of is universal in ;
- (2)
- it is equipped with a morphism factorising the content of into a pushout as follows;
- (3)
- for every functor in , the viewpoint along i is equal to the pre-composition of with the universal shifting along i as follows;
- (4)
- the context functor is sequential (see Section 2.7).
Proposition 8.
If a morphism is in (see end of Section 5.6) for every , then it has the rlp with respect to the arrow (see Diagram (9)).
Proof.
Let be a morphism that has the rlp with respect to the lifting system for every . For any , this means that it has the rlp with respect to the following arrow in , for every functor in :
It directly follows that f has the rlp with respect to the coproduct of these arrows over the set (seen as a discrete category), which may be identified to the arrow up to isomorphism as shown below:
It follows from classical facts that, since f has the rlp with respect to , it has the rlp with respect to any of its pushouts, and hence with respect to for any . It finally follows from Proposition 6 and the fact that the context functor is sequential that f has the rlp with respect to the arrow in . ☐
5.9. Morphisms of Oeuvres
Let be a numbered category. For every pair of oeuvres and , of respective themes Q and , a morphism of oeuvres from to consists, for every ordinal , of a regular morphism of tomes:
such that the underlying loose morphisms induce a morphism in the functor category (see Remark 7). The category whose objects are oeuvres for the numbered category and whose arrows are morphisms of oeuvres will be denoted by .
Remark 7.
The previous definition implies that all the arrows are equal to the same morphism for every . In addition, it forces the equality to hold in for every .
6. Constructors and Their Tomes
This section introduces the notion of constructor that allows one to associate systems of premodels with tomes. Constructors contain all the necessary information that permits the ‘elimination of quotients’. We will see that their definition already brings out what is meant to be analytic (or structural) and what is meant to be quotiented out. Even if they appear to comprise many components, the main goal of the items defined in Section 6.2 and Section 6.4 is to be able to define two sums whose forms look like the following type:
The hom-sets —which are defined in Section 6.4—are meant to ensure a certain functoriality (i.e., they are the monomials for a certain type of species [33]) while the hom-sets —which are defined in Section 6.2—are meant to contain the ‘squares’ that will enable us to perform our small object argument. In the sequel, I shall therefore try to give evoking names to the different parameters used to define these sums. In particular, one sum is to encode the structural data of our elimination of quotients while the other one is to encode the quotient acting on this data. To make the reader more confident with the items of Section 6.2 and Section 6.4, here is a preluding summary of the different notations used therein.
| 1st Hom | 2nd Hom | ||||||
| analytic sum | D | ||||||
| quotient sum |
6.1. Some More Notations
The following conventions are meant to ease the combinatorial description of a constructor and its associated tomes, which will be defined in Section 6.6.
Convention 4 (Vertebrae).
The diskad of a vertebra will be denoted by and seen as an arrow in . The other arrow in , which is induced by the ‘dual’ vertebra , will be denoted by and called the codiskad of v. Finally, the stem β and seed of v will be referred to by the notations and , respectively.
Convention 5 (Domains and codomains)
Let and be two categories and be a functor. In order to avoid too many notations in our reasonings, the image of an object X of in the arrow category will be denoted as . This implies that every morphism in gives a commutative diagram as follows:
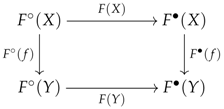

Similarly, for every functor , we will denote by and the “source” and “target” arrows of the squares involved in the image of H.
Example 45.
For every vertebra v in as displayed in Equation (3), the arrow is equal to . Thus, when the reader reads in Section 6.4, where is a functor mapping any element in I to the diskad of a certain vertebra in , they should think of the seed of the so-called vertebra.
Convention 6 (Closedness).
Let , and be three categories. The image of any functor of the form will later be denoted as for any pair of objects in – instead of the usual notation .
Convention 7 (Families).
Let be a category. In the sequel, we will denote by the obvious functor mapping a pair to the functor . Also, mainly for convenience, the images of any object in at some will be denoted by . This means that the equation holds for every .
Convention 8 (Families of arrows).
Convention 5 will be extended to in the obvious way: for every functor , we shall denote by and the obvious functors mapping any object to the families and , respectively.
Convention 9.
Later on, I shall often identify a set with a discrete category and identify many functions with functors. The reason for this is that we shall pre-compose these functions with functors going from discrete categories to non-trivial categories, which, for their parts, should really be seen as functors. This convention should thus ease the back and forth between set theory and category theory.
6.2. Preconstructors
This section introduces the concept of preconstructor. This notion tries to capture what it takes to specify the data of a localisation. For instance, in Modern Algebra, localising a ring requires one to specify:
- ☆
- the underlying set that one wants to act on, which is here the set R;
- ☆
- the subset by which one wants to localise the ring;
- ☆
- the operation that one wants to inverse, which is here given by the S-indexed family of group morphisms defined by the mappings ;
- ☆
- the type of inversion one wants to see happening on the maps .
Regarding this last item, the inversion would, for instance, be expressed in terms of a bijection for the type of localisation used in Classical Algebraic Geometry, but it would be expressed in terms of a quasi-isomorphism in the category of unbounded chain complexes in Derived Algebraic Geometry.
To pass from the earlier description to the formalism of preconstructors, one can try to describe what a preconstructor would be for the previous list of items, so that we could make the following associations (also, see the structure below): the data would specify the object R while the data would give the subset S; the data , and would enumerate the maps with theirs domains R and codomains R (which would be required to be independent of the indices in S); and the data and would specify the type of inversion one wants to see happening. We now give a formal definition.
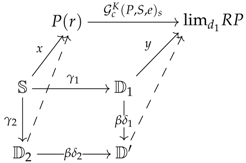
Let and be two categories and D be a small category. A preconstructor of type , let us call it , consists of a discrete category I together with:
- (a)
- two functors and , called the regulator and the localisor;
- (b)
- three functors as given below, which satisfy the string diagram axioms given underneath them (or the equations given just after);The previous string diagrams amount to saying that the following equations hold in the functor “category” for every ;
- (c)
- two functors and , called the analysor and the quotientor, such that the image encodes the diskad of a vertebra of stem for every ;
As mentioned in the preamble of Section 6, a preconstructor contains all the information that is necessary to define the parametrising ‘squares’ on which we will run the small-object-argument algorithm. These so-called parameters will be presented either as families (see Definition 5) or as formal sums (see Definition 6) – both presentations being useful.
Definition 5 (Families).
For any preconstructor as defined above, the analytic family of and the quotient family of are two functors and whose images are determined, for every arrow in and object , by the following mappings (or families) over :
Remark 8 (Concept of vertebra).
The relationship between the analytic family and the quotient family is established in item c) via the concept of vertebra. At this stage, this should suggest to the reader that the notion of vertebra subtly encompass both the idea of quotient—or coherence—via its stem and the idea of cellular structure—or ana-lysis—via its diskad.
Definition 6 (Species).
For any preconstructor as defined above, the analytic species of and the quotient species of are two functors and defined as follows, for every arrow in and object :
6.3. Preconstructor of a System of Premodels
Let be a system of R-premodels over a small category D in a category . The goal of this section is to associate any such system with a preconstructor of type . In this respect, define the set I to be the following leftmost disjoint sum:
Remark 9 (Encoding).
Any element θ in I may be presented as a pair where is a cone in K and v is a vertebra in .
By keeping the notational convention suggested by Remark 9, one defines the data of the preconstructor for the system of premodels as follows:
- (1)
- the regulator is given by the mapping ;
- (2)
- the localisor is given by the evaluation ;
- (3)
- the analysor is given by the mapping ;
- (4)
- the quotientor is given by the mapping ;
and because both equations:
hold for every , one may define the functor as the obvious functor satisfying the mapping on objects, so that the two associated functors and are defined as follows:
Remark 10 (Encoding).
For every arrow in and element θ in I, the image of the analytic species contains the tuples (The symbol is, here, preferred to the plain letter s as it could be confused with the notation (in bold) or thought to be related to the notation , which is not the case. I shall sometimes use s instead of when no confusion is possible) where: is a cone in K; v is a vertebra in ; is an element in and is a commutative square in of the form given below, on the left, for the notation , which may also be seen as the right commutative cube in when viewed from the bottom-left corner:

Similarly, the image of the quotient functor contains the tuples where: is a cone in K; v is a vertebra in ; is an element in and is an arrow in for the notation .
6.4. Constructors
This section introduces the concept of constructor. In comparison to the informal introduction of Section 6.2, a constructor should be seen as a structure giving all the data that we need to describe the localisation of the ring R by a subset S in terms of freely-added tuples and relations acting on these.
Specifically, one usually constructs the localisation by freely adding tuples of the form , for every and , to the set R. These tuples are often denoted as quotients . Because S has not been supposed to be a multiplicative set, one would also need to specify tuples of the form for every and where . The equivalence relations defined on the pairs are quite well-known: two pairs and are equivalent if there exists for which the following relation holds:
In the case of the elements of the form , it is less obvious how this should be done. A constructor can help us with this as it contains all the required structure for this type of general description without involving the need of focusing on the encoding.
In terms of the notations given below, in the definition of constructor, the data would specify the set of elements that are to be paired with elements in S; the data would specify the set of elements that are to be subject to relations of the form given earlier; the data and , which are used for coherence purposes, would be identities; the data and would specify the types of quotients one would like to see happening: they provide the seeds and the stems of the vertebrae given by the data coming from the preconstructor structure; the maps denoted by would map every element to (for the analytic links) and every pair where to a pair (for the quotient links); and the data j would specify how the set R injects into the localisation . With respect to the definition given below, all of these data would be associated with the canonical ring morphism .
We now give the definition of constructor. Let and be two categories and D be a small category. A constructor of type consists of a preconstructor of type , say as defined in Section 6.2, and a mapping that equips every object with a pair of sets together with:
- (1)
- two functors and called the analytic and quotient exponents;
- (2)
- two functors and called the analytic and quotient indicators;
- (3)
- a functor called the transitive analysor and, for every , a function , called the analytic link, of the following form:
- (4)
- a functor called the transitive quotientor and, for every , a function , called the quotient link, of the following form:
- (5)
- a functor , called the analytic section, satisfying the equalities , and so that the analytic link is an identity for every ;
For such a constructor, we define, for every object , an analytic functor and a quotient functor whose images and are given by the following formulae, respectively:
6.5. Constructor of a System of Premodels
Let be a system of R-premodels over a small category D in a category . The goal of this section is to associate any such system with a constructor of type . We shall, of course, use the preconstructor structure defined in Section 6.3. To define the supplementary structure, let us now define the following set (where denotes the set of objects of the elementary shape of ):
and let us associate every arrow in with two sets and as follows:
where the set is defined for every as the following sum, in which denotes a tuple of the form in and stands for the products of sets :
The initial section is taken to be the canonical monomorphism.
Remark 11 (Encoding).
It will turn out to be convenient to have conventional notations for any element , , or . In this respect, if one denotes:
- -
- by any tuple of cones in , for some positive integer n;
- -
- by any tuple in , for some tuple of cones as above;
- -
- by any tuple of morphisms living in for some object d in D;
the elements of the sets I, , and will be described as tuples of the form:
respectively, where , , and, obviously, .
Now, if one denotes by , , and any tuple of I, , and as displayed in Remark 11, one defines the mappings , , , , and associated with the constructor structure of as follows:
| Analytic Exponent | Quotient Exponent | |||
| on I | on I′ | |||
| otherwise | otherwise | |||
| Analytic Indicator | Quotient Indicator | |||
| on I | on I′ | |||
| otherwise | otherwise | |||
| Transitive Analysor | Transitive Quotientor | |||
| on I | on I′ | |||
| otherwise | otherwise | |||
Finally, one produces a constructor of type by defining the analytic link as an identity map when , and, otherwise, as a compositional iteration of the form:
where the triples , ⋯, are made out of the obvious components of and the functor maps any commutative square as given below, on the left, to the commutative trapezoid given on the right, where denotes the counit of the adjunction and the component is, here, seen as an arrow of the form with and otherwise:

For its part, the quotient link , which is defined for every , is given by a first application of the functor that maps any commutative square as given below, on the left, to the commutative trapezoid given on the right, where is the universal projection of the adjunction at z:
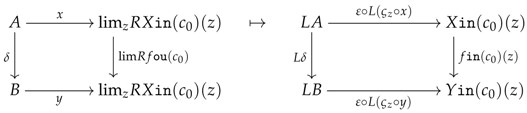 and, in the case where is not in , followed by successive iterations of the functor over the triples made out of the obvious components of (see Formula 15). It is easy to check that the initial section satisfies the axioms of item 5) of Section 6.4. The constructor associated with will later be referred to as .
and, in the case where is not in , followed by successive iterations of the functor over the triples made out of the obvious components of (see Formula 15). It is easy to check that the initial section satisfies the axioms of item 5) of Section 6.4. The constructor associated with will later be referred to as .
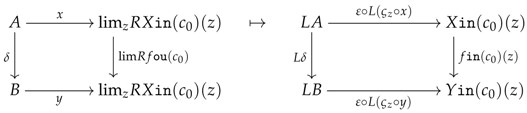
Remark 12.
In the case where the associated maps of our premodels are identities, the functors R and are trivial and the associated sets S are all equal to a fixed one, the set can be set empty for every and so that j can be defined as an identity. In this case, the validity of our results still holds for Examples 28 and 29, but not for Examples 30 and 31, which require to be as above. See Remark 16 and the proof of Theorem 3 for more insight.
Remark 13 (Encoding).
For every arrow in and object d in D, the image of the analytic functor contains the tuples and the tuples where: is a cone in K; v is a vertebra in ; n is a positive integer; , and are the tuples defined in Remark 11 and used to define the analytic link; t is an arrow in D of the form for the first type of tuple and an arrow otherwise; is an element in and is an arrow in as displayed in Equation (14) for the notation .
Similarly, the image of the quotient functor contains the tuples and the tuples where: is a cone in K; v is a vertebra in ; n is a natural number; , and are the tuples defined in Remark 11 and used to define the quotient link; z is an object of ; t is an arrow in D of the form for the first type of tuple and an arrow otherwise; is an element in and is an arrow in for the notation .
Remark 14 (Encoding).
It is not hard to see from Remark 13 that any type of tuple in may be written as a tuple of the form where the encoding of the parameter ϑ may vary. Similarly, it follows from Remark 13 that any tuple in may be written as a tuple where the encoding of the parameter ϑ may vary.
6.6. Tomes of a Constructor
Let denote a constructor of type as defined in Section 6.4. This section shows that may be associated with a variety of canonical tomes, each of them being used for specific purposes. The first one, called the operadic tome, is meant to be used in the small object argument (see Section 5) and is constructed out of the preconstructor structure of as follows: For every object , arrow in and , it is given by the functor defined by the following inclusion:
A second tome, called the analytic tome, is given by a functor and is defined on each term of —which denoted as below—as follows:
Explicitly, the functor maps any tuple in (see Remark 14) to the composite arrow given, below, by Equation (16) in :
A third tome, called the quotient tome, is given by a functor and is defined on each term of — which denoted as below — as follows:
Explicitly, the quotient tome maps any tuple in (see Remark 14) to the composite arrow given, below, by Equation (17) in :
The proofs of the following propositions follow from the previous definitions:
Proposition 9.
The operadic tome is natural in the variable . This amounts to saying that the mapping induces a functor .
Proposition 10.
The analytic tome is natural in the variable . This amounts to saying that the mapping induces a functor .
Proposition 11.
The quotient tome is natural in the variable . This amounts to saying that the mapping induces a functor .
6.7. Quotiented Arrows
Let denote a constructor of type as defined in Section 6.4. This section defines the concept of “quotient” whose essential idea is to restrict the quotient family of to certain parametrising “squares” only. In this respect, a -quotient for a morphism in consists of a collection of discrete categories, as given below, on the left, as well as a collection of functors as given on the right:
such that the inclusion holds for every element . We may associate any such -quotient with a functor defined as follows for every :
This functor will be called the species of . In much the same fashion as the quotient species of was used to define its quotient functor, we use the species of to define a third functor given by the following equation:
This functor will be referred to as the quotienting functor of .
Proposition 12.
The inclusions holding for every and induce functions of the form for every , which in turn induce a morphism in .
Proof.
By universality of the coproducts. ☐
Convention 10.
The natural transformation of Proposition 12 may be composed with the quotient tome of to give a natural transformation . Because this arrow lives in the functor category , it may be factorised into an epimonomorphism followed by a monomorphism as follows (this is an image factorisation):
For every object , the image will be thought of as the set , but quotiented by the obvious binary relation. In any case, the elements of and will be denoted as tuples where t is an arrow of the form ; s is an element in ; is an element in and is an element in .
Remark 15 (In preparation for Theorem 3).
Let be a morphism in as above. For every object , denote by the following sum of sets, which is defined with respect to the structure of f provided by the constructor :
The definition of -quotient for implies that any function of the form that maps a pair in to a pair in so that the equality is satisfied lifts to a function mapping any tuple in to the tuple in .
Example 46 (In preparation for Theorem 3).
In the case of a constructor associated with a system of R-premodels over a small category D in a category , the disjoint sum associated with a morphism in contains two types of tuples, which are of the form and with respect to the same notations given in Remark 13. For every and , if one takes r to be and to be , then it is possible to define a function with the following mapping rules, where stands for , stands for and stands for :
Because the following equations hold, it follows from Remark 15 that the function extends to a function :
In fact, the function also restricts to a function . To see this, take two tuples and in that are equivalent in , that is to say that have the same image under (see below, according to Equation (17)):
It follows that their images via are also equivalent in . This comes from the fact that the previous equation gives rise to the following one, after some obvious compositional operations on it (see the definitions for and in Section 6.5):
However, this last equation also amounts to saying that the images of and via are the same, and thus shows that restricts to a function .
Definition 7 (Quotiented arrows).
From now on, we shall speak of a-quotiented arrow in to refer to any arrow in that is equipped with a -quotient for f.
A -quotiented arrow as defined above will be denoted either as a pair or as a paired arrow . A morphism of -quotiented arrows, denoted as an arrow , will be understood as a morphism in . The category of -quotiented arrows and their morphisms will be denoted by .
6.8. Merolytic Functors and Their Tomes
Let denote a constructor of type as defined in Section 6.4 where has coproducts. For every -quotiented arrow , define the merolytic functor of as the coproduct of functors given below:
Then, define the merolytic tome of as the coproduct of the following cospan whose right leg is given by the rightmost arrow of Equation (18):
Proposition 13.
For every , the merolytic tome is natural in the variable . This amounts to saying that the mapping rule induces a functor .
Proof.
Follows from Propositions 10 to 12. ☐
Proposition 14.
For every , the mapping induces a functor .
Proof.
According to the definition of Section 5.5, it is sufficient to assign any arrow in to the arrow in . This mapping is functorial by functoriality of . ☐
Because the tome is functorial in , so is its content (see Section 5.4). In other words, the content gives us a commutative diagram in as follows:

The previous diagram will be referred to as the functorial content of .
6.9. Effectiveness of Quotiented Arrows
The goal of this section is to introduce what logicians could see as a concept of definability. The concept of effectiveness will allow us to designate those arrows that can be equipped with well-defined pushout factorisations in the category associated with a constructor. We prepare the notion of effectiveness by introducing the (almost-trivial) concept of realisability. Let denote a constructor of type as defined in Section 6.4 where has coproducts. A -quotiented arrow in will be said to be -realised if one may form a componentwise pushout square inside the functorial content of its merolytic tome as shown below:

The functor will then be called the -realisation of while the pair of arrows will be referred to as the -prefactorisation of .
Definition 8 (Effectiveness).
Let denote a constructor of type as defined in Section 6.4. A -quotiented arrow in will be said to be effective if it is -realised and its -prefactorisation in lifts to a factorisation of in , as shown in Equation (20), such that the arrow is an identity for every :


The leftmost factorisation of Equation (20) will be called the -factorisation of .
Remark 16.
Let be a given set and be the constructor of a system of R-premodels over a small category D in a category where every object in is such that S is equal to and e is made of identities only. In this case, the underlying functor is fully faithful and it follows that if has pushouts, then every -quotiented arrow in is effective. This means that the theorem given below becomes trivial, which explains why the set mentioned in Remark 12 may be set empty since it is not really needed anywhere else in the paper except for Theorem 3 (and Theorem 7, which is a copy of it). See Example 48 in the case where is defined as in Section 6.5.
Theorem 3.
Let be a system of R-premodels over a small category D in a category . If has pushouts and the inclusion is an identity, then every -quotiented arrow in is effective.
Proof.
For convenience, the symbol will be shortened to . Since has pushouts, every -quotiented arrow is -realised by definition. Let be an -quotiented arrow in . We are going to prove that the -realisation of has an R-premodel structure of the form and that this structure lifts the -prefactorisation of in to another one in . In this respect, fix and and denote and by r and , respectively. For simplicity, we will denote by the obvious morphism in whose components are given by the pair of arrows and in .
To prove the statement, we first need to define two functors. The first one is of the form and is induced by the following mappings, where stands for , stands for and stands for :
Note that the mappings on have already been given in Example 46. The second functor is of the form and maps any arrow to the map , where denotes the unit of the adjunction .
We are now going to show that the following diagram commutes:
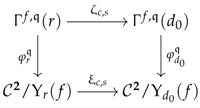
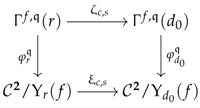
On the set , the calculation on a tuple goes as follows:
On the set , the calculation for goes as follows:
On the set , the calculation on a tuple goes as follows:
On the set , the calculation for goes as follows:
Now, the equation tells us that the content of the tome along is equal to the content of after applying the functor on it. More specifically, the equation means that the respective composites of Equations (22) and (23) are equal:
If one denotes by the unit of the adjunction , the definition of adjunction implies that the function is inverse of . Since the content appearing in Equation (22) may be factorised as in Diagram (19) on , an application of the inverse function of on the arrow represented by Equations (22) and (23) provides the following commutative diagram, where Equation (22) provides the inside while Equation (23) provides the outside.
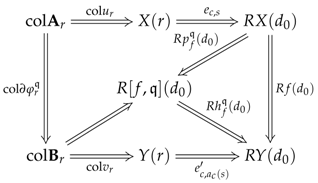

Now, because the top left corner of the previous diagram corresponds to the top left corner of the commutative square defining the -realisation of when evaluated at r, it follows that there exists a natural transformation making the following diagram commute.
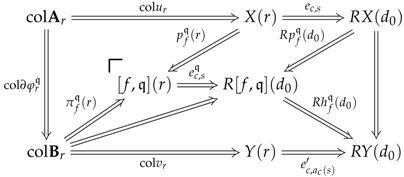

The previous diagram provides a morphism in the category of R-premodels . The universality of also provides a morphism in . These two morphisms obviously define a factorisation of the morphism in . Finally, since the second component of the morphism is the identity on S, its image via the functor is an identity for every (see Section 6.5). In other words, the arrow mentioned in Definition 8 is indeed an identity. ☐
Definition 9 (Fibered).
A system of R-premodels over a small category D in a category will be said to be fibered if the category has pushouts and the -factorisation of any -quotiented arrow (obtained in Theorem 3) lifts to .
Example 47.
By Theorem 3, any system of R-premodels where has pushouts and is identified with the category is fibered.
Example 48.
In the proof of Theorem 3, note that if the objects and are such that the associated arrows and are identities, then so is . This implies that any system of R-premodels where has pushouts and may be identified with the functor category is fibered (e.g., Examples 34–41)
Example 49.
In the proof of Theorem 3, note that if the objects and are such that the images of S and are equal to , then so is the -realisation . This implies that the system of Ω-premodels given in Example 42 is fibered.
Remark 17.
A system of R-premodels is not always fibered (e.g., Example 43), which is often due to a too strong restriction of the premodels via the inclusion . However, Theorem 3 shows that if is too strong, we might want to stay in to process most of our calculations. The idea would then be that it is possible to go back to at the very end of a transfinite calculation.
Example 50.
This example discusses the form that the -realisation takes when considering categories of models for a limit sketch. Let be a limit sketch seen as a croquis. Consider the system of premodels defined in Example 34 for the category . Recall that the vertebrae associated with any cone were of the following form:
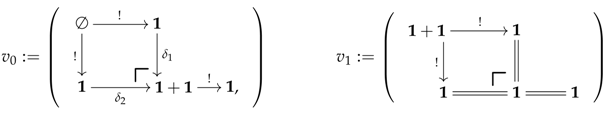
It follows from the definition of the transitive analysor and quotientor that, for any -quotiented arrow , the -realisation of evaluated at an object is defined over the following types of span:


The contribution of the left span to the construction of the -realisation is to add an element to while the contribution of the right span to the construction of the -realisation is to quotient a pair of elements in . After unravelling the indices that parametrise the two types of span, we may deduce that the colimit is of the following form, where and are the restrictions of to the vertebrae and , respectively:
After further unravelling the parameterisation of the rightmost summand, we may show that the colimit may be expressed as follows, where R is a binary relation on X in :
Concretely, the set is nothing but the set with respect to the notations of given in Remark 11 while the object is given by for the same notations.
Recall that, according to Remarks 12 and 16, the set could in fact be given by the set I itself in the present situation (i.e. premodels for a sketch). In this case, the expression of Equation (24) turns out to be as follows:
6.10. Rectification of Effective Quotiented Arrows
Let denote a constructor of type as defined in Section 6.9, with the usual notations, and be an effective -quotiented arrow in . Usually, effectiveness does not mean that the quotiented arrow is as we would like it to be. It is in fact necessary to rectify its defaults via a second quotient. The goal of this section is to define the ‘rectification’ of , which is nothing but a -quotient for the arrow .
To do so, let us define, for every element and , the associated functor of the following form:
First, define the discrete category to be the set . By definition, an element may be identified with an element , which may be sent to the arrow:
via the domain restriction . The arrow encoded by may be identified with an element in the image of the analytic tome of as follows (see Formula (16) and the assumption of the initial section ):
This therefore defines a function mapping any element to the tuple whose image via the merolytic tome is the arrow encoded by .
This being said, denote by r the element and, for every , denote by the function that picks out the element . From the point of view of these notations, we have showed that the image of the composite corresponds to the commutative square . However, this also means that the content of the merolytic tome of along is equal to the commutative Square (25) in as illustrated below:
Because the left arrow (i.e., the content) may be factorised as shown in Diagram (19), it follows that the commutative square encoding factorises as shown below, on the left:
The diagram displayed above, on the right, is for its part the image of the -factorisation of in via the functor . The definitions of the diagrams involved in Equation (26) imply that the commutative square factorises as follows, where the image is replaced with the diskad of a vertebra for which by definition:
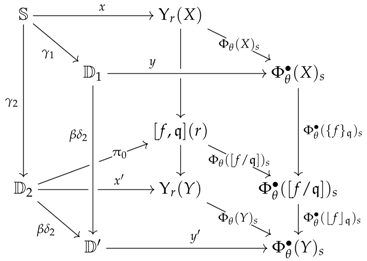

Notice that the previous commutative cube provides the following left commutative square:
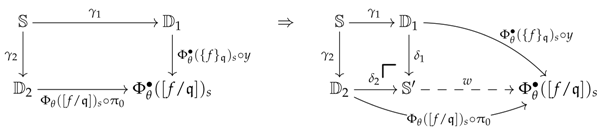

By using the structure of the vertebra , we may form a pushout inside so that we obtain a canonical arrow making the preceding right diagram commute. It is not hard to deduce from the universality of this pushout that both arrows:
are solutions for a same universal problem over (Diagram (27) might come in handy to visualise this fact). In particular, this means that the following diagram must commute:
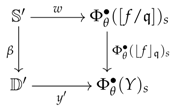

Because corresponds to the image , we have defined a functor mapping a commutative cube to the subset of consisting of Diagram (28) only. Thus, the images of are sets (or singletons) included in so that the collection of functors given below, denoted by , defines a -quotient for the arrow :
Definition 10 (Rectification).
The-rectification of the -quotiented arrow is the -quotiented arrow , which will sometimes be denoted by .
Later on, the diagram obtained in Equation (28), which is entirely determined by the image of the -rectification of above a cube at the parameters and , will be referred to as the obstruction square of for at .
Definition 11 (Ideal).
A -quotiented arrow will be said to be ideal if it is effective, its -rectification is effective and for every , and , there exists an arrow factorising the obstruction square of for at as follows:
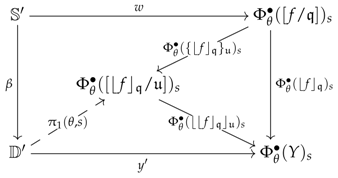

Remark 18 (Structure of narrative of degree 2).
Consider an ideal -quotiented arrow and a commutative cube in . According to the previous discussion, this cube may be factorised as in Diagram (27). Merging this factorisation of with: (1) the factorisation of the obstruction square of for at on its front face and (2) the -factorisation of the -rectification of on its back face leads to the following factorisation of (where the top front corner has been forgotten and ):
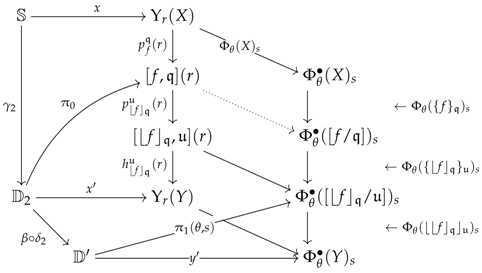

This means that the composite arrow given in Equation (30), whose the leftmost arrow is given by the content of the operadic tome , admits a lift in :
This last fact will later imply that we may construct a narrative of degree 2 out of the operadic tome.
Remark 19 (About π0).
This section discusses the encoding of the arrow that we have denoted . We shall use the same notations as that introduced at the beginning of the section. Recall that we defined the element , which we used to shift the merolytic tome of and obtain the leftmost diagram of Equation (26). Therefore, we have the following formula if we use the notation of Diagram (19):
If we now denote for some arrow , the functionality of and the construction of the merolytic tome of gives the following Equation:
This formula will later come in handy in the proof of Theorem 9.
Theorem 4.
Let be a system of R-premodels over a small category D in a category . If admits pushouts and the inclusion is an identity, then every -quotiented arrow is ideal.
Proof.
For convenience, the symbol will be shortened to . The present proof uses the construction made in the proof of Theorem 3. In particular, we shall use the notations defined thereof, such as and . Let be an -quotiented arrow in . By Theorem 3, it is effective and so is its -rectification . There now remains to show the existence of an arrow:
factorising the obstruction square of for any cube at any parameter and (see Diagram (29)).
First, recall that, for every , and cube , the obstruction square of for at is given by an arrow in of the following form:
By using the notations of Section 6.5 and the adjointness properties of R and , the preceding righthand arrow may be turned into the following arrow in for every :
Now, observe from the definitions of Section 6.5 that, for every and , we may define an object in , which precisely lands in the component of . From the notations of Section 6.5, the arrow given in Equation (31) may in fact be rewritten as follows (We have the identities and ):
It therefore follows from Formula (17) that the arrow given in Equation (31) may be identified with the image of Tuple (32) (see below) via the quotient tome :
In order to avoid overloading the next diagrams, denote by the functorial mapping and, for every , denote by the function that picks out Tuple (32) in for every . Now, to resume, the previous discussion showed that the image of the composite corresponds to the arrow . However, this is equivalent to saying that the content of the merolytic tome of along is equal to the arrow as illustrated below:
Because the rightmost arrow may be factorised as shown in Diagram (19), it follows that the commutative square encoded by factorises as follows:

The idea is now to obtain a factorisation of the form given in Equation (29) by reconstructing the obstruction square (from which the previous diagram is derived) without losing the factorisation.
First, note that, by definition of the quotient acting on (see Convention 10), the collection of arrows is natural in since the following tuples have the same images via the functor for every arrow in :
The functoriality of Diagram (19) over D and the naturality of in then implies that the earlier commutative diagram is natural over . Forming the limit of that diagram over and then applying the inverse of the function (which is given by the function if denotes the unit of ) provides a factorisation of the original obstruction square as follows:
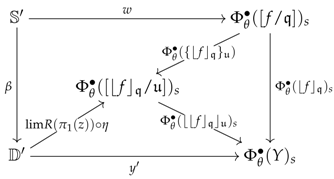

This finally shows that the -quotiented arrow is ideal. ☐
Example 51.
This example continues the discussion started in Example 50 (we shall use the same notations as those used thereof) in order to describe, in more details, the binary relation acting on (see Formula (24)) in the case where f is taken to be the canonical map . Recall that the quotient was meant to simplify the following expression:
Also, recall that, by definition, the binary relations contained in (see Remark 13 for the encoding of ) are those pairs that may be related to commutative diagrams as follows:

Precisely: The above diagram says that two elements will be identified if there exist a cone , a morphism and two elements and in such that the identities and hold and the elements and have the same image via the canonical map .
On the other hand, the binary relations contained in were given as part of our assumptions. However, in the sequel, the idea will be to define either as the empty binary relation or as we defined the set in Section 6.10. In the latter case, in order to make sense of , we need to suppose that the image takes the form given below for some functor and binary relation :
The quotient , which will later be shortened as , is supposed to identify pairs of elements coming from a previous -quotient . In this case, the pairs contained in the relation are those pairs that are the top parts of commutative diagrams of the form displayed below, where the leftmost commutative square is one of those obstruction squares constructed in Section 6.10:
Precisely: After unravelling the details of the construction of the corresponding obstruction square, the above diagram says that two elements:
will be identified if there exist a cone , say encoded by a natural transformation , an element , a morphism and two elements and living in of the form:
such that the following relations hold:
We can clearly see that the role of two binary relations and is to turn the canonical arrow into a surjection and an injection, respectively.
Example 52 (Comparison with Kelly’s construction).
Let us compare the quotients acting on the pushout object , as described in Examples 51 and 50 (where denotes the canonical arrow ), with those acting on the pushout object of Kelly’s construction [4]. Recall that, for each cone , the latter is given by a well-pointed endofunctor in . More specifically, if we take c to be a cone of the usual the form:
in D, then for every functor , the object can be computed in as the pushout object of the following span [4] (diag. (10.1), p. 31), whose components are further detailed below, while the natural transformation is the bottom arrow of the resulting pushout square:
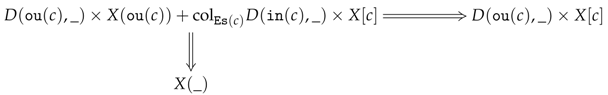
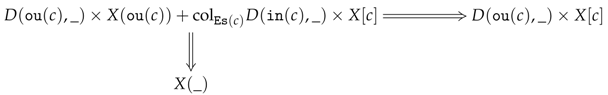
For every object , we can decompose the previous span in four parts as follows:
- (1)
- The arrow given below, part of the vertical leg, maps every pair , where t is an arrow and , to the element in :
- (2)
- The arrow given below, also part of the vertical leg, maps every pair , where t is an arrow in the colimit and is a tuple in , to the element in :
- (3)
- The arrow given below, part of the horizontal leg, is induced by the canonical arrow and maps every pair to the pair , where is the tuple in the limit object :
- (4)
- The arrow given below, also part of the horizontal leg, is induced by the canonical arrow and maps every pair , where t is an arrow for some object and , to the pair :
It takes a few lines of calculations to see that the pushout of the previous span evaluated at d can be described as a quotiented sum of the form:
where:
▹ identifies all pairs , where and , such that there exist and an arrow for which the following identities hold:
▹ identifies all pairs , where and , such that there exist and an arrow for which the following identities hold:
We can see that the definition of the relation exactly matches that of the relation given in Example 51. On the other hand, we can check that for every relation , as described in Example 51, there is an (obvious) element y for which both relations and are satisfied.
However, a relation of the form cannot be retrieved from the union of the relations and , given in Example 51. It can only be retrieved if one allows a use of these relations up to quotients. Indeed, the reader can check that the identification of the second line, below, cannot be made unless the one given in the fist line has already occured.
| elt. | Relation | elt. | |
| first identify | |||
| which then allows us to identify |
As mentioned in Section 1.4, Kelly’s construction is pursued by pushing out all the maps to give a natural transformation where identifies each component X appearing in the expression of the objects for every . We therefore obtain an expression as follows, for very object :
This expression should be compared with the (similar) expression of the -realisation obtained in Example 51, whose sum over K is, here, quotient-free:
Because the relations contained in can be written as a zigzag of relations in , we can construct an obvious arrow from to matching all the components together (here, the symbol ∼ stands for the obvious relation):
In fact, our earlier discussion showed that, if we denote and where and , then we can continue this process iteratively, by matching the components of the sum over K, so that we have arrows as follows:
One can check that all these arrows are compatible, in an obvious way, with the arrows and . However, one of our previous remarks on the fact that can only be retrieved from the relations and up to quotients shows that if there exists a dashed arrow making the following diagram commute:
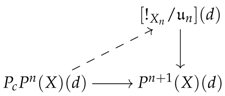

then this arrow must factorise through the following canonical arrow (see the reason below):
Indeed, otherwise we could derive a contradiction from every element of the form:
which must be identified with the element in via the relation , but must be left free in the expression of . The empty case obviously leads to the same conclusion.
If we now look at Formula (33), this factorisation means that that all the elements in the component of must be identified with elements in the other component . From the point of view of the relation at where t is taken to be the identity on , this means that the canonical arrow must be a surjection.
Finally, observe that, when , the arrow is also an injection because the images of are quotiented by the relations and hence the relation , which precisely characterises its injectiveness (see Example 51). In other words, the canonical arrow is a bijection, which makes the object a model for .
7. Combinatorial Categories and Their Oeuvres
The notion of combinatorial category encompasses all the assumptions that are necessary to the application of the small object argument in the case of systems of premodels.
7.1. Numbered Constructor
Let , be two categories and D be a small category. A numbered constructor of type consists of a constructor of type , where has coproducts, together with a limit ordinal such that the category admits colimits over every limit ordinal when seen as a preorder category. Such a structure will be denoted as a pair where will be equipped with its usual notational conventions.
7.2. Factorisable Morphisms
Let be a numbered constructor of type . A morphism in will be said to be -factorisable if it is equipped with a sequence of ideal -quotiented arrows in satisfying the following conditions:
- ▹
- initial case:;
- ▹
- successor cases:;
- ▹
- limit cases: for any (infinite) limit ordinal , the arrow is the colimit in of the following diagram over the category :
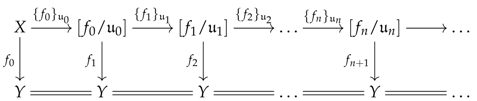
Convention 11.
For every (infinite) limit ordinal , the domain of the arrow will be denoted by . The object is by definition the colimit of the sequence of arrows where n runs over λ (see Diagram (34)). We will later denote by the associated canonical arrow .
By induction, we may show that the arrows and define a sequential functor with the following mapping rules:
Remark 20.
The functor turns the mapping into an obvious functor , which also lifts to the category via the mapping (see Diagram (34)).
Theorem 5.
Let κ denote a limit ordinal and be a system of R-premodels over a small category D in a category . If is cocomplete, R preserves colimits over every limit ordinal and the inclusion is an identity, then every morphism in may be equipped with the structure of a -factorisable morphism.
Proof.
First, the assumption that is cocomplete and R preserves colimits over every limit ordinal implies that admits colimits over every limit ordinal . We are now going to show that every morphism of the category may be equipped with the structure of a -factorisable morphism by induction. Let us define the sequence of -quotiented arrow as follows:
- ▹
- For the initial case, take to be the morphism and to be given by the collection of empty functors ;
- ▹
- By Theorem 4, the -quotiented arrow is ideal and we can take the next -quotiented arrow to be ;
- ▹
- For any (infinite) limit ordinal , the arrow is given by the colimit in of Diagram (35) over the category while is given by the collection of empty functors
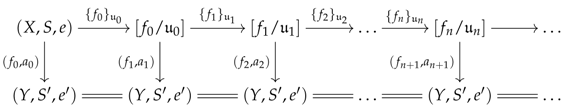
By Principle of Transfinite Induction, the preceding construction equip the morphism with the structure of a -factorisable morphism. ☐
Corollary 1.
Let κ denote a limit ordinal and be a fibered system of R-premodels over a small category D in a category . If is cocomplete and R preserves colimits over every limit ordinal , then every morphism in may be equipped with the structure of a -factorisable morphism.
Proof.
Follows from fiberedness and Theorem 5. ☐
Example 53 (Systems of premodels).
Let κ denote a limit ordinal and be a system of R-premodels over a small category D in a category where may be identified with the category of R-premodels – hence R is an identity. It follows from Example 48 and Corollary 1 that the morphisms of are all -factorisable.
Proposition 15.
Let be a -factorisable morphism. For every object d in D, the mapping induces an oeuvre of theme . This induces a functor whose images are strict narratives of degree 1.
Proof.
The fact that the mapping induces an oeuvre follows from Proposition 14 and Remark 20. One thus obtains an oeuvre of theme . It follows from Proposition 13 that the mapping defines a functor . The narrative structure is defined as follows:
- (1)
- for every , the set of events contains all the functors ;
- (2)
- for every and functor in , the viewpoint associated with the arrowis given by the -realisation of (see Diagram (19)) that may be inserted in the content , so that we obtain a lift for the previous composite that makes the following diagram commute.
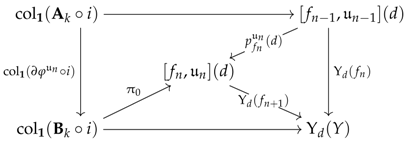 Note that the object must stand for X when .
Note that the object must stand for X when .
By definition (see Section 5.8), the previous narrative is strict. ☐
Proposition 16.
Let be a -factorisable morphism. For every object and , the mapping induces an oeuvre of theme that is equipped with the structure of a narrative of degree 2.
Proof.
The fact that the mapping induces an oeuvre follows from Proposition 9 and Remark 20. One thus obtains an oeuvre of theme . The narrative structure is defined as follows:
- (1)
- for every , the set of events contains all the functors ;
- (2)
- for every and functor in , the viewpoint is given by the pair defined in Section 6.10 if one replaces the functor with i and the -quotiented arrow with . As noticed in Remark 18, the version of Diagram (27) for these parameters provides the wanted lift.
This finishes the proof. ☐
7.3. Combinatorial Categories
Convention 12.
Let be a constructor as in Section 6.4. Recall that for every , the image encodes the diskad of a vertebra whose stem is given by . According to the conventions set in Section 4, if this vertebra is denoted by , the diskad is seen as an arrow . We shall let denote the set consisting of the domain and codomain of the coseed of the vertebra (i.e., the domain and codomain of ) for every object . Similarly, we shall let denote the set consisting of the coseeds of every vertebra for every object .
Remark 21.
For every object , the set may alternatively be seen as the set of domains of every codiskad for every object .
For every limit ordinal , a category will be said to be κ-combinatorial in a category if it is equipped with a numbered constructor of type such that:
- (1)
- every morphism in is -factorisable;
- (2)
- for every object f in and object in I, the functor , which is the context functor of the oeuvre , is -convergent.
Remark 22.
In practice, it is easy to prove that for every morphism in and object d in D, the context functor :
of the oeuvre is -convergent. This is generally due to the fact that the context functor is sequential and the vertebrae are rather “small”.
Example 54.
The following discussion continues the discussion began in Examples 50 and 51. In this respect, let be a limit sketch seen as a croquis and consider the system of premodels defined in Example 34 for the category . If one numbers the constructor with an ordinal , then for every morphism in and object d in D, the context functor:
of the oeuvre is U-convergent for any finite set U. This comes from the fact that any sequential functor of the form where is convergent with respect to finite sets. Now, in the case of the constructor , the set is made of the finite sets ∅, and , so the functor is -convergent.
Example 55.
Let denote the wide subcategory of restricted to inclusions defining relative CW-complex structures (see [17]). It is well-known that any sequential functor of the form , where , is convergent with respect to compact topological spaces (see Appendix of [17]). Since topological spheres and discs are compact, it follows that the functor associated with the constructors of the systems ofΩ-premodels defined in Examples 40 and 41 is -convergent when K is taken to be equal to and , respectively.
Example 56 (Systems of premodels).
Let be a fibered system of R-premodels over a small category D in a category . In addition, suppose that is cocomplete and R preserves colimits over every limit ordinal . Corollary 1 shows that every morphism in is -factorisable for any limit ordinal κ. Let us prove that the category becomes κ-combinatorial if:
- -
- κ is a well-chosen limit ordinal;
- -
- the statement of Remark 22 holds.
As specified by Remark 22, for every morphism in and object d in D, the context functor of the oeuvre is generally -convergent. Recall that this functor lifts to a functor landing in as follows:
Let c denote a cone of the form in K where is a functor . Let also g denote the functor defined in Example 11 where the cone ‘r’ used thereof is replaced with the natural transformation . By definition, the following equations hold for every ordinal , cone , vertebra and element :
In the case where the inequalities and hold, Example 20 says that the composite of the functor with the functor is -convergent. In other words, this shows that if is greater than or equal to the cardinality and , then the context functor of the oeuvre is -convergent.
Definition 12 (Lifting system).
Let be a combinatorial category as defined above. For every morphism in , every and , denote by the lifting system consisting of the functors picking out the codiskad .
Proposition 17.
For every morphism in , every and , the lifting system agrees with the narrative in the numbered category .
Proof.
To show that the lifting system in agrees with the narrative , which is generated by the operadic tomes for n running over , consider an ordinal and suppose that the functor in that admits a lift along ∂ as follows:
By definition, the functor picks out an element in which is therefore an element of . This means that we found a functor in the set of events whose composite with gives the lift as follows:
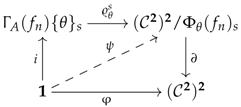

This exactly shows the statement of the proposition. ☐
Theorem 6.
Let κ be a limit ordinal and be a κ-combinatorial category as defined above. Every morphism may be factorised into two arrows:
such that, for every and , the arrow in has the rlp with respect to the codiskad of and, for every object d in D, the arrow has the llp with respect to every morphism in (see end of Section 5.6) for every .
Proof.
The factorisation is given by the image of the arrow via the functor defined in Remark 20. The statement on the arrow follows from Propositions 7 and 17 since the context functor:
of the oeuvre is -convergent (and hence -convergent for every ). The statement on the arrow follows from Propositions 8 and 15, which ensures that is a strict narrative for every object . ☐
Let be a limit ordinal. A category will be said to be trivially κ-combinatorial over a set if it is -combinatorial when equipped with the numbered constructor associated with the obvious category of -premodels whose set of vertebrae consists of the following degenerate vertebrae for every arrow :

Corollary 2 (Quillen’s small object argument).
Let be a trivially κ-combinatorial category over a set of arrows in . Every morphism in may be factorised into two arrows and where the arrow is in the class and the arrow is in the class .
Proof.
Theorem 6 implies that every morphism in may be factorised into two arrows and where the arrow is in the class and the arrow has the llp with respect to every morphism in for every . However, because of the triviality of our data, it follows that the equality holds for every . ☐
Remark 23.
For every system of R-premodels where: is cocomplete; preserves colimits over every limit ordinal and is combinatorial (see Example 56), Theorem 6 provides every arrow in with a factorisation:
where is an R-model and the arrow satisfies nice lifting properties. In the case of a category of premodels for a sketch, Example 50 shows that the ‘localisation’ admits a presentation as given in Theorem 2. There now remains to show that the arrow is universal. This is the goal of the next and last section.
8. Universal Property
This section discusses the universal properties of the factorisations provided by Theorem 6. To do so, we shall require our constructor to be ‘normal’ (see Section 8.1). An existential resut is given in Theorem 9 while a universal one is given in Theorem 8.
8.1. Normal Constructors
A constructor of type will be said to be normal if:
- (1)
- the categories and possess terminal objects (denoted by );
- (2)
- for every and , the functor preserves .
- (3)
- the mappings and (see Section 6.4) induce functors from to that extend the mappings , , and into obvious functors from to , , and , respectively;
Example 57.
The constructor associated with a system of R-premodels over a small category D in a category that possesses a terminal object is normal. Item (1) is straightforward and item (2) follows from the fact that preserves any terminal object by adjointness. The functoriality of the sets and is induced by the action of a morphism on the sets S and (see Section 6.5) while the functoriality of the functors , , and is straightforward .
Remark 24.
A consequence of item (3) is that the mappings and now induce functors and .
8.2. Quasi-Models and Models
Let be a normal constructor of type . For every object X in , there is an obvious morphism in given by the following commutative square:
Applying the functor (see Remark 24) on this morphism provides the following natural transformation in over D, which is natural in :
An object X in will be said to be a quasi-model of if for every object d in D, the function is surjective. A model of is a quasi-model X of that is equipped with a natural section of the natural surjection . Such a structure will be denoted as a pair .
Remark 25.
It follows from the definition of a surjection that an object is a quasi-model of if and only if for every object and tuple in , every commutative cube admits a lift as follows (where θ stands for ):
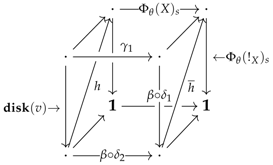

Remark 26.
The difference between a quasi-model and a model is that the lifts are chosen. Specifically, any model of is determined by a collection of lifts chosen for every object , element as follows:
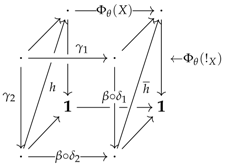

Indeed, if one denotes the previous commutative cube by and its upper commutative part seen as a degenerate commutative cube by , the section is determined by the following mapping rules:
The fact that such a mapping defines a natural section of the natural surjection is straightforward. Conversely, if a natural section was not of this form, we could find two arrows and such that the elements and would be sent to elements of the following form via the section :
However, the naturality of above the arrows t and also implies the equalities:
which show that the section has to be of the form previously given in the remark.
Example 58 (System of premodels).
Let be a system of R-premodels as in Example 57. The R-models are exactly given by the quasi-models of . By Remark 26, it is always possible to turn a quasi-model X into a model by using the axiom of choice on the different possible lifts.
Let now A be an object in . An A-quasi-model for the constructor consists of a morphism in where X is equipped with the structure of a quasi-model X. Similarly, an A-model for the constructor consists of a morphism in where X is equipped with the structure of a model . The latter structure will be denoted as a triple .
8.3. Quotiented Models
Let be a normal constructor of type and A be an object in . A -quotiented A-quasi-model consists of an -quotiented arrow in together with an A-quasi-model . Such a structure will be denoted as an arrow .
Remark 27 (In preparation of Definition 13).
In Definition 13, we define two new quotients that relies on the definition of . There is the quotient denoted by , which should be thought of as the collections of all commutative squares contained in (when viewed in ) whose top horizontal arrows are post-composed with the morphism (in ) while the bottom horizontal arrows consist of identities on the terminal object . The other quotient, denoted by , should be thought of as the collections of commutative squares contained in that admit lifts.
Definition 13.
For every -quotiented quasi-model where is given by a collection of functors , we may define a collection of functors:
whose component at the parameters and is given by the following image factorisation for every :
Then, we may define another collection of functors of the form:
whose component at the parameters and is obtained by pulling back the inclusion along the image of the morphism given in Equation (36) via the functor (see diagram below):
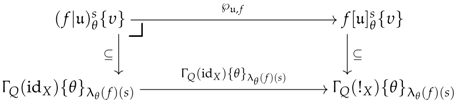
Definition 14 (Quotiented model).
A -quotiented A-model consists of a -quotiented arrow in together with an A-model such that for every element and , the transformation has a section . Such a structure will be denoted as an arrow .
For every -quotiented A-model , we may define two functors and given by the following sums for every :
These two functors give rise to two others and defined as the following sums over the set associated with :
It follows from the structure of that the functions , and induce an obvious sequence of natural transformations as follows:
Applying an image factorisation on the three composite arrows of codomain that results from the previous sequence leads to a new sequence of arrows as follows:
8.4. Tomes for Quotiented Models
Let be a normal constructor of type where has coproducts, A be an object in and be a -quotiented A-model. The merolytic tome of is the functor resulting from the coproduct of the following two functors for every :
This functor is therefore equipped with the following mapping rules:
Proposition 18.
The merolytic tome is natural in the variable . This amounts to saying that the mapping induces a functor .
Remark 28.
The naturality of over D extends to its content. In particular, it takes a few lines of straightforward calculations to see from the definitions of the functor and the functor that the top-left corner of the content of is equal to the top-left corner of the content of the tome :

The diagram given on the left of Remark 28 induces a commutative diagram in of the form given below. This diagram will be referred to as the functorial content of :

8.5. Effectiveness of Quotiented Models
Let be a normal constructor of type where has coproducts and A be an object in . A -quotiented A-model will be said to be -realised if one may form a pushout square inside the functorial content of its merolytic tome as shown below:
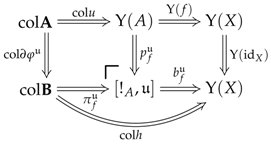

By Remark 28, the pushout square may be supposed to be exactly the same as that defined for the -realisation of . In particular, the following result holds.
Proposition 19.
A -quotiented A-model is -realised if and only if so is the -quotiented arrow .
Definition 15 (Effectiveness).
Let denote a constructor of type as defined in Section 6.4. A -quotiented A-model will be said to be effective if it is -realised and it is equipped with a factorisation of in , as given on the left of Equation (41), that lifts the factorisation of through the -realisation of along :
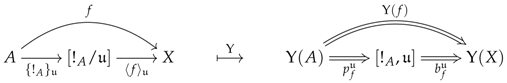
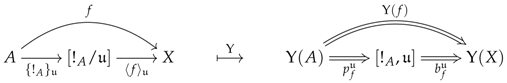
The leftmost factorisation of Equation (20) will be called the -factorisation of .
Theorem 7.
Let be a system of R-premodels over a small category D in a category . If has pushouts and the inclusion is an identity, then every -quotiented relative model is effective.
Proof.
Consider a relative model given by a morphism . The goal is to show that this morphism satisfies to the lifting conditions expressed in Equation (41) where the arrow is already constructed in Theorem 3. In fact, the proof of the present theorem is very similar to that of Theorem 3, except that it uses Diagram (42) instead of Diagram (21) for every and . As in the proof of Theorem 3, the symbols r and stand for the objects and in D, respectively:
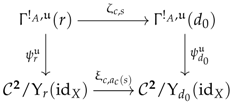
The proof that Diagram (42) commutes goes as in the proof of Theorem 3 by using Formula (39). Then, Diagram (42) may be used to show that the following diagram commutes:

The substantial information given by the previous diagram is the inner bottom commutative trapezoid, which shows that the lift exists; the desired factorisation is deduced by universality. ☐
Definition 16 (Strongly Fibered).
A system of R-premodels over a small category D in a category will be said to be strongly fibered if it is fibered and, for every -quotiented arrow , the -factorisation of any corresponding -quotiented -model (obtained in Theorem 3) lifts to .
Remark 29.
Let be a category with all pushouts. By Definitions 8 and 15, any subcategory of whose associated functor is fully faithful is necessarily strongly fibered. As a result, the category is strongly fibered. Thus, examples of strongly fibered systems of premodels are : Example 34–41.
Example 59.
For the same reasons put forward in Example 49, the system of Ω-premodels defined in Example 42 is strongly fibered.
Proposition 20.
Let be a normal constructor of type where has coproducts. Let be an effective -quotiented arrow in and be some effective A-model of . There exists a section turning the -quotiented -quasi-model into a -quotiented -model.
Proof.
Let us define the section , which must be a function of the following form for every and .
The idea is that the section is induced by the action of the section on the obstruction squares contained in the domain of Equation (43). On the other hand, the other section mentioned in the statement does play any role here.
First, recall that an obstruction square in is given by the lower front commutative square of a commutative cuboid as follows:

By using the factorisation , we can also obtain Diagram (44), whose lower trapezoid going from the arrow to the arrow , on the front face, is the image of our previous obstruction square via the canonical map:
induced by Diagram (36). By definition, this lower trapeziod is an element in the quotient :

To define our section , we simply need to explain how the lower trapezoid going from the arrow to the arrow , on the front face of the previous diagram, is mapped to an element in the following quotient:
We will do so by simply showing that this lower trapezoid admits a lift.
By assumption on the A-model , the outer cuboid of Diagram (44) admits a lift (see Remark 26). By universality of , this implies that the commutative diagram given below, on the left, must commute. The corresponding square given on the right then encodes an element in :
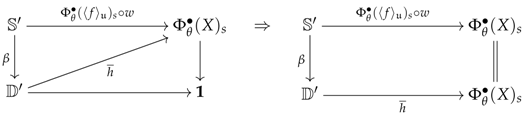
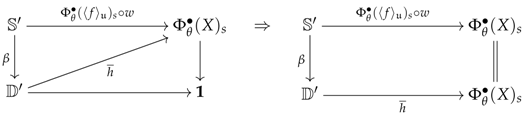
This finishes the description of the section for the parameters and .
The following theorem provides a universal property that only makes sense in the case of Examples 34 and 35. However, possible extensions of its assumptions (to a homotopical context) may be discussed so that the examples that were provided in Section 4.3 may be equipped with universal properties too; this will be discussed in a future work.
Theorem 8 (Universality).
Let be an effective -quotiented A-model such that the -quotiented arrow is also effective. If:
- (i)
- the transitive quotientor is a epimorphism in for every ;
- (ii)
- the arrow is a monomorphism is ;
- (iii)
- the trivial stem of is an epimorphism for every ;
- (iv)
- the functor is faithful;
- (v)
- the initial section is an isomorphism,
then every arrow in that factorises as shown below, on the left, and makes the succeeding diagram, on the right, commute must be equal to :
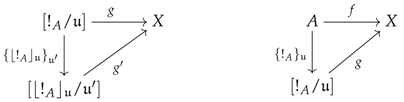
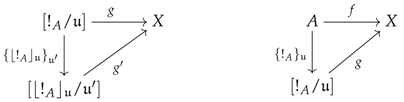
Proof.
Consider some arrow making the right diagram of the statement commute. Let d be an object in D. After application of on it and using the definition of the -realisation of , we obtain the following commutative diagram:
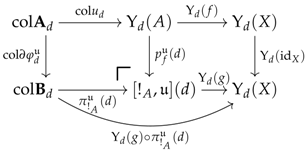

By universality of the -realisation and faithfulness of , the statement is proven if we show that the composite is equal to the arrow of Diagram (40) for every object . Equivalently, we need to show that, for every functor , the universal shifting of along i is equal to the composite . By definition, the universal shifting of the preceding diagram along any functor provides a diagram as given below, on the left. On the right is given the shifting of Diagram (40) along that same functor i:
Because the top vertical arrows of the previous two diagrams are the same and the transitive quotientor is an epimorphism, the shifting of along must be equal to . There only remains to check the same property for functors of the form .
Consider a functor . By assumption (v), the image of this functor is of the form where (since ) and . For this particular parameter , apply the functor on the two factorisations given in the statement. With these two factorisations, the diagram obtained in Remark 18 for the parameters gives a commutative diagram as follows (where ):

As shown in the diagram above, the composite is equal to . Because the two factorisations of the statement are also true when replacing g and with and , we similarly deduce that the composite is equal to . Because the trivial stem of is an epimorphism, the following equality must hold:
It is not hard to see that this equality implies the next one (Diagram (46) might help visualise this point if one imagines the arrows that were forgotten in the background):
Because is a monomorphism, we obtain the equation , which leads to the following one after post-composing with the arrow and using the bifunctoriality of :
Now, by Remark 19, we know that the composite is equal to the composite . According to the bottom part of the rightmost diagram of Equation (45), this means that the right-hand side of the previous equation corresponds to the component of the natural transformation h evaluated above the element picked out by the functor . This therefore concludes the proof of the statement. ☐
Example 60.
The vertebrae of Examples 34 and 35 satisfy assumptions (i), (iii) and (iv) of Theorem 8. Similarly, the -models generated by these examples, which are quasi-models of the associated constructor by Remark 25, or, in fact, actuals models, by Remark 26 and the axiom of choice, satisfy condition (ii). Finally, it follows from Remark 12 that condition (v) can also be satisfied in the case of these examples.
8.6. Factorisable Models
Let be a normal numbered constructor of type where has coproducts, A be an object in and be a model of . An A-model will be said to be -factorisable if the morphism is equipped with the structure of a -factorisable arrow, say , together with a sequence of effective -quotiented relative models satisfying the following conditions:
- ▹
- initial case:;
- ▹
- successor cases: is given by the arrow ;
- ▹
- limit cases: for any (infinite) limit ordinal , the arrow is the colimit in of the following diagram over the category .
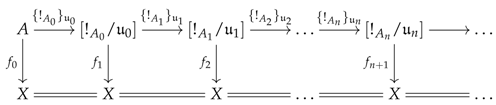
Remark 30.
Every -factorisable A-model is equipped with a factorisation of the Form (47), where the arrow is the image of the sequential functor (defined after Convention 11) above the arrow :

Later on, the arrow will be denoted as and called the localisation of . According to Theorem 6 and Remark 25, if the category is equipped with the structure of a κ-combinatorial category for the constructor , then the object must be a quasi-model of .
Theorem 9 (Weak localisation).
Let κ denote a limit ordinal and be a system of R-premodels over a small category D in a category . If is cocomplete, R preserves colimits over every limit ordinal and the inclusion is an identity, then every relative model of may be equipped with the structure of a -factorisable relative model.
Proof.
Let be a relative model of . By Theorem 5, the morphism may be equipped with the structure of a -factorisable arrow where:
- ▹
- is a collection of empty functors ;
- ▹
- the object is given by ;
- ▹
- For any (infinite) limit ordinal , the object is the colimit in of Diagram (48) over the category while is given by the collection of empty functors :
Because is made of empty functors, the identity on the empty set provides a section that turns into an obvious -quotiented -model. By Proposition 20, this model structure generates new model structures for all the finite successor ordinals of . These structures of relative model give rise to an -model by forming the colimit of the previous ones along the arrows . The same argument can be repeated for all ordinals of , since, for every infinite limit ordinal , the -quotient is made of empty functors. By Principle of Transfinite Induction, this shows that we can define a sequence of -quotiented relative models , which must be effective by Theorem 7 and where is given by . This concludes the proof by definition of a factorisable -model. ☐
Corollary 3.
Let κ denote a limit ordinal and be a strongly fibered system of R-premodels over a small category D in a category . If is cocomplete and R preserves colimits over every limit ordinal , then every relative model of may be equipped with the structure of a -factorisable relative model.
Proof.
This corollary is an obvious generalisation of Theorem 9 that takes advantage of the notion of strong fiberedness (see Definition 16). ☐
8.7. Elimination of Quotients
A normal numbered constructor of type will be said to eliminate quotients if the category is a -combinatorial category for the constructor and every canonical arrow is equipped with the structure of a -factorisable morphism such that every A-model is -factorisable for this structure.
Remark 31.
For every object A in , all A-models are equipped with the same localisation where is a quasi-model (see Remark 30). The way in which this arrow has been defined from the data of is the key of the so-called ‘elimination of quotients’.
Theorem 10.
Let be a normal numbered constructor of type that eliminates quotients. For every object A in , every quasi-model X and arrow in , there exists an arrow in making the following diagram commute:
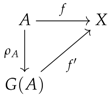
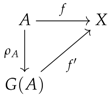
Proof.
By Remark 26 and the axiom of choice, every quasi-model X may be equipped with the structure of a model . It follows from Remark 30 that the diagram of the statement commutes. ☐
Example 61.
Save for Example 43, all the examples of Section 4.3 satisfy Corollary 3 (see Remark 29). Following Examples 54 and 55 for premodels valued in and and considering similar arguments for premodels valued in and , one can deduce from Example 56 that these examples are κ-combinatorial for some well-chosen ordinal κ. This means that these examples eliminate quotients and are equipped with a localisation of the form given in Theorem 10. In particular, this localisation tends to organise the different sorts of data appearing in the diskads of the systems in the form of bundles—this was explicited in Examples 50 and 51 in the case of the models for a limit sketch.
Remark 32.
Under the conditions of Theorem 8, the factorisation of Theorem 10 may be shown to be unique by using an obvious transfinite induction.
9. Concusions
9.1. Conclusions for Motivation 1
In Section 1.3, one of our main goals was to provide a language that would allow us to show strict universal properties from weak definitions. In this paper, we address this question in the form of Theorem 8. This theorem shows us what the main ingredients that are responsible for universal properties look like and most of them pertain to the sets of vertebrae associated with our systems of premodels (see conditions (i), (ii) and (iii)).
In fact, many sections and concepts were introduced in this paper because of these vertebrae. The need for each of these sections can be explained by the following storyline. At the centre of things is Section 4.3, which introduces the concept of system of premodels. This structure is a formal way to present the lifting problems associated with our vertebrae. To handle these lifting problems, we have to introduce the analytic and quotient species given in Definition 6. However, because these species need some formal setting, the concept of constructor is introduced in Section 6.4, which a fortiori motivates the introduction of preconstructors in Section 6.2. Note that the main purpose of the latter is to allow the handling of the premodel structure (e.g., the maps defined in Section 4.2) while the purpose of the former is to allow the handling of the vertebrae associated with systems of premodels. The way one handles the species is formalised via the tools of Section 5, in which is expressed our small object argument (Proposition 7). This section really allows us to see the big picture without introducing too much detail. On the other hand, from Section 6.6 to the end of Section 6, we give all the details of this big picture in the case of systems of premodels. We also use Section 7 to explain what it takes, in terms of required assumptions, to be able to apply the small object argument of Section 5. The need for Section 8 naturally presents itself if one is interested to know more about the universal properties satisfied by the models living in systems of premodels. As one is able to see there, this section heavily relies on the concept of species introduced in Section 6.4 and hence the concept of vertebra.
The fact that this last section relies so heavily on the vertebrae is not so surprising when one knows that vertebrae are meant to encode some sort of homotopical information and that, on the other hand, Homotopy Theory is all about coherence property. In fact, this idea of coherence—and universal property—coming from vertebrae is already discussed in my thesis [34] and this is exactly the spirit in which Theorem 8 should be regarded. In this respect, I will use the rest of this conclusion to explain why the formalism of systems of premodels is something that one might want to consider if one wants to solve higher coherence problem.
A way to put it would be to ask what happens if one starts changing the assumptions of Theorem 1 (see Section 1) in terms of homotopical properties. The notion of epimorphism used thereof could be replaced with a notion of epimorphism up to homotopy. For instance, the arrow could be called a weak epimorphism if for every pair of arrows for which the equation holds, we can form the pushout of with itself (see below) so that a given arrow factorises the universal arrow induced by f and g under as follows:
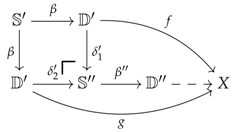

A quick look at the beginning of the proof of Theorem 8, in which should be viewed as the transitive quotientor , shows that such a notion of weak epimorphism would imply that the universal solution of the reflection would be unique up to a homotopy relation as defined in Equation (49). However, this type of statement would only hold if the vertebra:
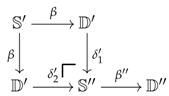 satisfies some nice compositional properties, and, more specifically, compositional properties of the type defined in [34]. In other words, our vertebra would need to satisfy axioms of the same type as those usually considered in the case of (co)limit sketches – the compositional properties would try to recapture the idea of composition of cells in (Higher) Category Theory.
satisfies some nice compositional properties, and, more specifically, compositional properties of the type defined in [34]. In other words, our vertebra would need to satisfy axioms of the same type as those usually considered in the case of (co)limit sketches – the compositional properties would try to recapture the idea of composition of cells in (Higher) Category Theory.

Interestingly, these axioms would also mingle different vertebrae together. For instance, it is interesting to note that our current discussion has made us consider two vertebrae: one for which is a stem (as usual) and one for which is both a seed and a coseed, given in Equation (50). This pair of vertebrae can be arranged in the form of the following diagram:
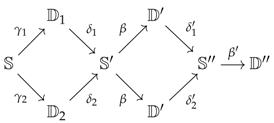

Such a commutative diagram defines what is called a spine (of degree 1) in [34]. There, spines are shown to be essential in the understanding of higher coherence results of the type mentioned above and one can see that these structures arise very naturally once one starts talking about universal properties. The degree of a spine hides a dimensional nature and it is interesting to note that this dimensional aspect already arises among the examples discussed in [14] (Section 4) when it is asked whether weak reflections can possess strict universal property such as functoriality and naturality.
In conclusion, the idea of universal property and coherence fits the language of systems of premodels nicely, so that these structures appear to be the right setting to address the question whether a class of algebraic objects defined via weak lifting properties can satisfy strict (or at least stricter than expected) universal properties—and an important part of the work to be done in this direction can already be perceived in [34].
9.2. Conclusions for Motivation 2
In Section 1.4, our other main goal was to prove Theorem 2, along with Propositions 1 and 2. These results were proven in different sections of the present paper. Before addressing the usefulness of these results, we briefly recapitulate their proof below.
Let be a limit sketch, seen as a croquis, and consider the system of premodels defined in Example 34 for the inclusion . First, Example 61 tells us that the reflector associated with a premodel (Also called a ‘presentation’ in Section 1.4) A in is given by Theorem 10. Its strict universal property then follows from Remark 32, where one needs to look at Example 60 in order to use Theorem 8. The functoriality of the reflection and the naturality of the reflector obviously follows from this (strict) universal property.
Now, if one consider the transfinite construction of the reflector given in Section 7.2, one may see that the transfinite sequence that gives rise to the reflector is of the desired form:
- -
- for Proposition 1 by using Example 50;
- -
- for Proposition 2 by using Example 52;
- -
- for Theorem 2 by using Examples 50–52, for which one needs to realise that a sum of the form:is the same thing as a left Kan extension of the form given in Equation (51), where K must regarded as a discrete category:
The question that now remains to be answered is: what is the combinatorial presentation given by Theorem 2 useful for? Recall that, according to Theorem 2, the reflector associated with a presentation X in is the transfinite composition of a sequence of arrows as follows:
where, for every , the object is the left Kan extension of the functor:
where, here, the functor denotes the sum :

The restriction of the quotient map (see Section 1.4) to the object gives us a way to organise the data of with respect to its fibres. Of course, this organisation is also present in Kelly’s construction via the quotients acting on (see Example 52), but this organisation is also unlikely to be the one that one wants to consider if one decides to study the combinatorial properties of the models. In fact, while Kelly’s construction forces us to consider an actual quotient of the object , the elimination of quotients leaves the object free of quotients, so that one can now use any other type of relations on without being forced to deal with the relations of the localisation. Furthermore, the formalism of quotient maps (formalised in terms of quotiented arrows in Section 6.7) makes compatibility and distributivity questions between potential new relations and those forced by the localisation much easier to study.
For instance, one could want to study the colimits of the category of models for . Recall that colimits in this category are given by the images of the reflection G on the corresponding colimits in the category of premodels , as shown below:
In addition, recall that a colimit of the form in can be seen as a quotiented sum:
The relations ∼ acting on the sum usually generates the type of identifications that one wants to study. Specifically, one usually wants to understand how these propagate through the transfinite constructions building the models. However, their propagation is usually non-obvious and requires some more-or-less non-trivial case-by-case analysis, depending on how complicated the theory is. This case-by-case analysis might not even depend on the quotients implied by the localisation and might instead depend on the properties of the objects . In order to be efficient and clear, this case-by-case analysis needs to be processed in a quotient-free environment separated from the quotients generated by the localisation, but what is better than a quotient map whose domain is a quotient-free left Kan extension of the form given in Equation (51) to make such a separation? Interestingly, the construction of the quotient maps has motivated the formalisation of the concept of quotient (in Section 6.7), so that our results open the door to the development of a new language to talk about quotients living in algebraic objects in general.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Recall that the category of sets is complete and cocomplete. The limit of a functor for some small category D is given by the set:
while the colimit of a functor for some small category D is given by the quotient set:
where ∼ denotes the binary relation whose relations are defined when there exists an object e and two arrow and in D such that the equation holds. Note that in the case where D is a preorder category for some ordinal , the binary relation ∼ is an equivalence relation.
Proof of Proposition 4.
A proof may be found in [35] (Corollaire 9.8). For the sake of self-containedness, the proof is recalled in this appendix. Let be a functor. An equivalence class for the equivalence relation ∼ will be denoted into brackets, i.e., . The notation:
will be used to mean that the collection is compatible with the action of the functor F in the appropriate way (see Equation (A1)). By definition, the following equations hold:
The natural transformation is given by the following mapping:
Let us prove its surjectiveness. Consider an element in of the following form:
By definition of the compatibility with the action of F, for any arrow in D, there exist arrows and in such that the next equation holds:
Since is a limit ordinal greater than or equal to , we may define the following supremum in :
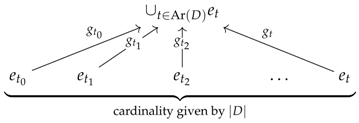

Denote the supremum by e. Note that for any pair of arrows and in D, the arrows and are equal in . The family made of the elements for every object d in D is then compatible with the action of F, since, for any arrow in D, the following equation holds from Equation (A2):
In addition, it is not hard to check that the mapping rule of the natural transformation includes the rule:
since . Let us now prove its injectiveness. Note that any equality implies the existence of cospans:
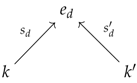 such that the identity holds for every object d in D. Now, define the following supremum, which will be denoted by :
such that the identity holds for every object d in D. Now, define the following supremum, which will be denoted by :
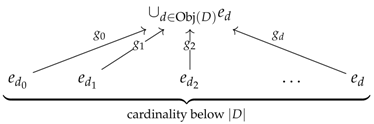


For every object d in D, the arrows are equal in . The same is true for . It follows that the equation:
holds, which implies the identity . ☐
Proof of Proposition 5.
We keep the convention set in the proof of Proposition 4. We only need to check that the diagram of the statement commutes. For any set X, the unit maps an element of to the constant collection . Similarly, for any functor , the unit maps an element of to the constant collection in . The diagram of the statement is therefore encoded by the following mapping rules:
In particular, this shows that the diagram commutes. ☐
References
- Adámek, J.; Rosický, J. Locally Presentable and Accessible Categories; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Borceux, F. Flat functors and Cauchy completeness. In Handbook of Categorical Algebra; Cambridge University Press: Cambridge, UK, 1994; Volume 1. [Google Scholar]
- Freyd, P.J.; Kelly, G.M. Categories of continuous functors. J. Pure Appl. Algebra 1972, 2, 169–191. [Google Scholar] [CrossRef]
- Kelly, G.M. A unified treatment of transfinite constructions for free algebras, free monoids, colimits, associated sheaves, and so on. Bull. Aust. Math. Soc. 1980, 22, 1–83. [Google Scholar] [CrossRef]
- Lawvere, W. Functorial Semantics of Algebraic Theories. Ph.D. Thesis, Columbia University, New York, NY, USA, 1963. [Google Scholar]
- Adámek, J.; Herrlich, H.; Rosický, J.; Tholen, W. On a generalized Small-Object Argument for the Injective Subcategory Problem. Cah. Topol. Geom. Differ. Categ. 2002, 43, 83–106. [Google Scholar]
- Hirschhorn, P.S. Model categories and their localizations. Math. Surv. Monogr. 2003, 99, 457. [Google Scholar]
- Quillen, D. Homotopical Algebra; Morel, J.M., Teissier, B., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1967; Volume 43. [Google Scholar]
- Garner, R. Understanding the small object argument. Appl. Categ. Struct. 2009, 17, 247–285. [Google Scholar] [CrossRef]
- Garner, R. Homomorphisms of higher categories. Adv. Math. 2010, 224, 2269–2311. [Google Scholar] [CrossRef]
- Batanin, M. Monoidal globular categories as natural environement for the theory of weak n-categories. Adv. Math. 1998, 136, 39–103. [Google Scholar] [CrossRef]
- Berger, C. A Cellular Nerve for Higher Categories. Adv. Math. 2002, 169, 118–175. [Google Scholar] [CrossRef]
- Tholen, W. Essential weak factorization systems. Contrib. Gen. Algebra 2001, 13, 321–333. [Google Scholar]
- Adámek, J.; Herrlich, H.; Rosický, J.; Tholen, W. Injective hulls are not natural. Algebra Universalis 2002, 48, 379–388. [Google Scholar] [CrossRef][Green Version]
- Poizat, B. Une théorie de Galois imaginaire. J. Symb. Log. 1983, 48, 1151–1170. [Google Scholar] [CrossRef]
- Shelah, S. Classification Theory and the Number of Nonisomorphic Models, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Grothendieck, A.; Colmez, P. Grothendieck-Serre Correspondence: Grothendieck’s Letter to Serre; American Mathematical Society: Paris, France, 2014. [Google Scholar]
- Kiss, E.W.; Kearnes, K. The Shape of Congruence Lattices; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- McKenzie, R. Some unsolved problems between lattice theory and equational logic. In Proceedings of the University of Houston Lattice Theory Conference, Houston, TX, USA, 22–24 March 1973; pp. 564–573. [Google Scholar]
- Brown, K. Abstract homotopy theory and generalized sheaf cohomology. Trans. Am. Math. Soc. 1973, 186, 419–458. [Google Scholar] [CrossRef]
- Pronk, D.A.; Warren, M.A. Bicategorical fibration structures and stacks. Theory Appl. Categ. 2014, 29, 836–873. [Google Scholar]
- Joyal, A.; Tierney, M. Strong stacks and classifying spaces. In Category Theory; Springer: Berlin, Germany, 1991. [Google Scholar]
- Maltsiniotis, G. Grothendieck ∞-Groupoids, and Still Another Definition Of ∞-Categories. arXiv, 2010; arXiv:1009.233. Available online: https://arxiv.org/abs/1009.2331 (accessed on 13 September 2010).
- Rezk, C. A model for the homotopy theory of homotopy theory. Trans. Am. Math. Soc. 2001, 353, 973–1007. [Google Scholar] [CrossRef]
- Stanculescu, A.E. Stacks and sheaves of categories as fibrant objects, I. Theory Appl. Categ. 2014, 29, 654–695. [Google Scholar]
- Simpson, C. Homotopy Theory of Higher Categories: From Segal Categories to n-Categories and Beyond. In New Mathematical Monographs; Cambridge University Press: Cambridge, UK, 2011; Volume 19. [Google Scholar]
- Métayer, F. Resolutions by Polygraphs. Theory Appl. Categ. 2003, 11, 148–184. [Google Scholar]
- Lane, S.M. Categories for the Working Mathematician, Graduate Texts in Mathematics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Dugger, D.; Isaksen, D.C. Weak Equivalences of Simplicial Presheaves; Priddy, S., Goerss, P., Eds.; Homotopy Theory: Relations With Algebraic Geometry, Group Cohomology, and Algebraic K-Theory; American Mathematical Society: Evanston, IL, USA, 2004; pp. 97–113. [Google Scholar]
- Lafont, Y.; Métayer, F.; Worytkiewicz, K. A folk model structure on omega-cat. Adv. Math. 2010, 224, 1183–1231. [Google Scholar] [CrossRef]
- Toën, B. The homotopy theory of dg-categories and derived Morita theory. Invent. Math. 2007, 167, 615–667. [Google Scholar] [CrossRef]
- Joyal, A. Foncteurs Analytiques Et Espèces De Structures. In Combinatoire énumérative; Springer: Berlin, Germany, 1986; pp. 126–159. [Google Scholar]
- Tuyéras, R. Sketches in Higher Category Theory; Macquarie University: Sydney, Australia, 2015. [Google Scholar]
- Artin, M.; Grothendieck, A.; Verdier, J.-L. Séminaire De Géométrie Algébrique Du Bois Marie–1963-64–Théorie Des Topos Et Cohomologie étale Des Schémas-(SGA 4)-Volume 1; Springer-Verlag: Berlin, Germany; New York, NY, USA, 1972; Volume 269, p. xix + 525. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).