Characterization of the Minimizing Graph of the Connected Graphs Whose Complements Are Bicyclic

Abstract

In a certain class of graphs, a graph is called minimizing if the least eigenvalue of its adjacency matrix attains the minimum. A connected graph containing two or three cycles is called a bicyclic graph if its number of edges is equal to its number of vertices plus one. Let ${\mathcal{G}}_{1,n}^c$ and ${\mathcal{G}}_{2,n}^c$ be the classes of the connected graphs of order n whose complements are bicyclic with exactly two and three cycles, respectively. In this paper, we characterize the unique minimizing graph among all the graphs which belong to ${\mathcal{G}}_n^c={\mathcal{G}}_{1,n}^c\cup {\mathcal{G}}_{2,n}^c$, a class of the connected graphs of order n whose complements are bicyclic.

1. Introduction

Let G be a finite, simple and undirected graph with the vertex-set $V(G)=\{v_i:1\le i\le n\}$ and the edge-set $E(G)$ such that $|V(G)|=n$ and $|E(G)|=m$ are order and size of the graph G, respectively. The adjacency matrix $\mathbf{A}(G)=\left[a_{i,j}\right]$ of the graph G is a matrix of order n, where $a_{i,j}=1$ if $v_i$ is adjacent to $v_j$ and $a_{i,j}=0$, otherwise. The zeros of $\det (\mathbf{A}(G)-\lambda \mathbf{I})$ are called the eigenvalues of $\mathbf{A}(G)$, where $\mathbf{I}$ is an identity matrix of order n. Since $\mathbf{A}(G)$ is real and symmetric, all the eigenvalues say that ${\lambda }_1(G)$, ${\lambda }_2(G)$, ..., ${\lambda }_n(G)$ are real and called the eigenvalues of the graph G. If ${\lambda }_1(G)$ is the least, then one can arrange the eigenvalues as ${\lambda }_1(G)\le {\lambda }_2(G)\le ...\le {\lambda }_n(G)$, and the eigenvector corresponding to the least eigenvalue is called the first eigenvector. For further study, we refer [1,2].

In 1957, Collatz and Sinogowitz investigated the spectrum of an undirected graph with respect to the adjacency matrix [3]. The literature on spectra of graphs has grown enormously since that time. The investigation on the spectral radius (largest eigenvalue) of graphs is an important topic in the theory of graph spectra [1,2,4,5,6]. In literature, the least eigenvalue received less attention comparatively to the spectral radius.

In a certain class of graphs, a graph is called minimizing if the least eigenvalue of its adjacency matrix attains the minimum. A graph G is called a nested split if its vertices can be ordered so that $jq\in E_G$ implies $ip\in E_G$, where $i\le j$ and $p\le q$. Let $\mathcal{G}(m,n)$ denote the class of connected graphs of order n and size m, where $0<m<$$\left(\genfrac{}{}{0pt}{}{n}{2}\right)$. Bell et al. [7] characterized the minimizing graphs in $\mathcal{G}(m,n)$ as follows.

Theorem 1.

Let G be a minimizing graph in $\mathcal{G}(m,n)$. Then, G is either (i) a bipartite graph; or (ii) a joining of two nested split graphs (not both totally disconnected).

It is observed that the complements of the minimizing graphs in $\mathcal{G}(m,n)$ are either disconnected or contain a clique of order greater than or equal to the half of the order of the graphs. This motivated discussion of the least eigenvalue of the graphs whose complements are connected and contain cliques of small sizes. Fan et al. [8] characterized the unique minimizing graph in the class of graphs of order n whose complements are trees. Wang et al. [9] characterized the unique minimizing graph in the class of graphs whose complements are unicyclic. Recently, the minimizing graph of the graphs which belong to ${\mathcal{G}}_{1,n}^c$ is studied in [10], where ${\mathcal{G}}_{1,n}^c$ is a class of the connected graphs of order n whose complements are bicyclic with exactly two cycles. In this note, we continue this study and characterize the unique minimizing graph among all the graphs which belong to a class of the connected graphs of order n whose complements are bicyclic with two or three cycles. The main result of this paper is stated as follows.

Theorem 2.

Let ${\mathcal{G}}_{1,n}$ and ${\mathcal{G}}_{2,n}$ be the classes of the bicyclic graphs of order n in which each bicyclic graph has exactly two and three cycles, respectively. Let ${\mathcal{B}}^c\in {\mathcal{G}}_n^c$ be a connected graph of order n such that its complement is a bicyclic graph i.e., $\mathcal{B}\in {\mathcal{G}}_{1,n}\cup {\mathcal{G}}_{2,n}$. Then:

$${\lambda }_{\min }(\mathcal{B}{(\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )}^c)\le {\lambda }_{\min }({\mathcal{B}}^c)$$

where $n\ge 30$ and equality holds if and only if $\mathcal{B}=\mathcal{B}(\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )$.

The results related to the bounds of the least eigenvalue can be found in [5,11]. For further study, we refer [12,13,14,15,16,17]. The rest of the paper is organized as follows: in Section 2, we present some basic definitions and terminologies that are frequently used in the main results and Section 3 includes the main results from the minimizing graph of the connected graphs whose complements are bicyclic.

2. Preliminaries

A star of size n is a tree that is obtained by joining one specific vertex to the remaining n vertices, where the fixed vertex is called center and all other vertices are called pendent vertices. It is denoted by ${\mathcal{K}}_{1,n}$ and its vertex-set and edge-set are defined as $V({\mathcal{K}}_{1,n})=\{v_i:1\le i\le n+1\}$ and $E({\mathcal{K}}_{1,n})=\{v_1{v}_i:2\le i\le n+1\}$, respectively. Moreover, ${\mathcal{S}}_{1,n}^1$ is a graph obtained by joining any one pair of pendent vertices of ${\mathcal{K}}_{1,n}$. If we choose a pair of pendent vertices of ${\mathcal{K}}_{1,n}$ consisting of $v_n$ and $v_{n+1}$, then $V({\mathcal{S}}_{1,n}^1)=\{v_i:1\le i\le n+1\}$ and $E({\mathcal{S}}_{1,n}^1)=\{v_1{v}_i:2\le i\le n+1\}\cup \left\{v_n{v}_{n+1}\right\}$ are the vertex-set and the edge-set of the graph ${\mathcal{S}}_{1,n}^1$, respectively. Similarly, ${\mathcal{S}}_{1,n}^2$ is a graph obtained by joining any two distinct pairs of pendent vertices of ${\mathcal{K}}_{1,n}$ such that $V({\mathcal{S}}_{1,n}^2)=V({\mathcal{S}}_{1,n}^1)$ and $E({\mathcal{S}}_{1,n}^2)=E({\mathcal{S}}_{1,n}^1)\cup \left\{v_{n-2}{v}_{n-1}\right\}$, where $(v_{n-2},v_{n-1})$ is chosen as the second pair of pendent vertices different from $(v_n,v_{n+1})$. If two chosen pairs of vertices have one vertex that is the same, then, by joining these pairs of vertices, we obtain the graph ${\mathcal{S}}_{1,n-1}^{\ast ,2}$ with the same vertex-set and the edge-set $E({\mathcal{S}}_{1,n}^{\ast ,2})=\{v_1{v}_i:2\le i\le n+1\}\cup \{v_{n-1}{v}_n,v_n{v}_{n+1}\}$.

Since bicyclic graphs are connected graphs in which the number of edges equals the number of vertices plus one. We conclude that ${\mathcal{S}}_{1,n}^2$ is a bicyclic graph with exactly two cycles and $n-4$ pendent vertices and ${\mathcal{S}}_{1,n}^{\ast ,2}$ is a bicyclic graph with exactly three cycles and $n-3$ pendent vertices. In particular, ${\mathcal{S}}_{1,4}^2$ is a bicyclic graph of order 5 with exactly two cycles and ${\mathcal{S}}_{1,3}^{\ast ,2}$ is a bicyclic graph of order 4 with three cycles. In the following definitions, we define some more graphs that are bicyclic.

Definition 1.

Let ${\mathcal{K}}_{1,p}$ be a star and ${\mathcal{S}}_{1,3}^{\ast ,2}$ be a bicyclic graph with three cycles and four vertices. The bicyclic graph denoted by $\mathcal{B}(p)$ is obtained by joining one pendent vertex of ${\mathcal{K}}_{1,p}$ with a vertex of degree 3 of the graph ${\mathcal{S}}_{1,3}^{\ast ,2}$, where $p\ge 2$. The vertex-set and the edge-set of $\mathcal{B}(p)$ are defined as $V(\mathcal{B}(p))=\{v_1^i:1\le i\le p-1\}\cup \{v_i:2\le i\le 5\}\cup \{v_6^i:1\le i\le 2\}$ and $E(\mathcal{B}(p))=\{v_1^i{v}_2:1\le i\le p-1\}\cup \{v_2{v}_3,v_3{v}_4,v_4{v}_5\}\cup \{v_4{v}_6^i:1\le i\le 2\}\cup \{v_5{v}_6^i:1\le i\le 2\}.$

Definition 2.

Let ${\mathcal{K}}_{1,p}$ be a star and ${\mathcal{S}}_{1,q}^{\ast ,2}$ be a bicyclic graph with three cycles and $q-3$ pendent vertices. The bicyclic graph denoted by $\mathcal{B}(p,q)$ is obtained by joining a pendent vertex of ${\mathcal{K}}_{1,p}$ with a pendent vertex of the graph ${\mathcal{S}}_{1,q}^{\ast ,2}$, where $p\ge 2$ and $q\ge 4$. The vertex-set and the edge-set of $\mathcal{B}(p,q)$ are defined as $V(\mathcal{B}(p,q))=\{v_1^i:1\le i\le p-1\}\cup \{v_i:2\le i\le 6\}\cup \{v_7^i:1\le i\le 2\}\cup \{v_8^i:1\le i\le q-4\}$ and $E(\mathcal{B}(p,q))=\{v_1^i{v}_2:1\le i\le p-1\}\cup \{v_2{v}_3,v_3{v}_4,v_4{v}_5,v_5{v}_6\}\cup \{v_5{v}_7^i:1\le i\le 2\}\cup \{v_5{v}_8^i:1\le i\le q-4\}\cup \{v_6{v}_7^i:1\le i\le 2\}$.

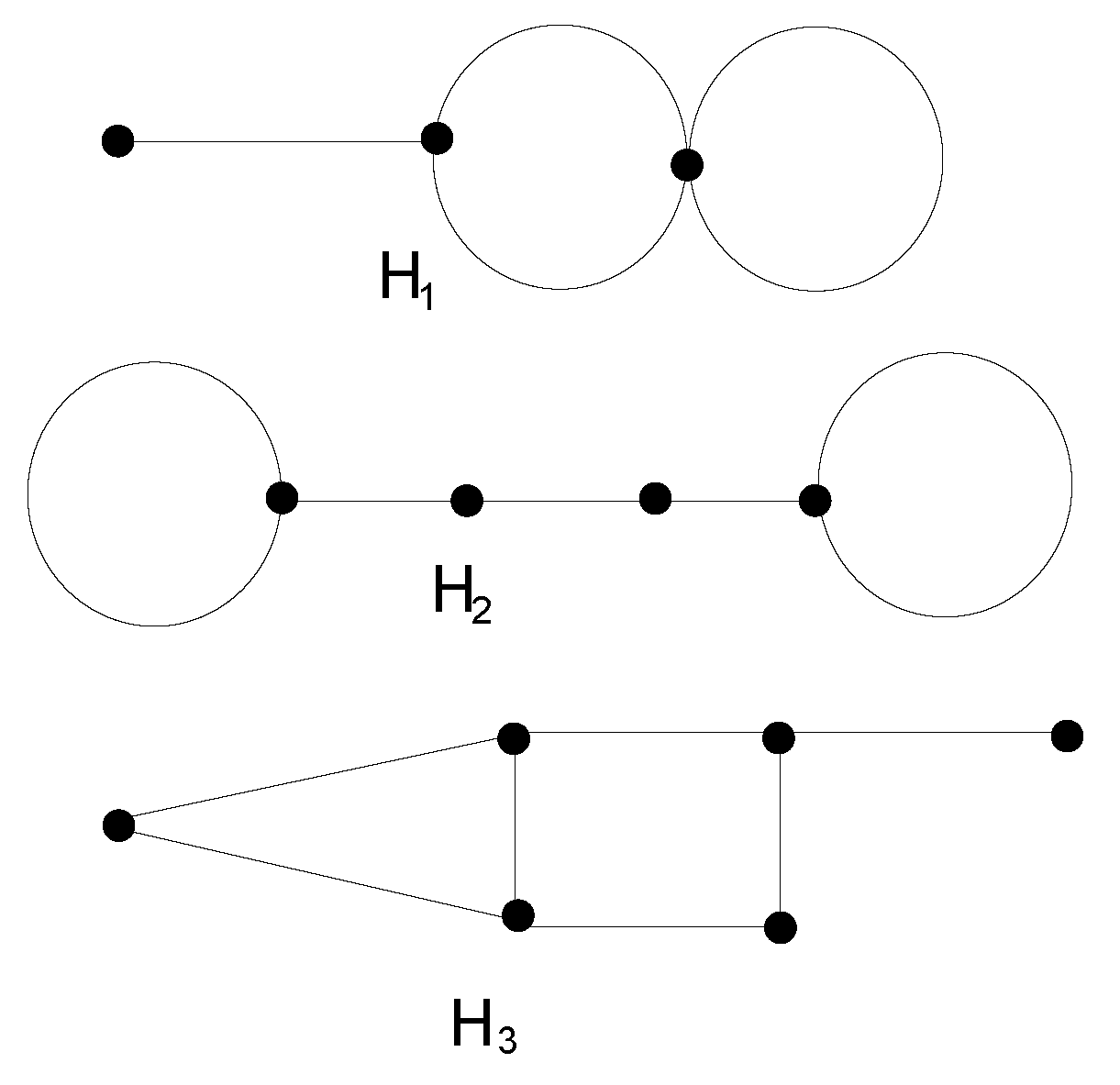
Let ${\mathcal{G}}_{1,n}$ and ${\mathcal{G}}_{2,n}$ be the classes of bicyclic graphs of order n such that each bicyclic graph has exactly two and three cycles, respectively. In particular, Figure 1 shows $H_1$ and $H_2$ as the examples of the bicyclic graphs with exactly two cycles that belong to ${\mathcal{G}}_{1,n}$, and $H_3$ as an example of the bicyclic graphs with exactly three cycles which belongs to ${\mathcal{G}}_{2,n}$. Let ${\mathcal{G}}_{1,n}^c$ be a class of the connected graphs of order n whose complements are bicyclic with exactly two cycles i.e., ${\mathcal{G}}_{1,n}^c=\{G^c:G^c\mathrm{is} \mathrm{connected}\mathrm{and}G\in {\mathcal{G}}_{1,n}\}$. Let ${\mathcal{G}}_{2,n}^c$ be a class of connected graphs of order n whose complements are bicyclic with exactly three cycles i.e., ${\mathcal{G}}_{2,n}^c=\{G^c:G^c\mathrm{is} \mathrm{connected}\mathrm{and}G\in {\mathcal{G}}_{2,n}\}$. Now, we define ${\mathcal{G}}_n^c={\mathcal{G}}_{1,n}^c\cup {\mathcal{G}}_{2,n}^c$ and note that ${({\mathcal{S}}_{1,n-1}^2)}^c$ and ${({\mathcal{S}}_{1,n-1}^{\ast ,2})}^c$ being disconnected do not belong to ${\mathcal{G}}_n^c$, where $n>4$.

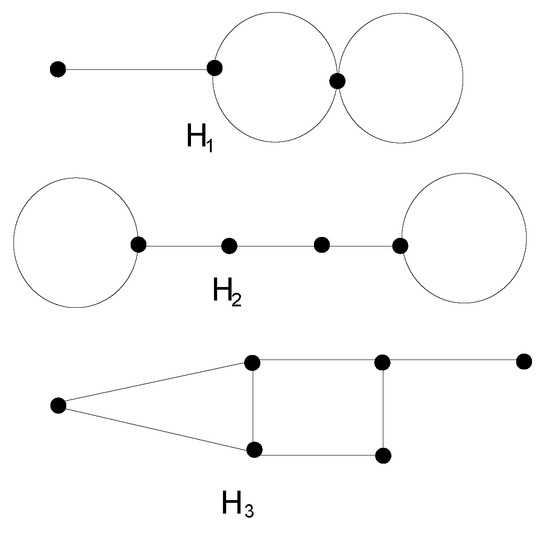
Figure 1. Bicyclic graphs.

By interlacing theorem, for a graph G containing at least one edge, we have ${\lambda }_{\min }(G)\le -1$. In particular, if G is a complete graph or disjoint union of complete graphs with at least one non-trivial copy, then ${\lambda }_{\min }(G)=-1$. Moreover, if G contains $K_{1,2}$ as an induced subgraph, then G verifies that ${\lambda }_{\min }(G)\le {\lambda }_{\min }(K_{1,2})=-\sqrt{2}$. Thus, for a graph G (tree), ${\lambda }_{\min }(G^c)=-1$ if and only if G is a star. Consequently, if G being a tree is not a star, then $G^c$ is connected and ${\lambda }_{\min }(G^c)<-1$. For a unicyclic graph G, ${\lambda }_{\min }(G^c)\le -1$, where equality holds if $G\cong {\mathcal{C}}_4$ (as ${({\mathcal{C}}_4)}^c$ is $2{\mathcal{P}}_2$, where ${\mathcal{P}}_2$ is a path of order 2). Similarly, for a bicyclic graph G with exactly three cycles, ${\lambda }_{\min }(G^c)\le -1$, where equality holds if $G\cong {\mathcal{S}}_{1,3}^{\ast ,2}$ and for a bicyclic graph G with exactly two cycles, ${\lambda }_{\min }(G^c)\le -2$, where equality holds if $G\cong {\mathcal{S}}_{1,n}^2$ for $n>3$.

A vector $\mathbf{X}\in {\mathcal{R}}^n$ is said to be defined on the graph G of order n, if there is a one to one map ϕ from $V(G)$ to the entries of $\mathbf{X}$ such that $\varphi (u)=X_u$ for each $u\in V(G)$. If $\mathbf{X}$ is an eigenvector of $\mathbf{A}(G)$, then it is naturally defined on $V(G)$, i.e., $X_u$ is the entry of $\mathbf{X}$ corresponding to the vertex u. Thus, it is easy to find that:

$${\mathbf{X}}^T\mathbf{A}(G)\mathbf{X}=2{\displaystyle \sum _{uv\in E(G)}}{X}_u{X}_v$$

(1)

and λ is an eigenvalue of G corresponding to the eigenvector $\mathbf{X}$ if and only if $\mathbf{X}\ne 0$. For each $v\in V(G)$, we obtain the following eigen-equation of the graph G:

$$\lambda X_v={\displaystyle \sum _{u\in N_G(v)}}{X}_u$$

(2)

where $N_G(v)$ is the set of neighbors of v in G. For an arbitrary unit vector $\mathbf{X}\in {\mathcal{R}}^n$:

$${\lambda }_{\min }(G)\le {\mathbf{X}}^T\mathbf{A}(G)\mathbf{X}$$

(3)

with equality if and only if $\mathbf{X}$ is a first eigenvector of G.

Moreover, if $G^c$ is a complement of the graph G, then $\mathbf{A}(G^c)=\mathbf{J}-\mathbf{I}-\mathbf{A}(G)$, where $\mathbf{J}$ and $\mathbf{I}$ are the all-ones matrix and the identity matrix of same size as of the adjacency matrix $\mathbf{A}(G)$, respectively. Thus, for any vector $\mathbf{X}\in {\mathcal{R}}^n:$

$${\mathbf{X}}^T\mathbf{A}(G^c)\mathbf{X}={\mathbf{X}}^T(\mathbf{J}-\mathbf{I})\mathbf{X}-{\mathbf{X}}^T\mathbf{A}(G)\mathbf{X}$$

(4)

Let ${\mathbf{X}}_1$ be the first eigenvector of the graph $\mathcal{B}{(p)}^c$ with entries corresponding to the vertices as defined in Definition 1. By Eigen-Equation (2), the vertices $v_1^i$ for $1\le i\le p-1$, $v_2$, $v_3$, $v_4$, $v_5$ and $v_6^i$ for $1\le i\le 2$ have values in ${\mathbf{X}}_1$, say $X_1$, $X_2$, $X_3$, $X_4$, $X_5$ and $X_6$, respectively. Moreover, if ${\lambda }_{\min }(\mathcal{B}{(p)}^c)={\lambda }_1$, then, we have:

$$\left\{\begin{array}{c}{\lambda }_1{X}_1=(p-2)X_1+X_3+X_4+X_5+2X_6,\hfill \\ {\lambda }_1{X}_2=X_4+X_5+2X_6,\hfill \\ {\lambda }_1{X}_3=(p-1)X_1+X_5+2X_6,\hfill \\ {\lambda }_1{X}_4=(p-1)X_1+X_2,\hfill \\ {\lambda }_1{X}_5=(p-1)X_1+X_2+X_3,\hfill \\ {\lambda }_1{X}_6=(p-1)X_1+X_2+X_3+X_6.\hfill \end{array}\right.$$

(5)

Take ${\mathbf{X}}_1={(X_1,X_2,X_3,X_4,X_5,X_6)}^T$. Then, the matrix equation of the above system of equations is $(\mathbf{A}-{\lambda }_1\mathbf{I}){\mathbf{X}}_1=0$, where $\mathbf{A}$ is a matrix of order 6. Thus, ${\lambda }_1$ is the least root of the polynomial:

$$f_1(\lambda ,p)=det(\mathbf{A}-\lambda \mathbf{I})=(-2+p)+(8-6p)\lambda +(6p){\lambda }^2+(-8+4p){\lambda }^3+(-4-4p){\lambda }^4-(1-p){\lambda }^5+{\lambda }^6.$$

(6)

Let ${\mathbf{X}}_2$ be the first eigenvector of the graph $\mathcal{B}{(p,q)}^c$ with entries corresponding to the vertices as defined in Definition 2. By Eigen-Equation (2), the vertices $v_1^i$ for $1\le i\le p-1$, $v_2$, $v_3$, $v_4$, $v_5$, $v_6$, $v_7^i$ for $1\le i\le 2$ and $v_8^i$ for $1\le i\le q-4$ have values in ${\mathbf{X}}_2$, say $X_1$, $X_2$, $X_3$, $X_4$, $X_5$, $X_6$, $X_7$ and $X_8$, respectively. Moreover, if ${\lambda }_{\min }(\mathcal{B}{(p,q)}^c)={\lambda }_2$, then we have:

$$\left\{\begin{array}{c}{\lambda }_2{X}_1=(p-2)X_1+X_3+X_4+X_5+X_6+2X_7+(q-4)X_8,\hfill \\ {\lambda }_2{X}_2=X_4+X_5+X_6+2X_7+(q-4)X_8,\hfill \\ {\lambda }_2{X}_3=(p-1)X_1+X_5+X_6+2X_7+(q-4)X_8,\hfill \\ {\lambda }_2{X}_4=(p-1)X_1+X_2+X_6+2X_7+(q-4)X_8,\hfill \\ {\lambda }_2{X}_5=(p-1)X_1+X_2+X_3,\hfill \\ {\lambda }_2{X}_6=(p-1)X_1+X_2+X_3+X_4+(q-4)X_8,\hfill \\ {\lambda }_2{X}_7=(p-1)X_1+X_2+X_3+X_4+X_7+(q-4)X_8,\hfill \\ {\lambda }_2{X}_8=(p-1)X_1+X_2+X_3+X_4+X_6+2X_7+(q-5)X_8.\hfill \end{array}\right.$$

(7)

Take ${\mathbf{X}}_2={(X_1,X_2,X_3,X_4,X_5,X_6,X_7,X_8)}^T$. Then, the matrix equation of the above system of equations is $(\mathbf{A}-{\lambda }_2\mathbf{I}){\mathbf{X}}_2=0$, where $\mathbf{A}$ is a matrix of order 8. Thus, ${\lambda }_2$ is the least root of the polynomial:

$$\begin{array}{ll}{f}_2(\lambda ,p,q)& =det(\mathbf{A}-\lambda \mathbf{I})\\ & =(-5+p+q)+(22-10p-6q+2pq)\lambda \\ & +(-12+20p+6q-7pq){\lambda }^2+(-30+2p+10q+2pq){\lambda }^3\\ & +(-5-11p-3q+7pq){\lambda }^4+(22-11p-11q+2pq){\lambda }^5\\ & +(17-6p-6q){\lambda }^6+(6-p-q){\lambda }^7+{\lambda }^8.\end{array}$$

(8)

.

Now, we state some results that are used in the main theorem.

Lemma 1.

[8] Let $\mathcal{T}$ be a tree with non-negative or non-positive real vectors $\mathbf{X}={(X_1,X_2,X_3,...,X_n)}^T$ defined on $\mathcal{T}$. The entries of $\mathbf{X}$ are ordered as $|X_1|\ge |X_2|\ge |X_3|\ge ...\ge |X_n|$, where $|V(\mathcal{T})|=n$. Then:

$${\displaystyle \sum _{uv\in E(\mathcal{T})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{K}}_{1,p})}}{X}_u{X}_v,$$

where $\mathbf{X}$ is defined on the star ${\mathcal{K}}_{1,p}$ such that its central vertex of degree $p=n-1$ has value $X_1$, and equality holds if and only if $\mathcal{T}={\mathcal{K}}_{1,n-1}$.

Lemma 2.

[9] Let $\mathcal{U}$ be a unicyclic graph with non-negative or non-positive real vectors $\mathbf{X}={(X_1,X_2,X_3,...,X_n)}^T$ defined on $\mathcal{U}$. The entries of $\mathbf{X}$ are ordered as $|X_1|\ge |X_2|\ge |X_3|\ge ...\ge |X_n|$, where $|V(\mathcal{U})|=n$. Then:

$${\displaystyle \sum _{uv\in E(\mathcal{U})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v,$$

where $\mathbf{X}$ is defined on the unicyclic graph ${\mathcal{S}}_{1,q}^1$ such that the vertex of degree $q=n-1$ has value $X_1$ and two vertices of degree two have values $X_2$ and $X_3$. The equality holds only if $\mathcal{U}={\mathcal{S}}_{1,q}^1$.

3. Main Results

In this section, we present the main results related to the minimizing graph of the connected graphs whose complements are bicyclic.

Lemma 3.

If $n\ge 8$, then ${\lambda }_{\min }(\mathcal{B}{(n-6,4)}^c)<{\lambda }_{\min }(\mathcal{B}{(n-5)}^c)$.

Proof. 

Consider ${\lambda }_1={\lambda }_{\min }(\mathcal{B}{(n-5)}^c)$ and ${\lambda }_2={\lambda }_{\min }(\mathcal{B}{(n-6,4)}^c)$ are the least roots of $f_1(\lambda ,n-5)$ and $f_2(\lambda ,n-6,4)$, respectively. Define

$$g(\lambda ,n-5)={(\lambda +1)}^2{f}_1(\lambda ,n-5).$$

Since ${\lambda }_1<-1$, ${\lambda }_1$ is the least root of $g(\lambda ,n-5)$. By (6) $f_1(-3.5,n-5)=113981-9666n$, $g(-3.5,n-5)\le 0$ for $n\ge 8$. Moreover, if $\lambda \to -\infty$. Then, $g(\lambda ,n-5)\to +\infty$, which implies ${\lambda }_1\le -3.5$. Now, for $\lambda \le -3.5$ and $n\ge 8$,

$$g(\lambda ,n-5)-f_2(\lambda ,n-6,4)=-(n-7)\lambda (2-3\lambda +7{\lambda }^3+2{\lambda }^4=-(n-7)\lambda (\lambda +1)(\lambda +3.3385)(0.5986-1.677\lambda +2{\lambda }^2)>0.$$

Consequently, $f_2(\lambda ,n-6,4)<g(\lambda ,n-4)$ for $\lambda \le -3.5$ and $n\ge 8$. In particular, ${\lambda }_2<{\lambda }_1$, which implies ${\lambda }_{\min }(\mathcal{B}{(n-6,4)}^c)<{\lambda }_{\min }(\mathcal{B}{(n-5)}^c)$ for $n\ge 8$.

Lemma 4.

Let p and q be positive integers such that $p\ge q\ge 5$ and $p+q+2=n$. Then,

$${\lambda }_{\min }(\mathcal{B}{(\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )}^c)\le {\lambda }_{\min }(\mathcal{B}{(p,q)}^c)$$

with equality if and only if $p=\lceil \frac{n-2}{2}\rceil$ and $q=\lfloor \frac{n-2}{2}\rfloor$, where, (a) $n\ge 30$ if $n\equiv 0(mod 2)$; and (b) $n\ge 25$ if $n\equiv 1(mod 2)$.

Proof. 

From Equation (8), we have:

$$f_2(-3,p,q)=712-248p+46q-42pq.$$

(9)

(a) If $n\equiv 0(\mathrm{mod}2)$, then $p=\frac{n-2}{2}$ and $q=\frac{n-2}{2}$. Thus, (9) becomes $f_2(-3,\frac{n-2}{2},\frac{n-2}{2})=-(n-4.7427)(n+10.3617)$ (b) If $n\equiv 1(\mathrm{mod}2)$, then $p=\frac{n-1}{2}$ and $q=\frac{n-3}{2}$. Thus, (9) becomes $f_2(-3,\frac{n-1}{2},\frac{n-3}{2})=-\frac{1}{2}(n-6.0108)(n+11.6298)$. From both cases (a) and (b), $f_2(-3,\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )<0$ for $n\ge 30$ and $n\ge 25$, respectively. This shows that ${\lambda }_2<-3$, where ${\lambda }_2$ is the least root of $f_2(\lambda ,p,q)$. Moreover:

$$\begin{array}{ll}{f}_2(\lambda ,p-1,q+1)& =\\ & +(-5+p+q)+(24-8p-8q+2pq)\lambda \\ & +(-19+13p+13q-7pq){\lambda }^2+(-24+4p+8q+2pq){\lambda }^3\\ & +(-4-4p-10q+7pq){\lambda }^4+(20-9p-13q+2pq){\lambda }^5\\ & +(17-6p-6q){\lambda }^6+(6-p-q){\lambda }^7+{\lambda }^8, \mathrm{and}\end{array}$$

$$\begin{array}{ll}& f_2(\lambda ,p,q)-f_2(\lambda ,p-1,q+1)\\ =& -2(p-q-1)\lambda (\lambda -\frac{1}{2})(\lambda +2)(\lambda +1+\sqrt{2})(\lambda +1-\sqrt{2}).\end{array}$$

We note that if $p>q+1$ and $\lambda <-3$, then $f_2(\lambda ,p,q)-f_2(\lambda ,p-1,q+1)>0$. In addition, $f_2(-3,p-1,q+1)<0$. Consequently:

$${\lambda }_{\min }(\mathcal{B}{(p-1,q+1)}^c)<{\lambda }_{\min }(\mathcal{B}{(p,q)}^c).$$

It follows that ${\lambda }_{\min }(\mathcal{B}{(\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )}^c)\le {\lambda }_{\min }(\mathcal{B}{(p,q)}^c)$, where equality holds if and only if $p=\lceil \frac{n-2}{2}\rceil$ and $q=\lfloor \frac{n-2}{2}\rfloor$.

Lemma 5.

Let $\mathcal{B}\in {\mathcal{G}}_n$ be a bicyclic graph of order n and $\mathbf{X}={(X_1,X_2,X_3,...,X_n)}^T$ be a non-negative or non-positive real vector defined on $\mathcal{B}$ such that the entries of $\mathbf{X}$ are ordered as $|X_1|\ge |X_2|\ge |X_3|\ge ...\ge |X_n|$:

(a)

If $\mathcal{B}\in {\mathcal{G}}_{1,n}$, then ${\displaystyle \sum _{uv\in E(\mathcal{B})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^2)}}{X}_u{X}_v,$ where $\mathbf{X}$ is defined on ${\mathcal{S}}_{1,n-1}^2$ such that one vertex of degree $n-1$ has value $X_1$ and four vertices of degree 2 have values $X_2$, $X_3$, $X_4$ and $X_5$, respectively. The remaining values $X_i$ for $6\le i\le n$ are assigned to the $n-5$ pendent vertices. The above equality holds only if $\mathcal{B}={\mathcal{S}}_{1,n-1}^2$,

(b)

${\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^2)}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^{\ast ,2})}}{X}_u{X}_v,$ where $\mathbf{X}$ is defined on ${\mathcal{S}}_{1,n-1}^{\ast ,2}$ such that one vertex of degree $n-1$, one vertex of degree 3 and two vertices of degree 2 have values $X_1$, $X_2$, $X_3$ and $X_4$, respectively. Furthermore, the remaining values are assigned to the $n-4$ pendent vertices,

(c)

If $\mathcal{B}\in {\mathcal{G}}_{2,n}$, then ${\displaystyle \sum _{uv\in E(\mathcal{B})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^{\ast ,2})}}{X}_u{X}_v$, where equality holds only if $\mathcal{B}={\mathcal{S}}_{1,n-1}^{\ast ,2}$.

Proof. 

(a) Without loss of generality, assume that $\mathbf{X}$ is non-negative. Otherwise, we consider $-\mathbf{X}$. Let v be a vertex of the bicyclic graph $\mathcal{B}$ with value $X_1$ assigned by the first eigenvector $\mathbf{X}$. Suppose that there exists a vertex u that is not adjacent with v. Since $\mathcal{B}$ is a connected graph, there exists a neighbor of u, say w, which is on the path of $\mathcal{B}$ containing v and u. If we delete $uw$ and add a new edge $vu$ in $\mathcal{B}$, then we have a new bicyclic graph $\tilde{\mathcal{B}}$ with exactly two cycles such that:

$${\displaystyle \sum _{uv\in E(\mathcal{B})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E(\tilde{\mathcal{B}})}}{X}_u{X}_v.$$

Repeating this process on the bicyclic graph $\tilde{\mathcal{B}}$ for the non-neighbor of v. Thus, we obtain a bicyclic graph which is infact a star $K_{1,n-1}$ with center v and two edges $u^{{}^{\prime }}{v}^{{}^{\prime }}$ and $u^{{}^{″}}{v}^{{}^{″}}$ that are non incident to the vertex v. Thus, we have:

$${\displaystyle \sum _{uv\in E(\mathcal{B})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E(\tilde{\mathcal{B}})}}{X}_u{X}_v\le {\displaystyle \sum _{i=2}^n}{X}_1{X}_i+X_{u^{{}^{\prime }}}{X}_{v^{{}^{\prime }}}+X_{u^{{}^{″}}}{X}_{v^{{}^{″}}}.$$

Since $X_2{X}_3+X_4{X}_5\ge X_{u^{{}^{\prime }}}{X}_{v^{{}^{\prime }}}+X_{u^{{}^{″}}}{X}_{v^{{}^{″}}}$ and ${\displaystyle \sum _{i=2}^n}{X}_1{X}_i+X_2{X}_3+X_4{X}_5={\mathcal{S}}_{1,n-1}^2$, we obtain:

$${\displaystyle \sum _{uv\in E(\mathcal{B})}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^2)}}{X}_u{X}_v.$$

The equality holds if v is adjacent to all other vertices and there are two non incident edges to the vertex v in $\mathcal{B}$, which implies that $\mathcal{B}={\mathcal{S}}_{1,n-1}^2$.

(b)

Since $X_3{X}_4\ge X_4{X}_5$:

$$\begin{array}{ll}{\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^2)}}{X}_u{X}_v& ={\displaystyle \sum _{i=2}^n}{X}_1{X}_i+X_2{X}_3+X_4{X}_5\\ & \le {\displaystyle \sum _{i=2}^n}{X}_1{X}_i+X_2{X}_3+X_3{X}_4\\ & ={\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^{\ast ,2})}}{X}_u{X}_v.\end{array}$$

Consequently, ${\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^2)}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in E({\mathcal{S}}_{1,n-1}^{\ast ,2})}}{X}_u{X}_v.$

(c)

Proof is similar to (a).

Lemma 6.

Let ${\mathcal{B}}^c\in {\mathcal{G}}_n^c$ be a connected graph order $n\ge 10$ such that its complement is a bicyclic graph and $\mathbf{X}$ be a first eigenvector of ${\mathcal{B}}^c$. Then, $\mathbf{X}$ has at least two positive and two negative entries.

Proof. 

Suppose, on the contrary, that only one vertex v of ${\mathcal{B}}^c$ has positive value assigned by $\mathbf{X}$. Since ${\mathcal{B}}^c$ is connected, $\mathcal{B}\ne {\mathcal{S}}_{1,n-1}^2$ and $\mathcal{B}\ne {\mathcal{S}}_{1,n-1}^{\ast ,2}$. Thus, there exists a vertex u as a neighbor of the vertex v in $\mathcal{B}$ such that $N_{\mathcal{B}}(u)\backslash \left\{v\right\}\ne \mathrm{\Phi }$, where $N_{\mathcal{B}}(u)$ is set of neighbors of u in $\mathcal{B}$. By (2) the eigen-equation of the vertex u for ${\mathcal{B}}^c$ is:

$$0\le {\lambda }_{\min }({\mathcal{B}}^c)X_u=\sum _{w\in N_{{\mathcal{B}}^c}(u)}{X}_w\le 0$$

(10)

This shows that $X_u=0$ and $X_w=0$ for each $w\in N_{{\mathcal{B}}^c}(u)$, where $N_{{\mathcal{B}}^c}(u)$ is set of neighbors of u in ${\mathcal{B}}^c$. Thus, all of the vertices of $N_{\mathcal{B}}(u)$ have non zero entries assigned by $\mathbf{X}$. Now, we discuss the following three cases:

(a)

When both of the vertices v and u are non-cycles. Then, we have three observations: (i) $N_{\mathcal{B}}(u)\backslash \left\{v\right\}\cap N_{\mathcal{B}}(v)\backslash \left\{u\right\}=\mathrm{\Phi }$; otherwise, $\mathcal{B}$ is not bicyclic; (ii) each pair of vertices of the set $N_{\mathcal{B}}(u)\backslash \left\{v\right\}$ is non adjacent; otherwise, B is not bicyclic; and (iii) at most one neighbor of u may be on any cycle; otherwise, u will be also on a cycle. Define $N_{\mathcal{B}}(u)\backslash \left\{v\right\}=\{s:s\mathrm{as} \mathrm{adjacent} \mathrm{to}u\mathrm{in}\mathcal{B}\}$ such that $X_s\ne 0$ for each $s\in N_{\mathcal{B}}(u)\backslash \left\{v\right\}$. Thus, the eigen-equation of the vertex v for the graph ${\mathcal{B}}^c$, ${\lambda }_{\min }({\mathcal{B}}^c)X_v={\displaystyle \sum _{t\in N_{{\mathcal{B}}^c}(v)}}{X}_t$ becomes ${\lambda }_{\min }({\mathcal{B}}^c)X_v={\displaystyle \sum _{s\in \mathcal{B}(u)\backslash \left\{v\right\}}}{X}_s$. By adding $X_v$ to both sides, we have:

$$(1+{\lambda }_{\min }({\mathcal{B}}^c))X_v=X_v+\sum _{s\in \mathcal{B}(u)\backslash \left\{v\right\}}{X}_s$$

(11)

Suppose that $s_0\in N_{\mathcal{B}}(u)\backslash \left\{v\right\}$ such that $s_0$ is non adjacent to s for each $s\in N_{\mathcal{B}}(u)\backslash \left\{v\right\}$, where $s\ne s_0$ as observed in (ii). Thus, the eigen-equation of the vertex $s_0$ for the graph ${\mathcal{B}}^c$ is ${\lambda }_{\min }({\mathcal{B}}^c)X_{s_0}={\displaystyle \sum _{s\in \mathcal{B}(u)\backslash \left\{s_0\right\}}}{X}_s$, which implies:

$$(1+{\lambda }_{\min }({\mathcal{B}}^c))X_{s_0}=X_{s_0}+\sum _{s\in \mathcal{B}(u)\backslash \left\{s_0\right\}}{X}_s$$

(12)

From (11) and (12), $(1+{\lambda }_{\min }({\mathcal{B}}^c))(X_{s_0}-X_v)=0$. Since $n\ge 10$, $\mathcal{B}\ne {\mathcal{S}}_{1,n-1}^2$, $\mathcal{B}\ne {\mathcal{S}}_{1,n-1}^{\ast ,2}$ and ${\lambda }_{\min }({\mathcal{B}}^c)<-1$. Consequently, $X_{s_0}=X_v$ are two positive entries of $\mathbf{X},$ which is a contradiction to our supposition.

(b)

When both the vertices are on the cycle(s). Here, we have two possibilities: (i) the vertex u is a common vertex of the cycles with degree of at least 4. Then, by (10), $X_u=0,$ which is a contradiction, as $\mathcal{B}$ is neither ${\mathcal{S}}_{1,n-1}^2$ nor ${\mathcal{S}}_{1,n-1}^{\ast ,2}$; (ii) the vertex u is not a common vertex of the cycles with degree of at least 4. If u and v are on a cycle of length 3, then there is a neighbor of u that is also a neighbor of v in $\mathcal{B}$, say z. If $N_{\mathcal{B}}(u)\backslash \left\{v\right\}=\left\{z\right\}$, then by the eigen-equation of v for ${\mathcal{B}}^c$, $X_v=0$, which is a contradiction. If $N_{\mathcal{B}}(u)\backslash \{v,z\}\ne \mathrm{\Phi }$, then we follow (a) and have all the vertices of $N_{\mathcal{B}}(u)\backslash \{v,z\}$ with the same value as v, which is again a contradiction. If u and v are on a cycle(s) of a length of at least 4, then $N_{\mathcal{B}}(u)\backslash \left\{v\right\}\cap N_{\mathcal{B}}(v)\backslash \left\{u\right\}=\mathrm{\Phi }$, and we have a contradiction using the procedure of (a).

(c)

When one vertex is on a cycle(s) and the other is a non-cycle, then $N_{\mathcal{B}}(u)\backslash \left\{v\right\}\cap N_{\mathcal{B}}(v)\backslash \left\{u\right\}=\mathrm{\Phi }$; otherwise, $\mathcal{B}$ is not a bicycle. If v is on a cycle and u is non-cycle, then by repeating (a), we have a contradiction. If u is on a cycle and v is non-cycle, then we have two possibilities: (i) if u is a common vertex of the cycles with a degree of at least 4; then, by (b) (i), we have a contradiction; (ii) if u is not a common vertex of the cycles with degree at least 4. Suppose that u is on a cycle of length 3, then u has neighbors $u_1$ and $u_2$ such that $u_1$ is adjacent to $u_2$ and one is a common vertex of the cycles, say $u_1$. By the eigen-equations for these two neighbors of u in ${\mathcal{B}}^c$, we have $X_{u_1}=X_{u_2}$, which is contradiction. If u is on a cycle of a length of at least 4, then, by (a), we have a contradiction. If u is a common vertex of two cycles, then the vertex which is non adjacent to all other neighbors of u has equal value to the value of v by (a), which is again a contradiction.

Therefore, $\mathbf{X}$ contains at least two positive entries. If we consider $-\mathbf{X}$, then we have at least two negative entries. Consequently, $\mathbf{X}$ has at least two positive and two negative entries.

Theorem 3.

Let ${\mathcal{G}}_{1,n}$ and ${\mathcal{G}}_{2,n}$ be the classes of the bicyclic graphs of order n in which each bicyclic graph has exactly two and three cycles, respectively. Let ${\mathcal{B}}^c\in {\mathcal{G}}_n^c$ be a connected graph of order n such that its complement is a bicyclic graph i.e $\mathcal{B}\in {\mathcal{G}}_{1,n}\cup {\mathcal{G}}_{2,n}$. Then:

$${\lambda }_{\min }(\mathcal{B}{(p,q)}^c)\le {\lambda }_{\min }({\mathcal{B}}^c)$$

where $p\ge q\ge 6$, $p+q+2=n\ge 30$ and equality holds if and only if $\mathcal{B}=\mathcal{B}(p,q)$.

Proof. 

Define $V_{+}=\{v:X_v\ge 0,v\in V(B^c)\}$ and $V_{-}=\{v:X_v<0,v\in V(B^c)\}$. By Lemma 6, both contain at least two elements. Suppose that ${\mathcal{B}}_{+}$ and ${\mathcal{B}}_{-}$ are subgraphs of $\mathcal{B}$ induced by $V_{+}$ and $V_{-}$, respectively. Moreover, assume that ${\mathcal{E}}^{{}^{\prime }}$ is a set of edges between $V_{+}$ and $V_{-}$ in $\mathcal{B}$. As $\mathcal{B}$ is connected, ${\mathcal{E}}^{{}^{\prime }}$ is non empty. Thus, we have:

$$\sum _{uv\in E(\mathcal{B})}{X}_u{X}_v=\sum _{uv\in {\mathcal{B}}_{+}}{X}_u{X}_v+\sum _{uv\in {\mathcal{B}}_{-}}{X}_u{X}_v+\sum _{uv\in {\mathcal{E}}^{{}^{\prime }}}{X}_u{X}_v$$

(13)

Now, for the edges of the cycles of $\mathcal{B}$, we have two cases: (i) all the edges of the cycles of $\mathcal{B}$ are only in ${\mathcal{B}}_{+}$ or ${\mathcal{B}}_{-}$; and (ii) both the subgraphs ${\mathcal{B}}_{+}$ and ${\mathcal{B}}_{-}$ contain the edges of the cycles of $\mathcal{B}$.

(i) Without loss of generality, we suppose that ${\mathcal{B}}_{+}$ does not include any edge of the cycles of $\mathcal{B}$; otherwise, we take $-\mathbf{X}$ as a first eigenvector. Let $\overline{\mathcal{B}}$ be a graph obtained from $\mathcal{B}$ such that the subgraph ${\overline{\mathcal{B}}}_{+}$ and ${\overline{\mathcal{B}}}_{-}$ of $\overline{\mathcal{B}}$ induced by ${\mathcal{B}}_{+}$ and ${\mathcal{B}}_{-}$ are tree and bicyclic, respectively (bicyclic with two cycles if $\mathcal{B}\in {\mathcal{G}}_{1,n}$ or bicyclic with three cycles if $\mathcal{B}\in {\mathcal{G}}_{2,n}$). By the deletion and addition of some edges in the tree ${\overline{\mathcal{B}}}_{+}$, we have a star $K_{1,p}$ with center $u^{{}^{\prime }}$, where $p+1=|V_{+}|\ge 7$ and $u^{{}^{\prime }}$ has a maximum modulus value among all the values of ${\overline{\mathcal{B}}}_{+}$ given by $\mathbf{X}$. Thus, by Lemma 1, we have:

$$\sum _{uv\in {\mathcal{B}}_{+}}{X}_u{X}_v\le \sum _{uv\in {\overline{\mathcal{B}}}_{+}}{X}_u{X}_v\le \sum _{uv\in {\mathcal{K}}_{1,p}}{X}_u{X}_v$$

Similarly, by the deletion and addition of some edges in the bicyclic subgraph ${\overline{\mathcal{B}}}_{-}$, we have ${\mathcal{S}}_{1,q}^2$ if $\mathcal{B}\in {\mathcal{G}}_{1,n}$ (or ${\mathcal{S}}_{1,q}^{\ast ,2}$ if $\mathcal{B}\in {\mathcal{G}}_{2,n}$) with $v^{{}^{\prime }}$ adjacent to all other vertices in ${\mathcal{S}}_{1,q}^2$ (or ${\mathcal{S}}_{1,q}^{\ast ,2}$). Moreover, $v^{{}^{\prime }}$ has maximum modulus value among all the values of ${\overline{\mathcal{B}}}_{-}$ and $q+1=|V_{-}|\ge 7$.

If $\mathcal{B}\in {\mathcal{G}}_{1,n}$, then by Lemma 5((a) and (b)), we have:

$$\sum _{uv\in {\mathcal{B}}_{-}}{X}_u{X}_v\le \sum _{uv\in {\overline{\mathcal{B}}}_{-}}{X}_u{X}_v\le \sum _{uv\in {\mathcal{S}}_{1,q}^2}{X}_u{X}_v\le \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}{X}_u{X}_v$$

If $\mathcal{B}\in {\mathcal{G}}_{2,n}$, then by Lemma 5(c), we have:

$$\sum _{uv\in {\mathcal{B}}_{-}}{X}_u{X}_v\le \sum _{uv\in {\overline{\mathcal{B}}}_{-}}{X}_u{X}_v\le \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}{X}_u{X}_v$$

In this case, we conclude that:

$$\sum _{uv\in {\mathcal{B}}_{+}}{X}_u{X}_v+\sum _{uv\in {\mathcal{B}}_{-}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}}{X}_u{X}_v$$

(ii) Let $\overline{\mathcal{B}}$ be a graph obtained from $\mathcal{B}$ such that both the subgraphs ${\overline{\mathcal{B}}}_{+}$ and ${\overline{\mathcal{B}}}_{-}$ induced by the subgraphs ${\mathcal{B}}_{+}$ and ${\mathcal{B}}_{-}$ of $\mathcal{B}$ are unicyclic. By the deletion and addition of some edges in ${\overline{\mathcal{B}}}_{+}$, we have ${\mathcal{S}}_{1,p}^1$ with $u^{{}^{\prime }}$ adjacent to all other vertices in ${\mathcal{S}}_{1,p}^1$. Moreover, $u^{{}^{\prime }}$ has a maximum modulus value among all the values of ${\overline{\mathcal{B}}}_{+}$ given by $\mathbf{X}$ and $p+1=|V_{+}|\ge 7$. Thus, by Lemma 1, we have:

$${\displaystyle \sum _{uv\in {\mathcal{B}}_{+}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\overline{\mathcal{B}}}_{+}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{S}}_{1,p}^1}}{X}_u{X}_v$$

Similarly, by the deletion and addition of some edges in ${\overline{\mathcal{B}}}_{-}$, we have ${\mathcal{S}}_{1,q}^1$ with $v^{{}^{\prime }}$ adjacent to all other vertices in ${\mathcal{S}}_{1,q}^1$. Moreover, $v^{{}^{\prime }}$ has a maximum modulus value among all the values of ${\overline{\mathcal{B}}}_{-}$ given by $\mathbf{X}$ and $q+1=|V_{-}|\ge 7$. Again, by Lemma 1, we have:

$${\displaystyle \sum _{uv\in {\mathcal{B}}_{-}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\overline{\mathcal{B}}}_{-}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v$$

From the above two inequalities, we have:

$${\displaystyle \sum _{uv\in {\mathcal{B}}_{+}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{B}}_{-}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{S}}_{1,p}^1}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v$$

Without loss of generality, assume that the modulus values of the vertices of ${\overline{\mathcal{B}}}_{-}$ are greater than the modulus values of the vertices of ${\overline{\mathcal{B}}}_{+}$ assigned by $\mathbf{X}$. Suppose that w and $w^{{}^{\prime }}$ are vertices in ${\overline{\mathcal{B}}}_{+}$ such that the edge $w{w}^{{}^{\prime }}$ is non incident with $u^{{}^{\prime }}$. Delete the edge $w{w}^{{}^{\prime }}$ and the edge the edge $r{r}^{{}^{\prime }}$, where r and $r^{{}^{\prime }}$ are vertices in ${\overline{\mathcal{B}}}_{-}$ such that the edge $r{r}^{{}^{\prime }}$ is non incident with $v^{{}^{\prime }}$, and use Lemma 5(b). Then:

$$\begin{array}{ll}{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,p}^1}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v& ={\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+X_w{X}_{w^{{}^{\prime }}}+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v\\ & \le {\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^1}}{X}_u{X}_v+X_r{X}_{r^{}}\\ & ={\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^2}}{X}_u{X}_v\\ & \le {\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}}{X}_u{X}_v\end{array}$$

Consequently, from both the cases:

$${\displaystyle \sum _{uv\in {\mathcal{B}}_{+}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{B}}_{-}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}}{X}_u{X}_v$$

(14)

Let $u^{{}^{″}}$ and $v^{{}^{″}}$ be the vertices of ${\mathcal{B}}_{-}$ and ${\mathcal{B}}_{+}$ with minimum modulus among all the vertices of ${\mathcal{B}}_{-}$ and ${\mathcal{B}}_{+}$, respectively. Then:

$${\displaystyle \sum _{uv\in {\mathcal{E}}^{{}^{\prime }}}}{X}_u{X}_v\le X_{u^{{}^{″}}}{X}_{v^{{}^{″}}}$$

(15)

Using (14) and (15) in (13), we have:

$${\displaystyle \sum _{uv\in \mathcal{B}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in {\mathcal{K}}_{1,p}}}{X}_u{X}_v+{\displaystyle \sum _{uv\in {\mathcal{S}}_{1,q}^{\ast ,2}}}{X}_u{X}_v+X_{u^{{}^{″}}}{X}_{v^{{}^{″}}}$$

(16)

Since $p\ge q\ge 6$, the vertices $u^{{}^{″}}$ and $v^{{}^{″}}$ can be taken from the pendent vertices of ${\mathcal{K}}_{1,p}$ and ${\mathcal{S}}_{1,q}^{\ast ,2},$ respectively. Thus, (16) becomes:

$${\displaystyle \sum _{uv\in \mathcal{B}}}{X}_u{X}_v\le {\displaystyle \sum _{uv\in \mathcal{B}(p,q)}}{X}_u{X}_v$$

Now, consider the following inequality:

$${\lambda }_{\min }({\mathcal{B}}^c)={\mathbf{X}}^T\mathbf{A}({\mathcal{B}}^c)\mathbf{X}={\mathbf{X}}^T(\mathbf{J}-\mathbf{I}-\mathbf{A}(\mathcal{B}))\mathbf{X}$$

$$={\mathbf{X}}^T(\mathbf{J}-\mathbf{I})\mathbf{X}-{\mathbf{X}}^T\mathbf{A}(\mathcal{B})\mathbf{X}$$

$$\hspace{1em}\hspace{1em}\ge {\mathbf{X}}^T(\mathbf{J}-\mathbf{I})\mathbf{X}-{\mathbf{X}}^T\mathbf{A}(\mathcal{B}(p,q))\mathbf{X}$$

$$\hspace{1em}={\mathbf{X}}^T\mathbf{A}(\mathcal{B}{(p,q)}^c)\mathbf{X}\ge {\lambda }_{\min }(\mathcal{B}{(p,q)}^c)$$

Consequently:

$${\lambda }_{\min }(\mathcal{B}{(p,q)}^c)\le {\lambda }_{\min }({\mathcal{B}}^c)$$

where $p\ge q\ge 6$, $p+q+2=n\ge 30$ and equality holds if and only if $\mathcal{B}=\mathcal{B}(p,q)$.

Now to complete the proof, we prove that the set ${\mathcal{E}}^{{}^{\prime }}$ consists of exactly one edge and the set $V_{+}$ does not contain any vertex with zero value given by $\mathbf{X}$. Before this, we prove that $X_3<X_1<X_2$ and $X_5<X_6<X_7<X_8<X_4$.

Suppose $\mathcal{B}(p,q)$ has labeled vertices as in Definition 2. Therefore, $v_2=u^{{}^{\prime }}$, $v_5=v^{{}^{\prime }}$, $v_3=u^{{}^{″}}$ and $v_4=v^{{}^{″}}$. The vertices $v_2$ and $v_3$ are unique in ${\mathcal{B}}_{+}$ with maximum and minimum moduli, and $v_4$ and $v_5$ are unique in ${\mathcal{B}}_{-}$ with maximum and minimum moduli, respectively. By Lemma 6, as $\mathbf{X}$ is the first eigenvector of the minimizing graph $\mathcal{B}(p,q)$, $X_1,X_2$, $X_3$ are non negative and $X_4,X_5,X_6,X_7,X_8$ are negative values of $\mathbf{X}$. Now, by (7), ${\lambda }_2(X_2-X_1)=-(p-2)X_1-X_3<0$ and ${\lambda }_2(X_1-X_3)=-X_1+X_3+X_4<0$, which implies $X_2-X_1>0$ and $X_1-X_3>0$. Therefore, $X_3<X_1<X_2$. Similarly, ${\lambda }_2(X_4-X_8)=X_8-X_3-X_4<0$, ${\lambda }_2(X_8-X_7)=-X_8+X_6+X_7<0$, ${\lambda }_2(X_7-X_6)=X_7<0$ and ${\lambda }_2(X_6-X_5)=X_4+(q-4)x_8<0$. Thus, $X_5<X_6<X_7<X_8<X_4$.

By (13)–(16) and the above discussion, we have ${\mathcal{B}}_{+}={\overline{\mathcal{B}}}_{+}={\mathcal{K}}_{1,p}$ and ${\mathcal{B}}_{-}={\overline{\mathcal{B}}}_{-}={\mathcal{S}}_{1,q}^{\ast ,2}$. Consequently, ${\mathcal{E}}^{{}^{\prime }}$ contains exactly one edge $u^{{}^{″}}{v}^{{}^{″}}=v_3{v}_4$. Now, if the value of $v_2$ is zero, i.e., $X_2=0$, then $X_1=X_3=0$ because $0<X_3<X_1<X_2$. By (7) $x_5=0$, which is a contradiction. If value of $v_1$ is zero i.e., $X_1=0$, then $X_3=0$ as $0<X_3<X_1$. Solving the first two equations of (7), $X_2=0$. This shows $X_5=0$, which is again a contradiction. If the value of $v_3$ is zero, i.e., $X_3=0$, then delete the edges $v_3{v}_4$ and $v_4{v}_5$, and join $v_4$ with $v_2$ and one of the pendent vertexes of ${\mathcal{S}}_{1,q}^{\ast ,2}$. Thus, we get a graph $\mathcal{B}(p+1,q-1)$ with the same $\mathbf{X}$ such that ${\lambda }_{min}(\mathcal{B}{(p+1,q-1)}^c)\le {\lambda }_{min}({\mathcal{B}}^c)$, which is a contradiction if $p\ge q$ by Lemma 4. Consequently, $V_{+}$ does not contain any vertex with zero value given by $\mathbf{X}$, which completes the proof.

Now, we give the proof of the main theorem (Theorem 2) of this paper, which is stated in Section 1 (Introduction).

Proof of Theorem 2. 

This proof follows Lemma 4 and Theorem 3.

4. Conclusions

Petrovi$\acute{\mathrm{c}}$ et al. [13] proved: if $G\in {\mathcal{G}}_n$ is any bicyclic graph of order n, then ${\lambda }_{\min }(G_4^{\ast })\le {\lambda }_{\min }(G)$ and equality holds if and only if $G=G_4^{\ast }$, where $G_4^{\ast }\cong S_{1,n-1}^{\ast ,2}$. It shows that $S_{1,n-1}^{\ast ,2}$ is a unique minimizing graph in ${\mathcal{G}}_n$, where ${\mathcal{G}}_n$ is a class of bicyclic graphs of order n. However, in this paper, we proved that $\mathcal{B}{(\lceil \frac{n-2}{2}\rceil ,\lfloor \frac{n-2}{2}\rfloor )}^c$ is a unique minimizing graph in ${\mathcal{G}}_n^c$, where ${\mathcal{G}}_n^c$ is a class of the connected graphs of order n whose complements are bicyclic.