Neutral, Leakage, and Mixed Delays in Quaternion-Valued Neural Networks on Time Scales: Stability and Synchronization Analysis

Abstract

Quaternion-valued neural networks (QVNNs) that have multiple types of delays (leakage, time-varying, distributed, and neutral) and defined on time scales are discussed in this paper. Quaternions form a 4D normed division algebra and allow for a better representation of 3D and 4D data. QVNNs have been proposed and applications have appeared lately. Time-scale calculus was developed to allow the joint treatment of systems, or any hybrid mixing of them, and was also applied with success to the analysis of dynamic properties for neural networks (NNs). Because of its generality, encompassing the common properties of discrete-time (DT) and continuous-time (CT) NNs, time-scale NNs dynamics research does not benefit from a fully-developed Lyapunov theory. So, Halanay-type inequalities have to be used instead. To this end, we provide a novel generalization of inequalities of Halanay-type on time scales specifically suited for neutral systems, i.e., systems with neutral delays. Then, this new lemma is employed to obtain sufficient conditions presented both as linear matrix inequalities (LMIs) and as algebraic inequalities for the exponential stability and exponential synchronization of QVNNs on time scales with the mentioned delay types. The model put forward in this paper has a generality which is appealing for practical applications, in which both DT and CT dynamics are interesting, and all the discussed types of delays appear. For both the DT and CT scenarios, four numerical applications are used to illustrate the four theorems put forward in this research.

1. Introduction

Over the last period, QVNNs have received increasing research interest. Introduced for the first time in [1], presently, they have applications in image classification, speech recognition, and signal processing (for a recent survey of QVNNs, see [2]). Because quaternions are four-dimensional numbers, they can better represent signals which were originally given in the 3D or 4D domains, without the need for decomposition into real-valued parts. Discovered by Hamilton in 1843, the quaternions are the first 4D normed division algebra that was put forward, which makes them amenable for use in NNs.

QVNNs are especially amenable to applications in domains where the data naturally has multidimensional correlated components, such as RGB image channels, which can be represented as quaternions, 3D rotations, which have a quaternion representation, or MIMO channels, which can also be encoded in the form of quaternions. In these contexts, the use of QVNNs provides better modeling of inter-channel relations, having fewer parameters than their real-valued counterparts, and thus being more efficient.

Owing to their popularity in applications, the dynamic properties of recurrent QVNNs have also begun to be studied in the recent past. Starting from paper [3], more and more papers are being published each year, discussing different dynamic properties of recurrent QVNNs, such as stability [4,5,6,7,8,9,10,11], fixed/finite-time stability [12,13], synchronization [14,15,16,17,18,19,20], fixed/finite-time synchronization [21,22,23,24,25,26], etc.

In implementations of NNs in the real-world, time delays occur due to the finite reaction time of circuit components, which might cause unwanted behavior. For this reason, it is essential to include time delays in the models used to study the dynamics of NNs [27]. Leakage delay may appear in the self-feedback term of NNs, which was considered a part of QVNN models in [4,10,28,29,30,31,32,33,34,35,36,37]. Then, distributed delays might arise as a result of the distribution, along the NN’s implementation paths, of conduction speeds. Distributed delays were added to QVNNs in [5,10,15,38,39,40,41,42,43,44]. When they are present together with the most popular types of delays that might appear in NNs, i.e., with time-varying delays, they are known as mixed delays. These were added to QVNN models in [17,26,29,30,33,45,46,47,48,49,50,51,52,53,54,55,56]. Finally, delays might appear in the derivative term of NNs, in which case, they are called neutral delays, and the resulting systems are called neutral systems. These systems exhibit more interesting dynamics than systems with the other types of delays and warrant particular study. It has als obeen proven that this type of delay appears in real-world brain response processes, which constitutes a further reason to add them to NN models. Indeed, they were considered in the context of QVNNs, most recently in [17,28,31,53,57,58,59,60,61,62,63].

However, most parts of the studies regarding the dynamics of NNs in general and QVNNs in particular are done in CT. However, in order to be implemented in circuits, NNs must be discretized in time, and there is the possibility that the dynamics of the CT model do not remain the same for its DT counterpart. For this reason, DT NNs were studied for the first time in [64]. Since then, studying the dynamics of DT NNs has become a standalone topic, which attracts more and more research interest as time passes. Discrete-time QVNN models were discussed in [4,9,19,65,66,67,68,69]. The paper [66] even separately discusses both the DT and the CT cases.

However, there is a solution to unify the study of DT and CT systems by employing time-scale calculus. Time-scale calculus was first proposed in [70] and has the advantage of encompassing both differential and difference equations in a single formulation or any combination of these. This type of generality allows for the unified study of both DT and CT NNs, or any hybrid mixing of them, also highlighting their commonalities. The calculus on time scales was further developed and synthesized in the books [71,72,73], which constitute the go-to references for further developments regarding time scales. In the context of NNs, time scales were first applied in [74]. Since then, the popularity of NN models on time scales has increased yearly. QVNNs on time scales were discussed in [9,28,35,52,75,76].

Unfortunately, the Lyapunov theory is not so developed for time scales as for differential or difference systems, since it is a more general setting, which has to encompass the common characteristics of both. For this reason, Halanay-type inequalities have been routinely employed to studying the dynamical properties of NNs defined on time scales. Several flavors of inequalities of Halanay-type have been discussed in the literature, over time; see [77,78,79,80,81]. Halanay-type inequalities on time scales were subsequently obtained by extending them to time scales in [82,83,84,85].

An interesting direction for studying time=scale NNs was proposed in papers [6,44,86,87,88,89,90], where different generalizations of Halanay-type inequalities for time scales are presented, which are then used to ascertain sufficient conditions for different dynamical properties of NNs defined on time scales. Unfortunately, none of these lemmas can be used for neutral systems, and this is the void the present paper aims to fill.

Considering all of the aforementioned issues, the paper’s primary highlights are as follows:

1.

A generalized Halanay-type inequality defined on time scales for neutral systems is provided, with a demonstration, which can be used for general neutral systems defined on time scales, not just for NNs.

2.

The very general QVNN model defined on time scales and with multiple types of delays (leakage, time-varying, distributed, and neutral) is presented.

3.

The application of the proposed generalization for a Halanay-type inequality is facilitated by the formulation of different types of general Lyapunov-like functions.

4.

Based on these, four theorems are proved, which formulate sufficient criteria given in terms of algebraic inequalities and LMIs which ensure that, for the discussed general model, the exponential stability and exponential synchronization properties are satisfied.

5.

For both the DT and CT scenarios, four numerical applications are used to illustrate the four theorems.

6.

The generality of the model allows it to be tailored for DT and CT NNs, or any hybrid mixing of them, and also for real-valued or complex-valued NNs, with possibly fewer types of delays. To our awareness, in the existing literature, the corresponding results have not yet been published.

The obtained results are applicable to real-world domains where recurrent QVNNs are used in order to study their dynamic properties, leading to model designs better fitted for these particular applications. The application domains of recurrent QVNNs include signal and image processing, robotic control, or memory and cognitive modeling.

The research is organized as follows. The basics of time-scale calculus, the generalization for neutral systems of the Halanay-type inequality, a few other lemmas, and the QVNN model are all the subject of Section 2. Then, the four main theorems, which all use the proposed lemma in their proofs, are given in Section 3, to ascertain the exponential stability and exponential synchronization properties of the introduced QVNNs, and are afterwards illustrated by way of numerical applications in Section 4. In Section 5, the research’s conclusions are provided.

Notations:$||·{||}_p$—$L_p$ norm, $p\in \{1,2\}$, $X<0$—X is negative definite, $X^T$—transpose of X, and ${\lambda }_{min}\left(X\right)$—smallest eigenvalue of X.

2. Preliminaries

Mainly based on [71], we first provide an introduction to time-scale calculus. A non-empty closed subset of the real number set $\mathbb{R}$, from which the topology and ordering are inherited, is called a time-scale $\mathbb{T}$. $\forall t\in \mathbb{T}$, the forward jump operator is defined as $\sigma \left(t\right):=inf\{\left.s\in \mathbb{T}\right|s>t\}$ and the backward jump operator as $\rho \left(t\right)=\sup \{\left.s\in \mathbb{T}\right|s<t\}$. The forward graininess function is defined as $\mu :\mathbb{T}\to [0,+\infty )$, $\mu \left(t\right):=\sigma \left(t\right)-t$, $\forall t\in \mathbb{T}$. Also put $\widehat{\mu }=\sup \{\left.\mu \left(t\right)\right|t\in \mathbb{T}\}$.

Once this is established, a point $t\in \mathbb{T}$ is right (left)-dense if $\sigma \left(t\right)=t$ ($\rho \left(t\right)=t$) and right (left)-scattered if $\sigma \left(t\right)>t$ ($\rho \left(t\right)<t$). ${\mathbb{T}}^{\kappa }:=\mathbb{T}\backslash \left\{m\right\}$, where m is the left-scattered maximum of $\mathbb{T}$, if it exists, otherwise ${\mathbb{T}}^{\kappa }:=\mathbb{T}$. If $f\left(t_1\right)={lim}_{\zeta \to t_1^{+}}f\left(\zeta \right)$ for any right-dense $t_1\in \mathbb{T}$, and ${lim}_{\zeta \to t_2^{-}}f\left(\zeta \right)$ exists for any left-dense $t_2\in \mathbb{T}$, then the function $f:\mathbb{T}\to \mathbb{R}$ is called rd-continuous. $C_{rd}(\mathbb{T},\mathbb{R})$ designates the set of all functions $f:\mathbb{T}\to \mathbb{R}$, which are rd-continuous. The jump operators are defined as $f^{\sigma }\left(t\right)=f\left(\sigma \left(t\right)\right)$ and $f^{\rho }\left(t\right)=f\left(\rho \left(t\right)\right)$, respectively, for a function $f:\mathbb{T}\to \mathbb{R}$. If $p\in C_{rd}(\mathbb{T},\mathbb{R})$ and $1+\mu \left(t\right)p\left(t\right)\ne 0$, $\forall t\in {\mathbb{T}}^{\kappa }$, then function $p:\mathbb{T}\to \mathbb{R}$ is said to be regressive, and we denote by $\mathcal{R}(\mathbb{T},\mathbb{R})$ the set of all regressive functions. The set ${\mathcal{R}}^{+}(\mathbb{T},\mathbb{R})$ denotes all positively regressive functions, which are functions $p:\mathbb{T}\to \mathbb{R}$, for which $p\in C_{rd}(\mathbb{T},\mathbb{R})$ and $1+\mu \left(t\right)p\left(t\right)>0$, $\forall t\in {\mathbb{T}}^{\kappa }$. We establish the following formula: $\forall p\in \mathcal{R}(\mathbb{T},\mathbb{R})$, $\ominus p\left(t\right):=-p\left(t\right)/(1+\mu (t\left)p\right(t\left)\right)$, $\forall t\in \mathbb{T}$. For any set $S\subseteq \mathbb{R}$, we define $S_{\mathbb{T}}=S\cap \mathbb{T}$.

Given a function $f:\mathbb{T}\to \mathbb{R}$, the number denoted by $f^{\Delta }\left(t\right)$ for $t\in {\mathbb{T}}^{\kappa }$, such that for $\forall \epsilon >0$, there exists a $\delta >0$, so that the subsequent inequality is valid $\forall s\in {(t-\delta ,t+\delta )}_{\mathbb{T}}$:

$$|f\left(\sigma \left(t\right)\right)-f\left(s\right)-f^{\Delta }\left(t\right)(\sigma \left(t\right)-s)|\le \epsilon |\sigma \left(t\right)-s|,$$

represents, if it exists, the $\Delta$-derivative of f at t. The function f is said to be $\Delta$-differentiable if the $\Delta$-derivative exists $\forall t\in {\mathbb{T}}^{\kappa }$.

The inverse operation of $\Delta$-differentiation is $\Delta$-integration, i.e., if $F^{\Delta }\left(t\right)=f\left(t\right)$, then

$${\int }_a^{b}f\left(s\right)\Delta s=F\left(b\right)-F\left(a\right),\forall a,b\in \mathbb{T}.$$

Lastly, for any regressive function $p\in \mathcal{R}(\mathbb{T},\mathbb{R})$, the $\Delta$-exponential function $e_p:\mathbb{T}\times \mathbb{T}\to \mathbb{R}$ is defined by the formula:

$$e_p(a,b)=e^{{\int }_a^b{\xi }_{\mu \left(s\right)}\left(p\left(s\right)\right)\Delta s},\forall a,b\in \mathbb{T},$$

where ${\xi }_{\mu \left(s\right)}$ represents the cylinder transformation, given as

$${\xi }_h\left(z\right)=\left\{\begin{array}{cc}{\displaystyle \frac{log(1+zh)}{h}},\hfill & h\ne 0\hfill \\ z,\hfill & h=0\hfill \end{array}\right..″$$

The subsequent lemmas regarding time scales are needed for proving our results:

Lemma 1

([71]). “If $f,g:\mathbb{T}\to \mathbb{R}$ are Δ-differentiable, then

(i) ${(f\left(t\right)+g\left(t\right))}^{\Delta }=f^{\Delta }\left(t\right)+g^{\Delta }\left(t\right)$;

(ii) ${\left(f\left(t\right)g\left(t\right)\right)}^{\Delta }=f^{\Delta }\left(t\right)g\left(t\right)+f\left(\sigma \left(t\right)\right)g^{\Delta }\left(t\right)=f\left(t\right)g^{\Delta }\left(t\right)+f^{\Delta }\left(t\right)g\left(\sigma \left(t\right)\right).$”

Lemma 2.

If $u,v\in C_{rd}(\mathbb{T},\mathbb{R})$ are non-negative functions and

$$u^{\Delta }\left(t\right)\le -{\alpha }_{1}u\left(t\right)+{\alpha }_2\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

$$v\left(t\right)\le {\alpha }_{4}u\left(t\right)+{\alpha }_5\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

$\forall t\in [t_0,+\infty )$, where the positive constants ${\alpha }_1,\dots ,{\alpha }_6$ are such that $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and

$${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}>0,$$

then

$$u\left(t\right)\le \underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t,t_0),$$

$$v\left(t\right)\le \underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }v\left(w\right)e_{\ominus \lambda }(t,t_0),$$

$\forall t\in [t_0,+\infty )$, where $\lambda >0$ satisfies

$$-\ominus \lambda \le {\alpha }_1-{\alpha }_2{e}^{\lambda \omega }-{\displaystyle \frac{{\alpha }_3{e}^{\lambda \omega }({\alpha }_4+{\alpha }_5{e}^{\lambda \omega })}{1-{\alpha }_6{e}^{\lambda \omega }}}.$$

(1)

Proof. 

Firstly, we consider function $F:\left[0,{\displaystyle \frac{1}{\omega }}ln{\displaystyle \frac{1}{{\alpha }_6}}\right)\times [t_0,+\infty )\to \mathbb{R}$, defined as

$$F(\lambda ,t)=-\ominus \lambda -{\alpha }_1+{\alpha }_2{e}^{\lambda \omega }+{\displaystyle \frac{{\alpha }_3{e}^{\lambda \omega }({\alpha }_4+{\alpha }_5{e}^{\lambda \omega })}{1-{\alpha }_6{e}^{\lambda \omega }}}.$$

Because of the hypothesis of the lemma, we have

$$F(0,t)=-{\alpha }_1+{\alpha }_2+{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}<0.$$

If we take the derivative of F with respect to $\lambda$, we can see that

$${\displaystyle \frac{\partial F(\lambda ,t)}{\partial \lambda }}={\displaystyle \frac{1}{{(1+\lambda \mu \left(t\right))}^2}}+{\alpha }_2\omega e^{\lambda \omega }+{\displaystyle \frac{{\alpha }_3\omega e^{\lambda \omega }({\alpha }_4+{\alpha }_5{e}^{\lambda \omega }(2-{\alpha }_6{e}^{\lambda \omega }))}{{(1-{\alpha }_6{e}^{\lambda \omega })}^2}}>0,$$

which, together with ${lim}_{\lambda \to {\displaystyle \frac{1}{\omega }}ln{\displaystyle \frac{1}{{\alpha }_6}}-0}F(\lambda ,t)=+\infty$ guarantees the existence of $\widehat{\lambda }\in \left(0,{\displaystyle \frac{1}{\omega }}ln{\displaystyle \frac{1}{{\alpha }_6}}\right)$, such that ${\sup }_{t\in {[t_0,+\infty )}_{\mathbb{T}}}F(\widehat{\lambda },t)=0$. For $\lambda \in (0,\widehat{\lambda }]$, we get that $F(\lambda ,t)\le 0$, $\forall t\in {[t_0,+\infty )}_{\mathbb{T}}$, which proves the existence of $\lambda >0$, so that (1) is true.

Inequality

$$-\ominus \lambda \le {\alpha }_1-{\alpha }_2{e}^{\lambda \omega }-{\displaystyle \frac{{\alpha }_3{e}^{\lambda \omega }({\alpha }_4+{\alpha }_5{e}^{\lambda \omega })}{1-{\alpha }_6{e}^{\lambda \omega }}},$$

implies that

$$-\ominus \lambda \le {\alpha }_1-{\alpha }_2{e}_{\ominus \lambda }(t-\omega ,t)-{\displaystyle \frac{{\alpha }_3{e}_{\ominus \lambda }(t-\omega ,t)({\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t-\omega ,t))}{1-{\alpha }_6{e}_{\ominus \lambda }(t-\omega ,t)}}.$$

Now, we define the function:

$$y\left(t\right)=\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t,t_0).$$

We are going to demonstrate that $u\left(t\right)\le y\left(t\right)$. The second inequality in the conclusion of the lemma is proved similarly. If we do not have $u\left(t\right)\le y\left(t\right)$, there are two possible cases.

In the first case, there exists a right-scattered $t_1\in {[t_0,+\infty )}_{\mathbb{T}}$ for which $u\left(w\right)\le y\left(w\right)$, $\forall w\in {[t_0,t_1]}_{\mathbb{T}}$, and $u\left(\sigma \left(t_1\right)\right)>y\left(\sigma \left(t_1\right)\right)$, and

$$\begin{array}{ccc}\hfill u\left(\sigma \left(t_1\right)\right)-y\left(\sigma \left(t_1\right)\right)& =& u\left(t_1\right)-y\left(t_1\right)+\mu \left(t_1\right)u^{\Delta }\left(t_1\right)-\mu \left(t_1\right)y^{\Delta }\left(t_1\right)\hfill \\ & =& u\left(t_1\right)-y\left(t_1\right)+\mu \left(t_1\right)\left(-{\alpha }_{1}u\left(t_1\right)+{\alpha }_2\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }v\left(w\right)\right.\hfill \\ & & \left.-\ominus \lambda \underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1,t_0)\right)\hfill \\ & \le & u\left(t_1\right)-y\left(t_1\right)+\mu \left(t_1\right)\left(-{\alpha }_{1}u\left(t_1\right)+{\alpha }_2\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }v\left(w\right)\right.\hfill \\ & & +{\alpha }_1\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1,t_0)-{\alpha }_2\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1-\omega ,t_0)\hfill \\ & & \left.-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t_1-\omega ,t_1))}{1-{\alpha }_6{e}_{\ominus \lambda }(t_1-\omega ,t_1)}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1-\omega ,t_0)\right)\hfill \\ & =& (u\left(t_1\right)-y\left(t_1\right))(1-{\alpha }_1\mu \left(t_1\right))+{\alpha }_2\mu \left(t_1\right)\left(\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }u\left(w\right)-y(t_1-\omega )\right)\hfill \\ & & +{\alpha }_3\mu \left(t_1\right)\left(\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }v\left(w\right)-{\displaystyle \frac{{\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t_1-\omega ,t_1)}{1-{\alpha }_6{e}_{\ominus \lambda }(t_1-\omega ,t_1)}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1-\omega ,t_0)\right)\hfill \\ & \le & 0,\hfill \end{array}$$

because $-{\alpha }_1\in {\mathcal{R}}^{+}$ and, from the hypotheses of the lemma, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t_1-\omega ,t_1)}{1-{\alpha }_6{e}_{\ominus \lambda }(t_1-\omega ,t_1)}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1-\omega ,t_0)& \ge & {\displaystyle \frac{{\alpha }_4+{\alpha }_5}{1-{\alpha }_6}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_1-\omega ,t_0)\hfill \\ & \ge & {\displaystyle \frac{{\alpha }_4+{\alpha }_5}{1-{\alpha }_6}}\underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }u\left(w\right)\hfill \\ & \ge & \underset{w\in {[t_1-\omega ,t_1]}_{\mathbb{T}}}{\sup }v\left(s\right),\hfill \end{array}$$

in which the last inequality is also obtained from the hypothesis of the lemma in the following way:

$$\begin{array}{ccc}\hfill v\left(t\right)& \le & {\alpha }_{4}u\left(t\right)+{\alpha }_5\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }v\left(w\right)\hfill \\ & \le & ({\alpha }_4+{\alpha }_5)\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }v\left(w\right)\hfill \\ & \iff \\ \hfill \underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }v\left(w\right)& \le & {\displaystyle \frac{{\alpha }_4+{\alpha }_5}{1-{\alpha }_6}}\underset{w\in {[t-\omega ,t]}_{\mathbb{T}}}{\sup }u\left(w\right).\hfill \end{array}$$

Thus, $u\left(\sigma \left(t_1\right)\right)\le y\left(\sigma \left(t_1\right)\right)$, which contradicts our initial assumption $u\left(\sigma \left(t_1\right)\right)>y\left(\sigma \left(t_1\right)\right)$.

In the second case, there exists a right-dense $t_2\in {[t_0,+\infty )}_{\mathbb{T}}$ for which $u\left(t_2\right)=y\left(t_2\right)$, $u\left(w\right)\le y\left(w\right)$, $\forall w\in {[t_0,t_2]}_{\mathbb{T}}$, and $u^{\Delta }\left(t_2\right)>y^{\Delta }\left(t_2\right)$. Then

$$\begin{array}{ccc}\hfill u^{\Delta }\left(t_2\right)-y^{\Delta }\left(t_2\right)& \le & -{\alpha }_{1}u\left(t_2\right)+{\alpha }_2\underset{w\in {[t_2-\omega ,t_2]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t_2-\omega ,t_2]}_{\mathbb{T}}}{\sup }v\left(w\right)-\ominus \lambda \underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_2,t_0)\hfill \\ & \le & \left(-{\alpha }_1+{\alpha }_2{e}_{\ominus \lambda }(t_2-\omega ,t_2)+{\displaystyle \frac{{\alpha }_3{e}_{\ominus \lambda }(t_2-\omega ,t_2)({\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t_2-\omega ,t_2))}{1-{\alpha }_6{e}_{\ominus \lambda }(t_2-\omega ,t_2)}}-\ominus \lambda \right)\hfill \\ & & \times \underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_2,t_0)\hfill \\ & \le & 0,\hfill \end{array}$$

because from the hypotheses of the lemma we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5{e}_{\ominus \lambda }(t_2-\omega ,t_2))}{1-{\alpha }_6{e}_{\ominus \lambda }(t_2-\omega ,t_2)}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_2-\omega ,t_0)& \ge & {\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}\underset{w\in {[t_0-\omega ,t_0]}_{\mathbb{T}}}{\sup }u\left(w\right)e_{\ominus \lambda }(t_2-\omega ,t_0)\hfill \\ & \ge & {\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}\underset{w\in {[t_2-\omega ,t_2]}_{\mathbb{T}}}{\sup }u\left(w\right)\hfill \\ & \ge & {\alpha }_3\underset{w\in {[t_2-\omega ,t_2]}_{\mathbb{T}}}{\sup }v\left(w\right).\hfill \end{array}$$

Thus, $u^{\Delta }\left(t_2\right)\le y^{\Delta }\left(t_2\right)$, which contradicts our initial assumption $u^{\Delta }\left(t_2\right)>y^{\Delta }\left(t_2\right)$.

Therefore, we proved by contradiction that $u\left(t\right)\le y\left(t\right)$, $\forall t\in {[t_0,+\infty )}_{\mathbb{T}}$. □

Lemma 3

([87]). “If $-\lambda \in {\mathcal{R}}^{+}$, $y\in C_{rd}(\mathbb{T},\mathbb{R})$, $z\in C_{rd}(\mathbb{T},\mathbb{R})$, then, $\forall t\in \mathbb{T}$,

$$y^{\Delta }\left(t\right)\le -\lambda y\left(t\right)+z\left(t\right)$$

implies

$${|y\left(t\right)|}^{\Delta }\le -\lambda |y\left(t\right)|+|z\left(t\right)|.″$$

On the other hand, the quaternion number set is defined as

$$\mathbb{H}=\{h=h^R+h^{I}i+h^{J}j+h^K\kappa |h^R,h^I,h^J,h^K\in \mathbb{R}\},$$

where $i,j,\kappa$ are the unit quaternions, and they satisfy $i^2=j^2={\kappa }^2=ij\kappa =-1$. The addition operation is defined as

$$h+g:=(h^R+g^R)+(h^I+g^I)i+(h^J+g^J)j+(h^K+g^K)\kappa ,$$

and the multiplication operation as

$$\begin{array}{ccc}\hfill hg& :=& h^R{g}^R-h^I{g}^I-h^J{g}^J-h^K{g}^K\hfill \\ & & +(h^R{g}^I+h^I{g}^R+h^J{g}^K-h^K{g}^J)i\hfill \\ & & +(h^R{g}^J-h^I{g}^K+h^J{g}^R+h^K{g}^I)j\hfill \\ & & +(h^R{g}^K+h^I{g}^J-h^J{g}^I+h^K{g}^R)\kappa ,\hfill \end{array}$$

which immediately leads to the conclusion that the multiplication of quaternions is not commutative.

The conjugate of a quaternion h is given as $\overline{h}:=h^R-h^{I}i-h^{J}j-h^K\kappa$, its inverse as $h^{-1}:={\displaystyle \frac{\overline{h}}{{|h|}^2}}$, and its norm as $|h|=\sqrt{\overline{h}h}=\sqrt{{\left(h^R\right)}^2+{\left(h^I\right)}^2+{\left(h^J\right)}^2+{\left(h^K\right)}^2}$. With the operations defined as above, the quaternion number set forms a normed division algebra.

In the following, we will study the dynamic properties of the QVNN model given, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$, by

$$h_i^{\Delta }\left(t\right)=-a_i{h}_i(t-\delta )+\sum _{j=1}^N{b}_{ij}{f}_j\left(h_j\left(t\right)\right)+\sum _{j=1}^N{c}_{ij}{f}_j\left(h_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{f}_j\left(h_j\left(s\right)\right)\Delta s+e_i{h}_i^{\Delta }(t-\theta )+I_i,$$

(2)

where $h\left(t\right)={(h_1\left(t\right),\dots ,h_N\left(t\right))}^T\in {\mathbb{H}}^N$ is the state vector at t, $A=\mathit{diag}(a_1,\dots ,a_N)\in {\mathbb{R}}^{N\times N}$, with $a_i>0$, is the feedback connection matrix, $B={\left(b_{ij}\right)}_{1\le i,j\le N}\in {\mathbb{H}}^{N\times N}$ is the connection matrix without delay, $C={\left(c_{ij}\right)}_{1\le i,j\le N}\in {\mathbb{H}}^{N\times N}$ is the connection matrix with delay, $D={\left(d_{ij}\right)}_{1\le i,j\le N}\in {\mathbb{H}}^{N\times N}$ is the distributed delay connection matrix, $E=\mathit{diag}(e_1,\dots ,e_N)\in {\mathbb{H}}^{N\times N}$ is the neutral delay connection matrix, $f_j:\mathbb{H}\to \mathbb{H}$ constitute the activation functions, $\forall j\in \{1,\dots ,N\}$, $I=(I_1,\dots ,I_N)\in {\mathbb{H}}^N$ is the external input vector, and the delays are leakage $\delta \in {\mathbb{R}}^{+}$, time-varying $\gamma :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, distributed $\eta \in {\mathbb{R}}^{+}$, and neutral $\theta \in {\mathbb{R}}^{+}$. The activation functions are also assumed to be of the form $f_j\left(h\right)=f_j^R\left(h\right)+f_j^I\left(h\right)i+f_j^J\left(h\right)j+f_j^K\left(h\right)\kappa$, $\forall h\in \mathbb{H}$, where $f_j^R,f_j^I,f_j^J,f_j^K:\mathbb{H}\to \mathbb{R}$. The time-varying delays are also assumed to satisfy $\gamma \left(t\right)\le \gamma$, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, for some $\gamma >0$, and we put $\pi :=\max \{\delta ,\gamma ,\eta ,\theta \}$.

Furthermore, the Lipschitz conditions will be assumed to be satisfied by the activation functions:

Assumption 1

([46]). “The activation functions $f_j$ satisfy the Lipschitz conditions:

$$||f_j\left(h\right)-f_j\left(h^{\prime }\right)||\le l_j||h-h^{\prime }||,$$

$\forall h,h^{\prime }\in \mathbb{H}$, $\forall j\in \{1,\dots ,N\}$, where $l_j>0$ are the Lipschitz constants. Moreover, we put $L:=\mathit{diag}(l_1,\dots ,l_N)$.”

Associated with System (2) are the initial conditions as follows:

$$h_i\left(t\right)={\chi }_i\left(t\right),\forall t\in {[-\pi ,0]}_{\mathbb{T}},$$

$\forall i\in \{1,\dots ,N\}$, where ${\chi }_i\in \mathcal{C}({[-\pi ,0]}_{\mathbb{T}},\mathbb{H})$ and the norm on $\mathcal{C}({[-\pi ,0]}_{\mathbb{T}},{\mathbb{H}}^N)$ is $||\chi ||:={\sum }_{i=1}^N{\sup }_{s\in {[-\pi ,0]}_{\mathbb{T}}}|{\chi }_i\left(s\right)|$.

In order to discuss synchronization, NN (2) will be considered as the drive NN, and we will define the corresponding response NN, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$, by

$$g_i^{\Delta }\left(t\right)=-a_i{g}_i(t-\delta )+\sum _{j=1}^N{b}_{ij}{f}_j\left(g_j\left(t\right)\right)+\sum _{j=1}^N{c}_{ij}{f}_j\left(g_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{f}_j\left(g_j\left(s\right)\right)\Delta s+e_i{g}_i^{\Delta }(t-\theta )+I_i-u_i\left(t\right),$$

(3)

and $g\left(t\right)={(g_1\left(t\right),\dots ,g_N\left(t\right))}^T\in {\mathbb{H}}^N$ represents the vector of states at t and $u\left(t\right)={(u_1\left(t\right),\dots ,u_N\left(t\right))}^T\in {\mathbb{H}}^N$ represents the control input at t, the significance of the other variables being the same as in (2).

For System (3), the initial conditions are assumed to be

$$g_i\left(t\right)={\psi }_i\left(t\right),\forall t\in {[-\pi ,0]}_{\mathbb{T}},$$

$\forall i\in \{1,\dots ,N\}$, and ${\psi }_i\in \mathcal{C}({[-\pi ,0]}_{\mathbb{T}},\mathbb{H})$.

Now, suppose that NN (2) possesses an equilibrium point (EP) that is unique and that is designated as $\tilde{h}=({\tilde{h}}_1,\dots ,{\tilde{h}}_N)\in {\mathbb{H}}^N$. If we take ${\mathfrak{h}}_i\left(t\right)=h_i\left(t\right)-\tilde{h}$, System (2) can be transformed as

$${\mathfrak{h}}_i^{\Delta }\left(t\right)=-a_i{\mathfrak{h}}_i(t-\delta )+\sum _{j=1}^N{b}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)+\sum _{j=1}^N{c}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{h}}_i^{\Delta }(t-\theta ),$$

(4)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$, in which ${\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)={\tilde{f}}_j({\mathfrak{h}}_j\left(t\right)+\tilde{h})-{\tilde{f}}_j\left(\tilde{h}\right),$$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall j\in \{1,\dots ,N\}$.

Associated with System (4), the initial conditions are as follows:

$${\mathfrak{h}}_i\left(t\right)=v_i\left(t\right)={\chi }_i\left(t\right)-\tilde{h},\forall t\in {[-\pi ,0]}_{\mathbb{T}},$$

$\forall i\in \{1,\dots ,N\}$, and $v_i\in \mathcal{C}({[-\pi ,0]}_{\mathbb{T}},\mathbb{H})$.

On the other hand, if ${\mathfrak{d}}_i\left(t\right)=g_i\left(t\right)-h_i\left(t\right)$, from the expressions of Systems (2) and (4), we are able to deduce that

$${\mathfrak{d}}_i^{\Delta }\left(t\right)=-a_i{\mathfrak{d}}_i(t-\delta )+\sum _{j=1}^N{b}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)+\sum _{j=1}^N{c}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{d}}_i^{\Delta }(t-\theta )-u_i\left(t\right),$$

(5)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$, in which ${\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)={\tilde{f}}_j({\mathfrak{d}}_j\left(t\right)+h_i\left(t\right))-{\tilde{f}}_j\left(h_i\left(t\right)\right),$$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall j\in \{1,\dots ,N\}$.

For the developments in this paper, we also need to write Systems (4) and (5) in matrix form as

$${\mathfrak{h}}^{\Delta }\left(t\right)=-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta ),$$

(6)

and, respectively, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$,

$${\mathfrak{d}}^{\Delta }\left(t\right)=-A\mathfrak{d}(t-\delta )+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+E{\mathfrak{d}}^{\Delta }(t-\theta )-u\left(t\right).$$

(7)

3. Main Results

Theorem 1.

If the following LMIs hold

$$\mathsf{\Omega }<0,\mathsf{\Phi }<0,$$

(8)

where

${\mathsf{\Omega }}_{1,1}=-PA-AP+L^T{R}_{1}L+{\alpha }_{1}P$, ${\mathsf{\Omega }}_{1,3}=-N_2^{*}$, ${\mathsf{\Omega }}_{1,6}=PB$, ${\mathsf{\Omega }}_{1,7}=PC$, ${\mathsf{\Omega }}_{1,8}=PD$, ${\mathsf{\Omega }}_{1,9}=PE$, ${\mathsf{\Omega }}_{2,2}=\widehat{\mu }P-N_1-N_1^{*}$, ${\mathsf{\Omega }}_{2,3}=-N_{1}A$, ${\mathsf{\Omega }}_{2,6}=N_{1}B-N_3^{*}$, ${\mathsf{\Omega }}_{2,7}=N_{1}C-N_4^{*}$, ${\mathsf{\Omega }}_{2,8}=N_{1}D-N_5^{*}$, ${\mathsf{\Omega }}_{2,9}=N_{1}E-N_6^{*}$, ${\mathsf{\Omega }}_{3,3}=-{\alpha }_{21}P-N_{2}A-A^{*}{N}_2^{*}$, ${\mathsf{\Omega }}_{3,6}=N_{2}B-A^{*}{N}_3^{*}$, ${\mathsf{\Omega }}_{3,7}=N_{2}C-A^{*}{N}_4^{*}$, ${\mathsf{\Omega }}_{3,8}=N_{2}D-A^{*}{N}_5^{*}$, ${\mathsf{\Omega }}_{3,9}=N_{2}E-A^{*}{N}_6^{*}$, ${\mathsf{\Omega }}_{4,4}=L^T{R}_{2}L-{\alpha }_{22}P$, ${\mathsf{\Omega }}_{5,5}=-{\alpha }_{23}P$, ${\mathsf{\Omega }}_{6,6}=-R_1+N_{3}B+B^{*}{N}_3^{*}$, ${\mathsf{\Omega }}_{6,7}=N_{3}C+B^{*}{N}_4^{*}$, ${\mathsf{\Omega }}_{6,8}=N_{3}D+B^{*}{N}_5^{*}$, ${\mathsf{\Omega }}_{6,9}=N_{3}E+B^{*}{N}_6^{*}$, ${\mathsf{\Omega }}_{7,7}=-R_2+N_{4}C+C^{*}{N}_4^{*}$, ${\mathsf{\Omega }}_{7,8}=N_{4}D+C^{*}{N}_5^{*}$, ${\mathsf{\Omega }}_{7,9}=N_{4}E+C^{*}{N}_6^{*}$, ${\mathsf{\Omega }}_{8,8}=N_{5}D+D^{*}{N}_5^{*}$, ${\mathsf{\Omega }}_{8,9}=N_{5}E+D^{*}{N}_6^{*}$, ${\mathsf{\Omega }}_{9,9}=-{\alpha }_{3}P+N_{6}E+E^{*}{N}_6^{*}$,

${\mathsf{\Phi }}_{1,1}=L^T{R}_{3}L-{\alpha }_{4}P$, ${\mathsf{\Phi }}_{1,3}=-N_8^{*}$, ${\mathsf{\Phi }}_{2,2}=-N_7-N_7^{*}$, ${\mathsf{\Phi }}_{2,3}=-N_{8}A$, ${\mathsf{\Phi }}_{2,6}=N_{7}B-N_9^{*}$, ${\mathsf{\Phi }}_{2,7}=N_{7}C-N_{10}^{*}$, ${\mathsf{\Phi }}_{2,8}=N_{7}D-N_{11}^{*}$, ${\mathsf{\Phi }}_{2,9}=N_{7}E-N_{12}^{*}$, ${\mathsf{\Phi }}_{3,3}=A^{*}PA-{\alpha }_{51}P-N_{8}A-A^{*}{N}_8^{*}$, ${\mathsf{\Phi }}_{3,6}=-A^{*}PB+N_{8}B-A^{*}{N}_9^{*}$, ${\mathsf{\Phi }}_{3,7}=-A^{*}PC+N_{8}C-A^{*}{N}_{10}^{*}$, ${\mathsf{\Phi }}_{3,8}=-A^{*}PD+N_{8}D-A^{*}{N}_{11}^{*}$, ${\mathsf{\Phi }}_{3,9}=-A^{*}PE+N_{8}E-A^{*}{N}_{12}^{*}$, ${\mathsf{\Phi }}_{4,4}=L^T{R}_{4}L-{\alpha }_{52}P$, ${\mathsf{\Phi }}_{5,5}=-{\alpha }_{53}P$, ${\mathsf{\Phi }}_{6,6}=B^{*}PB-R_3+N_{9}B+B^{*}{N}_9^{*}$, ${\mathsf{\Phi }}_{6,7}=B^{*}PC+N_{9}C+B^{*}{N}_{10}^{*}$, ${\mathsf{\Phi }}_{6,8}=B^{*}PD+N_{9}D+B^{*}{N}_{11}^{*}$, ${\mathsf{\Phi }}_{6,9}=B^{*}PE+N_{9}E+B^{*}{N}_{12}^{*}$, ${\mathsf{\Phi }}_{7,7}=C^{*}PC-R_4+N_{10}C+C^{*}{N}_{10}^{*}$, ${\mathsf{\Phi }}_{7,8}=C^{*}PD+N_{10}D+C^{*}{N}_{12}^{*}$, ${\mathsf{\Phi }}_{7,9}=C^{*}PE+N_{10}E+C^{*}{N}_{12}^{*}$, ${\mathsf{\Phi }}_{8,8}=D^{*}PD+N_{11}D+D^{*}{N}_{11}^{*}$, ${\mathsf{\Phi }}_{8,9}=D^{*}PE+N_{11}E+D^{*}{N}_{12}^{*}$, ${\mathsf{\Phi }}_{9,9}=E^{*}PE-{\alpha }_{6}P+N_{12}E+E^{*}{N}_{12}^{*}$,

in which $P\in {\mathbb{H}}^N$ is a positive definite (PD) matrix, $R_1,\dots ,R_4\in {\mathbb{R}}^{N\times N}$ are diagonal PD matrices, $N_1,\dots ,N_{12}\in {\mathbb{H}}^{N\times N}$ are any matrices, and there exist positive numbers ${\alpha }_1$, ${\alpha }_2={\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23}$, ${\alpha }_3$, ${\alpha }_4$, ${\alpha }_5={\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53}$, ${\alpha }_6$, which satisfy $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and

$${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}>0,$$

and Assumption 1 is also true, then the EP of NN (2) is exponentially stable.

Proof. 

At the beginning, we put forth the following Lyapunov-like function:

$$V\left(t\right)={\mathfrak{h}}^{*}\left(t\right)P\mathfrak{h}\left(t\right).$$

By considering Lemma 1, for the positive half trajectory of NN (6), V has its $\Delta$-derivative given by the subsequent substantiation:

$$\begin{array}{c}{V}^{\Delta }\left(t\right)\le {\mathfrak{h}}^{*}\left(t\right)P{\mathfrak{h}}^{\Delta }\left(t\right)+{\mathfrak{h}}^{\Delta *}\left(t\right)P\mathfrak{h}\left(t\right)+\widehat{\mu }{\mathfrak{h}}^{\Delta *}\left(t\right)P{\mathfrak{h}}^{\Delta }\left(t\right)\hfill \\ ={\mathfrak{h}}^{*}\left(t\right)P\left(-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right)\hfill \\ +{\left(-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right)}^{*}P\mathfrak{h}\left(t\right)\hfill \\ +\widehat{\mu }{\mathfrak{h}}^{\Delta *}\left(t\right)P{\mathfrak{h}}^{\Delta }\left(t\right).\hfill \end{array}$$

(9)

However, Assumption 1 assures us that the diagonal PD matrices $R_1,R_2\in {\mathbb{R}}^{N\times N}$ exist, so that $\forall t\in {[0,+\infty )}_{\mathbb{T}}$:

$$0\le {\mathfrak{h}}^{*}\left(t\right)L^T{R}_{1}L\mathfrak{h}\left(t\right)-\tilde{f}{\left(\mathfrak{h}\left(t\right)\right)}^{*}{R}_1\tilde{f}\left(\mathfrak{h}\left(t\right)\right),$$

(10)

$$0\le {\mathfrak{h}}^{*}(t-\gamma \left(t\right))L^T{R}_{2}L\mathfrak{h}(t-\gamma \left(t\right))-\tilde{f}{\left(\mathfrak{h}(t-\gamma \left(t\right))\right)}^{*}{R}_2\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right).$$

(11)

Moreover, for any matrices $N_1,\dots ,N_6\in {\mathbb{H}}^{N\times N}$, the next identity is true:

$$\begin{array}{c}\left({\mathfrak{h}}^{\Delta *}\left(t\right)N_1+{\mathfrak{h}}^{*}(t-\delta )N_2+\tilde{f}{\left(\mathfrak{h}\left(t\right)\right)}^{*}{N}_3+\tilde{f}{\left(\mathfrak{h}(t-\gamma \left(t\right))\right)}^{*}{N}_4+{\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s\right)}^{*}{N}_5+{\mathfrak{h}}^{\Delta *}(t-\theta )N_6\right)\\ \\ \times \left(-{\mathfrak{h}}^{\Delta }\left(t\right)-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right)=0.\end{array}$$

(12)

Now, in Lemma 2, we take, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$:

$$u\left(t\right):=V\left(t\right)={\mathfrak{h}}^{*}\left(t\right)P\mathfrak{h}\left(t\right),$$

$$v\left(t\right):={\mathfrak{h}}^{\Delta *}\left(t\right)P{\mathfrak{h}}^{\Delta }\left(t\right),$$

and, using Relations (9)–(12), we obtain

$$\begin{array}{ccc}\hfill u^{\Delta }\left(t\right)& \le & -{\alpha }_{1}u\left(t\right)+{\alpha }_{21}u(t-\delta )+{\alpha }_{22}u(t-\gamma \left(t\right))+{\alpha }_{23}u(t-\eta )+{\alpha }_{3}v(t-\theta )+{\xi }^{*}\left(t\right)\mathsf{\Omega }\xi \left(t\right)\hfill \\ & \le & -{\alpha }_{1}u\left(t\right)+({\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23})\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),\hfill \end{array}$$

in which Hypothesis (8) was used for the last inequality, and

$$\begin{array}{ccc}\hfill \xi \left(t\right)& =& \left[\begin{array}{ccccccc}{\mathfrak{h}}^{*}\left(t\right)& {\mathfrak{h}}^{\Delta *}\left(t\right)& {\mathfrak{h}}^{*}(t-\delta )& {\mathfrak{h}}^{*}(t-\gamma \left(t\right))& {\mathfrak{h}}^{*}(t-\eta )& \tilde{f}{\left(\mathfrak{h}\left(t\right)\right)}^{*}& \tilde{f}{\left(\mathfrak{h}(t-\gamma \left(t\right))\right)}^{*}\end{array}\right.\hfill \\ & & {\left.\begin{array}{cc}{\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)ds\right)}^{*}& {\mathfrak{h}}^{\Delta *}(t-\theta )\end{array}\right]}^{*}.\hfill \end{array}$$

This proves the validity of the first inequality from Lemma 2.

Going further, we have

$$\begin{array}{c}{\mathfrak{h}}^{\Delta *}\left(t\right)P{\mathfrak{h}}^{\Delta }\left(t\right)={\left(-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right)}^{*}P\hfill \\ \times \left(-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right).\hfill \end{array}$$

(13)

Similarly as above, we have, from Assumption 1, that there exist diagonal PD matrices $R_3,R_4\in {\mathbb{R}}^{N\times N}$ which satisfy, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$:

$$0\le {\mathfrak{h}}^{*}\left(t\right)L^T{R}_{3}L\mathfrak{h}\left(t\right)-\tilde{f}{\left(\mathfrak{h}\left(t\right)\right)}^{*}{R}_3\tilde{f}\left(\mathfrak{h}\left(t\right)\right),$$

(14)

$$0\le {\mathfrak{h}}^{*}(t-\gamma \left(t\right))L^T{R}_{4}L\mathfrak{h}(t-\gamma \left(t\right))-\tilde{f}{\left(\mathfrak{h}(t-\gamma \left(t\right))\right)}^{*}{R}_3\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right),$$

(15)

and any matrices $N_7,\dots ,N_{12}\in {\mathbb{H}}^{N\times N}$, so that

$$\begin{array}{c}\left({\mathfrak{h}}^{\Delta *}\left(t\right)N_7+{\mathfrak{h}}^{*}(t-\delta )N_8+\tilde{f}{\left(\mathfrak{h}\left(t\right)\right)}^{*}{N}_9+\tilde{f}{\left(\mathfrak{h}(t-\gamma \left(t\right))\right)}^{*}{N}_{10}+{\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s\right)}^{*}{N}_{11}+{\mathfrak{h}}^{\Delta *}(t-\theta )N_{12}\right)\\ \\ \times \left(-{\mathfrak{h}}^{\Delta }\left(t\right)-A\mathfrak{h}(t-\delta )+B\tilde{f}\left(\mathfrak{h}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{h}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{h}\left(s\right)\right)\Delta s+E{\mathfrak{h}}^{\Delta }(t-\theta )\right)=0.\end{array}$$

(16)

Relations (13)–(16) allow us to write

$$\begin{array}{ccc}\hfill v\left(t\right)& \le & {\alpha }_{4}u\left(t\right)+{\alpha }_{51}u(t-\delta )+{\alpha }_{52}u(t-\gamma \left(t\right))+{\alpha }_{53}u(t-\eta )+{\alpha }_{6}v(t-\theta )+{\xi }^{*}\left(t\right)\mathsf{\Phi }\xi \left(t\right)\hfill \\ & \le & {\alpha }_{4}u\left(t\right)+({\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53})\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),\hfill \end{array}$$

in which, again, Hypothesis (8) was used for the last inequality, which proves the validity of the second inequality in Lemma 2. So, applying Lemma 2, we obtain

$$\begin{array}{ccc}\hfill {\lambda }_{\min }{\left(P\right)||\mathfrak{h}\left(t\right)||}_2^2& \le & {\mathfrak{h}}^{*}\left(t\right)P\mathfrak{h}\left(t\right)\hfill \\ & \le & \underset{s\in {[-\pi ,0]}_{\mathbb{T}}}{\sup }u\left(s\right)e_{\ominus \lambda }(t,0),\hfill \end{array}$$

or, equivalently,

$${||\mathfrak{h}\left(t\right)||}_2\le \sqrt{{\displaystyle \frac{{\sup }_{s\in {[-\pi ,0]}_{\mathbb{T}}}u\left(s\right)}{{\lambda }_{\min }\left(P\right)}}}{\left(e_{\ominus \lambda }(t,0)\right)}^{{\displaystyle \frac{1}{2}}},$$

which allows us to infer the exponential stability of the EP of NN (2), precisely what we needed to prove. □

Remark 1.

The discussed model only takes into account time-varying delays, without taking into account robustness to variations or time-varying graininess, which may possibly occur in hybrid DT-CT scenarios. While we acknowledge the possibility that these may occur, we leave them as a potential future work direction, in order to not further complicate the obtained sufficient conditions.

Remark 2.

Theorem 1 gave sufficient conditions for the exponential stability of the EP of the general QVNN model (2) with leakage, time-varying, distributed, and neutral delays, defined on time scales. The results of the theorem are not directly comparable to other results in the literature, as such a general model has not yet been discussed to the best of our knowledge. However, the model can be particularized for DT or CT NNs, or hybrids of them, but also for real-valued or complex-valued NNs, which also are not present in the available literature in such a general form.

For the subsequent theorem, we need to assume that $\delta =0$, i.e., System (2) has no leakage delay:

$${\mathfrak{h}}_i^{\Delta }\left(t\right)=-a_i{\mathfrak{h}}_i\left(t\right)+\sum _{j=1}^N{b}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)+\sum _{j=1}^N{c}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{h}}_i^{\Delta }(t-\theta ),$$

(17)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$.

Theorem 2.

The following inequality is true, provided that numbers ${\rho }_i>0$, $0\le i\le N$ exist:

$${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}>0,$$

and $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, where

${\alpha }_1={min}_{1\le i\le N}\left\{a_i-{\sum }_{j=1}^N|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right\}$, ${\alpha }_2={\max }_{1\le i\le N}\left\{{\sum }_{j=1}^N|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i+{\sum }_{j=1}^N|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right\}$,

${\alpha }_3={\max }_{1\le i\le N}\left\{|e_i|\right\}$, ${\alpha }_4={\max }_{1\le i\le N}\left\{a_i+{\sum }_{j=1}^N|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right\}$,

${\alpha }_5={\max }_{1\le i\le N}\left\{{\sum }_{j=1}^N|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i+{\sum }_{j=1}^N|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right\}$, ${\alpha }_6={\max }_{1\le i\le N}\left\{|e_i|\right\}$,

and also when Assumption 1 is satisfied, then the EP of NN (2) is exponentially stable.

Proof. 

Initially, the subsequent function of Lyapunov type is put forward:

$$V\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{h}}_i\left(t\right)|.$$

For the positive half trajectory of NN (6), the $\Delta$-derivative of V has the explicitation shown below, obtained by also employing Lemma 3:

$$\begin{array}{c}{V}^{\Delta }\left(t\right)\le -{\displaystyle \sum _{i=1}^N}{a}_i{\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ij}|{\rho }_i{\int }_{t-\eta }^t|{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)|\Delta s+{\displaystyle \sum _{i=1}^N}|e_i|{\rho }_i|{\mathfrak{h}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le -{\displaystyle \sum _{i=1}^N}{a}_i{\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ji}|{\rho }_j{l}_i|{\mathfrak{h}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ji}|{\rho }_j{l}_i|{\mathfrak{h}}_i(t-\gamma \left(t\right))|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ji}|{\rho }_j\eta l_i{\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{h}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}|e_i|{\rho }_i|{\mathfrak{h}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le -{\displaystyle \sum _{i=1}^N}\left(a_i-{\displaystyle \sum _{j=1}^N}|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}\left({\displaystyle \sum _{j=1}^N}|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\sup }_{s\in {[t-\gamma ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}\left({\displaystyle \sum _{j=1}^N}|d_{ij}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right){\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}|e_i|{\sup }_{s\in {[t-\theta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i^{\Delta }\left(s\right)|.\hfill \end{array}$$

(18)

Next, in Lemma 2, we consider

$$u\left(t\right)=V\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{h}}_i\left(t\right)|,$$

$$v\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{h}}_i^{\Delta }\left(t\right)|.$$

Now, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, and from (18), we have

$$u^{\Delta }\left(t\right)\le -{\alpha }_{1}u\left(t\right)+{\alpha }_2\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

where ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ are the ones provided in the statement of the theorem. This proves the validity of the first inequality from Lemma 2.

Going further, we have

$$\begin{array}{c}{\displaystyle \sum _{i=1}^N}{\rho }_i|{\mathfrak{h}}_i^{\Delta }\left(t\right)|\le {\displaystyle \sum _{i=1}^N}{\rho }_i\left|-a_i{\mathfrak{h}}_i\left(t\right)+{\displaystyle \sum _{j=1}^N}{b}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^N}{c}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)\right.\hfill \\ \hfill \\ \left.+{\displaystyle \sum _{j=1}^N}{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{h}}_i^{\Delta }(t-\theta )\right|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}{a}_i{\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ij}|{\rho }_i{\int }_{t-\eta }^t|{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)|\Delta s+{\displaystyle \sum _{i=1}^N}|e_i|{\rho }_i|{\mathfrak{h}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}{a}_i{\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ji}|{\rho }_j{l}_i|{\mathfrak{h}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ji}|{\rho }_j{l}_i|{\mathfrak{h}}_i(t-\gamma \left(t\right))|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ji}|{\rho }_j\eta l_i{\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{h}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}|e_i|{\rho }_i|{\mathfrak{h}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}\left(a_i+{\displaystyle \sum _{j=1}^N}|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\rho }_i|{\mathfrak{h}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}\left({\displaystyle \sum _{j=1}^N}|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\sup }_{s\in {[t-\gamma ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}\left({\displaystyle \sum _{j=1}^N}|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right){\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}|e_i|{\sup }_{s\in {[t-\theta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{h}}_i^{\Delta }\left(s\right)|.\hfill \end{array}$$

(19)

Relation (19) gives

$$v\left(t\right)\le {\alpha }_{4}u\left(t\right)+{\alpha }_5\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, where ${\alpha }_4$, ${\alpha }_5$, ${\alpha }_6$ are the ones provided in the statement of the theorem, which proves the validity of the second inequality in Lemma 2.

This allows us to apply Lemma 2, which gives

$$\begin{array}{ccc}\hfill \underset{1\le i\le N}{min}\left\{{\rho }_i\right\}||\mathfrak{h}\left(t\right){||}_1& \le & \sum _{i=1}^N{\rho }_i|{\mathfrak{h}}_i\left(t\right)|\hfill \\ & \le & \underset{s\in {[-\pi ,0]}_{\mathbb{T}}}{\sup }u\left(s\right)e_{\ominus \lambda }(t,0),\hfill \end{array}$$

which is equivalent to

$${||\mathfrak{h}\left(t\right)||}_1\le {\displaystyle \frac{{\sup }_{s\in {[-\pi ,0]}_{\mathbb{T}}}u\left(s\right)}{{min}_{1\le i\le N}\left\{{\rho }_i\right\}}}{e}_{\ominus \lambda }(t,0),$$

which allows us to infer the exponential stability of the EP of NN (2), precisely what we had to prove. □

Remark 3.

The purpose of Theorem 2 was to provide sufficient conditions given as algebraic inequalities for the exponential stability of the EP of the very general QVNN model (2) having four types of delays and being defined on time scales, which has not yet been discussed in the literature, to our knowledge. Because of this, the obtained conditions are not comparable to those of other papers, as the models put forward are different. Nonetheless, the results of this theorem can be particularized for models with fewer types of delays, with real-valued or complex-valued parameters, and defined in DT or CT, or any combination of the two, for which no available results exist, also.

The subsequent state-feedback-type controller can be designed so as to obtain synchronization between drive NN (2) and response NN (3):

$$u\left(t\right)=K_1\mathfrak{d}\left(t\right)+K_2\mathfrak{d}(t-\delta )+K_3\mathfrak{d}(t-\gamma \left(t\right))+K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s+K_5{\mathfrak{d}}^{\Delta }(t-\theta ),$$

(20)

in which the real positive diagonal matrices $K_1,\dots ,K_5\in {\mathbb{R}}^{N\times N}$ are control gain matrices. By incorporating this control scheme, System (7) has the following form:

$$\begin{array}{c}{\mathfrak{d}}^{\Delta }\left(t\right)=-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\hfill \\ \hfill \\ +B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta ).\hfill \end{array}$$

(21)

Theorem 3.

If the following LMIs hold

$$\mathsf{\Omega }<0,\mathsf{\Phi }<0,$$

(22)

where

${\mathsf{\Omega }}_{1,1}=-P{K}_1-K_{1}P+L^T{R}_{1}L-N_2{K}_1-K_1{N}_2^{*}+{\alpha }_{1}P$, ${\mathsf{\Omega }}_{1,2}=-K_1{N}_1^{*}$, ${\mathsf{\Omega }}_{1,3}=-P(A+K_2)-N_2(A+K_2)-K_1{N}_3^{*}$, ${\mathsf{\Omega }}_{1,4}=-P{K}_3-N_2{K}_3-K_1{N}_4^{*}$, ${\mathsf{\Omega }}_{1,6}=PB+N_{2}B+K_1{N}_6^{*}$, ${\mathsf{\Omega }}_{1,7}=PC+N_{2}C+K_1{N}_7^{*}$, ${\mathsf{\Omega }}_{1,8}=-P{K}_4-N_2{K}_4-K_1{N}_5^{*}$, ${\mathsf{\Omega }}_{1,9}=PD+N_{2}D+K_1{N}_8^{*}$, ${\mathsf{\Omega }}_{1,10}=P(E-K_5)+N_2(E-K_5)+K_1{N}_9^{*}$, ${\mathsf{\Omega }}_{2,2}=\widehat{\mu }P-N_1-N_1^{*}$, ${\mathsf{\Omega }}_{2,3}=-N_1(A+K_2)-N_3^{*}$, ${\mathsf{\Omega }}_{2,4}=-N_1{K}_3-N_4^{*}$, ${\mathsf{\Omega }}_{2,6}=N_{1}B+N_6^{*}$, ${\mathsf{\Omega }}_{2,7}=N_{1}C+N_7^{*}$, ${\mathsf{\Omega }}_{2,8}=-N_1{K}_4-N_5^{*}$, ${\mathsf{\Omega }}_{2,9}=N_{1}D+N_8^{*}$, ${\mathsf{\Omega }}_{2,10}=N_1(E-K_5)+N_9^{*}$, ${\mathsf{\Omega }}_{3,3}=-N_3(A+K_2)-(A+K_2)N_3^{*}-{\alpha }_{21}P$, ${\mathsf{\Omega }}_{3,4}=-N_3{K}_3-(A+K_2)N_4^{*}$, ${\mathsf{\Omega }}_{3,6}=N_{3}B+(A+K_2)N_6^{*}$, ${\mathsf{\Omega }}_{3,7}=N_{3}C+(A+K_2)N_7^{*}$, ${\mathsf{\Omega }}_{3,8}=-N_3{K}_4-(A+K_2)N_5^{*}$, ${\mathsf{\Omega }}_{3,9}=N_{3}D+(A+K_2)N_8^{*}$, ${\mathsf{\Omega }}_{3,10}=N_3(E-K_5)+(A+K_2)N_9^{*}$, ${\mathsf{\Omega }}_{4,4}=L^T{R}_{2}L-N_4{K}_3-K_3{N}_4^{*}-{\alpha }_{22}P$, ${\mathsf{\Omega }}_{4,6}=N_{4}B+K_3{N}_6^{*}$, ${\mathsf{\Omega }}_{4,7}=N_{4}C+K_3{N}_7^{*}$, ${\mathsf{\Omega }}_{4,8}=-N_4{K}_4-K_3{N}_5^{*}$, ${\mathsf{\Omega }}_{4,9}=N_{4}D+K_3{N}_8^{*}$, ${\mathsf{\Omega }}_{4,10}=N_4(E-K_5)+K_3{N}_9^{*}$, ${\mathsf{\Omega }}_{5,5}=-{\alpha }_{23}P$, ${\mathsf{\Omega }}_{6,6}=-R_1-N_{6}B-B^{*}{N}_6^{*}$, ${\mathsf{\Omega }}_{6,7}=-N_{6}C-B^{*}{N}_7^{*}$, ${\mathsf{\Omega }}_{6,8}=B^{*}{N}_5^{*}+N_6{K}_4$, ${\mathsf{\Omega }}_{6,9}=-N_{6}D-B^{*}{N}_8^{*}$, ${\mathsf{\Omega }}_{6,10}=-N_6(E-K_5)-B^{*}{N}_9^{*}$, ${\mathsf{\Omega }}_{7,7}=-R_2-N_{7}C-C^{*}{N}_7^{*}$, ${\mathsf{\Omega }}_{7,8}=C^{*}{N}_5^{*}+N_7{K}_4$, ${\mathsf{\Omega }}_{7,9}=-N_{7}D-C^{*}{N}_8^{*}$, ${\mathsf{\Omega }}_{7,10}=-N_7(E-K_5)-C^{*}{N}_9^{*}$, ${\mathsf{\Omega }}_{8,8}=-N_5{K}_4-K_4{N}_5^{*}$, ${\mathsf{\Omega }}_{8,9}=N_{5}D+K_4{N}_8^{*}$, ${\mathsf{\Omega }}_{8,10}=N_5(E-K_5)+K_4{N}_9^{*}$, ${\mathsf{\Omega }}_{9,9}=-N_{8}D-D^{*}{N}_8^{*}$, ${\mathsf{\Omega }}_{9,10}=-N_8(E-K_5)-D^{*}{N}_9^{*}$, ${\mathsf{\Omega }}_{10,10}=-N_9(E-K_5)-{(E-K_5)}^{*}{N}_9^{*}-{\alpha }_{3}P$,

${\mathsf{\Phi }}_{1,1}=K_{1}P{K}_1+L^T{R}_{3}L-N_{11}{K}_1-K_1{N}_{11}^{*}+{\alpha }_{4}P$, ${\mathsf{\Phi }}_{1,2}=-K_1{N}_{10}^{*}$, ${\mathsf{\Phi }}_{1,3}=K_{1}P(A+K_2)-N_{11}(A+K_2)-K_1{N}_{12}^{*}$, ${\mathsf{\Phi }}_{1,4}=K_{1}P{K}_3-N_{11}{K}_3-K_1{N}_{13}^{*}$, ${\mathsf{\Phi }}_{1,6}=-K_{1}PB+N_{11}B+K_1{N}_{15}^{*}$, ${\mathsf{\Phi }}_{1,7}=-K_{1}PC+N_{11}C+K_1{N}_{16}^{*}$, ${\mathsf{\Phi }}_{1,8}=K_{1}P{K}_4-N_{11}{K}_4-K_1{N}_{14}^{*}$, ${\mathsf{\Phi }}_{1,9}=-K_{1}PD+N_{11}D+K_1{N}_{17}^{*}$, ${\mathsf{\Phi }}_{1,10}=-K_{1}P(E-K_5)+N_{11}(E-K_5)+K_1{N}_{18}^{*}$, ${\mathsf{\Phi }}_{2,2}=-N_{10}-N_{10}^{*}$, ${\mathsf{\Phi }}_{2,3}=-N_{10}(A+K_2)-N_{12}^{*}$, ${\mathsf{\Phi }}_{2,4}=-N_{10}{K}_3-N_{13}^{*}$, ${\mathsf{\Phi }}_{2,6}=N_{10}B+N_{15}^{*}$, ${\mathsf{\Phi }}_{2,7}=N_{10}C+N_{16}^{*}$, ${\mathsf{\Phi }}_{2,8}=-N_{10}{K}_4-N_{14}^{*}$, ${\mathsf{\Phi }}_{2,9}=N_{10}D+N_{17}^{*}$, ${\mathsf{\Phi }}_{2,10}=N_{10}(E-K_5)+N_{18}^{*}$, ${\mathsf{\Phi }}_{3,3}=(A+K_2)P(A+K_2)-N_{12}(A+K_2)-(A+K_2)N_{12}^{*}-{\alpha }_{51}P$, ${\mathsf{\Phi }}_{3,4}=(A+K_2)P{K}_3-N_{12}{K}_3-(A+K_2)N_{13}^{*}$, ${\mathsf{\Phi }}_{3,6}=-(A+K_2)PB+N_{12}B+(A+K_2)N_{15}^{*}$, ${\mathsf{\Phi }}_{3,7}=-(A+K_2)PC+N_{12}C+(A+K_2)N_{16}^{*}$, ${\mathsf{\Phi }}_{3,8}=(A+K_2)P{K}_4-N_{12}{K}_4-(A+K_2)N_{14}^{*}$, ${\mathsf{\Phi }}_{3,9}=-(A+K_2)PD+N_{12}D+(A+K_2)N_{17}^{*}$, ${\mathsf{\Phi }}_{3,10}=-(A+K_2)P(E-K_5)+N_{12}(E-K_5)+(A+K_2)N_{18}^{*}$, ${\mathsf{\Phi }}_{4,4}=K_{3}P{K}_3+L^T{R}_{4}L-N_{13}{K}_3-K_3{N}_{13}^{*}-{\alpha }_{52}P$, ${\mathsf{\Phi }}_{4,6}=-K_{3}PB+N_{13}B+K_3{N}_{15}^{*}$, ${\mathsf{\Phi }}_{4,7}=-K_{3}PC+N_{13}C+K_3{N}_{16}^{*}$, ${\mathsf{\Phi }}_{4,8}=K_{3}P{K}_4-N_{13}{K}_4-K_3{N}_{14}^{*}$, ${\mathsf{\Phi }}_{4,9}=-K_{3}PD+N_{13}D+K_3{N}_{17}^{*}$, ${\mathsf{\Phi }}_{4,10}=-K_{3}P(E-K_5)+N_{13}(E-K_5)+K_3{N}_{18}^{*}$, ${\mathsf{\Phi }}_{5,5}=-{\alpha }_{53}P$, ${\mathsf{\Phi }}_{6,6}=B^{*}PB-R_3-N_{15}B-B^{*}{N}_{15}^{*}$, ${\mathsf{\Phi }}_{6,7}=B^{*}PC-N_{15}C-B^{*}{N}_{16}^{*}$, ${\mathsf{\Phi }}_{6,8}=-B^{*}P{K}_4+B^{*}{N}_{14}^{*}+N_{15}{K}_4$, ${\mathsf{\Phi }}_{6,9}=B^{*}PD-N_{15}D-B^{*}{N}_{17}^{*}$, ${\mathsf{\Phi }}_{6,10}=B^{*}P(E-K_5)-N_{15}(E-K_5)-B^{*}{N}_{18}^{*}$, ${\mathsf{\Phi }}_{7,7}=C^{*}PC-R_4-N_{16}C-C^{*}{N}_{16}^{*}$, ${\mathsf{\Phi }}_{7,8}=-C^{*}P{K}_4+C^{*}{N}_{14}^{*}+N_{16}{K}_4$, ${\mathsf{\Phi }}_{7,9}=C^{*}PD-N_{16}D-C^{*}{N}_{17}^{*}$, ${\mathsf{\Phi }}_{7,10}=C^{*}P(E-K_5)-N_{16}(E-K_5)-C^{*}{N}_{18}^{*}$, ${\mathsf{\Phi }}_{8,8}=K_{4}P{K}_4-N_{14}{K}_4-K_4{N}_{14}^{*}$, ${\mathsf{\Phi }}_{8,9}=-K_{4}PD+N_{14}D+K_4{N}_{17}^{*}$, ${\mathsf{\Phi }}_{8,10}=-K_{4}P(E-K_5)+N_{14}(E-K_5)+K_4{N}_{18}^{*}$, ${\mathsf{\Phi }}_{9,9}=D^{*}PD-N_{17}D-D^{*}{N}_{17}^{*}$, ${\mathsf{\Phi }}_{9,10}=D^{*}P(E-K_5)-N_{17}(E-K_5)-D^{*}{N}_{18}^{*}$, ${\mathsf{\Phi }}_{10,10}={(E-K_5)}^{*}P(E-K_5)-N_{18}(E-K_5)-{(E-K_5)}^{*}{N}_{18}^{*}-{\alpha }_{6}P$,

in which $P\in {\mathbb{H}}^N$ is a PD matrix, $R_1,\dots ,R_4\in {\mathbb{R}}^{N\times N}$ are diagonal PD matrices, $N_1,\dots ,N_{18}\in {\mathbb{H}}^{N\times N}$ are any matrices, there exist positive numbers ${\alpha }_1$, ${\alpha }_2={\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23}$, ${\alpha }_3$, ${\alpha }_4$, ${\alpha }_5={\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53}$, ${\alpha }_6$, which satisfy $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and

$${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}>0,$$

and Assumption 1 is also true, then, under state feedback controller (20), exponential synchronization is achieved of the drive NN (2) and response NN (3).

Proof. 

Initially, we put forward the following Lyapunov-like function:

$$V\left(t\right)={\mathfrak{d}}^{*}\left(t\right)P\mathfrak{d}\left(t\right).$$

By considering Lemma 1, for the positive half trajectory of NN (21), V has its $\Delta$-derivative given by the following substantiation:

$$\begin{array}{c}{V}^{\Delta }\left(t\right)\le {\mathfrak{d}}^{*}\left(t\right)P{\mathfrak{d}}^{\Delta }\left(t\right)+{\mathfrak{d}}^{\Delta *}\left(t\right)P\mathfrak{d}\left(t\right)+\widehat{\mu }{\mathfrak{d}}^{\Delta *}\left(t\right)P{\mathfrak{d}}^{\Delta }\left(t\right)\hfill \\ \hfill \\ ={\mathfrak{d}}^{*}\left(t\right)P\left(-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ \left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right)\hfill \\ \hfill \\ +\left(-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ {\left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right)}^{*}P\mathfrak{d}\left(t\right)\hfill \\ \hfill \\ +\widehat{\mu }{\mathfrak{d}}^{\Delta *}\left(t\right)P{\mathfrak{d}}^{\Delta }\left(t\right).\hfill \end{array}$$

(23)

However, Assumption 1 assures us that the diagonal PD matrices $R_1,R_2\in {\mathbb{R}}^{N\times N}$ exist, so that $\forall t\in {[0,+\infty )}_{\mathbb{T}}$:

$$0\le {\mathfrak{d}}^{*}\left(t\right)L^T{R}_{1}L\mathfrak{d}\left(t\right)-\tilde{f}{\left(\mathfrak{d}\left(t\right)\right)}^{*}{R}_1\tilde{f}\left(\mathfrak{d}\left(t\right)\right),$$

(24)

$$0\le {\mathfrak{d}}^{*}(t-\gamma \left(t\right))L^T{R}_{2}L\mathfrak{d}(t-\gamma \left(t\right))-\tilde{f}{\left(\mathfrak{d}(t-\gamma \left(t\right))\right)}^{*}{R}_2\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right).$$

(25)

Moreover, for any matrices $N_1,\dots ,N_9\in {\mathbb{H}}^{N\times N}$, the following identity holds:

$$\begin{array}{c}\left[{\mathfrak{d}}^{\Delta *}\left(t\right)N_1+{\mathfrak{d}}^{*}\left(t\right)N_2+{\mathfrak{d}}^{*}(t-\delta )N_3+{\mathfrak{d}}^{*}(t-\gamma \left(t\right))N_4+{\left({\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right)}^{*}{N}_5\right.\hfill \\ \hfill \\ \left.-\tilde{f}{\left(\mathfrak{d}\left(t\right)\right)}^{*}{N}_6-\tilde{f}{\left(\mathfrak{d}(t-\gamma \left(t\right))\right)}^{*}{N}_7-{\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s\right)}^{*}{N}_8-{\mathfrak{d}}^{\Delta *}(t-\theta )N_9\right]\hfill \\ \hfill \\ \times \left[-{\mathfrak{d}}^{\Delta }\left(t\right)-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ \left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right]=0.\hfill \end{array}$$

(26)

Now, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, we take, in Lemma 2:

$$u\left(t\right):=V\left(t\right)={\mathfrak{d}}^{*}\left(t\right)P\mathfrak{d}\left(t\right),$$

$$v\left(t\right):={\mathfrak{d}}^{\Delta *}\left(t\right)P{\mathfrak{d}}^{\Delta }\left(t\right),$$

and, using Relations (23)–(26), we have

$$\begin{array}{ccc}\hfill u^{\Delta }\left(t\right)& \le & -{\alpha }_{1}u\left(t\right)+{\alpha }_{21}u(t-\delta )+{\alpha }_{22}u(t-\gamma \left(t\right))+{\alpha }_{23}u(t-\eta )+{\alpha }_{3}v(t-\theta )+{\xi }^{*}\left(t\right)\mathsf{\Omega }\xi \left(t\right)\hfill \\ & \le & -{\alpha }_{1}u\left(t\right)+({\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23})\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),\hfill \end{array}$$

in which Hypothesis (22) was used for the last inequality, and

$$\begin{array}{ccc}\hfill \xi \left(t\right)& =& \left[\begin{array}{ccccccc}{\mathfrak{d}}^{*}\left(t\right)& {\mathfrak{d}}^{\Delta *}\left(t\right)& {\mathfrak{d}}^{*}(t-\delta )& {\mathfrak{d}}^{*}(t-\gamma \left(t\right))& {\mathfrak{d}}^{*}(t-\eta )& \tilde{f}{\left(\mathfrak{d}\left(t\right)\right)}^{*}& \tilde{f}{\left(\mathfrak{d}(t-\gamma \left(t\right))\right)}^{*}\end{array}\right.\hfill \\ & & {\left.\begin{array}{ccc}{\left({\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right)}^{*}& {\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)ds\right)}^{*}& {\mathfrak{d}}^{\Delta *}(t-\theta )\end{array}\right]}^{*}.\hfill \end{array}$$

This proves the validity of the first inequality from Lemma 2.

Going further, we have

$$\begin{array}{c}{\mathfrak{d}}^{\Delta *}\left(t\right)P{\mathfrak{d}}^{\Delta }\left(t\right)=\left(-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ {\left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right)}^{*}P\hfill \\ \hfill \\ \times \left(-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ \left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right).\hfill \end{array}$$

(27)

Similarly as above, from Assumption 1, we have that diagonal PD matrices $R_3,R_4\in {\mathbb{R}}^{N\times N}$ exist, so that

$$0\le {\mathfrak{d}}^{*}\left(t\right)L^T{R}_{3}L\mathfrak{d}\left(t\right)-\tilde{f}{\left(\mathfrak{d}\left(t\right)\right)}^{*}{R}_3\tilde{f}\left(\mathfrak{d}\left(t\right)\right),$$

(28)

$$0\le {\mathfrak{d}}^{*}(t-\gamma \left(t\right))L^T{R}_{4}L\mathfrak{d}(t-\gamma \left(t\right))-\tilde{f}{\left(\mathfrak{d}(t-\gamma \left(t\right))\right)}^{*}{R}_4\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right),$$

(29)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, and, for any matrices $N_{10},\dots ,N_{18}\in {\mathbb{H}}^{N\times N}$, the following identity holds:

$$\begin{array}{c}\left[{\mathfrak{d}}^{\Delta *}\left(t\right)N_{10}+{\mathfrak{d}}^{*}\left(t\right)N_{11}+{\mathfrak{d}}^{*}(t-\delta )N_{12}+{\mathfrak{d}}^{*}(t-\gamma \left(t\right))N_{13}+{\left({\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right)}^{*}{N}_{14}\right.\hfill \\ \hfill \\ -\left.\tilde{f}{\left(\mathfrak{d}\left(t\right)\right)}^{*}{N}_{15}-\tilde{f}{\left(\mathfrak{d}(t-\gamma \left(t\right))\right)}^{*}{N}_{16}-{\left({\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s\right)}^{*}{N}_{17}-{\mathfrak{d}}^{\Delta *}(t-\theta )N_{18}\right]\hfill \\ \hfill \\ \times \left[-{\mathfrak{d}}^{\Delta }\left(t\right)-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\right.\hfill \\ \hfill \\ \left.+B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta )\right]=0.\hfill \end{array}$$

(30)

Relations (27)–(30) permit us to write

$$\begin{array}{ccc}\hfill v\left(t\right)& \le & {\alpha }_{4}u\left(t\right)+{\alpha }_{51}u(t-\delta )+{\alpha }_{52}u(t-\gamma \left(t\right))+{\alpha }_{53}u(t-\eta )+{\alpha }_{6}v(t-\theta )+{\xi }^{*}\left(t\right)\mathsf{\Phi }\xi \left(t\right)\hfill \\ & \le & {\alpha }_{4}u\left(t\right)+({\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53})\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),\hfill \end{array}$$

in which, again, Hypothesis (22) was used for the last inequality, which proves the validity of the second inequality in Lemma 2. So, applying Lemma 2, we obtain

$$\begin{array}{ccc}\hfill {\lambda }_{\min }{\left(P\right)||\mathfrak{d}\left(t\right)||}_2^2& \le & {\mathfrak{d}}^{*}\left(t\right)P\mathfrak{d}\left(t\right)\hfill \\ & \le & \underset{s\in {[-\pi ,0]}_{\mathbb{T}}}{\sup }u\left(s\right)e_{\ominus \lambda }(t,0),\hfill \end{array}$$

or, equivalently,

$${||\mathfrak{d}\left(t\right)||}_2\le \sqrt{{\displaystyle \frac{{\sup }_{s\in {[-\pi ,0]}_{\mathbb{T}}}u\left(s\right)}{{\lambda }_{\min }\left(P\right)}}}{\left(e_{\ominus \lambda }(t,0)\right)}^{{\displaystyle \frac{1}{2}}},$$

which allows us to infer the exponential synchronization, under state feedback controller (20), of drive NN (2) and response NN (3), thus ending the proof. □

Remark 4.

Theorem 3 gave sufficient conditions, expressed as LMIs, for the exponential synchronization of the drive QVNN (2) and response QVNN (3) having leakage, time-varying, distributed, and neutral delays and being defined on time scales. Because of the generality of the model, the results obtained are not directly comparable to others from the literature, as this type of model has not yet been put forward, as far as we know. However, the results of the theorem can be particularized for NN models with fewer delays, with real or complex values, and defined in DT or CT, or a mixing of the two. The corresponding models have also not yet been discussed in the literature.

In the context of our last theorem, we need to put System (21) in the following form:

$$\begin{array}{c}{\mathfrak{d}}_i^{\Delta }\left(t\right)=-k_{1i}{\mathfrak{d}}_i\left(t\right)-(a_i+k_{2i}){\mathfrak{d}}_i(t-\delta )-k_{3i}{\mathfrak{d}}_i(t-\gamma \left(t\right))-k_{4i}{\int }_{t-\eta }^t{\mathfrak{d}}_i\left(s\right)\Delta s+\sum _{j=1}^N{b}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)\hfill \\ \hfill \\ +\sum _{j=1}^N{c}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^N{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)\Delta s+(e_i-k_{5i}){\mathfrak{d}}_i^{\Delta }(t-\theta ),\hfill \end{array}$$

(31)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,\dots ,N\}$.

Theorem 4.

The following inequality is true, provided that numbers ${\rho }_i>0$, $0\le i\le N$ exist:

$${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}>0,$$

and $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, where

${\alpha }_1={min}_{1\le i\le N}\left\{k_{1i}-{\sum }_{j=1}^N|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right\}$,

${\alpha }_2={\max }_{1\le i\le N}\left\{a_i+k_{2i}+k_{3i}+{\sum }_{j=1}^N|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i+k_{4i}\eta +{\sum }_{j=1}^N|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right\}$, ${\alpha }_3={\max }_{1\le i\le N}\left\{|e_i|+k_{i5}\right\}$,

${\alpha }_4={\max }_{1\le i\le N}\left\{k_{1i}+{\sum }_{j=1}^N|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right\}$,

${\alpha }_5={\max }_{1\le i\le N}\left\{a_i+k_{2i}+k_{3i}+{\sum }_{j=1}^N|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i+k_{4i}\eta +{\sum }_{j=1}^N|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right\}$, ${\alpha }_6={\max }_{1\le i\le N}\left\{|e_i|+k_{i5}\right\}$,

and also Assumption 1 is satisfied, then, under the state feedback controller (20), drive NN (2) and response NN (3) are exponentially synchronized.

Proof. 

Initially, we put forth the subsequent function of Lyapunov type:

$$V\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{d}}_i\left(t\right)|.$$

By considering Lemma 3, for the positive half trajectory of NN (31), V has its $\Delta$-derivative explicitated as

$$\begin{array}{c}{V}^{\Delta }\left(t\right)\le -{\displaystyle \sum _{i=1}^N}{k}_{1i}{\rho }_i|{\mathfrak{d}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}(a_i+k_{2i}){\rho }_i|{\mathfrak{d}}_i(t-\delta )|+{\displaystyle \sum _{i=1}^N}{k}_{3i}{\rho }_i|{\mathfrak{d}}_i(t-\gamma \left(t\right))|+{\displaystyle \sum _{i=1}^N}{k}_{4i}{\rho }_i{\int }_{t-\eta }^t|{\mathfrak{d}}_i\left(s\right)|\Delta s\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ij}|{\rho }_i{\int }_{t-\eta }^t|{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)|\Delta s+{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\rho }_i|{\mathfrak{d}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le -{\displaystyle \sum _{i=1}^N}{k}_{1i}{\rho }_i|{\mathfrak{d}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}(a_i+k_{2i}){\rho }_i|{\mathfrak{d}}_i(t-\delta )|+{\displaystyle \sum _{i=1}^N}{k}_{3i}{\rho }_i{\mathfrak{d}}_i(t-\gamma \left(t\right))+{\displaystyle \sum _{i=1}^N}{k}_{4i}{\rho }_i\eta {\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ji}|{\rho }_j{l}_i|{\mathfrak{d}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ji}|{\rho }_j{l}_i|{\mathfrak{d}}_i(t-\gamma \left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ji}|{\rho }_j\eta l_i{\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\rho }_i|{\mathfrak{d}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le -{\displaystyle \sum _{i=1}^N}\left(k_{1i}-{\displaystyle \sum _{j=1}^N}|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\rho }_i|{\mathfrak{d}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}\left(a_i+k_{2i}\right){\sup }_{s\in [t-\delta ,t]}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}\left(k_{3i}+{\displaystyle \sum _{j=1}^N}|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\sup }_{s\in {[t-\gamma ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}\left(k_{4i}\eta +{\displaystyle \sum _{j=1}^N}|d_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right){\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\sup }_{s\in {[t-\theta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i^{\Delta }\left(s\right)|.\hfill \end{array}$$

(32)

Next, we can take in Lemma 2:

$$u\left(t\right)=V\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{d}}_i\left(t\right)|,$$

$$v\left(t\right)=\sum _{i=1}^N{\rho }_i|{\mathfrak{d}}_i^{\Delta }\left(t\right)|.$$

Now, $\forall t\in {[0,+\infty )}_{\mathbb{T}}$, from (32), we have

$$u^{\Delta }\left(t\right)\le -{\alpha }_{1}u\left(t\right)+{\alpha }_2\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_3\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

where ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are the ones provided in the statement of the theorem. This proves the validity of the first inequality from Lemma 2.

Going further, we have

$$\begin{array}{c}{\displaystyle \sum _{i=1}^N}{\rho }_i|{\mathfrak{d}}_i^{\Delta }\left(t\right)|\le {\displaystyle \sum _{i=1}^N}{\rho }_i\left|-k_{1i}{\mathfrak{d}}_i\left(t\right)-(a_i+k_{2i}){\mathfrak{d}}_i(t-\delta )-k_{3i}{\mathfrak{d}}_i(t-\gamma \left(t\right))-k_{4i}{\int }_{t-\eta }^t{\mathfrak{d}}_i\left(s\right)\Delta s+{\displaystyle \sum _{j=1}^N}{b}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)\right.\hfill \\ \hfill \\ \left.+{\displaystyle \sum _{j=1}^N}{c}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)+{\displaystyle \sum _{j=1}^N}{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)\Delta s+(e_i-k_{5i}){\mathfrak{d}}_i^{\Delta }(t-\theta )\right|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}{k}_{1i}{\rho }_i|{\mathfrak{d}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}(a_i+k_{2i}){\rho }_i|{\mathfrak{d}}_i(t-\delta )|+{\displaystyle \sum _{i=1}^N}{k}_{3i}{\rho }_i|{\mathfrak{d}}_i(t-\gamma \left(t\right))|+{\displaystyle \sum _{i=1}^N}{k}_{4i}{\rho }_i\eta {\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ij}|{\rho }_i|{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ij}|{\rho }_i{\int }_{t-\eta }^t|{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)|\Delta s+{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\rho }_i|{\mathfrak{d}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}{k}_{1i}{\rho }_i|{\mathfrak{d}}_i\left(t\right)|+{\displaystyle \sum _{i=1}^N}(a_i+k_{2i}){\rho }_i|{\mathfrak{d}}_i(t-\delta )|+{\displaystyle \sum _{i=1}^N}{k}_{3i}{\rho }_i{\mathfrak{d}}_i(t-\gamma \left(t\right))+{\displaystyle \sum _{i=1}^N}{k}_{4i}{\rho }_i\eta {\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|b_{ji}|{\rho }_j{l}_i|{\mathfrak{d}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|c_{ji}|{\rho }_j{l}_i|{\mathfrak{d}}_i(t-\gamma \left(t\right))|+{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}|d_{ji}|{\rho }_j\eta l_i{\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\rho }_i|{\mathfrak{d}}_i^{\Delta }(t-\theta )|\hfill \\ \hfill \\ \le {\displaystyle \sum _{i=1}^N}\left(k_{1i}+{\displaystyle \sum _{j=1}^N}|b_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\rho }_i|{\mathfrak{d}}_i\left(t\right))|+{\displaystyle \sum _{i=1}^N}\left(a_i+k_{2i}\right){\sup }_{s\in {[t-\delta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}\left(k_{3i}+{\displaystyle \sum _{j=1}^N}|c_{ji}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}{l}_i\right){\sup }_{s\in {[t-\gamma ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|+{\displaystyle \sum _{i=1}^N}\left(k_{4i}\eta +{\displaystyle \sum _{j=1}^N}|d_{ij}|{\displaystyle \frac{{\rho }_j}{{\rho }_i}}\eta l_i\right){\sup }_{s\in {[t-\eta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i\left(s\right)|\hfill \\ \hfill \\ +{\displaystyle \sum _{i=1}^N}(|e_i|+k_{i5}){\sup }_{s\in {[t-\theta ,t]}_{\mathbb{T}}}{\rho }_i|{\mathfrak{d}}_i^{\Delta }\left(s\right)|.\hfill \end{array}$$

(33)

Relation (33) gives

$$v\left(t\right)\le {\alpha }_{4}u\left(t\right)+{\alpha }_5\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }u\left(w\right)+{\alpha }_6\underset{w\in {[t-\pi ,t]}_{\mathbb{T}}}{\sup }v\left(w\right),$$

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, where ${\alpha }_4$, ${\alpha }_5$, ${\alpha }_6$ are the ones provided in the statement of the theorem, which proves the validity of the second inequality in Lemma 2.

This allows us to apply Lemma 2, which gives

$$\begin{array}{ccc}\hfill \underset{1\le i\le N}{min}\left\{{\rho }_i\right\}||\mathfrak{d}\left(t\right){||}_1& \le & \sum _{i=1}^N{\rho }_i|{\mathfrak{d}}_i\left(t\right)|\hfill \\ & \le & \underset{s\in {[-\pi ,0]}_{\mathbb{T}}}{\sup }u\left(s\right)e_{\ominus \lambda }(t,0),\hfill \end{array}$$

or, equivalently,

$${||\mathfrak{d}\left(t\right)||}_1\le {\displaystyle \frac{{\sup }_{s\in {[-\pi ,0]}_{\mathbb{T}}}u\left(s\right)}{{min}_{1\le i\le N}\left\{{\rho }_i\right\}}}{e}_{\ominus \lambda }(t,0),$$

which allows us to infer the exponential synchronization, under the state feedback controller (20), of the drive NN (2) and response NN (3), exactly what we needed to show. □

Remark 5.

The last theorem, Theorem 4, is concerned with putting forward sufficient conditions, expressed as algebraic inequalities, for the exponential synchronization of drive QVNN(2) and response QVNN (3) with four types of delays, defined on time scales. Such a general model has not yet been the focus of any of the literature, as far as we know, which means that our results are not directly comparable with other available ones. Nonetheless, the theorem can be particularized for models with fewer types of delays, with real-valued or complex-valued parameters, and for DT, CT, or hybrid NNs, which have also not yet been discussed in the literature.

4. Numerical Examples

Example 1.

To begin with, $\mathbb{T}=0.1\mathbb{Z}$ will be the time scale considered, and, in this case, $\widehat{\mu }=0.1$.

Let the subsequent two-neuron QVNN defined on time-scale $\mathbb{T}$ with neutral, leakage, and mixed delays be

$$h_i^{\Delta }\left(t\right)=-a_i{h}_i(t-\delta )+\sum _{j=1}^2{b}_{ij}{f}_j\left(h_j\left(t\right)\right)+\sum _{j=1}^2{c}_{ij}{f}_j\left(h_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^2{d}_{ij}{\int }_{t-\eta }^t{f}_j\left(h_j\left(s\right)\right)\Delta s+e_i{h}_i^{\Delta }(t-\theta )+I_i,$$

(34)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,2\}$.

Now, suppose that System (34) possesses an EP, designated as $\tilde{h}=({\tilde{h}}_1,{\tilde{h}}_1)\in {\mathbb{H}}^2$. By taking ${\mathfrak{h}}_i\left(t\right)=h_i\left(t\right)-\tilde{h}$, System (34) can be transformed as

$${\mathfrak{h}}_i^{\Delta }\left(t\right)=-a_i{\mathfrak{h}}_i(t-\delta )+\sum _{j=1}^2{b}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)+\sum _{j=1}^2{c}_{ij}{\tilde{f}}_j\left({\mathfrak{h}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^2{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{h}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{h}}_i^{\Delta }(t-\theta ),$$

(35)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,2\}$, in which ${\tilde{f}}_j\left({\mathfrak{h}}_j\left(t\right)\right)={\tilde{f}}_j({\mathfrak{h}}_j\left(t\right)+\tilde{h})-{\tilde{f}}_j\left(\tilde{h}\right),$$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall j\in \{1,2\}$.

The values of the parameter matrices will be the following:

$$A=\left[\begin{array}{cc}5& 0\\ 0& 6\end{array}\right],$$

$$B=0.1\left[\begin{array}{cc}-7+8i-2j+4\kappa & 3+9i-2j-2\kappa \\ -2-4i+2j-2\kappa & 4+3i+1j+4\kappa \end{array}\right],$$

$$C=0.1\left[\begin{array}{cc}-4+7i+2j+5\kappa & 8+5i+3j-5\kappa \\ 3+2i-2j+1\kappa & -5+5i+2j+4\kappa \end{array}\right],$$

$$D=0.1\left[\begin{array}{cc}2+8i+3j+9\kappa & 5+6i+8j-8\kappa \\ 3+2i-5j+2\kappa & -2-5i+7j+9\kappa \end{array}\right],$$

$$E=\left[\begin{array}{cc}0.3& 0\\ 0& 0.2\end{array}\right],$$

$$f_j\left(h\right)={\displaystyle \frac{1}{20}}\left({\displaystyle \frac{1}{1+e^{-h^R}}}+{\displaystyle \frac{1}{1+e^{-h^I}}}i+{\displaystyle \frac{1}{1+e^{-h^J}}}j+{\displaystyle \frac{1}{1+e^{-h^K}}}\kappa \right),\forall h\in \mathbb{H},\forall j\in \{1,2\},$$

which allows us to deduce that the activation functions fulfill Assumption 1, and

$$L=\left[\begin{array}{cc}0.025& 0\\ 0& 0.025\end{array}\right].$$

Also, we take $\delta =0.1$, $\gamma \left(t\right)=0.8$, $\eta =0.4$, and $\theta =0.2$; thus, $\gamma =0.8$ and $\pi =\max \{\delta ,\gamma ,\eta ,\theta \}=0.8$.

Lastly, if we take ${\alpha }_1=1.1$, ${\alpha }_{21}=0.1$, ${\alpha }_{22}=0.2$, ${\alpha }_{23}=0.3$${\alpha }_3=0.2$, ${\alpha }_4=1.4$, ${\alpha }_{51}=0.1$, ${\alpha }_{52}=0.2$, ${\alpha }_{53}=0.3$, ${\alpha }_6=0.1$, which yield ${\alpha }_2={\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23}=0.6$, ${\alpha }_5={\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53}=0.6$, and which satisfy $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and ${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}=0.0556>0$, and $R_1=\mathit{diag}(1.0419,1.0479)$, $R_2=\mathit{diag}(1.0036,1.0415)$, $R_3=\mathit{diag}(1.745,2.1202)$, $R_4=\mathit{diag}(1.9234,2.5495)$ (for the purpose of conciseness, the values of the other matrices are not shown), then we can verify that all the conditions in Theorem 1 are satisfied, from which we can infer the exponential stability of the EP of System (34).

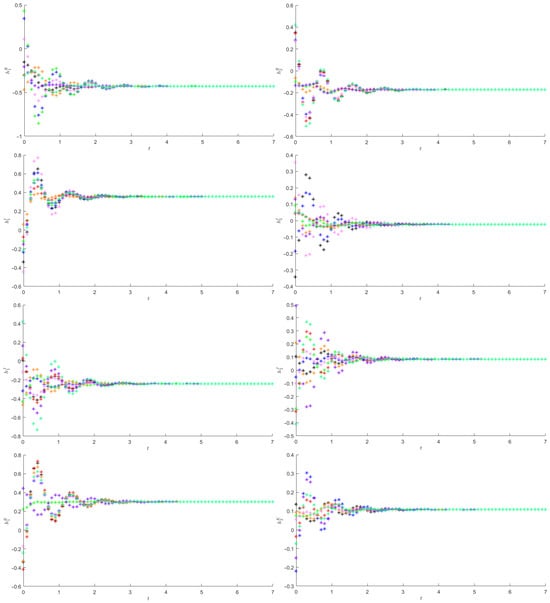
Figure 1 depicts, starting from 8 initial values, the quaternion components of the state trajectories of ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$.

Figure 1. The quaternion components of the state trajectories of ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$ in Example 1. Eight initial points are considered, which are depicted with different colors.

Example 2.

Consider again the time scale $\mathbb{T}=0.1\mathbb{Z}$ and also NN (34) with an unique EP, but with the following parameters:

$$A=\left[\begin{array}{cc}8& 0\\ 0& 9\end{array}\right],$$

$$B=0.1\left[\begin{array}{cc}-7+8i-2j+4\kappa & 3+9i-2j-2\kappa \\ -2-4i+2j-2\kappa & 4+3i+1j+4\kappa \end{array}\right],$$

$$C=0.1\left[\begin{array}{cc}-4+7i+2j+5\kappa & 8+5i+3j-5\kappa \\ 3+2i-2j+1\kappa & -5+5i+2j+4\kappa \end{array}\right],$$

$$D=0.1\left[\begin{array}{cc}2+8i+3j+7\kappa & 5+8i+8j-8\kappa \\ 3+2i-5j+2\kappa & -2-8i+9j+7\kappa \end{array}\right],$$

$$E=\left[\begin{array}{cc}0.3& 0\\ 0& 0.2\end{array}\right],$$

$$f_j\left(h\right)={\displaystyle \frac{1}{1+e^{-h^R}}}+{\displaystyle \frac{1}{1+e^{-h^I}}}i+{\displaystyle \frac{1}{1+e^{-h^J}}}j+{\displaystyle \frac{1}{1+e^{-h^K}}}\kappa ,\forall h\in \mathbb{H},\forall j\in \{1,2\},$$

which allows us to deduce that the activation functions fulfill Assumption 1, and

$$L=\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right].$$

The delays are now $\delta =0$ (leakage delay is not present), $\gamma \left(t\right)=0.5$, $\eta =0.2$, $\theta =0.3$, thus $\gamma =0.5$ and $\pi =\max \{\delta ,\gamma ,\eta ,\theta \}=0.5$.

Also, we compute ${\alpha }_1=6.8942$, ${\alpha }_2=1.1509$, ${\alpha }_3=0.3$, ${\alpha }_4=9.5715$, ${\alpha }_5=1.1509$, ${\alpha }_6=0.3$, which satisfy $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and ${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}=1.148>0,$ and take ${\rho }_1=1$, ${\rho }_2=2$. Thus, the requirements of Theorem 2 are met, so, by applying the theorem, we get that the EP of System (34) with the above-defined parameters is exponentially stable.

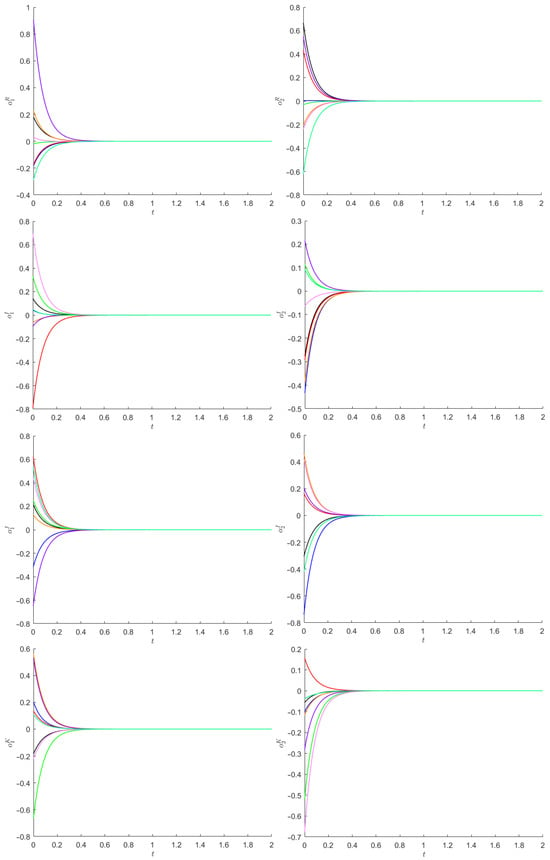
Figure 2 depicts, starting from 8 initial points, the quaternion components of the state trajectories of ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$.

Figure 2. The quaternion components of the state trajectories of ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$ in Example 2. Eight initial points are considered, which are depicted with different colors.

Example 3.

Now, consider the time scale $\mathbb{T}=\mathbb{R}$, and, in this case, $\widehat{\mu }=0$.

Also, for studying the synchronization problem, assume System (34) is the drive NN, and we will define the corresponding response NN by

$$g_i^{\Delta }\left(t\right)=-a_i{g}_i(t-\delta )+\sum _{j=1}^2{b}_{ij}{f}_j\left(g_j\left(t\right)\right)+\sum _{j=1}^2{c}_{ij}{f}_j\left(g_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^2{d}_{ij}{\int }_{t-\eta }^t{f}_j\left(g_j\left(s\right)\right)\Delta s+e_i{g}_i^{\Delta }(t-\theta )+I_i-u_i\left(t\right),$$

(36)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,2\}$.

Now, by putting ${\mathfrak{d}}_i\left(t\right)=g_i\left(t\right)-h_i\left(t\right)$, from the expressions of Systems (34) and (36), we are able to deduce that

$${\mathfrak{d}}_i^{\Delta }\left(t\right)=-a_i{\mathfrak{d}}_i(t-\delta )+\sum _{j=1}^2{b}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)+\sum _{j=1}^2{c}_{ij}{\tilde{f}}_j\left({\mathfrak{d}}_j(t-\gamma \left(t\right))\right)+\sum _{j=1}^2{d}_{ij}{\int }_{t-\eta }^t{\tilde{f}}_j\left({\mathfrak{d}}_j\left(s\right)\right)\Delta s+e_i{\mathfrak{d}}_i^{\Delta }(t-\theta )-u_i\left(t\right),$$

(37)

$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall i\in \{1,2\}$, in which ${\tilde{f}}_j\left({\mathfrak{d}}_j\left(t\right)\right)={\tilde{f}}_j({\mathfrak{d}}_j\left(t\right)+h_i\left(t\right))-{\tilde{f}}_j\left(h_i\left(t\right)\right),$$\forall t\in {[0,+\infty )}_{\mathbb{T}}$, $\forall j\in \{1,2\}$.

The subsequent state-feedback-type controller can be designed so as to synchronize drive NN (34) and response NN (36),

$$u\left(t\right)=K_1\mathfrak{d}\left(t\right)+K_2\mathfrak{d}(t-\delta )+K_3\mathfrak{d}(t-\gamma \left(t\right))+K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s+K_5{\mathfrak{d}}^{\Delta }(t-\theta ),$$

(38)

in which the real positive diagonal matrices $K_1,\dots ,K_5\in {\mathbb{R}}^{N\times N}$ are control gain matrices. By incorporating this control scheme, System (37) has the following form:

$$\begin{array}{c}{\mathfrak{d}}^{\Delta }\left(t\right)=-K_1\mathfrak{d}\left(t\right)-(A+K_2)\mathfrak{d}(t-\delta )-K_3\mathfrak{d}(t-\gamma \left(t\right))-K_4{\int }_{t-\eta }^t\mathfrak{d}\left(s\right)\Delta s\hfill \\ \hfill \\ +B\tilde{f}\left(\mathfrak{d}\left(t\right)\right)+C\tilde{f}\left(\mathfrak{d}(t-\gamma \left(t\right))\right)+D{\int }_{t-\eta }^t\tilde{f}\left(\mathfrak{d}\left(s\right)\right)\Delta s+(E-K_5){\mathfrak{d}}^{\Delta }(t-\theta ).\hfill \end{array}$$

(39)

The parameters are taken as

$$A=\left[\begin{array}{cc}0.8& 0\\ 0& 0.9\end{array}\right],$$

$$B=0.1\left[\begin{array}{cc}-7+1i-2j+4\kappa & 3+2i-2j-2\kappa \\ -2-4i+2j-2\kappa & 4+3i+1j+4\kappa \end{array}\right],$$

$$C=0.1\left[\begin{array}{cc}-4+7i+2j+5\kappa & 9+5i+3j-5\kappa \\ 3+2i-2j+1\kappa & -5+5i+2j+4\kappa \end{array}\right],$$

$$D=0.1\left[\begin{array}{cc}2+8i+3j+5\kappa & 5+8i+8j-5\kappa \\ 3+2i-5j+2\kappa & -2-8i+9j+2\kappa \end{array}\right],$$

$$E=\left[\begin{array}{cc}0.3& 0\\ 0& 0.2\end{array}\right],$$

$$f_j\left(h\right)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{1+e^{-h^R}}}+{\displaystyle \frac{1}{1+e^{-h^I}}}i+{\displaystyle \frac{1}{1+e^{-h^J}}}j+{\displaystyle \frac{1}{1+e^{-h^K}}}\kappa \right),\forall h\in \mathbb{H},\forall j\in \{1,2\},$$

from which we deduce that the activation functions satisfy Assumption 1 and

$$L=\left[\begin{array}{cc}0.25& 0\\ 0& 0.25\end{array}\right].$$

Then, we take $\delta =0.01$, $\gamma \left(t\right)=0.1|sint|$, $\eta =0.05$, $\theta =0.08$, thus $\gamma =0.1$ and $\pi =\max \{\delta ,\gamma ,\eta ,\theta \}=0.1$.

We design the control gain matrices as

$$K_1=\left[\begin{array}{cc}10.4& 0\\ 0& 10.3\end{array}\right],K_2=\left[\begin{array}{cc}0.4& 0\\ 0& 0.5\end{array}\right],K_3=\left[\begin{array}{cc}0.03& 0\\ 0& 0.05\end{array}\right],K_4=\left[\begin{array}{cc}0.2& 0\\ 0& 0.4\end{array}\right],K_5=\left[\begin{array}{cc}0.01& 0\\ 0& 0.02\end{array}\right],$$

and, furthermore, we take ${\alpha }_1=10$, ${\alpha }_{21}=0.2$, ${\alpha }_{22}=0.3$, ${\alpha }_{23}=0.4$, ${\alpha }_3=0.4$, ${\alpha }_4=0.4$, ${\alpha }_{51}=2.2$, ${\alpha }_{52}=2.3$, ${\alpha }_{53}=2.4$, ${\alpha }_6=0.1$, which means that ${\alpha }_2={\alpha }_{21}+{\alpha }_{22}+{\alpha }_{23}=0.9$, ${\alpha }_5={\alpha }_{51}+{\alpha }_{52}+{\alpha }_{53}=6.9$, and also that $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and ${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}=5.8556>0$. Finally, for $R_1=\mathit{diag}(0.46336,1.0832)$, $R_2=\mathit{diag}(0.36233,0.37425)$, $R_3=\mathit{diag}(1.9368,2.1147)$, $R_4=\mathit{diag}(1.7712,2.3323)$ (for the purpose of conciseness, the values of the other matrices are not shown), we can verify that all the conditions in Theorem 3 are satisfied, which allows us to conclude that System (34) is exponentially synchronized with System (36) under controller (38).

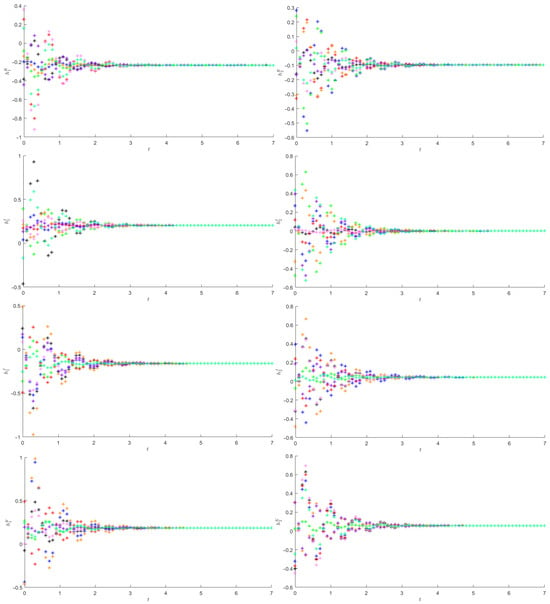
Figure 3 depicts, starting from 8 initial points, the quaternion components of the state trajectories of ${\mathfrak{d}}_1$ and ${\mathfrak{d}}_2$.

Figure 3. The quaternion components of the state trajectories of ${\mathfrak{d}}_1$ and ${\mathfrak{d}}_2$ in Example 3. Eight initial points are considered, which are depicted with different colors.

Example 4.

Lastly, time-scale $\mathbb{T}=\mathbb{R}$ will be taken, and the same Systems (34) and (36), and the same controller (38), but with the following parameters:

$$A=\left[\begin{array}{cc}0.8& 0\\ 0& 0.9\end{array}\right],$$

$$B=\left[\begin{array}{cc}-0.07+0.1i-0.02j+0.04\kappa & 0.03+0.12i-0.02j-0.02\kappa \\ -0.02-0.04i+0.02j-0.02\kappa & 0.04+0.03i+0.01j+0.04\kappa \end{array}\right],$$

$$C=\left[\begin{array}{cc}-0.04+0.07i+0.02j+0.05\kappa & 0.1+0.05i+0.03j-0.05\kappa \\ 0.03+0.02i-0.02j+0.01\kappa & -0.05+0.05i+0.02j+0.04\kappa \end{array}\right],$$

$$D=\left[\begin{array}{cc}0.02+0.08i+0.03j+0.15\kappa & 0.05+0.08i+0.08j-0.15\kappa \\ 0.03+0.02i-0.05j+0.02\kappa & -0.02-0.08i+0.1j+0.2\kappa \end{array}\right],$$

$$E=\left[\begin{array}{cc}0.03& 0\\ 0& 0.02\end{array}\right],$$

$$f_j\left(h\right)={\displaystyle \frac{1}{20}}\left({\displaystyle \frac{1}{1+e^{-h^R}}}+{\displaystyle \frac{1}{1+e^{-h^I}}}i+{\displaystyle \frac{1}{1+e^{-h^J}}}j+{\displaystyle \frac{1}{1+e^{-h^K}}}\kappa \right),\forall h\in \mathbb{H},\forall j\in \{1,2\},$$

which allows us to ascertain that

$$L=\left[\begin{array}{cc}0.025& 0\\ 0& 0.025\end{array}\right].$$

Also, we take $\delta =0.01$, $\gamma \left(t\right)=0.1|sint|$, $\eta =0.05$, $\theta =0.08$, thus $\gamma =0.1$ and $\pi =\max \{\delta ,\gamma ,\eta ,\theta \}=0.1$.

We design the control gain matrices as

$$K_1=\left[\begin{array}{cc}1.4& 0\\ 0& 1.3\end{array}\right],K_2=\left[\begin{array}{cc}0.04& 0\\ 0& 0.05\end{array}\right],K_3=\left[\begin{array}{cc}0.03& 0\\ 0& 0.05\end{array}\right],K_4=\left[\begin{array}{cc}0.2& 0\\ 0& 0.4\end{array}\right],K_5=\left[\begin{array}{cc}0.01& 0\\ 0& 0.02\end{array}\right].$$

Also, we compute ${\alpha }_1=1.2968$, ${\alpha }_2=1.0241$, ${\alpha }_3=0.04$, ${\alpha }_4=1.4059$, ${\alpha }_5=1.0241$, ${\alpha }_6=0.04$, which satisfy $-{\alpha }_1\in {\mathcal{R}}^{+}$, ${\alpha }_6<1$, and ${\alpha }_1-{\alpha }_2-{\displaystyle \frac{{\alpha }_3({\alpha }_4+{\alpha }_5)}{1-{\alpha }_6}}=0.1715>0,$ and take ${\rho }_1=1$, ${\rho }_2=2$. All the conditions of Theorem 4 are satisfied, from which we can conclude that System (34) is exponentially synchronized with System (36) under controller (38), with the above-defined parameters.

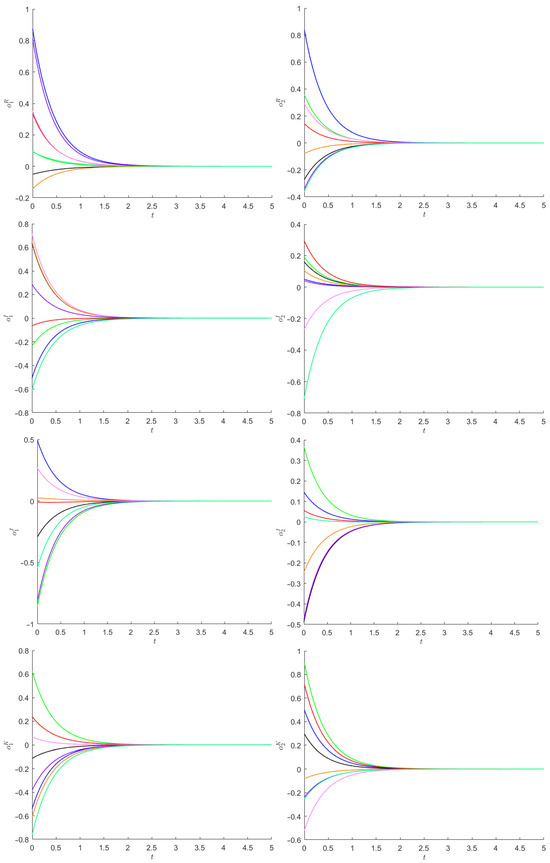
Figure 4 depicts, starting from 8 initial points, the quaternion components of the state trajectories of ${\mathfrak{d}}_1$ and ${\mathfrak{d}}_2$.

Figure 4. The quaternion components of the state trajectories of ${\mathfrak{d}}_1$ and ${\mathfrak{d}}_2$ in Example 4. Eight initial points are considered, which are depicted with different colors.

5. Conclusions

The present study was dedicated to putting forward a very generic QVNN model defined on time scales and having multiple types of delays (leakage, time-varying, distributed, and neutral), which was rarely, if ever, discussed before in the literature. The highlight of the contribution is a generalization of the Halanay-type inequality for neutral systems defined on time scales, which can be applied to any such systems, not just NNs. This proved lemma was then used in four theorems to ascertain sufficient criteria presented in terms of both LMIs and algebraic inequalities, which ensure the exponential stability and exponential synchronization properties for the proposed generic model. One numerical application illustrated each of the theorems for both the CT and DT cases.

The results obtained in this paper can be particularized for both CT and DT NNs, or any hybrid combination of the two, and for real-valued or complex-valued NNs with possibly fewer types of delays, which have not yet been discussed in the literature. Also, the proposed lemma can be applied to study different dynamical properties (like multistability, multiperiodicity, dissipativity, or passivity, for example) of other neutral systems defined on time scales, possible examples being NNs having impulsive effects, Markovian jumping parameters, or reaction–diffusion terms, other types of delays (unbounded delays), or different types of uncertainties, such as stochastic terms. The lemma could also be adapted to fractional-order NNs. These could all be interesting directions for future research.