Estimating the First, Hyper-Zagreb Index for Direct Product of F-Sum Graphs

Abstract

A chemical graph is an illustration of a chemical compound’s structural formula, where the edges indicate covalent bonding and the vertices depict atoms. In the study of (molecular) graphs, Zagreb indices and their variations are the most studied and well-investigated invariants due to their chemical applicability. To probe and investigate the most promising lower and upper bound of the appropriate topological index for a graph family is a problem of primal significance in extremal graph theory. Deng et al. computed the closed-form formulas for the Zagreb indices $M_1$ and $M_2$ for four novel operations known as F-sum graphs, proposed by Eliasi and Taeri in “Discrete Appl. Math. (2009) 157.” Subsequently, Buragohain et al. derived the formulas for $M_1$ and $M_2$ of four sum graphs in the context of the direct product. In this article, we investigate F-sum graphs formed through four newly defined graph operations associated with the direct product and establish lower bounds and upper bounds on the first hyper-Zagreb index $H{M}_1$ for these graphs. Finally, we validate our derived bounds by applying them to various examples, demonstrating the correctness and applicability of the results.

1. Introduction

Graph theory is a subject of fundamental significance in mathematics. Graphs are used to describe diverse problems of various contemporary fields in topological pictorial form. Graph theory found its origin in 1735 when Euler introduced the concept of the Eulerian circuit while providing a solution to the Königsberg bridges problem. Researchers of different disciplines, such as biology, computer science, and chemistry especially chemical graph theory have great attraction towards graph theory, due to its immense applications. In the recent past, chemical compounds have been studied extensively using graphs to represent the molecular structure of these compounds through their 2D lattice (molecular graph). The effective applications of chemical graph theory involve the association of physicochemical properties with chemical substances under study.

A topological abstraction of a molecule is called a molecular graph, which is always a simple graph in which the vertices portray the atoms while the edges symbolize the bonding between them. A topological invariant or index (TI) is a numerical parameter mathematically extracted from a molecular graph using graph parameters and is independent of the pictorial characterization or the labeling of a graph. Mathematical formulas of TIs involve degree, distance, the spectrum of adjacency matrix, and their combination. TIs help researchers working in mathematical chemistry, chemical graph theory, and cheminformatics to understand, develop, and design new chemical compounds in the context of their chemical, biological, and physical properties. Graph theory is a rapidly expanding field and offers a platform for mathematical modeling to develop prototype activity prediction models in drug discovery.

There are many applications of topological indices as implemented for creating chemical and other characteristics of molecules. In particular, researchers in the field of cheminformatics choose the appropriate and pertinent TIs in the analysis of QSPR/QSAR to conclude various characteristics such as melting and boiling point, density, toxicity, critical temperature, enthalpy of formation, surface area, and entropy of chemical compounds. Among the major classes of TIs, the frequently investigated and analyzed are the Zagreb indices, hyper-Zagreb indices, Wiener, Randić, Szeged, sum-connectivity, and atom-bond connectivity indices.

In 1947, Harry Wiener introduced the earliest known distance-related TI, called the Wiener index [1], and proved it to be a good estimator of the boiling point of alkanes. This milestone initiated a surge of interest in the development of various TIs, which later found significant applications in the design, analysis, and prediction of QSAR and QSPR. Among these, one of the most effective indices for predicting molecular branching in saturated hydrocarbons is the Randić connectivity index, proposed by Milan Randić in 1975 [2]. Another prominent class of classical degree-based topological indices includes the Zagreb indices, introduced by Gutman and Trinajstić in 1972 [3,4].

$$M_1(\Gamma )=\sum _{\begin{array}{c}s\in V(\Gamma )\end{array}}{\left(d\left(s\right)\right)}^2,M_2(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}d\left(s\right)d\left(r\right).$$

The equivalent mathematical formulation of $M_1(\Gamma )$ based on the degree structural characteristics of a molecular graph is given by

$$M_1(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}[d\left(s\right)+d\left(r\right)].$$

Zhou and Trinajstić, initiated the idea of the general sum-connectivity index (GSCI) [5] and is given as follows:

$${\chi }_{\gamma }(\Gamma )=\sum _{vw\in E(\Gamma )}{[d_{\Gamma }\left(v\right)+d_{\Gamma }\left(w\right)]}^{\gamma },\gamma \in R.$$

Inspired by the wide range of applications of the Zagreb indices, for a molecular graph $\Gamma$, V.R. Kulli (2017) introduced the concept of the 1st and 2nd Gourava index [6] and defined as follows:

$$G{O}_1(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}[d\left(s\right)+d\left(r\right)+d\left(s\right)d\left(r\right)].$$

$$G{O}_2(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}[d\left(s\right)+d\left(r\right)]\left[d\left(s\right)d\left(r\right)\right].$$

Ranjini et al. (2013) introduced the idea of the third re-defined Zagreb index [7] and formulated it as follows:

$$ReZ{M}_3(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}\left[d\left(s\right)d\left(r\right)\right)][d\left(r\right)+d\left(s\right)].$$

Initially, Ranjini introduced the topological index $ReZ{M}_3(\Gamma )$, which was subsequently followed by Kulli’s definition of $G{O}_2(\Gamma )$. Upon examination, it is evident that these two indices are equivalent, i.e., $ReZ{M}_3(\Gamma )=G{O}_2(\Gamma )$, highlighting the consistency between their respective formulations. In 2013, Shirdel et al. [8] proposed the first hyper-Zagreb index (FHZI), which is widely utilized in mathematical chemistry and cheminformatics to estimate thermodynamic, biological, and topological characteristics of organic compounds, polymers, and nanostructures. This index is defined as

$$H{M}_1(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}[d\left(s\right)+d\left(r\right)]{.}^2$$

Wang et al. [9] introduced the second hyper Zagreb index (2016) by integrating the degree products of adjacent vertices, which refines the classical Zagreb indices and provides a deeper insight into molecular structure. Its increased sensitivity to topological variations makes it a powerful tool for characterizing complex and branched molecular architectures. It is defined as follows:

$$H{M}_2(\Gamma )=\sum _{\begin{array}{c}sr\in E(\Gamma )\end{array}}{\left[d\left(s\right)d\left(r\right)\right]}^2.$$

Graph operations are essential tools for constructing new families of graphs, especially in the context of molecular structure modeling. Various established operations in graph theory enable the generation of complex and application-oriented graph structures. Some of the most widely used operations include the Cartesian $(\times )$, Strong $(⊠)$, Lexicographic, Corona $(\circ )$, and Direct $(\otimes )$ products.

The Cartesian product of two graphs, denoted by ${\Gamma }_1\times {\Gamma }_2$, was originally introduced by Whitehead and Russell in 1912. This product is defined on the vertex set $V\left({\Gamma }_1\right)\times V\left({\Gamma }_2\right)$, where adjacency between two vertices $(m,n)$ and $(r,s)$ in ${\Gamma }_1\times {\Gamma }_2$ holds if and only if either $m=r$ and $n\sim s$, or $m\sim r$ and $n=s$. The Cartesian product thus establishes a graph structure in which adjacency is inherited independently from each factor graph, preserving both local and global topological characteristics of the constituent graphs.

By applying certain unary graph operations to a given graph $\Gamma$, one can obtain four well-known derived graphs as follows:

• Subdivision Graph: The graph $\Gamma$ undergoes expansion to create $S\left(G\right)$ by introducing a new vertex to each edge of $\Gamma$.
• Triangle parallel graph: $R(\Gamma )$ is derived from $S(\Gamma )$ by connecting solid vertices along the original edges of $\Gamma$ that are associated with hollow vertices.
• Line superposition graph: $Q(\Gamma )$ can be formed from $S(\Gamma )$ by connecting pairs of new vertices with edges, where each pair shares an adjacent (solid) vertex.
• Total graph: $T(\Gamma )$ is formed by simultaneously applying both $R\left(G\right)$ and $Q(\Gamma )$ to $S(\Gamma )$.

An illustration of these derived graphs for the path graph $P_4$ is presented in Figure 1.

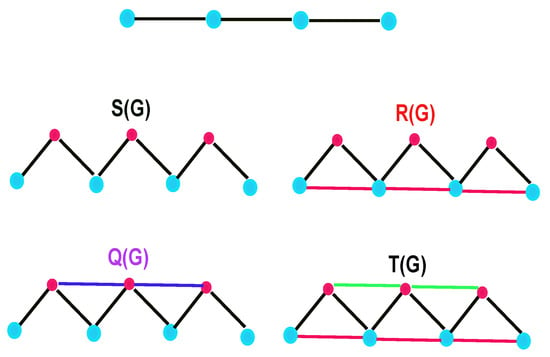
Figure 1. Path $P_4$ and its four related graphs.

In the F-sum graph ${\Gamma }_1{+}_F{\Gamma }_2$, where ${\Gamma }_1$ and ${\Gamma }_2$ are two simple, connected, and finite graphs, and F is an operation (chosen from S, R, Q, and T), the vertex set is defined as $V\left({\Gamma }_1{+}_F{\Gamma }_2\right)=V\left(F\left({\Gamma }_1\right)\right)\times V\left({\Gamma }_2\right)=(V\left({\Gamma }_1\right)\cup E\left({\Gamma }_1\right))\times V\left({\Gamma }_2\right)$. Two vertices, $(v_1,v_2)$ and $(w_1,w_2)$, in $V\left({\Gamma }_1{+}_F{\Gamma }_2\right)$ are adjacent if and only if: 1. $v_1=w_1\in V\left({\Gamma }_1\right)$ and $(v_2,w_2)\in E\left({\Gamma }_2\right)$, or 2. $v_2=w_2\in V\left({\Gamma }_2\right)$ and $(v_1,w_1)\in E\left(F\left({\Gamma }_1\right)\right)$. In the graph ${\Gamma }_{1F}{\Gamma }_2$, we note that there are $\left|V\right({\Gamma }_2\left)\right|$ copies of the graph $F\left({\Gamma }_1\right)$, and each of these copies is labeled with vertices of ${\Gamma }_2$. Specifically, in ${\Gamma }_1{+}_F{\Gamma }_2$, vertices corresponding to the original vertices of G are called solid vertices, while those corresponding to the edges $E\left({\Gamma }_1\right)$ are termed hollow vertices. To improve clarity, the process involves connecting solid vertices within the same copy of $F\left({\Gamma }_1\right)$, preserving their adjacency in ${\Gamma }_2$. In other words, solid vertices with identical labels in $F\left({\Gamma }_1\right)$ are joined if they are adjacent in ${\Gamma }_2$, see Figure 2.

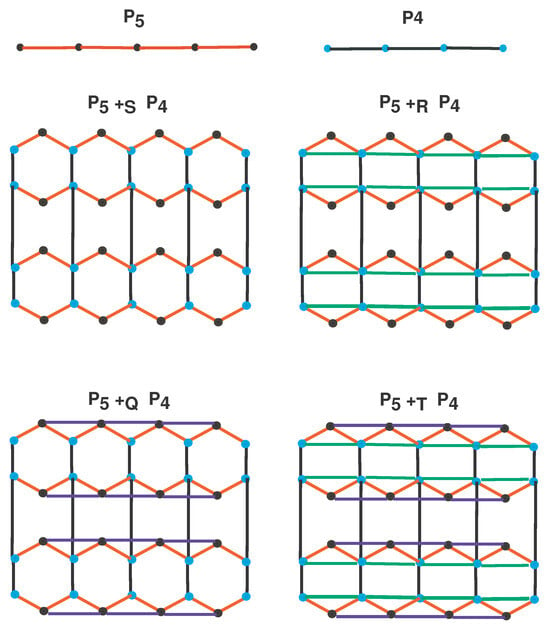
Figure 2. F-sum of $P_5$ with $P_4$.

In [10], Paul M. Weichsel (1962) proposed the idea of Direct product for two graphs ${\Gamma }_1$ and ${\Gamma }_2$ represented by $({\Gamma }_1\otimes {\Gamma }_2)$ with the vertex set $V({\Gamma }_1\otimes {\Gamma }_2)=V\left({\Gamma }_1\right)\times V\left({\Gamma }_2\right)$ and the set of edges $E({\Gamma }_1\otimes {\Gamma }_2)=(m,n)(r,s)\in E({\Gamma }_1\otimes {\Gamma }_2)$ satisfying the condition $mr\in E\left({\Gamma }_1\right)$ and $ns\in E\left({\Gamma }_2\right)$. The Direct product of $P_3$ with $C_3$ is described in Figure 3.

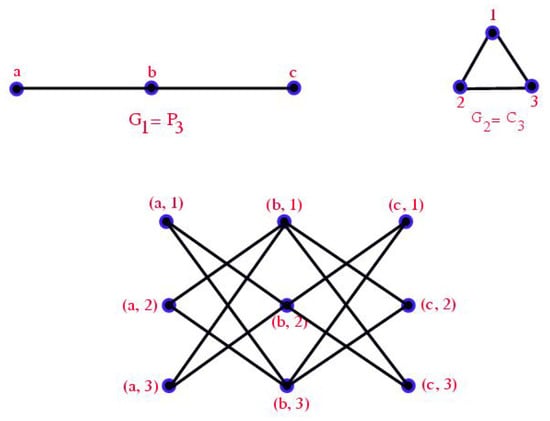
Figure 3. Direct product of $P_3$ with $C_3$.

F-sum graphs constitute a significant class of graph operations that integrate two graphs into a composite structure, providing an effective framework for modeling macromolecules, nanostructures, and polymeric systems. In this study, we employ the first hyper-Zagreb index $H{M}_1$ as a representative topological invariant (TI), since it encapsulates the structural features of both the forgotten and second Zagreb indices, thereby reflecting the molecular connectivity, branching complexity, $\pi$ electron energy, and the influence of local structural variations on the overall molecular topology. To establish bounds for selected topological indices corresponding to molecular graphs generated through graph operations, we adopt a systematic methodology that integrates combinatorial reasoning with algebraic formulation. Specifically, F-sum graphs are constructed using the Cartesian product between four unary transformations of a base graph ${\Gamma }_1$ and a secondary graph ${\Gamma }_2$. This framework can further be generalized through the use of other standard graph products, such as the Direct product.

The derivation of bounds on $H{M}_1$ for F-sum graphs relies fundamentally on formulating and applying the degree relations between the composite and its constituent base graphs. These relations are subsequently simplified to express the bounds in terms of known indices and parameters of the original graphs. Finally, the theoretical results are validated through illustrative case studies involving small-scale molecular graph examples. Again, the distinction between the F-sum graphs under Direct product and the simple Direct product of ${\Gamma }_1$ with ${\Gamma }_2$ lies in replacing ${\Gamma }_1$ with $F\left({\Gamma }_1\right)$, where F denotes one of the aforementioned four unary operations. The F-sum of $P_3$ with $P_3$ under the Direct product is presented in Figure 4.

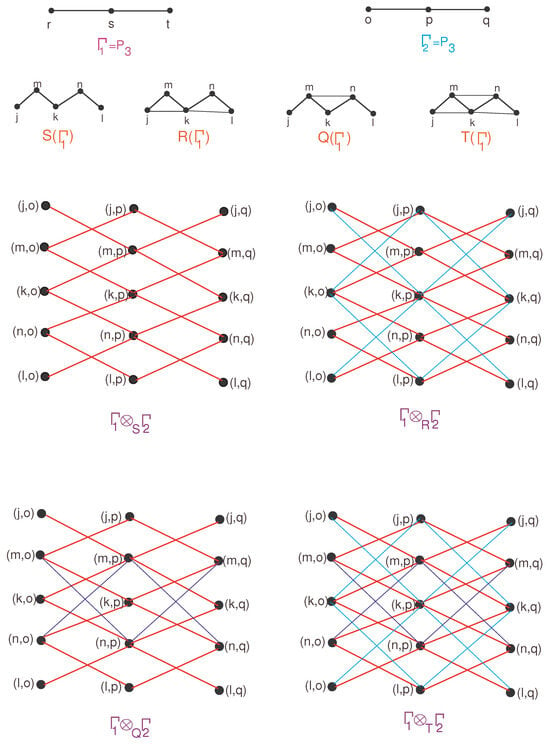
Figure 4. F-sum of $P_3$ with $P_3$ under Direct product.

In the ${\Gamma }_1{\otimes }_F{\Gamma }_2$ graph, the order and size are $(n_1+e_1)n_2$ and $2e_{F\left({\Gamma }_1\right)}\times e_2$, respectively. For graphs ${\Gamma }_1$ and ${\Gamma }_2$, it is easy to establish a degree relation between new graphs ${\Gamma }_1{\otimes }_F{\Gamma }_2$, where F is one of four unary operations S, R, Q, and T, and old (base) graphs that are presented below.

$$\begin{array}{c}\hfill d_{{\Gamma }_S}(a^{\prime },b^{\prime })=\left\{\begin{array}{c}{d}_{{\Gamma }_1}\left(a^{\prime }\right)d_{{\Gamma }_2}\left(b^{\prime }\right),if{a}^{\prime }\in V\left({\Gamma }_1\right)\hfill \\ 2d_{{\Gamma }_2}\left(b^{\prime }\right),if{a}^{\prime }\in V\left(S\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\hfill \end{array}\right.\end{array}$$

(1)

$$\begin{array}{cc}\hfill d_{{\Gamma }_R}(a^{\prime },b^{\prime })& =\left\{\begin{array}{cc}2d_{{\Gamma }_1}\left(a^{\prime }\right)d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left({\Gamma }_1\right)\hfill \\ 2d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left(R\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill d_{{\Gamma }_Q}(a^{\prime },b^{\prime })& =\left\{\begin{array}{cc}{d}_{{\Gamma }_1}\left(a^{\prime }\right)d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left({\Gamma }_1\right)\hfill \\ (d_{{\Gamma }_1}\left(w^{\prime }\right)+d_{{\Gamma }_1}\left(w^{″}\right)d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left(Q\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\hfill \end{array}\right.\hfill \end{array}$$

(3)

In expression (3) vertex $a^{\prime }$ is placed in edge $w^{\prime }{w}^{″}\in E\left({\Gamma }_1\right)$.

$$\begin{array}{cc}\hfill d_{{\Gamma }_T}(a^{\prime },b^{\prime })& =\left\{\begin{array}{cc}2d_{{\Gamma }_1}\left(a^{\prime }\right)d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left({\Gamma }_1\right)\hfill \\ (d_{{\Gamma }_1}\left(w^{\prime }\right)+d_{{\Gamma }_2}\left(w^{″}\right)d_{{\Gamma }_2}\left(b^{\prime }\right),\hfill & if{a}^{\prime }\in V\left(T\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\hfill \end{array}\right.\hfill \end{array}$$

(4)

In degree relation (4) the vertex $a^{\prime }$ is placed in the edge $w^{\prime }{w}^{″}\in E\left({\Gamma }_1\right)$.

In 2009, Khalifeh et al. and Eliasi et al. [11,12] offered the formulas of the Zagreb indices for four new graphs related to the Cartesian product (F-sum) and derived their Wiener index, respectively. In 2012, Pattabiraman et al. [13] used different topological indices to find a relation with graphs involving the Direct product. In 2014, Mahdieh found the sharp lower bound of the Narumi–Katayama index for different graph operations [14]. In 2016, Deng et al. [15] discerned exact formulas for Zagreb indices working with four new operations (F-sum) of graphs. In 2017, Sarala et al., Basavanagoud et al., and Imran et al. [16,17,18] determined the Zagreb indices for four-sum graphs related to the lexicographic product, the first hyper-Zagreb index for four-sum graphs related to the Cartesian product, and bounds on various TIs of graphs under Direct product, respectively. In 2018, Elumalai et al. [19] demonstrated improved bounds for the first hyper-Zagreb index with respect to simple connected graphs. In 2020, for the first time, Buragohain et al. and Basavanagoud et al. [20,21] introduced F-sum operations by replacing the Cartesian product with the Direct product and calculated formulas for Zagreb indices and co-indices, respectively. The VL index proved to be a good predictor of some physicochemical properties of hydrocarbons, and in 2021 Deepika [22] investigated and offered bounds on the VL index for F-sum graphs under Direct product. In this paper, we aim to derive and analyze lower and upper bounds on the first hyper-Zagreb index for the latest introduced F-sum graphs under Direct product. Further, we will provide support to and check the accuracy of our bounds by elaborating them for several specific examples.

2. Results and Discussion

This section presents the main results, where explicit formulas and bounds for the first hyper-Zagreb index of F-sum graphs under the Direct product ${\Gamma }_1{\otimes }_F{\Gamma }_2$ are derived. To streamline the notation throughout this discussion, we adopt the following conventions. Let ${\Gamma }_1$ and ${\Gamma }_2$ be two simple, connected, and finite graphs. Then we denote the following:

• $n_1=\left|V\left({\Gamma }_1\right)\right|$, $e_1=\left|E\left({\Gamma }_1\right)\right|$, $\delta \left({\Gamma }_1\right)$ = Smallest degree of ${\Gamma }_1$, $\Delta \left({\Gamma }_1\right)$ = Largest degree of ${\Gamma }_1$.
• $n_2=\left|V\left({\Gamma }_2\right)\right|$, $e_2=\left|E\left({\Gamma }_2\right)\right|$, $\delta (\Gamma )$ = Smallest degree of ${\Gamma }_2$, $\Delta \left({\Gamma }_2\right)$ = Largest degree of ${\Gamma }_2$.
• $|V\left(S\left({\Gamma }_1\right)\right)|=n_1+e_1$, $|E\left(S\left({\Gamma }_1\right)\right)|=2e_1$,
• $|V\left({\Gamma }_1{\otimes }_F{\Gamma }_2\right)|=(n_1+e_1)e_2$. $|E\left({\Gamma }_1{\otimes }_F{\Gamma }_2\right)|=2|E\left(F\left({\Gamma }_1\right)\right)| · e_2$,
• ${\Gamma }_S={\Gamma }_1{\otimes }_S{\Gamma }_2$, ${\Gamma }_R={\Gamma }_1{\otimes }_R{\Gamma }_2$, ${\Gamma }_Q={\Gamma }_1{\otimes }_Q{\Gamma }_2$, ${\Gamma }_T={\Gamma }_1{\otimes }_T{\Gamma }_2$.

Theorem 1. 

Let ${\Gamma }_1$ and ${\Gamma }_2$ be two connected, simple, and finite graphs, then the lower bound $L{B}_S$ the upper bound $U{B}_S$ of FHZI for graph $\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$ are

$$L{B}_S=e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_2(\delta {\left({\Gamma }_1\right)}^2+\delta {\left({\Gamma }_2\right)}^2)+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)\delta \left({\Gamma }_2\right)+8e_1{M}_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right).$$

$$U{B}_S=e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_2(\Delta {\left({\Gamma }_1\right)}^2+\Delta {\left({\Gamma }_2\right)}^2)+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)\Delta \left({\Gamma }_2\right)+8e_1{M}_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right).$$

Proof. 

To ensure that our calculations remain precise and accessible, let $d(a,b)=d_{\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)}(a,b)$ denote the degree of the vertex $(a,b)\in V\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$. Now, applying the definition of $H{M}_1$ to the graph operation S, together with the degree relation provided in Equation (1), we obtain

$$\begin{array}{cc}\hfill H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)& =\sum _{\begin{array}{c}(a_1^{\prime },b_1^{\prime })(a_2^{\prime },b_2^{\prime })\in E\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\\ \in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+2d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & +\sum _{\begin{array}{c}{a}_1\in V(S\left({\Gamma }_1\right)-V\left({\Gamma }_1\right))\\ a_1^{\prime }{a}_2^{\prime }\in E(S\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)+2d\left(a_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}1\end{array}}+\sum _{\begin{array}{c}2\end{array}}.\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}1\end{array}}& =\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+2d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+2d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left[{\left(d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)\right)}^2+4{\left(d\left(b_2^{\prime }\right)\right)}^2+4d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)d\left(b_2^{\prime }\right)\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(S\left({\Gamma }_1\right)\right)\end{array}}\left[e_2{\left(d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)\right)}^2+4e_2{\left(d\left(b_2^{\prime }\right)\right)}^2+4e_{2}d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)d\left(b_2^{\prime }\right)\right]\hfill \\ \hfill & =\left[e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+4e_2\left(2e_1\right){\left(d\left({\Gamma }_2\right)\right)}^2+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)d\left({\Gamma }_2\right)\right]\hfill \\ \hfill & =e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+8e_1{e}_2{\left(d\left({\Gamma }_2\right)\right)}^2+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)d\left({\Gamma }_2\right).\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}2\end{array}}& =\sum _{\begin{array}{c}{a}_1^{\prime }\in V(S\left({\Gamma }_1\right)-V\left({\Gamma }_1\right))\\ a_1^{\prime }{a}_2^{\prime }\in E(S\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)+2d\left(a_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V(S\left({\Gamma }_1\right)-V\left({\Gamma }_1\right))\\ a_1^{\prime }{a}_2^{\prime }\in E(S\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)+2d\left(a_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V(S\left({\Gamma }_1\right)-V\left({\Gamma }_1\right))\\ a_1^{\prime }{a}_2^{\prime }\in E(S\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left[{\left(d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right)}^2+4{\left(d\left(a_2^{\prime }\right)\right)}^2+4d\left(a_2^{\prime }\right)d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }\in V(S\left({\Gamma }_1\right)-V\left({\Gamma }_1\right))\\ a_1^{\prime }{a}_2^{\prime }\in E(S\left({\Gamma }_1\right)\end{array}}\left[H{M}_2\left({\Gamma }_2\right)+4e_2{\left(d\left(a_2^{\prime }\right)\right)}^2+4d\left(a_2^{\prime }\right)M_2\left({\Gamma }_2\right)\right]\hfill \\ \hfill & =\left[2e_{1}H{M}_2\left({\Gamma }_2\right)+4e_2\left(2e_1\right){\left(d\left({\Gamma }_1\right)\right)}^2+4M_2\left({\Gamma }_2\right)\left(2e_1\right)d\left({\Gamma }_1\right)\right]\hfill \\ \hfill & =2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_1{\left(d\left({\Gamma }_1\right)\right)}^2+8e_1{M}_2\left({\Gamma }_2\right)d\left({\Gamma }_1\right).\hfill \end{array}$$

(7)

Now, placing formulas derived in Equations (6) and (7) in Equation (5), we obtain the following:

$$\begin{array}{cc}\hfill H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)& =e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_2(d{\left({\Gamma }_1\right)}^2+d{\left({\Gamma }_2\right)}^2)+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)d\left({\Gamma }_2\right)\hfill \\ \hfill & +8e_1{M}_2\left({\Gamma }_2\right)d\left({\Gamma }_1\right).\hfill \end{array}$$

Now using minimum and maximum degrees of ${\Gamma }_1$ and ${\Gamma }_2$, we obtain the lower and the upper bound on FHZI for graph $\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$.

$$L{B}_S=e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_2(\delta {\left({\Gamma }_1\right)}^2+\delta {\left({\Gamma }_2\right)}^2)+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)\delta \left({\Gamma }_2\right)+8e_1{M}_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)$$

$$U{B}_S=e_{2}H{M}_2\left(S\left({\Gamma }_1\right)\right)+2e_{1}H{M}_2\left({\Gamma }_2\right)+8e_1{e}_2(\Delta {\left({\Gamma }_1\right)}^2+\Delta {\left({\Gamma }_2\right)}^2)+4e_2{M}_2\left(S\left({\Gamma }_1\right)\right)\Delta \left({\Gamma }_2\right)+8e_1{M}_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right).$$

□

Example 1. 

To calculate the upper and lower bounds of $H{M}_1$ using formulas calculated in Theorem 1. let ${\Gamma }_1=P_3$, ${\Gamma }_2=P_3$, $n_1=\left|V\left({\Gamma }_1\right)\right|=3$, $n_2=\left|V\left({\Gamma }_2\right)\right|=3$, $e_1=\left|E\left({\Gamma }_1\right)\right|=2$, $e_2=\left|E\left({\Gamma }_2\right)\right|=2$, $\delta \left({\Gamma }_1\right)=1$, $\delta \left({\Gamma }_2\right)=1$, $\Delta \left({\Gamma }_1\right)=2$, and $\Delta \left({\Gamma }_2\right)=2$. To evaluate the exact value of $H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$, it is necessary to obtain the edge partition of the graph $\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$, and it is observed that the graph contains 4, 4, and 8 vertices with degree pairs $(1,4)$, $(2,2)$, and $(4,2)$, respectively. Further, Table 1 comprises TI values of factor graphs involved in our results and essential to compute our examples. Then $L{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=400$ and $U{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=752$. We computed the exact value of $H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$ to be 452, and the bounds on $H{M}_1$ yield a good result as follows: $L{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=400\le H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=452\le U{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=752$.

Table 1. Certain relevant invariants of specific graphs.

Invariants/Specific Graphs	${\mathit{M}}_1$	${\mathit{M}}_2$	${\mathit{HM}}_1$	${\mathit{HM}}_2$	${\mathit{\chi }}_4$
$P_3$	6	4	18	8	162
$P_4$	10	8	34	24	418
$C_3$	12	12	48	48	768
$S\left(P_3\right)$	14	12		40	674
$S\left(P_4\right)$	22	20		72	1186

Example 2. 

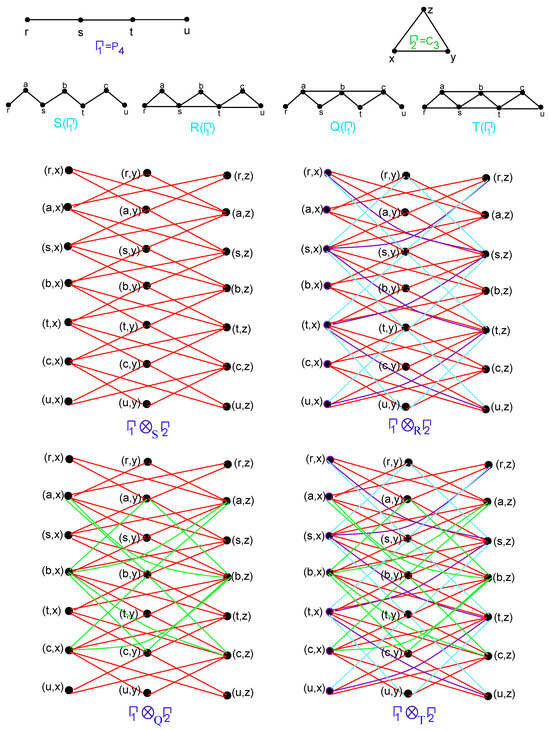
To compute the upper and lower bounds of $H{M}_1$ using formulas calculated in Theorem 1. let ${\Gamma }_1=P_4$, ${\Gamma }_2=C_3$, $n_1=\left|V\left({\Gamma }_1\right)\right|=4$, $n_2=\left|V\left({\Gamma }_2\right)\right|=3$, $e_1=\left|E\left({\Gamma }_1\right)\right|=3$, $e_2=\left|E\left({\Gamma }_2\right)\right|=3$, $\delta \left({\Gamma }_1\right)=1$, and $\delta \left({\Gamma }_2\right)=1$, $\Delta \left({\Gamma }_1\right)=2$, $\Delta \left({\Gamma }_2\right)=2$. The F-sum of $P_4$ with $C_3$ under the Direct product is illustrated in Figure 5.

Figure 5. F-sum of $P_4$ with $C_3$ under Direct product.

To calculate the actual value of $H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$, we require the edge partition of the graph $\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)$. The number of vertices having degree pairs $(2,2)$ and $(4,4)$ is observed to be 12 and 24, respectively. Using the formulas established in Theorem 1, together with the corresponding values of Table 1, we obtain $L{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=1560$, $U{B}_S\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=2064$, and $H{M}_1\left({\Gamma }_1{\otimes }_S{\Gamma }_2\right)=1968$. Clearly, our formulas provide a good estimate in this scenario.

Theorem 2. 

Let ${\Gamma }_1$ and ${\Gamma }_2$ be two connected, simple, and finite graphs; then the bounds on FHZI of graph $\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)$ are as follows:

$$L{B}_R=8e_{2}H{M}_2\left({\Gamma }_1\right)+24e_{1}H{M}_2\left({\Gamma }_2\right)+16M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)+16e_1{e}_2{\delta }^2\left({\Gamma }_1\right)+32e_1\delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right).$$

$$U{B}_R=8e_{2}H{M}_2\left({\Gamma }_1\right)+24e_{1}H{M}_2\left({\Gamma }_2\right)+16M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)+16e_1{e}_2{\Delta }^2\left({\Gamma }_1\right)+32e_1\Delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right).$$

Proof. 

Again, for vertex $(a,b)\in V\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)$, suppose $d(a,b)=d_{\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)}(a,b)$ symbolizes its degree. Then applying the definition of $H{M}_1$ for graph operation R and degree relation provided in Equation (2), we obtain the following:

$$\begin{array}{cc}\hfill H{M}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)& =\sum _{\begin{array}{c}(a_1^{\prime },b_1^{\prime })(a_2^{\prime },b_2^{\prime })\in E\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(R\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{″},b_2^{\prime })\right]}^2\hfill \\ \hfill & =2\sum _{\begin{array}{c}{a}_1^{\prime },a_2^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[2d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+2d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & +2\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_2^{\prime }\in V\left(R\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(R\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[2d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)+2d\left(a_1^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}3\end{array}}+\sum _{\begin{array}{c}4\end{array}}.\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}3\end{array}}& =8\sum _{\begin{array}{c}{a}_1^{\prime },a_2^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =8\sum _{\begin{array}{c}{a}_1^{\prime },a_2^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left[{\left(d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)\right)}^2+{\left(d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right)}^2+2d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]\hfill \\ \hfill & =8\left[e_{2}H{M}_2\left({\Gamma }_1\right)+e_{1}H{M}_2\left({\Gamma }_2\right)+2M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\right].\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}4\end{array}}& =8\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_2^{\prime }\in V\left(R\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(R\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)+d\left(a_1^{\prime }\right)\right]}^2\hfill \\ \hfill & =8\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_2^{\prime }\in V\left(R\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(R\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left[{\left(d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right)}^2+d^2\left(a_1^{\prime }\right)+2d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)d\left(a_1^{\prime }\right)\right]\hfill \\ \hfill & =8\sum _{\begin{array}{c}{a}_1^{\prime }\in V\left({\Gamma }_1\right)\\ a_2^{\prime }\in V\left(R\left({\Gamma }_1\right)\right)-V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left(R\left({\Gamma }_1\right)\right)\end{array}}\left[H{M}_2\left({\Gamma }_2\right)+e_2{d}^2\left(a_1^{\prime }\right)+2d\left(a_1^{\prime }\right)M_2\left({\Gamma }_2\right)\right]\hfill \\ \hfill & =8\left[2e_{1}H{M}_2\left({\Gamma }_2\right)+2e_1{e}_2{d}^2\left(a_1^{\prime }\right)+4e_{1}d\left(a_1^{\prime }\right)M_2\left({\Gamma }_2\right)\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \ge 16\left[e_{1}H{M}_2\left({\Gamma }_2\right)+e_1{e}_2{\delta }^2\left({\Gamma }_1\right)+2e_1\delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\right]\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \le 16\left[e_{1}H{M}_2\left({\Gamma }_2\right)+e_1{e}_2{\Delta }^2\left({\Gamma }_1\right)+2e_1\Delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\right]\hfill \end{array}$$

(11)

Now, using minimum and maximum degrees of ${\Gamma }_2$, to obtain the lower and upper bounds on the FHZI for the graph $\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)$ as follows:

$$L{B}_R=8e_{2}H{M}_2\left({\Gamma }_1\right)+24e_{1}H{M}_2\left({\Gamma }_2\right)+16M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)+16e_1{e}_2{\delta }^2\left({\Gamma }_1\right)+32e_1\delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right).$$

$$U{B}_R=8e_{2}H{M}_2\left({\Gamma }_1\right)+24e_{1}H{M}_2\left({\Gamma }_2\right)+16M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)+16e_1{e}_2{\Delta }^2\left({\Gamma }_1\right)+32e_1\Delta \left({\Gamma }_1\right)M_2\left({\Gamma }_2\right).$$

□

Example 3. 

Now we check the validity of our bounds derived in Theorem 2, for R-sum graph depicted in Figure 4 where ${\Gamma }_1=P_3={\Gamma }_2$. Using values of TI involved in our bounds from Table 1 the lower and upper bounds of $H{M}_1$ are computed as $L{B}_R\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=1232$, $U{B}_R\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=1680$. To calculate the exact value of $H{M}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)$, we require the edge partition of the graph ${\Gamma }_1{\otimes }_R{\Gamma }_2$. Upon observation, the edge-cardinality with degree of end-vertex pairs $(2,4)$, $(4,4)$, and $(2,8)$ is 8 in each case. The exact value is computed as $H{M}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=1600$. It is clearly observed that $L{B}_R=1232\le H{M}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=1600\le 1680=U{B}_R$.

Example 4. 

Again, to verify the accuracy of our results presented in Theorem 2 for the R-sum graph illustrated in Figure 5, where ${\Gamma }_1=P_4$ and ${\Gamma }_2=C_3$, we use the values of the topological indices involved in our bounds from Table 1. The lower and upper bounds for the $H{M}_1$ of the graph ${\Gamma }_1{\otimes }_R{\Gamma }_2$ are computed as $L{B}_R\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=6864$ and $U{B}_R\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=8448$, respectively. To determine the exact value of ${HM}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)$, it is necessary to obtain the edge partition of the graph ${\Gamma }_1{\otimes }_R{\Gamma }_2$. It is observed that the edge-cardinality with degree of end-vertex pairs $(8,8)$, $(4,4)$, and $(4,8)$ are 6, 12, and 36, in the respective order. Based on the edge partition described, the exact value is calculated as ${HM}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=7488$. This result satisfies the bound, $L{B}_R=6864\le {HM}_1\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)=7488\le 8448=U{B}_R$.

Theorem 3. 

Let ${\Gamma }_1$ and ${\Gamma }_2$ be two connected, simple and finite graphs then the upper and lower bound on FHZI of graph $\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)$ is

$$UB\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=2\left[e_2\delta ({{\Gamma }_1)}^2+e_2{\chi }_4\left({\Gamma }_1\right)+2M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right)+2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right)\right].$$

$$LB\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=2\left[e_2\delta {\left({\Gamma }_1\right)}^2+e_2{\chi }_4\left({\Gamma }_1\right)+2M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)+2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)\right].$$

Proof. 

For vertex $(a,b)$ belonging to Q-sum under Direct product $\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)$, suppose $d(a,b)=d_{\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)}(a,b)$ symbolizes the degree of $(a,b)$. Utilizing the definition of $H{M}_1$ and the degree relation illustrated by Equation (3), we obtain the following:

$$\begin{array}{cc}\hfill H{M}_1\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)& =\sum _{\begin{array}{c}(a_1^{\prime },b_1^{\prime })(a_2^{\prime },b_2^{\prime })\in E\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(Q\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2.\hfill \end{array}$$

(12)

The sum presented in Equation (12) can be divided into two sums, ${\sum }_{\begin{array}{c}5\end{array}}$ and ${\sum }_{\begin{array}{c}6\end{array}}$, based upon the edge classification. We proceed in the following manner. □

• Classification I: Suppose $\acute{b}$ be placed in edge $a_1^{\prime }{a}_2^{\prime }\in E\left({\Gamma }_1\right)$. Then

  $$\begin{array}{cc}\hfill \sum _{\begin{array}{c}5\end{array}}& =2\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(Q\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(b_1^{\prime }\right)+(d\left(a_1^{\prime }\right)+\acute{b})d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =2\sum _{\begin{array}{c}{a}_1^{\prime }\acute{b}\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d\left(a_1^{\prime }\right)d\left(b_1^{\prime }\right)+{(d\left(a_1^{\prime }\right)+d\left(\acute{b}\right))}^{2}d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =2\sum _{\begin{array}{c}{a}_1^{\prime }\acute{b}\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left[d{\left(a_1^{\prime }\right)}^{2}d{\left(b_1^{\prime }\right)}^2+{(d\left(a_1^{\prime }\right)+d\left(\acute{b}\right))}^{4}d{\left(b_2^{\prime }\right)}^2+2(d\left(a_1^{\prime }\right)+d\left(\acute{b}\right))d\left(a_1^{\prime }\right)d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]\hfill \\ \hfill & =2[\sum _{\begin{array}{c}{a}_1^{\prime }\acute{b}\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}d{\left(a_1^{\prime }\right)}^{2}d{\left(b_1^{\prime }\right)}^2+\sum _{\begin{array}{c}{a}_1^{\prime }\acute{b}\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{(d\left(a_1^{\prime }\right)+d\left(\acute{b}\right))}^{4}d{\left(b_2^{\prime }\right)}^2\hfill \\ \hfill & +\sum _{\begin{array}{c}{a}_1^{\prime }\acute{b}\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}2(d\left(a_1^{\prime }\right)+d\left(\acute{b}\right))d\left(a_1^{\prime }\right)d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)].\hfill \end{array}$$

  (13)

  Now, replacing sums of suitable TIs, lower and upper degrees of base graphs in Equation (13), we obtain the following results.

  $$\sum _{\begin{array}{c}5\end{array}}\le 2\left[e_2\delta {\left({\Gamma }_1\right)}^2+e_2{\chi }_4\left({\Gamma }_1\right)+2M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right)\right].$$

  (14)

  $$\sum _{\begin{array}{c}5\end{array}}\ge 2\left[e_2\delta {\left({\Gamma }_1\right)}^2+e_2{\chi }_4\left({\Gamma }_1\right)+2M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)\right].$$

  (15)
• Classification II: Suppose vertices $a_1^{\prime }$ and $a_2^{\prime }$ be placed in the edges $w_1{w}_2$ and $w_2{w}_3$ belonging to $E\left({\Gamma }_1\right)$. Then

  $$\begin{array}{cc}\hfill \sum _{\begin{array}{c}6\end{array}}& =2\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(Q\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[\left(d\left(w_1\right)+d\left(w_2\right)\right)d\left(b_1^{\prime }\right)+\left(d\left(w_2\right)+d\left(w_3\right)\right)d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =2\sum _{\begin{array}{c}{w}_1{w}_2,\\ w_2{w}_3\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}[{\left(d\left(w_1\right)+d\left(w_2\right)\right)}^{2}d{\left(b_1^{\prime }\right)}^2+{\left(d\left(w_2\right)+d\left(w_3\right)\right)}^{2}d{\left(b_2^{\prime }\right)}^2\hfill \\ \hfill & +2\left(d\left(w_1\right)+d\left(w_2\right)\right)\left(d\left(w_2\right)+d\left(w_3\right)\right)d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)]\hfill \\ \hfill & =2[\sum _{\begin{array}{c}{w}_1{w}_2,\\ w_2{w}_3\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left(d\left(w_1\right)+d\left(w_2\right)\right)}^{2}d{\left(b_1^{\prime }\right)}^2+\sum _{\begin{array}{c}{w}_1{w}_2,\\ w_2{w}_3\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left(d\left(w_2\right)+d\left(w_3\right)\right)}^{2}d{\left(b_2^{\prime }\right)}^2\hfill \\ \hfill & +2\sum _{\begin{array}{c}{w}_1{w}_2,\\ w_2{w}_3\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}\left(d\left(w_1\right)+d\left(w_2\right)\right)\left(d\left(w_2\right)+d\left(w_3\right)\right)d\left(a_2^{\prime }\right)d\left(b_2^{\prime }\right)]\hfill \end{array}$$

  (16)

  Now, replacing sums of suitable TIs, lower and upper degrees of base graphs in Equation (16), we obtain the following results.

  $$\sum _{\begin{array}{c}6\end{array}}\le 2\left[2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right)\right].$$

  (17)

  $$\sum _{\begin{array}{c}6\end{array}}\ge 2\left[2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)\right]$$

  (18)

  Combining Equations (14) with (17) and Equations (15) with (18), we obtain the desired upper and lower bounds of Q-sum under Direct product of ${\Gamma }_1$ with ${\Gamma }_2$.

Example 5. 

To examine the correctness of results established in Theorem 3 for Q-sum graphs, we again take ${\Gamma }_1=P_3={\Gamma }_2$. To calculate the bounds on FHZI using the required parameters and values of relevant TIs from Table 1, we have $L{B}_Q\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=1060$ and $U{B}_Q\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=1168$. To calculate the actual value of ${HM}_1\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)$, we require the edge partition of the graph ${\Gamma }_1{\otimes }_Q{\Gamma }_2$. It is observed that the edge-cardinality with end-vertex degree pairs $(1,6)$, $(2,6)$, $(2,3)$, $(3,4)$, and $(3,6)$ is 4 in each case. The actual calculated value is ${HM}_1\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=1072$. In this case, bounds given by our formulas work well.

Example 6. 

To compute the upper and lower bounds of ${HM}_1$ using formulas calculated in Theorem 3. Let ${\Gamma }_1=P_4$, ${\Gamma }_2=C_3$, $n_1=\left|V\left({\Gamma }_1\right)\right|=4$, $n_2=\left|V\left({\Gamma }_2\right)\right|=3$, $e_1=\left|E\left({\Gamma }_1\right)\right|=3$, $e_2=\left|E\left({\Gamma }_2\right)\right|=3$, $\delta \left({\Gamma }_1\right)=1$, $\delta \left({\Gamma }_2\right)=1$, $\Delta \left({\Gamma }_1\right)=2$, $\Delta \left({\Gamma }_2\right)=2$. For the actual value of ${HM}_1\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)$, we require partitioning of the edge set of graph $\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)$, and we detect edges whose end-vertices having degrees $(2,6)$, $(4,6)$, $(4,8)$, and $(6,8)$ are 12 each. The exact value of FHZI for the Q-sum graph is ${HM}_1\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=6690$. Using values of desired TIs from Table 1, the lower and upper bounds are $L{B}_Q\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=5586$ and $U{B}_Q\left({\Gamma }_1{\otimes }_Q{\Gamma }_2\right)=7044$. In this scenario the bounds computed perform well.

Theorem 4. 

Let ${\Gamma }_1$ and ${\Gamma }_2$ be two connected, simple, and finite graphs; then the upper and lower bound on the FHZI of graph $\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)$ are

$$UB\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)=8\left[e_{2}H{M}_2\left({\Gamma }_1\right)+e_{1}H{M}_2\left({\Gamma }_2\right)+2M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\right]+2\left[2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\Delta \left({\Gamma }_1\right)\right].$$

$$LB\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)=8\left[e_{2}H{M}_2\left({\Gamma }_1\right)+e_{1}H{M}_2\left({\Gamma }_2\right)+2M_2\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\right]+2\left[2H{M}_1\left({\Gamma }_1\right)M_1\left({\Gamma }_2\right)+4M_1\left({\Gamma }_1\right)M_2\left({\Gamma }_2\right)\delta \left({\Gamma }_1\right)\right].$$

Proof. 

Let $d(a,b)=d_{\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)}(a,b)$ represent the degree of the vertex $(a,b)$ in the T-sum graph under the Direct product, where $(a,b)\in V\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)$. Utilizing the definition of the first hyper-Zagreb index $H{M}_1$ for the T-sum graph in conjunction with Equation (4), we obtain

$$\begin{array}{cc}\hfill H{M}_1\left({\Gamma }_1{\otimes }_T{\Gamma }_2\right)& =\sum _{\begin{array}{c}(a_1^{\prime },b_1^{\prime })(a_2^{\prime },b_2^{\prime })\in E\left({\Gamma }_1{\otimes }_R{\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(T\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[d(a_1^{\prime },b_1^{\prime })+d(a_2^{\prime },b_2^{\prime })\right]}^2\hfill \\ \hfill & =2\sum _{\begin{array}{c}{a}_1^{\prime },a_2^{\prime }\in V\left({\Gamma }_1\right)\\ a_1^{\prime }{a}_2^{\prime }\in E\left({\Gamma }_1\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[2d\left(a_1^{\prime }\right)d\left(a_2^{\prime }\right)+2d\left(b_1^{\prime }\right)d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & +2\sum _{\begin{array}{c}{a}_1^{\prime }{a}_2^{\prime }\in E\left(T\left({\Gamma }_1\right)\right)\end{array}}\sum _{\begin{array}{c}{b}_1^{\prime }{b}_2^{\prime }\in E\left({\Gamma }_2\right)\end{array}}{\left[\left(d\left(w_1\right)+d\left(w_2\right)\right)d\left(b_1^{\prime }\right)+\left(d\left(w_2\right)+d\left(w_3\right)\right)d\left(b_2^{\prime }\right)\right]}^2\hfill \\ \hfill & =\sum _{\begin{array}{c}7\end{array}}+\sum _{\begin{array}{c}8\end{array}}.\hfill \end{array}$$

(19)

By definition, the T-sum graph is constructed by simultaneously applying the R and Q operations. Consequently, it inherits the edges from both the R-sum and Q-sum graphs. Therefore, ${\sum }_{\begin{array}{c}7\end{array}}$ and ${\sum }_{\begin{array}{c}8\end{array}}$ correspond exactly to Equations (9) and (16), respectively. By substituting Equations (9) and (18) into Equation (19), we obtain the required formula for the lower bound of $H{M}_1$ for T-sum graphs. Similarly, by substituting Equations (9) and (17) into Equation (19), the upper bound on $H{M}_1$ for T-sum graphs is derived. The validity of the formulas of bounds for T-sum under the Direct product will automatically be guaranteed for both examples of graphs $\left(P_3{\otimes }_T{P}_3\right)$ and $\left(P_4{\otimes }_T{C}_3\right)$ as T-sum is attained from R-sum and Q-sum, simultaneously. □

2.1. Numerical Illustration

To validate the derived closed-form relations, we evaluated the first hyper-Zagreb index for several representative tensor-based F-sum graphs. Table 2 lists numerical results for small cases of $P_n\otimes P_m$ and $C_n\otimes C_m$, confirming agreement with the analytical bounds established in Section 3.

Table 2. Computed values of ${HM}_1$ for selected tensor product graphs.

Graph/Indices	Expression of ${\mathit{HM}}_1$	Expression of ${\mathit{M}}_1$	Expression of ${\mathit{M}}_2$
$P_n\otimes P_m$	$128mn-240(m+n)+452$	$16mn-24(m+n)+36$	$16mn-32(m+n)+64$
$C_n\otimes C_m$	$128mn$	$16mn$	$16mn$
$C_n\otimes P_m$	$72m(n-1)$	$16mn-24n$	$16mn-32n$

These values exhibit linear growth consistent with the expected quadratic dependence on degree distribution, verifying the theoretical expressions for $H{M}_1$ under tensor and F-sum graph constructions.

2.2. Comparative Behavior of Related Indices

To further elucidate the sensitivity of the first hyper-Zagreb index $H{M}_1$, we compared its behavior with the classical first and second Zagreb indices, $M_1$ and $M_2$, respectively, over identical tensor product graphs. The analysis shows a consistent ordering

$$H{M}_1>M_1\ge M_2,$$

which holds across both acyclic and cyclic tensor combinations.

The numerical hierarchy in Table 3 confirms that $H{M}_1$ responds more strongly to local degree fluctuations and non-linear edge interactions, while $M_1$ primarily captures the total degree sum and $M_2$ emphasizes the multiplicities of the degrees of the pairs, $H{M}_1$ integrates both effects quadratically, resulting in enhanced sensitivity to branching, cyclicity, and vertex heterogeneity.

Table 3. Comparative values of ${HM}_1$, $M_1$, and $M_2$ indices for selected tensor product graphs.

Values/Graph	${\mathit{P}}_3\otimes {\mathit{P}}_3$	${\mathit{P}}_4\otimes {\mathit{P}}_3$	${\mathit{C}}_3\otimes {\mathit{C}}_3$	${\mathit{C}}_4\otimes {\mathit{C}}_3$	${\mathit{C}}_3\otimes {\mathit{P}}_3$	${\mathit{C}}_4\otimes {\mathit{P}}_3$
$M_1$	36	60	144	192	72	96
$M_2$	16	32	144	192	48	64
$H{M}_1$	64	576	1152	1536	432	576

This effect is most prominent in dense tensor products (e.g., $C_n\otimes C_m$), where vertex-degree distributions are highly non-uniform. The amplified $H{M}_1$ values reflect greater topological compactness and potential electron delocalization in corresponding molecular frameworks. Hence, $H{M}_1$ serves as a more discriminating topological descriptor for characterizing molecular complexity, stability, and conjugation density in QSPR and QSAR analyses.

Lemma 1. 

Let $P_n$ and $P_m$ be two paths of length n and m, respectively. Then values of $H{M}_1$ for the unary graph operations $(S,R,Q,T)$ under direct product are given as:

1. 

$H{M}_1\left(P_n{\otimes }_S{P}_m\right)=256mn-368m-480n+692$

2. 

$H{M}_1\left(P_n{\otimes }_R{P}_m\right)=1088mn-1856m-2032n+3472$

3. 

$H{M}_1\left(P_n{\otimes }_Q{P}_m\right)=2n^3(8mn-16m-15n+31)+16n(5mn-2m-10n+5)-112m+196$

4. 

$H{M}_1\left(P_n{\otimes }_T{P}_m\right)=2n^3(8mn-16m-15n+31)+16n(9mn+36m-18n-64)-1408m+2592$

Lemma 2. 

Let $C_n$ and $C_m$ be two paths of length n and m, respectively. Then values of $H{M}_1$ for the unary graph operations $(S,R,Q,T)$ under direct product are given as follows:

1. 

$H{M}_1\left(C_m{\otimes }_S{C}_n\right)=256mn$;

2. 

$H{M}_1\left(C_m{\otimes }_R{C}_n\right)=1088mn$;

3. 

$H{M}_1\left(C_m{\otimes }_Q{C}_n\right)=16mn(n^3+2n^2+5n+8)$;

4. 

$H{M}_1\left(C_m{\otimes }_T{C}_n\right)=16mn(n^3+2n^2+9n+56)$.

3. Conclusions

From a chemical graph theoretical perspective, tensor product operations enable the modeling of a wide range of molecular graphs, including lattice-like crystalline networks, nanotubes, nanotorus graphs, and polymeric or macromolecular structures. For instance, products such as $(P_n\otimes C_m)$ or $(C_n\otimes C_m)$ are used to represent periodic crystalline frameworks and nanostructured surfaces, while $(C_n\otimes P_m)$ can describe linear polymeric chains such as polyphenylene systems. Moreover, in combination with unary graph operations $F\in \{S,R,Q,T\}$, tensor-based F-sum graphs effectively characterize cross-linked polymer networks and paraline polymeric materials, including bakelite, vulcanite, and PMMA, see Table 4. For a broad class of graphs, particularly F-sum operations involving the Direct product, the computation of upper and lower bounds for a specific topological index $\left(H{M}_1\right)$ is a compelling and significant topic for researchers. Our efforts are directed toward addressing this problem. Specifically, we have derived and presented closed-form formulas for the lower and upper bounds of the first hyper-Zagreb index for four F-sum graph operations based on the Direct product, expressed in terms of the order, size, and topological indices of the original graphs. Furthermore, we extended our formulations to several specific circumstances by contrasting the precise value of $H{M}_1$ with bounds computed with the use of derived formulas. It is evident that the computed bounds perform adequately well and support the validity of our results. An intriguing direction for future research is to extend the results obtained for the first hyper-Zagreb index ($H{M}_1$) of F-sum graphs under the Direct product to other types of graph products, such as the standard (normal) product or the corona product. Another interesting and challenging problem is to determine the conditions under which the lower and upper bounds established in this work become equal.

Table 4. Chemical interpretation of tensor and F-sum graph operations for representative molecular and polymeric architectures.

Graph Operation	Representative Form	Chemical Analogy	Example Materials	Modeling Significance
Tensor (Direct) Product of Paths	$P_n\otimes P_m$	2D lattice or grid-like crystalline framework	Metal–organic frameworks, graphene sheets	Models periodic atomic connectivity and crystalline topology
Tensor Product of Cycles	$C_n\otimes C_m$	Toroidal or nanotubular structure	Carbon nanotorus, boron nitride nanotube	Captures curvature and cyclic conjugation patterns
Cycle–Path Tensor Product	$C_n\otimes P_m$	Linear or chain-type polymeric structure	Polyphenylene, polyethylene oxide	Represents sequentially repeating monomer units
Tensor-based F-sum Graphs ($F\in \{S,R,Q,T\}$)	$F\left({\Gamma }_1\right)\otimes {\Gamma }_2$	Cross-linked polymeric networks	Metal–organic frameworks, Zeolite, Crystalline polymer	Encodes branching, cross-link density, and local reactivity variation
Tensor Product of Derived Unary Graphs	$F\left({\Gamma }_1\right)\otimes F\left({\Gamma }_2\right)$	Nanostructured composite systems	Hybrid nanopolymers, supramolecular frameworks	Captures multilevel structural hierarchy (monomer → macrostructure)

The structural analogies summarized in Table 4 highlight how tensor and F-sum graph products serve as powerful abstractions for real molecular systems. These mappings provide a framework to interpret variations in $H{M}_1$ values in terms of molecular branching, cross-linking intensity, and topological symmetry.