Metric Dimensions of Metric Spaces over Vector Groups

Abstract

Let $(X,\rho )$ be a metric space. A subset A of X resolves X if every point $x\in X$ is uniquely identified by the distances $\rho (x,a)$ for all $a\in A$. The metric dimension of $(X,\rho )$ is the minimum integer k for which a set A of cardinality k resolves X. We consider the metric spaces of Cayley graphs of vector groups over $\mathbb{Z}$. It was shown that for any generating set S of $\mathbb{Z}$, the metric dimension of the metric space $X=X(\mathbb{Z},S)$ is, at most, $2\max S$. Thus, $X=X(\mathbb{Z},S)$ can be resolved by a finite set. Let $n\in \mathbb{N}$ with $n\ge 2$. We show that for any finite generating set S of ${\mathbb{Z}}^n$, the metric space $X=X({\mathbb{Z}}^n,S)$ cannot be resolved by a finite set.

1. Cayley Graphs

Let G be a finitely generated group and let $S\subseteq G$ be a finite generating set of G with $1\notin S$ and $S^{-1}=S$. The Cayley graph $X=X(G,S)$ is constructed by specifying its vertices and edges as follows:

$$V\left(X\right)=G,E\left(X\right)=\{gh:g,h\in G,g{h}^{-1}\in S\}.$$

This definition can be found in [1] (p. 34).

In the Cayley graph, the condition $S^{-1}=S$ ensures the graph is undirected, while the condition $1\notin S$ ensures the absence of loops. The requirement that S is a generating set for G guarantees that X is connected. The connectivity is important because the focus of this paper is on the metric properties of this particular family of Cayley graphs. The Cayley graphs presented in this paper are defined using the additive abelian group of vector groups over the integers.

The concepts of metric spaces, distances, and geodesics are fundamental, and readers may consult any book or monograph on metric spaces or distance geometry for further details. Our sources include [2,3]. The concept of the metric dimension of a metric space was first introduced in 1953 in [2]. It gained limited attention until 1975, when it was applied to graph vertices [4,5,6,7,8,9,10,11,12,13]. This concept has been extensively studied in graph theory, often motivated by its applications in radio and telecommunications, with a recent focus on geographic positioning systems (GPS). Determining the metric dimension is shown to be an NP-complete problem in [14].

As in [15], let X be a metric space with distance function $\rho :X\times X\to [0,+\infty )$. Let D be a nonempty subset of X with finite or countably infinite cardinality, which can be written as $D=\{v_1,v_2,\dots ,v_n,\dots \}$. If for every $x,y\in X$, the condition $x\ne y$ implies $\rho (v_i,x)\ne \rho (v_i,y)$ for at least one index i, then D is said to resolveX and is called a resolving set or simply a resolver for X. A resolving set of minimum cardinality is called a metric basis for X. The cardinality of the minimum resolving set is called the metric dimension of X, denoted by $\beta \left(X\right)$. Note that the condition for D to be resolving can be equivalently written as follows:

$$\forall i\in \{1,2,\dots ,n,\dots \},\rho (v_i,x)=\rho (v_i,y)\Rightarrow x=y.$$

In [15], the metric dimensions of the three classical geometric spaces were determined, and it was shown that $\beta \left(R\right)=3$ for each Riemann surface R. In [16,17], the metric dimensions of geometric spaces and metric manifolds were determined.

The focus of the present paper is on Cayley graphs of ${\mathbb{Z}}^n$. In [18], it was shown that for any generating set S of $\mathbb{Z}$, the metric dimension of the metric space $X=X(\mathbb{Z},S)$ is at most $2\max S$. Thus, $X=X(\mathbb{Z},S)$ can be resolved by a finite set. Let $n\ge 2$. We will show that for any finite generating set S of ${\mathbb{Z}}^n$, the metric space $X=X({\mathbb{Z}}^n,S)$ cannot be resolved by a finite set.

2. Convex Polytopes

As noted in [19] (p. 8), a set $K\subset {\mathbb{R}}^n$ is convex if, and only if, for every pair of distinct points $\alpha ,\beta \in K$, the closed segment connecting $\alpha$ and $\beta$ is entirely contained in K. The convex hull $convA$ of a subset A of ${\mathbb{R}}^n$ is defined as the intersection of all convex sets in ${\mathbb{R}}^n$ that contain A.

As in [19] (p. 10), let A be a subset of ${\mathbb{R}}^n$ and let $\alpha \in A$ with $\alpha \ne \overrightarrow{0}$. We say that a hyperplane

$$H=\{x\in {\mathbb{R}}^n:⟨x,\alpha ⟩=b\}$$

cuts A if there exist points $x_1,x_2\in A$ such that $⟨x_1,\alpha ⟩<b$ and $⟨x_2,\alpha ⟩>b$. A hyperplane H is said to support A if H does not cut A, and $\rho (A,H)=0$. In particular, H supports A if either

$$\sup \{⟨x,\alpha ⟩:x\in A\}=b\mathrm{or}\inf \{⟨x,\alpha ⟩:x\in A\}=b.$$

As in [19] (p. 17), let K be a convex subset of ${\mathbb{R}}^n$. A set $F\subseteq K$ is called a face of K if $F=\varnothing$, $F=K$, or if there exists a supporting hyperplane H of K such that $F=K\cap H$. ∅ and K are called the improper faces of K. For a polytope K, maximal proper faces are called facets of K.

Theorem 1

([20] (p. 59)). Let P be a polytope of dimension n in ${\mathbb{R}}^n$. Then, P has at least $n+1$ facets.

Lemma 1.

Let ${\alpha }_0\in {\mathbb{R}}^n$ with ${\alpha }_0\ne \overrightarrow{0}$ and $b\in \mathbb{R}$ with $b\ne 0$. Let $H=\{x\in {\mathbb{R}}^n:⟨x,{\alpha }_0⟩=b\}$ be a hyperplane of ${\mathbb{R}}^n$ and $H_0$ be the closed halfspace of ${\mathbb{R}}^n$ cut by H with 0. Let ${\alpha }_{r+1}\in H$, ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r\in H_0$, $r\in \mathbb{N}$ and $p_i\in \mathbb{R}$. If ${\displaystyle \sum _{i=1}^r}{p}_i{\alpha }_i={\alpha }_{r+1}$, then ${\displaystyle \sum _{i=1}^r}{p}_i\ge 1$.

Proof. 

Let ${\alpha }_0\in {\mathbb{R}}^n$ with ${\alpha }_0\ne \overrightarrow{0}$ and $b\in \mathbb{R}$ with $b\ne 0$. Suppose that $b>0$ and $H=\{x\in {\mathbb{R}}^n:⟨x,{\alpha }_0⟩=b\}$. According to the definition of $H_0$, we have $H_0=\{x\in {\mathbb{R}}^n:⟨x,{\alpha }_0⟩\le b\}$. Let ${\alpha }_i=(a_{i1},a_{i2},\dots ,a_{in})$, $i=\{0,1,\dots ,r+1\}$. Since ${\displaystyle \sum _{i=1}^r}{p}_i{\alpha }_i={\alpha }_{r+1}$, we have

$$\left\{\begin{array}{c}{p}_1{a}_{11}+p_2{a}_{21}+\cdots +p_r{a}_{r1}=a_{r+1,1}\hfill \\ p_1{a}_{12}+p_2{a}_{22}+\cdots +p_r{a}_{r2}=a_{r+1,2}\hfill \\ \cdots \hfill \\ p_1{a}_{1n}+p_2{a}_{2n}+\cdots +p_r{a}_{rn}=a_{r+1,n}\hfill \end{array}\right..$$

(1)

Since ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r\in H_0$, we have $a_{i1}{a}_{01}+a_{i2}{a}_{02}+\cdots +a_{in}{a}_{0n}\le b$, $i=\{1,2,\dots ,r\}$. Then, $a_{in}{a}_{0n}\le b-a_{i1}{a}_{01}-a_{i2}{a}_{02}-\cdots -a_{i,n-1}{a}_{0,n-1}$, $i=\{1,2,\dots ,r\}$. According to (1), we have

$$a_{r+1,n}={\displaystyle \sum _{i=1}^r}{p}_i{a}_{in}.$$

Hence,

$$\begin{array}{cc}\hfill a_{r+1,n}{a}_{0n}& ={\displaystyle \sum _{i=1}^r}{p}_i{a}_{in}{a}_{0n}\hfill \\ \hfill & \le {\displaystyle \sum _{i=1}^r}{p}_i\left(b-a_{i1}{a}_{01}-a_{i2}{a}_{02}-\cdots -a_{i,n-1}{a}_{0,n-1}\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^r}{p}_{i}b-\left({\displaystyle \sum _{i=1}^r}{p}_i{a}_{i1}{a}_{01}+{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i2}{a}_{02}+\cdots +{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i,n-1}{a}_{0,n-1}\right).\hfill \end{array}$$

According to (1), we have

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left({\displaystyle \sum _{i=1}^r}{p}_i{a}_{i1}{a}_{01}+{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i2}{a}_{02}+\cdots +{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i,n-1}{a}_{0,n-1}\right)\hfill \\ \hfill =& {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left(a_{r+1,1}{a}_{01}+a_{r+1,2}{a}_{02}+\cdots +a_{r+1,n-1}{a}_{0,n-1}\right).\hfill \end{array}$$

Then,

$$a_{r+1,n}{a}_{0n}\le {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left(a_{r+1,1}{a}_{01}+a_{r+1,2}{a}_{02}+\cdots +a_{r+1,n-1}{a}_{0,n-1}\right).$$

Hence, ${\displaystyle \sum _{i=1}^r}{p}_{i}b\ge ⟨{\alpha }_{r+1},{\alpha }_0⟩$. Since ${\alpha }_{r+1}\in H$, we have ${\displaystyle \sum _{i=1}^r}{p}_{i}b\ge ⟨{\alpha }_{r+1},{\alpha }_0⟩=b$. Since $b>0$, we have ${\displaystyle \sum _{i=1}^r}{p}_i\ge 1$.

Suppose, conversely, that $b<0$ and $H=\{x\in {\mathbb{R}}^n:⟨x,{\alpha }_0⟩=b\}$. According to the definition of $H_0$, we have $H_0=\{x\in {\mathbb{R}}^n:⟨x,{\alpha }_0⟩\ge b\}$. Let ${\alpha }_i=(a_{i1},a_{i2},\dots ,a_{in})$, $i=\{0,1,\dots ,r+1\}$. Since ${\displaystyle \sum _{i=1}^r}{p}_i{\alpha }_i={\alpha }_{r+1}$, we have

$$\left\{\begin{array}{c}{p}_1{a}_{11}+p_2{a}_{21}+\cdots +p_r{a}_{r1}=a_{r+1,1}\hfill \\ p_1{a}_{12}+p_2{a}_{22}+\cdots +p_r{a}_{r2}=a_{r+1,2}\hfill \\ \hfill \cdots \hfill \\ p_1{a}_{1n}+p_2{a}_{2n}+\cdots +p_r{a}_{rn}=a_{r+1,n}\hfill \end{array}\right..$$

(2)

Since ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r\in H_0$, we have $a_{i1}{a}_{01}+a_{i2}{a}_{02}+\cdots +a_{in}{a}_{0n}\ge b$, $i=\{1,2,\dots ,r\}$. Then, $a_{in}{a}_{0n}\ge b-a_{i1}{a}_{01}-a_{i2}{a}_{02}-\cdots -a_{i,n-1}{a}_{0,n-1}$, $i=\{1,2,\dots ,r\}$. According to (2), we have

$$a_{r+1,n}={\displaystyle \sum _{i=1}^r}{p}_i{a}_{in}.$$

Hence,

$$\begin{array}{cc}\hfill a_{r+1,n}{a}_{0n}& ={\displaystyle \sum _{i=1}^r}{p}_i{a}_{in}{a}_{0n}\hfill \\ \hfill & \ge {\displaystyle \sum _{i=1}^r}{p}_i\left(b-a_{i1}{a}_{01}-a_{i2}{a}_{02}-\cdots -a_{i,n-1}{a}_{0,n-1}\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^r}{p}_{i}b-\left({\displaystyle \sum _{i=1}^r}{p}_i{a}_{i1}{a}_{01}+{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i2}{a}_{02}+\cdots +{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i,n-1}{a}_{0,n-1}\right).\hfill \end{array}$$

According to (2), we have

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left({\displaystyle \sum _{i=1}^r}{p}_i{a}_{i1}{a}_{01}+{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i2}{a}_{02}+\cdots +{\displaystyle \sum _{i=1}^r}{p}_i{a}_{i,n-1}{a}_{0,n-1}\right)\hfill \\ \hfill =& {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left(a_{r+1,1}{a}_{01}+a_{r+1,2}{a}_{02}+\cdots +a_{r+1,n-1}{a}_{0,n-1}\right).\hfill \end{array}$$

Then,

$$a_{r+1,n}{a}_{0n}\ge {\displaystyle \sum _{i=1}^r}{p}_{i}b-\left(a_{r+1,1}{a}_{01}+a_{r+1,2}{a}_{02}+\cdots +a_{r+1,n-1}{a}_{0,n-1}\right).$$

Hence, ${\displaystyle \sum _{i=1}^r}{p}_{i}b\le ⟨{\alpha }_{r+1},{\alpha }_0⟩$. Since ${\alpha }_{r+1}\in H$, we have ${\displaystyle \sum _{i=1}^r}{p}_{i}b\le ⟨{\alpha }_{r+1},{\alpha }_0⟩=b$. Since $b<0$, we have ${\displaystyle \sum _{i=1}^r}{p}_i\ge 1$. □

3. Metric Spaces

Let $n\in \mathbb{N}$ with $n\ge 2$. In this section, we will show that for any finite generating set S of ${\mathbb{Z}}^n$, the metric space $X=X({\mathbb{Z}}^n,S)$ cannot be resolved using a finite set.

Lemma 2

([18]). Let A be a finitely generated additive abelian group and S be a finite generating set of A with $S={\left\{s_i\right\}}_{i=1}^p$, $-S=S$ and $0\notin S$. Then, for any $x,y\in X(A,S)$,

$$\rho (x,y)=\min \left\{{\displaystyle \sum _{i=1}^p}{a}_i:y-x={\displaystyle \sum _{i=1}^p}{a}_i{s}_i,a_i\in \mathbb{Z},a_i\ge 0\right\}.$$

Let A be a finitely generated additive abelian group. We assume that $S=\{-s_r,-s_{r-1},\cdots ,-s_1,s_1,\cdots ,s_{r-1},s_r\}$ is a generating set of A with $0\notin S$. Then, according to Lemma 2,

$$\begin{array}{cc}\hfill \rho (x,y)& =\min \left\{{\displaystyle \sum _{i=1}^r}{a}_i+{\displaystyle \sum _{i=1}^r}{b}_i:y-x={\displaystyle \sum _{i=1}^r}{a}_i{s}_i+{\displaystyle \sum _{i=1}^r}{b}_i(-s_i),a_i,b_i\in \mathbb{Z},a_i,b_i\ge 0\right\}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & =\min \left\{{\displaystyle \sum _{i=1}^r}(a_i+b_i):y-x={\displaystyle \sum _{i=1}^r}(a_i-b_i)s_i,a_i,b_i\in \mathbb{Z},a_i,b_i\ge 0\right\}.\hfill \end{array}$$

(4)

Proposition 1.

For any $x,y\in X(A,S)$,

$$\rho (x,y)=\min \left\{{\displaystyle \sum _{i=1}^r}\left|a_i\right|:y-x={\displaystyle \sum _{i=1}^r}{a}_i{s}_i,a_i\in \mathbb{Z}\right\}.$$

(5)

Proof. 

According to Equation (4), we have

$$\rho (x,y)=\min \left\{{\displaystyle \sum _{i=1}^r}(a_i+b_i):y-x={\displaystyle \sum _{i=1}^r}(a_i-b_i)s_i,a_i,b_i\in \mathbb{Z},a_i,b_i\ge 0\right\}.$$

Then, let $c_1,c_2,\cdots ,c_r,d_1,d_2,\cdots ,d_r$ be the nonnegative integers, such that

$${\displaystyle \sum _{i=1}^r}(c_i+d_i)=\min \left\{{\displaystyle \sum _{i=1}^r}(a_i+b_i):y-x={\displaystyle \sum _{i=1}^r}(a_i-b_i)s_i,a_i,b_i\in \mathbb{Z},a_i,b_i\ge 0\right\}$$

and

$$y-x={\displaystyle \sum _{i=1}^r}(c_i-d_i)s_i.$$

Suppose that there exists $i\in \{1,2,\cdots ,r\}$ such that $c_i>0$ and $d_i>0$. If $c_i>d_i$, then let $e_i=c_i-d_i$, $f_i=0$; if $d_i>c_i$, then let $e_i=0$, $f_i=d_i-c_i$. Hence, $c_i+d_i>e_i+f_i>0$ and $(c_i-d_i)s_i=(e_i-f_i)s_i$. If $c_i$ is replaced by $e_i$ and $d_i$ is replaced by $f_i$, then this leads to a contradiction in the minimality of ${\displaystyle \sum _{i=1}^r}(c_i+d_i)$. Therefore, for any $i\in \{1,2,\cdots ,r\}$, $c_i{d}_i=0$. Hence, there exist $a_1,a_2,\cdots ,a_r\in \mathbb{Z}$ such that $a_i=c_i-d_i$ and $|a_i|=c_i+d_i$. Therefore, we have Equation (5). □

From this point on, we assume that

$$S=\{-s_r,-s_{r-1},\cdots ,-s_1,s_1,\cdots ,s_{r-1},s_r\}$$

is a generating set of ${\mathbb{Z}}^n$ with $0\notin S$. Hence, according to Proposition 1, we have Equation (5).

Theorem 2

([21]). Let A be a finitely generated additive abelian group and S be a finite generating set of A with $0\notin S$ and $-S=S$. Let T denote the group of all translations of $X(A,S)$ and let $R=\{1,\rho \}$, where ρ is the reflection at 0. Then, $RT\le \mathit{Isom}X(A,S)$.

According to Theorem 2, any translation of $X({\mathbb{Z}}^n,S)$ is an isometry of $X({\mathbb{Z}}^n,S)$. Then, one of the two points may be chosen to be the origin, which we denote using 0. Hence,

$$\rho (0,x)=\min \left\{{\displaystyle \sum _{i=1}^r}\left|a_i\right|:x={\displaystyle \sum _{i=1}^r}{a}_i{s}_i,a_i\in \mathbb{Z}\right\}.$$

(6)

The convex hull $convS$ of a subset S of ${\mathbb{R}}^n$ is a convex polytopes in ${\mathbb{R}}^n$. If the dimension of $convS$ is less than n, then S is not a generating set of ${\mathbb{Z}}^n$. Hence, the dimension of $convS$ is equal to n. Let F be a facet of $convS$. Let H be a hyperplane of ${\mathbb{R}}^n$ with $F\subseteq H$. Let $S^{\prime }=S\cap F$. Since the dimension of F is $n-1$, $S^{\prime }$ contains n affinely independent vertices $s_1,s_2,\dots ,s_n$ of ${\mathbb{R}}^n$.

Lemma 3.

Let F be a facet of $convS$. Let H be a hyperplane of ${\mathbb{R}}^n$ with $F\subseteq H$. Then, $\overrightarrow{0}\notin H$.

Proof. 

Suppose that $\overrightarrow{0}\in H$. Then, H is a linear subspace of ${\mathbb{R}}^n$ with dimension $n-1$. This contradicts the condition that $s_1,s_2,\dots ,s_n$ are affinely independent vertices. Therefore, $\overrightarrow{0}\notin H$. □

Let $H_0$ be the closed halfspace of ${\mathbb{R}}^n$ cut by H with 0. Then $S\subseteq H_0$. Since $s_1,s_2,\dots ,s_n$ are affinely independent, for any $x\in {\mathbb{R}}^n$, there exist unique coefficients $c_1,c_2,\dots ,c_n\in \mathbb{R}$, such that $x={\displaystyle \sum _{i=1}^n}{c}_i{s}_i$. Let

$${\rho }^{\prime }(0,x)={\displaystyle \sum _{i=1}^n}\left|c_i\right|,x={\displaystyle \sum _{i=1}^n}{c}_i{s}_i.$$

The set

$$\left\{x\in {\mathbb{Z}}^n:x={\displaystyle \sum _{i=1}^n}{a}_i{s}_i,a_1,a_2,\dots ,a_n\in \mathbb{R},0\le a_1,a_2,\dots ,a_n<1\right\}$$

is denoted by $P\left(S^{\prime }\right)$. Let $m=max\{\rho (0,x):x\in P\left(S^{\prime }\right)\}$. The set

$$\left\{x\in {\mathbb{Z}}^n:x={\displaystyle \sum _{i=1}^n}{a}_i{s}_i,a_1,a_2,\dots ,a_n\in \mathbb{R},a_1,a_2,\dots ,a_n\ge 0\right\}$$

is denoted by $Q\left(S^{\prime }\right)$.

Lemma 4.

Let $x\in Q\left(S^{\prime }\right)$. Then, ${\rho }^{\prime }(0,x)\le \rho (0,x)$.

Proof. 

Since $x\in Q\left(S^{\prime }\right)$, there exist $c_1,c_2,\dots ,c_n\in \mathbb{R}$ with $c_i,c_1,c_2,\dots ,c_n\ge 0$ such that $x={\displaystyle \sum _{i=1}^n}{c}_i{s}_i$. If $c_1=c_2=\cdots =c_n=0$, then $x=0$. Hence, ${\rho }^{\prime }(0,x)=\rho (0,x)=0$.

Suppose that there exists $j\in \{1,2,\dots ,n\}$ such that $c_j>0$. According to Equation (6), there exist $a_1,a_2,\dots ,a_r\in \mathbb{Z}$ such that $x={\displaystyle \sum _{i=1}^r}{a}_i{s}_i$ and $\rho (0,x)={\displaystyle \sum _{i=1}^r}\left|a_i\right|$. Hence, ${\displaystyle \sum _{j=1}^n}{c}_j{s}_j=x={\displaystyle \sum _{i=1}^r}{a}_i{s}_i$. Since there exists $j\in \{1,2,\dots ,n\}$ such that $c_j>0$, there exists $p_{ji}\in \mathbb{R}$, $j\in \{1,2,\dots ,n\}$ and $i\in \{1,2,\dots ,r\}$ such that $a_i={\displaystyle \sum _{j=1}^n}{c}_j{p}_{ji}$. Then,

$${\displaystyle \sum _{j=1}^n}{c}_j{s}_j={\displaystyle \sum _{i=1}^r}{a}_i{s}_i={\displaystyle \sum _{i=1}^r}\left({\displaystyle \sum _{j=1}^n}{c}_j{p}_{ji}\right)s_i={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^r}{c}_j{p}_{ji}{s}_i={\displaystyle \sum _{j=1}^n}{c}_j\left({\displaystyle \sum _{i=1}^r}{p}_{ji}{s}_i\right).$$

Hence,

$${\displaystyle \sum _{i=1}^r}{p}_{ji}{s}_i=s_j.$$

According to the assumption of $convS$, F, H and $H_0$, we have $s_1,s_2,\dots ,s_n\in H$ and $s_1,s_2,\dots ,s_r\in H_0$. According to Lemma 1, we have ${\displaystyle \sum _{i=1}^r}{p}_{ji}\ge 1$. Since $c_1,c_2,\dots ,c_n\ge 0$, we have

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=1}^r}{c}_j{p}_{ji}& \ge c_j\hfill \\ \hfill {\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^r}{c}_j{p}_{ji}& \ge {\displaystyle \sum _{j=1}^n}{c}_j\hfill \end{array}$$

Therefore,

$$\rho (0,x)={\displaystyle \sum _{i=1}^r}\left|a_i\right|={\displaystyle \sum _{i=1}^r}\left|{\displaystyle \sum _{j=1}^n}{c}_j{p}_{ji}\right|\ge {\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^n}{c}_j{p}_{ji}\ge {\displaystyle \sum _{j=1}^n}{c}_j={\rho }^{\prime }(0,x).$$

 □

Here is an example of the inequality ${\rho }^{\prime }(0,x)<\rho (0,x)$.

Example 1.

Let $n=2$ and $S=\left\{\right(0,2),(0,1),(2,0),(1,0),(0,-2),(0,-1),(-2,0),(-1,0\left)\right\}$. Let $s_1=(0,2)$ and $s_2=(2,0)$. Then, the line segment $\left\{\right(a,2-a):0\le a\le 2\}$ is a facet of $convS$. Hence, $S^{\prime }=\{s_1,s_2\}$. Then,

$$(5,5)\in Q\left(S^{\prime }\right)=\left\{x\in {\mathbb{Z}}^2:x={\displaystyle \sum _{i=1}^2}{a}_i{s}_i,a_1,a_2\in \mathbb{R},a_1,a_2\ge 0\right\}=\{(a,b):a,b\in \mathbb{R},a,b\ge 0\}.$$

According to the definition of ${\rho }^{\prime }$ and ρ, we have ${\rho }^{\prime }(0,(5,5))=5<6=\rho (0,(5,5))$.

Note that the condition $x\in Q\left(S^{\prime }\right)$ is necessary.

Example 2.

Let $n=2$ and $S=\left\{\right(1,1),(1,-1),(-1,1),(-1,-1),(2,0),(-2,0\left)\right\}$. Let $s_1=(-1,1)$, $s_2=(1,1)$ and $s_3=(2,0)$. Then, the line segment $\left\{\right(a,1):-1\le a\le 1\}$ is a facet of $convS$. Hence, $S^{\prime }=\{s_1,s_2\}$. We have $s_3=(-1)s_1+\left(1\right)s_2\in X({\mathbb{Z}}^2,S)$ and $s_3\notin Q\left(S^{\prime }\right)$. Then,

$${\rho }^{\prime }(0,s_3)=|-1|+\left|1\right|=2>1=\rho (0,s_3).$$

Lemma 5.

For any $k_1,k_2,\dots ,k_n\in \mathbb{Z}$ with $k_1,k_2,\dots ,k_n\ge 0$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)={\displaystyle \sum _{i=1}^n}{k}_i.$$

Proof. 

According to Equation (6), we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)=\min \left\{{\displaystyle \sum _{i=1}^r}\left|a_i\right|:{\displaystyle \sum _{i=1}^n}{k}_i{s}_i={\displaystyle \sum _{i=1}^r}{a}_i{s}_i,a_i\in \mathbb{Z}\right\}.$$

Let $k_{n+1}=k_{n+2}=\cdots =k_r=0$. Then, ${\displaystyle \sum _{i=1}^n}{k}_i{s}_i={\displaystyle \sum _{i=1}^r}{k}_i{s}_i$. Hence,

$${\displaystyle \sum _{i=1}^n}{k}_i={\displaystyle \sum _{i=1}^n}\left|k_i\right|\in \left\{{\displaystyle \sum _{i=1}^r}\left|a_i\right|:{\displaystyle \sum _{i=1}^n}{k}_i{s}_i={\displaystyle \sum _{i=1}^r}{a}_i{s}_i,a_i\in \mathbb{Z}\right\}.$$

Hence,

$${\displaystyle \sum _{i=1}^n}{k}_i={\displaystyle \sum _{i=1}^n}\left|k_i\right|\ge \min \left\{{\displaystyle \sum _{i=1}^r}\left|a_i\right|:{\displaystyle \sum _{i=1}^n}{k}_i{s}_i={\displaystyle \sum _{i=1}^r}{a}_i{s}_i,a_i\in \mathbb{Z}\right\}=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right).$$

According to Lemma 4, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)\ge {\displaystyle \sum _{i=1}^n}{k}_i.$$

Therefore,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)={\displaystyle \sum _{i=1}^n}{k}_i.$$

 □

Lemma 6.

Let $m=max\{\rho (0,x):x\in P\left(S^{\prime }\right)\}$ and $t\in P\left(S^{\prime }\right)$. For any $k_1,k_2,\dots ,k_n\in \mathbb{Z}$ with $k_1,k_2,\dots ,k_n\ge 0$, we have

$${\displaystyle \sum _{i=1}^n}{k}_i\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)\le {\displaystyle \sum _{i=1}^n}{k}_i+m.$$

Proof. 

Let $t={\displaystyle \sum _{i=1}^n}{a}_i{s}_i\in P\left(S^{\prime }\right)$ with $0\le a_1,a_2,\dots ,a_n<1$ and $a_1,a_2,\dots ,a_n\in \mathbb{R}$. By Lemma 4, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)\ge {\rho }^{\prime }\left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)={\displaystyle \sum _{i=1}^n}(k_i+a_i)\ge {\displaystyle \sum _{i=1}^n}{k}_i.$$

According to the Triangle Inequality of metric spaces and Lemma 5, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)+\rho \left(0,t\right)\le {\displaystyle \sum _{i=1}^n}{k}_i+m.$$

Therefore,

$${\displaystyle \sum _{i=1}^n}{k}_i\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)\le {\displaystyle \sum _{i=1}^n}{k}_i+m.$$

 □

Lemma 7.

Let $t\in P\left(S^{\prime }\right)$ and $j\in \{1,2,\dots ,n\}$. Then there exist $N_1,N_2,\dots ,N_n\in \mathbb{Z}$ such that for any $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

Proof. 

Suppose that for any $N_1,N_2,\dots ,N_n\in \mathbb{Z}$, there exist $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$ such that

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\ne \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

According to the Triangle Inequality of metric spaces, we have

$$\rho \left(0,x\right)-1=\rho \left(0,x\right)-\rho \left(0,s_j\right)\le \rho \left(0,x+s_j\right)\le \rho \left(0,x\right)+\rho \left(0,s_j\right)=\rho \left(0,x\right)+1.$$

According to (6), for any $x\in {\mathbb{Z}}^n$, we have $\rho \left(0,x\right),\rho \left(0,x+s_j\right)\in \mathbb{Z}$. Then,

$$\begin{array}{cc}\hfill & \rho \left(0,x+s_j\right)=\rho \left(0,x\right)-1or\hfill \\ \hfill & \rho \left(0,x+s_j\right)=\rho \left(0,x\right)or\hfill \\ \hfill & \rho \left(0,x+s_j\right)=\rho \left(0,x\right)+1.\hfill \end{array}$$

Since

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\ne \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1,$$

we have

$$\begin{array}{cc}\hfill & \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)-1or\hfill \\ \hfill & \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right).\hfill \end{array}$$

Let $N_1=N_2=\dots =N_n=0$. According to the assumption of $N_1,N_2,\dots ,N_n$, there exist $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ such that

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\ne \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

Then,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right).$$

Let $K_1=max\{k_1,k_2,\dots ,k_n\}+1$. Then,

$$\begin{array}{cc}\hfill \rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_1{s}_i+s_j+t\right)& \le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_1-k_i)s_i-s_j\right)\hfill \\ \hfill & \le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_1-k_i)s_i-s_j\right)\hfill \\ \hfill & \le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_1-k_i)s_i-s_j\right)+\rho \left(0,t\right)\hfill \\ \hfill & \le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_1-k_i)s_i-s_j\right)+m.\hfill \end{array}$$

According to Lemma 5,

$$\begin{array}{cc}\hfill & \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_1-k_i)s_i-s_j\right)+m\hfill \\ \hfill =& {\displaystyle \sum _{i=1}^n}{k}_i+{\displaystyle \sum _{i=1}^n}(K_1-k_i)-1+m\hfill \\ \hfill =& n{K}_1+m-1.\hfill \end{array}$$

Then,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_1{s}_i+s_j+t\right)\le n{K}_1+m-1.$$

We are going to show that for any $g\in {\mathbb{Z}}^{+}$, there exists $K_g\in {\mathbb{Z}}^{+}$ such that

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_g{s}_i+s_j+t\right)\le n{K}_g+m-g.$$

The statement holds for $g=1$. Assume the statement holds for $g=l$. Let $N_1=N_2=\dots =N_n=K_l$. According to the assumption of $N_1,N_2,\dots ,N_n$, there exist $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge K_l,k_2\ge K_l,\dots ,k_n\ge K_l$ such that

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\ne \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

Then,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right).$$

Let $K_{l+1}=max\{k_1,k_2,\dots ,k_n\}+1$. Then,

$$\begin{array}{cc}\hfill & \rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_{l+1}{s}_i+s_j+t\right)\hfill \\ \hfill \le & \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)s_i-s_j\right)\hfill \\ \hfill \le & \rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)s_i-s_j\right)\hfill \\ \hfill \le & \rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_l{s}_i+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(k_i-K_l)s_i\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)s_i-s_j\right).\hfill \end{array}$$

According the assumption, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_l{s}_i+t\right)\le n{K}_l+m-l.$$

According to Lemma 5, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}(k_i-K_l)s_i\right)={\displaystyle \sum _{i=1}^n}(k_i-K_l)$$

and

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)s_i-s_j\right)={\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)-1.$$

Then,

$$\begin{array}{cc}\hfill & \rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_l{s}_i+t\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(k_i-K_l)s_i\right)+\rho \left(0,{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)s_i-s_j\right)\hfill \\ \hfill \le & n{K}_l+m-l+{\displaystyle \sum _{i=1}^n}(k_i-K_l)+{\displaystyle \sum _{i=1}^n}(K_{l+1}-k_i)-1\hfill \\ \hfill =& n{K}_{l+1}+m-(l+1).\hfill \end{array}$$

Then,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_{l+1}{s}_i+s_j+t\right)\le n{K}_{l+1}+m-(l+1).$$

Therefore, for any $g\in {\mathbb{Z}}^{+}$, there exists $K_g\in {\mathbb{Z}}^{+}$ such that

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_g{s}_i+s_j+t\right)\le n{K}_g+m-g.$$

Let $g=m+1$. Then,

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_{m+1}{s}_i+s_j+t\right)\le n{K}_{m+1}-1.$$

According to Lemma 6, we have

$$n{K}_{m+1}={\displaystyle \sum _{i=1}^n}{K}_{m+1}\le \rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_{m+1}{s}_i+s_j+t\right).$$

This contradicts

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{K}_{m+1}{s}_i+s_j+t\right)\le n{K}_{m+1}-1.$$

Therefore, there exist $N_1,N_2,\dots ,N_n$ such that for any $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

 □

Lemma 8.

Let $t\in P\left(S^{\prime }\right)$ and $j\in \{1,2,\dots ,n\}$. Let $N_1,N_2,\dots ,N_n\in \mathbb{Z}$ and for any $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

Let $C=\{c_1,c_2,\dots ,c_w\}\subseteq {\mathbb{Z}}^n$ be a finite set. Then, there exists $z\in {\mathbb{Z}}^n$ such that

$$C\subseteq z+{\displaystyle \sum _{i=1}^n}{N}_i{s}_i+Q\left(S^{\prime }\right).$$

Proof. 

According to Lemma 7, there exist $N_1,N_2,\dots ,N_n\in \mathbb{Z}$ such that for any $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

Since $s_1,s_2,\dots ,s_n$ are affinely independent, there exist $q_{j1},q_{j2},\dots ,q_{jn}\in \mathbb{Q}$ such that $c_j={\displaystyle \sum _{i=1}^n}{q}_{ji}{s}_i$, $j=1,2,\dots ,n$. Let $z={\displaystyle \sum _{i=1}^n}\left(\lfloor \min \{q_{1i},q_{2i},\dots ,q_{wi}\}\rfloor -N_i\right)s_i\in {\mathbb{Z}}^n$. Then, for any $c_j={\displaystyle \sum _{i=1}^n}{q}_{ji}{s}_i$, we have

$$\begin{array}{cc}\hfill c_j-z& ={\displaystyle \sum _{i=1}^n}\left(q_{ji}-\left(\lfloor \min \{q_{1i},q_{2i},\dots ,q_{wi}\}\rfloor -N_i\right)\right)s_i\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n}\left(\left(q_{ji}-\lfloor \min \{q_{1i},q_{2i},\dots ,q_{wi}\}\rfloor \right)+N_i\right)s_i\hfill \\ \hfill & \ge {\displaystyle \sum _{i=1}^n}{N}_i{s}_i.\hfill \end{array}$$

Hence,

$$c_j\in z+{\displaystyle \sum _{i=1}^n}{N}_i{s}_i+Q\left(S^{\prime }\right).$$

Therefore,

$$C\subseteq z+{\displaystyle \sum _{i=1}^n}{N}_i{s}_i+Q\left(S^{\prime }\right).$$

 □

Theorem 3.

Let $n\in \mathbb{N}$ with $n\ge 2$. Let S be a finite generating set of ${\mathbb{Z}}^n$. Let $C=\{c_1,c_2,\dots ,c_w\}\subseteq {\mathbb{Z}}^n$ be a finite set. Then, C does not resolve $X=X({\mathbb{Z}}^n,S)$.

Proof. 

According to Lemma 7, there exist $N_1,N_2,\dots ,N_n\in \mathbb{Z}$ such that for any $k_1,k_2,\dots ,k_n\in {\mathbb{Z}}^{+}$ with $k_1\ge N_1,k_2\ge N_2,\dots ,k_n\ge N_n$, we have

$$\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+s_j+t\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}{k}_i{s}_i+t\right)+1.$$

According to Lemma 8, we have $z\in {\mathbb{Z}}^n$, such that

$$C\subseteq z+{\displaystyle \sum _{i=1}^n}{N}_i{s}_i+Q\left(S^{\prime }\right).$$

Since $s_1,s_2,\dots ,s_n$ are affinely independent, there exist $p_1,p_2,\dots ,p_n\in \mathbb{Q}$ such that $z={\displaystyle \sum _{i=1}^n}{p}_i{s}_i$, $j=1,2,\dots ,n$. Then, for any $c_j={\displaystyle \sum _{i=1}^n}{q}_{ji}{s}_i$, we have

$$c_j-z={\displaystyle \sum _{i=1}^n}{q}_{ji}{s}_i-{\displaystyle \sum _{i=1}^n}{p}_i{s}_i={\displaystyle \sum _{i=1}^n}(q_{ji}-p_i)s_i$$

with

$$q_{ji}-p_i\ge N_i,i=1,2,\dots ,n.$$

According to Lemma 7, we have

$$\begin{array}{cc}\hfill & \rho \left(z-s_1,c_j\right)=\rho \left(0,c_j-z+s_1\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}(q_{ji}-p_i)s_i+s_1\right)\hfill \\ \hfill =& \rho \left(0,{\displaystyle \sum _{i=1}^n}(q_{ji}-p_i)s_i\right)+1=\rho \left(0,c_j-z\right)+1=\rho \left(z,c_j\right)+1\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \rho \left(z-s_2,c_j\right)=\rho \left(0,c_j-z+s_2\right)=\rho \left(0,{\displaystyle \sum _{i=1}^n}(q_{ji}-p_i)s_i+s_2\right)\hfill \\ \hfill =& \rho \left(0,{\displaystyle \sum _{i=1}^n}(q_{ji}-p_i)s_i\right)+1=\rho \left(0,c_j-z\right)+1=\rho \left(z,c_j\right)+1\hfill \end{array}$$

Hence, $\rho \left(z-s_1,c_j\right)=\rho \left(z-s_2,c_j\right)$. Therefore, C does not resolve $X=X({\mathbb{Z}}^n,S)$. □

Example 3.

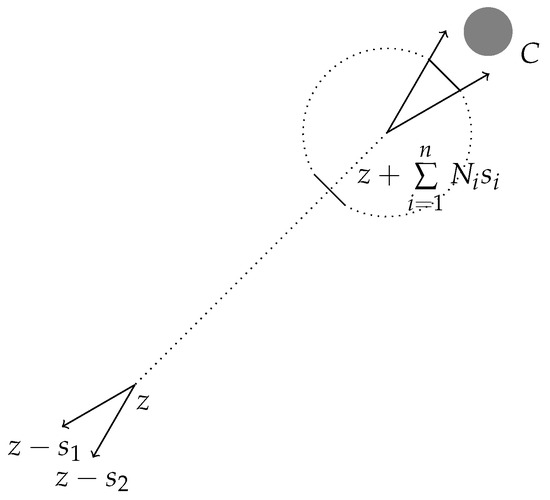
Let $n=2$ and $S=\left\{\left(1,2\right)\right.$, $\left(-1,-2\right)$, $\left(2,1\right)$, $\left(-2,-1\right)$, $\left(0,1\right)$, $\left(0,-1\right)$, $\left(1,0\right)$, $\left.\left(-1,0\right)\right\}$. Let $s_1=\left(1,2\right)$, $s_2=\left(2,1\right)$. Then, the line segment $\left\{\left(a,3-a\right):1\le a\le 2\right\}$ is a facet of $convS$. Hence, $S^{\prime }=\{s_1,s_2\}$. Then,

$$Q\left(S^{\prime }\right)=\left\{x\in {\mathbb{Z}}^2:x={\displaystyle \sum _{i=1}^2}{a}_i{s}_i,a_1,a_2\in \mathbb{R},a_1,a_2\ge 0\right\}.$$

Let $C=\left\{\right(0,0),(0,1),(1,1\left)\right\}$. Then, let $z=(-9,-9)$. Hence, $z-s_1=(-10,-11)$ and $z-s_2=(-11,-10)$. Then,

$$\rho (z-s_1,(0,0))=7=\rho (z-s_2,(0,0)),$$

$$\rho (z-s_1,(0,1))=8=\rho (z-s_2,(0,1)),$$

$$\rho (z-s_1,(1,1))=9=\rho (z-s_2,(1,1)),$$

Therefore, C does not resolve $X=X({\mathbb{Z}}^2,S)$ (see Figure 1).

Figure 1. An illustration of $\rho \left(z-s_1,c_j\right)=\rho \left(z-s_2,c_j\right)$, $c_j\in C$.

4. Conclusions

Let $n\in \mathbb{N}$ with $n\ge 2$. For any finite generating set S of ${\mathbb{Z}}^n$, we proved the metric space $X=X({\mathbb{Z}}^n,S)$ cannot be resolved by a finite set, which means the metric dimension of $X=X({\mathbb{Z}}^n,S)$ is infinite. There are several kinds of generalized metric dimensions, such as the edge metric dimension, strong metric dimension, mixed metric dimension, and so on. The generalized metric dimensions of $X=X({\mathbb{Z}}^n,S)$ should be discussed. Finally, we ask what the metric dimension of metric spaces of Cayley graphs of any finitely generating group is and how the choice of the generating set influences the metric properties of the metric spaces of Cayley graphs.

The metric dimensions of certain subspaces of $X=X({\mathbb{Z}}^n,S)$ remain to be determined. Additionally, which types of isometric subspaces of $X=X({\mathbb{Z}}^n,S)$ cannot be resolved by a finite set remains an open question. Furthermore, the metric dimensions of the metric spaces arising from Cayley graphs of non-abelian groups remain to be determined. This problem is particularly intriguing due to the added complexity introduced by the non-commutative nature of these groups.