Bayesian Estimation of R-Vine Copula with Gaussian-Mixture GARCH Margins: An MCMC and Machine Learning Comparison

Abstract

This study proposes Bayesian estimation of multivariate regular vine (R-vine) copula models with generalized autoregressive conditional heteroskedasticity (GARCH) margins modeled by Gaussian-mixture distributions. The Bayesian estimation approach includes Markov chain Monte Carlo and variational Bayes with data augmentation. Although R-vines typically involve computationally intensive procedures limiting their practical use, we address this challenge through parallel computing techniques. To demonstrate our approach, we employ thirteen bivariate copula families within an R-vine pair-copula construction, applied to a large number of marginal distributions. The margins are modeled as exponential-type GARCH processes with intertemporal capital asset pricing specifications, using a mixture of Gaussian and generalized Pareto distributions. Results from an empirical study involving 100 financial returns confirm the effectiveness of our approach.

1. Introduction

Over the past few decades, following the work of [1], who demonstrated that copula functions can capture non-linear comovement between variables, research on copula-based dependence structure models has grown rapidly. One of the key advantages of copulas, as multivariate distribution tools, is their ability to link different marginal distributions. As a result, copulas have been widely applied across various fields, including hydrology [2], energy [3], agricultural and forest meteorology [4], oceanology [5], computer science [6], insurance [7], and more widely in economics and finance [8,9].

A substantial body of literature demonstrates that copula models, particularly due to their ability to capture tail asymmetry, are highly effective for modeling dependence in quantitative risk management. Tail modeling plays a crucial role in risk assessment, where common measures include Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR), also known as expected shortfall. For formal definitions of risk measures, see [10]. Among multivariate dependence models, standard copulas are widely used. These typically fall into two main families: elliptical and Archimedean copulas (see [11,12,13,14] for details). However, standard multivariate copulas come with certain limitations—most notably, they rely on a single parameter to govern all pairwise tail dependencies. This becomes problematic in high-dimensional settings, where such a simplification can be unrealistic. This limitation was identified by [15], who introduced a more flexible class of models known as regular vine (R-vine) copulas. Two notable subclasses within the vine copula framework are the canonical vine (C-vine) and the drawable vine (D-vine) copulas [16]. Further discussion on vine copulas can be found in Section 2, and additional details are provided in Chapter 3 of [17].

It consists of two copula families: one is elliptical copulas—see Wichitaksorn et al. [11], Liang and Rosen [13] for recent studies—and the other is Archimedean copulas; see Michaelides et al. [14] and Górecki et al. [12] for recent studies.

In the existing literature, research on vine copulas—particularly R-vines—remains relatively limited. This is likely due to their structural complexity and the intensive computational effort required. Specifically, R-vines allow for a significantly larger number of possible tree structures compared to C-vines and D-vines, especially as the dimensionality increases. Despite these challenges, R-vines offer considerable flexibility as dependence models. Their wide range of possible structures makes them highly adaptable, and importantly, they overcome the parameter limitation of standard multivariate copulas. This added flexibility is particularly advantageous for analyzing tail dependence in high-dimensional financial data.

To our knowledge, there are few studies in the financial literature on R-vines with high dimensions. For instance, ref. [18] studied up to 398 dimensions on S&P500 constituents and ref. [19] studied 2131 dimensions, while other R-vine studies have examined the lower dimensions (less than 25). See, among others, the studies of R-vines in lower dimensions in [20,21,22,23,24,25]. For studies on copula models, see, among others, [26,27,28,29]. Hence, the study of R-vines in high dimensions is still scarce and needs more investigation. This observation is the starting point of our study. The model most closely related to ours is that of [30], which studies R-vines in application to 16-dimensional financial indices using the quasi-maximum likelihood estimation (QMLE) method.

Given standardized residuals, vine copula models can be applied across five different classes: mixed R-vines, mixed C-vines, mixed D-vines, all-t R-vines, and the standard multivariate Gaussian copula. This study utilizes seven bivariate copula families. Based on the test proposed by [31] and likelihood comparisons, previous research has identified mixed R-vines as the best-performing models—an approach we adopt in this study.

Our first contribution is to extend this analysis to 100 dimensions of financial data using constituents of the S&P500, which, to our knowledge, has not been explored in this context. The second contribution is the expansion of the copula family set from seven to thirteen bivariate copulas, including two-parameter BB families and additional Archimedean copulas. This broader selection allows for a more accurate capture of tail asymmetries observed in financial data. Further details are provided in Section 4. Our third contribution lies in the modeling of the marginal distributions. We employ the intertemporal capital asset pricing model (ICAPM), originally proposed by [32], with an asymmetric GARCH model featuring a mixture innovation. This approach enhances the filtration of volatility clustering and yields deeper insights into risk premia across individual financial returns. Unlike [30], who used an ARMA-GARCH model with a single Student-t innovation, we incorporate a mixture of one Gaussian and two heavy-tailed distributions, offering a more flexible representation of return dynamics.

Another key contribution of this study lies in the estimation methodology. In the existing literature, quasi-maximum likelihood estimation (QMLE) is widely used for copula models; see, for example, [33,34,35]. However, QMLE has notable limitations—it is highly sensitive to initial parameter values and often suffers from convergence issues [36]. To address these shortcomings, we employ more efficient estimation techniques, specifically Bayesian Markov chain Monte Carlo (MCMC) and variational Bayes (considered as machine learning) methods, to estimate our proposed R-vine dependence models. These methods are also compatible with the two main subclasses of vine copulas: C-vines and D-vines. While Bayesian MCMC and machine learning approaches are computationally intensive, we mitigate the associated costs by incorporating parallel computing. Additionally, we use QMLE estimates as initial values to improve convergence speed in the Bayesian MCMC and machine learning algorithms.

Our study explores these advanced methods in two distinct ways. First, we apply the random walk Metropolis–Hastings (rw-MH) algorithm for Bayesian MCMC estimation. Second, we implement the variational Bayes method—both with and without data augmentation (VBDA)—as proposed by [37], to estimate the multivariate dependence structure. Furthermore, we propose an alternative, more efficient variational approximation to reduce computational time, the details of which are presented in the simulation study in the Supplementary Material. For related surveys on MLE, Bayesian, and machine learning methods, see [38,39,40,41], among others.

The remainder of the paper is structured as follows. Section 2 introduces the graph-theoretical framework for high-dimensional regular vine (R-vine) copulas, including the two special subclasses—C-vines and D-vines—as well as the marginal models. Section 3 outlines the Bayesian inference and machine learning algorithms used to estimate general R-vine dependence models. Section 4 presents empirical results based on 100-dimensional financial data. Section 5 offers concluding remarks. Details on the simulation study and data generation algorithms are provided in the Supplementary Material.

2. Graph Theory

2.1. Regular Vines in n-by-n Matrix Representation

This section provides the theoretical background on regular vine (R-vine) copulas, along with two important subclasses: canonical vine (C-vine) and drawable vine (D-vine) copulas, all represented in an n-dimensional graphical model framework. In graph theory, an R-vine is represented as a sequence of tree structures composed of nodes N and edges E. An R-vine ($\mathcal{V}$) in n-dimensions is defined as a nested set of $n-1$ trees. The first tree ($T=1$) consists of n nodes and $n-1$ edges, each representing a pair of variables. Each edge in $T=1$ becomes a node in the second tree ($T=2$), which then has $n-1$ nodes and $n-2$ edges. The construction follows the proximity condition, meaning that connected nodes in $T=2$ must share a common node from $T=1$.

This nesting continues: in the third tree ($T=3$), there are $n-2$ nodes and $n-3$ edges, and again, any two connected nodes must share a common node from $T=2$. This process continues until the final tree ($T_{n-1}$), which has two nodes and a single edge. These two nodes must share all remaining nodes from the previous tree. For further definitions and examples—including complete unions, conditioning sets, and conditional sets of an edge—refer to [30]. Additional theoretical details and properties of vine copulas can be found in [17,42,43,44].

A convenient approach for developing an algorithm in a vine graphical model is to store the trees in an n-by-n matrix. The authors of [30] proposed using a lower triangular matrix $\mathcal{M}$ to represent vines as a tree structure in n dimensions; see Figure 1.

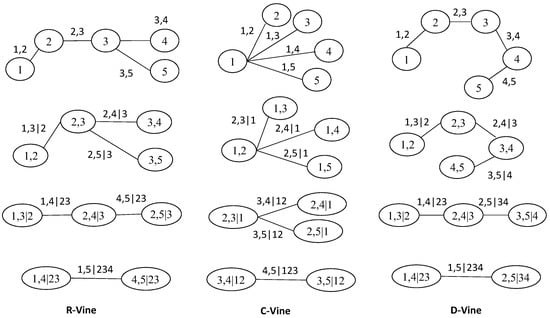
Figure 1. An illustrative example of vine copula graphical model in five dimensions.

Definition 1

(Matrix Constraint Set). Let $\mathcal{M}=\left(m_{i,k}\right)$ be a lower triangular n-by-n matrix where $i,k=1,\dots ,n$. The $i^{th}$ constraint set for $\mathcal{M}$ is

$$\mathcal{CM}\left(i\right)=\left\{(\{m_{k,k},m_{i,k}\},\mathcal{D})\right|i=k+1,\dots ,n,\mathcal{D}=\{m_{i+1,k},\dots ,m_{n,k}\}\}$$

for $i=n-1,\dots ,1$. Otherwise, $\mathcal{D}=\varnothing$ (if $i=n$). Hence, $\mathcal{D}$ is the conditioning set and $\{m_{k,k},m_{i,k}\}$ is the conditioned set.

In other words, every pair variable within the constraint set is built up from a diagonal element $m_{k,k}$ plus another element in the same column $m_{i,k}$ conditioning on set of $\mathcal{D}=\{m_{i+1,k},\dots ,m_{n,k}\}$. Otherwise, $\mathcal{D}=\varnothing$ when i equal to n. To illustrate Definition 1, the 5-by-5 matrix $\mathcal{M}$ of Figure 1 can be constructed as

$$\begin{array}{cccc}\hfill {\mathcal{M}}^R& =\left(\begin{array}{ccccc}1& & & & \\ 5& 5& & & \\ 4& 4& 2& & \\ 3& 2& 4& 3& \\ 2& 3& 3& 4& 4\end{array}\right), \hfill & \hfill {\mathcal{M}}^C=\left(\begin{array}{ccccc}5& & & & \\ 4& 4& & & \\ 3& 3& 3& & \\ 2& 2& 2& 2& \\ 1& 1& 1& 1& 1\end{array}\right), & {\mathcal{M}}^D=\left(\begin{array}{ccccc}5& & & & \\ 1& 4& & & \\ 2& 1& 3& & \\ 3& 2& 1& 2& \\ 4& 3& 2& 1& 1\end{array}\right)\hfill \end{array}$$

Once a 5-by-5 matrix is constructed, it becomes straightforward to generalize the construction to an $\mathcal{M}$ matrix for any dimension n. For different constructions of upper triangular matrices representing vines in graphical theory, see [17] (Chapter 3).

2.2. Multivariate Regular Vines Density

This section introduces the matrix $\mathcal{M}$ within a numerical framework for computing multivariate regular vine copula densities, including both multivariate canonical vine (C-vine) and drawable vine (D-vine) structures in n-dimensions. In the previous section, we generated an n-by-n matrix $\mathcal{M}$ satisfying a proximity condition. Building on this, the n-dimensional multivariate vine copula density is now formulated using two additional n-by-n matrices: the bivariate copula type matrix $\mathcal{T}=\left(t_{i,k}\right)$ and its associated parameter matrix $\mathcal{P}=\left({\mathfrak{p}}_{i,k}\right)$ where $i=n,\dots ,2$ and $k=n-1,\dots ,1$.

We begin by expressing the vine copula density as a product of pairwise copula functions. According to Sklar’s theorem, a copula C is a multivariate distribution function that links a joint distribution to its marginals $F_1\left(x_1\right),\dots ,F_n\left(x_n\right)$ [1]. Thus, the multivariate copula distribution can be written as:

$$F(x_1,\dots ,x_n) = C\{F_1\left(x_1\right),\dots ,F_n\left(x_n\right)\}$$

for n-dimensional data. After that, vine copula density in n-dimensions can be expressed in graph theory. In product indexing, the C-vine density is

$$\prod _{j=1}^{n-1}\prod _{i=1}^{n-j}{c}_{j,j+i|1,\dots ,j-1}\left\{F\left(x_j\right|x_1,\dots ,x_{j-1}),F\left(x_{j+i}\right|x_1,\dots ,x_{j-1})\right\}.$$

(1)

The D-vine density is

$$\prod _{j=1}^{n-1}\prod _{i=1}^{n-j}{c}_{i,i+j|i+1,\dots ,i+j-1}\left\{F\left(x_i\right|x_{i+1},\dots ,x_{i+j-1}),F\left(x_{i+j}\right|x_{x+1},\dots ,x_{i+j-1})\right\}.$$

(2)

The R-vine density is

$$\prod _{i=1}^{n-1}\prod _{e\in E_i}{c}_{C_{e,a},C_{e,b}|D_e}(F_{C_{e,a}|D_e}\left(X_{C_{e,a}}\right|{\mathbf{X}}_{D_e}),F_{C_{e,b}|D_e}\left(X_{C_{e,b}}\right|{\mathbf{X}}_{D_e})).$$

(3)

In a D-vine, each node in a given tree $T_i$ can be connected to only one edge. In contrast, within a C-vine, a specific node in tree $T_i$ must have $n-j$ edges. The D-vine structure allows for more independence assumptions compared to the C-vine. However, the C-vine can be advantageous when there is prior knowledge of a particular variable that strongly influences the dataset. The R-vine represents the most general form, offering significantly greater flexibility in modeling complex dependency structures.

Figure 1 provides an example of a five-dimensional regular vine copula density. The complete R-vine copula density depicted in this figure can be expressed as follows:

$$\begin{array}{cc}\hfill f(x_1,x_2,x_3,x_4,x_5)& =c_{1,2}·c_{2,3}·c_{3,4}·c_{3,5} (\mathrm{unconditional} \mathrm{pairs})\hfill \\ \hfill & \times c_{1,3|2}·c_{2,4|3}·c_{2,5|3}·c_{1,4|23}·c_{4,5|23}·c_{1,5|234} (\mathrm{conditional} \mathrm{pairs})\hfill \end{array}$$

where $c_{u,v|k}$ stands for $c_{u,v|k}(F_{u|k}\left(x_u\right|x_k),F_{v|k}\left(x_v\right|x_k))$. All definitions and further details can be found, among others, in [15] for C-vines and D-vines, and in [30] for R-vines. Next, we present R-vine density using matrix representation ${\mathcal{M}}^{*}$, ${\mathcal{T}}^{*}$, and ${\mathcal{P}}^{*}$ in Figure 2, which can be used for its special cases.

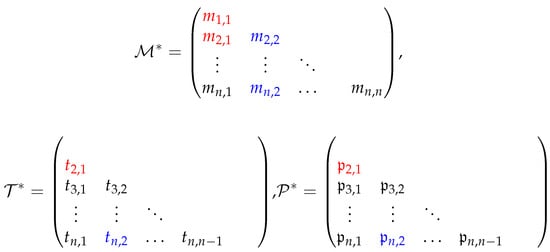
Figure 2. Vine copula specification in n-by-n matrix representation including ${\mathcal{T}}^{*}$, ${\mathcal{P}}^{*}$ and ${\mathcal{M}}^{*}$.

In Figure 2, the red label corresponds to the last tree, $n-1$. The conditioned set is $\{m_{1,1},m_{2,1}\}\in {\mathcal{M}}^{*}$, and the conditioning set $\mathcal{D}$ includes all elements $m_{i,1}, i=3,\dots ,n$. The associated bivariate copula type and parameter are $t_{2,1}$ and ${\mathfrak{p}}_{2,1}$, respectively.

The blue label represents the first tree, $T_1$. Here, the conditioned set is $\{m_{2,2},m_{n,2}\}\in {\mathcal{M}}^{*}$, and the conditioning set $\mathcal{D}$ is ∅. The corresponding bivariate copula type and parameter are $t_{n,2}$ and ${\mathfrak{p}}_{n,2}$, respectively.

From a graph-theoretical perspective, the regular vine copula density can therefore be described as:

$$f_{1,\dots ,n}=\prod _{k=1}^n{f}_k\prod _{k=n-1}^1\prod _{i=n}^{k+1}{c}_{m_{k,k},m_{i,k}|m^{*}}(F_{m_{k,k}|m^{*}},F_{m_{i,k}|m^{*}}),$$

(4)

where $m^{*}$ is $m_{i+1,k},\dots ,m_{n,k}\in {\mathcal{M}}^{*}$ with bivariate copula types ${\mathcal{T}}^{*}$, bivariate copula parameters ${\mathcal{P}}^{*}$, and the corresponding densities in Equations (1)–(3). For the R-vine density algorithm, see Algorithm 2.1 of [30].

2.3. Marginal Model and Distribution

This section presents our proposed marginal model, which combines elements of the ICAPM and an asymmetric GARCH model with a mixture distribution. This hybrid approach is designed to capture key stylized facts of financial returns, such as volatility clustering and time-varying heteroskedasticity. The model offers several advantages, including the incorporation of risk premium information and the ability to account for asymmetric shocks and fat-tailed behavior in financial data.

Our marginal model is similar to that of [45], who employed Gaussian innovations; however, we adopt a more flexible mixture innovation to better reflect the complexity of financial return distributions. Furthermore, we extend this framework to the multivariate setting in order to analyze dependence structures using regular vine copulas.

The ICAPM we use in this study follows [32], which is a linear-in-variance function of financial returns and is given by

$$y_t={\lambda }_1+{\lambda }_2{\mathfrak{h}}_t +{\epsilon }_t,$$

(5)

where $y_t$ is the financial returns at time $t=\{1,\dots ,T\}$, ${\lambda }_1$ is a risk-free rate, ${\lambda }_2$ is a risk premium, ${\mathfrak{h}}_t$ is a conditional volatility, ${\epsilon }_t=\sqrt{{\mathfrak{h}}_t}{z}_t$ is an innovation with zero mean and the conditional variance (or volatility) ${\mathfrak{h}}_t$, and $z_t$ is the independent and identically distributed (iid) random variable with zero mean and unit variance from a mixture distribution. To deal with the heteroskedastic returns, we use an exponential-type GARCH model or EGARCH(p,q,r) given by

$$log{\mathfrak{h}}_t=\omega +\sum _{i=1}^p{\gamma }_i{z}_{t-i}+\sum _{j=1}^q{\delta }_j{\left|z\right|}_{t-j}+\sum _{k=1}^r{\nu }_{k}log{\mathfrak{h}}_{t-k}.$$

(6)

where $\omega$ is a constant, ${\gamma }_i$ measures the direct innovation effects, ${\delta }_j$ is the asymmetry parameter for the leverage effects, and ${\nu }_k$ is the volatility persistence parameter. For details on the EGARCH model, see [46], as well as the surveys on asymmetric GARCH models, including EGARCH, in [47,48]. Regarding the distribution of innovations in the marginal model, we employ a mixture distribution originally proposed by [49] for use with the ARMA-GARCH model and standard copulas. In contrast, our study applies this mixture distribution within an ICAPM-EGARCH framework combined with regular vine copulas.

The mixture distribution consists of three components: one Gaussian distribution and two generalized Pareto distributions (GPDs) derived from extreme value theory (EVT). The GPD components are specifically designed to capture asymmetric fat tails—one of the most significant features observed in financial return data [50].

The mixture distribution has a flexible property. It can be represented by either a finite set of distribution functions (cdf), $P_k\left(x_t\right)$, or density functions (pdf), $p_k\left(x_t\right)$, $k =1,\dots ,K$. The mixture distribution and its density are a weighted sum such that $F\left(x_t\right)={\sum }_{k=1}^K{w}_k{P}_k\left(x_t\right)$ and $f\left(x_t\right)={\sum }_{k=1}^K{w}_k{p}_k\left(x_t\right)$, respectively. $w>0$ is a weight and $\sum w=1$. If the mixing weight w is pre-specified, it can also represent the quantile level of the mixture distribution. Given the three components, the mixture pdf is given by

$$p\left(x_t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{{\beta }^L}}{\left(1+{\xi }^L{\displaystyle \frac{\left(x_t-{\mu }^L\right)}{{\beta }^L}}\right)}^{-{\displaystyle \frac{1}{{\xi }^L}}-1}\hfill & ,x_t\le {\mathsf{\Phi }}^{-1}\left({\alpha }^L\right)\hfill \\ \varphi \left(x_t\right)\hfill & ,{\mathsf{\Phi }}^{-1}\left({\alpha }^L\right)<x_t<{\mathsf{\Phi }}^{-1}\left({\alpha }^R\right)\hfill \\ {\displaystyle \frac{1}{{\beta }^R}}{\left(1+{\xi }^R{\displaystyle \frac{\left(x_t-{\mu }^R\right)}{{\beta }^R}}\right)}^{-{\displaystyle \frac{1}{{\xi }^R}}-1}\hfill & ,x_t\ge {\mathsf{\Phi }}^{-1}\left({\alpha }^R\right),\hfill \end{array}\right.$$

(7)

where ${\alpha }^L$ and ${\alpha }^R$ are a pre-specified quantile, $\mu =(-\infty ,\infty )$ is a location parameter, $\beta =(0,\infty )$ is a scale parameter, $\xi =(-\infty ,\infty )$ is a shape parameter, and L and R denote the left and right tails, respectively. The support of $x_t\sim GPD(\mu ,\beta ,\xi )$ is $x_t\ge 0$ when $\xi =[0,\infty )$ and $x_t=[\mu ,\mu -\beta /\xi ]$ when $\xi =(-\infty ,0)$, and $\xi =[0,1/2]$ represents a fat tail and exists at least up to the second moment. For more details on the moment property, see [51,52].

The GPDs, in a sense of generalization, consist of an ordinary Pareto distribution, an exponential distribution, and a short-tailed, Pareto type II distribution. Further details of the GPD used in the peak-over-threshold method are found in ([10] Chapter 5). Note that $\varphi \left(·\right)$ and ${\mathsf{\Phi }}^{-1}\left(·\right)$ are the standard Gaussian pdf and its inverse cdf, respectively.

3. Bayesian Inference and Machine Learning in the Graphical Model

This section outlines the parameter estimation techniques used in our study, which include both Bayesian and machine learning approaches. For the Bayesian framework here, we refer to the Markov chain Monte Carlo (MCMC), while the variational Bayes is considered a machine learning method. Though both methods are computationally demanding and mathematically intricate, they are well-suited for cases where the posterior distribution of the marginal models is intractable—as is the case in our analysis.

Specifically, we apply the random walk Metropolis–Hastings (rw-MH) MCMC algorithm proposed by [53], along with the variational Bayes method developed by [37], both with and without data augmentation. These methods are used to estimate model parameters and to analyze the R-vine copula dependence structure.

To support and enhance the efficiency of these estimation procedures, we also incorporate plug-in parallel computing and the quasi-maximum likelihood estimation (QMLE) method. These additions help reduce computational time while preserving estimation accuracy, thereby facilitating the integration of Bayesian inference and machine learning techniques in a computationally feasible manner.

3.1. Full Likelihood Function

It is important to first discuss a likelihood function since this is a connection between Bayesian MCMC and machine learning methods. Given the observed n-dimensional data, the full log-likelihood function of our model is

$$\begin{array}{cc}\hfill \mathsf{\Lambda }\left(\theta \right|y_{k,i,t})& =\sum _{k=1}^{n}log\left(f_k\right)\sum _{k=n-1}^1\sum _{i=n}^{k+1}log\left(c_{m_{k,k},m_{i,k}|m^{*}}(F_{m_{k,k}|m^{*}},F_{m_{i,k}|m^{*}})\right)\hfill \\ \hfill & =\sum _{k=1}^n\sum _{t=1}^{T}log[q_k^L{p}_L^{GPD}\left(x_{k,t}\right)+(1-q_k^L-q_k^R)p^G\left(x_{k,t}\right)+q_k^R{p}_R^{GPD}\left(x_{k,t}\right)]\hfill \\ & \sum _{k=n-1}^1\sum _{i=n}^{k+1}\sum _{t=1}^{T}log\left(c_{t_{m_{k,k},m_{i,k}|m^{*}}}(F_{t_{m_{k,k}|m^{*}}},F_{t_{m_{i,k}|m^{*}}})\right),\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill p_L^{GPD}\left(x_{k,t}\right)& ={\displaystyle \frac{1}{\sqrt{{\mathfrak{h}}_t^k}\left(1-{\xi }^{L,k}\right){\left(1-2{\xi }^{L,k}\right)}^{1/2}}}{\left(1+{\displaystyle \frac{{\xi }^{L,k}\left(y_{k,t}-{\lambda }_1^k-{\lambda }_2^k{\mathfrak{h}}_t^k\right)}{\sqrt{{\mathfrak{h}}_t^k}\left(1-{\xi }^{L,k}\right){\left(1-2{\xi }^{L,k}\right)}^{1/2}}}\right)}^{-{\displaystyle \frac{1}{{\xi }^{L,k}}}-1},\hfill \\ \hfill p^G\left(x_{k,t}\right)& ={\displaystyle \frac{1}{{\left(2\pi {\mathfrak{h}}_t^k\right)}^{1/2}}}exp\left[{\displaystyle \frac{-{\left(y_{k,t}-{\lambda }_1^k-{\lambda }_2^k{\mathfrak{h}}_t^k\right)}^2}{2{\mathfrak{h}}_t^k}}\right],\hfill \\ \hfill p_R^{GPD}\left(x_{k,t}\right)& ={\displaystyle \frac{1}{\sqrt{{\mathfrak{h}}_t^k}\left(1-{\xi }^{R,k}\right){\left(1-2{\xi }^{R,k}\right)}^{1/2}}}{\left(1+{\displaystyle \frac{{\xi }^{R,k}\left(y_{k,t}-{\lambda }_1^k-{\lambda }_2^k{\mathfrak{h}}_t^k\right)}{\sqrt{{\mathfrak{h}}_t^k}\left(1-{\xi }^{R,k}\right){\left(1-2{\xi }^{R,k}\right)}^{1/2}}}\right)}^{-{\displaystyle \frac{1}{{\xi }^{R,k}}}-1},\hfill \end{array}$$

which is compatible with Equation (4). $c_t$ is a unique bivariate copula pdf. $F_t$ is a mixture cdf which is defined in Section 2.3. $x_t$ is a standardized residual given by Equation (5). The parameter $\theta$ in parameter space $\mathsf{\Theta }$ is $\theta =\{{\lambda }_1^k,{\lambda }_2^k,{\xi }^{L,k},{\xi }^{R,k},{\omega }^k,{\gamma }^k,{\delta }^k,{\nu }^k,{\mathcal{P}}^{*}\}$. In n dimensions, there are at least ${\displaystyle \frac{n(n+15)}{2}}$ parameters that need to be estimated. The number of parameters grows proportionally to the number of dimensions. From our R-vine copula-based models, there are at least 606 parameters in 30 dimensions and 6094 parameters in 100 dimensions, respectively. Notably, the trade-off between flexibility and parsimony needs to be taken into account. This leads to a research area of regularization or shrinkage method where the most common shrinkage methods are, for instance, lasso and ridge—see [54,55,56], among others. However, we leave this for further research.

3.2. Bayesian MCMC Estimation

Due to the intractable nature of the likelihood, a Bayesian approach is a good candidate for the estimation. Hence, this section discusses the rw-MH algorithm, enhanced with the QMLE and parallel computing to improve computational efficiency. Given the large number of parameters in vine copula models, we adopt the Inference for Margins (IFM) approach [57], which enables the parallelization of marginal model estimation and significantly accelerates the overall computation. Regarding the choice of prior distributions, we use an informative prior, especially the uniform distribution, in the estimation with the hyperparameter values following previous studies.

In summary, Algorithm 1 outlines the procedure for obtaining the parameter estimates ${\widehat{\mathcal{P}}}^{*}$ for the R-vine copula model and $\widehat{\theta }$ for the marginal models. The process begins by constructing the maximum matrix $\mathbb{M}$ from ${\mathcal{M}}^{*}$, where each element ${\mathbf{m}}_{i,k}$ in $\mathbb{M}$ represents the maximum value among all entries in the k-th column from row i to row n.

The algorithm proceeds in several parallelized steps. The first loop performs data standardization in parallel. In the second loop, the algorithm computes the independent pairwise copulas in the first tree, $T_1$, of the R-vine model—also in parallel. The third loop handles the dependent pairs in the subsequent trees $T_i$, for $i=2,\dots ,n-1$.

Algorithm 1 Parallel algorithm of regular vine copulas model using random walk chain Metropolis–Hastings sampling MCMC and maximum likelihood estimation.

Require:  $y_t$   1: Calculate ${\mathbb{M}}_{i,k}={\mathbf{m}}_{i,k}|i=n,k=1,\dots ,n$. ${\mathbf{m}}_{n,k}=\mathit{max}$$\{m_{i,k},\dots ,m_{n,k}\}$ for all $k=n,\dots ,1$. m is spanning tree maximisation.   2: parfor $i_g\leftarrow 1,n$ do        ▹ estimate margin parameters from Equations (5)–(7), do parallel   3:       Perform ${\widehat{\theta }}_{i_g}^{QMLE,Margins}$←${arg\; max}_{\theta \in \mathsf{\Theta }}log\left(f_{i_g}(\theta \mid y_{i_g})\right)$.   4:       Perform ${\widehat{\theta }}_{i_g}^{rmMH,Margins}|({\widehat{\theta }}_{i_g}^{QMLE,Margins}, y_{i_g})$ via call Algorithm 2   5:       Calculate $z_{t,i_g}$ via standardized $y_{t,i_g}|{\widehat{\theta }}_{Margins,i_g}^{rmMH}$.   6:       Calculate $u_{i_g}=F_{i_g}\left(z_{t,i_g}\right)\sim Unif(0,1)$.   7: end parfor   8: Allocate $V^{direct}=\left(v_{i,k}^{direct}\right)$ where $i=n$ and $k=1,\dots ,n$.   9: Allocate $(v_{n,1}^{direct},\dots ,v_{n,n}^{direct})=(u_1,\dots ,u_n)$. 10: parfor $k\leftarrow 1,n-1$ do                                                                    ▹ first tree, do parallel 11:       Perform ${\widehat{\mathfrak{p}}}_{n,k}^{QMLE},BI{C}^{QMLE}$←${arg\; max}_{\theta \in \mathsf{\Theta }}log\left(c(z_{n,k}^{\left(2\right)},z_{n,k}^{\left(1\right)};t_{n,k})\right)$ using Equation (8) for copula candidate. 12:       Find ${\widehat{\mathfrak{p}}}_{n,k}^{QMLE},t_{n,k}$ by min$\left\{BI{C}^{QMLE}\right\}$ 13:       Set $z_{n,k}^{\left(1\right)}=v_{n,k}^{direct}$ and $z_{n,k}^{\left(2\right)}=v_{i,(n-{\mathbf{m}}_{n,k}+1)}^{direct}$. 14:       Perform ${\widehat{\mathfrak{p}}}_{n,k}^{rmMH}\left|\right(z_{n,k}^{\left(1\right)}, z_{n,k}^{\left(2\right)}, {\widehat{\mathfrak{p}}}_{n,k}^{QMLE}$) using Equation (8) via call Algorithm 2 15:       Calculate $v_{n-1,k}^{direct}=h(z_{n,k}^{\left(1\right)},z_{n,k}^{\left(2\right)}|t_{n,k},{\widehat{\mathfrak{p}}}_{n,k}^{rmMH})$ 16:       Calculate $v_{n-1,k}^{indirect}=h(z_{n,k}^{\left(2\right)},z_{n,k}^{\left(1\right)}|t_{n,k},{\widehat{\mathfrak{p}}}_{n,k}^{rmMH})$ 17: end parfor 18: for $k\leftarrow n-2,1$ do                            ▹ column iteration, iteration for tree $n-1$ to tree 2 19:       for $i\leftarrow n-1,k+1$ do                                                                         ▹ row iteration 20:             Calculate ${\mathbb{M}}_{i,k}={\mathbf{m}}_{i,k}$. ${\mathbf{m}}_{i,k}=\mathit{max}$$\{m_{i,k},\dots ,m_{n,k}\}$. 21:             Set $z_{i,k}^{\left(1\right)}=v_{i,k}^{direct}$. 22:             if ${\mathbf{m}}_{i,k}=m_{i,k}$ then 23:                $z_{i,k}^{\left(2\right)}=v_{i,(n-{\mathbf{m}}_{i,k}+1)}^{direct}$ 24:             else 25:                $z_{i,k}^{\left(2\right)}=v_{i,(n-{\mathbf{m}}_{i,k}+1)}^{indirect}$ 26:             end if 27:             Perform ${\widehat{\mathfrak{p}}}_{i,k}^{QMLE},BI{C}^{QMLE}$←${arg\; max}_{\theta \in \mathsf{\Theta }}log\left(c(z_{i,k}^{\left(2\right)},z_{i,k}^{\left(1\right)};t_{i,k})\right)$ using Equation (8) for copula candidate. 28:             Find ${\widehat{\mathfrak{p}}}_{i,k}^{QMLE},t_{i,k}$ by min$\left\{BI{C}^{QMLE}\right\}$ 29:             Perform ${\widehat{\mathfrak{p}}}_{i,k}^{rmMH}|(z_{i,k}^{\left(2\right)},z_{i,k}^{\left(1\right)},t_{i,k},{\widehat{\mathfrak{p}}}_{i,k}^{QMLE})$ using Equation (8) via call Algorithm 2 30:             Calculate $v_{i-1,k}^{direct}=h(z_{i,k}^{\left(1\right)},z_{i,k}^{\left(2\right)}|t_{i,k},{\widehat{\mathfrak{p}}}_{i,k}^{rmMH})$ 31:             Calculate $v_{i-1,k}^{indirect}=h(z_{i,k}^{\left(2\right)},z_{i,k}^{\left(1\right)}|t_{i,k},{\widehat{\mathfrak{p}}}_{i,k}^{rmMH})$ 32:       end for 33: end for 34: return ${\widehat{\mathcal{P}}}^{*}$, ${\widehat{\mathcal{T}}}^{*}$, ${\widehat{\mathcal{M}}}^{*}$, $\widehat{\theta }$

To ensure better convergence, the algorithm initially employs the QMLE to provide starting values for the rw-MH sampler, described in Algorithm 2, which functions as a subroutine within Algorithm 1.

The function $c(u,v;t,\mathfrak{p})$ denotes a specific bivariate copula density, parameterized by copula type t and parameter $\mathfrak{p}$. The terms $v_{i,k}^{direct}$ and $v_{i,k}^{indirect}$ refer to recursive conditional cumulative distribution functions (cdfs), often denoted by $h(u,v|t,\mathfrak{p})$, which are fundamental components in the construction of conditional copulas in vine structures.

$$\begin{array}{cc}\hfill v_{i,k}^{direct}& =C\left(v_{m_{k,k}}\right|u_{m_{i+1,k}},u_{m_{i+2,k}},\dots ,u_{m_{n,k}}),\hfill \\ \hfill v_{i,k}^{indirect}& =C\left(v_{m_{i+1,k}}\right|u_{m_{k,k}},u_{m_{i+2,k}},\dots ,u_{m_{n,k}}),\hfill \end{array}$$

(9)

for all $n\ge i>1$. Denote that $h(u,v|t,\mathfrak{p})=C_{2|1}\left(v\right|u;\theta ,\delta )$. $C(u,v;\theta ,\delta )=G(x,y;\theta ,\delta )$ where $G(x,y;\theta ,\delta )$ is a bivariate survival function and $x,y$ are monotonically decreasing transforms. Therefore, the conditional cdf is $C_{2|1}\left(v\right|u;\theta ,\delta )={\displaystyle \frac{\partial G}{\partial x}}.{\displaystyle \frac{\partial x}{\partial u}}.$ See [30] for further discussion.

Algorithm 2 presents the rw-MH sampling method used as part of the MCMC procedure in Algorithm 1. In general, the performance of the Metropolis–Hastings algorithms is sensitive to the choice of initial values ($\theta ,\mathsf{\Omega }$) where $\mathsf{\Omega }$ is a covariance matrix. The first stage of the rw-MH algorithm involves a burn-in period, during which early samples of $\theta$ are discarded. A longer burn-in period increases computational time, and its length largely depends on how close the initial values are to the target distribution.

To address this, our approach initializes the algorithm with parameter estimates obtained via the QMLE. This helps achieve a reasonable acceptance rate more quickly— approximately 50% in our implementation.

The proposal step involves an increment random variable z, which follows a Gaussian distribution, $z\sim N(0,c\mathsf{\Omega })$, where c is a constant scaling factor. This constant is tuned to ensure an appropriate acceptance rate for the sampler. For further details on the MH algorithm, see [53] (Exercise 17.5 and Exercise 11.18).

Algorithm 2 Random walk Metropolis–Hastings algorithm

Require:  $\mathsf{\Lambda }\left(\theta \right|y),{\widehat{\theta }}^{QMLE},{\widehat{\mathsf{\Sigma }}}^{QMLE},c,nburn,nrep$.   1: Calculate ${\mathsf{\Sigma }}^{*}=c\times {\widehat{\mathsf{\Sigma }}}^{QMLE}$.   2: Set ${\theta }^1={\widehat{\theta }}^{QMLE}$.   3: $$   4: for  $i\leftarrow 2,nburn+nrep$  do   5:       Draw a candidate ${\theta }^{*}={\theta }^{i-1}+z$   6:       Draw an acceptance probability $$\alpha ({\theta }^{i-1},{\theta }^{*})=min\left[{\displaystyle \frac{\mathsf{\Lambda }\left({\theta }^{*}\right|y)}{\mathsf{\Lambda }\left({\theta }^{i-1}\right|y)}},1\right]$$   7:       Set ${\theta }^i={\theta }^{*}$ with probability $\alpha ({\theta }^{i-1},{\theta }^{*})$. Otherwise, set ${\theta }^i={\theta }^{i-1}$.   8: end for   9: $$ 10: Calculate posterior means ${\widehat{\theta }}^{rwMH}$ from the draws $\theta$ and whatever posterior inference of interest are needed. 11: return  ${\widehat{\theta }}^{rwMH}$

3.3. Variational Bayes Estimation

This section introduces an alternative algorithm based on the variational Bayes (VB) method, which integrates Bayesian inference with machine learning to estimate n-dimensional general regular vine copula models. Specifically, we apply the variational Bayes with (and without) data augmentation (VBDA) approach originally developed for a drawable vine structure by [37,58].

In this study, we extend the VBDA method to accommodate the more general class of regular vines by incorporating an additional stopping criterion. This enhancement is designed to reduce the number of iterative learning steps, thereby improving computational efficiency.

We explore three versions of the variational Bayes estimation method: one without data augmentation (VBDA0), and two with data augmentation (VBDA1 and VBDA2). All three methods rely on latent variables during estimation. To address convergence challenges and reduce computational time, we also incorporate plug-in QMLE estimates and leverage parallel computing techniques.

The augmented posterior density is

$$p(\theta ,\mathbf{u}|y)={\displaystyle \frac{f(y,\mathbf{u},\theta )}{f\left(y\right)}}=\left(c\left(\mathbf{u}\right|\theta )p\left(\theta \right)\prod _{t=1}^T\mathcal{I}(a_t\le u_t<b_t)\right)/f\left(y\right).$$

where $p\left(\theta \right)$ is the prior density. $f\left(y\right)$ is the marginal likelihood function. $c\left(\mathbf{u}\right|\theta )$ is the copula density. $\mathcal{I}$ is the indicator function. VB estimation approximates $p(\theta ,\mathbf{u}|y)$ by a tractable density $q_{\lambda }(\theta ,\mathbf{u})$ in a so-called variational approximation. This estimation corresponds to minimizing the Kullback–Leibler (KL) divergence

$$KL(q_{\lambda }(\theta ,\mathbf{u})\left|\right|p(\theta ,\mathbf{u}|y))=\int log\left({\displaystyle \frac{q_{\lambda }(\theta ,\mathbf{u})}{p(\theta ,\mathbf{u}|y)}}\right)q_{\lambda }(\theta ,\mathbf{u}) d\theta du$$

or maximizing the lower bound of the logarithm of the marginal likelihood (or the evidence lower bound (ELBO)), given by

$$\mathcal{L}\left(\lambda \right)=\int log\left({\displaystyle \frac{p\left(\theta \right)f(y,\mathbf{u}|\theta )}{q_{\lambda }(\theta ,\mathbf{u})}}\right)q_{\lambda }(\theta ,\mathbf{u}) d\theta du,$$

where $\theta$ and $\mathbf{u}$ are independent. For further details and examples of VB methods, see, among others, [59,60]. Also, see [61,62], among others, for reviews of VB inference in machine learning.

The density approximation of $q_{\lambda }$ can be written as $q_{\lambda }(\theta ,\mathbf{u})=q_{{\lambda }^a}\left(\theta \right)q_{{\lambda }^b}\left(\mathbf{u}\right)$. The specification of $q_{{\lambda }^a}$ and $q_{{\lambda }^b}$ is crucial. $q_{{\lambda }^a}$ has parameter ${\lambda }^a$ while $q_{{\lambda }^b}$ has parameter ${\lambda }^b$ with the support on $[a_1,b_1)\times \dots \times [a_T,b_T)$. This study selects the choice of $\mathbf{u}$ approximation as follows:

$$\begin{array}{cc}\hfill VBDA0:q_{{\lambda }^b}\left(u\right)& =0,\hfill \\ \hfill VBDA1:q_{{\lambda }^b}\left(u\right)& =\prod _{t=1}^T{\displaystyle \frac{1}{b_t-a_t}}\mathcal{I}(a_t\le u_t<b_t),\hfill \\ \hfill VBDA2:q_{{\lambda }^b}\left(u\right)& =\prod _{t=1}^T{\displaystyle \frac{\varphi (x_t;{\mu }_t,{\mathsf{\Omega }}_t)}{(b_t-a_t)\varphi \left(x_t\right)}}.\hfill \end{array}$$

VBDA2 nests VBDA1, which covers a wide range of data dependencies with an effective mean field approximation. VBDA1 is expected to be more accurate for data with low dependence. ${\lambda }^b=\{{\mu }_1,\dots ,{\mu }_T,log {\omega }_1,\dots ,log {\omega }_T\}$, ${\mathsf{\Omega }}_t=diag({\omega }_1,\dots ,{\omega }_T)$, and $\varphi$ is the standard normal density.

To approximate $\theta$, we adopt a commonly used variational distribution $q_{{\lambda }^a}$, specifically the multivariate normal (Gaussian) distribution with mean M and covariance matrix $\mathsf{\Sigma }$, denoted as $N(M,\mathsf{\Sigma })$. In the context of R-vine models, a large number of parameter estimates are required. The use of a tractable multivariate normal distribution makes it relatively straightforward to compute the gradient of $log q_{{\lambda }^a}\left(\theta \right)$.

Moreover, the structure of $\mathsf{\Sigma }$ contributes to improving the accuracy of the gradient estimates. In particular, when $\mathsf{\Sigma }$ is expressed using its factorized form $\mathsf{\Sigma }=B{B}^{\prime }+D^2$, the gradient of this factorization has been derived and shown to be computationally efficient [63].

Algorithm 3 shows the VBDA algorithm with stochastic gradient ascent optimization. Note that, in Algorithm 1, Algorithm 2 is replaced by Algorithm 3 in order to perform VBDA method in the R-vine model. This approach is tractable posterior distribution.

Algorithm 3 Variational Bayes data augmentation with control variates and ADADELTA learning rate

Require:  $\mathsf{\Lambda }\left(\theta \right|y),DA,{\lambda }^{\left(0\right)},{\mu }^{QMLE},S,nVB,c,t_w,P,\rho ,ϵ.$   1: Set $k=1$.   2: Initialize $\lambda |{\mu }^{QMLE}$.   3: Generate $({\theta }_s^{\left(k\right)},{\mathbf{u}}_s^{\left(k\right)})\sim q_{{\lambda }^k}\left(\theta ,u\right)$ for $s=1,\dots ,S$ where   4: $q_{{\lambda }^b}\left(\mathbf{u}\right)$ could be i. $DA0$ii. $DA1$ or iii. $DA2$ and $q_{{\lambda }^a}\left(\theta \right)\sim N(M_{\theta },{\mathsf{\Sigma }}_{\theta })$.   5: Calculate ${\varsigma }_i^{\left(k\right)}=({\varsigma }_1^{\left(k\right)},\dots ,{\varsigma }_m^{\left(k\right)})$ with $${\varsigma }_i^{\left(k\right)}={\displaystyle \frac{cov\left(\left[log h(\theta ,\mathbf{u})-log q_{\lambda }(\theta ,\mathbf{u})\right]\times {\nabla }_{{\lambda }_i}log q_{\lambda }(\theta ,\mathbf{u}),{\nabla }_{{\lambda }_i}log q_{\lambda }(\theta ,\mathbf{u})\right)}{var({\nabla }_{{\lambda }_i}log q_{\lambda }(\theta ,\mathbf{u}))}}$$   6: Set $k=k+1$.   7: while stopping rule is not satisfied do   8:       Generate $({\theta }_s^{\left(k\right)},{\mathbf{u}}_s^{\left(k\right)})\sim q_{{\lambda }^k}\left(\theta ,u\right)$ for $s=1,\dots ,S$.   9:       Calculate ${\nabla }_{\lambda }\left(\widehat{\mathcal{L}\left({\lambda }^{\left(k\right)}\right)}\right)={\left(g_{{\lambda }_1}^{\left(k\right)},\dots ,g_{{\lambda }_m}^{\left(k\right)}\right)}^{\prime }$ $$\begin{array}{cc}\hfill g_{{\lambda }_i}^{\left(k\right)}& ={\displaystyle \frac{1}{S}}\sum _{s=1}^S\left(logh({\theta }_s^{\left(k\right)},{\mathbf{u}}_s^{\left(k\right)})-log{q}_{\lambda }({\theta }_s^{\left(k\right)},{\mathbf{u}}_s^{\left(k\right)})-{\varsigma }_i^{(k-1)}\right)\hfill \\ & \times {\nabla }_{{\lambda }_i}log{q}_{\lambda }({\theta }_s^{\left(k\right)},{\mathbf{u}}_s^{\left(k\right)})\hfill \end{array}$$ 10:     Calculate ${\varsigma }_i^{\left(k\right)}=({\varsigma }_1^{\left(k\right)},\dots ,{\varsigma }_m^{\left(k\right)})$. 11:     Perform $\Delta {\lambda }^{\left(k\right)}\leftarrow$ the ADADELTA method. 12:     Set ${\lambda }^{(k+1)}={\lambda }^{\left(k\right)}+\Delta {\lambda }^{\left(k\right)}$ 13:     Calculate $\widehat{LB}\left({\lambda }^{(k+1)}\right)={\displaystyle \frac{1}{S}}{\sum }_{s=1}^S\left(logh({\theta }_s^{\left(k+1\right)},{\mathbf{u}}_s^{\left(k+1\right)})-log{q}_{\lambda }({\theta }_s^{\left(k+1\right)},{\mathbf{u}}_s^{\left(k+1\right)})\right)$ 14:     if $k>c$ then 15:          Calculate ${\overline{LB}}_{k-t_w}=1/t_w{\sum }_{i=1}^{t_w}{\widehat{LB}(\lambda }^{(k-i+1)})$ 16:          if $\overline{LB}\left({\lambda }^{(k-t_w)}\right)>max\left(\overline{LB}\right)$ then 17:               $patience=0$. 18:               Collect ${\lambda }^{(*)}\leftarrow {\lambda }^{(k+1)}$. 19:          else 20:               $patience=patience+1$. 21:          end if 22:          if $patience>P$ then 23:               stop. 24:          end if 25:       end if 26:       Set $k=k+1$. 27: end while 28: return  ${\lambda }^{(*)}$

A brief overview of the procedure is as follows:

Three VB estimators for regular vine dependence models are introduced in Line 4, where the specification of $q_{\left(u\right)}$ can be one of DA0, DA1, or DA2. To initiate the algorithm, an initial value for the variational parameter, ${\lambda }^{\left(0\right)}$, is required, typically initialized using QMLE estimates ${\mu }^{QMLE}$.

In Line 12, the lower bound (LB) is updated iteratively as follows: ${\lambda }^{(k+1)}={\lambda }^{\left(k\right)}+{\rho }^{\left(k\right)}\widehat{{\nabla }_{\lambda }\mathcal{L}\left({\lambda }^{\left(k\right)}\right)}$. Here, ${\rho }^{\left(k\right)}$ is the learning rate, and ${\nabla }_{\lambda }\widehat{\mathcal{L}\left({\lambda }^{\left(k\right)}\right)}$ is an unbiased estimate of the gradient of the lower bound $\mathcal{L}$, computed using the ADADELTA optimization method (Line 11). For further details on adaptive learning rate techniques like ADADELTA, see [64].

The gradient of the lower bound, ${\nabla }_{\lambda }\mathcal{L}\left(\lambda \right)$, is expressed as the expectation:

$${\nabla }_{\lambda }\mathcal{L}\left(\lambda \right)=E_q({\nabla }_{\lambda }log q_{\lambda }(\theta ,\mathbf{u})\{log h(\theta ,\mathbf{u})-log q_{\lambda }(\theta ,\mathbf{u})\})$$

where $p(\theta ,\mathbf{u}|y)\propto f(y,\mathbf{u}\left|\theta \right)p\left(\theta \right)=h(\theta ,\mathbf{u})$ represents the unnormalized posterior distribution.

To reduce the variance of this unbiased gradient estimator, a control variate vector $\varsigma$ is employed. Consequently, the unbiased estimator of the gradient is given by $\widehat{{\nabla }_{\lambda }\mathcal{L}\left({\lambda }^{\left(k\right)}\right)}={(g_{{\lambda }_1},\dots ,g_{{\lambda }_m})}^{\prime }$ where $g_{\lambda }={\displaystyle \frac{1}{S}}{\sum }_{s=1}^S\left(log h({\theta }_s,{\mathbf{u}}_s)-log q_{\lambda }({\theta }_s,{\mathbf{u}}_s)\right){\nabla }_{\lambda }log q_{\lambda }({\theta }_s,{\mathbf{u}}_s)$ where $g_{\lambda }={\displaystyle \frac{1}{S}}{\sum }_{s=1}^S\left(log h({\theta }_s,{\mathbf{u}}_s)-log q_{\lambda }({\theta }_s,{\mathbf{u}}_s)\right){\nabla }_{\lambda }log q_{\lambda }({\theta }_s,{\mathbf{u}}_s)$ and m is the number of elements in $\lambda$, and SS is the number of Monte Carlo samples.

For a more detailed discussion of the VBDA algorithm, refer to [30] (Section 3).

The stopping rule for the algorithm terminates the iterative procedure if

(i.)

There is a fixed number of stochastic gradient ascent steps, $nVB$, or

(ii.)

The moving average $\widehat{LB}$ is not improved, ${\overline{LB}}_{k-t_w}=1/t_w{\sum }_{i=1}^{t_w}{\widehat{LB}(\lambda }^{(k-i+1)})$, which is referred to as the $patience$ parameter and $patience=patience+1$ in Line 20 and the whole procedure stops when $patience>$ maximum patience P in Line 22–23, and

(iii.)

All of the above conditions will be checked when the $k^{th}$ iteration is greater than a constant c.

Finally, ${\lambda }^{(*)}$ is collected when ${\overline{LB}}_{k-t_w}$ is greater than $max\left(\overline{LB}\right)$ [60]. Note that the simulation study in Bayesian inference and machine learning including the rw-MH algorithm and the VBDA algorithm can be found in the Supplementary Material. The results show that, in general, the VB methods perform better than the others.

4. Empirical Study

4.1. Data

This study analyzes financial market time series data with up to 100 dimensions. For the training set, we selected the daily adjusted closing prices of the top 100 Nasdaq-listed stocks by market capitalization, covering the period from 2 January 2009 to 20 September 2021, where we intentionally avoided the impact of the 2008 global financial crisis. Only stocks listed before 2009 were included, resulting in a total of 3201 daily observations. The test set spans from 21 September 2021 to 21 December 2021, comprising 65 daily observations. All data were obtained from Yahoo Finance using MATLAB 2022a’s data feed function. The experiments were implemented in MATLAB and conducted on a laptop equipped with an 11th Gen Intel(R) Core(TM) i7-1185G7 processor (3.00 GHz) and 32 GB of RAM.

After completing data cleaning, we obtained 100 stock indices for use in our empirical study. A full list of these indices is provided in Appendix C. To evaluate the performance of the proposed models described in Section 2, we conducted two empirical experiments using two datasets: one consisting of all 100 time series and another with only the last 30 stock indices. The goal of these experiments was to assess the scalability and effectiveness of the proposed model as the dimensionality increases.

The descriptive statistics of the dataset are summarized as follows. The top five business sectors represented in our analysis are technology (22 firms), health care (18 firms), finance (11 firms), consumer services (11 firms), and capital goods (8 firms). The total market capitalization of the selected stocks is USD 30,814 billion, accounting for approximately 46% of the total market capitalization on the Nasdaq exchange.

All stocks exhibit a positive mean return, with return values ranging from −39.02% to 52.29%. The standard deviation ranges from 1.06% to 3.67%, while skewness values range between −1.04 and 1.56. Kurtosis spans from 5.95 to 47.26. These statistics indicate that the return distributions are asymmetric and exhibit heavy tails.

Additionally, the Jarque–Bera test statistics for all returns strongly reject the null hypothesis of normality at the 1% significance level, confirming that the return distributions deviate significantly from normality.

4.2. Regular Vine Distribution Selection

Multivariate copula models can be fitted to n-dimensional time series data using a two-stage sequential approach [30]. In the first stage, a univariate marginal model is selected and fitted separately to each time series to obtain standardized residuals, which are then transformed into marginally uniform variables. In this study, we apply our proposed marginal model, detailed in Section 2.3, and compare its performance to a widely used benchmark: the ARMA(1,1)-GARCH(1,1) model with Student-t innovations.

In the second stage, the dependence structure among the transformed residuals is modeled using a multivariate copula. It is well established in the literature that different pairs of financial variables exhibit varying degrees of asymmetry and tail dependence. Traditional multivariate copulas are generally unable to capture such heterogeneous dependence structures. Vine copulas, however, are specifically designed to address this limitation.

While D-vine and C-vine copulas are effective in modeling complex dependencies, they are constrained by their predefined path structures. To overcome this limitation, we investigate the use of regular vine (R-vine) copulas—a more flexible and general class that encompasses both D-vines and C-vines as special cases. R-vines offer significantly greater modeling capacity due to their extensive variety of possible tree structures and pair-copula combinations.

In fact, for high-dimensional datasets, the number of possible R-vine structures grows rapidly, with the total number given by ${\displaystyle \frac{n!}{2}}{2}^{\left({\displaystyle \genfrac{}{}{0pt}{}{n-2}{2}}\right)}$ [65], underscoring their flexibility and complexity compared to standard copula models and their vine subclasses.

The following tasks are the sequential steps of fitting an R-vine copula with marginal specification:

(a)

Standardize the residuals of the returns using the univariate marginal model.

(b)

Select the R-vine path structure of the tree, $\mathcal{M}=(N,E)$, given by maximized empirical $Kendal{l}^{\prime }s \tau$ via

b.1

Formulation of empirical $Kendal{l}^{\prime }s \tau$ of all possible pairs variable, ${\widehat{\tau }}_{i,k}$, $1\le i<k\le n$;

b.2

Performing the spanning tree maximization (the sum of absolute empirical $Kendal{l}^{\prime }s \tau$)

$$max\sum _{e=\{i,k\} in spanning tree}\left|{\widehat{\tau }}_{i,k}\right|;$$

b.3

For each edge, selection of bivariate copula family $t_{i,k}$ and its parameter(s) ${\mathfrak{p}}_{i,k}$ from all possible bivariate copula candidates via Bayesian information criterion (BIC) value.

(c)

Iterate Step (b) from the first tree $T_1$ (unconditional tree, ${\widehat{\tau }}_{i,k}$) to the last tree $T_{n-1}$ (conditional tree, ${\widehat{\tau }}_{i,k|D}$ where D is the proximity condition).

The methodology described above yields a complete specification of a regular vine copula, including $\mathcal{M},\mathcal{T},\mathcal{P}$. The QMLE is employed in Step b.3 to estimate all relevant parameters. This full specification is then used as the foundation for our Bayesian inference and machine learning procedures.

It is important to note that, for the first tree in the vine structure, parallel computation is feasible due to the independence of the path structure in R-vines. The method proceeds as follows:

• Step 1 (Tree 1): A parallel computation technique is applied to estimate ${\widehat{\tau }}_{1,k}$ for $k=1,\dots ,n-1$.
• Step 2: A FOR loop is used to compute ${\widehat{\tau }}_{i,k}$ where $i<k,i=n-1,\dots ,2, k=1,\dots ,n-2$.

For more details on the maximum spanning tree algorithm used in this context, see [30].

Our study employs a range of bivariate copula functions to capture the diverse (a)symmetrical dependence structures present in financial time series data. While the core families considered include the Gaussian, Student-t, Gumbel, and Frank copulas—consistent with the approach of [30]—we extend the analysis by incorporating a total of 13 copula families. The complete list of candidate bivariate copula families used in this study is provided below:

• Gaussian/Normal copula presents symmetric and no tail dependence.
• Student-t copula presents symmetric and upper and lower tail dependence.
• Frank copula presents symmetric and tail independence.
• Clayton copula presents asymmetric and lower tail dependence.
• B5/Joe, Gumbel, and Galambos copulas present asymmetric and different upper and lower tail dependence.
• BB1, BB3, BB4, BB5, BB7 and BB10 copulas present asymmetric and different upper and lower tail dependence.

Details of the bivariate copula distributions and their key dependence structure properties are summarized in Appendix A. These include the cumulative distribution functions, lower and upper tail dependence orders, and rank-based dependence measures. For additional discussion on copula properties, see, among others, [17] (Chapter 4) and [66] (Appendix).

We also conducted Ljung–Box tests on the standardized residuals from all proposed models. The results confirm the independence of the residuals. Full details of these tests are provided in Appendix B.

4.3. Empirical Results

In this section, we present the empirical results obtained from our proposed Bayesian models and estimation methods for R-vine copulas. A comprehensive set of 13 bivariate copula families is employed within the regular vine structure to capture complex dependence patterns.

For the univariate margins, we apply the mixture distribution defined in Equation (7) to the ICAPM-EGARCH models, which are designed to capture key features of financial time series data such as volatility clustering and heavy tails.

As a benchmark, we use the traditional QMLE method and compare its performance with our proposed approaches, including the rw-MH algorithm and the VBDA methods. These methods are implemented in the R-vine copula framework for dimensions of up to 100. In total, the empirical study involves the estimation of up to 4950 bivariate copula functions and 6138 parameters.

The experimental results, summarized in Table 1 and Table 2, indicate that the VBDA1 method delivers the best performance in terms of marginal likelihood on the training set. On the test set, the variational Bayes approaches—particularly VBDA1—demonstrate substantial improvements in forecasting accuracy as the dimensionality increases, making them strong candidates for high-dimensional modeling. Specifically, as both the number of dimensions and the forecast horizon grow, VBDA1 provides more accurate variability estimates. In contrast, the QMLE method performs relatively poor in higher dimensions and longer forecast horizons. However, in the case of 30 dimensions with a three-month forecast window, QMLE outperforms the other methods.

Table 1. Performance comparison of 30 dimensions.

Model	Method	Training Data						Test Data
		MarLik	AIC	BIC	Loglik	Last nVB Step	Time	1 Month		3 Months
								MAD	RMSE	MAD	RMSE
MD1	QMLE	n.a.	302,512	302,955	−150,347	n.a.	23	1.22	1.63	1.43	1.94
MD1	rw-MH	1,381,159	300,006	302,968	−149,107	n.a.	1484	1.22	1.63	1.42	2.03
MD1	VBDA0	1,395,092	320,038	323,005	−159,122	944	3586	1.50	2.57	1.54	2.26
MD1	VBDA1	1,402,133	328,476	331,339	−163,360	489	1465	1.45	2.31	1.48	2.21
MD1	VBDA2	1,395,652	318,248	321,177	−158,234	728	10,530	1.35	2.01	1.54	2.19
MD2	QMLE	n.a.	298,389	298,677	−148,359	n.a.	28	1.22	1.63	1.41	2.04

Notes: MD1 = R-vine–ICAPM–EGARCH–Mixture model. MD2 = R-vine–ARMA–GARCH–Student-t model. The acceptance rate of the rw-MH method is 49%. Time is computational time in minutes. n.a. = not available. MarLik = marginal log-likelihood. MAD = mean absolute deviation. RMSE = root mean square error. Bold font indicates better results.

Table 2. Performance comparison of 100 dimensions.

Model	Method	Training Data					Test Data
		MarLik	AIC	BIC	Loglik	Last nVB Step	1 Month		3 Months
							MAD	RMSE	MAD	RMSE
MD1	QMLE	n.a.	969,425	1,015,504	−477,779	n.a.	1.18	1.59	1.35	1.85
MD1	rw-MH	4,372,594	906,846	948,133	−446,490	n.a.	1.17	1.58	1.34	1.85
MD1	VBDA0	4,483,822	915,862	956,847	−451,037	1116	1.19	1.60	1.37	1.90
MD1	VBDA1	4,485,991	963,895	1,005,219	−475,009	567	1.21	1.63	1.34	1.86
MD1	VBDA2	4,482,233	917,936	959,083	−452,053	1086	1.19	1.61	1.37	1.89
MD2	QMLE	n.a.	964,942	1,010,414	−475,638	n.a.	1.20	1.61	1.34	1.88

Notes: MD1 = R-vine–ICAPM–EGARCH–Mixture model. MD2 = R-vine–ARMA–GARCH–Student-t model. The acceptance rate of the rw-MH method is 48%. Time is computational time in minutes. n.a. = not available. MarLik = marginal log-likelihood. MAD = mean absolute deviation. RMSE = root mean square error. Bold font indicates better results.

For 100-dimensional data, VBDA1 achieves the best forecasting performance based on the mean absolute deviation (MAD). Meanwhile, both the rw-MH and QMLE methods yield the best performance in terms of root mean square error (RMSE) for the three-month test set, while rw-MH shows the strongest performance in one-month forecasts at the 100-dimensional level.

Figure 3 illustrates a representative example of the empirical results for a normalized R-vine copula contour plot and rank-based dependence measures. These results are based on the univariate ICAPM-EGARCH–mixture marginal model using the VBDA2 estimation method in a 30-dimensional setting.

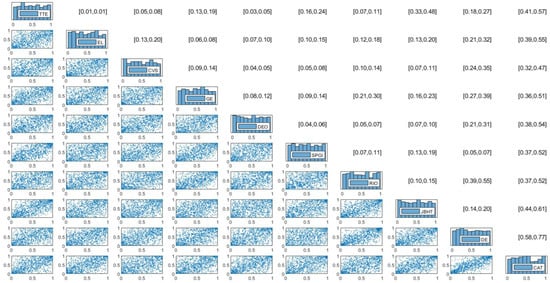
Figure 3. Estimation results of normalized mixed R-vine copula contour plot, Kendall’s $\widehat{\tau }$, and Spearman’s $\widehat{{\rho }_s}$ for 10 stock indices in the 30-dimensional cases using R-vine–ICAPM–EGARCH–Mixture model and VBDA2 method. Notes: Due to space, only 10 representative stocks are shown. Contour plots are shown in the lower triangular matrix while [Kendall’s $\widehat{\tau }$, Spearman’s $\widehat{{\rho }_s}$] are shown in the upper triangular matrix.

Due to space, we present a normalized 10-dimensional subset of the R-vine contour plot for selected stock indices. The stock names appear along the diagonal of the matrix. The lower triangular part of the matrix displays the R-vine copula contours, where each row corresponds to the $i^{th}$ tree ($i=1,\dots ,9$) derived from the full 30-dimensional dataset. The upper triangular matrix shows the empirical Kendall’s ${\widehat{\tau }}^k$ and Spearman’s ${\widehat{{\rho }_s}}^k$, where the $k^{th}$ column ($k=10,\dots ,2$) corresponds to tree ${\widehat{\mathcal{T}}}_i$ for $i=1,\dots ,9)$.

Similarly, Figure 4 provides an empirical example of the normalized 10-dimensional R-vine contour plots and rank-based dependence measures from the 100-dimensional analysis, using the VBDA1 method. Complete empirical results—including Kendall’s $\widehat{\tau }$, Spearman’s $\widehat{{\rho }_s}$, and the estimated vine matrices $\widehat{\mathcal{M}}$ and $\widehat{\mathcal{T}}$ for both figures—are available in the Supplementary Materials.

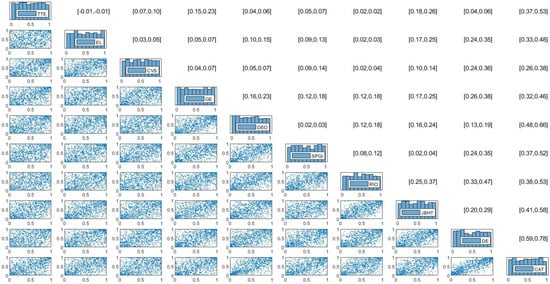
Figure 4. Estimation results of normalized mixed R-vine copula contour plot, Kendall’s $\widehat{\tau }$, and Spearman’s $\widehat{{\rho }_s}$ for 10 stock indices in the 100-dimensional cases using R-vine–ICAPM–EGARCH–Mixture model and VBDA1 method. Notes: Due to space, only 10 representative stocks are shown. Contour plots are shown in the lower triangular matrix while [Kendall’s $\widehat{\tau }$, Spearman’s $\widehat{{\rho }_s}$] are shown in the upper triangular matrix.

Table 1 summarizes the model performance for the 30-dimensional case. Based on the training dataset, the proposed VBDA1–R-vine–ICAPM–EGARCH–mixture model delivers the best performance in terms of marginal likelihood. The next best performers are the VBDA2 and VBDA0 methods, respectively. Among all estimation methods, VBDA2 is the most computationally intensive, which explains its longer runtime for R-vine copula estimation. VBDA1, while still relatively complex, requires less computing time than VBDA2 and converges more efficiently than simpler methods such as VBDA0 due to its favorable convergence properties.

An illustration of the convergence behavior of the evidence lower bound (ELBO) for all VBDA methods is shown in Figure 5, using the stock index pair (DE, CAT) as an example. Additionally, Figure 6 presents the first tree structure from the spanning tree maximization algorithm for the VBDA2–R-vine–ICAPM–EGARCH–mixture model. In contrast, when evaluating by Akaike information criterion (AIC), Bayesian information criterion (BIC), and log-likelihood values, the QMLE–R-vine–ARMA–GARCH–Student-t model achieves the best performance. The second-best performance under these criteria is the rw-MH-based R-vine–ICAPM–EGARCH–mixture model, which achieves a favorable acceptance rate in the MH algorithm.

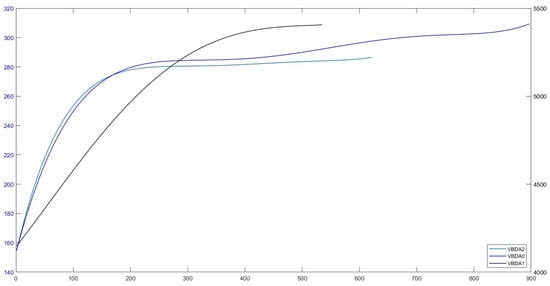
Figure 5. An example of ELBO convergence across VBDA methods for a pair of stocks (DE, CAT), using a Student-t copula in the 30-dimensional case. Note: The ELBO values of VBDA0 are plotted against the right y-axis while those of VBDA1 and VBDA2 are plotted against the left y-axis.

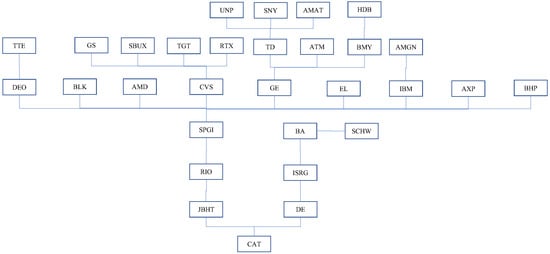
Figure 6. An example of Tree 1 in the 30-dimensional case of an R-vine copula using VBDA2 within the R-vine–ICAPM–EGARCH–Mixture model.

For the test dataset, forecasting performance was evaluated over one-month and three-month horizons using the MAD and RMSE metrics. In terms of forecast errors, the QMLE and rw-MH methods show comparable predictive performance and emerge as the best-performing models overall. Interestingly, within the variational Bayes framework, VBDA1 demonstrates improved performance—especially as the forecast horizon increases—outperforming the other VBDA variants based on MAD values. This trend is further supported by the experimental results.

Table 2 summarizes the performance of the proposed models in the 100-dimensional setting, using both training and test datasets. Overall, as the number of dimensions increases to 100, the performance of variational Bayes methods improves noticeably.

Among all approaches, the Bayesian inference and machine learning methods—particularly the Variational Bayes with Data Augmentation Type 1 (VBDA1)—outperform the traditional QMLE method, especially in terms of the mean absolute deviation (MAD) for the three-month forecast horizon. The VBDA1–R-vine–ICAPM–EGARCH–mixture model achieves the lowest three-month MAD, accurate to three decimal places, indicating superior forecasting accuracy.

These findings suggest that variational Bayes—specifically, the VBDA1 algorithm—performs effectively in high-dimensional settings. Both the training and test results confirm that the VBDA1–R-vine–ICAPM–EGARCH–mixture model surpasses all competing models in terms of marginal likelihood and three-month MAD forecast error.

Based on the model comparisons, the rw-MH algorithm combined with the R-vine-ICAPM-EGARCH-Mixture model emerges as the most outstanding, particularly due to its reasonable acceptance rate. Variational Bayes inference also performs exceptionally well, with the VBDA0-R-vine-ICAPM-EGARCH-Mixture model ranking as the second most preferable according to the AIC and BIC values. While the traditional QMLE method shows a decline in performance on the training data, it still remains a viable alternative for the test data.

Table 3 and Table 4 summarize the copula families and their parameter counts across models and methods for 30- and 100-dimensional settings, as selected by Algorithm 1. In total, there are 435 pair-copula functions in 30 dimensions and 4950 in 100 dimensions. In the 30-dimensional case, the best-performing method—VBDA1—estimates 638 parameters, which is the second-lowest among all methods. Conversely, in the 100-dimensional case, VBDA1 estimates 6138 parameters—the highest. This indicates that better model performance does not necessarily correspond to a smaller number of parameters. Among the selected bivariate copula families, the elliptical copulas—Student-t and Gaussian—fit the empirical data best, followed by Archimedean families. The Student-t, Gaussian, and Frank copulas together account for at least 68% of all copulas used, implying that approximately 32% of the data exhibit asymmetric or tail dependence characteristics. In 30 dimensions, the most frequently selected families are Student-t and Frank, while in 100 dimensions, the elliptical copulas dominate. Notably, the BB6 copula was not selected in the 30-dimensional case, and the BB10 copula was not used in the 100-dimensional case.

Table 3. Summary of copula families and their parameter numbers across models and methods for 30 dimensions.

Model	R-Vine–ICAPM–EGARCH–Mixture					Competing Model *
Estimation Method	VBDA0	VBDA1	VBDA2	rw-MH	QMLE	QMLE
Total Parameter Estimates **	657	638	650	656	682	606
Copula Family	Number of Parameters
Gaussian	53	73	54	37	39	44
Student-t	156	119	151	156	143	118
Frank	111	111	114	124	121	178
Clayton	19	23	24	29	31	24
Gumbel	17	12	12	14	16	6
B5/Joe	8	4	8	3	7	6
Galambos	5	9	8	7	3	6
BB1	6	10	9	4	7	3
BB3	1	1	3	1	1	0
BB4	1	5	1	1	0	0
BB6	0	0	0	0	0	0
BB7	12	15	14	12	12	1
BB10	46	53	37	47	55	49

Notes: * The competing model is the R-vine–ARMA–GARCH–Student-t model. ** Including the copula and marginal distribution parameters.

Table 4. Summary of copula families and their parameter numbers across models and methods for 100 dimensions.

Model	R-Vine–ICAPM–EGARCH–Mixture					Competing Model *
Estimation Method	VBDA0	VBDA1	VBDA2	rw-MH	QMLE	QMLE
Total Parameter Estimates **	6094	6138	6115	6133	6133	6133
Total Copula Family	4950
Gaussian	1537	1659	1535	1527	1527	1527
Student-t	1226	1526	1215	1207	1207	1207
Frank	617	777	625	633	633	633
Clayton	528	254	526	526	526	526
Gumbel	440	228	446	452	452	452
B5/Joe	196	70	193	193	193	193
Galambos	178	185	174	173	173	173
BB1	141	157	142	141	141	141
BB3	51	40	49	43	43	43
BB4	24	47	29	34	34	34
BB6	6	3	10	11	11	11
BB7	6	4	6	10	10	10
BB10	0	0	0	0	0	0

Notes: * The competing model is R-vine–ARMA–GARCH–Student-t model. ** Including the copula and marginal distribution parameters.

In this study, we apply the ICAPM–EGARCH–mixture with R-vine copula, which we believe is a useful model. However, this might be subject to the model misspecification, which can be a limitation of this study. The computing performance is another possible limitation, which can be improved, but we leave for future research. A practical implementation from the practitioner’s viewpoint poses an interesting challenge to be validated in the future.

5. Concluding Remarks

This study introduces the variational Bayes methods—with and without data augmentation types 1 and 2—for Bayesian inference and machine learning, alongside the rw-MH Bayesian MCMC approach and the competing QMLE method, applied to regular vine copula models in graph theory for n-dimensional data. Standard multivariate copulas often face limitations due to having a single control parameter, a problem that worsens as dimensionality increases. Although C-vine and D-vine copulas offer more flexibility by allowing different bivariate copula choices and tree constructions, they impose restrictions on the tree path structure. To overcome this, we employ the more general R-vine copula, which eliminates the tree path structure constraint and provides richer insights into the relationships within financial data. This study considers 13 candidate bivariate copula families for the R-vine model, though the algorithm easily accommodates additional families. Furthermore, our proposed model is fully compatible with the special subclasses of C-vine and D-vine copulas and can be applied to n-dimensional data analysis.

Furthermore, this study is the first to introduce a mixture distribution into the R-vine model, enhancing its flexibility. The mixture distribution combines a Gaussian distribution with two generalized Pareto distributions within a univariate marginal intertemporal capital asset pricing model and an asymmetric GARCH framework, capturing additional risk premium stylized facts of specific financial securities. Additionally, the study presents a parallel R-vine with margins algorithm for Bayesian inference and machine learning, a bivariate copula selection algorithm within the R-vine framework, and an R-vine with margins data simulation algorithm. Importantly, our proposed algorithm can compute the joint distribution for arbitrary R-vine copulas.

In conclusion, our study produces the R-vine tree path dependence structure, pair-copula types, and parameter estimates in n-dimensions. The univariate marginal model captures individual stock risk premiums and risk-free rates. Our proposed model, particularly the VBDA1–R-vine–ICAPM–EGARCH–mixture model, outperforms competing approaches. Moreover, we demonstrate that the traditional QMLE estimation method significantly deteriorates as dimensionality increases.

For future research, there are numerous avenues to explore depending on specific interests. For instance, the model could be applied to higher-frequency data or extended with alternative copula families such as factor copulas or rotated copulas. The copula selection criteria could also be modified—using Spearman’s ${\rho }_s$ or other relevant measures tailored to particular financial contexts instead of Kendall’s $\tau$. Additionally, the framework can be adapted to other domains, such as high-dimensional portfolio optimization and higher-dimensional datasets. From a computational perspective, further development could involve implementing the algorithm on high-performance computing platforms to reduce computational time in Bayesian inference and machine learning.