Asymptotics of Closeness Centralities of Graphs

Abstract

Given a connected graph G with n vertices, the distance between two vertices is the number of edges in a shortest path connecting them. The sum of the distances in a graph G from a vertex v to all other vertices is denoted by $S{D}_G\left(v\right)$. The closeness centrality of a vertex in a graph was defined by Bavelas to be $C_C\left(v\right)={\displaystyle \frac{n-1}{S{D}_G\left(v\right)}}$ and the closeness centrality of G is $C_C\left(G\right)={\displaystyle \sum _{v\in G}}{\displaystyle \frac{n-1}{S{D}_G\left(v\right)}}$. We consider the asymptotic limit of $C_C\left(G\right)$ as the number of vertices tends to infinity and provide an elegant and insightful proof of a 2025 result by Britz, Hu, Islam, and Tang, ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(P_n\right)=\pi$, using uniform convergence and Riemann sums. We applied the same technique for the union of a cycle $C_m$ and path $P_n$ and the union of a path and a complete graph. We prove that of all graphs, paths have the minimum closeness centrality. Next we show for any $c\in [\pi ,\infty )$, there exists a sequence of graphs $\left\{G_n\right\}$ such that ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(G_n\right)=c$. In addition, we investigate the mean distance of a graph, $\overline{l}\left(G\right)={\displaystyle \frac{1}{n(n-1)}}{\displaystyle \sum _{v\in V\left(G\right)}}SD\left(v\right)$ and the normalized closeness centrality, ${\overline{C}}_C\left(G\right)={\displaystyle \frac{1}{n}}{C}_C\left(G\right)$. We verify a conjecture of Britz, Hu, Islam, and Tang that the set of products $\{\overline{l}\left(G\right){\overline{C}}_C\left(G\right):G\mathrm{is}\mathrm{finite}\mathrm{and}\mathrm{connected}\}$ is dense in $[1,2)$.

1. Introduction

Given a graph G, the distance between two vertices is the number of edges in a shortest path connecting them. We consider the sum of the distances from a given vertex to all other vertices. The sum of the distances in a graph G from a vertex v will be denoted by $S{D}_G\left(v\right)$ or simply $SD\left(v\right)$ when the graph G is clear. This measure is equivalent to the transmission of a vertex introduced by Handa [1]. As noted in [2], motivation for this metric comes from a variation of the famous Traveling Salesman Problem where the salesman must return to the starting point v after each delivery. The length of the salesman’s tour will be $2S{D}_G\left(v\right)$. This is related to the closeness centrality of a vertex or a graph, defined by Bavelas in 1950 [3]. The closeness centrality of a vertex v in a graph is $C_C\left(v\right)={\displaystyle \frac{n-1}{S{D}_G\left(v\right)}}$. Then $C_C\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\displaystyle \frac{n-1}{S{D}_G\left(v\right)}}$.

Closeness centrality has been used to identify important individuals in social networks [4] and has been used to analyze the impact on coauthorship networks [5]. Asymptotic behavior for graph centrality properties have been studied for decades. A practical application of this asymptotic analysis is to identify trends that emerge as networks expand over time. In 2000, Barrat and Weigt [6] investigated asymptotic properties of small-world network models. In 2013 Ek, VerSchneider, and Narayan [7] determined the asymptotic behavior of the global efficiency of a path. In this paper we investigate the asymptotic behavior of $C_C\left(G\right)$.

We present a new approach for determining the asymptotic behavior of $C_C\left(G\right)$ for various families of graphs. We recast the sum of the distances as a Riemann sum and then replace the discrete values with a continuous function. Then we determine the asymptotic value of the closeness centrality by computing the definite integral.

We present an elegant and more powerful proof of a result of Britz, Hu, Islam, and Tang [8], showing that ${\displaystyle \underset{n\to \infty }{lim}}$$C_C\left(P_n\right)=\pi$. In addition, we resolve a conjecture from their paper, showing that the numbers $\overline{l}$$C_C\left(G\right)$ for all connected graphs G form a dense subset of the interval $[1,2)$. We also establish a universal lower bound for $C_C\left(G\right)$ and show that this bound is tight when G is a path.

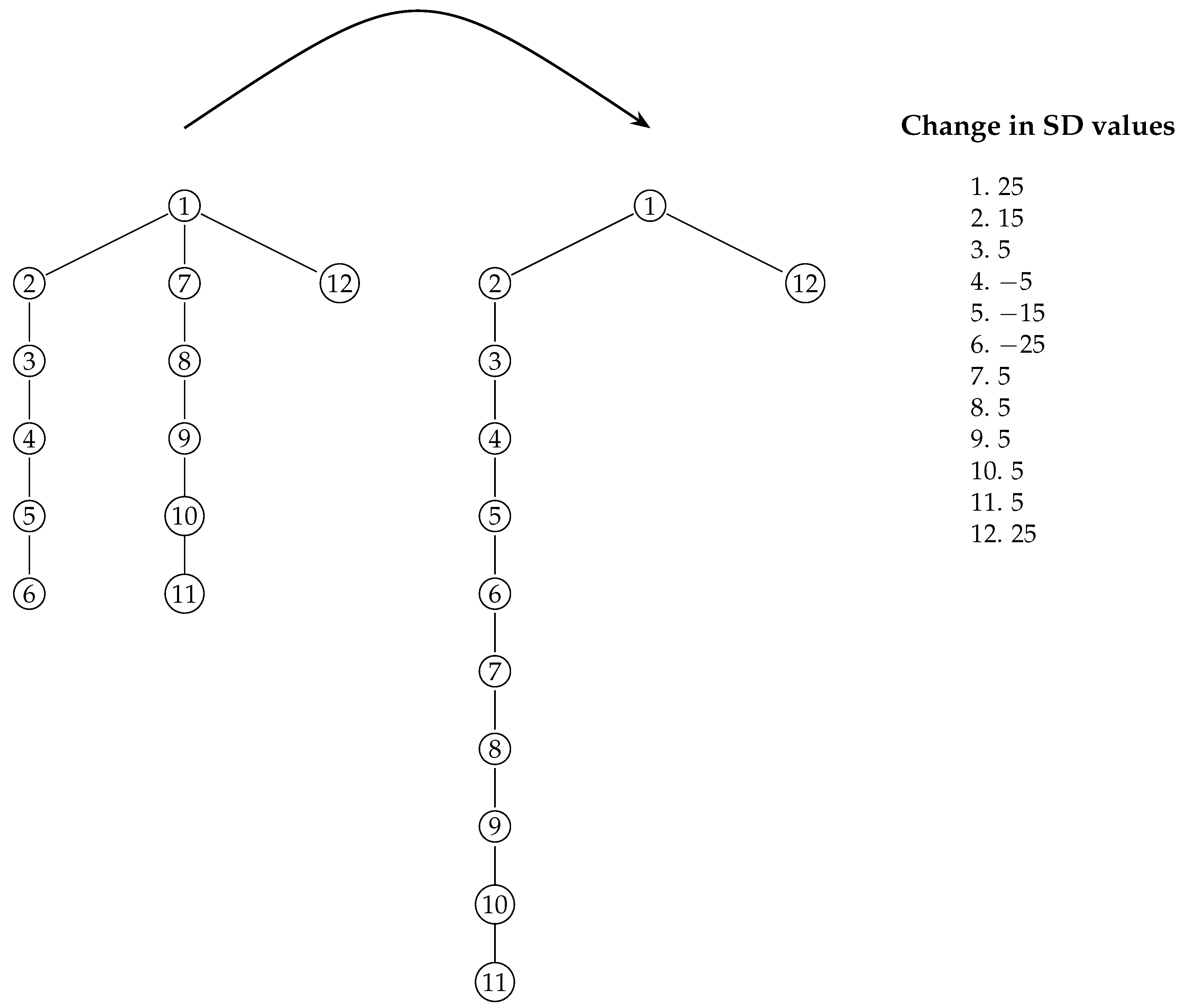
2. Asymptotics of Closeness Centralities of a Path

We provide an alternative proof for ${\displaystyle \underset{n\to \infty }{lim}}$$C_C\left(P_n\right)=\pi$ in Lemma 2. We start by presenting a combinatorial formula for $SD$ values for vertices in a path in Lemma 1.

Lemma 1.

Let $G=P_n$ with vertices $v_1,v_2,\dots ,v_n$. Then $SD\left(v_j\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n-j+1}{2}}\right)$.

Proof. 

Consider a vertex $v_i$. The distances from $v_j$ to each of the vertices $v_{j-1},v_{j-2},\dots ,v_1$ are $1,2,3,\dots ,j-1$, respectively, which sum to $\left({\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right)$. The distances from $v_j$ to each of the vertices $v_{j+1},v_{j+2},\dots ,v_n$ is $1,2,3,\dots ,n-j$, respectively, which sum to $\left({\displaystyle \genfrac{}{}{0pt}{}{n-j+1}{2}}\right)$. □

We next restate a lemma of Britz, Hu, Islam, and Tang [8]. In their proof they used approximations through lower and upper bounds which converge asymptotically as n grows large. We provide an alternative proof using a novel technique. Starting with the formula from Lemma 1 we let $S_n={\displaystyle \sum _{j=1}^n}{\displaystyle \frac{n}{SD\left(v_j\right)}}={\displaystyle \frac{n}{n-1}}{C}_C\left(P_n\right)$. Then we can view $S_n$ as a Riemann sum over the partition ${\left\{{\displaystyle \frac{j}{n}}\right\}}_{j=1}^n$. Then after carefully changing this to a sum over a continuous domain we can calculate ${\displaystyle \underset{n\to \infty }{lim}}$$C_C\left(P_n\right)$ using a definite integral. We obtain the same stunning result from [8] that ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(P_n\right)=\pi$.

Lemma 2.

${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(P_n\right)=\pi$

Proof. 

Let $x_j={\displaystyle \frac{j}{n}}$ and we have

$$\begin{array}{cc}\hfill S_n& ={\displaystyle \sum _{j=1}^n}\left({\displaystyle \frac{1}{n}}\right){\displaystyle \frac{n^2}{j^2-j-jn+\frac{n(n+1)}{2}}}\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^n}\left({\displaystyle \frac{1}{n}}\right){\displaystyle \frac{1}{(j^2-j-jn+\frac{n(n+1)}{2})\frac{1}{n^2}}}\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^n}\left({\displaystyle \frac{1}{n}}\right){\displaystyle \frac{1}{x_j^2-\frac{n+1}{n}{x}_j+\frac{n+1}{2n}}}.\hfill \end{array}$$

Define a sequence of functions $\left\{g_n\right\}$ as $g_n:[0,1]\to \mathbb{R}$ where $g_n\left(x\right)={\displaystyle \frac{1}{x^2-\frac{n+1}{n}x+\frac{n+1}{2n}}}$ for each $n\in \mathbb{N}$. Now define function $g:[0,1]\to \mathbb{R}$, $g\left(x\right)={\displaystyle \frac{1}{x^2-x+\frac{1}{2}}}$ and we claim that sequence $\left\{g_n\right\}$ uniformly converges to g (see Appendix A Lemma A1). Returning to the sum, we have

$$S_n={\displaystyle \sum _{j=1}^n}{g}_n\left(x_j\right){\displaystyle \frac{1}{n}}.$$

Let $ϵ>0$ and by uniform convergence there exists $N>0$ such that for all $n>N$, we have $|g\left(x\right)-g_n\left(x\right)|<ϵ$ for each $x\in [0,1]$. Let $n>N$ and we have

$$\begin{array}{cc}\hfill \left|{\displaystyle \sum _{j=1}^n}{\displaystyle \frac{1}{n}}(g\left(x_j\right)-g_n\left(x_j\right))\right|& \le {\displaystyle \sum _{j=1}^n}{\displaystyle \frac{1}{n}}|g\left(x_j\right)-g_n\left(x_j\right)|\hfill \\ \hfill & <{\displaystyle \sum _{j=1}^n}{\displaystyle \frac{1}{n}}ϵ\hfill \\ \hfill & =ϵ.\hfill \end{array}$$

Thus ${\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{j=1}^n}{\displaystyle \frac{1}{n}}(g\left(x_j\right)-g_n\left(x_j\right))=0\Rightarrow {\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{j=1}^n}{g}_n\left(x_j\right){\displaystyle \frac{1}{n}}={\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{j=1}^n}g\left(x_j\right){\displaystyle \frac{1}{n}}$. Note that the limit on the right is of the right-hand Riemann sum of the function g over the interval $[0,1]$ with sequence of partitions $p_n={\left\{{\displaystyle \frac{j}{n}}\right\}}_{j=1}^n$. Since g is Riemann integrable, we have that

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \frac{n}{n-1}}{C}_C\left(P_n\right)& ={\displaystyle \underset{n\to \infty }{lim}}{S}_n\hfill \\ \hfill & ={\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{j=1}^n}g\left(x_n\right){\displaystyle \frac{1}{n}}\hfill \\ \hfill & ={\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2-x+\frac{1}{2}}}dx\hfill \\ \hfill & =\pi .\hfill \end{array}$$

□

Lower Bound for Closeness Centralities

We will show that the lower bound for the closeness centrality of a graph is ${\displaystyle \frac{n\pi }{n+2}}$, where n is the number of vertices. We begin with trees. The technique will be as follows. We start with a tree with a vertex v of degree at least three. Then we remove one of the branches and append it to one of the other branches. Informally, we are ’flattening’ a tree, making it more like a path. This is illustrated in Figure 1.

Surprisingly the negative $SD\left(v\right)$ values perfectly cancel out. To see this consider the change in $S{D}_T$ and $S{D}_W$ values for the vertices $v_j$ and $v_{s+2-j}$. We note that the only distances that may change involve the vertices $v_{s+2},v_{s+3},\dots ,v_{s+l+1}$.

For $1\le j\le \lfloor (s+1)/2\rfloor$, we have $S{D}_T\left(v_j\right)={\sum }_{i=1}^l(i+j-1)$ and $S{D}_W\left(v_j\right)={\sum }_{i=2}^{l+1}(s+i-j)$. For $1\le j\le \lfloor (s+1)/2\rfloor$, we have $S{D}_T\left(v_{s+2-j}\right)={\sum }_{i=2}^{l+1}(s+i-j)$ and $S{D}_W\left(v_{s+2-j}\right){\sum }_{i=1}^l(i+j-1)$.

Hence the negative changes in $SD$ values $v_j$ where $\lfloor (s+1)/2\rfloor +1\le j\le s+1$ cancel out with the postive changes in $SD$ values $v_j$ where $1\le j\le \lfloor (s+1)/2\rfloor$.

For the remaining vertices the change in $SD\left(v\right)$ values will be positive. Hence sum of the closeness centrality values will decrease.

Lemma 3.

Let T be a tree with a vertex $v_1$ of degree at least three with two pendant paths $P_s$ and $P_t$. Let $V\left(P_s\right)=v_1,v_2,\dots ,v_s$ and $E\left(P_s\right)=\left\{v_i{v}_{i+1}\right|1\le i\le s-1\}$ and let $V\left(P_t\right)=$$v_{s+1},v_{s+2},\dots ,v_{s+t}$ and $E\left(P_t\right)=\left\{v_i{u}_{i+1}\right|s+1\le i\le s+t-1\}$. Let W be a tree where $V\left(W\right)=V\left(T\right)$ and $E\left(W\right)=\left\{v_i{v}_{i+1}\right|1\le i\le s-1\}\cup \left\{v_{i+1}{u}_1\right\}\cup \left\{v_i{v}_{i+1}\right|s+1\le i\le s+t-1\}$. Then $C_C\left(W\right)\le C_C\left(T\right)$.

Proof. 

We will proceed with $s\ge 2$. Then $S{D}_T\left(v_i\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{i+t}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{s+1-i}{2}}\right)+i$ when $1\le i\le s$, and $S{D}_T\left(v_i\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{s+t+1-i}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{i}{2}}\right)$ when $s+1\le i\le s+t$. For W, we have $S{D}_W\left(v_i\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{i}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{s+t+1-i}{2}}\right)$ for $1\le i\le s+t$.

We examine the differences between the $SD$ values of the same vertices between trees T and W. We consider two cases, first where the vertices are on the path with S vertices and then where the vertices are on the path with T vertices. We consider two cases.

Case 1.

Let $1\le i\le s$ $S{D}_W\left(v_i\right)-S{D}_T\left(v_i\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{i+1}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{s+t+1-i}{2}}\right)-\left(\left({\displaystyle \genfrac{}{}{0pt}{}{i+t}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{s+1-i}{2}}\right)+i\right)=t-2it+st$

• Subcase 1 (a): When s is even: $t-2\left({\displaystyle \frac{s}{2}}+k\right)t+st=t-2kt$
• $t-2\left({\displaystyle \frac{s}{2}}-(k-1)\right)t+st=2kt-tS{D}_T\left(v_i\right)=-S{D}_T\left(v_{s+1-i}\right)$
• Subcase 1 (b): When s is odd:
• $t-2\left({\displaystyle \frac{s+1}{2}}+k\right)t+st=-2kt$
• $t-2\left({\displaystyle \frac{s+1}{2}}-k\right)t+st=2kt$
• $S{D}_T\left(v_i\right)=-S{D}_T\left(v_{s+1-i}\right)$
• and when $k=0$, $S{D}_T\left(v_i\right)=S{D}_T\left(v_{s+1-i}\right)$.

Case 2.

Let $s+1\le i\le s+t$

$\left({\displaystyle \genfrac{}{}{0pt}{}{i+1}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{s+t+1-i}{2}}\right)-\left(\left({\displaystyle \genfrac{}{}{0pt}{}{s+t+1-i}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{i}{2}}\right)+i-s+1\right)=s-1$. We note that for all vertices $v\in V\left(G\right)-V\left(T\right)$ that $S{D}_T\left(v\right)\le S{D}_W\left(v\right)$. □

We note that the differences $S{D}_W\left(v_i\right)-S{D}_T\left(v_i\right)$ perfectly cancel out with $S{D}_W\left(v_{s+1-i}\right)$−$S{D}_T\left(v_{s+i-i}\right)$. However we need to show that the reciprocals of the $SD$ values $C_{C_W}\left(v_i\right)-C_{C_T}\left(v_i\right)$ overcompensate for $C_{C_W}\left(v_{s+1-i}\right)-C_{C_T}\left(v_{s+i-i}\right)$. To do this we apply a basic result from number theory that we restate in our next lemma.

Lemma 4.

For positive integers $a,x$, and k, $\left({\displaystyle \frac{1}{a}}-{\displaystyle \frac{1}{a+x}}\right)+\left({\displaystyle \frac{1}{a+x+k}}-{\displaystyle \frac{1}{a+k}}\right)>0$.

Proof. 

${\displaystyle \frac{x}{a(a+x)}}>{\displaystyle \frac{x}{(a+k)(a+x+k)}}$

$\hspace{1em}\iff {\displaystyle \frac{x}{a(a+x)}}+{\displaystyle \frac{-x}{(a+k)(a+x+k)}}>0$

$\hspace{1em}\iff {\displaystyle \frac{a+x-a}{a(a+x)}}+{\displaystyle \frac{a+k-(a+x+k)}{(a+k)(a+x+k)}}>0$

$\hspace{1em}\iff \left({\displaystyle \frac{1}{a}}-{\displaystyle \frac{1}{a+x}}\right)+\left({\displaystyle \frac{1}{a+x+k}}-{\displaystyle \frac{1}{a+k}}\right)>0.$ □

Lemma 5.

For any tree $T_n$ with n vertices, $C_C\left(T_n\right)\ge C_C\left(P_n\right)$.

Proof. 

If $T_n$ is a path, then we are done. If not we combine two pendant paths into a single path using Lemma 3. Iterating this process will result in a path with a lower closeness centrality than the original tree. □

Theorem 1.

For any graph G with n vertices, $C_C\left(G\right)\ge C_C\left(P_n\right)$.

Proof. 

Given a graph G a minimum distance spanning tree $T_n$ can be obtained using Dijkstra’s algorithm [9]. Here $d_G(v_i,v_j)\le d_T(v_i,v_j)$ for all pairs of vertices $(v_i,v_j)$. Hence ${\displaystyle \frac{1}{d_{T_n}(v_i,v_j)}}\le {\displaystyle \frac{1}{d_G(v_i,v_j)}}$ for all pairs of vertices $(v_i,v_j)$. This implies $CC\left(G\right)\ge CC\left(T_n\right)$. Combining this with Lemmas 3 and 5 we have $C_C\left(G\right)\ge C_C\left(T_n\right)\ge C_C\left(P_n\right)$. □

3. Asymptotics

We will generalize the method used to prove Lemma 2 by replacing the sum of $SD$ values with a Riemann sum. We do this by extending the SD functions to a sequence of continuous functions that uniformly converge, and then compute an integral of the limit. We next provide tools from analysis, which will be useful in obtaining the results in this section.

Lemma 6.

Let $I\subseteq \mathbb{R}$ be a closed interval, and suppose that the sequence of functions $f_n:I\to \mathbb{R}$ uniformly converges to the continuous function $f:I\to \mathbb{R}$ on I. If f is either strictly negative or positive, then there exists $N>0$ such that $f_n$ is also strictly negative or positive accordingly for all $n>N$.

Proof. 

Without loss of generality suppose that f is strictly positive and by the EVT, it attains a minimum value of $m>0$. By uniform convergence, there exists $N>0$ such that for all $n>N$ we have

$$\begin{array}{cccc}& \hfill & \hfill |f_n\left(x\right)-f\left(x\right)|& <{\displaystyle \frac{m}{2}}\hfill \\ \hfill \Rightarrow & \hfill & \hfill -{\displaystyle \frac{m}{2}}& <f_n\left(x\right)-f\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill f\left(x\right)-{\displaystyle \frac{m}{2}}& <f_n\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill 0<m-{\displaystyle \frac{m}{2}}& <f_n\left(x\right)\hfill \end{array}$$

as desired. □

Lemma 7.

Let $I\subseteq \mathbb{R}$ be a closed interval and suppose that $\left(f_n\right)$ is a sequence of functions that uniformly converge to a continuous function $f:I\to \mathbb{R}$ on I. If $f_n\left(x\right)\ne 0$ and $f\left(x\right)\ne 0$ for all $n\ge 1$ and $x\in I$, then $\left({\displaystyle \frac{1}{f_n}}\right)\rightrightarrows {\displaystyle \frac{1}{f}}$. In addition. the function ${\displaystyle \frac{1}{f}}:I\to \mathbb{R}$ is continuous.

Proof. 

Since f has no roots in I, by the IVT, it must either be positive or negative on I. Without loss of generality, suppose that f is positive on I and by the EVT, f attains a minimum at $x_{min}\in I$. Let $m=f\left(x_{min}\right)$ and by uniform convergence, there exists $N_0>0$ such that for all $n>N_0$

$$\begin{array}{cccc}& \hfill & \hfill |f_n\left(x\right)-f\left(x\right)|& <{\displaystyle \frac{m}{2}}\hfill \\ \hfill \Rightarrow & \hfill & \hfill -{\displaystyle \frac{m}{2}}& \le f_n\left(x\right)-f\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill f\left(x\right)-{\displaystyle \frac{m}{2}}& \le f_n\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill m-{\displaystyle \frac{m}{2}}& \le f_n\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill 0<{\displaystyle \frac{m}{2}}& \le f_n\left(x\right)\hfill \\ \hfill \Rightarrow & \hfill & \hfill 0<{\displaystyle \frac{1}{|f_n\left(x\right)|}}& \le {\displaystyle \frac{2}{m}}\hfill \end{array}$$

for all $x\in I$.

Let $ϵ>0$ and by uniform convergence there exists $N_1>0$ such that for all $n>N_1$, $|f-f_n|<{\displaystyle \frac{m^2ϵ}{4}}$. Suppose $n>max\{N_0,N_1\}$ and we have

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{1}{f_n}}-{\displaystyle \frac{1}{f}}\right|& ={\displaystyle \frac{1}{\left|f\right||f_n|}}|f_n-f|\hfill \\ \hfill \hspace{0.17em}& \le {\left({\displaystyle \frac{2}{m}}\right)}^2|f_n-f|\hfill \\ \hfill \hspace{0.17em}& <{\displaystyle \frac{4}{m^2}}{\displaystyle \frac{m^2ϵ}{4}}\hfill \\ \hfill \hspace{0.17em}& =ϵ\hfill \end{array}$$

for all $x\in I$. Therefore $\left({\displaystyle \frac{1}{f_n}}\right)$ uniformly converges to ${\displaystyle \frac{1}{f}}$ on I. As a composition of continuous functions $f:I\to {\mathbb{R}}^{+}$ and ${\displaystyle \frac{1}{x}}:{\mathbb{R}}^{+}\to \mathbb{R}$, continuity of ${\displaystyle \frac{1}{f}}$ follows immediately. □

Lemma 6 can be used to weaken the conditions of the above Lemma so that for some $N>0$, ${\displaystyle \frac{1}{f_n}}\rightrightarrows {\displaystyle \frac{1}{f}}$ while using the restriction $n>N$. For the purposes of this paper, it suffices to assume $N=1$ without loss of generality.

Lemma 8.

Let $I\subseteq \mathbb{R}$ be a closed interval, and suppose that the sequence of functions $(f_n:I\to \mathbb{R})$ uniformly converges to the continuous function $f:I\to \mathbb{R}$ on I. Suppose that ${\left\{x_k^n\right\}}_{k=1}^{m_n}\subseteq I$ is a family of sequences indexed by $n\in {\mathbb{Z}}^{+}$.

If either ${\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^{m_n}}f\left(x_k^n\right){\displaystyle \frac{1}{m_n}}\mathit{or}{\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^{m_n}}{f}_n\left(x_k^n\right){\displaystyle \frac{1}{m_n}}$ converge, then the limits coincide.

Proof. 

Let $\epsilon >0$ and there exists $N>0$ such that for all $n>N$, $|f-f_n|<ϵ,\forall x\in D$. Suppose $n>N$ and we have

$$\begin{array}{cc}\hfill |{\displaystyle \sum _{k=1}^{m_n}}f\left(x_k^n\right)-f_n\left(x_k^n\right)|{\displaystyle \frac{1}{m_n}}\le & {\displaystyle \sum _{k=1}^{m_n}}|f\left(x_k^n\right)-f_n\left(x_k^n\right)|{\displaystyle \frac{1}{m_n}}\hfill \\ \hfill <& {\displaystyle \sum _{k=1}^{m_n}}ϵ{\displaystyle \frac{1}{m_n}}\hfill \\ \hfill =& m_nϵ{\displaystyle \frac{1}{m_n}}\hfill \\ \hfill =& ϵ\hfill \end{array}$$

Thus ${\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^{m_n}}(f\left(x_k^n\right)-f_n\left(x_k^n\right)){\displaystyle \frac{1}{m_n}}=0$ as desired. □

In the special case that the sequences $p_n={\left\{{\displaystyle \frac{k}{n}}\right\}}_{k=1}^n$ are partitions of the unit interval, we can compute the limit of Riemann sums ${\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^n}{f}_n\left({\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}$ by replacing $f_n$ with the limit f. Since $f:[0,1]\to \mathbb{R}$ is continuous, and therefore Riemann integrable, the sum reduces to the integral

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^n}f\left({\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}={\displaystyle \underset{0}{\overset{1}{\int }}}f\left(x\right)dx.\end{array}$$

By the above Lemma, this integral is the value of ${\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{k=1}^n}{f}_n\left({\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}$.

3.1. Union of a Path and Complete Graph

Let $m,n$ be non-negative integers, and $P_n\cup K_m$ will denote a path with n vertices joined to a vertex of a complete graph with m vertices. The vertices of the path will be labeled $v_1$ through $v_n$ where $v_1=v_{n+1}$ is the junction vertex, and the vertices in the complete graph are labeled $v_{n+1}$ through $v_{n+m}$.

We next determine the $SD$ values of $P_n\cup K_m$ considering three different cases:

• Both vertices are on the path:
  If $v_j,v_i\in P_n$, then $d(v_i,v_j)=|j-i|.$
• Both distinct vertices are on the complete graph:
  If $v_i,v_j\in K_m$, then $d(v_i,v_j)=1.$
• One vertex is in the path and the other is in the complete subgraph.
  Without loss of generality, suppose that $v_i\in P_n$ and $v_j\in K_m/\left\{v_{n+1}\right\}$, then the shortest path from $v_i$ to $v_j$ is obtained by first traveling from $v_i$ to $v_1$ and then from $v_1=v_{n+1}$ to $v_j$. Thus

  $$\begin{array}{cc}\hfill d(v_i,v_j)=& d(v_i,v_1)+d(v_{n+1},v_j)\hfill \\ \hfill =& i-1+1=i.\hfill \end{array}$$

  Now suppose that $v_j\in P_n$ and we have

  $$\begin{array}{cc}\hfill SD\left(v_j\right)=& {\displaystyle \sum _{k=1}^n}d(v_j,v_k)+{\displaystyle \sum _{k=n+2}^{n+m}}d(v_j,v_k)\hfill \\ \hfill =& {\displaystyle \sum _{k=1}^n}|j-i|+{\displaystyle \sum _{k=n+2}^{n+m}}j\hfill \\ \hfill =& \left({\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n-j+1}{2}}\right)+(m-1)j.\hfill \end{array}$$

If $v_j\in K_m/\left\{v_{n+1}\right\}$, then

$$\begin{array}{cc}\hfill SD\left(v_j\right)=& {\displaystyle \sum _{k=1}^n}d(v_j,v_k)+{\displaystyle \sum _{k=n+2}^{n+m}}d(v_j,v_k)\hfill \\ \hfill =& {\displaystyle \sum _{k=1}^n}k+{\displaystyle \sum _{k=n+2}^{n+m}}d(v_j,v_k)\hfill \\ \hfill =& \left({\displaystyle \genfrac{}{}{0pt}{}{n+1}{2}}\right)+{\displaystyle \sum _{k=n+2,k\ne j}^{n+m}}1\hfill \\ \hfill =& \left({\displaystyle \genfrac{}{}{0pt}{}{n+1}{2}}\right)+m-2.\hfill \end{array}$$

Theorem 2.

Let p be a positive real number and suppose that $\left(n_k\right)$ and $\left(m_k\right)$ are strictly increasing sequences of positive integers such that ${\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{m_k}{n_k}}=p$. Let $S_k=P_{n_k}\cup K_{m_k}$, then

$$\begin{array}{cc}\hfill & {\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(S_k\right)=(1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx+2p+2p^2\hfill \\ \hfill & {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)}{{(n_k+m_k)}^3}}={\displaystyle \frac{p+\frac{1}{3}}{{(1+p)}^3}}.\hfill \end{array}$$

Proof. 

We will first show the centrality result and let $N_k=n_k+m_k$ and note that $S_k$ has $N_k-1$ vertices. Thus

$$\begin{array}{cc}\hfill C_C\left(S_k\right)=& {\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{N_k-2}{SD\left(v_j\right)}}+{\displaystyle \sum _{j=n_k+2}^{N_k}}{\displaystyle \frac{N_k-2}{SD\left(v_j\right)}}\hfill \\ \hfill \Rightarrow {\displaystyle \frac{N_k}{N_k-2}}{C}_C\left(S_k\right)=& {\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{N_k^2}{SD\left(v_j\right)}}{\displaystyle \frac{1}{N_k}}+{\displaystyle \sum _{j=n_k+2}^{N_k}}{\displaystyle \frac{N_k}{SD\left(v_j\right)}}\hfill \\ \hfill =& {\displaystyle \frac{n_k}{N_k}}{\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{N_k^2}{SD\left(v_j\right)}}{\displaystyle \frac{1}{n_k}}+{\displaystyle \sum _{j=n_k+2}^{N_k}}{\displaystyle \frac{N_k}{SD\left(v_j\right)}}\hfill \\ \hfill =& A_k+B_k.\hfill \end{array}$$

Define sequence of functions $f_k:[0,1]\to \mathbb{R}$ where

$$\begin{array}{c}\hfill f_k\left(x\right)={\displaystyle \frac{1}{N_k^2}}\left(\left({\displaystyle \genfrac{}{}{0pt}{}{n_{k}x}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n_k-n_{k}x+1}{2}}\right)+(m_k-1)\left(n_{k}x\right)\right)\end{array}$$

and we will show that

$$\begin{array}{c}\hfill f_k\rightrightarrows f\left(x\right)={\displaystyle \frac{x^2}{2{(1+p)}^2}}+{\displaystyle \frac{{(1-x)}^2}{2{(1+p)}^2}}+{\displaystyle \frac{px}{{(1+p)}^2}}.\end{array}$$

The functions $f_k\left(x\right)$ were obtained by reparameterizing $SD\left(v_j\right)$ so that $f\left({\displaystyle \frac{j}{n_k}}\right)={\displaystyle \frac{SD\left(v_j\right)}{N_k^2}}$, for $1\le j\le n_k$. This strategy will be used again for the next family of graphs. Now let $a_k\left(x\right)={\displaystyle \frac{1}{N_k^2}}\left({\displaystyle \genfrac{}{}{0pt}{}{n_{k}x}{2}}\right)$, $b_k\left(x\right)={\displaystyle \frac{1}{N_k^2}}\left({\displaystyle \genfrac{}{}{0pt}{}{n_k-n_{k}x+1}{2}}\right)$, and $c_k\left(x\right)={\displaystyle \frac{1}{N_k^2}}(m_k-1)\left(n_{k}x\right)$ and we have 3 cases.

• $a_k\rightrightarrows a\left(x\right)={\displaystyle \frac{x^2}{2{(1+p)}^2}}$:
  We have

  $$\begin{array}{cc}\hfill |a_k\left(x\right)-a\left(x\right)|=& |{\displaystyle \frac{x^2}{2{(1+p)}^2}}-{\displaystyle \frac{\left(n_{k}x\right)(n_{k}x-1)}{2N_k^2}}|\hfill \\ \hfill =& |{\displaystyle \frac{x^2}{2{(1+p)}^2}}-{\displaystyle \frac{n_k^2{x}^2}{2N_k^2}}+{\displaystyle \frac{n_{k}x}{2N_k^2}}|\hfill \\ \hfill \le & {\displaystyle \frac{x^2}{2}}|{\displaystyle \frac{1}{{(1+p)}^2}}-{\displaystyle \frac{n_k^2}{N_k^2}}|+{\displaystyle \frac{x}{2}}\left|{\displaystyle \frac{n_k}{N_k^2}}\right|\hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}|{\displaystyle \frac{1}{{(1+p)}^2}}-{\displaystyle \frac{n_k^2}{N_k^2}}|+{\displaystyle \frac{1}{2}}\left|{\displaystyle \frac{n_k}{N_k^2}}\right|\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}|{\displaystyle \frac{1}{{(1+p)}^2}}-{\displaystyle \frac{1}{{(1+\frac{m_k}{n_k})}^2}}|+{\displaystyle \frac{1}{2N_k}}\left|{\displaystyle \frac{1}{(1+\frac{m_k}{n_k})}}\right|.\hfill \end{array}$$
  This is true for all $x\in [0,1]$ and recall that ${\displaystyle \frac{m_k}{n_k}}\to p$ and $N_k\to \infty$. Thus ${\displaystyle \frac{1}{{(1+\frac{m_k}{n_k})}^2}}\to {\displaystyle \frac{1}{{(1+p)}^2}}$ and it is also clear that the right term of the last inequality goes to 0 uniformly for all $x\in [0,1].$ Then $a_k\rightrightarrows a$
• $b_k\left(x\right)\rightrightarrows b\left(x\right)={\displaystyle \frac{{(x-1)}^2}{2{(p+1)}^2}}$
  The proof is similar to the first case.
• $c_k\left(x\right)\rightrightarrows c\left(x\right)={\displaystyle \frac{px}{{(1+p)}^2}}$

  $$\begin{array}{cc}\hfill |c\left(x\right)-c_k\left(x\right)|=& \left|{\displaystyle \frac{px}{{(1+p)}^2}}-{\displaystyle \frac{1}{N_k^2}}(m_k-1)\left(n_{k}x\right)\right|\hfill \\ \hfill \le & \left|{\displaystyle \frac{p}{{(1+p)}^2}}-{\displaystyle \frac{m_k{n}_k}{N_k^2}}\right|+\left|{\displaystyle \frac{n_k}{N_k^2}}\right|.\hfill \end{array}$$

It can be shown that ${\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{m_k{n}_k}{N_k^2}}={\displaystyle \frac{p}{{(1+p)}^2}}$ and since $N_k\to \infty$, the last inequality goes to 0 uniformly for all $x\in [0,1]$. The sum of the sequences $f_k=a_k+b_k+c_k$ uniformly converges to the sum of the limits $f\left(x\right)=a+b+c$. Note that $f\left(x\right)=0$ if and only if $x^2+x(p-1)+{\displaystyle \frac{1}{2}}=0$, which has discriminant ${(p-1)}^2-2$. Then for all $p\in [0,\sqrt{2}+1)$, $f\left(x\right)$ has no real roots. Now suppose $p\ge \sqrt{2}+1$, and since $x\ge 0$, it follows

$$\begin{array}{c}\hfill x^2+x(p-1)+{\displaystyle \frac{1}{2}}\ge {\displaystyle \frac{1}{2}}.\end{array}$$

The continuous function $f:[0,1]\to \mathbb{R}$ has no nonnegative roots for $p>0$ and by Lemma 6, there exists $N>0$ such that $f_k$ has no roots for all $k\ge N$. Without loss of generality suppose $N=1$, and by Lemma 7, sequence $\left\{{\displaystyle \frac{1}{f_k}}\right\}$ uniformly converges to continuous function ${\displaystyle \frac{1}{f}}$ on $[0,1]$. Let ${\{x_j^k={\displaystyle \frac{j}{n_k}}\}}_{j=1}^{n_k}$ be a sequence of partitions of $[0,1]$, and we have

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}}{A}_k=& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{n_k}{N_k}}·{\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{1}{f_k\left(\frac{j}{n_k}\right)}}{\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}{\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{1}{f\left(x_j^k\right)}}{\displaystyle \frac{1}{n_k}}\hfill & \hfill & \hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}{\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{{(1+p)}^2}{x^2+x(p-1)+\frac{1}{2}}}dx\hfill & \hfill & \hfill \\ \hfill =& (1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx.\hfill \end{array}$$

Furthemore

$$\begin{array}{cc}\hfill B_k=& {\displaystyle \sum _{j=n_k+2}^{N_k}}{\displaystyle \frac{N_k}{SD\left(v_j\right)}}\hfill \\ \hfill =& {\displaystyle \sum _{j=n_k+2}^{N_k}}{\displaystyle \frac{N_k}{\left(\genfrac{}{}{0pt}{}{n_k+1}{2}\right)+m_k-2}}\hfill \\ \hfill =& {\displaystyle \frac{N_k(m_k-2)}{\left(\genfrac{}{}{0pt}{}{n_k+1}{2}\right)+m_k-2}}\hfill \\ \hfill =& {\displaystyle \frac{1}{\frac{1}{N_k(m_k-2)}\left(\genfrac{}{}{0pt}{}{n_k+1}{2}\right)+\frac{1}{N_k}}}.\hfill \end{array}$$

It is clear that ${\displaystyle \frac{1}{N_k(m_k-2)}}\left({\displaystyle \genfrac{}{}{0pt}{}{n_k+1}{2}}\right)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{n_k}{N_k}}\right)\left({\displaystyle \frac{n_k+1}{m_k-2}}\right)$ converges to ${\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{1+p}}{\displaystyle \frac{1}{p}}$ so that $B_k\rightrightarrows 2(p+1)p$. Thus

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(S_k\right)=& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{N_k}{N_k-2}}{C}_C\left(S_k\right)\hfill \\ \hfill =& {\displaystyle \underset{k\to \infty }{lim}}{A}_k+{\displaystyle \underset{k\to \infty }{lim}}{B}_k\hfill \\ \hfill =& (1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx+2(p+1)p\hfill \end{array}$$

as desired. As for the sum of distances, we have

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)}{N_k^3}}=& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{n_k}{N_k}}\left({\displaystyle \sum _{j=1}^{n_k}}{\displaystyle \frac{SD\left(v_j\right)}{N_k^2}}{\displaystyle \frac{1}{n_k}}\right)+{\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{1}{N_k^3}}{\displaystyle \sum _{j=n_k+2}^{N_k}}SD\left(v_j\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}\left({\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \sum _{j=1}^{n_k}}{f}_k\left({\displaystyle \frac{j}{n}}\right){\displaystyle \frac{1}{n_k}}\right)+{\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{m_k-1}{N_k^3}}\left(\left({\displaystyle \genfrac{}{}{0pt}{}{n_k+1}{2}}\right)+m_k-2\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}\left({\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \sum _{j=1}^{n_k}}f\left(x_j^k\right){\displaystyle \frac{1}{n_k}}\right)+{\displaystyle \frac{p}{2{(1+p)}^3}}.\hfill \end{array}$$

The left-hand side of the last expression is the Riemann sum of f over the interval $[0,1]$ obtained by Lemma 8, and the right-hand limit can be easily computed knowing that ${\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{n_k}{N_k}}={\displaystyle \frac{1}{1+p}}$ and ${\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{m_k}{N_k}}={\displaystyle \frac{p}{1+p}}$. Thus

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)}{N_k^3}}=& {\displaystyle \frac{1}{{(1+p)}^3}}{\displaystyle \underset{0}{\overset{1}{\int }}}{x}^2+x(p-1)+{\displaystyle \frac{1}{2}}dx+{\displaystyle \frac{p}{2{(1+p)}^3}}\hfill \\ \hfill =& {\displaystyle \frac{p+\frac{1}{3}}{{(1+p)}^3}}.\hfill \end{array}$$

□

The function $S:{\mathbb{R}}_{\ge }0\to \mathbb{R}$, defined as $S\left(p\right)=(1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx+2(p+1)p$, will be called the shooting star centrality. Now we have the following result.

Corollary 1.

For every $c\in [\pi ,\infty )\cap \mathbb{R}$, there exists a sequence of graphs $G_n$ such that ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(G_n\right)=c.$

Proof. 

Suppose $c>\pi$, and note that

$$\begin{array}{cc}\hfill 0\le & (1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx⟹\hfill \\ \hfill 2(p+1)p\le & (1+p){\displaystyle \underset{0}{\overset{1}{\int }}}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{1}{2}}}dx+2(p+1)p=S\left(p\right)⟹\hfill \\ \hfill {\displaystyle \underset{p\to \infty }{lim}}S\left(p\right)=& \infty .\hfill \end{array}$$

Thus there exists $p_0>0$ such that $c<S\left(p_0\right)$ and by the IVT, there exists $p\in (0,p_0)$ such that $S\left(p\right)=c$. Let $\left({\displaystyle \frac{m_k}{n_k}}\right)$ be a sequence of convergents of p with strictly growing numerator and denominator. Since ${\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{m_k}{n_k}}=p$, then ${\displaystyle \underset{k\to \infty }{lim}}{C}_C(P_{n_k}\cup K_{m_k})=S\left(p\right)=c$. If $c=\pi$, then ${\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(P_k\right)=\pi$ by Lemma 2. □

As a consequence of Theorem 1, we have $C_C\left(G\right)\ge {\displaystyle \frac{\pi n}{n+2}}$. This provides the following result complementary to the above Corollary.

Theorem 3.

Let $\mathcal{C}$ denote the set of all graph centralities. Then $\mathcal{C}\cap [0,\pi ]$ is not dense in $[0,\pi ]$.

Proof. 

Let $\alpha \in [0,\pi ]$ be an irrational number and suppose that $A=\mathcal{C}\cap [0,\pi ]$ is dense in $[0,\pi ]$. Then α is a limit point of A and there exists a sequence of finite connected graphs $\left(G_k\right)$ such that ${\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(G_k\right)=\alpha$. If $|G_k|$ is unbounded, then we can extract a subsequence of graphs $H_k$ with increasing order such that ${\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(H_k\right)=\alpha$. However, by the above inequality,

$$\begin{array}{cc}\hfill & C_C\left(H_k\right)\ge {\displaystyle \frac{\pi |H_k|}{|H_k|+2}}\hfill \\ \hfill ⟹& {\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(H_k\right)\ge \pi \hfill \end{array}$$

which is a contradiction. Thus $|G_k|$ is bounded, and let $N>0$ be the size of the largest graph. Let $R_n$ denote the finite set of distinct connected graphs of $n\in {\mathbb{Z}}^{+}$ vertices up to isomorphism. Then we have $|C_C\left(R_{|G_k|}\right)|\le |R_{|G_k|}|\le {\displaystyle \sum _{j=1}^N}\left|R_j\right|$, and each term $C_C\left(G_k\right)$ has upmost ${\displaystyle \sum _{j=1}^N}\left|R_j\right|$ of the same choices. Therefore, the sequence $C_C\left(G_k\right)$ has finitely many distinct terms which are all rational. But since the sequence converges, there exists $N_0>0$ such that all $C_C\left(G_k\right)$ are equal for $k>N$ and the limit α is rational, which is a contradiction. Thus α is not a limit point of $A,$ so that it cannot be dense in $[0,\pi ]$ as desired. □

Let $C\left(\pi \right)$ denote the set of graph closeness centralities greater than $\pi$. Corollary 1 shows that $C\left(\pi \right)$ is a dense subset of $[\pi ,\infty )$. A related result can be obtained by considering the normalized centrality and mean distance of a connected graph G with n vertices as defined by Britz, Hu, Islam, and Tang [8]:

$$\begin{array}{cc}\hfill {\overline{C}}_C\left(G\right)=& {\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=1}^n}{\displaystyle \frac{n-1}{SD\left(v_k\right)}}\hfill \\ \hfill \overline{l}\left(G\right)=& {\displaystyle \frac{1}{n(n-1)}}{\displaystyle \sum _{k=1}^n}SD\left(v_k\right).\hfill \end{array}$$

They showed that $1\le \overline{l}\left(G\right){\overline{C}}_C\left(G\right)<2$ for all finite connected graphs G and conjectured the set of all such values, $\mathcal{L}=\left\{\overline{l}\left(G\right){\overline{C}}_C\left(G\right)\right\}$ is dense in $[1,2]$. Let $p\in {\mathbb{R}}^{+}$ and define integer sequences $\left\{m_k\right\}$, $\left\{n_k\right\}$ the same way as in the above theorem. Then for the sequence of star graphs $S_k=P_{n_k}\cup K_{m_k}$ we have

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}}\overline{l}\left(S_k\right){\overline{C}}_C\left(S_k\right)=& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)C_C\left(S_k\right)}{{(N_k-1)}^2(N_k-2)}}\hfill \\ \hfill =& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)}{N_k^3}}{C}_C\left(S_k\right)\hfill \\ \hfill =& {\displaystyle \underset{k\to \infty }{lim}}{\displaystyle \frac{SD\left(S_k\right)}{N_k^3}}·{\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(S_k\right)\hfill \\ \hfill =& {\displaystyle \frac{p+\frac{1}{3}}{{(1+p)}^3}}S\left(p\right)=\overline{S}\left(p\right).\hfill \end{array}$$

The function $\overline{S}\left(p\right):{\mathbb{R}}_{\ge 0}\to \mathbb{R}$ is continuous and note that $\overline{S}\left(0\right)={\displaystyle \frac{\pi }{3}}$. Furthermore, it can be shown that ${\displaystyle \underset{p\to \infty }{lim}}\overline{S}\left(p\right)=2$ (see Appendix A Lemma A5), which converges from below, and we have the following result by applying the IVT as in Corollary 1.

Corollary 2.

The set $\mathcal{L}\cap [{\displaystyle \frac{\pi }{3}},2]$ is dense in $[{\displaystyle \frac{\pi }{3}},2]$

3.2. Mean Distance

Let G be a connected graph of n vertices. Doyle and Graver, ref. [10] defined the mean distance of G as

$$\begin{array}{c}\hfill \mu \left(G\right)={\displaystyle \frac{1}{n(n-1)}}SD\left(G\right)\end{array}$$

and presented that $\mu \left(P_n\right)={\displaystyle \frac{n+1}{3}}$ is a tight upper bound for the mean distance $\mu$. It follows that $SD\left(P_n\right)={\displaystyle \frac{n^3-n}{3}}$ is a tight upper bound for $SD\left(G\right)$, and we will define the normalized mean distance as $\overline{SD}\left(G\right)={\displaystyle \frac{SD\left(G\right)}{SD\left(P_n\right)}}={\displaystyle \frac{SD\left(G\right)}{\frac{n^3-n}{3}}}$. It is clear that

$$\begin{array}{c}\hfill 0<\overline{SD}\left(G\right)\le 1\end{array}$$

for all finitely connected graphs G and let $\overline{SD}\subseteq [0,1]$ denote the set of all such values.

Theorem 4.

The set $\overline{SD}$ is dense in $[0,1]$

Proof. 

Let $p\in {\mathbb{R}}^{+}$ and let $\left(n_k\right),\left(m_k\right)$ be strictly increasing sequence of positive integers whose ratio converges to p. Then by Theorem 2,

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}\overline{SD}\left(S_{n_k,m_k}\right)=& \underset{k\to \infty }{lim}3{\displaystyle \frac{SD\left(S_{n_k,m_k}\right)}{{(N_k-1)}^3-(N_k-1)}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}3{\displaystyle \frac{SD\left(S_{n_k,m_k}\right)}{N_k^3}}\hfill \\ \hfill =& {\displaystyle \frac{3p+1}{{(1+p)}^3}}=f\left(p\right).\hfill \end{array}$$

The function $f:{\mathbb{R}}_{\ge 0}\to [0,1]$ is continuous and $\underset{p\to \infty }{lim}f\left(p\right)=0$ so that by a similar application of the IVT as in Corollary 1, the desired result follows. □

4. Balloon Graphs

Let $B_{2n}$ denote a balloon graph consisting of a cycle $C_n$ attached to a path $P_n$, each containing n vertices. The junction vertex of the cycle and path will be labeled $v_1$. Traveling clockwise around the cycle, its vertices will be labeled $v_1,v_2,\dots ,v_n,v_{n+1}$ where $v_1$ and $v_{n+1}$ are the same vertex. Starting at $v_{n+1}$, the vertices of the path will be labeled from left to right as $v_{n+1},v_{n+2},\dots ,v_{2n}$.

Now we have the following theorem:

Theorem 5.

${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(B_{2n}\right)={\displaystyle \frac{4arctan\left(\frac{2}{\sqrt{3}}\right)}{\sqrt{3}}}+4ln\left({\displaystyle \frac{5}{3}}\right)$

Proof. 

First we will find the shortest distance $d(v_i,v_j)$ between vertices $v_i,v_j\in B_{2n}$ and we have 3 cases:

• $v_i,v_j\in C_n$
  If both vertices are on the cycle, then the shortest distance is given by the minor arc between them. Without loss of generality, suppose that $1\le i<j\le n$ and the shortest path is either travel clockwise from $v_i$ to $v_j$, giving a distance of $j-i$. Or we travel counterclockwise by going from $v_i$ to $v_1$ and then jumping from $v_1$ to $v_n$. From here we go from $v_n$ to $v_j$ giving a total distance of $(i-1)+1+(n-j)=n-(j-i)$. Thus in general

  $$d(v_i,v_j)=min\left\{\right|j-i|,n-|j-i\left|\right\}={\displaystyle \frac{n}{2}}-\left||j-i|-{\displaystyle \frac{n}{2}}\right|.$$
• $v_i,v_j\in P_n$
  If both vertices are on the path then $d(v_i,v_j)=|i-j|$ where $i,j\in [n+1,2n].$
• $v_i\in P_n$ and $v_j\in C_n$
  If the vertices are on different components of the graph, then it suffices to consider when $v_i\in P_n$ and $v_j\in C_n$. The shortest path is given by first going from $v_i$ to $v_{n+1}=v_1$ and then from $v_1$ to $v_j$ giving

  $$\begin{array}{cc}\hfill d(v_i,v_j)& =d(v_i,v_1)+d(v_1,v_j)\hfill \\ \hfill & =i-(n+1)+\left({\displaystyle \frac{n}{2}}-\left|j-1-{\displaystyle \frac{n}{2}}\right|\right).\hfill \end{array}$$

  Now suppose that $v_j\in P_n$ and we have

  $$\begin{array}{cc}\hfill SD\left(v_j\right)=& \sum _{k=1}^{2n}d(v_j,v_k)\hfill \\ \hfill =& \sum _{k=1}^{n}d(v_j,v_k)+\sum _{k=n+2}^{2n}d(v_j,v_k)\hfill \\ \hfill =& \sum _{k=1}^n(d(v_1,v_k)+d(v_1,v_j))+\left(\sum _{k=n+1}^{2n}|j-k|\right)-d(v_1,v_j)\hfill \\ \hfill =& S{D}_{C_n}\left(v_1\right)+(n-1)d(v_1,v_j)+\sum _{k=1}^n|j-n-k|\hfill \\ \hfill =& S{D}_{C_n}\left(v_1\right)+S{D}_{P_n}\left(v_j\right)+(n-1)(j-n-1)\hfill \\ \hfill =& 2\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{j-n}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{2n-j+1}{2}}\right)+(n-1)(j-n-1).\hfill \end{array}$$

When expanding $S{D}_{P_n}\left(v_j\right)$ we need to replace j with $j-n$ since $n+1\le j\le 2n$. If $v_j\in C_n$ then

$$\begin{array}{cc}\hfill SD\left(v_j\right)=& \sum _{k=1}^{2n}d(v_j,v_k)\hfill \\ \hfill =& \sum _{k=1}^{n}d(v_j,v_k)+\sum _{k=n+2}^{2n}d(v_j,v_k)\hfill \\ \hfill =& S{D}_{C_n}\left(v_j\right)+\left(\sum _{k=n+1}^{2n}d(v_k,v_{n+1})+d(v_1,v_j)\right)-d(v_j,v_{n+1})\hfill \\ \hfill =& S{D}_{C_n}\left(v_j\right)+S{D}_{P_n}\left(v_1\right)+(n-1)d(v_1,v_j)\hfill \\ \hfill =& 2\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)+(n-1)\left({\displaystyle \frac{n}{2}}-\left|j-1-{\displaystyle \frac{n}{2}}\right|\right).\hfill \end{array}$$

Define a sequence of functions $f_n:[0,1]\to \mathbb{R}$ as

$$f_n\left(x\right)={\displaystyle \frac{1}{n^2}}\left(2\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)+(n-1)\left({\displaystyle \frac{n}{2}}-\left|nx-1-{\displaystyle \frac{n}{2}}\right|\right)\right)$$

Note that $f_n\left({\displaystyle \frac{j}{n}}\right)={\displaystyle \frac{SD\left(v_j\right)}{n^2}}$ for $1\le j\le n$, and we will show that $f_n\rightrightarrows f$ where $f\left(x\right)={\displaystyle \frac{5}{4}}-\left|x-{\displaystyle \frac{1}{2}}\right|$. Now we have

$$\begin{array}{c}\hfill f_n\left(x\right)=L_n-{\displaystyle \frac{n-1}{n}}\left|x-{\displaystyle \frac{1}{n}}-{\displaystyle \frac{1}{2}}\right|\end{array}$$

where $L_n={\displaystyle \frac{1}{n^2}}(2\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right))+{\displaystyle \frac{n-1}{2n}}$. It can be shown that $L_n\to {\displaystyle \frac{5}{4}}$ and it is clear that ${\displaystyle \frac{n-1}{n}}\left|x-{\displaystyle \frac{1}{n}}-{\displaystyle \frac{1}{2}}\right|\rightrightarrows \left|x-{\displaystyle \frac{1}{2}}\right|$. Their difference uniformly converges to the difference of the limits, which is ${\displaystyle \frac{5}{4}}-|x-{\displaystyle \frac{1}{2}}|$.

Now define new sequence of functions $g_n:[1,2]\to \mathbb{R}$ as

$$\begin{array}{c}\hfill g_n\left(x\right)={\displaystyle \frac{1}{n^2}}(2\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{nx-n}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{2n-nx+1}{2}}\right)+(n-1)(nx-n-1)).\end{array}$$

Note that $g_n\left(x\right)$ can be expressed as the sum of 4 functions defined as

$$\begin{array}{cc}\hfill g_{n,1}\left(x\right)=& {\displaystyle \frac{2}{n^2}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)\hfill \\ \hfill g_{n,2}\left(x\right)=& {\displaystyle \frac{1}{n^2}}\left({\displaystyle \genfrac{}{}{0pt}{}{nx-n}{2}}\right)\hfill \\ \hfill g_{n,3}\left(x\right)=& {\displaystyle \frac{1}{n^2}}\left({\displaystyle \genfrac{}{}{0pt}{}{2n-nx+1}{2}}\right)\hfill \\ \hfill g_{n,4}\left(x\right)=& {\displaystyle \frac{1}{n^2}}(n-1)(nx-n-1).\hfill \end{array}$$

It can be shown that each function converges to the following over $[1,2]$:

$$\begin{array}{cc}\hfill & g_{n,1}\rightrightarrows {\displaystyle \frac{1}{4}}\hfill \\ \hfill & g_{n,2}\rightrightarrows {\displaystyle \frac{{(x-1)}^2}{2}}\hfill \\ \hfill & g_{n,3}\rightrightarrows {\displaystyle \frac{{(x-2)}^2}{2}}\hfill \\ \hfill & g_{n,4}\rightrightarrows x-1.\hfill \end{array}$$

The sum $g_n$ uniformly converges to the function

$$\begin{array}{cc}\hfill g\left(x\right)=& {\displaystyle \frac{1}{4}}+{\displaystyle \frac{{(x-1)}^2}{2}}+{\displaystyle \frac{{(x-2)}^2}{2}}+x-1\hfill \\ \hfill =& {(x-1)}^2+{\displaystyle \frac{3}{4}}.\hfill \end{array}$$

Note that continuous functions f and g have no roots on $[0,1]$ and $[1,2]$, respectively, so that by Lemma 7, ${\displaystyle \frac{1}{f_n}}\rightrightarrows {\displaystyle \frac{1}{f}}$ and ${\displaystyle \frac{1}{g_n}}\rightrightarrows {\displaystyle \frac{1}{g}}$, which are both continuous. Define a sequence of partitions $q_n={\{x_k^n={\displaystyle \frac{n+k}{n}}\}}_{k=1}^n$, and note that $g\left(x_k^n\right)={\displaystyle \frac{SD\left(v_k\right)}{n^2}}$ for vertices on the path component of $B_{2n}$. Similarly, define a sequence of partitions $p_n={\{y_k^n={\displaystyle \frac{k}{n}}\}}_{k=1}^n$ and we have:

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{C}_C\left(B_{2n}\right)=& \underset{n\to \infty }{lim}\sum _{k=1}^{2n}{\displaystyle \frac{2n}{SD\left(v_k\right)}}\hfill \\ \hfill =& \underset{n\to \infty }{lim}2\sum _{k=1}^n{\displaystyle \frac{n^2}{SD\left(v_k\right)}}{\displaystyle \frac{1}{n}}+2\sum _{k=n+1}^{2n}{\displaystyle \frac{n^2}{SD\left(v_k\right)}}{\displaystyle \frac{1}{n}}\hfill \\ \hfill =& \underset{n\to \infty }{lim}2\sum _{k=1}^n{\displaystyle \frac{1}{f_n\left(y_k^n\right)}}{\displaystyle \frac{1}{n}}+2\sum _{k=1}^n{\displaystyle \frac{1}{g_n\left(x_k^n\right)}}{\displaystyle \frac{1}{n}}\hfill \\ \hfill =& \underset{n\to \infty }{lim}2\sum _{k=1}^n{\displaystyle \frac{1}{f\left(y_k^n\right)}}{\displaystyle \frac{1}{n}}+2\sum _{k=1}^n{\displaystyle \frac{1}{g\left(x_k^n\right)}}{\displaystyle \frac{1}{n}}\hfill & \hfill & \hfill \\ \hfill =& 2\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{\frac{5}{4}-|y-\frac{1}{2}|}}dy+2\underset{1}{\overset{2}{\int }}{\displaystyle \frac{1}{{(x-1)}^2+\frac{3}{4}}}dx\hfill & \hfill & \\ \hfill =& {\displaystyle \frac{4arctan\left(\frac{2}{\sqrt{3}}\right)}{\sqrt{3}}}+4ln\left({\displaystyle \frac{5}{3}}\right).\hfill \end{array}$$

□

Generalized Balloon Graph Asymptotic

Let $B_{n,m}$ denote a graph consisting of a path $P_n$ joined with a cycle $C_m$ at a single vertex. Starting at the junction vertex $v_1$, the cycle will be labeled $v_1$ through $v_m$ traveling clockwise. Meanwhile, the path will be labeled $v_{m+1}$ through $v_{n+m}$ where $v_{m+1}=v_1$ is the junction vertex.

This class of graphs will be referred to as balloon graphs, and the $SD$ values are as follows.

Lemma 9.

Let $B_{n,m}$ denote a balloon graph and suppose $v_j\in B_{n,m}$ is a vertex, then

$$\begin{array}{c}\hfill SD\left(v_j\right)=\left\{\begin{array}{cc}R(n,m)+(n-1)({\displaystyle \frac{m}{2}}-|j-1-{\displaystyle \frac{m}{2}}\left|\right),\hfill & 1\le j\le m\hfill \\ R(n,m)-\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)+(m-1)(j-m-1)+\left({\displaystyle \genfrac{}{}{0pt}{}{j-m}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{N-j+1}{2}}\right),\hfill & m+1\le j\le N\hfill \end{array}\right.\end{array}$$

where $N=n+m$ and $R(n,m)=\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{m}{2}\rceil +1}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{m-\lceil \frac{m}{2}\rceil +1}{2}}\right)-\lceil {\displaystyle \frac{m}{2}}\rceil +\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right).$

Proof. 

We will calculate the $SD$ values by separately considering the cycle $C_m$ and path $P_n$ components and adjusting for path going though the junction vertex. Suppose $1\le j\le m$, i.e, $v_j$ is on the cycle component. Then

$$\begin{array}{cc}\hfill SD\left(v_j\right)=& \sum _{k=1}^{m}d(v_k,v_j)+\sum _{k=m+2}^{N}d(v_k,v_j)\hfill \\ \hfill =& \sum _{k=1}^{m}d(v_k,v_j)+\sum _{k=m+2}^N(d(v_j,v_1)+d(v_{m+1},v_k))\hfill \\ \hfill =& \sum _{k=1}^{m}d(v_k,v_j)+(n-1)d(v_j,v_1)+\sum _{k=m+2}^{N}d(v_{m+1},v_k)\hfill \\ \hfill =& S{D}_{C_m}\left(v_j\right)+(n-1)d(v_j,v_1)+S{D}_{P_n}\left(v_1\right).\hfill \end{array}$$

By symmetry of the cycle, $S{D}_{C_m}\left(v_j\right)=S{D}_{C_m}\left(v_1\right)$, and note that the shortest distance between two vertices $v_k,v_j\in C_m$ along the cycle is given by the minor arc between them, which has length $d(v_j,v_k)=min\left\{\right|k-j|,m-|k-j\left|\right\}={\displaystyle \frac{m}{2}}-|{\displaystyle \frac{m}{2}}-|j-k||$. Thus

$$\begin{array}{cc}\hfill S{D}_{C_m}\left(v_1\right)=& \sum _{k=1}^{m}min\{k-1,m-k+1|\}\hfill \\ \hfill =& {\displaystyle \sum _{k\le \lceil {\displaystyle \frac{m}{2}}\rceil }}min\{k-1,m-k+1|\}+{\displaystyle \sum _{k\ge \lceil {\displaystyle \frac{m}{2}}\rceil +1}}min\{k-1,m-k+1|\}\hfill \\ \hfill =& \sum _{k=1}^{\lceil {\displaystyle \frac{m}{2}}\rceil }(k-1)+\sum _{k=\lceil {\displaystyle \frac{m}{2}}\rceil +1}^m(m-k+1)\hfill \\ \hfill =& \sum _{k=1}^{\lceil {\displaystyle \frac{m}{2}}\rceil }(k-1)+\sum _{k=1}^{m-\lceil {\displaystyle \frac{m}{2}}\rceil }k\hfill \\ \hfill =& \left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{m}{2}\rceil +1}{2}}\right)-\lceil {\displaystyle \frac{m}{2}}\rceil +\left({\displaystyle \genfrac{}{}{0pt}{}{m-\lceil \frac{m}{2}\rceil +1}{2}}\right)\hfill \\ \hfill =& R(n,m)-\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right).\hfill \end{array}$$

Now we have

$$\begin{array}{cc}\hfill SD\left(v_j\right)=& R(n,m)+(n-1)d(v_j,v_1)+S{D}_{P_n}\left(v_1\right)-\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)\hfill \\ \hfill =& R(n,m)+(n-1)({\displaystyle \frac{m}{2}}-|{\displaystyle \frac{m}{2}}-j+1|).\hfill \end{array}$$

If $v_j\in P_n$, then

$$\begin{array}{cc}\hfill SD\left(v_j\right)=& \sum _{k=1}^{m}d(v_k,v_j)+\sum _{k=m+2}^{N}d(v_k,v_j)\hfill \\ \hfill =& \sum _{k=1}^m(d(v_k,v_1)+d(v_{m+1},v_j))+\sum _{k=m+1}^{N}d(v_k,v_j)-d(v_{m+1},v_j)\hfill \\ \hfill =& S{D}_{C_m}\left(v_1\right)+(m-1)d(v_{m+1},v_j)+S{D}_{P_n}\left(v_j\right)\hfill \\ \hfill =& R(n,m)-\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)+(m-1)(j-m-1)+\left({\displaystyle \genfrac{}{}{0pt}{}{j-m}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{N-j+1}{2}}\right).\hfill \end{array}$$

□

Theorem 6.

Let $p\in {\mathbb{R}}^{+}$ and suppose that $\left(m_k\right),\left(n_k\right)$ are strictly increasing sequences of positive integers such that ${\displaystyle \frac{m_k}{n_k}}\to p$. Then

$$\begin{array}{cc}\hfill & {\displaystyle \underset{k\to \infty }{lim}}{C}_C\left(B_{n_k,m_k}\right)=2(p+1)\left(ln\left({\displaystyle \frac{p^2+2p+2}{p^2+2}}\right)+{\displaystyle \frac{1}{\sqrt{2p+1}}}arctan\left({\displaystyle \frac{2\sqrt{2p+1}}{p^2+2p}}\right)\right),\hfill \\ \hfill & {\displaystyle \underset{k\to \infty }{lim}}\overline{l}\left(B_{n_k,m_k}\right)={\displaystyle \frac{p^3+2p^2+4p+\frac{4}{3}}{4{(1+p)}^3}}.\hfill \end{array}$$

Proof. 

Let $N_k=n_k+m_k$ and the closeness centrality of $B_{n_k,m_k}$ is

$$\begin{array}{cc}\hfill C_C\left(B_{n_k,m_k}\right)=& \sum _{j=1}^{m_k}{\displaystyle \frac{N_k-2}{SD\left(v_j\right)}}+\sum _{j=m_k+2}^{N_k}{\displaystyle \frac{N_k-2}{SD\left(v_j\right)}}\hfill \\ \hfill =& A_k+B_k\hfill \end{array}$$

and we will consider the right and left-hand sums separately. Define a sequence of functions $f_k:[0,1]\to \mathbb{R}$ as

$$\begin{array}{c}\hfill f_k\left(x\right)={\displaystyle \frac{1}{N_k^2}}\left(R(n_k,m_k)+(n_k-1)({\displaystyle \frac{m_k}{2}}-|{\displaystyle \frac{m_k}{2}}-m_{k}x+1\left|\right)\right).\end{array}$$

It can be shown that

$$\begin{array}{c}\hfill f_k\left(x\right)\rightrightarrows f\left(x\right)={\displaystyle \frac{p^2+2p+2-4p|x-\frac{1}{2}|}{4{(1+p)}^2}}\end{array}$$

(See Appendix A Lemma A6) on $[0,1]$. This sequence was chosen such that $f_k\left({\displaystyle \frac{j}{n_k}}\right)={\displaystyle \frac{SD\left(v_j\right)}{N_k^2}}$ for $1\le j\le m_k$. Since ${\displaystyle \frac{1}{2}}-|x-{\displaystyle \frac{1}{2}}|\ge 0$ for all $x\in [0,1]$, it follows $f:[0,1]\to {\mathbb{R}}^{+}$ is strictly positive, in addition to being continuous. By Lemma 7, sequence $\left\{{\displaystyle \frac{1}{f_k}}\right\}$ uniformly converges to continuous function ${\displaystyle \frac{1}{f}}$, and we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}{\displaystyle \frac{N_k}{N_k-2}}{A}_k=& \underset{k\to \infty }{lim}\sum _{j=1}^{m_k}{\displaystyle \frac{N_k^2}{SD\left(v_j\right)}}{\displaystyle \frac{1}{N_k}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}{\displaystyle \frac{m_k}{N_k}}\sum _{j=1}^{m_k}{\displaystyle \frac{1}{f_k\left(\frac{j}{m_k}\right)}}{\displaystyle \frac{1}{m_k}}\hfill \\ \hfill =& {\displaystyle \frac{p}{1+p}}\underset{k\to \infty }{lim}\sum _{j=1}^{m_k}{\displaystyle \frac{1}{f\left(\frac{j}{m_k}\right)}}{\displaystyle \frac{1}{m_k}}\hfill & \hfill & \hfill \\ \hfill =& {\displaystyle \frac{p}{1+p}}\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{f\left(x\right)}}dx\hfill & \hfill & \hfill \\ \hfill =& {\displaystyle \frac{p}{1+p}}\underset{0}{\overset{1}{\int }}{\displaystyle \frac{4{(1+p)}^2}{p^2+2p+2-4p|x-\frac{1}{2}|}}dx\hfill \\ \hfill =& 4p(1+p)\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{p^2+2p+2-4p|x-\frac{1}{2}|}}dx.\hfill \end{array}$$

Now we will consider $B_k$. Define new sequence of functions $g_k:[0,1]\to \mathbb{R}$ as

$$\begin{array}{c}\hfill g_k\left(x\right)=R(n_k,m_k)-\left({\displaystyle \genfrac{}{}{0pt}{}{n_k}{2}}\right)+(m_k-1)(n_{k}x-1)+\left({\displaystyle \genfrac{}{}{0pt}{}{n_{k}x}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n_k-n_{k}x+1}{2}}\right).\end{array}$$

Note that $g_k\left({\displaystyle \frac{j}{n_k}}\right)=SD\left(v_{j+m_k}\right)$ for $1\le j\le n_k$ and using a very similar process as in Lemma A6, it can be shown that

$$\begin{array}{c}\hfill g_k\left(x\right)\rightrightarrows g\left(x\right)={\displaystyle \frac{4x^2+4x(p-1)+2+p^2}{4{(1+p)}^2}}.\end{array}$$

Furthermore, $g\left(x\right)$ has a root iff $x^2+x(p-1)+{\displaystyle \frac{p^2+2}{4}}$ does as well, which has a negative discriminant ${(p-1)}^2-{(p+2)}^2$. Therefore $g\left(x\right)$ has no roots in $[0,1]$ and by Lemma 7, sequence of functions $\left\{{\displaystyle \frac{1}{g_k}}\right\}$ uniformly converges to continuous function ${\displaystyle \frac{1}{g}}$ on $[0,1].$ Now we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}{\displaystyle \frac{N_k}{N_k-2}}{B}_k=& \underset{k\to \infty }{lim}\sum _{j=m_k+2}^{N_k}{\displaystyle \frac{N_k^2}{SD\left(v_j\right)}}{\displaystyle \frac{1}{N_k}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}{\displaystyle \frac{n_k}{N_k}}\sum _{j=2}^{n_k}{\displaystyle \frac{N_k^2}{SD\left(v_{j+m_k}\right)}}{\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}\underset{k\to \infty }{lim}\sum _{j=2}^{n_k}{\displaystyle \frac{1}{g_k\left(\frac{j}{n_k}\right)}}{\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}\underset{k\to \infty }{lim}\sum _{j=2}^{n_k}{\displaystyle \frac{1}{g\left(\frac{j}{n_k}\right)}}{\displaystyle \frac{1}{n_k}}\hfill & \hfill & \hfill \\ \hfill =& {\displaystyle \frac{1}{1+p}}\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{g\left(x\right)}}dx\hfill & \hfill & \hfill \\ \hfill =& (1+p)\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{2+p^2}{4}}}dx.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}{C}_C\left(B_{n_k,m_k}\right)=& 4p(1+p)\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{p^2+2p+2-4p|x-\frac{1}{2}|}}dx+(1+p)\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{x^2+x(p-1)+\frac{2+p^2}{4}}}dx\hfill \\ \hfill =& 2(p+1)\left(ln\left({\displaystyle \frac{p^2+2p+2}{p^2+2}}\right)+{\displaystyle \frac{1}{\sqrt{2p+1}}}arctan\left({\displaystyle \frac{2\sqrt{2p+1}}{p^2+2p}}\right)\right)\hfill \\ \hfill =& B\left(p\right)\hfill \end{array}$$

(see Appendix A Lemmas A2 and A3).

As for the mean sum of distance, we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}\overline{l}\left(B_{n_k,m_k}\right)=& \underset{k\to \infty }{lim}{\displaystyle \frac{SD\left(B_{n_k,m_k}\right)}{N_k^3}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}{\displaystyle \frac{m_k}{N_k}}\sum _{j=1}^{m_k}{\displaystyle \frac{SD\left(v_j\right)}{N_k^2}}{\displaystyle \frac{1}{m_k}}+\underset{k\to \infty }{lim}{\displaystyle \frac{n_k}{N_k}}\sum _{j=2}^{n_k}{\displaystyle \frac{SD\left(v_{j+m_k}\right)}{N_k^2}}{\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}{\displaystyle \frac{m_k}{N_k}}\sum _{j=1}^{m_k}{f}_k\left({\displaystyle \frac{j}{m_k}}\right){\displaystyle \frac{1}{m_k}}+\underset{k\to \infty }{lim}{\displaystyle \frac{n_k}{N_k}}\sum _{j=2}^{n_k}{g}_k\left({\displaystyle \frac{j}{n_k}}\right){\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& \underset{k\to \infty }{lim}{\displaystyle \frac{m_k}{N_k}}\sum _{j=1}^{m_k}f\left({\displaystyle \frac{j}{m_k}}\right){\displaystyle \frac{1}{m_k}}+\underset{k\to \infty }{lim}{\displaystyle \frac{n_k}{N_k}}\sum _{j=2}^{n_k}g\left({\displaystyle \frac{j}{n_k}}\right){\displaystyle \frac{1}{n_k}}\hfill \\ \hfill =& {\displaystyle \frac{p}{1+p}}\underset{0}{\overset{1}{\int }}{\displaystyle \frac{p^2+2p+2-4p|x-\frac{1}{2}|}{4{(1+p)}^2}}dx+{\displaystyle \frac{1}{1+p}}\underset{0}{\overset{1}{\int }}{\displaystyle \frac{4x^2+4x(p-1)+2+p^2}{4{(1+p)}^2}}dx\hfill \\ \hfill =& {\displaystyle \frac{p^3+2p^2+4p+\frac{4}{3}}{4{(1+p)}^3}}\hfill \\ \hfill =& B_0\left(p\right).\hfill \end{array}$$

□

Theorem 7.

The set $\mathcal{L}$ is dense in $[1,2]$, where $\mathcal{L}=\{\overline{l}\left(G\right){\overline{C}}_C\left(G\right):\mathrm{G}\mathrm{is}\mathrm{finite}\mathrm{and}\mathrm{connected}\}.$

Proof. 

It can be shown that $\underset{p\to \infty }{lim}B\left(p\right)=4$ and $\underset{p\to \infty }{lim}{B}_0\left(p\right)={\displaystyle \frac{1}{4}}$ (see Appendix A Lemma A4), which corresponds to the balloon graph having relatively negligible vertices on the path component compared to the cycle so that it overall behaves like the latter. The limit of the products is 1 and $B\left(0\right)B_0\left(0\right)={\displaystyle \frac{\pi }{3}}$, which is attributed to the path graph. By continuity of $f\left(p\right)=B\left(p\right)B_0\left(p\right)$, for each $y\in (1,{\displaystyle \frac{\pi }{3}})$ there exists $p\in (0,\infty )$ such that $f\left(p\right)=y$. Choose strictly increasing sequence of positive integers $\left(m_k\right),\left(n_k\right)$ such that $\underset{k\to \infty }{lim}{\displaystyle \frac{m_k}{n_k}}=p$ and we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}\overline{l}\left(B_{n_k,m_k}\right){\overline{C}}_C\left(B_{n_k,m_k}\right)=& \underset{k\to \infty }{lim}{\displaystyle \frac{SD\left(B_{n_k,m_k}\right)}{{(n_k+m_k)}^3}}{C}_C\left(B_{n_k,m_k}\right)\hfill \\ \hfill =& B_0\left(p\right)B\left(p\right)\hfill \\ \hfill =& y.\hfill \end{array}$$

Thus, every point of $[1,{\displaystyle \frac{\pi }{3}}]$ is a limit point of $\mathcal{L}\cap [1,{\displaystyle \frac{\pi }{3}}]$, which is then dense in $[1,{\displaystyle \frac{\pi }{3}}]$. By applying Corollary 2, we obtain the entire result. □

5. Conclusions

We verify a conjecture of Britz, Hu, Islam, and Tang that the set of products $\{\overline{l}\left(G\right){\overline{C}}_C\left(G\right):G\mathrm{is}\mathrm{finite}\mathrm{and}\mathrm{connected}\}$ is dense in $[1,2)$. The use of Riemann sums provides a method that is computationally advantageous for precisely determining asymptotics of closeness centralities. The key benefit is the use of integration for calcuating asymptotic behavior of complicated combinatorial forumulae. It would be interesting to see how the methods in this paper can be used for other families of graphs. The density results are connected to the inverse Wiener index problem [11], where one starts with a prescribed sum of distances over all pairs of vertices and seeks a tree with this index. The following problem presents a problem that could provide a bridge between our work and the inverse Wiener index problem. There is also a potential index to the Harary index [12].

Problem 1.

Determine ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(G\right)$ where G is a tree.

The next problem is a natural extension of the first problem.

Problem 2.

Determine ${\displaystyle \underset{n\to \infty }{lim}}{C}_C\left(G\right)$ where G is a unicyclic graph.

We have started developing quasi-simple curve theory to demonstrate how closeness centrality can be calculated with just calculus. This would provide a segue to a natural definition of closeness centrality for piecewise smooth curves.